Generalized Sliding Mode Observers for Simultaneous Fault Reconstruction in the Presence of Uncertainty and Disturbance
Abstract
:1. Introduction
2. Description of the Problem
3. Robust Actuator Faults Reconstruction
4. Robust Sensor Fault Reconstruction
5. Simultaneous Sensor and Actuator Faults Reconstruction
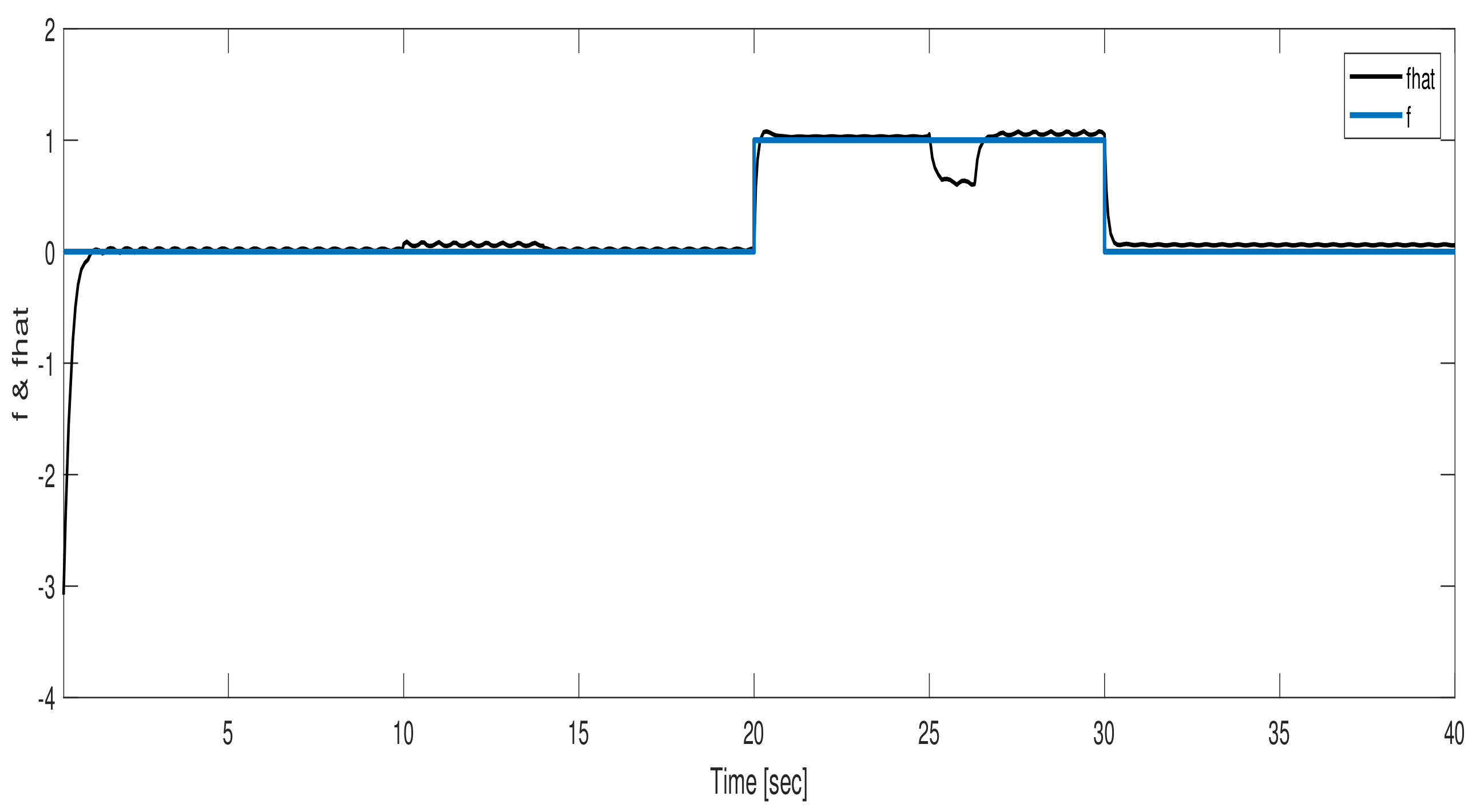
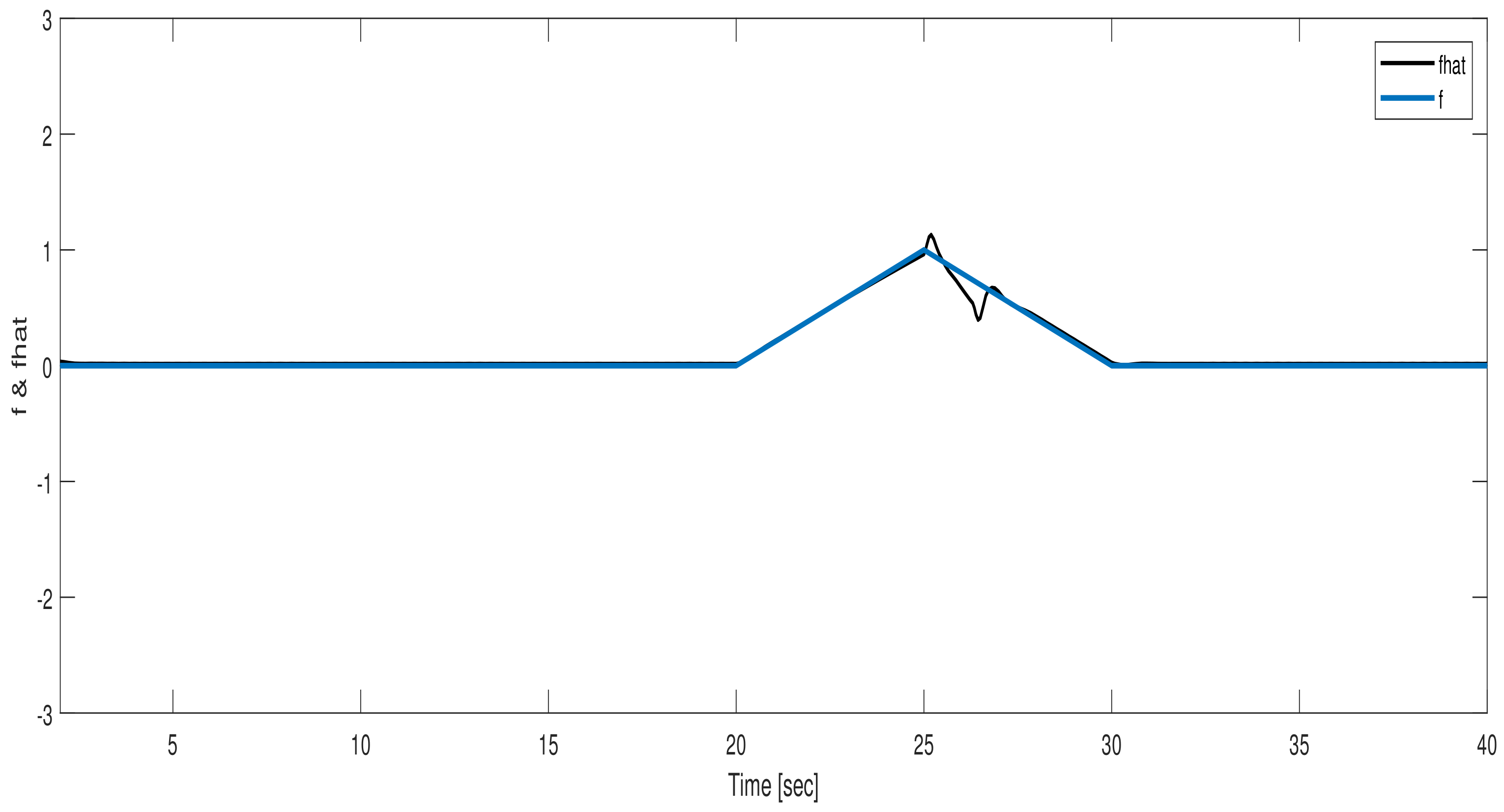
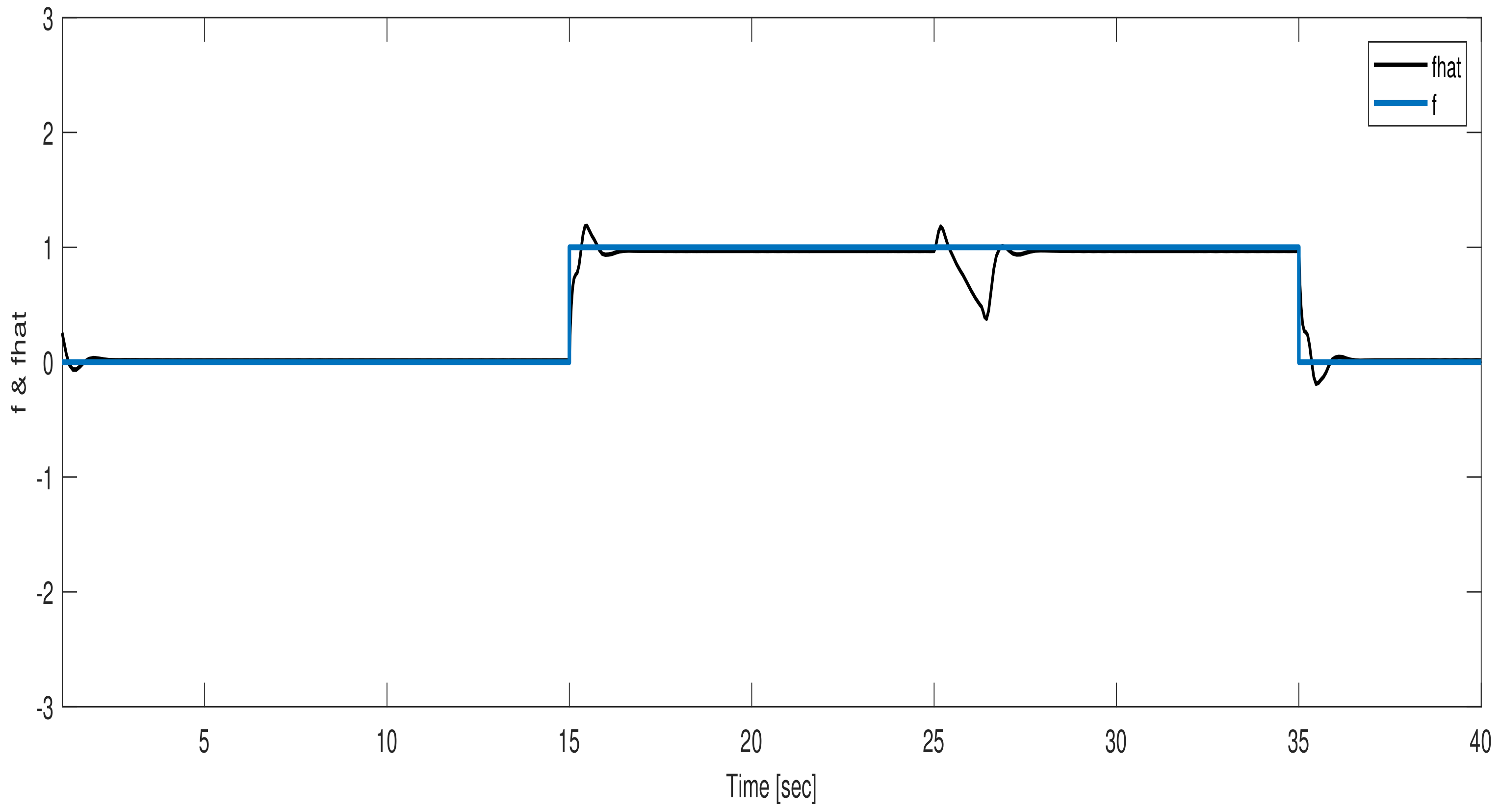
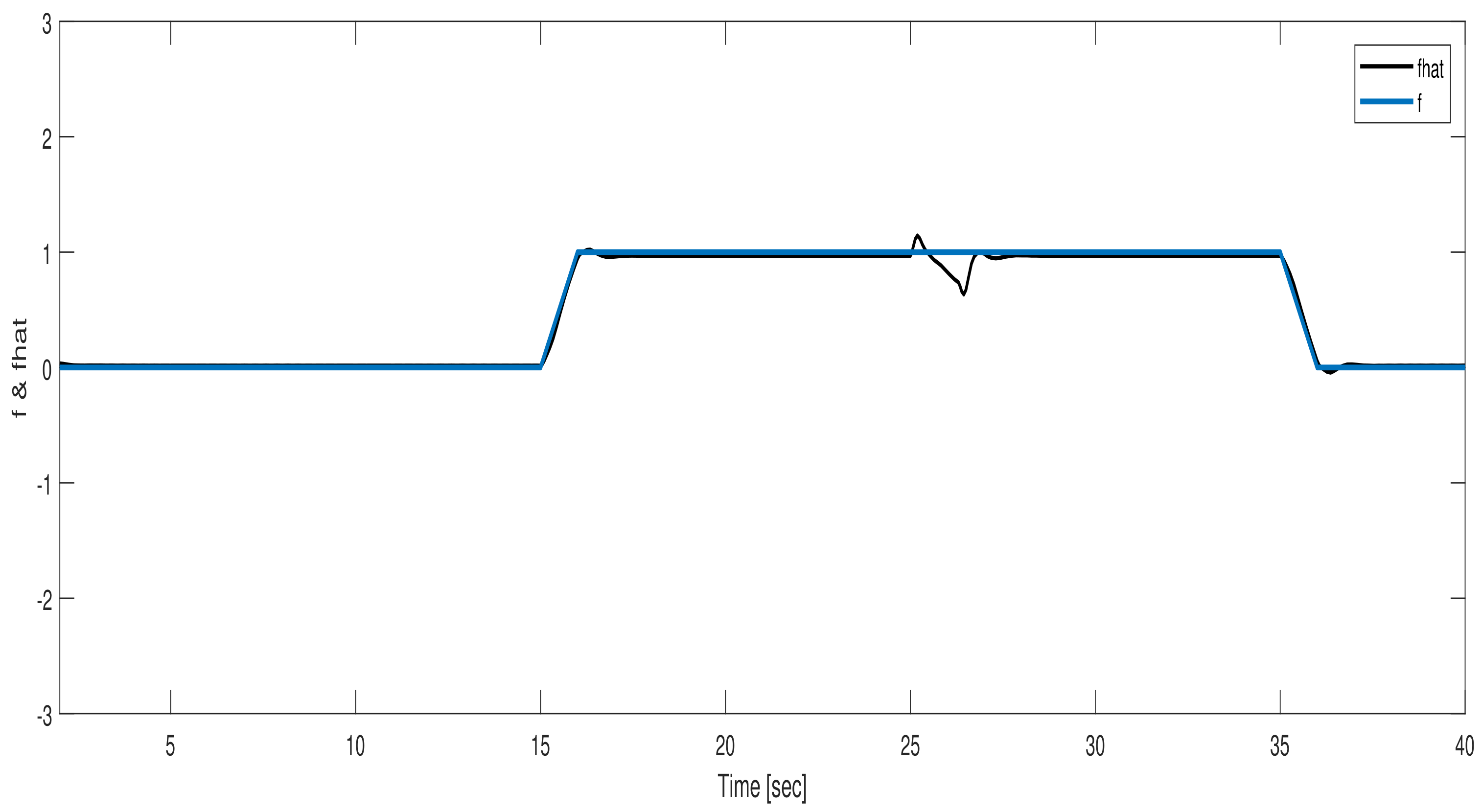
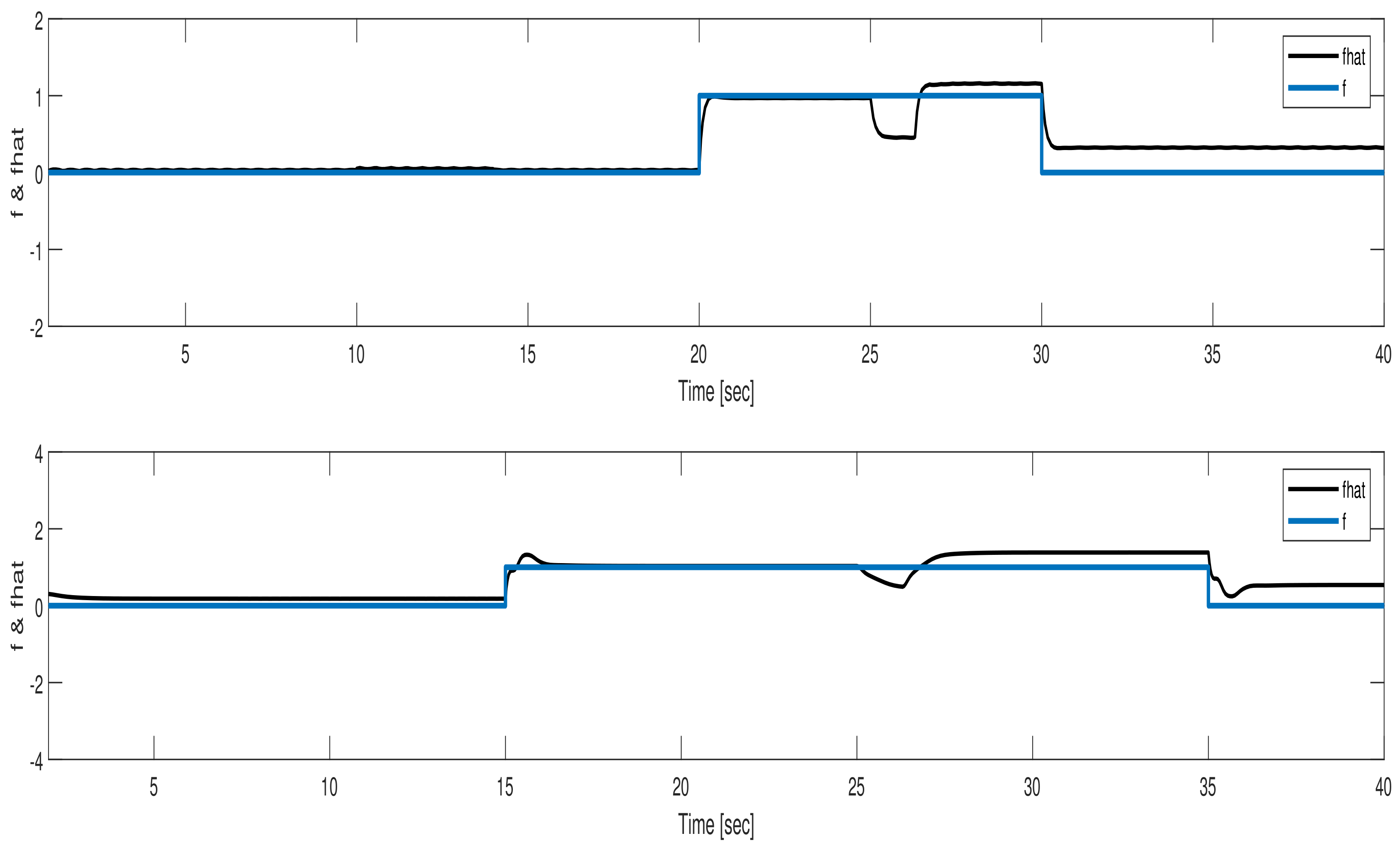
6. Simulation Results
6.1. Actuator Fault Reconstruction
6.2. Sensor Fault Reconstruction
6.3. Simultaneous Actuator and Sensor Faults
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saif, M.; Guan, Y. A new approach to robust fault detection and identification. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 685–695. [Google Scholar] [CrossRef]
- Zhang, A.A.; Lv, B.C.; Zhang, C.Z.; She, D.Z. Finite time fault tolerant attitude control-based observer for a rigid satellite subject to thruster faults. IEEE Access 2017, 5, 16808–16817. [Google Scholar] [CrossRef]
- Ghanbarpour, K.; Bayat, F.; Jalilvand, A. Wind turbines sustainable power generation subject to sensor faults: Observer-based MPC approach. Int. Trans. Electr. Energy Syst. 2020, 30, e12174. [Google Scholar] [CrossRef]
- Taherkhani, A.; Bayat, F. Wind turbines robust fault reconstruction using adaptive sliding mode observer. IET Gener. Transm. Distrib. 2019, 13, 3096–3104. [Google Scholar] [CrossRef]
- Yin, S.; Huang, Z. Performance monitoring for vehicle suspension system via fuzzy positivistic C-means clustering based on accelerometer measurements. IEEE/ASME Trans. Mechatron. 2014, 20, 2613–2620. [Google Scholar] [CrossRef]
- Zhang, B.; Lu, S. Fault-tolerant control for four-wheel independent actuated electric vehicle using feedback linearization and cooperative game theory. Control Eng. Pract. 2020, 101, 104510. [Google Scholar] [CrossRef]
- Sakthivel, R.; Selvaraj, P.; Mathiyalagan, K.; Park, J.H. Robust fault-tolerant Hinf control for offshore steel jacket platforms via sampled-data approach. J. Frankl. Inst. 2015, 352, 2259–2279. [Google Scholar] [CrossRef]
- Gonzalez-Prieto, I.; Duran, M.J.; Rios-Garcia, N.; Barrero, F.; Martin, C. Open-switch fault detection in five-phase induction motor drives using model predictive control. IEEE Trans. Ind. Electron. 2017, 65, 3045–3055. [Google Scholar] [CrossRef]
- Su, X.; Liu, X.; Song, Y.D. Fault-tolerant control of multiarea power systems via a sliding-mode observer technique. IEEE/ASME Trans. Mechatron. 2017, 23, 38–47. [Google Scholar] [CrossRef]
- Ghanbarpour, K.; Bayat, F.; Jalilvand, A. Dependable power extraction in wind turbines using model predictive fault tolerant control. Int. J. Electr. Power Energy Syst. 2020, 118, 105802. [Google Scholar] [CrossRef]
- Guzman, J.; Lopez-Estrada, F.R.; Estrada-Manzo, V.; Valencia-Palomo, G. Actuator fault estimation based on a proportional-integral observer with nonquadratic Lyapunov functions. Int. J. Syst. Sci. 2021, 52, 1938–1951. [Google Scholar] [CrossRef]
- Tan, C.P.; Edwards, C. Sliding mode observers for robust detection and reconstruction of actuator and sensor faults. Int. J. Robust Nonlinear Control 2003, 13, 443–463. [Google Scholar] [CrossRef]
- Sharma, R.; Aldeen, M. Fault detection in nonlinear systems with unknown inputs using sliding mode observer. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 432–437. [Google Scholar]
- Rayankula, V.; Pathak, P.M. Fault Tolerant Control and Reconfiguration of Mobile Manipulator. J. Intell. Robot. Syst. 2021, 101, 1–18. [Google Scholar] [CrossRef]
- Van Nguyen, T.; Ha, C. Experimental study of sensor fault-tolerant control for an electro-hydraulic actuator based on a robust nonlinear observer. Energies 2019, 12, 4337. [Google Scholar] [CrossRef] [Green Version]
- Selvaraj, P.; Kaviarasan, B.; Sakthivel, R.; Karimi, H.R. Fault-tolerant SMC for Takagi–Sugeno fuzzy systems with time-varying delay and actuator saturation. IET Control. Theory Appl. 2017, 11, 1112–1123. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Dolvis, L.G.; Jacques, K.; Lien, C.H.; Sambas, A. A new five-dimensional four-wing hyperchaotic system with hidden attractor, its electronic circuit realisation and synchronisation via integral sliding mode control. Int. J. Model. Identif. Control 2019, 32, 30–45. [Google Scholar] [CrossRef]
- Mobayen, S.; Fekih, A.; Vaidyanathan, S.; Sambas, A. Chameleon Chaotic Systems With Quadratic Nonlinearities: An Adaptive Finite-Time Sliding Mode Control Approach and Circuit Simulation. IEEE Access 2021, 9, 64558–64573. [Google Scholar] [CrossRef]
- Hou, Y.Y.; Fang, C.S.; Lien, C.H.; Vaidyanathan, S.; Sambas, A.; Mamat, M.; Johansyah, M.D. Rikitake dynamo system, its circuit simulation and chaotic synchronization via quasi-sliding mode control. Telkomnika 2021, 19, 1291–1301. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, Z.; Tan, X.; Xie, D.; Dai, W. Sensors fault diagnosis and active fault-tolerant control for PMSM drive systems based on a composite sliding mode observer. Energies 2019, 12, 1695. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Zhu, F. FDI design for uncertain nonlinear systems with both actuator and sensor faults. Asian J. Control. 2015, 17, 213–224. [Google Scholar] [CrossRef]
- Taherkhani, A.; Bayat, F.; Mobayen, S.; Bartoszewicz, A. Dependable Sensor Fault Reconstruction in Air-Path System of Heavy-Duty Diesel Engines. Sensors 2021, 21, 7788. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X. Sensor bias fault detection and isolation in a class of nonlinear uncertain systems using adaptive estimation. IEEE Trans. Autom. Control 2011, 56, 1220–1226. [Google Scholar] [CrossRef]
- Defoort, M.; Veluvolu, K.C.; Rath, J.J.; Djemai, M. Adaptive sensor and actuator fault estimation for a class of uncertain Lipschitz nonlinear systems. Int. J. Adapt. Control. Signal Process. 2016, 30, 271–283. [Google Scholar] [CrossRef]
- You, F.; Li, H.; Wang, F.; Guan, S. Robust fast adaptive fault estimation for systems with time-varying interval delay. J. Frankl. Inst. 2015, 352, 5486–5513. [Google Scholar] [CrossRef]
- Selvaraj, P.; Sakthivel, R.; Kwon, O.M. Synchronization of fractional-order complex dynamical network with random coupling delay, actuator faults and saturation. Nonlinear Dyn. 2018, 94, 3101–3116. [Google Scholar] [CrossRef]
- Selvaraj, P.; Sakthivel, R.; Ahn, C.K. Observer-based synchronization of complex dynamical networks under actuator saturation and probabilistic faults. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 1516–1526. [Google Scholar] [CrossRef]
- Pinto, H.L.D.C.P.; Oliveira, T.R.; Hsu, L. Sliding mode observer for fault reconstruction of time-delay and sampled-output systems—A Time Shift Approach. Automatica 2019, 106, 390–400. [Google Scholar] [CrossRef]
- Yang, C.; Liu, J.; Zeng, Y.; Xie, G. Real-time condition monitoring and fault detection of components based on machine-learning reconstruction model. Renew. Energy 2019, 133, 433–441. [Google Scholar] [CrossRef]
- Harkat, M.F.; Mansouri, M.; Abodayeh, K.; Nounou, M.; Nounou, H. New sensor fault detection and isolation strategy–based interval-valued data. J. Chemom. 2020, 34, e3222. [Google Scholar] [CrossRef]
- Lee, D.J.; Park, Y.; Park, Y.S. Robust H∞ Sliding Mode Descriptor Observer for Fault and Output Disturbance Estimation of Uncertain Systems. IEEE Trans. Autom. Control 2012, 57, 2928–2934. [Google Scholar] [CrossRef]
- Ben Brahim, A.; Dhahri, S.; Ben Hmida, F.; Sellami, A. Simultaneous actuator and sensor faults reconstruction based on robust sliding mode observer for a class of nonlinear systems. Asian J. Control 2017, 19, 362–371. [Google Scholar]
- Brahim, A.B.; Dhahri, S.; Hmida, F.B.; Sellami, A. Simultaneous actuator and sensor faults estimation design for LPV systems using adaptive sliding mode observers. Int. J. Autom. Control 2021, 15, 1–27. [Google Scholar] [CrossRef]
- You, G.; Xu, T.; Su, H.; Hou, X.; Li, J. Fault-tolerant control for actuator faults of wind energy conversion system. Energies 2019, 12, 2350. [Google Scholar] [CrossRef] [Green Version]
- Tan, C.P.; Edwards, C. An LMI approach for designing sliding mode observers. Int. J. Control 2001, 74, 1559–1568. [Google Scholar] [CrossRef]
- Alwi, H.; Edwards, C.; Tan, C.P. Fault Detection and Fault-Tolerant Control Using Sliding Modes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control. Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Mahmoud, C.; Pascal, G. H∞ design with pole placement constraints: An LMI approach. IEEE Trans. Autom. Control 1996, 41, 358–367. [Google Scholar]


| Theorem 5 | 29.04 | 99.07 |
| [32] | 32.61 | 103.87 |
| Improvement (%) | 10.9 | 4.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taherkhani, A.; Bayat, F.; Hooshmandi, K.; Bartoszewicz, A. Generalized Sliding Mode Observers for Simultaneous Fault Reconstruction in the Presence of Uncertainty and Disturbance. Energies 2022, 15, 1411. https://doi.org/10.3390/en15041411
Taherkhani A, Bayat F, Hooshmandi K, Bartoszewicz A. Generalized Sliding Mode Observers for Simultaneous Fault Reconstruction in the Presence of Uncertainty and Disturbance. Energies. 2022; 15(4):1411. https://doi.org/10.3390/en15041411
Chicago/Turabian StyleTaherkhani, Ashkan, Farhad Bayat, Kaveh Hooshmandi, and Andrzej Bartoszewicz. 2022. "Generalized Sliding Mode Observers for Simultaneous Fault Reconstruction in the Presence of Uncertainty and Disturbance" Energies 15, no. 4: 1411. https://doi.org/10.3390/en15041411
APA StyleTaherkhani, A., Bayat, F., Hooshmandi, K., & Bartoszewicz, A. (2022). Generalized Sliding Mode Observers for Simultaneous Fault Reconstruction in the Presence of Uncertainty and Disturbance. Energies, 15(4), 1411. https://doi.org/10.3390/en15041411







