Numerical Investigation of the Sensitivity of the Acoustic Power Level to Changes in Selected Design Parameters of an Axial Fan
Abstract
:1. Introduction
2. Numerical Simulations
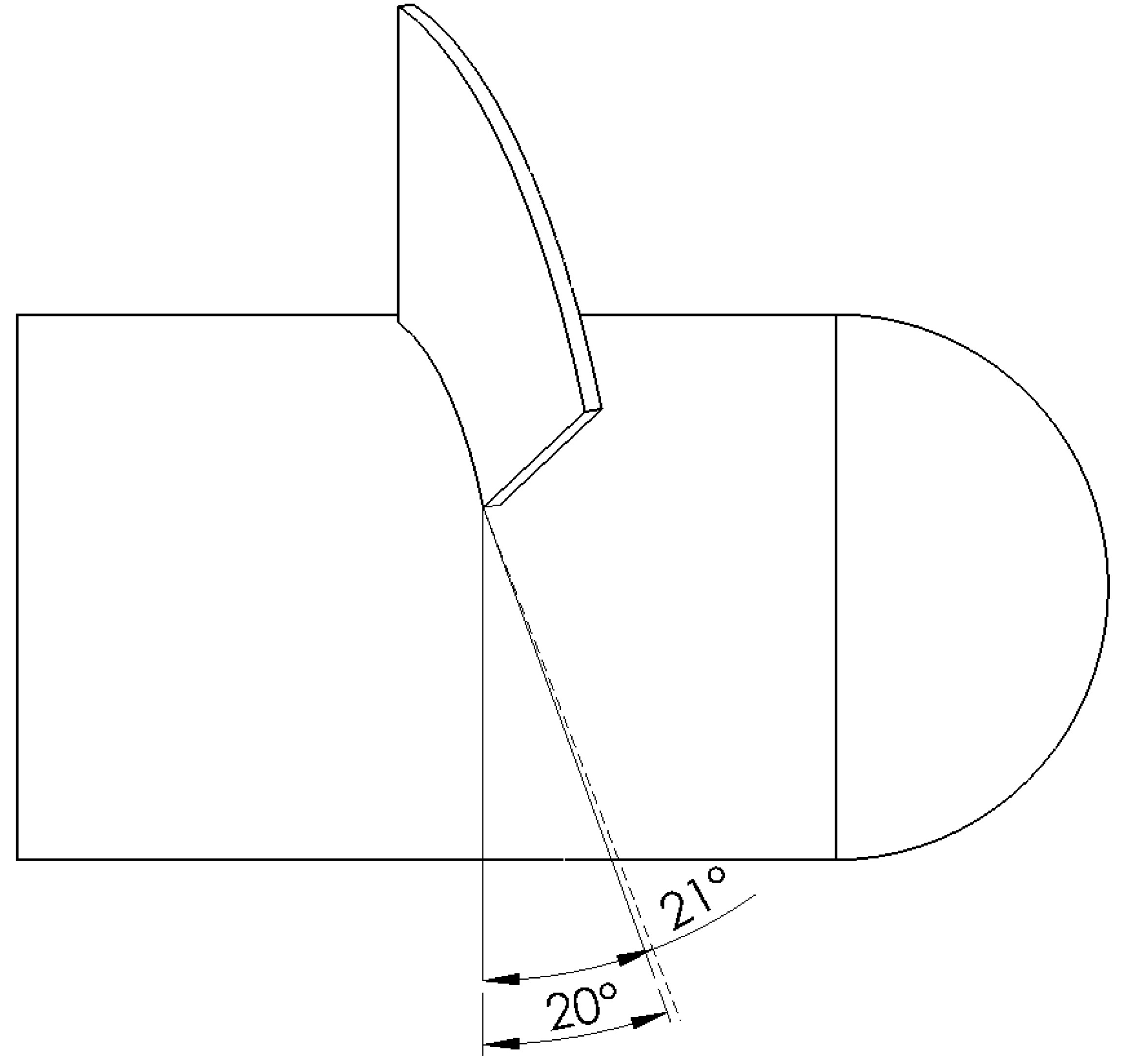
2.1. Research Object
2.2. Mathematical Model
2.3. Boundary Conditions and Solver Settings
3. Results
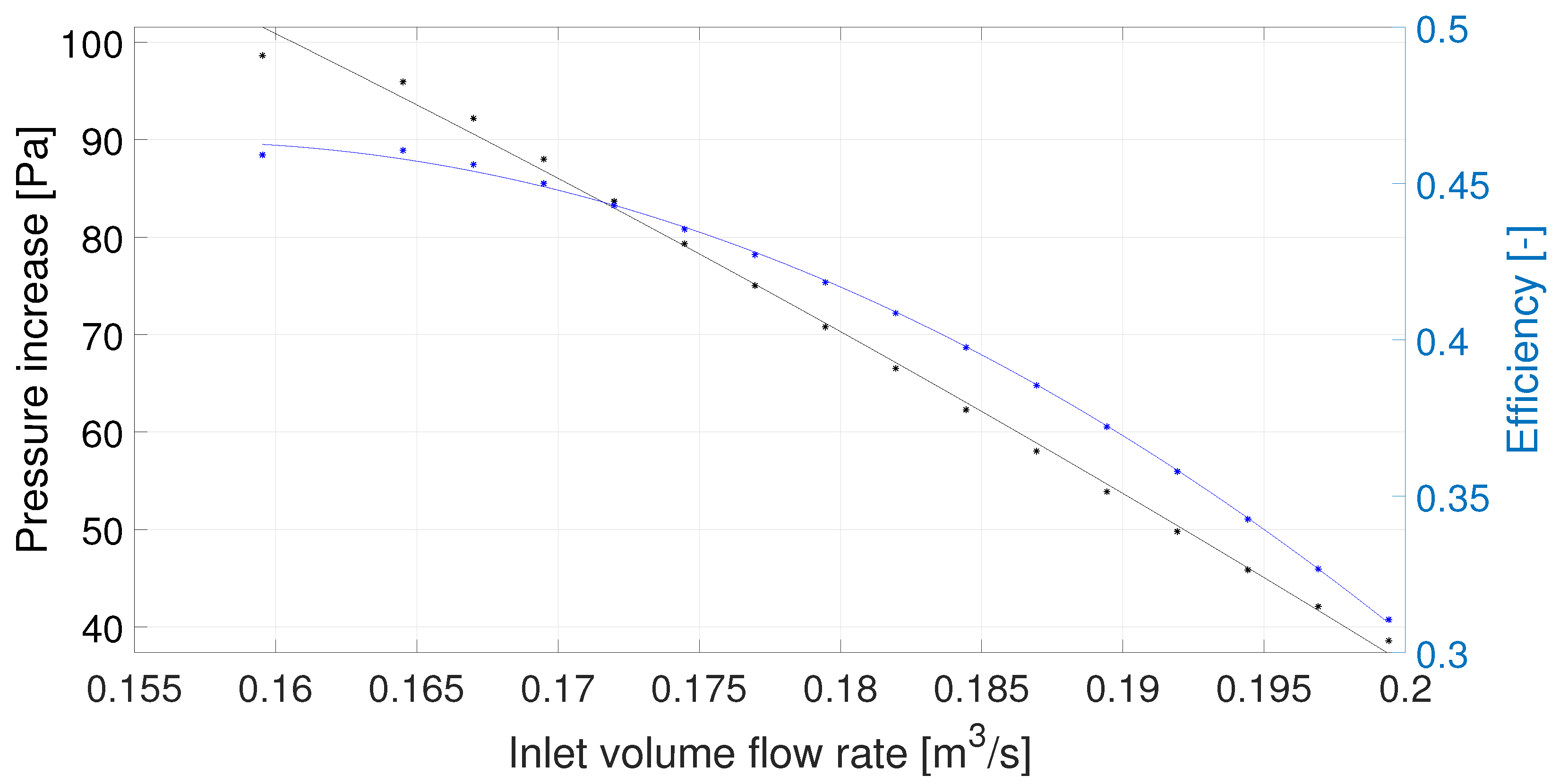
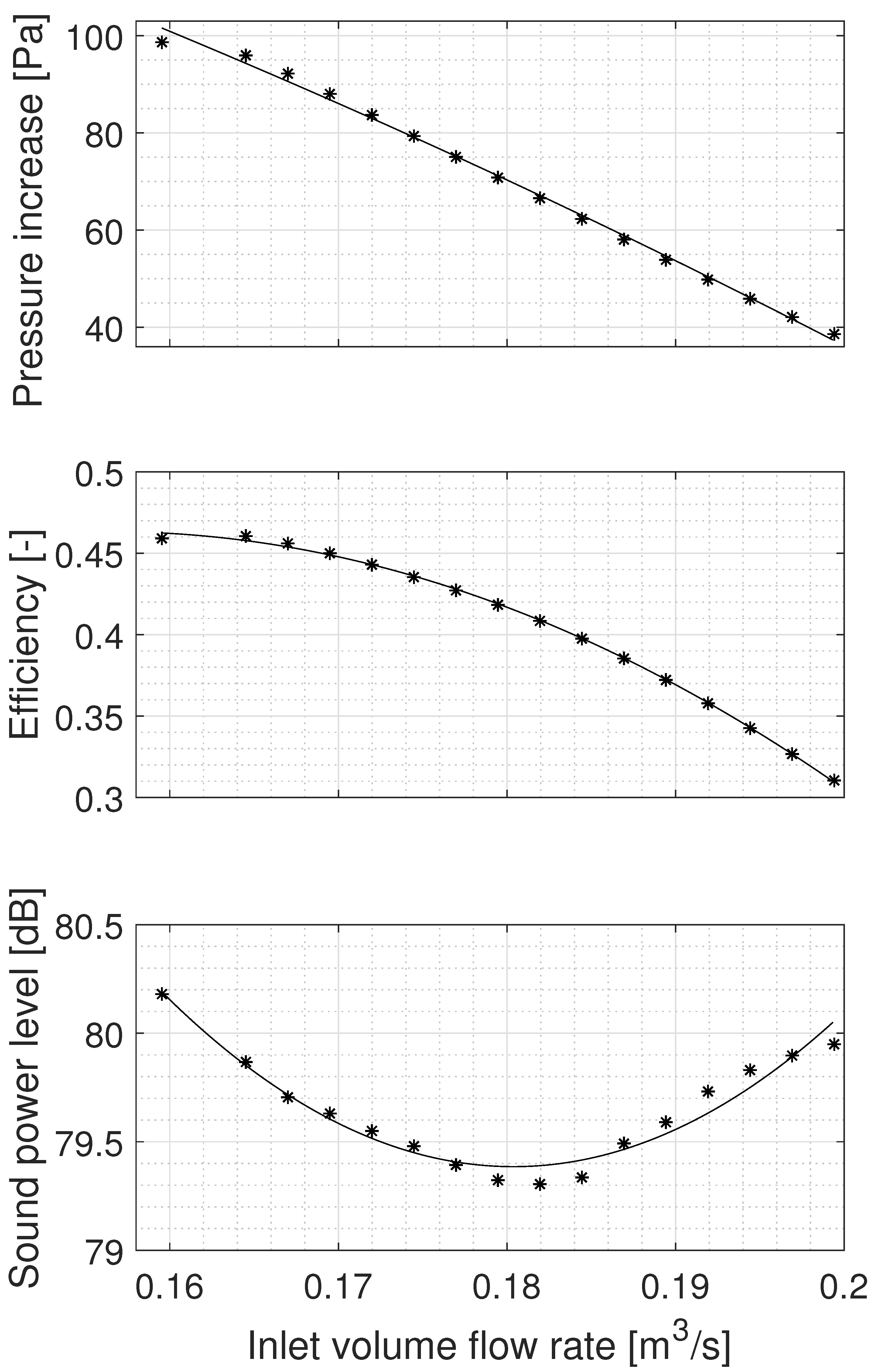
3.1. Fan Characteristics
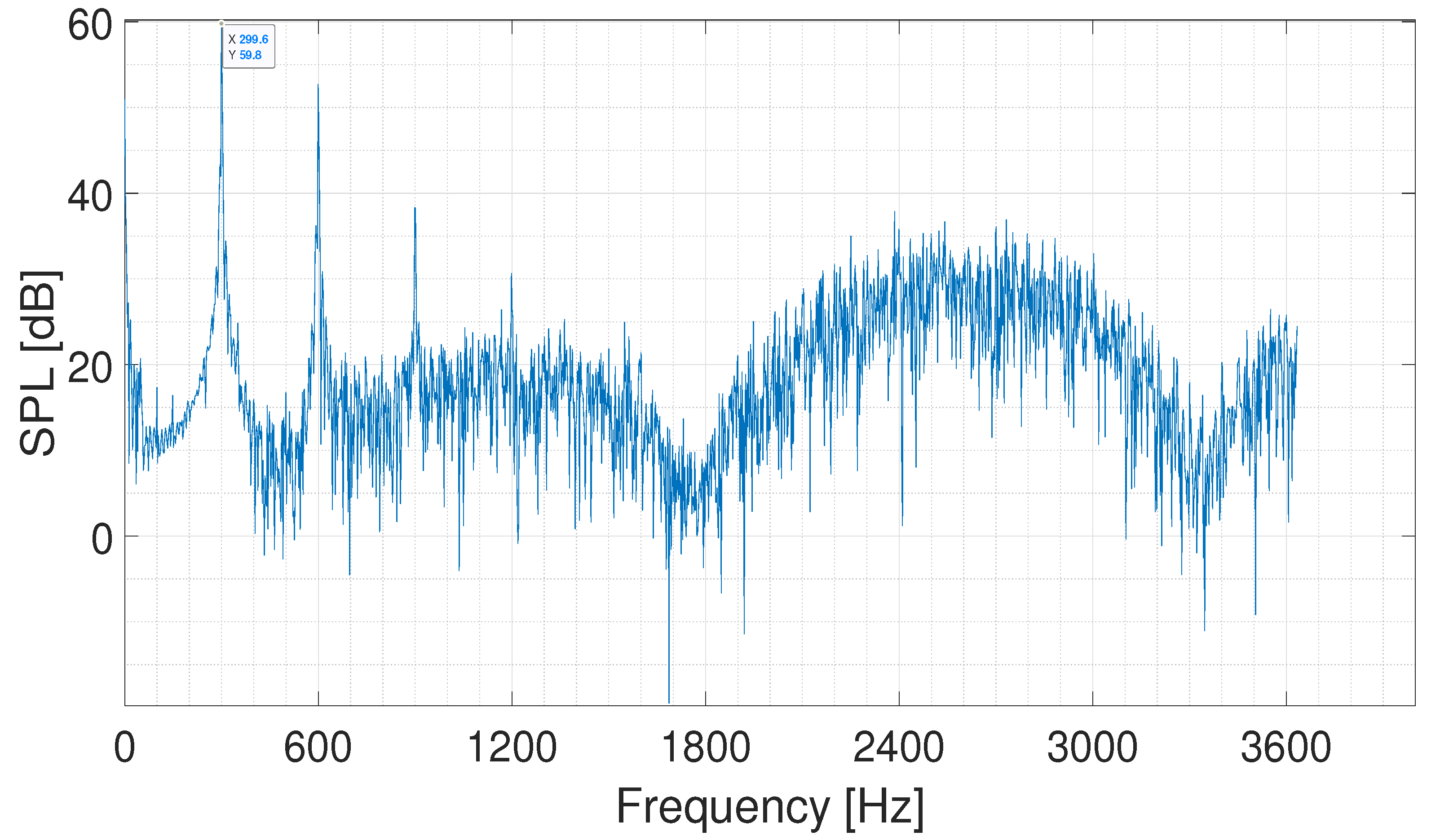
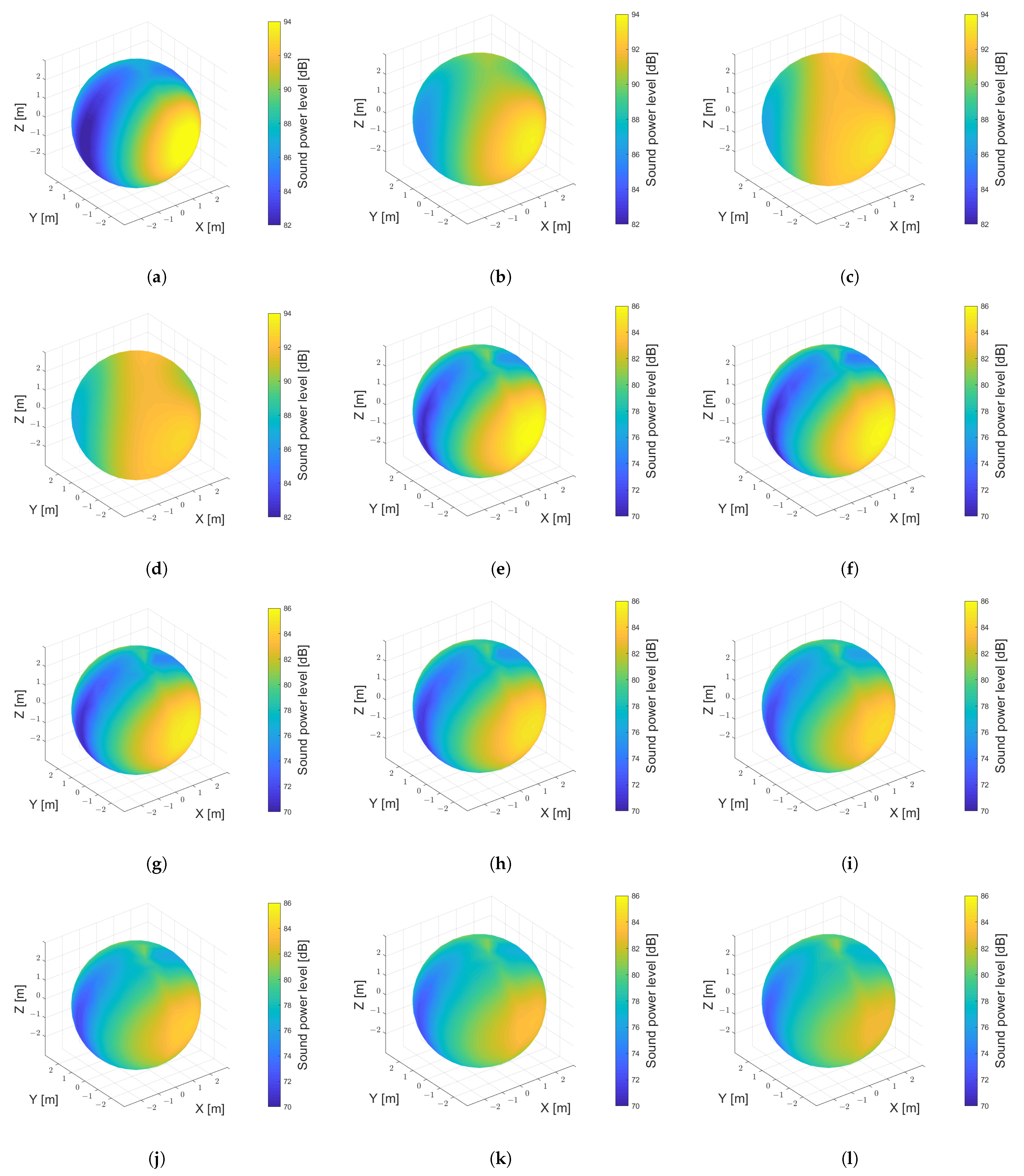
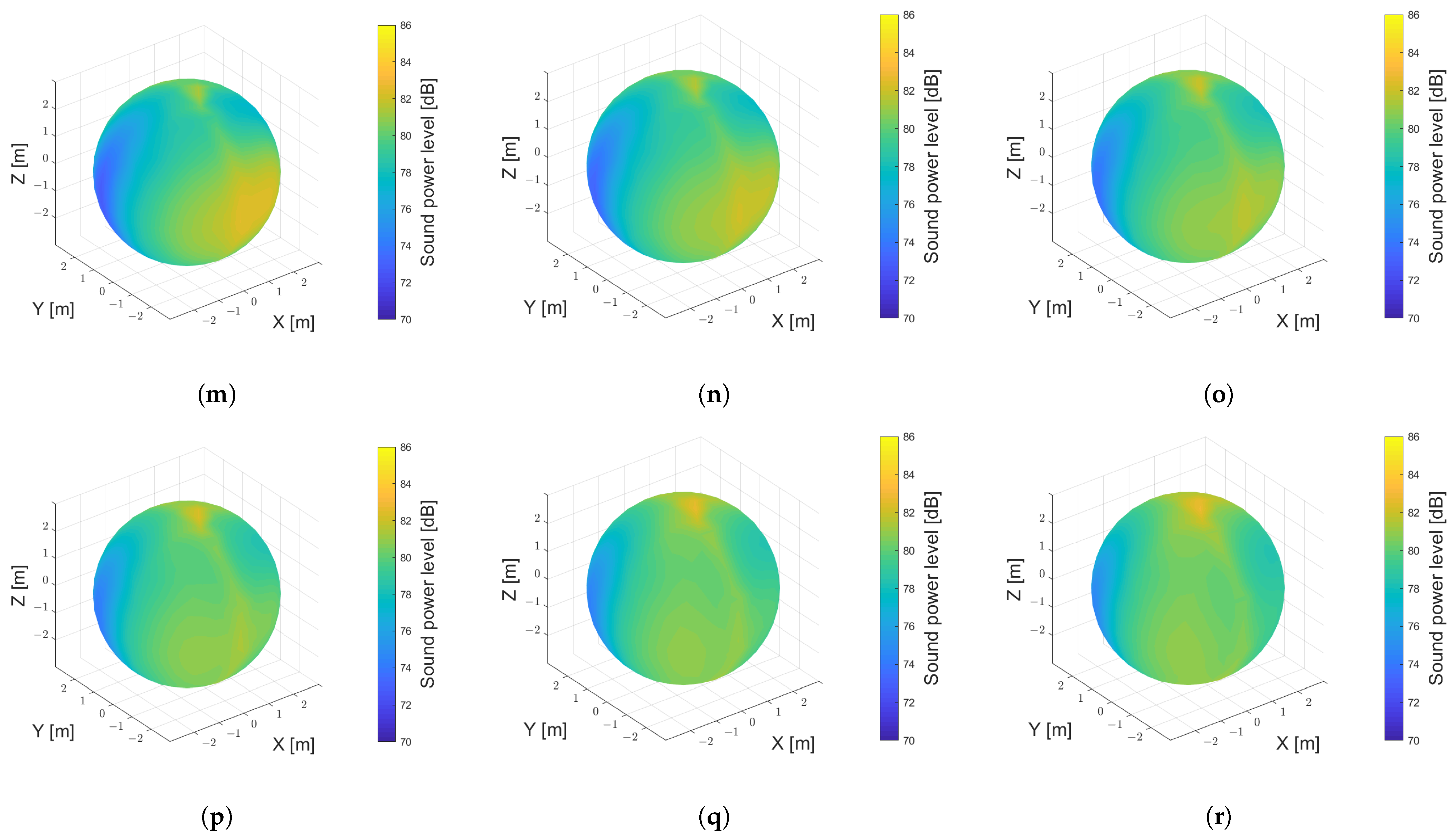
3.2. Aerodynamic Noise Characteristics
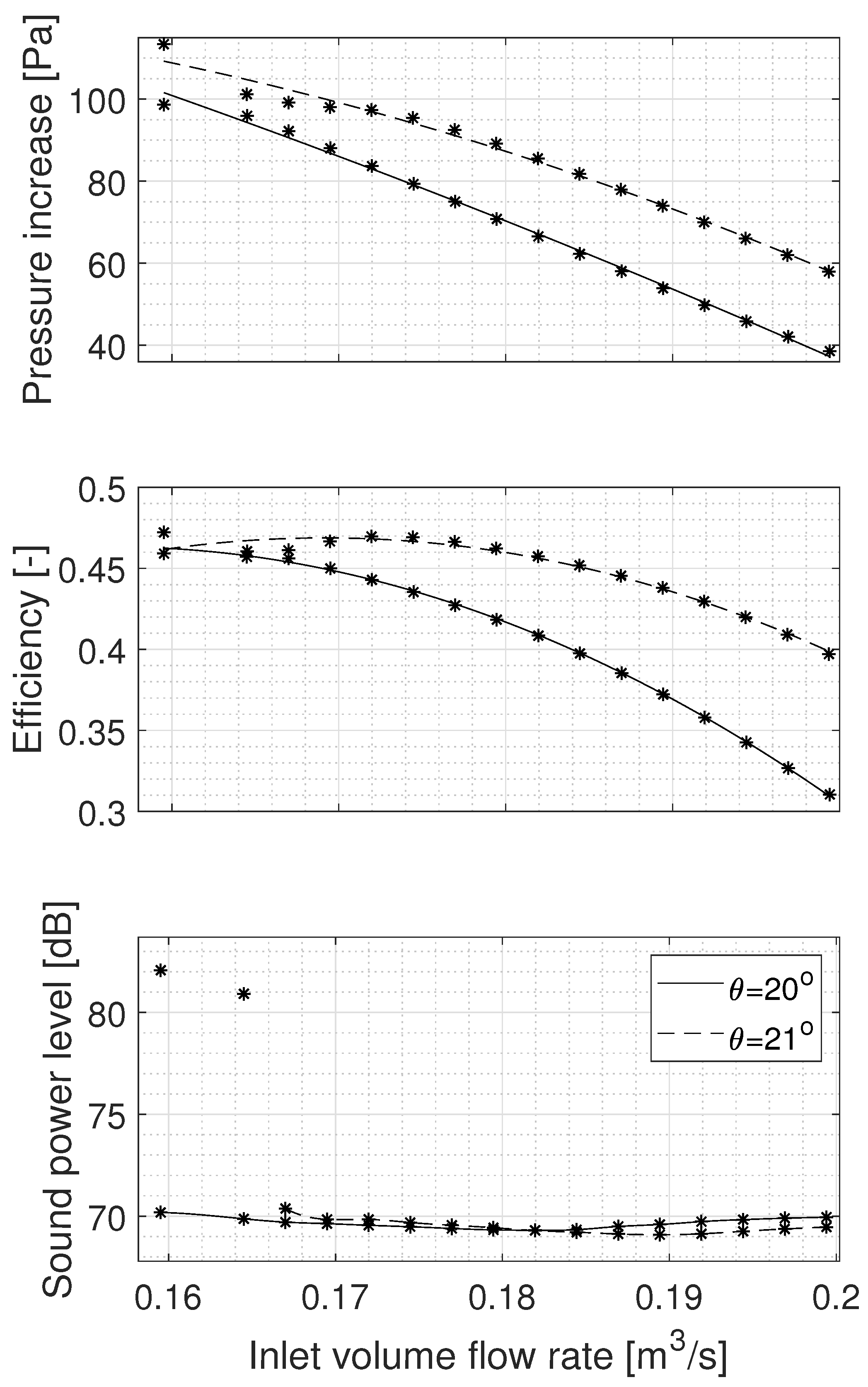
3.3. Sensitivity of the Fan Parameters to the Change of the Blade Angle
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BPF | blade pass frequency |
| CFD | computational fluid dynamics |
| DDES | delayed detached eddy simulations |
| DNS | direct numerical simulations |
| FFT | fast Fourier transform |
| FW-H | Ffowcs Williams and Hawkings analogy |
| MRF | multiple reference frame |
| LES | large eddy simulation |
| SST | shear stress transport |
| URANS | unsteady Reynolds-averaged Navier–Stokes |
References
- Czajka, I. Modeling of Acoustic Phenomena in Aerodynamic Flows; Volume 365, Dissertations, Monographs; AGH: Krakow, Poland, 2019. [Google Scholar]
- Kissner, C.; Guérin, S.; Seeler, P.; Billson, M.; Chaitanya, P.; Carrasco Laraña, P.; de Laborderie, H.; François, B.; Lefarth, K.; Lewis, D.; et al. ACAT1 Benchmark of RANS-Informed Analytical Methods for Fan Broadband Noise Prediction—Part I—Influence of the RANS Simulation. Acoustics 2020, 2, 539–578. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically I. General theory. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1952, 211, 564–587. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically II. Turbulence as a source of sound. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1954, 222, 1–32. [Google Scholar] [CrossRef]
- Lighthil, M.J. Jet Noise. AIAA J. 1963, 1, 1507–1517. [Google Scholar] [CrossRef]
- Curle, N. The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 231, 505–514. [Google Scholar] [CrossRef]
- Williams, J.F.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1969, 321–342. [Google Scholar] [CrossRef]
- Williams, J.F.; Hawkings, D. Theory relating to the noise of rotating machinery. J. Sound Vib. 1969, 10, 10–21. [Google Scholar] [CrossRef]
- Schmitz, F.; Yu, Y. Transonic Rotor Noise: Theoretical and Experimental Comparisons; National Aeroacoustics and Space Administration: Washington, DC, USA, 1982; pp. 319–330. [Google Scholar]
- Brentner, K.S.; Farassat, F. Modeling aerodynamically generated sound of helicopter rotors. Prog. Aerosp. Sci. 2003, 39, 83–120. [Google Scholar] [CrossRef] [Green Version]
- Konstantinov, M.; Wagner, C. Numerical Simulation of the Sound Generation and the Sound Propagation from Air Intakes in an Aircraft Cabin; New results in numerical and experimental fluid mechanics XI; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef] [Green Version]
- Sundström, E.; Semlitsch, B.; Mihăescu, M. Acoustic signature of flow instabilities in radial compressors. J. Sound Vib. 2018, 434, 221–236. [Google Scholar] [CrossRef]
- Al-Am, J.; Clair, V.; Giauque, A.; Boudet, J.; Gea-Aguilera, F. A Parametric Study on the LES Numerical Setup to Investigate Fan/OGV Broadband Noise. Int. J. Turbomach. Propuls. Power 2021, 6, 12. [Google Scholar] [CrossRef]
- Guérin, S.; Kissner, C.; Seeler, P.; Blázquez, R.; Carrasco Laraña, P.; de Laborderie, H.; Lewis, D.; Chaitanya, P.; Polacsek, C.; Thisse, J. ACAT1 Benchmark of RANS-Informed Analytical Methods for Fan Broadband Noise Prediction: Part II—Influence of the Acoustic Models. Acoustics 2020, 2, 617–649. [Google Scholar] [CrossRef]
- Biedermann, T.M.; Czeckay, P.; Hintzen, N.; Kameier, F.; Paschereit, C.O. Applicability of Aeroacoustic Scaling Laws of Leading Edge Serrations for Rotating Applications. Acoustics 2020, 2, 579–594. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Lu, C. Flow and Noise Characteristics of Centrifugal Fan in Low Pressure Environment. Processes 2020, 8, 985. [Google Scholar] [CrossRef]
- Kholodov, P.; Moreau, S. Identification of Noise Sources in a Realistic Turbofan Rotor Using Large Eddy Simulation. Acoustics 2020, 2, 691–706. [Google Scholar] [CrossRef]
- Zarri, A.; Christophe, J.; Moreau, S.; Schram, C. Influence of Swept Blades on Low-Order Acoustic Prediction for Axial Fans. Acoustics 2020, 2, 812–832. [Google Scholar] [CrossRef]
- Zarri, A.; Christophe, J.; Schram, C.F. Low-Order Aeroacoustic Prediction of Low-Speed Axial Fan Noise. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019; p. 2760. [Google Scholar] [CrossRef]
- Herold, G.; Zenger, F.; Sarradj, E. Influence of blade skew on axial fan component noise. Int. J. Aeroacoustics 2017, 16, 418–430. [Google Scholar] [CrossRef]
- Sanjosé, M.; Moreau, S. Fast and accurate analytical modeling of broadband noise for a low-speed fan. J. Acoust. Soc. Am. 2018, 143, 3103–3113. [Google Scholar] [CrossRef] [PubMed]
- Ding, H.; Chang, T.; Lin, F. The Influence of the Blade Outlet Angle on the Flow Field and Pressure Pulsation in a Centrifugal Fan. Processes 2020, 8, 1422. [Google Scholar] [CrossRef]
- Mo, J.o.; Choi, J.h. Numerical Investigation of Unsteady Flow and Aerodynamic Noise Characteristics of an Automotive Axial Cooling Fan. Appl. Sci. 2020, 10, 5432. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, C.; He, R.; Li, K.; Zhang, Q. Numerical Study on the Acoustic Characteristics of an Axial Fan under Rotating Stall Condition. Energies 2017, 10, 1945. [Google Scholar] [CrossRef] [Green Version]
- Chan, K.; Saltelli, A.; Scott, E.M. Sensitivity Analysis; Wiley: Chichester, UK, 2000. [Google Scholar]
- Klieber, M.; Antunez, H.; Hien, T.; Kowalczyk, P. Parameter Sensitivity in Nonlinear Mechanics; Wiley: Chichester, UK, 1997. [Google Scholar]
- MRÓZ, Z.; HAFTKA, R.T. Sensitivity of buckling loads and vibration frequencies of plates. Stud. Appl. Mech. 1988, 19, 255–266. [Google Scholar]
- Zheng, C.; Zhao, W.; Gao, H.; Du, L.; Zhang, Y.; Bi, C. Sensitivity analysis of acoustic eigenfrequencies by using a boundary element method. J. Acoust. Soc. Am. 2021, 149, 2027–2039. [Google Scholar] [CrossRef] [PubMed]
- Romik, D.; Czajka, I.; Suder-Dębska, K. Numerical Investigations of the Design Parameters’ Influence on the Noise of Radial Fan; Polish Acoustical Society, Department of Krakow: Krakow, Poland, 2019; pp. 133–149. [Google Scholar]
- Romik, D.; Czajka, I. On the Modelling of the Aeroacoustics Phenomena Generated by Axial Fan; AGH: Krakow, Poland, 2019; pp. 122–131. [Google Scholar]
- Romik, D.; Czajka, I. Influence of Turbulence Models on Numerical Investigation of Axial Fans Efficiency; Department of Power Systems and Environmental Protection Facilities, Faculty of Mechanical Engineering and Robotics, AGH: Krakow, Poland, 2019; pp. 71–79. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Launder, B.E., Spalding, D.B., Eds.; Academic Press: London, UK; New York, NY, USA, 1972; p. 7. 169p. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries La Canada: La Canada, CA, USA, 1998; Volume 2. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Brentner, K.S.; Farassat, F. Analytical comparison of the acoustic analogy and Kirchhoff formulation for moving surfaces. AIAA J. 1998, 36, 1379–1386. [Google Scholar] [CrossRef] [Green Version]
- Chima, R.; Liou, M. Comparison of the AUSM(+) and H-CUSP Schemes for Turbomachinery Applications. In Proceedings of the Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003. [Google Scholar] [CrossRef] [Green Version]
- Barth, T.; Jespersen, D. The design and application of upwind schemes on unstructured meshes. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989. [Google Scholar] [CrossRef]
- McAlpine, A. Aeroacoustics of Low Mach Number Flows: Fundamentals, Analysis and Measurement S. Glegg and W. Devenport Academic Press, Elsevier, The Boulevard, Langford Lane, OX5 1GB, Kidlington, Oxford, UK. xiii; 537pp. 2017. Illustrated. £97. ISBN 978-0-12-809651-2. Aeronaut. J. 2018, 122, 2030–2032. [Google Scholar] [CrossRef] [Green Version]
- Fortuna, S.; Czajka, I. Experimental Verification of Selected Equations Describing the Sound Power Level in Fans. Turbomachinery 2010, nr 138, 21–32. [Google Scholar]
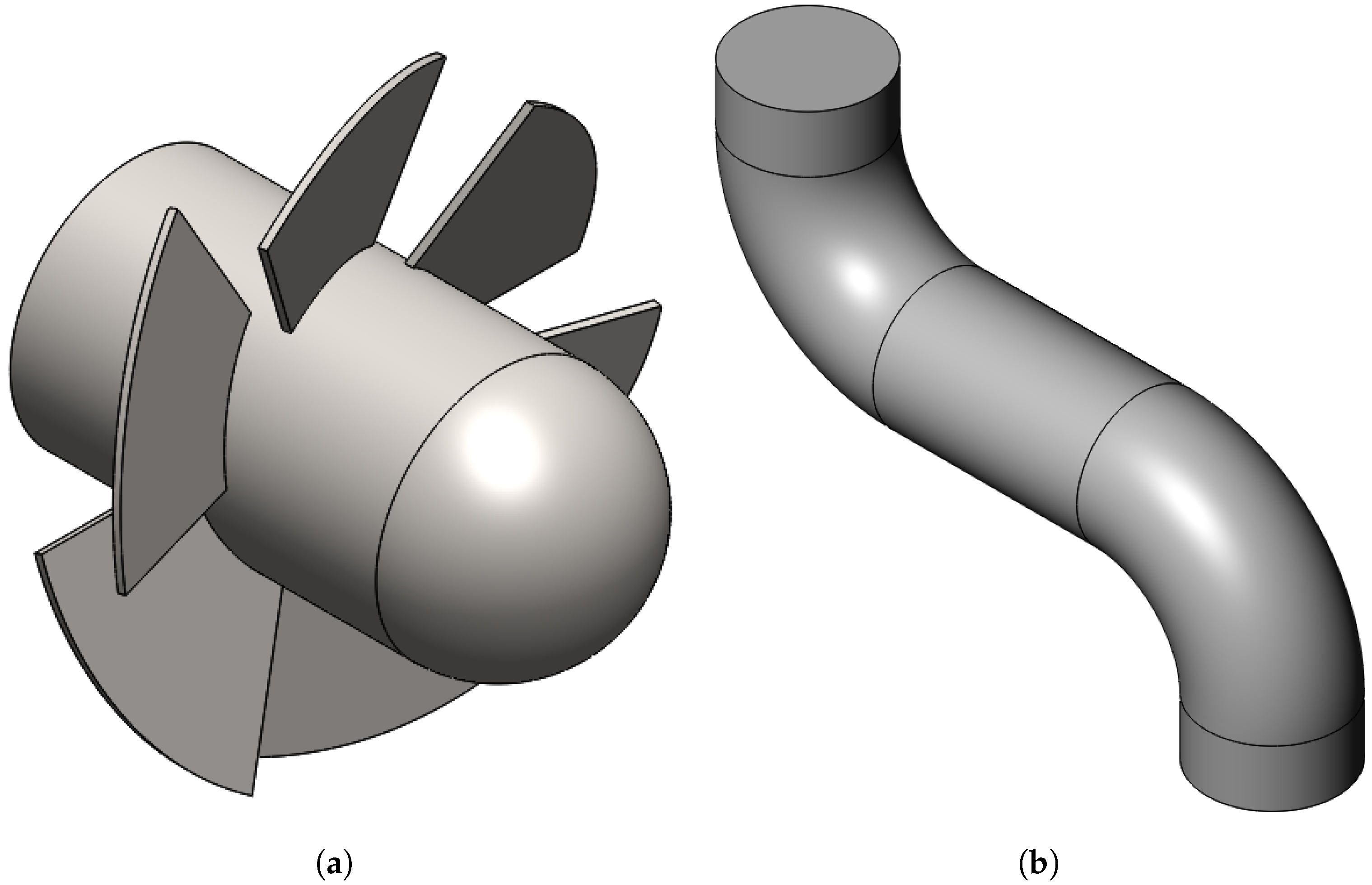
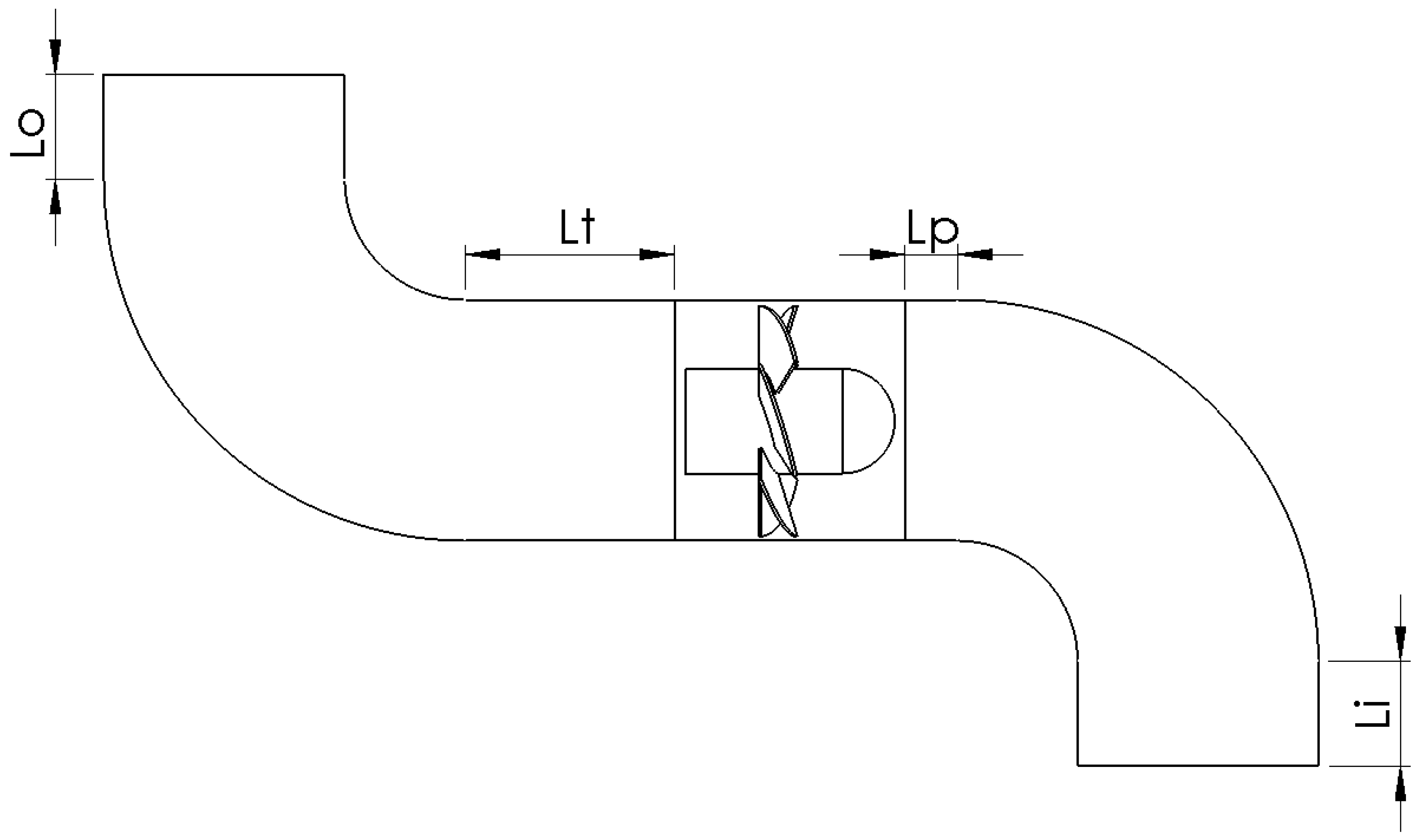

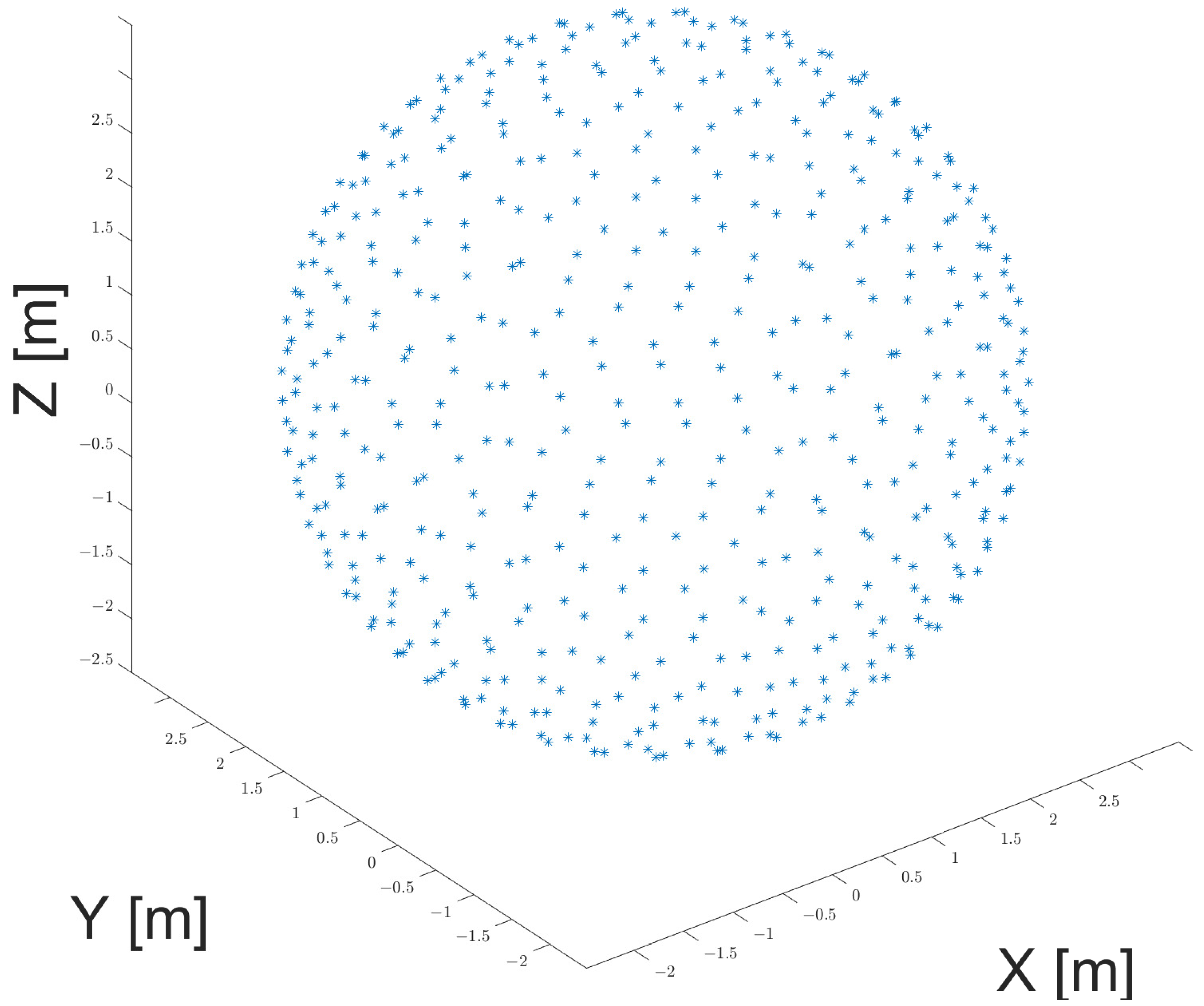

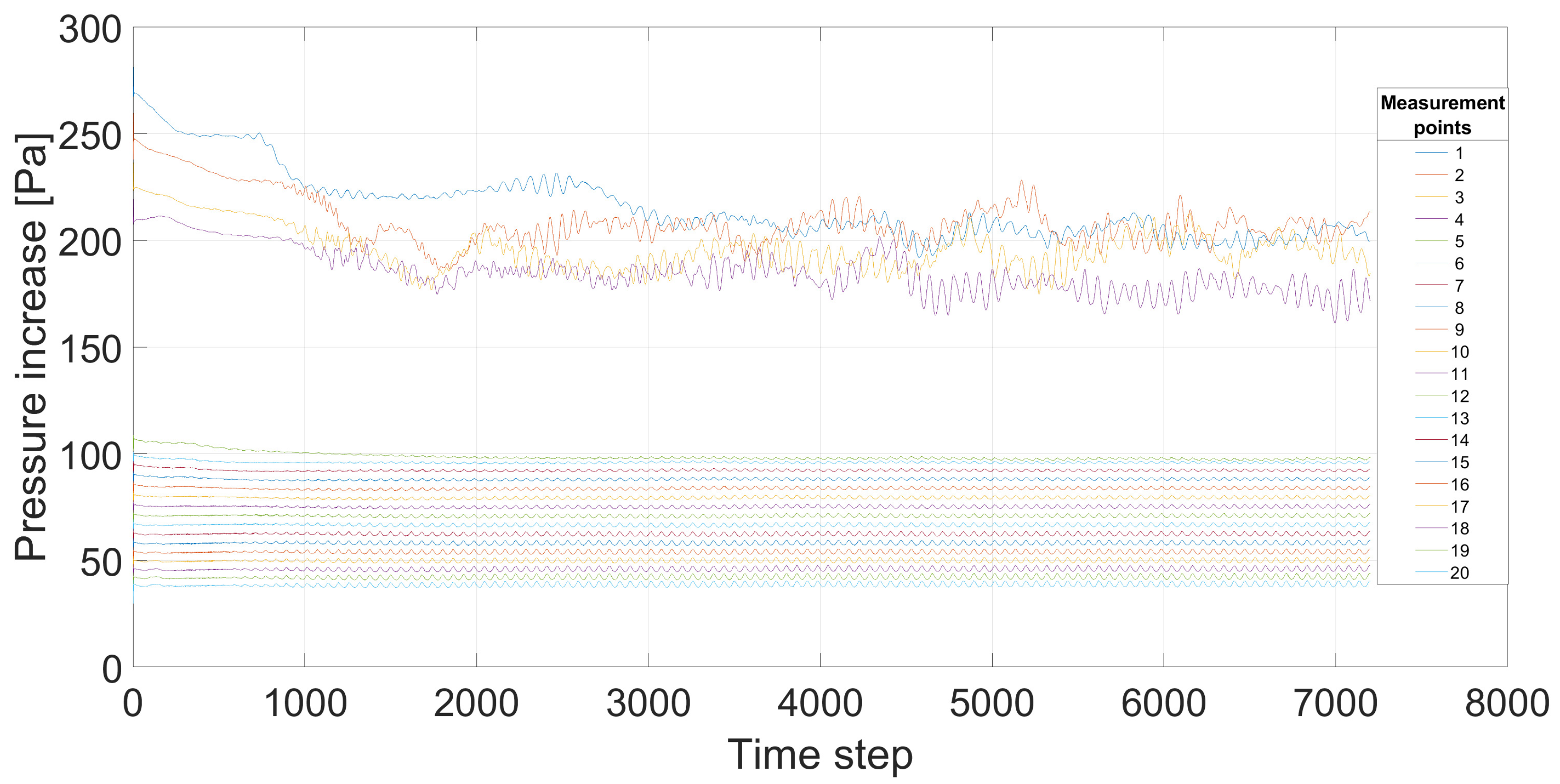
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Rotational speed | n | r·min | 3000 |
| Number of blade | z | - | 6 |
| Rotor diameter | D | mm | 220 |
| Hub diameter | mm | 100 | |
| Hub length | mm | 200 | |
| Inlet/outlet diameter | / | mm | 230 |
| Inlet/outlet length | mm | 100 | |
| Blade angle | 20 |
| Boundary Condition | Symbol | Unit | Value/Zone |
|---|---|---|---|
| Operating pressure | Pa | 101,325 | |
| Inlet pressure | Pa | 0 | |
| Outlet pressure | Pa | 0 | |
| Mesh motion | n | r·min | 3000 |
| Interface | - | - | rotor/duct contact area |
| Wall | - | - | rotor/duct walls |
| Time step | t | s |
| Nr | Volume Flow Rate (m/s) | Percentage (%) | Nr | Volume Flow Rate (m/s) | Percentage (%) |
|---|---|---|---|---|---|
| 1 | 0.0997 | 50.00 | 11 | 0.1770 | 88.75 |
| 2 | 0.1097 | 55.00 | 12 | 0.1795 | 90.00 |
| 3 | 0.1196 | 60.00 | 13 | 0.1820 | 91.25 |
| 4 | 0.1246 | 62.50 | 14 | 0.1845 | 92.50 |
| 5 | 0.1595 | 80.00 | 15 | 0.1869 | 93.75 |
| 6 | 0.1645 | 82.50 | 16 | 0.1894 | 95.00 |
| 7 | 0.1670 | 83.75 | 17 | 0.1919 | 96.25 |
| 8 | 0.1695 | 85.00 | 18 | 0.1944 | 97.50 |
| 9 | 0.1720 | 86.25 | 19 | 0.1969 | 98.75 |
| 10 | 0.1744 | 87.50 | 20 | 0.1994 | 100.00 |
| Nr | SWL [dB] | Nr | SWL [dB] |
|---|---|---|---|
| 1 | 88.47 | 11 | 79.39 |
| 2 | 89.96 | 12 | 79.32 |
| 3 | 90.88 | 13 | 79.30 |
| 4 | 90.80 | 14 | 79.33 |
| 5 | 80.18 | 15 | 79.49 |
| 6 | 79.87 | 16 | 79.59 |
| 7 | 79.70 | 17 | 79.73 |
| 8 | 79.63 | 18 | 79.83 |
| 9 | 79.55 | 19 | 79.90 |
| 10 | 79.48 | 20 | 79.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romik, D.; Czajka, I. Numerical Investigation of the Sensitivity of the Acoustic Power Level to Changes in Selected Design Parameters of an Axial Fan. Energies 2022, 15, 1357. https://doi.org/10.3390/en15041357
Romik D, Czajka I. Numerical Investigation of the Sensitivity of the Acoustic Power Level to Changes in Selected Design Parameters of an Axial Fan. Energies. 2022; 15(4):1357. https://doi.org/10.3390/en15041357
Chicago/Turabian StyleRomik, Dawid, and Ireneusz Czajka. 2022. "Numerical Investigation of the Sensitivity of the Acoustic Power Level to Changes in Selected Design Parameters of an Axial Fan" Energies 15, no. 4: 1357. https://doi.org/10.3390/en15041357
APA StyleRomik, D., & Czajka, I. (2022). Numerical Investigation of the Sensitivity of the Acoustic Power Level to Changes in Selected Design Parameters of an Axial Fan. Energies, 15(4), 1357. https://doi.org/10.3390/en15041357






