1. Introduction
One of the fundamental requirements of nuclear reactor safety is to ensure that heat produced in the reactor core is removed at a sufficient rate to prevent overheating, which can lead to fuel failure and, if all other defense-in-depth release barriers fail, radioactive emissions to the environment. Reactor safety design largely relies on computational analyses. The modeling of an operating nuclear reactor typically involves a multi-stage calculation sequence that solves the coupled problem between core neutronics, thermal hydraulics and fuel behavior. The outer boundary conditions of the core physics problem are further coupled to a system-scale model, which covers the primary and secondary reactor circuits, along with their associated components and sub-systems.
The VTT Technical Research Centre of Finland has a long history of using in-house computational tools for reactor modeling. The development dates back to the construction of the first Finnish power reactors in the 1970s, in particular the two VVER-440 reactor units at the Loviisa nuclear power plant. The main motivation was to establish sufficient national competence to perform independent reactor safety analyses at a time when no computer codes meeting Western quality standards were available for modeling the hexagonal core geometry of VVER-type reactors. Two-dimensional reactor core simulator HEXBU [
1] was developed for this purpose and later upgraded to its three-dimensional version HEXBU-3D [
2]. The development of the first transient analysis code TRAWA [
3] was started soon after. The Three-Mile-Island accident in 1979 created a need for improved plant-scale analyses, which prompted the development of the SMABRE system code [
4].
The development of these codes continued through the 1980s and 1990s, while the constant improvements in computer capacity allowed the implementation of increasingly elaborate computational methods. Three-dimensional transient analysis codes HEXTRAN [
5] and TRAB3D [
6] developed at that time have been actively used until today. As a parallel project, VTT started developing the Apros process simulator [
7] together with the Imatran Voima company (predecessor of Fortum) for the system-scale analyses of nuclear and conventional power plants and industrial processes. Apros has been used for the computational safety analyses of all Finnish power reactors, and the code is still actively developed.
The development of computational tools and methods during past decades enabled maintaining a high level of national competence in reactor safety. However, the evolution of computer platforms, high-performance parallel computing and introduction of advanced new methodologies eventually lead to a situation where the maintenance and further development of the old core simulator and transient analysis codes was no longer practically feasible. One of the major issues was that the original developers of these codes were close to retirement, and the responsibilities had to be passed on to the next generation of experts. Since the source-code level understanding of computational methods was considered essential for preserving national competence, it was decided that the generation shift should be accompanied by the complete renewal of the core physics calculation system.
Work on a new core physics framework Kraken [
8] was started in 2017. Kraken is essentially a modular multi-physics platform, which enables coupling different neutronics, thermal hydraulics and fuel behavior solvers into various reduced-order and high-fidelity computational sequences. The work builds on the previous development of VTT’s Serpent Monte Carlo code [
9], which was started in 2004. Serpent has been specifically designed for reactor physics applications, and has been widely used for both production of homogenized group constants for nodal diffusion codes and as a high-fidelity neutronics solver in coupled multi-physics simulations.
This paper is a review on the current status, applications and planned future development of the Kraken framework. A brief overview of the coupled core physics problem is provided in the following section. The computational modules and coupling platform in Kraken are introduced in
Section 3. Recent work and applications are discussed in
Section 4 and the future plans in
Section 5. The last section is left for summary and conclusions.
2. The Coupled Core Physics Problem
The modeling of an operating nuclear reactor involves solving a coupled problem between neutronics, thermal hydraulics and the thermo-mechanical behavior of nuclear fuel. Fission power is coupled to heat transfer and coolant flow via physical feedbacks, which determine the core response to perturbations in the operating state. The capability to model the dynamic response of the reactor core after reactivity insertions and other initiating events is put to practice in transient analyses, which determine important safety margins for reactor operation. The core physics model also forms the first key component in a long calculation chain in system-scale analyses. The thermal hydraulics model of the core is coupled to primary coolant flow, the simulation of which is handled using calculation codes that also account for the operation of pumps, valves, heat exchangers and other primary circuit components, as well as the turbine cycle, generator, electrical systems and automation.
Core neutronics are also affected by long-term changes in the isotopic compositions and the mechanical properties of fuel materials. The depletion of fissile uranium and burnable absorbers and the build-up of plutonium, minor actinides and fission products changes the neutronic characteristics of fuel over core life, which must be taken into account by burnup calculations. Mechanical changes, such as fuel swelling and cladding creep, are directly reflected in the heat transfer properties, and consequently, the coupled solution. These long-term changes are accounted for by fuel cycle simulations, which provide the initial state for transient safety analyses and form the basis of in-core fuel management and loading pattern optimization.
The common denominator in core physics calculations is the need to obtain a three-dimensional steady-state or time-dependent solution for the core power distribution at the resolution of a single fuel pin, preferably within the accuracy of a few percent. What complicates the solution is that the coupling between neutronics, heat transfer, coolant flow and fuel burnup transforms a computational task comprised of a number of independent linear problems into a complex non-linear problem requiring iterations between the solvers. Obtaining a converged solution becomes computationally expensive, which practically rules out the use of high-fidelity methods for routine core-level design and safety analyses.
The conventional methodology applied to core physics calculations is instead based on a number of approximations. For the neutronics solution this implies a multi-stage calculation scheme, in which the physical complexity of the transport problem is gradually reduced, while simultaneously increasing the scale of the modeled system. The input for the reduced-order core-level neutronics model is obtained via spatial homogenization, in which the physical characteristics of the fuel is reduced into a handful of assembly-wise few-group constants. The multi-stage calculation scheme is capable of providing sufficiently accurate results within a reasonable computational cost, largely because much of the actual transport physics is included in the homogenized few-group constants.
The methods applied to coupled core physics calculations also depend on the modeled system. For light water reactors (LWRs), the neutronics solution is typically based on two-group diffusion theory. Reduced-order neutronics codes developed for conventional pressurized and boiling water reactors, however, may not be directly applicable to fast reactors, high-temperature gas-cooled reactors (HTGRs) or other non-LWR reactor types. Even SMR-scale LWR cores may require more advanced neutronics models, as the peripheral fuel assemblies located next to the radial reflector occupy a larger fraction of core volume compared to traditional large LWRs.
The same applies to methods used for thermal hydraulics and fuel behavior. Coolant flow and heat transfer phenomena in water-cooled reactors are fundamentally different from reactors cooled by liquid metal or gas. In most reactors, the nuclear fuel is loaded into the core in the form of cylindrical pellets encapsulated inside metallic cladding tubes. There is some variation in the geometry, as well as the materials used for fuel and cladding. There are also reactor types, in which the fuel is fundamentally different. HTGRs use micro-particle fuel, in which the fissile material is in the form of microscopic kernels encapsulated inside multiple protective layers and mixed with a graphite matrix. In molten salt reactors (MSRs), the fuel is in liquid state, mixed with the coolant salt flowing through the reactor core.
Even though high-fidelity methods are not a practical approach for routine design and safety analyses, they can often be a useful option for best-estimate analyses and to complement the results of reduced-order calculation tools. Nodal diffusion methods, for example, can be verified by continuous-energy Monte Carlo simulations, for which the accuracy is much less dependent on the physical characteristics of the modeled system. In a similar way, system- or component-scale thermal hydraulics calculations can be verified by computational fluid dynamics (CFD), albeit at a very high computational cost.
3. The Kraken Computational Framework
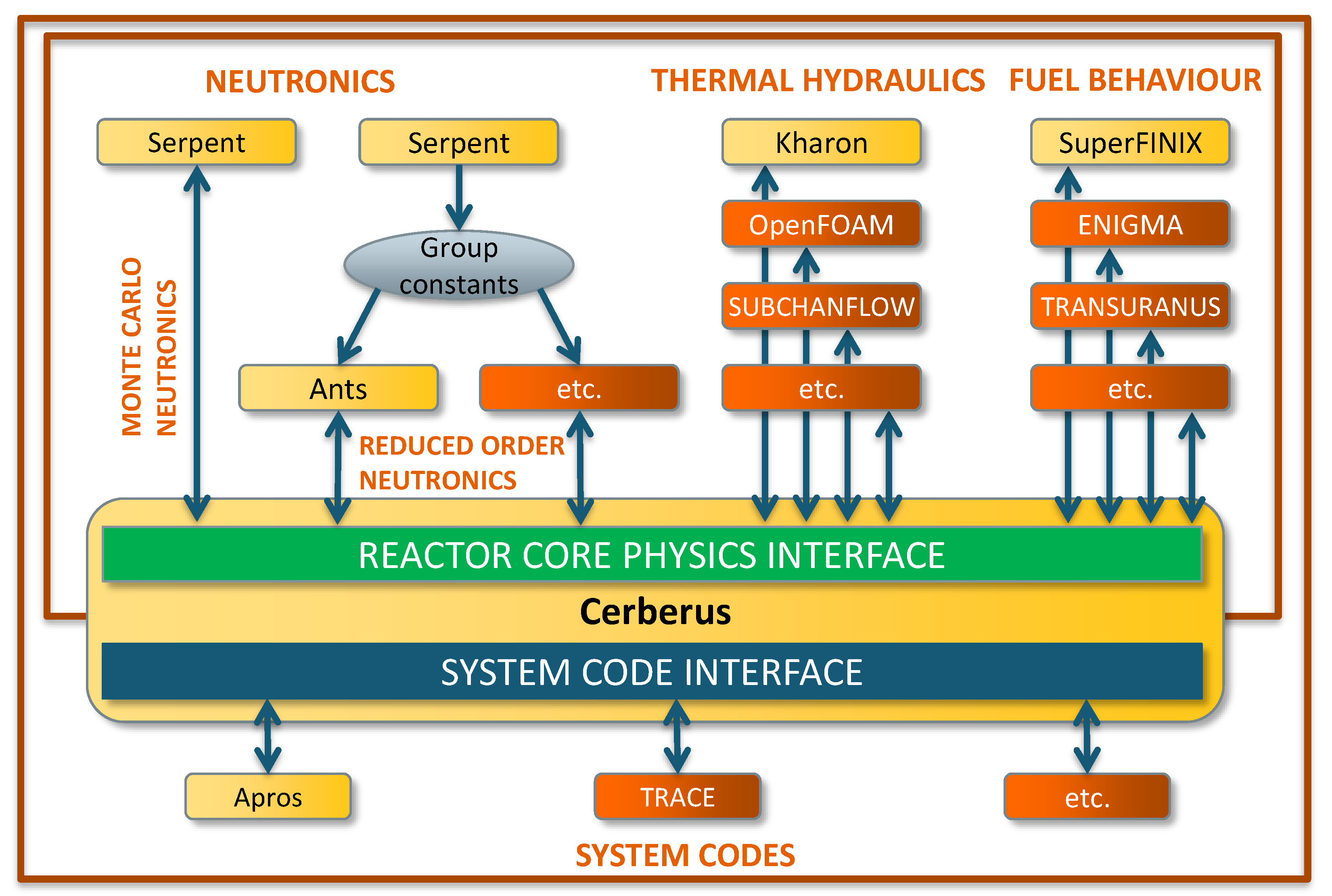
The Kraken framework is VTT’s state-of-the-art modular multi-physics platform for coupling neutronics, thermal hydraulics and fuel behavior solvers into various high-fidelity and reduced-order computational sequences. The platform itself provides an interface for the exchange of input and output data between the solvers, together with driver modules to handle the communication and user interaction. A schematic view of the framework is presented in
Figure 1, and computational modules are described in the following subsections. The main focus is in the core physics solution, which can be further coupled to system-scale simulations through external boundary conditions.
3.1. Serpent
The Serpent Monte Carlo neutron and photon transport code has been developed at VTT since 2004 [
9]. The code is publicly distributed by the OECD/NEA Data Bank and RSICC and currently has more than 1000 users in 250 organizations around the world. The distribution for non-commercial research and educational use is free of charge, but the code can also be used for commercial applications with a separate commercial software license. The project started out as a simplified Monte Carlo code dedicated to reactor physics, but the applications have been considerably diversified over the years. In addition to reactor modeling, Serpent is also used for fusion neutronics and various radiation transport applications.
The role of Serpent in the Kraken framework is twofold. The code is used for generating homogenized group constant data for reduced-order neutronics solvers, most importantly the Ants nodal neutronics code described in the following subsection. For this purpose, Serpent features an automated run sequence for history and branch calculations, and the capability to produce homogenized microscopic and macroscopic reaction cross sections and diffusion coefficients in infinite and critical spectra, as well as discontinuity factors and other parameters typically used by nodal diffusion codes [
10,
11]. Before starting the development of the Ants code in 2017, group constants generated using Serpent were used with the Ares nodal diffusion code [
12,
13] and the neutronics model in Apros. Outside VTT, Serpent has been extensively used, in particular with DYN3D [
14] and PARCS [
15].
Serpent can also be used as a high-fidelity neutronics solver in coupled multi-physics applications. Material temperature and density distributions from thermal hydraulics and fuel behavior codes can be passed into Serpent using a multi-physics interface that is structurally separated from the geometry model. The same interface can be used for passing power distributions in the opposite direction. This capability was implemented several years before starting the development of the Kraken framework [
16]. More recent additions include the capability to perform coupled neutron–photon transport calculations for the explicit treatment of gamma heating [
17,
18] and a collision-based domain decomposition scheme to enable reactor-scale burnup calculations with millions of depletion zones [
19].
Computer capacity is still a major limiting factor for coupled multi-physics simulations involving a Monte-Carlo-based neutronics solution, but the use of Serpent for reactor-scale coupled burnup simulations and transient analyses has already been demonstrated in supercomputers [
20,
21].
3.2. Ants
Ants is a modern multi-group nodal neutronics solver capable of performing steady state, burnup and transient calculations in rectangular and hexagonal fuel geometry [
22,
23]. The solution is based on a combination of the analytic function expansion nodal method (AFEN) and the flux expansion nodal method (FENM), used for solving the diffusion equation. Ants has been specifically developed for the Kraken framework since 2017 and to utilize Serpent-generated group constant data. The main advantage of using the continuous-energy Monte Carlo method for group constant generation is that the same Serpent–Ants calculation sequence can be applied to a wide range of fuel and reactor types without application-specific limitations.
The nodal solution in Ants can be refined by utilizing an intra-nodal mesh in both rectangular and hexagonal geometries. In the hexagonal case, the radial subdivision is achieved by using a triangular nodal solution [
24]. Ants also features a pin power reconstruction scheme for both rectangular and hexagonal cores. Preliminary support for nuclide composition tracking using a microscopic depletion approach has been recently added to Ants [
11].
3.3. FINIX / SuperFINIX
FINIX [
25] is a fuel behavior module developed at VTT since 2012 for the purpose of multi-physics simulations. The code was originally designed for internal coupling, for example, to replace outdated fuel models in VTT’s legacy transient analysis codes or to provide temperature feedback for Serpent simulations. FINIX is publicly distributed by the OECD/NEA Data Bank. The code has a small user base, with most of the users applying it as an internally coupled fuel behavior solver with Serpent.
FINIX solves the thermo-mechanical behavior of a single fuel rod under neutron irradiation conditions, taking into account both thermal effects and changes in rod geometry. The thermal and mechanical models are coupled by internal pressure and fuel-cladding gap heat conductance, which are functions of rod temperature and dimensions. Both the heat equation and the mechanical behavior are solved radially in one-dimensional cylindrical geometry independently for several axial nodes. The node-wise solutions are coupled together via internal pressure, which is solved simultaneously for the entire rod. This approach is generally referred to as the 1.5-dimensional model. The dependence of physical quantities on local parameters, such as temperature and burnup, are based on publicly available material correlations.
When the FINIX code was adopted as part of the Kraken framework, the execution of individual runs was assigned to a wrapper module called SuperFINIX [
26], which handles the core-level fuel behavior solution by running a large number of parallel rod-level calculations. The solution provides the fuel temperatures for the coupled simulation.
3.4. Kharon
Kharon is a closed-channel two-phase steady-state thermal hydraulics module based on the porous-medium approximation. Being a closed-channel steady-state solver implies its applications are limited to time-independent simulations with a closed assembly geometry or no appreciable cross-flows. The original motivation for developing Kharon was to have a light-weight TH solver to complete the multi-physics coupling during the early development stages of the Kraken framework. Even though Kharon was essentially designed as a placeholder for a more advanced methodology, the code has shown good results in routine fuel cycle simulations coupled to Ants and SuperFINIX [
27]. The module has been used, for example, in the core design analyses of VTT’s LDR-50 district heating reactor concept (see
Section 4.2).
3.5. Cerberus
Communication between the solver modules is handled using the Cerberus Python package. Cerberus is essentially a high-level code-agnostic interface that provides the methods for socket-based communication, exchange of field data, iteration algorithms, etc. The Python-based functionality is complemented by a reactor simulator module [
27], which provides a user interface for reactivity control, core reloading operations and other features needed to perform routine fuel cycle simulations. The simulator also collects the relevant output data and evaluates several safety-related parameters, such as reactivity feedback coefficients, control rod worths, shutdown margins and power peaking factors.
3.6. The Apros Process Simulator
The commercial Apros software [
7] developed by VTT and Fortum is intended for dynamic simulations of industrial processes and conventional and nuclear power plants. In Finland, the code has been widely used for system-scale analyses of the power reactors at Loviisa and Olkiluoto. Apros includes several solvers for two-phase flows and models for pipes, pumps, valves, electric components and plant automation. The code also features a point-kinetics and one- and three-dimensional neutronics models for the reactor core.
Apros is not an integral part of the Kraken framework, but it can be coupled to the outer boundary conditions of the core physics solution. This approach combines the state-of-the-art methodology developed for Kraken to the capability to construct complicated plant-scale models. So far, such applications have been limited to steady-state calculations with one-way coupling, by obtaining the reactor pressure and core inlet flow conditions for the Kharon module from Apros simulations. The capabilities of the system code interface in Kraken are planned to be extended to dynamic simulations with two way coupling within the near future (see
Section 5.2).
3.7. Third-Party Solvers
The Kraken framework is designed to be code-agnostic, in the sense that any computational module in the coupled sequence can be replaced with another tool performing the same task. This applies to both modules developed at VTT and third-party solvers. However, there are two main reasons why the primary focus is on in-house modules. First, the purpose of the new system is to replace VTT’s legacy codes developed several decades ago by people who have since then been retired. The renewal process is not limited to computational tools—there is also a new generation of experts using these tools in their everyday work. It is believed that the development of new codes and methods is by far the the best way to accomplish this generation shift.
Second, third-party calculation tools often come with restriction in their scope of applications. The SUBCHANFLOW thermal hydraulics solver, for example, has been successfully coupled to Serpent and extensively used for multi-physics simulations within the EU Horizon 2020 project McSAFE [
28]. The code provides a methodology that is superior to the Kharon thermal hydraulics module, but the software license limits the applications to non-commercial research. Similar limitations apply to the TRACE system code, which has been coupled to Kraken simulations for research purposes [
29]. Since the Kraken framework is intended to be used for both non-commercial research and commercial work, it was decided that the development should primarily rely on modules owned by VTT or unrestricted open-source software, such as OpenFOAM [
30].
4. Example Applications
The Kraken framework has been developed for four years now, and so far, most of the efforts have been devoted to implementing new methods and establishing the couplings between the modular solvers. The work has also involved the verification and validation of the implemented methodology, as well as practical applications.
4.1. Verification and Validation of the Ants Code
The Ants nodal neutronics solver is a novel code, and a major component of the Kraken framework. The verification and validation of the solution methods is therefore one of the main topics of on-going work. The three nodal models of Ants have been initially verified during their implementation. The results have been published separately for the rectangular [
22], hexagonal [
23] and triangular lattice types [
24].
The pin power reconstruction capabilities in Ants have been verified against high-fidelity Serpent reference solutions. For a rectangular geometry, this has been carried out in the context of the initial hot zero power core calculations of the BEAVRS benchmark [
31]. Similar verification for hexagonal geometries is under way. The test cases include the Khmelnitsky 2 initial core [
32,
33] and the VVER-440 and VVER-1000 full core benchmarks [
34,
35].
The transient nodal solution of Ants is currently being verified against international reactor kinetics and dynamics benchmarks such as the TWIGL [
36], LMW [
37], LRA [
38,
39,
40] and the AER-DYN benchmarks [
41,
42].
In addition to verification by code-to-code comparisons, Ants has been validated by comparison against experimental data in the context of simulating the BEAVRS and Khmelnitsky 2 initial core zero power physics tests [
31,
43].
4.2. VTT’s District Heating Reactor Project
In February 2020, VTT initiated the development of a 50 MW SMR for the purpose of district heating and other low-temperature applications. The purpose of the project is to support the Finnish national climate goals, in particular, the phase-out of coal in energy production by the end of this decade. The technology is developed under the name “Low-temperature District Heating and Desalination reactor”, or LDR.
The LDR-50 reactor module is currently in the conceptual design phase. System-scale design and safety analyses have been carried out using the Apros code and core physics simulations using the Ants–Kharon–SuperFINIX sequence in Kraken. This work has involved initial and equilibrium core design and the evaluation of safety parameters, such as control rod ejection worths, shut-down margins and reactivity feedback coefficients. The reactor is operated without soluble boron, which required implementing a control rod algorithm in the reactor simulator module to maintain a flat power distribution throughout the operating cycle.
The first results of VTT’s district heating reactor project have been published in three papers at the ICONE-28 conference in August 2021 [
44,
45,
46]. More recent core design analyses also involve load-follow scenarios, in which the reactor power and operating temperature follow the demand of the district heating network [
47].
5. Future Development
The original goal set for Kraken development was that the new computational framework would gradually replace VTT’s legacy codes used for the safety analyses of Finnish power reactors. Another major motivation for developing new methodologies was to extend the modeling capabilities to next-generation reactor types. Some of the near-term plans are discussed in the following.
5.1. Ants Development
Since the Ants code forms one of the major components of the coupled code sequence, implementing new features and capabilities in the nodal solution also plays a major role in Kraken development. Ants is already capable of performing steady-state, transient and burnup calculations for both rectangular and hexagonal core geometries, so most of the work is related to refining the existing methodology.
Specific topics include the implementation of an axial rehomogenization model to handle material discontinuities separately from the general axial nodalization. This capability improves the treatment of control rods inserted partially inside the nodes. Advanced time-integration methods have been planned for burnup calculations to enable longer time steps without compromising the accuracy. The forward flux solution will be complemented by an adjoint solution, which can be used, for example, for calculating adjoint-weighted time constants, reactivity coefficients and sensitivities.
As a related effort, improved group constant models are being developed to reduce the overall computational cost of the Serpent–Ants calculation sequence. This is accomplished by optimizing the parametrization in such way that the number of computationally expensive Monte Carlo simulations could be reduced while maintaining the high level of accuracy.
5.2. Improved Thermal Hydraulics Models
While the thermal-hydraulic module Kharon served its purpose in the early stages of Kraken development, it has several limitations that prevent its more general use in safety assessments. The solution is based on parallel 1D channels, one for each fuel assembly, which do not exchange information between each other. Therefore, its use is limited to closed-channel fuel assemblies or configurations with negligible crossflow. Furthermore, the solution is time-independent, which completely rules out transient simulations. Finally, the implemented mass and heat transfer model was explicitly created for water and steam phases. While these shortcomings could be amended, the work required would eventually approach that of developing an in-house CFD code.
When considering suitable candidates for future thermal-hydraulics modules to be included in Kraken, the third party open source software package OpenFOAM [
30] conforms to most of the requirements set out at the beginning of Kraken development. Its open source code base provides the possibility for source-code level understanding, similar to an in-house code. OpenFOAM consists of several different solvers, purpose-built for different applications and a wide range of physics. New solvers can be constructed from an extensive library of available tools. The software is actively developed and maintained. New functionality and models can be easily added on top of the existing ones. The GNU General Public License of OpenFOAM enables both academic and commercial use, including further development of the source code.
It is planned that the functionality associated with the OpenFOAM–Kraken coupling will be collected into a library, which can be easily included on top of any existing solver, with minimal modifications to the solver itself, thereby remaining fully versatile. In addition to serving as a core thermal-hydraulic solver, the computational domain could be expanded to cover a larger region, for example, the reactor pressure vessel internals or the whole primary loop.
The capability to run system-scale transient simulations involving pump trips, loss-of-coolant accidents and other events involving components outside the reactor core require a computational model that extends beyond the Kraken framework. This is accomplished by coupling the outer boundary conditions of the thermal hydraulics solution to a system-scale simulation (see
Figure 1). Alternatively, the TH solver in Kraken can be replaced by the core TH component of the system code. Some preliminary calculations with one-way Apros–Kraken coupling have already been carried within VTT’s district heating reactor project [
46,
47], and the data exchange is planned to be extended to both ways in the near future.
5.3. Verification and Validation of Coupled Calculation Sequences
Applying the Kraken framework to nuclear reactor safety analyses requires comprehensive verification and validation of the entire system. So far, the efforts have been primarily focused on individual modules, in particular the Ants code, as discussed in
Section 4.1. The next step is to extend the V&V efforts to coupled code sequences.
The work has begun with the modeling of the first and second operating cycles of a 1000 MWe PWR featured in the BEAVRS benchmark [
48]. The calculation is run using the reactor simulator module in Kraken, driving the Ants–Kharon–SuperFINIX code sequence. The calculation utilizes the fuel cycle simulation capabilities in Kraken, including fuel shuffling between the two cycles. The results including boron letdown curves, power distributions and zero power physics tests will be reported in a journal article currently under preparation. Similar fuel cycle simulations are planned for a hexagonal VVER-1000 reactor, as described in the Khmelnitsky 2 benchmark [
32].
A coupling between Kraken and the TRACE system code was recently established [
29], and the code sequence will be tested within the near future using the V1000CT-2 [
49] exercise 2 and the Kalinin 3 Coolant Transient Benchmark [
50] exercise 3. Similar tests will be later carried out for the Kraken–Apros system code coupling.
5.4. Non-LWR Applications
So far, the development of Kraken has been focused on conventional large and SMR-scale LWRs, but the long-term plan is to extend the capabilities to various next-generation non-LWR reactor types. These plans have been taken into consideration from the beginning of the project. The neutronics solution in the Ants code, for example, relies on a multi-group model instead of the traditional two-group approach commonly used with LWR calculations. Since the group constant data are obtained from continuous-energy Monte Carlo simulations, there are no major limitations associated with the underlying transport model.
The first non-LWR reactor type to be considered is the high-temperature gas-cooled reactor with a prismatic core. The Ants code already features hexagonal and triangular nodal models, which can be applied to these types of geometries. The challenges for the reduced-order neutronics solution are instead related to certain characteristic features of gas-cooled reactors. The vertical coolant channels extending through the core form long streaming paths for neutrons, which challenges the current diffusion-based nodal models in Ants. One potential solution is to expand the nodal model to higher-order transport methods. Another topic for future work is the group constant model, in which the parametrization relies on LWR-specific state variables, such as coolant density and boron concentration.
The development of OpenFOAM-based thermal hydraulics solvers (see
Section 5.2) provides sufficient tools for the modeling of a wide range of reactor coolants, including the helium gas flow in HTGRs. Models based on the porous medium approximation can be easily applied to both prismatic and pebble-bed type cores. Heat conduction through graphite can be accommodated into the same solver module.
The 1.5-dimensional model in the FINIX code enables the modeling of traditional cylindrical fuel rods used in conventional PWRs and BWRs, and the capabilities can be extended to MOX, ATF and other advanced fuels by implementing new correlations in the material libraries. Similar fuels are used in fast reactors, although accounting for the thermal expansion effects may require some additional work. The modeling of the micro-particle fuel used in HTGRs, however, requires more fundamental changes in the source code. The development of a thermomechanical particle fuel model has already been started. In the first development stage, the main objective is to provide realistic temperature distributions for pebble-bed and prismatic HTGR cores for the coupled solution.
5.5. REMS: A Response Matrix Solver for Reactor Dosimetry Applications
Nodal neutronics methods in the Ants code are not sufficient for the routine surveillance of the neutron dose on the reactor pressure vessel wall and other ex-core components. The Serpent code, on the other hand, is not a practical choice for such applications due to the high computational cost of the Monte Carlo simulation. As a solution, an alternative two-step reduced-order calculation scheme is being developed for reactor dosimetry. The deterministic code REMS relies on multi-group cross section data and nodal responses pre-calculated by Serpent. The responses are generated for nodes of Cartesian or hexagonal geometry with embedded meshes of different types in order to replicate as closely as possible the main geometrical features of the reactor core and surrounding structures. The dosimetry problem is then solved by coupling adjacent nodes via interface currents. The aim of REMS is to be able to model dosimeter activation and neutron dose during complex, multi-step irradiations.
REMS receives most of its input data from Serpent and does not provide any feedback to the core physics solution. The future plans to include REMS into the Kraken framework aim at the simultaneous validation of Serpent and REMS for dosimetry applications, as well as the transfer of pin power distributions from Serpent to REMS. Given that REMS is expected to run considerably faster than Serpent, a possibility also exists to quantify the effect of the Monte Carlo statistics on the deterministic dosimetry solution by executing REMS each time new response matrix data are written to external files by Serpent during a simulation.
6. Summary and Conclusions
In 2017, the VTT Technical Research Centre of Finland launched the development of Kraken, a new computational framework for solving the coupled core physics problem. The aim of the development is to replace VTT’s outdated legacy codes used for the deterministic safety analyses of Finnish power reactors but also to provide a modern calculation system for the modeling of SMRs and other emerging reactor technologies. Since the development is carried out by a new generation of experts, the project also has a considerable educational role. The work supports the efforts to maintain a high-level of national competence in reactor safety by providing source-code-level understanding on the tools and methods.
The Kraken framework is comprised of neutronics, thermal hydraulics and fuel behavior solvers, which can be coupled together to form various high-fidelity and reduced-order computational sequences. The neutronics solution relies on VTT’s Serpent Monte Carlo code, which can be used either for producing homogenized group constants for the new Ants nodal neutronics code, or as a high-fidelity solver in the coupled sequence. In the current setup, the thermal mechanical solution is provided by the FINIX fuel behavior module and the thermal hydraulics solution by the Kharon single-channel solver. The core physics solution can be further coupled to a system code, such as TRACE or Apros, which enables modeling the reactor core as part of the power plant process.
The development of the Kraken framework is still under way, and so far, the applications have been limited to verification and validation tasks, and the core design of VTT’s LDR-50 district heating SMR. Major near-term plans include implementing more advanced OpenFOAM based thermal hydraulics models into the coupled code sequence, and in general extending the capabilities of Kraken to new reactor types, in particular, high-temperature gas-cooled reactors.
Validation also plays a major role for future work, since the new calculation system is intended to be used for the independent safety analyses of Finnish reactors. This involves identifying suitable benchmarks and experimental data. The scope covers three separate fields of physics: neutronics, thermal hydraulics and fuel behavior, as well as the full coupled problem. Performing the analyses to demonstrate the quality requires considerable effort. Expanding the scope from conventional LWRs to emerging next-generation reactor technologies further complicates the validation, as the experimental data may be scarce or unavailable in the public domain.