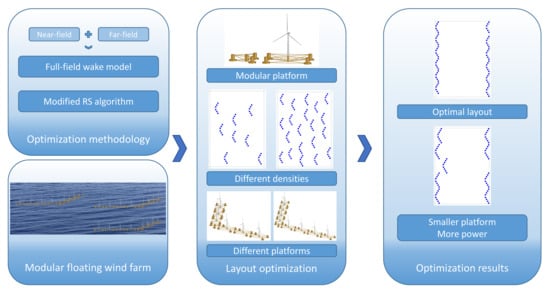
Layout Optimization of a Modular Floating Wind Farm Based on the Full-Field Wake Model
Abstract
:1. Introduction
2. Methodology of the Layout Optimization
2.1. Full-Field Wake Model
2.2. Optimization Algorithm
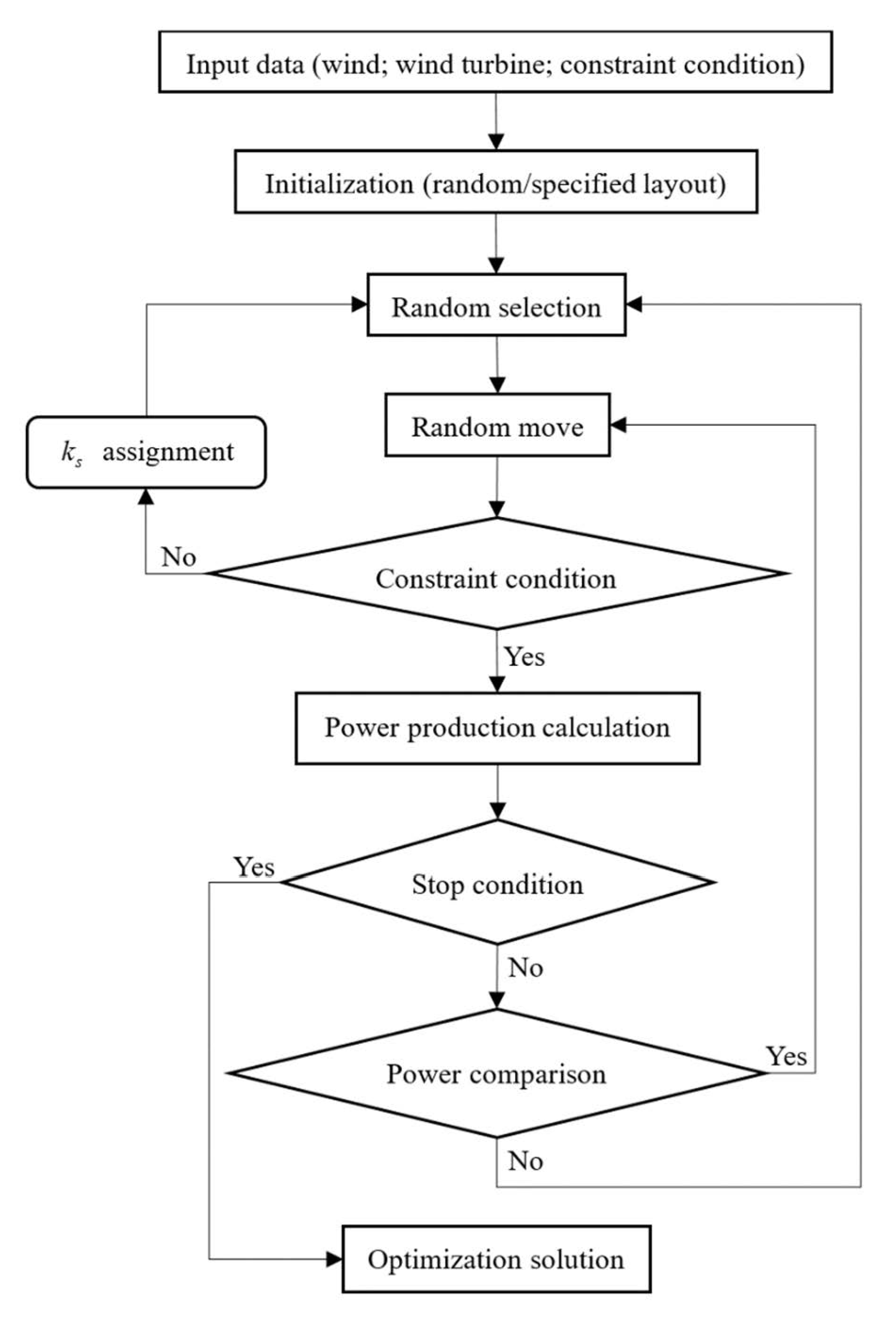
2.3. Optimization Framework
3. Layout Optimization of a Modular Floating Wind Farm
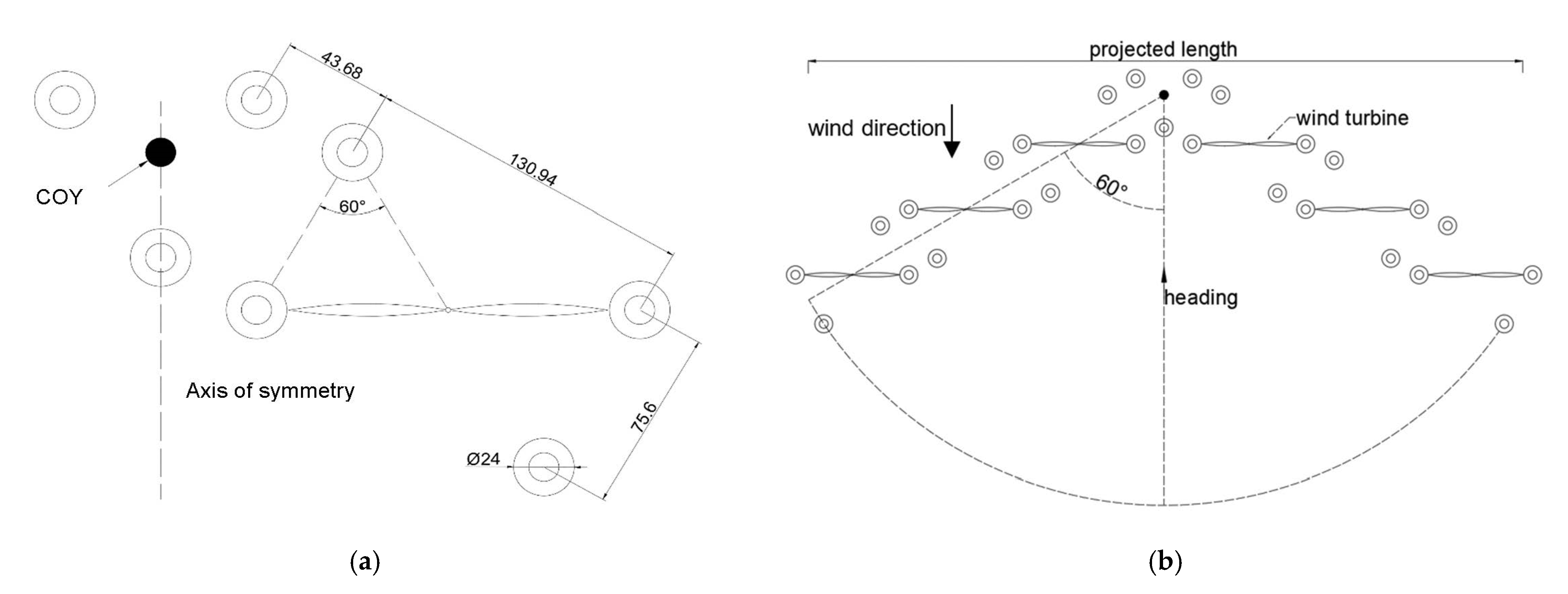
3.1. Structural Module
3.2. Problem Description
4. Results and Discussion
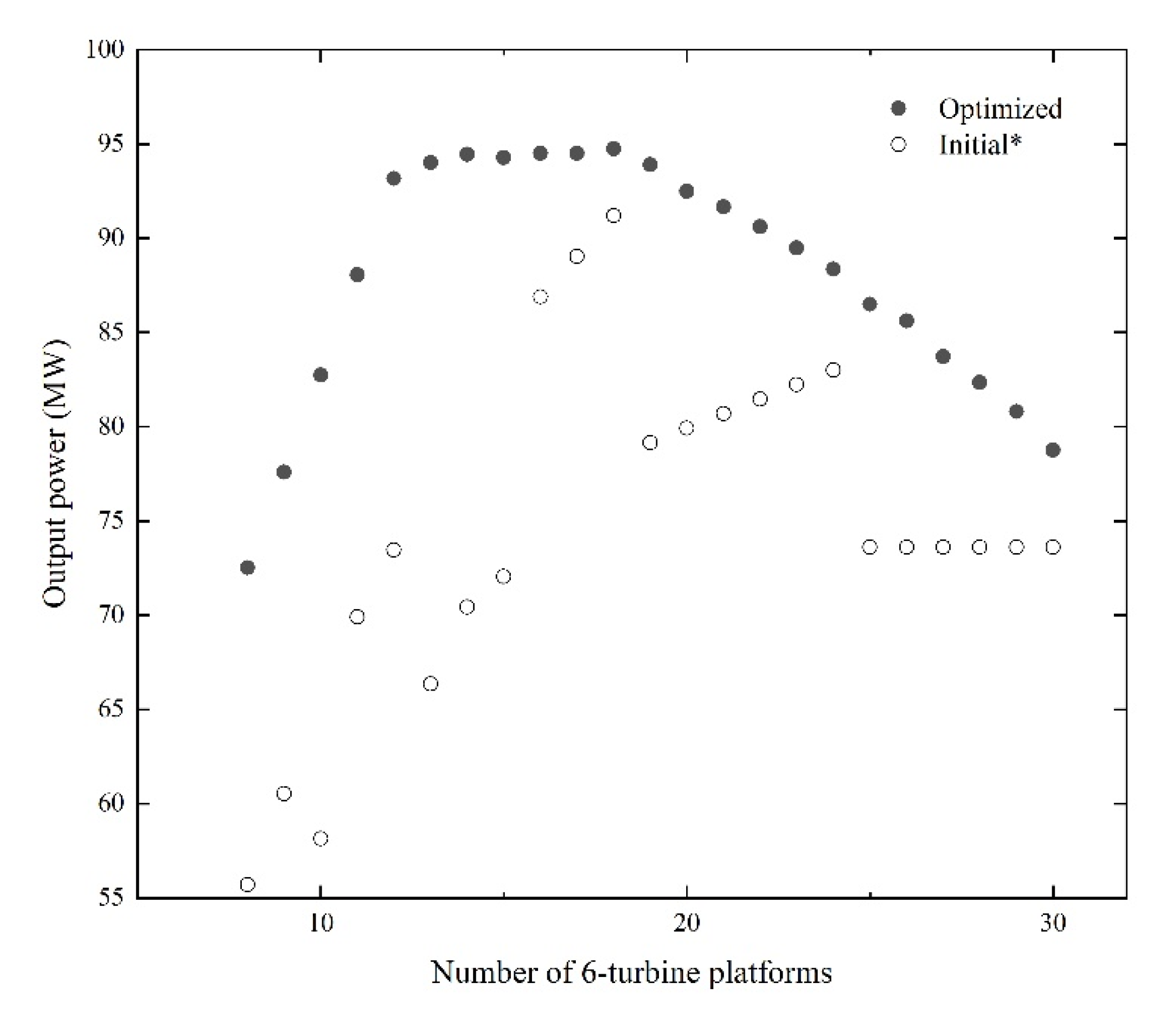
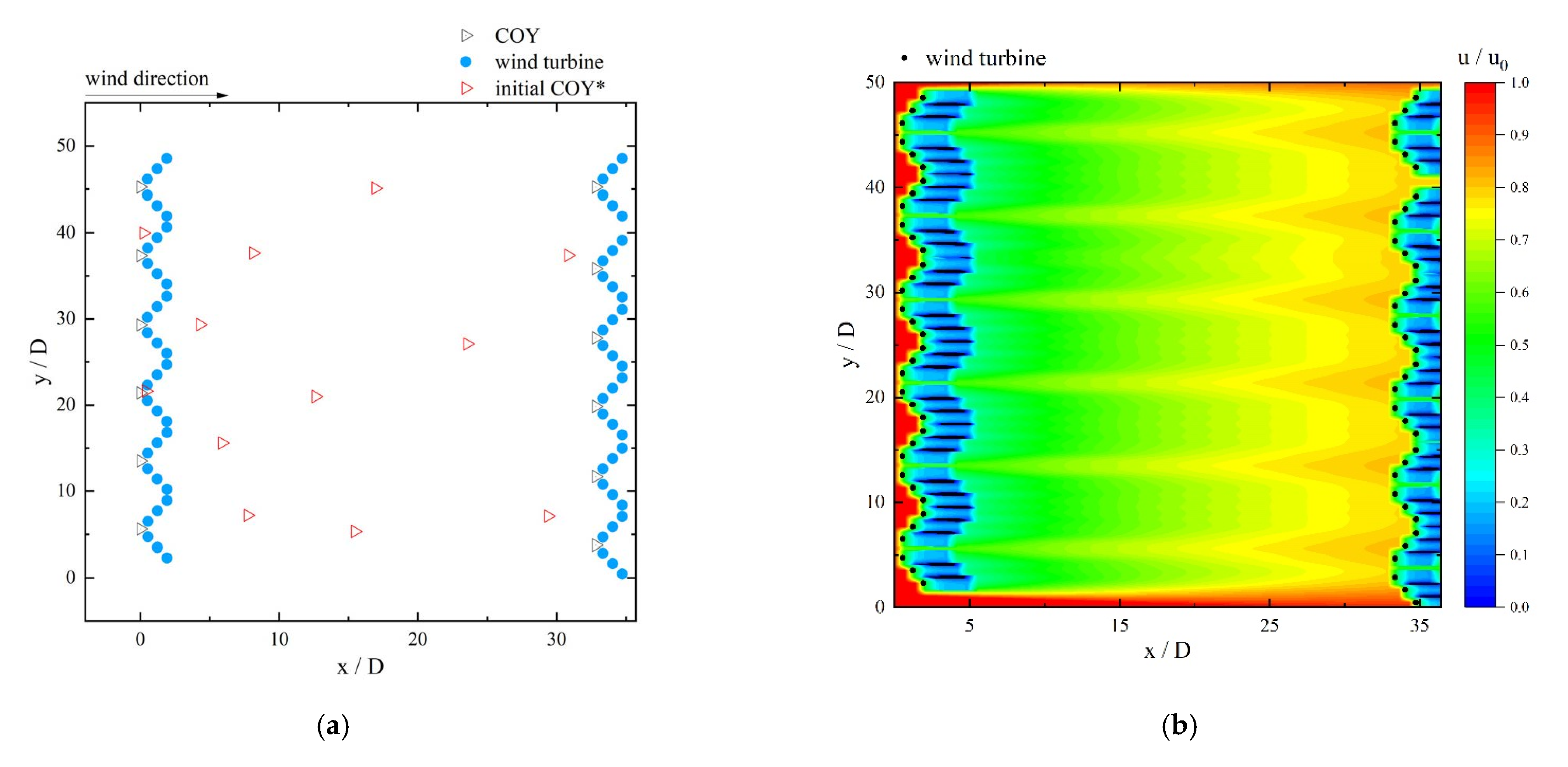
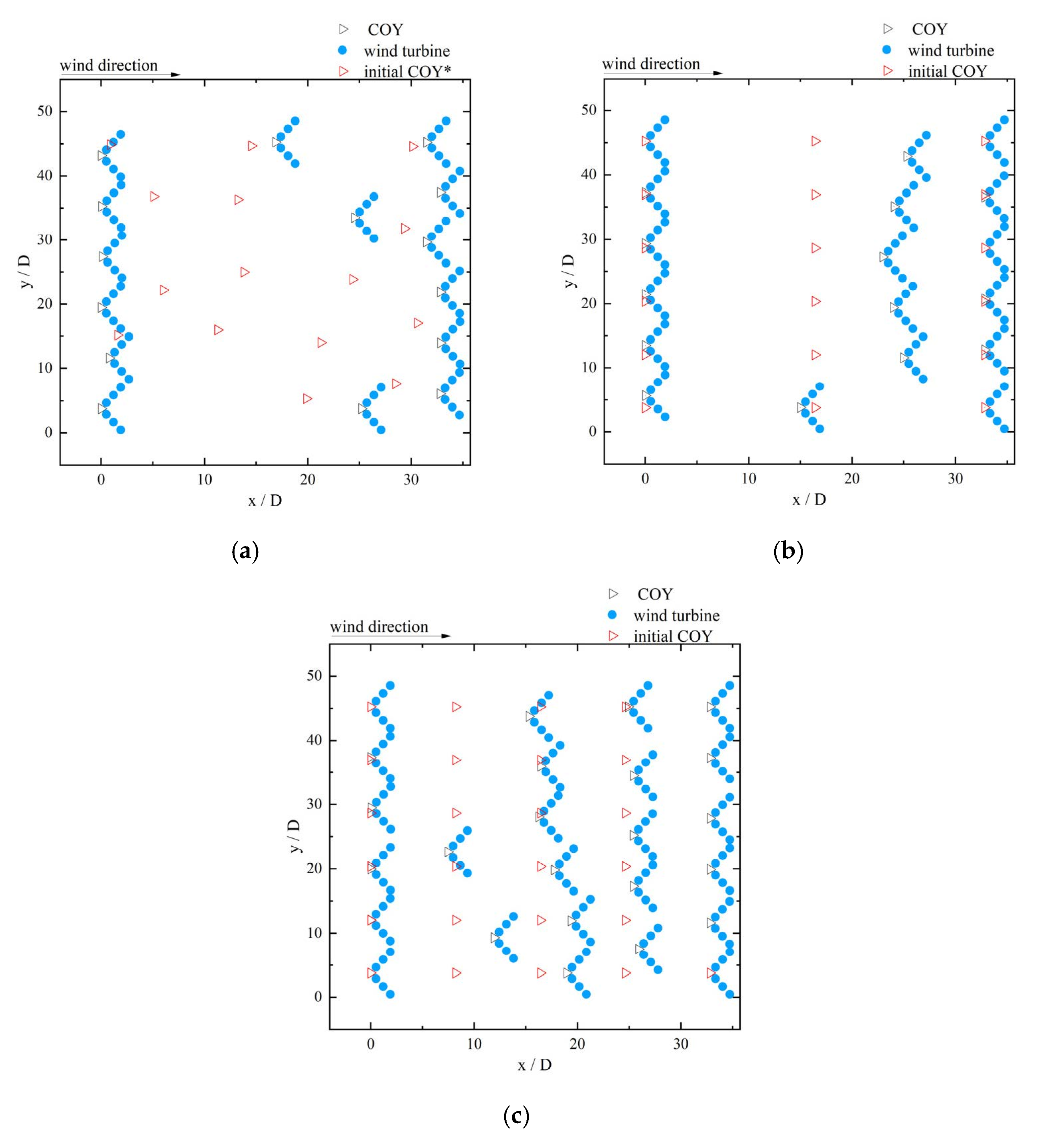
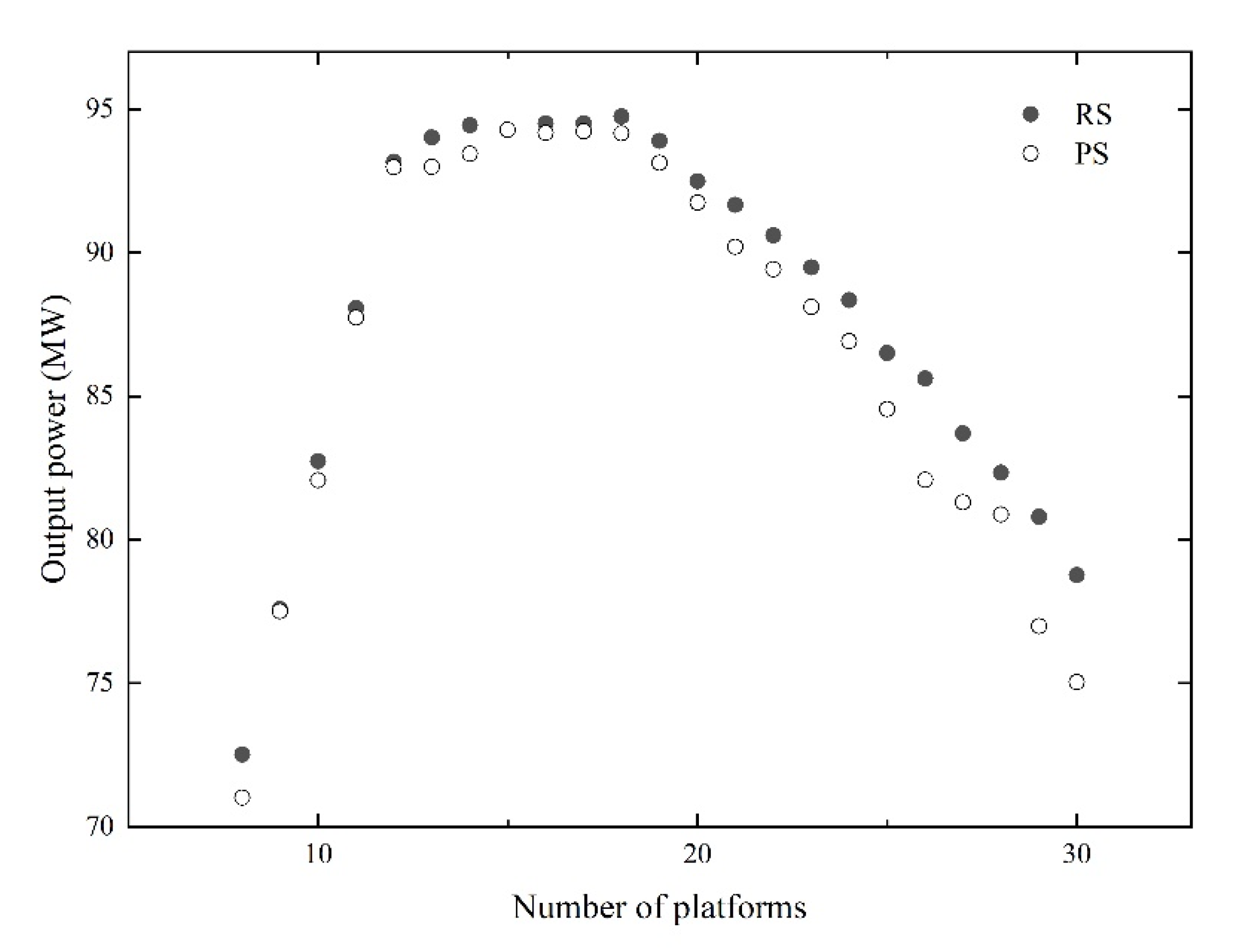
4.1. Optimization of Six-Turbine Platforms
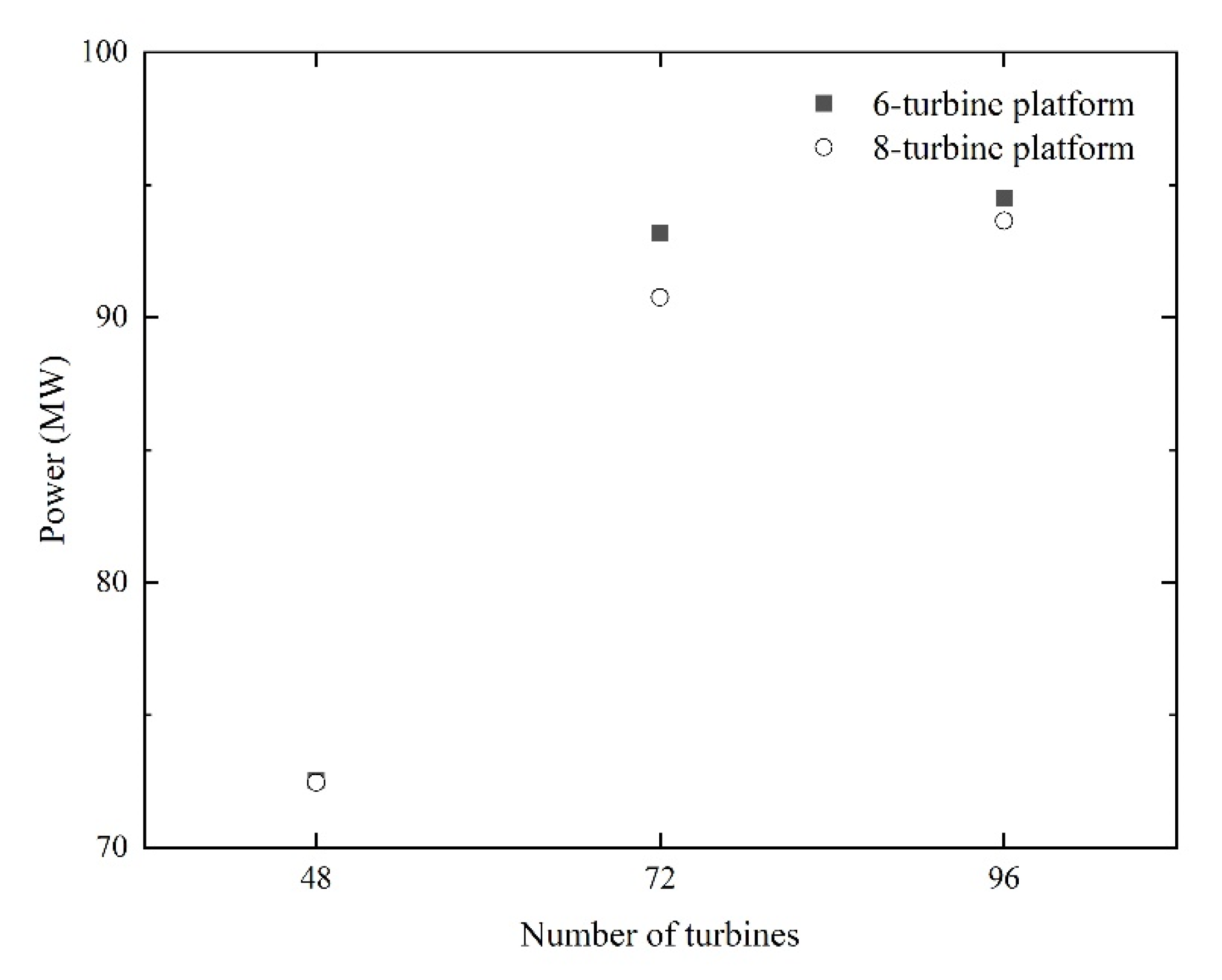
4.2. Optimization of Eight-Turbine Platforms
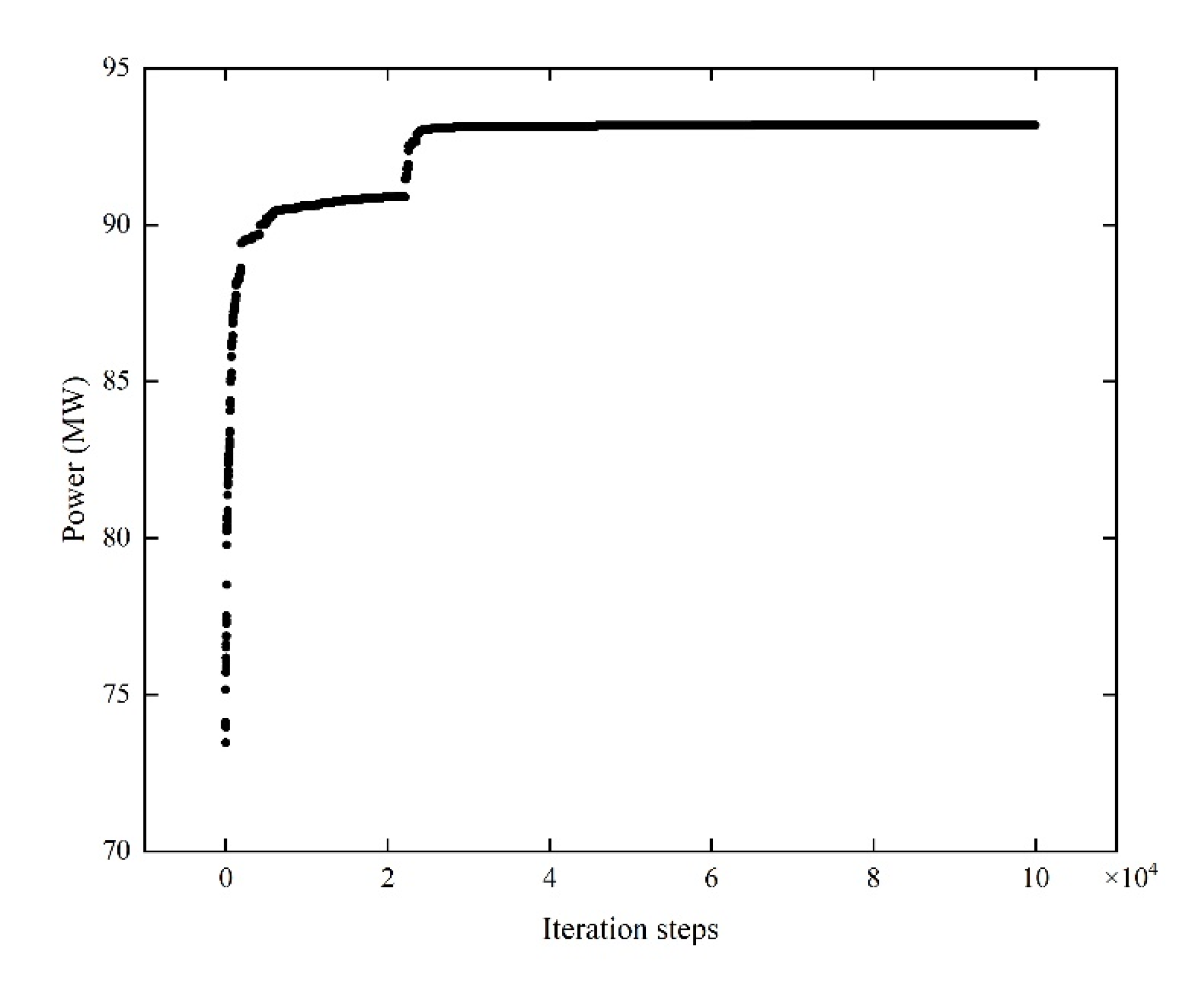
4.3. Comparison of Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | induction factor (dimensionless) |
| Ct | thrust coefficient (dimensionless) |
| D | rotor diameter (m) |
| dis | axial distance from the wind turbine to divide the near and far fields (m) |
| dmin | minimal distance between wind turbines or platforms (m) |
| dx | axial distance of the target point from the wind turbine (m) |
| H | hub height of the wind turbine (m) |
| I0 | freestream turbulence intensity (dimensionless) |
| krand | random number (dimensionless) |
| ks | scale factor (dimensionless) |
| Lmax | length of the long edge of the wind farm (m) |
| n | number of the wind turbines affecting the target point (dimensionless) |
| ns | number of steps of the infeasible random move before a feasible move (dimensionless) |
| nwt | total number of turbines in the wind farm (dimensionless) |
| P | power production of the wind turbine (kW) |
| Psum | power production of the wind farm (kW) |
| r | distance between the calculated point and the rotor shaft of the wind turbine in the radial direction (m) |
| rd | wake radius at d x (m) |
| ris | radial distance of the intersection (m) |
| ΔS | distance of a random move (m) |
| u | wake velocity of the calculated point (m/s) |
| u0 | freestream velocity (m/s) |
| x, y | wind turbine position in the wind direction & cross-wind direction, respectively (m) |
| z0 | surface roughness height (m) |
| Subscripts | |
| i, j | variables of the points or turbines i and j, respectively |
| m, * | variables after modification and before modification, respectively |
References
- Lee, J.; Zhao, F. Global Wind Report 2021; Global Wind Energy Council: Brussels, Belgium, 2021. [Google Scholar]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook, 2nd ed.; John Wiley & Sons: Chichester, UK, 2011; p. 619. [Google Scholar]
- Jensen, N.O. A Note on Wind Generator Interaction; Risø-M-2411; Risø National Laboratory: Roskilde, Denmark, 1983. [Google Scholar]
- Katic, I.; Højstrup, J.; Jensen, N.O. A Simple Model for Cluster Efficiency. In Proceedings of the European Wind Energy Association Conference and Exhibition, Rome, Italy, 7–9 October 1986. [Google Scholar]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-Turbine and Wind-Farm Flows: A Review. Bound-Lay. Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Larsen, G.C.; Højstrup, J.; Madsen, H.A. Wind fields in wakes. In Proceedings of the 1996 European Union Wind Energy Conference, Göteborg, Sweden, 20–24 May 1996. [Google Scholar]
- Frandsen, S.; Barthelmie, R.; Pryor, S.; Rathmann, O.; Larsen, S.; Højstrup, J.; Thøgersen, M. Analytical modelling of wind speed deficit in large offshore wind farms. Wind Energy 2006, 9, 39–53. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. A new analytical model for wind-turbine wakes. Renew. Energy 2014, 70, 116–123. [Google Scholar] [CrossRef]
- Tian, L.; Zhu, W.; Shen, W.; Zhao, N.; Shen, Z. Development and validation of a new two-dimensional wake model for wind turbine wakes. J. Wind Eng. Ind. Aerodyn. 2015, 137, 90–99. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Huang, P.; Sun, H. A Novel Analytical Wake Model with a Cosine-Shaped Velocity Deficit. Energies 2020, 13, 3353. [Google Scholar] [CrossRef]
- Liu, H.; Fu, J.; Liang, Z.; Zhang, Y.; Liang, Z.; Xiao, Z. A simple method of fast evaluating full-field wake velocities for arbitrary wind turbine arrays on complex terrains. Renew. Energy 2021. submitted. [Google Scholar]
- Mosetti, G.; Poloni, C.; Diviacco, B. Optimization of wind turbine positioning in large windfarms by means of a genetic algorithm. J. Wind. Eng. Ind. Aerodyn. 1994, 51, 105–116. [Google Scholar] [CrossRef]
- Beyer, H.G.; Rüger, T.; Schäfer, G.; Waldl, H.P. Optimization of wind farm configurations with variable number of turbines. In Proceedings of the European Union Wind Energy Conference, Göteborg, Sweden, 20–24 May 1996. [Google Scholar]
- Grady, S.A.; Hussaini, M.Y.; Abdullah, M.M. Placement of wind turbines using genetic algorithms. Renew. Energy 2005, 30, 259–270. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W.Z. Optimization of Wind Farm Layout: A Refinement Method by Random Search. In Proceedings of the 2013 International Conference on aerodynamics of Offshore Wind Energy Systems and wakes, Lyngby, Denmark, 17–19 June 2013. [Google Scholar]
- Feng, J.; Shen, W.Z. Solving the wind farm layout optimization problem using random search algorithm. Renew. Energy 2015, 78, 182–192. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W.Z. Co-optimization of the shape, orientation and layout of offshore wind farms. J. Phys. Conf. Ser. 2020, 1618, 42023. [Google Scholar] [CrossRef]
- Hwang, B.; Kim, H.; Lee, S. Wind farm layout optimization using multidisciplinary model. J. Mech. Sci. Technol. 2018, 32, 2919–2924. [Google Scholar] [CrossRef]
- Kirchner-Bossi, N.; Porté-Agel, F. Realistic Wind Farm Layout Optimization through Genetic Algorithms Using a Gaussian Wake Model. Energies 2018, 11, 3268. [Google Scholar] [CrossRef] [Green Version]
- Farajifijani, R.; Ahmadian, S.; Ebrahimi, S.; Ghotbi, E. Wind Farm Layout Optimization Problem Using Joint Probability Distribution of CVaR Analysis. In Proceedings of the 2019 IEEE 9th Annual Computing and Communication Workshop and Conference, Las Vegas, NV, USA, 7–9 January 2019; pp. 7–12. [Google Scholar]
- Zhang, J.; Jiang, Y. Joint optimization of the number, type and layout of wind turbines for a new offshore wind farm. J. Renew. Sustain. Energy 2020, 12, 053308. [Google Scholar] [CrossRef]
- Shin, J.; Baek, S.; Rhee, Y. Wind Farm Layout Optimization Using a Metamodel and EA/PSO Algorithm in Korea Offshore. Energies 2021, 14, 146. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, A.G.; Serrano-González, J.; Burgos-Payán, M.; Riquelme-Santos, J.M. Realistic Optimization of Parallelogram-Shaped Offshore Wind Farms Considering Continuously Distributed Wind Resources. Energies 2021, 14, 2895. [Google Scholar] [CrossRef]
- Kheirabadi, A.C.; Nagamune, R. Modeling and Power Optimization of Floating Offshore Wind Farms with Yaw and Induction-based Turbine Repositioning. In Proceedings of the 2019 American Control Conference, Philadelphia, PA, USA, 10–12 July 2019; pp. 5458–5463. [Google Scholar]
- Serrano González, J.; Burgos Payán, M.; Riquelme Santos, J.M.; González Rodríguez, Á.G. Optimal Micro-Siting of Weathervaning Floating Wind Turbines. Energies 2021, 14, 886. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H. A Novel Structural Configuration of Modular Floating Wind Farms with Self-Adaptive Property. J. Offshore Mech. Arct. Eng. 2021, 143, 052002. [Google Scholar] [CrossRef]
- Brogna, R.; Feng, J.; Sørensen, J.N.; Shen, W.Z.; Porté-Agel, F. A new wake model and comparison of eight algorithms for layout optimization of wind farms in complex terrain. Appl. Energy 2020, 259, 114189. [Google Scholar] [CrossRef]
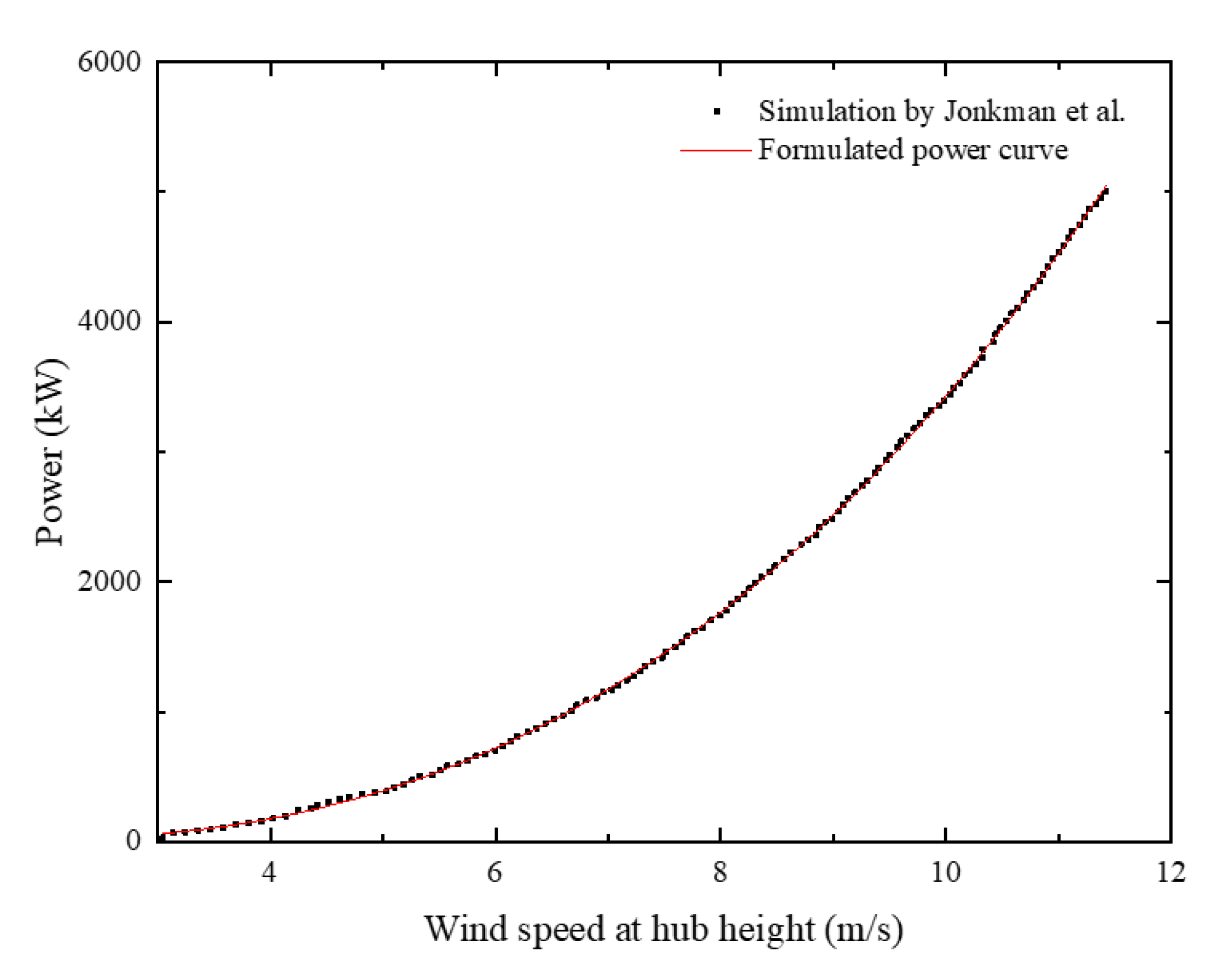
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; NREL/TP-500-38060; National Renewable Energy Laboratory: Golden, CO, USA, 2009.
- Hansen, K.S.; Barthelmie, R.J.; Jensen, L.E.; Sommer, A. The impact of turbulence intensity and atmospheric stability on power deficits due to wind turbine wakes at Horns Rev wind farm. Wind Energy 2012, 15, 183–196. [Google Scholar] [CrossRef] [Green Version]
- Westerhellweg, A.; Cañadillas, B.; Kinder, F.; Neumann, T. Wake Measurements at alpha ventus—Dependency on Stability and Turbulence Intensity. J. Phys. Conf. Ser. 2014, 555, 12106. [Google Scholar] [CrossRef] [Green Version]
| Earlier Study | Wake Model | Optimization Algorithm | Feature | |
|---|---|---|---|---|
| Distribution | Number of Turbines | |||
| Mosetti et al. [12] | Jensen | GA | grid | variable |
| Beyer et al. [13] | Jensen | GA | grid | variable |
| Grady et al. [14] | Jensen | GA | grid | variable |
| Feng and Shen [15,16,17] | Jensen | RS | coordinate | specified or fixed |
| Hwang et al. [18] | Larsen | NSGA2 | coordinate | fixed |
| Kirchner-Bossi and Porté-Agel [19] | Gaussian | GA | coordinate | fixed |
| Farajifijani et al. [20] | Jensen | fmincon | coordinate | fixed |
| Zhang and Jiang [21] | Jensen | IQPSO | coordinate | variable |
| Shin et al. [22] | Jensen | EA, PSO | coordinate | fixed |
| Gonzalez-Rodriguez et al. [23] | Jensen | NGEA | coordinate | fixed |
| Kheirabadi and Nagamune [24] | modified FLORIS | SQP | coordinate | fixed |
| González et al. [25] | Frandsen | GA | coordinate | fixed |
| Type of Platforms | Number of Platforms | Number of Turbines |
|---|---|---|
| 6-turbine | 8–30 | 48, 54, 60, …, 180 |
| 8-turbine | 6, 9, 12 | 48, 72, 96 |
| Parameter | Value |
|---|---|
| 8 | |
| 0.003 | |
| 0.07 | |
| 0.97 | |
| 90 | |
| 126 | |
| [0, 4410] | |
| [0, 6174] | |
| of 6-turbine platform | 994.78 |
| of 8-turbine platform | 1311.78 |
| Number of Turbines | Power (kW) | |
|---|---|---|
| 6-Turbine Platform | 6-Turbine Platform | |
| 48 | 72,524.39 | 72,448.36 |
| 72 | 93,167.43 | 90,752.69 |
| 96 | 94,506.95 | 93,635.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Liu, H. Layout Optimization of a Modular Floating Wind Farm Based on the Full-Field Wake Model. Energies 2022, 15, 809. https://doi.org/10.3390/en15030809
Liang Z, Liu H. Layout Optimization of a Modular Floating Wind Farm Based on the Full-Field Wake Model. Energies. 2022; 15(3):809. https://doi.org/10.3390/en15030809
Chicago/Turabian StyleLiang, Zhichang, and Haixiao Liu. 2022. "Layout Optimization of a Modular Floating Wind Farm Based on the Full-Field Wake Model" Energies 15, no. 3: 809. https://doi.org/10.3390/en15030809
APA StyleLiang, Z., & Liu, H. (2022). Layout Optimization of a Modular Floating Wind Farm Based on the Full-Field Wake Model. Energies, 15(3), 809. https://doi.org/10.3390/en15030809