Machine Learning Approach for Maximizing Thermoelectric Properties of BiCuSeO and Discovering New Doping Element

Abstract

Machine learning (ML) has increasingly received interest as a new approach to accelerating development in materials science. It has been applied to thermoelectric materials research for discovering new materials and designing experiments. Generally, the amount of data in thermoelectric materials research, especially experimental data, is very small leading to an undesirable ML model. In this work, the ML model for predicting ZT of the doped BiCuSeO was implemented. The method to improve the model was presented step-by-step. This included normalizing the experimental ZT of the doped BiCuSeO with the pristine BiCuSeO, selecting data for the BiCuSeO doped at Bi-site only, and limiting important features for the model construction. The modified model showed significant improvement, with the R² of 0.93, compared to the original model (R² of 0.57). The model was validated and used to predict the ZT of the unknown doped BiCuSeO compounds. The predicted result was logically justified based on the thermoelectric principle. It means that the ML model can guide the experiments to improve the thermoelectric properties of BiCuSeO and can be extended to other materials.

1. Introduction

Electricity consumption is increasing continuously as a result of technological progress. Thermoelectric is one of the interesting alternative energy technologies, which can convert heat to electricity and vice versa. This technology provides many benefits, such as environmentally friendly energy sources, scalability, and silent operation. Unfortunately, the generic thermoelectric bulk modules perform with an efficiency of about 3–5% [1], which is lower than other alternative energy sources such as solar cells with an efficiency of up to 30% [2]. In order to develop a better thermoelectric performance, thermoelectric materials, the heart of the technology, need to be better developed. The key performance of thermoelectric materials is determined from the dimensionless Figure-of-Merit (ZT), defined as ZT = $\frac{S^2\sigma }{k}T$ [3] where T, σ S, and k are the absolute temperature, electrical conductivity, Seebeck coefficient, and thermal conductivity, respectively. Various methods have been investigated to enhance ZT, and thus, the performance of the material.

Traditional approaches to investigate thermoelectric materials are by experiments and computational methods based on density functional theory (DFT). In general, experimenting requires expertise, instrument, and advanced technology, which consume considerable resources. Furthermore, it is difficult to control overall variables and may require a long acquisition period. Alternatively, the computational simulation needs less time and is profitable in complete control over the essential variables. Nonetheless, there are also many challenges for the DFT simulation related to microstructures of material. It needs high-performance computing apparatus, usually in large computing clusters, which is difficult to be accessed by individuals. Additionally, the simulation was merely employed to some specific systems and required approximations to minimize runtime on complex systems. To accelerate the development and discovery of novel thermoelectric materials, machine learning (ML) becomes an attractive approach. ML is a data-driven method that utilizes statistical mathematics to analyze the data. It can predict micro and macro properties and the correlation between the parameters of the materials [4].

To accelerate the material research, advances and applications of ML have been developed continuously [4,5,6,7]. The ML was currently supported by several online databases, algorithms, and frameworks [8,9]. The ML model for predicting materials properties was usually implemented via a classical algorithm, such as regression, determined by $y_i=a_0+a_1{x}_1+a_2{x}_2+\dots +a_n{x}_n$, i = 1, 2, … n, where $y_i$ is the target or predicting value, a_i is the regression coefficient automatically calculated by an ML algorithm, and x_i is the feature or descriptor for representing the character of materials. Even though there are many ways to generate the features, Magpie is the software that originates features for material science by using physical properties. They are operated with mathematics requiring only chemical formula [10]. Furthermore, the features have the potential to build an ML model with advantages in a comfortable and quick method for searching new candidate materials [11,12]. With many advantages, ML has the potential to be a new approach to accelerate the discovery of thermoelectric material with high performance.

Related Work

Recently, ML applications in thermoelectric materials have been increasingly investigated due to high accuracy and less time-consuming. For example, Iwasaki et al. reported the ML model that accelerated the discovery of new candidate materials by generating features from the chemical formula confirmed with the experiment [12]. In their investigation for the spin-driven thermoelectric effect (STE) device, the descriptors for training the ML model were generated automatically from the composition with a composition-based feature vector (CBFV) [13]. The results showed that some features, such as atomic weight, spin, and orbital angular momenta, play an important role in thermopower. In addition, Wang et al. studied the Cu_xBi₂Te_2.85+ySe_0.15 system with ML [14]. The correlation between microstructure and thermoelectric properties was investigated with the principal component analysis (PCA) and the regression algorithm. Furthermore, apart from predicting the properties of new materials, ML could design the experimental conditions to obtain a high ZT value. Hou et al. presented an effective way to find the optimal chemical composition of the Al₂Fe₃Si₃ thermoelectric compound [15]. With the Bayesian Optimization (BO) algorithm, ML can be applied to the experiment effectively. The power factor can be improved by about 40% compared to the sample with the initial Al/Si ratio of 0.9. Moreover, the author claimed that the framework of this study could be extended to the extrinsic doping of Al₂Fe₃Si₃. These related works can be summarized in

Table 1. Summary of the research investigating thermoelectric properties with ML.

Datasets	Input	Output	R2	Remark	Ref.
112	temperature, chemical potential, atomic radius, etc.	Thermopower	-	Thermopower improved an order of magnitude	[13]
17	chemical composition	ZT	0.99	design experiment condition providing high ZT	[14]
5	Al/Si ratio	Power factor	-	increase 40% of power factor	[15]

.

The previous related research generally exploited the data from the first principle calculation or from one laboratory. Our present work made a contribution over the previous related research by exploring the experimental datasets available in literature to construct the ML model. We then used the model to predict the thermoelectric properties of BiCuSeO. BiCuSeO is a class of thermoelectric oxides considered a new candidate for high-performance p-type thermoelectric materials [16]. Even though the material was only discovered in 2010, thermoelectric researchers have paid much attention to this compound, and continuous publications have been reported since then [17,18,19,20,21,22,23,24]. This compound has a complex ZrSiCuAs layered structure, as shown in Figure 1. It consists of the conducting (Cu₂Se₂)²⁻ layers alternatively stacked by the insulating (Bi₂O₃)²⁺ layers. Due to distinct functionalities and the weak bonding between these two layers, BiCuSeO showed outstanding thermoelectric properties and outperformed most thermoelectric oxides [25]. Therefore, intense research interest is focusing on BiCuSeO to lift the thermoelectric performance and ZT even higher. The most common approach to enhance ZT is by extrinsic doping some elements into the BiCuSeO structure to lower thermal conductivity, increase carrier concentration, and optimize electrical transport properties [25,26,27]. Nevertheless, since there are numerous available dopants, tedious experiments are required. Therefore, ML could be a wise choice to address the issue by providing guidance for appropriate effective doping of BiCuSeO.

In this work, the ML model was constructed to provide the guidelines for effective doping of the BiCuSeO system. The ML model was built and tested by collecting data from available published articles (2010–present). Step-by-step, we improved the accuracy of our model so that the predicted ZT value from the model closely matched with the experiment. We then extracted the features/descriptors representing the characteristics of materials and discussed their correlation to the physical parameters of the materials. Finally, we used the ML model to predict the suitable dopants in the BiCuSeO system, which can improve thermoelectric properties and lift the ZT of the doped compound with respect to the pristine BiCuSeO. We truly believe that our work and technique would be very useful for experimental researchers working to improve the thermoelectric properties of the BiCuSeO compounds.

2. Materials and Methods

Thermoelectric databases for the BiCuSeO compounds were collected from published articles from 2010 to the present (available in the supplementary information, Table S1). They were then tabulated in Excel for the convenience to import into the Jupyter Notebook software. The descriptors or features for building classical ML models were generated from the collected chemical formula via Magpie. The physical and chemical properties of the element were manipulated by mathematical operators, such as average, summation, min, mode, max, and median, and a total of 154 features were obtained. Then, the total datasets were split into a training set (85%) and a test set (15%). The training set was used to teach ML to find the pattern of the data, whereas the test set was used to test the accuracy of the model. Due to the small size of datasets compared to other ML research in materials science [11], the models were built by using different regression algorithms [28], namely, forest regression (RF), Gradient Boosting Regressor (GBR), kneighbor regressor (KN), extraboost tree (ET) and xgboost (XGB). These regression algorithms were determined from a simple linear relationship according to:

$$y_i=a_0+a_1{x}_1+a_2{x}_2+\dots +a_n{x}_n,i=1,2,\dots n,$$

(1)

where $y_i$ is the target or predicting value, a_i is the regression coefficient automatically calculated by an ML algorithm, and x_i is the features or descriptors for representing the character of materials. The algorithm which showed the best performance was selected.

Two metrics were used to evaluate the model’s accuracy, i.e., (1) the coefficient of determination (R²) and (2) the root mean squared error (RMSE). The R² was determined by:

$$R^2=1-\frac{SSE}{SST},$$

(2)

where

$$SSE={{\displaystyle \sum }}_{i=1}^n{\left\{y_i-\widehat{y_i}\right\}}^2,$$

and

$$\mathrm{SST}={{\displaystyle \sum }}_{i=1}^n{\left\{y_i-\overline{y},\right\}}^2$$

and the RMSE was determined by:

$$RMSE=\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2 }$$

(3)

where $y_i$, $\widehat{y_i}, \mathrm{and} \overline{y}$ are defined as experimental, predicted, and average target value or ZT.

The features or descriptors that are important to the model were exposed automatically via the function method from the regression model. Additionally, before bringing the model to use, a final step was to validate the model by Leave One Out Cross Validation (LOOCV). Finally, we used our ML model to predict the ZT value of the BiCuSeO compounds doped at the Bi site (Bi_1-xA_xCuSeO, where A is the dopant and x was set to 0.02). To discover a candidate to maximize the ZT value, the dopant (element A) was not in the original datasets and could possibly be done by experiments. Converting the materials into the numerical feature vectors benefits thermoelectric material researchers to build the ML model and discover new candidate material with the only chemical formula.

In the next section, we presented the results for improving the ML model step-by-step until obtaining the desirable ML model. The processes along with the thermoelectric principle of BiCuSeO material were discussed.

3. Results and Discussions

Firstly, the data of BiCuSeO research reporting ZT values were extracted from literature (a total of 264 datasets). Then, the ML model was constructed using CBFV to generate 154 features from the chemical formula. Due to relatively small datasets compared to other ML research in materials science [11], several regression algorithms were employed. The algorithm which showed the best performance was selected.

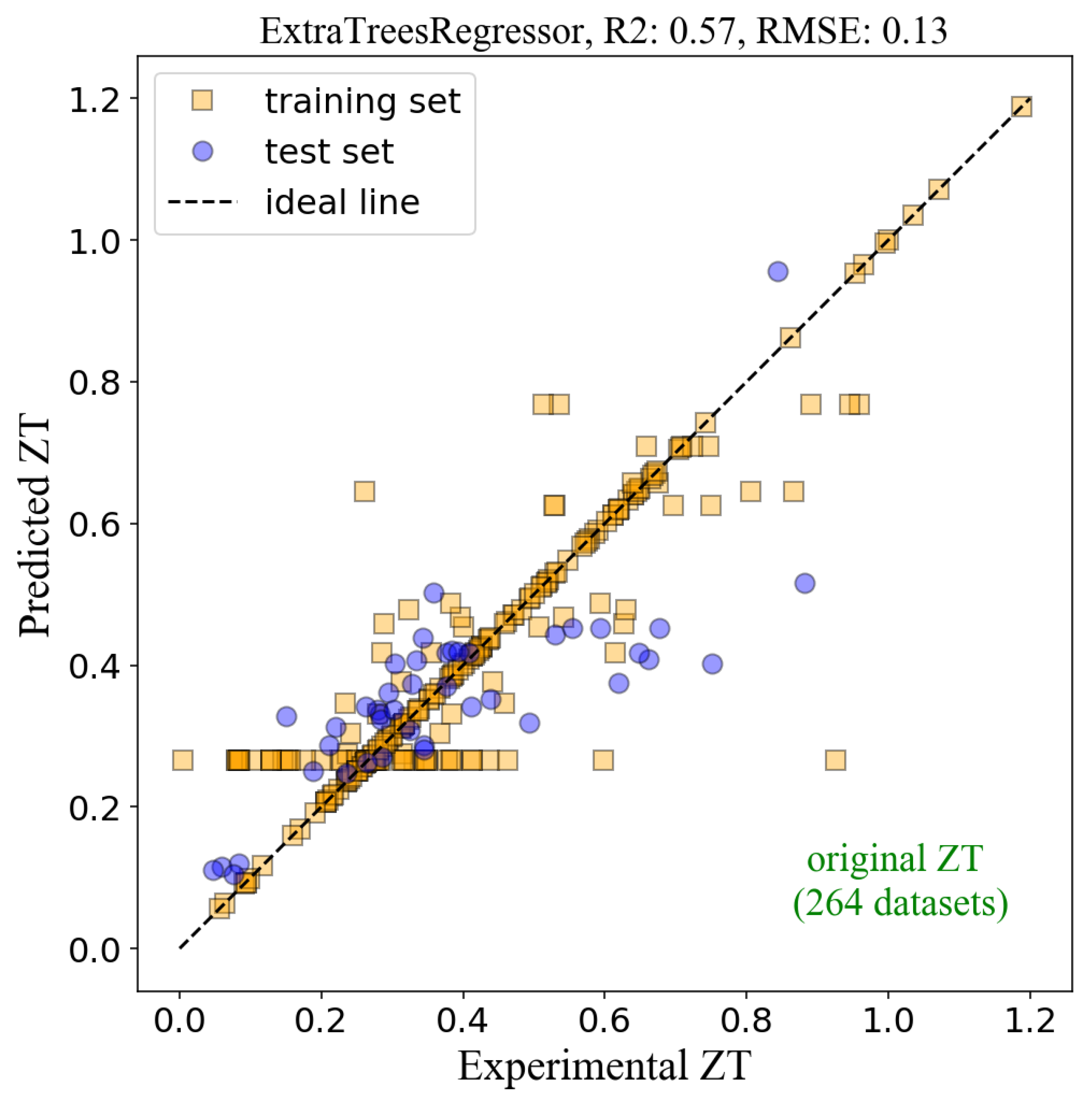
The results from the ML model are plotted in Figure 2. The x-axis is the experimental ZT, referring to the reported ZT values extracted from the literature. The y-axis is called the ‘predicted ZT’, the ZT values predicted from the ML model based on the exact chemical formula of BiCuSeO compounds. All related features (a total of 154 features) were included in the model. The orange circles represent data from the training set, whereas the blue squares refer to data from the test set. The dotted line plotted as a guide-to-eyes is an ideal line when the predicted value perfectly matches the experiment. We evaluated the accuracy of the model using two metrics: (1) the coefficient of determination (R²), and (2) the root mean squared error (RMSE). R² accounts for how well the model can capture the correlation between the features and the ZT value, whereas RMSE is used to evaluate the model accuracy regarding the error from prediction. The perfect fit would result in the R² of 1 and RMSE of 0.

Figure 2 shows the R² of 0.57 and the RMSE of 0.13 from the test set. The R² value is relatively low, implying that the model is not very accurate. The model inaccuracy lies in the original data from the experiment database. The reported ZT values of the pristine BiCuSeO from several research groups varied significantly. For example, Farooq et al. reported the ZT of 0.25 [29], but Yang et al. reported the ZT of 0.42 [30] for the same compound (BiCuSeO). These points are explicitly shown in Figure 2, where the orange squares line up horizontally at the ‘predicted ZT’ around 0.3. The discrepancy was due to the experimental details, such as processing parameters, microstructures, etc., which strongly affect the ML performance because the ML models were trained with the features that were extracted from chemical formulas only. The variations from experimental parameters were not included in the ML model, resulting in the model’s inaccuracy.

To improve the model’s accuracy, we had to eliminate the experimental dependent variables. To do that, we normalized the experimental ZT by the ZT of the pristine BiCuSeO from each publication. For instance, Farooq et a. reported the ZT of BiCuSeO and Bi_0.99Cd_0.01CuSeO of 0.25 and 0.43 [29], while Yang reported the ZT of BiCuSeO and Bi_0.98Pb_0.02CuSeO of 0.42 and 0.66 [30]. By normalizing, the ‘experimental ZT_normalized’ of Farooq’s BiCuSeO and Bi_0.8Cd_0.2CuSeO became 1.0 and 1.72, whereas ‘experimental ZT_normalized’ of Yang’s BiCuSeO and BiCu_0.8Zn_0.2SeO were 1.0 and 1.57. The normalization can be determined as $Z{T}_{normalized}=\frac{Z{T}_{doped}}{Z{T}_{undoped}}$. In other words, by using this process, the ‘experimental ZT_normalized’ of the pristine BiCuSeO from any publication was turned into unity. The ‘experimental ZT_normalized’ of the doped BiCuSeO thus indicated the ratio of improvement between the doped BiCuSeO and the pristine BiCuSeO. The ML model was then reconstructed such that the ZT was only related to the chemical formulas, and other experimental dependent variables were eliminated.

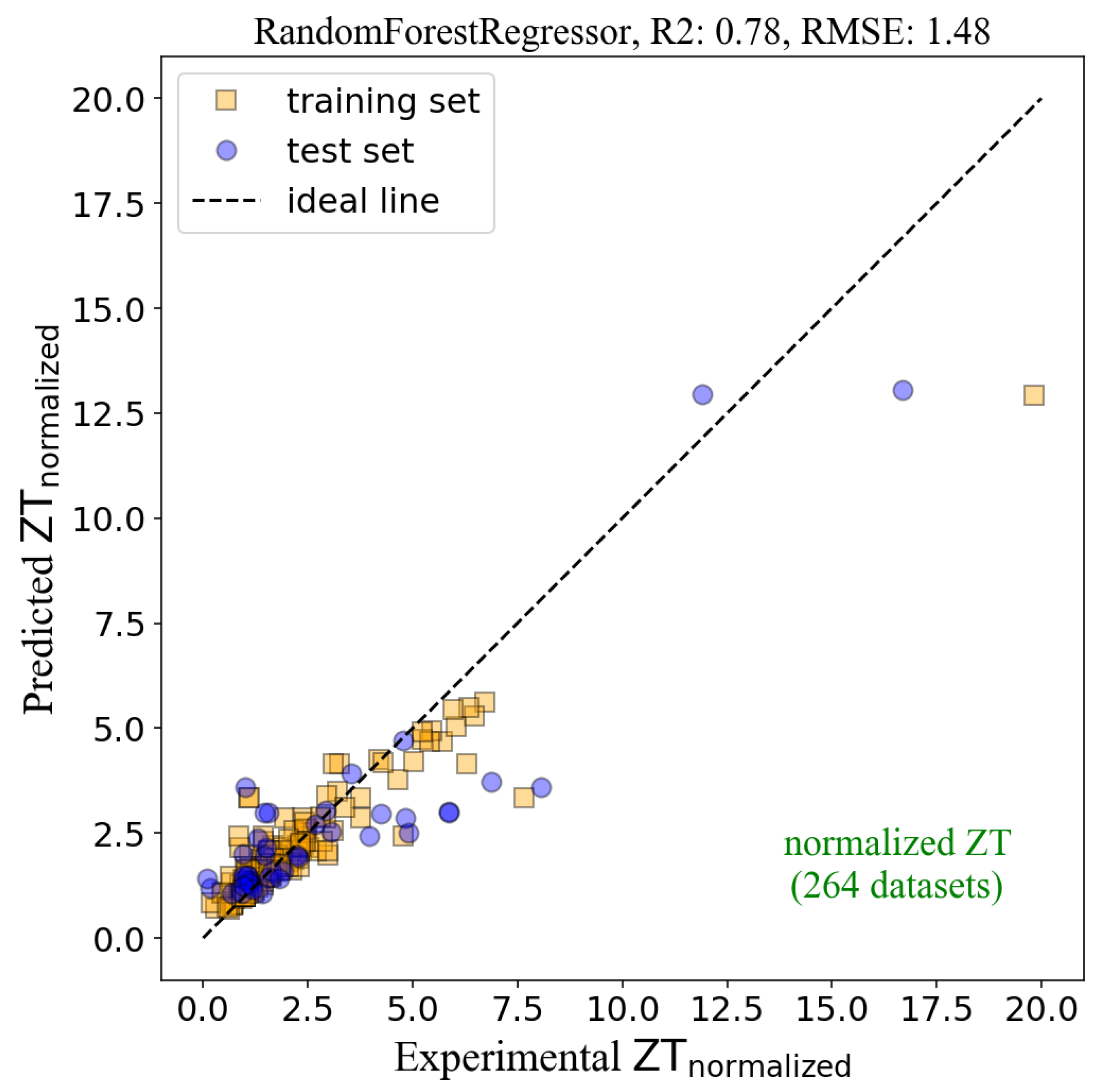
The results from the ML model after normalizing all 264 datasets are presented in Figure 3, with the R² of 0.78 and RMSE of 1.48 for the test set. The R² of 0.78 in Figure 3 is larger than the R² of 0.57 in Figure 2, indicating the improvement of the model’s accuracy. However, the higher RMSE (1.48) in Figure 3 compared to Figure 2 (RMSE = 0.13) does not mean that its prediction’s error is worse. In fact, it is incorrect to compare the RMSE between the two figures because the data ranges are not the same. The scales in both axes in Figure 2 range between 0 and 1.2, whereas Figure 3 ranges from 0 to 20.0. Hence, it is expected that the RMSE in Figure 3 tends to be higher.

Although the R² for the ML model in Figure 3 is relatively high, there are still outliers that deviated from the ideal line, for instance, the orange square and the blue circle on the right of the figure, leading to the reduction of R². This situation occurred even when the selected features in the model were already optimized. Therefore, we tried improving our ML model further by analyzing the original datasets. We found that the outliers and inaccuracy of the model could be from the different doping sites in the BiCuSeO compound. In general, doping elements in BiCuSeO is done by substituting atoms at different sites, written in a chemical formula Bi_1-xA_xCu_1-yB_ySe_1-zC_zO_1-wD_w, where A, B, C, and D are dopants. Sometimes, dual dopings were done at one or more sites. The purpose of doping in each site is different, such as lowering thermal conductivity, bandgap engineering, and tuning electrical transport properties [17]. We assumed that our ML model could not capture the pattern from the data including all variations. Therefore, we analyzed the data and grouped the datasets into a few sub-groups. The major sub-group (145datasets) was the BiCuSeO compound doped at the Bi site (Figure 1), for instance, Bi_0.98K_0.02CuSeO [31]. This group is vital from the thermoelectric perspective. The BiCuSeO structure consists of two layers: the conducting (Cu₂Se₂)²⁻ layers and the insulating (Bi₂O₃)²⁺ layers. The electrical transport pathway is mainly limited to the Cu₂Se₂ layers, whereas the Bi₂O₂ layers behave as a charge reservoir [32]. Thus, doping at the Bi site provides extra charge carriers for thermoelectric power factor tuning without interrupting the carrier transport. Therefore, the ML was reconstructed based on these datasets.

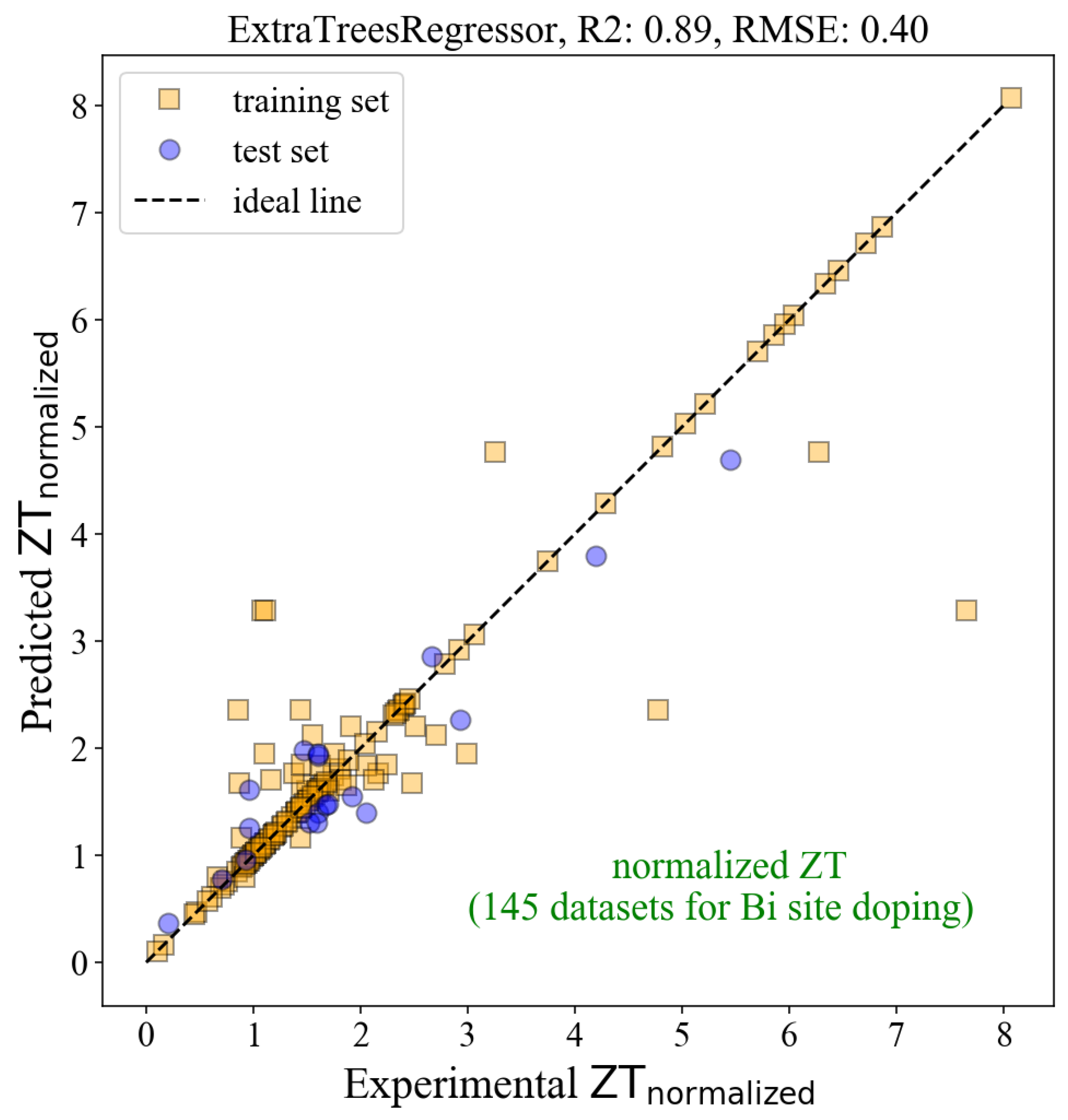
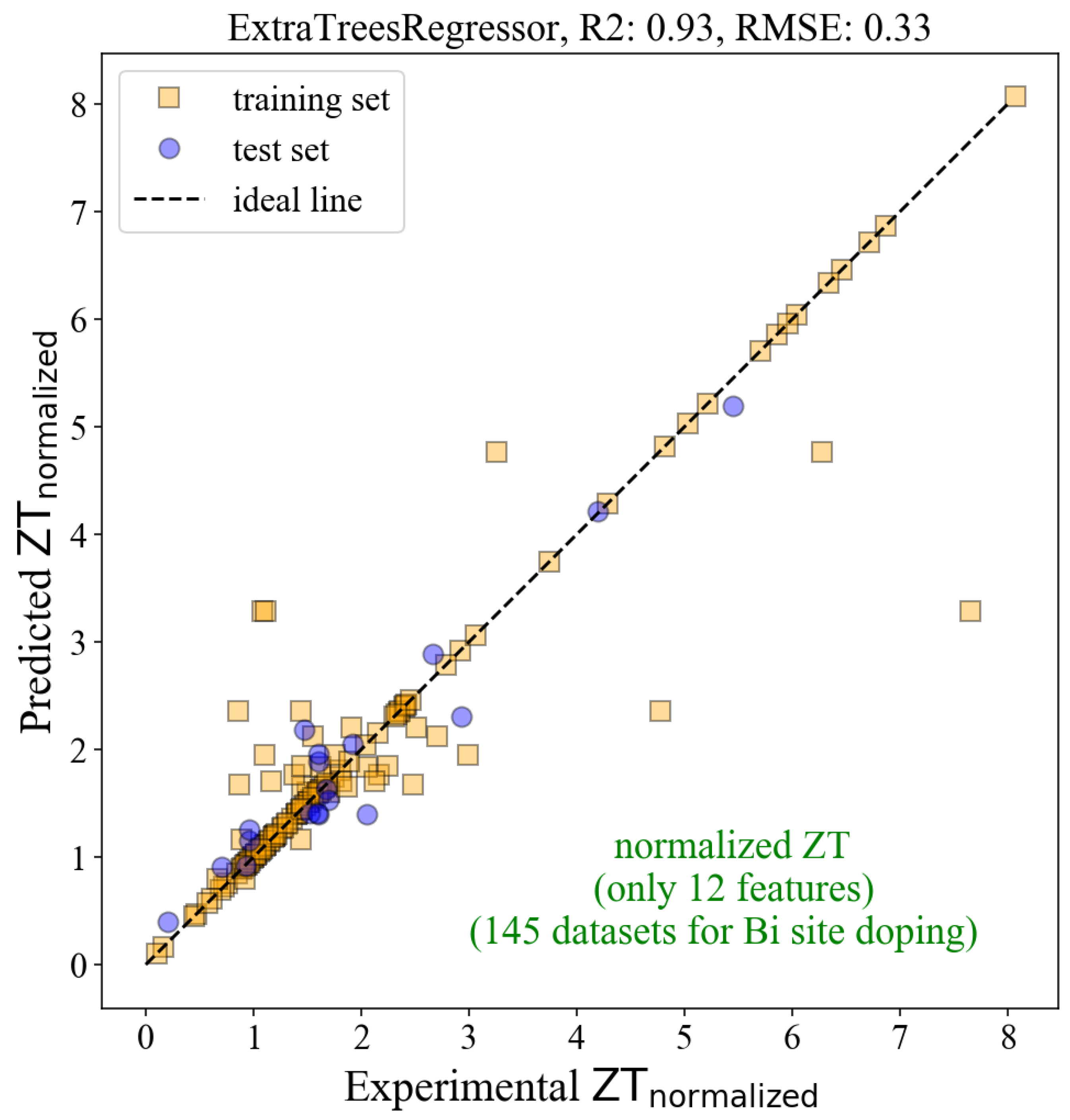
Figure 4 shows the results from the ML model based on 144 datasets for the Bi-doped BiCuSeO. The R² was considerably increased to 0.89, with the RMSE of 0.40, indicating the improvement of the model’s accuracy. 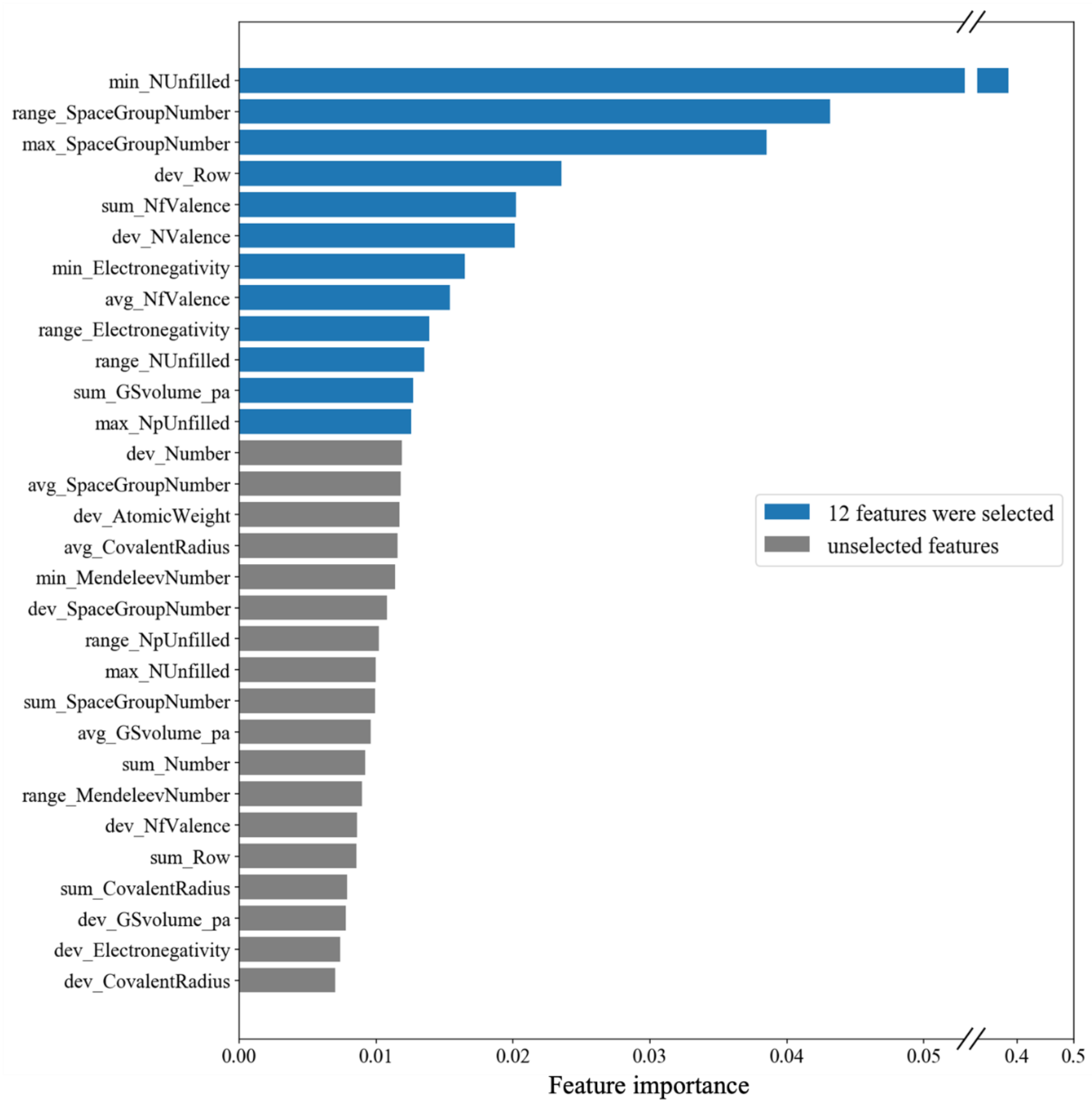However, decreasing the amount of data and using many features (154 features) could lead to overfitting, which means the model shows high performance on the training dataset but low performance on the test set [33]. To address the issue, we exported the features or descriptors representing the material characteristics from our ML model and ranked them according to their importance to the model. There were a total of 154 generated features, but the first 30 important features are shown in Figure 5. We then optimized the ML model by including only the important features. We have tried including the first 3, the first 6, the first 9… and so on important features in the model. The best-performance model was obtained when the first 12 important features (as highlighted in Figure 5) were used. Figure 6 shows the results from such a model, with the R² of 0.93 and the RMSE of 0.33 for the test set, an improvement in accuracy from the model in Figure 4. If one compared the model in Figure 6 to the primitive model in Figure 2, the accuracy performance increased >63%. However, before bringing the model to use, the generalization of the model was carried out via Leave One Out Cross Validation (LOOCV). This method is appropriate, particularly for small-size datasets [5]. The validation resulted in the RMSE of 0.71 for the training dataset, which means that the predicted ZT_normalized values from the model have an error of ±0.71.

The physical meaning of the important features in Figure 5 is worth discussing. The most important feature is the min_NUnfilled. The prefix min refers to the minimum number of the element’s properties obtained from Magpie software, whereas the NUnfilled accounts for the total number of unfilled electrons in electronic shells (s, p, d, f). For example, the NUnfilled of He is 0 from its electronic configuration (1s²), whereas the electronic configuration of Na is 1s² 2s² 2p⁶ 3s¹ resulting in the NUnfilled of 1. In the case of the BiCuSeO compound, the NUnfilled of Bi, Cu, Se, and O is 3, 1, 2, and 2, respectively, and hence, the min_NUnfilled of BiCuSeO is 1, according to the minimum NUnfilled of Cu. For the doped compound, such as Bi_0.94Mg_0.03Pb_0.03CuSeO, the min_NUnfilled of this compound is 0 because the NUnfilled of Mg equals 0. By using Pearson correlation analysis, it was found that the lower the min_NUnfilled, the higher the ZT_normalized. The lowest min_NUnfilled (0) was found in the BiCuSeO doped with, for example, Mg, Ca, Sr, Ba. These elements are divalent ions (Mg²⁺, Ca²⁺, Sr²⁺, Ba²⁺). When they were substituted for Bi³⁺, an extra +1 charge was generated for charge neutralization. This extra charge increased the carrier concentration of the BiCuSeO system, leading to optimization of power factors [17,34,35]. Therefore, it is reasonable for min_NUnfilled to be the most important feature for our ML model.

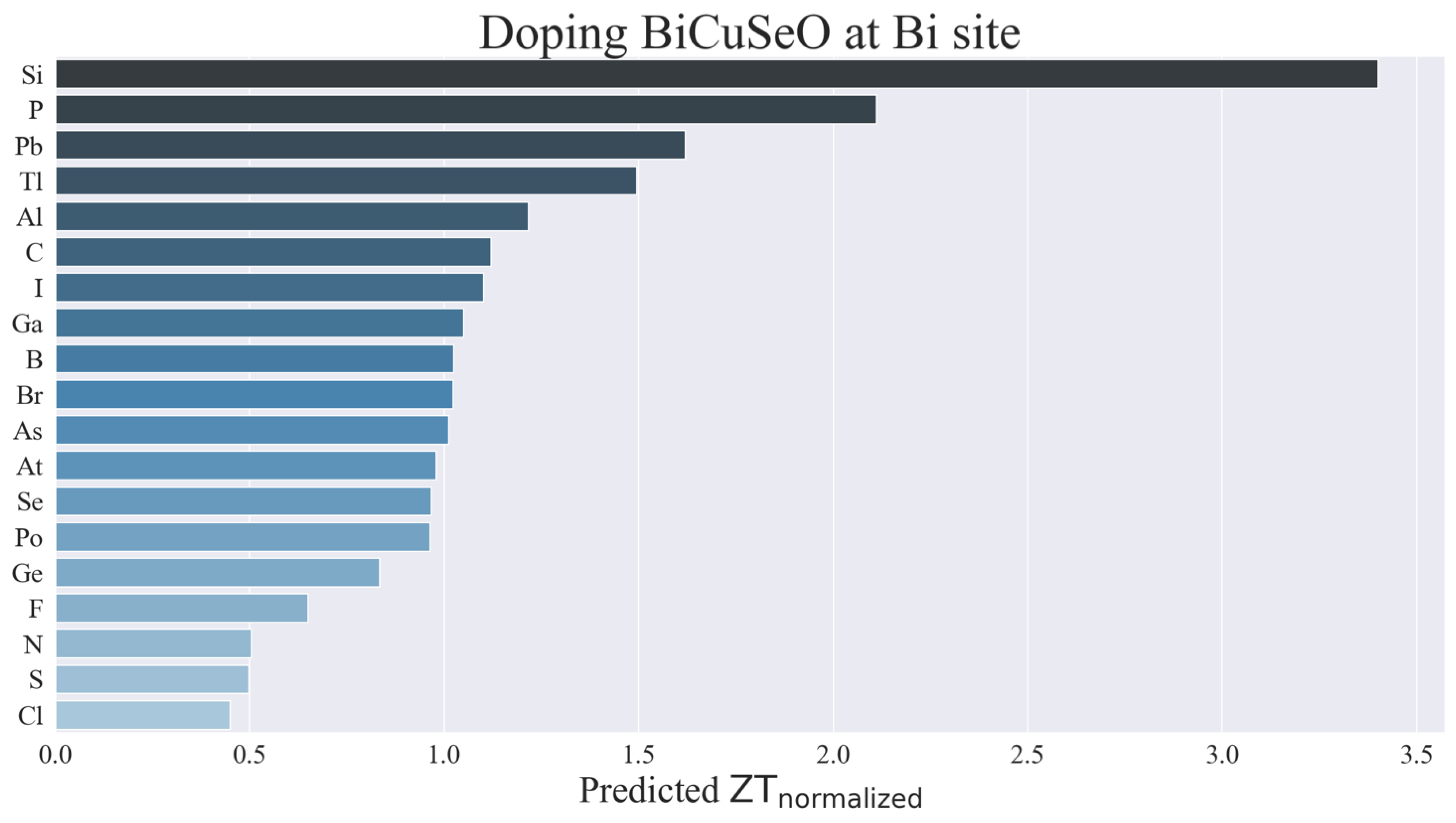
Finally, we used the optimized ML model to predict ZT_normalized of the doped BiCuSeO at Bi-site (Bi_1-xA_xCuSeO, where A is the dopant and x = 0.02). We selected some elements that were not already in the model datasets, and such elements could be synthesized experimentally. Figure 7 shows the predicted ZT_normalized value for some candidate materials. The highest ZT_normalized belongs to the Si-doped compound, which is reasonably justified. It was reported that doping light elements at the Bi-site in BiCuSeO could promote carrier mobility from the decreased carrier scattering [36]. Since Si can be considered as a light element, doping Si for Bi is likely to promote carrier mobility and increase ZT. Moreover, the DFT simulation of the Si doping at Bi-site showed the increased electrical conductivity, with a slight decrease in the Seebeck coefficient, from the modified electronic band near the Femi level, resulting in a large power factor. On the other hand, the Cl-doped compound exhibited the lowest ZT_normalized value from the model. This result is understandable. The previous experiment reported that doping Cl at Se-site negatively affected the ZT value, by increasing both electrical resistivity and thermal conductivity [37]. Thus, Cl is unlikely to be a good candidate for doping in BiCuSeO.

The step-by-step development of the ML model with improving performance was presented. It was used to guide a new candidate material for enhancing ZT value. However, the limited data from experiments was an obstacle to constructing the accurate ML model. Apart from that, it was also found that training the ML model requires both good and bad results. Generally, most published articles reported only good results (large ZT), but in fact, various data (positive or negative results) are necessary to improve the ML model.

4. Conclusions

We have developed the ML model for predicting the thermoelectric Figure-of-Merit (ZT) of the BiCuSeO compounds. The model was improved step-by-step to achieve relatively high accuracy. The ML initially showed a relatively low R² of 0.57. We then improved the model’s accuracy by normalizing the experimental ZT of the doped BiCuSeO with the pristine BiCuSeO. The modified ML model showed improved accuracy with an R² of 0.78. Furthermore, we selected the data for the BiCuSeO doped at Bi-site only and reconstructed the model. The R² increased to 0.89, indicating the enhanced model’s accuracy. Last but not least, only 12 important features were used in the model, which resulted in the increased R² to 0.93 and the RMSE of 0.33. Furthermore, the most important feature, min_NUnfilled, was discussed and correlated to the physical parameters of materials. The model predicted the substantial ZT improvement for the Si-doped BiCuSeO material, which is scientifically sound from the thermoelectric principle. Therefore, the ML model of this work can provide a guideline for experimental researchers for improving the thermoelectric properties of BiCuSeO and can be extended to other thermoelectric materials.