Abstract
The work in this article analyses the impact of time-delays on distributed real-time simulation stability and accuracy with respect to different decoupling points as well as the impact of decoupling point selection on system modes. We perform analysis of the system modes and participation matrix of the system and determine suitable points that negligibly modify the system modes to decouple the original system. From this analysis, a non-intrusive delay-based model partitioning method for distributing real-time simulations that exploits the flexibility in the context of selecting decoupling points is developed.
1. Introduction
With the surge of power electronics and renewable energy sources integration in modern power systems, the need for real-time power system simulations and Power Hardware-in-the-Loop (PHiL) studies is constantly increased [1]. Real-time simulations in modern power systems are considered as an essential tool for the grid and device testing [2,3,4]. However, this constant increase of the device number and the sizes of grids simulated in real-time environment poses a challenge to simulating models in one simulation unit.
The issue of splitting into subsystems and assigning subsystems to different processing resources while ensuring simulation stability and the required level of simulation fidelity in distributed real-time power system simulations is a challenging task and an open research question. Distributed simulations are used when we want or need to have a real-time simulation of a system that cannot be simulated on just one OPAL-RT target or RTDS rack.
This is the case even for simulations running on different CPU cores in one simulator unit since at least a one time step delay between partitions must to be considered. The impact of that one time step delay on the simulation performance is not negligible. In the following, both terms—a partition and a subsystem—are going to be used interchangeably. The contribution of this paper is the method for non-intrusive delay-based model partitioning of distributed real-time simulations developed via analysis of the delay impact on distributed real-time simulation modes at different decoupling points.
2. Literature Review and Related Work on System Partitioning
The most common real-time power system solvers fall into three main categories: nodal analysis-based (as in Hypersim of OPAL-RT and RTDS real-time simulator), state-space formulation solvers (as in Simscape Power System from MATLAB and eMEGAsim from OPAL-RT) and the most recent state-space nodal (SSN) [5,6] formulation that combines the previously mentioned two approaches. The method in this paper performs system analysis using the state-space system formulation.
Research efforts have previously been made to convert nodal power system representation to the state-space formulation if the method is going to be applied in an automated manner on the nodal based power system simulators [7]. Different algorithms and methods have been proposed in the literature for power system simulation partitioning in different contexts. Partitioning methods can be classified based on the used methodology, application and partitioning objective. The most commonly used methodologies are graph-based and eigenvalue-based.
From the application perspective, three main groups are present: methods for parallel computing of the power system solution where the partitioning objective is the reduction of computational complexity when distributing the simulation, methods for the partitioning of multi-rate simulations where the partitioning objectives are the stability and accuracy of the multi-rate simulation and methods for a distributed system simulation where the focus lies on the system simulation stability and accuracy as in methods for multi-rate simulations.
The main difference between distributed system simulations and parallel system simulations is the inclusion of the delays between partitions in the case of distributed system simulations. While the methods dealing with parallel computing partition the system to parallelize the computing of a network solution on one simulation unit, assuming no delays between partitions in one simulation time step, distributed system simulations simulate partitions (representing one monolithic system) on different computational units.
They are, therefore, affected by time delays occurring between computational units. The main focus of this paper is system partitioning for distributed simulations. Therefore, our literature review focuses on the methods already existing for this application, the explanation for why some other currently existing partitioning algorithms cannot be directly used in this application, and papers that have similar methodologies to the one analysed in this paper.
The standard method for power system model partitioning for real-time applications is the travelling-wave method. Here, decoupling is achieved via a travelling-wave transmission line model whose travel time is greater than or equal to the simulation time step used [8,9]. Therefore, natural decoupling of the system is achieved. Assuming the speed of light and simulation time step of s, the line length should be at least 15 km in order to naturally decouple the system.
For many transmission networks, this method was sufficient. However, in distribution networks where longer transmission lines do not exist, this method is inapplicable, and decoupling of the system poses greater challenges. Artificially increasing the line length brings in large capacitance and inaccurate results—for example, grid voltages becoming unusually high [10]. The standard method for system partitioning for parallel processing of the system solution is diakoptics, which was developed to reduce the computational burden of the matrix inversion by tearing the power system into sub-problems that are solved independently with the introduction of additional calculations [11,12].
In the original form, as with other parallel processing partitioning methods, diakoptics does not include a delay that could occur between sub-problems solved independently. Therefore, it cannot be applied directly on distributed real-time power system simulations where at least one time step delay should be considered. In [13], partitioning was included by optimizing the CPU load computation and communication between CPUs, and the optimal number of portions was found in the context of parallel computing applications. From the perspective of the methodology, this method is graph-based partitioning as in [14].
Graph-based system partitioning methods are widely used for the parallel computing of system solutions. However, they cannot be directly used for distributed real-time simulations without modifications needed to include the delays occurring between two simulation units. The analysis and method developed in this paper are based on modal analysis. Circuit latency and modal analysis have already been exploited to determine network partitions. However, in multi-rate power system simulation applications, it is applied to finding decoupling points and subsystems suitable for decoupling small and large simulation time steps [7,15].
In [16], a delay-based method for the decoupling of system equations was proposed for offline system simulation. The idea in the paper is similar to the one used in our work since the paper searched for variables that can be delayed one time step and enable the matrix sparsity needed for parallel processing of the system solution, but did not address, in the original form, distributed system simulations (delayed interface quantities between subsystems are the combination of different system states and inputs and contribute to different elements in a Jacobian system matrix).
A detailed explanation of multi-core simulations of power system transients and methods for system partitioning can be found in [17]; however, none of them address the distributed simulation partitioning issue. Coupling point analysis and motivation for methods for decoupling point selection in distributed real-time simulations can be found in [18], where it is shown how the location of the coupling point can affect the fidelity of the distributed simulation.
3. Motivation
3.1. Distributed Real-Time Power System Simulations
A real-time simulation is a distributed real-time power system simulation if we divide a monolithic model of the system. In the literature, this is also called a naturally coupled system (NCS), on subsystems simulated on different simulation units. The simulation decoupling point is where the monolithic system partitioning is made, and delays occur when interface variables are exchanged. This point is known in the literature as the point of connection (POC).
In this paper, the ideal transformer model (ITM) [19] is assumed to be used as an interface algorithm because of its simplicity and accuracy, as represented in Figure 1, and all further analysis is done assuming ITM as the interface algorithm between subsystems. Though a highly accurate interface algorithm, ITM is proven to have stability issues when used in distributed simulation applications [19]. The model partitioning methodology in this paper aims to determine appropriate decoupling points to preserve the simulation stability while using the ITM interface and acting non-intrusive.
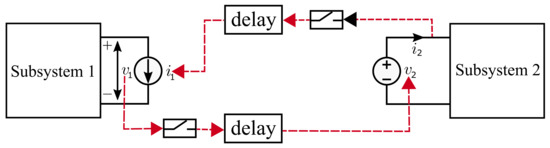
Figure 1.
Distributed simulation or PHiL.
Subsystems in the Figure 1 visualizing partitioning problem can represent simulators or real devices based on the application—distributed simulation or PHiL. The main focus of the paper is the first application. Digital real-time power system simulators use a fixed-step solver with a common simulation time step in electromagnetic transient programs (EMTPs) of 50 s. The term time step is used to describe the time between two consecutive instantaneous outputs of the solver.
The time step is related to the sampling frequency of the simulation and determines the frequency bandwidth of signals that can be accurately reproduced. With this time step up to 2–3 kHz can be simulated based on a common rule of thumb that suggests a time step size of a 10-times smaller value of the period of the fastest frequency following disturbance [20]. The delay between two subsystems in this work is always deterministic and a multiple of the simulation time step.
A variable that is transferred from one subsystem to another is referred to as an interface variable. The interface variable is sampled and delayed before being applied to the receiving subsystem. The sampling period is the time difference between two consecutive sending samples of interface variables from one subsystem to another. In this paper, only delays occurring between two subsystems are considered, and the sampling period is assumed to be equal to the simulation time step of the subsystems. Both subsystems are simulated with the same time step s.
3.2. Simulation Examples Explaining Paper Motivation
Let us observe the example system (simple circuit) in Figure 2 with two possible points in which the system can be decoupled: A and B.

Figure 2.
System decoupling example 1.
Let us assume our circuit has the following parameters mH, mF, mH, mF, mH, mF, , , and . This system was partitioned in two decoupling points making a distributed system simulation. The system was simulated with a defined fixed delay between two subsystems, where s is the simulation time step that is the same for both subsystems. Decoupling the system in decoupling point A leads to stability issues for the distributed system simulation for or delay ms. For decoupling point B, the simulation stays stable up to the last simulated delay of , thus, ms. Let us observe the example system two in Figure 3, with two possible points in which the system can be decoupled: A and B.
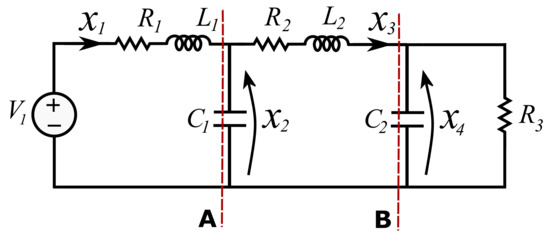
Figure 3.
System decoupling example 2.
Let us assume our circuit has the following parameters mH, mF, mH, mF, , and and that distributed versions are made as in the previous example. Decoupling the system in decoupling point A leads to stability issues for the distributed system simulation, even for or delay ms. For decoupling point B, the simulation stays stable up to the last simulated delay of or ms. These motivation examples show that distributed simulations have stability issues in specific decoupling points. In contrast, another decoupling point would not have a stability problem for the predefined delay and would, therefore, be a better decoupling point candidate in terms of the distributed simulation stability.
4. Mathematical Background of Analysis and Methodology
4.1. State-Space Representation of Partitioned System Model
In the case of distributed real-time simulations, both digital simulator units solve the system in the discrete time-domain. It is, thus, a straightforward approach to perform analysis of the distributed system model in the discrete time-domain. To perform modal analysis on the distributed system simulation model, the time-invariant state-space model of the two connected subsystems with the inclusion of delays is derived.
The implicit integration method typically used in real-time power system simulators is the trapezoidal method, which is numerically A-stable. If this method is applied to the set of stable linear system equations, the time step of the simulation influences only the accuracy of the system simulation and not the numerical stability. In the modelling of the two coupled subsystems in this section, trapezoidal integration was applied to discretize the state-space subsystem models. Let us first assume that we have two state-space subsystem models represented in Figure 4.
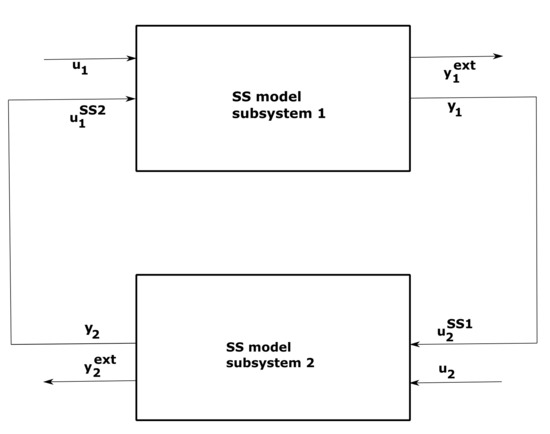
Figure 4.
Coupled subsystem state-space representation without delayed outputs.
State-space models of the subsystems one and two in the discrete time-domain can be represented by Equations (1) and (2) respectively:
where k is the current time step, is the future time step, and , . With simple manipulation over the matrices, the combined state-space model of those two subsystem models can be described by Equation (3), where and I is the unity matrix of the required size.
If we assume that delayed outputs of the state-space subsystem models are inputs of the other state-space subsystem model, this means that , , and their connection is visualized in Figure 5.
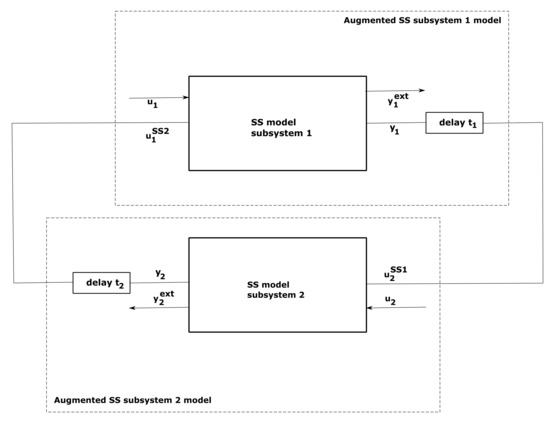
Figure 5.
Coupled subsystem state-space representation with delayed outputs.
We assume that time delays between two subsystems are deterministic and multiples of the simulation time step of the subsystems and , where is the simulation time step.
If we augment the states and input vectors up to the output delays as in Equation (4) for the subsystem 1 model, a new augmented state-space model of subsystem 1 can be developed, as in Equations (5) and (6). Here, n is the number of states in subsystem 1, p is the number of external inputs in subsystem 1 (size of vector ), s is the number of inputs coming from another subsystem (size of vector ), m is the number of outputs going to another subsystem (size of vector ), is a unity matrix of size , and is a zero matrix of size .
4.2. Modal Analysis
Modal analysis has been applied to various power system problems, especially in the domain of inter-area oscillations [21] and Wide-Area Measurement System (WAMS) applications [22,23,24,25]. The modal analysis represents small-signal stability analysis applied to linearized system models. This analyses the stability of the power system around its equilibrium point before or after the disturbances and gives information about system oscillations: how many modes the system has and their frequencies and dampings.
A systematic procedure for assigning state variables and finding the dynamical equations of the system can be found in [26] if a dynamic system is a linear time-invariant (LTI) electric network. An electrical grid is the interconnection of different electrical elements. With some assumptions, all dynamic components in power systems (generators, dynamic loads, lines, regulation and control) can be described by a set of differential and algebraic equations:
where is state vector of size n, represents the system inputs, contains algebraic variables of the system, f is a set of differential equations, and g is set of algebraic (without derivatives) equations based on Kirchhoff’s law. The state-space model of the system is a linear representation of Equation (7) at some equilibrium point. If ) is an equilibrium point of the system (given for example by the load flow calculations):
using the first order Taylor approximation around leads to:
In order to simplify Equations (9) and (10), , , , , , are introduced. In the same manner, , and are partial derivatives of in . It can be easily derived that:
where , with the assumption that is not singular. If we assume that observable outputs of the system are represented via the function , and, using the same notation, it can be derived that:
where and . In the state-space representation of the system, matrix A is specific for the system for a given equilibrium point, whereas B, C and D depend on the chosen inputs and outputs of the system. The system is characterized by the state matrix A and, more precisely, the eigenvalues of matrix A.
The poles of the system are the eigenvalues of the matrix A. These poles can be real and complex if matrix A is real, and the real part of all system eigenvalues needs to be negative, to ensure the stability of the system. The real eigenvalue of A is the system mode, and complex eigenvalues appear in conjugate pairs representing one system mode. The eigenvalue of matrix A is a scalar parameter that fulfils the equation:
were is n by 1 vector, and n is the size of the square matrix A. To find the eigenvalues, we can rewrite Equation (13) in form. For a non-trivial solution, that means:
Equation (14) is a characteristic equation with n solutions that are eigenvalues of A. For any eigenvalue , the n-column vector that satisfies
is the (right) eigenvector of A associated with . Similarly, n-row vector that satisfies:
is the left eigenvector associated with . In order to express the eigenproperties of A, modal matrices (in the literature also called transformation matrices) are introduced:
It can be easily derived that matrices and are orthogonal [27] and satisfy , , where . If is the right eigenvector, then is as well, and the same counts for and , where k is scalar. Therefore, and can be normalized so that they satisfy and .
Using the transformation matrix , we can transform the system in the new base () where the modes are decoupled () and show that the right eigenvector represents the relative activity of the state variables when a particular mode is excited and represents how state variable will be impacted by the excitation of the mode j where magnitudes of the elements in represent a degree of activities of n state variables in the ith mode, and the angles of elements show the phase shifting of the state variables with regard to the mode.
Thus, a larger means that state variable is more impacted by mode j. The overall variation of the mode is the sum of the impacts of all system modes. The left eigenvector gives the combination of state variables displayed in the ith mode. Similarly to the case of the right eigenvectors, if is the jth element of the , the larger the value is, the larger is the influence of the state on mode i.
Analysing the connection of system modes and system states looking individually at right and left eigenvectors can cause a problem due to scaling and the units of state variables (the elements of the right and left eigenvectors depend on the units and scaling of the state variables). To overcome this issue, a participation matrix [27,28] is introduced:
with
where is the kth element of the right eigenvector and is the kth element of the left eigenvector . The element is called the participation factor. The influence of the specific eigenvalues (poles or modes) on the states of the system can be measured using a participation matrix.
When and are normalized and orthogonal, we have and . For this paper, a relative participation matrix is used as introduced in [29], normalizing the state influence on the modes. The relative participation of the kth state variable on the ith mode is as in Equation (20), representing this influence as a percentage.
We assume that the ith mode has influence on the kth state if as in [30].
5. Analysis and Non-Intrusive Delay-Based System Partitioning
5.1. Analysis
As we saw in Section 3.2, certain decoupling points are more challenging than others. Our methodology focuses on finding how challenging a specific decoupling point is in terms of simulation stability and, if possible, suggesting other decoupling points that would lead to stability of the simulation for the specified delay with preserved fidelity. This was done with the application of modal analysis explained in Section 4.2 and verified on the examples from Section 3.2 modelled using distributed the state-space modelling approach from Section 4.1.
Considering only the simulation of stable monolithic systems, the real parts of all eigenvalues should be negative (). Real eigenvalue corresponds to the non-oscillatory mode. Each complex conjugate pair of eigenvalues is associated with one complex conjugate mode. For complex pairs of eigenvalues , the natural frequency of oscillation is determined by , and the damping ratio is , where , and .
The damping ratio determines the rate of transient response decay of the amplitude of oscillation of complex conjugate mode, and the frequency of oscillations is determined by as . Following the rule of thumb, the simulation time step needed to capture oscillations of the complex conjugate mode is 10-times smaller than the period of oscillation of the mode [20], which results in , and this value we define as the critical time constant of the complex conjugated mode .
The dynamic properties of the system modes determined by damping and the frequency of the oscillations determine the dynamic properties of the system, transient response of the system and, therefore, the overall system dynamics. System modes that influence the states in both subsystems, assuming we have two subsystems, are interaction modes. Local modes are all the modes that are not interaction modes for a specified decoupling point. Modes of the system were defined in the same manner but for another application in [30].
Modes that are interaction modes are the modes impacted by partitioning the system, while local modes are not impacted by partitioning, and therefore delays occur between partitions. Modes of different distributed simulation models were observed in the z-domain to determine which modes moved in the z-domain, thereby, changing the system response and leading to simulation instability.
We observed that local modes of the distributed simulations do not change the value and move in the z-domain significantly, even with significantly increased delays between subsystems. Interaction modes move more, even with only one time step delay if the dynamic of the mode is comparable with the delay and, therefore, change the distributed simulation system response as will be shown in Section 5.2.1.
5.2. Methodology
Avoiding decoupling points in which critical modes are interaction modes can allow greater delays while preserving the stability of the real-time simulation, and since the modes are not significantly moving, thus, preserving simulation fidelity. The method developed in this paper focuses on selecting model decoupling points in which the critical modes of the monolithic model are not significantly modified and proposes possible time delays to preserve the simulation stability.
We define critical modes of the system as complex conjugate modes of the system that have comparable dynamic properties with the time delays we expect between two subsystems and, therefore, are sensitive to delays between subsystems in the case that they are interaction modes. Critical modes of the system are all the complex conjugate modes for which Equation (21) is fulfilled, where is the expected time delay between two subsystems.
Value should be rounded down to the first discrete , where m is an integer. The stronger the coupling between two subsystems from the perspective of critical mode is, the larger is the influence of decoupling on critical system mode and, therefore, the distributed system simulation. If is a set of the subsystem states in subsystem w, the relative influence of system mode i on this subsystem can be defined as . Here it is important to define the coupling index between two subsystems m and s with respect to the system mode i as in Equation (22) where m is the subsystem with the smaller relative influence of the mode i, and s opposite.
The maximal coupling index of two subsystems for the system mode i is , and if the system mode is the local mode, . The partitioning methodology of this paper is assumed to be performed on a monolithic system model in the continuous time domain. Since eigenvectors of the system are the same in the continuous and discrete time domain, the participation matrix is also [31].
Therefore, performing participation matrix analysis on the monolithic system model in the continuous time domain is possible without losing correctness. Eigenvalues of the continuous and discrete time domain are connected by bilinear transformation as in Equation (23), where is a discrete eigenvalue, and differential equations are discretized with the trapezoidal rule. In the case simulation, time step is small enough compared to the time constants of the system, discretization does not influence the response of the modes, and continuous eigenvalues can be considered without losing correctness.
The delay margin for preserving distributed simulation stability cannot be found as a precise value observing only critical mode i properties because is determined relying on the simulation rule of thumb. Though, empirically on different distributed system simulations, a delay margin for the stability of the distributed system is assured from the perspective of delays occurring between subsystems is found and looks as in Equation (24).
Here, i is a critical system mode, is critical time constant of that mode, is the damping of that mode, and is a coupling index of the critical system mode i for the decoupling point. As expected, with a decreasing coupling index between two subsystems, increases. In the case of several critical coupling modes, the smallest of all should be taken.
If the simulation is stable for greater delays, it cannot be answered using this methodology. However, it eliminates the possibility that the simulation is unstable because of the critical mode that disturbances can excite. If the delay d that we expect between partitions is larger than , we suggest decreasing the delay until Equation (25) is fulfilled or changing the decoupling point in order to preserve the simulation stability.
The non-intrusive delay-based model partitioning method is explained step-by-step and applied on examples from Section 3.2, and the methodology diagram is shown in Figure 6.
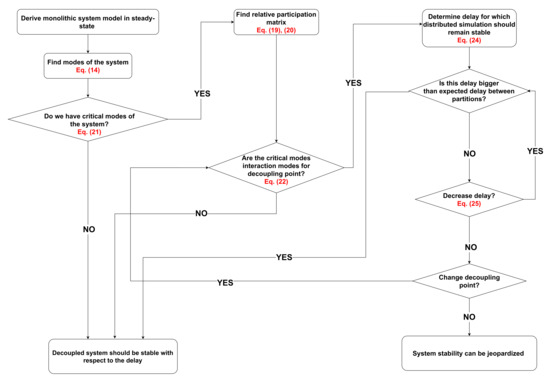
Figure 6.
Logical flow of the method application.
The method developed in this paper can be applied in PHiL applications determining how suitable and challenging the point is in which we want to connect the device from the real-time simulation perspective if a suitable model of the device can be found.
5.2.1. Method and Analysis Exemplification
Let us first analyse example system one in Figure 2. Following the methodology, one should find a monolithic system model, find the modes of the system, and check if there are some critical modes with the predefined delay of using Equation (21). As the first step, the monolithic system model is derived with as the system input and all system states as outputs. Matrix A of the system is:
with system states as in Figure 2, . From this matrix and the parameters given in Section 3.2, we find that system has four modes with the characteristics presented in Table 1.

Table 1.
Example system 1 modes.
If the expected delay between subsystems can go up to , for , where s, using Equation (21), can be classified as a critical mode of the system. The next step in our distributed system analysis is finding the relative participation matrix of the system using Equation (20):
From the relative participation matrix, it follows that influences state of the system with , state with and state with and has a negligible impact on states , and . In the case of decoupling point A, this mode is interaction mode. For decoupling point A, the influence of critical on the states is divided between the subsystems on and . Therefore, for decoupling point A, the coupling index between subsystem with respect to critical is In the case of decoupling point A, critical mode is interaction mode, and one can say that the stability of distributed system simulation can be assured for delays smaller than ms. Since this delay ms is smaller than the s = 0.5 ms, we suggest to decrease the delay in order to preserve the stability of the simulation or change the decoupling point, and use decoupling point B for example.
In the case of decoupling point B, critical is not the interaction mode. Therefore, following the methodology, it is expected that critical mode will not be sensitive to delays occurring between subsystems, since it is localized in one of the subsystems, and a decoupled system should be stable with respect to the delay. Distributed simulations of this system were done up to the delay of , , and s, and decoupling points A and B. A distributed system (partitioned system) is simulated with V and transience is made in s with input change to V.
Distributed simulations showed that, in the case of decoupling point A, the system becomes unstable for , while, for decoupling point B, the system remained stable up to the last simulated delay of . In order to analyse the delay impact on the distributed system modes, the distributed system model was derived as in Section 4.1, and in Table 2, we can observe the value of critical system mode with respect to delays between partitions.

Table 2.
Example system 1, mode 1, for decoupling point A.
Since the model of the distributed system is made in the discrete time domain mode, values in the continuous time domain in the table are made using Equation (23). In the further analysis, we use the term ’decoupled system’, for a system that is made, as in Section 4.1, without delays occurring between subsystems (Figure 4), but with the separate discretization of the two subsystems (partitions). This model is made to see how the separate discretization of the subsystems influenced the system modes before applying delays between subsystems.
The critical system mode that is the interaction mode in the case of decoupling point A, is highly impacted via decoupling in this point and leads to the distributed system instability. It is interesting to observe that the damping and of the coupling mode decrease with the increased delay. For decoupling point B, critical mode is localized with coupling index . In the case of decoupling point B, for the monolithic model in the continuous and discrete domain, decoupled system model and distributed system model for delays up to .
This example shows that the critical system mode leads to instability of the distributed system simulation for the decoupling point, in which this mode was the interaction mode. In contrast, the same critical mode does not change its value with the increased delay between subsystems when it is the local mode for some other decoupling point. Therefore, in avoiding the critical modes as interaction modes, one can preserve the distributed system stability, and indirectly, since the critical mode is not moving and changing the distributed system response the simulation fidelity as well. The system is simulated for both decoupling points A and B and delay to show simulation fidelity. In Figure 7 is presented response for both decoupling points after transient at s, showing that not only the stability of the simulation is preserved in the case of decoupling point B. This point shows greater fidelity of the simulation as well.
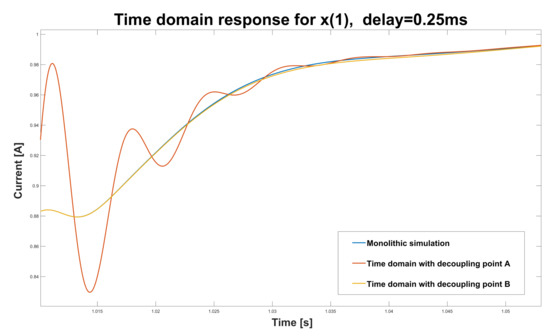
Figure 7.
Response of in system example 1 after the disturbance—decoupling points A and B.
The fidelities of the output variables are calculated using Equation (26) for each variable i and every simulation point k.
Since the critical interaction mode is the one changing its value with decoupling in decoupling point A, the fidelity of the partitioned system simulation in decoupling point B is better even for as can be seen in Figure 8. From Figure 8, it can be concluded that, for all simulation points, decoupling point B shows better simulation fidelity compared to decoupling point A, and the monolithic system response is preserved. In the case that we have highly underdamped or an extremely fast critical system mode acting as the coupling mode, this can lead to instability of the simulation even after relatively small delays of and , and this is observed on example system two from Figure 3.
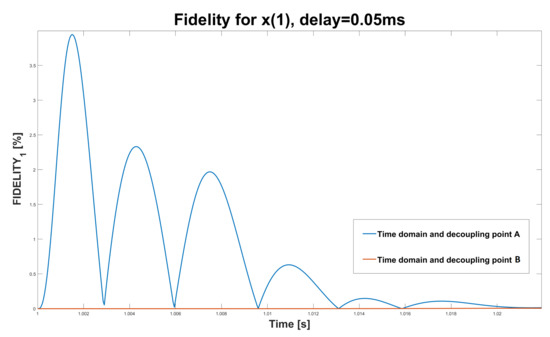
Figure 8.
The fidelity of in example 1 after a disturbance—decoupling points A and B.
Assuming a delay between subsystems up to , , using Equation (21) critical system mode , with ms, and can be found. In the case of decoupling point A, the critical system mode is coupling system mode with . Using Equation (24), one can say that the stability of distributed system simulation in decoupling point A is assured for delays smaller than ms; thus, .
The distributed system was simulated with V, and transient is made in s with input change to V. Indeed, in the case of decoupling point A, the distributed system simulation was stable for one time step delay; therefore, , and for , the distributed system simulation was unstable. In the case of decoupling point B, critical mode is localized with , and the distributed system simulation in decoupling point B showed extreme resiliency towards the delays (the last simulated delay was ).
6. Testing of the Method on the Realistic Power System Model
The previously analysed non-intrusive delay-based model partitioning method is verified in power system applications on the part of the CIGRE low voltage European grid benchmark [32], presented in Figure 9. This grid is a representative distribution system benchmark used as the benchmark system for Hardware-in-the-Loop testing of distributed energy resources [1].
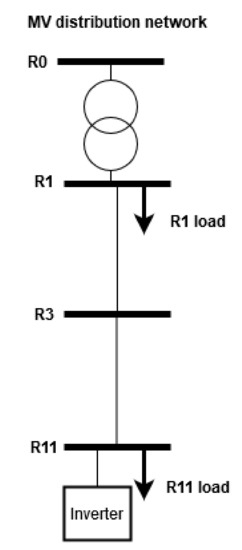
Figure 9.
Part of the CIGRE European low voltage topology.
The lines of the benchmark are shorter than 15 km; therefore, natural decoupling into subsystems is not possible for the simulation time step of s. Part of the grid until node R11 is taken for this use-case, and the inverter is placed in node R11 representing a renewable energy source or battery system. The grid is modelled as a single phase balanced network with L-R lines using parameters from the report [32].
Loads are modelled as constant impedance loads represented as L-R elements, while the inverter is modelled with its L-C filter. Therefore, this work focuses on the physical properties and modes introduced with filter dynamics. In Table 3 are the parameters of the inverter where is the rated power of the inverter, is the switching frequency of the inverter, is the inverter filter capacitance, and is the inverter inductance.

Table 3.
Inverter parameters.
The parameters of the inverter are calculated using Equations (27), where is current ripple, is the rated active power for a power factor of , and adopting a capacitor is assumed.
In the literature, system models are usually developed focusing on individual system components, such as inverters, lines and transformers [33,34] or merged micro-grid models [35], which are inapplicable for the modelling of a distribution system. In this paper, the overall distribution system model in the state-space domain is made using the approach from [36]. Following the partitioning methodology, one should find if the system has critical system modes using Equation (21). If we determine that the expected delay between partitions can be up to delay , this system has one critical mode—that is with , and ms.
Observing the relative participation matrix, the critical mode is purely influencing the inverter filter dynamics and line R1–R11 connecting that inverter. In the case of decoupling point R11, that mode is the coupling mode with a coupling factor between subsystems Using Equation (24), the stability of the simulation with respect to the delay is assured for ms. Therefore, in the case of , it is suggested to change the decoupling point, since the delay cannot be decreased.
The partitioning methodology would suggest that one should choose a decoupling point for which the inverter and line connecting the inverter are in one subsystem, localizing the critical system mode. The power system model described here is simulated in decoupling point R11 and for delays Indeed, in the case of decoupling point R11, the distributed system simulation never reaches a stable operating point after a disturbance for one time step delay.
In contrast, choosing decoupling point R1 leads to a stable and accurate distributed system simulation even for the larger delays, and thus it is shown that the partitioning methodology developed in this paper suggests a better decoupling point. A comparison of time responses of the inductance current for decoupling point R1 and a monolithic system simulation for and in one of the sinusoidal peaks can be seen in Figure 10.
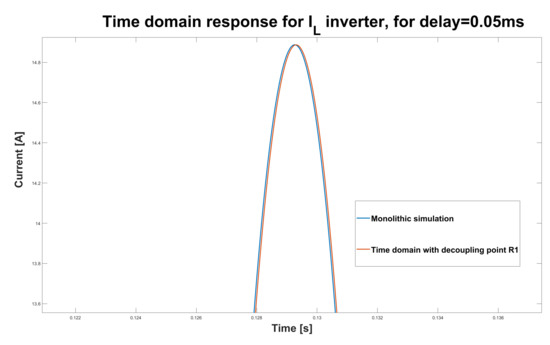
Figure 10.
Time response of for decoupling point R1 and monolithic system simulation.
The behaviour that inverter modes are not only influencing the inverter but also the line connecting that inverter was noticed in applying modal analysis and looking at the participation matrix on different power system models. This can be a helpful finding for researchers who want to extend or use this analysis for PHiL and multi-rate simulations applications.
7. Conclusions
Partitioning a system for distributed real-time simulation applications poses challenges in terms of the stability and accuracy of the simulation, and these issues were addressed in this paper. In this paper, we developed and analysed analytical models of distributed real-time simulations. We found that interaction system modes were more impacted by the partitioning of the systems and delays occurring between partitions. With localizing critical system modes, one can preserve the distributed system simulation stability.
The paper showed that the stability of the distributed simulations can be analysed by observing the critical modes of the system, and stable partitioning with regard to delays can be made using the non-intrusive delay-based method developed in the paper. The method acts non-intrusively on the monolithic system model and preserves the simulation fidelity. Verification results of the method on the representative grid are useful for developing automatized partitioning solutions for benchmark distribution system models.
Author Contributions
Conceptualization, M.B. and M.S.; methodology, M.B.; software, M.B.; validation, M.B. and M.S.; formal analysis, M.B.; investigation, M.B.; resources, M.B. and M.S.; data curation, M.B.; writing—original draft preparation, M.B.; writing—review and editing, M.B.; visualization, M.B.; supervision, A.M.; project administration, A.M.; funding acquisition, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Regional Development Fund grant number EFRE-0500029.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kotsampopoulos, P.; Lagos, D.; Hatziargyriou, N.; Faruque, M.O.; Lauss, G.; Nzimako, O.; Forsyth, P.; Steurer, M.; Ponci, F.; Monti, A.; et al. A Benchmark System for Hardware-in-the-Loop Testing of Distributed Energy Resources. IEEE Power Energy Technol. Syst. J. 2018, 5, 94–103. [Google Scholar] [CrossRef]
- Guillaud, X.; Faruque, M.O.; Teninge, A.; Hariri, A.H.; Vanfretti, L.; Paolone, M.; Dinavahi, V.; Mitra, P.; Lauss, G.; Dufour, C.; et al. Applications of Real-Time Simulation Technologies in Power and Energy Systems. IEEE Power Energy Technol. Syst. J. 2015, 2, 103–115. [Google Scholar] [CrossRef] [Green Version]
- Benigni, A.; Monti, A.; Dougal, R.A. Latency-Based Approach to the Simulation of Large Power Electronics Systems. IEEE Trans. Power Electron. 2014, 29, 3201–3213. [Google Scholar] [CrossRef]
- Bélanger, J.; Venne, P.; Paquin, J.-N. The What, Where and Why of Real-Time Simulation. Available online: https://blob.opal-rt.com/medias (accessed on 12 January 2022).
- Dufour, C.; Mahseredjian, J.; Belanger, J. A Combined State-Space Nodal Method for the Simulation of Power System Transients. IEEE Trans. Power Deliv. 2011, 26, 928–935. [Google Scholar] [CrossRef]
- Martinez-Velasco, J.A. Transient Analysis of Power Systems: Solution Techniques, Tools and Applications. 2019. Available online: https://www.wiley.com/en-us/Transient+Analysis+of+Power+Systems%3A+Solution+Techniques%2C+Tools+and+Applications-p-9781118352342 (accessed on 12 January 2022).
- Hollman, J.A.; Marti, J.R. Step-by-step eigenvalue analysis with EMTP discrete-time solutions. IEEE Trans. Power Syst. 2010, 25, 1220–1231. [Google Scholar] [CrossRef] [Green Version]
- Watson, N.; Arrillaga, J. Power Systems Electromagnetic Transients Simulation; Institution of Engineering and Technology: Stevenage, UK, 2019; pp. 193–198. [Google Scholar]
- Dommel, H.W. Digital Computer Solution of Electromagnetic Transients in Single-and Multiphase Networks. IEEE Trans. Power Appar. Syst. 1969, 88, 388–399. [Google Scholar] [CrossRef]
- Dyck, M.; Nzimako, O. Real-time simulation of large distribution networks with distributed energy resources. CIRED Open Access Proc. J. 2017, 2017, 1402–1405. [Google Scholar] [CrossRef] [Green Version]
- Brameller, A.; John, M.N.; Scott, M.R. Practical Diakoptics for Electrical Networks; Brameller, A., John, M.N., Scott, M.R., Eds.; Chapman & Hall: London, UK, 1969; 242p. [Google Scholar]
- Kron, G. Diakoptics: The Piecewise Solution of Large-Scale Systems; Madconald Technical Books; Macdonals: London, UK, 1963. [Google Scholar]
- Zhang, P.; Marti, J.; Dommel, H. Network partitioning for real-time power system simulation. In Proceedings of the 2005 International Conference on Power System Transients, Montreal, QC, Canada, 19–23 June 2005; pp. 1–6. [Google Scholar]
- Karypis, G.; Kumar, V. Multilevel Algorithms for Multi-Constraint Graph Partitioning. In Proceedings of the 1998 ACM/IEEE Conference on Supercomputing, San Jose, CA, USA, 7–13 November 1998; p. 28. [Google Scholar] [CrossRef]
- Moreira, F.A.; Martí, J.R. Latency suitability for the time-domain simulation of electromagnetic transients through network eigenanalysis. In Proceedings of the International Conference on Power Systems Transients (IPST), New Orleans, LA, USA, 28 September–2 October 2003. [Google Scholar]
- Tzounas, G.; Milano, F. Delay-based Decoupling of Power System Models for Transient Stability Analysis. IEEE Trans. Power Syst. 2020. [Google Scholar] [CrossRef]
- Uriarte, F.M. Multicore Simulation of Power System Transients; IET Power and Energy Series; The Institution of Engineering and Technology: London, UK, 2013; Volume 67. [Google Scholar]
- Ersal, T.; Gillespie, R.B.; Brudnak, M.; Stein, J.L.; Fathy, H.K. Effect of coupling point selection on distortion in Internet-distributed hardware-in-the-loop simulation. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 3096–3103. [Google Scholar] [CrossRef]
- Ren, W.; Steurer, M.; Baldwin, T.L. Improve the Stability and the Accuracy of Power Hardware-in-the-Loop Simulation by Selecting Appropriate Interface Algorithms. IEEE Trans. Ind. Appl. 2008, 44, 1286–1294. [Google Scholar] [CrossRef]
- Abourida, S.; Bélanger, J.; Jalili-Marandi, V. Real-Time Power System Simulation: EMT vs. Phasor. In OPAL-RT Technologies: White Paper: opWP150620-sa-revA; OPAL-RT Technologies Inc.: Montreal, QC, Canada, 2016. [Google Scholar]
- Dussaud, F. An Application of Modal Analysis in Electric Power Systems to Study Inter-Area Oscillations; KTH: Stockholm, Sweden, 2015. [Google Scholar]
- Susuki, Y.; Chakrabortty, A. Introduction to Koopman Mode Decomposition for Data-Based Technology of Power System Nonlinear Dynamics. IFAC-PapersOnLine 2018, 51, 327–332. [Google Scholar] [CrossRef]
- Barocio, E.; Pal, B.; Thornhill, N.; Messina, A.R. A Dynamic Mode Decomposition Framework for Global Power System Oscillation Analysis. IEEE Trans. Power Syst. 2015, 30, 2902–2912. [Google Scholar] [CrossRef]
- Alassaf, A.; Fan, L. Dynamic Mode Decomposition in Various Power System Applications. In Proceedings of the 2019 North American Power Symposium (NAPS), Wichita, KS, USA, 13–15 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ramos, J.J.; Kutz, J.N. Dynamic Mode Decomposition and Sparse Measurements for Characterization and Monitoring of Power System Disturbances. arXiv 2019, arXiv:1906.03544. [Google Scholar]
- Chen, C.T. Linear System Theory and Design; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Kundur, P.; Balu, N.; Lauby, M. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Perezarriaga, I.; Verghese, G.; Schweppe, F. Selective Modal Analysis with Applications to Electric Power Systems, PART I: Heuristic Introduction. IEEE Trans. Power Appar. Syst. 1982, 101, 3117–3125. [Google Scholar] [CrossRef]
- Kunjumuhammed, L.; Pal, B.; Gupta, R.; Dyke, K. Stability Analysis of a PMSG-Based Large Offshore Wind Farm Connected to a VSC-HVDC. IEEE Trans. Energy Convers. 2017, 32, 1166–1176. [Google Scholar] [CrossRef]
- Beerten, J.; D’Arco, S.; Suul, J.A. Identification and Small-Signal Analysis of Interaction Modes in VSC MTDC Systems. IEEE Trans. Power Deliv. 2016, 31, 888–897. [Google Scholar] [CrossRef] [Green Version]
- Pöller, M.A. Discrete Time State Space Analysis of Electrical Networks. In Proceedings of the International Conference on Power Systems Transients, Rio de Janeiro, Brazil, 24–28 June 2001. [Google Scholar]
- CIGRE Task Force C6.04. Benchmark Systems for Network Integration of Renewable and Distributed Energy Resources. 2014. Available online: https://e-cigre.org/publication (accessed on 12 January 2022).
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Prodanovic, M.; Green, T.C. Control and filter design of three-phase inverters for high power quality grid connection. IEEE Trans. Power Electron. 2003, 18, 373–380. [Google Scholar] [CrossRef] [Green Version]
- Schiffer, J.; Zonetti, D.; Ortega, R.; Stankovic, A.; Sezi, T.; Raisch, J. A survey on modeling of microgrids—From fundamental physics to phasors and voltage sources. Automatica 2016, 74, 135–150. [Google Scholar] [CrossRef] [Green Version]
- Angioni, A. Uncertainty Modeling for Analysis and Design of Monitoring Systems for Dynamic Electrical Distribution Grids; RWTH Aachen University: Aachen, Germany, 2019. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).