Experimental Study of Horizontal Flow Boiling Heat Transfer Coefficient and Pressure Drop of R134a from Subcooled Liquid Region to Superheated Vapor Region
Abstract
1. Introduction
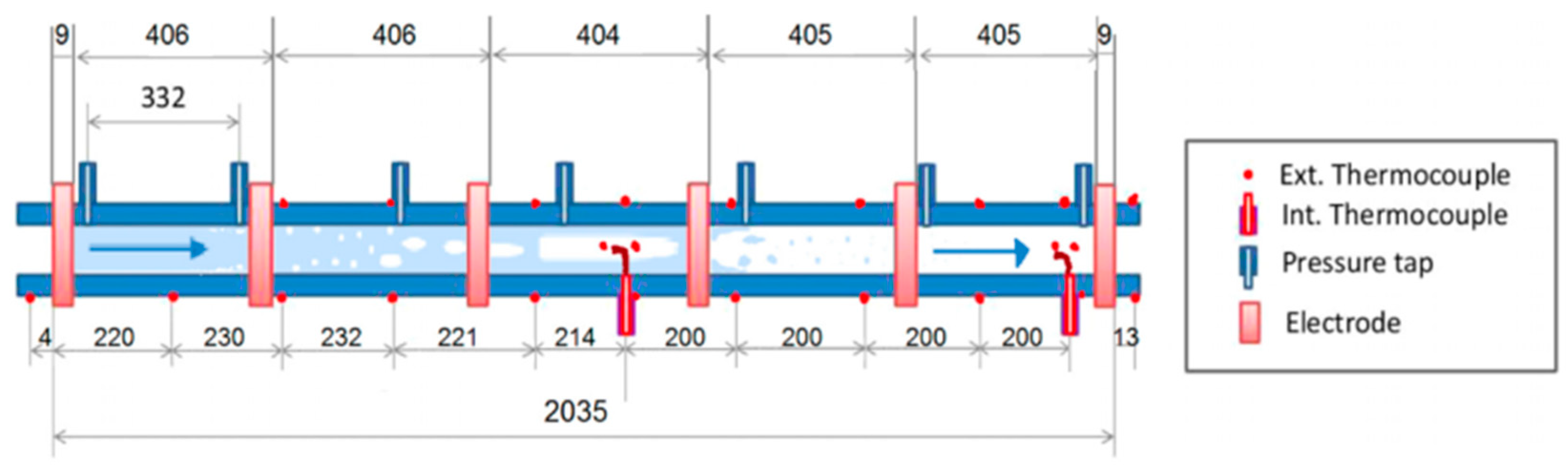
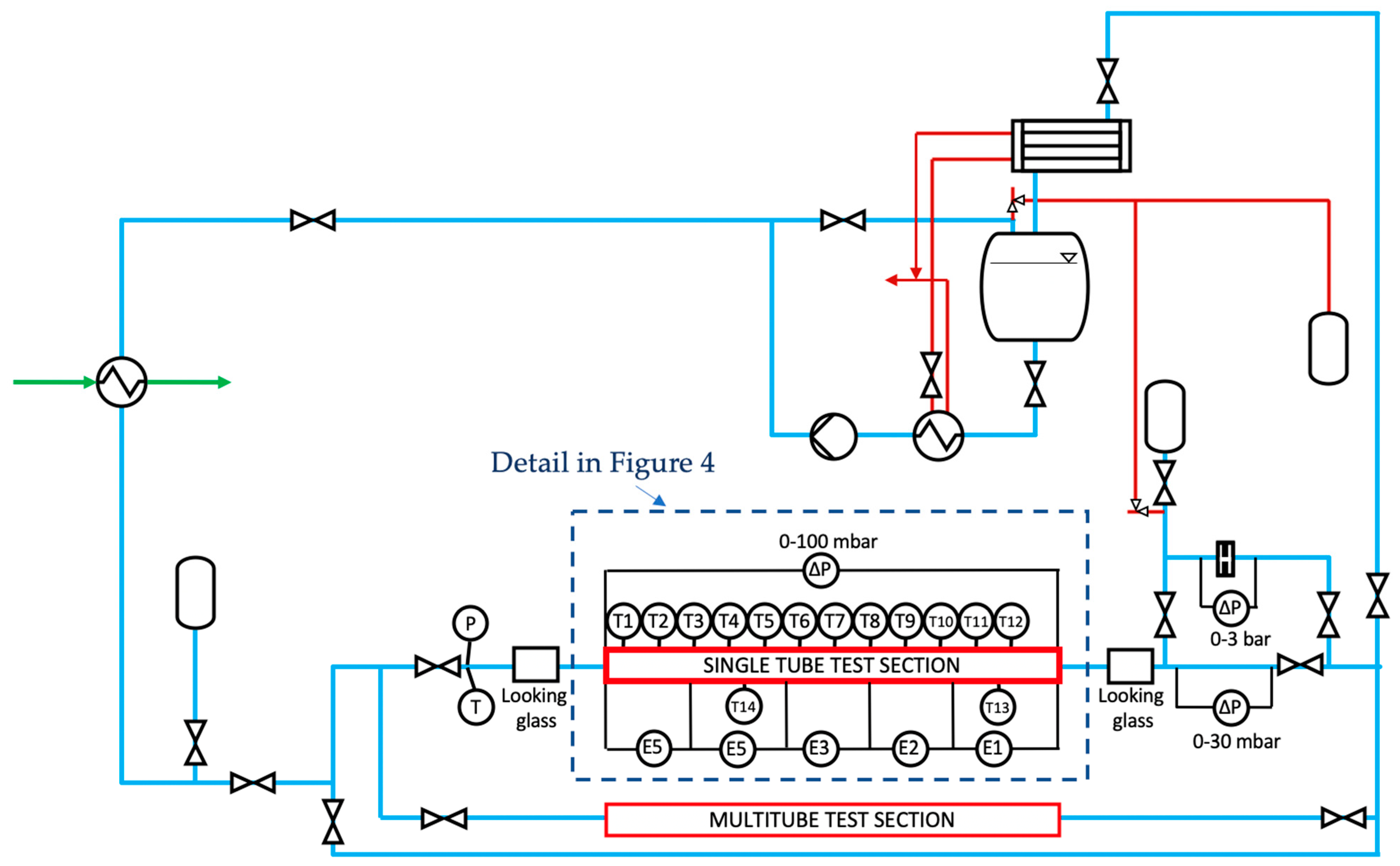
2. Experimental Set Up
2.1. Measurement
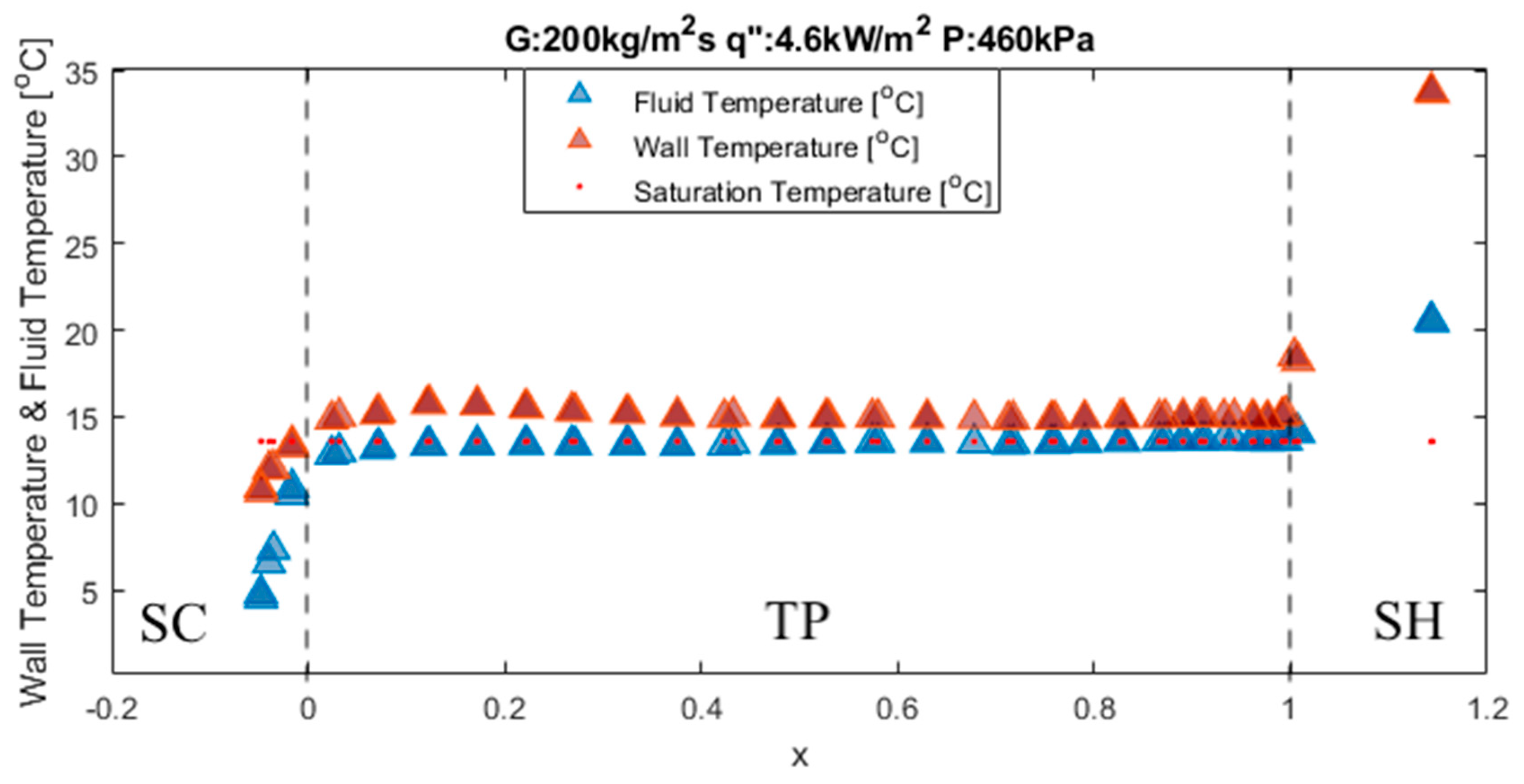
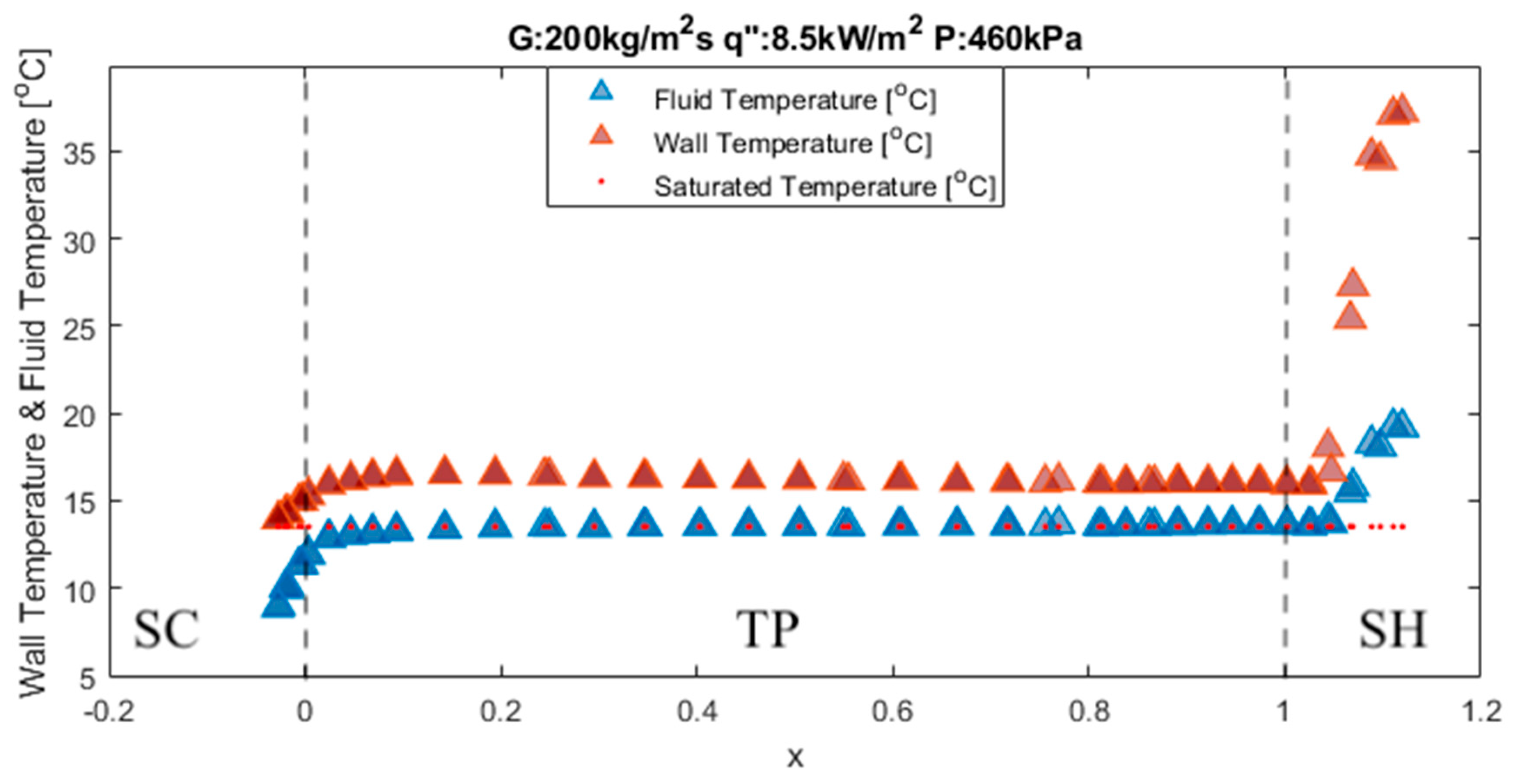
2.2. Fluid Temperature
2.3. Heat Flux
2.4. Vapor Quality
2.5. Accuracy of Measurement
2.6. Data Reduction
2.7. Frictional Pressure Drop
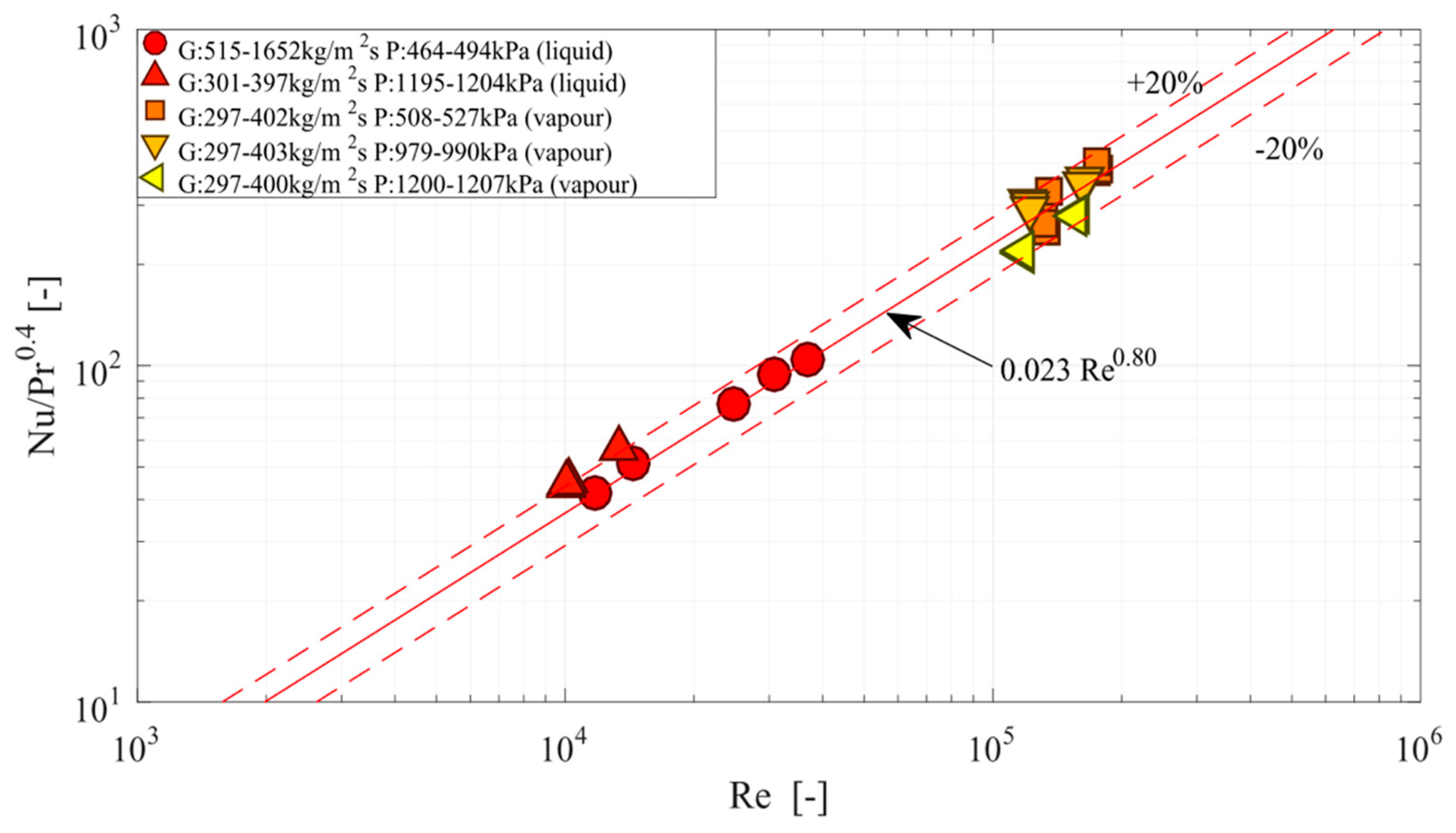
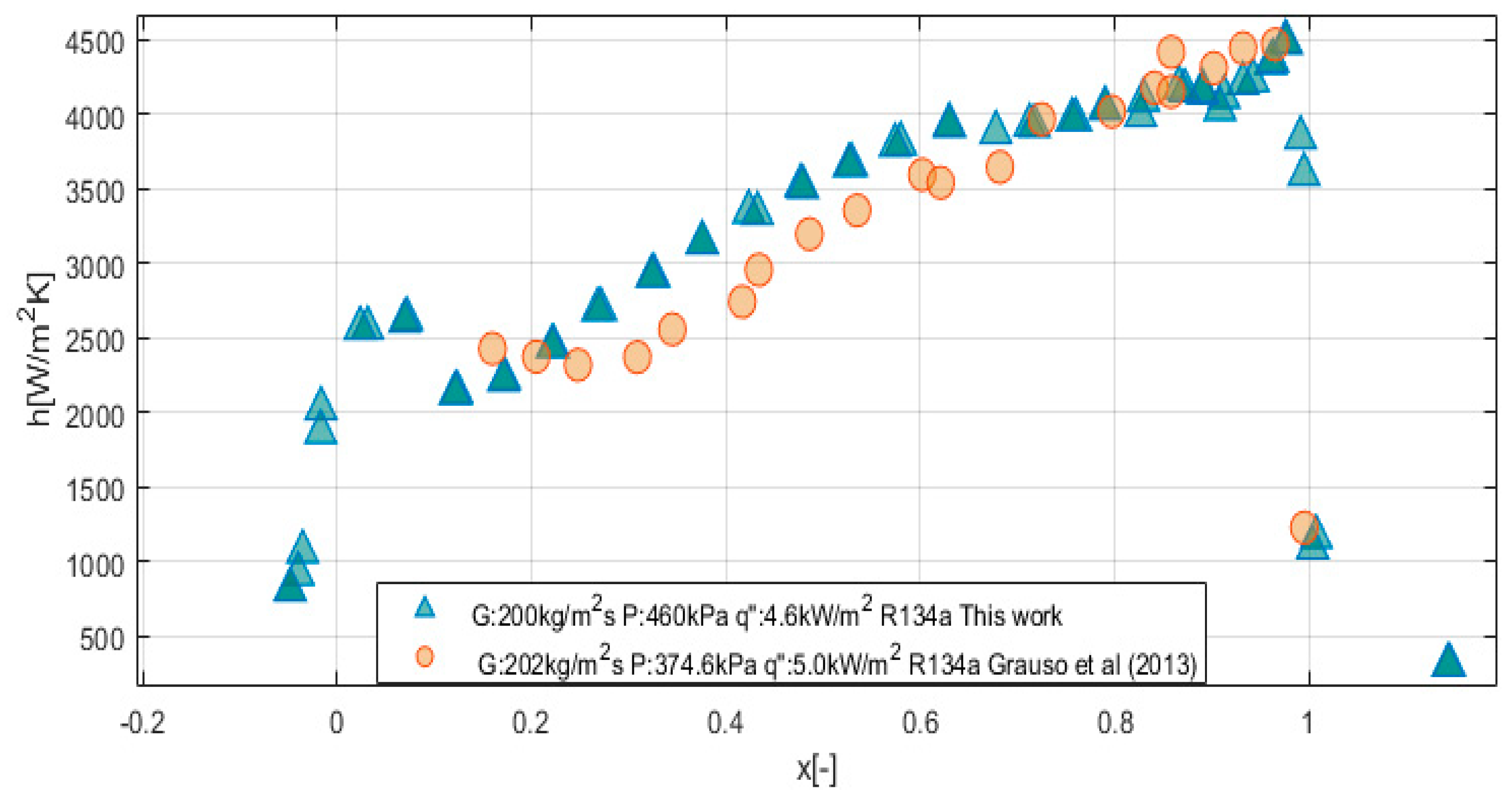
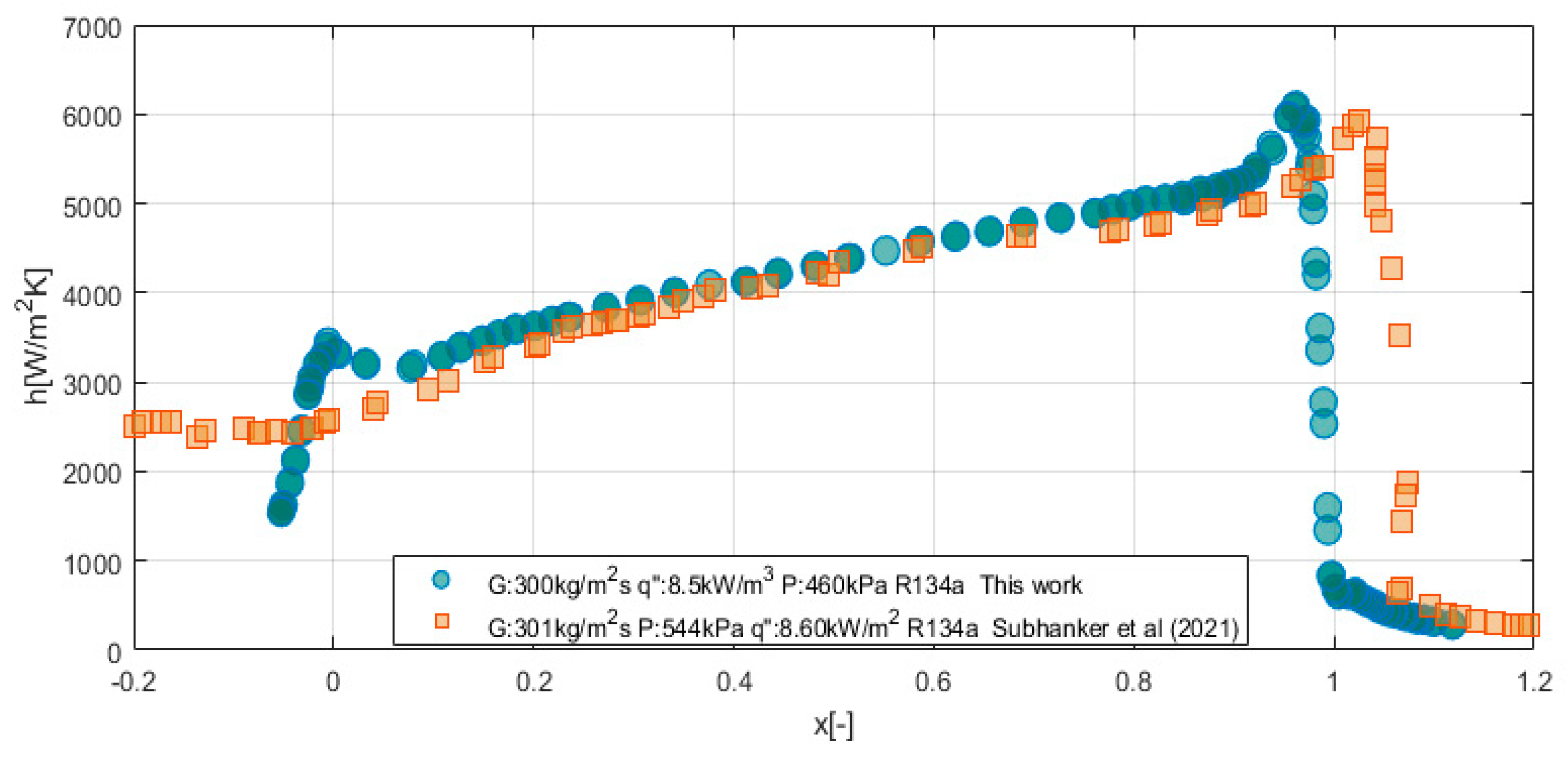
2.8. Experimental Validation
2.9. Experimental Method
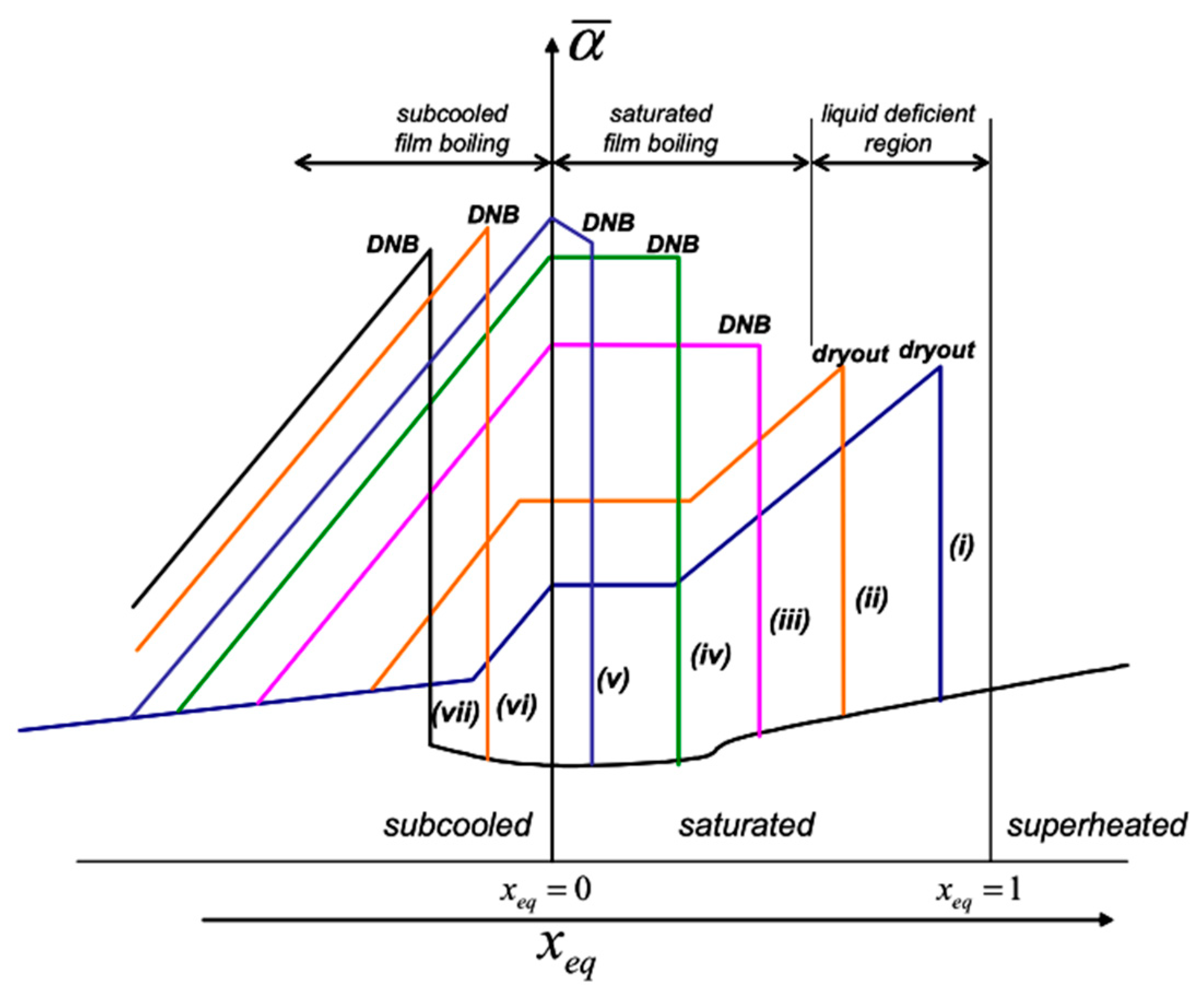
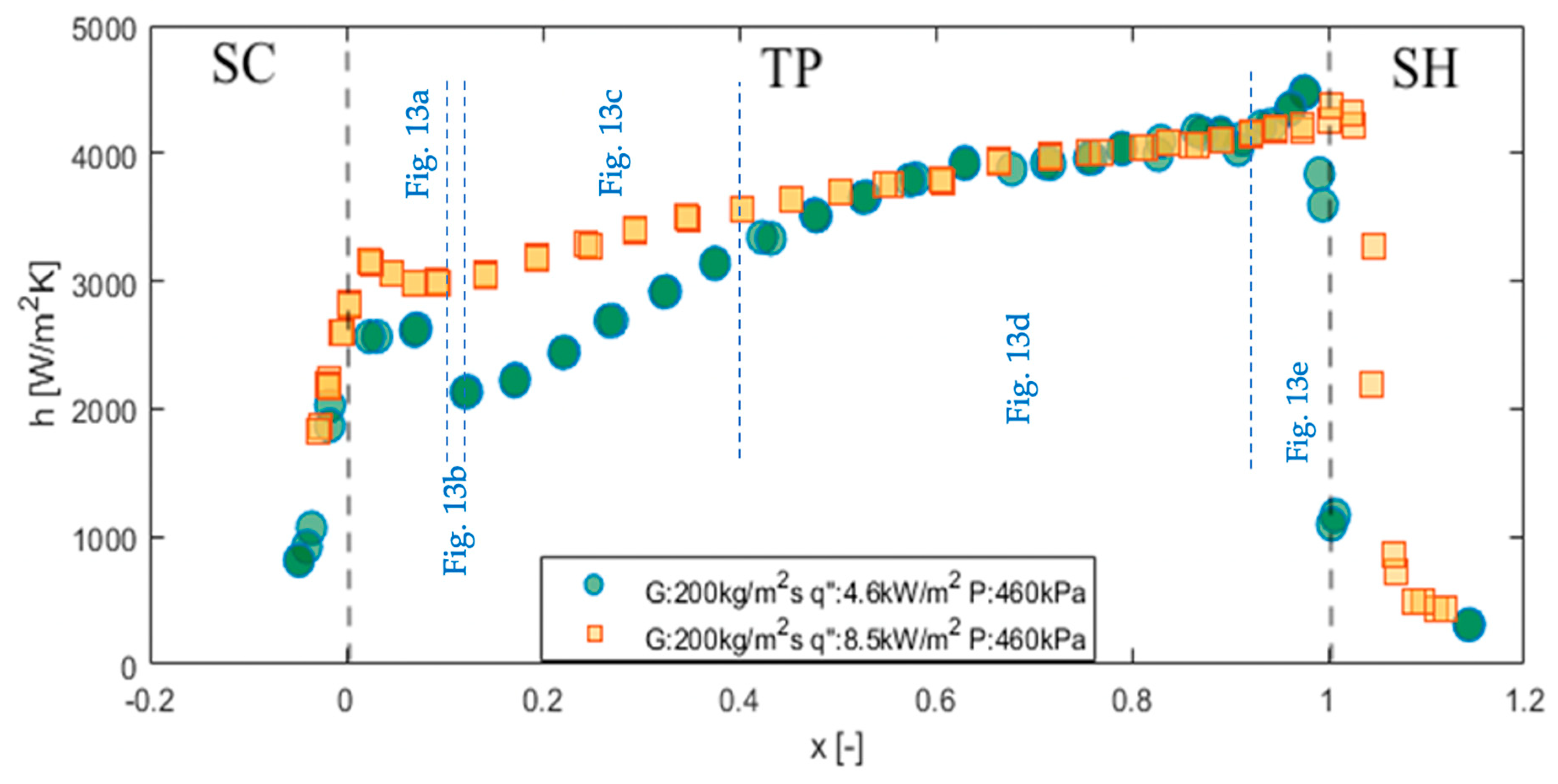
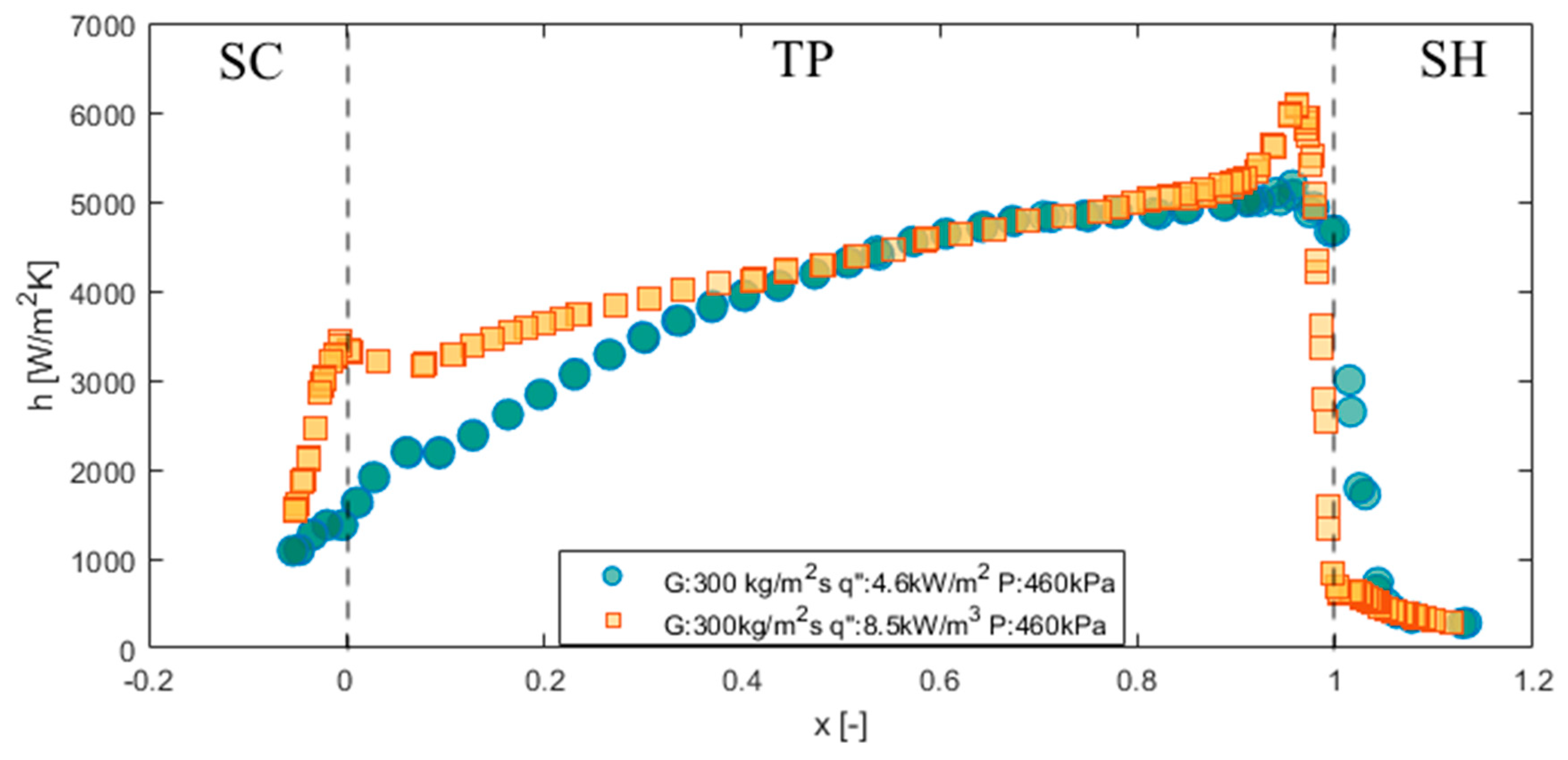
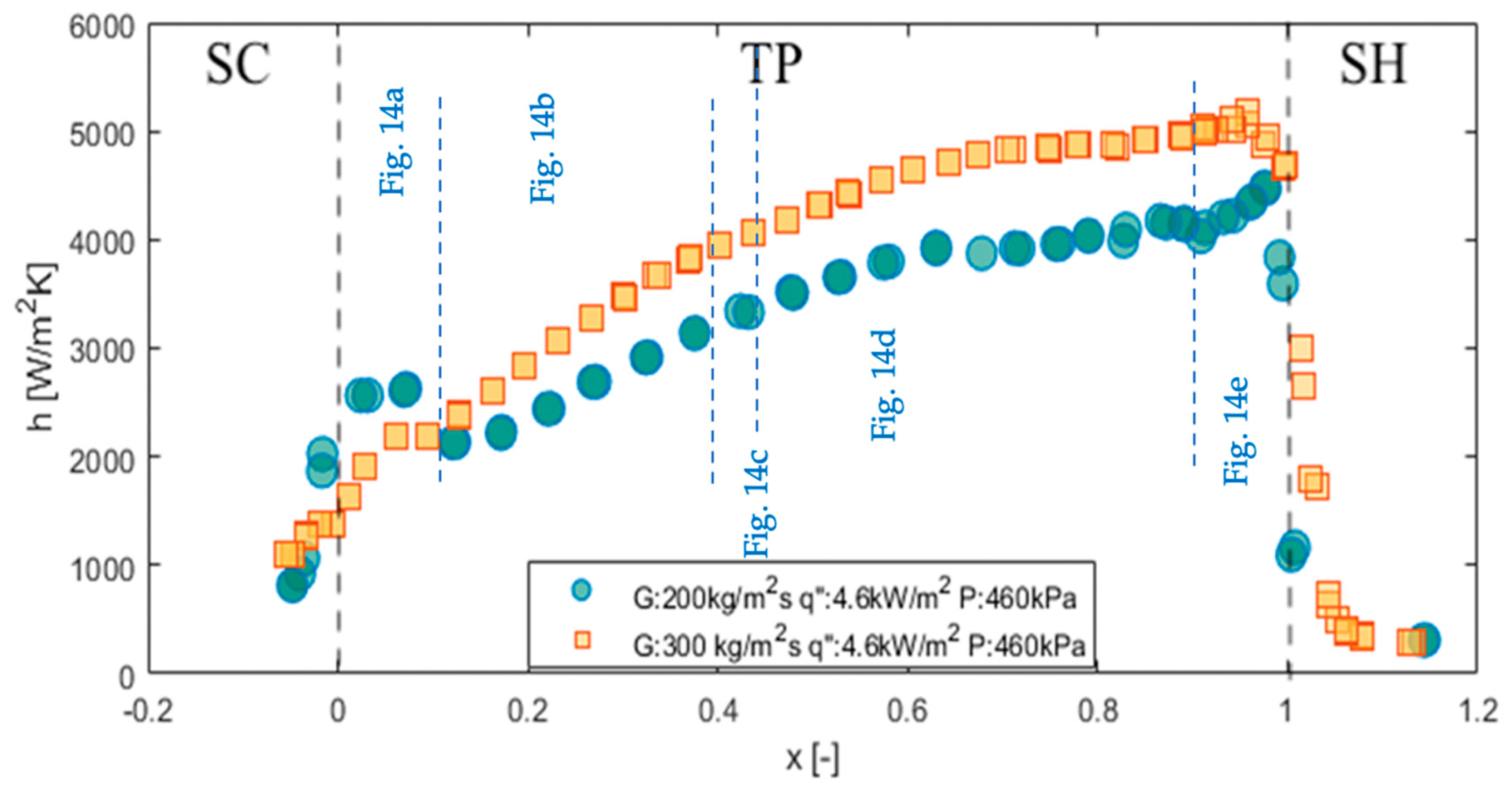
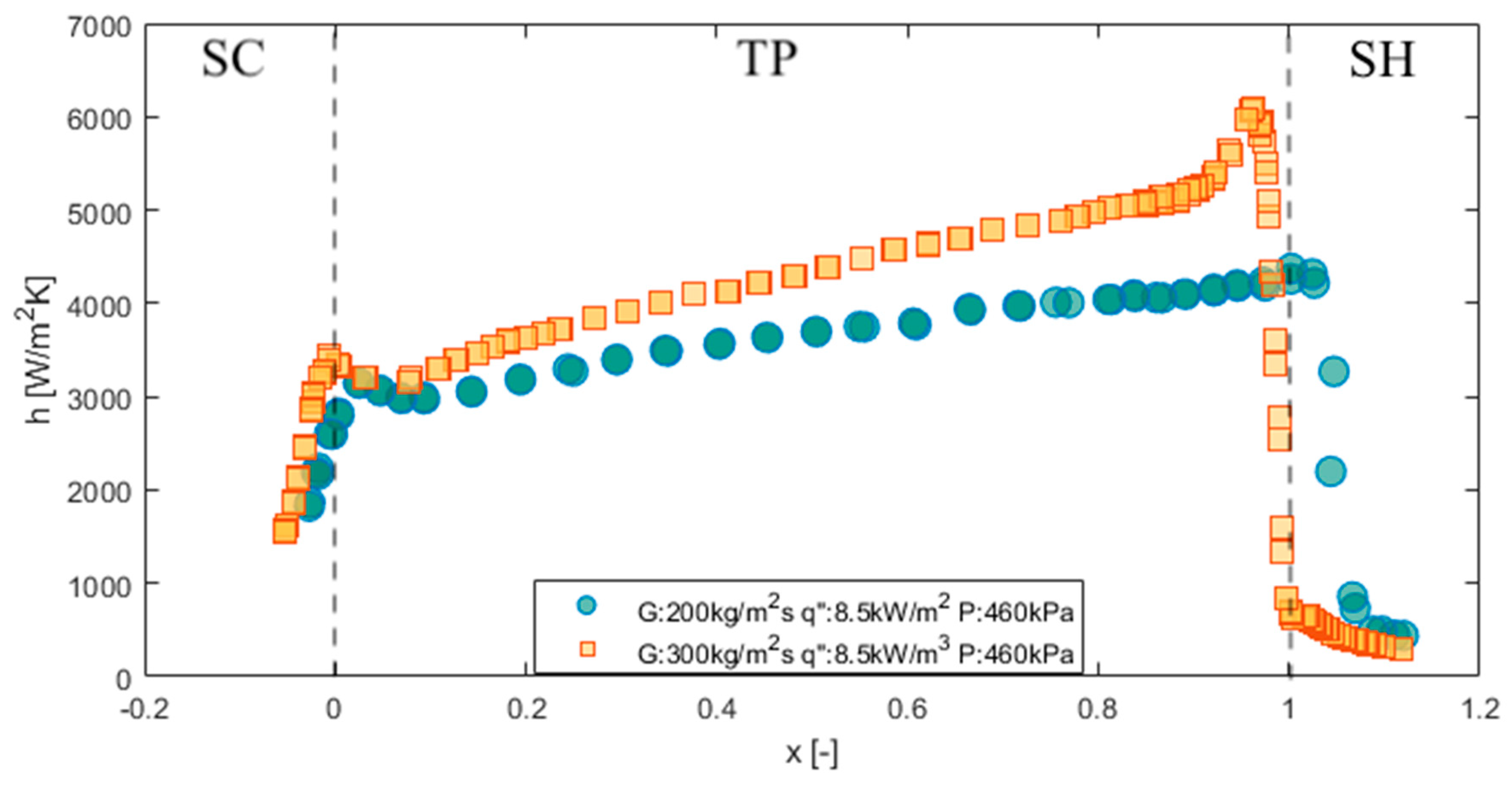
3. Results and Discussion
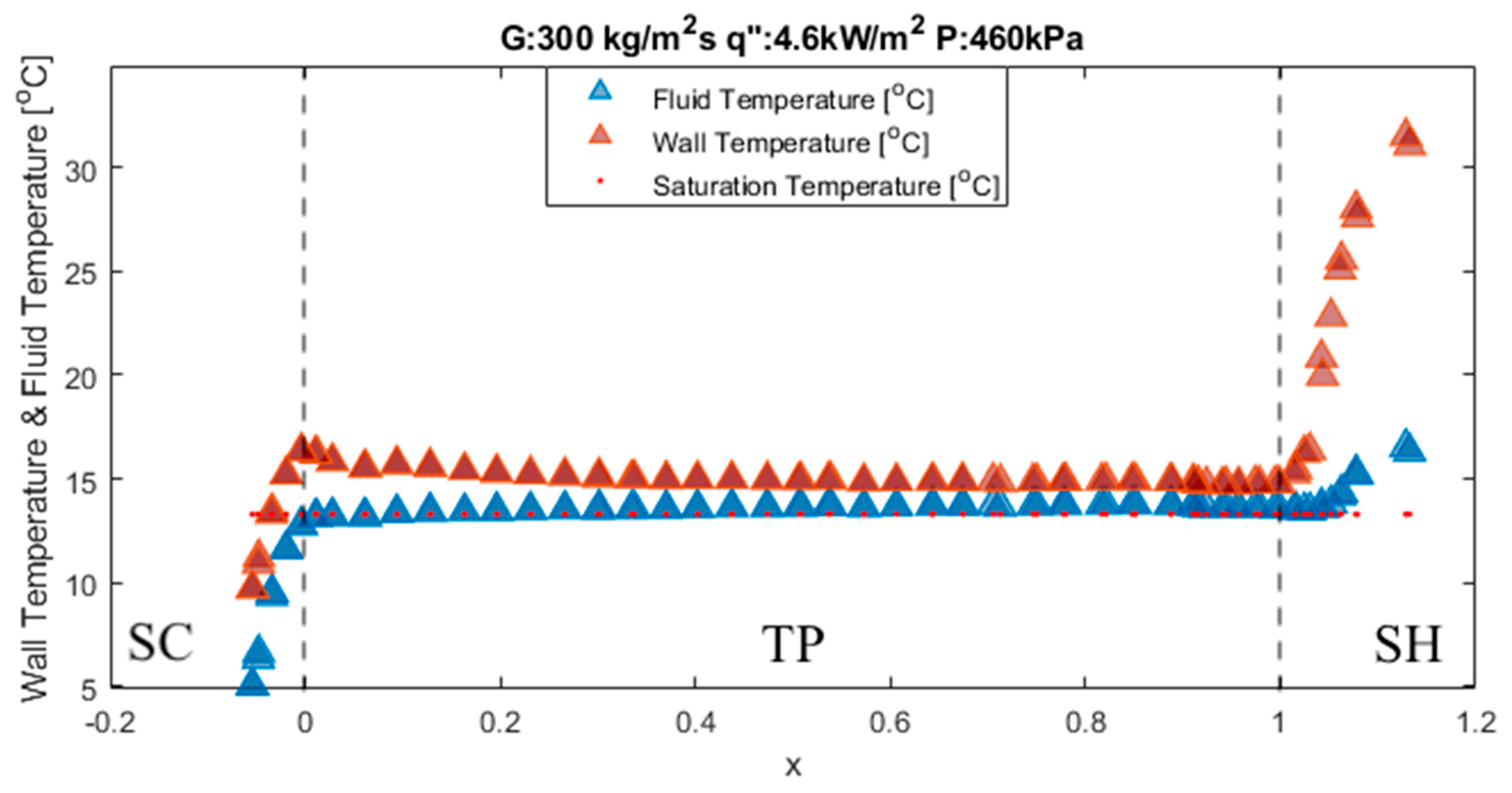
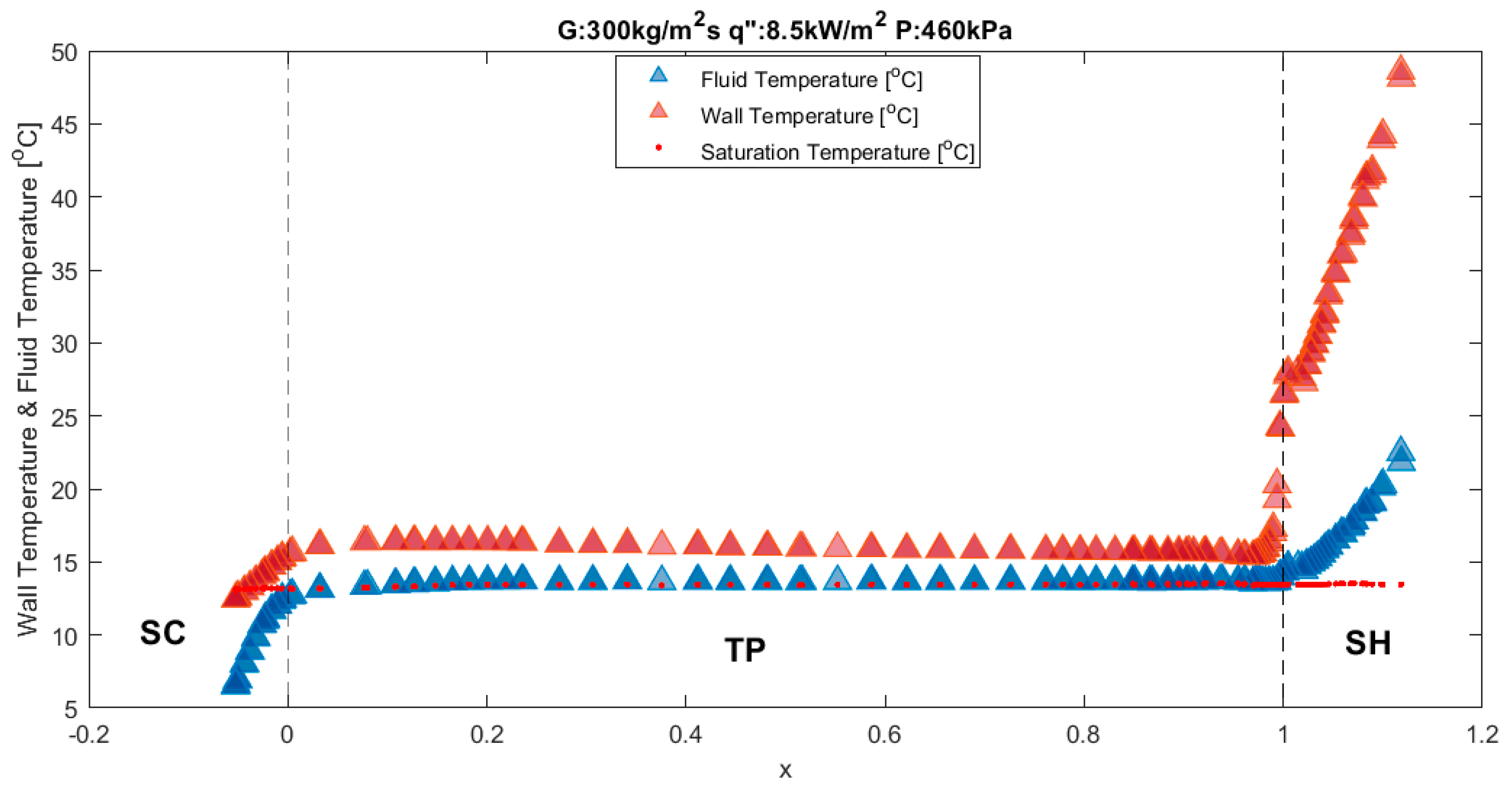
3.1. Subcooled Region
3.2. Two-Phase Region (Saturated Region)

3.3. Dry-Out Incipience and CHF
3.4. Superheated Region
Visualization of Flow Pattern
3.5. Temperature Profile
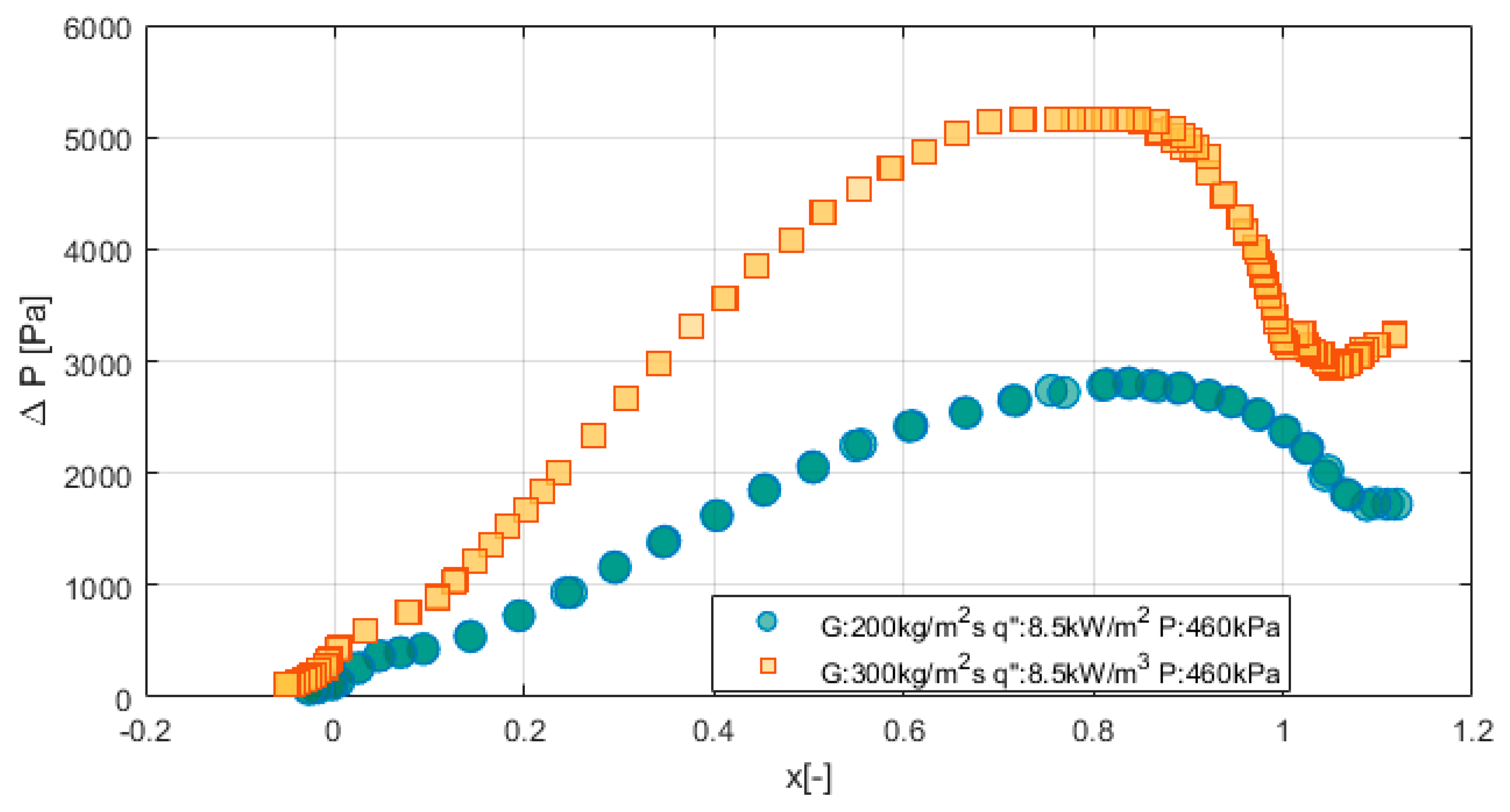
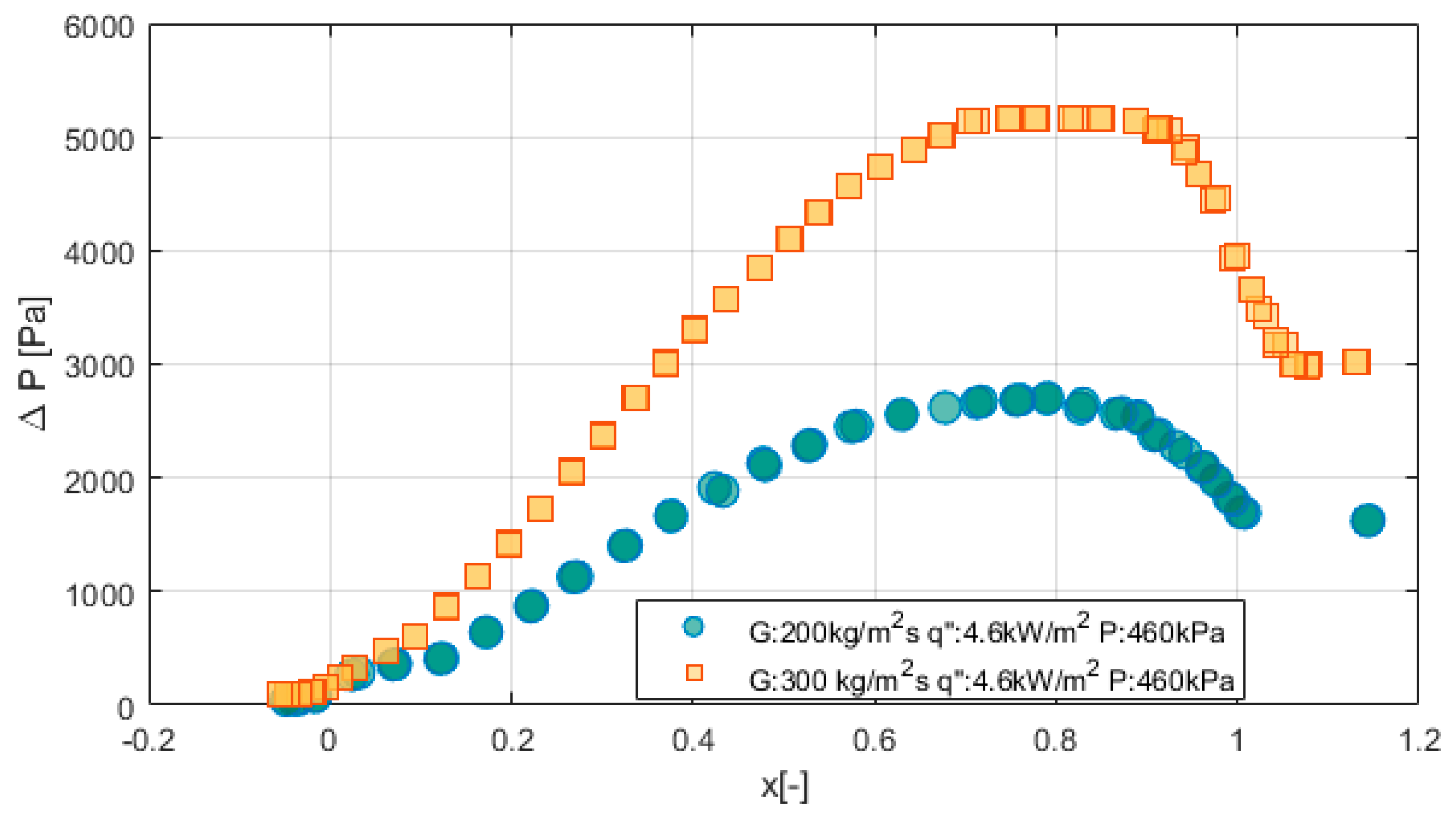
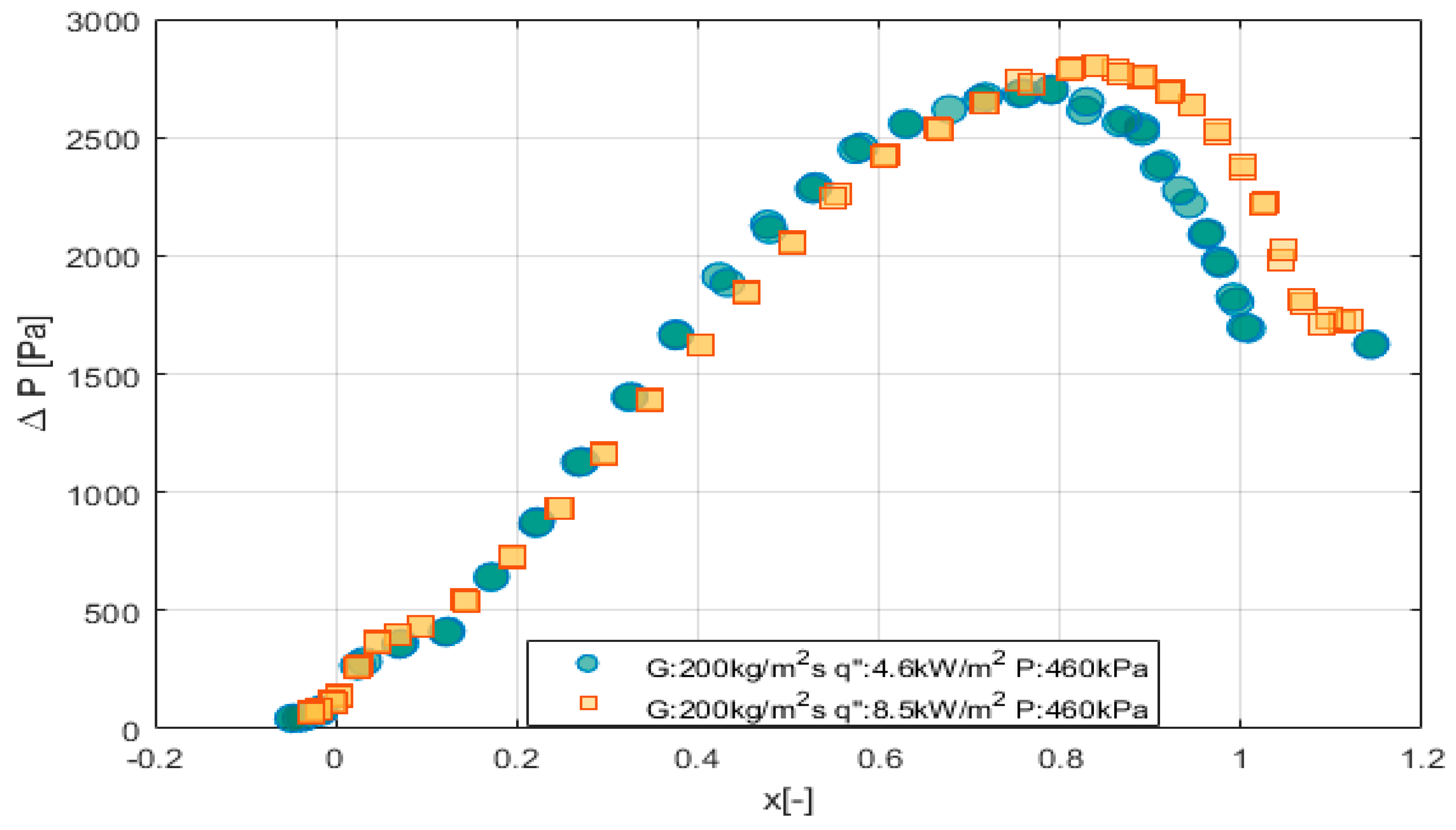
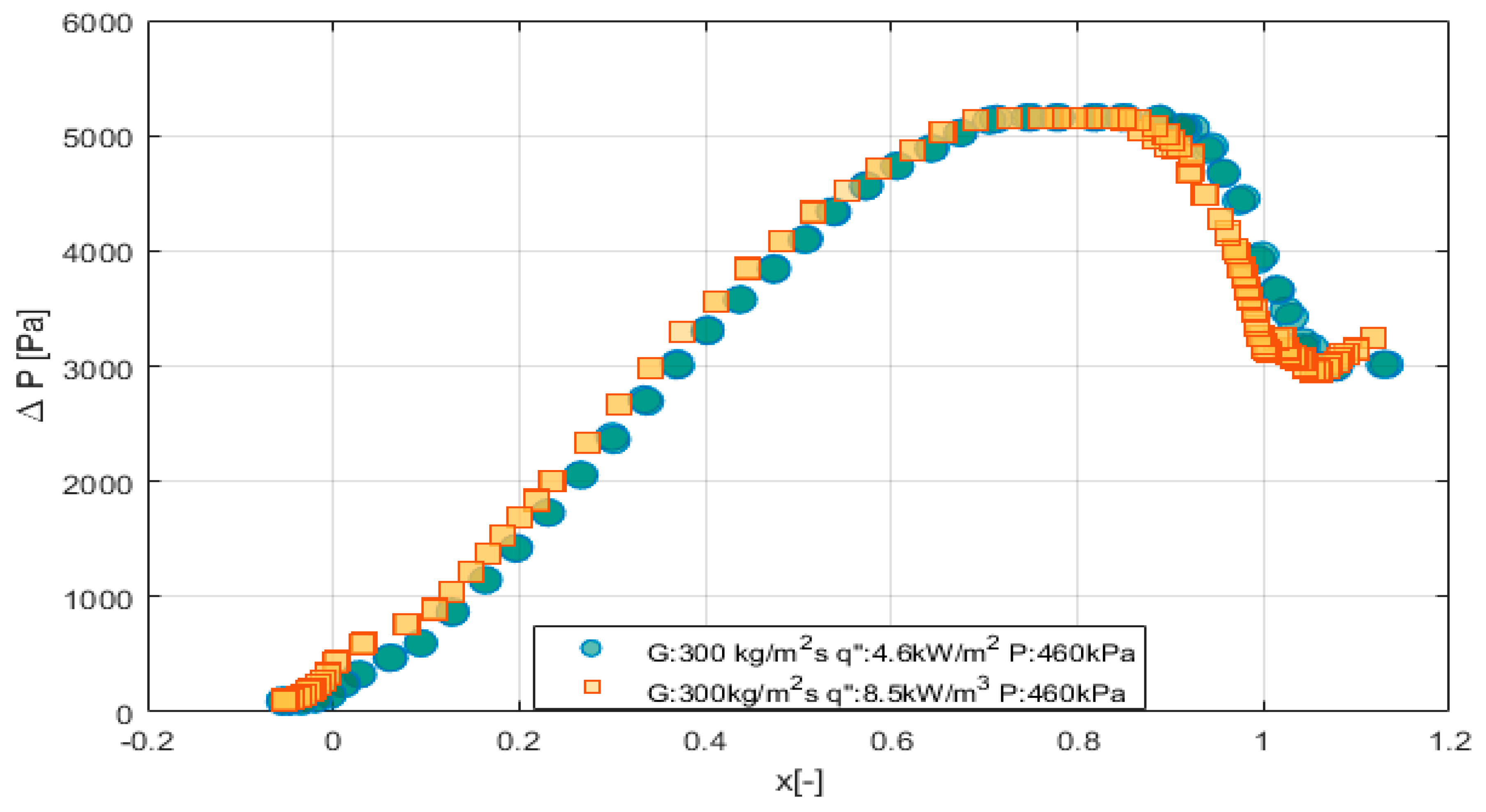
4. Pressure Drop
5. Conclusions
- At the low saturation pressure and heat flux conditions studied, a maximum peak of the heat transfer coefficient near the vapor quality of zero (0) was observed. This peak was sensitive to heat flux and insensitive to mass flux.
- After the local maximum peak of the heat transfer coefficient reached near zero vapor quality, heat transfer coefficient deterioration is observed until a local minimum is reached. The decrease in heat transfer coefficient to a local minimum is observed at a low vapor quality region below 0.1 (i.e., x < 0.1).
- Heat flux had a considerable impact on the heat transfer coefficient in the low-vapor-quality region. However, this influence was reduced as vapor quality increased. The influence of mass flux in the low vapor quality region was mild, except at low heat fluxes. In the high vapor quality region, the effect of mass flux on the heat transfer coefficient was highly pronounced. Generally, in the low vapor quality region, nucleate boiling heat transfer was the dominant mechanism controlling the heat transfer coefficient, whereas in the high vapor quality region, convective heat transfer was the dominant mechanism.
- The flow patterns observed were recorded with a high-speed camera to help analyze the results. The main flow patterns observed were slug, intermittent in the low-quality region, and annular and dry-out to mist in the high-quality region.
- Pressure drop varied as a function of vapor quality and mass flux in the two-phase region and superheated vapor region. There was no significant effect of heat flux on pressure drop.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| D | Channel diameter (m) |
| h | Heat transfer coefficient (W/(m2 K)) |
| G | Mass flux (kg/(m2s)) |
| k | Thermal conductivity of liquid (W/(m K)) |
| Nu | Nusselt number (hD/k) |
| Pr | Prandtl number |
| PrL | Liquid phase Prandtl number |
| PrV | Vapor phase Prandtl number |
| ReL | Liquid Reynolds number |
| Tsub | Inlet subcooling (K) |
| ReV | Vapor Reynolds number |
| Re2φ | Two-phase Reynolds |
| x | Vapor quality |
| q″ | Heat Flux (Wm−2) |
| hlv | Latent heat of vaporization (J/(kg K) |
| hl | Specific enthalpy of liquid (J/(kg K)) |
| g | Acceleration due to gravity (ms−2) |
| A | Cross section area (m2) |
| Tw,i | Inner wall temperature (K) |
| Tf | Fluid temperature (K) |
References
- Del Col, D. Flow boiling of halogenated refrigerants at high saturation temperature in a horizontal smooth tube. Exp. Therm. Fluid Sci. 2010, 34, 234–245. [Google Scholar] [CrossRef]
- Copetti, J.B.; Macagnan, M.H.; Zinani, F.; Kunsler, N.L.F. Flow boiling heat transfer and pressure drop of R-134a in a mini tube: An experimental investigation. Exp. Therm. Fluid Sci. 2011, 35, 636–644. [Google Scholar] [CrossRef]
- Xu, Y.; Fang, X.; Li, G.; Li, D.; Yuan, Y. An experimental study of flow boiling heat transfer of R134a and evaluation of existing correlations. Int. J. Heat Mass Transf. 2016, 92, 1143–1157. [Google Scholar] [CrossRef]
- Kamel, M.S.; Lezsovits, F.; Hussein, A.K. Experimental studies of flow boiling heat transfer by using nanofluids A critical recent review. J. Therm. Anal. Calorim. 2019, 138, 4019–4043. [Google Scholar] [CrossRef]
- Van den Bergh, W.J.; Moran, H.R.; Dirker, J.; Markides, C.N.; Meyer, J.P. Effect of low heat and mass fluxes on the boiling heat transfer coefficient of R-245fa. Int. J. Heat Mass Transf. 2021, 180, 121743. [Google Scholar] [CrossRef]
- Simon, J.R.; Bandhauer, T.M. An experimentally validated evaporative phase change heat transfer model for low mass flux applications using R134a in plate heat exchangers. Int. J. Refrig. 2021, 131, 604–614. [Google Scholar] [CrossRef]
- Fang, X.; Zhuang, F.; Chen, C.; Wu, Q.; Chen, Y.; Chen, Y.; He, Y. Saturated flow boiling heat transfer: Review and assessment of prediction methods. Heat Mass Transf. 2019, 55, 197–222. [Google Scholar] [CrossRef]
- Smith, M.K.; Wattelet, J.P.; Newell, T.A. A Study of Evaporation Heat Transfer Coefficient Correlations at Low Heat and Mass Fluxes for Pure Refrigerants and Refrigerant Mixtures; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1993. [Google Scholar]
- Charnay, R.; Revellin, R.; Bonjour, J. Flow boiling heat transfer in minichannels at high saturation temperatures: Part I—Experimental investigation and analysis of the heat transfer mechanisms. Int. J. Heat Mass Transf. 2015, 87, 636–652. [Google Scholar] [CrossRef]
- Charnay, R.; Revellin, R.; Bonjour, J. Flow boiling heat transfer in minichannels at high saturation temperatures: Part II—Assessment of predictive methods and impact of flow regimes. Int. J. Heat Mass Transf. 2015, 87, 653–672. [Google Scholar] [CrossRef]
- Charnay, R.; Revellin, R.; Bonjour, J. Flow boiling characteristics of R-245fa in a minichannel at medium saturation temperatures. Exp. Therm. Fluid Sci. 2014, 59, 184–194. [Google Scholar] [CrossRef]
- Charnay, R.; Bonjour, J.; Revellin, R. Experimental investigation of R-245fa flow boiling in minichannels at high saturation temperatures: Flow patterns and flow pattern maps. Int. J. Heat Fluid Flow 2014, 46, 1–16. [Google Scholar] [CrossRef]
- Wijayanta, A.T.; Miyazaki, T.; Koyama, S. Note on refrigerant R134a flow maldistribution in a header type evaporator. Int. J. Refrig. 2018, 95, 1–9. [Google Scholar] [CrossRef]
- Dorao, C.A.; Drewes, S.; Fernandino, M. Can the heat transfer coefficients for single-phase flow and for convective flow boiling be equivalent? Appl. Phys. Lett. 2018, 112, 064101. [Google Scholar] [CrossRef]
- Dorao, C.A.; Fernandez, O.B.; Fernandino, M. Experimental Study of Horizontal Flow Boiling Heat Transfer of R134a at a Saturation Temperature of 18.6 °C. J. Heat Transf. 2017, 139, 111510. [Google Scholar] [CrossRef]
- Tibiriçá, C.B.; Ribatski, G. Flow boiling in micro-scale channels-Synthesized literature review. Int. J. Refrig. 2013, 36, 301–324. [Google Scholar] [CrossRef]
- Paul, S.; Fernandino, M.; Dorao, C.A. On the scaling of convective boiling heat transfer coefficient. Int. J. Heat Mass Transf. 2021, 164, 120589. [Google Scholar] [CrossRef]
- Kanizawa, F.T.; Tibiriçá, C.B.; Ribatski, G. Heat transfer during convective boiling inside microchannels. Int. J. Heat Mass Transf. 2016, 93, 566–583. [Google Scholar] [CrossRef]
- Da Silva Lima, R.J.; Quibén, J.M.; Thome, J.R. Flow boiling in horizontal smooth tubes: New heat transfer results for R-134a at three saturation temperatures. Appl. Therm. Eng. 2009, 29, 1289–1298. [Google Scholar] [CrossRef]
- Celen, A.; Dalkılıç, A.S. A complete evaluation method for the experimental data of flow boiling in smooth tubes. Int. Commun. Heat Mass Transf. 2017, 89, 108–121. [Google Scholar] [CrossRef]
- Filho, E.P.B.; Jabardo, J.M.S. Convective boiling performance of refrigerant R-134a in herringbone and microfin copper tubes. Int. J. Refrig. 2006, 29, 81–91. [Google Scholar] [CrossRef]
- Chiapero, E.M.; Fernandino, M.; Dorao, C.A. Experimental results on boiling heat transfer coefficient, frictional pressure drop and flow patterns for R134a at a saturation temperature of 34 °C. Int. J. Refrig. 2014, 40, 317–327. [Google Scholar] [CrossRef]
- Balachander, P.; Raja, B.; Lal, D.M. Evaporative heat transfer characteristics of R404A and R134a under varied heat flux conditions. Exp. Heat Transf. 2012, 25, 254–265. [Google Scholar] [CrossRef]
- Jabardo, J.M.S.; Filho, E.P.B. Convective boiling of halocarbon refrigerants flowing in a horizontal copper tube—An experimental study. Exp. Therm. Fluid Sci. 2000, 23, 93–104. [Google Scholar] [CrossRef]
- Barbosa, J.R.; Hewitt, G.F. A Thermodynamic Nonequilibrium Slug Flow Model. J. Heat Transfer. 2005, 127, 323–331. [Google Scholar] [CrossRef]
- Barbosa, J.R. Two-phase non-equilibrium models: The challenge of improving phase change heat transfer prediction. J. Braz. Soc. Mech. Sci. Eng. 2005, 27, 31–45. [Google Scholar] [CrossRef][Green Version]
- Collier, J.G. Convective Boiling and Condensation; McGraw-Hill: Maidenhead, UK, 1981. [Google Scholar]
- Kandlikar, S.G. Development of a flow boiling map for suboooled and saturated flow boiling of different fluids inside circular tubes. J. Heat Transf. 1991, 113, 190–200. [Google Scholar] [CrossRef]
- Kandlbinder, T. Experimental Investigation of Forced and Boiling of Hydrocarbons Mixtures. Ph.D. Thesis, University of London, London, UK, 1997. [Google Scholar]
- Urso, M.E.D.; Wadekar, V.V.; Hewitt, G.F. Flow Boiling at Low Mass Flux. Available online: http://www.ihtcdigitallibrary.com/jp/conferences/4eae15a77edee960,7dccb3ab77120b0d,7385d00257f4745d.html (accessed on 31 October 2021).
- Chiapero, E.M.; Fernandino, M.; Dorao, C. Research, and Undefined 2012. Study of the Influence of Axial Conduction in a Boiling Heated Pipe. Available online: https://www.sciencedirect.com/science/article/pii/S0263876211004795 (accessed on 26 October 2021).
- Lemmon, E.; McLinden, M.; Huber, M. NIST Standard Reference Database 23-NIST Thermodynamic and Transport Properties REFPROP, Version 7.0. 2002. Available online: https://www.nist.gov/publications/nist-standard-reference-database-23-nist-thermodynamic-and-transport-properties-refprop (accessed on 26 October 2021).
- Enoki, K.; Ono, M.; Okawa, T.; Akisawa, A.; Mori, H.; Kristiawan, B.; Wijayanta, A.T. Two-phase flow regimes of refrigerant R134a in an oscillating horizontal rectangular minichannel conduit. Int. J. Refrig. 2020, 118, 261–268. [Google Scholar] [CrossRef]
- Sorum, M. Experimental Investigation of the Impact in the Heat Transfer Coefficient and Pressure Drop during Boiling Flow Instabilities. Master’s Thesis, University of Kragujevac, Kragujevac, Serbia, June 2014. [Google Scholar]
- Dittus, F.W.; Boelter, L.M.K. Communications in Heat and Undefined 1985. Heat Transfer in Automobile Radiators of the Tubular Type. Available online: https://www.researchgate.net/profile/Ildiko-Kurucz/post/correlation_for_the_Nusselt_number_in_channel/attachment/59d642c979197b807799e63b/AS%3A440040569479168%401481925255396/download/1-s2.0-073519338590003X-main.pdf (accessed on 26 October 2021).
- Grauso, S.; Mastrullo, R.; Mauro, A.W.; Thome, J.R.; Vanoli, G.P. Flow pattern map, heat transfer and pressure drops during evaporation of R-1234ze(E) and R134a in a horizontal, circular smooth tube: Experiments and assessment of predictive methods. Int. J. Refrig. 2013, 36, 478–491. [Google Scholar] [CrossRef]
- Dorao, C.A. Engineering Science and Undefined 2015. Effect of Inlet Pressure and Temperature on Density Wave Oscillations in a Horizontal Channel. Available online: https://www.sciencedirect.com/science/article/pii/S0009250915002213 (accessed on 26 October 2021).
- Park, I.W.; Ryu, J.; Fernandino, M.; Dorao, C.A. Can flow oscillations during flow boiling deteriorate the heat transfer coefficient? Appl. Phys. Lett. 2018, 113, 154102. [Google Scholar] [CrossRef]
- La Forgia, N.; Dorao, C.A.; Fernandino, M. Experimental investigation and discussion of heat transfer mechanisms during flow boiling in mini-channels using refrigerant R134A. In Proceedings of the ASME 2016 14th International Conference on Nanochannels, Microchannels, and Minichannels, ICNMM 2016, Collocated with the ASME 2016 Heat Transfer Summer Conference and the ASME 2016 Fluids Engineering Division Summer Meeting, Washington, DC, USA, 10–14 July 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Sørum, M.; Dorao, C.A. Experimental study of the heat transfer coefficient deterioration during density wave oscillations. Chem. Eng. Sci. 2015, 132, 178–185. [Google Scholar] [CrossRef]
- Ruspini, L.C. Experimental and Numerical Investigation on Two-Phase Flow. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2013. [Google Scholar]
- Balasubramanian, K.; Lee, P.S.; Teo, C.J.; Chou, S.K. Flow boiling heat transfer and pressure drop in stepped fin microchannels. Int. J. Heat Mass Transf. 2013, 67, 234–252. [Google Scholar] [CrossRef]
- Charnay, R. Experimental Study of Flow Boiling in Horizontal Minichannels at High Saturation Temperature. Ph.D. Thesis, INSA Lyon, Villeurbanne, France, 2015. [Google Scholar]
- Deng, H.; Fernandino, M.; Dorao, C.A. Flow boiling in a horizontal tube at high vapor qualities. In Proceedings of the ASME 2016 14th International Conference on Nanochannels, Microchannels, and Minichannels, ICNMM 2016, Collocated with the ASME 2016 Heat Transfer Summer Conference and the ASME 2016 Fluids Engineering Division Summer Meeting, Washington, DC, USA, 10–14 July 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Copetti, J.B.; Macagnan, M.H.; Kunsler, N. Boiling of R-134a in horizontal mini tube. J. Braz. Soc. Mech. Sci. Eng. 2011, 33, 220–226. [Google Scholar] [CrossRef][Green Version]



| Experimental Condition | Mass Flux (G (kg/(m2s)) | Heat Flux (q″ (kW/m2)) | Saturation Pressure (P (kPa)) |
|---|---|---|---|
| 1 | 200 | 4.6 | 460 |
| 2 | 200 | 8.5 | 460 |
| 3 | 300 | 4.6 | 460 |
| 4 | 300 | 8.5 | 460 |
| Properties | Saturation Pressure = 460 kPa |
|---|---|
| Saturation Pressure | 13.150 °C |
| Liquid Density | 1250.0 kg/m3 |
| Vapor Density | 22.397 kg/m3 |
| Liquid Enthalpy | 217.92 KJ/kg |
| Vapor Enthalpy | 406.06 KJ/kg |
| Liquid Viscosity | 2.258 × 10−4 Pa·s |
| Vapor Viscosity | 1.1219 × 10−5 Pa·s |
| Liquid Conductivity | 86.247 mW/m·K |
| Vapor Conductivity | 12.690 mW/m·K |
| Surface Tension | 9.6121 mN/m |
| Variable | Symbol | Accuracy | Information |
|---|---|---|---|
| Mass flux | G | 0.2 % of the reading | Given by the supplier |
| Pressure drop | ΔP | 0.075 % full scale (fs = 50 kPa) | Given by the supplier |
| Absolute pressure | P | 0.04 % full scale (fs = 25 bar) | Given by the supplier |
| Temperature | T | 0.1 K | Inhouse calibration |
| Heat flux | q″ | 3% of the reading | Inhouse calibration |
| Parameter | Symbol | Error |
|---|---|---|
| Mass flux | G | ±10 kg/m2s |
| Inlet pressure | Pi | ±10 kPa |
| Inlet temperature | Ti | ±0.2 °C |
| Heat flux (all 5 zones) | q″ | ±<40 W |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bediako, E.G.; Dančová, P.; Vít, T. Experimental Study of Horizontal Flow Boiling Heat Transfer Coefficient and Pressure Drop of R134a from Subcooled Liquid Region to Superheated Vapor Region. Energies 2022, 15, 681. https://doi.org/10.3390/en15030681
Bediako EG, Dančová P, Vít T. Experimental Study of Horizontal Flow Boiling Heat Transfer Coefficient and Pressure Drop of R134a from Subcooled Liquid Region to Superheated Vapor Region. Energies. 2022; 15(3):681. https://doi.org/10.3390/en15030681
Chicago/Turabian StyleBediako, Ernest Gyan, Petra Dančová, and Tomáš Vít. 2022. "Experimental Study of Horizontal Flow Boiling Heat Transfer Coefficient and Pressure Drop of R134a from Subcooled Liquid Region to Superheated Vapor Region" Energies 15, no. 3: 681. https://doi.org/10.3390/en15030681
APA StyleBediako, E. G., Dančová, P., & Vít, T. (2022). Experimental Study of Horizontal Flow Boiling Heat Transfer Coefficient and Pressure Drop of R134a from Subcooled Liquid Region to Superheated Vapor Region. Energies, 15(3), 681. https://doi.org/10.3390/en15030681





