Remaining Useful Life Estimation for Underground Cable Systems Based on Historical Health Index
Abstract
1. Introduction
2. Health Index Monitoring System
2.1. Data Collection
2.2. Operating Factor
2.3. Health Index Calculation
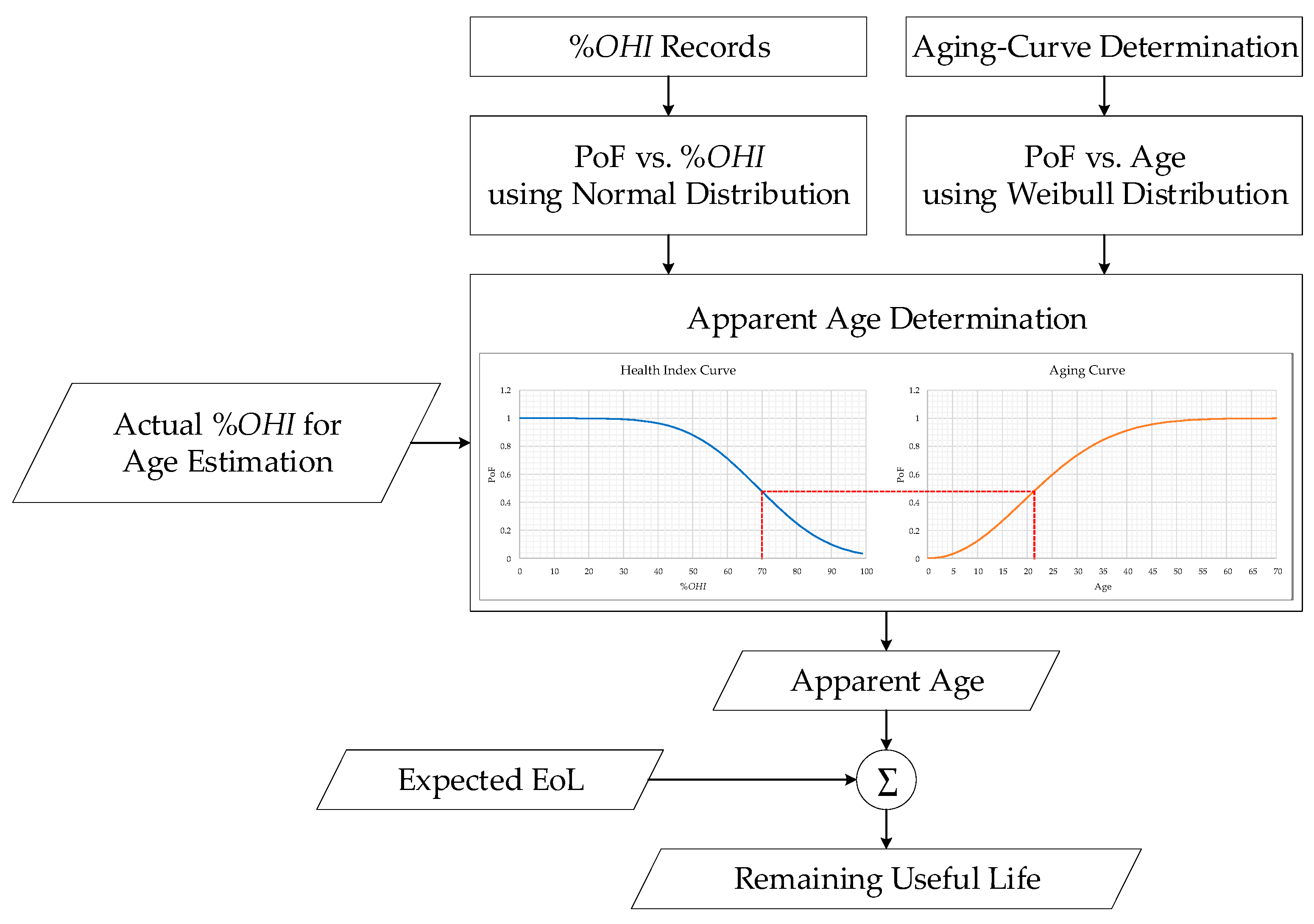
3. Remaining Useful Life Estimation
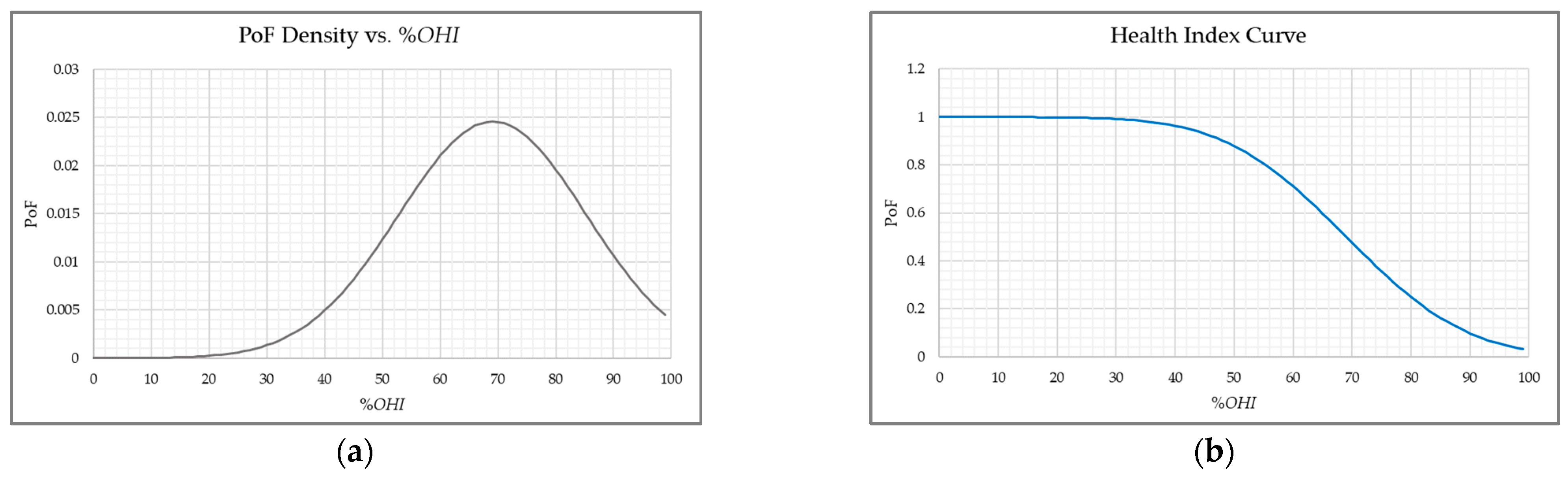
3.1. Health Index Curve Using Normal Distribution
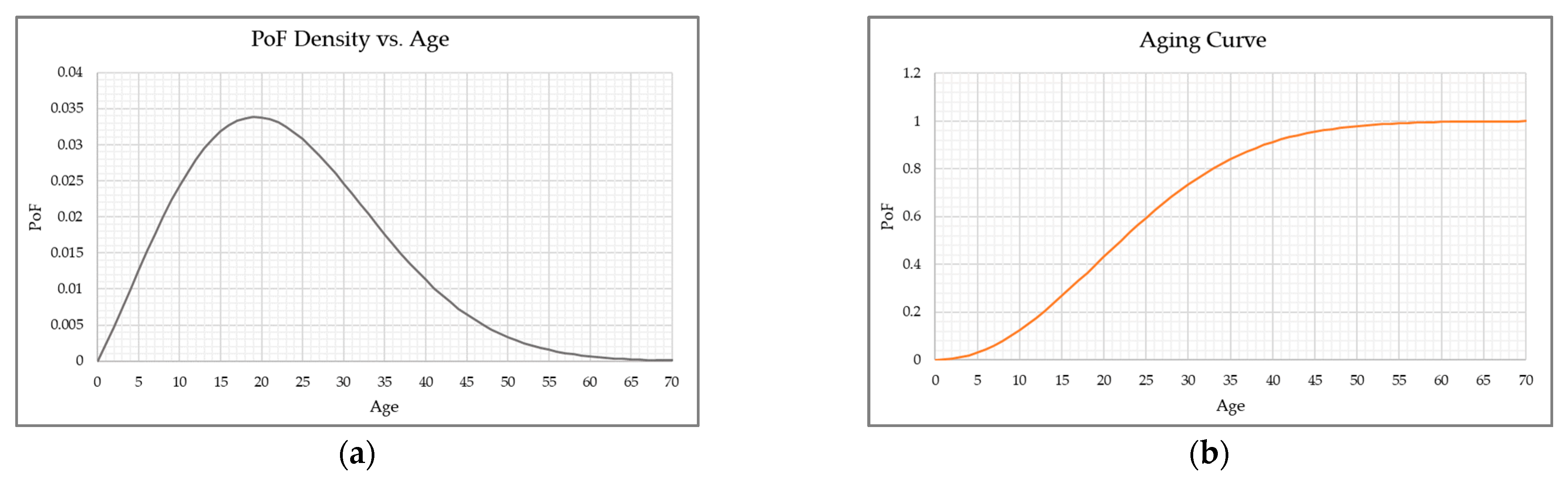
3.2. Aging Curve Using Weibull Distribution
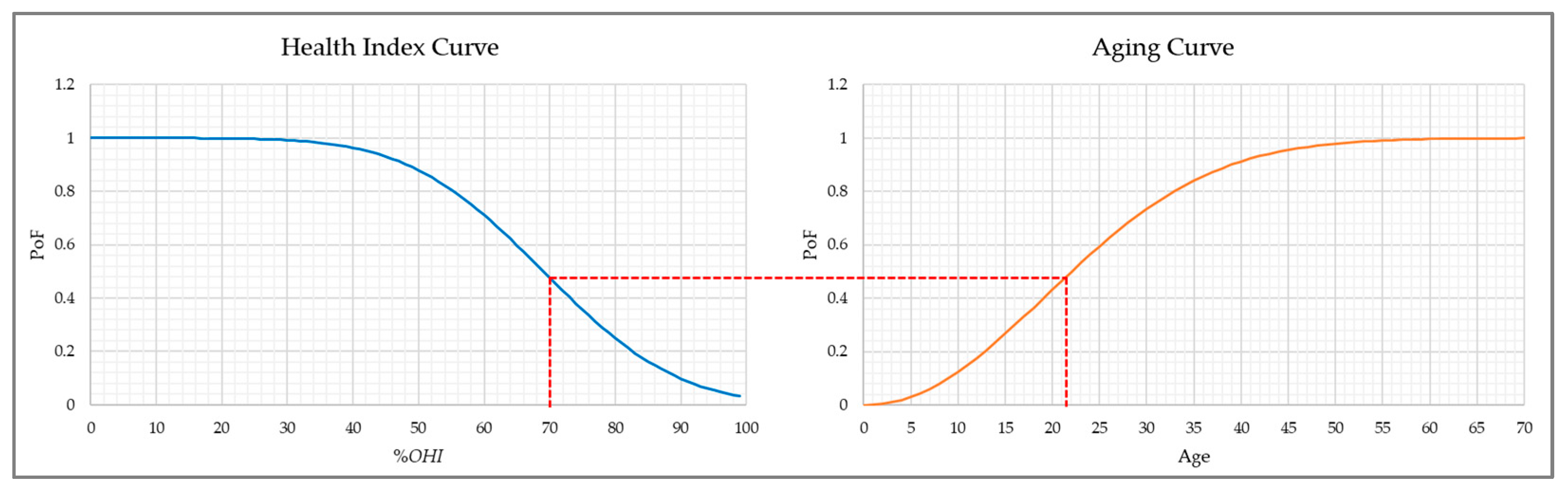
3.3. System Age Prediction
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mazzanti, G. Life and Reliability Models for High Voltage DC Extruded Cables. IEEE Electr. Insul. Mag. 2017, 33, 42–52. [Google Scholar] [CrossRef]
- Bicen, Y. Trend Adjusted Lifetime Monitoring of Underground Power Cable. Electr. Power Syst. Res. 2017, 143, 189–196. [Google Scholar] [CrossRef]
- Gulski, E.; Jongen, R. Condition Based Maintenance of Transmission Power Cables. IEEE Trans. Power Deliv. 2022, 37, 1588–1597. [Google Scholar] [CrossRef]
- IEEE Std 400-2012; Guide for Field Testing and Evaluation of the Insulation of Shielded Power Cable Systems Rated 5 kV and Above. Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2012. [CrossRef]
- Zhang, Z.; Assala, P.D.S.; Wu, L. Residual Life Assessment of 110 kV XLPE Cable. Electr. Power Syst. Res. 2018, 163, 572–580. [Google Scholar] [CrossRef]
- CIGRE. Remaining Life Management of Existing AC Underground Lines; WG B1.09; Technical Brochure No. 358; CIGRE: Paris, France, 2008. [Google Scholar]
- IEEE Std 400.2-2013; Guide for Field Testing of Shielded Power Cable Systems Using Very Low Frequency (VLF)(Less than 1 Hz). Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2013. [CrossRef]
- IEEE Std 4-2013; Standard for High-Voltage Testing Techniques. Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2013. [CrossRef]
- Buhari, M.; Levi, V.; Awadallah, S.K.E. Modelling of Ageing Distribution Cable for Replacement Planning. IEEE Trans. Power Syst. 2016, 31, 3996–4004. [Google Scholar] [CrossRef]
- Mazzanti, G. The Effects of Seasonal Factors on Life and Reliability of High Voltage AC Cables Subjected to Load Cycles. IEEE Trans. Power Deliv. 2020, 35, 2080–2088. [Google Scholar] [CrossRef]
- Naranpanawe, L.; Ma, H.; Saha, T.K.; Lee, C.; Ghosal, A. A Practical Health Index for Overhead Conductors: Experience from Australian Distribution Networks. IEEE Access 2020, 8, 218863–218873. [Google Scholar] [CrossRef]
- Liu, Y.; Xv, J.; Yuan, H.; Lv, J.; Ma, Z. Health Assessment and Prediction of Overhead Line Based on Health Index. IEEE Trans. Ind. Electron. 2019, 66, 5546–5557. [Google Scholar] [CrossRef]
- Foros, J.; Istad, M. Health Index, Risk and Remaining Lifetime Estimation of Power Transformers. IEEE Trans. Power Deliv. 2020, 35, 2612–2620. [Google Scholar] [CrossRef]
- Somsak, T.; Suwanasri, T.; Suwanasri, C. Condition Assessment of Underground Cable System Using Health Index and Conditional Multiplying Factor. In Proceedings of the 21st International Symposium on High Voltage Engineering (ISH 2019), Budapest, Hungary, 26–30 August 2019; pp. 763–776. [Google Scholar] [CrossRef]
- Li, S.; Wu, G.; Dong, H.; Yang, L.; Zhen, X. Probabilistic Health Index-Based Apparent Age Estimation for Power Transformers. IEEE Access 2020, 8, 9692–9701. [Google Scholar] [CrossRef]
- Melchor-Hernández, C.L.; Rivas-Dávalos, F.; Maximov, S.; Coria, V.; Moreno-Goytia, E.L. An Analytical Method to Estimate the Weibull Parameters for Assessing the Mean Life of Power Equipment. Int. J. Electr. Power Energy Syst. 2015, 64, 1081–1087. [Google Scholar] [CrossRef]
- Tsimberg, Y.; Lotho, K.; Dimnik, C.; Wrathall, N.; Mogilevsky, A. Determining Transmission Line Conductor Condition and Remaining Life. In Proceeding of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–5. [Google Scholar] [CrossRef]
- CIGRE. Asset Management Decision Making using different Risk Assessment Methodologies; WG C1.25; Technical Brochure No. 541; CIGRE: Paris, France, 2013. [Google Scholar]
- Liu, S.; Wang, Y.; Tian, F. Prognosis of Underground Cable via Online Data-Driven Method with Field Data. IEEE Trans. Ind. Electron. 2015, 62, 7786–7794. [Google Scholar] [CrossRef]
- Li, W. Evaluating Mean Life of Power System Equipment with Limited End-of-Life Failure Data. IEEE Trans. Power 2004, 19, 236–242. [Google Scholar] [CrossRef]
- Chimunda, S.; Nyamupangedengu, C. A Reliability Assessment Model for an Outdoor 88kV XLPE Cable Termination. Electr. Power Syst. Res. 2019, 177, 105979. [Google Scholar] [CrossRef]
- Montanari, G.C.; Fabiani, D.; Ciani, F. Partial Discharge and Aging of AC Cable Systems Under Repetitive Voltage Transient Supply. In Proceeding of the 2016 IEEE Electrical Insulation Conference (EIC), Montreal, QC, Canada, 19–22 June 2016; pp. 379–382. [Google Scholar] [CrossRef]
- CIGRE. Maintenance of HV Cable Systems; WG B1.60; Technical Brochure No. 825; CIGRE: Paris, France, 2021. [Google Scholar]
- Somsak, T.; Suwanasri, T.; Suwanasri, C. Lifetime Estimation Based Health Index and Conditional Factor for Underground Cable System. Energies 2021, 14, 8113. [Google Scholar] [CrossRef]
- CIGRE. Generic Guidelines for Life Time Condition Assessment of HV Assets and Related Knowledge Rules; WG B1.17; Technical Brochure No. 420; CIGRE: Paris, France, 2010. [Google Scholar]
- Jahromi, A.; Piercy, R.; Cress, S.; Service, J.; Fan, W. An Approach to Power Transformer Asset Management Using Health Index. IEEE Electr. Insul. Mag. 2009, 25, 20–34. [Google Scholar] [CrossRef]
- Thind, B.S.; Reddy, G.N.; Thomas, A.J.; Reddy, C.C. Modified Damage Equalization Method for Lifetime Estimation of Dielectrics. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 1118–1126. [Google Scholar] [CrossRef]
- Shaban, A.H.; Resen, A.K.; Bassil, N. Weibull Parameters Evaluation by Different Methods for Windmills Farms. Energy Rep. 2020, 6, 188–199. [Google Scholar] [CrossRef]
- IEC 62539; IEEE 930; Guide for the Statistical Analysis of Electrical Insulation Breakdown Data. IEC: Geneva, Switzerland; IEEE: Piscataway, NJ, USA, 2007. [CrossRef]
- Hamad, A.A.; Ghunem, R.A. A Techno-Economic Framework for Replacing Aged XLPE Cables in the Distribution Network. IEEE Trans. Power Deliv. 2020, 35, 2387–2393. [Google Scholar] [CrossRef]
- Liao, Y.; Liu, H.; Yuan, J.; Xu, Y.; Zhou, W.; Zhou, C. A Holistic Approach to Risk-Based Maintenance Scheduling for HV Cables. IEEE Access 2019, 7, 118975–118985. [Google Scholar] [CrossRef]


| Main Group | Detail |
|---|---|
| technical information | route name, model type, conductor size, installation date, manufacturing date, manufacturer, installation company, system voltage, current ampacity |
| operating information | service age, load level, number of failures, number of repairs, network configuration, route length, number of joints, laying environment |
| inspection and test results | visual inspection, PD inspection, IRT inspection, grounding resistance measurement, sheath current measurement |
| Considering Item | Criteria | ||
|---|---|---|---|
| Normal | Satisfactory | Risk | |
| service age (yrs.) | <20 | 20–30 | >30 |
| load level (%) | <60 | 60–80 | >80 |
| Number of failures (times) | 0 | 1–3 | >3 |
| Number of repairs (times) | <3 | 3–6 | >6 |
| network configuration | network | loop | redial |
| route length (km) | <1 | 1–3 | >3 |
| number of joints | <10 | 10–30 | >30 |
| laying environment | no | road, building | vibration |
| Testing Method | Output Value | Criteria | ||
|---|---|---|---|---|
| Good | Satisfactory | Bad | ||
| PD inspection | PD pattern | no PD/corona | surface | internal |
| amplitude (internal PD), (pC) | <50 | 50–300 | >300 | |
| amplitude (surface PD), (nC) | <0.5 | 0.5–2 | >2 | |
| trending of amplitude | stable | slight | significant | |
| IRT inspection | ΔT phase-ambient (°C) | <10 | 10–15 | >15 |
| ΔT phase-phase (°C) | <5 | 5–10 | >10 | |
| sheath current | increment of sheath current (%) | <5 | 5–10 | >10 |
| grounding resistance | grounding resistance (Ω) | <10 | 10–25 | 25 |
| visual inspection | cable jacket | normal | repaired | cracked |
| cable supporting structure | normal | stained | broken | |
| cable shield grounding | normal | loose | broken | |
| splice condition | normal | - | bloated | |
| termination condition | normal | dirty | bloated | |
| manhole gate | normal | stained | lost | |
| manhole wall | normal | small crack | broken | |
| manhole floor | normal | small crack | broken | |
| manhole cleaning | clean | dirty | flooded | |
| manhole ground connection | normal | loose | broken | |
| duct bank water ingress | no water | some leakage | high pressure | |
| duct bank general condition | normal | small crack | broken | |
| number of available ducts | many | a few | unavailable | |
| System Name | Conductor Size (mm2) | Length (m) | Number of Joints | Laying Environment | Load Percentage | Year in Service |
|---|---|---|---|---|---|---|
| EF01 | 800 | 2194 | 36 | road, building | 67 | 20 |
| EF02 | 800 | 3712 | 39 | road, building | 49 | 27 |
| EF03 | 800 | 2446 | 30 | road, building | 34 | 37 |
| EF04 | 800 | 2150 | 30 | road, building | 24 | 42 |
| EF05 | 400 | 2011 | 39 | road, building | 65 | 29 |
| EF06 | 400 | 2057 | 18 | vibration | 32 | 35 |
| EF07 | 400 | 1523 | 18 | road, building | 37 | 39 |
| EF08 | 800 | 3150 | 27 | vibration | 29 | 39 |
| EF09 | 800 | 7942 | 81 | vibration | 37 | 31 |
| EF10 | 400 | 1439 | 12 | vibration | 63 | 32 |
| EF11 | 800 | 5315 | 60 | vibration | 47 | 29 |
| EF12 | 800 | 1208 | 9 | vibration | 63 | 35 |
| EF13 | 300 | 1853 | 18 | vibration | 62 | 30 |
| System Name | Start Year | End-of-Life Year | ||||
|---|---|---|---|---|---|---|
| %HIS | OF | %OHI | %HIS | OF | %OHI | |
| EF01 | 98.58 | 0.89 | 87.56 | 59.28 | 0.78 | 46.11 |
| EF02 | 99.23 | 0.90 | 89.43 | 60.30 | 0.82 | 49.32 |
| EF03 | 98.85 | 0.92 | 90.61 | 61.73 | 0.80 | 49.34 |
| EF04 | 99.04 | 0.92 | 90.79 | 58.55 | 0.80 | 46.98 |
| EF05 | 99.23 | 0.92 | 90.96 | 59.13 | 0.80 | 47.27 |
| EF06 | 99.23 | 0.93 | 92.49 | 56.22 | 0.83 | 46.68 |
| EF07 | 98.65 | 0.93 | 91.95 | 56.49 | 0.82 | 46.20 |
| EF08 | 99.04 | 0.92 | 90.79 | 59.71 | 0.76 | 45.52 |
| EF09 | 98.08 | 0.90 | 88.39 | 59.09 | 0.80 | 47.24 |
| EF10 | 99.04 | 0.92 | 91.40 | 58.46 | 0.80 | 46.74 |
| EF11 | 98.08 | 0.89 | 87.48 | 53.43 | 0.81 | 43.04 |
| EF12 | 100 | 0.93 | 92.90 | 56.02 | 0.79 | 44.44 |
| EF13 | 99.04 | 0.91 | 90.48 | 60.01 | 0.81 | 48.34 |
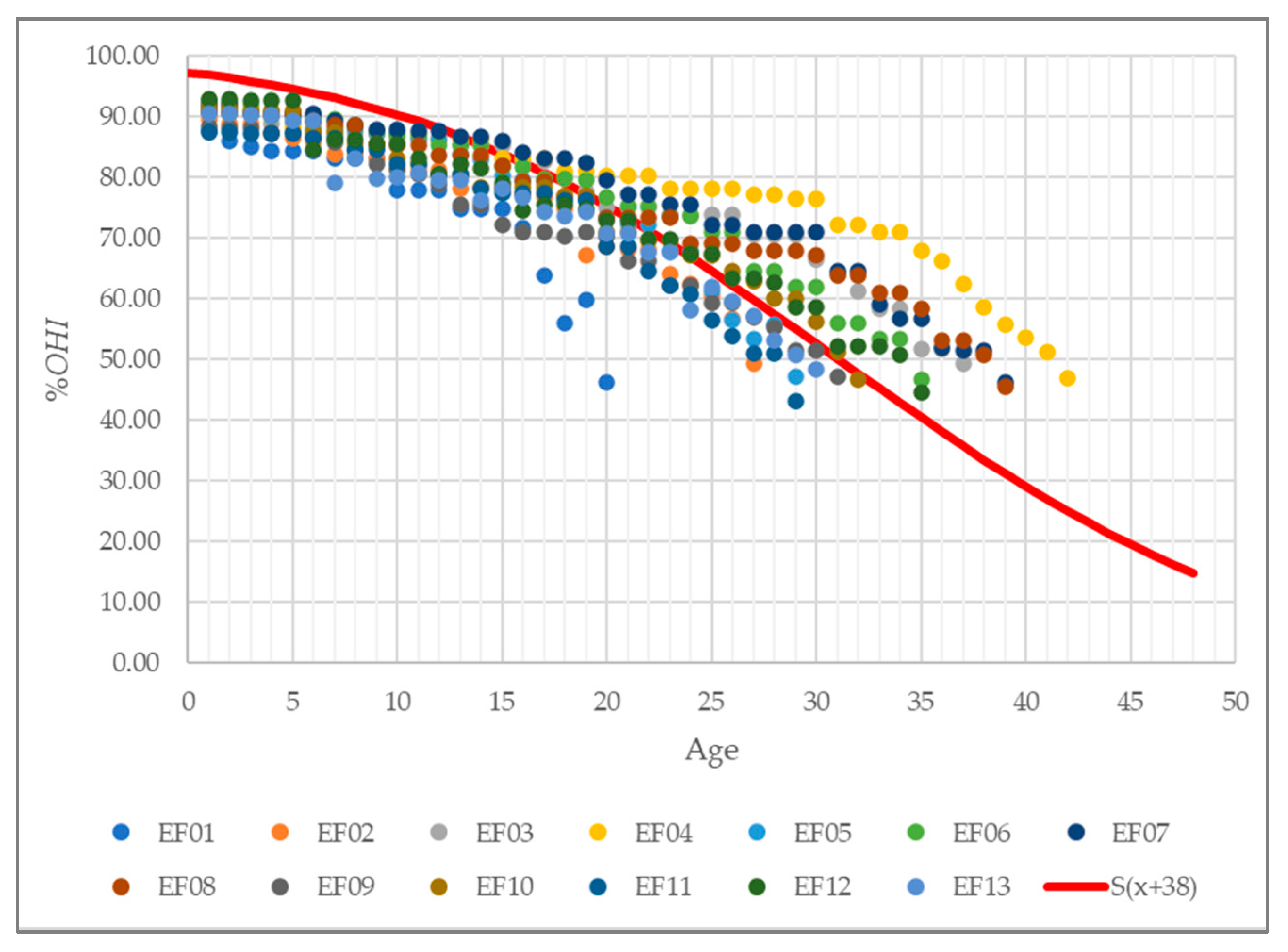
| Recorded Year | %OHI of Retired Underground Cable Systems | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EF01 | EF02 | EF03 | EF04 | EF05 | EF06 | EF07 | EF08 | EF09 | EF10 | EF11 | EF12 | EF13 | |
| 0 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 1 | 87.56 | 89.43 | 90.61 | 90.79 | 90.96 | 92.49 | 91.95 | 90.79 | 88.39 | 91.40 | 87.48 | 92.90 | 90.48 |
| 3 | 85.05 | 88.91 | 90.61 | 90.43 | 90.43 | 91.95 | 90.56 | 90.43 | 88.04 | 91.04 | 87.14 | 92.54 | 90.13 |
| 5 | 84.25 | 86.53 | 88.89 | 88.16 | 89.95 | 90.21 | 90.39 | 90.43 | 87.35 | 91.04 | 87.14 | 92.54 | 89.31 |
| 7 | 83.11 | 83.69 | 87.12 | 87.82 | 87.82 | 89.49 | 89.31 | 88.67 | 85.77 | 87.31 | 86.45 | 86.23 | 78.97 |
| 9 | 83.11 | 83.07 | 87.12 | 87.12 | 87.12 | 87.51 | 87.77 | 85.14 | 82.15 | 85.48 | 84.62 | 85.42 | 79.76 |
| 11 | 77.85 | 81.22 | 86.30 | 87.12 | 86.25 | 86.81 | 87.72 | 85.14 | 80.44 | 82.15 | 82.15 | 83.01 | 80.78 |
| 13 | 74.87 | 78.11 | 85.14 | 86.25 | 83.69 | 85.13 | 86.65 | 83.63 | 75.53 | 80.45 | 80.44 | 82.16 | 79.49 |
| 15 | 74.87 | 78.07 | 85.14 | 83.17 | 80.23 | 81.60 | 86.94 | 82.00 | 72.26 | 78.23 | 77.38 | 79.04 | 78.14 |
| 17 | 63.78 | 76.63 | 82.63 | 83.17 | 79.43 | 79.83 | 83.12 | 79.21 | 71.01 | 78.23 | 77.38 | 75.57 | 74.17 |
| 19 | 59.87 | 67.11 | 77.65 | 80.90 | 76.24 | 79.43 | 82.31 | 76.84 | 71.01 | 76.95 | 76.10 | 74.78 | 74.24 |
| 20 | 46.11 | 68.03 | 74.95 | 80.27 | 72.10 | 75.22 | 77.19 | 73.32 | 66.25 | 71.06 | 68.46 | 72.91 | 70.83 |
| 27 | 49.32 | 70.50 | 77.20 | 53.31 | 64.47 | 70.99 | 67.95 | 56.81 | 62.95 | 50.91 | 63.31 | 57.24 | |
| 29 | 70.50 | 76.44 | 47.27 | 61.96 | 70.99 | 67.95 | 51.48 | 60.06 | 43.04 | 58.59 | 50.69 | ||
| 30 | 66.49 | 76.44 | 61.96 | 70.99 | 67.11 | 51.48 | 56.17 | 58.59 | 48.34 | ||||
| 31 | 64.09 | 72.24 | 55.85 | 64.54 | 63.84 | 47.24 | 51.29 | 52.19 | |||||
| 32 | 61.22 | 72.24 | 55.85 | 64.54 | 63.84 | 46.74 | 52.19 | ||||||
| 35 | 51.57 | 67.95 | 46.68 | 56.66 | 58.23 | 44.44 | |||||||
| 37 | 49.34 | 62.41 | 51.43 | 53.06 | |||||||||
| 39 | 55.85 | 46.20 | 45.52 | ||||||||||
| 42 | 46.98 | ||||||||||||
| 1st yr. OF | 0.89 | 0.90 | 0.92 | 0.92 | 0.92 | 0.93 | 0.93 | 0.92 | 0.90 | 0.92 | 0.89 | 0.93 | 0.91 |
| end yr. OF | 0.78 | 0.82 | 0.80 | 0.80 | 0.80 | 0.83 | 0.82 | 0.76 | 0.80 | 0.80 | 0.81 | 0.79 | 0.81 |
 End-of-life (%OHI < 50).
End-of-life (%OHI < 50).| Actual Age | %OHIavg | Apparent Age | %Error (Age Difference) | Actual Age | %OHIavg | Apparent Age | %Error (Age Difference) |
|---|---|---|---|---|---|---|---|
| 1 | 90.40 | 8.71 | 770.612 | 22 | 69.61 | 21.59 | 1.872 |
| 2 | 90.13 | 8.84 | 341.967 | 23 | 67.98 | 22.81 | 0.838 |
| 3 | 89.79 | 9.00 | 200.076 | 24 | 66.30 | 24.08 | 0.335 |
| 4 | 89.23 | 9.28 | 131.914 | 25 | 64.93 | 25.14 | 0.552 |
| 5 | 88.94 | 9.42 | 88.474 | 26 | 63.38 | 26.35 | 1.363 |
| 6 | 87.63 | 10.09 | 68.221 | 27 | 60.85 | 28.37 | 5.079 |
| 7 | 86.29 | 10.80 | 54.322 | 28 | 60.31 | 28.81 | 2.877 |
| 8 | 86.12 | 10.90 | 36.214 | 29 | 58.03 | 30.67 | 5.767 |
| 9 | 85.03 | 11.49 | 27.708 | 30 | 57.18 | 31.38 | 4.591 |
| 10 | 83.95 | 12.11 | 21.074 | 31 | 54.26 | 33.82 | 9.097 |
| 11 | 83.61 | 12.30 | 11.833 (max error) | 32 | 53.69 | 34.30 | 7.198 |
| 12 | 82.62 | 12.88 | 7.327 | 33 | 52.54 | 35.27 | 6.893 |
| 13 | 81.66 | 13.46 | 3.510 | 34 | 52.25 | 35.52 | 4.476 |
| 14 | 80.95 | 13.89 | 0.805 | 35 | 50.28 | 37.22 | 6.344 |
| 15 | 79.70 | 14.66 | 2.236 | 36 | 49.38 | 38.00 | 5.556 |
| 16 | 78.19 | 15.63 | 2.330 | 37 | 48.88 | 38.43 | 3.871 |
| 17 | 77.24 | 16.25 | 4.426 | 38 | 48.42 | 38.83 | 2.190 |
| 18 | 75.47 | 17.43 | 3.156 | 39 | 47.39 | 39.73 | 1.868 |
| 19 | 74.88 | 17.84 | 6.123 | 40 | 47.21 | 39.89 | 0.286 (min error) |
| 20 | 71.26 | 20.38 | 1.918 | 41 | 47.03 | 40.04 | 2.334 |
| 21 | 70.51 | 20.93 | 0.346 | 42 | 46.71 | 40.33 | 3.985 |
| average error | 3.79% | ||||||
| Feeder | Latest %OHI | Actual Age | Expected EoL | Apparent Age | RUL |
|---|---|---|---|---|---|
| F01 | 87.82 | 8 | 40 | 9.99 | 30.01 |
| F02 | 80.44 | 12 | 40 | 14.20 | 25.80 |
| F03 | 75.57 | 17 | 40 | 17.37 | 22.63 |
| F04 | 79.21 | 17 | 40 | 14.97 | 25.03 |
| F05 | 71.06 | 21 | 40 | 20.53 | 19.47 |
| F06 | 72.10 | 22 | 40 | 19.78 | 20.22 |
| F07 | 70.96 | 25 | 40 | 20.60 | 19.40 |
| F08 | 67.07 | 25 | 40 | 23.49 | 16.51 |
| F09 | 60.97 | 33 | 40 | 28.28 | 11.72 |
| F10 | 53.06 | 36 | 40 | 34.84 | 5.16 |
| %OHI | Condition | Recommendation | Goals |
|---|---|---|---|
| 100–75 | good | normal maintenance | minimal maintenance |
| 75–50 | satisfactory | increase maintenance period, repair minor defections | defects localization, maintain system condition, prolong the RUL |
| <50 | bad (EoL) | urgent action required | fully replacement if no possibility to extend the RUL |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Somsak, T.; Suwanasri, T.; Suwanasri, C. Remaining Useful Life Estimation for Underground Cable Systems Based on Historical Health Index. Energies 2022, 15, 9447. https://doi.org/10.3390/en15249447
Somsak T, Suwanasri T, Suwanasri C. Remaining Useful Life Estimation for Underground Cable Systems Based on Historical Health Index. Energies. 2022; 15(24):9447. https://doi.org/10.3390/en15249447
Chicago/Turabian StyleSomsak, Tanachai, Thanapong Suwanasri, and Cattareeya Suwanasri. 2022. "Remaining Useful Life Estimation for Underground Cable Systems Based on Historical Health Index" Energies 15, no. 24: 9447. https://doi.org/10.3390/en15249447
APA StyleSomsak, T., Suwanasri, T., & Suwanasri, C. (2022). Remaining Useful Life Estimation for Underground Cable Systems Based on Historical Health Index. Energies, 15(24), 9447. https://doi.org/10.3390/en15249447








