OrcaFlex Modelling of a Multi-Body Floating Solar Island Subjected to Waves
Abstract
1. Introduction
2. Test Case Definition
2.1. Floats and PV Panel Properties
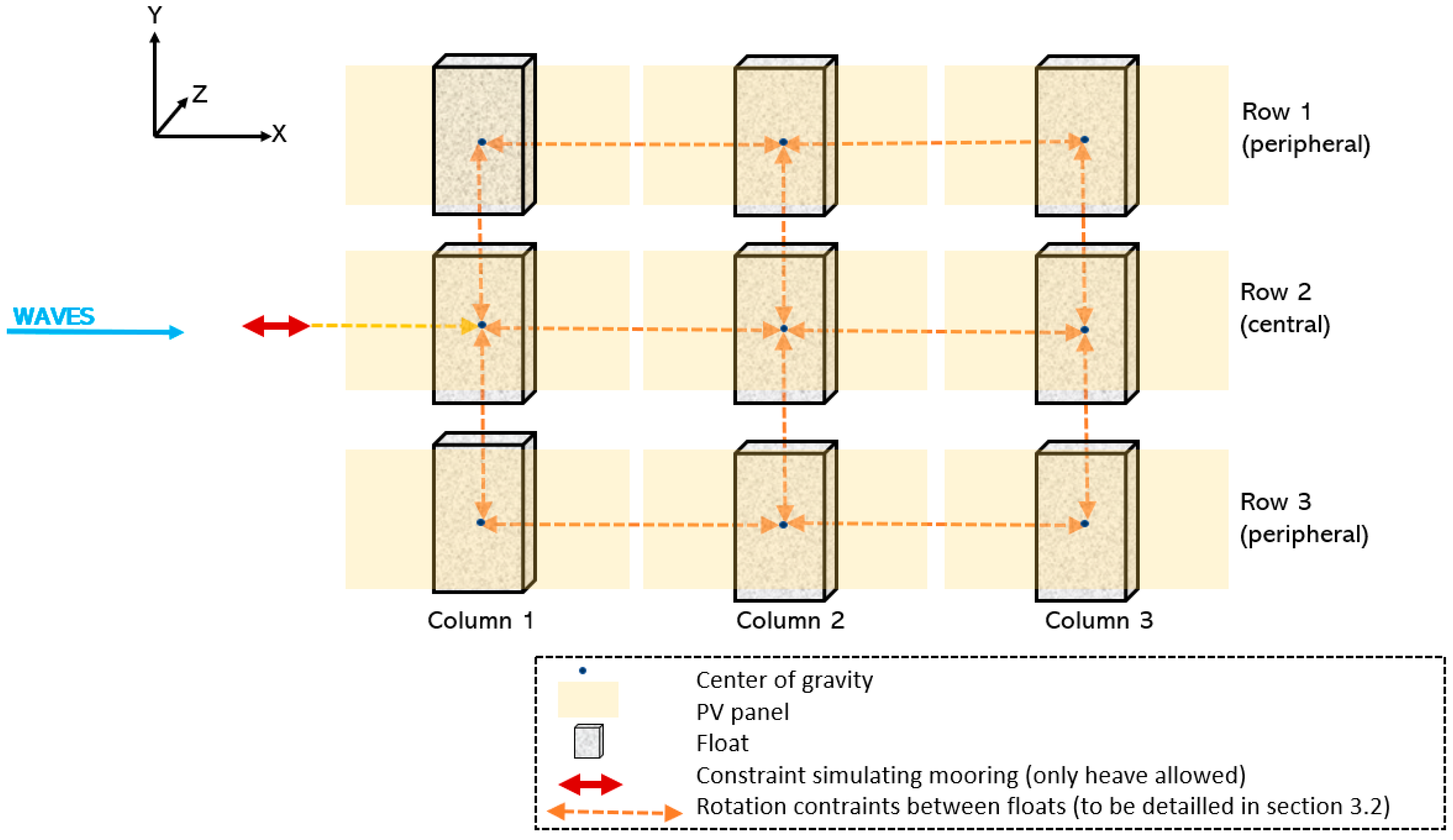
2.2. Island Definition
2.3. Environmental Conditions
3. OrcaFlex Modelling
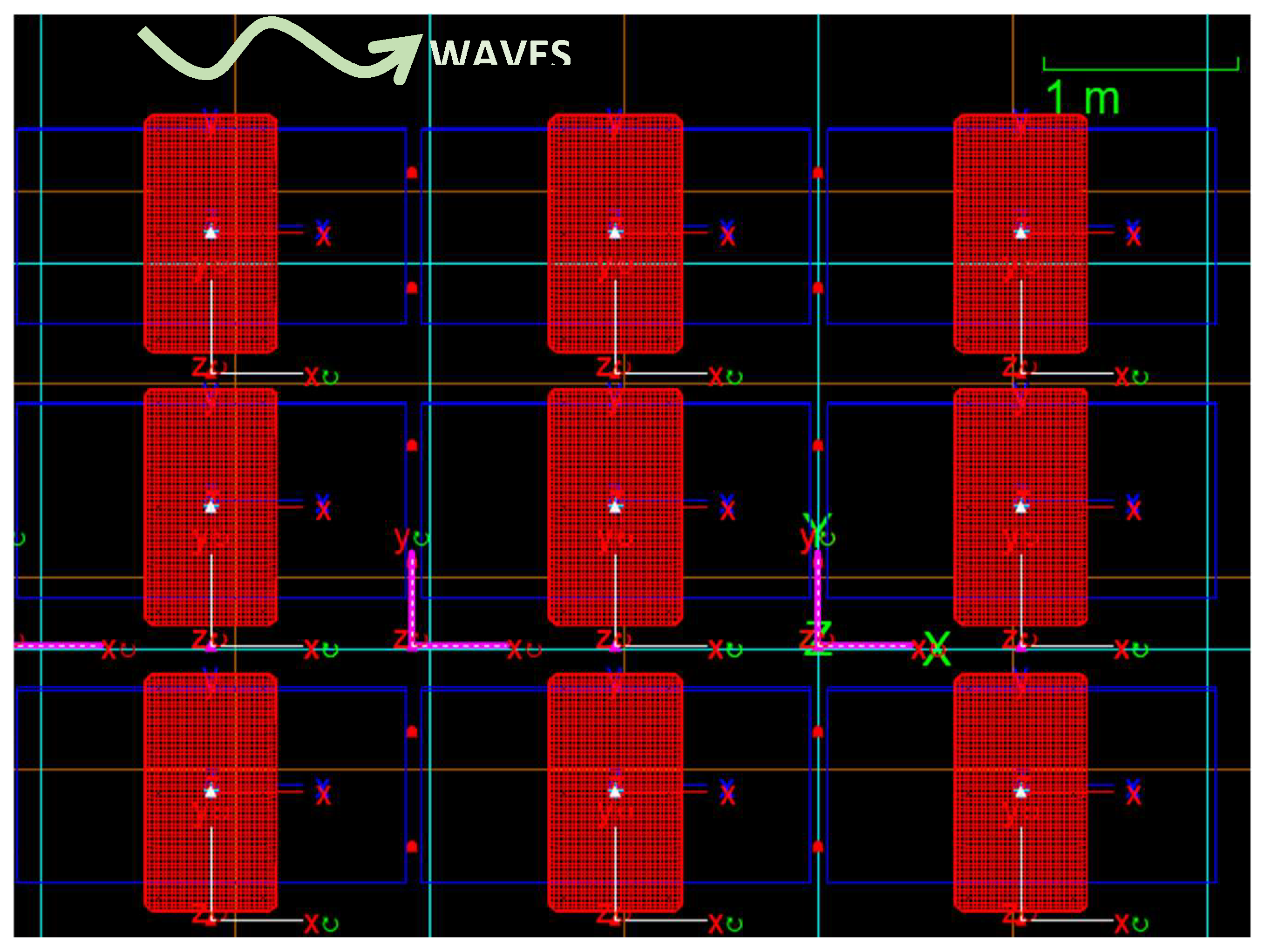
3.1. Presentation of the Modelled System
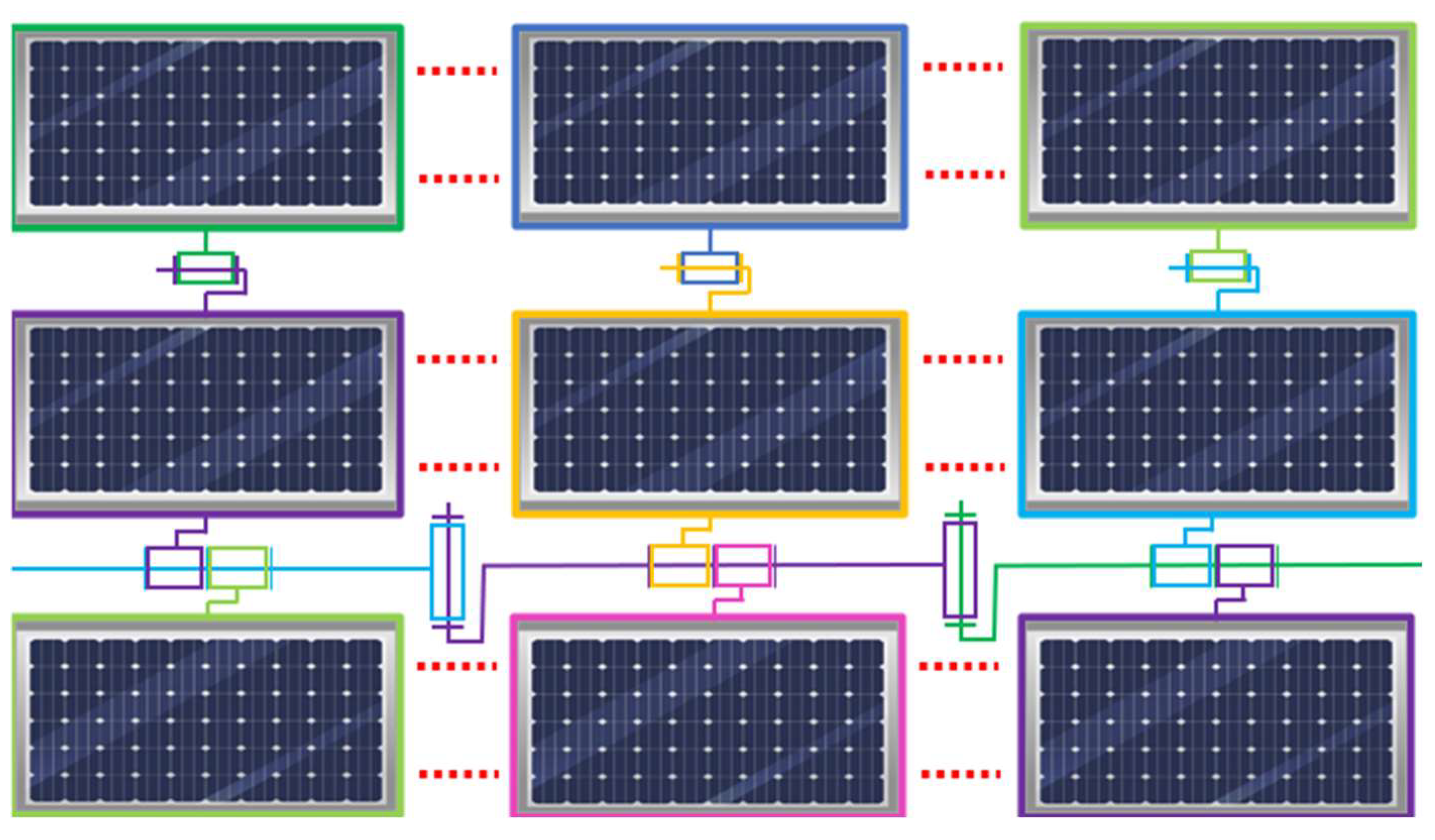
- PV panels are represented by 6D buoys (OrcaFlex objects defined by their mass, volume and inertial properties, with six degrees of freedom).
- Each PV panel is mounted on an individual float.
- No pathway for intervention is considered.
- No electrical component is considered.
- Mooring is not considered. The float ensemble is limited by a constraint that blocks all the motions but heave, which is located upstream of the first row.
- Panels are interconnected by rotation constraints (detailed in Section 3.2).
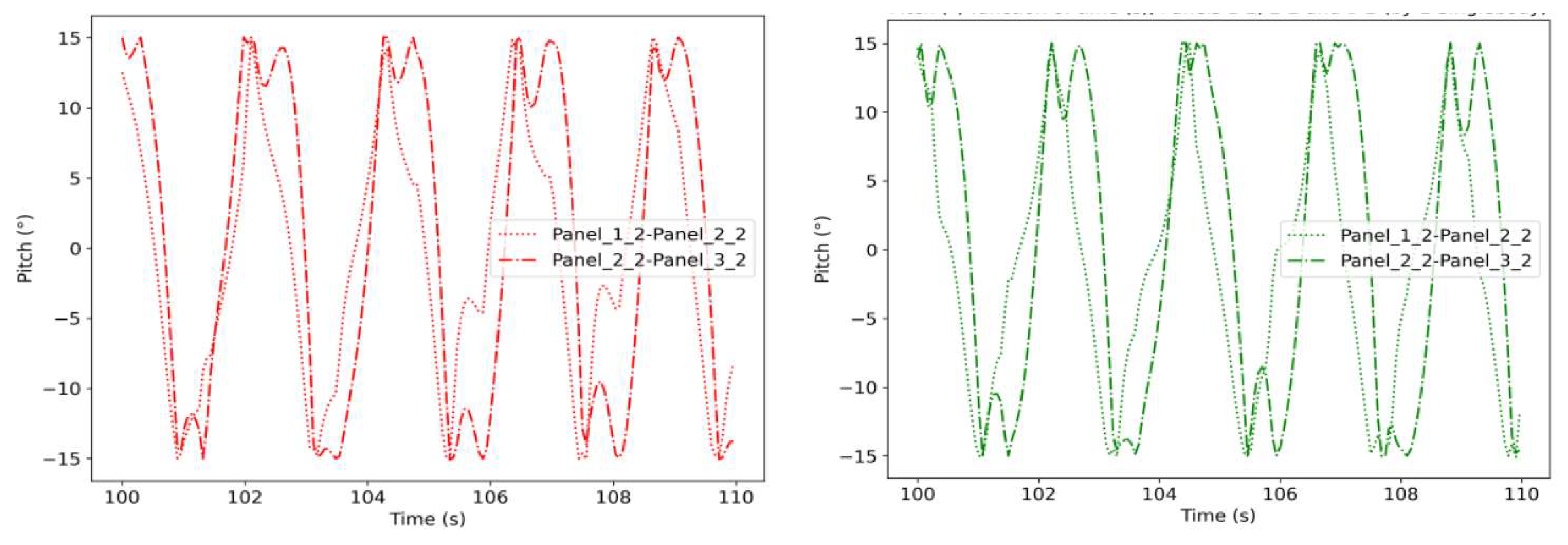
3.2. Definition of Mechanical Joints between Floats
- -
- All the constraints have a 15° limit. In the model, this translates to a connection with no stiffness for an angular displacement lower than 15° and with a quasi-infinite stiffness when the angular displacement exceeds 15°. The 15° limit is imposed gradually to avoid hysteresis movements. Constraints (both X- and Y-constraints) are connected to the floats’ centres of gravity.
- -
- All springs have infinite stiffness. The length of the links is the result of an optimisation between the smallest length and the smallest computation time. Eventually, the best compromise was found to be m. Springs are located at the following positions:
- ∘
- Mid-distance between two floats’ centres of gravity in the horizontal direction.
- ∘
- Mid-distance between the float’s centre and the float’s extremity in the vertical direction (both up and down).
3.3. Interactions between Waves and Potential Flow Theory
3.4. Modelling Strategies
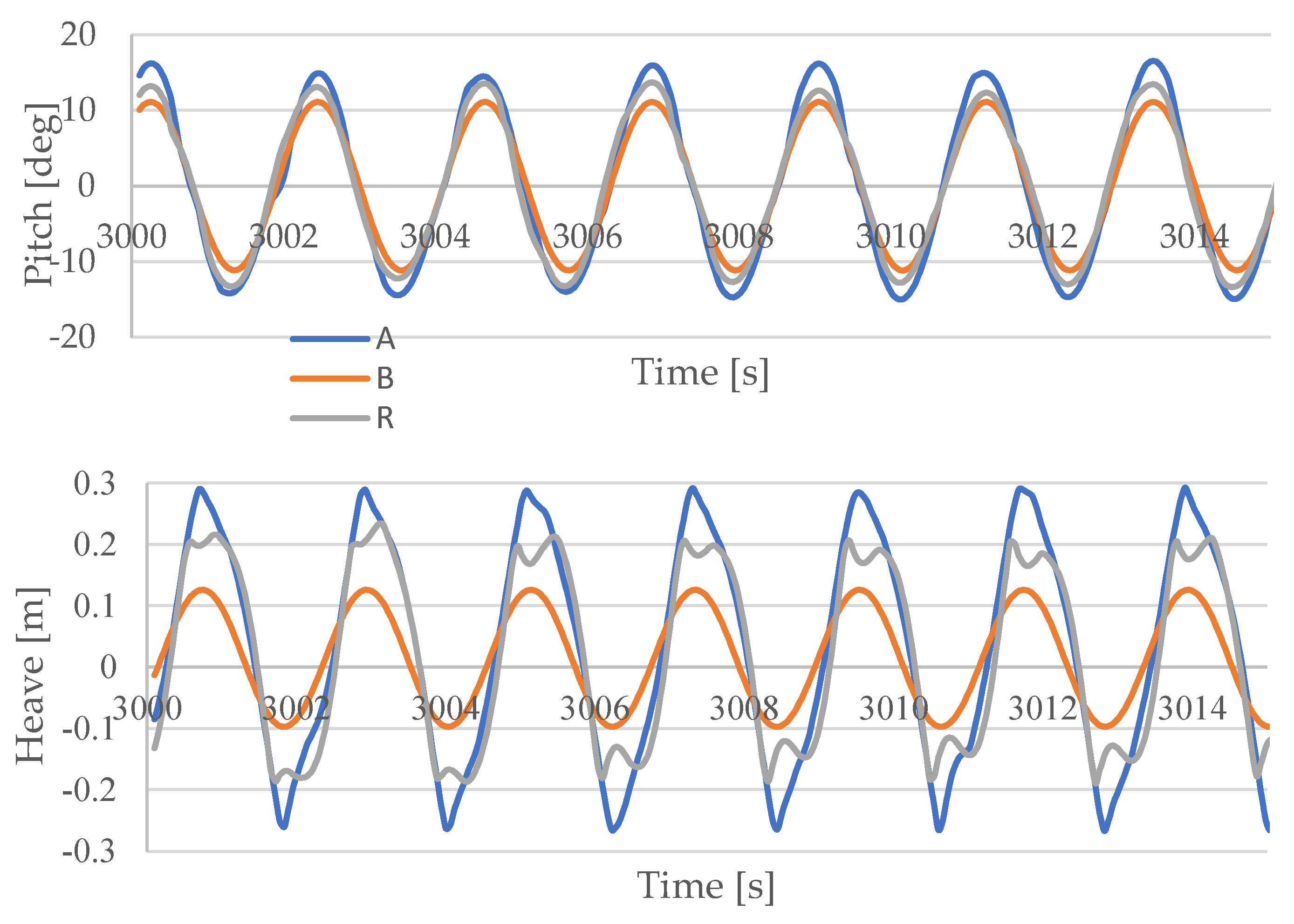
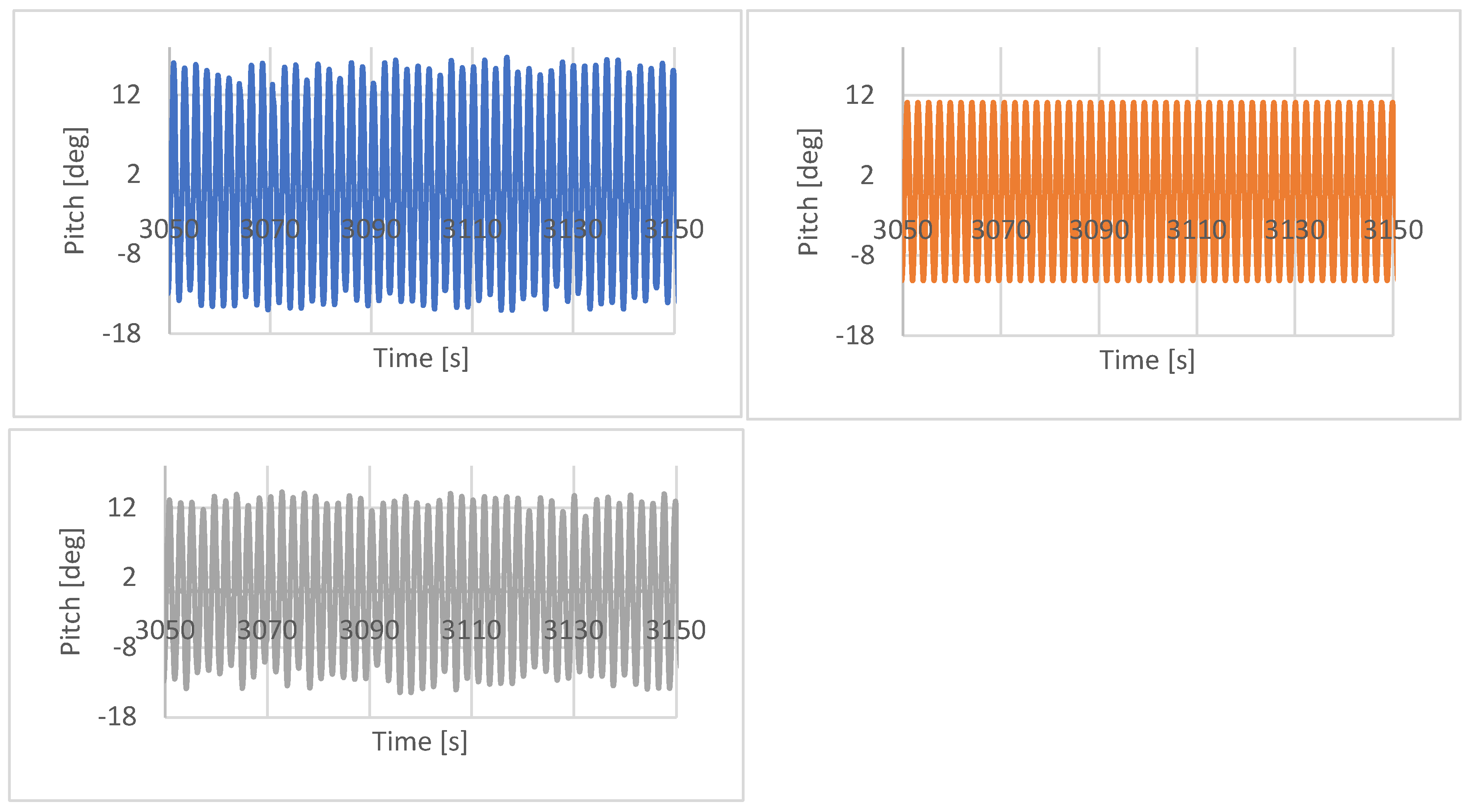
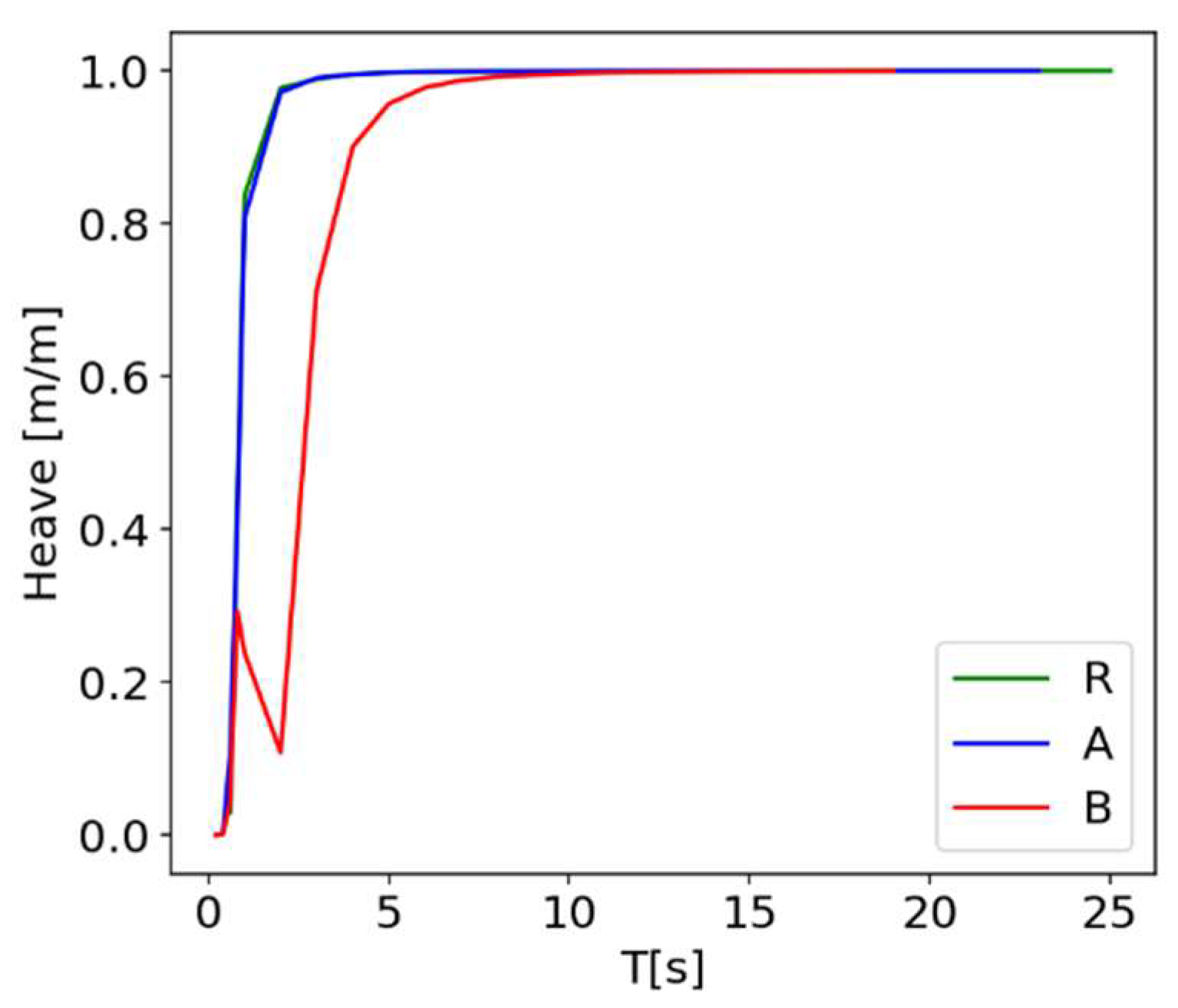
- Model A: a single float is considered alone. In this case, the HDB is calculated for a single float and is applied to each float separately. Therefore, all floats behave as if they were alone and hydrodynamic interactions are not considered. It is considered to be a “single-body” approach.
- Model B: a rigid ensemble with all nine floats is considered. It is considered to be a “rigid body” approach.
- Model R: all nine floats are considered in the OrcaWave model and the potential equations are solved for each float individually. Hydrodynamic interactions between the floats are accounted for. It is considered to be a “multi-body” approach.
- For model A: the same HDB is applied to all floats.
- For model B: only one HDB is applied to the rigid 3 × 3 ensemble.
- For model C: an HDB, including different data for each float, is applied to the ensemble.
3.5. Hydrodynamic Interactions between Floats
4. Results and CPU Time Optimization
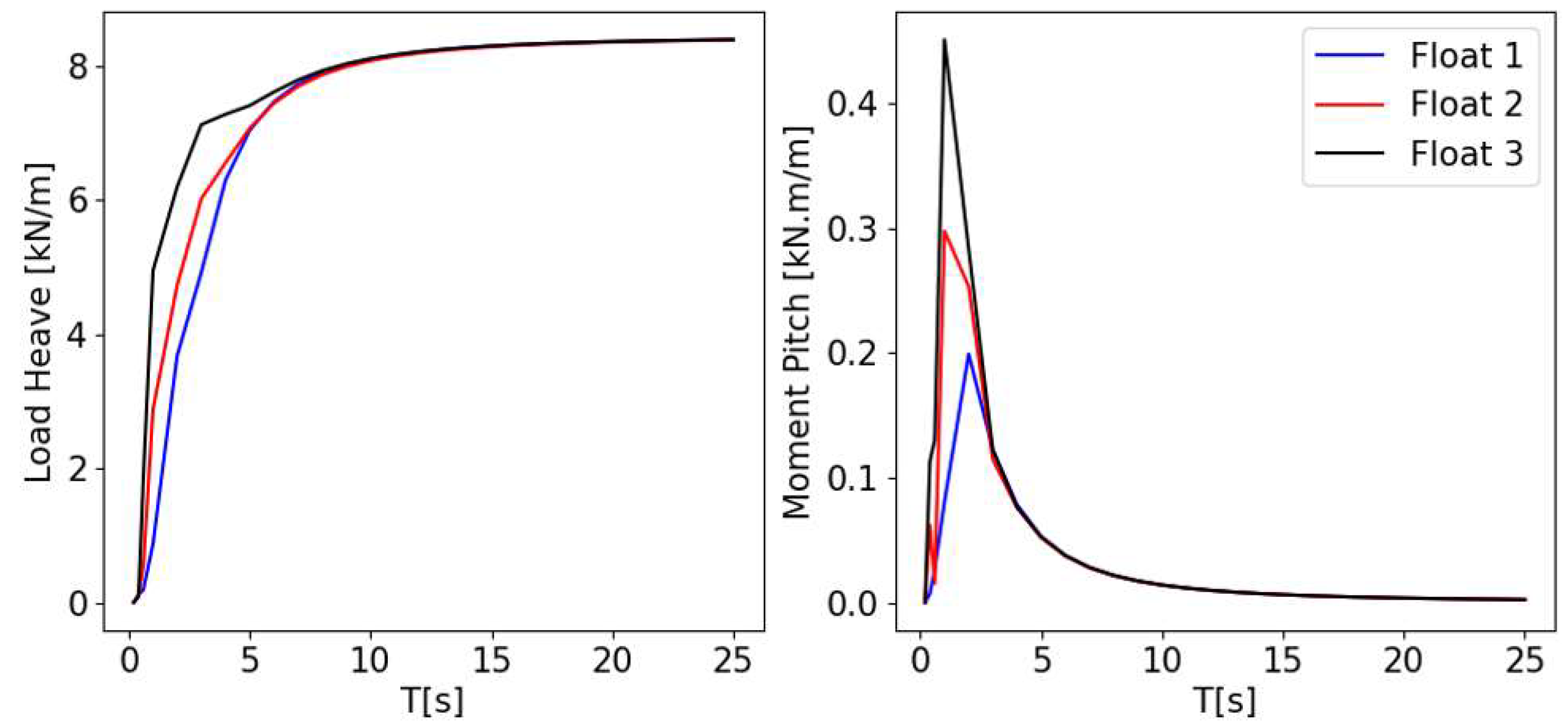
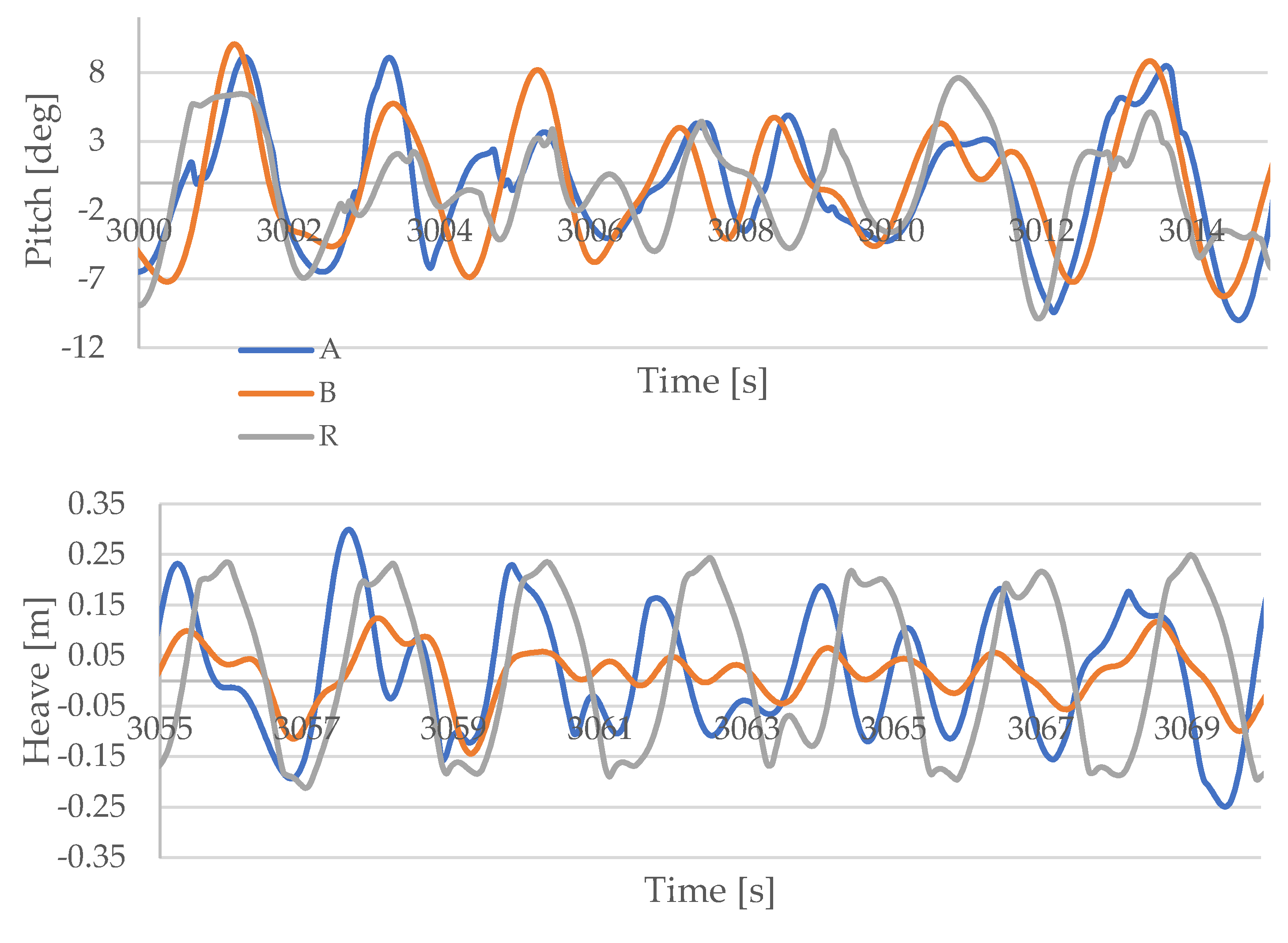
4.1. Results of Regular Waves
4.2. Results of Irregular Waves
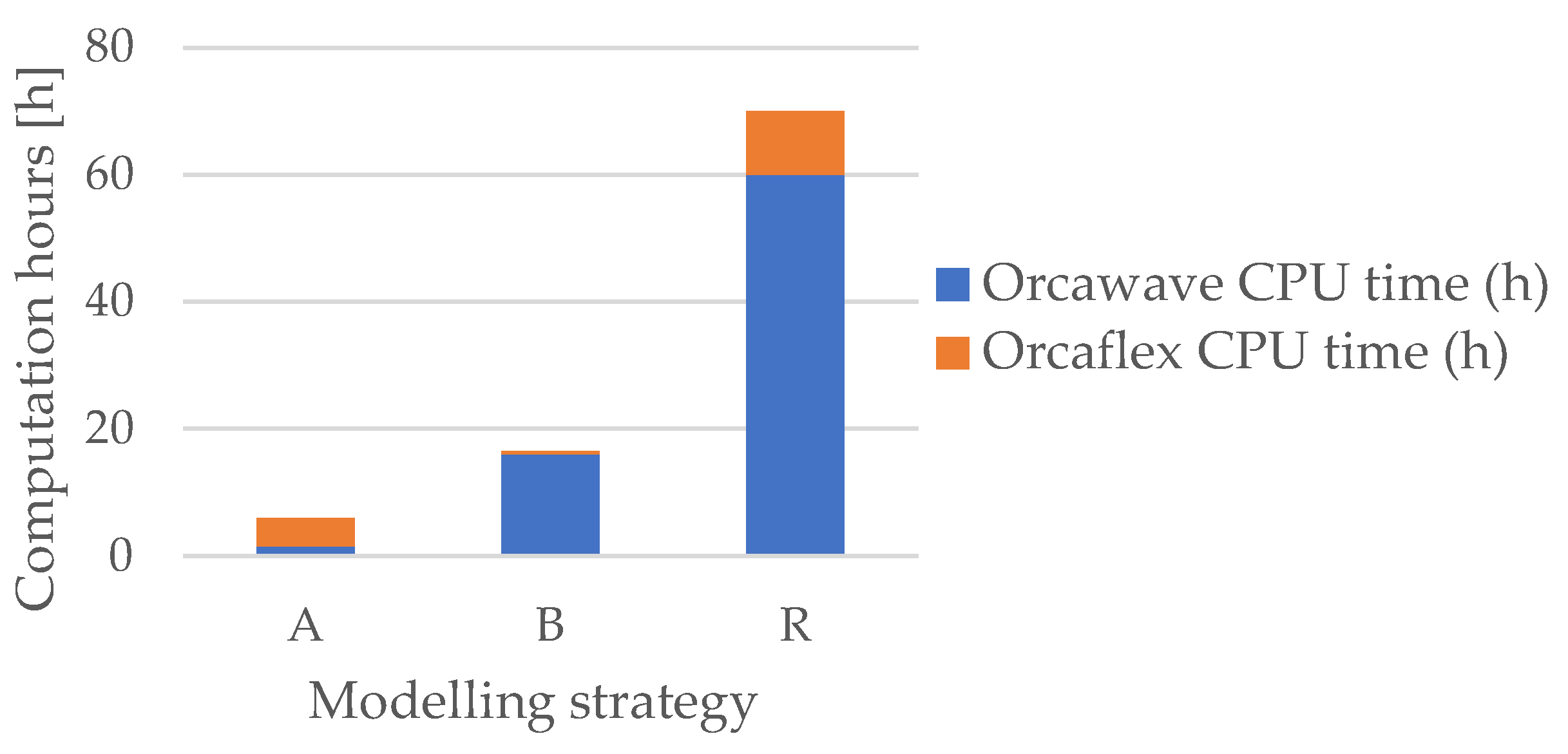
4.3. CPU Time
5. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Bank Group; ESMAP; SERIS. Where Sun Meets the Water, Floating Solar Market Report; World Bank Group: Washington, DC, USA, 2018. [Google Scholar]
- Perez, M.; Perez, R.; Ferguson, C.R.; Schlemmer, J. Deploying effectively dispatchable PV on reservoirs: Comparing floating PV to other renewable technologies. Sol. Energy 2018, 174, 837–847. [Google Scholar] [CrossRef]
- Claus, R.; López, M. Key issues in the design of floating photovoltaic structures for the marine environment. Renew. Sustain. Energy Rev. 2022, 164, 112502. [Google Scholar] [CrossRef]
- Friel, D.; Karimirad, M.; Whittaker, T.; Doran, W.; Howlin, E. A review of photovoltaic design concepts and installed variations. In Proceedings of the 4th International Conference on Offshore Renewable Energy, Glasgow, UK, 29–30 August 2019. [Google Scholar]
- Sahu, A.; Yadav, N.; Sudhakar, K. Floating photovoltaic power plant: A review. Renew. Sustain. Energy Rev. 2016, 66, 815–824. [Google Scholar] [CrossRef]
- Trapani, K.; Redón Santafé, M. A review of floating photovoltaic installations: 2007–2013. Prog. Photovolt. Res. Appl. 2015, 23, 524–532. [Google Scholar] [CrossRef]
- Ikhennicheu, M.; Danglade, B.; Pascal, R.; Arramounet, V.; Trébaol, Q.; Gorintin, F. Analytical method for loads determination on floating solar farms in three typical environments. Sol. Energy 2021, 219, 34–41. [Google Scholar] [CrossRef]
- [Reportage] Akuo Revient sur les Causes de L’incendie sur sa Centrale Flottante O’MEGA 1. PV Magazine, 28 February 2022.
- OrcaFlex ©, Version 11.0; Orcina: Ulverston, UK.
- Sethuraman, L.; Venugopal, V. Hydrodynamic response of a stepped-spar floating wind turbine: Numerical modelling and tank testing. Renew. Energy 2013, 52, 160–174. [Google Scholar] [CrossRef]
- Viuff, T.; Xiang, X.; Leira, B.; Øiseth, O. Code-to-code verification of end-anchored floating bridge global analysis. In Proceedings of the 37th International Conference on Offshore Mechanics and Arctic Engineering, Madrid, Spain, 17–22 June 2018; pp. 1–9. [Google Scholar]
- Xiang, X.; Viuff TLeira, B.; Øiseth, O. Impact of hydrodynamic interaction between pontoons on global responses of a long floating bridge under wind waves. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018; Volume 7A. [Google Scholar]
- Suzuki, H.; Bhattacharya, B.; Fujikubo, M.; Hudson, D.A.; Riggs, H.R.; Seto, H.; Shin, H.; Shugar, T.A.; Yasuzawa, Y.; Zong, Z. ISSC Committee Vi.2: Very large floating structures. In Proceedings of the 16th International Ship and Offshore Structures Congress, Southampton, UK, 20–25 August 2006. [Google Scholar]
- Sree, D.; Law, A.; Pang, D.; Tan, S.; Wang CKew, J.; Seow, W.; Lim, V. Fluid-structural analysis of modular floating solar farms under wave motion. Sol. Energy 2022, 233, 161–181. [Google Scholar] [CrossRef]
- Song, J.; Kim, J.; Lee, J.; Kim, S.; Chung, W. Dynamic response of multiconnected floating solar panel systems with vertical cylinders. J. Mar. Sci. Eng. 2022, 10, 189. [Google Scholar] [CrossRef]
- Ocean Sun Technology. Available online: https://oceansun.no/ (accessed on 21 April 2022).
- Ciel et Terre Technology. Available online: www.ciel-et-terre.net (accessed on 12 June 2022).
- DNVGL-RP-C205; Environmental Conditions and Environmental Loads. DNV: Høvik, Norway, 2019.
- Isifloating Technology. Available online: www.isifloating.com (accessed on 14 August 2022).
- Molin, B. Hydrodynamique des Structures Offshores; Editions TECHNIP: Paris, France, 2020. [Google Scholar]
- OrcaWave ©, Version 11.0; Orcina: Ulverston, UK.
- Ansys, Version 15; Ansys: Canonsburg, PA, USA.
- Newman, J.N. Algorithms for the free-surface Green function. J. Eng. Math. 1985, 19, 57–67. [Google Scholar] [CrossRef]
- Cummins, W.E. The Impulse Response Function and Ship Motions; Report no. DTMB-1661; Washington, DC, USA, 1962. [Google Scholar]
- DNVGL-RP-0584; Design, Development and Operation of Floating Solar Photovoltaic Systems. DNV: Høvik, Norway, 2021.




| Property | Unit | Value |
|---|---|---|
| Float length (x) | (m) | 1.23 |
| Float width (y) | (m) | 0.69 |
| Float height (z) | (m) | 0.40 |
| Float draft | (m) | 0.05 |
| Spacing between floats (x) * | (m) | 2.09 |
| Spacing between floats (y) * | (m) | 1.50 |
| Float mass | (kg) | 16 |
| PV panel mass | (kg) | 30 |
| PV panel tilt | (deg) | 10 |
| PV panel CoG position above water surface | (m) | 0.43 |
| Environmental Condition | Unit | Value |
|---|---|---|
| Wind speed | (m/s) | 40 |
| Fetch | (m) | 3000 |
| Water depth MSL | (m) | 90 |
| Wave Hs | (m) | 0.9 |
| Wave Tp | (s) | 2.2 |
| Pros | Cons | Example of Behavior in Regular Waves | |
|---|---|---|---|
| Single body-A | Requires very little computation time. | No hydrodynamic interactions between floats. |  |
| Rigid body-B | Very fast OrcaFlex calculations. | No hydrodynamic interactions nor dynamic motions between floats. | 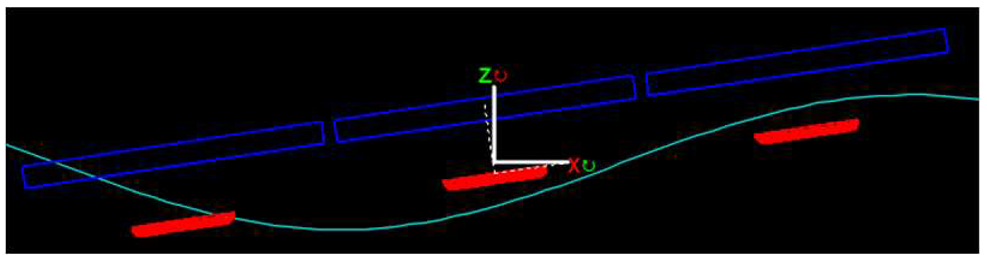 |
| Multi-body-R | Accounts for hydrodynamic interactions between floats. | Requires high computation time. | 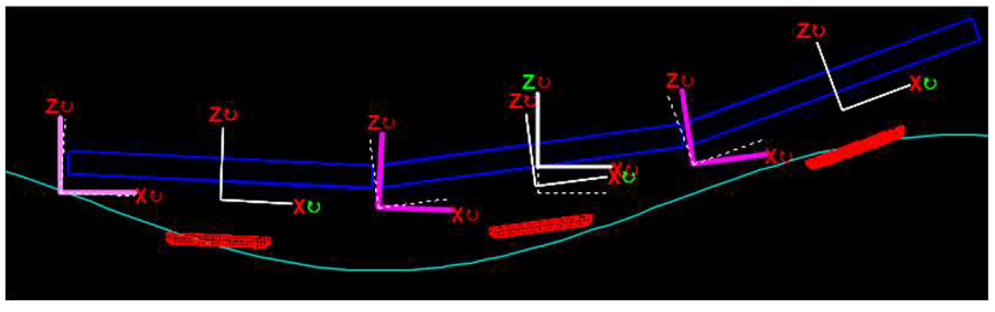 |
| R | A | B | |
|---|---|---|---|
| Mean (Z) (m) | 0.442 | 0.449 | 0.441 |
| Std (Z) (m) | 0.152 | 0.176 | 0.079 |
| R | A | B | |
|---|---|---|---|
| Mean (Z) (m) | 0.443 | 0.443 | 0.444 |
| Std (Z) (m) | 0.107 | 0.127 | 0.061 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ikhennicheu, M.; Blanc, A.; Danglade, B.; Gilloteaux, J.-C. OrcaFlex Modelling of a Multi-Body Floating Solar Island Subjected to Waves. Energies 2022, 15, 9260. https://doi.org/10.3390/en15239260
Ikhennicheu M, Blanc A, Danglade B, Gilloteaux J-C. OrcaFlex Modelling of a Multi-Body Floating Solar Island Subjected to Waves. Energies. 2022; 15(23):9260. https://doi.org/10.3390/en15239260
Chicago/Turabian StyleIkhennicheu, Maria, Arthur Blanc, Benoat Danglade, and Jean-Christophe Gilloteaux. 2022. "OrcaFlex Modelling of a Multi-Body Floating Solar Island Subjected to Waves" Energies 15, no. 23: 9260. https://doi.org/10.3390/en15239260
APA StyleIkhennicheu, M., Blanc, A., Danglade, B., & Gilloteaux, J.-C. (2022). OrcaFlex Modelling of a Multi-Body Floating Solar Island Subjected to Waves. Energies, 15(23), 9260. https://doi.org/10.3390/en15239260






