Numerical Modeling of Shell-and-Tube-like Elastocaloric Regenerator
Abstract
1. Introduction
2. Methods
2.1. Experimental Determination of Superelastic and Elastocaloric Properties
2.2. Phenomenological Modeling
2.3. Numerical Modeling of the AeCR
- the HTF flow is incompressible, with no flow maldistributions,
- the HTF properties are defined according to the mean temperature,
- the stress throughout the AeCR is constant,
- the strain within the segment of the AeCR is constant,
- the mechanical loading and unloading are adiabatic,
- a step on and off function of the fluid flow period is assumed,
- the strain is kept constant during the HTF flow period,
- it is assumed that the energy released during unloading is fully recovered.
3. Results and Discussion
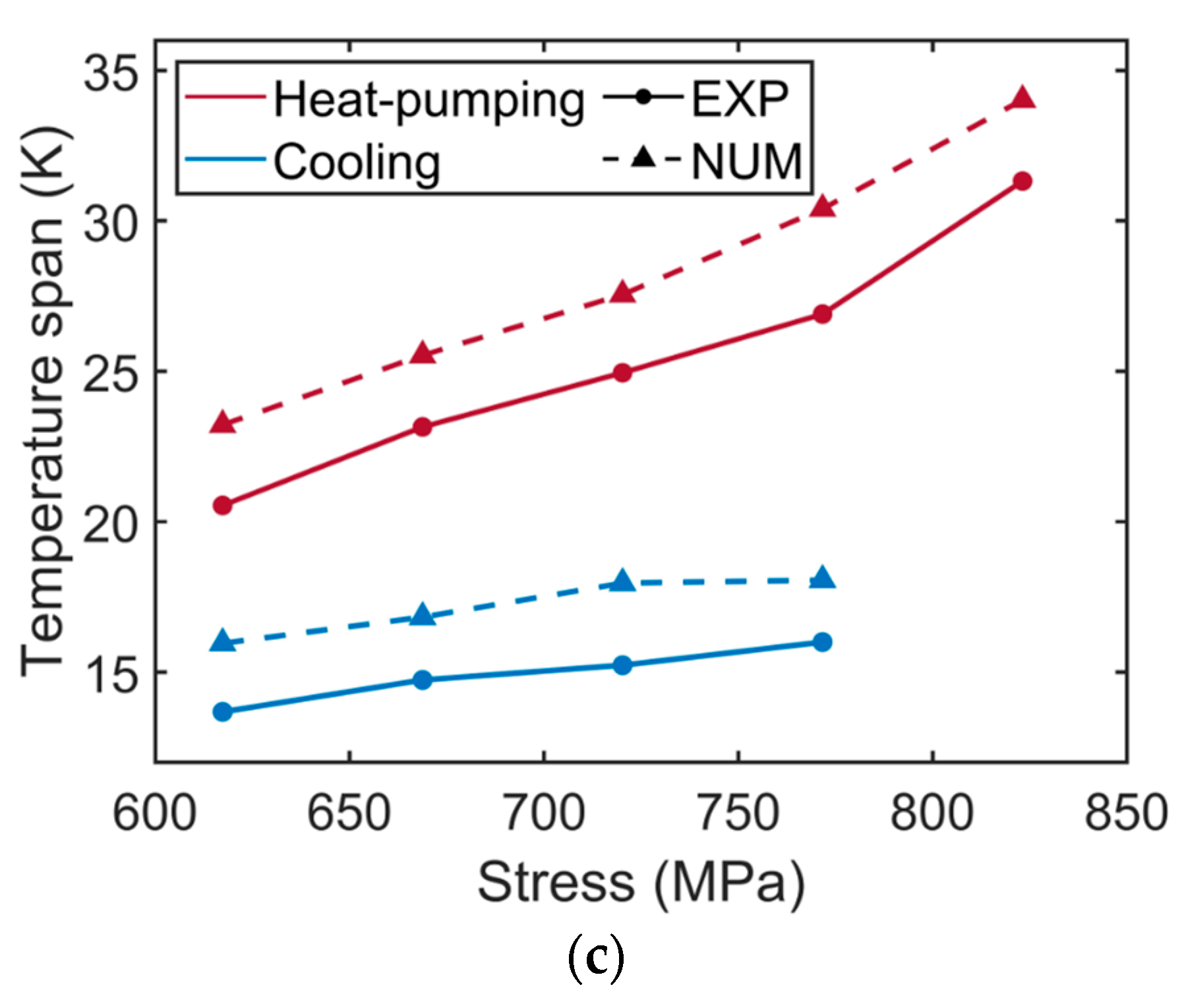
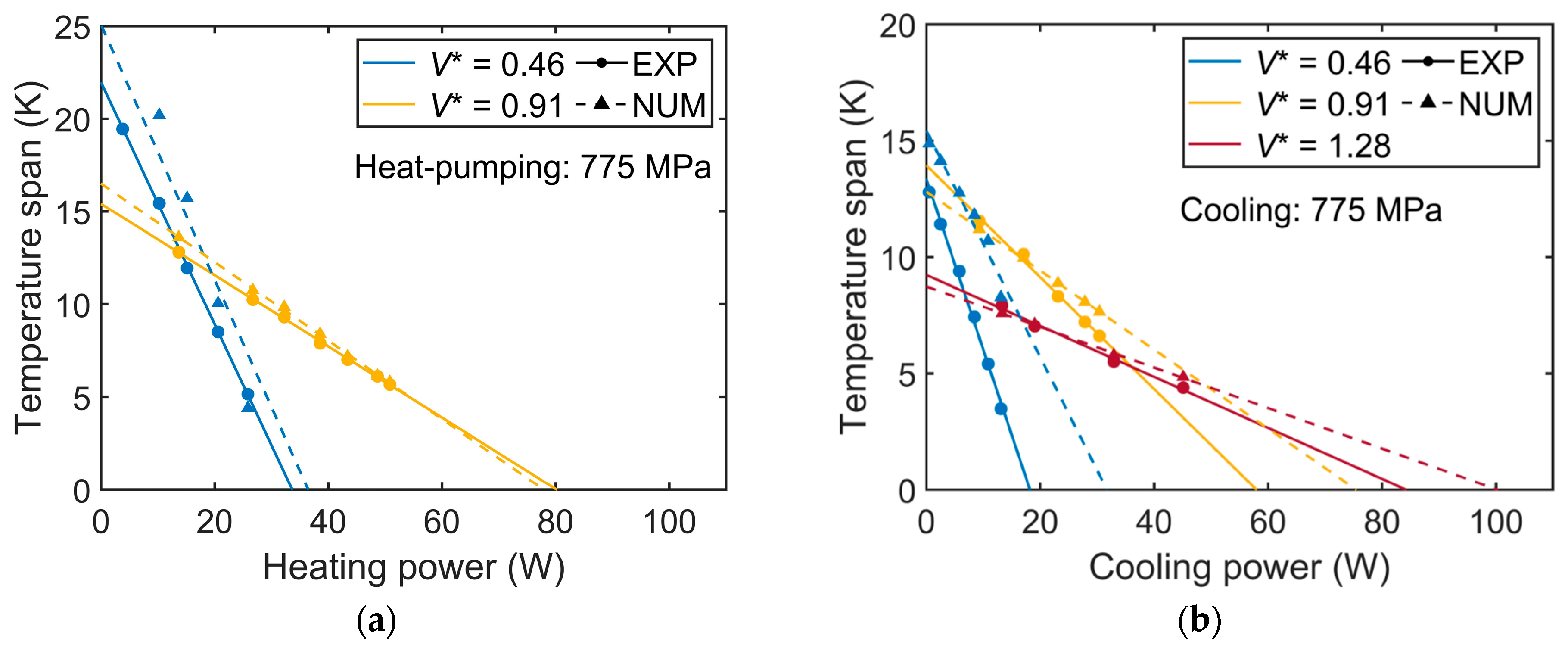
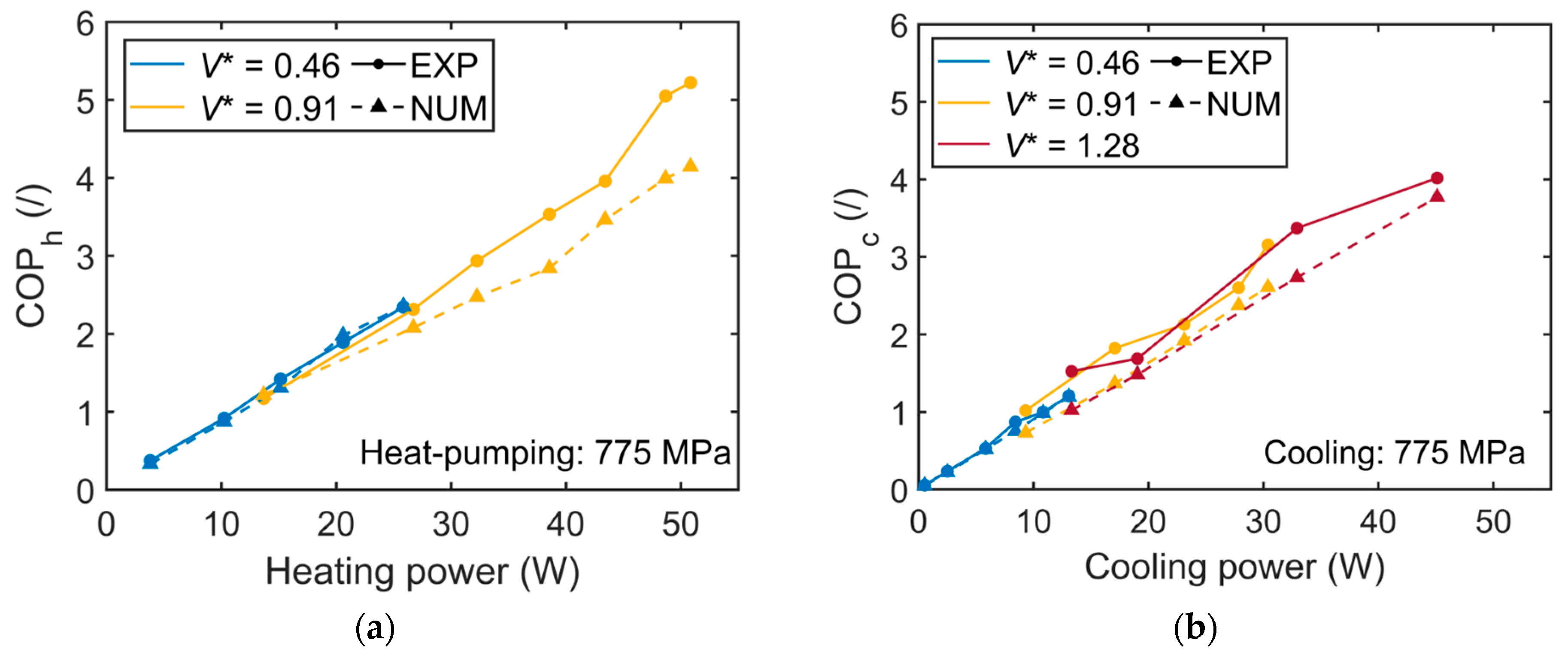
3.1. Model Verification against the Experimental Results
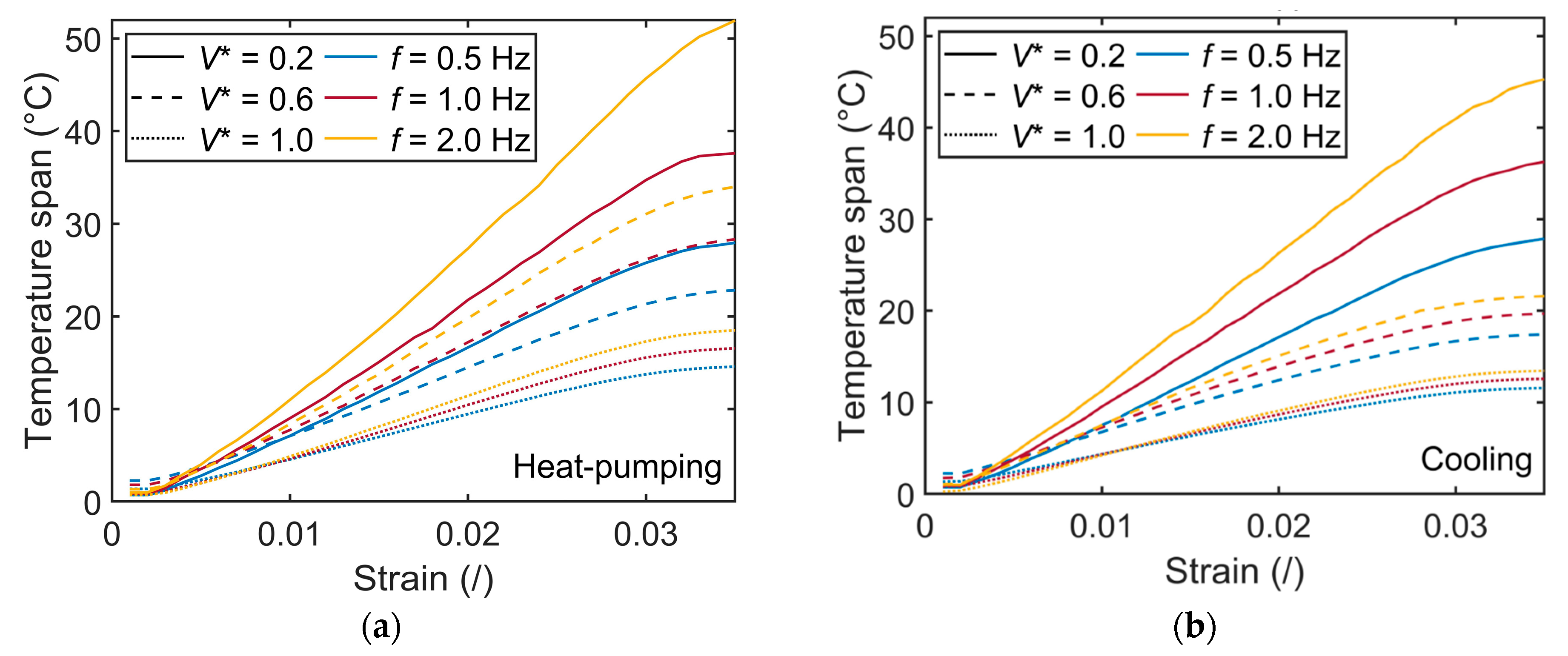
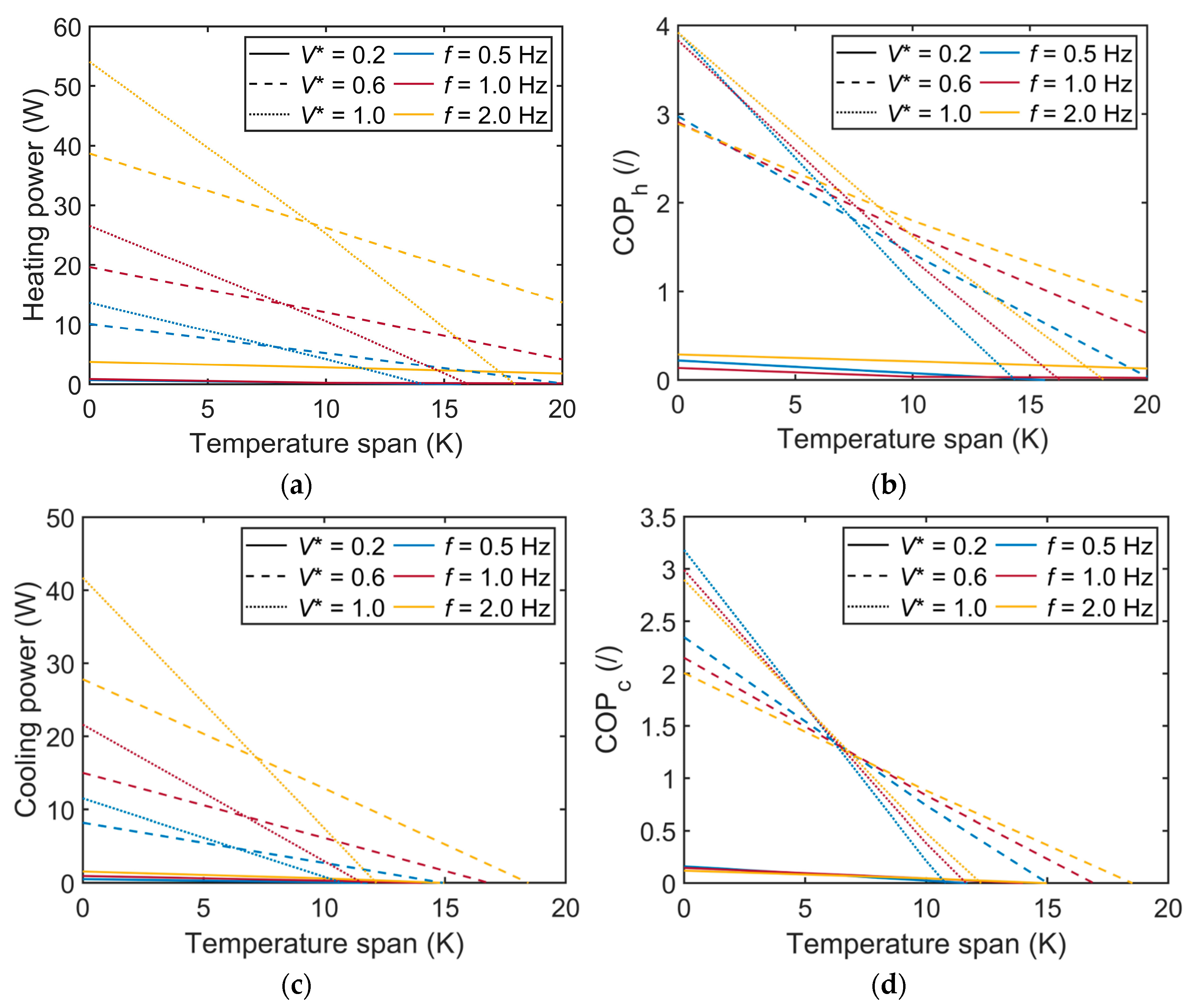
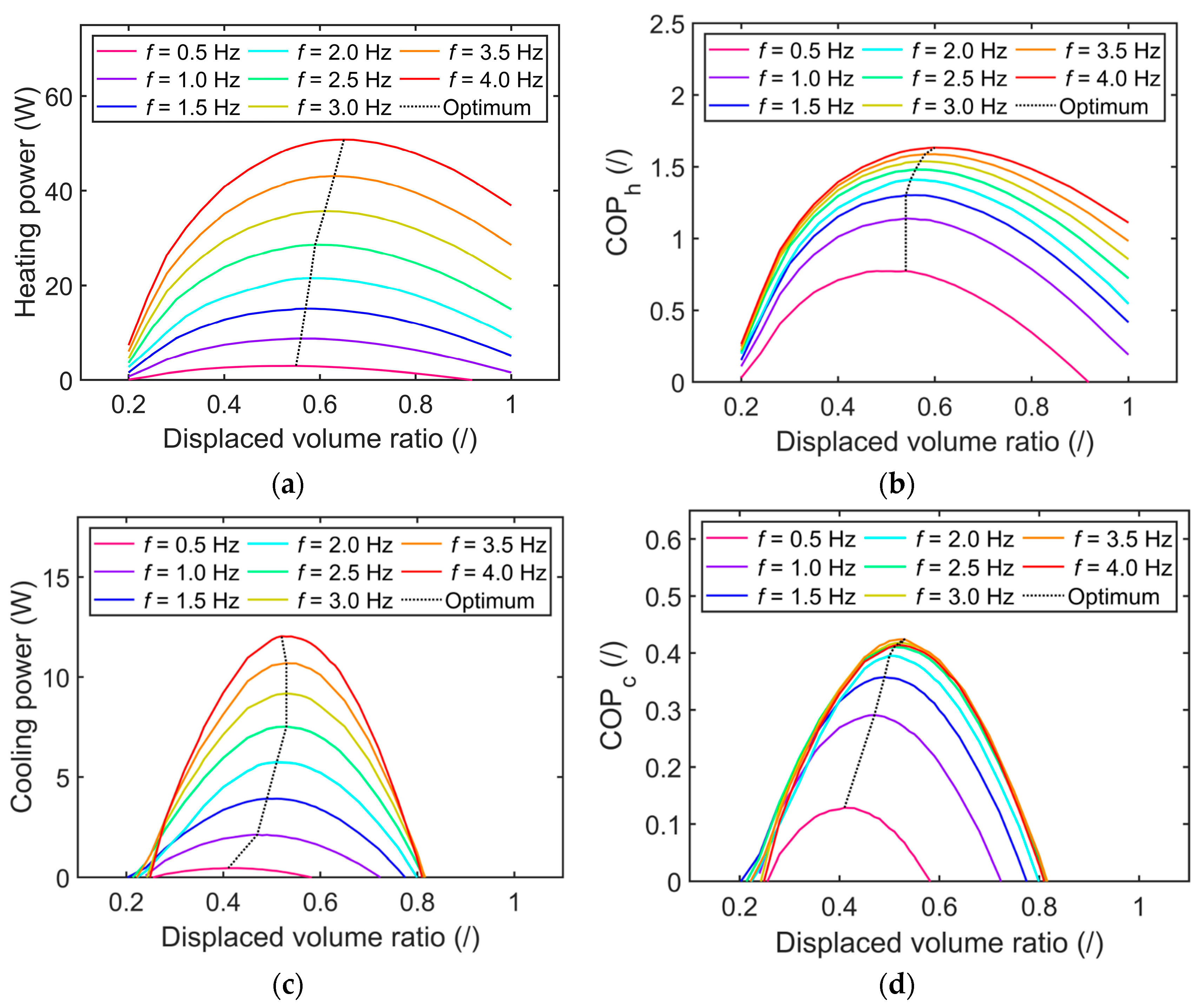
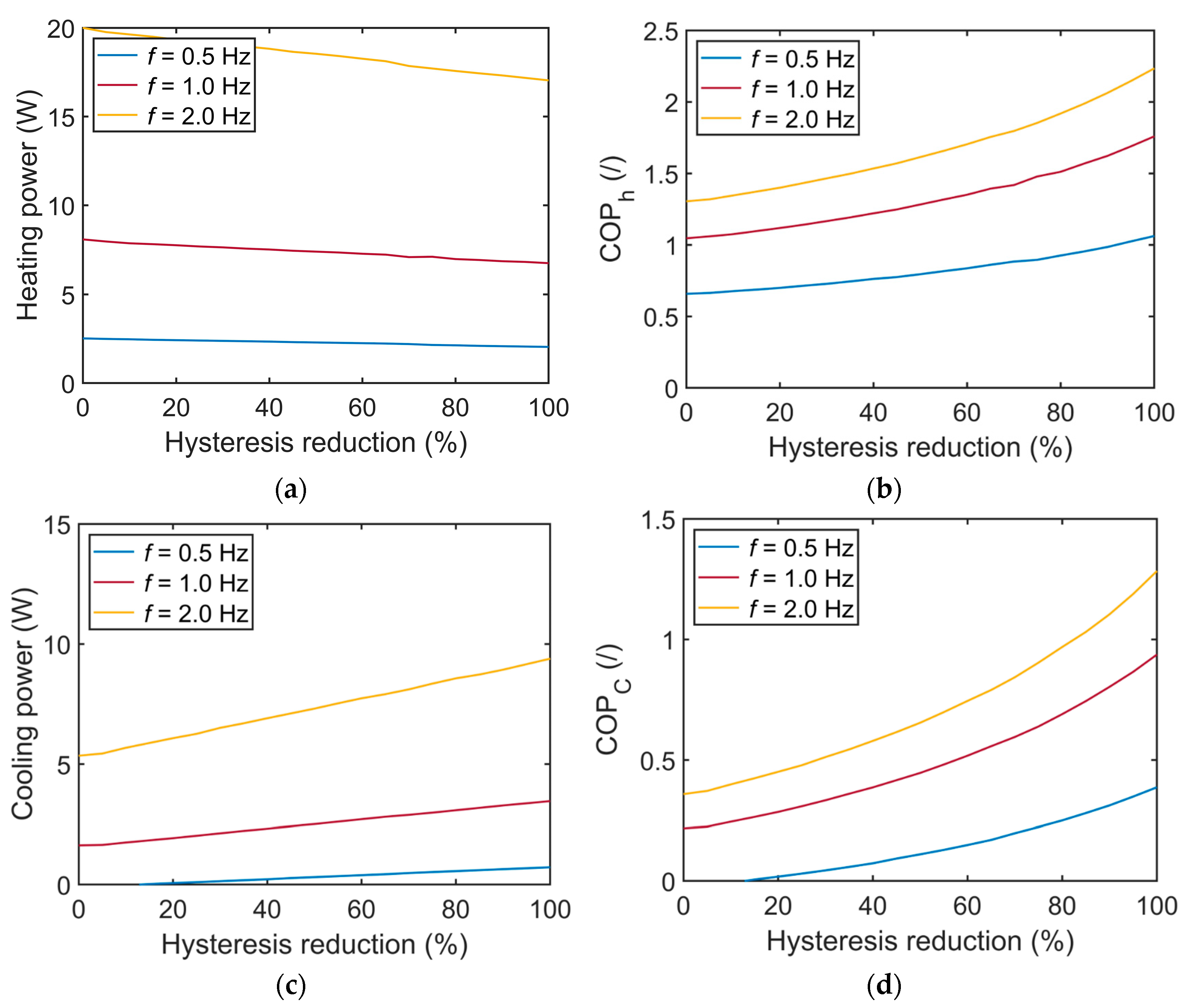
3.2. Impact of the Operating Conditions and Hysteresis Losses
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description | Units |
| Roman | ||
| A | area | (m2) |
| c | specific heat | (J·kg−1·K−1) |
| COP | coefficient of performance | (/) |
| d | inner diameter | (m) |
| D | outer diameter | (m) |
| dh | hydraulic diameter | (m) |
| E | Young’s modulus | (GPa) |
| F | friction factor | (/) |
| f | frequency | (Hz) |
| h | convective heat transfer coefficient | (W·m−2·K−1) |
| H | height | (m) |
| k | thermal conductivity | (W·m−1·K−1) |
| L | length | (m) |
| m | mass | (kg) |
| mass flow rate | (kg·s−1) | |
| Mp | martensite peak temperature | (K) |
| nt | number of tubes | (/) |
| ns | number of segments | (/) |
| Nu | Nusselt number | (/) |
| p | pressure | (Pa) |
| Pr | Prandtl number | (/) |
| Q | heat | (J) |
| thermal power | (W) | |
| R | thermal resistance | (K·W−1) |
| Re | Reynolds number | (/) |
| s | specific entropy | (J·kg−1·K−1) |
| S | spacing | (m) |
| T | temperature | (K) |
| t | time | (s) |
| v | velocity | (m·s−1) |
| V | volume | (m3) |
| V* | the displaced fluid volume ratio | (/) |
| mechanical power | (W) | |
| x | segment | (/) |
| y | a spatial node within the segment | (/) |
| Greek | ||
| δ | thickness | (m) |
| σ | stress | (MPa) |
| ϵ | emissivity | (/) |
| ε | strain | (/) |
| ρ | density | (kg·m−3) |
| μ | dynamic viscosity | (Pa·s) |
| τ | time | (s) |
| Subscripts | ||
| a | ambient | |
| ad | adiabatic | |
| A | austenite | |
| baf | baffles | |
| c | cold | |
| ef | effective | |
| f | fluid | |
| h | hot | |
| ht | heat transfer | |
| hyst | hysteresis | |
| H | housing | |
| i | inlet | |
| in | inside | |
| iso | isothermal | |
| irr | irreversibility | |
| L | loading | |
| mech | mechanical | |
| o | outlet | |
| out | outside | |
| pump | pumping | |
| reg | regenerator | |
| s | solid | |
| tot | total | |
| trans | transformation | |
| UL | unloading |
Appendix A
| Material properties | ||||||
| eCM | HTF | housing | ||||
| V | (m3) | 0.000119 | ||||
| c | (J·kg−1·K−1) | Equation (6) | 726 | |||
| ρ | (kg·m−3) | 6450 | 5523 | |||
| k | (W·m−1·K−1) | 8.6/18 | 10.9 | |||
| μ | (Pa·s) | / | / | |||
| Geometrical properties | ||||||
| D | (m) | 0.003 | ||||
| d | (m) | 0.0025 | ||||
| S | (m) | 0.0003 | ||||
| H | (m) | 0.008 | ||||
| δsup | (m) | 0.004 | ||||
| nt | (/) | 18 | ||||
| ns | (/) | 4 | ||||
| Aht,L | (m2) | for heat transfer from eCM to HTF | ||||
| for heat transfer from HTF to housing | ||||||
| Aht,UL | (m2) | for heat transfer from eCM to HTF | ||||
| 0.00443 for heat transfer from HTF to housing | ||||||
| Aht,a | (m2) | 0.0187 | ||||
| Aht,sup | (m2) | 0.00012 | ||||
| dh | (m) | [72] | ||||
| L | (m) | 0.082 | ||||
| Thermohydraulic properties | ||||||
| Re | (/) | |||||
| Nu | (/) | [65] | ||||
| F | (/) | [65] | ||||
| Ta | (°C) | 25 ± 1.5 | ||||
| hout | (W·m−2·K−1) | 90 | ||||
| hin | (W·m−2·K−1) | |||||
| heff | (W·m−2·K−1) | [83] [84] | ||||
| Ra | (m2·K·W−1) | |||||
| Rbaf,f | (m2·K·W−1) | |||||
| Rbaf,s | (m2·K·W−1) | |||||
References
- Ozone Secretariat. Handbook for the Montreal Protocol on Substances That Deplete the Ozone Layer, 14th ed.; Ozone Secretariat: Nairobi, Kenya, 2020. [Google Scholar]
- Kauffeld, M. Current long-term alternative refrigerants and their applications. In Proceedings of the 31st Informatory Note on Refrigeration Technologies, International Institute of Refrigeration, Paris, France, 1 April 2016. [Google Scholar]
- McLinden, M.O.; Brown, J.S.; Brignoli, R.; Kazakov, A.F.; Domanski, P.A. Limited options for low-global-warming-potential refrigerants. Nat. Commun. 2017, 8, 14476. [Google Scholar] [CrossRef] [PubMed]
- IEA. Average Efficiency of New Air Conditioners 2000–2020 and in the Net Zero Scenario; IEA: Paris, France; Available online: https://www.iea.org/data-and-statistics/charts/average-efficiency-of-new-air-conditioners-2000-2020-and-in-the-net-zero-scenario (accessed on 12 September 2022).
- Kitanovski, A. Energy Applications of Magnetocaloric Materials. Adv. Energy Mater. 2020, 10, 1903741. [Google Scholar] [CrossRef]
- Ismail, M.; Yebiyo, M.; Chaer, I.A. Review of Recent Advances in Emerging Alternative Heating and Cooling Technologies. Energies 2021, 14, 502. [Google Scholar] [CrossRef]
- Goetzler, W.; Zogg, R.; Young, J.; Johnson, C. Energy Savings Potential and RD & D Opportunities for Non-Vapor-Compression HVAC Technologies; United States Department of Energy: Washington, DC, USA, 2014; p. 3673. [CrossRef]
- OECD/IEA. The Future of Cooling Opportunities for Energy-Efficient Air Conditioning Together Secure Sustainable. 2018. Available online: www.iea.org/t&c/ (accessed on 12 September 2022).
- Bruederlin, F.; Bumke, L.; Chluba, C.; Ossmer, H.; Quandt, E.; Kohl, M. Elastocaloric Cooling on the Miniature Scale: A Review on Materials and Device Engineering. Energy Technol. 2018, 6, 1588–1604. [Google Scholar] [CrossRef]
- Kalizan, J.; Tušek, J. Caloric Micro-Cooling: Numerical modelling and parametric investigation. Energy Convers. Manag. 2020, 225, 113421. [Google Scholar] [CrossRef]
- Babapoor, A.; Aziz, M.; Karimi, G. Thermal management of a Li-on battery using carbon fiber-PCM composites. Appl. Therm. Eng. 2015, 62, 281–290. [Google Scholar] [CrossRef]
- Bo, Z.; Li, Z.; Yang, H.; Li, C.; Wu, S.; Xu, C.; Xiong, G.; Mariotti, D.; Yan, J.; Cen, K.; et al. Combinatorial atomistic-to-AI prediction and experimental validation of heating effects in 350 F supercapacitor modules. Int. J. Heat Mass Transf. 2021, 171, 121075. [Google Scholar] [CrossRef]
- Kabirifar, P.; Žerovnik, A.; Ahčin, Ž.; Porenta, L.; Brojan, M.; Tušek, J. Elastocaloric Cooling: State-of-the-art and Future Challenges in Designing Regenerative Elastocaloric Devices. J. Mech. Eng. 2019, 65, 615–630. [Google Scholar] [CrossRef]
- Rodriguez, C.; Brown, L.C. The thermal effect due to stress-induced martensite formation in Β-CuAlNi single crystals. Metall. Mater. Trans. A 1980, 11, 147–150. [Google Scholar] [CrossRef]
- Hou, H.; Qian, S.; Takeuchi, I. Materials, physics and systems for multicaloric cooling. Nat. Rev. Mater. 2022, 7, 633–652. [Google Scholar] [CrossRef]
- Qian, S. Thermodynamics of elastocasloric cooling and heat pump cycles. Appl. Therm. Eng. 2023, 219, 119540. [Google Scholar] [CrossRef]
- Frenzel, J.; Wieczorek, A.; Opahle, I.; Maaß, B.; Drautz, R.; Eggeler, G. On the effect of alloy composition on martensite start temperatures and latent heats in Ni–Ti-based shape memory alloys. Acta Mater. 2015, 90, 213–231. [Google Scholar] [CrossRef]
- Wieczorek, A.; Frenzel, J.; Schmidt, M.; Maass, B.; Seelecke, S.; Schütze, A.; Eggeler, G. Optimizing Ni–Ti-based shape memory alloys for ferroic cooling. Funct. Mater. Lett. 2017, 10, 1740001. [Google Scholar] [CrossRef]
- Chluba, C.; Ge, W.; de Miranda, R.L.; Strobel, J.; Kienle, L.; Quandt, E.; Wuttig, M. Ultralow-fatigue shape memory alloy films. Science 2015, 348, 1004–1007. [Google Scholar] [CrossRef] [PubMed]
- Chluba, C.; Ossmer, H.; Zamponi, C.; Kohl, M.; Quandt, E. Ultra-Low Fatigue Quaternary TiNi-Based Films for Elastocaloric Cooling. Shape Mem. Superelasticity 2016, 2, 95–103. [Google Scholar] [CrossRef]
- Mañosa, L.; Jarque-Farnos, S.; Vives, E.; Planes, A. Large temperature span and giant refrigerant capacity in elastocaloric Cu-Zn-Al shape memory alloys. Appl. Phys. Lett. 2013, 103, 211904. [Google Scholar] [CrossRef]
- Qian, S.; Geng, Y.; Wang, Y.; Pillsbury, T.E.; Hada, Y.; Yamaguchi, Y.; Fujimoto, K.; Hwang, Y.; Radermacher, R.; Cui, J.; et al. Elastocaloric effect in CuAlZn and CuAlMn shape memory alloys under compression. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150309. [Google Scholar] [CrossRef]
- Xiao, F.; Bucsek, A.; Jin, X.; Porta, M.; Planes, A. Giant elastic response and ultra-stable elastocaloric effect in tweed textured Fe-Pd single crystals. Acta Mater. 2022, 223, 117486. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, D.; Li, Y. Exploring Magnetic Elastocaloric Materials for Solid-State Cooling. Shape Mem. Superelasticity 2017, 3, 192–198. [Google Scholar] [CrossRef]
- Tong, W.; Liang, L.; Xu, J.; Wang, H.J.; Tian, J.; Peng, L.M. Achieving enhanced mechanical, pseudoelastic and elastocaloric properties in Ni-Mn-Ga alloys via Dy micro-alloying and isothermal mechanical cyclic training. Scr. Mater. 2022, 209, 114393. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, Q.; Li, C.; Fu, Y.; Zhang, H.; Ye, Z.; Zhou, X.; Li, Q.; Wang, T.; Wang, S.; et al. Solid-state cooling by elastocaloric polymer with uniform chain-lengths. Nat. Commun. 2022, 13, 9. [Google Scholar] [CrossRef] [PubMed]
- Bennacer, R.; Liu, B.; Yang, M.; Chen, A. Refrigeration performance and the elastocaloric effect in natural and synthetic rubbers. Appl. Therm. Eng. 2022, 204, 117938. [Google Scholar] [CrossRef]
- Imran, M.; Zhang, X. Recent developments on the cyclic stability in elastocaloric materials. Mater. Des. 2020, 195, 109030. [Google Scholar] [CrossRef]
- Chen, J.; Lei, L.; Fang, G. Elastocaloric cooling of shape memory alloys: A review. Mater. Today Commun. 2021, 28, 102706. [Google Scholar] [CrossRef]
- Imran, M.; Zhang, X. Reduced dimensions elastocaloric materials: A route towards miniaturized refrigeration. Mater. Des. 2021, 206, 109784. [Google Scholar] [CrossRef]
- Tušek, J.; Engelbrecht, K.; Eriksen, D.; Dall’Olio, S.; Tušek, J.; Pryds, N. A regenerative elastocaloric heat pump. Nat. Energy 2016, 1, 16134. [Google Scholar] [CrossRef]
- Kirsch, S.M.; Welsch, F.; Michaelis, N.; Schmidt, M.; Wieczorek, A.; Frenzel, J.; Eggeler, G.; Schütze, A.; Seelecke, S. NiTi-Based Elastocaloric Cooling on the Macroscale: From Basic Concepts to Realization. Energy Technol. 2018, 6, 1567–1587. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, K.; Kan, Q.; Yin, H.; Sun, Q. Ultra-high fatigue life of NiTi cylinders for compression-based elastocaloric cooling. Appl. Phys. Lett. 2019, 115, 93902. [Google Scholar] [CrossRef]
- Snodgrass, R.; Erickson, D. A multistage elastocaloric refrigerator and heat pump with 28 K temperature span. Sci. Rep. 2019, 9, 18532. [Google Scholar] [CrossRef]
- Ahčin, Ž.; Dall’Olio, S.; Žerovnik, A.; Baškovič, U.Ž.; Porenta, L.; Kabirifar, P.; Cerar, J.; Zupan, S.; Brojan, M.; Klemenc, J.; et al. High-performance cooling and heat pumping based on fatigue-resistant elastocaloric effect in compression. Joule 2022, 6, 2338–2357. [Google Scholar] [CrossRef]
- Bachmann, N.; Fitger, A.; Maier, L.M.; Mahlke, A.; Schäfer-Welsen, O.; Koch, T.; Bartholomé, K. Long-term stable compressive elastocaloric cooling system with latent heat transfer. Commun. Phys. 2021, 4, 194. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Sun, W.; Qian, S.; Liu, J. A compact elastocaloric refrigerator. Innovation 2022, 3, 100205. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhu, Y.; Cheng, S.; Yao, S.; Sun, Q. Enhancing cooling performance of NiTi elastocaloric tube refrigerant via internal grooving. Appl. Therm. Eng. 2022, 213, 118657. [Google Scholar] [CrossRef]
- Emaikwu, N.; Catalini, D.; Muehlbauer, J.; Hwang, Y.; Takeuchi, I.; Radermacher, R. Experimental Investigation of a Staggered-Tube Active Elastocaloric Regenerator. Int. J. Refrig. 2022, in press. [CrossRef]
- Li, X.; Cheng, S.; Sun, Q. A compact NiTi elastocaloric air cooler with low force bending actuation. Appl. Therm. Eng. 2022, 215, 118942. [Google Scholar] [CrossRef]
- Barclay, J.A.; Steyer, W.A. Active Magnetic Regenerator. U.S. Patent 4332135A, 1 June 1982. [Google Scholar]
- Torelló, A.; Lheritier, P.; Usui, T.; Nouchokgwe, Y.; Gérard, M.; Bouton, O.; Hirose, S.; Defay, E. Giant temperature span in electrocaloric regenerator. Science 2020, 370, 125–129. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Lai, C.; Li, J.; Zhang, Z.; Zhang, H.; Hou, S.; Wang, F.; Zhao, J.; Zhang, C.; Miao, H.; et al. Elastocaloric cooler for waste heat recovery from proton exchange membrane fuel cells. Energy 2022, 238, 121789. [Google Scholar] [CrossRef]
- Al-Hamed, K.H.M.; Dincer, I.; Rosen, M.A. Investigation of elastocaloric cooling option in a solar energy-driven system. Int. J. Refrig. 2020, 120, 340–356. [Google Scholar] [CrossRef]
- Qian, S.; Ling, J.; Hwang, Y.; Radermacher, R.; Takeuchi, I. Thermodynamics cycle analysis and numerical modeling of thermoelastic cooling systems. Int. J. Refrig. 2015, 56, 65–80. [Google Scholar] [CrossRef]
- Luo, D.; Feng, Y.; Verma, P. Modeling and analysis of an integrated solid state elastocaloric heat pumping system. Energy 2017, 130, 500–514. [Google Scholar] [CrossRef]
- Tušek, J.; Engelbrecht, K.; Millán-Solsona, R.; Mañosa, L.; Vives, E.; Mikkelsen, L.P.; Pryds, N. The Elastocaloric Effect: A Way to Cool Efficiently; Supporting Information. Adv. Energy Mater. 2015, 5, 1500361. [Google Scholar] [CrossRef]
- Qian, S.; Wang, Y.; Xu, S.; Chen, Y.; Yuan, L.; Yu, J. Cascade utilization of low-grade thermal energy by coupled elastocaloric power and cooling cycle. Appl. Energy 2021, 298, 117269. [Google Scholar] [CrossRef]
- Sebald, G.; Komiya, A.; Jay, J.; Coativy, G.; Lebrun, L. Regenerative cooling using elastocaloric rubber: Analytical model and experiments. J. Appl. Phys. 2020, 127, 94903. [Google Scholar] [CrossRef]
- Zhu, Y.; Hur, J.; Cheng, S.; Sun, Q.; Li, W.; Yao, S. Modelling of elastocaloric regenerators with enhanced heat transfer structures. Int. J. Heat Mass Transf. 2021, 176, 121372. [Google Scholar] [CrossRef]
- Tušek, J.; Engelbrecht, K.; Pryds, N. Elastocaloric effect of a Ni-Ti plate to be applied in a regenerator-based cooling device. Sci. Technol. Built Environ. 2016, 22, 489–499. [Google Scholar] [CrossRef]
- Tan, J.; Wang, Y.; Xu, S.; Liu, H.; Qian, S. Thermodynamic cycle analysis of heat driven elastocaloric cooling system. Energy 2020, 197, 117261. [Google Scholar] [CrossRef]
- Qian, S.; Wang, Y.; Yuan, L.; Yu, J. A heat driven elastocaloric cooling system. Energy 2019, 182, 881–899. [Google Scholar] [CrossRef]
- Qian, S.; Yuan, L.; Yu, J.; Yan, G. Numerical modeling of an active elastocaloric regenerator refrigerator with phase transformation kinetics and the matching principle for materials selection. Energy 2017, 141, 744–756. [Google Scholar] [CrossRef]
- Cirillo, L.; Rosaria Farina, A.; Greco, A.; Masselli, C. The optimization of the energy performances of a single bunch of elastocaloric elements to be employed in an experimental device. Therm. Sci. Eng. Prog. 2022, 27, 101152. [Google Scholar] [CrossRef]
- Qian, S.; Yuan, L.; Hou, H.; Takeuchi, I. Accurate prediction of work and coefficient of performance of elastocaloric materials with phase transformation kinetics. Sci. Technol. Built Environ. 2018, 24, 673–684. [Google Scholar] [CrossRef]
- Ulpiani, G.; Saliari, M.; Bruederlin, F.; Kohl, M.; Ranzi, G.; Santamouris, M. On the cooling potential of elastocaloric devices for building ventilation. Sol. Energy 2021, 230, 298–311. [Google Scholar] [CrossRef]
- Bachmann, N.; Schwarz, D.; Bach, D.; Schäfer-Welsen, O.; Koch, T.; Bartholomé, K. Modeling of an Elastocaloric Cooling System for Determining Efficiency. Energies 2022, 15, 5089. [Google Scholar] [CrossRef]
- Heintze, O.; Seelecke, S. A coupled thermomechanical model for shape memory alloys-From single crystal to polycrystal. Mater. Sci. Eng. A 2008, 481–482, 389–394. [Google Scholar] [CrossRef]
- Yuan, L.; Wang, Y.; Yu, J.; Greco, A.; Masselli, C.; Qian, S. Numerical study of a double-effect elastocaloric cooling system powered by low-grade heat. Appl. Therm. Eng. 2023, 218, 119302. [Google Scholar] [CrossRef]
- Bachmann, N.; Fitger, A.; Unmüßig, S.; Bach, D.; Schäfer-Welsen, O.; Koch, T.; Bartholomé, K. Phenomenological model for first-order elastocaloric materials. Int. J. Refrig. 2022, 136, 245–253. [Google Scholar] [CrossRef]
- Hess, T.; Vogel, C.; Maier, L.M.; Barcza, A.; Vieyra, H.P.; Schäfer-Welsen, O.; Wöllenstein, J.; Bartholomé, K. Phenomenological model for a first-order magnetocaloric material. Int. J. Refrig. 2020, 109, 128–134. [Google Scholar] [CrossRef]
- Griffith, L.D.; Alho, B.P.; Czernuszewicz, A.; Ribeiro, P.O.; Slaughter, J.; Pecharsky, V.K. Toward efficient elastocaloric systems: Predicting material thermal properties with high fidelity. Acta Mater. 2021, 217, 117162. [Google Scholar] [CrossRef]
- de Oliveira, N.A.; von Ranke, P.J. Theoretical aspects of the magnetocaloric effect. Phys. Rep. 2010, 489, 89–159. [Google Scholar] [CrossRef]
- Ahčin, Ž.; Liang, J.; Engelbrecht, K.; Tušek, J. Thermo-hydraulic evaluation of oscillating-flow shell-and-tube-like regenerators for (elasto)caloric cooling. Appl. Therm. Eng. 2021, 190, 116842. [Google Scholar] [CrossRef]
- Porenta, L.; Trojer, J.; Brojan, M.; Tušek, J. Experimental investigation of buckling stability of superelastic Ni-Ti tubes under cyclic compressive loading: Towards defining functionally stable tubes for elastocaloric cooling. Int. J. Solids Struct. 2022, 256, 111948. [Google Scholar] [CrossRef]
- Tušek, J.; Engelbrecht, K.; Mikkelsen, L.P.; Pryds, N. Elastocaloric effect of Ni-Ti wire for application in a cooling device. J. Appl. Phys. 2015, 117, 124901. [Google Scholar] [CrossRef]
- Miyazaki, S.; Imai, T.; Igo, Y.; Otsuka, K. Effect of cyclic deformation on the pseudoelasticity characteristics of Ti-Ni alloys. Metall. Trans. A 1986, 17, 115–120. [Google Scholar] [CrossRef]
- Porenta, L.; Kabirifar, P.; Žerovnik, A.; Cebron, M.; Žužek, B.; Dolenec, M.; Brojan, M.; Tušek, J. Thin-walled Ni-Ti tubes under compression: Ideal candidates for efficient and fatigue-resistant elastocaloric cooling. Appl. Mater. Today 2020, 20, 100712. [Google Scholar] [CrossRef]
- Brey, W.; Nellis, G.; Klein, S. Thermodynamic modeling of magnetic hysteresis in AMRR cycles. Int. J. Refrig. 2014, 47, 85–97. [Google Scholar] [CrossRef]
- Kitanovski, A.; Tušek, J.; Tomc, U.; Plaznik, U.; Ožbolt, M.; Poredoš, A. Magnetocaloric Energy Conversion—From Theory to Applications; Springer: Berlin, Germany, 2015. [Google Scholar] [CrossRef]
- Žukauskas, A. Heat Transfer from Tubes in Crossflow. Adv. Heat Transf. 1987, 18, 87–159. [Google Scholar] [CrossRef]
- Trevizoli, P.V.; Barbosa, J.R. Thermal-hydraulic behavior and influence of carryover losses in oscillating-flow regenerators. Int. J. Therm. Sci. 2017, 113, 89–99. [Google Scholar] [CrossRef]
- Masche, M.; Ianniciello, L.; Tušek, J.; Engelbrecht, K. Impact of hysteresis on caloric cooling performance. Int. J. Refrig. 2021, 121, 302–312. [Google Scholar] [CrossRef]
- Hess, T.; Maier, L.M.; Bachmann, N.; Corhan, P.; Schäfer-Welsen, O.; Wöllenstein, J.; Bartholomé, K. Thermal hysteresis and its impact on the efficiency of first-order caloric materials. J. Appl. Phys. 2020, 127, 75103. [Google Scholar] [CrossRef]
- Lu, B.; Song, M.; Zhou, Z.; Liu, W.; Wang, B.; Lu, S.; Wu, C.; Yang, L.; Liu, J. Reducing mechanical hysteresis via tuning the microstructural orientations in Heusler-type Ni44.8Mn36.9In13.3Co5.0 elastocaloric alloys. J. Alloys Compd. 2019, 785, 1023–1029. [Google Scholar] [CrossRef]
- Yuan, B.; Zhu, X.; Zhang, X.; Qian, M. Elastocaloric effect with small hysteresis in bamboo-grained Cu–Al–Mn microwires. J. Mater. Sci. 2019, 54, 9613–9621. [Google Scholar] [CrossRef]
- Ahadi, A.; Kawasaki, T.; Harjo, S.; Ko, W.S.; Sun, Q.; Tsuchiya, K. Reversible elastocaloric effect at ultra-low temperatures in nanocrystalline shape memory alloys. Acta Mater. 2019, 165, 109–117. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, X.; Qian, M. Reversible elastocaloric effects with small hysteresis in nanocrystalline Ni-Ti microwires. AIP Adv. 2018, 8, 125002. [Google Scholar] [CrossRef]
- Lin, H.; Hua, P.; Sun, Q. Effects of grain size and partial amorphization on elastocaloric cooling performance of nanostructured NiTi. Scr. Mater. 2022, 209, 114371. [Google Scholar] [CrossRef]
- Kabirifar, P.; Trojer, J.; Brojan, M.; Tušek, J. From the elastocaloric effect towards an efficient thermodynamic cycle. J. Phys. Energy 2022, 4, 44009. [Google Scholar] [CrossRef]
- Schmidt, M.; Kirsch, S.M.; Seelecke, S.; Schütze, A. Elastocaloric cooling: From fundamental thermodynamics to solid state air conditioning. Sci. Technol. Built Environ. 2016, 22, 475–488. [Google Scholar] [CrossRef]
- Jeffreson, C.P. Prediction of breakthrough curves in packed beds: II. Experimental evidence for axial dispersion and intraparticle effects. AIChE J. 1972, 18, 416–420. [Google Scholar] [CrossRef]
- Engelbrecht, K.L.; Nellis, G.F.; Klein, S.A. The effect of internal temperature gradients on regenerator matrix performance. J. Heat Transf. 2006, 128, 1060–1069. [Google Scholar] [CrossRef]

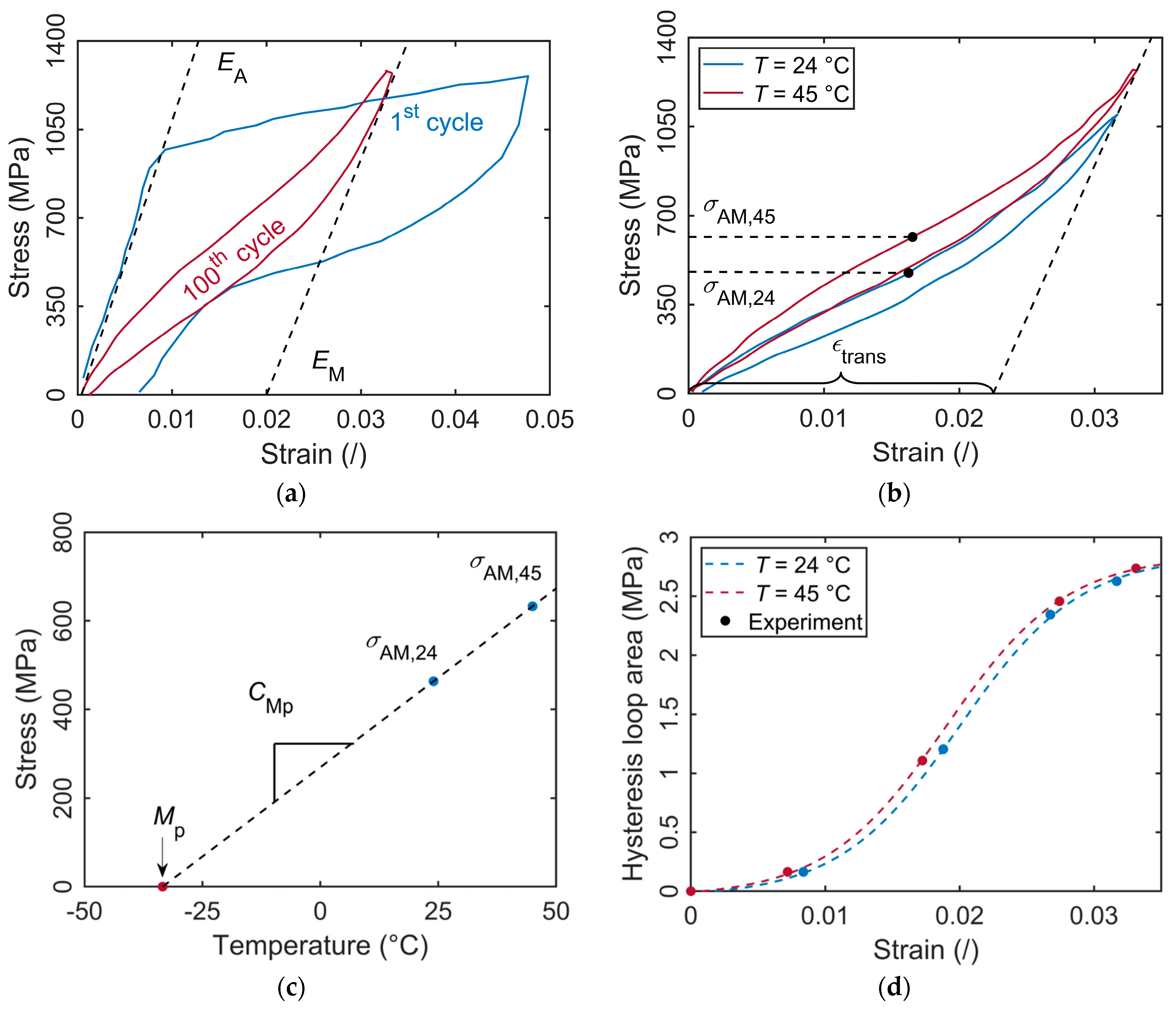

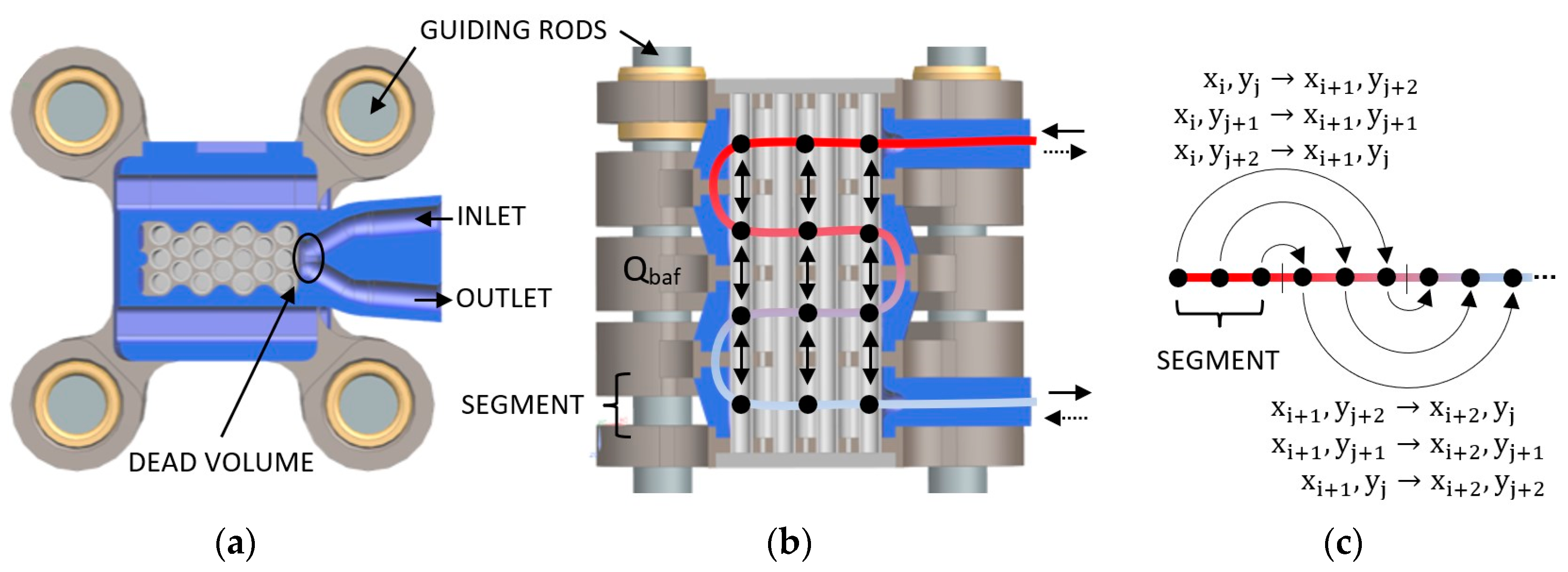

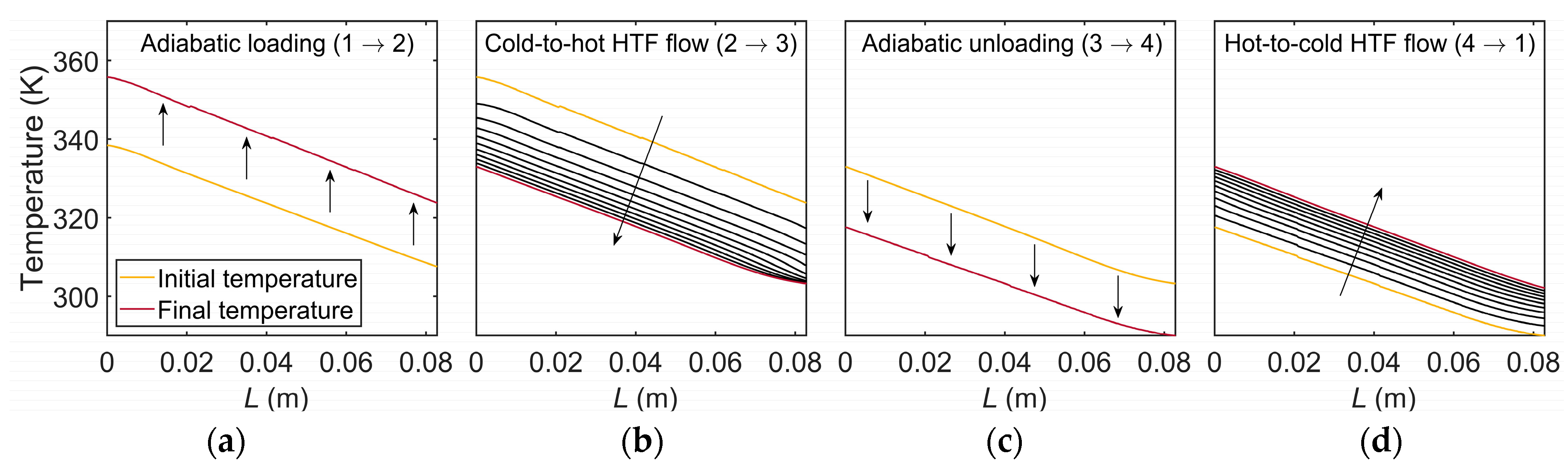
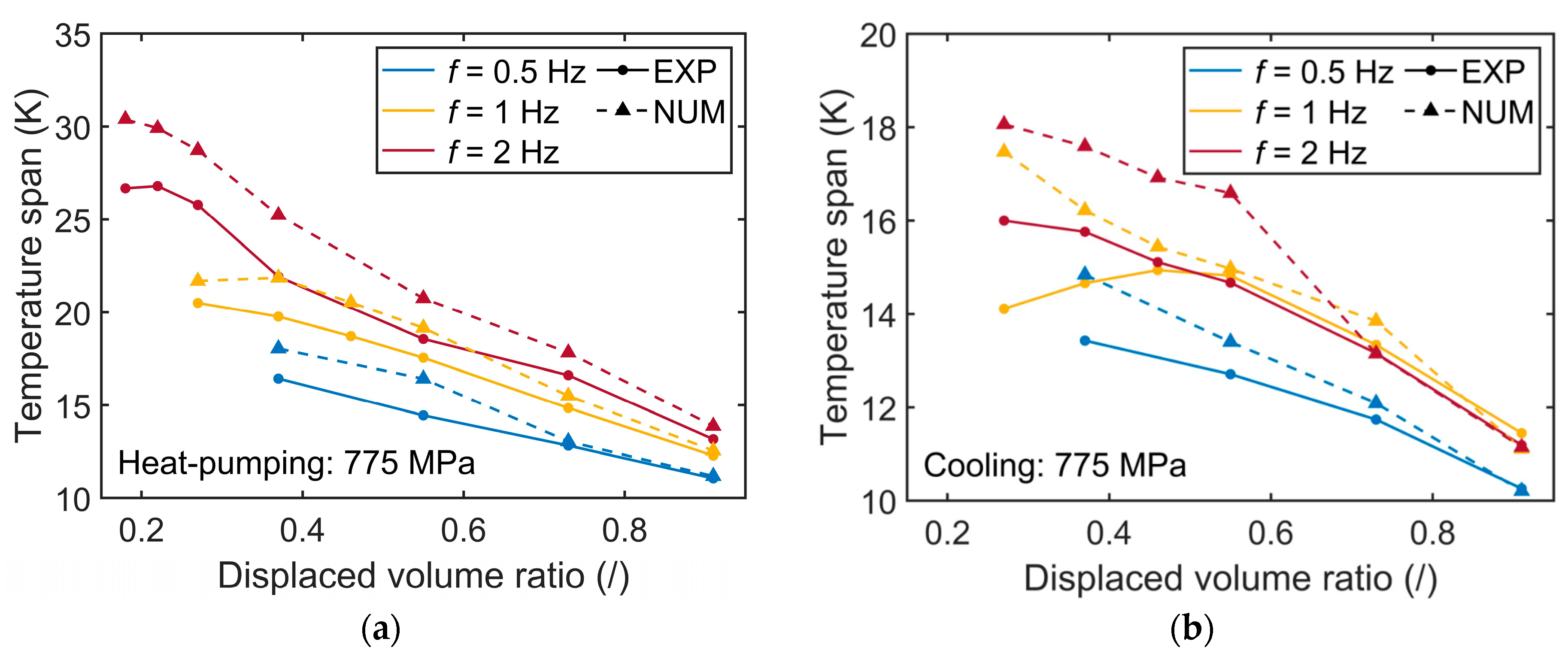
| EA (GPa) | σAM,24 (MPa) | σAM,45 (MPa) | εtrans (/) | CMp (MPa·K−1) | Mp (K) | Ms (K) | Mf (K) |
|---|---|---|---|---|---|---|---|
| 113.3 | 463 | 633 | 0.0225 | 7.83 | 239 | 315 | 163 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahčin, Ž.; Kabirifar, P.; Porenta, L.; Brojan, M.; Tušek, J. Numerical Modeling of Shell-and-Tube-like Elastocaloric Regenerator. Energies 2022, 15, 9253. https://doi.org/10.3390/en15239253
Ahčin Ž, Kabirifar P, Porenta L, Brojan M, Tušek J. Numerical Modeling of Shell-and-Tube-like Elastocaloric Regenerator. Energies. 2022; 15(23):9253. https://doi.org/10.3390/en15239253
Chicago/Turabian StyleAhčin, Žiga, Parham Kabirifar, Luka Porenta, Miha Brojan, and Jaka Tušek. 2022. "Numerical Modeling of Shell-and-Tube-like Elastocaloric Regenerator" Energies 15, no. 23: 9253. https://doi.org/10.3390/en15239253
APA StyleAhčin, Ž., Kabirifar, P., Porenta, L., Brojan, M., & Tušek, J. (2022). Numerical Modeling of Shell-and-Tube-like Elastocaloric Regenerator. Energies, 15(23), 9253. https://doi.org/10.3390/en15239253








