A Review of the Optimization and Control Techniques in the Presence of Uncertainties for the Energy Management of Microgrids

Abstract

This paper reviews the current techniques used in energy management systems to optimize energy schedules into microgrids, accounting for uncertainties for various time frames (day-ahead and real-time operations). The current uncertainties affecting applications, including residential, commercial, virtual power plants, electric mobility, and multi-carrier microgrids, are the main subjects of this article. We outline the most recent modeling approaches to describe the uncertainties associated with various microgrid applications, such as prediction errors, load consumption, degradation, and state of health. The modeling approaches discussed in this article are probabilistic, possibilistic, information gap theory, and deterministic. Then, the paper presents and compares the current optimization techniques, considering the uncertainties in their problem formulations, such as stochastic, robust, fuzzy optimization, information gap theory, model predictive control, multiparametric programming, and machine learning techniques. The optimization techniques depend on the model used, the data available, the specific application, the real-time platform, and the optimization time. We hope to guide researchers to identify the best optimization technique for energy scheduling, considering the specific uncertainty and application. Finally, the most challenging issues to enhance microgrid operations, despite uncertainties by considering new trends, are discussed.

1. Introduction

A microgrid is a cluster of distributed generators—wind turbines, photovoltaic (PV) systems, thermal units, microhydropower plants—and controllable or uncontrollable loads, operating at low and medium voltage levels [1]. Storage units and electrical vehicles (EVs) can be part of the clusters [2]. The microgrid can operate in a grid-connected or islanded mode, while a supervisory control system is responsible for its operation. In a grid-connected mode, the supervisory control manages the grid synchronization, acts in case of grid disturbance or failure, regulates the power and energy flows between the microgrid and the grid, and ensures an adequate level of power quality at the point of common coupling [3]. Commonly, the microgrid has an energy management system (EMS) at the supervisory and control level [4], which has the objective of (i) monitoring and processing the available data (i.e., environmental, electrical, and operating parameters) [5], (ii) forecasting the generation capability [6], the load profile [7], the consumer behavior [8], and the energy market dynamic behavior [9], (iii) optimizing the energy flow among distributed generators and loads, e.g., by minimizing the operation cost, maximizing the self-consumption of the produced renewable energy [10], and (iv) developing the offline or online energy scheduling [11].

To develop the various functions of the EMS, intelligent algorithms, modeling, and optimization techniques have been used [12]. The energy schedule and the optimization of the energy flows will depend on the time frame (real-time [13], day-ahead [14], intra-day scheduling [15]), the input and forecast data, and the specific application of the microgrid (home, building, residential, or industry) [16]. Usually, for energy scheduling and energy flow optimization, the value of the forecast power generated by the renewable sources, the load consumption, the electricity price, and other parameters, such as the state of health of the microgrid, are considered as certain variables (e.g., [17]). In reality, they are inherently affected by an amount of uncertainty that needs to be taken into account, affecting the result of the smart grid-optimized management [18]. For instance, PV power forecasting can be affected by time-varying clouding [19], soiling, and PV module degradation [20], which are usually not accounted for in the EMS optimization problem. As for the batteries of the EVs that are connected to the microgrid, their initial state of charge depends on the driving pattern [21,22], the battery type, and degradation [23], on the ambient temperature, and on a number of further uncertain parameters that make the EMS operation more complicated [24]. The same conclusion holds for residential applications because of the dependency of energy consumption on inherently uncertain parameters, e.g., the comfort level, occupancy, and user behaviors [25]. Failures in the power system [26] as electrical lines, outages of power generators, variability of power reserve, and loss of communication could also affect the resiliency of the normal operation of the microgrid [27].

Thus, including the uncertainties in the optimization algorithm can help enhance the resiliency and overall performance of the different types of microgrids [28]. Depending on the type of uncertainty, the modeling, and the optimization technique to adopt may be different. For instance, wind speed, solar irradiance, load consumption, and electricity market prices are often modeled through suitable probability functions, which are accounted for in EMS-oriented stochastic optimization procedures [29]. In addition, when no previous data are considered, other uncertain factors can be modeled by fixing the range of variation to examine the worst and best case operation at each time step. For these cases, robust and fuzzy optimization techniques have been used to search for the optimal operation point considering a degree of satisfaction [18]. Novel techniques have been emerging in the last years as information gap theory [30], multiparametric programming [2], and machine learning [31], which can help to find an optimal schedule in real-time operation.

Recent review papers on EMSs focused on (a) architecture [4], (b) communication [32], (c) optimization techniques ([3,10]), (d) operation and control [33], and (e) specific applications, such as residential [11], building [34], and virtual power plants [35], but they lacked focus on the uncertainties of EMSs. In this sense, few papers have approached EMSs by accounting for uncertainties, i.e., ([1,36]). A small section in reference [36] focused on modeling uncertainties for virtual power plants. However, they did not discuss the optimization techniques and the different types of uncertainties. The work developed by K.Kumar et al. [1] presented a review of the modeling techniques of uncertainties in power generation, only focusing on energy sources. However, the authors of [36] did not present the optimization techniques used with this type of modeling. Regarding the optimization techniques discussed with uncertainties, [18] focused on stochastic and robust optimization, but no other techniques were reviewed. The authors of [37] also discussed optimization techniques, accounting for uncertainties but with the objective of long-term planning.

Table 1. An overview of the review papers on EMS for microgrids. The papers are organized by year of publication and whether they cover optimization and modeling when uncertainties are considered.

Reference	Model Uncertainties	Optimization Techniques with Uncertainties	Survey	Year	Focus
[1]	x	-	2007–2016	2016	Renewable energy availability, heat demand, and load demand
[4]	-	-	2005–2014	2016	Architecture, control, common optimization algorithms: heuristic and mathematical methods
[38]	-	x	2001–2015	2016	Optimization objectives, heuristic methods, stochastic programming, model predictive control and neural network.
[35]	x	x	2002–2016	2017	Energy scheduling for reliability, uncertainty, demand response, emissions, and multi-objective. The  uncertainty discussions are covered in a small section where only probabilistic modeling is discussed.
[18]	x	-	2000–2017	2018	Robust, and stochastic approach for uncertainty modeling in energy systems
[3]	x	x	2002–2017	2018	Robust, stochastic programming and model predictive control. It reviews the architecture, control, and  communication. The uncertainties models are not well described
[16]	-	-	2001–2020	2020	Architecture, technologies, and  market analysis.
[39]	x	x	1989–2019	2020	Artificial intelligence and machine learning for energy demand.
[10]	x	-	2000–2020	2021	Traditional optimization techniques, the architecture, control, of microgrids. Only a small section is dedicated to uncertainties.
[11]	-	-	2005–2020	2021	dc microgrid architecture, control, optimization algorithms, and software.
[17]	-	-	2002–2020	2021	Architecture and control
[37]	-	x	2002–2021	2022	Control methods: game theory, multi-agent and artificial intelligence, stochastic and robust optimization

provides an overview of recent review papers on EMSs and microgrids. It indicates whether each study addresses uncertainty, modeling, and optimization strategies, and some comments are provided. Notably, these reviews did not provide in-depth discussions on the modeling and optimization strategies utilized for EMSs when uncertainty was incorporated. Furthermore, there is a lack of discussion on which uncertainties are significant depending on the microgrid application and which modeling and optimization techniques are used in each. Similarly, an analysis of how EMSs accounting for uncertainties can be embedded in real-time operations has not been proposed until now.

Therefore, to the best of our knowledge, a survey on EMS optimization and modeling techniques when uncertainties are considered needs to be included in the literature. Furthermore, this paper identifies the main uncertainties affecting EMSs, the common modeling techniques used, the optimization approach, the software, the platform used, and the new challenges to overcome for better EMS performances; we conducted a comprehensive literature review of more than one hundred papers dedicated to modeling uncertainties, EMSs, microgrids, and optimization techniques by considering uncertainties.

In this paper, we identify the uncertain parameters that are being considered in residential, commercial, virtual power plants, multi-carrier microgrids, and electric mobility. The modeling and optimization techniques discussed in this paper are stochastic, robust, deterministic optimization, information gap decision theory, model predictive control, multiparametric programming, and machine learning techniques. Moreover, this paper provides a deep discussion about the future and the challenges that new EMSs have to overcome, taking into account uncertainties in new microgrid applications.

The paper is structured as follows. Section 2 explains the systematic literature review. Afterward, the current uncertainties in various microgrid applications are discussed in Section 3. Then, the techniques that are used to model the uncertain parameters are described in Section 4. Next, a critical comparison between consolidated optimization techniques and new approaches for day-ahead and real-time optimization is given in Section 5. The common algorithms used are described in Section 6. Additionally, details about hardware and software implementation are provided in Section 7. A final discussion about future trends and challenges is presented in Section 8.

2. Systematic Literature Review

For the literature review, four consecutive steps were followed: search, appraisal, synthesis, and analysis [40]. For the first step, “search”, the scientific databases used were Scopus, IEEE Xplorer, and Google Scholar. The search for review papers was restricted to the years between 2016 and 2022 and the research papers from 2014 to 2022. The search strings created were:

• S1: microgrid + review + EMS + uncertainties;
• S2: review + modeling + optimization + uncertainties + energy;
• S3: microgrid + EMS + uncertainties + optimization;
• S4: microgrid + EMS + uncertainties + optimization + real-time.

The second stage, “appraisal”, involved the following: (i) giving a quality assessment to verify if the publication was within the scope of the current study, (ii) the accessibility of the article, and (iii) all the words of the string were included. Initially, 1038 review papers regarding the first two strings were found. For S3, a total of 2404 publications were found, and for S4, there was a total of 63 publications. After the quality assessment, 180 articles were used for further review.

Then for the third stage, “synthesis”, we looked for specific features of interest for this study: the uncertainty model, optimization technique used when uncertainty was considered, validation, software, and uncertainty. Then, these features were considered in the fourth stage, “analysis”, to discuss the uncertainty models and the optimization techniques used for EMSs in microgrids. The analysis is presented in the following sections of this paper.

3. Uncertainties in Microgrids

The inputs of any control system have a level of confidence depending on many factors. Some inputs may depend on the randomness of nature or unpredictable human behavior, so they are intrinsically affected by an uncertainty level [41]. For instance, the wind forecast may show a standard deviation error between 40% and 50% for 24 h ahead of the horizon and 20% for 1 h ahead. In the case of solar irradiance, the standard deviation error can vary between 10% and 50% (for 24 h ahead) and from 1 to 10% (for 1 h ahead) [6].

Depending on the microgrid under analysis, the uncertain parameters to account for may have different natures and require different representations. This section analyzes the current uncertainties taken into account in the EMSs for various microgrids: residential and commercial, virtual power plants, electric mobility, and multi-carrier microgrids. A summary of the various uncertainties considered and neglected in the literature depending on the application is in

Table 2. Uncertainties considered in various applications.

Uncertainty	Residential and Commercial	Virtual Power Plants	Electric Mobility	Multi-Carrier Microgrids
Renewable energy power production	x	x	x	x
Ambient conditions: solar irradiance, humidity, precipitation, wind speed, temperature	x	x	x	x
Electricity price	x	x	x	x
Electricity consumption	x	x	x	x
Power reserve	-	-	-	x
Voltage and frequency variations	-	-	-	x
Electrical failures	x	-	-	-
Use of appliances	x	-	-	-
Connection/disconnection EV	x	x	x	x
Parking availability	-	-	x	-
Parking queues	-	-	x	-
User’s comfort	x	-	x	-
State of charge of battery	x	x	x	x
Driving pattern	-	-	x	-
State of health: battery, electrical system, PV modules, generators	x	x	x	-
Remaining use of life	x	x	x	-
CO${}_2$ emissions	x	-	-	-
Future installed capacity	-	-	-	x
Future load demand	-	-	-	x
House and building occupancy	x	-	-	-
Maintenance	-	-	-	x
Power reserves	-	-	-	-

.

3.1. Residential and Commercial–Industrial Applications

The main components used in residential and commercial–industrial applications are appliances, air conditioning, and heating systems, PV systems, energy storage systems (ESSs), and EVs. For these applications, the principal task of the EMS is to reduce the overall energy cost while maintaining the comfort requirements. The level of independence from the grid, which can be optimized by maximizing self-consumption and self-sufficiency, is also considered. Uncertainties affecting the electricity price, the electrical demand, the temperature of the living rooms, and the power generated from the PV array are usually accounted for [42]. Some studies have considered further uncertainties, home occupancy, energy price, PV power generation forecast, and solar irradiance. When EVs are included in the study, the uncertainties affecting the charging time, connection, and disconnection [43] are also considered. However, there are further uncertainties that are not taken into account for residential and commercial–industrial applications. Some of the uncertainties that could be included to enhance the performance of these EMSs are the power generation state (connection or disconnection), the state of the ESS, and the CO${}_2$ emissions factor.

3.2. Virtual Power Plants

Virtual power plants (VPPs) have three main objectives: maximize the profit, minimize the risk, and guarantee the spinning reserve. When VPPs include PV systems and wind turbines, the error related to the forecast of the generated power and the weather conditions are considered uncertainties. The energy flows are controlled by considering uncertainties, such as electricity price, abrupt fluctuations, electricity demand, and power reserve [44]. In [45], the authors include uncertainties related to EVs, such as the charging time, the power capacity, the state of charge, the number of vehicles connected, and the charging period. Other uncertainties are the transmission line and generator outages [35].

Because the VPP aggregates various power generators at different locations, the uncertainties affecting the regular operation to guarantee power according to the grid codes are still drawbacks. For instance, the power reserve, ramps-up and ramps-down, the losses due to curtailment, and maintenance are not commonly part of theuncertainties of the EMS [46]. Moreover, it is not considered the variation of the CO${}_2$ emissions due to the interaction of the grid.

3.3. Electric Mobility

EVs are included in some studies where EMSs are used to optimize parking lot operations. In this case, the primary goals are to minimize the operation costs, maximize the time when the charging points are available, and reduce CO${}_2$ emissions. The uncertainties affecting the arrival time, departure time, daily driving distance, driving behavior, connection, and disconnection time are accounted for [47]. Although these uncertainties can be handled by fixing arrival and departure times or using economic incentives, they can affect the user’s comfort. Other uncertainties, such as parking availability and queues, are also considered in [48]. Other uncertainties included in the EMS are weather forecasts, power production forecasts, electricity prices, and demand [47]. The battery’s state of charge and degradation costs are also considered. Other uncertainties regarding human behavior, such as the level of anxiety due to the level of the battery’s energy, are also considered in some studies (e.g., [49]).

For the optimal operations of parking lots, the optimization is usually developed one day ahead, then the schedule is rectified in real-time as the number of vehicles and the charging times change. Even though the minimization of CO${}_2$ emissions is an essential aspect, no studies considering the uncertainty affecting this parameter are available in the literature. When EVs are connected to a microgrid, the batteries embedded in the vehicles can be considered as additional storage elements that can support the ancillary services of the grid, sometimes using a vehicle-to-grid (V2G) configuration. In this case, the EMS aims to determine the best charging cycle to reduce EV battery degradation. The impact of the charging cycle is not considered uncertain, but it plays an essential role in the battery’s life expectancy. Other uncertainties that are not considered in current studies are the amount of power and the required time interval to provide active power as part of the ancillary services.

In maritime applications, “all-electric ships” are considered moving microgrids. In this case, the uncertainties are solar irradiance, ambient temperature, wind speed, and direction, and the swinging direction of the ship [50]. Other uncertainties, such as the ship’s occupancy, speed, comfort level, state of the battery, and degradation, have not yet been considered in any study. The uncertainties related to the availability of charging points in seaports have not yet been accounted for in the current literature.

3.4. Multi-Carrier Microgrids

Multi-carrier microgrids consist of various distributor generators and microgrids that are connected to the medium voltage level; thus, they have to comply with the electrical system regulations [51]. In this case, distribution system operators (DSOs) schedule the energy flows by maximizing profit and reducing the operation risk. Uncertainties impacting power generation production, energy price, and load demand are typically considered. In the literature, voltage and frequency fluctuations, electrical failures, and generator outages are considered uncertainties [52]. For planning purposes, long-term uncertainties are the future installed capacity and load demand [53].

To enhance the energy management where multi-carrier microgrids are taken into account, uncertainties such as power reserves, variability of the CO${}_2$ emissions, and responses regarding ancillary services could be introduced. Moreover, the degradation and life span of the various microgrids are also necessary for long-term planning.

4. Modeling Techniques for Uncertainties in Microgrid Optimization

The design of a microgrid EMS requires a suitable representation of the uncertainties, which can be modeled by using different approaches: (i) probabilistic, (ii) possibilistic, (iii) information gap theory, and (iv) deterministic (Figure 1).

4.1. Probability Distribution Modeling

A probability distribution function (PDF) describes the behavior of a random variable based on its likelihood to happen. There are two main types of PDFs according to the nature of the variable: (i) discrete and (ii) continuous [54]. Discrete PDFs are used when the variable can assume a discrete number of values or binary positions. For example, the discrete probability distribution can model the random connection or disconnection (0 or 1) of generators in a microgrid. Another example is the number of EVs in a parking lot. Instead, a continuous probability distribution is used for variables that assume continuous values, so the probability it assumes a specific value is almost zero. Solar irradiance, ambient temperature, and wind speed are good examples of these variables.

The most common types of discrete PDFs are binomial, Poisson, and uniform distribution. This PDF is widely used as it well models the time-independent discrete operation. For example, the Poisson distribution is often used to model driving behaviors and EV charging patterns, the initial state of charge, and the number of EVs connected to a microgrid [55]. This type of function is also used to model random spikes in electricity prices [56,57], and to model the errors in the prediction of PV and wind energy production [58]. Binomial distribution functions have been used to model transformer failures due to overloads related to the increasing number of EVs connected to the grid [59]. Binomial distribution functions are suitable to model EVs’ random connection and disconnection [60]. Lastly, uniform distributions are employed to model the state of charge, and the number of EVs connected to the grid [61]. In the literature, uncertainties related to the connection or disconnection of microgrids and the failure of PV generators, wind turbines, or ESSs have not yet been modeled using the PDFs mentioned above.

With reference to the management of microgrids and smart grids, Gaussian and Weibull are the most used continuous PDFs. Gamma, Beta, Rayleigh, Bernoulli, and log-normal have also been employed. The Gaussian distribution function is preferred for those applications where the data have a symmetric distribution, as in the case of errors in the wind [62,63] and PV power forecasting [64]. These distributions have been used to model the state of health [65,66], and the state of charge of EV batteries [67]. The same representation is commonly chosen to model the load consumption [68], the charging duration of an EV battery, the arrival, the departure time of EVs [69], and the temperature variation inside a house or building [70].

Weibull, Gamma, Beta, Rayleigh, Bernoulli, and log-normal are commonly used in the case of asymmetrical data and represent ideal choices to model ambient conditions, such as wind speed and variations of solar irradiance due to clouds. The Weibull distribution and Beta distribution perform well for wind speed and solar irradiance forecasts, respectively [71]. Weibull’s distribution functions have also been used to model the effect of degradation, the remaining useful life, cycle prediction, and reliability for PV modules [72,73], lead acid batteries [74], and lithium batteries [75,76]. The log-normal function has been used to model the travel distance and time of an EV [77]. A summary of the most common probability distributions and their applications is given in

Table 3. Main probability distribution functions in microgrid applications.

Type	Multi-Carrier Microgrid	Renewable Energy	Load	Electricity Price	EV	Energy Storage
Poisson		forecast error	connection/disconnection	spikes	arrival/departure	state of charge
			random occupancy		connection/disconnection
					number of EVs
Binomial	generator outages				connection/disconnection
	transformers failures
Uniform	generator outages		load consumption		state of charge	state of charge
					number of Evs
Gaussian		forecast error	heating loads	price variation	charging time	state of health
		solar irradiance	cooling loads		arrival/departure	state of charge
		sky index
		PV power	load profile
		temperature
Beta		solar irradiance
Weibull		PV power				degradation
		wind power
		degradation
Gamma					travel time
					travel distance

.

4.2. Possibility Theory

Building a reliable probability function depends on the availability of historical data. Whenever these are not available, the uncertainty can be modeled as the degree of possibility for a situation to occur. In order to model uncertainties, Bayesian statistics or fuzzy sets [78] require less precise information than the one used in the case of the probabilistic distribution.

The degree of possibility that a situation occurs can be added to model the uncertainty when there is a lack of information to build a reliable probability function [78]. The uncertainties can be represented by fuzzy sets as bounds or intervals or by their degree of affection on the measured variable that helps to model the possibility that an event happens [79]. The main advantage of this technique is that it does not need precise information. In the case of fuzzy sets, a function represents the degree of membership of a variable or parameter, thus the possibility that these can have a specific value. The function can be a trapezoid, a triangle, or a rectangle, depending on the variable’s membership limits [79]. For instance, Figure 2 shows a function used to represent the forecast of an active power that can vary between $P_a$ and $P_b$, while the most probable value is $P_b^{\prime }$. Fuzzy prediction intervals are widely employed to forecast wind and PV power generation and electric load variations during the day [80]. In [81], it is used to forecast the errors in predicting solar irradiance, wind speed, ambient temperature, and home internal heat. Possibility theory can also handle uncertainty, such as electricity load demand [82], parking availability [83], and the connection or disconnection of EVs from the grid [84].

Although the design of fuzzy sets does not require any historical data, the boundaries and the nominal value that the variable or parameter can assume are known. For instance, the availability of at least one space when parking at noon is uncertain, and it is difficult to assign to it a membership number. A fuzzy membership degree is adopted, especially when few historical data are available or previous knowledge of the system is lacking [79]. This representation can be combined with probabilistic functions when a reasonable amount of information is available. For instance, in [85], the load demand and power generation are modeled using the historical database with probabilistic distribution functions. Instead, fuzzy sets are used to model random events such as quick variations of weather conditions, spikes in prices, and peak demand. On the other hand, Bayesian models represent the degree of belief that an event can occur and use a probability expression. This model includes previous knowledge of the probability of occurrence of the variable combined with the likelihood a specific event happens [86]. Therefore, Bayesian models can represent the random variable as a network of different states, the so-called Bayesian network, with conditional probability. This network helps to model the variable or parameter as a consequence of other events. For example, in Figure 3, an acyclic graph referring to the air conditioning behavior in a house is shown. Each value of the ambient temperature and household occupancy has its own probability of occurrence, both affecting the probability that the state of the air conditioning assumes a given value. Such an approach is also helpful to model the degradation of batteries and PV solar cells, as every state depends on the previous one [87] (See

Table 4. Modeling uncertainties with possibility theory.

Type	Multi-Carrier Microgrid	Renewable Energy	Load	Electricity Price	EV	Energy Storage
Fuzzy sets	Non applied	forecast error	forecast error	forecast error	total charging amount	maximum charging rate
		spikes of solar irradiance	sudden variations	spikes	connection/disconnection	initial state of charge
		PV power	home internal heat		parking availability	final state of charge
		Wind power	load power	maximum profit	maximum charging rate
			connection/disconnection	operation cost	initial state of charge
					final state of charge
					battery level anxiety
					driving pattern
Bayesian	failure	forecast error	variations	peak price	connection/disconnection
	outages	PV power	use factor of appliances		driving pattern
	reliability	Wind power	load variation
		Minimum power	connection/disconnection
		Maximum power	heating system
			cooling system
			peak load

). In the literature, a Dirichlet-based model based on Bayesian modeling is used to model the uncertainty set, where the set can vary over time depending on the previous information. The set becomes narrower depending on available data and is based on known probability distribution functions. Every probability function is linked to a different possibility weight, which will vary. For instance, in [88], the authors use an imprecise Dirichlet model-based nonparametric ambiguity set to represent the uncertainty set of a wind power generator’s power production. Every time, the function varies, and the ambiguity set is constructed with all the possible probability functions. Then, the polyhedron set varies its lower and upper limits as the confidence level varies. A similar approach is used to model PV power production and load consumption in [89].

4.3. Information Gap Theory

The information gap theory models the uncertainty radius between what is known and what could be known [90]. This approach allows for a model of severe uncertainty without needing a historical database or a reliable statistical function, making it suitable to model the uncertain error between the forecast and the accurate data [91,92]. The technique is based on the interval or unknown radius, depending on the preferred outcome (Figure 4). For instance, in the presence of an uncertain PV power production, if the objective is to reduce the cost of operation, the decision maker searches for the maximum radius of PV power that the system can handle to minimize the objective function value. On the contrary, the decision maker searches for the minimum uncertainty radius to warranty a specific objective function value to increase the profit.

The uncertainty gap is modeled through energy-bound, envelope-bound, Minkowski, slope-bound, Fourier-bound, and hybrid models [90]. Envelope-bound and slope-bound models are the most used for microgrid and electrical system applications. Commonly, the information gap theory is used to model the error of forecast variables [93] as, for example, electricity price [94], load profile [95], renewable power generation [96], and degradation of batteries [97] (see

Table 5. Main applications of Information Gap Theory.

Multi-Carrier Microgrid	Renewable Energy	Load	Electricity Price	EV	Energy Storage
not applied	forecast error	forecast error	forecast error	Not applied
	thermal power	load power	intervals of bidding prices
	PV power		maximum price
	wind power		minimum price

). Although information gap theory is able to handle severe uncertainties, it has not yet been applied to model the forecast error of CO${}_2$, the state of health and the state of charge of batteries, or the driven pattern for EVs.

4.4. Deterministic Theory

The uncertainty as forecast errors and maximum and minimum variations can be modeled by bound intervals or by robust sets. To find the limits for the intervals, sensitivity analysis or interval arithmetic are commonly employed [78].

The sensitivity analysis aims to identify which input variables or parameters change, more or less significantly, the model’s performance by affecting its output. Additionally, it simultaneously identifies sets of variables or parameters affecting system performance. Thus, it can enhance the model by adding errors, importance weights, or sensitivity coefficient to one or more specific inputs [98]. In microgrid applications, sensitivity analyses evaluate the uncertainty affecting the load [99], the power generation [100], failures occurrence [26], the batteries’ degradation [101], the EV penetration [102], the power generation profits [103], and CO${}_2$ emission forecasts [104].

Interval arithmetic models the uncertainty through a lower and an upper bound of the range, wherein all the values are equiprobable. However, this technique cannot handle internal errors due to arithmetic round-offs; correlations or series truncations are given false wide limitations [105]. The Affine arithmetic is an improved method that considers the correlation among input and output variables by giving a more realistic output bound. The Taylor model is also used to represent the bounds in the form of a function that varies with time [106]. In power systems, these techniques have been commonly used to model the uncertainty of voltage magnitude, and voltage phase for power flow analysis [107]. In microgrids, problems related to load modeling [108], power generation [109], and electricity prices [110] have been afforded.

In addition to representing the uncertainty in common intervals, it can take the shape of robust sets (e.g., intervals), so they can be included in robust optimization or multiparametric programming. The sets can be a box, ellipsoidal, polyhedral, cardinality constrained, and norm uncertainty [111]. These robust sets describe the variation of the uncertain variable considering maximum, minimum, mean values, correlation, deviation, covariance, and confidence parameters. An explanation of the construction of these sets is given in [112,113,114]. The uncertainties in energy price, wind and PV power production, and power demand are modeled by their peak values, confidence, and variance level. In [115], a polyhedral set is employed to represent future installed capacity and peak demand to provide microgrid protection in the worst-case scenario. It is worth mentioning that the size of the set depends on the time variance of the application. For instance, long-term uncertainty, as the maximum future demand will not be the same as the maximum demand that can occur in the next hour. In microgrids, these models are used for planning, optimization, and scheduling, considering worst and best-case scenarios. The analysis of the upper and lower bounds or the size of the set can be developed by observation, statistical analysis of historical data, or policy regulations. The set can also vary and be adjusted depending on the historical data. Depending on the set’s shape, these variable sets can take the name of flying brick [116] and flexible envelope [117], commonly used for modeling the electricity price (see

Table 6. Main characteristics and applications of deterministic theory.

Type	Multi-Carrier Microgrids	Renewable Energy	Load	Electricity Price	EV	Energy Storage
Intervals	max/min number of generators	forecast error	max/min consumption	forecast error	max/min number of cars	max/min state of charge
	max/min voltage	max/min production	max/min number of appliances	max/min price	max/min charging points
	max/min frequency
Robust sets	Installed capacity	forecast error	discomfort level	market price	not applied
		wind power	variation of temperature
		solar power	expected demand
			consumption

).

The models for uncertain parameters are used to develop the EMS and are included in the optimization algorithm. The basic mathematical modeling and the main characteristics are summarized in

Table 7. Summary of the uncertainty models.

	Probability Theory	Possibility Theory	Information Gap Theory	Deterministic
Type of uncertainty	Randomness	ambiguity	unmeasured uncertainty	measured uncertainty
Output of the model	Probability density function/ cumulative density function	Membership function	Uncertain uncertainty set	exact interval
General mathematical form	e.g., Normal PDF		e.g., envelope	e.g., min/max
	$N(u,{\sigma }^2)$	$U_A\left(x\right)$	$U(\alpha ,\tilde{u})$	$x\subset [min\left(\tilde{u}\right),max\left(\tilde{u}\right)]$
			$|u\left(t\right)-\widetilde{u\left(t\right)}|\le \alpha |\widetilde{u\left(t\right)}|$

. This table provides a general mathematical formulation, where ${\sigma }^2$ is the covariance, and $\alpha$ is the uncertain envelope size. The studies presented in [91,118,119], make an in deep mathematical analysis for each category. The following section reviews the optimization techniques that can embed uncertainties.

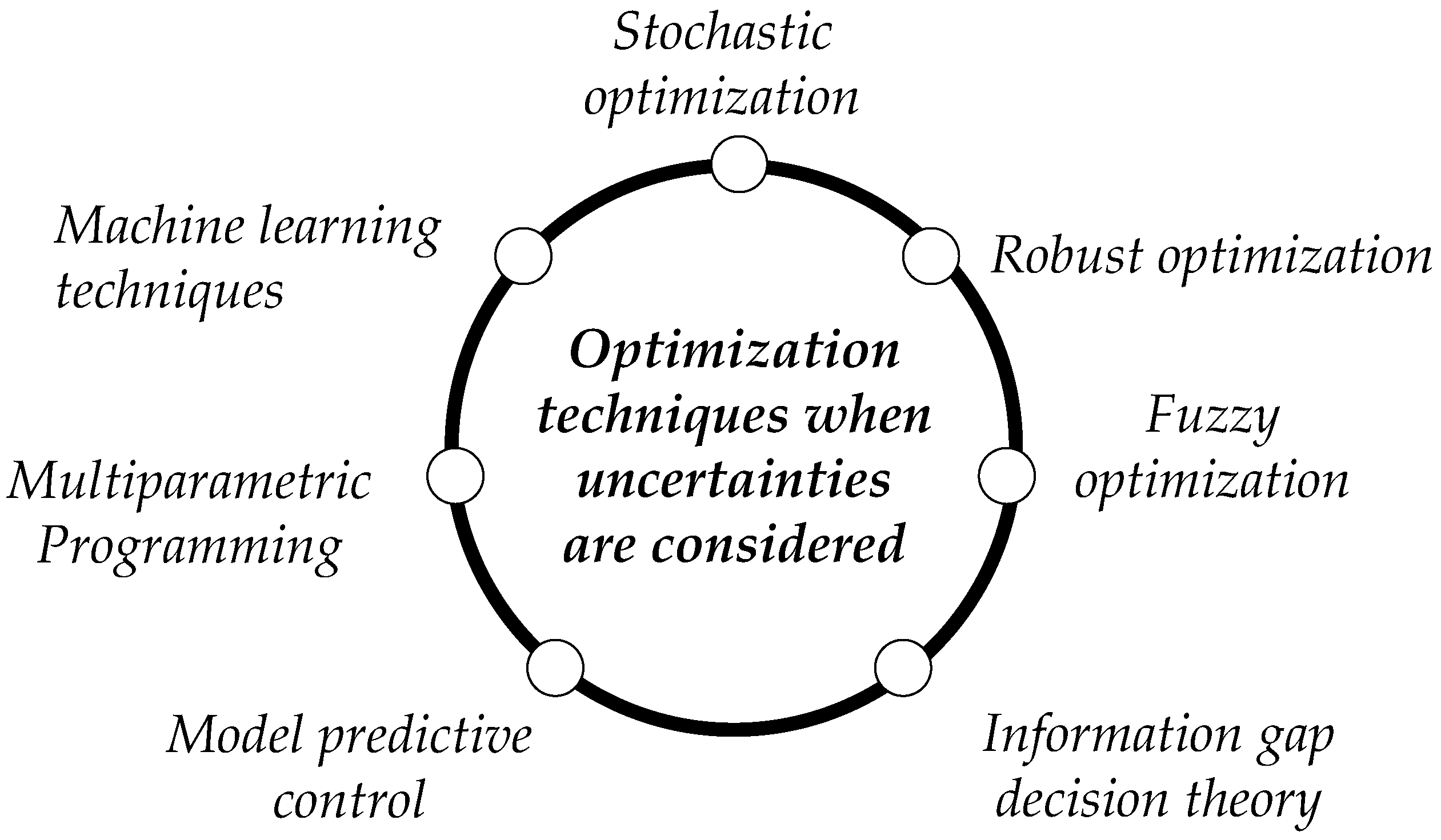
5. Optimization Techniques with Uncertainties

Optimization techniques managing uncertainties, such as stochastic and robust optimization, fuzzy optimization, information gap decision theory, model predictive control, and multiparametric programming, are commonly used for microgrid applications. A summary of each technique for one-stage and multiple stages optimization is introduced in the following. The advantages and drawbacks of their application in the microgrid context are presented. Furthermore, machine learning techniques for optimization purposes in uncertain environments are also reviewed (see Figure 5).

5.1. Stochastic Programming

Stochastic optimization techniques can be used to optimize an objective function’s value, even by modeling random variables by probabilistic functions.

In stochastic programming, there can be two stages and multiple stages of optimization (Figure 6). In the case of two stages, the optimization is divided into two steps. In the first step, the day-ahead optimization searches for the best point of operation with the forecasted data. In the second stage, the real-time operation corrects the optimization using the actual value only in case a perturbation occurs. Commonly, the first stage evaluates all the possible scenarios; but in the second one, only specific scenarios are considered [120,121]. A multistage optimization uses scenario trees to adjust the decision at different time steps, depending on the current information and future uncertainties [120]. The authors in [122] propose an energy management method based on multistage stochastic programming to reduce the daily purchase cost. The uncertainties considered are the load profile and the PV power generation, which are forecasted using long-term memory. The correlation among the uncertain parameters is accounted for to create several scenarios. The response of the microgrid for one day ahead that works as a base model is optimized. Then, the system is evaluated every fifteen minutes to recalculate the best microgrid operating condition by considering the actual data and the scenarios created in the previous stages. Stochastic optimization has been broadly used in EMSs, although it requires a computation time that increases with the number of uncertainties and scenarios.

One of the common approaches to optimizing with uncertainties in stochastic programming is chance-constrained optimization. In this case, the algorithm searches for a solution with a high confidence level by ensuring the highest probability of meeting the different constraints. In [123], this technique optimizes home energy management, considering electricity prices and loads as uncertainties. This study’s main objective is to minimize the electricity cost by ensuring the probability of complying with constraints. If the forecast error increases, then the operating cost increases significantly. Another approach in stochastic programming is adding conditional value at risk (CVaR) in the objective function. CVaR is used when the variability of a profit is expected due to the stochastic behavior of the uncertainties. For instance, in [25], this approach is used to consider the risk of load loss to minimize the operation costs and $\mathrm{C}{\mathrm{O}}_2$ emissions.

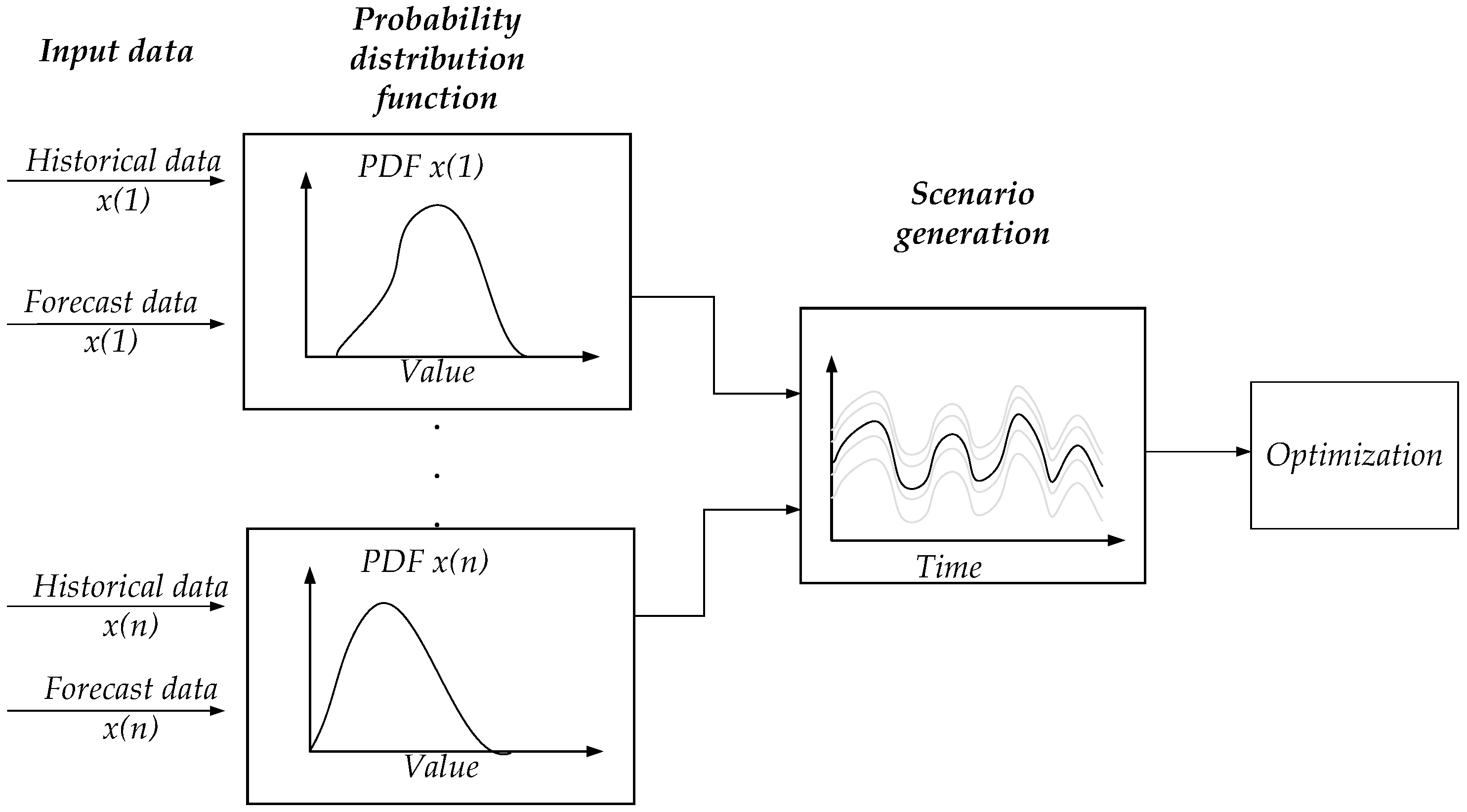
All the variables are managed by simulating all the possible scenarios through sampling methods, the Monte Carlo simulation, Latin-hypercube, and Markov chain. The Monte Carlo simulation is based on the generation of random samples and of “what if” scenarios related to the input variables or parameters in order to keep into account their statistical behavior [124]. The scenarios are constructed by the random propagation of uncertainties that usually is defined by probabilistic functions. This technique can handle different uncertain variables simultaneously, allowing the discovery of possible correlations among them (Figure 7). The main drawback of this approach is that the computation time can be very high for a large set of variables and scenarios.

There are three types of Monte Carlo simulation techniques, depending on how the problem is sampled: (i) sequential, (ii) non-sequential, and (iii) pseudo-sequential. The sequential Monte Carlo simulation approach is to preserve the time series’ characteristics representing the input data. Thus, the analysis is developed in a chronological way [125]. In [126], a sequential Monte Carlo method is used to estimate the possible scenarios when considering simultaneously electric, cooling, and heating demand together with the solar irradiance; in this case, both the demand and the solar irradiance are modeled as a uniform distribution. A non-sequential Monte Carlo simulation generates samples by the current states of the variables, each one not depending on the previous or future samples [125]. This type of Monte Carlo simulation technique is often used to determine scenarios related to random failures of generators or the sudden increase or decrease of power due to intermittent renewable generation [127]. Pseudo-sequential methods generate the scenarios by including both random and chronological variables. In [128], an application concerning the generation of scenarios related to the driving characteristics of an EV (time-dependent) and the battery characteristics (random states of charge) are presented. The Monte Carlo simulation is broadly used for scenario generation for its later application in stochastic optimization in power systems [125] and microgrids EMS [29].

Similar to Monte Carlo simulations, Latin hypercube-based methods generate scenarios as functions of random variables or parameters. The main difference with the Monte Carlo simulation is that this approach generates a smaller number of samples by considering the same probability distribution for all the parameters. This technique requires a computing time lower than the one needed by a Monte Carlo simulation, with the same accuracy of the result [124]. This technique has been used to assess the reliability of power systems [129,130], and to generate power generation scenarios of microgrids in the presence of uncertainties affecting the forecast of power generation [131]. The Monte Carlo simulation has also been used to create different scenarios regarding V2G applications, considering the arrival time and the state of charge of the batteries as random variables [132].

Markov chain is described as a first-order function in which the transition to the next state depends on the current state but not on the sequence of past events [118]. They are commonly applied to model EV status [133], queues in parking lots [134], and driven patterns [21]. As for driven patterns, the defined states to form a Markov chain can be the electricity price [135], the energy level of the battery [21], or the state of the vehicle (low charging, fast charging, parking, commuting) [136]. The transition between one state and another can be defined by a probability matrix built with Monte Carlo simulation, as explained in [136].

Table 8. Uncertainties considered with sample techniques.

Phenomena	Monte Carlo	Latin Hypercube	Markov Chain
Renewable energy power production	x	x
Driver pattern	x	x	x
State of charge of battery	x
Electricity price	x	x	x
Degradation battery price
Electricity consumption/load profile	x	x
Connection/disconnection EV	x		x
Electrical failures	x
Ambient conditions: solar irradiance, humidity, precipitation, wind speed	x
Generators failures/reliability	x	x
Through life cost
Risk planning	x	x
Microgrid operation	x
Power flow direction	x
Range anxiety/ battery level anxiety			x

shows each technique’s common uncertainties considered in the case studies.

However, these techniques can be helpful for one-day ahead optimization, but for real-time, they have the drawback of high computation time. Thus, stochastic dynamic programming is used for the case of real-time operation, as the uncertainties are incorporated at every time interval. Then, the optimal response can be chosen by using game theory to reduce the computation time, and the memory requirement [137,138].

5.2. Robust Optimization

Robust optimization methods aim to achieve a feasible solution for any value of the uncertain parameters modeled as a robust set. At the same time, the solution should be optimal for the worst uncertainty realization within the robust set. There are three main advantages of using robust optimization, i.e., (i) it is tractable as the size of the problem does not increase exponentially as is the case of stochastic programming, (ii) it requires less computation time than probabilistic or stochastic programming as there is not a large number of scenarios, and (iii) it provides a conservative solution for every possible uncertain parameter. The robust set should be carefully modeled according to the time frame and application to profit from these advantages [111]. The most robust solution could be, at the same time, the most expensive or the riskiest one, especially if the robust set is not carefully chosen (Figure 8). In microgrids and smart grids, robustness under uncertainties ensures that energy management does not overestimate the power production or underestimate the load demand, which might lead to an increase in the price or an increase in the CO${}_2$ footprint.

The literature presents three robust optimization formulations: Soyster’s worst-case scenario, Ben-Tal, and Nemirovski’s nonlinear optimization, and a formulation proposed by Bertsimas and Sim [139]. The latter is the most used technique in microgrids, as it is flexible and linear. In contrast with the other formulations, it adds a parameter, i.e., the “budget of uncertainty” and its main goal is to control the trade-off between robustness and flexibility [140]. A new approach is robust distributional optimization, where a budget of uncertainty is not used. Instead, a confidence interval probability is applied, and the uncertainty sets are given by the predicted means and the variances of the uncertain parameter. In [14], robust distributional scheduling for a hybrid microgrid is presented and compared with a traditionally robust optimization. The operation cost is higher for three case scenarios: day ahead, short-term, and real-time optimization.

Single-stage and multiple-stage [111] are two types of robust optimization methods close to stochastic programming. In the former, the decision is implemented before the uncertainty happens, but considering, in most cases, the worst-case scenario (here and now). Thus, this solution is risky and cannot be the most economical one. It is commonly used in day-ahead energy scheduling and long-term planning; see [141,142]. The second one, also called robust adaptable optimization, is utilized when real-time management is possible. It consists of three stages: the first stage gives the planning strategy before uncertainty occurs; the second represents the uncertainty realization in the worst-case scenario within a robust set. The third level takes the decision when uncertainty occurs (wait and see decisions) [143]. In adaptive robust optimization, stochastic programming might be the first optimization stage. For instance, in [144], the use of stochastic adaptive robust optimization to maximize the profit in a virtual power plant is described. In the first stage, stochastic optimization is developed, considering a set of scenarios of the market prices for the day ahead scheduling. Then, adaptive robust optimization is applied, considering the wind turbine power production as uncertainty for online energy management. The processing time of up to 35 min for the first stage and, in contrast, one minute for the second stage represents a limitation for practical applications.

5.3. Information Gap Decision Theory

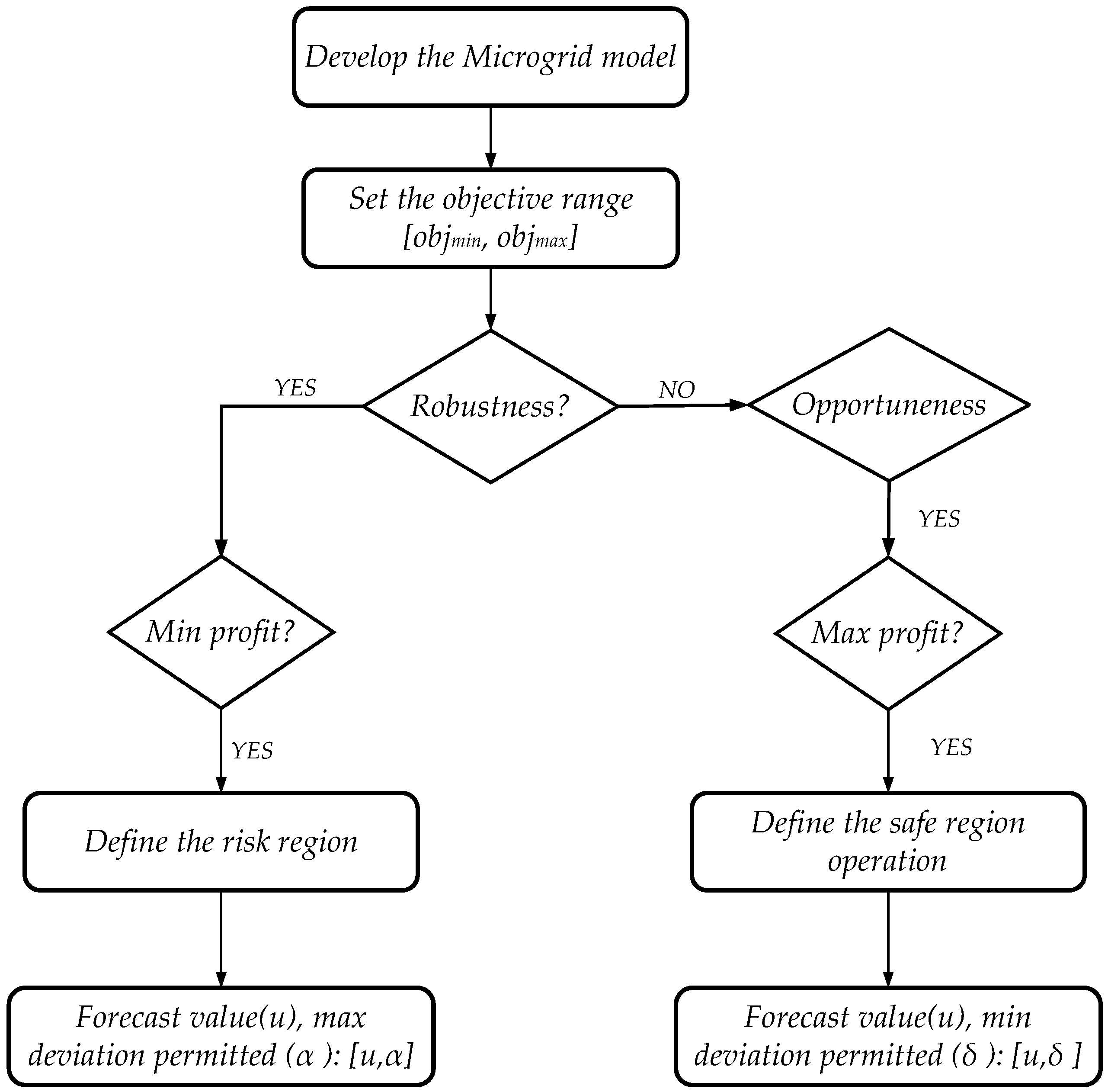
The information gap decision theory (IGDT) supports the decision-makers in managing the system by determining the uncertainty band. Two formulations are adopted: robust or risk-averse strategy and opportunity or risk seeker strategy. The former aims to search for the maximum uncertainty level the system can handle to comply with the desired objective function, for example, a critical cost. The main objective is to minimize the risk of failure (immunity to failure). The second method aims at determining the minimum uncertainty radius that the system can have so the desired objective function is maximized, for example, the profit. The opportunity function aims to optimize the success risk (immunity to windfall gain) (Figure 9). The decision-makers can follow one or more strategies simultaneously, depending on the operation of the system [90].

Microgrid energy management systems use these approaches to maximize profit or reduce operational costs. The uncertainties considered are market price [52], wind and PV power, and load consumption [145]. These are evaluated in a predefined critical revenue. In literature, IGDT is used for risk-averse strategy instead of risk seeker. However, ref. [146] uses both strategies where the system chooses one of them depending on the hour of the day to maximize the profit depending on the uncertainty of the peak prices. One of the main disadvantages of this technique is that it cannot be used for short-term uncertainty, as the information gap is too small. IGDT is preferable, but not limited, for long-term uncertainties as load demand and market prices tend to have a larger gap.

5.4. Model Predictive Control

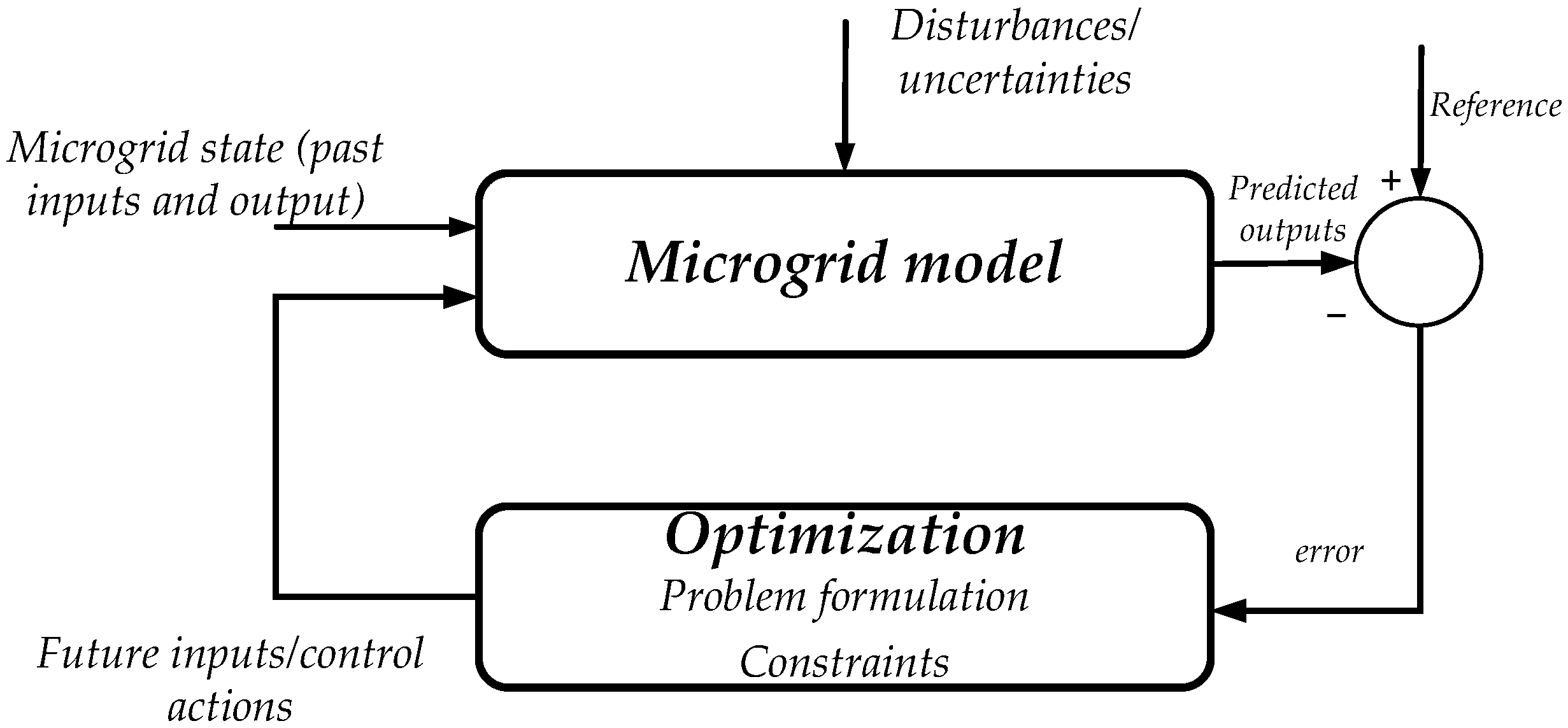
Model predictive control (MPC) is an optimization strategy based on the model of the system. This control looks for the best point of operation in small-time frames, considering the real-time inputs and the actual value of the optimized variable. Each time step, the control system reads, optimizes, and decides based on the microgrid’s model and the available data. This control technique works under possible system perturbations due to uncertainties that can be modeled as a set of bounds. The disturbance model can use robust sets (worst-case scenario), polyhedral, or impulse response (Figure 10). In [147], the authors model the uncertainties of temperature and solar irradiance using adaptive robust sets and the optimization of the greenhouse’s energy management is developed with MPC. Nevertheless, the uncertainty can be modeled using fuzzy intervals, and the MPC can optimize at every time step for a defined prediction horizon but looking for a robust optimization, as explained in [81].

Similar to stochastic and robust optimization, MPC can be applied for various optimization stages depending on the time horizon. Depending on the time step, it can be applied for day-ahead, intraday, and real-time optimization. Commonly, MPC is used for the second stage, or the real-time operation, to correct the energy schedule calculated at the beginning of the day [15]. Moreover, the first stage could use robust and stochastic optimization to calculate the energy schedule by taking into account various uncertainties and, in the case of stochastic optimization, various scenarios (e.g., [149,150]). However, the MPC can be robust by adequately choosing the uncertainty model. For instance, ref. [151] focuses on using robust model predictive control for a multi-carrier microgrid, taking into account the electrical grid and the gas network, where the uncertainty is modeled using a robust set.

However, the main disadvantage is the computation time, as it can be too expensive depending on the number of variables, constraints, and uncertainties. For instance, ref. [152] presents a model predictive control to manage the energy schedule of a microgrid considering renewable power generation, load, and price forecasts to minimize the operating cost. Any variation of these data outside the predicted values will cause the model predictive control to calculate the best point of operation for each power generator and ESSs again.

5.5. Multiparametric Programming

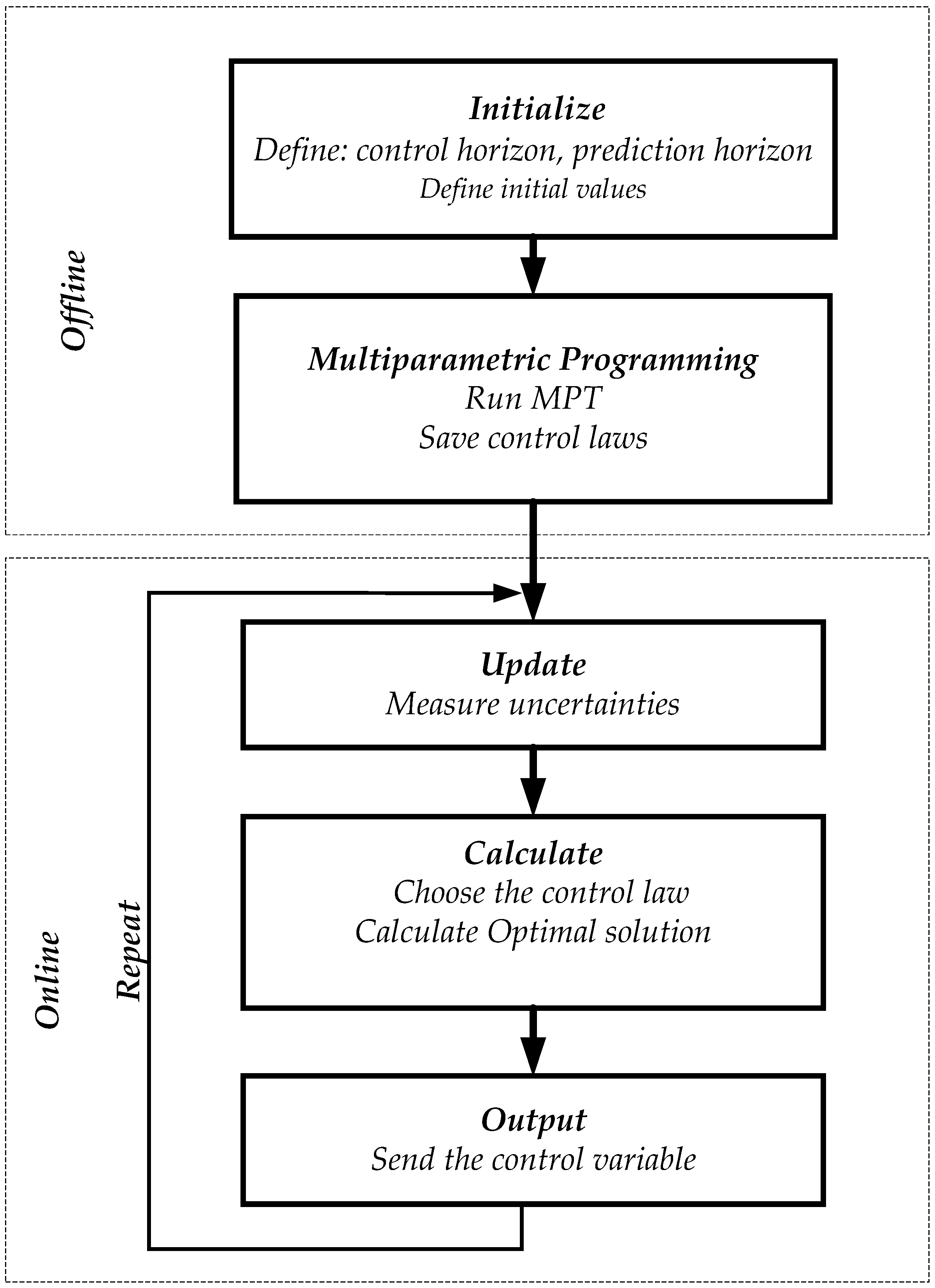
Multiparametric programming has been developed to reduce the MPC’s computational burden and solve optimization problems offline. The main goal of multiparametric programming is to look for objective functions and constraints as a function of all sets of uncertain parameters that vary between upper and lower bounds. Then, it constructs regions where these objective functions are valid, depending on the uncertain parameter variations. The construction of these regions is developed offline and can be done at the beginning of the day. Then, in real-time operation, the system evaluates the actual value of the uncertain parameters and searches for the active region. When the region is found, the system solves the actual optimization function subject to the different constraints with the real values of the uncertainties. The main advantage of multiparametric programming is the small computational burden in online mode, which can be applied only if the parameters are known in real-time operation [153]. This technique has been commonly applied in batch scheduling, control, and optimization of process system engineering [154]. However, multiparametric programming has not been extensively utilized in microgrids and power systems. In [155], this technique has been used to dispatch energy considering the minimal cost operation of a microgrid. The uncertainties considered are the load consumption, wind, and PV power error forecast. Once the regions are built and the actual data are acquired, the optimal point of operation is searched. Another example is presented in [156], where multiparametric programming is used to manage the energy schedule of a combined energy system (heat and power units) where the demand and the state of the power units and heating system are considered uncertainties (Figure 11). In [2], multiparametric programming is applied in a real-time energy management system for a PV-based charged station where five uncertainties were considered: PV production, EV power consumption, the battery’s state of charge, electricity price, and CO${}_2$ emissions.

5.6. Fuzzy Optimization

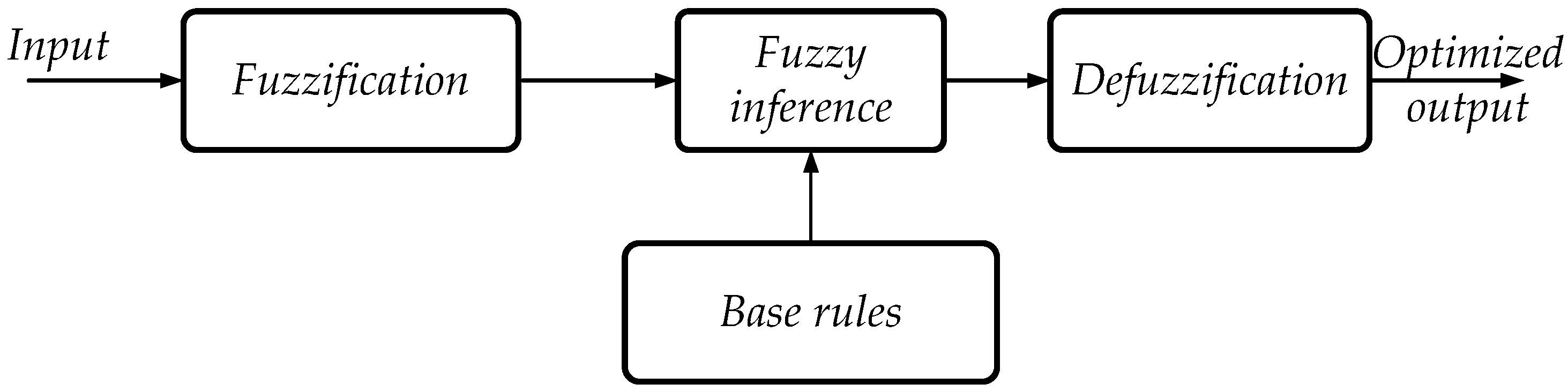
This optimization technique is based on the degree of membership condition (function) satisfaction. The fuzzy logic control operation uses three main steps: fuzzification, fuzzy inference, and defuzzification (Figure 12). Fuzzification translates the numerical input values into fuzzy sets categorized as linguistic variables. Moreover, these fuzzy sets give a degree of membership to the inputs. For instance, the power from renewable energy can be classified as low, medium, high, and super high. In the case of “low”, it means there is a lack of renewable energy, and if it is “super high”, it implies a surplus of energy. After the fuzzification, the fuzzy sets are analyzed in the next block: fuzzy inference to obtain a decision; for instance, the decision could imply the charging or discharging of a battery depending on the availability of renewable energy, price, and demand. The use of fuzzy rules helps make the decision. These rules are expressed again in linguistic terminology. For instance, if the availability of renewable energy is low and the battery’s SoC is low, the battery could be charged by the grid only if the electricity price is low. These rules are expressed as if-then scenarios, and the combination of them can obtain a final decision on the microgrid’s performance. After a decision is made, the result is defuzzified, where the decision is translated to an actual value, such as the exact power to charge or discharge a battery [157]. The response of the EMS will depend entirely on the input variables elected, the fuzzy sets, and the fuzzy rules [158].

The study presented in [47] does not individually model the uncertainties as market price, battery state, and departure time. However, it defines a satisfaction function to the constraints that include various uncertainties as a group. The main advantage (compared to other techniques) is tractability, as it does not increase with the number of uncertainties. This type of optimization has been applied for the management of the energy flows in virtual power plants [158], the management of parking lots [47], and V2G applications [159].

5.7. Machine Learning

Machine learning techniques are emerging tools for data forecasting, parametric identification, scheduling, and control of microgrids. The main types of machine learning are supervised, unsupervised, and reinforcement learning. For supervised learning, it looks to find the best function according to the historical data considered as input. It is commonly used for forecasting uncertain parameters, such as load demand, electricity price, and power generation from wind and solar systems. Common supervised learning algorithms used for this application are kernel-based tree methods, support vector machines, the Gaussian process, and support vector regression [39]. However, these techniques show low performance and are less accurate for forecasting parameters. A promising strategy for forecasting is deep learning, which can present a mean error between 1 and 5% for the estimation of the wind speed and around 0.5% for the one solar irradiance, depending on the season [20]. These techniques have also been used for the parameter estimation of batteries, e.g., state of charge, remaining useful life, and the state of health [160].

In the case of unsupervised learning, it looks to detect patterns in the data given. In microgrids, this strategy is usually managed by clustering techniques, where each group of loads, distribution generators, or multi-carrier microgrids can be in a specific cluster [12]. For instance, it can be used to classify the load demand and time-varying price tariffs [161].

Reinforcement learning is a promising technique for the real-time management of microgrids under uncertain environments. It does not require an explicit model of the uncertainty, but it constantly learns from the real-time operation. The problem is formulated using a Markov decision process where at each step, the agent receives the representation of the environment state and decides an action for the next time step with a numerical reward. As it is an active learning process, the agent looks for the best schedule option at the current time step by looking at the possible best outcomes in the future [39]. The use of this technique for the real-time microgrids EMS is explained in [162]. Here, the states are defined by the uncertainty and correlation between the energy, the demand, the electricity price, and the state of charge of the battery. The schedule constantly adapts to the electricity price, load, and power generation trend. Recently, similar approaches have been used for energy management in smart grids [163], V2G applications [164], and ESSs [165].

However, reinforcement learning has a drawback in real-time operation when there is extreme non-linearity and various uncertainties [166]. Thus, deep reinforcement learning is a machine learning technique that seems more suitable for real-time energy management of microgrids, as it can handle non-linearities. Moreover, its main advantage is that it can make a decision in real time and can handle non-convex data [167]. For instance, deep reinforcement learning is proposed in [162] to optimize the energy management of a microgrid, where it uses a proximal policy optimization to learn the optimal energy management of a common MPC. However, the drawback of using deep reinforcement learning is that it needs a large amount of training data set considering abrupt changes in power production, load connection/disconnection, variations of electricity price, and CO${}_2$ emissions. A possible solution for this drawback is using a double-deep Q-learning method, as it is explained in [165]. This technique updates its memory every time and constantly creates new data sets.

5.8. Comparison

A comparison of the different optimization techniques, including their main characteristics, advantages and disadvantages, the model of uncertainty, the computation time, and the input data type, are shown in

Table 9. Characteristics of the optimization techniques for microgrids under uncertainties.

Optimization Technique	Uncertainty Model	Input Data	Stages		Computation Time
			Day Ahead	Real Time
Stochastic Optimization	Probabilistic function	Forecast	Yes	Yes	High
	Fuzzy sets	Estimated
	Intervals	Deterministic
	Robust sets
Robust optimization	Robust sets Intervals	Forecast	Yes	Yes	Medium
	Intervals	Estimated
	Fuzzy sets	Deterministic
Information gap decision theory		Forecast	Yes	Yes	Medium
	Variable interval	Estimated
		Deterministic
Multiparametric	Robust sets	Forecast	No	Yes	Low
	Intervals	Estimated
		Deterministic
MPC	Probabilistic function	Forecast	No	Yes	High
	Intervals	Estimated
		Deterministic
Fuzzy optimization	Fuzzy sets	Forecast	Yes	No	Medium
		Estimated
		Deterministic
Machine learning	Does not require	Forecast	No	Yes	Low
		Estimated
		Deterministic

and

Table 10. Comparison of the optimization techniques for microgrids under uncertainties.

Optimization Technique	Main Characteristics	Pros	Cons	Preferred Applications
Stochastic programming	Scenarios based	easy to implement	High computational time	day-ahead optimization
			intractable	electrical distribution
			reduce operational cost	short-term uncertainty
				large VPPs
Robust optimization	worst-case scenario	reduce risky operation	Increment cost	Long-term decisions
		Robust		electrical distribution
		tractable		day-ahead optimization
IGDT	worst and base case scenario	non-data set	inflexible	long-term uncertainties
	known outcome	tractable	complex
Multiparametric programming	creates critical regions	reduce online computation	intractable	real time systems
	offline calculation	low use of memory	solution grows exponentially	residential and commercial microgrids
				small applications
MPC	Model the system	online optimization	needs the model of the system	small time frames decisions
	Predicts the next step	no previous data set	high computation time	react to uncertainties
		tractable		parking lots
		enhanced transient response		electric mobility
		receives real time feedback		residential and commercial microgrids
				real-time operation
Fuzzy optimization	membership function satisfaction	tractable	increase exponentially	day-ahead scheduling
		flexible	reduced accuracy	parking lots
		rapid operation		VPPs
		precision		day-ahead scheduling
				V2G
Machine learning		adaptable	requires historic data set	real time operation
		flexible	problems with unexpected changes in short-term	VPPs
		small online computation time	offline time	digital twins
				residential and commercial microgrids
				electric mobility

. Each technique discussed previously has its advantages and drawbacks; this section focuses on the specific application regarding the type of uncertainty and its common use. Thus, this section is a guideline for selecting the best technique for a specific scenario.

Stochastic programming is the most used technique to optimize the energy schedule in microgrids by accounting for uncertainties. Probabilistic functions are mainly used for modeling the inaccuracy in forecasting the amount of power production [19], the energy price, and the load profile. They are also used for modeling stochastic variables, such as solar irradiance, wind speed, cloud index, ambient temperature, peak prices, and connection or disconnection of generators. EV charging time, arrival, and departure time are also modeled through probabilistic functions or sampling techniques. Unfortunately, the increasing number of variables and the need to consider the uncertainties significantly increase the problem’s difficulty, with significant consequences on the computation time.

Another widely used technique is robust optimization, where uncertainties are modeled using robust sets. The typical uncertainties modeled by these robust sets are the electricity price, the power generation, and the power demand forecast errors. As this technique looks for the worst-case scenario, the energy scheduling reduces the time of dependency on PV systems, wind, or energy storage, affecting one of the main goals of microgrids, which is the reduction of CO${}_2$ emissions. Other techniques, such as information gap decision theory and fuzzy optimization, have recently been applied, but not for real-time applications and only for one-day ahead scheduling. These techniques may give good results in the real-time optimization of virtual power plants, V2G, and parking lots.

The modeling and optimizing method depends on the available data type, application, and required computation time. For the forecasting of power production, probability distributions are a good option, as the input data follow a specific function that can be extracted only if there are enough data. The same applies to any machine learning technique, as training data are the base of their performance. However, the data can be fuzzified when the dataset is limited, but the primary limits and the average value are available. If only the limits are known, then robust sets can be used. If there is no information regarding the uncertainty, then information gap theory is applied to search the limits based on the outcome of the microgrid.

Depending on the model used, the decision maker chooses the optimization technique accordingly. The probability theory is based on the generation of scenarios. The uncertainty can be modeled by a probability distribution, fuzzy or fixed intervals, as in the case of robust sets. Due to the generation of scenarios, the computation time is the main drawback of this technique. The other techniques, such as fuzzy, robust, and information gap decision theory, have a specific uncertainty model. These are usually applied to schedule energy flows considering worst-case scenarios. Even though the optimization under the worst-case scenario can lead to a safe and low-risk schedule, it is important to mention that it can increase the operation cost. Therefore, it is advisable that in the modeling stage, the developer defines the maximum and minimum values depending on the application and the time frame of the optimization.

Multiparametric programming has not been used extensively in the microgrids context. This technique could be used when the system can collect the data of the uncertainties at every time step. This technique can be combined with model predictive control, significantly reducing online applications’ optimization time. So, its point of strength is the short optimization time.

In the case of model predictive control, its main advantage is that it can adapt the optimal point in real-time, taking into account the prediction of the states of the microgrid. However, when the microgrid has too many components, its optimization time can be a drawback. Thus, its combination with other techniques, such as machine learning, multiparametric programming, and robust and stochastic optimization to develop the optimal solution offline could help reduce the optimization time in online mode. In distribution system operator(s) (DSO), stochastic programming and model predictive control are the preferred techniques for optimizing the energy flow when multi-carrier microgrids, virtual power plants, and distributor generators are considered. Although there are other techniques, such as info-gap decision theory and multi-parametric programming, its application by DSO is not widespread due to its complexity [18].

6. Optimization Algorithms

The algorithms used to solve the optimization problem, taking into account uncertainties, can be divided into traditional, meta-heuristic/heuristic, and hyper-heuristics. The uncertainties, the objective function, and the constraints are adapted according to the optimization technique used: robust, stochastic, multiparametric, IGDT or MPC. In the case of traditional methods, in microgrids, mixed integer linear and quadratic programming are the most used due to the nature of the loads and generators (on/off) (e.g., [168]). However, one of the challenges is to linearize the problem formulation for a shorter computation time. The authors in [169] have proposed a mixed-integer quadratically constrained programming. However, this solution cannot always be adapted for the optimization technique, as is the case with multiparametric programming; at the moment, it can only handle non-integer and non-quadratically constrained programming as the critical regions could increase exponentially.

Meta-heuristic and heuristic methodologies are designed to reduce the computational time of traditional methodologies, to be flexible, and handle nonlinear problems. The algorithms commonly used are genetic algorithm, particle swarm optimization, evolutionary optimization algorithm, and agents based [38]. The study in [170] proposes a hybrid evolutionary optimization algorithm to solve a microgrid’s stochastic multi-objective optimization, taking into account the wind power forecast as an uncertainty. The algorithm helped reduce the computational burden and the optimization time to search for a convergence operation point. In [171], it is shown that using a genetic algorithm reduces the computational optimization time by 23%. A deep review of these algorithms and their mathematical approaches to energy management can be found in [10].

In the case of hyper-heuristics, its focus is to search for the optimal solution in a heuristic space, so it can be used not only to solve one specific problem under a particular space but also beyond the conventional domain. It selects or generates a low-level heuristic to solve the problem, and can be constructive or perturbative. In the case of selection constructive hyper-heuristic, the techniques used are local search, population-based, and hybrid approaches. Evolutionary algorithms and population-based methods are used when it is selection perturbative. On the other hand, generating constructive hyper-heuristic creates an initial solution that can be optimized further by using genetic algorithms. In this case, it is generation perturbative; it uses conditional statements to search for the solution [172]. The most suitable algorithms used in microgrids for any of these hyper-heuristic methodologies are ants colony, genetic algorithm, and particle swarm optimization, as it is presented in [173].

7. Software

In order to develop an energy management system, MATLAB can be used for modeling the system as it provides tools for robust, stochastic, multiparametric, and fuzzy optimization. Furthermore, MATLAB has a complete library of the different machine learning techniques to work with a large amount of data. Even though the problem formulation can be developed in MATLAB, researchers prefer to use GAMS [174] or YALMIP [141] when the problem formulation is complex or when there are uncertainties in the system. In these cases, the optimization of the problem can be developed using the following solvers: IBM ILOG^® CPLEX^®, Gurobi, and others depending on the problem that can be linear, nonlinear, convex, or non-convex. In [175], an energy management system developed in LABVIEW is used to control a microgrid. In this case, the formulation of the problem is written in GAMS, while the optimization problem is solved by IBM ILOG^® CPLEX^®.

In the case of a microgrid, the main components are a central controller that reads, optimizes, and sends the output signals to the local controllers of each component of the microgrid. dSPACE and have been used as central controllers in many applications. dSPACE works with a MATLAB Simulink environment to create the real-time code used for the control. Moreover, different solvers such as GAMS or CPLEX can be used for the optimization task [176]. Another popular programmable processor is the NI-compactRIO from National Instruments. This is used with a data acquisition card (NI-DAQ) that reads the input data. In this case, LABVIEW is used to control, monitor, and optimize the microgrid [177]. The control of the microgrid can be developed by combining any of this equipment and software. In [178], dSPACE controls the microgrid, LABVIEW is used for the data acquisition, and MATLAB is used for the energy management system that links to GAMS for optimization purposes. The central computer where MATLAB and LABVIEW run is also used for data storage. For small applications such as home energy management systems, Raspberry PI is often used. The control and optimization codes can be directly developed in the Raspberry PI [179,180]. However, they can also be linked with MATLAB and other solvers for optimization and LABVIEW for data acquisition.

It is worth mentioning that the computation time depends both on the number of components to control and on the optimization technique. Concerning

Table 11. Comparison of different optimization techniques regarding the computation time.

Components	Methodology	Uncertainties	Time Horizon	Resolution	Execution Time	Software	Ref.
Diesel generator	IGDT	PV power	24 h	1 h	546.9 s	GAMS	[145]
PV system		load power
ESS
load
Diesel generator	Probabilistic	PV power	24 h	1 h	131,494.4 s	GAMS	[145]
PV system		load power
ESS
load
ESS	IGDT	market price	24 h	30 min	360 s	GAMS	[181]
load
smart appliances
thermal storage system
ESS	Robust optimization	market price	24 h	1 h	0.59 s	MATLAB/CPLEX	[174]
PV system		PV generation
flexible load
Wind turbine	Stochastic Adaptive Robust Optimization	wind power	24 h	1 h	2100 s	CPLEX/GAMS	[144]
ESS		market price
flexible load
Thermal generators	Fuzzy optimization	wind power	24 h	1 h	9 s	MATLAB/CVX	[158]
PV systems		PV power
Wind turbines
industrial load
commercial load
households
Thermal generators	Probabilistic/Monte Carlo	wind power	24 h	1 h	2609.4 s	MATLAB/CVX	[158]
PV systems		PV power
Wind turbines
industrial load
commercial load
households
heating system	Multiparametric programming	initial state heat storage	3 h	1 h	32,660 s	MATLAB/CPLEX	[156]
loads		initial electricity production
combined heat and power units		demand for heat
		electricity consumption
CIGRE model	Deep reinforcement learning	PV power	24 h	1 h	0.5 ms	Python	[167]
		load
CIGRE model	MPC	PV power	24 h	1 h	228 ms	Python	[167]
		load

, the highest execution times are for stochastic optimization and multiparametric programming. Meanwhile, fuzzy, IGDT, and robust optimization can solve the problem formulation in less than six minutes. In the case of multiparametric programming, the execution time depends on the number of uncertainties and regions. Nevertheless, the execution time is shorter during the second optimization stage (online mode), even a few seconds. The computation time also depends on the time horizon and its resolution. From Table 11, it can be seen that most applications have a time horizon of one day ahead with one hour of resolution.

8. Challenges and Future Trends

Microgrid energy management systems need to consider the uncertainties related to various sources to make the energy schedule more realistic. Each modeling and optimization technique attempts to tackle this issue specifically for applications such as virtual power plants, home energy management, electric mobility, and multi-carrier microgrids. The methods presented here focused on typical uncertainties, such as power generation and electricity price, but many are still missing. To the best of the authors’ knowledge, although uncertainties related to the degradation of PV modules and batteries are widely studied, they are not considered when the microgrid energy management optimization process is developed. Moreover, the impact of uncertainties on the state of charge and health of batteries are neither broadly studied. Usually, these variables are considered operation constraints in the optimization technique. Even though virtual power plants and V2G participate in ancillary services, uncertainties such as power reserve, time, and frequency deviation have not been considered. EV’s arrival, departure, and charging time uncertainties are usually considered, but their modeling is almost rough because of the human interaction that usually affects the real-time operation. The errors from these models can be reduced by using economic incentives. Including these uncertainties is the first challenge to overcome for a proper energy management system.

One common problem of microgrid EMSs is that they do not consider CO${}_2$ emissions. Few cases consider CO${}_2$ as a parameter for a specific constraint in the optimization algorithm, but it is not considered an uncertainty. Because the power from the grid comes from different sources, the corresponding CO${}_2$ emissions are variable and uncertain. The data for calculating these emissions depend on the available information for the considered location and time. They are affected by uncertainties that need to be included in the day-ahead schedule. Thus, the inclusion of CO${}_2$ emissions as part of the uncertainties and the objective function is a challenge to overcome in the following years.

Another challenge is finding a common technique suitable for every type of uncertainty and optimization. In this regard, the methods recalled in this paper offer a range of versatility depending on the application (

Table 12. Summary of the articles reviewed depending on the optimization technique used. (RO: Robust optimization, SO: stochastic optimization, FO: fuzzy optimization, IGDT: information-gap decision theory, MPC: model predictive control, MP: multiparametric programming, ML: machine learning, MS: multiple stages, RT: real time).

Reference	SO	RO	FO	IGDT	MPC	MP	ML	MS	RT	Year
[2]					x	x			x	2022
[5]										2022
[13]									x	2022
[88]		x						x		2022
[89]							x			2022
[171]	x									2022
[44]		x						x		2019
[12]							x		x	2020
[15]								x		2020
[25]	x									2020
[30]				x						2020
[50]							x			2020
[64]							x			2020
[92]				x						2020
[94]				x						2020
[97]				x				x		2020
[147]		x			x		x			2020
[155]					x	x				2020
[164]							x			2020
[165]							x			2020
[14]		x			x			x		2019
[31]							x			2019
[45]	x									2019
[93]				x				x		2019
[122]	x								x	2019
[140]		x								2019
[145]				x						2019
[162]							x			2019
[170]	x									2019
[180]									x	2019
[53]		x								2018
[58]							x			2018
[81]		x	x							2018
[82]	x		x							2018
[121]	x									2018
[123]	x									2018
[131]	x									2018
[141]	x	x								2018
[146]				x						2018
[184]							x			2018
[166]							x			2018
[181]				x						2018
[43]	x								x	2017
[47]			x							2017
[84]			x							2017
[95]				x						2017
[96]				x						2017
[142]		x						x		2017
[144]	x	x						x		2017
[158]			x							2017
[52]				x						2016
[149]	x				x			x		2016
[150]	x	x			x					2016
[176]									x	2016
[177]									x	2016

). However, at the same time, they can have drawbacks, such as computation time, scalability, or the need for historical data. Although stochastic and robust techniques are the most used methodologies, they are not the best options when optimization time is a constraint, or there are not enough historical data. On the contrary, multiparametric programming reduces the optimization time. However, it depends on the measurement of the uncertainty in real-time operations, which could be a drawback when this is not possible. Although machine learning techniques have been used especially for predicting uncertainties when historical data are available, they have not been applied much in the context of microgrids for energy optimization. Thus, a future scenario is to use machine learning to teach the microgrid how to react depending on the variations of the uncertainties, such as electricity price, CO${}_2$ emissions, load behavior, and ESS parameters, considering the energy mix from the grid. In this sense, the Internet of Things concept can enhance machine learning techniques by improving the data collection from houses, buildings, EVs, parking lots, virtual power plants, and even the electrical grid.

With the advance of the internet of things, modeling, and platforms, the development of a digital twin of various microgrids can be a reality. The digital twin can be an exact replica of a microgrid that can adapt over time and provide various services, such as predictive maintenance and a variation of operations, taking into account the statistical analysis of uncertain parameters (e.g., degradation and thermal stress) [182]. For this new trend of research, adaptable models of uncertain parameters are necessary to develop together with the statistical analysis of the information. Thus, in this case, machine learning techniques could help the development of digital twins for microgrids [183].

9. Conclusions

This paper presents a review of the techniques used for uncertainty modeling in the context of microgrid optimization and management. Current and future trends in the different microgrid environments are also discussed.

In recent literature, a number of uncertainties related to the operation of EVs, virtual power plants, home, and building energy management are accounted for. Uncertainties affect the electricity market prices, the load and power generation forecasts, and the errors forecast. Modeling some key uncertainties (e.g., materials degradation, state of health of batteries, and the user’s behavior) is more challenging and, thus, neglected.

Uncertainties are represented by using probabilistic functions, intervals, robust sets, information gap theory, and fuzzy sets. The selection of the model depends mainly on the type of available data and the application. Energy management systems aim to minimize the price, maximize the user’s comfort, or minimize CO${}_2$ emissions. When uncertainties are involved, the optimization techniques that can be applied are stochastic, robust, fuzzy optimization, model predictive control, multiparametric programming, information gap decision theory, and machine learning techniques. Among these, model predictive control, stochastic, and robust optimization are the most used for microgrid management.