Numerical Investigation of Flow Past Bio-Inspired Wavy Leading-Edge Cylinders
Abstract
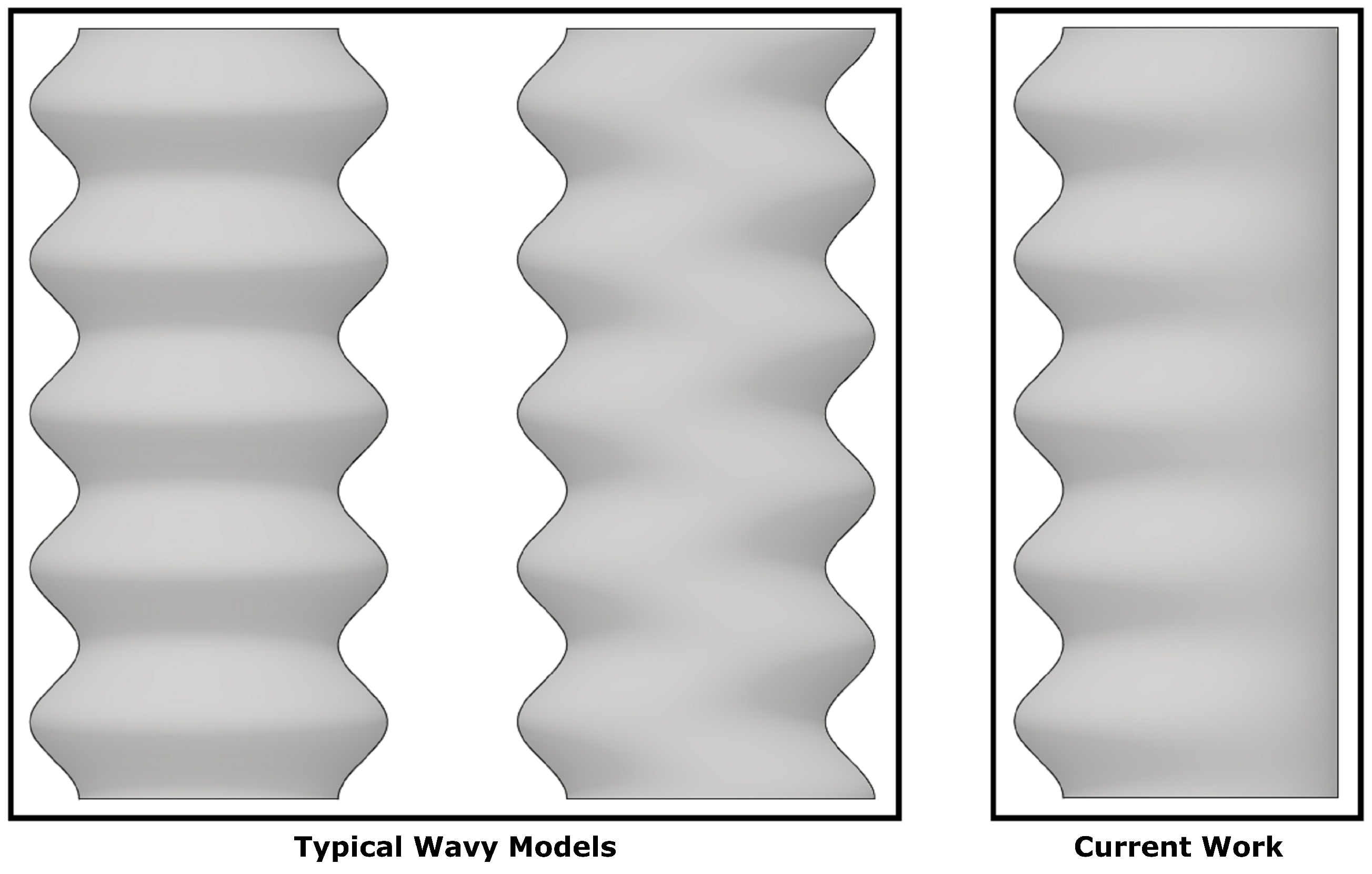
:1. Introduction
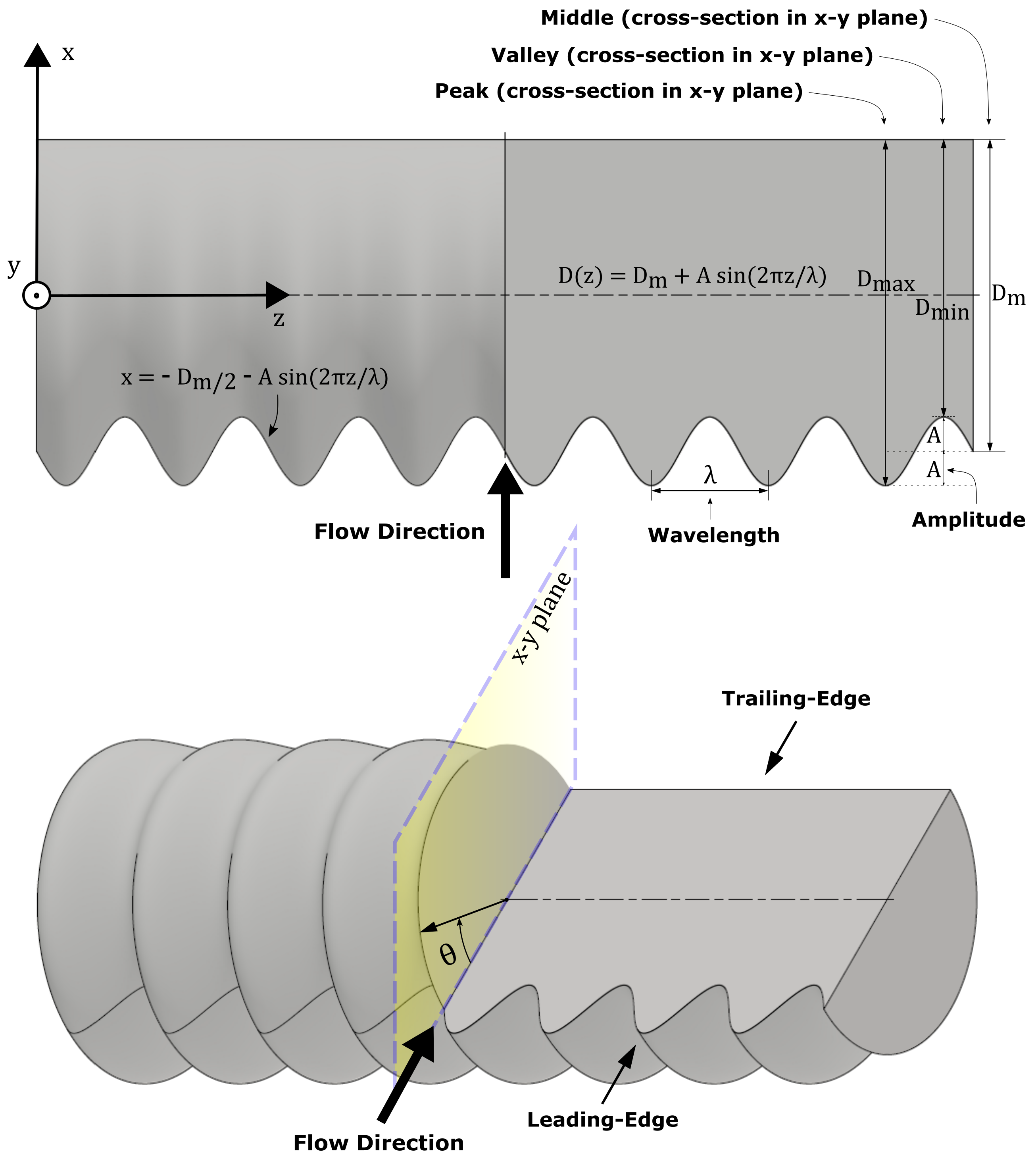
2. Materials and Methods
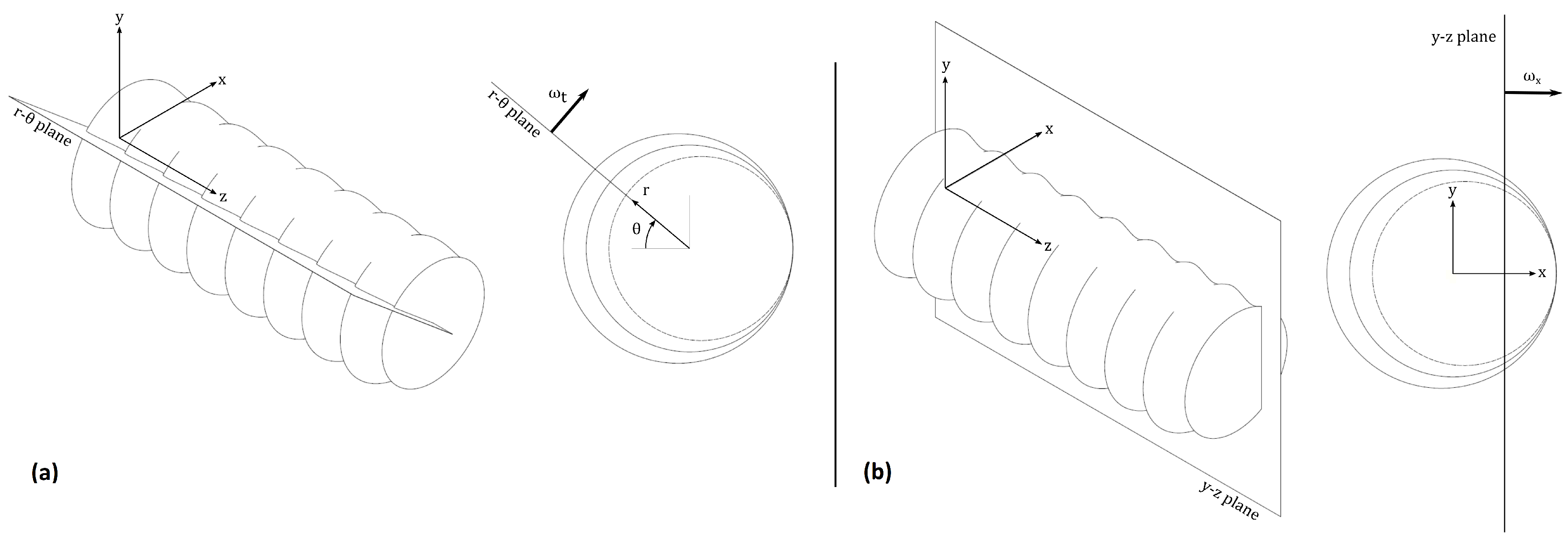
2.1. Computational Domain and Baseline Mesh
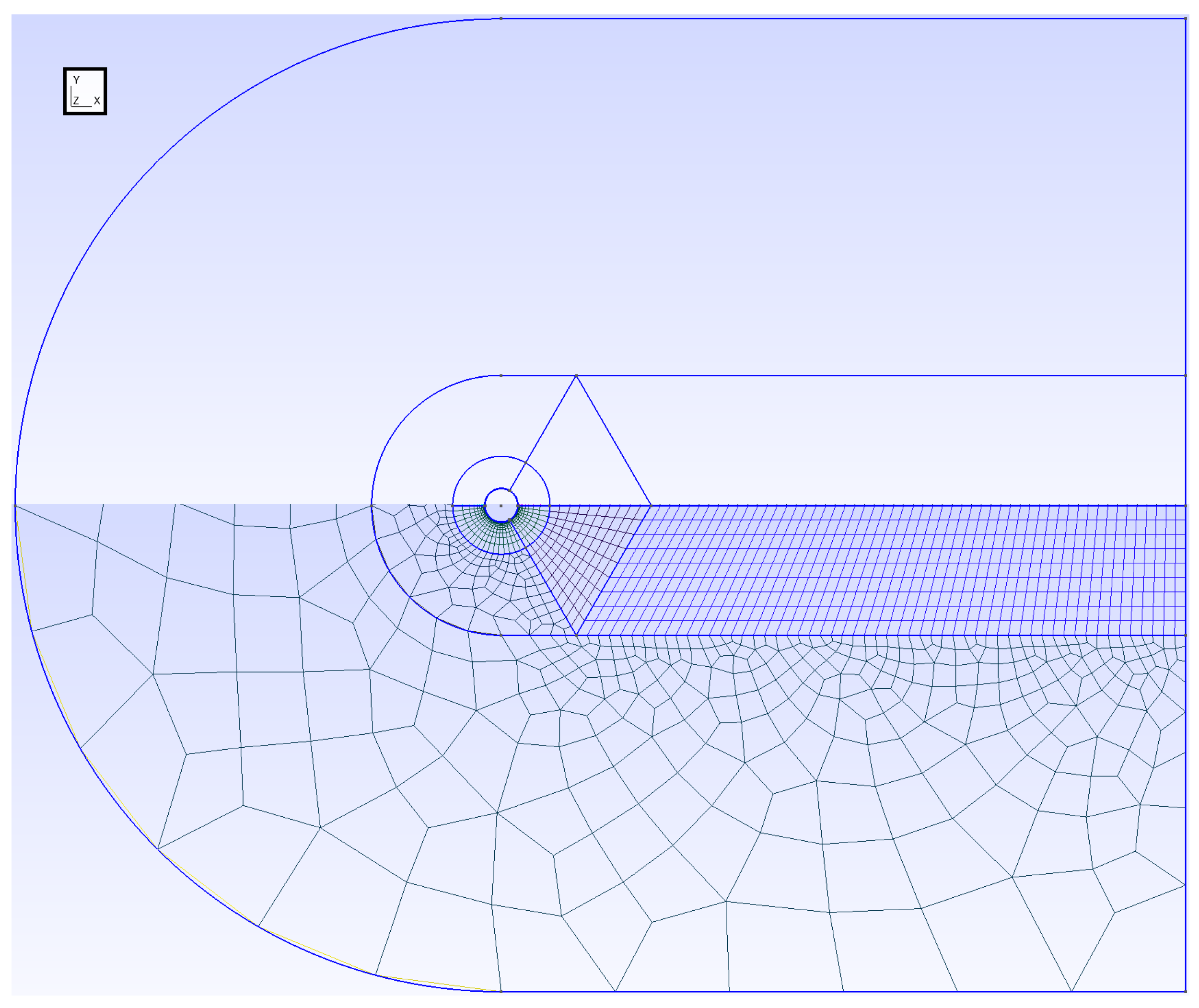
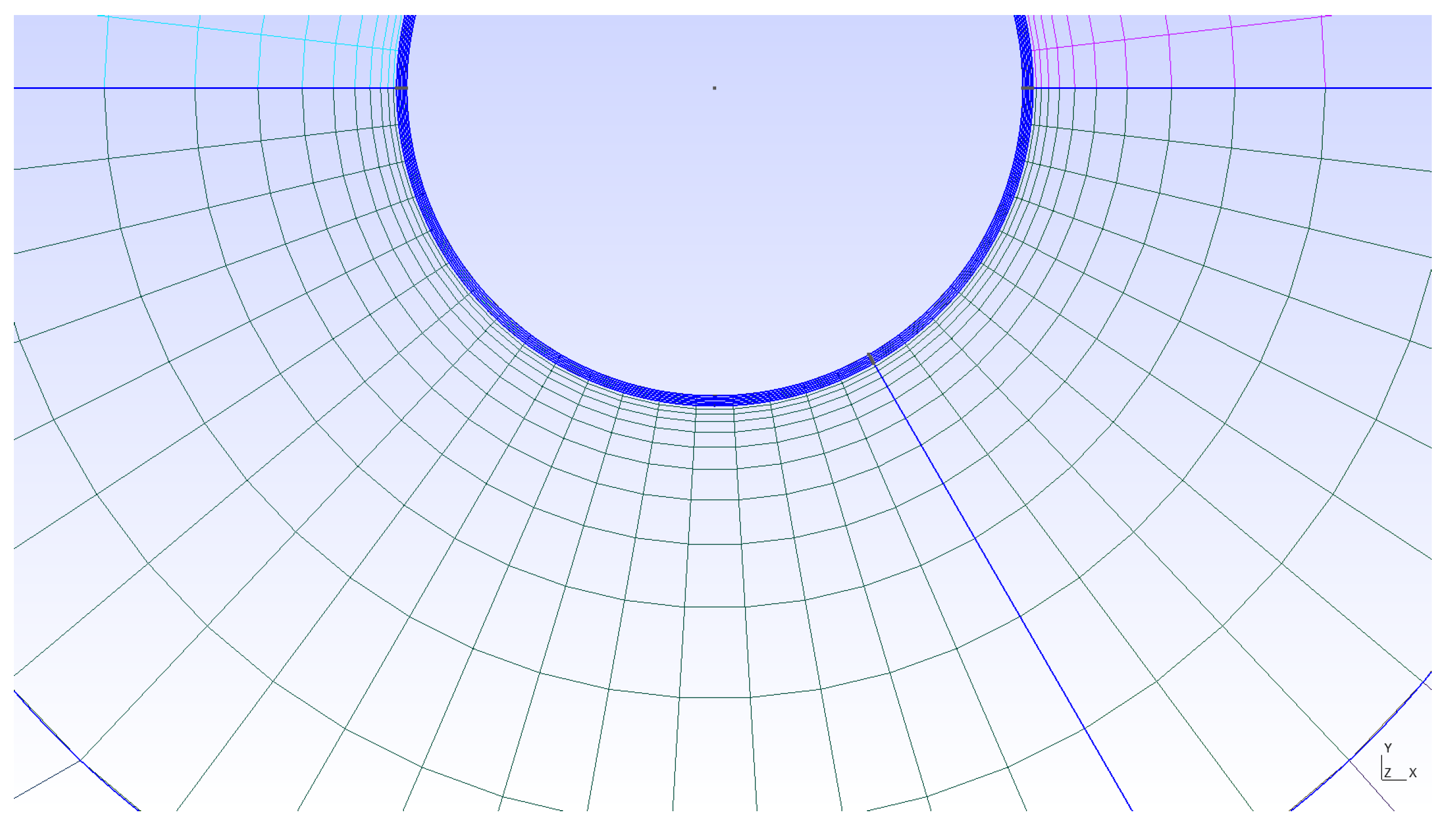
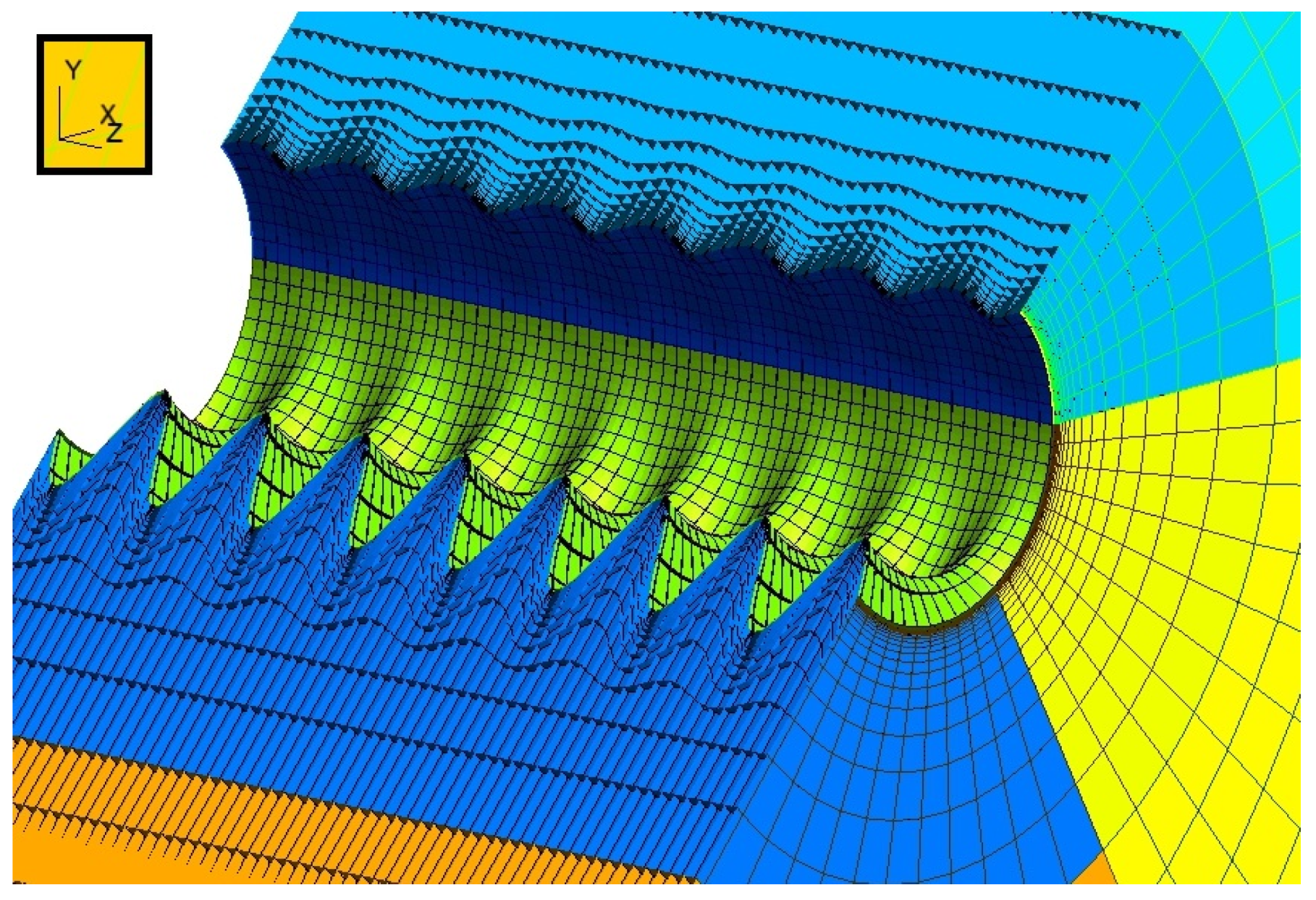
2.2. Mesh Generation
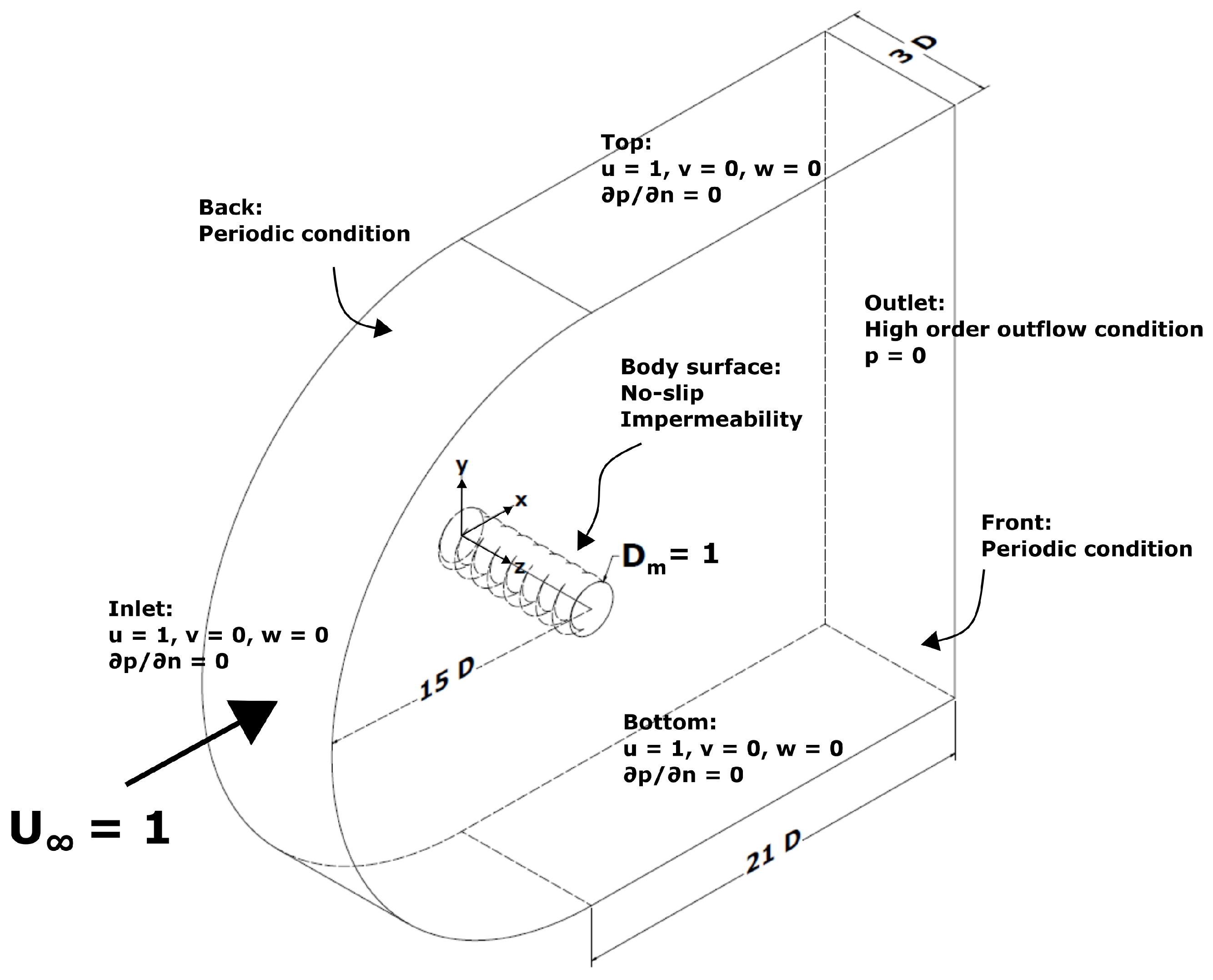
2.3. Boundary and Initial Conditions
- Viscous wall (no-slip and impermeability) conditions at the cylinder surface, along with Neumann condition for the pressure (, where n denotes the unit vector normal to the relevant surface);
- Periodic condition connecting the opposite surfaces in the spanwise direction (back and front planes in Figure 6);
- Dirichlet boundary condition for the velocity () at the inlet surface, along with Neumann condition for the pressure (); these same conditions were applied for the outermost top and bottom domain surfaces shown in Figure 6;
- Nektar’s high-order outflow boundary condition at the outlet surface, which enforces a Dirichlet condition for the pressure () while allowing for velocity fluctuations across the outlet.
2.4. Simulation Details and Cases
2.5. Mesh Dependence Study
3. Results and Discussion
3.1. Numerical Validation
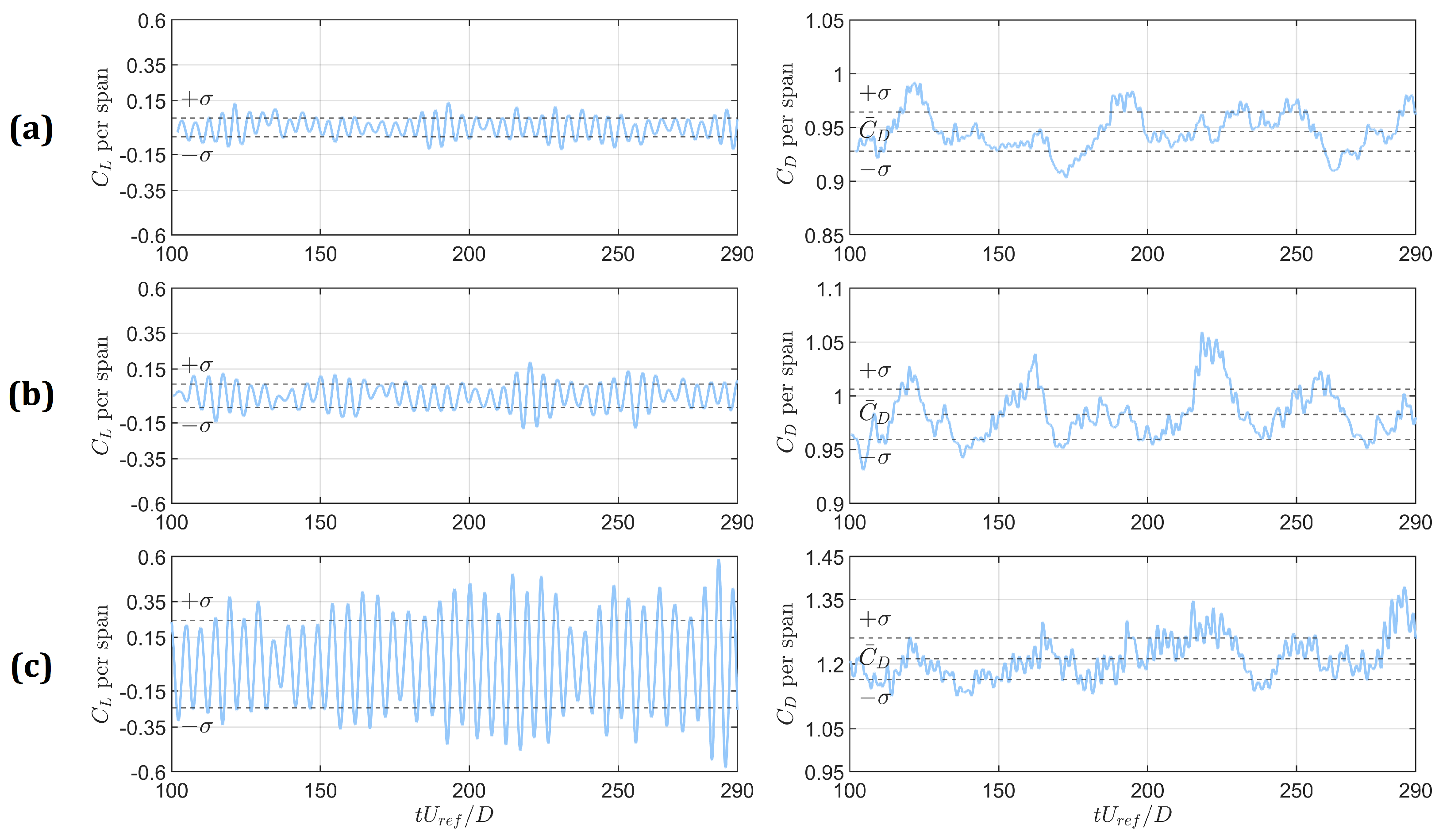
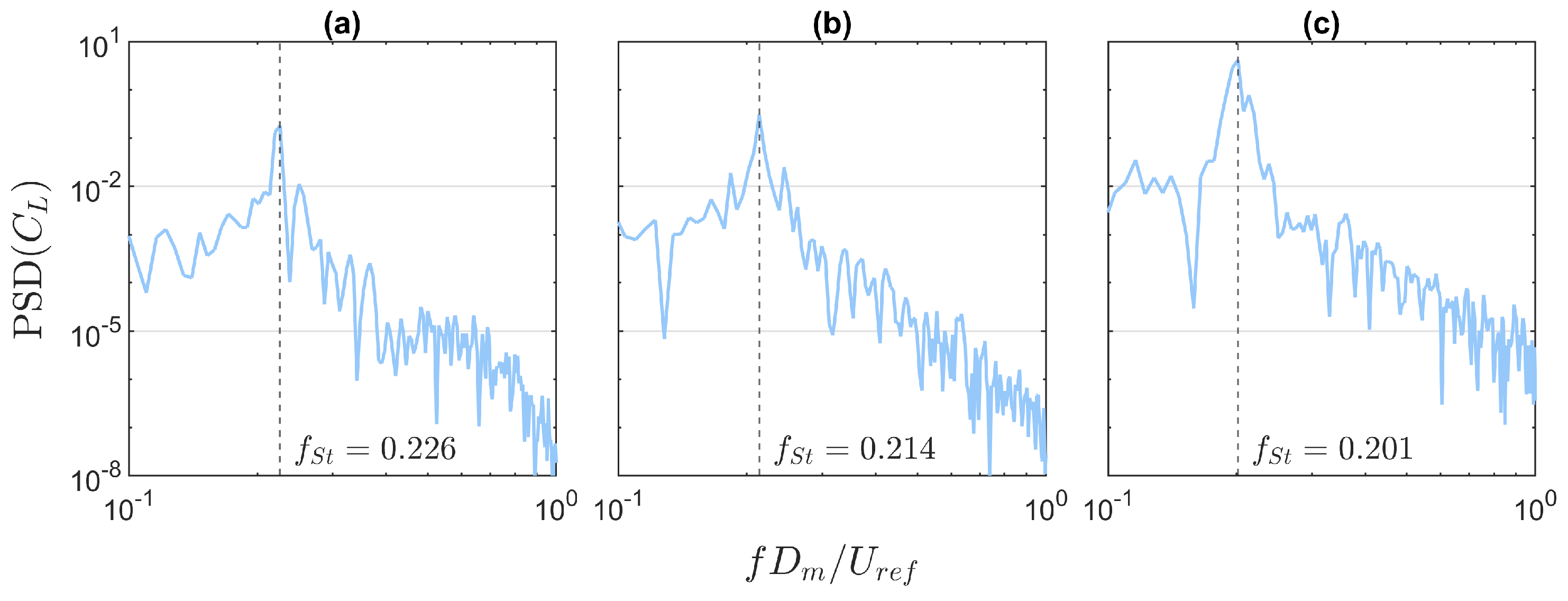
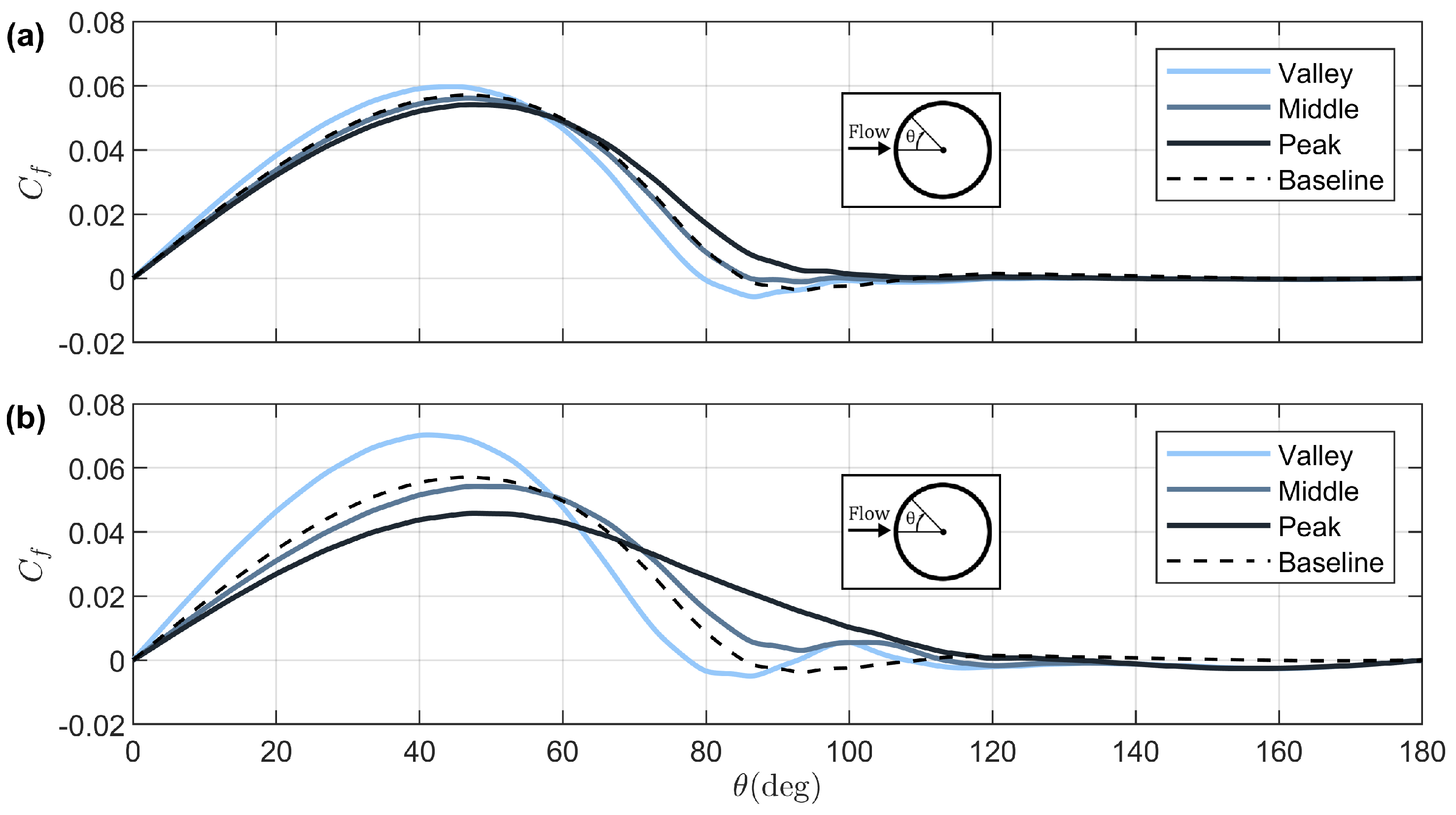
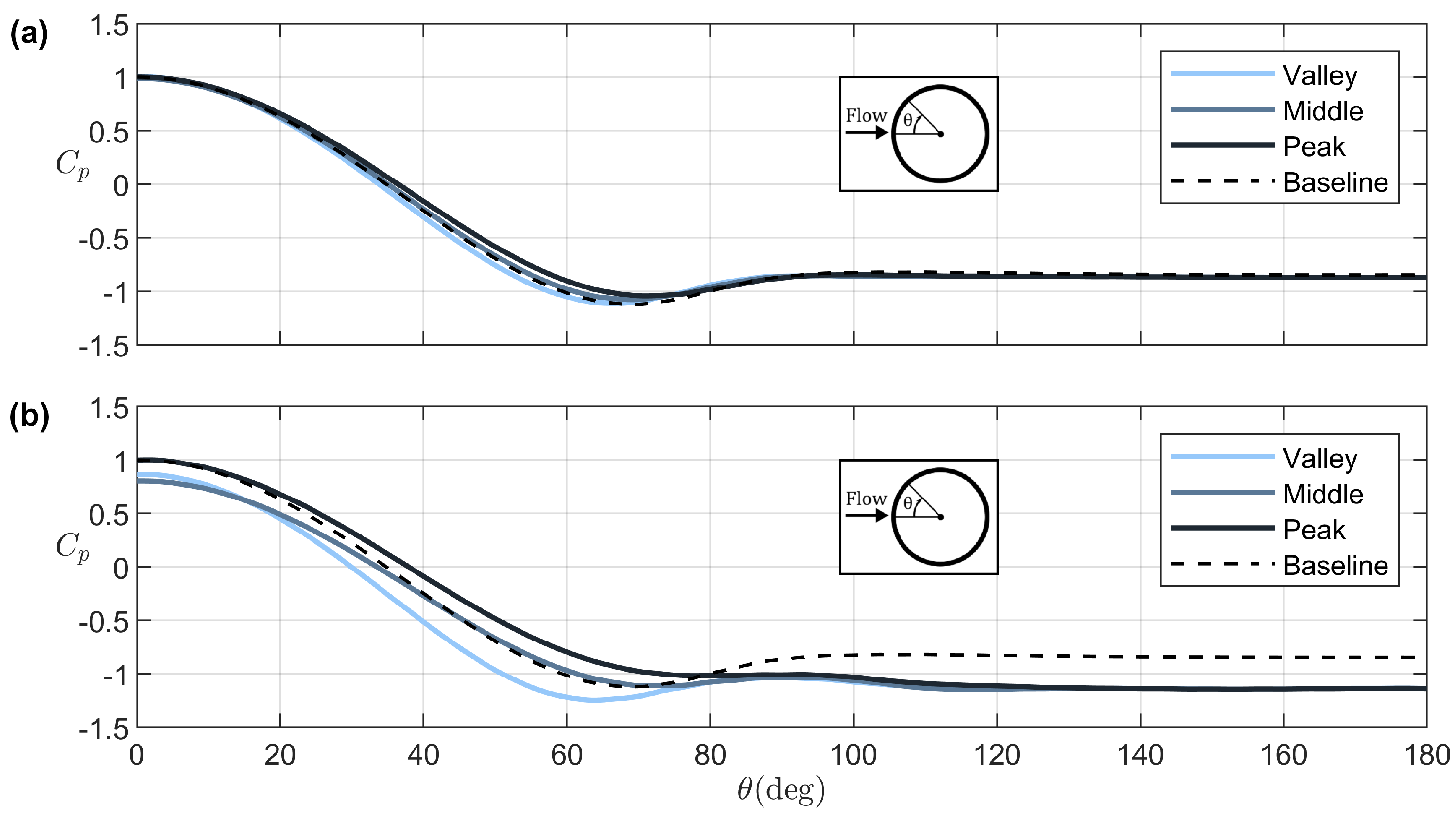
3.2. Changes in Drag, Lift, and Shedding Frequency
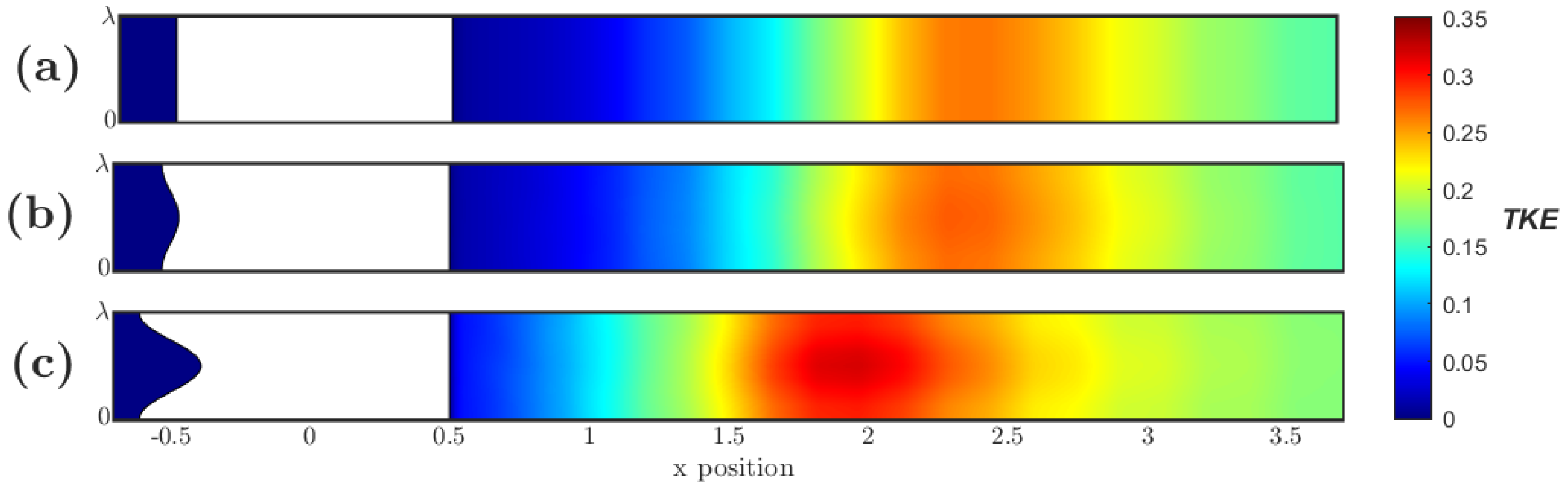
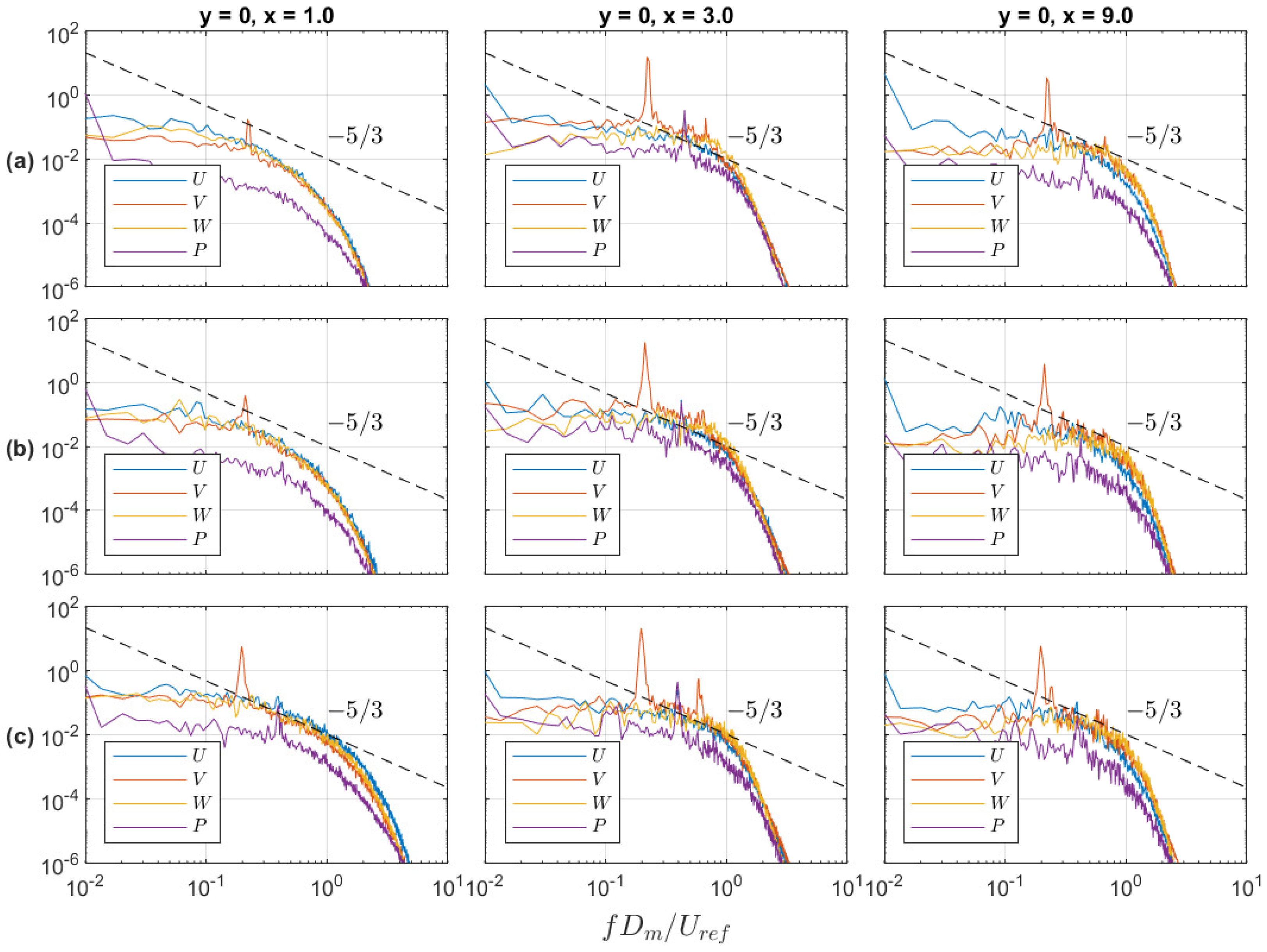
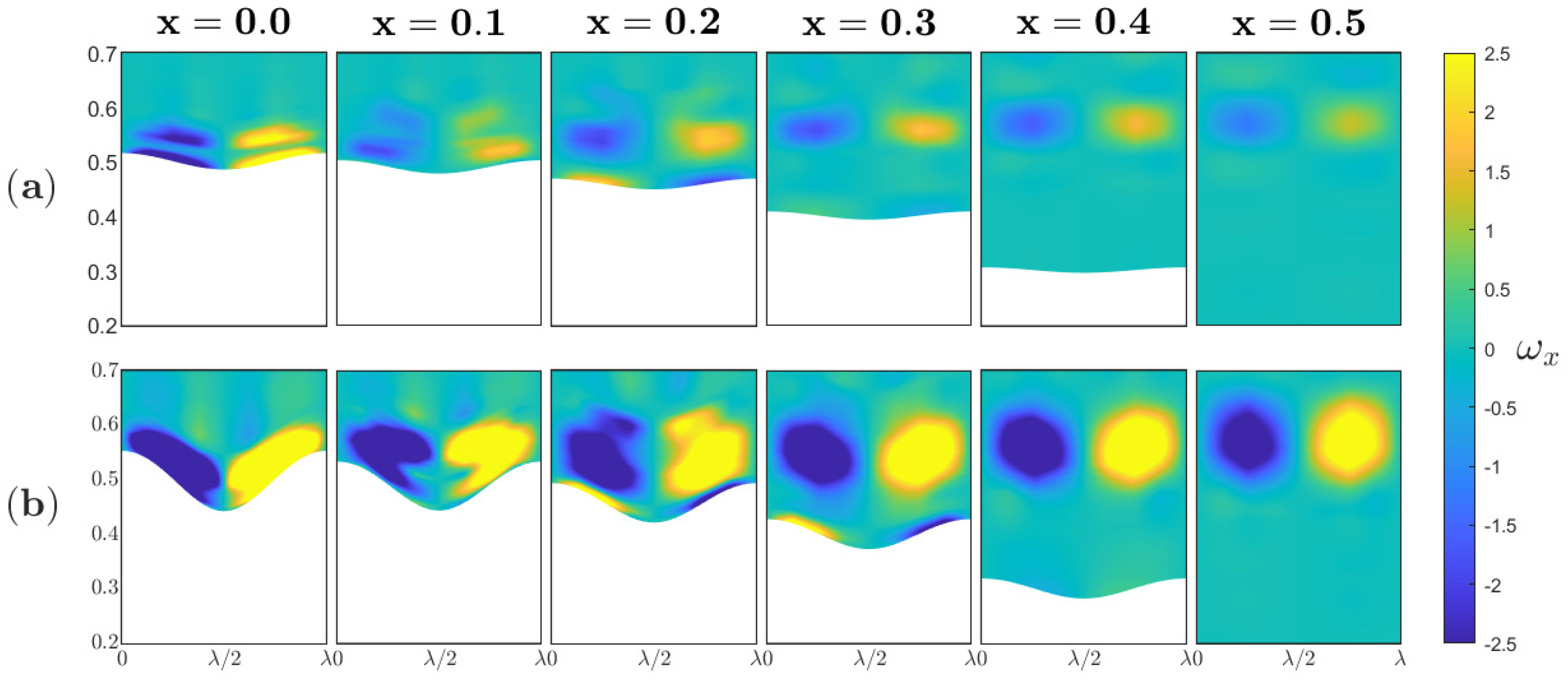
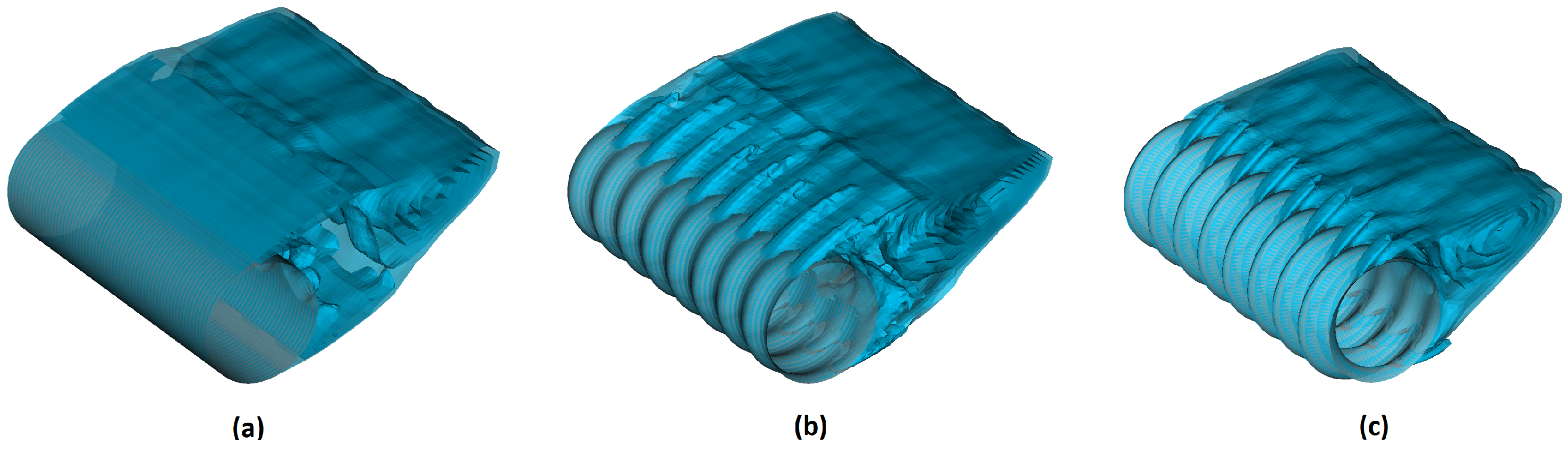
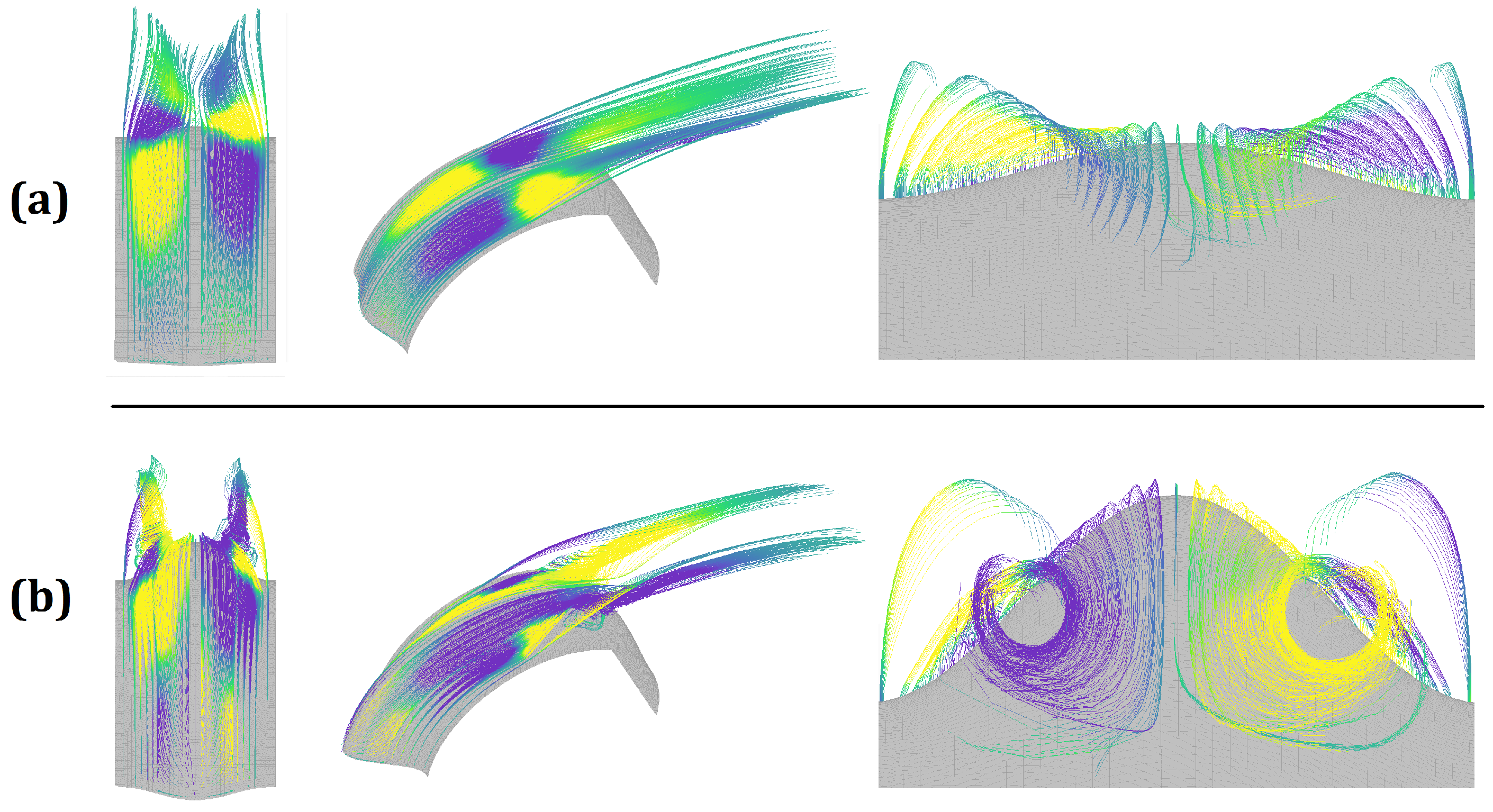
3.3. Flow Field Analysis and Coherent Structures
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roshko, A. Perspectives on bluff body aerodynamics. J. Wind Eng. Ind. Aerodyn. 1993, 49, 79–100. [Google Scholar] [CrossRef]
- Williamson, C.H.K. Three-dimensional wake transition. J. Fluid Mech. 1996, 328, 345–407. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Flow Around Circular Cylinders—Fundamentals; Oxford University Press: Oxford, UK, 1997; Volume 1. [Google Scholar]
- Bearman, P.W. Vortex Shedding from Oscillating Bluff Bodies. Annu. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Wang, R.; Xin, D.; Ou, J. Experimental investigation on suppressing circular cylinder VIV by a flow control method based on passive vortex generators. J. Wind Eng. Ind. Aerodyn. 2019, 187, 36–47. [Google Scholar] [CrossRef]
- Fish, F.E.; Battle, J.M. Hydrodynamic design of the humpback whale flipper. J. Morphol. 1995, 225, 51–60. [Google Scholar] [CrossRef]
- Miklosovic, D.S.; Murray, M.M.; Howle, L.E.; Fish, F.E. Leading-edge tubercles delay stall on humpback whale (Megaptera novaeangliae) flippers. Phys. Fluids 2004, 16, L39–L42. [Google Scholar] [CrossRef]
- Johari, H.; Henoch, C.; Custodio, D.; Levshin, A. Effects of leading-edge protuberances on airfoil performance. AIAA J. 2007, 45, 2634–2642. [Google Scholar] [CrossRef]
- Hansen, K.; Kelso, R.; Dally, B. The effect of leading edge tubercle geometry on the performance of different airfoils. In Proceedings of the 7th World Conference on Experimental Heat Transfer, Fluid Mechanics and Thermodynamics, Krakow, Poland, 28 June–3 July 2009. [Google Scholar]
- de Paula, A.A.; Meneghini, J.; Kleine, V.G.; Girardi, R.D. The wavy leading edge performance for a very thick airfoil. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Rocha, F.A.; de Paula, A.A.; de Sousa, M.; Cavalieri, A.V.; Kleine, V.G. Lift enhancement by wavy leading edges at Reynolds numbers between 700,000 and 3,000,000. In Proceedings of the 36th AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Seyhan, M.; Sarioglu, M.; Akansu, Y.E. Influence of Leading-Edge Tubercle with Amplitude Modulation on NACA 0015 Airfoil. AIAA J. 2021, 59, 3965–3978. [Google Scholar] [CrossRef]
- Ferreira, P.H.; Moura, R.C.; de Araújo, T.B. Experimental Investigation of a Wavy Leading Edge Cylinder. In Proceedings of the AIAA Aviation 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022. [Google Scholar]
- Ahmed, A.; Bays-Muchmore, B. Transverse flow over a wavy cylinder. Phys. Fluids A Fluid Dyn. 1992, 4, 1959–1967. [Google Scholar] [CrossRef]
- Zhang, W.; Daichin; Lee, S.J. PIV measurements of the near-wake behind a sinusoidal cylinder. Exp. Fluids 2005, 38, 824–832. [Google Scholar] [CrossRef]
- Lam, K.; Lin, Y.F. Large eddy simulation of flow around wavy cylinders at a subcritical Reynolds number. Int. J. Heat Fluid Flow 2008, 29, 1071–1088. [Google Scholar] [CrossRef]
- Lin, Z.; Yu-feng, L. Force reduction of flow around a sinusoidal wavy cylinder. J. Hydrodyn. Ser. B 2009, 21, 57–96. [Google Scholar]
- Lam, K.; Lin, Y.F.; Zou, L.; Liu, Y. Investigation of turbulent flow past a yawed wavy cylinder. J. Fluids Struct. 2010, 26, 1078–1097. [Google Scholar] [CrossRef]
- Zhao, R.; Xu, J.; Yan, C.; Yu, J. Scale-adaptive simulation of flow past wavy cylinders at a subcritical Reynolds number. Acta Mech. Sin. 2011, 27, 660–667. [Google Scholar] [CrossRef]
- Bai, H.L.; Zang, B.; New, T.H. The near wake of a sinusoidal wavy cylinder with a large spanwise wavelength using time-resolved particle image velocimetry. Exp. Fluids 2019, 60, 15. [Google Scholar] [CrossRef]
- Karthik, K.; Jeyakumar, S.; Sebastin, J.S. Optimization of wavy cylinder for aerodynamic drag and aeroacoustic sound reduction using computational fluid dynamics analysis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 1–13. [Google Scholar] [CrossRef]
- Zhang, Z.; Tu, J.; Zhang, K.; Yang, H.; Han, Z.; Zhou, D.; Xu, J.; Zhang, M. Vortex characteristics and flow-induced forces of the wavy cylinder at a subcritical Reynolds number. Ocean Eng. 2021, 222, 108593. [Google Scholar] [CrossRef]
- Moura, R.C. On the Use of Spectral Element Methods for Under-Resolved Simulations of Transitional and Turbulent Flows. Ph.D. Thesis, Imperial College London, London, UK, 2017. [Google Scholar]
- Moura, R.C.; Mengaldo, G.; Peiró, J.; Sherwin, S.J. On the eddy-resolving capability of high-order discontinuous Galerkin approaches to implicit LES/under-resolved DNS of Euler turbulence. J. Comput. Phys. 2017, 330, 615–623. [Google Scholar] [CrossRef]
- Moura, R.C.; Sherwin, S.J.; Peiró, J. Linear dispersion-diffusion analysis and its application to under-resolved turbulence simulations using discontinuous Galerkin spectral/hp methods. J. Comput. Phys. 2015, 298, 695–710. [Google Scholar] [CrossRef]
- Moura, R.C.; Sherwin, S.J.; Peiró, J. Modified equation analysis for the discontinuous Galerkin formulation. In Spectral and High Order Methods for Partial Differential Equations—ICOSAHOM 2014; Springer: Cham, Switzerland, 2015; pp. 375–383. [Google Scholar]
- Moura, R.C.; Sherwin, S.J.; Peiró, J. Eigensolution analysis of spectral/hp continuous Galerkin approximations to advection-diffusion problems: Insights into spectral vanishing viscosity. J. Comput. Phys. 2016, 307, 401–422. [Google Scholar] [CrossRef]
- Moura, R.C.; Mengaldo, G.; Peiró, J.; Sherwin, S.J. An LES setting for DG-based implicit LES with insights on dissipation and robustness. In Proceedings of the 11th International Conference on Spectral and High Order Methods (under review), Rio de Janeiro, Brazil, 27 June–1 July 2016. [Google Scholar]
- Mengaldo, G.; Moura, R.C.; Giralda, B.; Peiró, J.; Sherwin, S.J. Spatial eigensolution analysis of discontinuous Galerkin schemes with practical insights for under-resolved computations and implicit LES. Comput. Fluids 2017, 169, 349–364. [Google Scholar] [CrossRef]
- Moura, R.C.; Peiró, J.; Sherwin, S.J. On the accuracy and robustness of implicit LES/under-resolved DNS approaches based on spectral element methods. In Proceedings of the 10th International Symposium on Turbulence and Shear Flow Phenomena, Chicago, IL, USA, 7–9 July 2017. [Google Scholar]
- Mengaldo, G.; De Grazia, D.; Moura, R.C.; Sherwin, S.J. Spatial eigensolution analysis of energy-stable flux reconstruction schemes and influence of the numerical flux on accuracy and robustness. J. Comput. Phys. 2018, 358, 1–20. [Google Scholar] [CrossRef]
- Fernandez, P.; Moura, R.C.; Mengaldo, G.; Peraire, J. Non-modal analysis of spectral element methods: Towards accurate and robust large-eddy simulations. Comput. Method. Appl. M. 2019, 346, 43–62. [Google Scholar] [CrossRef]
- Moura, R.C.; Peiró, J.; Sherwin, S.J. Implicit LES approaches via discontinuous Galerkin methods at very large Reynolds. In Direct and Large-Eddy Simulation XI; Springer: Cham, Switzerland, 2019; pp. 53–59. [Google Scholar]
- Moura, R.C.; Peiró, J.; Sherwin, S.J. Under-resolved DNS of non-trivial turbulent boundary layers via spectral/hp CG schemes. In Direct and Large Eddy Simulation XII; Springer: Cham, Switzerland, 2020; pp. 389–395. [Google Scholar]
- Moura, R.C.; Fernandez, P.; Mengaldo, G.; Sherwin, S.J. Viscous diffusion effects in the eigenanalysis of (hybridisable) DG methods. In Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2018; Springer: Cham, Switzerland, 2020; pp. 371–382. [Google Scholar]
- Moura, R.C.; Fernandes, L.D.; Silva, A.F.C.; Mengaldo, G.; Sherwin, S.J. Spectral/hp element methods’ linear mechanism of (apparent) energy transfer in Fourier space: Insights into dispersion analysis for implicit LES. J. Comput. Phys. 2022, 471, 111613. [Google Scholar] [CrossRef]
- Martins, Y.W.G.; Malatesta, V.; Moura, R.C. Numerical study of the flow past an inclined flat plate via spectral/hp element methods with novel stabilization. In Proceedings of the 26th International Congress of Mechanical Engineering, Virtual Event, 22–26 November 2021. [Google Scholar]
- Moura, R.C.; Cassinelli, A.; da Silva, A.F.C.; Burman, E.; Sherwin, S.J. Gradient jump penalty stabilisation of spectral/hp element discretisation for under-resolved turbulence simulations. Comput. Methods Appl. Mech. Eng. 2022, 388, 114200. [Google Scholar] [CrossRef]
- Moura, R.C.; Aman, M.; Peiró, J.; Sherwin, S.J. Spatial eigenanalysis of spectral/hp continuous Galerkin schemes and their stabilisation via DG-mimicking spectral vanishing viscosity: Application to high Reynolds number flows. J. Comput. Phys. 2019, 406, 109112. [Google Scholar] [CrossRef]
- Cantwell, C.D.; Moxey, D.; Comerford, A.; Bolis, A.; Rocco, G.; Mengaldo, G.; de Grazia, D.; Yakovlev, S.; Lombard, J.; Ekelschot, D.; et al. Nektar++: An open-source spectral/hp element framework. Comput. Phys. Commun. 2015, 192, 205–219. [Google Scholar] [CrossRef]
- Moxey, D.; Cantwell, C.D.; Bao, Y.; Cassinelli, A.; Castiglioni, G.; Chun, S.; Juda, E.; Kazemi, E.; Lackhove, K.; Marcon, J.; et al. Nektar++: Enhancing the capability and application of high-fidelity spectral/hp element methods. Comput. Phys. Commun. 2020, 249, 1–18. [Google Scholar] [CrossRef]
- Lombard, J.W.; Moxey, D.; Sherwin, S.J.; Hoessler, J.F.A.; Dhandapani, S.; Taylor, M.J. Implicit large-eddy simulation of a wingtip vortex. AIAA J. 2016, 54, 506–518. [Google Scholar] [CrossRef]
- Serson, D.; Meneghini, J.R.; Sherwin, S.J. Direct numerical simulations of the flow around wings with spanwise waviness. J. Fluid Mech. 2017, 826, 714–731. [Google Scholar] [CrossRef]
- Wang, R.; Wu, F.; Xu, H.; Sherwin, S.J. Implicit large-eddy simulations of turbulent flow in a channel via spectral/hp element methods. Phys. Fluids 2021, 33, 035130. [Google Scholar] [CrossRef]
- Mengaldo, G.; Moxey, D.; Turner, M.; Moura, R.C.; Jassim, A.; Taylor, M.; Peiro, J.; Sherwin, S.J. Industry-relevant implicit large-eddy simulation of a high-performance road car via spectral/hp element methods. SIAM Rev. 2021, 63, 723–755. [Google Scholar] [CrossRef]
- Karniadakis, G.; Sherwin, S.J. Spectral/hp Element Methods for Computational Fluid Dynamics; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Raza, S.A.; Irawan, Y.H.; Chern, M. Effect of boundary conditions and domain size on the turbulent flow characteristics over a circular cylinder. J. Chin. Inst. Eng. 2021, 44, 659–672. [Google Scholar] [CrossRef]
- Ali, H.; Khan, N.B.; Jameel, M.; Khan, A.; Sajid, M.; Munir, A.; Ahmed, A.E.; Alharbi, K.A.M.; Galal, A.M. Numerical investigation of the effect of spanwise length and mesh density on flow around cylinder at Re = 3900 using LES model. PLoS ONE 2022, 17, e0266065. [Google Scholar] [CrossRef] [PubMed]
- Geuzaine, C.; Remacle, J.F. Gmsh: A three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Beaudan, P.; Moin, P. Numerical Experiments on the Flow Past a Circular Cylinder at Sub-Critical Reynolds Number; Technical Report No. TF-62; Thermosciences Division, Department of Mechanical Engineering, Stanford University: Stanford, CA, USA, 1994. [Google Scholar]
- Kravchenko, A.G.; Moin, P. Numerical studies of flow over a circular cylinder at Re = 3900. Phys. Fluids 2000, 12, 403–417. [Google Scholar] [CrossRef]
- Norberg, C. Effects of Reynolds Number and a Low-Intensity Freestream Turbulence on the Flow around a Circular Cylinder; Technical Report Publication 87/2; Department of Applied Thermodynamics and Fluid Mechanics, Chalmers University of Technology: Gothenburg, Sweden, 1987. [Google Scholar]
- Ong, L.; Wallace, J.M. The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 1996, 20, 441–453. [Google Scholar] [CrossRef]
- Lourenco, L.M.; Shih, C. Characteristics of the Plane Turbulent Near Wake of a Circular Cylinder. A Particle Image Velocimetry Study. Engineering 1993. [Google Scholar]
- Tremblay, F. Direct and Large-Eddy Simulation of Flow around a Circular Cylinder at Subcritical Reynolds Numbers. Ph.D. Thesis, Technische Universität München (TUM), Munich, Germany, 2002. [Google Scholar]
- Norberg, C. Fluctuating lift on a circular cylinder: Review and new measurements. J. Fluids Struct. 2003, 17, 57–96. [Google Scholar] [CrossRef]


| Case | Type | ||
|---|---|---|---|
| Baseline | Straight | - | - |
| A03 | Wavy | 0.03 | 0.375 |
| A11 | Wavy | 0.11 | 0.375 |
| Case | Time Step | CPU Time (h) |
|---|---|---|
| Baseline | 898 | |
| A03 | 1321 | |
| A11 | 1980 |
| Case | |||||
|---|---|---|---|---|---|
| Fine | 156.080 | 3902 | 40 | 0.939 | 0.046 |
| Medium | 92.832 | 2901 | 32 | 0.946 | 0.052 |
| Coarse 1 | 49.024 | 1532 | 32 | 1.054 | 0.195 |
| Coarse 2 | 20.944 | 1309 | 16 | 1.054 | 0.203 |
| Author | Nature | ||||
|---|---|---|---|---|---|
| Norberg [52] | Experimental | 0.98 | 0.84 | 0.21 | - |
| Ong and Wallace [53] | Experimental | 0.99 | - | 0.21 | 86 |
| Lourenco and Shih [54] cited in [50] | Experimental | 0.99 | 0.88 | 0.22 | 89 |
| Beaudan and Moin [50] | DNS | 0.96 | 0.89 | 0.216 | 85.3 |
| Tremblay [55] | DNS | 1.03 | 0.93 | 0.215 | 86.5 |
| Kravchenko and Moin [51] | Classic LES | 1.04 | 0.93 | 0.21 | 88 |
| Present work | Implicit LES | 0.95 | 0.84 | 0.226 | 86 |
| Case | Valley | Peak | Middle | |||
|---|---|---|---|---|---|---|
| Baseline | 0.226 | 0.052 | 0.946 | 0.946 | 0.946 | 0.946 |
| A03 | 0.214 | 0.066 | 0.983 | 0.941 | 1.024 | 0.977 |
| A11 | 0.201 | 0.245 | 1.212 | 1.068 | 1.316 | 1.184 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, P.H.; de Araújo, T.B.; Carvalho, E.O.; Fernandes, L.D.; Moura, R.C. Numerical Investigation of Flow Past Bio-Inspired Wavy Leading-Edge Cylinders. Energies 2022, 15, 8993. https://doi.org/10.3390/en15238993
Ferreira PH, de Araújo TB, Carvalho EO, Fernandes LD, Moura RC. Numerical Investigation of Flow Past Bio-Inspired Wavy Leading-Edge Cylinders. Energies. 2022; 15(23):8993. https://doi.org/10.3390/en15238993
Chicago/Turabian StyleFerreira, Paulo Henrique, Tiago Barbosa de Araújo, Eduardo Oliveira Carvalho, Lucas Dantas Fernandes, and Rodrigo Costa Moura. 2022. "Numerical Investigation of Flow Past Bio-Inspired Wavy Leading-Edge Cylinders" Energies 15, no. 23: 8993. https://doi.org/10.3390/en15238993
APA StyleFerreira, P. H., de Araújo, T. B., Carvalho, E. O., Fernandes, L. D., & Moura, R. C. (2022). Numerical Investigation of Flow Past Bio-Inspired Wavy Leading-Edge Cylinders. Energies, 15(23), 8993. https://doi.org/10.3390/en15238993






