Design and Robust Performance Analysis of Low-Order Approximation of Fractional PID Controller Based on an IABC Algorithm for an Automatic Voltage Regulator System
Abstract
1. Introduction
- -
- For the first time, the low-order approximation of a FOPID controller based on the ABC algorithm (named IABC/LOA-FOPID) is used.
- -
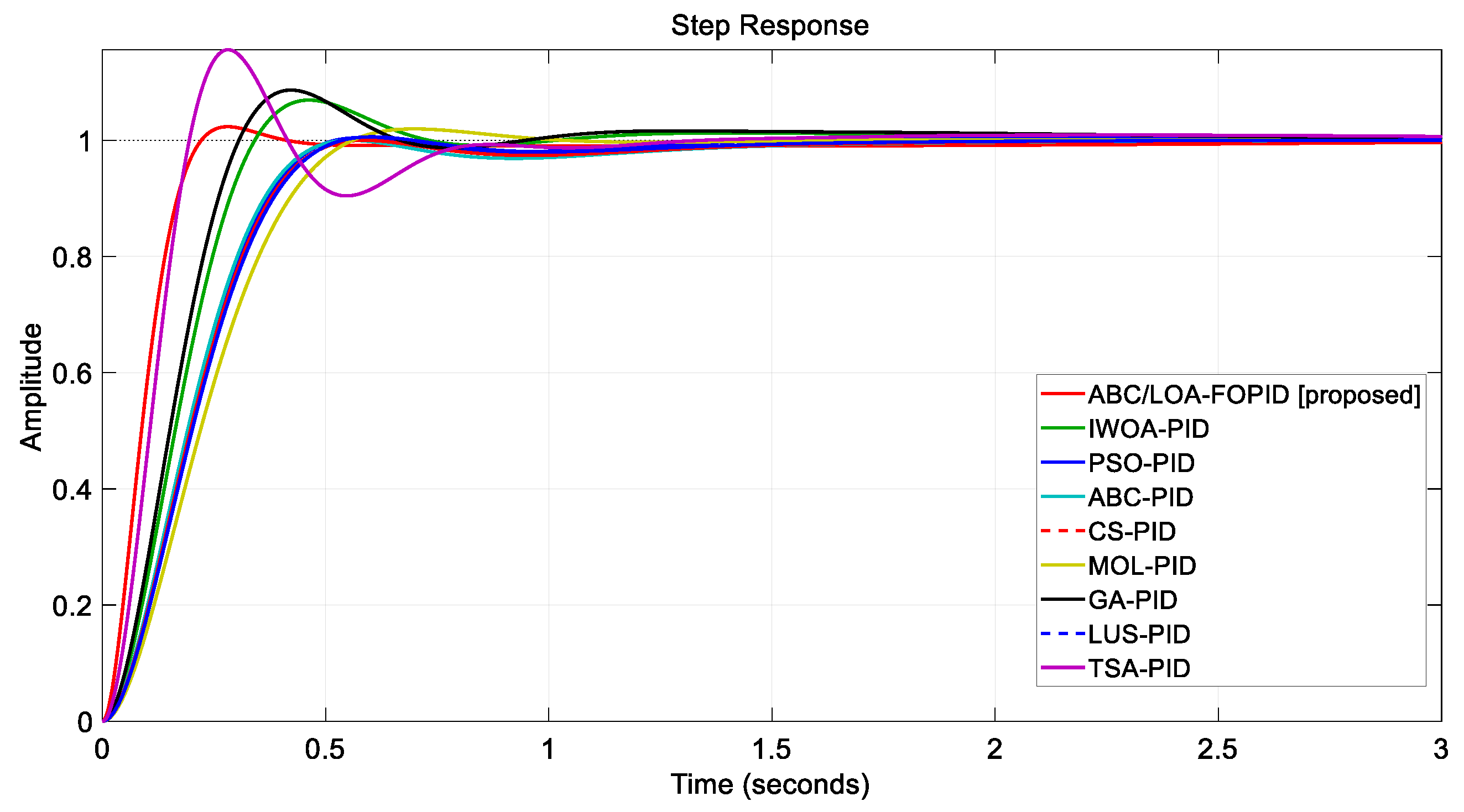
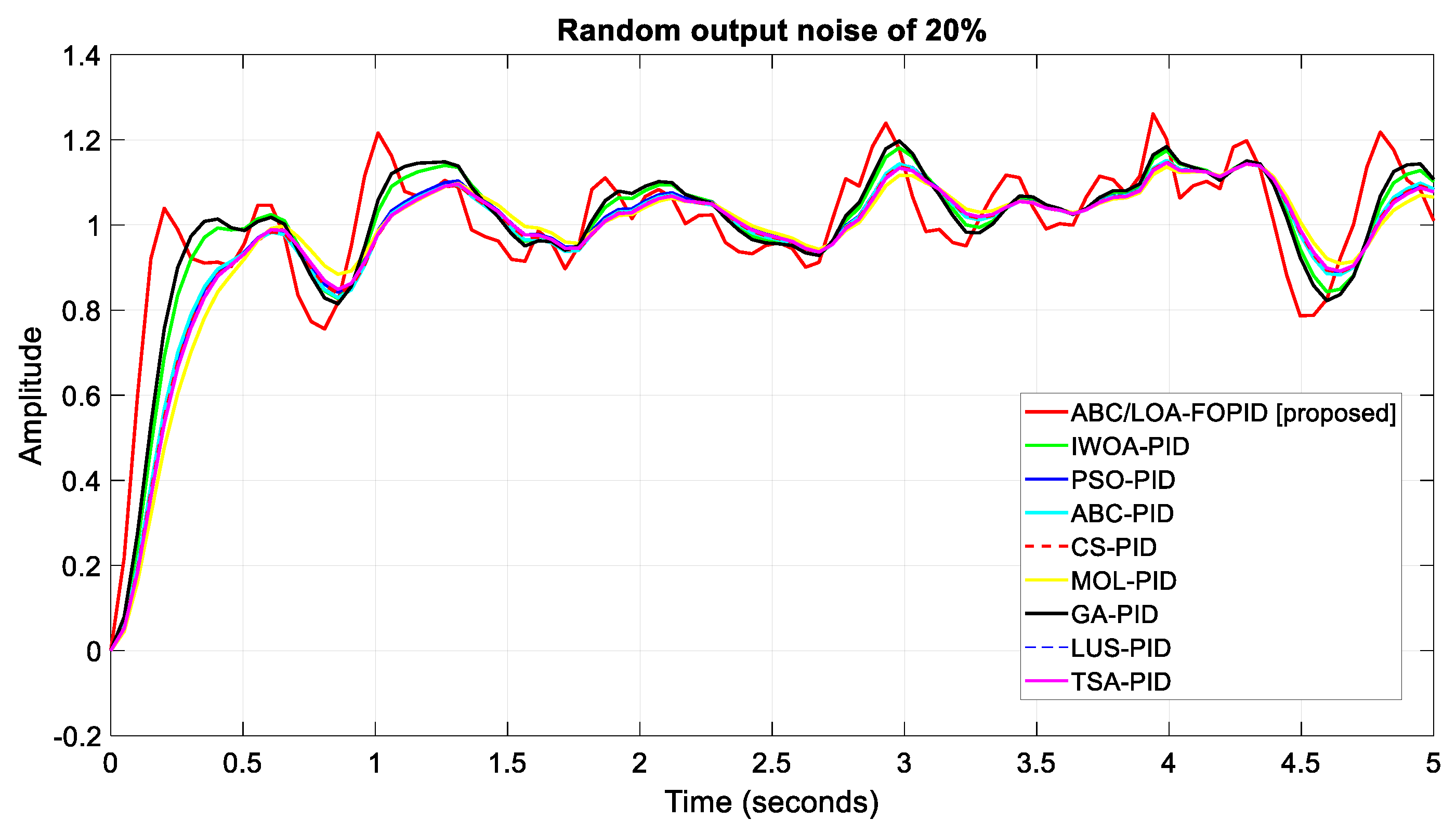
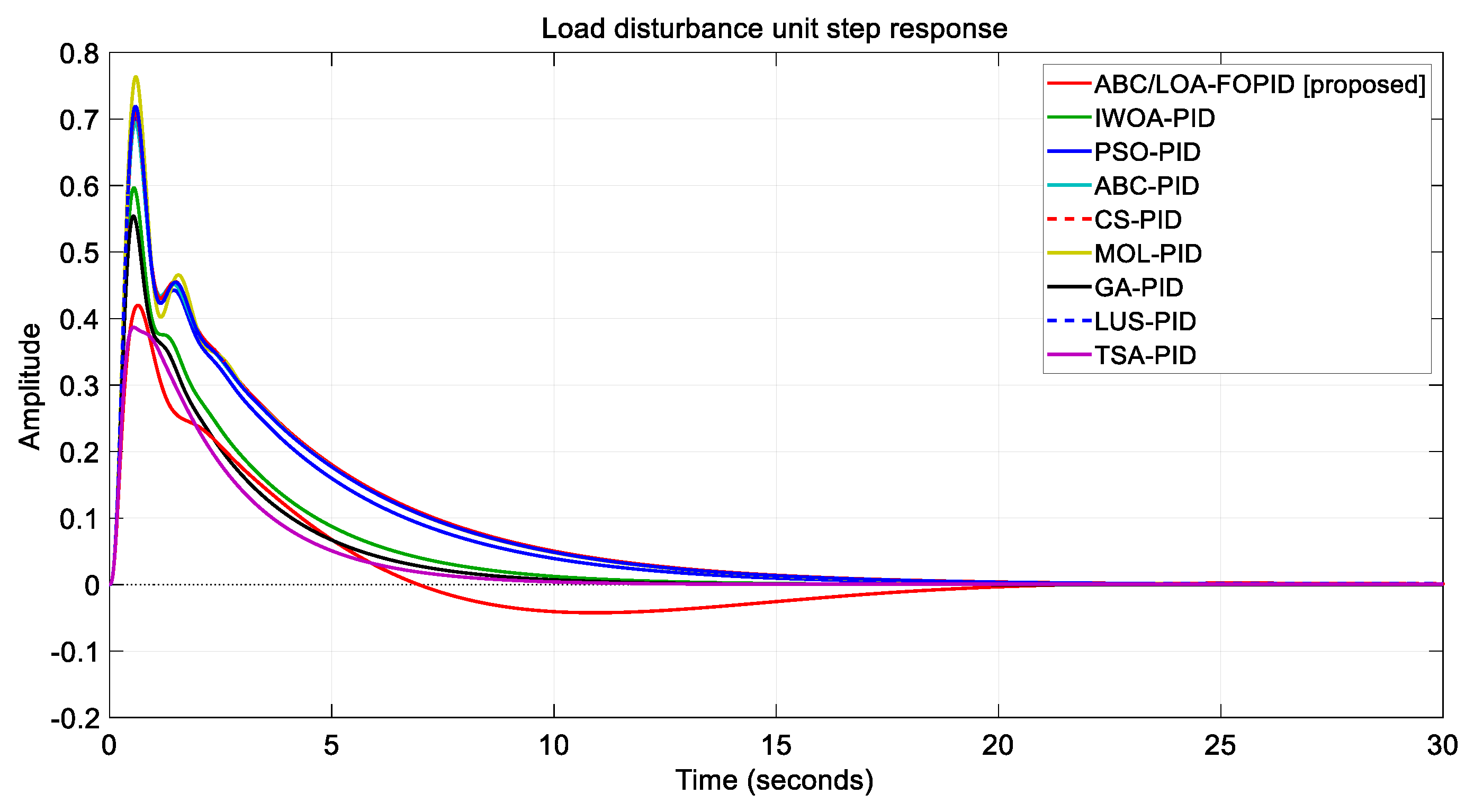
- In terms of transient response performance, the proposed IABC/LOA-FOPID controller was thoroughly compared to various strategies in the literature, such as IWOA-PID [21], PSO-PID [12], ABC-PID [15], CS-PID [26], MOL-PID [28], GA-PID [12], LUS-PID [31], and TSA [23]. The findings of the research clearly show that the LOA-FOPID controller tuned by IABC is better.
- -
- To investigate the system’s behavior, several robustness tests are specifically studied. All along the experiments, the LOA-FOPID regulator optimized by ABC outperforms the classical or fractional PID controller, whose parameters have been optimized by the other methods that have been researched in the literature.
2. Materials and Methods
2.1. AVR System Description and Modeling
2.2. Fractional Calculus
2.3. Stability of Fractional Order Systems
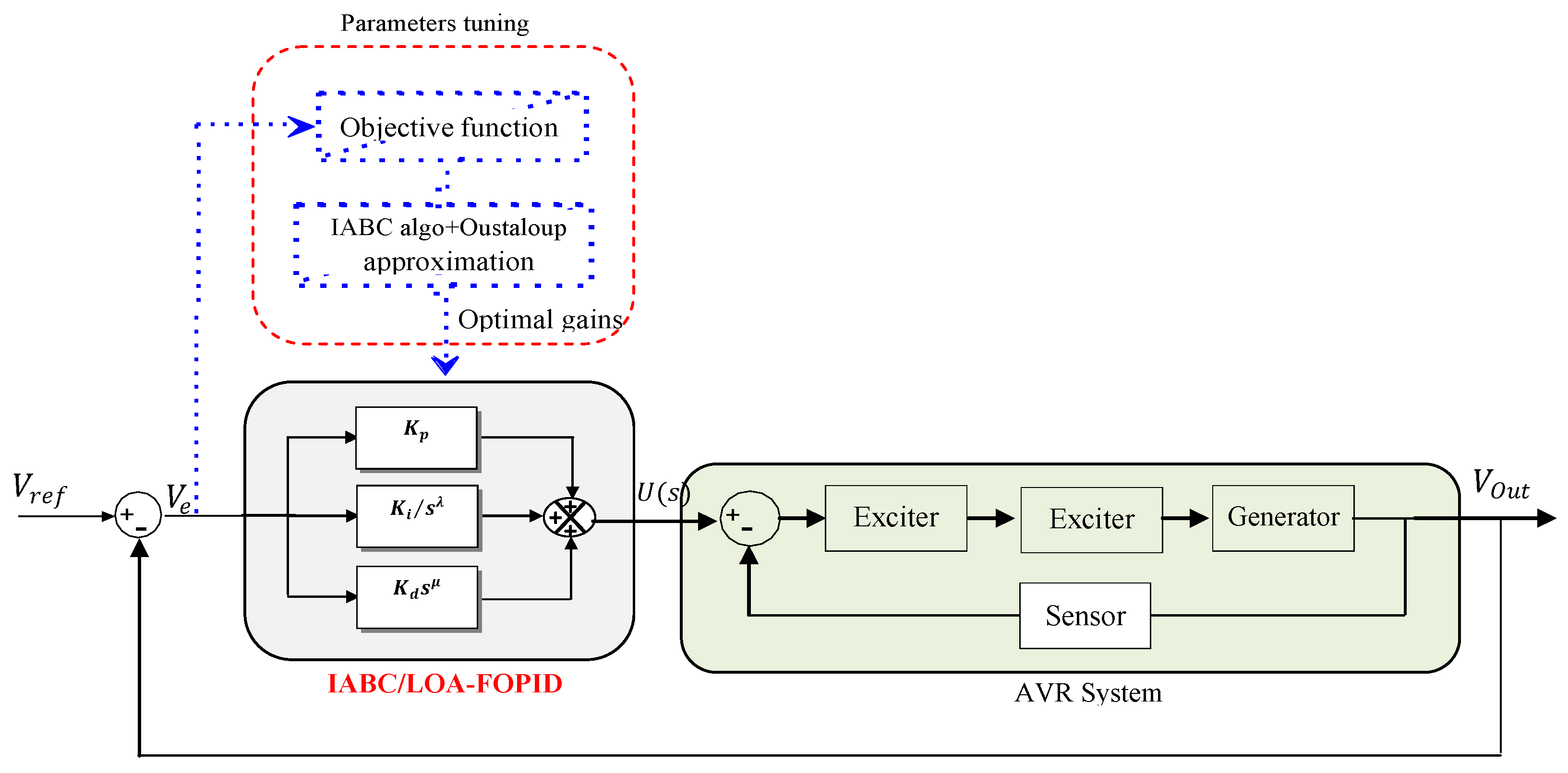
3. Fractional PID Controller Based on IABC Algorithm
3.1. ABC Algorithm
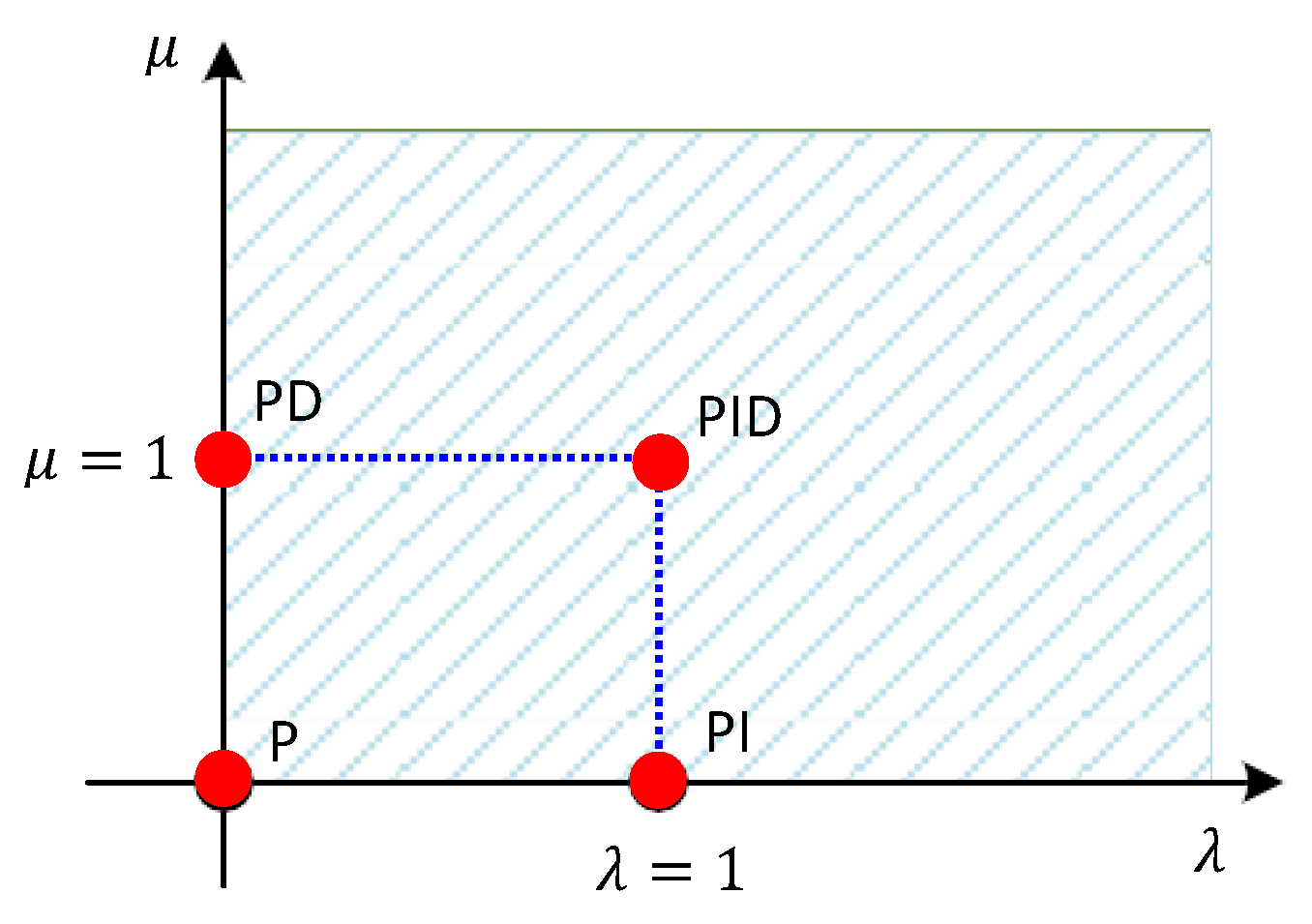
3.2. Fractional Order PID Controller
3.3. Design of the FOPID Controller Using IABC
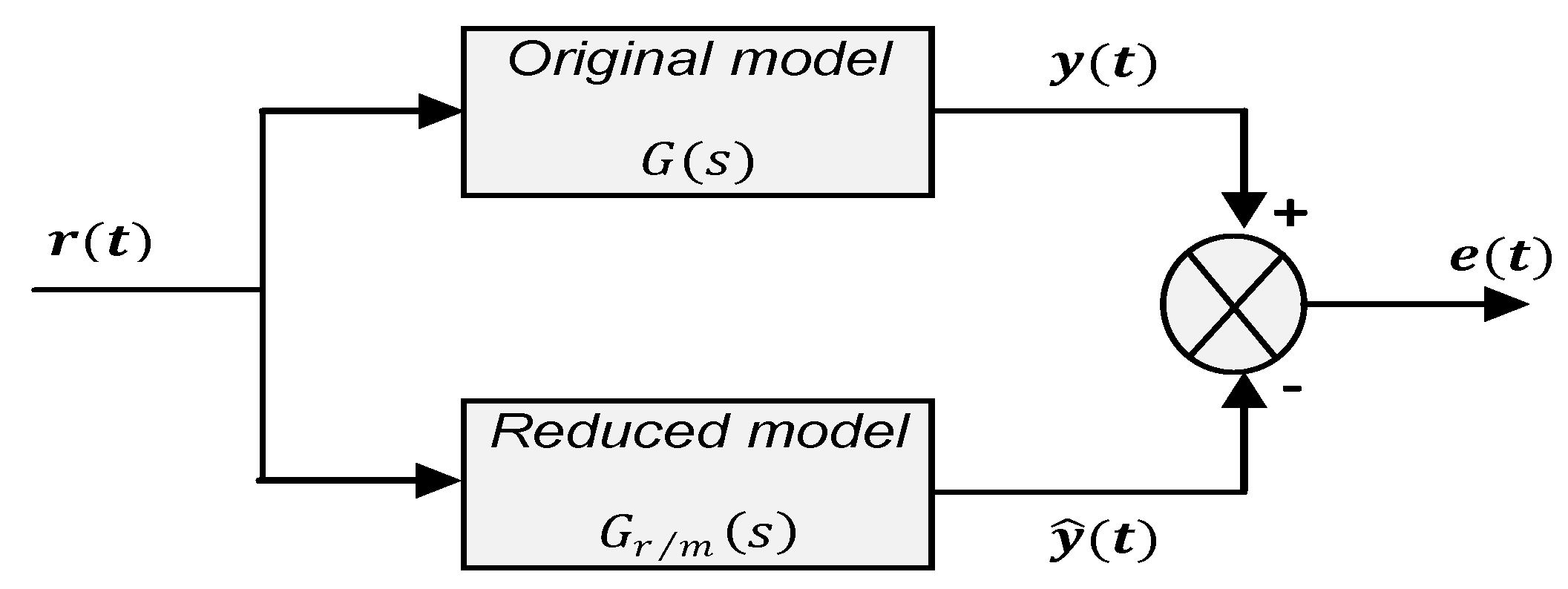
3.4. Sub-Optimal Reduction Algorithm
- Choose an initial simplified model .
- Get an error function
- Use the Powell optimization method [55] to iterate a step to obtain a better estimation of the model.
- Set , go to step 2 until an optimal LOA model is obtained.
4. Results and Discussion
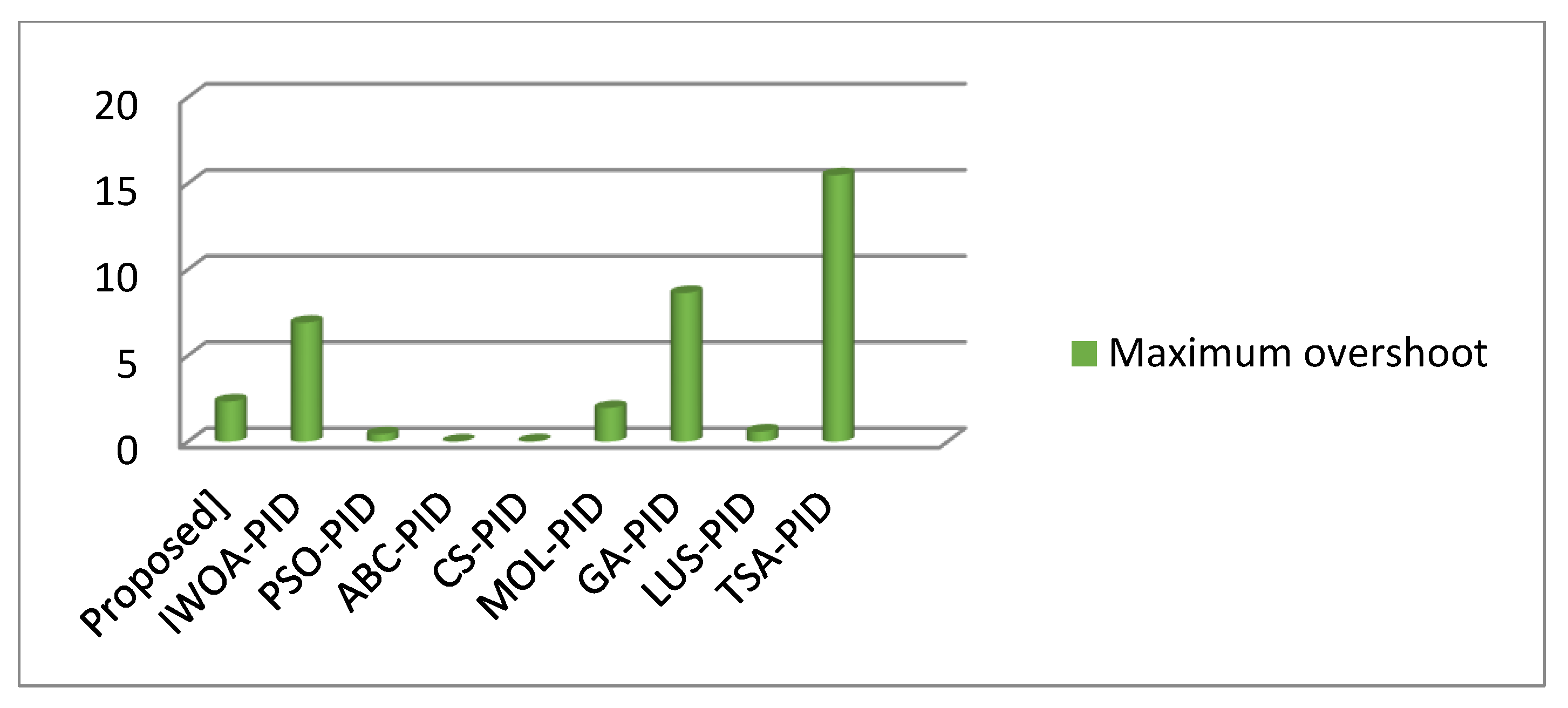
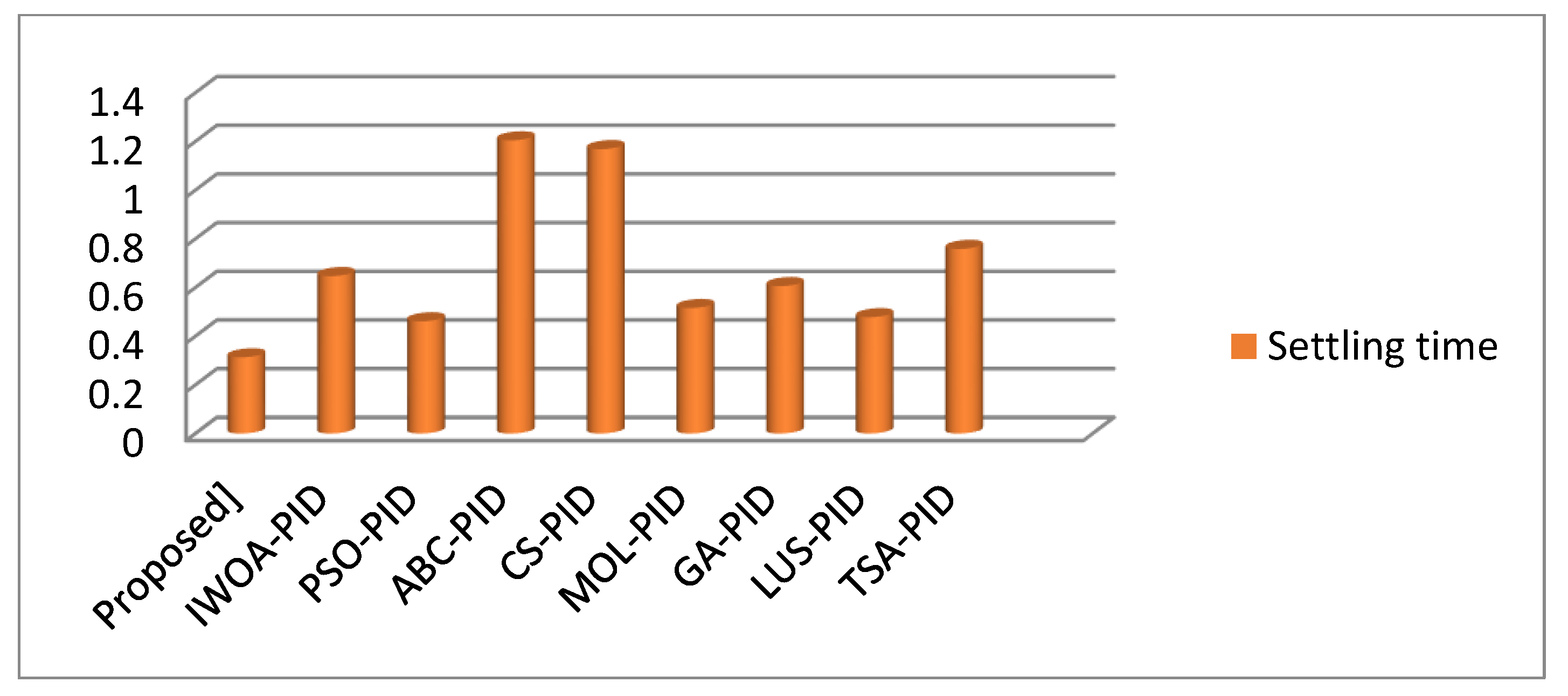
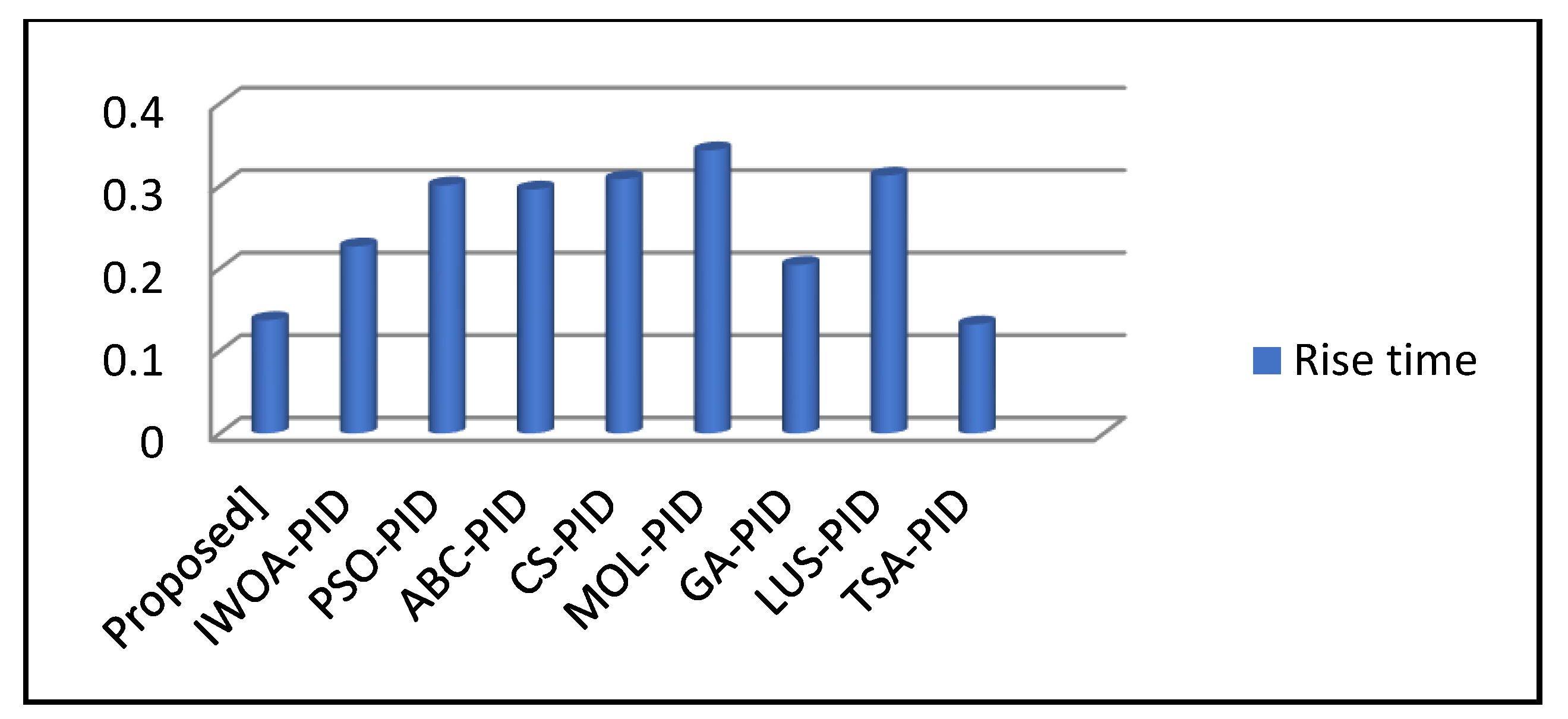
4.1. Transient Response Analysis Comparison
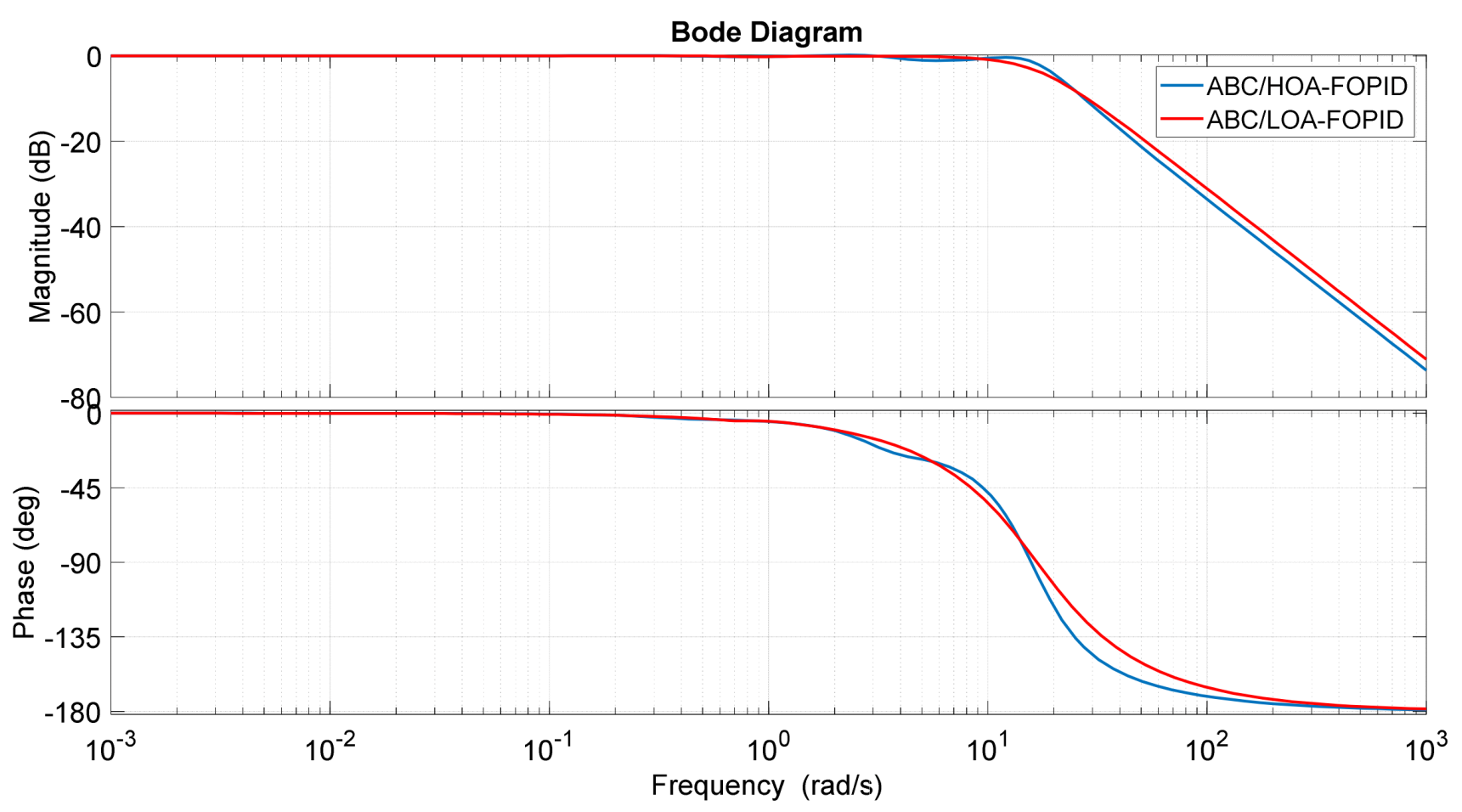
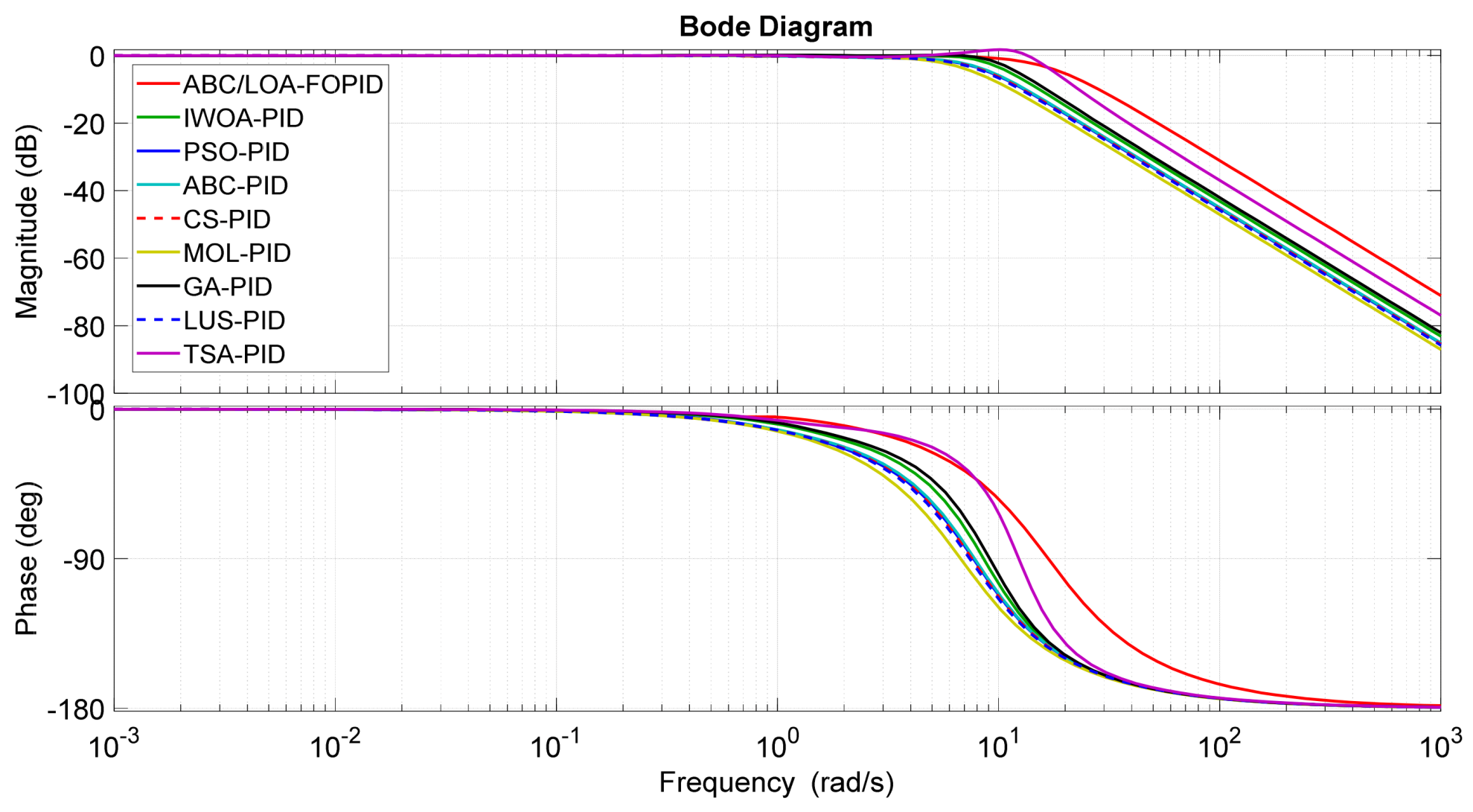
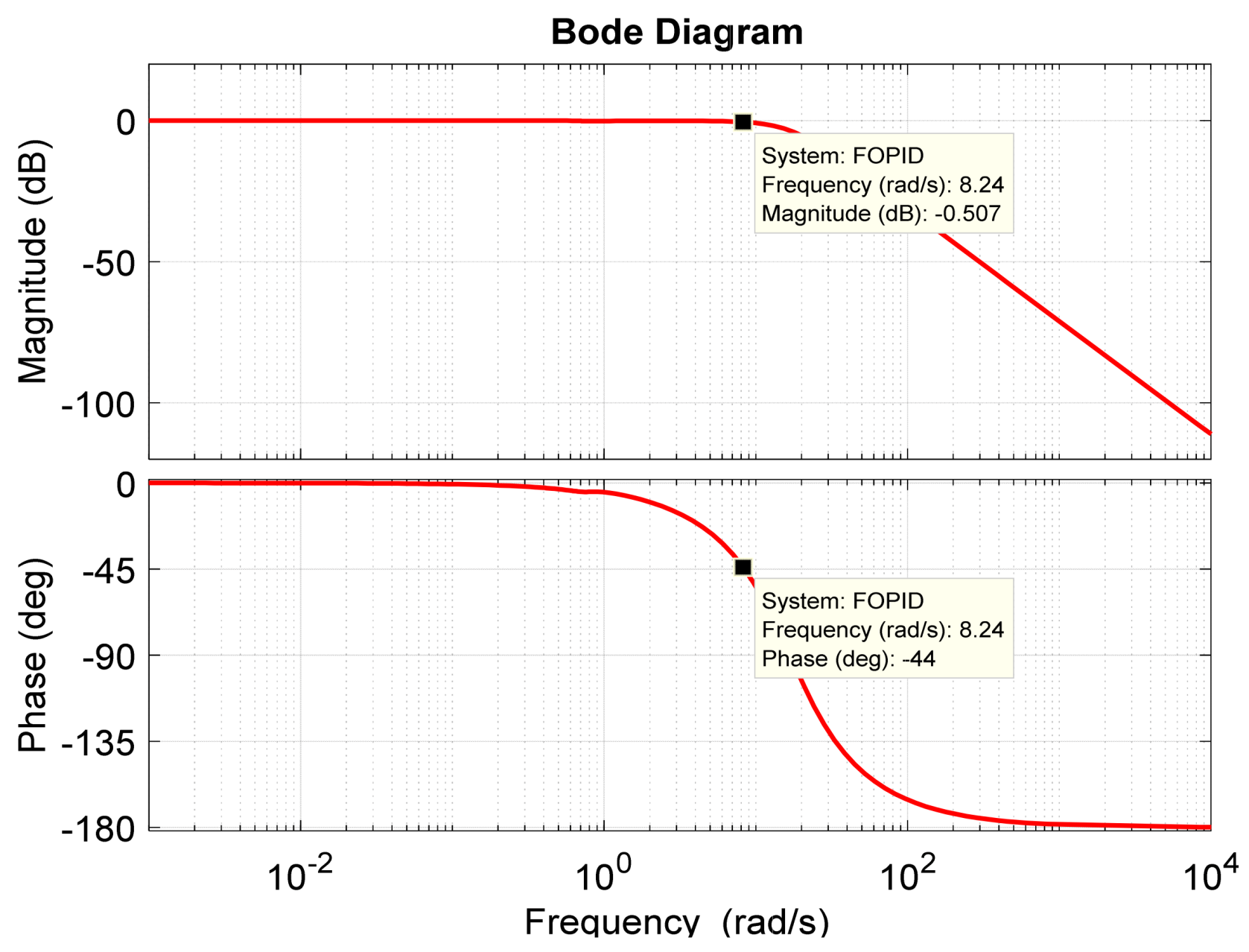
4.2. Comparison of Frequency Domain Analyses
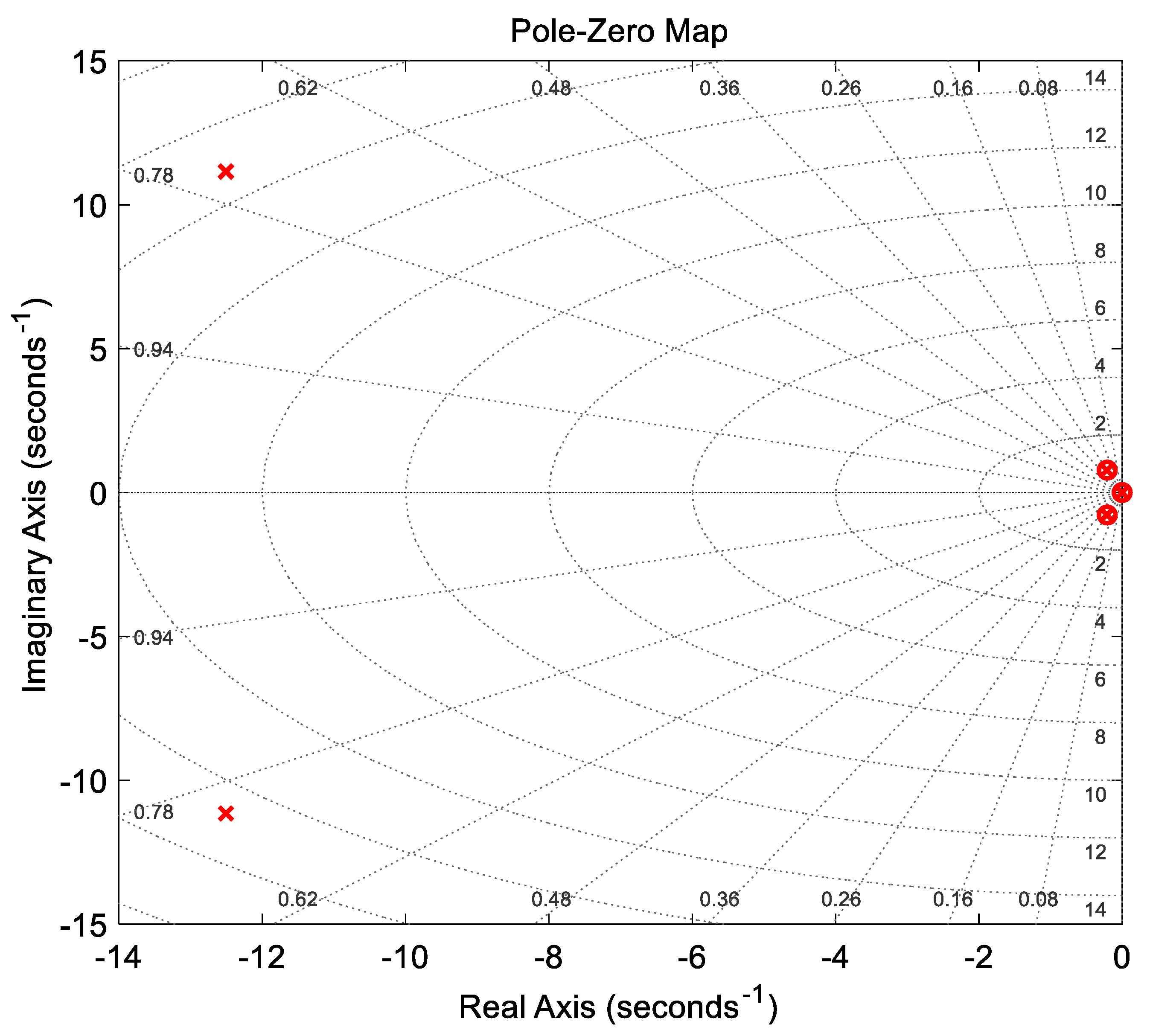
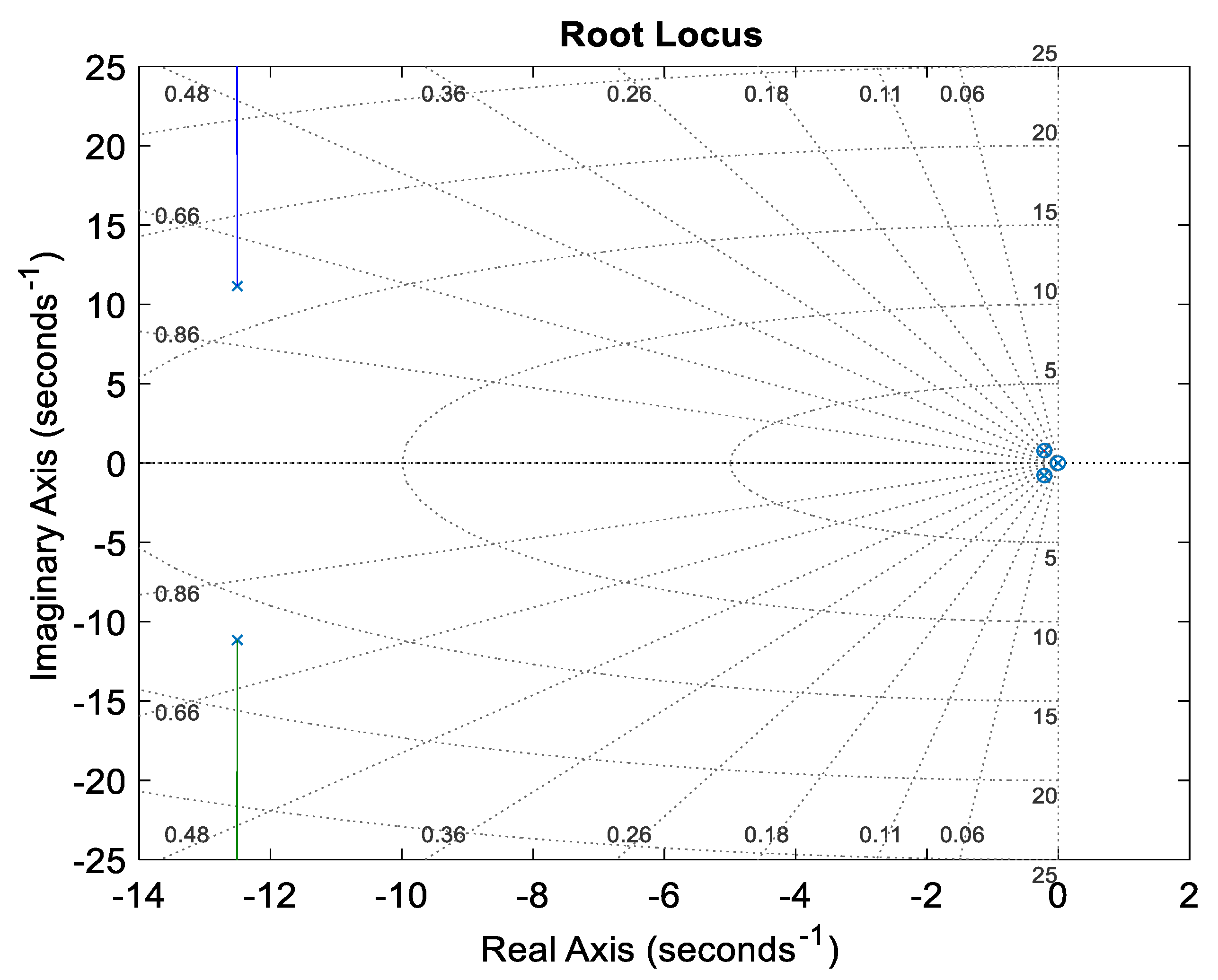
4.3. Stability Assessment
4.4. Noise Attenuation
4.5. Analysis of Robustness Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hasanien, H.M. Design optimization of PID controller in automatic voltage regulator system using Taguchi combined genetic algorithm method. IEEE Syst. J. 2012, 7, 825–831. [Google Scholar] [CrossRef]
- Ćalasan, M.; Micev, M.; Radulović, M.; Zobaa, A.F.; Hasanien, H.M.; Abdel Aleem, S.H. Optimal PID Controllers for AVR System Considering Excitation Voltage Limitations Using Hybrid Equilibrium Optimizer. Machines 2021, 9, 265. [Google Scholar] [CrossRef]
- Kiran, H.U.; Tiwari, S.K. Hybrid BF-PSO Algorithm for Automatic Voltage Regulator System. In Proceedings of the International Conference on Innovative Computing and Communications, Delhi, India, 20–21 February 2021; Springer: Singapore, 2021; pp. 145–153. [Google Scholar]
- Kang, H.I.; Kwon, M.W.; Bae, H.G. Comparative Study of PID Controller Designs Using Particle Swarm Optimizations for Automatic Voltage Regulators. In Proceedings of the 2011 International Conference on Information Science and Applications, Jeju Island, Republic of Korea, 26–29 April 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–5. [Google Scholar]
- Chatterjee, S.; Mukherjee, V. PID controller for automatic voltage regulator using teaching–learning based optimization technique. Int. J. Electr. Power Energy Syst. 2016, 77, 418–429. [Google Scholar] [CrossRef]
- Solanki, A.; Rathore, A. Optimization of PIDA controller for AVR System Using GSA. In Proceedings of the 2018 IEEE 3rd International Conference on Computing, Communication and Security (ICCCS), Kathmandu, Nepal, 25–27 October 2018; pp. 236–239. [Google Scholar]
- Micev, M.; Ćalasan, M.; Oliva, D. Fractional order PID controller design for an AVR system using Chaotic Yellow Saddle Goatfish Algorithm. Mathematics 2020, 8, 1182. [Google Scholar] [CrossRef]
- Dastranj, M.R.; Rouhani, M.; Hajipoor, A. Design of optimal fractional order PID controller using PSO algorithm. Int. J. Comput. Theory Eng. 2012, 4, 429. [Google Scholar] [CrossRef]
- Sun, J.; Wu, L.; Yang, X. Optimal Fractional Order PID Controller Design for AVR System Based on Improved Genetic Algorithm. In Proceedings of the 2020 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 25–27 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 351–355. [Google Scholar]
- Micev, M.; Calasan, M.; Radulovic, M. Optimal design of real PID plus second-order derivative controller for AVR system. In Proceedings of the 2021 25th International Conference on Information Technology (IT), Szczecin, Poland, 16–20 February 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–4. [Google Scholar]
- Bhullar, A.K.; Kaur, R.; Sondhi, S. Modified neural network algorithm based robust design of AVR system using the Kharitonov theorem. Int. J. Intell. Syst. 2022, 37, 1339–1370. [Google Scholar] [CrossRef]
- Zwe-Lee, G. A particle swarm optimization approach for optimum design of PID controller in AVR system. IEEE Trans. Energy Convers. 2004, 19, 384e391. [Google Scholar]
- Panda, M.K.; Pillai, G.N.; Kumar, V. Design of an interval type-2 fuzzy logic controller for automatic voltage regulator system. Electr. Power Compon. Syst. 2011, 40, 219–235. [Google Scholar] [CrossRef]
- Kalyan, C.H.; Rao, G.S. Impact of communication time delays on combined LFC and AVR of a multi-area hybrid system with IPFC-RFBs coordinated control strategy. Prot. Control. Mod. Power Syst. 2021, 6, 1–20. [Google Scholar] [CrossRef]
- Gozde, H.; Taplamacioglu, M.C. Comparative performance analysis of artificial bee colony algorithm for automatic voltage regulator (AVR) system. J. Frankl. Inst. 2011, 348, 1927–1946. [Google Scholar] [CrossRef]
- Sahib, M. A novel optimal PID plus second order derivative controller for AVR system. Eng. Sci. Technol. Int. J. 2014, 18, 1–13. [Google Scholar] [CrossRef]
- Kumar Kuri, R.; Paliwal, D.; Sambariya, D.K. Grey Wolf Optimization Algorithm based PID controller design for AVR Power system. In Proceedings of the 2019 2nd International Conference on Power Energy Environment and Intelligent Control (PEEIC), Toronto, ON, Canada, 2–4 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 233–237. [Google Scholar]
- Mosaad, A.M.; Attia, M.A.; Abdelaziz, A.Y. Comparative performance analysis of AVR controllers using modern optimization techniques. Electr. Power Compon. Syst. 2018, 46, 2117–2130. [Google Scholar] [CrossRef]
- Çelik, E. Incorporation of stochastic fractal search algorithm into efficient design of PID controller for an automatic voltage regulator system. Neural Comput. Appl. 2018, 30, 1991–2002. [Google Scholar] [CrossRef]
- Mosaad, A.M.; Attia, M.A.; Abdelaziz, A.Y. Whale optimization algorithm to tune PID and PIDA controllers on AVR system. Ain Shams Eng. J. 2019, 10, 755–767. [Google Scholar] [CrossRef]
- Habib, S.; Abbas, G.; Jumani, T.A.; Bhutto, A.A.; Mirsaeidi, S.; Ahmed, E.M. Improved Whale Optimization Algorithm for Transient Response, Robustness, and Stability Enhancement of an Automatic Voltage Regulator System. Energies 2022, 15, 5037. [Google Scholar] [CrossRef]
- Hekimoğlu, B. Sine-cosine algorithm-based optimization for automatic voltage regulator system. Trans. Inst. Meas. Control. 2019, 41, 1761–1771. [Google Scholar] [CrossRef]
- Köse, E. Optimal control of AVR system with tree seed algorithm-based PID controller. IEEE Access 2020, 8, 89457–89467. [Google Scholar] [CrossRef]
- Jarrah, A.; Zaitoun, M. Optimized implementation of AVR system using particle swarm optimization. Int. J. Comput. Sci. Eng. 2022, 25, 272–284. [Google Scholar]
- Ekinci, S.; Hekimoğlu, B. Improved kidney-inspired algorithm approach for tuning of PID controller in AVR system. IEEE Access 2019, 7, 39935–39947. [Google Scholar] [CrossRef]
- Bingul, Z.; Karahan, O. A novel performance criterion approach to optimum design of PID controller using cuckoo search algorithm for AVR system. J. Frankl. Inst. 2018, 355, 5534–5559. [Google Scholar] [CrossRef]
- Dogruer, T.; Can, M.S. Design and Robustness Analysis of Fuzzy PID Controller for Automatic Voltage Regulator System Using Genetic Algorithm. Trans. Inst. Meas. Control 2022, 44, 1862–1873. [Google Scholar] [CrossRef]
- Panda, S.; Sahu, B.K.; Mohanty, P.K. Design and performance analysis of PID controller for an automatic voltage regulator system using simplified particle swarm optimization. J. Frankl. Inst. 2012, 349, 2609–2625. [Google Scholar] [CrossRef]
- Bhullar, A.K.; Kaur, R.; Sondhi, S. Enhanced crow search algorithm for AVR optimization. Soft Comput. 2020, 24, 11957–11987. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, J.; Yang, X.; Ling, Y. Optimization of PID controller based on water wave optimization for an automatic voltage regulator system. Inf. Technol. Control. 2019, 48, 160–171. [Google Scholar] [CrossRef]
- Mohanty, P.K.; Sahu, B.K.; Panda, S. Tuning and assessment of proportional–integral–derivative controller for an automatic voltage regulator system employing local unimodal sampling algorithm. Electr. Power Compon. Syst. 2014, 42, 959–969. [Google Scholar] [CrossRef]
- Rao, G.S.; Kalyan CN, S.; Kumar, C.V.; Goud, B.S.; Kumar, M.K.; Reddy, C.R. Automatic Voltage Regulator Using Global Optimization Algorithms Based on Traditional Controller. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Blondin, M.J.; Sanchis, J.; Sicard, P.; Herrero, J.M. New optimal controller tuning method for an AVR system using a simplified Ant Colony Optimization with a new constrained Nelder–Mead algorithm. Appl. Soft Comput. J. 2018, 62, 216–229. [Google Scholar] [CrossRef]
- Naga Sai Kalyan, C.H.; Sambasiva Rao, G. Frequency and voltage stabilisation in combined load frequency control and automatic voltage regulation of multiarea system with hybrid generation utilities by AC/DC links. Int. J. Sustain. Energy 2020, 39, 1009–1029. [Google Scholar] [CrossRef]
- Mok, R.; Ahmad, M.A. Fast and optimal tuning of fractional order PID controller for AVR system based on memorizable-smoothed functional algorithm. Eng. Sci. Technol. Int. J. 2022, 35, 101264. [Google Scholar] [CrossRef]
- Odili, J.B.; Mohmad Kahar, M.N.; Noraziah, A. Parameters-tuning of PID controller for automatic voltage regulators using the African buffalo optimization. PLoS ONE 2017, 12, e0175901. [Google Scholar] [CrossRef]
- Zhou, G.; Li, J.; Tang, Z.; Luo, Q.; Zhou, Y. An improved spotted hyena optimizer for PID parameters in an AVR system. Math. Biosci. Eng. 2020, 17, 3767–3783. [Google Scholar] [CrossRef]
- Pachauri, N. Water cycle algorithm-based PID controller for AVR. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2020, 39, 551–567. [Google Scholar] [CrossRef]
- Sikander, A.; Thakur, P.; Bansal, R.C.; Rajasekar, S. A novel technique to design cuckoo search based FOPID controller for AVR in power systems. Comput. Electr. Eng. 2018, 70, 261–274. [Google Scholar] [CrossRef]
- Idir, A.; Kidouche, M.; Bensafia, Y.; Khettab, K.; Tadjer, S.A. Speed control of DC motor using PID and FOPID controllers based on differential evolution and PSO. Int. J. Intell. Eng. Syst. 2018, 20, 21. [Google Scholar] [CrossRef]
- Khan, I.A.; Alghamdi, A.S.; Jumani, T.A.; Alamgir, A.; Awan, A.B.; Khidrani, A. Salp swarm optimization algorithm-based fractional order PID controller for dynamic response and stability enhancement of an automatic voltage regulator system. Electronics 2019, 8, 1472. [Google Scholar] [CrossRef]
- Idir, A.; Khettab, K.; Bensafia, Y. Design of an Optimally Tuned Fractionalized PID Controller for DC Motor Speed Control Via a Henry Gas Solubility Optimization Algorithm. Int. J. Intell. Eng. Syst. 2022, 15, 59–70. [Google Scholar]
- Verma, S.K.; Devarapalli, R. Fractional order PIλDμ controller with optimal parameters using Modified Grey Wolf Optimizer for AVR system. Arch. Control. Sci. 2022, 32, 429–450. [Google Scholar]
- Idir, A.; Canale, L.; Tadjer, S.A.; Chekired, F. High Order Approximation of Fractional PID Controller based on Grey Wolf Optimization for DC Motor. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/ICPS Europe), Prague, Czech Republic, 28 June–1 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- dos Santos Coelho, L. Tuning of PID controller for an automatic regulator voltage system using chaotic optimization approach. Chaos Solitons Fractals 2009, 39, 1504–1514. [Google Scholar] [CrossRef]
- Bensafia, Y.; Khettab, K.; Idir, A. A Novel Fractionalized PID controller Using The Sub-optimal Approximation of FOTF. Alger. J. Signals Syst. 2022, 7, 21–26. [Google Scholar] [CrossRef]
- Garrappa, R. A Grünwald-Letnikov scheme for fractional operators of Havriliak-Negami type. Recent Adv. Appl. Model. Simul. 2014, 34, 70–76. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science Business Media: Berlin, Germany, 2010. [Google Scholar]
- Bensafia, Y.; Khettab, K.; Idir, A. An Improved Robust Fractionalized PID Controller for a Class of Fractional-Order Systems with Measurement Noise. Int. J. Intell. Eng. Syst. 2018, 11, 200–207. [Google Scholar] [CrossRef]
- Busłowicz, M. Stability analysis of continuous-time linear systems consisting of n subsystems with different fractional orders. Bull. Pol. Acad. Sciences. Tech. Sci. 2012, 60, 279–284. [Google Scholar] [CrossRef]
- Radwan, A.G.; Soliman, A.M.; Elwakil, A.S.; Sedeek, A. On the stability of linear systems with fractional-order elements. Chaos Solitons Fractals 2009, 40, 2317–2328. [Google Scholar] [CrossRef]
- Zhang, D.L.; Tang, Y.-G.; Guan, X.-P. Optimum design of fractional order PID controller for an AVR system using an improved artificial bee colony algorithm. Acta Autom. Sin. 2014, 40, 973–979. [Google Scholar] [CrossRef]
- Du, H.; Liu, P.; Cui, Q.; Ma, X.; Wang, H. PID Controller Parameter Optimized by Reformative Artificial Bee Colony Algorithm. J. Math. 2022, 2022, 3826702. [Google Scholar] [CrossRef]
- Xue, D.; Chen, Y.Q. Sub-Optimum H2 rational approximations to fractional-order linear systems. In Proceedings of the ASME 2005 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Long Beach, CA, USA, 24–28 September 2005; pp. 1–10. [Google Scholar]
- Xue, D.; Atherton, D.P. A suboptimal reduction algorithm for linear systems with a time delay. Int. J. Control. 1994, 60, 181–196. [Google Scholar] [CrossRef]
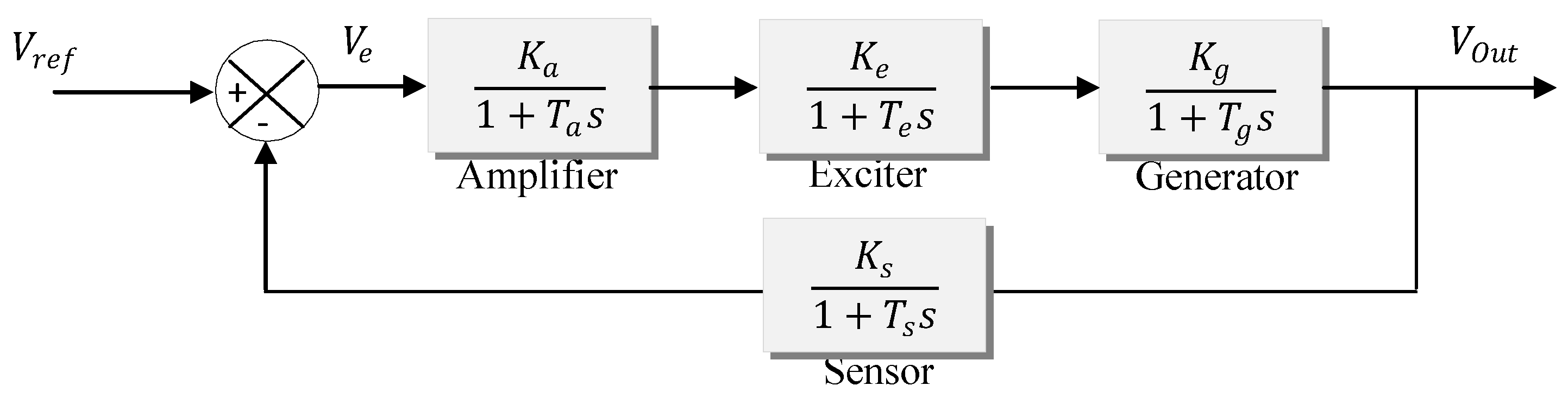


| Component of AVR System | Transfer Function | Gain Range | Time Constant Range [s] |
|---|---|---|---|
| Amplifier | |||
| Exciter | |||
| Generator | |||
| Sensor |
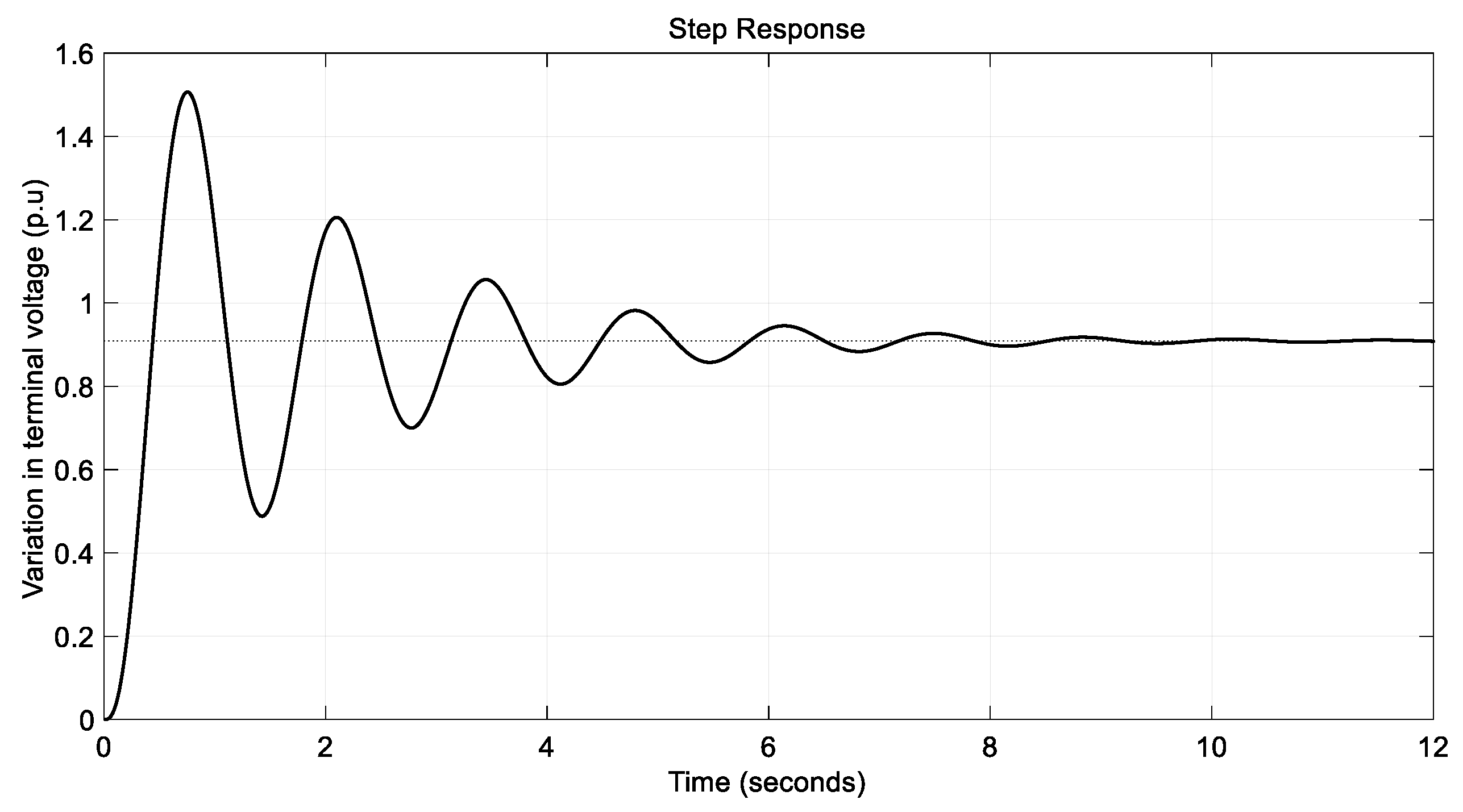
| Controller Type | Mp [%] | ts [s] | tr [s] |
|---|---|---|---|
| AVR without controller | 65.7226 | 6.9865 | 0.2607 |
| Parameter | Value |
|---|---|
| Population size | |
| Maximum cycle number | |
| Dimension for optimization problem | 5 |
| Controller Type | Kp | Ki | Kd | λ | μ |
|---|---|---|---|---|---|
| IABC/LOA-FOPID [Proposed] | 1.9605 | 0.4922 | 0.2355 | 1.4331 | 1.5508 |
| IWOA-PID [21] | 0.8167 | 0.6898 | 0.2799 | 1 | 1 |
| PSO-PID [12] | 0.6254 | 0.4577 | 0.2187 | 1 | 1 |
| ABC-PID [15] | 0.6352 | 0.4235 | 0.2241 | 1 | 1 |
| CS-PID [26] | 0.6198 | 0.4165 | 0.2126 | 1 | 1 |
| MOL-PID [28] | 0.5857 | 0.4189 | 0.1772 | 1 | 1 |
| GA-PID [12] | 0.8851 | 0.7984 | 0.3158 | 1 | 1 |
| LUS-PID [31] | 0.6190 | 0.4222 | 0.2058 | 1 | 1 |
| TSA [23] | 1.1281 | 0.9567 | 0.5671 | 1 | 1 |
| Controller Type | Maximum Overshoot Mp [%] | Settling Time ts [s] | Rise Time tr [s] | IAE |
|---|---|---|---|---|
| IABC/LOA-FOPID [Proposed] | 2.3323 | 0.3129 | 0.1373 | 0.109 |
| IWOA-PID [21] | 6.9064 | 0.6466 | 0.2266 | 0.3150 |
| PSO-PID [12] | 0.4349 | 0.4609 | 0.3007 | 0.2917 |
| ABC-PID [15] | 0.0081 | 1.2041 | 0.2957 | 0.2892 |
| CS-PID [26] | 0.0198 | 1.1681 | 0.3082 | 0.2916 |
| MOL-PID [28] | 1.9547 | 0.5154 | 0.3432 | 0.3086 |
| GA-PID [12] | 8.6338 | 0.6055 | 0.2042 | 0.3048 |
| LUS-PID [31] | 0.5896 | 0.4778 | 0.3125 | 0.2930 |
| TSA-PID [23] | 15.4763 | 0.7582 | 0.1321 | 0.3553 |
| Controller Type | Gain Margin Gm [db] | Phase Margin φm [°] | Bandwidth Bw [Hz] |
|---|---|---|---|
| ABC/LOA-FOPID [Proposed] | Inf | 178.7980 | 15.7280 |
| IWOA-PID [21] | Inf | 161.6094 | 9.6571 |
| PSO-PID [12] | Inf | 173.8067 | 7.5015 |
| ABC-PID [15] | Inf | 180 | 7.6998 |
| CS-PID [26] | Inf | 180 | 7.3393 |
| MOL-PID [28] | Inf | 180 | 6.3391 |
| GA-PID [12] | Inf | 116.3886 | 10.6594 |
| LUS-PID [31] | Inf | 180 | 7.1673 |
| TSA-PID [23] | Inf | 77.3967 | 16.2326 |
| PID Tuning Methods | Closed-Loop Poles | Damping Ratio | Frequency [rad/s] | Time Constant [s] |
|---|---|---|---|---|
| ABC/LOA-FOPID [Proposed] | −2.49 × 10−3 | 1.00 | 2.49 × 10−3 | 4.01 × 10+2 |
| −2.16 × 10−1 + 7.75 × 10−1i | 2.68 × 10−1 | 8.05 × 10−1 | 4.64 | |
| −2.16 × 10−1 + 7.75 × 10−1i | 2.68 × 10−1 | 8.05 × 10−1 | 4.64 | |
| −1.25 × 10+1 + 1.12 × 10+1i | 7.46 × 10−1 | 1.68 × 10+1 | 8.00 × 10−2 | |
| −1.25 × 10+1 + 1.12 × 10+1i | 7.46 × 10−1 | 1.68 × 10+1 | 8.00 × 10−2 | |
| IWOA-PID [21] | −1.01 × 10+2 | 1.00 | 1.01 × 10+2 | 9.92 × 10−3 |
| −1.35 + 6.77 × 10−1i | 8.93 × 10−1 | 1.51 | 7.43 × 10−1 | |
| −1.35 + 6.77 × 10−1i | 8.93 × 10−1 | 1.51 | 7.43 × 10−1 | |
| −5.02 + 7.09i | 5.78 × 10−1 | 8.68 | 1.99 × 10−1 | |
| −5.02 + 7.09i | 5.78 × 10−1 | 8.68 | 1.99 × 10−1 | |
| PSO-PID [12] | −1.01 × 10−2 | 1.00 | 1.01 × 10+2 | 9.94 × 10−3 |
| −1.30 + 3.92 × 10−1i | 9.58 × 10−1 | 1.36 | 7.67 × 10−1 | |
| −1.30 + 3.92 × 10−1i | 9.58 × 10−1 | 1.36 | 7.67 × 10−1 | |
| −5.14 + 5.91i | 6.56 × 10−1 | 7.84 | 1.94 × 10−1 | |
| −5.14 + 5.91i | 6.56 × 10−1 | 7.84 | 1.94 × 10−1 | |
| ABC-PID [15] | −1.01 × 10+2 | 1.00 | 1.01 × 10+2 | 9.94 × 10−3 |
| −1.12 | 1.00 | 1.12 | 8.97 × 10−1 | |
| −1.50 | 1.00 | 1.50 | 6.66 × 10−1 | |
| −5.13 + 6.04i | 6.47 × 10−1 | 7.93 | 1.95 × 10−1 | |
| −5.13 + 6.04i | 6.47 × 10−1 | 7.93 | 1.95 × 10−1 | |
| CS-PID [26] | −1.01 × 10+2 | 1.00 | 1.01 × 10+2 | 9.94 × 10−3 |
| −1.07 | 1.00 | 1.07 | 9.31 × 10−1 | |
| −1.62 | 1.00 | 1.62 | 6.15 × 10−1 | |
| −5.11 + 5.76i | 6.63 × 10−1 | 7.70 | 1.96 × 10−1 | |
| −5.11 + 5.76i | 6.63 × 10−1 | 7.70 | 1.96 × 10−1 | |
| MOL-PID [28] | −1.00 × 10+2 | 1.00 | 1.00 × 10+2 | 9.95 × 10-3 |
| −1.06 | 1.00 | 1.06 | 9.41 × 10−1 | |
| −2.11 | 1.00 | 2.11 | 4.74 × 10−1 | |
| −4.92 + 4.72i | 7.21 × 10−1 | 6.82 | 2.03 × 10−1 | |
| −4.92 + 4.72i | 7.21 × 10−1 | 6.82 | 2.03 × 10−1 | |
| GA-PID [12] | −1.00 × 10+2 | 1.00 | 1.01 × 10+2 | 9.91 × 10−3 |
| −1.29 + 8.20 × 10−1i | 8.43 × 10−1 | 1.52 | 7.78 × 10−1 | |
| −1.29 + 8.20 × 10−1i | 8.43 × 10−1 | 1.52 | 7.78 × 10−1 | |
| −5.03 + 7.73i | 5.45 × 10−1 | 9.23 | 1.99 × 10−1 | |
| −5.03 + 7.73i | 5.45 × 10−1 | 9.23 | 1.99 × 10−1 | |
| LUS-PID [31] | −1.01 × 10+2 | 1.00 | 1.01 × 10+2 | 9.94 × 10−3 |
| −1.06 | 1.00 | 1.06 | 9.40 × 10−1 | |
| −1.74 | 1.00 | 1.74 | 5.75 × 10−1 | |
| −5.06 + 5.57i | 6.73 × 10−1 | 7.53 | 1.97 × 10−1 | |
| −5.06 + 5.57i | 6.73 × 10−1 | 7.53 | 1.97 × 10−1 | |
| TSA-PID [23] | −1.01 × 10+2 | 1.00 | 1.02 × 10+2 | 9.85 × 10−3 |
| −9.26 × 10−1 + 8.22 × 10−1i | 7.48 × 10−1 | 1.24 | 1.08 | |
| −9.26 × 10−1 + 8.22 × 10−1i | 7.48 × 10−1 | 1.24 | 1.08 | |
| −5.05 + 1.13 × 10+1i | 4.07 × 10−1 × 10−1 | 1.24 × 10+1 | 1.98 × 10−1 | |
| −5.05 + 1.13 × 10−1i | 4.07 × 10−1 | 1.24 × 10+1 | 1.98 × 10−1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Idir, A.; Canale, L.; Bensafia, Y.; Khettab, K. Design and Robust Performance Analysis of Low-Order Approximation of Fractional PID Controller Based on an IABC Algorithm for an Automatic Voltage Regulator System. Energies 2022, 15, 8973. https://doi.org/10.3390/en15238973
Idir A, Canale L, Bensafia Y, Khettab K. Design and Robust Performance Analysis of Low-Order Approximation of Fractional PID Controller Based on an IABC Algorithm for an Automatic Voltage Regulator System. Energies. 2022; 15(23):8973. https://doi.org/10.3390/en15238973
Chicago/Turabian StyleIdir, Abdelhakim, Laurent Canale, Yassine Bensafia, and Khatir Khettab. 2022. "Design and Robust Performance Analysis of Low-Order Approximation of Fractional PID Controller Based on an IABC Algorithm for an Automatic Voltage Regulator System" Energies 15, no. 23: 8973. https://doi.org/10.3390/en15238973
APA StyleIdir, A., Canale, L., Bensafia, Y., & Khettab, K. (2022). Design and Robust Performance Analysis of Low-Order Approximation of Fractional PID Controller Based on an IABC Algorithm for an Automatic Voltage Regulator System. Energies, 15(23), 8973. https://doi.org/10.3390/en15238973