1. Introduction
An automated drilling operation requires the analysis of drilling dynamics in real time. Among the drilling dynamics are fluid flow inside the drill string and annulus, drill string dynamics (rotation and axial movement), and drilling bit dynamics. Additionally, the success of a drilling operation is also dependent upon the drilling crew’s understanding of these dynamics during the drilling process. These dynamics, however, have coupled effects to one another, and a thorough perception of drilling problems related to each of these issues requires knowledge about other dynamics occurring at the same time.
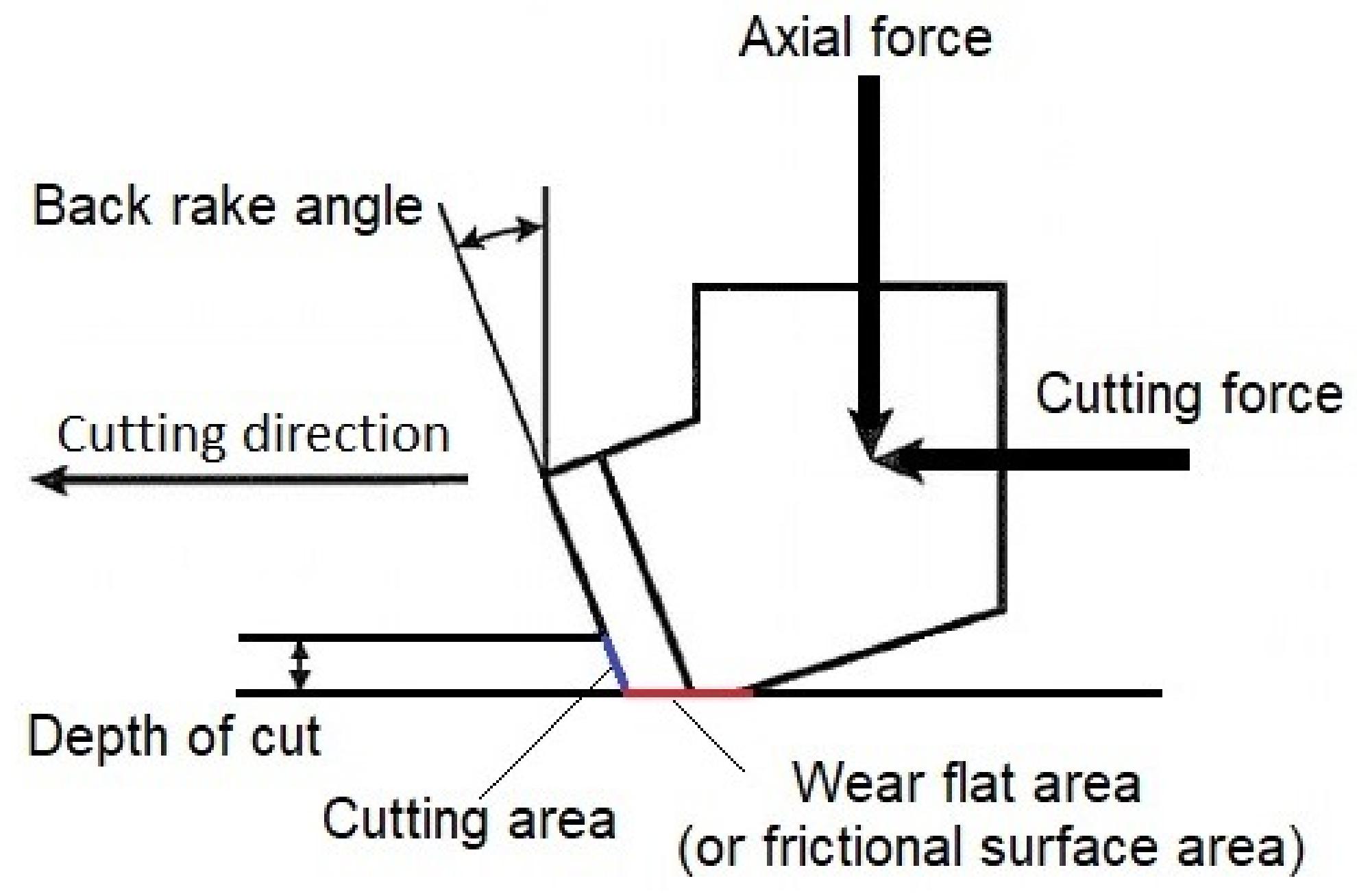
A study of drill string dynamics based on energy consumption during drilling requires an understanding of the processes occurring at drilling bits. In drilling bits, instant interactions at the interface between the cutter and the rock are the governing criterion. Further, in order to evaluate polycrystalline diamond compact bits (PDC) in real time and after drilling, knowledge of the interaction between cutters and rock is necessary. When such studies are conducted, the forces and stresses on the cutter should also be considered, as otherwise, much of the instant and significant local effects of rock cutting would be lost as a result of drilling. Additionally, an accurate bit–rock interaction law should be incorporated into the study of the torsional vibration of drill string. The value and spatial distribution of stresses on cutters, derived from the bit–rock interaction model, depend on the applied drilling parameters (the torque on bit, the weight on bit, rotary speed, and hydraulic forces) and design characteristics of PDC bits (rake angles, bit profile, cutter size, and cutter distribution, wear flat area, and chamfer angle).
It is not possible to model the dynamics of a drilling bit analytically; therefore, studying the processes that occur at the interface between the cutter and rock requires experimental techniques. Compared to full-scale testing, single cutter testing offers greater insight into the dynamics of cutter–rock interaction. It is more versatile to perform a single cutter test rather than a full-scale test if the objective is to accurately control both the downhole and the operating conditions during the cutting test [
1]. There has been a significant amount of research conducted on both the theoretical and experimental aspects of cutter–rock interaction models. In the analysis of PDC bit design in geothermal applications, Glowka [
2,
3] performed an extensive experimental and theoretical study. During the course of the study, it became apparent that the PDC cutter wear rate was strongly influenced by the frictional temperature, the abrasiveness of the rock, and the stresses that developed at the interface between the cutter and the rock. Based on cutter–rock interaction forces, Detournay and Defournay [
4] developed a phenomenological model to study the drilling response of drag bits and verified the model through experiments. The same concept was then modified by Dagrain et al. [
5] to investigate the influence of cutter geometry on cutter forces. In addition to the above research, a complementary model was developed to determine the relationship between the weight on bit, the torque on bit, the penetration rate, and angular velocity of drag bits [
6].
Generally speaking, cutter–rock interaction research is focused on investigating the effects of confining pressure, cutter geometry design parameters (back-rake and side-rake angles), cutting area and wear height, as well as rock drillability.
Confining Pressure. In porous media, one of the most promising factors is the effect of confining pressure or dynamic pore pressure on the forces and stresses distributed within the rock by cutting action. Using the single cutter test, researchers have found that mechanical specific energy increases even at low confining pressures [
7,
8]. Using poroelastic laws, mechanical stresses can affect the pore pressure inside a rock as long as the rock undergoes stress distribution [
8,
9]. It has also been reported that the mechanical properties of the crushed rock in front of cutters may affect the force required to drill through the rock [
10]. Aside from this, when cutters are not cleaned with drilling fluid, friction on the cutter surface dissipates significant energy compared to intrinsic specific energy [
9]. A single cutter and drilling process is further studied under confining pressure, and both of them verified that fluid pressure influences specific energy, stresses, and how the cutting are removed ahead of the bit [
1,
10,
11,
12,
13,
14]. In experiments conducted by Rafatian et al. [
8], a nonlinear relationship was validated at low confining pressures up to 150 psi.
Cutter Geometry Parameters (Back-Rake and Side-Rake Angles). Studies have demonstrated that cutting forces (vertical and cutting forces) are minimal at back-rake angles of around 15° [
7,
11,
15,
16]. In addition, specific energy and back-rake angle exhibit a nonlinear relationship. According to Coudyzer and Richard [
17], an increase in specific energy up to five-fold occurs when the back-rake angle is increased from 10° to 60°. Furthermore, they found that side rake angles up to 45 degrees have only a minor impact on specific energy. At atmospheric and confining pressures, Rajabov et al. [
7] investigated the influence of back and side-rake angles on cutting forces. Their results showed that specific energy increases with an increase in back-rake angle when the confining pressure remains constant. According to the authors, Mechanical specific energy (MSE) is negligible between 0- and 30-degree side-rake angles, but can increase by threefold when the side-rake angle increases from 30 to 60 degrees. However, such values of side-rake angles are not applicable in PDC bits with circular cutters unless non-circular cutters with in-built side-rake angles (similar to cutters introduced in the work by Liu et al. [
18]) are implemented during manufacturing.
Cutting Area and Wear Height. Due to instantaneous changes in the contact area, PDC cutter modeling focuses on the cutter–rock interface and how it affects full-scale bit performance. Besides the normal force from the weight on the bit, the contact area between the cutter and rock is also dependent on the wear condition of the cutter. The effects of the cutting area on applied forces have been extensively investigated experimentally [
2,
3,
11,
16,
19]. Experimental and theoretical studies were conducted to evaluate the lapping effect of the adjacent cutter on the surface area [
20,
21,
22]. In experiments with single cutters, forces were found to be linearly related to the cutting area [
16]; however, in the case of overlapping cutters, the normal and cutting forces are related to the contact area in a power relationship [
15].
To optimize drilling operations and decide when to terminate the PDC bit run, all modeling efforts should include a continuous calculation of the cutter wear state during drilling. This concept can be applied when designing cutter placement during the manufacture of bits by developing a reliable cutter wear model [
23,
24]. Studies of blunt and new cutters have highlighted the importance of changes in the geometry of cutters on the force state. A comprehensive mathematical representation of the relationship between frictional surface area and force distribution has been provided by Detournay et al. [
4,
6,
14]. In the course of cutter wear, frictional contact develops beneath cutters and dominates force distribution on cutters [
1,
6,
25,
26,
27].
Rock Drillability. During drilling operations, rock mechanical properties cannot be controlled, so all design parameters and drilling parameters should be selected to overcome varying rock drillability. In drilling, the drillability of rock changes as a result of changes in the lithology, porosity, permeability, compaction, and cementation material of the rock. In spite of the fact that there has been only limited research conducted on rock drillability, almost all of the previous studies mentioned here have conducted experimental and analytical studies of different types of rock.
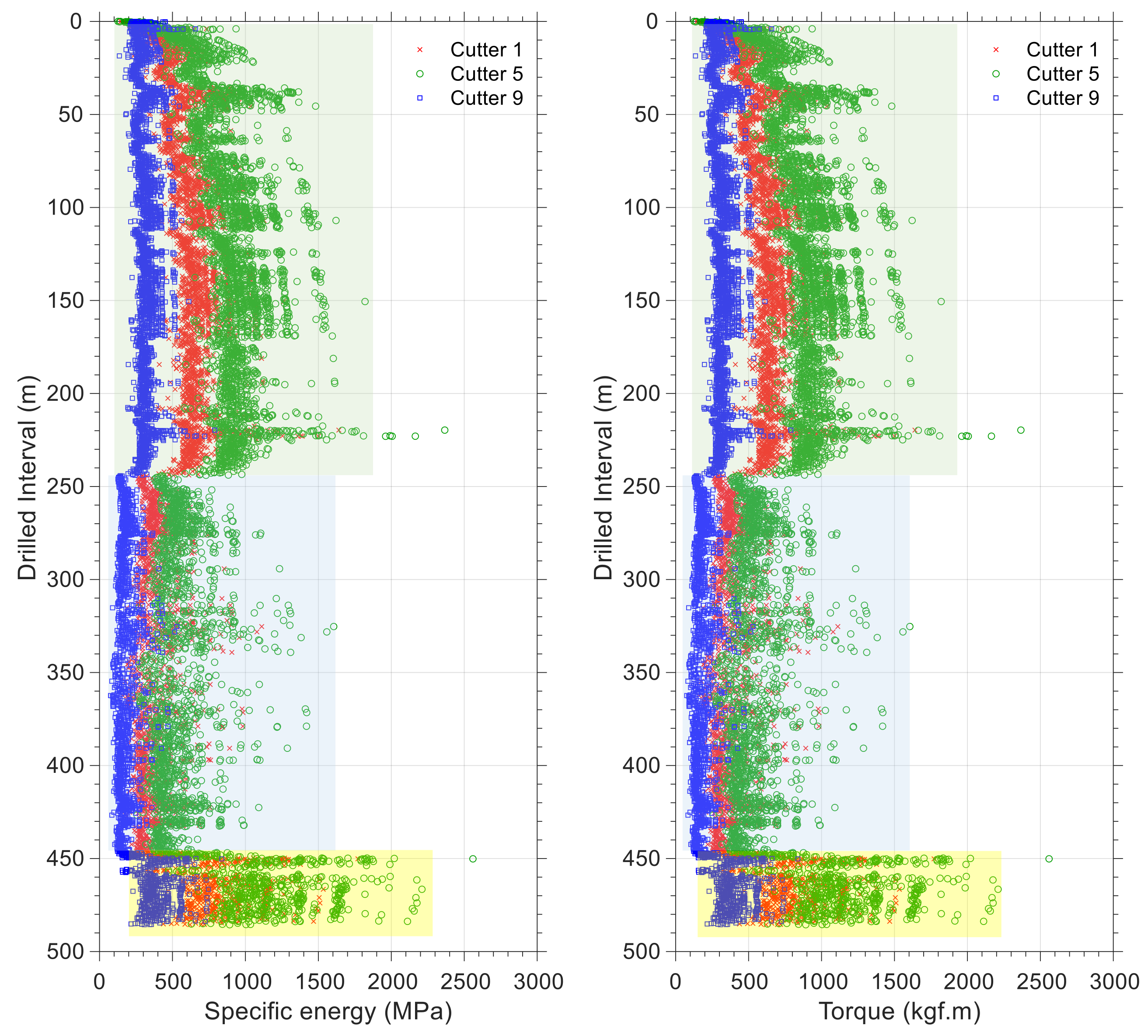
Table 1 provides a summary of rock properties (such as friction angle, shear stress, and uniaxial and confined compressive stress) utilized in this study. A dash indicates that no data exist for the rock referred to in the cited reference.
As a result of experiments conducted on three rock types, namely Carthage limestone, Berea sandstone, and Catoosa shale, Sinor and Warren [
28] developed a drag bit wear model. The study by Wang et al. [
16] examined four different rock types (shale, marble, granite, and limestone) and established drillability ranges between 5.0 and 7.0. In this study, the effect of rock drillability is acknowledged by parameter
K [
15,
16] and plugged in the cutter force formulations. When downhole measurements of weight on bit and torque on bit are provided by the enhanced measurement system (EMS), the algorithm developed in this study could be employed to estimate rock drillability in real time (as an indicator of change in lithology). Moreover, in post-drilling analysis, the results of the estimation of rock drillability could be compared to techniques that determine the compressive strength of rock or classify rock types using wireline logging data [
29,
30,
31].
This literature review indicates that parameters such as back-rake angle, contact area, cutter worn height, frictional contact area, rock drillability, and differential pressure contribute to cutter–rock interaction performance; however, cutting speed and side-rake angle are considered to have negligible effects [
32].
As our knowledge and expertise develop, PDC bits have become increasingly useful in optimizing drilling operations by optimizing the penetration rates. Due to the fact that they do not contain any moving parts, they are durable, and they are capable of continuing to drill for an extended period of time.
A number of approaches can be used to optimize drilling operations by studying the processes at the bit. It should be noted that some models attempt to predict or estimate the rate of penetration in order to determine when to change the bit. In addition, some approaches use a cutter wear equation to estimate the bit status during drilling [
33,
34,
35]. The concept of specific energy (SE) dissipated by a given bit has been utilized to address the variation in penetration rate and to optimize drilling performance [
36,
37,
38]. Due to the complexity of drilling with polycrystalline drilling bits (PDCs), there are no dedicated drilling models, and the majority of analyses conducted to study drilling dynamics are based on the concept of specific energy [
37,
39,
40,
41].
The concept of specific energy introduced by Teale [
42] has been applied to the implementation of PDC bits in two ways. One method of analyzing historical data on bit runs and selecting the optimal bit is by utilizing specific energy as a computational or measurement tool. According to research performed by Hussain [
36], bit run and selection could be based on a cost per foot approach and a specific energy analysis. Second, and most commonly, real-time requirements are analyzed to determine when it is most appropriate to pull out a bit. Waughman et al. [
39] utilized the concept of specific energy and logging while drilling data for the purpose of identifying formation types and tracking status of the bit in comparison to benchmark values recorded when the bit was new. Based on surface recorded data, Dupriest and Koederitz [
37] applied the concept of SE to optimize drilling rates.
Considering the influence of each cutter on the overall performance of the PDC bit is the most advantageous, but also the most complex method of modeling the performance of a PDC bit. It is possible to model and evaluate the efficiency of any PDC bit using a general model of forces acting on cutters, as well as the part of the dynamics of the drill string that is related to the drilling bit. An experimental model was developed by Glowka [
2,
3] based on a single cutter analysis under atmospheric conditions in order to describe the cutting process of PDC bits. The results were analyzed to provide equations relating force on the cutter to rock type, cut depth, and cutter wear. This was followed by implementing a model for evaluating the performance and wear of PDC bits [
3]. Liang et al. [
43] developed an equation to estimate the cutting and normal force on cutters based on experimental data regarding cutting area, rock drillability, back-rake angle, cutter wear height, and arc length coefficient.
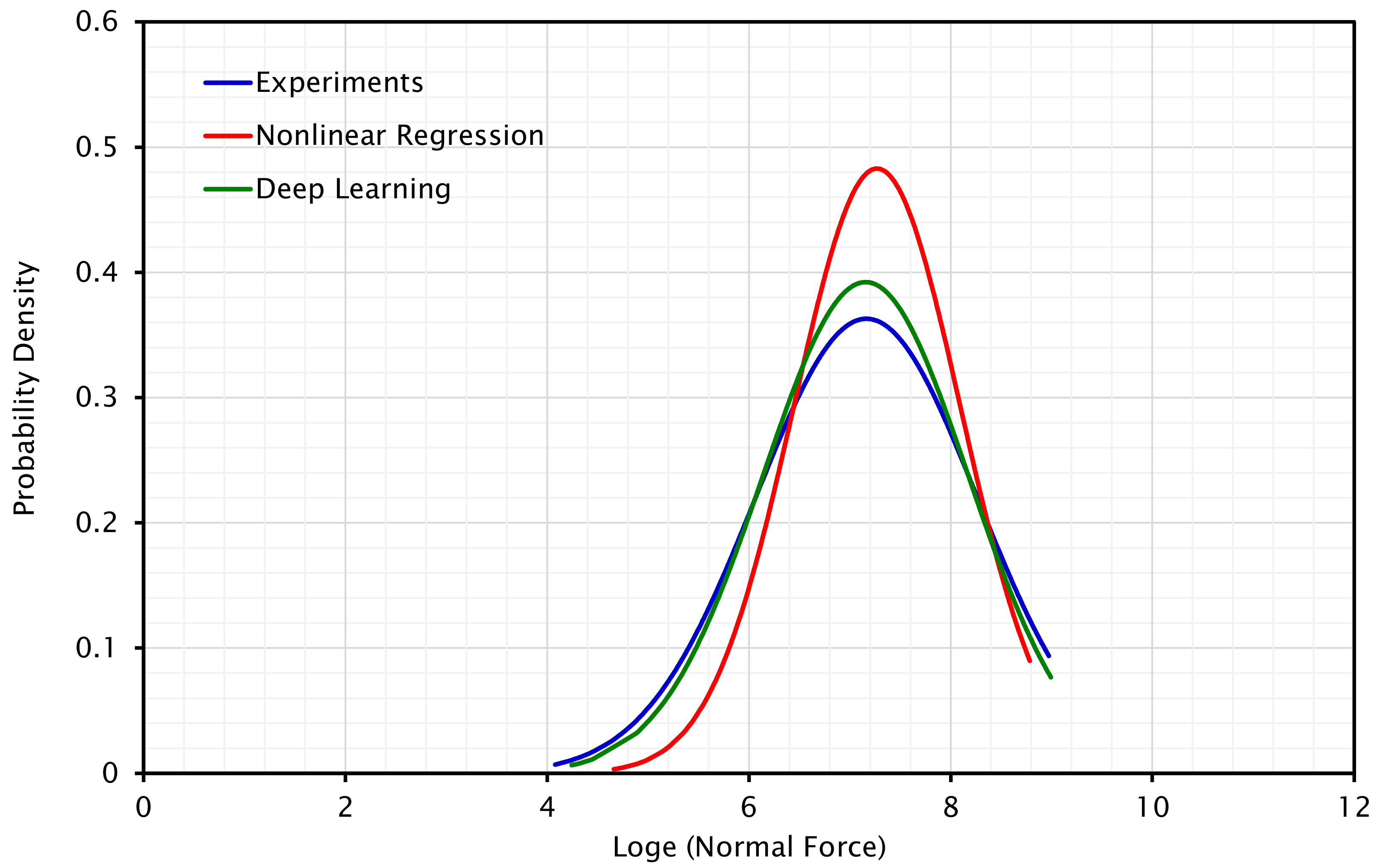
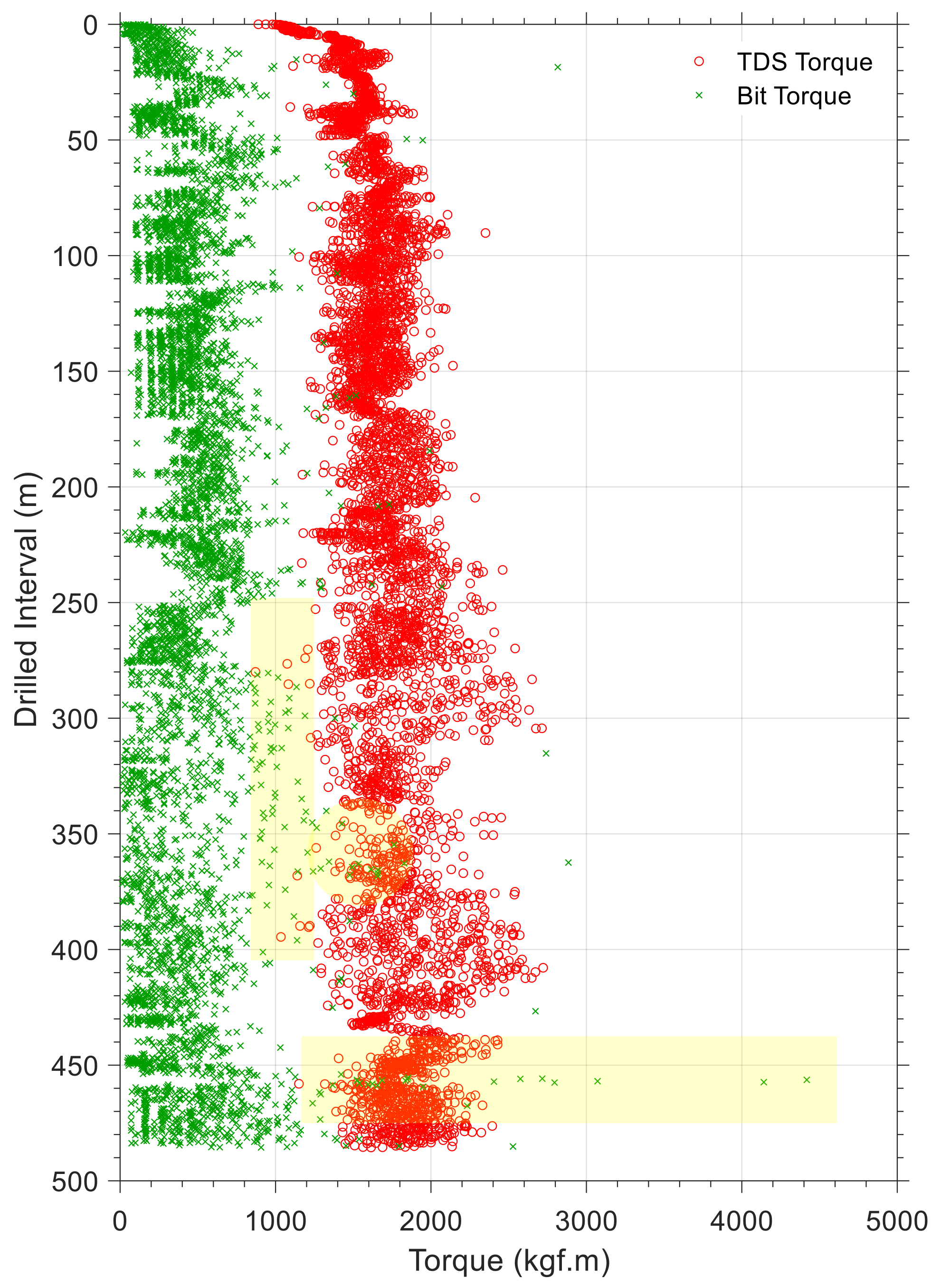
Historically, specific energy models and cutter–rock interaction models have been employed to estimate the performance of PDC bits. In spite of this, none of these methods considered the actual bit design parameters and the actual drilling conditions, such as the weight on the bit, rotational speed, the torque on the bit, and differential pressure at the bottom of the hole. This study proposes a novel approach for estimating forces on drilling bit cutters and evaluating specific energy at these cutters by using data analytics and experimentally derived models of cutter–rock interaction. A combination of surface recorded data and downhole drilling measurements gathered via wired drill pipe and along-string sensors is incorporated in the modeling process. A PDC bit is expressed as equivalent cutters and blades, and the status of each equivalent cutter could be simulated from input data from measurements based on specific energy theory. The torque at the bit is estimated using the approach and compared to the torque delivered to the drill string at the surface. Based on the comparison, one could be able to determine how much energy is dissipated by friction between the drill string and the borehole wall. This provides a sophisticated indicator for predicting and estimating the initiation and progress of downhole drilling problems such as annular pack off and fluid leaks.
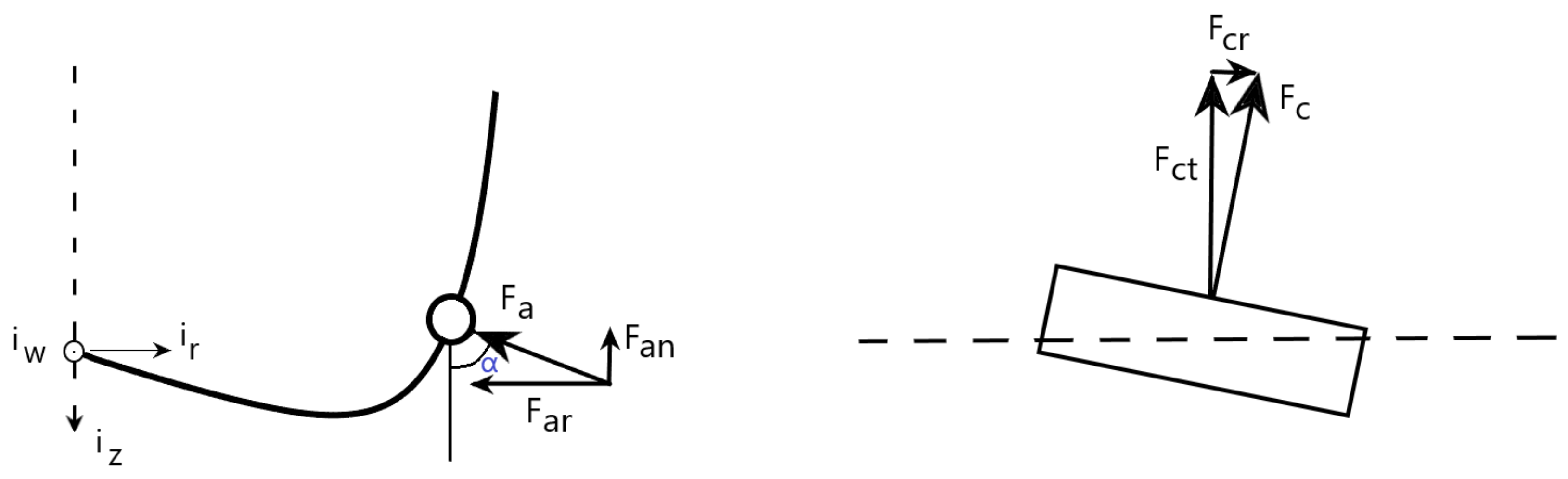
The novelty of the present study is that it develops two equations to estimate normal force, , (force that is parallel to the axis of the bit) and cutting force, , (force perpendicular to the axis of the bit and in the direction of movement of the cutters) considering all design, operational, and rock parameters. In this context, the design specifications of a PDC bit include cutter diameter, back-rake angle, and in-built wear flat area; operational factors comprise confining pressure at the bottom of the hole and rate of penetration; and rock parameter is characterized as drillability. In this study, experimental data from the literature are collected and analyzed using nonlinear regression algorithms. Thereafter, these equations were integrated into the bit and cutter models so that they could be related to weights and torques on the bit. A recursive least squares technique is used to handle real-time measurements for the purpose of studying the dynamics of the drill string and bit in real time. The remainder of this research paper is organized as follows. The first part of this paper is devoted to the development of mathematical equations for cutter–rock interaction. A description of the approach for studying the dynamics of drilling is provided in the second part. In this section, we discuss specific energy and how measurements are linked to developed models using data analytics. We conclude our paper with the results and discussion of two case studies (two bit runs in a inch section) from the Norwegian continental shelf.
Table 1.
Physical properties of rock for data utilized in this study.
Table 1.
Physical properties of rock for data utilized in this study.
| References | Rock Name | Bulk Density | Porosity | | Poisson’s Ratio | Young Modulus |
|---|
| | | (gr/cc) | (%) | (kpsi) | | (Mpsi) |
|---|
| Rajabov et al. [7] | Carthage Marble | 2.63 | 1–2 | 9–12 | 0.27 | 4–5 |
| | Torrey Buff Sandstone | 2.54 | 7.9 | 9–11 | 0.22 | 1.5–1.6 |
| | Mancos Shale | 2.47 | 16 | 5–7 | 0.2 | 4.6 |
| Glowka [2,3] | Berea Sandsone | - | - | 7.1 | - | - |
| | Sierra White Granite | - | - | 21.5 | - | - |
| | Tennessee Marble | - | - | 17.8 | - | - |
| | (Holton Limestone) |
| Akbari et al. [11,12] | Carthage Marble | - | - | 14.48 | - | - |
| Richard et al. [44] | Fontenoille Sandstone | - | - | 13.775 | - | - |
| | Moka Limestone | - | - | 9.425 | - | - |
| | Lens Limestone | - | - | 4.35 | - | - |
| | Voges Sandstone | - | 20 | 2.32 | - | - |
| | Nurabup Sandstone | - | 41 | 1.16 | - | |
| | MC Field Sandstone | - | 24.5 | 1.015 | - | - |
| Majidi et al. [45] | Indiana Limestone | - | 11–16 | 7 | - | - |
| | Carthage Marble | - | 1–2 | 9–11.7 | - | - |
| | | | | | Tensile Strength (kpsi) |
| Wang et al. [16] | Shale | - | - | 9.764 | 0.81 |
| | Marble | - | - | 12.294 | 0.90 |
| | Granite | - | - | 13.656 | 1.017 |
| | Limestone | - | - | 15.013 | 1.141 |