Experimental Study on Flow Boiling Characteristics in Continuous and Segmented Microchannels with Vapor Venting Membrane
Abstract
1. Introduction
2. PTFE Membrane and Experimental Set-Up
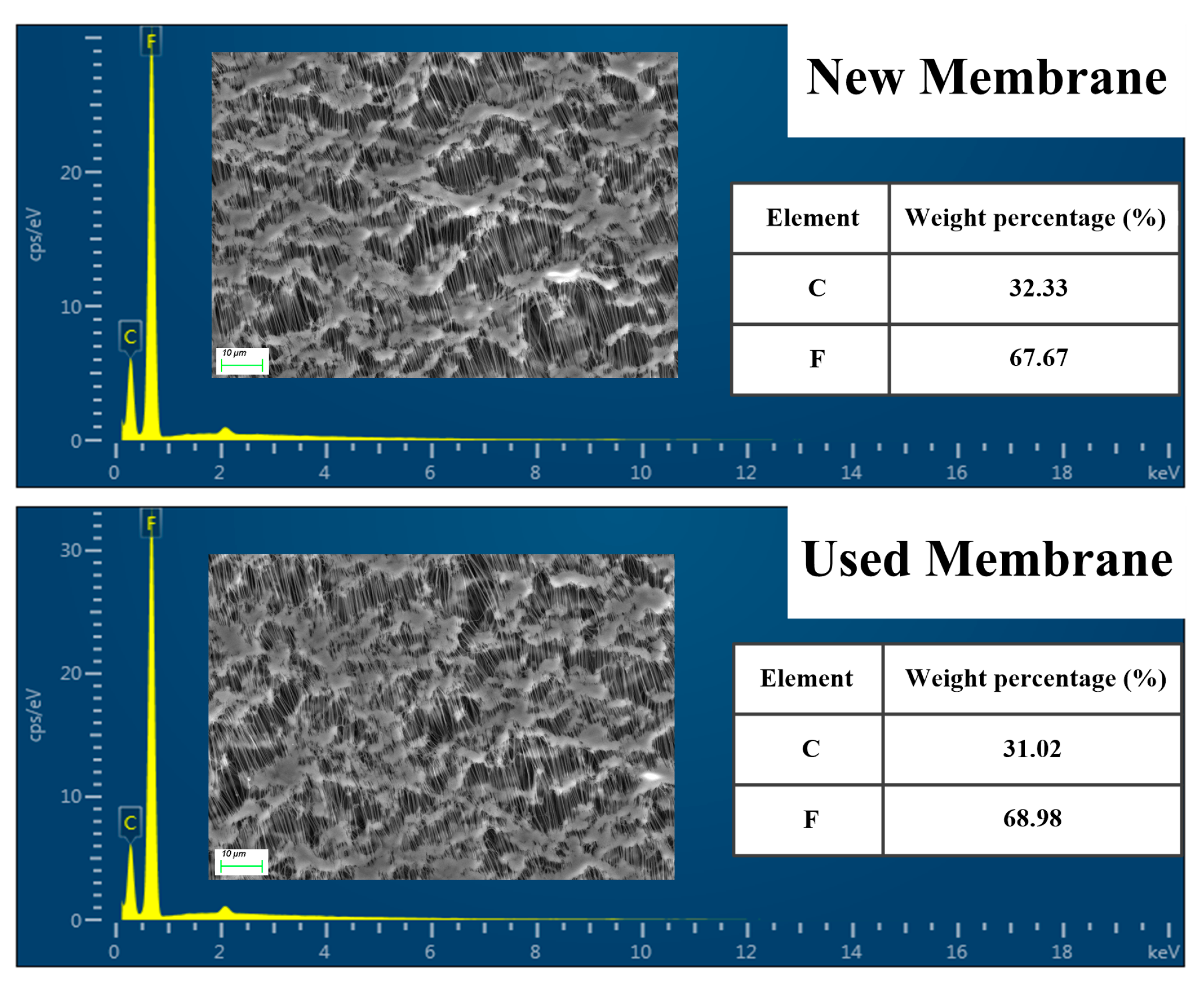
2.1. Characterization of Vapor Venting Membrane
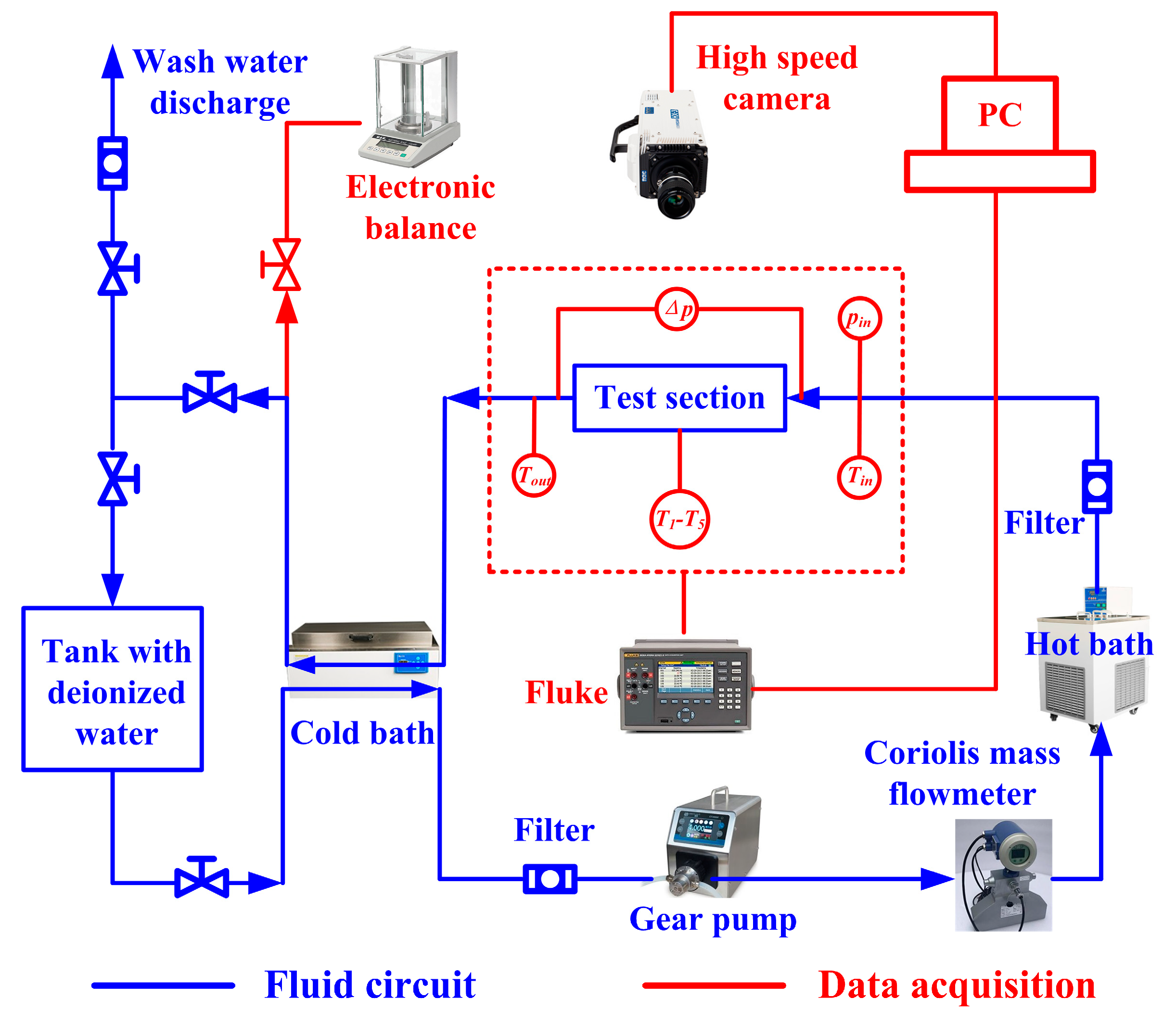
2.2. Experimental Set-Up
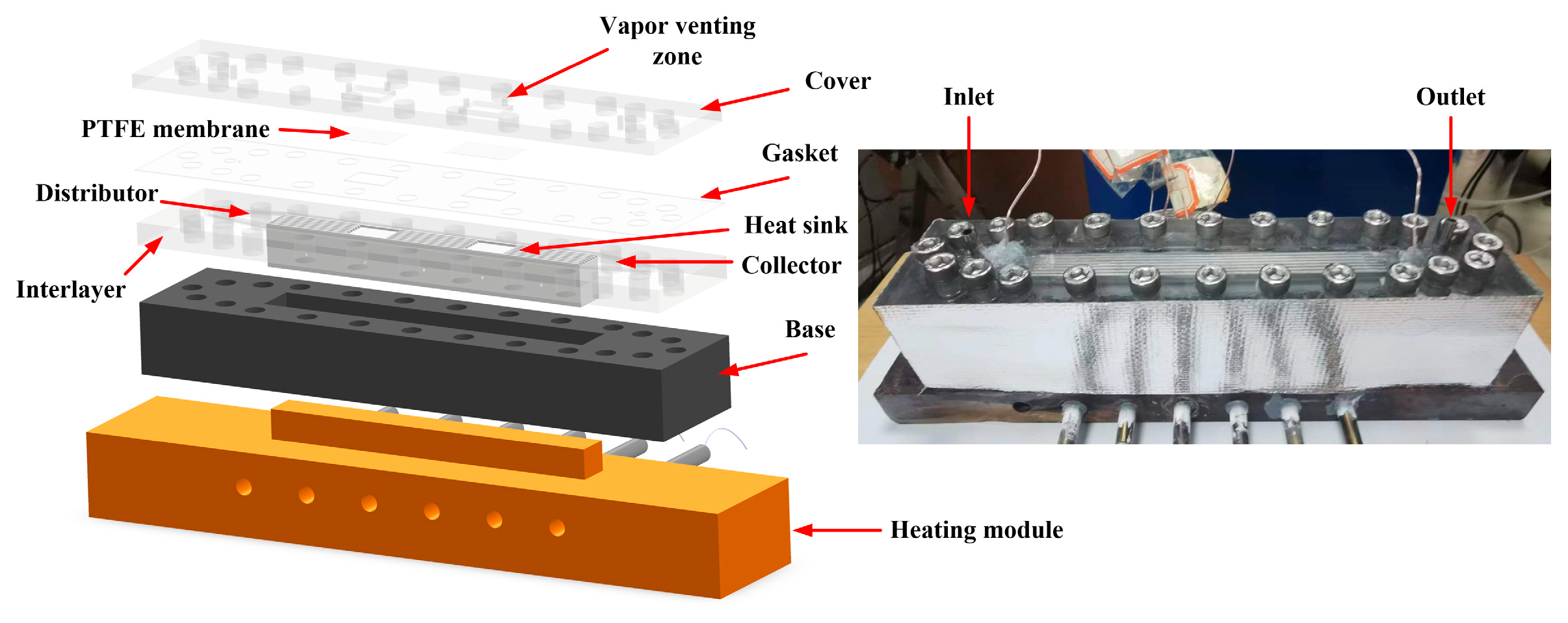
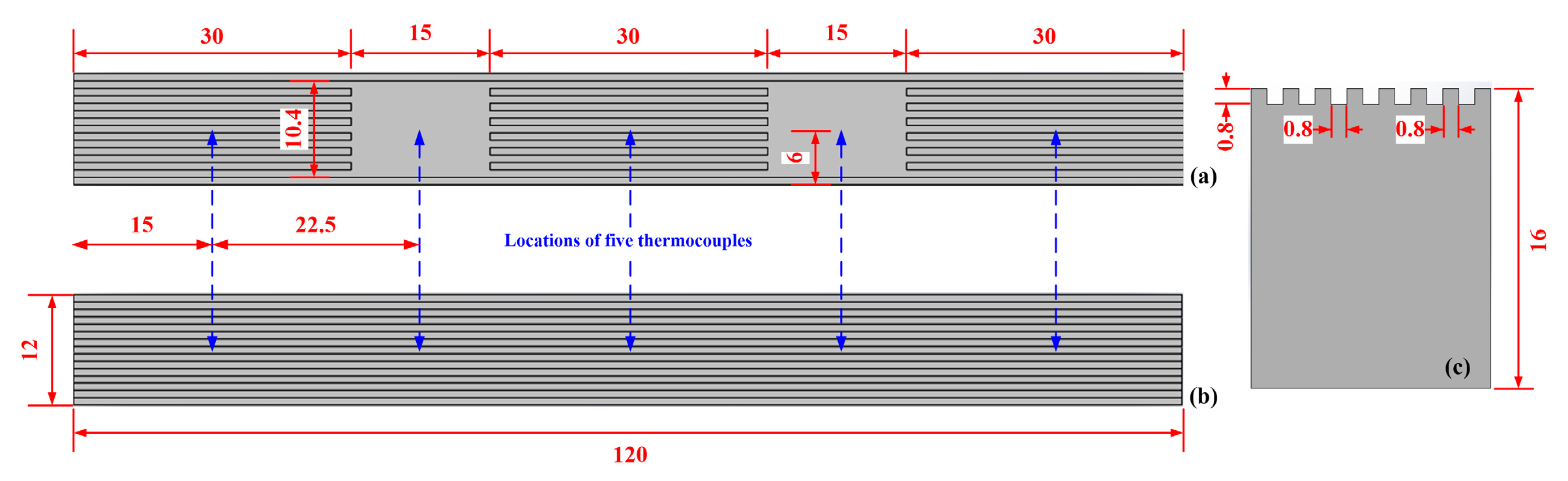
2.3. Test Module
3. Experimental Method and Data Processing
3.1. Determination of Heat Loss
3.2. Data Reduction of Two-Phase Flow Region
3.3. Uncertainty Analysis
3.4. Validation Study
4. Results and Discussion
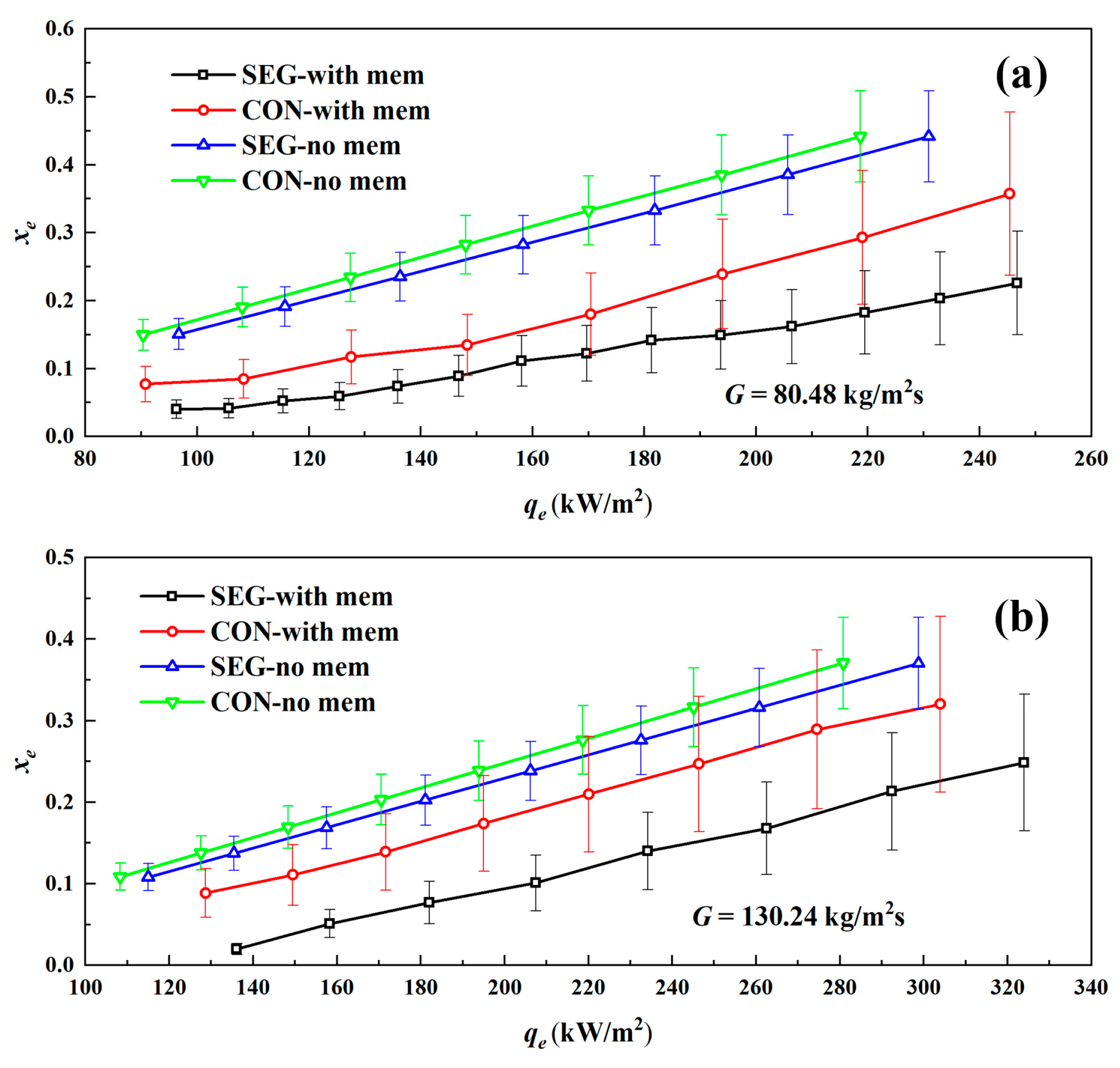
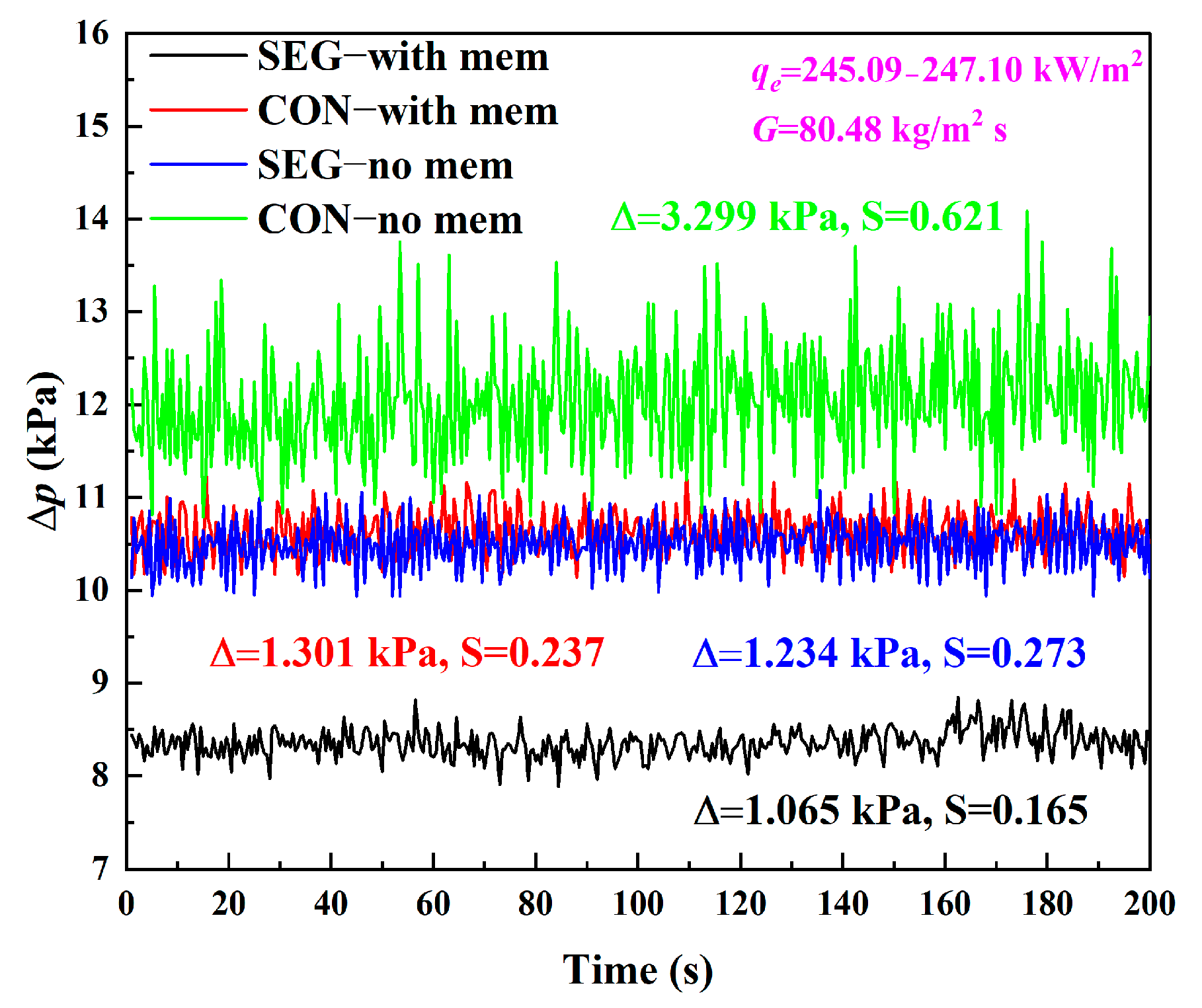
4.1. Pressure Drop and Bubble Motion
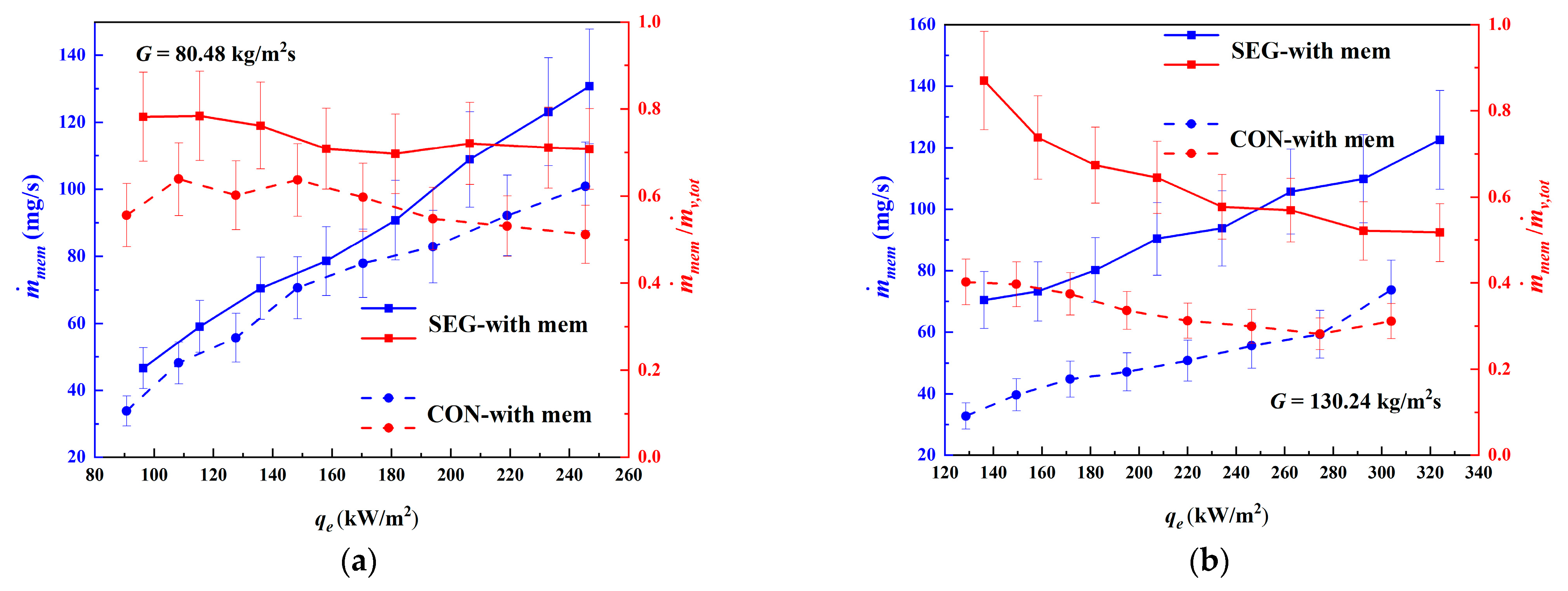
4.2. Heat Transfer Characteristics
4.3. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tuckerman, D.B.; Pease, R.F.W. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Mao, N.; Zhuang, J.; He, T.; Song, M. A critical review on measures to suppress flow boiling instabilities in microchannels. Heat Mass Transf. 2021, 57, 889–910. [Google Scholar] [CrossRef]
- Lee, H.; Liu, D.; Yao, S. Flow instability of evaporative micro-channels. Int. J. Heat Mass Transf. 2010, 53, 1740–1749. [Google Scholar] [CrossRef]
- Kingston, T.A.; Weibel, J.A.; Garimella, S.V. High-frequency thermal-fluidic characterization of dynamic microchannel flow boiling instabilities: Part 1—Rapid-bubble-growth instability at the onset of boiling. Int. J. Multiph. Flow 2018, 106, 179–188. [Google Scholar] [CrossRef]
- Law, M.; Lee, P.S. A comparative study of experimental flow boiling heat transfer and pressure characteristics in straight and oblique-finned microchannels. Int. J. Heat Mass Transf. 2015, 85, 797–810. [Google Scholar] [CrossRef]
- Prajapati, Y.K.; Pathak, M.; Khan, M.K. A comparative study of flow boiling heat transfer in three different configurations of microchannels. Int. J. Heat Mass Transf. 2015, 85, 711–722. [Google Scholar] [CrossRef]
- Li, W.; Yang, F.; Alam, T.; Qu, X.; Peng, B.; Khan, J.; Li, C. Enhanced flow boiling in microchannels using auxiliary channels and multiple micronozzles (I): Characterizations of flow boiling heat transfer. Int. J. Heat Mass Transf. 2018, 116, 208–217. [Google Scholar] [CrossRef]
- Ma, J.; Li, W.; Ren, C.; Khan, J.A.; Li, C. Realizing highly coordinated, rapid and sustainable nucleate boiling in microchannels on HFE-7100. Int. J. Heat Mass Transf. 2019, 133, 1219–1229. [Google Scholar] [CrossRef]
- Sitar, A.; Golobic, I. Effect of nucleation cavities on enhanced boiling heat transfer in microchannels. Nanoscale Microscale Thermophys. Eng. 2016, 20, 33–50. [Google Scholar] [CrossRef]
- Deng, D.; Xie, Y.; Huang, Q.; Wan, W. On the flow boiling enhancement in interconnected reentrant microchannels. Int. J. Heat Mass Transf. 2017, 108, 453–467. [Google Scholar] [CrossRef]
- Deng, D.; Chen, L.; Wan, W.; Fu, T.; Huang, X. Flow boiling performance in pin fin- interconnected reentrant microchannels heat sink in different operational conditions. Appl. Therm. Eng. 2019, 150, 1260–1272. [Google Scholar] [CrossRef]
- Liu, T.; Li, P.; Liu, C.; Gau, C. Boiling flow characteristics in microchannels with very hydrophobic surface to superhydrophilic surface. Int. J. Heat Mass Transf. 2011, 54, 126–134. [Google Scholar] [CrossRef]
- Morshed, A.; Yang, F.; Ali, M.Y.; Khan, J.A.; Li, C. Enhanced flow boiling in a microchannel with integration of nanowires. Appl. Therm. Eng. 2012, 32, 68–75. [Google Scholar] [CrossRef]
- Li, D.; Wu, G.; Wang, W.; Wang, Y.; Liu, D.; Zhang, D.; Chen, Y.; Peterson, G.; Yang, R. Enhancing flow boiling heat transfer in microchannels for thermal management with monolithically-integrated silicon nanowires. Nano Lett. 2012, 12, 385–3390. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Wu, H.; Cheng, P. Pressure drop and heat transfer of Al2O3-H2O nanofluids through silicon microchannels. J. Micromech. Microeng. 2009, 19, 105020. [Google Scholar] [CrossRef]
- Xu, L.; Xu, J. Nanofluid stabilizes and enhances convective boiling heat transfer in a single microchannel. Int. J. Heat Mass Transf. 2012, 55, 5673–5686. [Google Scholar] [CrossRef]
- Hassan, M.; El-Zahar, E.R.; Khan, S.U.; Rahimi-Gorji, M.; Ahmad, A. Boundary layer flow pattern of heat and mass for homogenous shear thinning hybrid-nanofluid: An experimental data base modeling. Numer. Methods Part. Differ. Equ. 2020, 37, 1234–1249. [Google Scholar] [CrossRef]
- Duursma, G.; Sefiane, K.; Dehaene, A.; Harmand, S.; Wang, Y. Flow and heat transfer of single-and two-phase boiling of nanofluids in microchannels. Heat Transf. Eng. 2015, 36, 1252–1265. [Google Scholar] [CrossRef]
- Liang, G.; Mudawar, I. Review of single-phase and twophase nanofluid heat transfer in macro-channels and micro-channels. Int. J. Heat Mass Transf. 2019, 136, 324–354. [Google Scholar] [CrossRef]
- Zhou, P.; Goodson, K.; Santiago, J. Vapor Escape Microchannel Heat Exchanger. U.S. Patent 699415107, 7 February 2006. [Google Scholar]
- Meng, D.; Kim, J.; Kim, C.J. A degassing plate with hydrophobic bubble capture and distributed venting for microfluidic devices. J. Micromech. Microeng. 2006, 16, 419–424. [Google Scholar] [CrossRef]
- Meng, D.; Cubaud, T.; Ho, C.M.; Kim, C.J. A methanol-tolerant gas-venting microchannel for a microdirect methanol fuel cell. J. Microelectromech. Syst. 2007, 16, 1403–1410. [Google Scholar] [CrossRef]
- Alexander, B.R.; Wang, E. Design of a Microbreather for Two-Phase Microchannel Heat Sinks. Nanoscale Microscale Thermophys. Eng. 2009, 13, 151–164. [Google Scholar] [CrossRef]
- David, M.P.; Miler, J.; Steinbrenner, J.E.; Yang, Y.; Touzelbaev, M.; Goodson, K.E. Hydraulic and Thermal Characteristics of a Vapor Venting Two-Phase Microchannel Heat Exchanger. Int. J. Heat Mass Transf. 2011, 54, 5504–5516. [Google Scholar] [CrossRef]
- David, M.P.; Steinbrenner, J.E.; Miler, J.; Goodson, K.E. Adiabatic and Diabatic Two-phase Venting Flow in a Microchannel. Int. J. Multiph. Flow 2011, 37, 1135–1146. [Google Scholar] [CrossRef]
- Salakij, S.; Liburdy, J.A.; Pence, D.V. Modeling Criteria for Extraction Regime Transitions for Microscale In-site Vapor Extraction Applications. Int. J. Heat Mass Transf. 2015, 84, 214–224. [Google Scholar] [CrossRef]
- Mohiuddin, A.; Loganathan, R.; Gedupudi, S. Experimental investigation of flow boiling in rectangular mini/micro-channels of different aspect ratios without and with vapour venting membrane. Appl. Therm. Eng. 2020, 168, 114837. [Google Scholar] [CrossRef]
- Dang, C.; Jia, L.; Peng, Q.; Yin, L.; Qi, Z. Comparative study of flow boiling heat transfer and pressure drop of HFE-7000 in continuous and segmented microchannels. Int. J. Heat Mass Transf. 2020, 148, 119038. [Google Scholar] [CrossRef]
- Steinke, M.E.; Kandlikar, S.G. An experimental investigation of flow boiling characteristics of water in parallel microchannels. J. Heat Transf. 2004, 126, 518–526. [Google Scholar] [CrossRef]
- Mahmoud, M.M.; Karayiannis, T.G.; Kenning, D.B.R. Surface effects in flow boiling of R134a in microtubes. Int. J. Heat Mass Transf. 2011, 54, 3334–3346. [Google Scholar] [CrossRef][Green Version]
- Pike-Wilson, E.A.; Karayiannis, T.G. Flow boiling of R245fa in 1.1mm diameter stainless steel, brass and copper tubes. Exp. Therm. Fluid Sci. 2014, 59, 166–183. [Google Scholar] [CrossRef]
- Mirmanto, M. Heat transfer coefficient calculated using a linear pressure gradient assumption and measurement for flow boiling in microchannels. Int. J. Heat Mass Transf. 2014, 79, 269–278. [Google Scholar] [CrossRef]
- Wang, Y.; Sefiane, K. Effects of heat flux, vapour quality, channel hydraulic diameter on flow boiling heat transfer in variable aspect ratio micro-channels using trans-parent heating. Int. J. Heat Mass Transf. 2012, 55, 2235–2243. [Google Scholar] [CrossRef]
- Mathew, J.; Lee, P.S.; Wu, T.; Yap, C.R. Experimental study of flow boiling in a hybrid microchannel-microgap heat sink. Int. J. Heat Mass Transf. 2019, 135, 1167–1191. [Google Scholar] [CrossRef]
- Jayaramu, P.; Gedupudi, S.; Das, S.K. Influence of heating surface characteristics on flow boiling in a copper microchannel: Experimental investigation and assessment of correlations. Int. J. Heat Mass Transf. 2019, 128, 290–318. [Google Scholar] [CrossRef]
- Shah, R.K. A correlation for laminar hydrodynamic entry length solutions for circular and noncircular ducts. J. Fluids Eng. 1978, 100, 177–179. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Kays, W.M.; London, A.L. Compact Heat Exchangers; McGraw-Hill: New York, NY, USA, 1984. [Google Scholar]
- Kandlikar, S.G.; Garimella, S.V.; Li, D.; Colin, S.; King, M. Heat Transfer and Fluid Flow in Minichannels and Microchannels; Elsevier: Waltham, MA, USA, 2006. [Google Scholar]
- Dharaiya, V.V.; Kandlikar, S.G. Numerical investigation of heat transfer in rectangular microchannels under H2 boundary condition during developing and fully developed laminar flow. ASME J. Heat Transf. 2012, 134, 020911. [Google Scholar] [CrossRef]
- Wu, H.; Cheng, P. Visualization and measurements of periodic boiling in silicon microchannels. Int. J. Heat Mass Transf. 2003, 46, 2603–2614. [Google Scholar] [CrossRef]
- Hetsroni, G.; Mosyak, A.; Pogrebnyak, E.; Segal, Z. Periodic boiling in parallel microchannels at low vapor quality. Int. J. Multiph. Flow 2006, 32, 1141–1159. [Google Scholar] [CrossRef]
- Wang, G.; Cheng, P. An experimental study of flow boiling instability in a single microchannel. Int. Commun. Heat Mass Transf. 2008, 35, 1229–1234. [Google Scholar] [CrossRef]
- Lv, Y.; Xia, G.; Cheng, L.; Ma, D. Experimental study on the pressure drop oscillation characteristics of the flow boiling instability with FC-72 in parallel rectangle microchannels. Int. Commun. Heat Mass Transf. 2019, 108, 104289. [Google Scholar] [CrossRef]
- Qu, W.; Mudawar, I. Flow boiling heat transfer in two-phase micro-channel heat sinks: I. Experimental investigation and assessment of correlation methods. Int. J. Heat Mass Transf. 2003, 46, 2755–2771. [Google Scholar] [CrossRef]
- Fang, C.; David, M.; Rogacs, A.; Goodson, K. Volume of fluid simulation of boiling two-phase flow in a vapor-venting microchannel. Front. Heat Mass Transf. 2010, 1, 013002. [Google Scholar] [CrossRef]

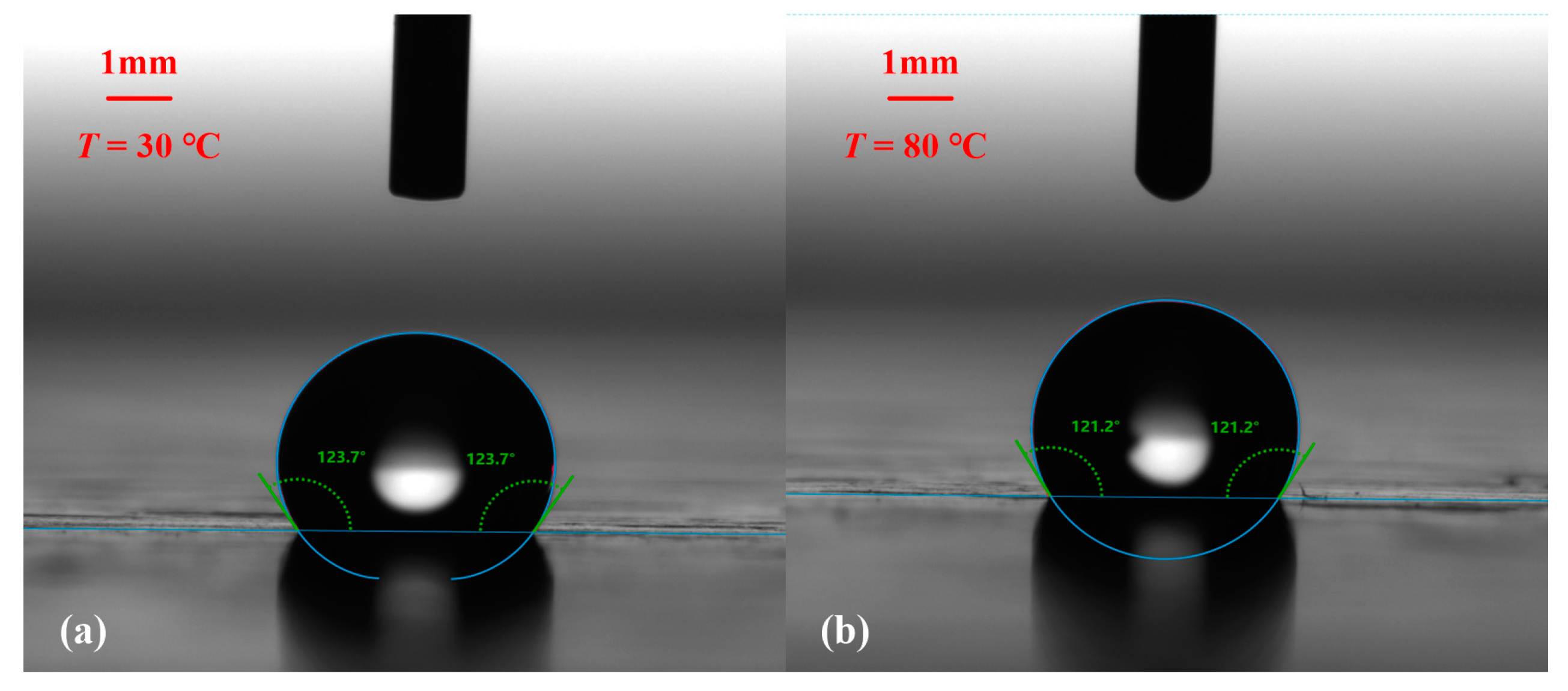








| Membrane | Pore Size (μm) | Porosity (%) | Operating Temperature (°C) | Thickness (μm) |
|---|---|---|---|---|
| PTFE (T050A047A) | 0.50 | 78 | −120~260 | 75 |
| Quantity | Uncertainty |
|---|---|
| Microchannel dimension | 0.01 mm, 0.1–1.2% |
| Temperature (T) | 0.62 K, 0.5–0.9% |
| Voltage (U) | 1 V, 0.5–1% |
| Inlet mass flow-rate () | 1 mL/min, 2.9–4.5% |
| Outlet mass flow-rate () | 0.6 g/min, 5.7–12.3% |
| Pressure drop (p) | 6.5 Pa, 0.3–2.3% |
| Mass flow-rate of vapor through the membrane () | 6.4–13.1% |
| Effective heat flux (qe) | 4.1–8.3% |
| Mass flux (G) | 3.1–6.9% |
| Single-phase Nusselt number (Nu) | 4.5–9.3% |
| Single-phase friction factor (f) | 6.7–18.5% |
| Exit quality without membrane () | 7.2–15.2% |
| Exit quality with membrane () | 15.7–33.7% |
| Subcooled length () | 7.8–14.7% |
| Two-phase heat transfer coefficient () | 4.8–9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Wei, M. Experimental Study on Flow Boiling Characteristics in Continuous and Segmented Microchannels with Vapor Venting Membrane. Energies 2022, 15, 8756. https://doi.org/10.3390/en15228756
Li S, Wei M. Experimental Study on Flow Boiling Characteristics in Continuous and Segmented Microchannels with Vapor Venting Membrane. Energies. 2022; 15(22):8756. https://doi.org/10.3390/en15228756
Chicago/Turabian StyleLi, Shanwei, and Min Wei. 2022. "Experimental Study on Flow Boiling Characteristics in Continuous and Segmented Microchannels with Vapor Venting Membrane" Energies 15, no. 22: 8756. https://doi.org/10.3390/en15228756
APA StyleLi, S., & Wei, M. (2022). Experimental Study on Flow Boiling Characteristics in Continuous and Segmented Microchannels with Vapor Venting Membrane. Energies, 15(22), 8756. https://doi.org/10.3390/en15228756





