1. Introduction
The electrification of transport has increased in the past years, leading to a fast increase in the electricity demand over the distribution grid. To study the integration of a massive amount of EVs into the distribution grids, the impact of uncontrolled EV charging on the grid utilities was explored in several benchmarking studies [
1,
2,
3,
4,
5,
6]. Based on these benchmark studies, ample smart charging methods have been developed and studied in recent years [
7,
8]. These algorithms in general are challenging to implement and have a trade-off between operating functionalities, input information and computational power. There are plentiful simpler and easier-to-implement EV charging methods that require much less communication and computation. Some of the methods are applicable for a broader spectrum of scenarios or offer a competitive, or even superior, performance [
9,
10,
11].
It is our interest to explore what minimalism can bring to EV charging scheduling methods and to evaluate their effectiveness. In addition, it is also vital to assess the short-term EV charging methods before the innovative charging algorithms are ready to be launched with the support of relevant protocols and regulations [
12].
In this paper, three representative pragmatic rule-based EV charging scheduling methods are selected or proposed based on existing popular simple EV charging scheduling methods. The generic fundamental mechanism of the three methods is to control the EV charging power based on different criteria. A systematic analysis and comparison of their efficacy, including grid congestion mitigation, economic benefits and charging demand fulfilment, were carried out. In addition, this study provides an elementary reference point for the assessment of future-developed algorithms. It must be noted that different charging schemes can have diverse impacts on other factors, such as battery lifetime. However, the focus of our study is the above-mentioned three aspects and, therefore, the influence on the battery performance is beyond the scope of this research.
1.1. Background on Advanced Smart EV Charging Algorithms
Most of the controlled charging of electric vehicles (EVs) shares one or more of the four prevailing primary targets [
13,
14,
15,
16]: (i) grid impact mitigation, (ii) profit maximisation, (iii) enhancing the service to EV users and (iv) increasing the utilisation of renewable energy resources. To achieve multiple targets with one charging method, EV charging power is usually not the only parameter that must be tuned, especially in complex systems where other relevant parties are involved [
13,
17,
18,
19]. On top of that, complex structures, such as hierarchical control schemes and multi-level optimisations, are composed [
18,
20,
21,
22], which, in turn, increase the requirement for the amount, accuracy and speed of the communication [
13,
15,
17]. For example, the EV charging management system proposed in paper [
17] suggests a bidding process within a transactive market in which the EV fleet information, as well as the EV users’ preference towards the clearing price, is requested beforehand. Similarly, study [
18] investigates a systematic supply–demand balance, PV power generation and energy storage, as well as the V2G performance, within its EV charging optimisation problem using both hourly and day-ahead predictive data. The EV smart charging method proposed in research [
19] not only incorporates battery lifetime protection and PV power generation into the stochastic dynamic programming but also integrates grid capacity, as well as energy storage optimisation, in its objective function.
The above-mentioned primary targets become competitive towards each other under some operational conditions. For example, it is suggested in [
14] that prioritizing peak shaving can approximately half the maximum demand but leads to a 5–10% increase in average energy costs as a trade-off. Further, while the method proposed in [
15] successfully satisfies the load congestion and voltage droop constraints relative to 70% of exceeded constraints in the uncontrolled method, it is suggested that location-specific customer demands may lead to a fairness challenge that needs further investigation. An interesting approach in [
16] attempts to include fairness in imposing grid limitations by setting priority criteria for coordinated EV charging depending on the available parking time and energy demand of the connected cars. These leading algorithms highlight the importance of multi-objective optimisation for minimizing a defined system cost function to address the underlying trade-offs using accurate information and fast communication between different agents.
Complex hierarchical control structures are often employed to incorporate multiple functions in advanced EV charging algorithms. Paper [
20] proposes a two-level hierarchical charging coordination algorithm where the upper-level controller is in charge of the grid power dispatch and the station-level controller manages the local charging scheduling. The algorithm in [
21] has three levels of actions, and each has different functionalities. The first level participates in the day-ahead (DA) or real-time (RT) market and obtains the quantity of cleared energy, the second level aims to optimally dispatch the energy budget obtained from level one to the EVs in the system and, finally, the objective of the third level is to respond to the up and down regulation requests.
Apart from trade-offs and compound structures associated with multi-objective optimisation, smart charging algorithms also deal with uncertain load demand forecasting, renewable energy generation and the arrival/departure time of the EVs, usually by employing a multi-timescale optimisation scheme. In [
22], a building operational cost reduction of approximately 6% was achieved using a two-stage algorithm for DA scheduling and RT operation compared to the baseline case, where only a prediction of the PV output was considered. Similarly, an algorithm developed in [
18] optimises the system in four stages along the time scale from the prediction to DA, hourly ahead and, finally, to RT, to show that even though the EV energy consumption is the same, the overall cost with an hour-ahead schedule is 1.55 times higher than RT control, mainly due to uncertainty in PV generation.
All of the above-mentioned challenges would become exponentially difficult in real-environment applications, which consecutively makes simple charging methods compelling.
1.2. Simple and Practical Charging Scheduling Approach
Meanwhile, simple yet pragmatic EV charging algorithms have been suggested and tested in preceding works. Simple charging algorithms usually focus on regulating the EV charging procedure with three common approaches: reducing the charging cost, alleviating the grid impact and tuning the charging power from the user’s point of view. This section gives an overview of simple charging methods.
1.2.1. Charging Cost Reduction Methods
The most popular reason for EV charge scheduling is cost reduction. The electricity price, such as the DA price or time of use (TOU) price, can reflect the grid loading level to some degree and is often selected as the price signal.
The objective of [
23] is to minimise the EV charging cost based on the TOU price from a regulated market. This heuristic algorithm sorts the charging power from both temporal and magnitude perspectives and the expected outcome is that the charging requests of EV users are fulfilled with a lower cost in contrast to uncontrolled charging. In the end, 52.92% to 61.19% of the energy demand shifted from the highest to the lowest loaded time window (peak → flat → valley time), with a 39.67% to 51.52% cost reduction in contrast to uncontrolled charging. Similarly, a linear optimisation problem is formulated in [
24] to minimise the EV charging cost from an aggregator’s point of view. This method was implemented in combination with three charging power adjustment programs with cost incentives, among which, the users can pick in their own favor. The hourly price used in [
24] was calculated based on the real-time cost of electricity generation, transmission and distribution. It was observed that, with a 50% EV penetration level, the charging peak power at midnight is reduced to around 50% relative to uncontrolled charging. In addition, the EV aggregator saves at least 5% in charging cost compared to the uncontrolled charging scenario and the savings increase further with increasing levels of EV penetration.
However, a deficiency of the price signal as the sole dependent charging control method is that it could cause a second load peak that can sometimes overtake the uncontrolled charging load peak; this negative side effect should not be overlooked. This is due to the simultaneous charging stimulated by the unified off-peak tariff in the system. Study [
25] implemented a TOU price-based time-control EV charging method where different off-peak tariff starting moments in combination with various begin-to-charge schemes were investigated. It was found that this method could shift the EV charging demand into off-peak hours and mitigate the under-voltage violation in comparison to the uncontrolled charging method. Although the second peak in the load demand on the service transformer was observed starting between 11 p.m. to 12 a.m, this value did not exceed the peak observed for uncontrolled charging that occurred between 8 p.m–10 p.m. A similar trend in the minimal voltage was also encountered. It was concluded that the beginning moment of the off-peak tariff needs to be carefully demonstrated so that the balance between grid loading and charging completion can be obtained. The TOU price-based EV start charging time control method was also tested in [
26] and it was noticed that a secondary peak appeared due to the simultaneous EV charging, but the peak was still around 20% less than the peak induced by uncontrolled charging. In addition to the time control charging method inducing the second peak issue, optimisation programming could also produce the same side effect. Study [
27] proposed an EV charging optimisation method with the objective to minimise the charging price by referring to the DA spot market price. The results suggest that even though the charging cost is reduced by 11–16% with the proposed method, using only hourly price information is not sufficient. Simulations on actual grid data revealed the highest increment in system energy loss of 4.3% relative to uncontrolled charging in a residential area, whereas no significant difference in the commercial area was observed.
The employment of extra constraints might effectively balance out the second peak issue. For instance, study [
28] presents a cost minimisation charging method based on a time-varying electricity price that reflects the net system demand, including the wind generation, as well as the EV demand. The results indicate that, as opposed to uncontrolled charging, the average peak loading of the grid reduces up to 8%, whereas the net present value of the grid investments increases by 25% in the low-wind-generation scenario. Incorporating the grid-related constraints directly into the model produces a more adequate effect. The charging profile of two TOU tariff-based delayed charging methods—concurrent or with Poisson distribution—was studied in [
29], and it was found that both methods lead to a narrower peak time window with a higher peak value. However, with the grid condition limitation being considered in the form of a distribution system loading margin, the maximum EV penetration level was improved from the worst case of 8.5% to the best case of 142.6%. A loss-optimal charge strategy was used in helping to defer the infrastructure reinforcement of the distribution network in [
27], and a 100% EV penetration was achieved as opposed to 49% in the price-optimal case. The network peak load minimisation method proposed in [
28] not only decreases the average peak grid loading by at least 5% compared to the cost minimisation method, but also helps to reduce the future grid component reinforcement requirement on MV distribution cables by 49.9% relative to the 29.5% of the cost minimisation method.
1.2.2. Grid Impact Mitigation Methods
Aside from the electricity price, the grid performance is often selected as the primary goal of the EV charging regulation method, considering the potential grid limitation violation caused by the massive EV charging demand as well as the competition between primary goals. In doing so, the grid characteristics are frequently integrated into the system model.
For example, the grid loss optimisation method developed in [
27] adapts grid congestion indicators, such as the transformer and the line loading, as well as the voltage variations, into constraints. Alternatively, grid power limitation in a half-hour step was used in [
16] to prevent overloading, but this method requires communication with the system operator for the grid power limit, as well as the load demand with prediction. Incorporating grid features into the optimisation is the most straightforward way to mitigate overloading issues. However, it also means that strong nonlinear features are introduced into the optimisation problem, which leads to complex non-linear (NL) programming solutions that increase the solving time. In addition, these methods often use centralised control schemes and request a high-level knowledge of the grid, which means a high requirement in communication and computational power [
30,
31].
Decentralised control methods using locally available information such as node voltage as a reference is another common direct approach. The premise is that the node voltage measured at any given time is a function of grid loading in the associated branch and, therefore, the information on grid congestion can be extracted locally without communication. Study [
25] formed a distributed optimisation problem, with its objective to minimise the local voltage deviation at every EV connection node. The results reveal that the peak load demand is largely shifted to the off-peak hours and the voltage droop issue is significantly improved with at least a 4.26% increased minimal voltage. Another popular method is the well-known voltage droop method, where the power drawn by the EV varies in proportion to the measured node voltage according to a heuristically set droop gain. A simple voltage droop charging method was studied in research [
32]. The simulation results of a real urban residential LV grid revealed that the voltage droop charging method improves the minimal voltage by 14.7% and lowers the voltage unbalance factor by 32% as opposed to the uncontrolled charging. Nevertheless, the minimum voltage value of the grid is still under 0.9 p.u. with a maximum of 10.4% of the time duration in one week. This is probably related to a relatively low voltage droop response range being selected (0.85 to 0.9 p.u.). Study [
33] proposed a phase-wise voltage-droop-based reactive power control algorithm. The phase-to-neutral voltage unbalance was alleviated by up to 56% and the minimum voltage was also improved by up to 6.3% with a negligible energy loss in contrast to the reference scenario.
Despite the persuasive grid overloading prevention ability, this strategy may lead to an unfair energy transfer to EVs connected at downstream nodes. This is because such locations are further away from the substation and have a relatively greater drop in voltage due to the higher impedance of the distribution branch [
34].
To establish a fair utilisation of grid resources among vehicle owners while simultaneously alleviating the grid congestion, ref. [
35] adapted the threshold voltage at each node in accordance with its distance from the substation based on a learning algorithm using measured data. The peak power drawn increases by approximately 10–20% as the charging power of all houses reaches its equilibrium point compared to its initial status. However, this method requests the full information of the whole grid, including geographic information, as well as the grid local profile. A fair control scheme was proposed in paper [
36] by using an exponential voltage droop curve, and the charging rate was altered based on the state of charge (SoC) of the EVs. This method successfully decreased the peak in the system load by 10–15%. Furthermore, the difference in time to fully charge between EVs connected at different nodes was scaled down to 60–70% with the SoC-involved adjustment in comparison with the SoC-free adjustment. This control method is only effective with a maximum of 50% EV penetration, and EVs at the far end will not be able to be fully charged if the EV penetration keeps growing. An EV SoC and local voltage-dependent fuzzy logic communication-free charging method was developed in [
37]. Additionally, a zero membership function was assigned to the voltage range 0.95–1.025 p.u. to avoid the extensive voltage-reliant sensitivity of the charging rate. The performance comparison between the proposed method versus the traditional voltage droop method suggested a similar capability of grid overloading reduction, where the difference in the minimum voltage at the same far-end node was only 0.0023 p.u. Nevertheless, the proposed method has an outstanding strength in unfair charging realignment. The difference in the time until full charge between the upstream and downstream node-connected EV decreased by almost three hours relative to the traditional voltage droop charging method. Paper [
11] introduced a rule-based decentralised charging method using historical node voltage data, as well as EV SoC information, to determine the charging rate. Both under-voltage and transformer overloading probability decreased significantly in comparison to uncontrolled charging. The results also imply that embedding extra information such as the EV arrival/departure time, urgency and charging energy demand into the algorithm would not certainly enhance the after-effect. Although an 11.5% charging cost saving was obtained, the transformer loading probability was up to 26% higher with a 0.42% higher failure to the supply rate.
As we can conclude from the above-reviewed paper, extra efforts, such as a sophisticated control scheme and additional information, are always requested to reconcile grid congestion and charging fairness.
1.2.3. EV User-Centric Charging Methods
Third-party information is not always a necessity in EV charging coordination. The EV charging impact alleviation in LV distribution grids can be attained by flattening or staggering the high EV charging powers from each other and from the base load demand. This can be achieved based solely on the charging-demand-related information, which makes this method EV-user-centric, as its primary constraint is the accomplishment of EV charging demand. Examples of popular EV-user-centric charging methods are: reduced power charging (also called average rate charging or individual peak shaving), delayed charging and random charging (with a random rate and/or at random times).
Charging by departure and individual peak shaving methods are investigated in [
38]. In this study, the individual peak shaving presents a significant improvement in load peak reduction (up to 60%) while enhancing the PV self-consumption by 3.9% points. However, individual peak shaving is not as effective in grid impact mitigation during the night. Moreover, the charging by departure method could cause a slightly higher evening peak compared to the uncontrolled charging and has an insignificant increase in the PV self-consumption rate.
Four charging methods that fall into random charging or delayed charging categories were studied in [
9]: random-in-window with fixed (RIW-FR) or varying rates (RIW-VR), pure-random charging and charging by departure. Among all methods, RIW-VR charging has the best efficacy in both charging peak reduction and load valley filling and RIW-FR is the runner-up, followed by the pure-random charging method. Nevertheless, similar to other research, the charging by departure method shifts the charging load to a later moment with the side effect of creating a second peak, even though this peak is lower than the one with uncontrolled charging.
User participation was included in [
24], where three charging programs could be selected by users before the charging starts. The charging programs were allocated by different average charging speeds and matching charging prices. Depending on the program selection and the charging energy request, the charging time for each user varies. The simulation results of a distribution feeder in Ecuador prove that, with a user-selected average power charging method, the peak charging demand was reduced to around 38% of the uncontrolled charging peak power. If the minimal possible charging power is applied, the charging peak demand reduction can be up to half of the peak caused by uncontrolled charging [
39]. It was also reported that the reduced charging power method with a charging rate depending on price could save an 11.8% cost per EV per day in Winter [
40].
1.3. Contributions and the Paper Structure
To what extent the individual criterion is effective in EV charging scheduling and how it influences the system performance is essential and interesting. In this paper, one method from each approach introduced in the previous section was selected and investigated. They are the price-signal-based method (PSM) for charging cost reduction, voltage droop method (VDM) for grid impact mitigation and the average rate method (ARM) for a user-centric charging approach. Each method only utilises single and specific information as a control reference, where PSM only uses the price signal, VDM solely employs the local voltage value and ARM just exploits user-provided charging session knowledge.
Since each charge scheduling method only considers one factor, the pros and cons of each method are magnified while the trade-offs between them are pronounced. Node voltages correlate well with the loading patterns of the local grid; thus, VDM discriminates against the chargers located downstream of the central substation. On the other hand, PSM can eliminate this location-specific charging behaviour, but communication for price signals is necessary. Furthermore, both VDM and PSM aim to postpone the EV charging demand based on heuristically chosen slopes independent of the user information; hence, these methods are vulnerable to the possibility of incomplete charging events. The ARM takes into account only the EV user input data, which contain the parking time and energy demand information to guarantee that the EV charging requirements are met. However, the charging method is unaware of the grid operating conditions and its performance becomes user dependent.
It is important to benchmark the advanced smart EV charging algorithms using simplified methods targeting either a single objective or ones that are structurally less complex in their implementation to ensure scalability. By studying the fundamental impact of every single factor with our chosen three charging methods, the benchmark criteria are then provided for the reference of future smart charging evaluation. The contributions of our work are listed as follows:
Three simple charging methods were compared vertically with each other and with uncontrolled charging from several perspectives: grid congestion prevention, charging cost minimisation and EV charging completion.
The comparison was accomplished by means of grid simulations. The simulations on six real LV distribution grids jointly with four EV penetration levels (0, 20, 50, 80%) were investigated in two representative seasons (winter, summer).
The practical limitation of charging protocol IEC61851 was deliberated, where the charging current has a minimum value of 6 A with discrete incremental steps.
An in-depth analysis with respect to different charging price schemes is carried out
In
Section 2, the mathematical principles for the considered charge scheduling methods (PSM, ARM and VDM) are described in detail. The system description of six grid types in the Netherlands, simulation methodology, key assumptions and measured statistical data pertaining to the energy demand, arrival and departure time of EVs is discussed in
Section 3. Simulation results related to the grid performance in terms of transformer and line loading and the node voltage droop with the considered charging schemes are compared with UNC in
Section 4. In
Section 5, the impact of the PSM scheme is explored in more detail. The trade-offs associated with charging demand fulfilment and charging costs are quantified in
Section 6 and, finally, the key conclusions are highlighted in
Section 7.
2. EV Charging Scheduling Methods
In this paper, the per-unit format of charging power/current is presented since the rated charging power/current differs for every EV and charger brand. The base EV charging power/current (
/
) per unit calculation of each EV and charger combination is introduced in Equation (
1), wherein
/
represent the maximum charging power/current of EV
j, and
/
is the maximum charging power/current of the charger at which EV
j is connected to it. Therefore, the base EV charging power/current means the maximum allowable charging power/current for a particular EV–charger pair.
One of the most commonly applied AC charger with EV communication protocols in Europe is IEC61851. The charger gives an upper limit of charging current via a pulse-width modulation (PWM) signal through the control pilot (CP) of the connector. According to this protocol, the lowest non-zero charging current set-point is 6 A [
41]. Even though the EV is the master in the negotiation, it was assumed in this paper that the EV charging current always follows the set-point given by the chargers [
42]. The constant-voltage (CV) battery charging stage was not considered in the control scheme in this paper. Therefore, 6 A was set as the minimum charging current in this study. In addition, the charging current/power of the EVs and the set-point given by the charger are not continuous [
41]. A discrete charging scheme was then applied and the resolution of the charging current set-point was set to be 1 A. Three charging methods are explained in the following context, and their control scheme illustrations are presented in
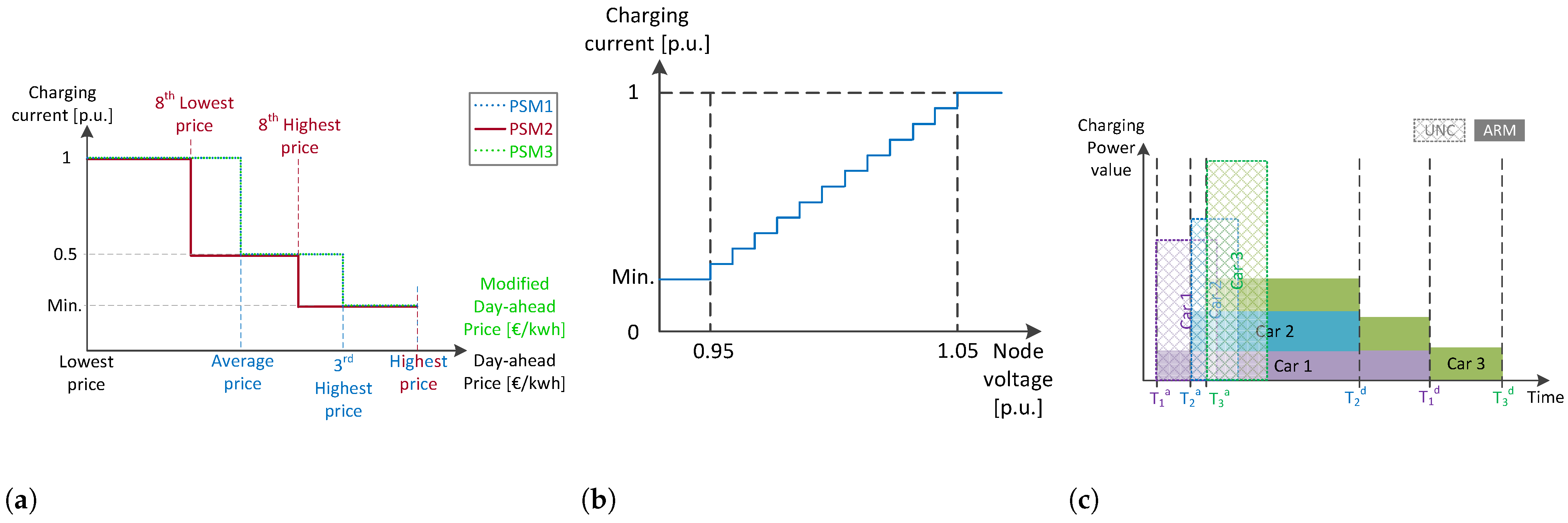
Figure 1.
2.1. Price Signal Method
The idea of the PSM is inspired by the commonly applied TOU-tariff-based time control charging method introduced in
Section 1 and a field implemented in the pilot project “Flexpower” in Amsterdam, The Netherlands [
43]. The TOU method controls the on and off charging status based on the peak–valley price time window and the Flexpower project increases or decreases the charging current limit based on the time of day. The PSM combines two approaches, and the idea is to limit the EV charging current solely based on the electricity price. This price signal could be a predicted intra-day market (IDM) price, a day-ahead market (DAM) price, a predicted market price that reflects the grid congestion or a different type of market price that is available prior to the activation moment of the charging scheduler. In the European market, the DAM price for the next whole day is released one day ahead at 12:00 noon, and the price is fixed for every hour [
44]. The APX Dutch DAM price is then selected as the price signal for PSM due to its advantages of having an early accessibility and a long duration that lasts for 24 h [
45]. Without the necessity of collecting local information such as local voltage or the user departure time and charging energy demand, the maximum allowable per unit charging rate of all of the connected EVs is tuned by referring to the DAM price signals.
In this study, we propose a three-price-segment scheme where the price of the next day is divided into three high (
), medium (
) and low (
) segments and each segment corresponds to one charging current level. An hourly DAM price signal means that the charging power adjustment is also in a step of one hour. The hourly PSM charging current (
) for EV
j is limited based on the hourly DAM price (
), which is demonstrated in Equation (
2).
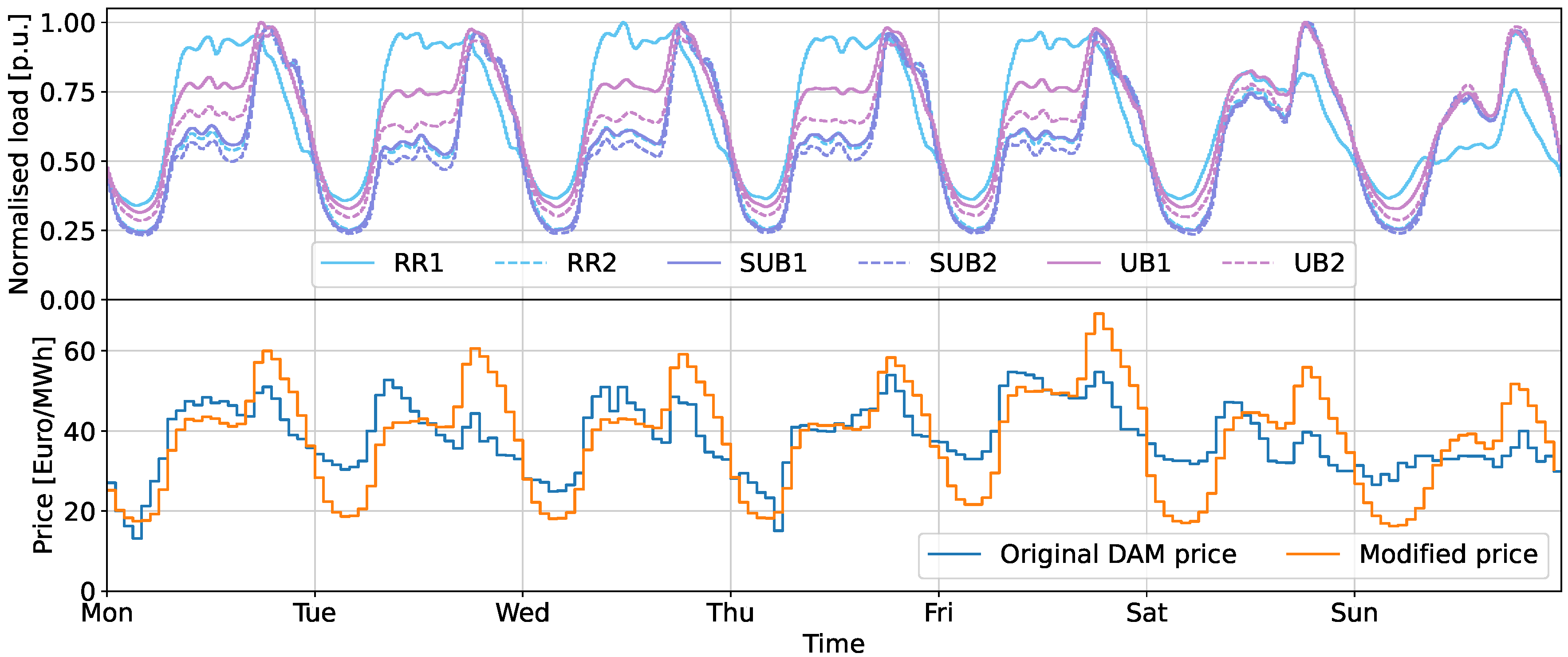
Energy prices such as DAM or IDM prices only reflect the supply–demand relation from an energy production–consumption balance perspective but not from a power transmission and distribution perspective. Hence, a separate congestion market is required to factor in the grid loading conditions or to adjust the energy prices in such a way that it can reflect grid congestion as well. To compare how close the DAM price reflects the grid congestion, the normalised grid total baseloads of all six grids and the DAM price of the same time period are plotted in
Figure 2. From this plot, it can be observed that even though the DAM price shows a day-and-night price fluctuation and there are two peak hours during the day, the load variation is not well replicated by the price signal. Unfortunately, there is no mature congestion market available in the Netherlands [
46] that contains the grid loading information. Hence, a modified DAM price signal is proposed based on the Dutch DAM price. The new price signal is modified by referring to the average base power consumption trend of all six grids, and it shares the same daily mean values as the original DAM price. The curve of the modified price signal can be seen in
Figure 2.
Moreover, how the price segment division impacts the effectiveness of PSM is also appealing to study. Two price segment division methods were thus explored. One method is to divide the daily 24 h price into three parts: the top three prices as , all prices below the daily average price as and the rest of the prices in between, which are categorised as . This method inhibits the time window, during which, the EV charge has a minimal current in order to reduce the limitation on the charging demand as much as possible. The second segment division method is to simply divide the 24 h into three equal parts that are each 8 h long. This division method means that the EVs can be charged with full current for only 8 h of a day, and, in another 8 h, the EV can only be charged with its lowest possible current.
To cover two price signals and two price segment division methods, three PSM schemes are proposed and studied in this paper. The scheme detail is summarised in
Table 1 and the schematic of three PSM control schemes is shown in
Figure 1a.
2.2. Voltage Droop Method
The VDM tested in this paper is simply the traditional voltage droop method [
34]. A voltage droop response range of 0.95–1.05 p.u., within which, the charging current increases proportionally, was selected to confine the voltage fluctuation within the allowable range as much as possible [
47]. When the voltage surpasses the droop response range, the charging current was set to its min/max value. The regulation rules are listed in Equation (
3).
The VDM was set to only take actions at every fixed time step to prevent the massive oscillations of the current. The trigger timing of the VDM can be adjusted and is synchronised with the simulation time steps. The charging current alteration versus node voltage is plotted in
Figure 1b.
2.3. Average Rate Method
The ARM is relatively simple yet fairly effective for grid congestion prevention, and it was selected from existing work [
39]. The ARM reduces the charging impact on the grid while acknowledging the user’s requirement and will ensure the full charge of the EV if the user indeed departs as indicated. The ARM spreads out the charging process along the whole EV parking duration, which is only possible if each of the EV users’ arrival time
, departure time
and required energy demand
are known. The diagram of the ARM is shown in
Figure 1c.
Equation (
4) depicts how the charging power of EV
j (
) is determined. The
was calculated and compared with the base power of the EV and charger combination (
) as well as the minimal charging power
, which was determined by the minimum charging current of 6 A. Afterwards, the ARM charging power was rounded so that the charging current is an integer.
The effectiveness of the ARM is directly related to the duration of the EV parking time within a certain range: the longer the EV parks, the more likely the charging power is to get lower. However, the charging power cannot be infinitely small due to the constraint. This constraint leads to the EV parking duration and energy demand being no longer important after a certain threshold. All EVs will be charged with the minimal power in that situation. On the contrary, a very short parking time could deteriorate the efficacy of the ARM when the value of is close to . Additionally, the performance of the ARM is also sensitive to the arrival time; for example, if an EV arrives 1–2 h before the peak hour and leaves after the peak hour. Compared to the UNC, with which, the charging process would have been finished before the peak hour, the ARM prolongs the charging process starting from the valley moment and unnecessarily extends the whole charging process to the peak hours. This might lead to an elevated peak loading in the grid.
3. Simulation Methodology and System Information
The comparison of three different EV charging scheduling methods was accomplished by PowerFactory simulations and Python data analysis. The simulations of six grids with four EV penetration levels in one winter week and one summer week were conducted with 10 min resolution. Three charging methods were compared with each other, as well as compared to the UNC method from grid performance and charging cost perspectives, as well as charging completion perspective. UNC method was designated in this paper as immediate EV charging with its rated power as soon as the EV is plugged into the charger.
The six tested grids were real Dutch LV distribution grids provided by the Dutch Distribution system operator (DSO). The tested grids were categorised into three types based on their geographical and functional features, namely rural (RR) grids, suburban (SUB) grids and urban (UB) grids, with two grids per type being considered. The detailed grid features can be found in
Table 2.
The grid baseload profile was modelled based on the load features that were contained in the grid models and the Dutch standardised load profiles [
48]. The standard profiles for a 1000 kWh yearly energy consumption load is presented in
Figure 3. The profile name in the figure depicts the electrical load type in various scales and patterns. The PV profile modelling was based on a previous study [
49]. The one-minute resolution sample profile of a 1 kWp PV installation is shown in
Figure 4. It was assumed in this study that RR grids have 25% PV penetration, SUB grids contain a 15% PV penetration and, in UB grid, there is only 5% PV penetration. It was also assumed that, for each installation, the PV peak power is 2.5 kW [
50,
51].
In this study, the EV data consisted of two parts: one part is the EV fleet composition and the other part is the EV users’ charging habits, including EV arrival time, EV parking time, energy requests and the EV charging frequency. The EV fleet selection was based on the Dutch market data [
52]. Top 10 EV models whose battery capacities vary from 35.8 to 90 kWh were modelled in the simulation. The EV charging behaviour data are based on a study that contains 1.5 M real EV charging sessions from charger measurements [
53,
54]. The charging sessions can be classified into three typical groups subject to their temporal–spatial features, such as charging location, time of arrival and parking duration. These three groups were identified as home, semi-public and public charging session types, as explained in [
6]. The share of charging session groups per grid type is as follows: 70% of the total charging sessions in RR grids are home type and this value is 50% for SUB grid and 25% for UB grids. The rest of the charging sessions were equally divided into semi-public and public types [
52]. The probability distribution curves of EV arrival time, EV connection time and charging energy requests of three charging session types are shown in
Figure 5.
Finally, the modelling of EV charging profile was accomplished by combining the EV fleet data and the EV charging behaviour. The EV chargers were modelled as LV loads in the grid, and they were all assumed to be three-phase AC chargers with a 32 A max per phase connection. The increase in EV penetration was modelled as the growth in EV charging sessions, and, subsequently, the rising charger numbers. The EV charging sessions, the location and the capacity of the chargers in the lower EV penetration level were retained. This modelling method also ensures that the only difference between a higher and a lower EV penetration level in a particular grid is the additional EV charging sessions. In addition, all of the charging sessions, including arrival–departure time, arrival SoC and energy demand, were exactly the same for the four charging methods. A detailed description of the grid models and how the simulation data were generated can be found in our previous work [
55].
4. Comparative Simulation Results for Grid Performance with Different Charging Schemes
In this section, the impact of ARM, VDM and PSM1 on the grid performance in terms of grid congestion alleviation, loading value distribution and overloading on each element is assessed and compared with UNC.
4.1. Grid Congestion Alleviation and Charging Session Feature Correlations
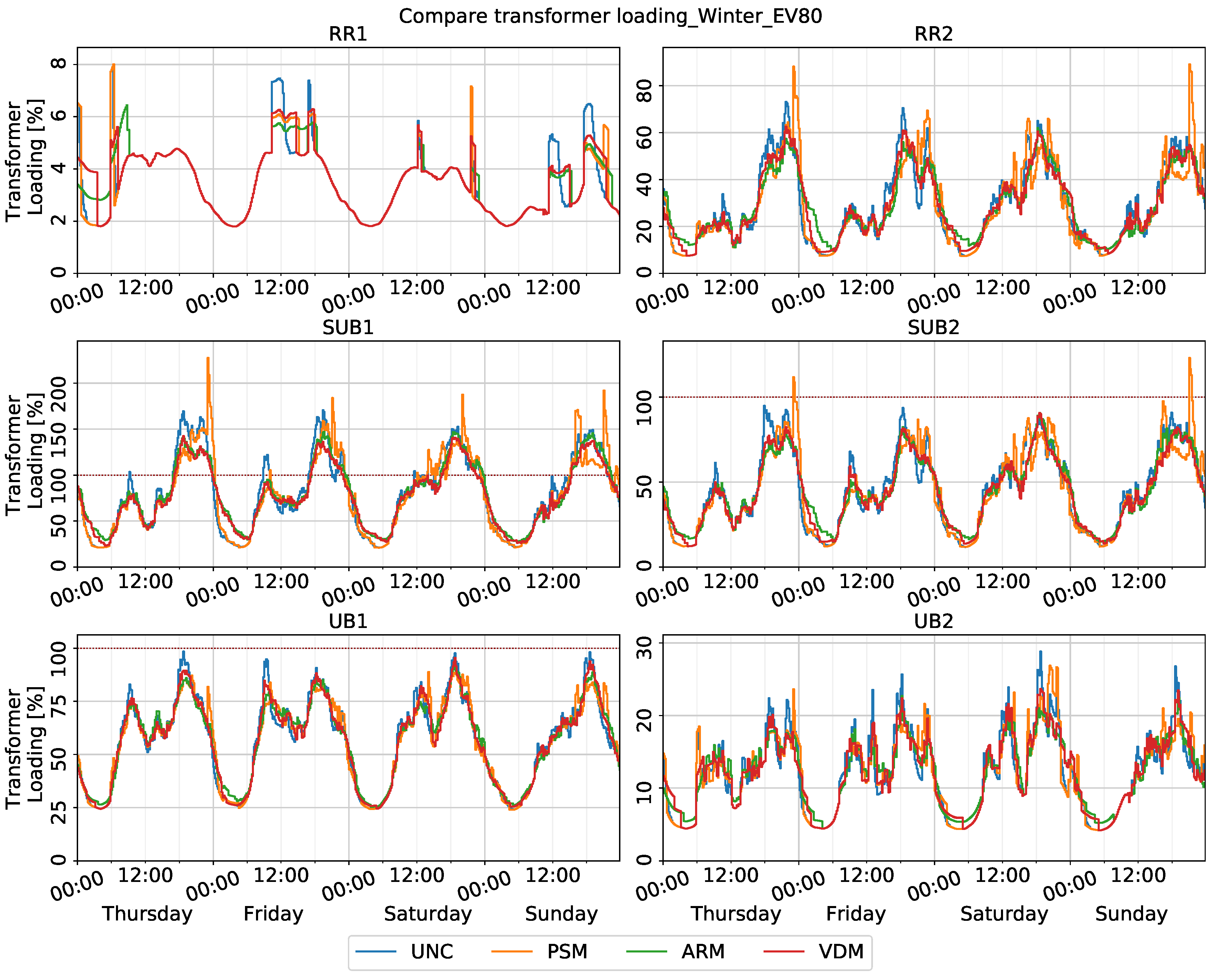
In
Figure 6, the transformer loading of four charging methods in an EV 80% scenario in winter is presented, with time as the x-axis. It can be observed that the peak transformer loading is reduced with the ARM and VDM relative to UNC, whereas it is higher with PSM1. This tendency is particularly relevant for both SUB grids as well as UB2 and RR2 with a high EV penetration, posing a risk of higher overloads if the PSM is used. For example, in the SUB1 grid with EV80 scenario, the topmost transformer loading value of the PSM is 28.7% higher than the UNC and 59.71% higher than the VDM highest transformer loading value.
However, while the PSM mitigates the morning peaks and partial evening peaks that are spotted in UNC, shifted new spikes arise later in the evening between 19:00 and 24:00. This is because the PSM curtails the EV charging power and restricts the energy being delivered during the high-energy-price period. When the energy price drops so that the power restriction is lifted, the stockpiled charging demand of yet-connected EVs is released simultaneously, resulting in an abrupt power spike. It can be inferred that this shifted excessive peak demand phenomenon is exacerbated when the most frequent EV arrival time coincides with the peak of the baseload. This is especially the case when a long parking time is expected in the arrived EVs, which is typical for home charging sessions, as shown in the arrival distribution curve exhibited in
Figure 5. On the other hand, semi-public and public charging sessions have relatively short parking times and the EVs arrive less frequently in the evening, which coincides with the base-load peak moment. It is also less likely to have a public or semi-public charging session with a duration that extends beyond the evening peak hours and, therefore, most charging events are expected to be completed before the peak hour restriction imposed by the PSM is lifted. Consequently, the shifted peak phenomenon induced by the PSM is significant for SUB grids, in which, home chargers are dominant, and is not observable in UB grids where a higher proportion of public and semi-public charging sessions occur. Based on these inferences, it is suggested that grids with a higher proportion of home chargers are more sensitive to the worsening of the peak load due to PSM charging. At the same time, the expected benefit in terms of cost minimisation and charging demand fulfilment can be lower where short parking times and uniform arrival times dominate, as is the case with public and semi-public chargers; this shall be explored in subsequent sections. Additionally, the profile in
Figure 6 shows a peak loading shifting phenomenon between weekdays and weekends, but no essential charging method performance change is observed.
4.2. Loading Value Distribution Exploration
The numerical distribution analysis on loading values was performed in our study and the maximum line loading among all lines at every moment in one winter week is shown in
Figure 7. The bottom and top edge of the box indicate the 25–75% quantile of the data distribution and the top and the bottom of the I-shape line mark the 1.5–98.5% quantile of the data distribution. The short dashed line in the middle of the colour box signifies the median of all of the data points and the white dot points out the average value of this data group. From this plot, one can recognise that the PSM still exacerbates the line overloading issue, yet it does lower the 25–75% quantile range relative to the UNC results. It is further observed that a slight reduction in the average value of maximum line loading is achieved with the PSM, ARM and VDM-based charging relative to the UNC method, except for three cases in the PSM (RR1 with EV20 and 50, UB1 with EV20) and two cases in the VDM (RR1 with EV20 and 50). The highest reduction in the mean value of the maximum line loading of 7.74% is reached by the VDM in the SUB1 grid with the EV80 scenario. This result hints that all three charging methods are useful in reducing line loading in the majority of cases. Regarding transformer loading, the margin of the mean and median loading value among all cases is less than 3.5%. In addition, the 25–75% quantile range of the PSM is enlarged in comparison to UNC whereas both the ARM and VDM have a narrower 25–75% quantile range. This implies that the ARM and VDM are effective in not only lowering the peak loading but also in smoothing the loading curve, which makes the data points more concentrated around their median values. This can be clearly pinpointed in
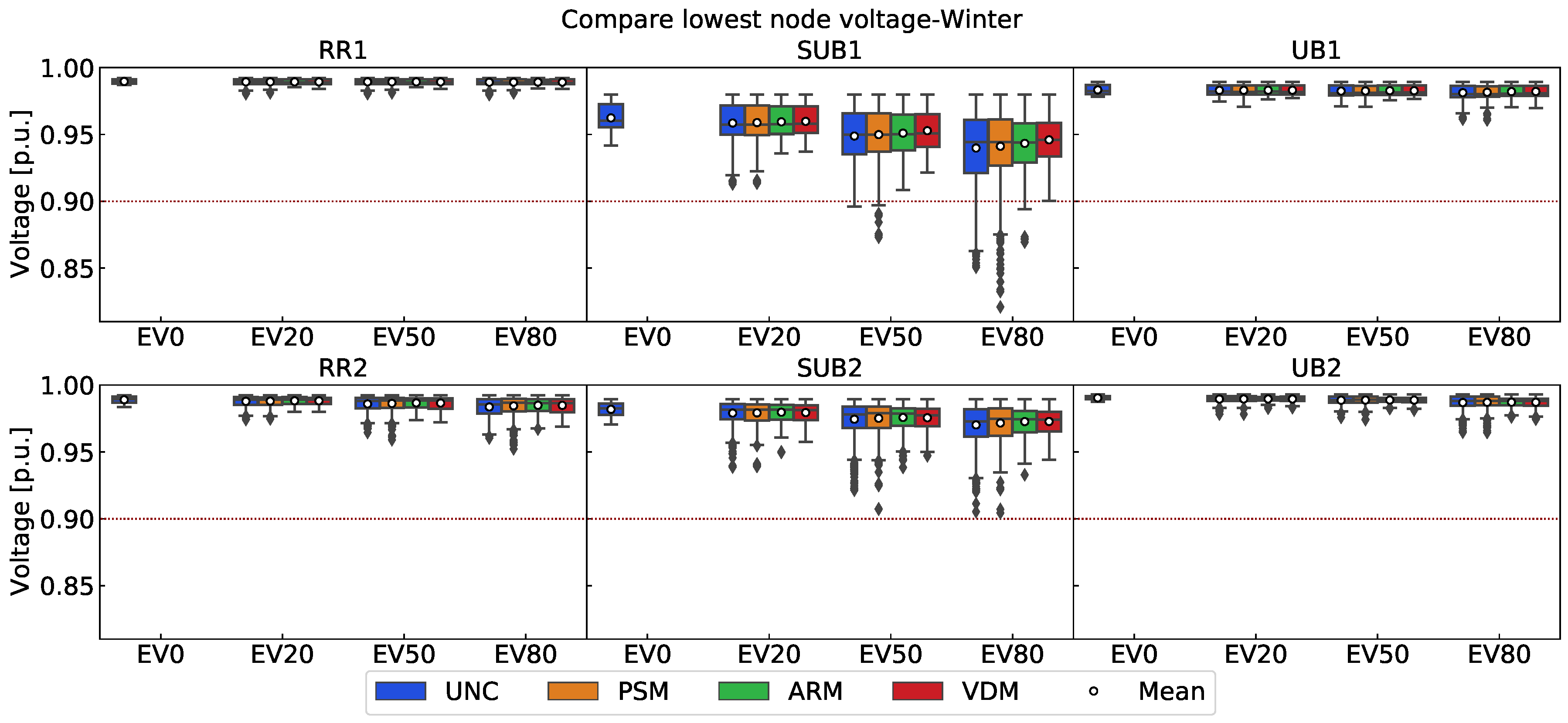
Figure 6 as well. The distribution analysis of the minimum node voltage delivers a consistent conclusion, as can be observed in
Figure 8. Additionally, the VDM charging scheme performs the best in limiting the greatest voltage drop in the grid, even compared to the ARM.
4.3. Overloading Assessment on Individual Element
A spatial examination of line loading and node voltage distribution along the course of the branch reveals how four charging methods diverge the congestion level of each line and each node.
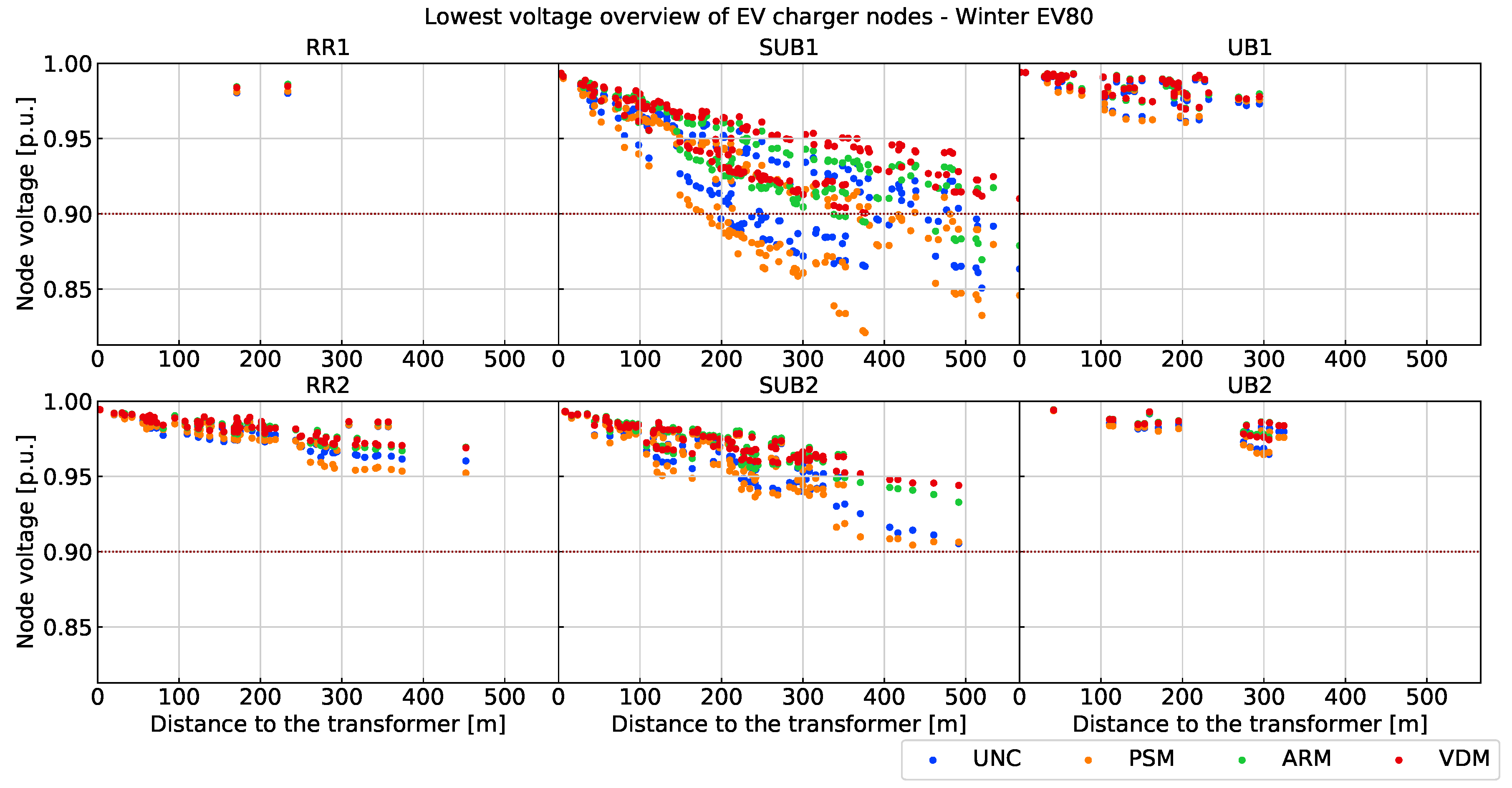
A scatter plot of the minimum voltage of each EV-connected node versus their distance toward the transformer is presented in
Figure 9. The minimal node voltage decreases proportionally to their distance to the transformer. The VDM successfully brings the lowest node voltage back from 0.8506 p.u. with UNC to above 0.9 p.u.. Moreover, the percentage of nodes that ever encountered under-voltage with the VDM reaches 0% instead of 23.53% for UNC. The ARM also has a considerable under-voltage avoidance ability, where, in the SUB1 grid, the minimum voltage is improved to 0.8695 p.u., whereas the percentage of nodes that have under-voltage problems drops to 5.27% Even though the PSM aggravates the voltage droop problem, none of the nodes experience under-voltage in RR, UB and SUB2 grids.
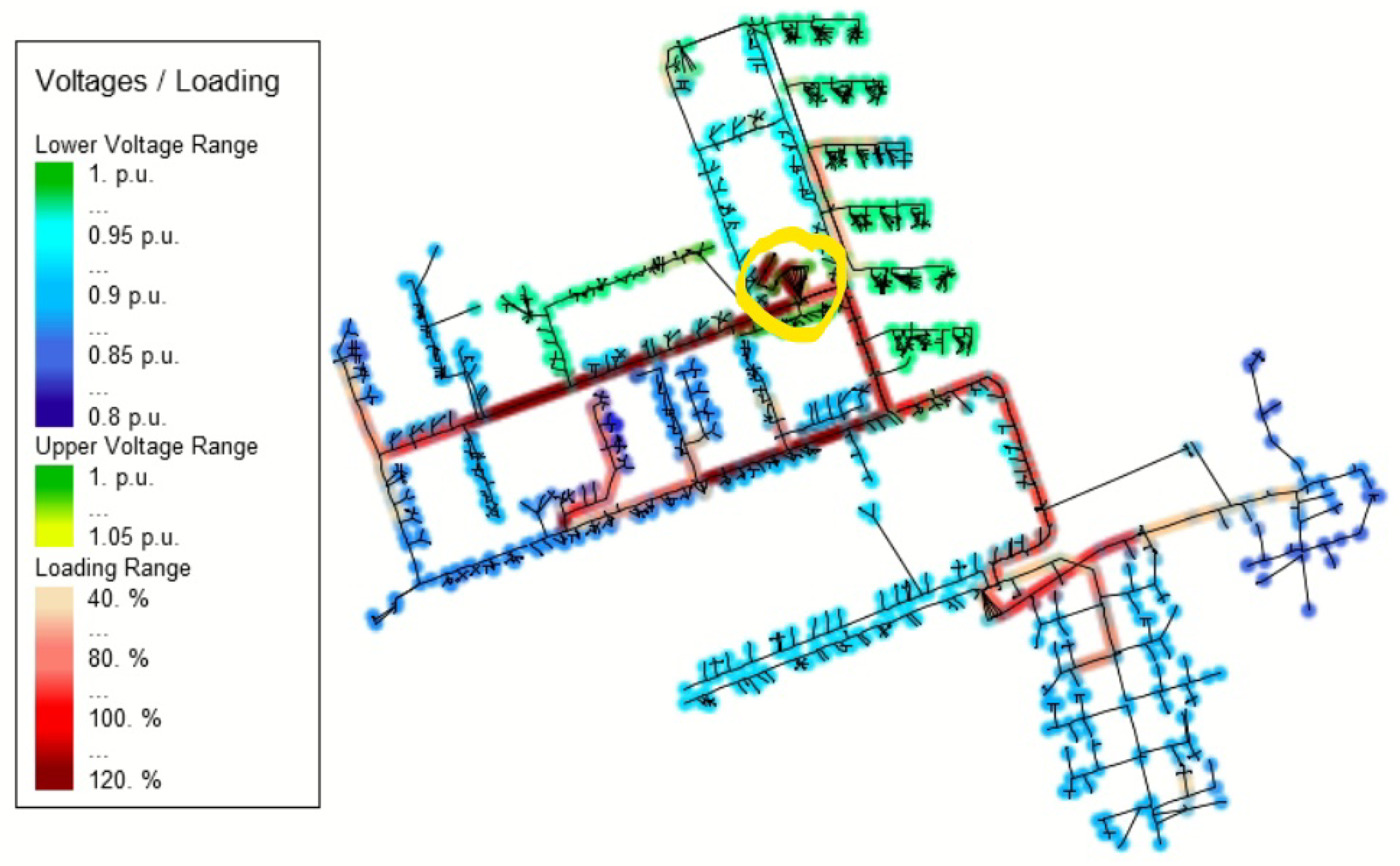
The PSM aggravates the maximum loading of a large number of lines, especially the lines that are closer to the transformer in SUB and UB grids. Many of these lines are part of the main branches; this implies that a simultaneous load growth happens in their downstream sub-branches. The raised loadings that are developed in the sub-branches are passed on to the upper stream main feeders and thus cause this excessive and aggregated main feeder overloading. One example can be seen in
Figure 10, in which, the grid loading heatmap of the SUB1 grid with the PSM1 charging method with EV 80% penetration in winter is exhibited. This heatmap is captured at the highest line loading moment, and the yellow circle denotes the location of the transformer.
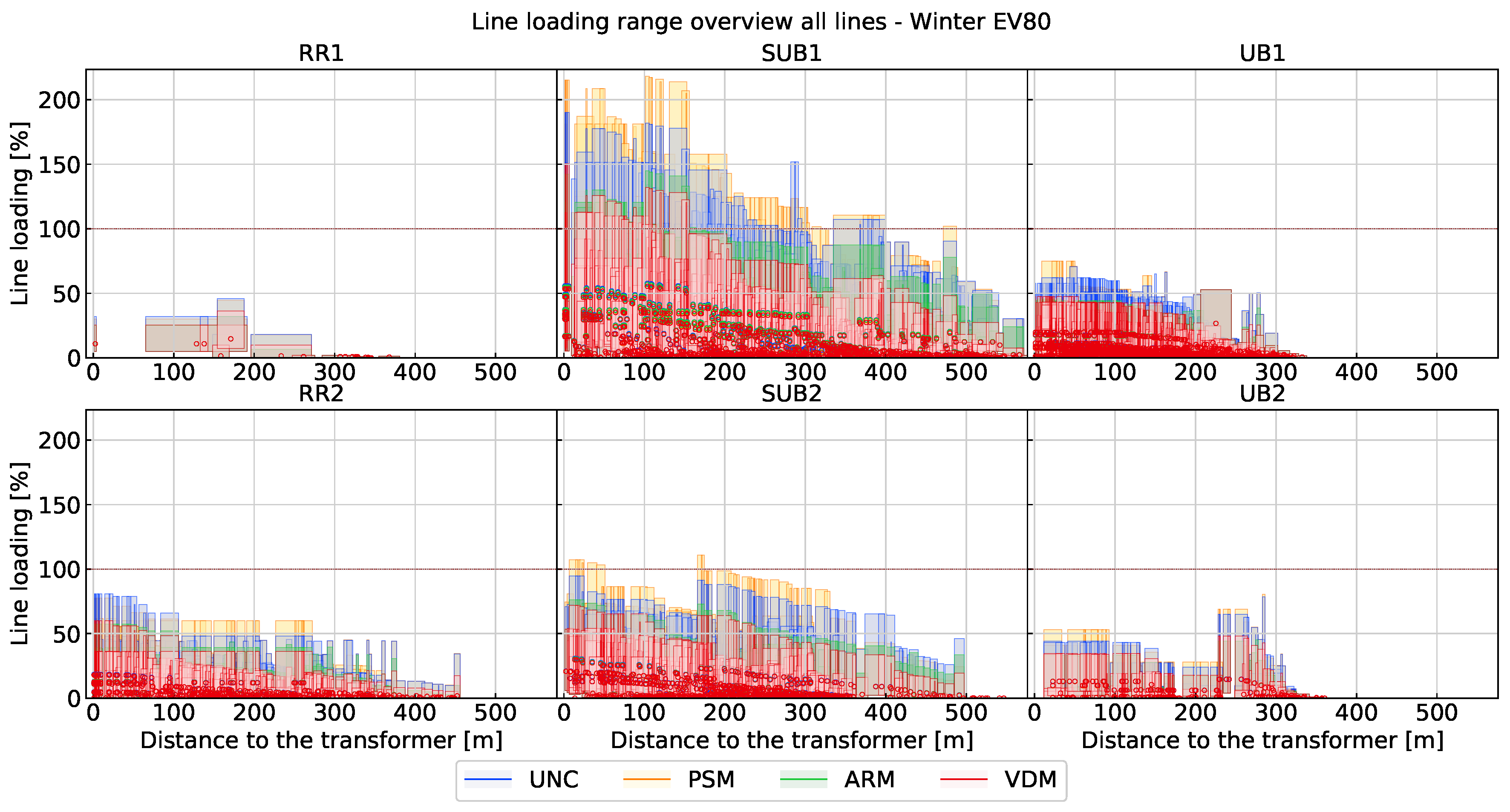
In addition, for every charging method in a particular grid, the maximum line loading has a tendency to decline when its distance to the transformer increases. This trend is clearly shown in the loading distribution plot (
Figure 11) of all lines during the whole simulation period. The ARM has the smallest slope of line loading versus distance to the transformer in comparison with other charging methods. That is due to the ARM being the only method that curtails the charging power at every possible moment, and the charging power is constant once the procedure starts. As for the VDM, it curtails the maximum loading of every line the most among all charging methods.
After all, the ARM successfully restrains the charging current of every charging session at every moment within a very low range. A total of 92.61% of the charging current is lower than 10 A for the ARM, whereas this value is 46.49% for UNC, 60.33% for PSM1 and 82.79% for VDM.
4.4. Key Takeaways
The VDM functions the best in mitigating the grid loading in all grids from three aspects, and the ARM is the runner-up. Although a previous study [
20] obtained a non-ideal grid congestion relief effect using a droop response range lower than 0.9 p.u, our results suggest that the VDM is a parameter-sensitive method. If the voltage boundary is set properly, the grid congestion mitigation could be improved considerably. At the same time, the VDM achieves the given performance solely based on local node voltage measurement, which can be preferable when user information regarding the parking time and energy demand is not available consistently, which is an essential requirement for the ARM.
Despite the fact that the PSM exacerbates the grid peak loading magnitude in SUB and RR grids, it still contributes to shortening the overloading duration even in the most overloaded SUB1 grid with an 80% EV penetration. The grid, 69.74% of the time, does not have any kind of grid limitation violation, and the PSM improves it to 70.54% of the time. This value is 72.22% for the ARM and 73.81% for the VDM. The PSM causes worse overloading spikes in grids with a large portion of home charging sessions, but it works well to alleviate the loading in UB grids by shifting the charging demand peak to a later less congested moment. Therefore, the proposed PSM is still a good choice for grids with lower EV penetration levels and with a lower portion of home charging sessions, particularly considering the benefits related to charging costs, as shall be later explored.
5. PSM Scheme Analysis
To further explore the grid performance deterioration due to the shifted higher peak caused by the PSM, the total EV charging power per grid with three PSM schemes of the EV 80% scenario are compared in this section. The purpose is to see the grid impact when different heuristic restrictions are imposed by using different price signals and various price segment division methods. The sum of all EV charging power with three PSM schemes in three grids (one each type) for four days in winter (two weekdays and two weekends) with an EV 80% penetration level is shown in
Figure 12. The sum EV charging power of UNC, as well as the total baseload power, are also presented for reference. The daily price segment schematics of three PSM schemes are displayed in the same plot.
From this graph, it can be spotted that the evening peaks of the EV charging power are postponed and substantially boosted by all PSM schemes in comparison with UNC. This transition happens when the price segment switches from medium to low, causing the charging current limit to shift from 50% to no limit. PSM2 delays the evening peaks further and it decreases the peak amplitude compared to PSM1. This is because PSM2 has a longer duration of low and medium price segments than PSM1, and the EVs have less time to charge with a higher power during the day. On Saturday afternoon at 14:00, PSM2 causes an extremely high power spike in comparison to PSM1 and PSM3. The reason behind this can be found in the PSM2 price segment plot. On Saturday at 14:00, the price jumped from the high segment to the low segment, which means that the charging current limit leaps directly from the minimum level to the maximum level. All of the connected EVs that were charging with minimum current were all tuned to their maximum charging current simultaneously, leading to this high peak value. Comparatively, PSM3 has the best relative performance regarding delaying the power peak as close to the valley moment as possible and lowering the peak power values with the help of the baseload trend adapted price signal. For the overnight charging EVs, the switch to the maximum charging current moment can be further delayed to between 2 and 6 a.m. the next day when the baseload hits its lowest point.
The natural limitation of the PSM is that, for every round of the price division segment update, it only looks at the 24 h time window from 00:00 to 00:00 the next day, though most home charging sessions with EVs arriving at night would stay overnight. Nonetheless, the renewed price segment starts at 00:00, making the overnight charging control lack continuity. There are two approaches that could potentially resolve this problem. One is to diminish the length of the low price segment and, additionally, to force the medium–maximum charging current transition moment to occur only between 2 and 6 a.m. Another approach is to renew the price segment with a higher frequency and shorten the total control length from 24 h to, for example, 12 h. Because the DAM price of the next day releases at 12:00, the price of the next day can be involved in the new price segment division after 12:00. A potential beneficial point at which to renew the price segment is 18:00, when the evening peak starts. Once the price segment division plan and update frequency are improved as recommended, we believe that the PSM can also be quite effective in lowering the grid loading.
6. Charging Process Evaluation
In this section, how the charging process is influenced by three methods is evaluated from charging cost and charging satisfaction perspectives.
6.1. Charging Completion
It is assumed that, with UNC, the charging process is terminated when the EV battery is full or when the charged energy reaches the user’s expectation. For the exact same charging session, the energy charged with UNC is set as a target for comparison. Due to the nature of the ARM, all of the charging requests input by users in advance are fulfilled, but thus is not the case for the PSM and VDM. This is primarily due to the fact that these techniques do not factor in the information related to the energy demand or the parking time of the EV. The comparison of the charging demand completion of EV 80% in one winter week is displayed in
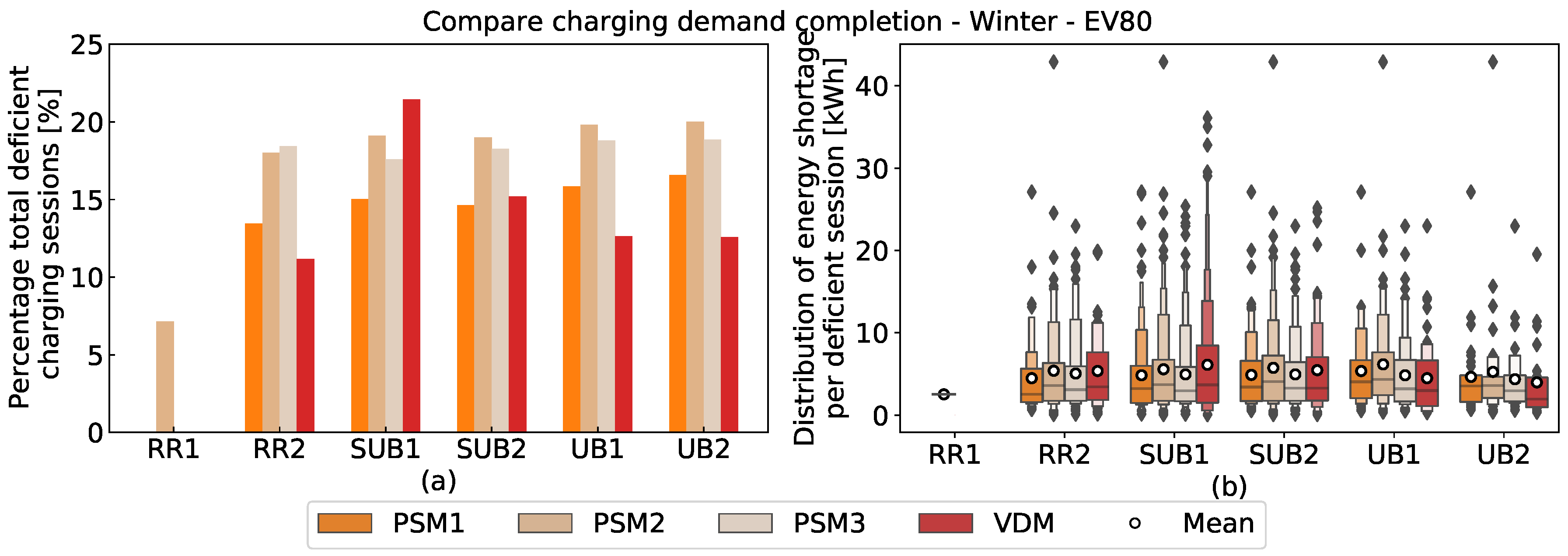
Figure 13. In this figure, (a) shows the percentage events of total events whose charged energy is less than the UNC method, whereas (b) shows, among all of these deficient charging events, the distribution of per-session incomplete charging energy.
From
Figure 13, it can be noticed that the charging completion of the VDM is similar to or better than the PSM, except for SUB grids. This is correlated with the grid congestion levels. The VDM directly responds to the grid condition and, in the simulations of this research, the node voltage value is strongly synchronised with the overall grid congestion. For SUB grids, there are more occasions with a longer duration of grid overloading in comparison with the other two types of grids as shown in
Section 4. The VDM limits the charging current, especially when the voltage is low, whereas SUB1 grids have the highest duration and scale of voltage drops, leading to a strict charging current limitation. As a result, the energy demand of 20.04% of sessions in SUB1 grids is not fulfilled because of the limitation in comparison with the PSM (on average 17.07%) and ARM (0%).
For all grids, all PSM schemes have a similar and stable influence regarding charging completion in both percentages of the deficient session and deficient energy per session. It is easy to interpret that all EVs in all grids use the same centralised control rule and that no other variables are involved in this charging tuning procedure, unlike the VDM, which uses varying local voltages. However, among the three PSM charging schemes, PSM2 has the highest charging demand incomplete rate. As explained in
Section 5, the control scheme of PSM2 extends the duration of maximum and medium price segments, which correspond to the minimum and 50% of the full charging current. This means that more EVs have to charge with a lower power for a longer time, which might be even longer than the EV parking time, eventually causing this highest unfinished charging ratio.
6.2. Charging Cost
How three charging methods influence the charging cost in comparison with UNC is studied in this section. Both absolute and relative costs were analysed considering the charging demand completion rate as diverse between methods, even with the exact same charging session. The total charging cost (
) and the total charging energy (
) from all six grids, as well as the ratio of total savings (
) and the total energy-deficient ratio (
) of all charging methods with respect to UNC with 80% EV in winter are summarised in
Table 3.
It should be noted that the total energy charged with the ARM being higher than UNC is due to the simulation setup and the data resolution. For every time step (10 min in the simulation), the charging current of the ARM is constant and the minimum value is 6 A; thus, the minimum chargeable energy for a three-phase connection EV per step is 0.69 kWh. If the energy to be charged by referring to UNC is less than this value, the higher charged energy situation happens. In the meantime, there is an overcharge prevention mechanism to ensure that SoC never exceeds 1. From this table, it can be perceived that both the PSM and ARM reduce the charging cost and that PSM2 saves the most expenses. For the PSM, the value of the saved cost is correlated with the energy-deficient ratio, whereas the ARM does not compromise the energy being delivered. On the other hand, the VDM is the only method that costs more to charge but obtains less energy for EV users.
Every charging session has various energy demands and uses divergent price values. Hence, a comparative charging cost factor () is introduced for a fair comparison, with the charging sessions of UNC as the benchmark.
For every charging session, the relative charging cost of method
(one of PSM, ARM and VDM) is first calculated by
, where
is the charging cost of session
k with method
and
is the charging cost of the same session but charged with UNC. Since not all of the energy demand is fulfilled in every charging session, especially with methods PSM and VDM, a charging fulfilment correction factor is introduced to correct the charging cost reduction due to the charging energy deficiency. The correction factor is calculated by
, where
is the delivered energy with method UNC and
is the charging energy delivered with method
. The equation of the
calculation is shown in Equation (
5).
The comparative charging cost factor
of every charging session with all charging schedule methods is visualised in the box plot in
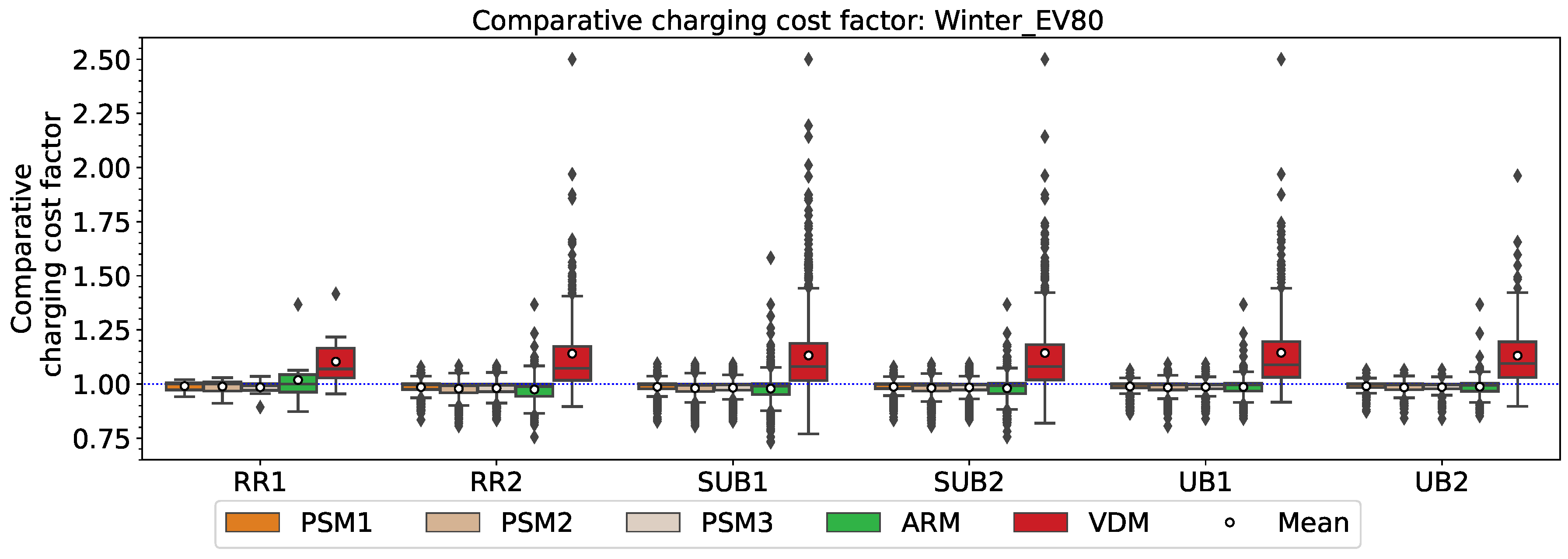
Figure 14. From this figure, it can be concluded that both the ARM and PSM can reduce the charging price decently. Aside from the ARM in RR1, the PSM and ARM both have a mean
value lower than 1 in all of the other grids. On average, 31.63% of PSM charging sessions have a
value higher than 1 and they are solely caused by unfulfilled charging energy requests. With the ARM, this value is 30.83%. On the contrary, on average, 83.12% of VDM sessions have a significantly higher
value because of both the high charging cost and unfinished charging requests. On the other hand, the VDM is excellent from a grid congestion perspective as seen in the previous section. The
difference among PSM1, PSM2 and PSM3 is negligible. PSM2 has the lowest minimum
value, as it has prolonged half and minimum charging limit time windows, where many EVs are charged more during the low price window.
7. Conclusions
Simple smart charging techniques such as the PSM, ARM and VDM were compared with UNC in terms of the grid performance, charging demand fulfilment and economic benefits. These trends were quantified for different grid types with an increasing EV penetration for summer and winter, and the following are the main observations:
The VDM is the most effective in improving the grid performance peak and median loading, as well as the node voltage drops relative to UNC, whereas the PSM can worsen the performance, particularly for suburban grids, where the percentage of home chargers is high.
The ARM is most effective in simultaneously improving the grid performance and meeting the user energy demand. On the contrary, both the PSM and VDM lead to 10–20% unfinished charging sessions, with a total energy deficiency ratio of 4–8%.
The PSM can reduce the total charging cost by 6–11% relative to UNC and the ARM leading to cost savings of 2–4%. On the other hand, the VDM increases the charging cost by 0–2%.
From the study results, we can conclude that the PSM can be a preferred strategy for achieving a charging cost reduction where the grid performance is not a bottleneck for the given EV penetration. We also have confidence in the PSM concerning grid congestion alleviation if (1) the price signal can reflect the base load fluctuating and (2) the price segment division is updated so that the beginning moment of full power charging for overnight EVs can be shifted to 2–6 a.m. At the same time, the VDM should be preferred if user information on the parking time and energy demand is not consistently available. The ARM provides the best balance in the trade-offs associated with the mitigation of grid congestion and price reduction, as well as charging completion. However, user information related to the EV parking time and energy demand is necessary. The qualitative benefits and operational requirements of the explored charging schemes are summarised in
Table 4.
For future work, several points can be covered further. Sensitivity analyses on more PSM price signal sources, as well as price segment division methods, can be beneficial. It could be appealing to investigate how the voltage droop response range impacts the VDM performance. In addition, it is worth inspecting how the node voltage fluctuates in between voltage droop command signal intervals. Last but not the least, the EV battery lifetime is a critical aspect that must be investigated in future work to compare the performance of these different charging methods.
Author Contributions
Y.Y.: Conceptualisation, methodology, software, validation, formal analysis, investigation, visualisation, writing—original draft; A.S.: Validation, formal analysis, writing, editing; G.R.C.M.: Reviewing, supervision; P.B.: Supervision, project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Electric Mobility Europe (EMEurope).
Acknowledgments
This research is part of the Orchestrating Smart Charging in mass Deployment (OSCD) project, which is funded by Electric Mobility Europe (EMEurope). The authors would like to thank Dutch DSO Enexis for providing the grid data. We would also like to thank the project partner ElaadNL for their support in EV charging data.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| EV | Electric Vehicle | TOU | Time of Use |
| LV | Low Voltage | SoC | State of Charge |
| UNC | Uncontrolled Charging | DAM | Day-ahead Market |
| PSM | Price-Signal Method | IDM | Intra-day Market |
| ARM | Average Rate Method | DSO | Distribution System Operator |
| VDM | Voltage Droop Method | RR | Rural |
| DA | Day Ahead | SUB | Suburban |
| RT | Real Time | UB | Urban |
References
- Lillebo, M.; Zaferanlouei, S.; Zecchino, A.; Farahmand, H. Impact of large-scale EV integration and fast chargers in a Norwegian LV grid. J. Eng. 2019, 2019, 5104–5108. [Google Scholar] [CrossRef]
- Calearo, L.; Thingvad, A.; Suzuki, K.; Marinelli, M. Grid Loading Due to EV Charging Profiles Based on Pseudo-Real Driving Pattern and User Behavior. IEEE Trans. Transp. Electrif. 2019, 5, 683–694. [Google Scholar] [CrossRef]
- Crozier, C.; Morstyn, T.; McCulloch, M. The opportunity for smart charging to mitigate the impact of electric vehicles on transmission and distribution systems. Appl. Energy 2020, 268, 114973. [Google Scholar] [CrossRef]
- Wagh, S.; Yu, Y.; Shekhar, A.; Mouli, G.C.R.; Bauer, P. Aggregated Impact of EV Charger Type and EV Penetration level in Improving PV Integration in Distribution Grids. In Proceedings of the 2021 IEEE Transportation Electrification Conference Expo (ITEC), Chicago, IL, USA, 23–25 June 2021. [Google Scholar]
- Stiasny, J.; Zufferey, T.; Pareschi, G.; Toffanin, D.; Hug, G.; Boulouchos, K. Sensitivity analysis of electric vehicle impact on low-voltage distribution grids. Electr. Power Syst. Res. 2021, 191, 106696. [Google Scholar] [CrossRef]
- Yu, Y.; Shekhar, A.; Mouli, G.C.R.; Bauer, P.; Refa, N.; Bernards, R. Impact of Uncontrolled Charging with Mass Deployment of Electric Vehicles on Low Voltage Distribution Networks. In Proceedings of the 2020 IEEE Transportation Electrification Conference Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; pp. 766–772. [Google Scholar] [CrossRef]
- Nimalsiri, N.I.; Mediwaththe, C.P.; Ratnam, E.L.; Shaw, M.; Smith, D.B.; Halgamuge, S.K. A Survey of Algorithms for Distributed Charging Control of Electric Vehicles in Smart Grid. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4497–4515. [Google Scholar] [CrossRef]
- Hussain, M.T.; Sulaiman, D.N.B.; Hussain, M.S.; Jabir, M. Optimal Management strategies to solve issues of grid having Electric Vehicles (EV): A review. J. Energy Storage 2021, 33, 102114. [Google Scholar] [CrossRef]
- Mobarak, M.H.; Bauman, J. Vehicle-Directed Smart Charging Strategies to Mitigate the Effect of Long-Range EV Charging on Distribution Transformer Aging. IEEE Trans. Transp. Electrif. 2019, 5, 1097–1111. [Google Scholar] [CrossRef]
- Dimitroulis, P.; Alamaniotis, M. A fuzzy logic energy management system of on-grid electrical system for residential prosumers. Electr. Power Syst. Res. 2022, 202, 107621. [Google Scholar] [CrossRef]
- Cardona, J.E.; López, J.C.; Rider, M.J. Decentralized electric vehicles charging coordination using only local voltage magnitude measurements. Electr. Power Syst. Res. 2018, 161, 139–151. [Google Scholar] [CrossRef]
- Hogeveen, P.; Steinbuch, M.; Verbong, G.; Wargers, A. Revisiting static charge schedules for electric vehicles as temporary solution to low-voltage grid congestion with recent charging and grid data. Sustain. Energy Grids Netw. 2022, 31, 100701. [Google Scholar] [CrossRef]
- Chandra Mouli, G.R.; Kefayati, M.; Baldick, R.; Bauer, P. Integrated PV Charging of EV Fleet Based on Energy Prices, V2G, and Offer of Reserves. IEEE Trans. Smart Grid 2019, 10, 1313–1325. [Google Scholar] [CrossRef]
- Frendo, O.; Gaertner, N.; Stuckenschmidt, H. Real-Time Smart Charging Based on Precomputed Schedules. IEEE Trans. Smart Grid 2019, 10, 6921–6932. [Google Scholar] [CrossRef]
- Zhou, K.; Cai, L. Randomized PHEV Charging Under Distribution Grid Constraints. IEEE Trans. Smart Grid 2014, 5, 879–887. [Google Scholar] [CrossRef]
- Kumar, K.N.; Sivaneasan, B.; So, P.L. Impact of Priority Criteria on Electric Vehicle Charge Scheduling. IEEE Trans. Transp. Electrif. 2015, 1, 200–210. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, Q.; Shahidehpour, M.; Li, C.; Huang, S.; Wei, W. Transactive Real-Time Electric Vehicle Charging Management for Commercial Buildings With PV On-Site Generation. IEEE Trans. Smart Grid 2019, 10, 4939–4950. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, B.; Kezunovic, M. Optimized Operational Cost Reduction for an EV Charging Station Integrated With Battery Energy Storage and PV Generation. IEEE Trans. Smart Grid 2019, 10, 2096–2106. [Google Scholar] [CrossRef]
- Liao, Y.T.; Lu, C.N. Dispatch of EV Charging Station Energy Resources for Sustainable Mobility. IEEE Trans. Transp. Electrif. 2015, 1, 86–93. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, S.; Ye, J. A Novel Online Scheduling Algorithm and Hierarchical Protocol for Large-Scale EV Charging Coordination. IEEE Access 2019, 7, 101376–101387. [Google Scholar] [CrossRef]
- Vagropoulos, S.I.; Kyriazidis, D.K.; Bakirtzis, A.G. Real-Time Charging Management Framework for Electric Vehicle Aggregators in a Market Environment. IEEE Trans. Smart Grid 2016, 7, 948–957. [Google Scholar] [CrossRef]
- Wu, D.; Zeng, H.; Lu, C.; Boulet, B. Two-Stage Energy Management for Office Buildings With Workplace EV Charging and Renewable Energy. IEEE Trans. Transp. Electrif. 2017, 3, 225–237. [Google Scholar] [CrossRef]
- Cao, Y.; Tang, S.; Li, C.; Zhang, P.; Tan, Y.; Zhang, Z.; Li, J. An Optimized EV Charging Model Considering TOU Price and SOC Curve. IEEE Trans. Smart Grid 2012, 3, 388–393. [Google Scholar] [CrossRef]
- Clairand, J.M.; Rodríguez-García, J.; Álvarez Bel, C. Smart Charging for Electric Vehicle Aggregators Considering Users’ Preferences. IEEE Access 2018, 6, 54624–54635. [Google Scholar] [CrossRef]
- Dubey, A.; Santoso, S. Electric Vehicle Charging on Residential Distribution Systems: Impacts and Mitigations. IEEE Access 2015, 3, 1871–1893. [Google Scholar] [CrossRef]
- Olivella-Rosell, P.; Villafafila-Robles, R.; Sumper, A.; Bergas-Jané, J. Probabilistic Agent-Based Model of Electric Vehicle Charging Demand to Analyse the Impact on Distribution Networks. Energies 2015, 8, 4160–4187. [Google Scholar] [CrossRef]
- Steen, D.; Tuan, L.A.; Carlson, O.; Bertling, L. Assessment of Electric Vehicle Charging Scenarios Based on Demographical Data. IEEE Trans. Smart Grid 2012, 3, 1457–1468. [Google Scholar] [CrossRef]
- Veldman, E.; Verzijlbergh, R.A. Distribution Grid Impacts of Smart Electric Vehicle Charging From Different Perspectives. IEEE Trans. Smart Grid 2015, 6, 333–342. [Google Scholar] [CrossRef]
- Humayd, A.S.B.; Bhattacharya, K. A Novel Framework for Evaluating Maximum PEV Penetration Into Distribution Systems. IEEE Trans. Smart Grid 2018, 9, 2741–2751. [Google Scholar] [CrossRef]
- Zaferanlouei, S.; Lakshmanan, V.; Bjarghov, S.; Farahmand, H.; Korpås, M. BATTPOWER application: Large-scale integration of EVs in an active distribution grid–A Norwegian case study. Electr. Power Syst. Res. 2022, 209, 107967. [Google Scholar] [CrossRef]
- Fahmy, S.; Gupta, R.; Paolone, M. Grid-aware distributed control of electric vehicle charging stations in active distribution grids. Electr. Power Syst. Res. 2020, 189, 106697. [Google Scholar] [CrossRef]
- Leemput, N.; Geth, F.; Van Roy, J.; Delnooz, A.; Büscher, J.; Driesen, J. Impact of Electric Vehicle On-Board Single-Phase Charging Strategies on a Flemish Residential Grid. IEEE Trans. Smart Grid 2014, 5, 1815–1822. [Google Scholar] [CrossRef]
- Phase-wise enhanced voltage support from electric vehicles in a Danish low-voltage distribution grid. Electr. Power Syst. Res. 2016, 140, 274–283. [CrossRef]
- Lehfuss, F.; Nöhrer, M. Evaluation of different control algorithm with low-level communication requirements to increase the maximum electric vehicle penetration. CIRED-Open Access Proc. J. 2017, 2017, 1750–1754. [Google Scholar] [CrossRef][Green Version]
- Ucer, E.; Kisacikoglu, M.C.; Yuksel, M.; Gurbuz, A.C. An Internet-Inspired Proportional Fair EV Charging Control Method. IEEE Syst. J. 2019, 13, 4292–4302. [Google Scholar] [CrossRef]
- Al-Awami, A.T.; Sortomme, E.; Asim Akhtar, G.M.; Faddel, S. A Voltage-Based Controller for an Electric-Vehicle Charger. IEEE Trans. Veh. Technol. 2016, 65, 4185–4196. [Google Scholar] [CrossRef]
- Faddel, S.; Mohamed, A.A.; Mohammed, O.A. Fuzzy logic-based autonomous controller for electric vehicles charging under different conditions in residential distribution systems. Electr. Power Syst. Res. 2017, 148, 48–58. [Google Scholar] [CrossRef]
- Van Roy, J.; Leemput, N.; Geth, F.; Salenbien, R.; Büscher, J.; Driesen, J. Apartment Building Electricity System Impact of Operational Electric Vehicle Charging Strategies. IEEE Trans. Sustain. Energy 2014, 5, 264–272. [Google Scholar] [CrossRef]
- Kefayati, M.; Baldick, R. Harnessing demand flexibility to match renewable production using localized policies. In Proceedings of the 2012 50th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 1–5 October 2012; pp. 1105–1109. [Google Scholar]
- Tushar, W.; Yuen, C.; Huang, S.; Smith, D.B.; Poor, H.V. Cost Minimization of Charging Stations With Photovoltaics: An Approach With EV Classification. IEEE Trans. Intell. Transp. Syst. 2016, 17, 156–169. [Google Scholar] [CrossRef]
- IEC 61851-1; Electric Vehicle Conductive Charging System—Part 1: General requirements. International Standard. International Electrotechnical Commission: Geneva, Switzerland, 2017.
- Mouli, G.R.C.; Kaptein, J.; Bauer, P.; Zeman, M. Implementation of dynamic charging and V2G using Chademo and CCS/Combo DC charging standard. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 27–29 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Bons, P.; Buatois, A.; Ligthart, G.; van den Hoed, R.; Warmerdam, J. Amsterdam Flexpower Operational Pilot: A Detailed Analysis of the Effect of Applying a Static Smart Charging Profile for Public Charging Infrastructure; Project Report; Amsterdam University of Applied Science, Nuon, Liander and ElaadNL, Interreg, North Sea Region: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Hu, J.; Harmsen, R.; Crijns-Graus, W.; Worrell, E.; van den Broek, M. Identifying barriers to large-scale integration of variable renewable electricity into the electricity market: A literature review of market design. Renew. Sustain. Energy Rev. 2018, 81, 2181–2195. [Google Scholar] [CrossRef]
- Day-ahead Prices. ENTSO-E Transparency Platform. Available online: transparency.entsoe.eu (accessed on 19 August 2021).
- Congestion Management Research-Zeeland. C1-Public Information, TenneT TSO B.V. 2021. Available online: https://www.tennet.eu (accessed on 19 August 2021).
- EN-50160; Voltage Characteristics of electricity supplied by Public Distribution Systems. European Standard: Brussels, Belgium, 2010.
- Verbruiksprofielen-Profielen 2018. De Vereniging Nederlandse EnergieDataUitwisseling (NEDU). Available online: https://www.nedu.nl (accessed on 20 April 2021).
- Mouli, G.C.; Bauer, P.; Zeman, M. System design for a solar powered electric vehicle charging station for workplaces. Appl. Energy 2016, 168, 434–443. [Google Scholar] [CrossRef]
- Zonnestroom; Vermogen Bedrijven en Woningen, Regio (Indeling 2018), 2012–2018. Centraal Bureau voor de Statistiek. Available online: https://opendata.cbs.nl (accessed on 20 April 2021).
- Factsheets Zon. Rijksdienst voor Ondernemend Nederland (RVO). Available online: www.rvo.nl (accessed on 20 April 2021).
- Statistics Electric Vehicles and Charging in The Netherlands Up to and Including November 2018; Rijksdienst voor Ondernemend Nederland (RVO): Den Haag, The Netherlands, 2018.
- Elaad Open Data Platform, 2018. Elaad. Available online: https://platform.elaad.io/ (accessed on 11 May 2021).
- Refa, N.; Hubbers, N. Impact of Smart Charging on EVs Charging Behaviour Assessed from Real Charging Events. In Proceedings of the 32th International Electric Vehicle Symposium, Lyon, France, 19–22 May 2019. [Google Scholar]
- Yu, Y.; Reihs, D.; Wagh, S.; Shekhar, A.; Stahleder, D.; Mouli, G.R.C.; Lehfuss, F.; Bauer, P. Data-Driven Study of Low Voltage Distribution Grid Behaviour With Increasing Electric Vehicle Penetration. IEEE Access 2022, 10, 6053–6070. [Google Scholar] [CrossRef]
Figure 1.
Illustration of three charging methods’ control mechanism: (a) PSM, (b) VDM, (c) ARM.
Figure 1.
Illustration of three charging methods’ control mechanism: (a) PSM, (b) VDM, (c) ARM.
Figure 2.
Normalised baseloads of six grids compare with two price signals.
Figure 2.
Normalised baseloads of six grids compare with two price signals.
Figure 3.
Sample load profile for a 1000 kWh yearly energy consumption in both seasons.
Figure 3.
Sample load profile for a 1000 kWh yearly energy consumption in both seasons.
Figure 4.
Sample PV profile for a 1 kW installation in winter and summer.
Figure 4.
Sample PV profile for a 1 kW installation in winter and summer.
Figure 5.
EV behaviour distribution curves. ( Only EV arrival time has weekday–weekends differences; the other two have the same distribution throughout the whole week).
Figure 5.
EV behaviour distribution curves. ( Only EV arrival time has weekday–weekends differences; the other two have the same distribution throughout the whole week).
Figure 6.
Comparison of transformer loading versus time of three methods with 80% EV penetration in winter.
Figure 6.
Comparison of transformer loading versus time of three methods with 80% EV penetration in winter.
Figure 7.
Comparison of maximum line loading distribution for one winter week.
Figure 7.
Comparison of maximum line loading distribution for one winter week.
Figure 8.
Comparison of per time step minimal node voltage distribution for one winter week.
Figure 8.
Comparison of per time step minimal node voltage distribution for one winter week.
Figure 9.
Minimal node voltage of EV charger connected nodes versus the distance to the transformer with EV 80% penetration level in winter.
Figure 9.
Minimal node voltage of EV charger connected nodes versus the distance to the transformer with EV 80% penetration level in winter.
Figure 10.
Grid loading heatmap of SUB1 grid with PSM with EV 80% penetration in winter, highest line loading moment.
Figure 10.
Grid loading heatmap of SUB1 grid with PSM with EV 80% penetration in winter, highest line loading moment.
Figure 11.
Line loading distribution of all lines versus the distance to the transformer with EV 80% penetration level in winter.
Figure 11.
Line loading distribution of all lines versus the distance to the transformer with EV 80% penetration level in winter.
Figure 12.
Comparison of total charging power under the three PSM study schemes for three grids (top three plots), with the corresponding price signals (bottom three plots).
Figure 12.
Comparison of total charging power under the three PSM study schemes for three grids (top three plots), with the corresponding price signals (bottom three plots).
Figure 13.
Comparison of charging demand satisfaction of EV 80% scenario in winter. (a) Percentage of total deficient charging sessions; (b) Distribution of unfinished charging energy per session.
Figure 13.
Comparison of charging demand satisfaction of EV 80% scenario in winter. (a) Percentage of total deficient charging sessions; (b) Distribution of unfinished charging energy per session.
Figure 14.
Comparative charging cost factor of EV 80% scenario in winter.
Figure 14.
Comparative charging cost factor of EV 80% scenario in winter.
Table 1.
PSM methods explanation.
Table 1.
PSM methods explanation.
| Method | PSM1 | PSM2 | PSM3 |
|---|
| Price signal | DAM price | DAM price | Modified DAM price |
| Price segment division | : Top 3 prices
: Below daily average
: The rest | Equally divided into 8 h | : Top 3
: Below daily average
: The rest |
Table 2.
Summary of grids’ characteristics.
Table 2.
Summary of grids’ characteristics.
| Grid | No. Households | Yearly Energy Consumption [MWh] | PV Installation [kWp] | Avg. Line Length [m] | Longest Feeder Length [m] | No. Transformer and Capacity [kVA] |
|---|
| RR1 | 3 | 98.0 | 2.5 | 22.8 | 367.8 | 1 × 400 kVA |
| RR2 | 133 | 486.8 | 87.5 | 7.9 | 452.2 | 1 × 400 kVA |
| SUB1 | 475 | 1394.1 | 180 | 7.3 | 566.0 | 1 × 400 kVA |
| SUB2 | 266 | 800.8 | 100 | 8.1 | 546.6 | 1 × 400 kVA |
| UB1 | 283 | 1680.2 | 37.5 | 4.4 | 332.5 | 1 × 400 kVA |
| UB2 | 122 | 261.0 | 17.5 | 10.3 | 360.4 | 1 × 400 kVA |
Table 3.
Total charging cost and energy failed to deliver comparison.
Table 3.
Total charging cost and energy failed to deliver comparison.
| Season | Compare Items | UNC | PSM1 | PSM2 | PSM3 | ARM | VDM |
|---|
| Winter | [€] | 1900.79 | 1766.25 | 1701.88 | 1737.29 | 1834.32 | 1902.00 |
| [%] | - | 7.08 | 10.46 | 8.60 | 3.50 | −0.06 |
| [kWh] | 45,664.63 | 43,671.41 | 42,576.50 | 43,137.44 | 45,763.09 | 43,711.11 |
| [%] | - | 4.36 | 6.76 | 5.53 | 0 | 4.28 |
| Summer | [€] | 2789.20 | 2599.73 | 2510.90 | 2617.83 | 2721.22 | 2844.47 |
| [%] | - | 6.79 | 9.98 | 6.14 | 2.44 | −1.98 |
| [kWh] | 45,664.63 | 43,666.40 | 42,368.90 | 43,205.43 | 45,763.09 | 44,119.27 |
| [%] | - | 4.38 | 7.22 | 5.39 | 0 | 3.38 |
Table 4.
Performance comparison.
Table 4.
Performance comparison.
| Benchmark Index | Grid Performance | Charging Cost | Unfinished Charging | Fairness | Communication | Forecasting |
|---|
| PSM | − | | − | O | − | − |
| VDM | + | + | O | − | | O |
| ARM | | − | − | | − | O |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).