Optimal DG Placement in Power Systems Using a Modified Flower Pollination Algorithm
Abstract
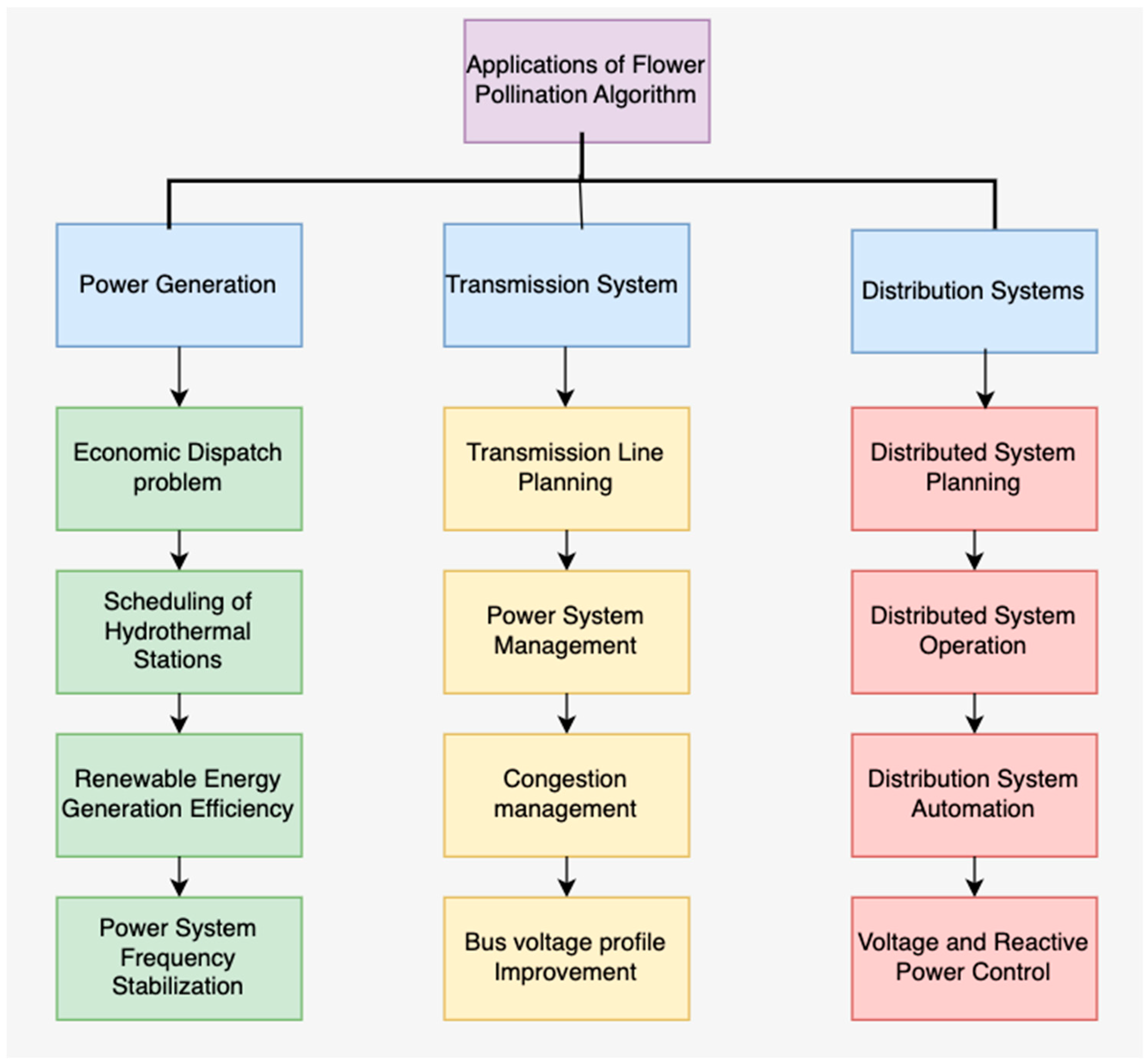
1. Introduction
- Evaluation the optimal DG location and size while satisfying all the network constraints.
- Comparing different state-of-the-art techniques in terms of their efficiency and power loss.
- Testing the method on different bus systems.
2. Materials and Methods
2.1. Problem Formulation with System Model
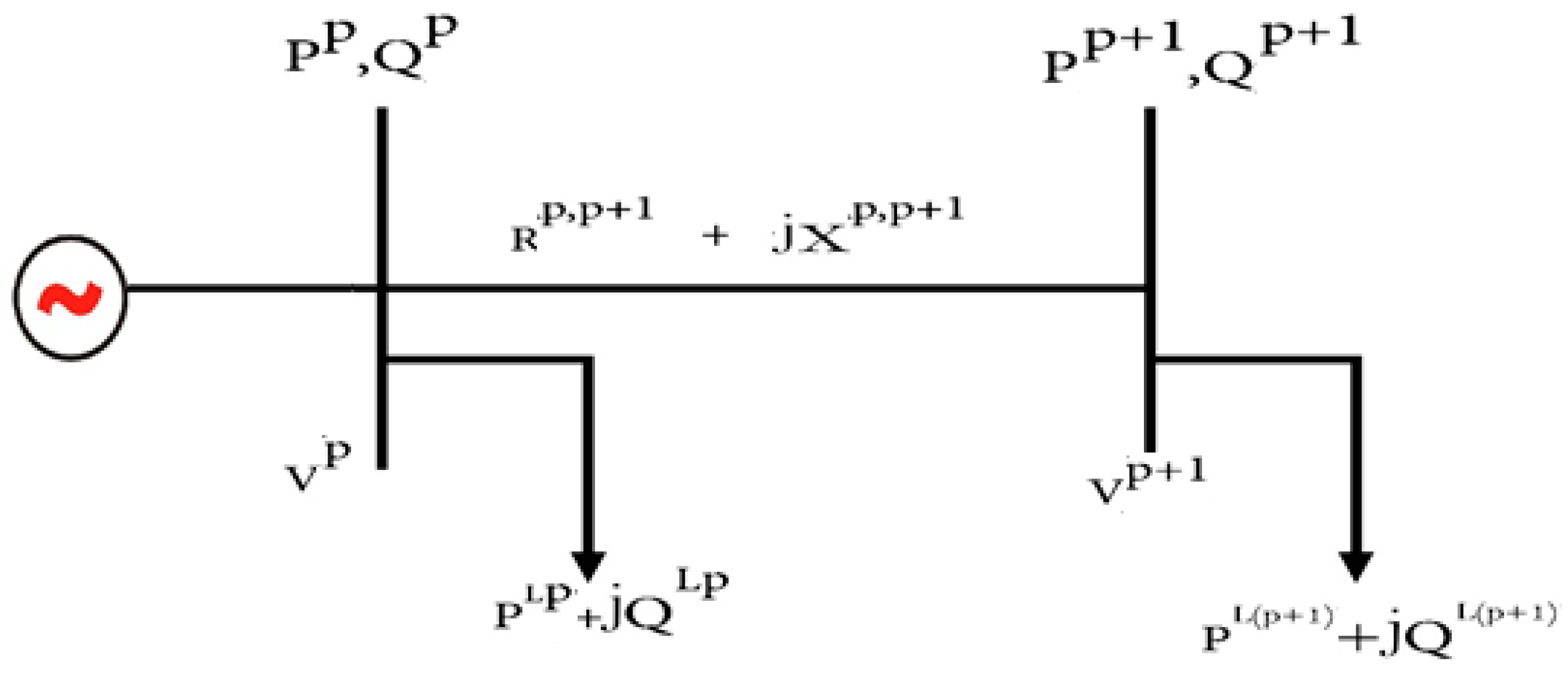
2.1.1. Power Flow Calculation
- is the real power flow which is flowing from bus p;
- is the real power load which is at bus p;
- is the real power load which is at bus p + 1;
- is the reactive power flow which is flowing from bus p;
- is the reactive power load which is at bus p;
- is the reactive power load which is at bus p + 1;
- is the reactance which is between the buses p and p + 1;
- is the resistance which is between the buses p and p + 1;
- is the voltage which is at bus p + 1;
- is the voltage which is at bus p;
- is the total power loss which is in the system.
2.1.2. Power Loss Minimization
- is the minimization of power loss;
- is the Ith bus’s active powers load;
- is the Ith bus’s reactive powers load;
- is the number of branches in the distribution network;
- is the Ith bus’s voltage magnitude;
- is the Ith branch’s resistance.
2.1.3. Real Power Balance and Reactive Power Balance
- is the Ith DG unit’s active power output;
- is the Jth bus’s active power load demand;
- is the Kth branch’s active power loss;
- is the slack bus’s active power provided;
- is the Ith DG unit’s reactive power output;
- is the Jth bus’s reactive power load demand;
- is the Kth branch’s reactive power loss;
- is the slack bus’s reactive power provided;
- is the distribution network’s number of buses;
- is the total number of DG units presented in the power system.
2.1.4. Radial Configuration Constraint
- is the total number of tie switches in the distribution network;
- is the number of lines in the loop network;
- is the number of lines in the radial network.
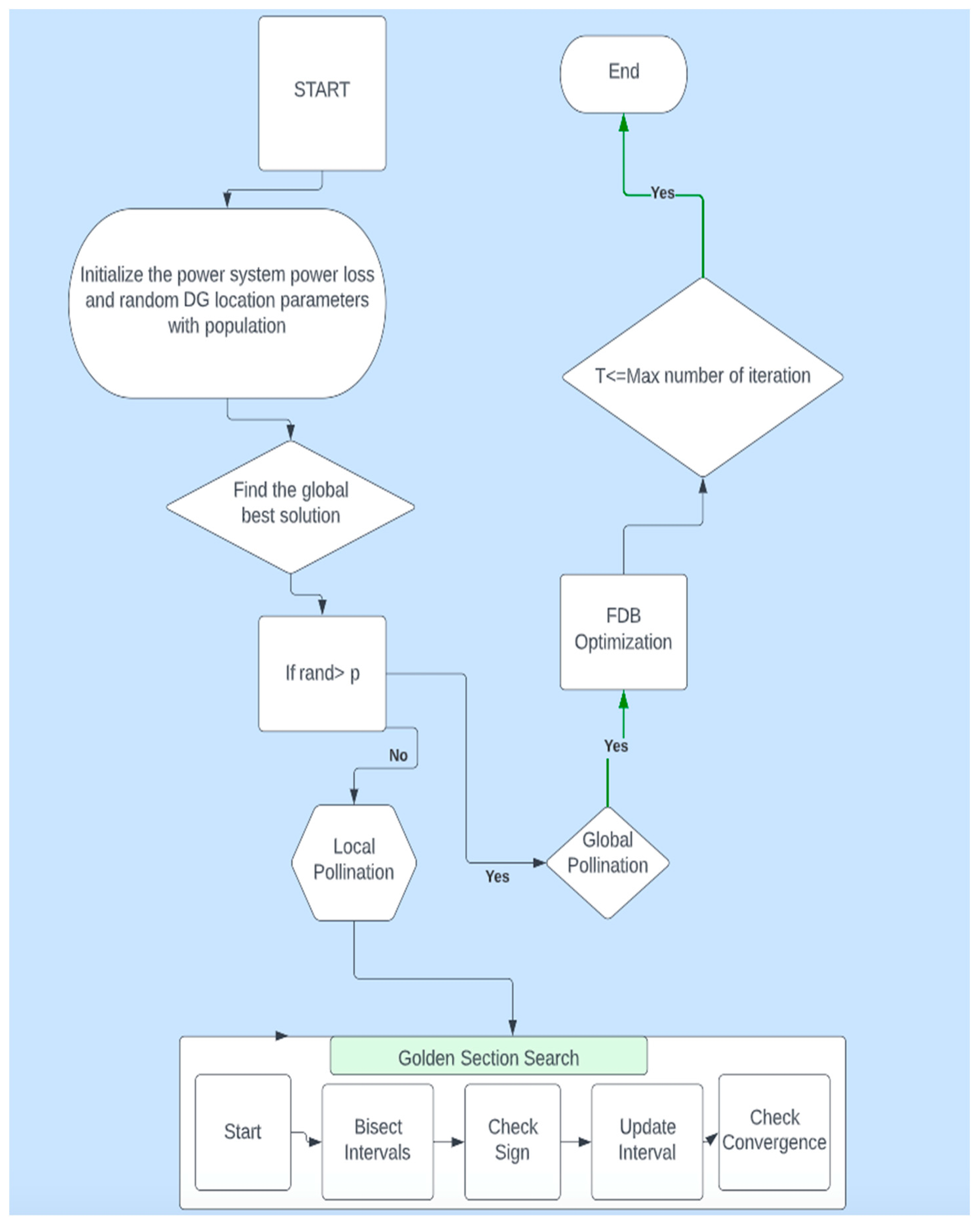
2.2. Detailed Description of Algorithm
2.2.1. Process of Flower Pollination Algorithm
- Rule 1: Global pollination refers to cross-pollination process and biotic pollination. Based on levy flight operation, it moves away to carry pollinators.
- Rule 2: Local pollination utilizes both self-pollination as well as abiotic pollination.
- Rule 3: Insects or pollinators with developed flower constancy equates to a reproduction probability. The probability of reproduction is directly proportional to the similarity function involved.
- Rule 4: Based on switch probability, the switching or interaction of both the global and local pollination is controllers, which lightly biased to local pollination.
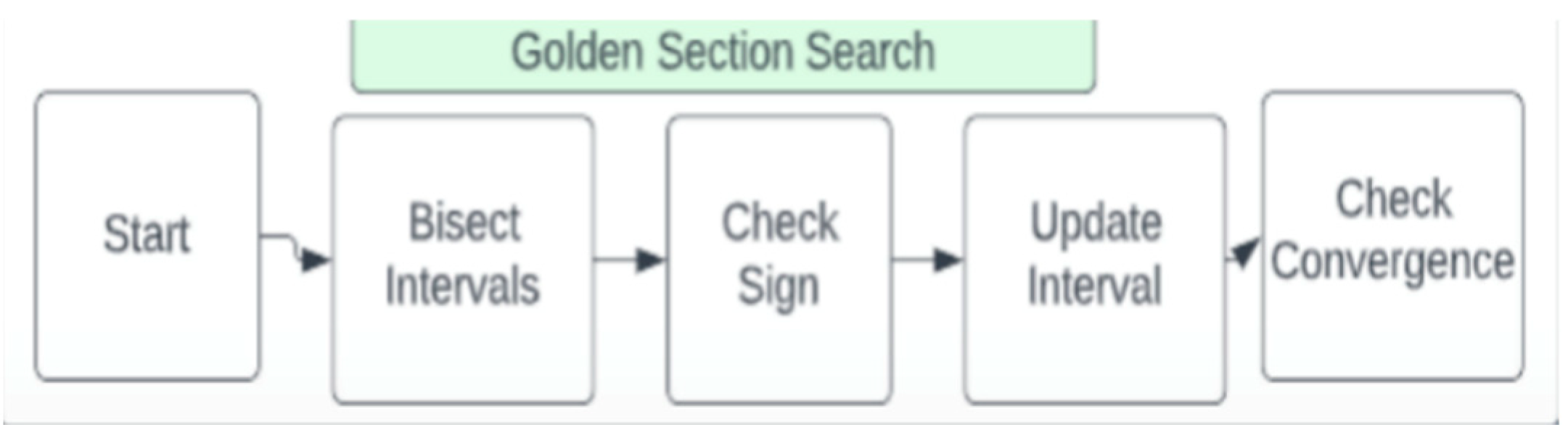
2.2.2. Process of Golden Search Algorithm
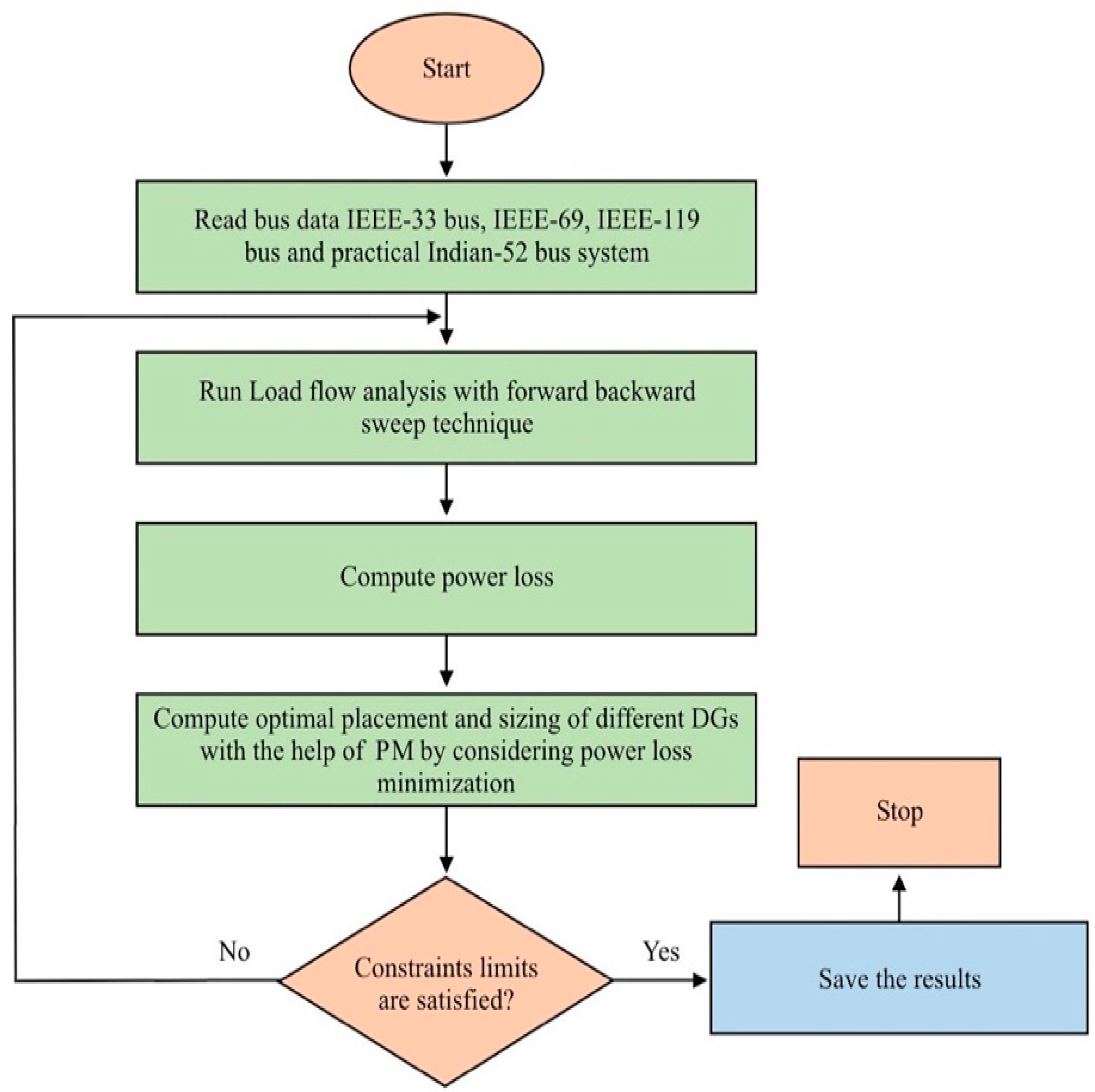
2.2.3. Proposed Methodology Process
3. Results
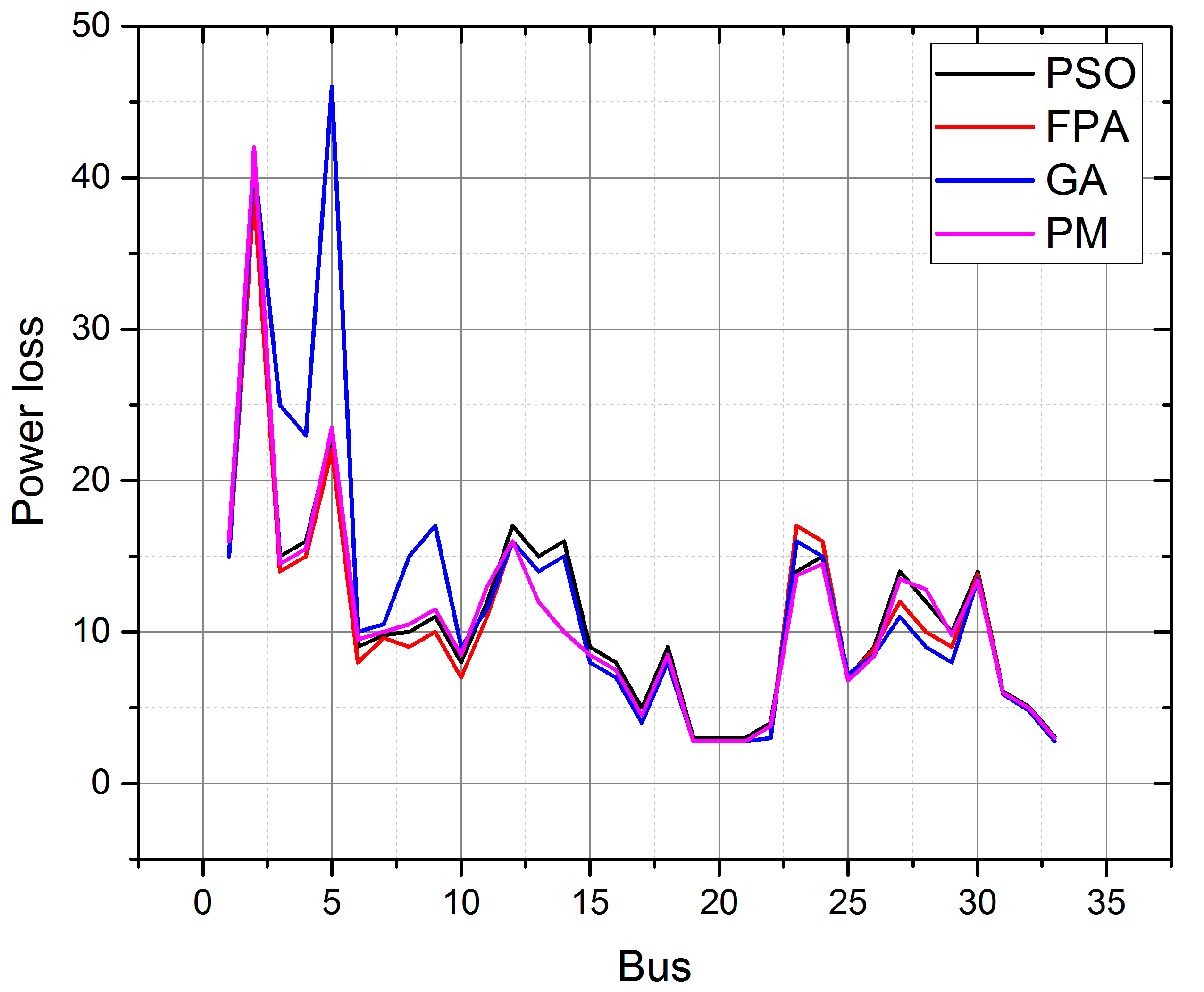
3.1. IEEE 33 Bus System Performance Analysis
3.2. IEEE 69 Bus System Performance Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- New Energy Outlook 2021: BLOOMBERGNEF: Bloomberg Finance LP. BloombergNEF. (n.d.). Available online: https://about.bnef.com/new-energy-outlook/ (accessed on 2 September 2022).
- Jafari, A.; Ganjeh Ganjehlou, H.; Khalili, T.; Behnam, M.-I. A two-loop hybrid method for optimal placement and scheduling of switched capacitors in distribution networks. IEEE Access 2020, 8, 38892–38906. [Google Scholar] [CrossRef]
- Suresh, M.C.V.; Edward, J.B. A hybrid algorithm based optimal placement of DG units for loss reduction in the distribution system. Appl. Soft Comput. 2020, 91, 106191. [Google Scholar] [CrossRef]
- Katyara, S.; Shaikh, M.F.; Shaikh, S.; Khand, Z.H.; Staszewski, L.; Bhan, V.; Majeed, A.; Shah, M.A.; Zbigniew, L. Leveraging a Genetic Algorithm for the Optimal Placement of Distributed Generation and the Need for Energy Management Strategies Using a Fuzzy Inference System. Electronics 2021, 10, 172. [Google Scholar] [CrossRef]
- Angalaeswari, S.; Sanjeevikumar, P.; Jamuna, K.; Leonowicz, Z. Hybrid PIPSO-SQP Algorithm for Real Power Loss Minimization in Radial Distribution Systems with Optimal Placement of Distributed Generation. Sustainability 2020, 12, 5787. [Google Scholar] [CrossRef]
- Montoya, O.D.; Molina-Cabrera, A.; Chamorro, H.R.; Alvarado-Barrios, L.; Rivas-Trujillo, E. A Hybrid Approach Based on SOCP and the Discrete Version of the SCA for Optimal Placement and Sizing DGs in AC Distribution Networks. Electronics 2021, 10, 26. [Google Scholar] [CrossRef]
- Saddique, M.W.; Haroon, S.S.; Amin, S.; Bhatti, A.R.; Sajjad, I.A.; Liaqat, R. Optimal placement and sizing of shunt capacitors in radial distribution system using polar bear optimization algorithm. Arab. J. Sci. Eng. 2021, 46, 873–899. [Google Scholar] [CrossRef]
- Ettehadi, M.; Ghasemi, H.; Vaez-Zadeh, S. Voltage stability-based DG placement in distribution networks. IEEE Trans. Power Deliv. 2012, 28, 171–178. [Google Scholar] [CrossRef]
- Esmaili, M.; Firozjaee, E.C.; Shayanfar, H.A. Optimal placement of distributed generations considering voltage stability and power losses with observing voltage-related constraints. Appl. Energy 2014, 113, 1252–1260. [Google Scholar] [CrossRef]
- Aman, M.; Jasmon, G.; Mokhlis, H.; Bakar, A. Optimal placement and sizing of a DG based on a new power stability index and line losses. Int. J. Electr. Power Energy Syst. 2012, 43, 1296–1304. [Google Scholar] [CrossRef]
- Samala, R.K.; Rosalina, K.M. Optimal Allocation of Multiple Photo-Voltaic and/or Wind-Turbine Based Distributed Generations in Radial Distribution System Using Hybrid Technique with Fuzzy Logic Controller. J. Electr. Eng. Technol. 2021, 16, 101–113. [Google Scholar] [CrossRef]
- Babu, M.R.; Kumar, C.V.; Anitha, S. Simultaneous Reconfiguration and Optimal Capacitor Placement Using Adaptive Whale Optimization Algorithm for Radial Distribution System. J. Electr. Eng. Technol. 2021, 16, 181–190. [Google Scholar] [CrossRef]
- Palanisamy, R.; Muthusamy, S.K. Optimal Siting and Sizing of Multiple Distributed Generation Units in Radial Distribution System Using Ant Lion Optimization Algorithm. J. Electr. Eng. Technol. 2021, 16, 79–89. [Google Scholar] [CrossRef]
- Ramadan, A.; Ebeed, M.; Kamel, S.; Nasrat, L. Optimal power flow for distribution systems with uncertainty. In Uncertainties in Modern Power Systems; Academic Press: Cambridge, MA, USA, 2021; pp. 145–162. [Google Scholar] [CrossRef]
- Raut, U.; Mishra, S. A new Pareto multi-objective sine cosine algorithm for performance enhancement of radial distribution network by optimal allocation of distributed generators. Evol. Intell. 2020, 14, 1635–1656. [Google Scholar] [CrossRef]
- Quoc, S.N.; Ngoc, D.V. Symbiotic Organism Search Algorithm for Power Loss Minimization in Radial Distribution Systems by Network Reconfiguration and Distributed Generation Placement. Math. Probl. Eng. 2020, 2020, 1615792. [Google Scholar] [CrossRef]
- Prakash, P. Optimal DG Allocation Using Particle Swarm Optimization. In Proceedings of the 2021 International Conference on Artificial Intelligence and Smart Systems (ICAIS), Tamilnadu, India, 25–27 March 2021; pp. 940–944. [Google Scholar] [CrossRef]
- Oudjana, S.H.; Zine, R.; Mosbah, M.; Khattara, A.; Arif, S. Optimal placement of distributed generation based pv source in electrical power system for LVSI improvement using GA algorithm. In Proceedings of the International Conference in Artificial Intelligence in Renewable Energetic Systems 2020, Tipasa, Algeria, 22–24 November 2020; Springer: Cham, Switzerland; pp. 252–259. [Google Scholar] [CrossRef]
- Mahdad, B. Optimal reconfiguration and reactive power planning based fractal search algorithm: A case study of the Algerian distribution electrical system. Eng. Sci. Technol. Int. J. 2018, 22, 78–101. [Google Scholar] [CrossRef]
- Kashem, M.A.; Ganapathy, V.; Jasmon, G.B. On-line Network Reconfiguration for Enhancement of Voltage Stability in Distribution Systems Using Artificial Neural Networks. Electr. Power Compon. Syst. 2001, 29, 361–373. [Google Scholar] [CrossRef]
- Fathy, A.; Yousri, D.; Abdelaziz, A.Y.; Ramadan, H.S. Robust approach based chimp optimization algorithm for minimizing power loss of electrical distribution networks via allocating distributed generators. Sustain. Energy Technol. Assess. 2021, 47, 101359. [Google Scholar] [CrossRef]
- Sabarinath, G.; Gowri Manohar, T. Application of Bird Swarm Algorithm for Allocation of Distributed Generation in an Indian Practical Distribution Network. Int. J. Intell. Syst. Appl. 2019, 7, 54–61. [Google Scholar] [CrossRef]
- Khoubseresht, O.; Shayanfar, H. The role of demand response in optimal sizing and siting of distribution energy resources in distribution network with time-varying load: An analytical approach. Electr. Power Syst. Res. 2020, 180, 106100. [Google Scholar] [CrossRef]
- Al-Ammar, E.A.; Farzana, K.; Waqar, A.; Aamir, M.; Ullah, S.; Haq, A.U.; Zahid, M.; Batool, M. ABC algorithm based optimal sizing and placement of DGs in distribution networks considering multiple objectives. Ain Shams Eng. J. 2020, 12, 697–708. [Google Scholar] [CrossRef]
- Yang, H.; Liu, X.; Guo, Y.; Zhang, P. Fault Location of Active Distribution Networks Based on the Golden Section Method. Math. Probl. Eng. 2020, 2020, 6937319. [Google Scholar] [CrossRef]
- Mahendran, G.; Govindaraju, C. Flower pollination algorithm for distribution system phase balancing considering variable demand. Microprocess. Microsyst. 2020, 74, 103008. [Google Scholar] [CrossRef]
- Pandya, K.S.; Joshi, S.K. CHAOS enhanced Flower Pollination Algorithm for Optimal Scheduling of Distributed Energy Resources in Smart Grid. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Singapore, 22–25 March 2018. [Google Scholar] [CrossRef]
- Yousri, D.; Babu, T.S.; Allam, D.; Ramachandaramurthy, V.K.; Beshr, E.; Eteiba, M.B. Fractional Chaos Maps with Flower Pollination Algorithm for Partial Shading Mitigation of Photovoltaic Systems. Energies 2019, 12, 3548. [Google Scholar] [CrossRef]
- Arai, H.; Arafune, T.; Shibuya, S.; Kobayashi, Y.; Asami, K.; Kobayashi, H. Fibonacci sequence weighted SAR ADC as golden section search. In Proceedings of the 2017 International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS), Xiamen, China, 6–9 November 2017; pp. 657–662. [Google Scholar] [CrossRef]
- yyc9268 (December 18,2021) YYC9268/numerical_optimization: Implementation of Several Local Optimization Methods, GitHub. Available online: https://github.com/yyc9268/Numerical_optimization (accessed on 20 October 2022).
- Lubin, T.; Razik, H.; Rezzoug, A. On-line efficiency optimization of a synchronous reluctance motor. Electr. Power Syst. Res. 2007, 77, 484–493. [Google Scholar] [CrossRef]
- Prakash, D.B.; Lakshminarayana, C. Multiple DG placements in radial distribution system for multi objectives using Whale Optimization Algorithm. Alex. Eng. J. 2018, 57, 2797–2806. [Google Scholar] [CrossRef]
- Hassan, A.S.; Sun, Y.; Wang, Z. Multi-objective for optimal placement and sizing DG units in reducing loss of power and enhancing voltage profile using BPSO-SLFA. Energy Rep. 2020, 6, 1581–1589. [Google Scholar] [CrossRef]
- Amarendra, A.; Srinivas, L.R.; Rao, R.S. Contingency Analysis in Power System- Using UPFC and DVR Devices with RDOA. Technol. Econ. Smart Grids Sustain. Energy 2022, 7, 17. [Google Scholar] [CrossRef]
- Almabsout, E.A.; El-Sehiemy, R.A.; An, O.N.U.; Bayat, O. A hybrid local Search-Genetic algorithm for simultaneous placement of DG units and shunt capacitors in radial distribution systems. IEEE Access 2020, 8, 54465–54481. [Google Scholar] [CrossRef]
- Yang, X.S. Flower Pollination Algorithm for Global Optimization. In Unconventional Computation and Natural Computation 2012. UCNC 2012; Lecture Notes in Computer Science; Durand-Lose, J., Jonoska, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 7445. [Google Scholar] [CrossRef]
- Yang, X.S.; Karamanoglu, M.; He, X.S. Multi-objective flower algorithm for optimization. Procedia Comput. Sci. 2013, 18, 861–868. [Google Scholar] [CrossRef]
- Yousri, D.; Elaziz, M.A.; Mirjalili, S. Fractional-order calculus-based flower pollination algorithm with local search for global optimization and image segmentation. Knowl. Based Syst. 2020, 197, 105889. [Google Scholar] [CrossRef]
- Liang, X.; Liang, W.; Xiong, J. Intelligent diagnosis of natural gas pipeline defects using improved flower pollination algorithm and artificial neural network. J. Clean. Prod. 2020, 264, 121655. [Google Scholar] [CrossRef]
- Yang, X.-S. ature-Inspired Algorithms and Applied Optimization; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Truong, K.H.; Nallagownden, P.; Elamvazuthi, I.; Vo, D.N. A quasi-oppositional-chaotic symbiotic organisms search algorithm for optimal allocation of DG in radial distribution networks. Appl. Soft Comput. 2020, 88, 106067. [Google Scholar] [CrossRef]
- Adithiyaa, T.; Chandramohan, D.; Sathish, T. Flower Pollination Algorithm for the Optimization of Stair casting parameter for the preparation of AMC. Mater. Today Proc. 2020, 21, 882–886. [Google Scholar] [CrossRef]
- Chen, Y.; Pi, D. An innovative flower pollination algorithm for continuous optimization problem. Appl. Math. Model. 2020, 83, 237–265. [Google Scholar] [CrossRef]
- Rai, K.; Seksena, S.B.L.; Thakur, A.N. A Comparative Assessment of Genetic and Golden Search Algorithm for Loss Minimization of Induction Motor Drive. In Modelling, Simulation and Intelligent Computing; Lecture Notes in Electrical Engineering; Goel, N., Hasan, S., Kalaichelvi, V., Eds.; Springer: Singapore, 2020; Volume 659. [Google Scholar] [CrossRef]
- Aras, S.; Gedikli, E.; Kahraman, H.T. A novel stochastic fractal search algorithm with fitness-Distance balance for global numerical optimization. Swarm Evol. Comput. 2021, 61, 100821. [Google Scholar] [CrossRef]
- Dhivya, S.; Arul, R. Hybrid Flower Pollination Algorithm for Optimization Problems. In Proceedings of the International Conference on Computational Intelligence and Sustainable Technologies, Greater Noida, India, 20–21 May 2022; Algorithms for Intelligent Systems. Das, K.N., Das, D., Ray, A.K., Suganthan, P.N., Eds.; Springer: Singapore, 2022. [Google Scholar] [CrossRef]

| Genetic Algorithm (GA) | |||
| No | Description | Notation | Value |
| 1 | Population/Generation Combination | P/G | 60:20 |
| 2 | Probability of Crossover | %C | 0.9 |
| 3 | Probability of Mutation | %M | 0.2 |
| 4 | Maximum number of iterations | Niter | 350 |
| 5 | Population Size | Ns | 60 |
| Particle Swarm Optimistion (PSO) | |||
| No | Description | Notation | Value |
| 1 | Cognitives Constant | C1 | 2 |
| 2 | Social Constant | C2 | 2 |
| 3 | Inertia Weight | w | Linear reduction from 0.9 to 0.4 |
| 4 | Probability Switch | P | 0.8 |
| 5 | Maximum number of iterations | Niter | 350 |
| 6 | Population Size | Ns | 60 |
| Flower Pollination Algorithm (FPA) | |||
| No | Description | Notation | Value |
| 1 | Maximum number of iterations | Niter | 350 |
| 2 | Golden ratio | C | 0.618 |
| 3 | Probability switch | P | 0.8 |
| 4 | Population | Ns | 60 |
| Proposed Method (PM) | |||
| No | Description | Notation | Value |
| 1 | Maximum number of iterations | Niter | 350 |
| 2 | Golden ratio | C | 0.618 |
| 3 | Probability switch | P | 0.8 |
| 4 | Population | Ns | 60 |
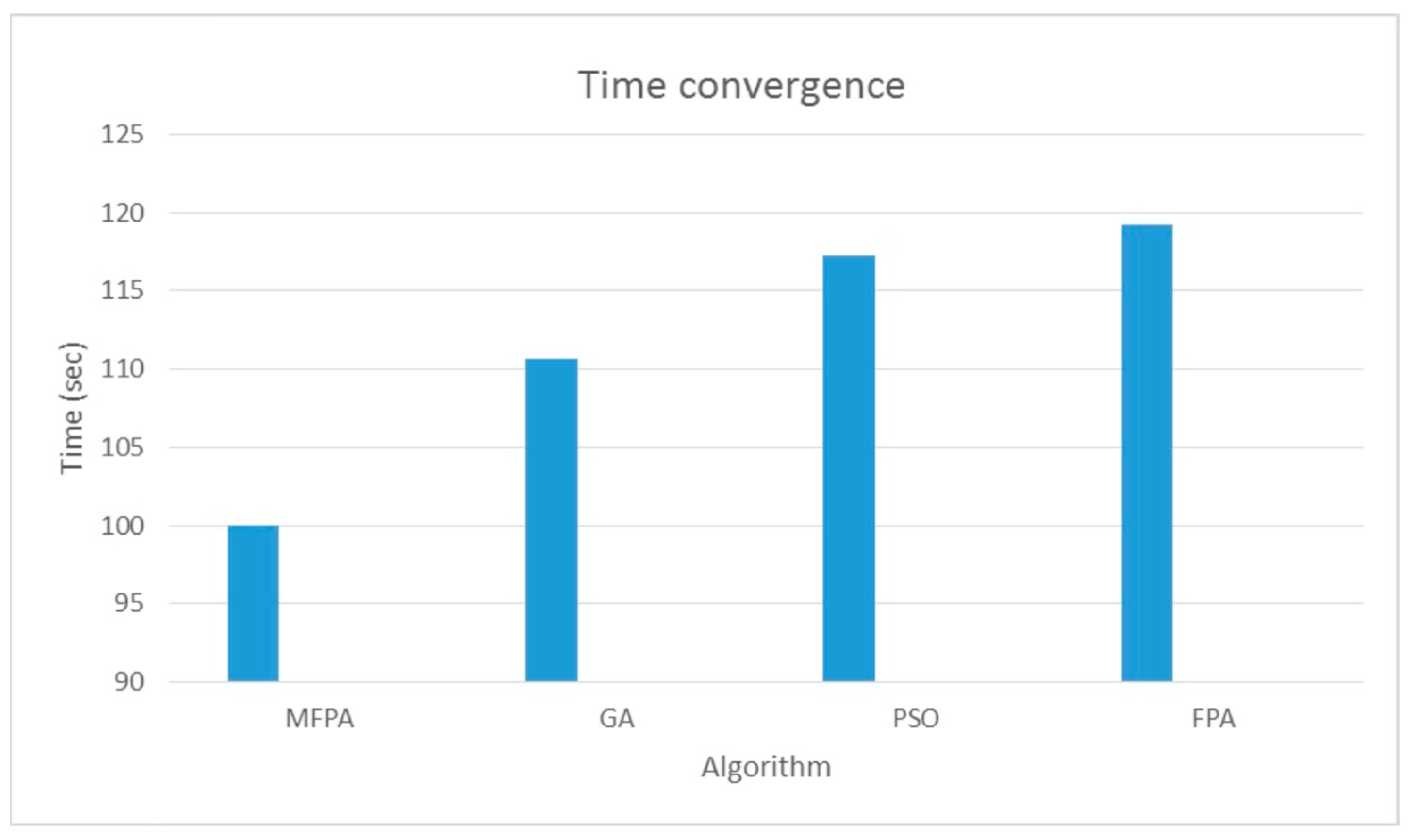
| No | Algorithm | Stopping Criteria | Time Convergence |
|---|---|---|---|
| 1 | Genetic Algorithm | Exhaustion-based Stopping Criteria | 110.65 |
| 2 | Particle Swarm Algorithm | Movement-based Stopping Criteria | 117.245 |
| 3 | Flower Pollination Algorithm and | Movement-based Stopping Criteria | 119.255 |
| 4 | proposed method | Movement-based Stopping Criteria | 100 |
| GA | PSO | FPA | Modified FPA | |||
|---|---|---|---|---|---|---|
| DGs location (bus number) | Solar | 30 | 14 | 10 | 9 | |
| Wind | 24 | 24 | 29 | 29 | ||
| Biogas | 14 | 30 | 14 | 13 | ||
| DG optimal size | P (kW) | Solar | 492 | 340 | 400 | 396 |
| Wind | 627 | 701 | 580 | 567 | ||
| Biogas | 349 | 396 | 400 | 555 | ||
| Q (kVar) | Solar | 40 | 19 | 19 | 23 | |
| Wind | 111 | 72 | 32 | 31 | ||
| Biogas | 83 | 121 | 80 | 63 | ||
| Power factor | Solar | 0.99677 | 0.8688 | 0.97677 | 0.99839 | |
| Wind | 0.98459 | 0.99477 | 0.98689 | 0.99851 | ||
| Biogas | 0.97273 | 0.95624 | 0.96564 | 0.99368 | ||
| Best power loss (kW) | 205.968 | 275.565 | 275.565 | 193.363677 | ||
| Worst Power loss | 319.045 | 346.881 | 346.469 | 248.385615 | ||
| Mean Power loss | 242.491 | 310.469 | 310.469 | 200.95 | ||
| Standard deviation | 29.9714 | 24.5554 | 24.5554 | 8.71297325 | ||
| GA | PSO | FPA | Modified FPA | |||
|---|---|---|---|---|---|---|
| DGs location (bus number) | Solar | 18 | 11 | 15 | 12 | |
| Wind | 51 | 18 | 64 | 62 | ||
| Biogas | 61 | 61 | 30 | 36 | ||
| DG optimal size | P (kW) | Solar | 199 | 431 | 440 | 238 |
| Wind | 315 | 846 | 370 | 184 | ||
| Biogas | 805 | 966 | 890 | 819 | ||
| Q (kVAr) | Solar | 48 | 196 | 45 | 21 | |
| Wind | 49 | 38 | 50 | 15 | ||
| Biogas | 94 | 633 | 83 | 75 | ||
| Power factor | Solar | 0.97262 | 0.9105 | 0.97568 | 0.99607 | |
| Wind | 0.98801 | 0.99899 | 0.97546 | 0.99649 | ||
| Biogas | 0.99332 | 0.8366 | 0.98453 | 0.99589 | ||
| Best power loss (kW) | 133.878 | 162.212 | 141.235 | 126.383916 | ||
| Worst Power loss | 181.364 | 192.529 | 160.458 | 152.611128 | ||
| Mean Power loss | 151.8 | 170.166 | 145.128 | 134.67 | ||
| Standard deviation | 15.8572 | 14.9133 | 6.235494 | 5.69932973 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramshanker, A.; Isaac, J.R.; Jeyeraj, B.E.; Swaminathan, J.; Kuppan, R. Optimal DG Placement in Power Systems Using a Modified Flower Pollination Algorithm. Energies 2022, 15, 8516. https://doi.org/10.3390/en15228516
Ramshanker A, Isaac JR, Jeyeraj BE, Swaminathan J, Kuppan R. Optimal DG Placement in Power Systems Using a Modified Flower Pollination Algorithm. Energies. 2022; 15(22):8516. https://doi.org/10.3390/en15228516
Chicago/Turabian StyleRamshanker, Abinands, Jacob Raglend Isaac, Belwin Edward Jeyeraj, Jose Swaminathan, and Ravi Kuppan. 2022. "Optimal DG Placement in Power Systems Using a Modified Flower Pollination Algorithm" Energies 15, no. 22: 8516. https://doi.org/10.3390/en15228516
APA StyleRamshanker, A., Isaac, J. R., Jeyeraj, B. E., Swaminathan, J., & Kuppan, R. (2022). Optimal DG Placement in Power Systems Using a Modified Flower Pollination Algorithm. Energies, 15(22), 8516. https://doi.org/10.3390/en15228516







