Abstract
We investigate whether oil-price uncertainty helps forecast the international stock returns of ten advanced and emerging countries. We consider an out-of-sample period of August 1925 to September 2021, with an in-sample period between August 1920 and July 1925, and employ a quantile-predictive-regression approach, which is more informative relative to a linear model, as it investigates the ability of oil-price uncertainty to forecast the entire conditional distribution of stock returns Based on a recursive estimation scheme, we draw the following main conclusions: the quantile-predictive-regression approach using oil-price uncertainty as a predictor statistically outperforms the corresponding quantile-based constant-mean model for all ten countries at certain quantiles (capturing normal, bear, and bull markets), and over specific forecast horizons, compared to forecastability being detected for eight countries under the linear predictive model. Importantly, we detect forecasting gains in many more horizons (at particular quantiles) compared to the linear case. In addition, an oil-price uncertainty-based state-contingent spillover analysis reveals that the ten equity markets are connected more tightly at the upper regime, suggesting that heightened oil-market volatility erodes the benefits from diversification across equity markets.
JEL Classification:
C22; C53; G15; Q41
1. Introduction
The extensive literature on investment under uncertainty and real options suggest that high oil-price uncertainty creates cyclical fluctuations in investment by lowering firms’ incentive for current investment [1,2]. This, in turn, impacts cash flows generated by a firm and the discount rate used to calculate stock prices and, hence, negatively impacts stock prices and/or returns [3]. In addition, because stock prices are the sum of discounted cash flows, including dividends, oil-price uncertainty can adversely affect stock prices by decreasing the overall profit that a firm generally uses to pay dividends, with this resulting from the fact that firms need to bear additional costs to avoid the risk associated with oil-price uncertainty [4]. Furthermore, in the wake of the recent financialization of the oil market after the Global Financial Crisis [5], there is an increase in oil price volatility, signaling higher economic uncertainty and the tightening of funding constraints for financial intermediaries, which are systematic factors in the stock market. Overall, the theoretical prediction is that oil-price uncertainty negatively impacts stock prices and/or returns via the investment and dividends channels. This hypothesis is widely empirically validated for developed economies [6,7,8,9,10] and emerging countries [11,12,13,14]. Ref. [15] employed a multi-factor model to show that oil-price risk tends to strongly affect a large set of emerging stock market returns. Moreover, the negative relationship between oil uncertainty and stock prices in a global vector-autoregressive model for a set of 26 advanced and developing countries considered together covering 90% of the world’s Gross Domestic Product (GDP) has been validated [16].
Given that in-sample tests of predictability might not translate into out-of-sample gains, we aim to extend the empirical literature on the nexus between oil-price uncertainty and stock markets by analyzing the role of West Texas Intermediate (WTI) crude-oil-price volatility (traditionally used in the literature mentioned above as a metric for oil-price uncertainty) for the stock returns of Canada, France, Germany, India, Italy, Japan, South Africa, Switzerland, the United Kingdom (UK), and the United States (US) over the monthly period from August 1920 to September 2021. From a statistical perspective, such a forecasting analysis is important because it is deemed as a more robust test of predictability compared to an in-sample analysis [17]. Moreover, because we use the longest available data sample in our empirical analysis, we avoid the issue of a possible sample-selection bias. At the same time, we also cover extreme fluctuations in the oil price associated with a wide range of historical events involving the interwar period, the Great Depression, the Korean and Vietnam wars, the two oil shocks, the Gulf war, the 9/11 attack, the Iraq invasion, the Global Financial Crisis, the Arab Spring, the oil-price collapse of 2014 to 2016, the US-China trade war, and, of course, the more recent swings in the price of oil due to the outbreak of the COVID-19 pandemic. The focus on the G7 countries and Switzerland, besides the early-established stock markets of two emerging economies, is purely driven by the availability of data on stock prices over this long sample period. Moreover, our decision to analyze the stock markets of these ten (advanced and emerging) economies is motivated by their importance in the global economy, with these countries representing nearly two-thirds of global net wealth and nearly half of world output [18]. Naturally, the impact of oil-price uncertainty on the equity-market system of these economies would translate into a global effect.
Besides the statistical validation of the role of oil-price uncertainty for stock returns based on a full-fledged out-of-sample forecasting experiment, the empirical results we document in this research also possess value for investors, academics, and policymakers. For instance, practitioners in finance require real-time forecasts of stock returns for asset allocation, while academics are particularly interested in stock-returns forecasts because they hold important lessons for measures of market efficiency and also help to refine asset-pricing models [19]. Moreover, it is well-established that stock returns serve as a leading indicator for macroeconomic variables [20], and the accurate forecasting of stock returns would entail valuable information to policymakers in terms of designing optimal policy responses to oil price uncertainty.
Naturally, the existing literature on forecasting international stock returns is vast, based on a wide array of (linear and nonlinear) models and (macroeconomic, financial, technical, and behavioral) predictors. Hence, providing a detailed review is beyond the scope of this paper; interested readers should refer to [21,22,23,24,25,26,27,28,29,30], for further information regarding this area of research. Even though the role of the oil price and/or returns in forecasting stock returns has been extensively analyzed [31,32,33,34], our contribution to this important and significant area of research is that we are the first to incorporate the role of oil-price uncertainty in forecasting international stock returns of advanced and emerging countries using over a century of data.
At this stage, it is important to outline the econometric approach we rely on to conduct our forecasting experiment. Traditionally, as discussed in detail in the papers cited above, the literature on predicting stock returns has relied on linear models. However, more recently, the focus has shifted to developing models that accommodate the well-established nonlinear relationship between stock returns and their predictors [35,36,37,38,39]. Against this backdrop, we consider the standard linear predictive-regression approach and use a predictive quantile-regression approach for our forecasting analysis. We argue that, due to non-linearity and non-normality patterns, which exist in our dataset based on formal statistical tests, a linear regression approach might not be adequate for exploring the ability of oil-price uncertainty to forecast the entire distribution of the stock returns of the ten countries.
The quantiles-based approach enables us to have a complete characterization of the forecastability of the entire conditional distribution of stock returns through a set of conditional quantiles rather than only its conditional mean, as is the case with the standard linear regression approach [40]. Looking at just the conditional mean of stock returns is likely to ‘hide’ interesting characteristics, as it can lead us to conclude that a predictor, in our case oil-price uncertainty, has poor forecasting performance, while it is valuable for forecasting certain parts of the conditional distribution of stock returns. In addition, business cycle fluctuations are likely to induce the slope coefficients associated with the predictor to vary across quantiles [41] to the extent that oil-price uncertainty may contain significant information for the lower or upper quantiles but not for the entire conditional distribution of stock returns. The quantile-predictive regression approach, which allows us to integrate this information, would, thus, lead to additional benefits over the standard linear and other popular nonlinear approaches.
Furthermore, in terms of modeling non-linearity, on the one hand, unlike the Markov-switching and the smooth threshold models, we do not need to specify the number of regimes of stock returns (for instance, bear and bull) in an ad hoc fashion with the quantile -based approach. On the other hand, the quantile approach has added advantages over the non- or semi-parametric neural networks and time-varying approaches, as we can study each point of the conditional distribution characterizing the state of the stock market. As the quantile-based approach studies the entire conditional distribution, which captures various stock market states, it adds an inherent time-varying component to the estimation process. By pursuing a recursive estimation of both the conditional-mean and predictive quantile-based approaches over the out-of-sample period, we make both the models have time-varying parameters in the forecast evaluation part of the sample, and in the process, do not provide the quantiles-based approach with an upper-hand in terms of estimation, besides its inherent advantage of being able to provide information on the entire conditional distribution of stock returns.
Overall, the quantile-based approach is more efficient and more robust than the linear approach, which focuses on the conditional mean only, in the presence of non-normality, non-linearity, and outliers [42], with the latter possibly leading to the emergence of regime changes in the relationship between oil-price uncertainty and stock returns (which, unsurprisingly, given the usage of over a century of data, we show to exist in our sample based on tests of multiple structural breaks). The fact that the quantile-based approach is not sensitive to outliers is particularly important in our forecasting context, as this implies that the quantile forecasts are still accurate in the presence of large positive or negative returns in the sample and, therefore, the produced forecasts are robust.
To the best of our knowledge, this is the first paper to analyze the role of oil-price uncertainty in forecasting the historical stock returns of ten advanced and emerging countries spanning over 100 years of monthly data. In other words, we extend the existing literature based on post-World War II and in-sample analyses that might not translate into out-of-sample gains into a full-fledged forecasting experiment relating oil uncertainty and stock returns with the longest possible data available to avoid a sample-selection bias. At the same time, using a quantiles-based approach, which is robust to non-linearity, regime changes, and non-normality, provides a time-varying approach to drawing correct forecast-related inferences over such a long span of data for the entire conditional distribution of stock returns.
While the focus is on forecasting, to provide an angle of economic and investment implications of our results, we also conduct an analysis involving regimes-dependent (smooth-transition, besides threshold, Markov-switching, and quantiles-based) methods of connectedness of the ten stock markets, with the regimes contingent on the high- and low-levels of oil-price uncertainty. In the process, we test the so-called correlation-asymmetry phenomena reported in a number of studies [43] that refer to the asymmetric pattern in which stock returns tend to be more correlated (connected) during bear-market regimes (as well as during periods of extreme price fluctuations). This is likely when oil-price uncertainty is high, given the theoretical and empirical evidence of the negative nexus between stock returns and a highly volatile oil market. Understandably, if connectedness is high across the ten markets when oil uncertainty is in its upper regime, then portfolio diversification opportunities across international equity markets are likely to erode, with all the stock returns experiencing a bearish phase. This issue has also not been dealt with before in the literature based on historical data, which, in turn, is likely to provide robust information, as we take the aspect of the length of the sample out of question here and simultaneously rely on time-varying methods.
It must be emphasized at this stage that the usage of the longest possible data available on the stocks and oil markets, as well as the implementation of regime-specific approaches for forecasting and spillover analyses, helps us to avoid any biases involving the choice of the sample period, while incorporating time-variation in the evolution of the relationships. In the process, our study can provide relatively robust conclusions for investors, policymakers, and even academics, when making their respective decisions. We organize the remainder of our paper as follows. Section 2 describes the methodologies we use in our empirical analysis. Section 3 discusses the data, our empirical results are presented in Section 4, and in Section 5, we conclude the paper.
2. Predictive Regression Models
In this section, we provide the technical details associated with the linear and quantile-based predictive regression models that we implement in our forecasting analysis.
The classical linear predictive mean-regression model is given by:
where is the observed cumulated stock returns over time period t + 1 to t + h, xi,t is a specific regressor/predictor at time , which in our work is oil-price uncertainty, and is the error term assumed to be independent with zero mean and variance . The ordinary least squares (OLS) estimators, , of the parameters in the predictive mean-regression model are estimated by minimizing the quadratic expected loss, , with respect to the parameters, . The point forecast of stock returns at time , is obtained as: .
The aforementioned model is primarily devised to predict the mean of , not the entire conditional distribution of stock returns. Ref. [40] showed that quantile-regression estimators are more efficient and robust than mean regression estimators in cases where nonlinearities and deviations from normality exist, with both these features existing in our data (as discussed below). Hence, we consider the predictive quantile-regression model of the following form:
where , and is assumed independent derived from an error distribution with the -th quantile equal to 0. Model (2) implies the -th quantile of given is where the intercept and the coefficients depend upon . The estimators of the parameters of the predictive quantile-regression model in Equation (2), , are obtained by minimizing the sum , where the so called check function is being used, The forecast of the -th quantile of the distribution of stock returns at time is .
3. Data
The stock-index raw data are denominated in respective local currencies for Canada (S&P TSX 300 Composite Index), France (CAC All-Tradable Index), Germany (CDAX Composite Index), India (Bombay Stock Exchange (BSE) Index), Italy (Banca Commerciale Italiana Index), Japan (Nikkei 225 Index), South Africa (Johannesburg Stock Exchange All Share (JSE-ALSI) Index), Switzerland (All Share Stock Index), the UK (FTSE All Share Index), and the US (S&P500 Index). The local currency stock indexes of the nine countries (except for the US) are converted to US dollars using the bilateral dollar-based exchange rates and then divided by the US Consumer Price Index (CPI) to get to the real stock prices. The WTI oil price in US dollars is also deflated by the US CPI to get the corresponding real oil price. All our raw data are obtained from the Global Financial Data. (https://globalfinancialdata.com/ (accessed on 1 October 2021)).
We then compute log returns in percentages for the stock and oil prices. Following the early work of ref. [6], and the extant literature on oil-price uncertainty (ref. [44], who relied on the Vector Autoregression (VAR)-GARCH-in-Mean model to relate oil uncertainty with low-frequency macroeconomic variables), we fit a Generalized Autoregressive Conditional Heteroskedasticity (GARCH(1,1)) model to obtain the conditional variance of the log returns of oil, which in turn serves as our metric of oil-price uncertainty (OIL_UNC) (Complete details of the estimation results of the GARCH(1,1) model are available upon request from the authors. As suggested by an anonymous referee, a formal test of ARCH effects on the squared residuals recovered from the mean-equation of real log returns of oil prices on a constant revealed that the null hypothesis of no ARCH effects is rejected at the highest level of significance at various lags. This suggested that modeling oil price uncertainty with a GARCH(1,1) model on monthly data, given that daily data is not available for analysis, is appropriate and does not lead to any misspecifications. Details of these results are also available upon request from the authors.) Based on a balanced data set, our monthly sample period covers the period from August 1920 to September 2021 at the time of writing this paper.
Figure A1 at the end of the paper (Appendix A) plots the stock-market returns and the GARCH(1,1)-based oil-price conditional volatility (OIL_UNC). In addition, as can be seen from the summary statistics of the variables reported in Table A1 (Appendix A), all ten stock log returns and OIL_UNC are not normally distributed based on the rejection of the null hypothesis under the Jarque-Bera test at the highest level of significance. Heavy tails of the variables under consideration provide a preliminary motivation to look at a predictive quantile-based approach.
4. Empirical Findings
4.1. Forecasting Results
We use an in-sample period from August 1920 to July 1925 (i.e., 60 months). Then the models in Equations (1) and (2) are estimated recursively over the out-of-sample period from August 1925 to September 2021 to produce forecasts at horizons (h) of 1-, 3-, 6-, 9-, 12, 18-, and 24-month-ahead. The choice of this in-sample period ensures that all regime changes, as determined by the multiple structural break tests of [45] applied to Equation (1) and reported in Table A2, fall over the out-of-sample period. In this manner, given the recursive estimation of both the predictive linear and predictive quantile-based regressions, we ensure that the latter does not enjoy any unfair advantage in terms of being inherently a nonlinear model, with non-linearity at least arising because of structural breaks. Non-linearity in the relationship between stock returns and OIL_UNC is overwhelmingly confirmed by the [46] (BDS) test when applied to the residuals of Equation (1), with the test rejecting the null hypothesis of i.i.d. at all possible dimensions at the highest possible level of significance, as shown in Table A3. The results from the structural instability analysis, as well as the non-linearity test, highlight, on the one hand, the inappropriateness of the linear predictive regression model given in Equation (1) and, on the other hand, indicate the necessity to employ a predictive quantile-based approach, as in Equation (2), when forecasting stock returns based on the information content of OIL_UNC.
In any event, for the sake of completeness and comparability, we also present the forecasting results from the predictive linear regression model in Table 1, besides the same from the predictive quantile-based approach, where we use the following quantiles for the latter: = 0.10, 0.20, 0.30….0.90. The entries in the table report the ratio of the Mean Square Forecast Errors (MSFEs) of Equation (1) relative to the same of the constant-mean (random-walk (RW)) model, i.e., , and the same for Equation (2) relative to the quantiles-based RW model, i.e., . If the ratio is less than one, the model with the predictor outperforms the model without it. It is also important, however, to test whether the superior performance of the model with the OIL_UNC, if it holds, is statistically different from the corresponding benchmark. Given that the model featuring oil-price uncertainty nests its associated benchmark, we use the MSE-F test statistic of ref. [47] to check whether, in cases where the ratio is less than one, the model with oil-price uncertainty significantly outperforms the one without it. The MSE-F test statistic is given as follows: MSE-F = (MSFER/MSFEUR − 1) × (T-R-h + 1), where MSFER and MSFEUR are the mean square forecast error of the restricted (without OIL_UNC) and unrestricted (with OIL_UNC) models, respectively, with T being the total sample size, R the length of the in-sample, and h the forecast horizon under consideration. A positive and significant MSE-F indicates that the forecasts from the unrestricted model are statistically superior to those from the restricted model. Given our set-up, the 1%, 5%, and 10% critical values derived from Table 4 of [47] (p. 732) are 3.951, 1.518, and 0.616, respectively.

Table 1.
Forecasting results.
Since we use the MSFE to evaluate forecast errors, we assume that a forecast consumer uses a squared-error loss function to study the predictive performance of both the linear regression and the quantiles-based approach. Alternatively, a quantile-based loss function (check function) could be used to evaluate the forecast errors implied by the quantile-based approach. This quantiles-based loss function is asymmetric (except in the special case where the conditional median is being analyzed) and accounts for the fact that the quantile-regression model adjusts forecasts of stock returns upward or downward depending on the quantile under scrutiny [48,49,50]. In this paper, we use the standard quadratic loss function, which has been used in recent research in a quantile-regression context [51], because using the MSFE for both approaches ensures that the results for the forecast evaluations are comparable across the two different approaches. From the perspective of a forecast consumer, the upward and downward adjustments of forecasts made under the quantile-based approach can then be interpreted as a data-driven pragmatic attempt to explore potential improvements in the forecasting performance of oil-price uncertainty by moving from a linear to a quantiles-based forecasting approach, where the underlying ceteris-paribus assumption is that the squared-error loss function and, thus, the preferences of a forecast consumer are the same for both approaches.
As can be seen from Table 1, for the predictive linear-regression model, the model with OIL_UNC surpasses the benchmark model in terms of forecasting performance in 13 instances, which happens to be the case at h = 1 and 6 for Canada; h = 24 for France, India, Japan, and Switzerland; h = 9 for Germany; h = 6, 9, and 18 for the UK, and; h = 1, 3, and 6 for the US. There is no evidence of stock-returns forecastability due to OIL_UNC for Italy and South Africa at any of the seven forecasting horizons considered. However, more importantly, out of the 13 cases where the model with OIL_UNC outperforms the benchmark, the forecasting gains, based on the MSE-F test, are statistically significant at the 1% level in nine cases, 5% in three cases, and 10% in the remaining one case. The evidence is generally mixed, with forecastability primarily observed at medium- to long-horizons for oil importers (France, Germany, India, Japan, Switzerland, and the UK) and at shorter horizons for oil exporters such as Canada and the US.
Given the evidence of non-normality and non-linearity (including structural breaks), these results are not surprising, besides being unreliable. Thus, we progressed to the predictive quantile-based approach. For Canada, significant forecastability based on the information content of OIL_UNC is observed for at least one conditional quantile, particularly at the lower end (i.e., τ = 0.30, 0.50–0.60 and 0.80 at h = 3; 0.10–0.40 and 0.70–0.90 at h = 6; 0.10–0.30 at h = 9, and; τ = 0.10–0.20 at h = 12 and 18) overall forecast horizon, except for h = 24. Hence, a stronger predictive effect is observed at lower forecast horizons regarding the coverage of the quantiles. For France, strong forecastability is observed at h = 24 over the conditional median and beyond, i.e., τ = 0.50 to 0.90, but the OIL_UNC also plays a role in predicting a bearish market (i.e., τ = 0.10 at h = 9, 12, 18, and; τ = 0.20 at h = 9 and 12). For Germany, while forecastability is observed for τ = 0.2–0.4 at h = 1 and at τ = 0.4 at h = 6, the same is observed at primarily higher conditional quantiles (i.e., τ = 0.60–0.70 for h = 12, and 0.70–0.80 for h = 18. For India, although evidence of forecastability at the shortest horizon (h = 1) could not be found, it is indeed observed primarily at higher quantiles (i.e., 0.70 onwards up to 0.90) for h = 3 to 18, with the strongest predictability observed at h = 24 covering virtually the entire conditional distribution (i.e., τ = 0.10 to 0.80). Compared to the predictive linear-regression model, under which Italian and South African stock returns were completely unpredictable based on the information content of OIL_UNC, now with the quantile-based approach, stock returns for Italy are consistently forecastable over all seven horizons considered for at least one conditional quantile, and, in particular, for below the median (τ = 0.10–0.40). Moderately higher quantiles are also predictable at h = 1 and 24. A story similar to that for Italy also holds for South Africa, with higher conditional quantiles (τ = 0.60–0.90) being forecastable at h = 1, 18, and 24, besides the lower quantiles (τ = 0.10–0.40) at h = 1 to 18. For Japan, barring h = 18, oil-price uncertainty can forecast at least one conditional quantile of stock returns (primarily around the median and at τ = 0.90) for the remaining forecast horizons, with the broadest evidence in terms of quantile coverage (τ = 0.20–0.90) at h = 24. For Switzerland, the forecastability of stock returns is observed at all seven horizons considered for at least one conditional quantile, with the largest quantile coverage, just as in the case of Japan, being at h = 24 (τ = 0.30–0.90). The other horizons depict forecastability at each end of the conditional distribution, except for h = 18, where the benchmark is outperformed at τ = 0.60. For the UK, apart from h = 1 and 24, at least two conditional quantiles are forecastable due to OIL_UNC, especially on and around the moderate quantiles below the median. At h = 18, the coverage of the predictable τ is equal to 0.10–0.80. Finally, for the US, at least one conditional quantile of stock returns can be accurately forecasted based on the information contained in OIL_UNC at h = 1, 3, 6, 12, and 18, especially in the bearish phase, although the normal market condition and the bullish-regime (i.e., τ = 0.50–0.90) is also forecastable at h = 1 to 6-month-ahead. For all the significant cases (with three instances of insignificance, even though the benchmark model was outperformed) of out-of-sample predictability detected under the quantile regression, three cases carry significance at the 5% level and four at the 10% level, with the rest being at the 1% level.
Despite the heterogeneity of the results across the stock markets, the quantile regression model with OIL_UNC as a predictor outperforms the prevailing quantile benchmark for all ten countries at certain quantiles, capturing normal, bear, and bull markets over specific forecast horizons. This differs from the predictive linear regression model, which picks up forecasting gains for eight countries (except Italy and South Africa). Moreover, we unveil forecasting gains in many more horizons (at particular quantiles) compared to the linear case. Our results depict the advantages of resorting to a non-linear approach that renders it possible to shed light on the entire conditional distribution of stock returns rather than just the conditional mean while analyzing the predictive relationship of oil-price uncertainty for international stock returns, which depicts non-normality. Besides the statistical importance of our findings, our results also hold value for academics, investors, and policymakers seeking to optimize their respective decisions during bull, bear, and normal stock-market phases in the wake of changes in oil-price uncertainty.
Table A4 provides the results for the forecasting experiment when we use an in-sample period of 120 months, i.e., from August 1920 to July 1930, with August 1930 to September 2021 being the out-of-sample period. As seen from this table, the basic conclusions derived for the shorter in-sample period from August 1920 to July 1925, as reported in Table 1, continue to hold for the longer in-sample period. This observation shows that our forecasting results are robust relative to a reasonable variation of the length of the in- and out-of-sample periods in terms of the superiority of the quantile predictive regression relative to its linear counterpart.
Overall, despite the forecasting gains being country-specific, i.e., observed for specific parts of the conditional distributions of stock returns and forecasting horizons, our findings depict the importance of relying on a quantiles-based approach over a linear predictive regression method, traditionally used in the literature. Our observations highlight that the quantile predictive regression is more informative for investors aiming to design their optimal portfolios in the wake of oil-price uncertainty shocks and associated market states across various forecasting horizons since out-of-sample predictability is detected in more cases under the quantile regression model relative to the linear framework. In essence, portfolio weights involving the international equity markets will vary based on their underlying states following hikes in oil market volatility.
4.2. Regimes-Based Connectedness Results and Investment Implications
Table 2 displays the regime-dependent connectedness metrics based on a smooth transition vector autoregressive (STVAR) model [52,53,54], computed in the same way as in ref. [55] (DY). The lag order of the STVAR models is 1, which is determined by the Bayesian information criterion (BIC) in a linear VAR model. Oil uncertainty is the threshold variable. The lower regime relates to the below-threshold (low uncertainty) periods, while the upper regime corresponds to the above-threshold (high uncertainty) periods. The STVAR smoothness and threshold parameter estimations are 44.876 and 59.709, respectively. The DY spillover index as a measure of the total connectedness measure is estimated as 62.60% in the low oil-price-uncertainty regime, while it is 83.58% in the high oil-price-uncertainty regime. Thus, there is a much stronger connectedness in the high-uncertainty regime, where more than four-fifths of the total spillover is due to cross-links across the stock markets and oil-price uncertainty. Indeed, many of the cross-links in both regimes are with oil-price uncertainty. In the low-uncertainty regime, Canada, France, Germany, India, Italy, the UK, and the US are significantly influenced by the oil market as volatility receivers. There are also a few strong connectedness links among stock markets in the low-uncertainty regime. For example, the spillover from Canada, Franca, Germany, Italy, and the US to Switzerland and the spillover from India, the UK, and the US to South Africa are substantial. A similar pattern is also observed in the high-uncertainty regime.

Table 2.
Regime dependent connectedness based on STVAR model.
In the high-uncertainty regime, the predictive power of oil-price uncertainty is stronger for almost all stock markets except South Africa. Indeed, the spillover estimates from oil-price uncertainty to stock returns are all above 90% for Canada, France, Italy, Japan, Switzerland, the UK, and the US, while they are above 80% for Germany and India. Although oil-price uncertainty is the key predictor variable for all stock returns in both regimes, its predictive capacity is much higher in the high-uncertainty regime. In the high-uncertainty regime, 95.53% of the spillover received by the ten stock markets comes from oil-price uncertainty, while this figure is only 70.68% in the low-uncertainty regime. Comparing the total spillover across the regimes, we observe that 88.93% of the total spillover of 11,000 in the high-uncertainty regime is accounted for by oil-price uncertainty, while this proportion falls to 53.32% in the low-uncertainty regime. Another noteworthy result for both regimes is related to the net-spillover estimates. In both regimes, all ten stock markets are net receivers, while oil-price uncertainty is the only net transmitter. All stock markets receive higher spillover from others in the high-uncertainty regime. For example, the net spillovers received by South Africa, Japan, Germany, and India are 2.18, 1.65, 1.63, and 1.31 times higher in the high-uncertainty regime, respectively, compared to the low-uncertainty regime. A further observation is that oil-price uncertainty does not receive any spillover from stock returns in the high-uncertainty regime, while the spillover from others to oil-price uncertainty in the low-uncertainty regime is also negligible.
Overall, oil-price uncertainty is the key variable governing and generating spillover connectedness for the ten stock markets, where its influence is much greater during high-uncertainty periods. The main findings from the STVAR model are summarized in the network analysis provided in Figure 1.
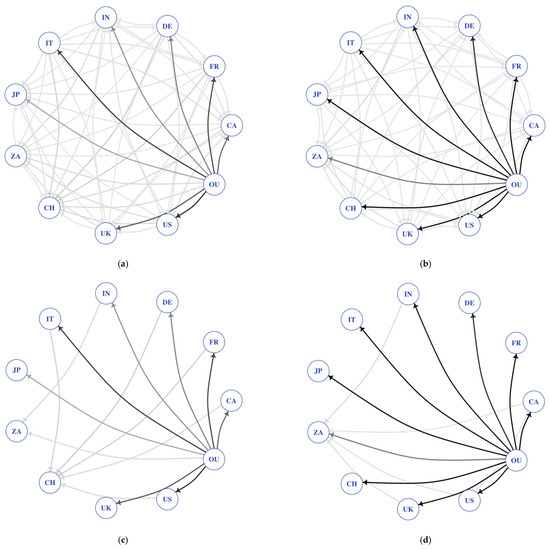
Figure 1.
Connectedness based on the STVAR model. Net connectedness is based on the pairwise net spillovers obtained from the STVAR model estimates reported in Table 2. Thresholding sets values below the 75th percentile of the spillover to zero. Darker color intensity indicates stronger links. (a) Net connectedness without thresholding in the lower regime. (b) Net connectedness without thresholding in the upper regime. (c) Net connectedness with thresholding in the lower regime. (d) Net connectedness with thresholding in the upper regime.
In addition, it should be noted that the conclusions from the STVAR model are also verified robustly in Table A5, Table A6 and Table A7, under the Threshold VAR (TVAR), Markov-switching VAR (MSVAR), and Quantile VAR (QVAR), respectively [56,57]. Our findings related to connectedness, thus, suggest that international portfolio allocation across stock markets would be relatively more difficult during episodes of heightened oil-price uncertainty, which is likely to result in bearish stock markets. The fact that higher oil-price uncertainty tends to have a stronger negative effect on stock returns when stock markets are in their lower conditional quantiles, i.e., during their bearish states, is evident, especially for the short forecast horizons, for Canada, France, Germany, Switzerland, and the US (Appendix A Figure A2). For Italy, Japan, and India, the coefficients estimated for the lower conditional quantiles are also generally negative, but, as the results for India demonstrate, they are not necessarily larger (in absolute value) than their counterparts in the upper conditional quantiles. Figure A2 plots the full-sample-based quantile response of the average, rather than cumulative, stock returns due to scale issues in the graphical representation (without compromising on the sign) across the ten countries due to OIL_UNC () for the various forecast horizons (h = 1, 3, 6, 9, 12, 18 and 24), covering the entire sample period of August 1920 to September 2021. This finding is in line with the correlation asymmetry phenomena, which states that stock returns tend to be more correlated (connected) during bear-market regimes, which are linked to higher oil-price volatility, thus making portfolio allocation across international equity markets difficult in the wake of an oil-price uncertainty shock.
5. Conclusions
The importance of accurate forecasting of stock returns for academics, practitioners in finance, and policymakers is well-recognized. However, stock-return forecasting is highly challenging because it inherently contains a sizable unpredictable component. Naturally, many models and predictors have been used in earlier literature.
In this regard, given that in-sample predictability does not necessarily translate into out-of-sample forecasting gains, we aim to extend the structural analyses-type literature on the oil-price uncertainty/stock-returns nexus by forecasting real stock returns of ten developed and emerging markets (Canada, France, Germany, India, Italy, Japan, South Africa, Switzerland, the UK, and the US) based on the information content of oil-price uncertainty. We investigated the forecastability of the stock returns of these markets based on over a century of monthly historical data (August 1920 to September 2021) and relied upon a predictive quantile-based approach to account for non-linearity and non-normality, which existed in our data based on statistical tests, while forecasting the entire conditional distribution of stock returns.
Our results show that the out-of-sample predictive content of oil-price uncertainty for stock returns is country-specific, as the effect is quite heterogeneous across countries and cannot be generalized. However, oil-price uncertainty produces significant forecasting gains for stock returns of all ten countries considered, though the specificity of the conditional quantiles and forecast horizon varies across the countries. In general, however, the coverage of predictability is associated with normal, bear, and bull-market states, as well as short-, medium-, and long-run horizons. When compared to the common predictive linear-regression approach, we find that the quantile results of forecastability encompass all ten markets rather than eight under the former. In addition, under the quantiles-based approach, the forecasting gains are detected at many more horizons (at particular quantiles) compared to the linear predictive regression. Our results thus highlight the importance of studying the entire distribution based on a framework that can account for non-linearity and non-normality rather than performing just a conditional mean-based analysis, which might be misleading as it is likely to miss important information contained for certain parts of the distribution of stock returns.
In addition, using a regimes-based spillover analysis, we find that the connectedness among the ten international stock markets, though predicted differently by oil-price uncertainty, is stronger in the wake of heightened oil-price uncertainty. This finding, in turn, implies that international portfolio diversification opportunities across stock markets are limited in the wake of large unfavorable uncertainty shocks related to the oil market. With our analyses relying on the longest possible data samples and time-varying methods, our findings can be considered robust and independent of the period of analyses.
Our results further demonstrate that policymakers who use movements in real stock returns following oil-price-uncertainty shocks as a leading indicator for low-frequency macroeconomic variables would be better served by tracing the differently-behaving entire conditional distribution of stock returns rather than just its conditional mean when designing policies aimed at mitigating business-cycle fluctuations and ensuring recovery out of a recession.
In light of the widespread evidence of cross-market volatility spillovers [58], as part of future research, it is interesting to analyze the second-moment predictability-effect of oil-price uncertainty on stock returns, i.e., on stock-market volatility, based on the historical dataset used in our paper. At the same time, with oil market uncertainty likely associated with geopolitical events [59] to which traditional equity markets are exposed [60], future analysis could delve into the issue of forecasting historical stock returns and volatility due to geopolitical acts and threats.
Author Contributions
Conceptualization, R.G.; Methodology, M.B., R.G. and C.P.; Software, M.B., R.G. and C.P.; Validation, C.P.; Formal Analysis, M.B., R.G. and C.P.; Investigation, M.B., R.G. and C.P.; Resources, R.G.; Data Curation, R.G.; Writing—Original Draft Preparation, R.G.; Writing—Review & Editing, M.B. and C.P.; Visualization, M.B. and C.P.; Supervision, C.P.; Project Administration, C.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is available from the authors upon request.
Acknowledgments
We would like to thank two anonymous referees for many helpful comments. However, any remaining errors are solely ours.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Summary statistics.
Table A1.
Summary statistics.
| Canada | France | Germany | India | Italy | Japan | |
| Statistic | CA | FR | DE | IN | IT | JP |
| Mean | 0.206 | 0.394 | 0.187 | −0.106 | 0.319 | 0.358 |
| S.D. | 4.592 | 5.503 | 8.073 | 6.253 | 7.058 | 6.034 |
| Min | −32.011 | −28.017 | −147.279 | −64.254 | −30.782 | −26.279 |
| Max | 20.589 | 24.256 | 68.264 | 27.690 | 46.811 | 51.287 |
| Skewness | −1.106 | −0.253 | −4.717 | −1.119 | 0.760 | 0.580 |
| Kurtosis | 5.618 | 1.822 | 100.959 | 13.170 | 5.591 | 7.124 |
| JB | 1852.385 *** | 182.403 *** | 521,844.876 *** | 9063.431 *** | 1706.435 *** | 2647.451 *** |
| South Africa | Switzerland | UK | US | Oil Uncertainty (OIL_UNC) | ||
| Statistic | ZA | CH | UK | US | OU | |
| Mean | 0.040 | 0.159 | 0.024 | 0.310 | 70.975 | |
| S.D. | 5.954 | 4.374 | 5.165 | 4.406 | 165.337 | |
| Min | −31.650 | −28.479 | −34.430 | −30.753 | 1.008 | |
| Max | 27.201 | 28.778 | 36.116 | 41.484 | 2536.770 | |
| Skewness | −0.048 | −0.510 | −0.178 | −0.465 | 7.922 | |
| Kurtosis | 3.156 | 4.988 | 6.059 | 11.969 | 89.223 | |
| JB | 507.507 *** | 1317.739 *** | 1872.398 *** | 7319.968 *** | 416,781.610 *** |
Note: Table reports the descriptive statistics on the stock log returns of Canada (CA), France (FR), Germany (DE), India (IN), Italy (IT), Japan (JP), South Africa (ZA), Switzerland (CH), the UK, the US, and the oil price uncertainty based on the GARCH(1,1,)-based volatility estimate of the WTI oil log-returns series. Along with the mean, standard deviation (SD), minimum and maximum values, skewness, and excess kurtosis, the table includes the Jarque-Bera test of normality (JB), with *** indicating significance at the 1% level.

Table A2.
BDS test results.
Table A2.
BDS test results.
| Canada (CA) | |||||
| Horizon | m | ||||
| 2 | 3 | 4 | 5 | 6 | |
| 1 | 5.4804 *** | 7.2432 *** | 7.7305 *** | 8.0552 *** | 8.3996 *** |
| 3 | 30.0470 *** | 29.8887 *** | 30.0940 *** | 30.5043 *** | 31.2106 *** |
| 6 | 48.8757 *** | 49.5146 *** | 50.2101 *** | 51.8332 *** | 54.7206 *** |
| 9 | 59.7664 *** | 61.5225 *** | 63.5063 *** | 66.8864 *** | 71.8290 *** |
| 12 | 66.6430 *** | 69.3991 *** | 72.3594 *** | 76.7925 *** | 83.0177 *** |
| 18 | 73.4330 *** | 77.3927 *** | 81.6248 *** | 87.7516 *** | 96.1108 *** |
| 24 | 73.9455 *** | 77.8864 *** | 82.5771 *** | 89.3594 *** | 98.4716 *** |
| France (FR) | |||||
| Horizon | m | ||||
| 2 | 3 | 4 | 5 | 6 | |
| 1 | 6.3620 *** | 7.2471 *** | 7.9322 *** | 8.4771 *** | 9.2419 *** |
| 3 | 32.0595 *** | 31.0787 *** | 31.0264 *** | 31.4570 *** | 32.2572 *** |
| 6 | 50.4667 *** | 50.4568 *** | 50.7707 *** | 52.1863 *** | 54.5124 *** |
| 9 | 60.2360 *** | 62.0011 *** | 63.7013 *** | 66.6309 *** | 70.9955 *** |
| 12 | 71.1355 *** | 74.1394 *** | 77.2470 *** | 81.9037 *** | 88.3707 *** |
| 18 | 78.0588 *** | 82.0287 *** | 86.4896 *** | 92.8287 *** | 101.4192 *** |
| 24 | 84.1488 *** | 89.0199 *** | 94.7484 *** | 102.8983 *** | 113.8628 *** |
| Germany (DE) | |||||
| Horizon | m | ||||
| 2 | 3 | 4 | 5 | 6 | |
| 1 | −0.0304 | −0.0408 | −0.0489 | −0.0558 | −0.0619 |
| 3 | 22.1413 *** | 19.8431 *** | 17.8224 *** | 16.2627 *** | 15.0398 *** |
| 6 | 49.1776 *** | 49.8417 *** | 50.7371 *** | 52.9877 *** | 56.5639 *** |
| 9 | 57.4173 *** | 59.4958 *** | 61.9414 *** | 65.7028 *** | 70.9413 *** |
| 12 | 64.2860 *** | 67.0138 *** | 70.1761 *** | 75.0193 *** | 81.7098 *** |
| 18 | 65.8235 *** | 69.5390 *** | 73.6751 *** | 79.6903 *** | 87.8614 *** |
| 24 | 68.1973 *** | 72.3469 *** | 77.2291 *** | 84.2390 *** | 93.6809 *** |
| India (IN) | |||||
| Horizon | m | ||||
| 2 | 3 | 4 | 5 | 6 | |
| 1 | 6.6610 *** | 7.8605 *** | 8.7403 *** | 9.7294 *** | 10.8895 *** |
| 3 | 34.2447 *** | 33.4717 *** | 33.1863 *** | 33.8146 *** | 35.2266 *** |
| 6 | 55.9590 *** | 56.5965 *** | 57.3946 *** | 59.3295 *** | 62.5465 *** |
| 9 | 68.4950 *** | 70.3921 *** | 72.5318 *** | 75.9896 *** | 81.2207 *** |
| 12 | 82.4923 *** | 85.7183 *** | 89.1765 *** | 94.5480 *** | 102.2504 *** |
| 18 | 100.5006 *** | 105.5870 *** | 111.3451 *** | 119.6967 *** | 130.9977 *** |
| 24 | 101.6299 *** | 107.1692 *** | 113.8164 *** | 123.5633 *** | 136.7903 *** |
| Italy (IT) | |||||
| Horizon | m | ||||
| 2 | 3 | 4 | 5 | 6 | |
| 1 | 8.1219 *** | 9.9043 *** | 11.8050 *** | 12.9516 *** | 14.0496 *** |
| 3 | 31.1155 *** | 31.2116 *** | 32.0832 *** | 33.2771 *** | 34.8462 *** |
| 6 | 45.0681 *** | 46.1790 *** | 47.1035 *** | 49.0987 *** | 52.1795 *** |
| 9 | 52.6023 *** | 54.2944 *** | 56.5492 *** | 60.0800 *** | 64.952 *** |
| 12 | 58.6007 *** | 61.2763 *** | 64.2609 *** | 68.9322 *** | 75.3187 *** |
| 18 | 65.6667 *** | 68.8835 *** | 72.6163 *** | 78.1481 *** | 85.6733 *** |
| 24 | 72.3672 *** | 76.4420 *** | 81.2412 *** | 88.1203 *** | 97.4060 *** |
| Japan (JP) | |||||
| Horizon | m | ||||
| 2 | 3 | 4 | 5 | 6 | |
| 1 | 7.7895 *** | 10.5237 *** | 12.3909 *** | 13.5504 *** | 14.7601 *** |
| 3 | 32.6978 *** | 33.0664 *** | 33.4913 *** | 34.4981 *** | 36.0140 *** |
| 6 | 46.1696 *** | 47.9324 *** | 49.0691 *** | 51.0530 *** | 54.0522 *** |
| 9 | 56.6341 *** | 59.0716 *** | 61.5812 *** | 65.3488 *** | 70.3983 *** |
| 12 | 64.5106 *** | 67.6304 *** | 71.1540 *** | 76.2769 *** | 83.1049 *** |
| 18 | 70.9028 *** | 75.1158 *** | 79.5581 *** | 85.7982 *** | 94.2258 *** |
| 24 | 72.6994 *** | 77.0989 *** | 82.1197 *** | 89.3549 *** | 99.0218 *** |
| South Africa (ZA) | |||||
| Horizon | m | ||||
| 2 | 3 | 4 | 5 | 6 | |
| 1 | 8.2964 *** | 9.4845 *** | 10.8520 *** | 11.6503 *** | 12.7213 *** |
| 3 | 34.1471 *** | 33.4270 *** | 33.7088 *** | 34.5045 *** | 35.8966 *** |
| 6 | 57.9810 *** | 58.3660 *** | 58.8450 *** | 60.6053 *** | 63.7685 *** |
| 9 | 72.9328 *** | 75.2876 *** | 77.8432 *** | 81.9912 *** | 87.8248 *** |
| 12 | 80.7393 *** | 84.4037 *** | 88.4145 *** | 94.6587 *** | 103.1594 *** |
| 18 | 83.4895 *** | 88.1933 *** | 93.5529 *** | 101.3645 *** | 111.9483 *** |
| 24 | 92.3261 *** | 97.6548 *** | 103.8140 *** | 112.8047 *** | 125.0195 *** |
| Switzerland (CH) | |||||
| Horizon | m | ||||
| 2 | 3 | 4 | 5 | 6 | |
| 1 | 7.4940 *** | 7.8755 *** | 9.0694 *** | 9.7816 *** | 10.7581 *** |
| 3 | 31.9384 *** | 30.7749 *** | 30.6713 *** | 31.4211 *** | 32.7586 *** |
| 6 | 49.7216 *** | 50.8735 *** | 52.0055 *** | 54.1263 *** | 57.3040 *** |
| 9 | 63.0756 *** | 65.3880 *** | 67.7258 *** | 71.4613 *** | 76.8146 *** |
| 12 | 71.2159 *** | 74.5311 *** | 78.1453 *** | 83.4362 *** | 90.5305 *** |
| 18 | 83.8940 *** | 88.6358 *** | 94.0200 *** | 101.6712 *** | 111.9015 *** |
| 24 | 85.7254 *** | 90.8166 *** | 96.7568 *** | 105.1647 *** | 116.4791 *** |
| UK | |||||
| Horizon | m | ||||
| 2 | 3 | 4 | 5 | 6 | |
| 1 | 7.3849 *** | 9.5479 *** | 10.6744 *** | 11.9226 *** | 12.6929 *** |
| 3 | 26.9010 *** | 27.2498 *** | 27.9282 *** | 28.9153 *** | 30.2618 *** |
| 6 | 41.1060 *** | 41.7911 *** | 42.3479 *** | 43.6310 *** | 45.9965 *** |
| 9 | 48.1450 *** | 49.6972 *** | 51.4142 *** | 54.0192 *** | 57.7359 *** |
| 12 | 52.6877 *** | 54.8292 *** | 57.1575 *** | 60.8198 *** | 65.7464 *** |
| 18 | 62.3997 *** | 65.7829 *** | 69.4332 *** | 74.7400 *** | 81.8649 *** |
| 24 | 65.9381 *** | 69.7089 *** | 73.9110 *** | 79.8362 *** | 87.8560 *** |
| US | |||||
| Horizon | m | ||||
| 2 | 3 | 4 | 5 | 6 | |
| 1 | 7.2639 *** | 8.4353 *** | 9.4870 *** | 10.3174 *** | 11.2059 *** |
| 3 | 33.4457 *** | 33.8675 *** | 34.6486 *** | 35.9221 *** | 37.9822 *** |
| 6 | 50.0905 *** | 50.9738 *** | 52.1340 *** | 54.4882 *** | 58.1975 *** |
| 9 | 58.4171 *** | 60.6130 *** | 63.3531 *** | 67.6082 *** | 73.4821 *** |
| 12 | 65.5209 *** | 68.5206 *** | 71.9698 *** | 77.0623 *** | 84.1272 *** |
| 18 | 69.3140 *** | 72.9984 *** | 77.4758 *** | 83.9991 *** | 92.7723 *** |
| 24 | 71.3134 *** | 75.2479 *** | 80.0222 *** | 86.9867 *** | 96.3795 *** |
Note: m stands for the number of (embedded) dimensions which embed the time series into m-dimensional vectors by taking each m successive points in the series; Test applied to residuals of Equation (1): ; entries correspond to the null hypothesis of i.i.d. residuals based on the z-statistic of the BDS (Brock et al., 1996) [46] test), with *** indicating significance at the 1% level.

Table A3.
Multiple structural break test results.
Table A3.
Multiple structural break test results.
| Canada (CA) | |
| Horizon | Dates |
| 1 | 1940M12, 1956M08, 1975M01 |
| 3 | |
| 6 | |
| 9 | 1937M07, 1952M11, 1967M11, 1982M11, 2000M11 |
| 12 | 1937M09, 1957M02, 1975M08, 1990M10, 2006M09 |
| 18 | 1937M08, 1957M02, 1975M11, 1990M10, 2006M11 |
| 24 | 1937M09, 1952M07, 1967M05, 1983M08, 2001M06 |
| France (FR) | |
| Horizon | Dates |
| 1 | 1939M10, 1962M05 |
| 3 | 1939M11, 1962M06 |
| 6 | 1940M02, 1962M06 |
| 9 | 1940M04, 1960M06, 1975M06, 1990M06, 2006M10 |
| 12 | 1940M06, 1960M09, 1975M09, 1990M09, 2006M10 |
| 18 | 1940M12, 1960M12, 1975M11, 1990M10, 2006M11 |
| 24 | 1940M06, 1961M02, 1975M12, 1990M10, 2006M12 |
| Germany (DE) | |
| Horizon | Dates |
| 1 | 1935M10, 1950M12, 1966M03, 1982M09, 2000M03 |
| 3 | 1935M11, 1951M01, 1966M04, 1982M09, 2000M05 |
| 6 | 1936M02, 1951M03, 1966M04, 1982M11, 2000M06 |
| 9 | 1936M04, 1951M04, 1966M04, 1982M12, 2000M09 |
| 12 | 1936M07, 1951M07, 1966M07, 1982M12, 2000M11 |
| 18 | 1950M01, 1964M12, 1983M02, 2001M02 |
| 24 | 1950M07, 1965M05, 1982M12, 2000M11 |
| India (IN) | |
| Horizon | Dates |
| 1 | 1940M12, 1956M04, 1976M07, 1991M08, 2006M09 |
| 3 | 1940M12, 1956M05, 1976M07, 1991M08, 2006M09 |
| 6 | 1941M03, 1956M08, 1976M07, 1991M08, 2006M09 |
| 9 | 1941M06, 1956M09, 1975M10, 1990M10, 2005M10 |
| 12 | 1947M07, 1968M03, 1987M05, 2002M06 |
| 18 | 1948M01, 1969M01, 1986M04, 2002M04 |
| 24 | 1948M05, 1977M05, 1995M09 |
| Italy (IT) | |
| Horizon | Dates |
| 1 | |
| 3 | |
| 6 | 1939M06, 1961M07, 1978M05 |
| 9 | 1939M06, 1960M10, 1975M10, 1990M10, 2006M10 |
| 12 | 1939M07, 1960M10, 1975M10, 1990M10, 2006M10 |
| 18 | 1939M10, 1960M12, 1975M11, 1990M10, 2006M11 |
| 24 | 1939M11, 1962M06, 1979M02, 2001M02 |
| Japan (JP) | |
| Horizon | Dates |
| 1 | |
| 3 | |
| 6 | 1944M12, 1960M01, 1975M02, 1990M03, 2005M04 |
| 9 | 1945M04, 1960M04, 1975M04, 1990M04, 2005M05 |
| 12 | 1945M07, 1960M07, 1975M07, 1990M07, 2005M07 |
| 18 | 1947M12, 1962M11, 1989M10, 2004M09 |
| 24 | 1948M01, 1962M11, 1990M02, 2004M12 |
| South Africa (ZA) | |
| Horizon | Dates |
| 1 | 1940M06, 1974M02 |
| 3 | 1941M05, 1956M09, 1974M04, 1991M07, 2006M09 |
| 6 | 1941M05, 1961M09, 1981M01, 2000M10 |
| 9 | 1941M05, 1961M11, 1981M02, 2001M01 |
| 12 | 1947M05, 1962M05, 1981M05, 2001M03 |
| 18 | 1947M10, 1962M09, 1981M11, 2001M02 |
| 24 | 1948M06, 1963M04, 1982M02, 2000M12 |
| Switzerland (CH) | |
| Horizon | Dates |
| 1 | 1945M04, 1962M03, 1982M08, 1998M08 |
| 3 | 1945M05, 1962M04, 1982M09, 1998M08 |
| 6 | 1945M08, 1962M05, 1982M11, 1998M08 |
| 9 | 1945M09, 1962M05, 1982M11, 1998M09 |
| 12 | 1939M01, 1962M05, 1982M12, 2001M03 |
| 18 | 1939M06, 1962M07, 1983M02, 1999M07 |
| 24 | 1939M06, 1962M10, 1983M07, 2000M01 |
| UK | |
| Horizon | Dates |
| 1 | 1941M08, 1956M12, 1974M04, 1990M12, 2006M09 |
| 3 | 1941M06, 1967M05, 1982M09 |
| 6 | 1941M10, 1957M01, 1975M01, 1991M04, 2006M09 |
| 9 | 1941M10, 1956M12, 1975M01, 1991M04, 2006M10 |
| 12 | 1941M07, 1957M01, 1975M01, 1990M01, 2006M10 |
| 18 | 1941M10, 1957M03, 1975M04, 1990M03, 2006M11 |
| 24 | 1941M09, 1957M03, 1975M01, 1989M11, 2006M12 |
| US | |
| Horizon | Dates |
| 1 | |
| 3 | |
| 6 | 1937M04, 1952M05, 1967M08, 1982M09, 1999M09 |
| 9 | 1937M05, 1952M07, 1967M11, 1982M11, 2000M08 |
| 12 | 1937M06, 1952M06, 1968M01, 1983M01, 2000M04 |
| 18 | 1937M05, 1952M04, 1967M03, 1983M02, 2000M09 |
| 24 | 1937M09, 1952M07, 1967M05, 1983M04, 2000M11 |
Note: Test applied to Equation (1): ; entries correspond to the break dates based on Bai and Perron (2003) [45] tests of multiple structural breaks.

Table A4.
Alternative forecasting results.
Table A4.
Alternative forecasting results.
| Canada (CA) | ||||||||||
| Horizon | Linear | Quantile | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 1 | 1.0096 | 1.0539 | 1.0207 | 1.0063 | 1.0056 | 1.0692 | 1.0225 | 1.0565 | 1.0541 | 1.0681 |
| 3 | 1.1653 | 0.9834 *** | 1.0260 | 1.0137 | 1.1749 | 1.1579 | 1.3767 | 1.1520 | 1.0041 | 1.1533 |
| 6 | 1.0695 | 3.6724 | 2.8853 | 1.5703 | 1.0828 | 1.0428 | 0.9909 *** | 1.0160 | 1.7642 | 2.5774 |
| 9 | 1.0097 | 1.0775 | 1.0009 | 1.0102 | 1.0289 | 1.0012 | 1.0055 | 1.0082 | 1.0198 | 1.1721 |
| 12 | 1.0426 | 1.1246 | 1.0181 | 0.9767 *** | 1.0041 | 0.9960 *** | 1.0777 | 1.0577 | 1.0481 | 1.0280 |
| 18 | 1.0415 | 0.9319 *** | 1.0219 | 0.9984 ** | 1.0093 | 1.0224 | 1.0306 | 1.0739 | 0.9909 *** | 0.9967 ** |
| 24 | 1.1414 | 1.1748 | 1.0304 | 1.2822 | 1.0970 | 1.0810 | 1.0539 | 1.0424 | 0.9874 *** | 0.9849 *** |
| France (FR) | ||||||||||
| Horizon | Linear | Quantile | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 1 | 1.0313 | 1.0527 | 1.0000 | 1.0215 | 1.0231 | 1.1059 | 1.0470 | 1.0838 | 1.1175 | 1.1217 |
| 3 | 1.1494 | 0.9469 *** | 0.9420 *** | 1.1186 | 1.1266 | 1.1617 | 1.1589 | 1.0852 | 1.1215 | 1.0157 |
| 6 | 1.0095 | 1.0188 | 0.9864 *** | 1.0475 | 1.0057 | 1.0044 | 1.0184 | 0.9977 ** | 0.9696 *** | 1.0002 |
| 9 | 1.0015 | 1.0973 | 1.0783 | 1.0000 | 0.9929 *** | 0.9913 *** | 1.0098 | 0.9977 ** | 0.9986 ** | 1.1446 |
| 12 | 0.9937 *** | 1.0030 | 0.9432 *** | 0.9674 *** | 1.0113 | 1.0188 | 0.9883 *** | 0.9917 *** | 1.0205 | 1.0648 |
| 18 | 1.0137 | 0.9867 *** | 1.1046 | 1.0585 | 1.0279 | 1.0175 | 1.0282 | 0.9880 *** | 1.1046 | 0.9785 *** |
| 24 | 1.3594 | 1.1084 | 1.0417 | 1.5507 | 1.3332 | 1.3228 | 1.3951 | 1.4304 | 1.2986 | 2.5698 |
| Germany (DE) | ||||||||||
| Horizon | Linear | Quantile | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 1 | 1.0279 | 1.1018 | 0.9898 *** | 1.0360 | 1.0204 | 1.0448 | 1.1372 | 1.0048 | 1.1026 | 1.0208 |
| 3 | 1.1151 | 0.9379 *** | 1.0549 | 1.2953 | 1.1239 | 1.1144 | 1.0876 | 1.0256 | 1.0308 | 1.0686 |
| 6 | 1.0230 | 1.0046 | 0.9894 *** | 1.0064 | 1.0024 | 1.0043 | 1.0321 | 1.0120 | 1.0740 | 1.0010 |
| 9 | 1.0030 | 1.2079 | 0.9989 * | 1.0230 | 1.0217 | 0.9938 *** | 0.9912 *** | 0.9995 | 1.0267 | 0.9872 *** |
| 12 | 0.9980 ** | 1.0389 | 0.9968 ** | 1.0012 | 0.9947 *** | 0.9985 ** | 0.9969 ** | 1.0231 | 0.9805 *** | 1.0071 |
| 18 | 1.0313 | 0.9988 * | 1.0337 | 1.0673 | 1.0675 | 1.0283 | 1.0253 | 1.0513 | 0.9915 *** | 0.9369 *** |
| 24 | 1.9997 | 1.2953 | 1.3754 | 1.6164 | 1.7809 | 2.1678 | 2.3916 | 2.3820 | 3.2277 | 4.1536 |
| India (IN) | ||||||||||
| Horizon | Linear | Quantile | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 1 | 1.0978 | 1.4814 | 1.0274 | 1.2574 | 1.1813 | 1.1473 | 1.1468 | 1.0286 | 1.1446 | 1.0188 |
| 3 | 1.0085 | 1.0727 | 1.0415 | 1.4281 | 1.1178 | 1.0832 | 0.9824 *** | 0.9711 *** | 1.0006 | 1.0187 |
| 6 | 1.0248 | 1.0924 | 0.9995 | 1.0007 | 1.0071 | 1.0155 | 1.0914 | 1.0631 | 1.0370 | 0.9494 *** |
| 9 | 1.0184 | 1.0396 | 1.0065 | 1.0293 | 1.0306 | 0.9973 ** | 0.9981 ** | 0.9995 | 0.9757 *** | 1.1052 |
| 12 | 0.9998 | 1.0349 | 0.9828 *** | 0.9998 | 1.0011 | 1.0048 | 1.0216 | 0.9920 *** | 0.9639 *** | 1.0069 |
| 18 | 1.0422 | 0.9695 *** | 0.9801 *** | 1.0793 | 1.1084 | 1.0888 | 1.1171 | 1.0380 | 0.9846 *** | 1.0141 |
| 24 | 1.0024 | 1.0503 | 0.9541 *** | 1.0345 | 1.0017 | 1.0018 | 1.0207 | 1.0009 | 1.0319 | 1.0166 |
| Italy (IT) | ||||||||||
| Horizon | Linear | Quantile | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 1 | 1.1823 | 0.7720 *** | 1.1620 | 1.5118 | 1.4267 | 1.2264 | 1.1427 | 1.1004 | 1.1092 | 1.0123 |
| 3 | 1.1822 | 1.0281 | 1.7459 | 1.4004 | 1.3863 | 1.0002 | 1.0119 | 0.9681 *** | 1.0874 | 1.0138 |
| 6 | 1.0074 | 0.8750 *** | 1.0080 | 1.0002 | 1.0014 | 0.9872 *** | 1.0717 | 1.0194 | 1.0022 | 1.0442 |
| 9 | 1.2124 | 1.0220 | 1.1897 | 1.1015 | 1.0460 | 1.0197 | 1.1358 | 1.4979 | 1.2484 | 1.3853 |
| 12 | 1.0000 | 1.0521 | 1.0373 | 0.9943 *** | 1.0061 | 0.9979 ** | 1.0209 | 1.0349 | 1.0578 | 1.1765 |
| 18 | 1.0291 | 1.0006 | 1.0080 | 1.0531 | 1.0765 | 1.1013 | 1.0739 | 1.0585 | 1.0108 | 0.9812 *** |
| 24 | 1.0053 | 1.0635 | 1.0201 | 1.0394 | 1.0173 | 1.0704 | 1.0097 | 0.9958 *** | 1.0163 | 1.0753 |
| Japan (JP) | ||||||||||
| Horizon | Linear | Quantile | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 1 | 1.2420 | 0.9940 *** | 1.2484 | 1.7484 | 1.6886 | 1.3154 | 1.1184 | 1.0560 | 1.0853 | 1.0603 |
| 3 | 1.2625 | 1.7774 | 1.7937 | 1.0878 | 1.0151 | 1.0109 | 1.0547 | 1.1246 | 1.0573 | 1.1131 |
| 6 | 1.0223 | 0.9873 *** | 1.0180 | 1.0746 | 1.0076 | 1.0391 | 1.0806 | 1.0392 | 0.9947 *** | 1.0003 |
| 9 | 1.0012 | 1.0090 | 1.0027 | 1.0031 | 1.0031 | 1.0054 | 0.9999 | 1.0020 | 1.0002 | 1.0206 |
| 12 | 0.9974 ** | 1.0620 | 1.0324 | 0.9806 *** | 1.0010 | 0.9980 ** | 1.0126 | 1.0178 | 1.0751 | 1.1429 |
| 18 | 1.0002 | 1.5033 | 1.0417 | 1.0012 | 1.0367 | 1.1547 | 1.0448 | 0.9856 *** | 0.9976 ** | 1.0058 |
| 24 | 1.0025 | 1.1077 | 1.0006 | 1.0076 | 1.1255 | 1.0761 | 1.0774 | 1.0424 | 1.0013 | 0.9898 *** |
| South Africa (ZA) | ||||||||||
| Horizon | Linear | Quantile | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 1 | 1.4650 | 0.9945 *** | 1.8966 | 2.1014 | 1.9733 | 1.8073 | 1.9312 | 1.2950 | 1.0204 | 0.9817 *** |
| 3 | 1.0708 | 1.4051 | 1.3542 | 1.1024 | 0.9813 *** | 1.0104 | 1.0200 | 1.0921 | 1.0107 | 1.0261 |
| 6 | 0.9947 *** | 1.0304 | 1.0222 | 0.9977 ** | 1.0135 | 0.9369 *** | 0.9627 *** | 1.0376 | 1.0192 | 1.0136 |
| 9 | 0.9999 | 1.0205 | 1.0358 | 0.9965 *** | 1.0090 | 0.9984 ** | 1.0001 | 1.0009 | 0.9941 *** | 1.0138 |
| 12 | 1.0070 | 1.0895 | 0.9975 ** | 0.9957 *** | 0.9749 *** | 0.9918 *** | 1.0050 | 0.9994 * | 1.0011 | 0.9736 *** |
| 18 | 1.0216 | 1.0691 | 1.1364 | 1.0466 | 1.0634 | 1.0373 | 1.0168 | 1.0039 | 0.9895 *** | 1.0167 |
| 24 | 1.0402 | 1.1938 | 1.0024 | 1.0669 | 1.1141 | 1.1288 | 1.1311 | 1.1342 | 0.9889 *** | 1.0083 |
| Switzerland (CH) | ||||||||||
| Horizon | Linear | Quantile | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 1 | 1.0279 | 1.0496 | 1.0018 | 1.0119 | 1.0090 | 0.9998 | 1.0692 | 1.1040 | 1.1118 | 1.1047 |
| 3 | 0.9998 | 1.2222 | 1.1021 | 1.0053 | 1.0216 | 1.1108 | 1.0138 | 0.8667 *** | 1.0533 | 1.0154 |
| 6 | 1.0565 | 0.9798 *** | 1.0370 | 1.0100 | 0.9812 *** | 1.1639 | 1.1867 | 1.0328 | 1.0160 | 1.0183 |
| 9 | 1.0301 | 1.1459 | 1.0247 | 1.0025 | 1.0043 | 1.0047 | 1.0113 | 1.0100 | 1.0238 | 1.0247 |
| 12 | 1.0419 | 0.9803 *** | 0.9976 ** | 1.0122 | 1.0058 | 1.1001 | 1.0572 | 1.0242 | 1.0173 | 0.9930 *** |
| 18 | 1.0600 | 1.0691 | 1.0739 | 1.1491 | 1.0879 | 1.0784 | 1.0828 | 1.0381 | 0.9783 *** | 1.0375 |
| 24 | 1.0990 | 0.9874 *** | 0.9947 *** | 1.1388 | 1.2852 | 1.2089 | 1.1239 | 1.0596 | 1.0010 | 1.1398 |
| UK | ||||||||||
| Horizon | Linear | Quantile | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 1 | 1.0434 | 1.0109 | 1.0136 | 1.0100 | 0.9996 | 1.0531 | 1.0868 | 1.2331 | 1.1611 | 1.0767 |
| 3 | 1.0323 | 1.4793 | 1.0448 | 1.0267 | 1.0649 | 1.0963 | 1.0343 | 0.9485 *** | 0.9670 *** | 0.9797 *** |
| 6 | 1.0012 | 1.2523 | 1.0781 | 1.0078 | 1.0069 | 1.0031 | 1.0022 | 0.9990 * | 1.0072 | 1.1252 |
| 9 | 1.0847 | 1.0446 | 1.0154 | 1.0109 | 1.0584 | 1.0510 | 1.0718 | 1.0722 | 1.0875 | 1.0844 |
| 12 | 1.3548 | 1.2745 | 1.2623 | 1.3162 | 1.3016 | 1.2363 | 1.2374 | 1.1294 | 1.0468 | 1.0564 |
| 18 | 1.0766 | 1.1655 | 1.0600 | 1.0944 | 1.1366 | 1.1212 | 1.0326 | 1.0043 | 1.0045 | 1.0186 |
| 24 | 1.1771 | 1.0165 | 1.4577 | 1.2638 | 1.1698 | 1.1418 | 1.2222 | 1.1263 | 1.0788 | 0.9917 *** |
| US | ||||||||||
| Horizon | Linear | Quantile | ||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| 1 | 1.0497 | 1.0348 | 1.0002 | 0.9872 *** | 0.9995 | 1.1256 | 1.0973 | 1.1177 | 1.1432 | 1.0528 |
| 3 | 1.3280 | 0.9840 *** | 1.3684 | 1.0353 | 1.0276 | 1.0337 | 1.0000 | 2.7862 | 1.4646 | 1.3231 |
| 6 | 1.0004 | 1.0385 | 0.9756 *** | 0.9718 *** | 0.9942 *** | 1.0033 | 1.0291 | 1.0555 | 1.0440 | 1.0169 |
| 9 | 1.0755 | 0.9941 *** | 0.9895 *** | 0.9877 *** | 1.0202 | 1.0466 | 1.0866 | 1.0581 | 1.0790 | 1.0206 |
| 12 | 1.0067 | 1.0155 | 1.0299 | 1.0278 | 1.0109 | 1.0037 | 0.9989 * | 0.9788 *** | 1.0072 | 1.0008 |
| 18 | 1.0942 | 1.1269 | 1.1496 | 1.1291 | 1.1904 | 1.0899 | 1.0626 | 1.0094 | 1.0057 | 1.0084 |
| 24 | 1.4691 | 1.8355 | 1.9966 | 1.5954 | 1.4648 | 1.3589 | 1.2509 | 1.2500 | 1.2216 | 1.0107 |
Note: In-sample: August 1920 to July 1930; Out-of-sample: August 1930 to September 2021; ***, **, and * indicate significance for the MSE-F statistic of McCracken (2007) [47] at 1%, 5%, and 10% levels respectively, while τ specifies the quantile; MSFEUR/MSFER signifies the Mean Square Forecast Error (RMSFE) ratio of the corresponding linear () or quantile regression () models over the one generated by the benchmarks ( or ).

Table A5.
Regime dependent connectedness based on the TVAR model.
Table A5.
Regime dependent connectedness based on the TVAR model.
| Lower Regime | ||||||||||||
| CA | FR | DE | IN | IT | JP | ZA | CH | UK | US | OIL_UNC | From | |
| CA | 26.75 | 7.13 | 5.38 | 5.24 | 5.59 | 2.09 | 1.48 | 6.80 | 0.79 | 13.46 | 25.29 | 73.25 |
| FR | 3.28 | 24.97 | 4.25 | 0.44 | 5.70 | 1.71 | 0.09 | 4.20 | 0.34 | 2.06 | 52.95 | 75.03 |
| DE | 1.49 | 2.48 | 71.54 | 0.24 | 2.63 | 1.49 | 0.04 | 2.75 | 0.23 | 1.24 | 15.88 | 28.46 |
| IN | 2.16 | 0.37 | 0.35 | 36.20 | 0.33 | 0.08 | 5.44 | 0.68 | 2.73 | 3.90 | 47.76 | 63.80 |
| IT | 0.96 | 1.88 | 1.95 | 0.14 | 23.71 | 1.04 | 0.01 | 1.26 | 0.16 | 0.89 | 67.98 | 76.29 |
| JP | 1.84 | 3.31 | 2.41 | 0.16 | 5.59 | 69.87 | 0.06 | 2.48 | 0.72 | 1.15 | 12.41 | 30.13 |
| ZA | 1.63 | 0.11 | 0.09 | 11.89 | 0.04 | 0.04 | 65.67 | 0.42 | 7.13 | 6.96 | 6.03 | 34.33 |
| CH | 6.16 | 8.74 | 9.54 | 1.54 | 7.16 | 2.63 | 0.33 | 20.06 | 0.38 | 4.88 | 38.59 | 79.94 |
| UK | 0.15 | 0.45 | 0.13 | 2.85 | 0.52 | 0.48 | 4.43 | 0.06 | 21.22 | 2.26 | 67.45 | 78.78 |
| US | 4.64 | 1.53 | 1.36 | 3.52 | 1.90 | 0.47 | 2.90 | 1.71 | 1.83 | 7.59 | 72.55 | 92.41 |
| OU | 0.01 | 0.01 | 0.01 | 0.01 | 0.03 | 0.08 | 0.01 | 0.00 | 0.00 | 0.00 | 99.85 | 0.15 |
| To | 22.33 | 26.00 | 25.49 | 26.02 | 29.49 | 10.10 | 14.78 | 20.37 | 14.31 | 36.80 | 406.88 | 57.51 |
| Net | −50.91 | −49.03 | −2.97 | −37.78 | −46.80 | −20.03 | −19.55 | −59.57 | −64.47 | −55.61 | 406.73 | |
| Upper Regime | ||||||||||||
| CA | FR | DE | IN | IT | JP | ZA | CH | UK | US | OIL_UNC | From | |
| CA | 2.20 | 0.61 | 0.43 | 0.40 | 0.51 | 0.19 | 0.13 | 0.55 | 0.13 | 1.05 | 93.80 | 97.80 |
| FR | 0.48 | 3.58 | 0.55 | 0.07 | 0.89 | 0.31 | 0.01 | 0.62 | 0.10 | 0.45 | 92.96 | 96.42 |
| DE | 0.37 | 0.61 | 18.72 | 0.20 | 0.73 | 0.18 | 0.02 | 0.69 | 0.04 | 0.28 | 78.16 | 81.28 |
| IN | 0.37 | 0.09 | 0.07 | 7.21 | 0.12 | 0.02 | 0.99 | 0.14 | 0.42 | 0.69 | 89.88 | 92.79 |
| IT | 0.25 | 0.51 | 0.47 | 0.11 | 6.04 | 0.32 | 0.00 | 0.32 | 0.03 | 0.26 | 91.70 | 93.96 |
| JP | 0.16 | 0.33 | 0.36 | 0.04 | 0.49 | 6.40 | 0.00 | 0.25 | 0.05 | 0.11 | 91.80 | 93.60 |
| ZA | 0.57 | 0.09 | 0.04 | 4.87 | 0.02 | 0.03 | 27.08 | 0.20 | 2.88 | 2.70 | 61.52 | 72.92 |
| CH | 0.31 | 0.44 | 0.44 | 0.07 | 0.38 | 0.15 | 0.02 | 0.99 | 0.03 | 0.29 | 96.88 | 99.01 |
| UK | 0.01 | 0.09 | 0.04 | 0.60 | 0.08 | 0.08 | 0.82 | 0.01 | 4.53 | 0.54 | 93.20 | 95.47 |
| US | 2.03 | 0.76 | 0.62 | 1.59 | 0.98 | 0.20 | 1.34 | 0.79 | 0.79 | 3.40 | 87.51 | 96.60 |
| OU | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 100.00 | 0.00 |
| To | 4.55 | 3.53 | 3.01 | 7.95 | 4.21 | 1.46 | 3.33 | 3.55 | 4.47 | 6.36 | 877.42 | 83.62 |
| Net | −93.25 | −92.89 | −78.27 | −84.83 | −89.75 | −92.14 | −69.58 | −95.46 | −91.00 | −90.24 | 877.42 | |
Note: See Note to Table A1. The table reports the regime-dependent connectedness measures computed in a similar manner to Diebold and Yilmaz (2012). The lag order of the TVAR models is selected by the Bayesian information criterion (BIC) in a linear VAR model. The threshold variable is the oil uncertainty. The lower regime corresponds to regime periods below the estimated threshold (low uncertainty), while the upper regime corresponds to periods above the threshold (high uncertainty). The TVAR threshold parameter estimate is 55.961. Boldface denotes the overall spillover index.

Table A6.
Regime-dependent connectedness based on the MSVAR model.
Table A6.
Regime-dependent connectedness based on the MSVAR model.
| Regime 1 | ||||||||||||
| CA | FR | DE | IN | IT | JP | ZA | CH | UK | US | OIL_UNC | From | |
| CA | 83.24 | 0.21 | 0.04 | 0.07 | 0.21 | 0.01 | 0.64 | 1.47 | 0.18 | 8.58 | 5.33 | 16.76 |
| FR | 1.61 | 58.10 | 0.13 | 0.05 | 0.90 | 0.02 | 0.12 | 9.52 | 0.22 | 0.57 | 28.76 | 41.90 |
| DE | 1.16 | 0.00 | 55.40 | 0.09 | 2.67 | 0.18 | 0.54 | 0.59 | 0.62 | 1.99 | 36.77 | 44.60 |
| IN | 0.05 | 0.03 | 0.80 | 35.89 | 0.04 | 0.01 | 0.00 | 0.65 | 0.22 | 0.18 | 62.13 | 64.11 |
| IT | 1.19 | 0.00 | 0.13 | 0.01 | 88.78 | 2.07 | 0.67 | 2.13 | 0.01 | 0.22 | 4.78 | 11.22 |
| JP | 0.20 | 0.07 | 0.10 | 0.71 | 0.91 | 50.52 | 0.18 | 1.26 | 0.89 | 4.86 | 40.30 | 49.48 |
| ZA | 0.14 | 0.06 | 0.03 | 0.17 | 0.02 | 0.08 | 31.56 | 0.00 | 0.24 | 0.14 | 67.56 | 68.44 |
| CH | 1.80 | 0.03 | 0.02 | 0.10 | 0.12 | 0.00 | 0.20 | 94.26 | 0.07 | 0.82 | 2.58 | 5.74 |
| UK | 7.07 | 0.02 | 0.38 | 4.45 | 0.49 | 0.26 | 0.24 | 0.16 | 55.44 | 10.80 | 20.68 | 44.56 |
| US | 5.68 | 0.02 | 0.01 | 0.28 | 0.02 | 0.03 | 0.03 | 2.85 | 1.02 | 37.80 | 52.25 | 62.20 |
| OU | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 99.99 | 0.01 |
| To | 18.90 | 0.45 | 1.65 | 5.93 | 5.40 | 2.67 | 2.62 | 18.62 | 3.47 | 28.18 | 321.13 | 37.18 |
| Net | 2.15 | −41.45 | −42.95 | −58.18 | −5.82 | −46.81 | −65.82 | 12.88 | −41.09 | −34.02 | 321.12 | |
| Regime 2 | ||||||||||||
| CA | FR | DE | IN | IT | JP | ZA | CH | UK | US | OIL_UNC | From | |
| CA | 18.84 | 0.03 | 0.03 | 0.13 | 0.01 | 0.06 | 1.62 | 2.49 | 0.01 | 0.16 | 76.63 | 81.16 |
| FR | 0.92 | 9.37 | 0.05 | 0.01 | 0.67 | 0.21 | 0.97 | 0.17 | 0.00 | 0.48 | 87.16 | 90.63 |
| DE | 1.14 | 0.04 | 23.32 | 0.52 | 0.01 | 0.55 | 3.17 | 9.05 | 1.48 | 3.28 | 57.43 | 76.68 |
| IN | 5.83 | 0.64 | 0.06 | 49.80 | 0.14 | 0.52 | 7.67 | 0.17 | 3.49 | 14.80 | 16.89 | 50.20 |
| IT | 28.46 | 4.85 | 2.62 | 0.24 | 26.22 | 10.02 | 0.62 | 0.31 | 1.62 | 10.91 | 14.13 | 73.78 |
| JP | 3.87 | 0.56 | 4.10 | 0.38 | 0.35 | 23.42 | 1.30 | 4.52 | 0.21 | 31.14 | 30.15 | 76.58 |
| ZA | 0.34 | 0.40 | 0.00 | 0.56 | 0.02 | 0.23 | 13.32 | 0.76 | 1.62 | 2.23 | 80.51 | 86.68 |
| CH | 2.03 | 0.27 | 0.07 | 0.03 | 0.06 | 0.02 | 6.65 | 63.14 | 0.31 | 2.50 | 24.91 | 36.86 |
| UK | 19.76 | 2.31 | 0.02 | 0.31 | 0.44 | 0.05 | 4.82 | 6.48 | 34.87 | 6.61 | 24.34 | 65.13 |
| US | 6.10 | 0.03 | 0.01 | 0.11 | 0.01 | 0.52 | 2.11 | 4.74 | 1.10 | 23.65 | 61.62 | 76.35 |
| OU | 0.04 | 0.01 | 0.00 | 0.05 | 0.02 | 0.02 | 0.02 | 0.01 | 0.11 | 0.06 | 99.66 | 0.34 |
| To | 68.50 | 9.13 | 6.97 | 2.35 | 1.72 | 12.19 | 28.94 | 28.69 | 9.95 | 72.18 | 473.76 | 64.94 |
| Net | −12.66 | −81.50 | −69.71 | −47.85 | −72.06 | −64.39 | −57.74 | −8.17 | −55.18 | −4.17 | 473.42 | |
Note: See Notes to Table A1. The table reports the regime-dependent connectedness measures computed in a similar manner to Diebold and Yilmaz (2012) [55]. The lag order of the MSVAR models is selected by the Bayesian information criterion (BIC) in a linear VAR model. Regime 1 corresponds to lower variance (low uncertainty) estimates, while upper Regime 2 corresponds to higher variance (high uncertainty) estimates. Boldface denotes the overall spillover index.

Table A7.
Regime dependent connectedness based on the QVAR model.
Table A7.
Regime dependent connectedness based on the QVAR model.
| The 0.10−th Quantile of Oil Uncertainty | ||||||||||||
| CA | FR | DE | IN | IT | JP | ZA | CH | UK | US | OIL_UNC | From | |
| CA | 43.17 | 8.03 | 2.70 | 4.29 | 3.82 | 1.88 | 1.59 | 11.86 | 0.42 | 22.18 | 0.05 | 56.83 |
| FR | 9.78 | 53.01 | 3.97 | 0.64 | 7.10 | 3.01 | 0.11 | 15.01 | 0.91 | 6.44 | 0.01 | 46.99 |
| DE | 4.42 | 5.14 | 71.77 | 0.45 | 3.66 | 1.12 | 0.07 | 9.80 | 0.13 | 3.41 | 0.02 | 28.23 |
| IN | 5.74 | 0.86 | 0.77 | 61.60 | 0.63 | 0.29 | 10.11 | 2.13 | 5.22 | 12.57 | 0.09 | 38.40 |
| IT | 5.44 | 8.40 | 3.22 | 0.44 | 64.02 | 3.63 | 0.04 | 8.80 | 0.54 | 5.43 | 0.03 | 35.98 |
| JP | 3.79 | 4.60 | 1.46 | 0.10 | 4.53 | 76.43 | 0.05 | 5.91 | 0.82 | 2.30 | 0.01 | 23.57 |
| ZA | 2.04 | 0.11 | 0.06 | 10.48 | 0.04 | 0.03 | 64.76 | 0.55 | 8.83 | 13.03 | 0.08 | 35.24 |
| CH | 12.64 | 12.41 | 5.91 | 1.78 | 6.19 | 3.21 | 0.50 | 47.34 | 0.16 | 9.79 | 0.05 | 52.66 |
| UK | 2.98 | 1.38 | 0.58 | 6.44 | 0.77 | 0.80 | 9.97 | 1.25 | 63.92 | 11.88 | 0.04 | 36.08 |
| US | 20.44 | 5.10 | 2.13 | 8.32 | 3.79 | 1.02 | 7.48 | 9.15 | 5.50 | 37.03 | 0.04 | 62.97 |
| OU | 0.05 | 0.01 | 0.00 | 0.00 | 0.05 | 0.00 | 0.01 | 0.10 | 0.05 | 0.01 | 99.73 | 0.27 |
| To | 67.32 | 46.04 | 20.80 | 32.95 | 30.58 | 15.00 | 29.93 | 64.54 | 22.59 | 87.04 | 0.42 | 37.93 |
| Net | 10.49 | −0.95 | −7.43 | −5.45 | −5.39 | −8.57 | −5.30 | 11.88 | −13.50 | 24.07 | 0.15 | |
| The 0.90−th Quantile of Oil Uncertainty | ||||||||||||
| CA | FR | DE | IN | IT | JP | ZA | CH | UK | US | OIL_UNC | From | |
| CA | 19.21 | 11.79 | 6.23 | 3.22 | 9.45 | 8.73 | 4.50 | 12.71 | 5.31 | 15.22 | 3.63 | 80.79 |
| FR5 | 11.35 | 19.54 | 6.43 | 5.14 | 10.31 | 9.16 | 6.37 | 12.89 | 7.57 | 10.16 | 1.07 | 80.46 |
| DE | 5.04 | 5.03 | 11.88 | 4.76 | 4.05 | 4.67 | 4.31 | 5.82 | 3.76 | 4.55 | 46.12 | 88.12 |
| IN | 5.39 | 6.59 | 5.57 | 21.46 | 6.29 | 7.80 | 12.03 | 6.38 | 10.03 | 3.93 | 14.52 | 78.54 |
| IT | 9.40 | 10.21 | 6.13 | 5.13 | 18.95 | 8.69 | 5.98 | 10.30 | 6.72 | 9.06 | 9.44 | 81.05 |
| JP | 9.93 | 10.31 | 6.02 | 6.41 | 9.82 | 21.70 | 7.41 | 10.61 | 7.89 | 8.99 | 0.90 | 78.30 |
| ZA | 7.73 | 8.76 | 5.81 | 11.54 | 7.36 | 8.34 | 20.16 | 8.62 | 11.05 | 5.38 | 5.26 | 79.84 |
| CH | 12.65 | 12.10 | 7.80 | 4.09 | 9.92 | 9.18 | 5.34 | 19.76 | 6.47 | 11.61 | 1.08 | 80.24 |
| UK | 6.84 | 9.25 | 4.74 | 11.06 | 8.40 | 8.80 | 12.46 | 8.07 | 24.74 | 3.11 | 2.51 | 75.26 |
| US | 16.22 | 11.41 | 6.65 | 2.64 | 9.98 | 8.82 | 3.01 | 13.25 | 3.88 | 19.57 | 4.58 | 80.43 |
| OU | 3.79 | 3.58 | 6.52 | 4.77 | 2.68 | 3.75 | 4.02 | 4.14 | 3.14 | 3.41 | 60.21 | 39.79 |
| To | 88.34 | 89.05 | 61.90 | 58.76 | 78.26 | 77.93 | 65.43 | 92.78 | 65.83 | 75.42 | 89.12 | 76.62 |
| Net | 7.55 | 8.59 | −26.22 | −19.77 | −2.79 | −0.37 | −14.41 | 12.54 | −9.43 | −5.01 | 49.33 | |
Note: See Notes to Table A1. The table reports the regime-dependent connectedness measures computed in a similar manner to Diebold and Yilmaz (2012) [55]. The lag order of the QVAR models is selected by the Bayesian information criterion (BIC) in a linear VAR model. Boldface denotes the overall spillover index.
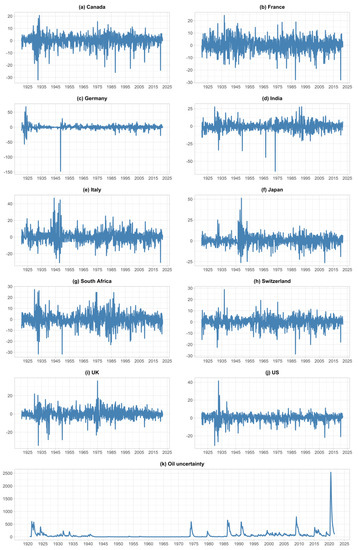
Figure A1.
Stock returns and oil uncertainty series.
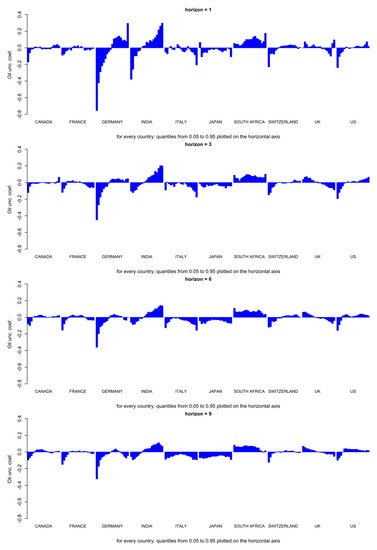
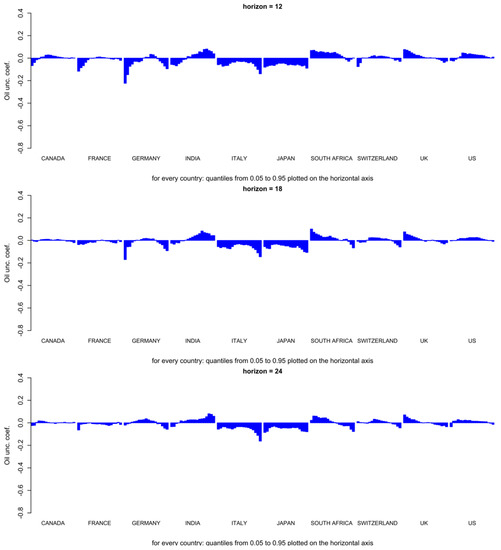
Figure A2.
Full-sample quantiles-based response of stock returns to oil price uncertainty (OIL_UNC).
References
- Bernanke, B.S. Irreversibility, uncertainty, and cyclical investment. Q. J. Econ. 1983, 98, 85–106. [Google Scholar] [CrossRef]
- Pindyck, R. Irreversibility, uncertainty, and investment. J. Econ. Lit. 1991, 29, 1110–1148. [Google Scholar]
- Swaray, R.; Salisu, A.A. A firm-level analysis of the upstream-downstream dichotomy in the oil-stock nexus. Glob. Financ. J. 2018, 37, 199–218. [Google Scholar] [CrossRef]
- Demirer, R.; Jategaonkar, S.P.; Khalifa, A.A.A. Oil price risk exposure and the cross-section of stock returns: The case of net exporting countries. Energ. Econ. 2015, 49, 140–142. [Google Scholar] [CrossRef]
- Christoffersen, P.; Pan, X.N. Oil volatility risk and expected stock returns. J. Bank. Financ. 2018, 95, 5–26. [Google Scholar] [CrossRef]
- Sadorsky, P. Oil price shocks and stock market activity. Energ. Econ. 1999, 21, 449–469. [Google Scholar] [CrossRef]
- Masih, R.; Peters, S.; de Mello, L. Oil price volatility and stock price fluctuations in an emerging market: Evidence from South Korea. Energ. Econ. 2011, 33, 975–986. [Google Scholar] [CrossRef]
- Alsalman, Z. Oil price uncertainty and the U.S. stock market analysis based on a GARCH in mean VAR model. Energ. Econ. 2016, 59, 251–260. [Google Scholar] [CrossRef]
- Diaz, E.M.; Molero, J.C.; de Gracia, F.P. Oil price volatility and stock returns in the G7 economies. Energ. Econ. 2016, 54, 417–430. [Google Scholar] [CrossRef]
- Rahman, S. Oil price volatility and the US stock market. Empir. Econ. 2021, 61, 1461–1489. [Google Scholar] [CrossRef]
- Jiranyakul, K. Does oil price uncertainty transmit to the Thai stock market? J. Econ. Financ. Stud. 2014, 2, 16–25. [Google Scholar] [CrossRef][Green Version]
- Aye, G.C. Does oil price uncertainty matter for stock returns in South Africa? Investig. Manag. Financ. Innov. 2015, 12, 179–188. [Google Scholar]
- Bass, A. Does oil prices uncertainty affect stock returns in Russia: A bivariate GARCH-in-mean approach. Int. J. Energ. Econ. Policy 2017, 7, 224–230. [Google Scholar]
- Benavides, D.R.; García, M.A.M.; Reyes, L.F.H. Uncertainty of the international oil price and stock returns in Mexico through an SVAR-MGARCH. Contad. Adm. 2019, 64, 1–16. [Google Scholar]
- Basher, S.A.; Sadorsky, P. Oil price risk and emerging stock markets. Glob. Financ. J. 2006, 17, 224–251. [Google Scholar] [CrossRef]
- Salisu, A.A.; Gupta, R. Oil Price Uncertainty Shocks and Global Equity Markets: Evidence from a GVAR Model. J. Risk Financ. Manag. 2022, 15, 355. [Google Scholar] [CrossRef]
- Campbell, J.Y. Viewpoint: Estimating the equity premium. Can. J. Econ. 2008, 41, 1–21. [Google Scholar] [CrossRef]
- Salisu, A.A.; Pierdzioch, C.; Gupta, R. Geopolitical risk and forecastability of tail risk in the oil market: Evidence from over a century of monthly data? Energy 2021, 235, 121333. [Google Scholar] [CrossRef]
- Rapach, D.E.; Zhou, G. Forecasting stock returns. In Handbook of Economic Forecasting, 2nd ed.; (Part A); Elliott, G., Timmermann, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 328–383. [Google Scholar]
- Stock, J.H.; Watson, M.W. Forecasting output and inflation: The tole of asset prices. J. Econ. Lit. 2003, 41, 788–829. [Google Scholar] [CrossRef]
- Rapach, D.E.; Strauss, J.K.; Zhou, G. International Stock Return Predictability: What is the Role of the United States? J. Financ. 2013, 68, 1633–1662. [Google Scholar] [CrossRef]
- Aye, G.C.; Balcilar, M.; Gupta, R. International stock return predictability: Is the role of US time-varying? Empirica 2017, 44, 121–146. [Google Scholar] [CrossRef]
- Gupta, R.; Majumdar, A.; Wohar, M.E. The Role of current account balance in forecasting the US equity premium: Evidence from a quantile predictive regression approach. Open Econ. Rev. 2017, 28, 47–59. [Google Scholar] [CrossRef]
- Gupta, R.; Huber, F.; Piribauer, P. Predicting international equity returns: Evidence from time-varying parameter vector autoregressive models. Int. Rev. Financ. Anal. 2020, 68, 101456. [Google Scholar] [CrossRef]
- Huber, F.; Krisztin, T.; Piribauer, P. Forecasting equity indices using large Bayesian VARs. B. Econ. Res. 2017, 69, 288–308. [Google Scholar] [CrossRef][Green Version]
- Jordan, S.J.; Vivian, A.J.; Wohar, M.E. Forecasting market returns: Bagging or combining? Int. J. Forecast. 2017, 33, 102–120. [Google Scholar] [CrossRef]
- Jordan, S.J.; Vivian, A.J.; Wohar, M.E. Stock returns forecasting with metals: Sentiment vs. fundamentals. Eur. J. Financ. 2018, 24, 458–477. [Google Scholar] [CrossRef]
- Christou, C.; Gupta, R.; Jawadi, F. Does Inequality Help in Forecasting Equity Premium in a Panel of G7 Countries? N. Am. J. Econ. Financ. 2021, 57, 101456. [Google Scholar] [CrossRef]
- Salisu, A.A.; Gupta, R. Commodity prices and forecastability of international stock returns over a century: Sentiments versus fundamentals with focus on South Africa. Emerg. Mark. Financ. Trade 2022, 58, 2620–2636. [Google Scholar] [CrossRef]
- Rapach, D.E.; Zhou, G. Asset pricing: Time-series predictability. Oxf. Res. Encycl. Econ. Financ. 2022; in press. [Google Scholar]
- Narayan, P.K.; Gupta, R. Has oil price predicted stock returns for over a century? Energ. Econ. 2015, 48, 18–23. [Google Scholar] [CrossRef]
- Gupta, R.; Wohar, M.E. Forecasting oil and stock returns with a Qual VAR using over 150 years of data. Energ. Econ. 2017, 62, 181–186. [Google Scholar] [CrossRef]
- Degiannakis, S.A.; Filis, G.; Arora, V. Oil prices and stock markets: A review of the theory and empirical evidence. Energ. J. 2018, 39, 85–130. [Google Scholar] [CrossRef]
- Smyth, R.; Narayan, P.K. What do we know about oil prices and stock returns? Int. Rev. Financ. Anal. 2018, 57, 148–156. [Google Scholar] [CrossRef]
- Guidolin, M.; Hyde, S.; McMillan, D.; Ono, S. Non-linear predictability in stock and bond returns: When and where is it exploitable? Int. J. Forecast. 2009, 25, 373–399. [Google Scholar] [CrossRef]
- Gupta, R.; Majumdar, A. Incorporating Economic Policy Uncertainty in US Equity Premium Models: A Nonlinear Predictability Analysis. Financ. Res. Lett. 2016, 18, 291–296. [Google Scholar]
- Demirer, R.; Pierdzioch, C.; Zhang, H. On the Short-Term Predictability of Stock Returns: A Quantile Boosting Approach. Financ. Res. Lett. 2017, 22, 35–41. [Google Scholar] [CrossRef]
- Gupta, R.; Mwamba, J.W.M.; Wohar, M.E. The role of partisan conflict in forecasting the US equity premium: A nonparametric approach. Finance Res. Lett. 2018, 25, 131–136. [Google Scholar] [CrossRef]
- Gupta, R.; Pierdzioch, C.; Vivian, A.J.; Wohar, M.E. The predictive value of inequality measures for stock returns: An analysis of long-span UK data using quantile random forests. Financ. Res. Lett. 2019, 29, 315–322. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Meligkotsidou, L.; Panopoulou, E.; Vrontos, I.D.; Vrontos, S.D. A Quantile Regression Approach to Equity Premium Prediction. J. Forecast. 2014, 33, 558–576. [Google Scholar] [CrossRef]
- Gebka, B.; Wohar, M.E. Stock return distribution and predictability: Evidence from over a century of daily data on the DJIA index. Int. Rev. Econ. Financ. 2019, 60, 1–25. [Google Scholar] [CrossRef]
- Das, S.; Demirer, R.; Gupta, R.; Mangisa, S. The effect of global crises on stock market correlations: Evidence from scalar regressions via functional data analysis. Struct. Chang. Econ. Dyn. 2019, 50, 132–147. [Google Scholar] [CrossRef]
- Elder, J.; Serletis, A. Oil Price Uncertainty. J. Money Credit. Bank 2010, 42, 1137–1159. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef]
- Brock, W.A.; Scheinkman, J.A.; Dechert, W.D.; LeBaron, B. A test for independence based on the correlation dimension. Econom. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- McCracken, M.W. Asymptotics for out of sample tests of Granger causality. J. Econom. 2007, 140, 719–752. [Google Scholar] [CrossRef]
- Pierdzioch, C.; Risse, M.; Rohloff, S. The international business cycle and gold-price fluctuations. Q. Rev. Econ. Financ. 2014, 54, 292–305. [Google Scholar] [CrossRef]
- Pierdzioch, C.; Risse, M.; Rohloff, S. Fluctuations of the real exchange rate, real interest rates, and the dynamics of the price of gold in a small open economy. Empir. Econ. 2016, 51, 1481–1499. [Google Scholar] [CrossRef]
- Gupta, R.; Pierdzioch, C.; Do Economic Conditions of U.S. States Predict the Realized Volatility of Oil-Price Returns? A Quantile Machine-Learning Approach. Financial Innovation, Forthcoming. Available online: https://ideas.repec.org/p/pre/wpaper/202216.html (accessed on 18 August 2022).
- Ren, X.; Duan, K.; Tao, L.; Shi, Y.; Yan, C. Carbon prices forecasting in quantiles. Energ. Econ. 2022, 108, 105862. [Google Scholar] [CrossRef]
- Balcilar, M.; Ozdemir, Z.A.; Ozdemir, H.; Wohar, M.E. Fed’s unconventional monetary policy and risk spillover in the US financial markets. Q. Rev. Econ. Financ. 2020, 78, 42–52. [Google Scholar] [CrossRef]
- Balcilar, M.; Roubaud, D.; Usman, O.; Wohar, M.E. Moving out of the linear rut: A period-specific and regime-dependent exchange rate and oil price pass-through in the BRICS countries. Energ. Econ. 2021, 98, 105249. [Google Scholar] [CrossRef]
- Balcilar, M.; Roubaud, D.; Usman, O.; Wohar, M.E. Testing the asymmetric effects of exchange rate pass-through in BRICS countries: Does the state of the economy matter? World Econ. 2021, 44, 188–233. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Better to give than receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Bouri, E.; Kang, S.H.; Saeed, T. Regime specific spillover across cryptocurrencies and the role of COVID-19. Financ. Innov. 2021, 7, 5. [Google Scholar] [CrossRef] [PubMed]
- Balcilar, M.; Ozdemir, Z.A.; Ozdemir, H.; Aygun, G.; Wohar, M.E. Effectiveness of monetary policy under the high and low economic uncertainty states: Evidence from the major Asian economies. Empir. Econ. 2022, 63, 1741–1769. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Cunado, J.; Gupta, R.; Wohar, M.E. Volatility spillovers across global asset classes: Evidence from time and frequency domains. Q. Rev. Econ. Financ. 2018, 70, 194–202. [Google Scholar] [CrossRef]
- Demirer, R.; Gupta, R.; Suleman, M.T.; Wohar, M.E. Time-varying rare disaster risks, oil returns and volatility. Energ. Econ. 2018, 75, 239–248. [Google Scholar] [CrossRef]
- Sohag, K.; Hammoudeh, S.; Elsayed, A.H.; Mariev, O.; Safonova, Y. Do geopolitical events transmit opportunity or threat to green markets? Decomposed measures of geopolitical risks. Energ. Econ. 2022, 111, 106068. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).