Thermal Performance in Convection Flow of Nanofluids Using a Deep Convolutional Neural Network

Abstract

This study develops a geometry adaptive, physical field predictor for the combined forced and natural convection flow of a nanofluid in horizontal single or double-inner cylinder annular pipes with various inner cylinder sizes and placements based on deep learning. The predictor is built with a convolutional-deconvolutional structure, where the input is the annulus cross-section geometry and the output is the temperature and the Nusselt number for the nanofluid-filled annulus. Profiting from the proven ability of dealing with pixel-like data, the convolutional neural network (CNN)-based predictor enables an accurate end-to-end mapping from the geometry input and the desired nanofluid physical field. Taking the computational fluid dynamics (CFD) calculation as the basis of our approach, the obtained results show that the average accuracy of the predicted temperature field and the coefficient of determination R² are more than 99.9% and 0.998 accurate for single-inner cylinder nanofluid-filled annulus; while for the more complex case of double-inner cylinder, the results are still very close, higher than 99.8% and 0.99, respectively. Furthermore, the predictor takes only 0.038 s for each nanofluid field prediction, four orders of magnitude faster than the numerical simulation. The high accuracy and the fast speed estimation of the proposed predictor show the great potential of this approach to perform efficient inner cylinder configuration design and optimization for nanofluid-filled annulus.

1. Introduction

Heat transfer enhancement has been a leading topic of research and study in many engineering areas in the past five decades [1]. The related techniques are developed to improve the performance of heat transfer systems, to save energy, and to conserve limited natural resources. One commonly used technique is the modification of the system’s geometry structure to increase the effective heat transfer surface or to generate turbulence. Another method is related to the application of nanofluids, introduced by Choi in 1995 [2]; this has attracted significant attention in scientific community. Through adding very small solid particles (<100 nm) to a base liquid, the nanofluid heat transfer properties have been largely improved compared to conventional fluids [3], and thereby nanofluids have become promising working fluids to improve the efficiency of heat transfer systems [4].

Annulus enclosure, as an essential structure, has been used in various engineering applications, such as solar collectors, nuclear reactors, thermal storage systems, and electronic cooling systems. A large number of investigations tried to enhancing the heat transfer efficiency of annulus enclosures using the above techniques. Abu-Nada et al. compared the heat transfer performance of a horizontal annulus enclosure using four filled nanofluids [5]. The results showed the type of nanoparticles, and the particle concentrations have significant influence on the heat transfer with high Rayleigh numbers. Similarly, Wang et al. [6] investigated the influence of CuO nanoparticle volume fraction and its mean diameter on the temperature distribution of a three-dimensional natural convection flow in a horizontal annular structure. Furthermore, several articles also investigated the nanofluids transfer in a vertical annulus structure. Sankar et al. [7] studied the conjugate heat transfer in nanofluid with different nanoparticles in a vertical enclosed annular gap. Berrahil et al. [8] reported a numerical investigation of natural convection of a nanofluid in a heated vertical annulus under a uniform magnetic field.

Various types of annulus geometry, for example, the semi-annulus [9], the elliptical annuals [10], the two-square duct annulus [11], and the inner triangular annulus [12] of nanofluid-filled enclosures have attracted the interest of scientists. For these studies, besides the parametric analysis for nanofluid properties, the effects of geometrical parameters on the thermal performance of the annulus, such as the angle of turn, the inclination angle, and the inner cylinder size and placement have also been considered. Arefmanesh et al. [11] and Yu et al. [13] reported the numerical study of natural convection in square-square and cylinder–cylinder nanofluid-filled annulus, respectively, where the effect of the aspect ratio on the flow and heat transfer patterns were investigated; their results indicated that the flow was more stable with a larger-gapped annulus. The natural convection heat transfer in the inner triangular cylinder annulus was studied successively by Xu et al. [12] and Mehrizi et al. [14], where the former focused on geometrical parameters, such as the inner triangular size and the inclinaiton angles, while the latter concentrated on the inner triangular eceentricity locations. The results showed that the rotation of the inner triangular cylinder changed the local Nusselt number in the peak position; the largest average Nusselt number occured when the inner cylinder was at the lowest position of the annulus vertical centerline.

A large number of numerical simulations have been carried out for the nanofluid properties and the annulus geometry. In these studies, each simulation required solving a large number of partial differential equations. Therefore, the above studies do not seem to be economical or efficient. Over the past five years, many scientists have been attracted by the artificial neural network (ANN) due to its powerful ability of dealing with highly nonlinear problems, and they have started building a reduced-order model (ROM) based on ANN to study heat transfer problems. Saeedan et al. [15] proposed a CFD study to look at the performance of a nanofluid-filled double pipe helically baffled heat exchanger. The neural network was applied to predict the Nusselt number, the pressure drop, Reynolds number, concentration, and the physical properties of particles. Maddah et al. [16] applied ANN to predict the exegetic efficiency in a double-pipe heat exchanger equipped with twisted tapes using experimental data; there were five designed parameters as inputs for the ANN. Ashouri et al. [17] used a deep neural network to predict the Nusselt number for a two dimensional square enclosure. It is worth noting that all the above ANN-based thermal system predictors achieve high accuracy with the determination coefficient R² > 0.99.

Recently a few studies have considered using nanofluids physical field prediction in heat transfer problems using deep convolutional neural networks. Two nanofluid-filled microchannels with three cylindrical grooves etched [18] and two grooves [19] in the upper plate were used and studied in the same year; both studies used the limited experimental data as the input. Then, the physical fields were reconstructed and the corresponding performance parameters, the Nusselt number and the Fanning friction factor, were extracted from the generated predicted fields. Later, the former study considered the auxiliary tasks in the deep learning-based model, which can greatly improve the performance of the main task [20]. The later study applied the physics-informed deep learning method to the same microchannel [21]. Compared with the convolutional neural network (CNN), the physical interpretability has been improved by introducing conservation laws in loss functions.

Furthermore, several studies have investigated the geometry adaptive reduced order models in heat transfer and fluid flow problems using the convolutional neural network (CNN). The CNN-based model uses the flow field as pixel level figures/matrix; therefore, it can be adapted to any geometry easily. Peng et al. successively applied CNN to a heat conduction [22] problem and then to the steady-state heat convection [23] problem with varied geometries. In both studies, a signed distance function (SDF) is proposed to represent the geometry of the problem. Subsequently, the authors also used CNN structure to rapidly predict the steady flow [24] and unsteady flow [25] over objects with arbitrary geometry and various boundary conditions where the input matrix is composed of the nearest wall signed distance function (NWSDF). The results of all the studies show the high accuracy and efficiency of the proposed network model, indicating the geometry adaptive ability of the CNN-based reduced order model.

Inspired by the above studies, we apply CNN to build a ROM to predict the temperature field and the local Nusselt (Nu) number for nanofluid-filled single-inner-cylinder annulus with random inner cylinder size and location and also for a nanofluid-filled double-inner-cylinder annulus with a random inner cylinder location. Using the SDF annulus geometry as the input, the proposed network model enables the direct output of the temperature and the local Nusselt number fields, that is, an end-to-end mapping between the geometry and the physical field is established. Then we perform the numerical calculation to obtain a reference basis to evaluate the performance of the proposed predictor. According to our literature review, this is the first time that a geometry adaptive network model has been developed to estimate the Nusselt number field in nanofluids flowing in horizontal annular pipes using deep convolutional neural network, which can be used to design and optimize the geometry of annular pipes for enhancing the heat transfer in a thermal system. The rest of this paper is structured as follows: in Section 2, we discuss the method, including the preparation of the datasets and the establishment of the nanofluid field predictor. Then the results of the temperature and the Nusselt number distribution predictions of are presented and discussed in Section 3. Finally, a few concluding remarks are made at the end of the paper.

2. Methods

This section presents the dataset preparation and the building of the deep learning-based nanofluid field predictor. The CFD method is used to create raw data, which are regarded as labeled data to train, validate, and evaluate the predictor. According to the research task, the raw data consist of the annulus geometry and the simulated temperature and the Nu number field of the nanofluid in single and double-inner-cylinder annulus.

The predictor is a deep convolutional neural network (CNN), consisting of five convolution layers followed by four deconvolution layers, which enable finding and solving highly nonlinear relationships in the real-world complex problems. In this study, we want to predict the temperature field and the Nu number field. The input of the predictor is the 2D cross-section geometry of the annulus enclosure, prepared by the nearest wall signed distance function (NWSDF), which can provide more spatial information and therefore produce better performance in the nanofluid field prediction for a geometry-adaptive task [26].

2.1. Preparation of Dataset

2.1.1. Mathematical Framework

In this work, we do not consider any chemical or electromagnetic effects. The governing equations are the conservation equations for mass, momentum, and the energy equations [27].

• Governing Equations

Conservation of mass:

$$\begin{array}{c}\frac{\partial \rho }{\partial t}+\mathrm{div}\left(\rho \mathit{u}\right)=0\end{array}$$

(1)

where $\partial /\partial t$ is the partial derivative with respect to time, $div$ is the divergence operator, $\mathit{u}$ is the velocity vector, and $\rho$ is the density of the fluid. If the fluid is incompressible, then it can only undergo isochoric (i.e., volume preserving) motions and $\mathrm{div} \mathit{u}=0$.

Conservation of momentum:

$$\begin{array}{c}\rho \frac{\mathrm{d}u}{\mathrm{d}t}=\mathrm{div} \mathbf{T}+\rho \mathbf{b}\end{array}$$

(2)

where $\mathrm{d}/\mathrm{d}t$ is the total time derivative given by $\frac{\mathrm{d}(.)}{\mathrm{d}t}=\frac{\partial (.)}{\partial t}+\left[\mathrm{grad}(.)\right]\mathbf{v}$ and $grad$ is the gradient operator, T is the Cauchy stress tensor and $b$ is the body force. The balance of angular momentum indicates that the stress tensor is symmetric.

Conservation of energy:

$$\begin{array}{c}\frac{\mathrm{d}e}{\mathrm{d}t}=\mathbf{T}:\mathbf{L}-\mathrm{div} \mathit{q}+\rho r\end{array}$$

(3)

where $e$ is the internal energy density, $L$ is the velocity gradient, $\mathit{q}$ is the heat flux vector, and $r$ is the specific radiant energy, which is neglected in this study. $T:L$ represents the viscous dissipation, and $\mathit{q}$ represents the heat conduction. In general, thermodynamical considerations require that the second law of thermodynamics (the entropy inequality) be applied; in this paper, however, we do not consider the entropy law [28].

2.

Constitutive Equations

Looking at the above equations, we can see that constitutive relations for the body force, the stress tensor, the heat flux vector, the radiation term, and the internal energy are required. In this problem, we ignore the effects of radiation, and we assume $e=\rho \epsilon$, where $\epsilon =C_{p}T$, that $T$ is the temperature and $C_p$ is the heat capacity. For the heat flux vector, we use the traditional Fourier’s assumption where

$$\begin{array}{c}\mathit{q}=-k\mathrm{gradT}\end{array}$$

(4)

and $k$ is the (constant) thermal conductivity. In general, the thermal conductivity of nanofluids (suspension with particles) is not constant; it can be a function of temperature, shear rate, concentration, etc. [29,30,31]. For a recent review of the heat flux vector, see [32,33,34].

The body (buoyancy) force is given by $\rho \mathit{b}=\rho \left(T\right)\mathit{g}$; in general, for a nanofluid composed of a fluid and particles, the density will also depend on the volume fraction. In this paper, we ignore this effect. Here we use the usual Boussinesq assumption [35,36,37,38,39,40] where the density is expressed as:

$$\begin{array}{c}\rho ={\rho }_{ref}\left(1-\beta \left(T-T_{ref}\right)\right)\end{array}$$

(5)

where $\beta ={-\frac{1}{\rho }\frac{\partial \rho }{\partial T}|}_{T_{ref}}$ is the coefficient of thermal expansion, which is assumed to be constant, and ${\rho }_{ref}$ is the density of the suspension at the reference temperature $T_{ref}$.

As mentioned in the Introduction, nanofluids are made by adding nanoscale particles in low volumetric fractions to a fluid to enhance or improve their rheological, mechanical, optical, and thermal properties. For the stress tensor of nanofluids, we can say that in general, they behave as non-Newtonian fluids, with yield stress [41,42] or exhibiting viscoelasticity [43], thixotropy, and their viscosity can depend on shear rate, temperature, concentration of the nano particles, etc. That is, in general, the shear viscosity $\mu \left(\Psi \right)$ can be a function of one or all the following: (1) time, (2) shear rate, (3) concentration, (4) temperature, (5) pressure, (6) electric field, (7) magnetic field, etc. Thus, in general, $\mu \left(\Psi \right)=\mu \left(t,\pi ,T,\phi ,p,\mathit{E},\mathit{B},\dots \right)$ where $t$ is the time. $\pi$ is some measure of the shear rate (for example, $\dot{\gamma }=\sqrt{2tr{D}^2})$, where $tr$ is the trace operator, $T$ is the temperature, $\phi$ is the concentration, $p$ is the pressure, $\mathit{E}$ is the electric field, and $\mathit{B}$ is the magnetic field. There are also studies which indicate that some nanofluids can be assumed to behave as Newtonian fluids [8,44,45]. For the sake of simplicity and in order to test our new numerical approach, in this paper, we assume that the stress tensor for the nanofluid is given by the traditional Navier–Stokes fluid model, where:

$$\begin{array}{c}\mathbf{T}=-p\mathbf{I}+2\mu \mathbf{D}\end{array}$$

(6)

where $I$ is the identity tensor. $\mu$ is the constant shear viscosity, and $D$ is the symmetric part of the velocity gradient $D=1/2\left[\mathrm{grad} \mathit{u}+{\left(\mathrm{grad} \mathit{u}\right)}^T\right]$.

3.

The expanded form of the governing equations

We should mention that an implicit assumption made in many buoyance-driven flows, including our paper, is that while the fluid is mechanically incompressible, i.e., $\mathrm{div} \mathit{u}=0,$ thermally the fluid is assumed to be compressible, via the Boussinesq approximation [46].

Substituting Equations (4)–(6) into Equations (1)–(3), we obtain the basic equations of motion and heat transfer which need to be solved:

$$\begin{array}{c}\mathrm{div} \mathit{u}=0\end{array}$$

(7)

$$\begin{array}{c}\frac{\partial \mathit{u}}{\partial t}+\left(\mathrm{grad}\mathit{u}\right)\mathit{u}=-\frac{1}{\rho }\mathrm{grad}p+\nu \mathrm{div}\left(D\right)-\beta \left(T-T_0\right)\mathit{g}\end{array}$$

(8)

where $\nu , \rho$, and $\beta$ are the kinematic viscosity, density, and the thermal expansion coefficient of the nanofluid with constant values at reference temperature, respectively. $g$ is the gravitational constant.

$$\begin{array}{c}\frac{\partial T}{\partial \mathrm{t}}+\left(\mathrm{grad}T\right).\mathit{u}=\alpha \mathbf{D}:\mathbf{L}\end{array}$$

(9)

where $\alpha$ is the thermal diffusivity. We also define the local Nusselt number:

$$\begin{array}{c}Nu=-\frac{\partial T}{\partial n}\end{array}$$

(10)

where n is the unit outward normal to the boundary surface of the annulus. We use the following non-dimensional parameters:

$$\begin{array}{c}{T}^{*}=\frac{T-T_0}{T_1-T_0},N{u}^{*}=Nu\ast \frac{L_r}{T_1-T_0},\end{array}$$

(11)

where $T_1$ and $T_0$ are reference temperatures for the hot and cold walls, respectively. $L_r$ is a reference length and $L_r=\mathrm{R}-\mathrm{r}$.

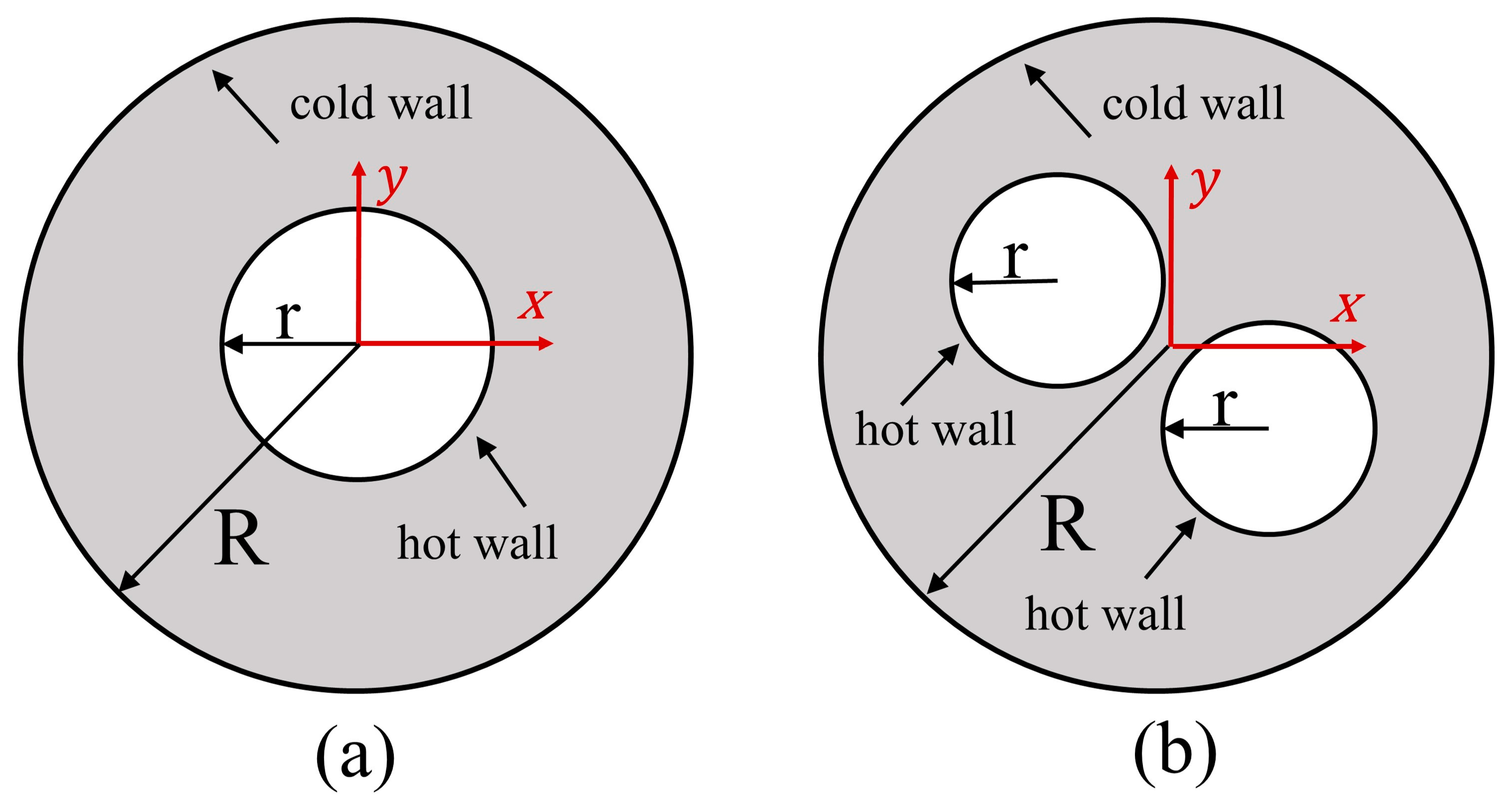
2.1.2. Physical Model and Numerical Simulation

The convection heat transfer in a nanofluid in enclosures is investigated in this study. Two common annulus enclosure structures are designed: horizontal placed annular pipes with single inner cylinder and double inner cylinders. Both are assumed to be two-dimensional problems. The inner cylinders are considered as the heat source with constant temperature T₁, while T₀ (<T₁) is set for the outer wall of the enclosures. The nanofluid works as the cooling fluid with the initial temperature T₀. The initial condition for the velocity is: $\mathit{u}=\mathbf{0}$ and for the fluid domain, the boundary conditions are: $\mathit{u}=\mathbf{0}$ for the inner and the outer cylinders. We use 5% Fe₃O₄ nanofluid in this study; the values of the material parameters are used according to [40] and listed in

Table 1. Physical properties of 5% Fe₃O₄ nanofluid.

$\mathit{\nu }$ (m2/s)	$\mathit{\rho }$ (kg/m3)	$\mathit{\beta }$ (1/K)	$\mathit{\alpha }$ (m2/s)
$8.484\times {10}^{-4}$	1209	$28.565\times {10}^{-5}$	$1.248\times {10}^{-7}$

.

This study focuses on building a nanofluid field predictor of annulus enclosure with geometry adaptive ability; therefore, we need to generate some data with various inner cylinder diameters and positions to train the predictor. For the single cylinder annulus, as shown in Figure 1a, the external radius is fixed, designed as R. The inner cylinder radius r is randomly set to be between 0.24R and 0.44R, and the placement is randomly limited to a concentric circular area where the diameter is 0.2R. In the double inner cylinder case, as shown in Figure 1b, the radius of both the double inner-annulus is 0.3R and randomly distributed without crossing. Each case generates one type of dataset and creates 400 geometries. This design method of the dataset creates a strong robustness for the geometry for the ROM.

All the geometries are meshed with Gmsh and simulated in OpenFOAM. Then, the obtained temperature field and the Nu number field are considered as the basis to guide the training of the predictor.

2.2. Establishment of the Nanofluid Field Predictor

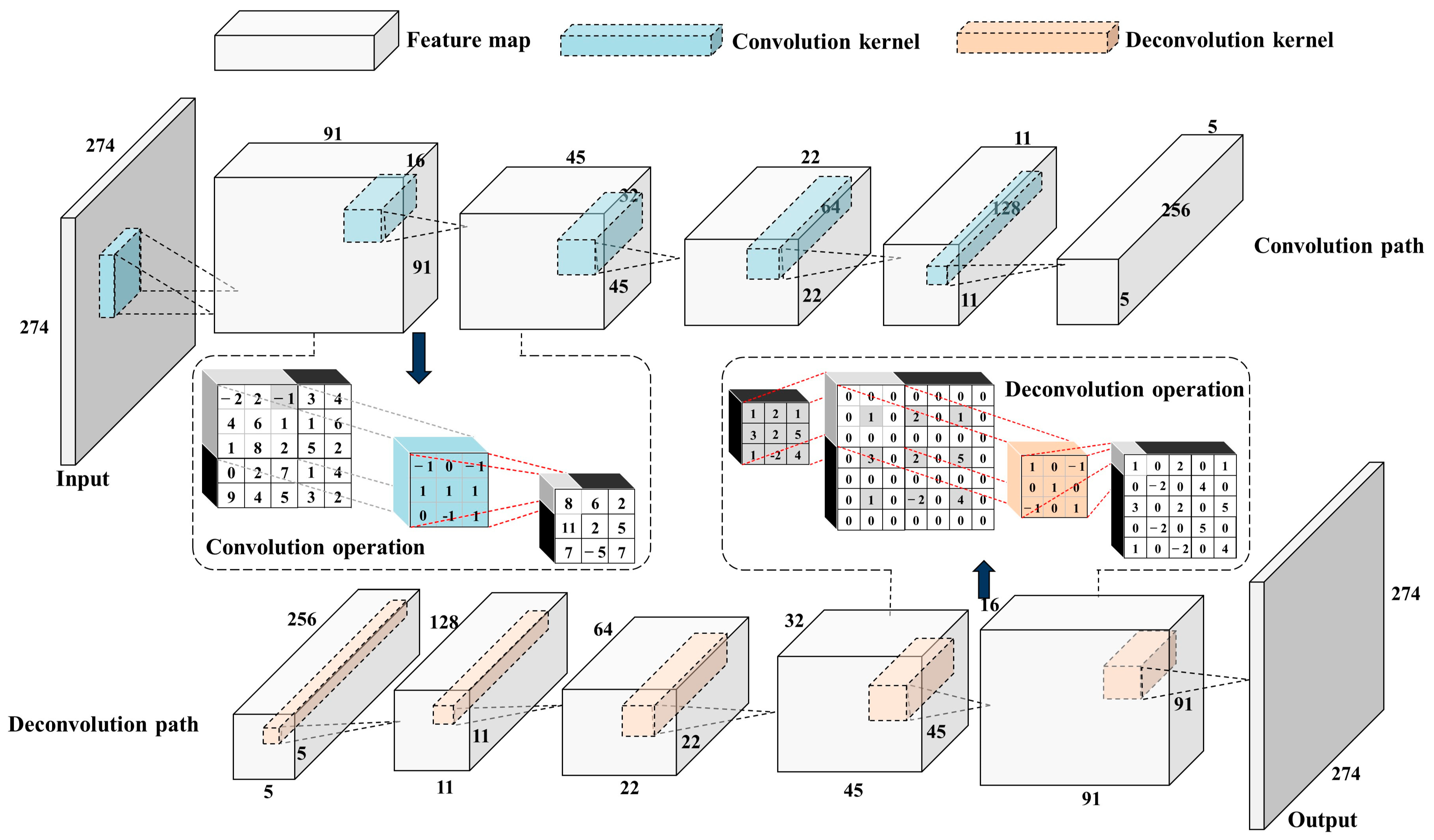
2.2.1. Architecture Design of the Nanofluid Field Predictor

The structure of the proposed deep learning-based predictor is illustrated in Figure 2, consisting of an encoding path and decoding path. The encoding path is composed of five convolutional layers, each layer compresses the feature map of the previous layer using the convolution kernel, and finally the highly encoded intrinsic feature of $5\times 5$ is obtained from the NWSDF-presented geometry input matrix of $274\times 274$. Then the four deconvolution layers form the deconvolution path to analyze the encoded feature and expand it to the original size. Thereby, the mapping between the geometry and the physics is established.

In the encoding part, the main operation is a convolution operation and the calculation is expressed as [47]:

$$\begin{array}{c}{z}^l=a^{l-1} \ast k^l+b^l\end{array}$$

(12)

where $\ast$ is the convolution operation symbol, $z^l$ is the output of the l-th layer, $a^{l-1}$ is the output of the previous layer, and $k^l$ and $b^l$ are the weight coefficient and the bias vector of the l-th layer, respectively.

The transpose convolution operation is performed in the deconvolution path, which is one special convolutional operation and similar to the convolution operation. Generally, a padding process is required to expand the matrix dimension before transposing the convolution calculation. The subfigure of Figure 2 briefly explains the method on how to convolve and deconvolve a matrix in 2D—please refer to [47] for more details.

Furthermore, the activation function is added after each convolution or deconvolution operation allowing the neural networks to establish more complex mapping relationships between the data. The output value $z^l$ calculated in Equation (12) is further converted by the activation function, then with the deep learning-based predictor; thus, we have the nonlinear fitting capability. The exponential linear unit (ELU) activation function is used in this study, where [48]:

$$\begin{array}{c}{a}^l=ELU\left(z^l\right)\end{array}$$

(13)

$$\begin{array}{c}ELU\left(x\right)=\{\begin{array}{c}x\\ \alpha \left(e^x-1\right)\end{array}\end{array}$$

(14)

2.2.2. Model Training and Evaluation Method

Model training is a continuous process where the main objective is to minimize the loss function by updating the two parameters, namely, the weight coefficient and the bias vector of the neural network. In our study, the mean square field error loss is applied as the criterion to evaluate the difference between the predicted field and the numerical simulated field, the latter is regarded as the labeled data, generated in the numerical simulation tool—OpenFOAM7. The loss function is defined as [49]:

$$\begin{array}{c}loss=\frac{1}{n_{bc}\times H\times W}{\displaystyle \sum }_{n=1}^{n_{bc}}{\displaystyle \sum }_{i=1}^H{\displaystyle \sum }_{j=1}^W{\left(\widehat{y}-y\right)}^2\end{array}$$

(15)

where $n_{bc}$ represents the training batch size in a training session. H and W are the height and the width of the reconstructed field, respectively. $\widehat{y}$ is the predicted result, and $y$ is the corresponding simulated result. In this study, the Adam optimizer [50] is adopted to optimize the loss value.

The determination coefficient R² is used for the error measurement of the predicted scalar:

$$\begin{array}{c}{R}^2=1-\frac{{{\displaystyle \sum }}_{n=1}^N{\left(y^n-{\widehat{y}}^n\right)}^2}{{{\displaystyle \sum }}_{n=1}^N{\left(y^n-\overline{y}\right)}^2}\end{array}$$

(16)

where $\overline{y}$ represents the average of the simulated result. If the value of R² is closer to 1, then the prediction is more accurate.

3. Results and Discussions

The geometry adaptive field predictor of nanofluid convection in the annulus is constructed based on the proposed convolutional–deconvolutional neural network and the training method. This section will first present the performance test of the predictor on two kinds of physical field predictions, namely, the temperature field and the local Nusselt number distribution. Then the network model analysis will be investigated.

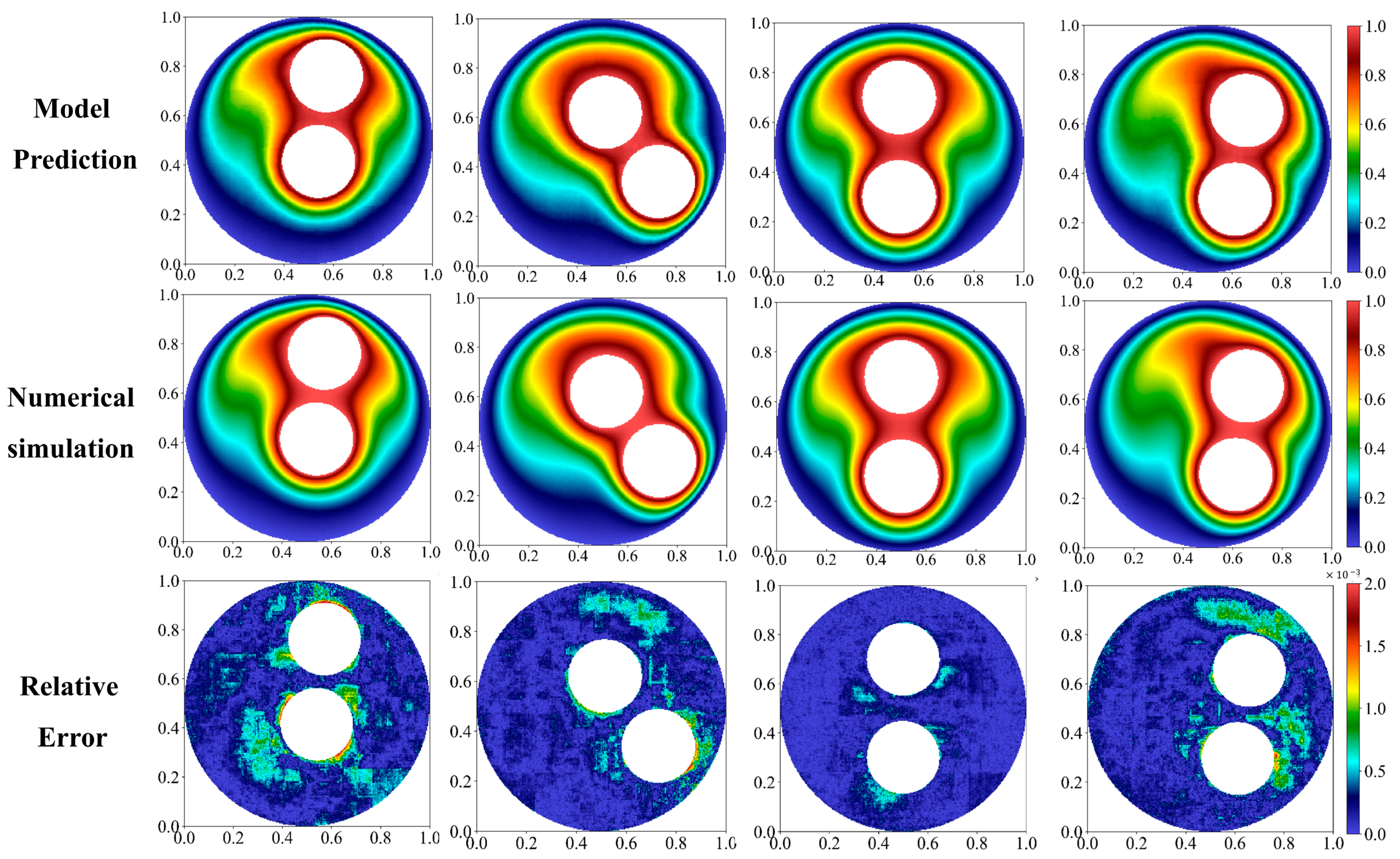
3.1. Temperature Prediction Results of the Geometry Adaptive Predictor

The temperature field predictions of the nanofluid-filled annulus on test data are shown in Figure 3 with four representative cases. Three rows illustrate, respectively, the predicted results, the numerical simulation (true results), and the error analysis. To test the geometry adaptive ability of the model, as mentioned before, the test dataset is independent of training and validation datasets. As seen from the predicted and the simulated results, heat is transferred from the inner cylinder to the periphery, and accordingly, the temperature decreases in the same direction. Furthermore, heat is transferred faster towards the upper center of the annulus. Therefore, for the cases in the first and the fourth columns, the left-right symmetrical annulus leads to a left-right symmetric temperature prediction. As seen from the error distribution of the third row, the absolute error values are very small, where the most points are less than 0.02% and all the points are less than 0.1%, which means the accuracy is higher than 99.9%. Most of the larger error points appear around the inner cylinder, where there is a big temperature gradient. It is more difficult to learn the heat transfer mechanism of the left–right asymmetrical nanofluid-filled annulus for the proposed geometry adaptive predictor.

Figure 4 shows the predicted and the true (simulated) temperature fields in a double-inner-cylinder annulus on test dataset. Similar to the temperature prediction of a single-inner-cylinder annulus, four representative cases are chosen to study the generalization ability of the proposed predictor. As shown in the first and the second rows of Figure 4, the temperature fields of the predicted and the numerical simulation are very close, showing that the highly nonlinear relationship between the 2D cross-section of annulus geometry and the nanofluid temperature field is accurately established. The warmer inner cylinder mainly transfers the heat along the direction of the outer diameter, with a small deviation to the upper center of the external cylinder. The error distribution in the figures on the third row show more extended error areas and higher error values than the cases of single-inner-cylinder annulus. This seems reasonable since the double-inner-cylinder annulus has a more complex geometry, and the predictor must learn the temperature field between the inner cylinder and the external cylinder; in addition, there are also the saddle points between the two inner cylinders. Thereby, the predictor has more difficulty to master the temperature distribution in the nanofluid area. However, the maximum error of the four cases are all less than 0.2%, and the average errors are about 0.05%. The larger errors tend to be on the surface of the inner cylinders where there is a large temperature gradient.

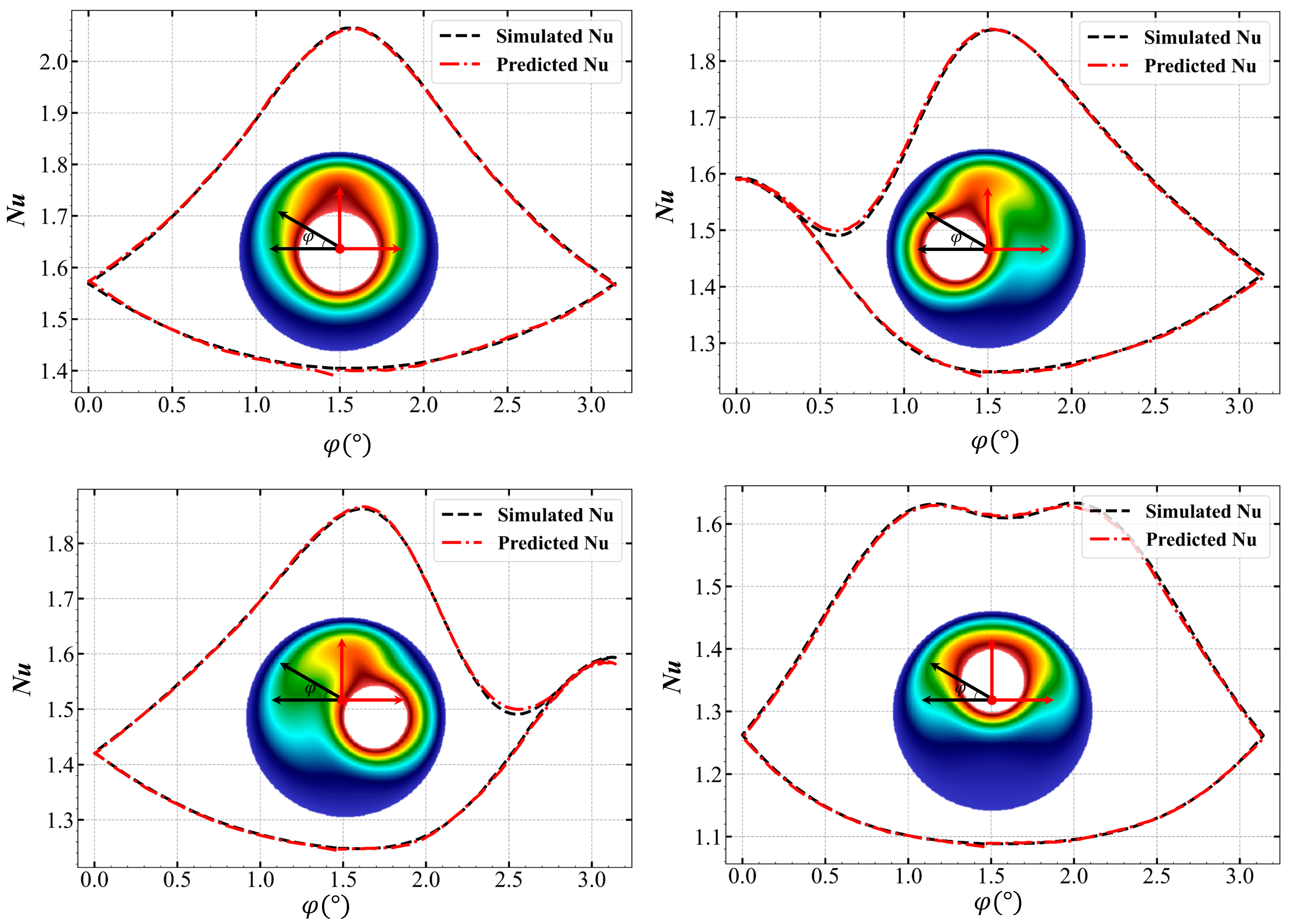
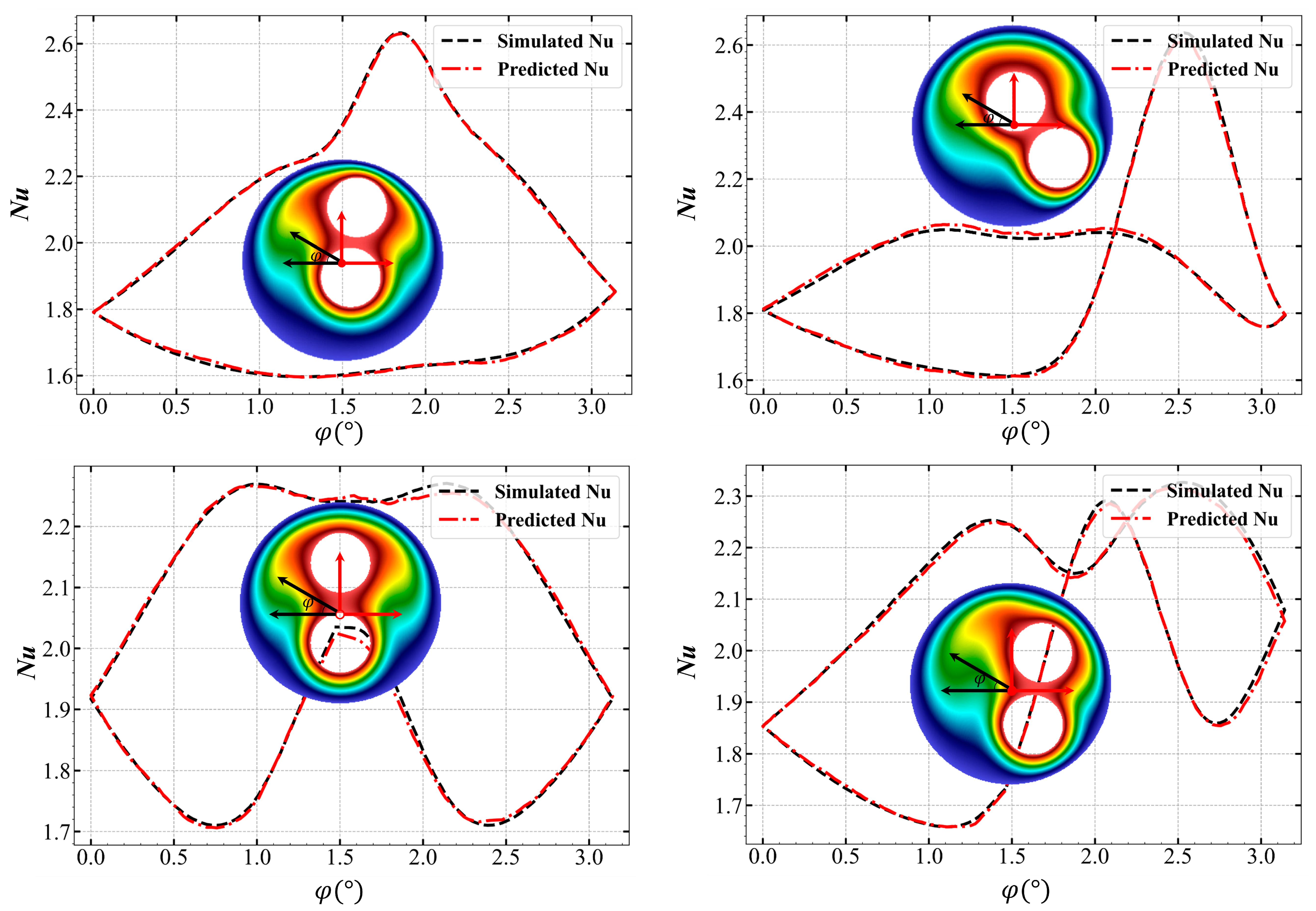
3.2. Nusselt Number Prediction of the Geometry Adaptive Predictor

The Nusselt number is a dimensionless physical quantity describing the rate of energy transfer from the surface. In this subsection, the local Nusselt number distributions in single-inner-cylinder and double-inner-cylinder annulus are investigated. Although the predictor has been trained to estimate the local Nusselt number of the whole nanofluid domain outward normal to the boundary surface, we concentrate our studies to highlight the results on the outer walls of the external cylinder.

First, we look at the local Nusselt number distribution along the angular direction of the outer wall, as shown in Figure 5, where the same four inner-cylinder test data as in Section 3.1 are used. The black dashed curve represents the simulated Nu, calculated according to Equation (10) using the temperature results of our numerical simulation in OpenFOAM. The red dash line represents the predicted Nu, mapped directly from the cross-section geometry of the annulus. We also show the corresponding temperature field in subfigure to clearly show the relationship between the temperature distribution and the Nu distribution. As seen from the comparison between the four sets of curves, the simulated and the predicted Nu are very close. The predictor ‘learns’ the Nu distribution of the outer wall along the angular direction, where all the curves form a closed loop without self-intersect where the largest Nu always occurs in the top area of the cylinder. Looking at the definition of the local Nusselt number given in Equation (10), we can see that its value is proportional to the temperature gradient normal to the boundary. Therefore, the results indicate that on the surface of the outer wall, the highest temperature gradient always occurs in the top area of the annulus.

We also compare the average Nu of the outer walls on 60 test data shown in Figure 6. The left subfigure fits the 60 data results with a straight line, which nearly overlaps with the line y = x, indicating that the predicted Nu numbers agree well with the simulated ones. Furthermore, the coefficient of determination R² reaches 0.9987. The right subfigure directly presents the 60 predicted and the simulated Nu values, which also show the high accuracy of the Nu number prediction in the single-inner-cylinder annulus.

Turning now to the Nu number prediction results of the double-inner-cylinder annulus, we use the four cases in Section 3.1. We can see from Figure 7, that the Nu number curves of the outer walls have more complex shapes: two of the four curves self-intersect and the maximum value of the Nu number and the location of its occurrence vary. In general, when the inner cylinder is closer to the outer wall, then where the temperature gradient is larger, the Nu value is higher. However, only small deviations are found between the simulated and the predicted curves. The results further confirm the accuracy of the proposed nanofluid field predictor.

The left subfigure of Figure 8 shows the coefficient of determination R² between the simulated and the predicted average Nu numbers obtained from the clouds of points. Although the accuracy is lower than the single-inner-cylinder predictions, the R² value is still higher than 0.99, and most of the points fall on the black line, which is very close to y = x. The right subfigure of Figure 8 compares the average Nu values of the outer wall for 80 samples; the results are consistent with the previous ones, where the predicted Nu agree well with the simulated ones.

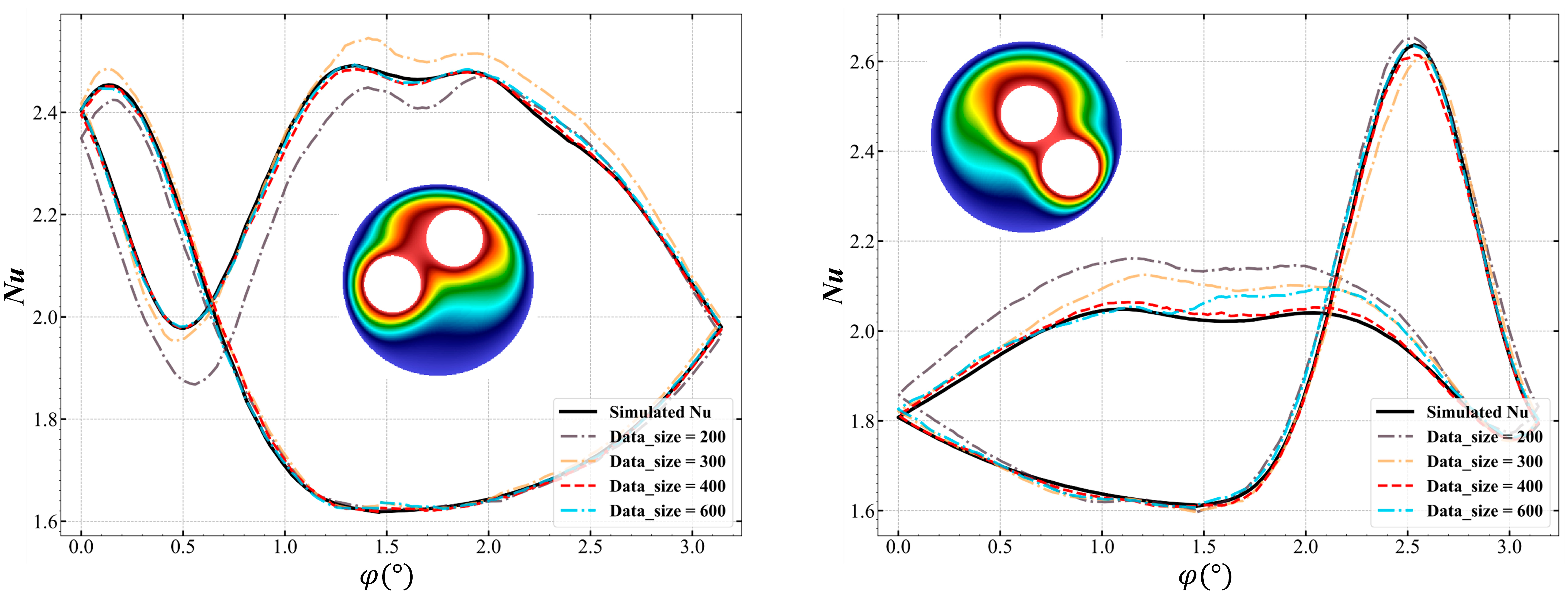
3.3. Influence of Data Size

The training data size is a key hyperparameter of deep learning-based models. A good choice of the data size not only facilitates the training but also helps the designer to build a more efficient predictor. Briefly, it can be said that too little training data may result in a poor estimation. However, generating large numbers of data is time-consuming and sometimes it is not possible to find enough data sources. Furthermore, it is reported that sometimes large data sizes may lead to a decrease in accuracy [51]. As a result, we discuss the effect of the data size for the proposed model. Four training data sizes are designed: 200, 300, 400, and 600 data, and then the value of the determination coefficient between the simulated and the predicted Nu number and the Nu curves with various data size are compared.

As shown in Figure 9, the coefficient of determination R² increases with the augmentation of the data size, the highest value is 0.9934 with the data size of 600. However, the R² values of the other three data sizes are not far behind, especially the R² of 400 data, which is 0.9901—very close to the value of for the 600 data. Figure 10 provides the Nusselt number curves of two representative double-inner-cylinder annuli with various data size, where we can clearly see the discrepancy of the curves. The curves of the 200 and the 300 data show relatively large errors, and the curve of the 400 data seems to agree best with the simulated results. Therefore, considering both the time required for data generation and the model training, as well as the above model analysis, the data size of 400 is chosen in our study.

The computational cost of the temperature and the Nu number estimations using network predictor and numerical solver are listed in

Table 2. Time usage of network model prediction and numerical solver calculation.

		Time Cost	Pretreatment
Network predictor	Temperature	0.0382 s	0.032 s (NWSDF)
	Nu number	0.0388 s
Numerical solver	data	430 s	3.09 s (mesh)

. Each numerical simulation can handle the Nu field and the temperature field together. Therefore, time is saved and the results for the two field predictions for the same time costs, 430 s, are given in Table 2. It takes more time for the Nu calculation because it is based on the data of the temperature field prediction. Moreover, what stands out in this table is the markedly different usage time between the numerical simulation and the network prediction, where the prediction time for the network predictor is only about 0.038 s, four orders of magnitude faster compared to the numerical simulation. This may be explained by the fact that for either temperature or Nu prediction, the proposed predictor can directly obtain the required information from the established end-to-end mapping using the corresponding annulus geometry as input, where no further equations need to be solved. In addition, the pretreatment process of the network predictor takes very little time. Therefore, together, the two small time costs assure faster and even real-time predictions of the proposed predictor.

4. Conclusions

Nanofluids, as popular working fluids, have been used to enhance the heat transfer efficiency in many thermal systems due to their higher thermal conductivity achieved by adding nanoparticles to the base fluid. Annulus enclosure, as an essential geometry, has been used in various thermal engineering applications.

Therefore, this paper builds a purely data-driven geometry adaptive model to predict convection in a nanofluid flowing in horizontal annular pipes using a deep convolutional neural network. The numerical simulations are performed in OpenFOAM to obtain the reference values for the temperature field and the Nusselt number distribution. Five convolutional layers followed by four deconvolutional layers create the structure of the proposed predictor, and with the NWSDF presented annulus geometry input, it can accurately and reasonably predict quickly the temperature field of the nanofluid and the Nusselt number distribution on the outer wall of a single or double-inner-cylinder annulus. The following conclusions can be drawn from the present study:

• For the case of single inner cylinder, the predictor can adapt both the inner cylinder size and the placement, where the accuracy of the temperature field is higher than 99.9% and the coefficient of determination $R^2$ of the Nusselt number prediction reaches 0.9987.
• For the case of the double-inner-cylinder annulus, which has a more complex geometry, the temperature prediction accuracy and the $R^2$ values of the Nusselt number prediction are not far from the results of the single-inner-cylinder case, 99.8% and 0.9901, respectively, with the inner ring placement adaptive ability.
• In addition, the proposed predictor takes much less time in both the nanofluid field prediction and the input data pretreatment. In particular, the prediction time is four orders faster.

In conclusion, with the fast and accurate estimation of the temperature and the Nusselt number fields, the proposed predictor can be expected to realize the rapid inner cylinder configuration design for the nanofluid-filled horizontal annular pipes.