A Review of Recent Aerodynamic Power Extraction Challenges in Coordinated Pitch, Yaw, and Torque Control of Large-Scale Wind Turbine Systems
Abstract
1. Introduction
- 1.
- This study represents the first attempt to review and evaluate the impact of climate change on the maximum aerodynamic power extraction of a super-large WTS.
- 2.
- Mathematical modeling of climate change, such as temperature and rainfall effects, is constructed to investigate power production techniques in WTS effectively.
- 3.
- A brief representation of coordinated pitch, yaw, and generator torque control technologies for super-large WTS are presented.
- 4.
- Finally, we present a variety of simulation case studies to demonstrate the impact of climate change on aerodynamic power generation in super-large WTS and the limitations of coordinated pitch/yaw and generator torque control techniques.
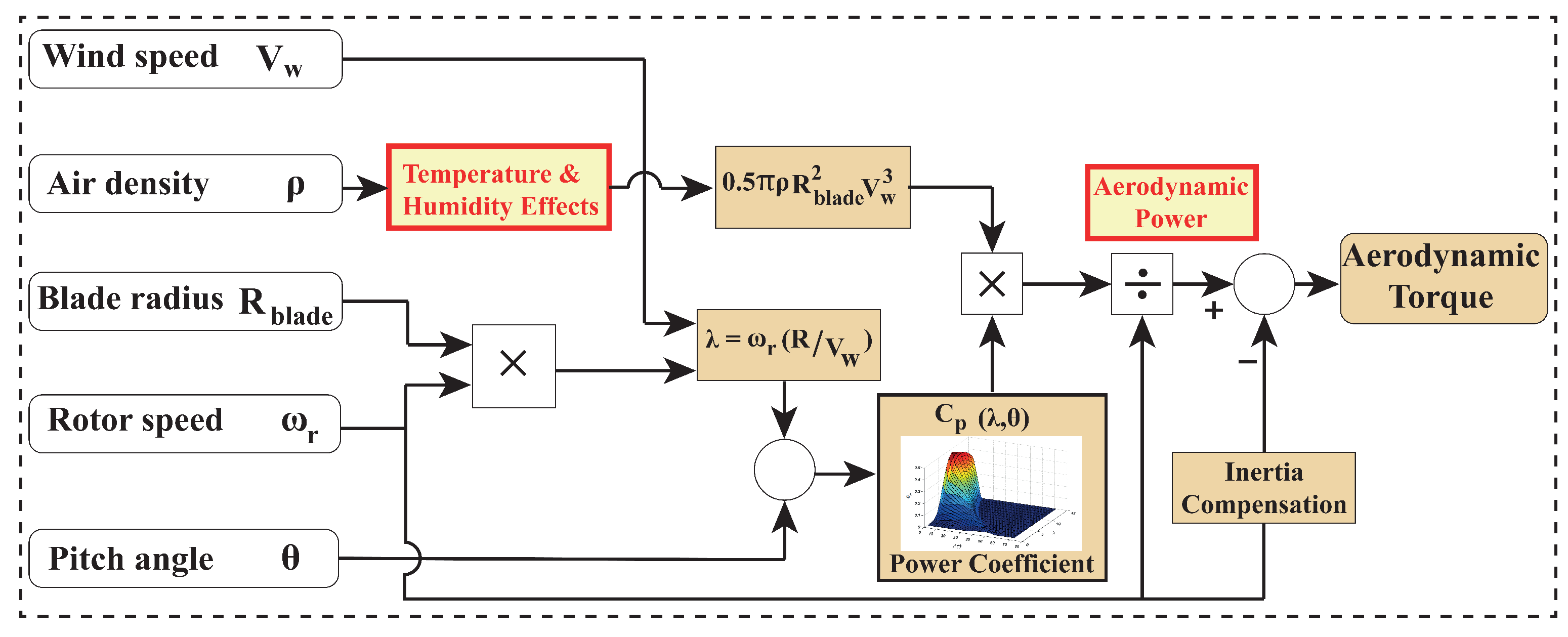
2. Aerodynamic Power Extraction Challenges in Super-Large WTS
3. Temperature and Humidity Effects in Super-Large WTSs
3.1. Mathematical Modeling of the Temperature and Humidity Effects in WTS
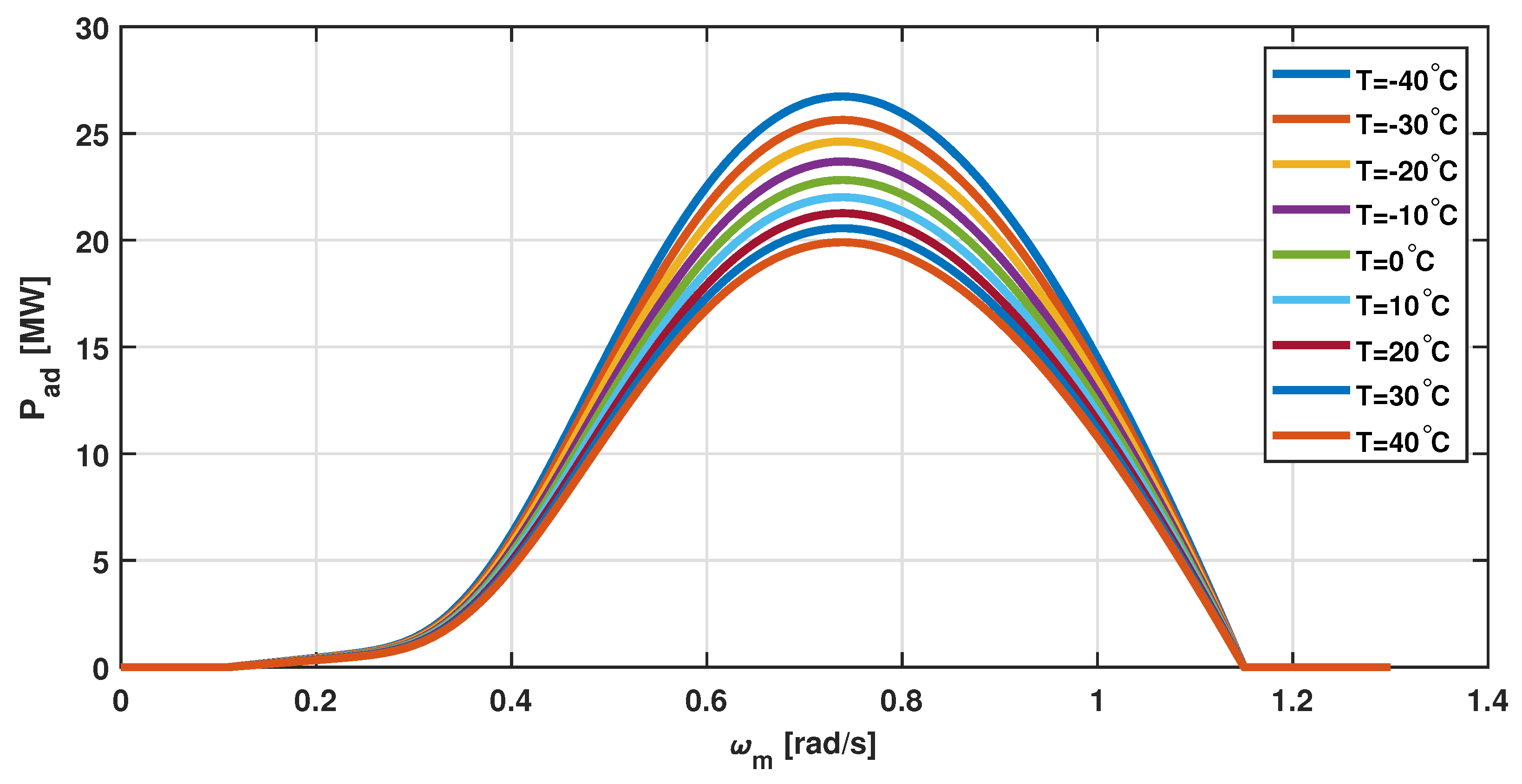
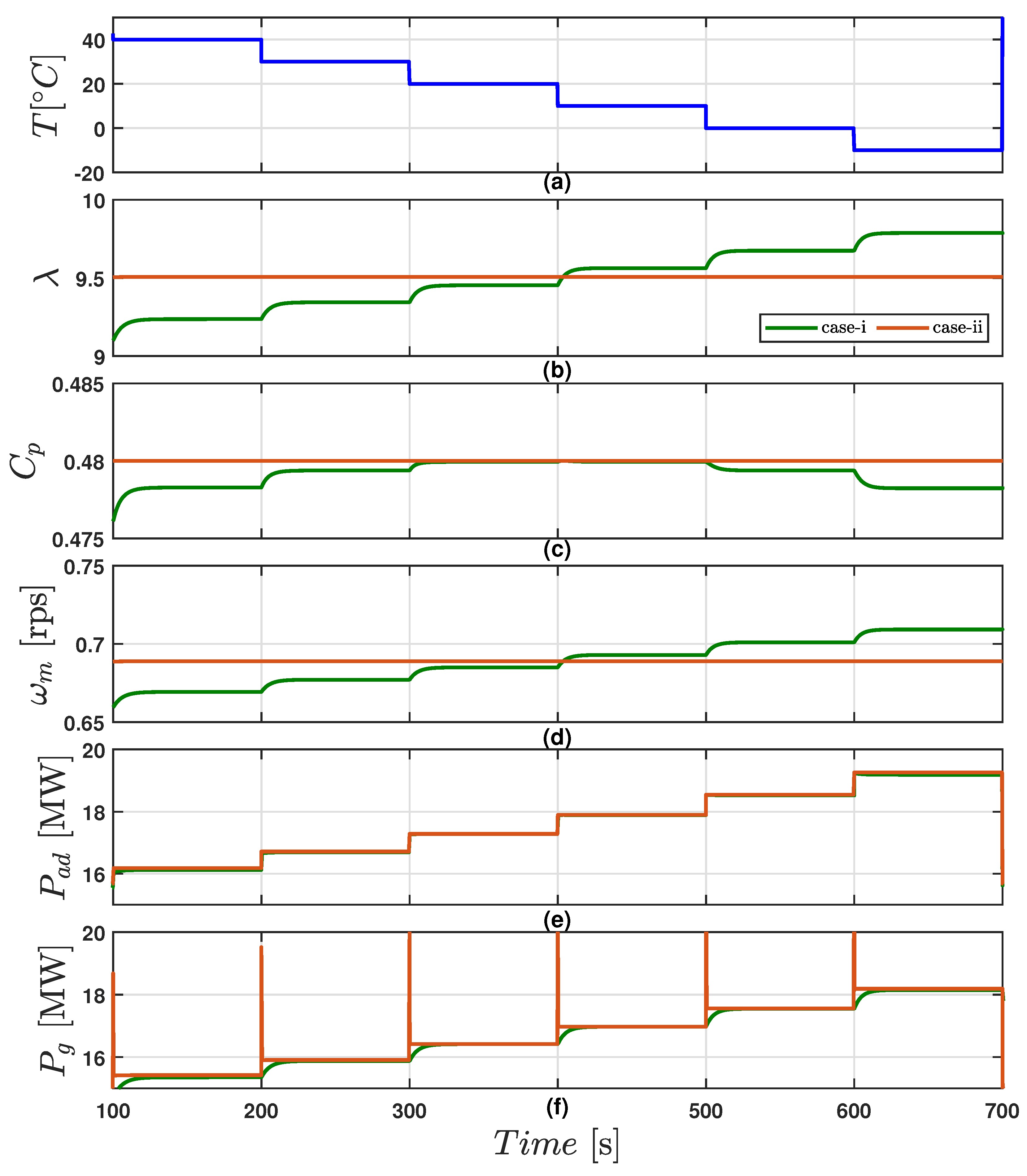
3.2. Performance of WTS Operation under Temperature and Humidity Effects
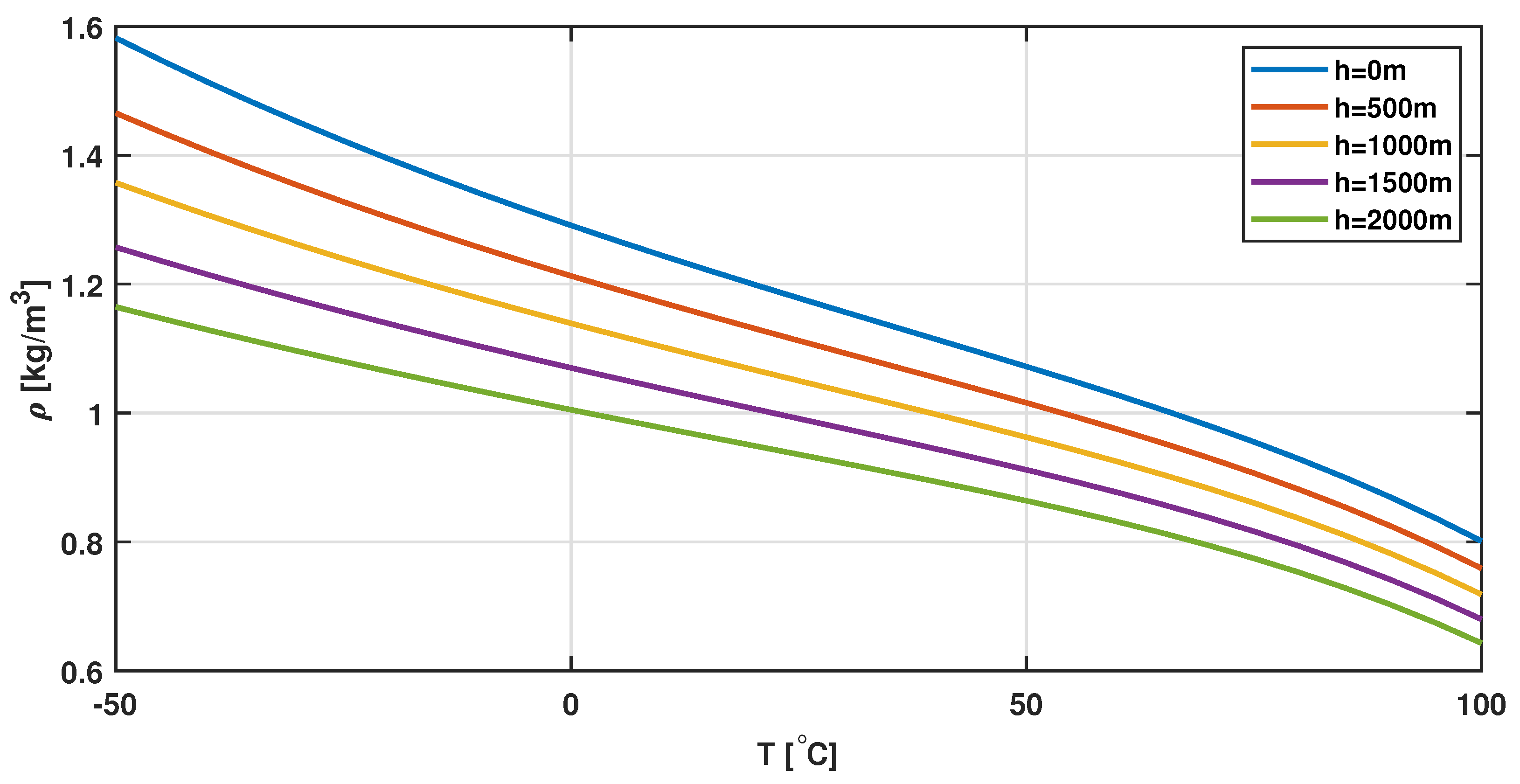
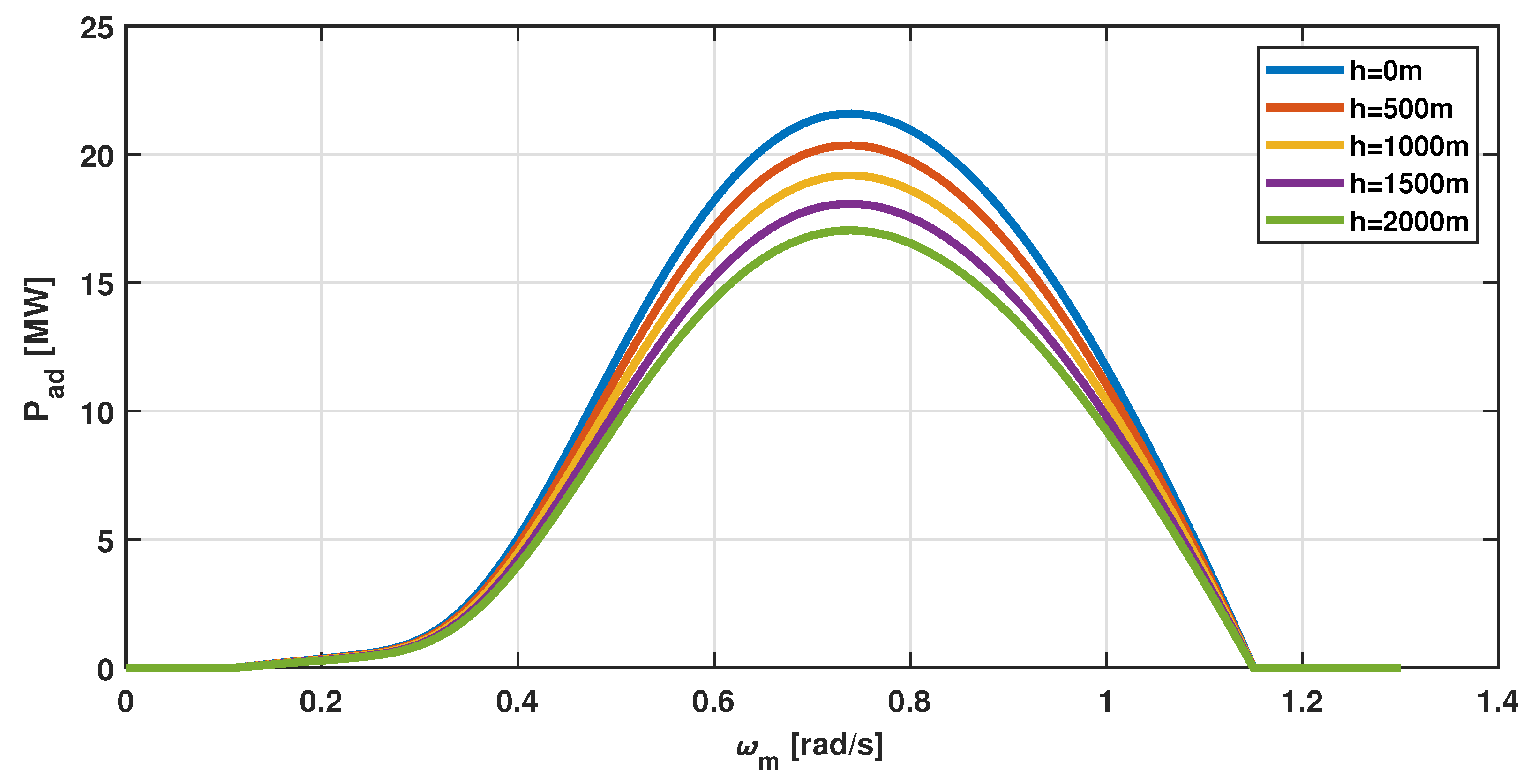
3.2.1. Simulation Results for Super-Large WTS under Varying Environmental Conditions
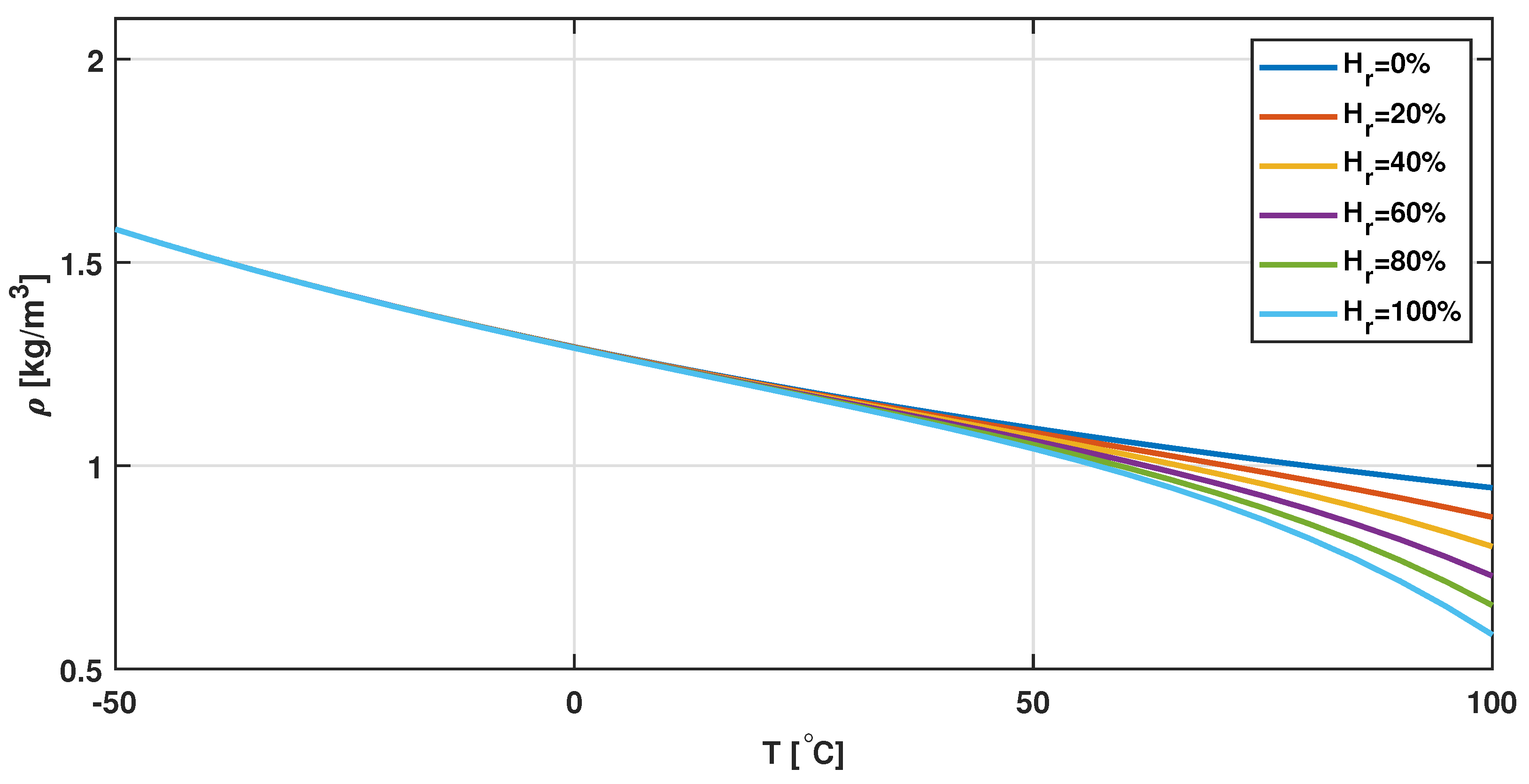
3.2.2. Simulation Results for Super-Large WTS with Varying Temperature and Constant Relative Humidity
- i.
- First, the given standard value of = 1.225 kg/m is considered under varying temperature operations.
- ii.
- The results are compared for an identical temperature profile with varying .
3.2.3. Simulation Results for a Super-Large WTS with Constant Temperature and Varying Relative Humidity
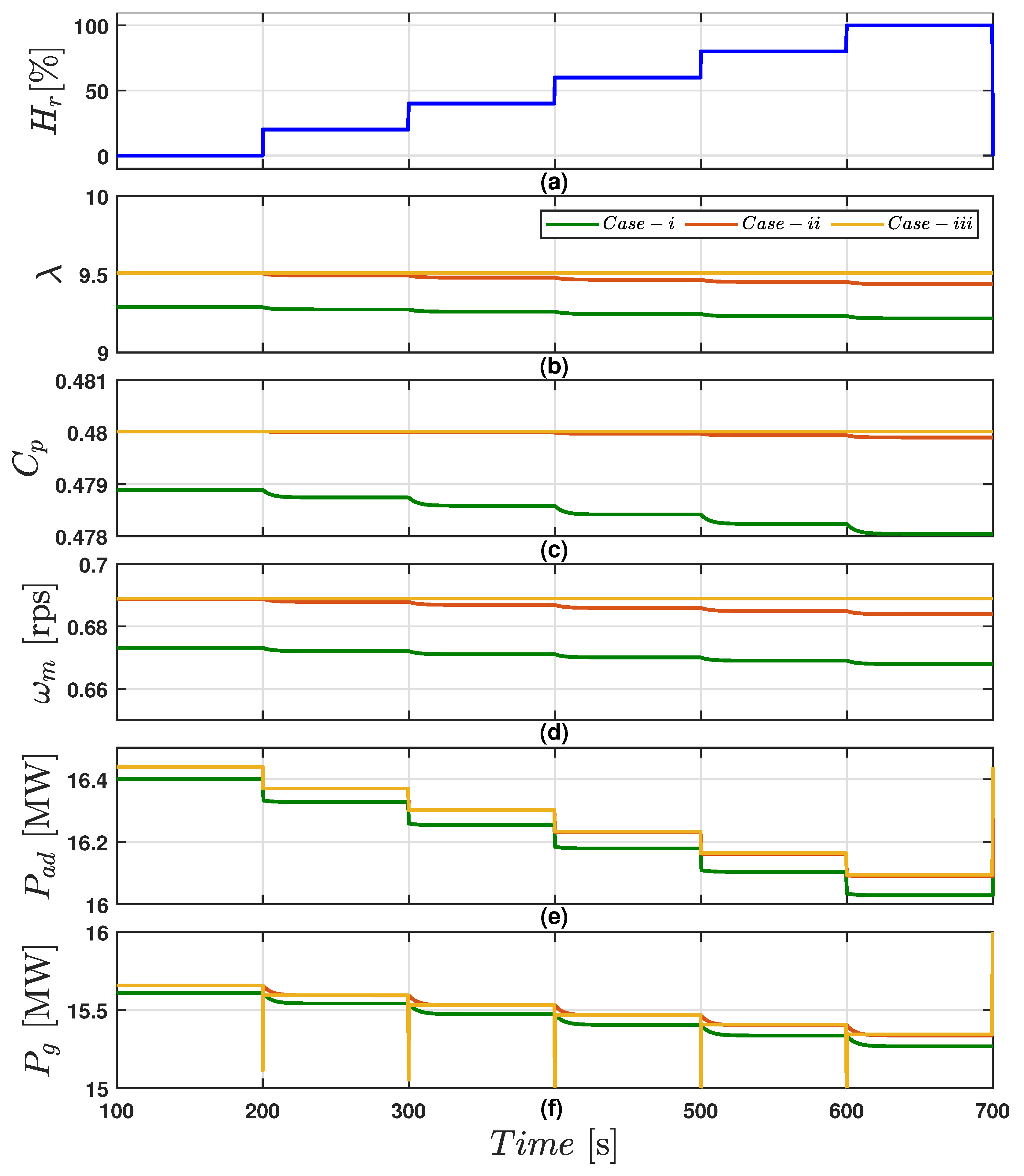
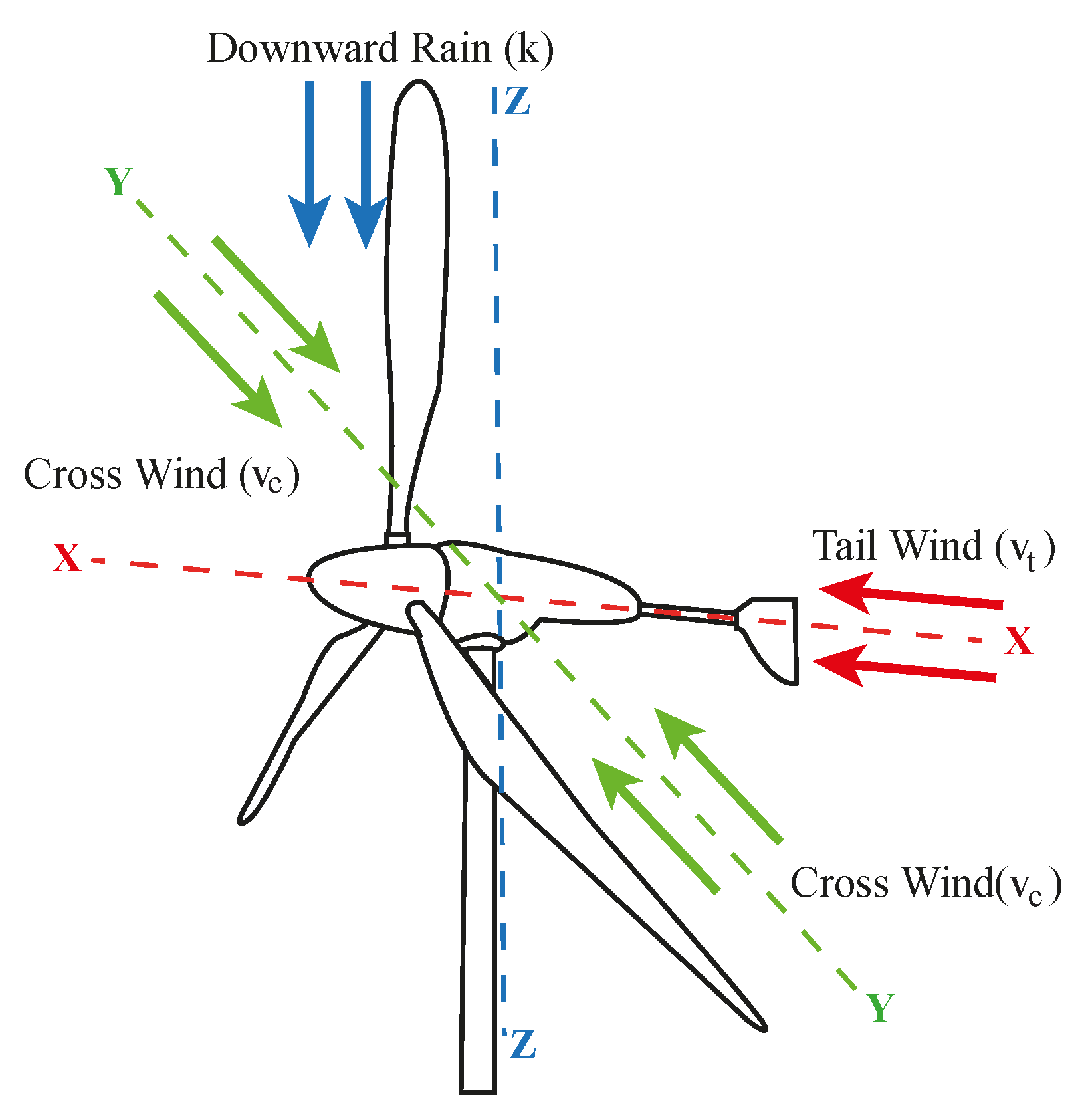
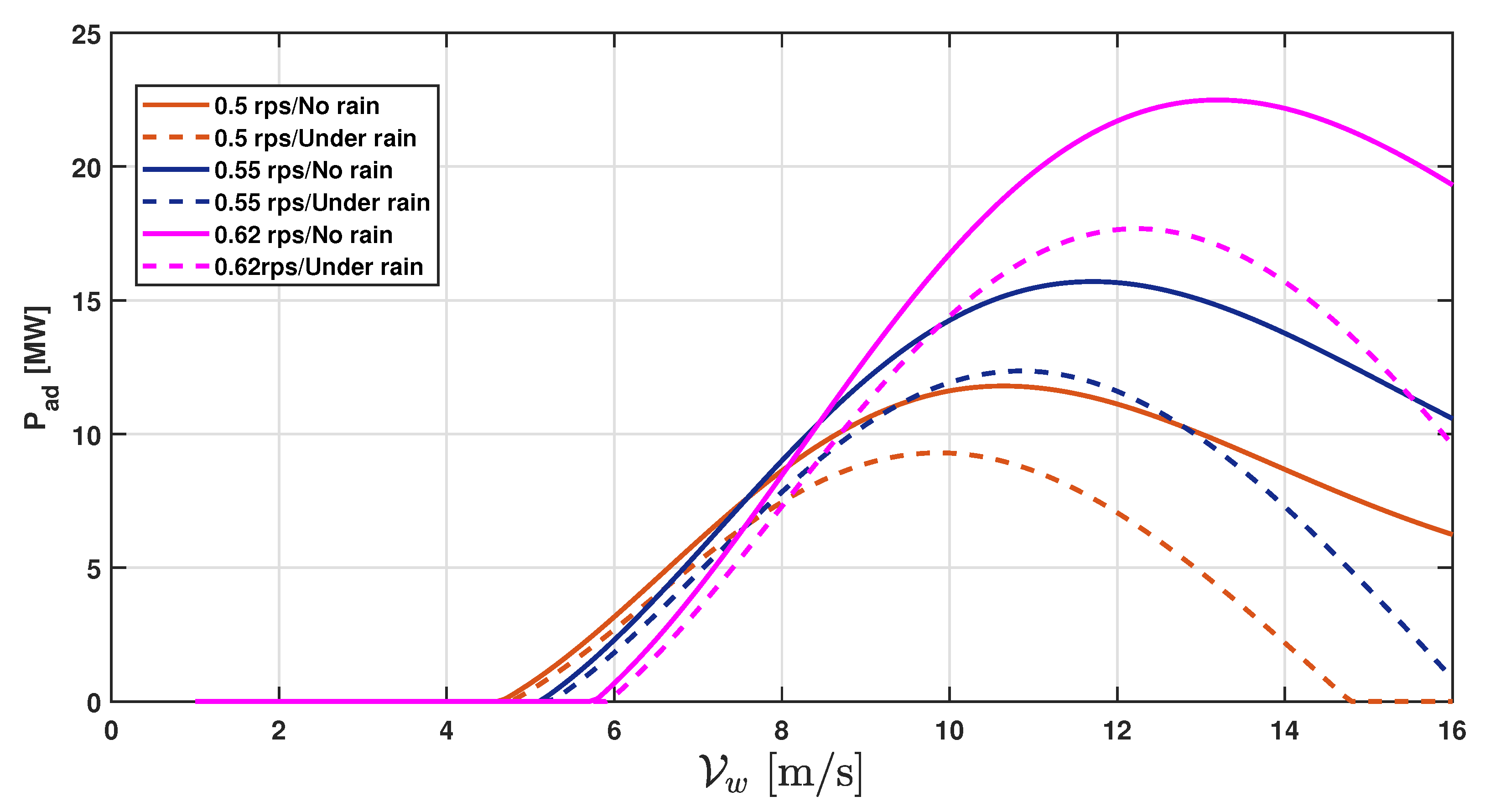
4. Rainfall Effects on Super-Large Wind Turbine Systems
Mathematical Modelling of Rainfall Effects in Super-Large WTSs
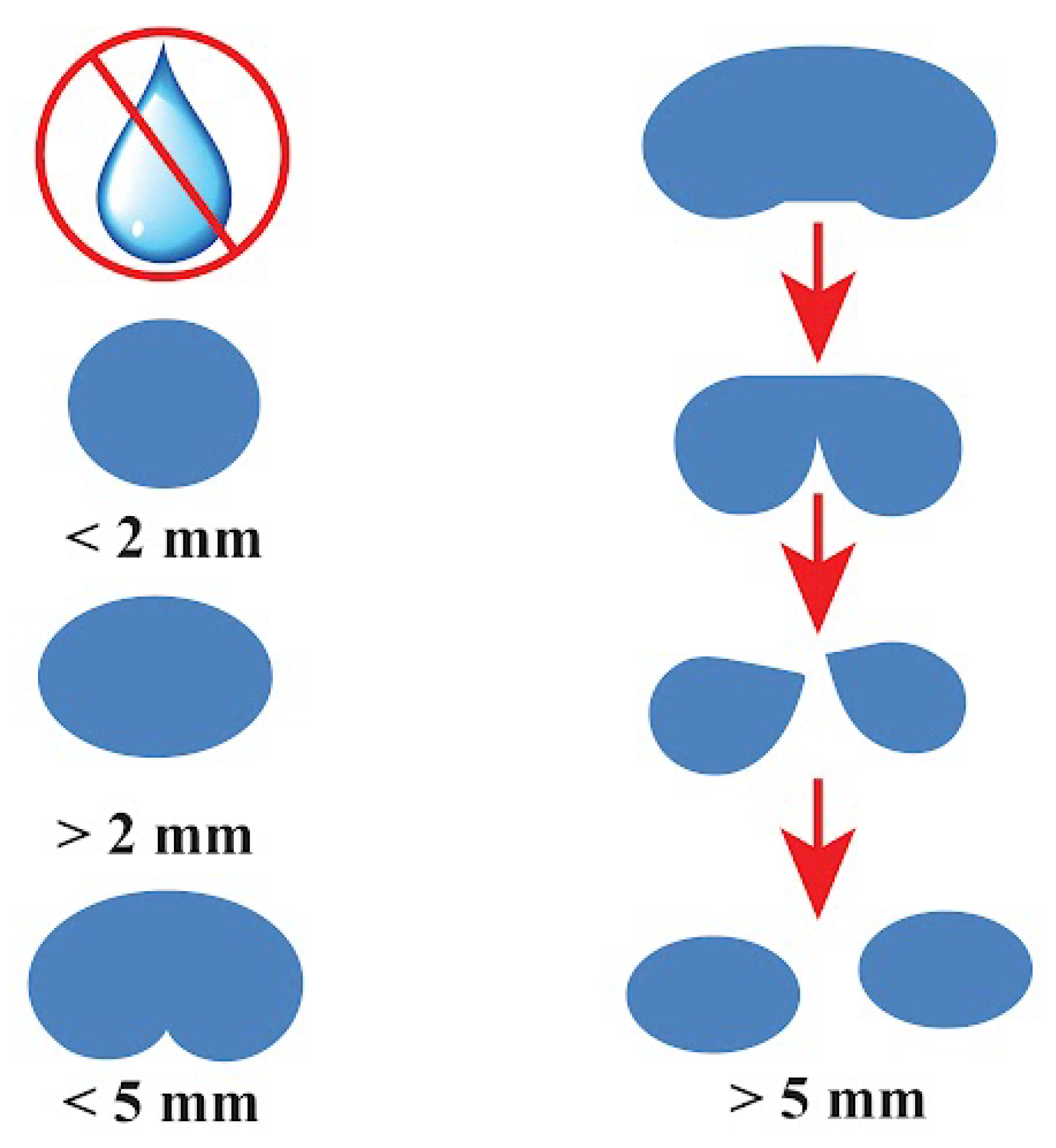
Wetness Modeling of the WT Blades
5. Recent Pitch, Yaw, and Torque Control Methods for Super-Large WTS with and without Environmental Changes
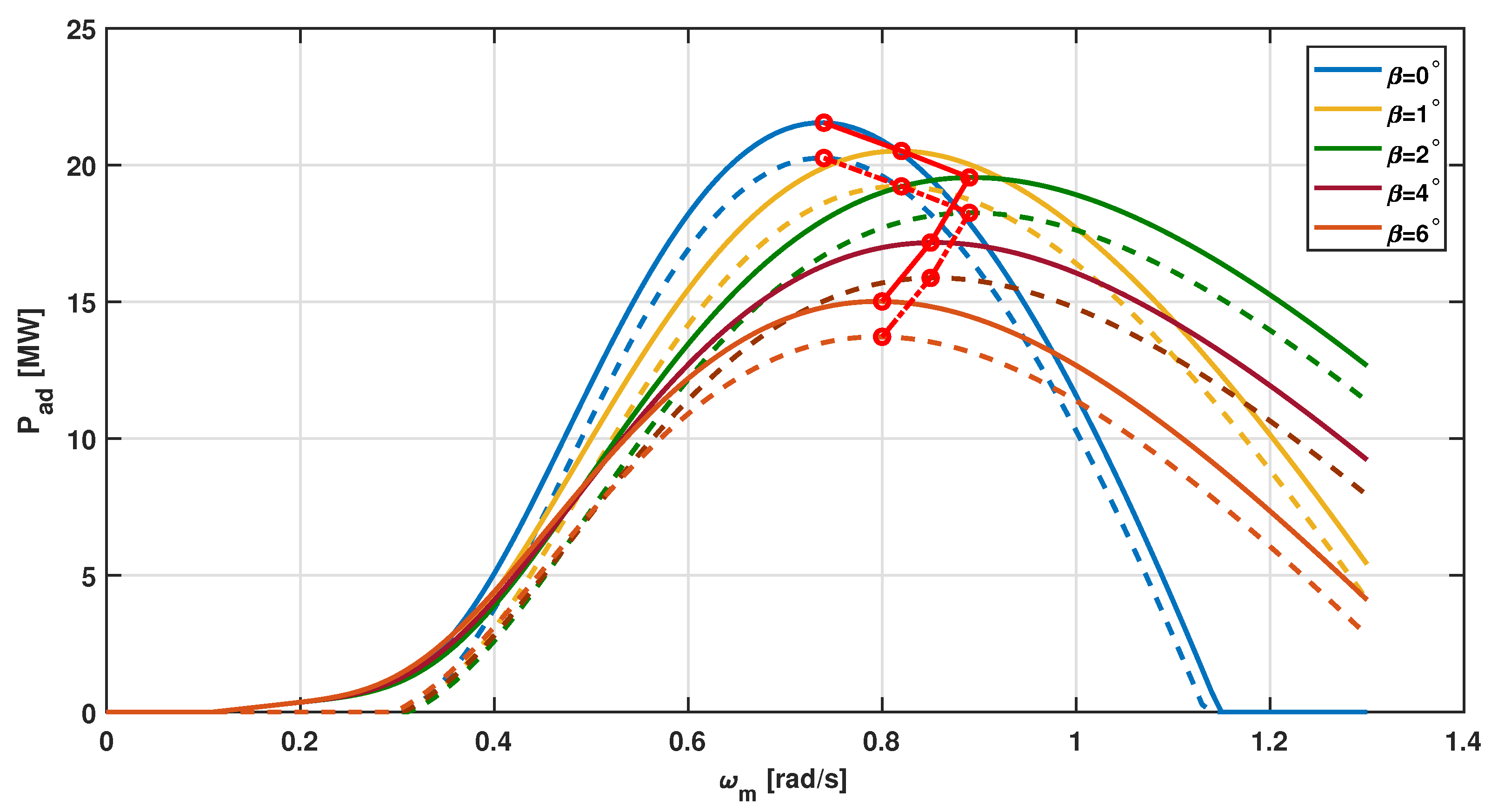
5.1. Review of Pitch Control for Super-Large WTS
- (1)
- To maintain a constant rotor speed, the generator torque must often remain constant to achieve stable output power operation.
- (2)
- To track the active power reference and real-time balancing between the aerodynamic (input) and electric (output) power of the super-large WTS.
5.2. Coordinated Pitch and Generator Speed Control for Active Power Regulation of Super-Large WTSs
5.3. Review of Yaw Control for Large-Scale WTS
- (1)
- Maximizing the energy capture of a wind turbine by aligning the nacelle of WT exactly with the direction of wind velocity under region-2 operation.
- (2)
- Ensuring load reduction and maximum energy capture by establishing a coordinated pitch and yaw control with minimum actuation for efficient operation.
- (3)
- Decreasing a single WT’s fatigue load, and maximizing the total amount of power produced by a wind farm while optimizing load.
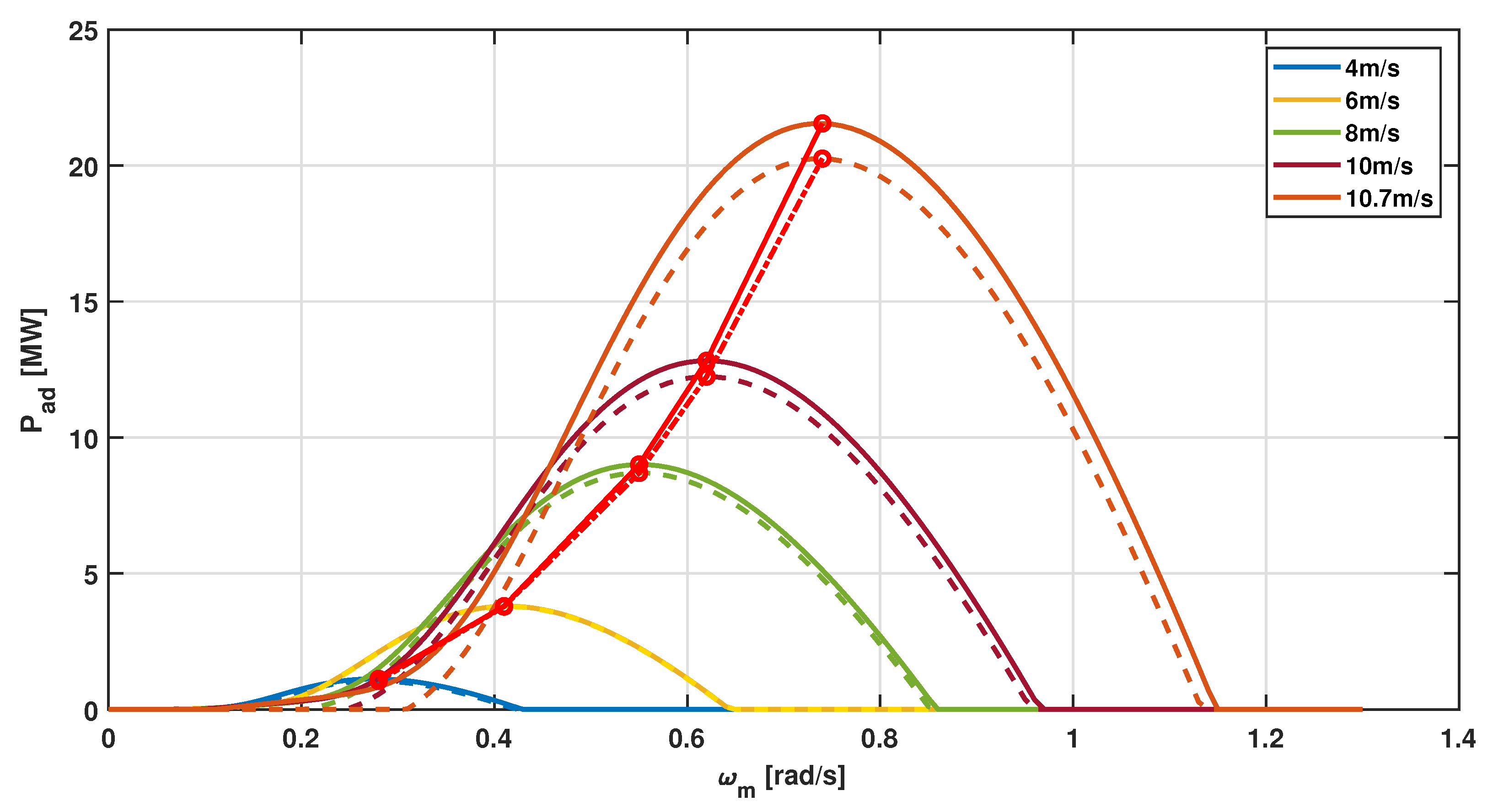
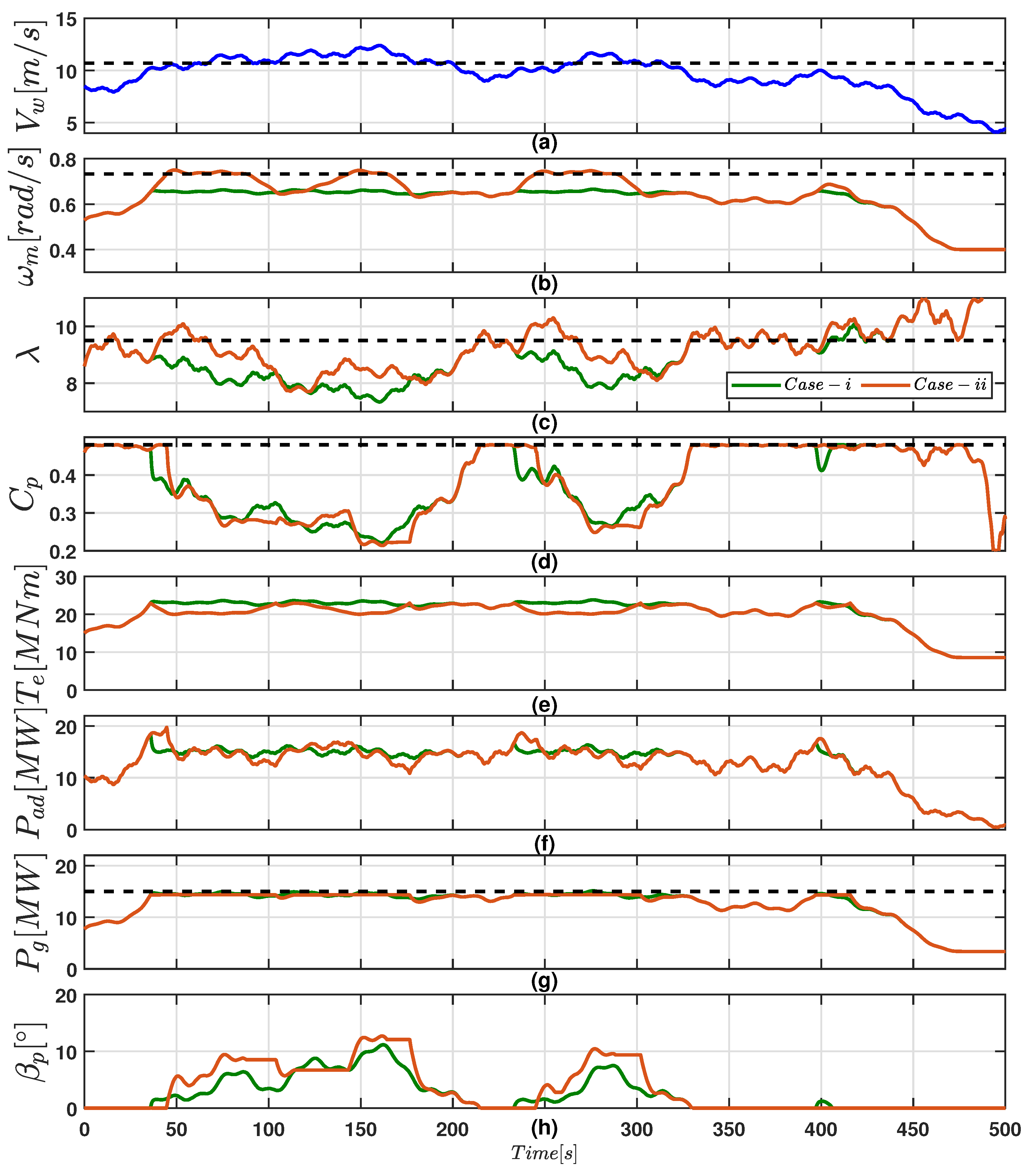
6. Validation Example
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mayilsamy, G.; Natesan, B.; Joo, Y.H.; Lee, S.R. Fast Terminal Synergetic Control of PMVG-Based Wind Energy Conversion System for Enhancing the Power Extraction Efficiency. Energies 2022, 15, 2774. [Google Scholar] [CrossRef]
- Jones, D. Global Electricity Review 2021. Available online: https://ember-climate.org/project/global-electricity-review-2021/ (accessed on 1 September 2022).
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Ramasamy, T.; Abdul Basheer, A.; Tak, M.H.; Joo, Y.H.; Lee, S.R. An Effective DC-Link Voltage Control Strategy for Grid-Connected PMVG-Based Wind Energy Conversion System. Energies 2022, 15, 2931. [Google Scholar] [CrossRef]
- Global Wind Energy Counci. Global Wind Report 2022; Global Wind Energy Council: Brussels, Belgium, 2022. [Google Scholar]
- Yesudhas, A.A.; Joo, Y.H.; Lee, S.R. Reference Model Adaptive Control Scheme on PMVG-Based WECS for MPPT under a Real Wind Speed. Energies 2022, 15, 3091. [Google Scholar] [CrossRef]
- Anbalagan, P.; Joo, Y.H. Dissipative-based Sampled-data Control for TS Fuzzy Wind Turbine System Via Fragmented-delayed State Looped Functional Approach. 2022. Available online: https://www.researchsquare.com/article/rs-1525158/v1 (accessed on 1 September 2022).
- Shanmugam, L.; Joo, Y.H. Stabilization of permanent magnet synchronous generator-based wind turbine system via fuzzy-based sampled-data control approach. Inf. Sci. 2021, 559, 270–285. [Google Scholar] [CrossRef]
- Venkateswaran, R.; Yesudhas, A.A.; Lee, S.R.; Joo, Y.H. Integral sliding mode control for extracting stable output power and regulating DC-link voltage in PMVG-based wind turbine system. Int. J. Electr. Power Energy Syst. 2023, 144, 108482. [Google Scholar] [CrossRef]
- Asim, T.; Islam, S.Z.; Hemmati, A.; Khalid, M.S.U. A review of recent advancements in offshore wind turbine technology. Energies 2022, 15, 579. [Google Scholar] [CrossRef]
- Belabbas, B.; Allaoui, T.; Tadjine, M.; Denai, M. Comparative study of back-stepping controller and super twisting sliding mode controller for indirect power control of wind generator. Int. J. Syst. Assur. Eng. Manag. 2019, 10, 1555–1566. [Google Scholar] [CrossRef]
- Chen, S.; Hu, W.; Du, Y.; Wang, S.; Zhang, C.; Chen, Z. Three-stage relaxation-weightsum-correction based probabilistic reactive power optimization in the distribution network with multiple wind generators. Int. J. Electr. Power Energy Syst. 2022, 141, 108146. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, Y.; Zhang, D. Optimal ancillary control for frequency regulation of wind turbine generator based on improved fatigue load sensitivity. Int. J. Electr. Power Energy Syst. 2022, 137, 107751. [Google Scholar] [CrossRef]
- Palanimuthu, K.; Mayilsamy, G.; Lee, S.R.; Jung, S.Y.; Joo, Y.H. Comparative analysis of maximum power extraction and control methods between PMSG and PMVG-based wind turbine systems. Int. J. Electr. Power Energy Syst. 2022, 143, 108475. [Google Scholar] [CrossRef]
- Wu, B.; Lang, Y.; Zargari, N.; Kouro, S. Power Conversion and Control of Wind Energy Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Venkateswaran, R.; Joo, Y.H. Retarded sampled-data control design for interconnected power system with DFIG-based wind farm: LMI approach. IEEE Trans. Cybern. 2021, 52, 5767–5777. [Google Scholar] [CrossRef] [PubMed]
- Menezes, E.J.N.; Araújo, A.M.; Da Silva, N.S.B. A review on wind turbine control and its associated methods. J. Clean. Prod. 2018, 174, 945–953. [Google Scholar] [CrossRef]
- Ghoudelbourk, S.; Dib, D.; Omeiri, A.; Azar, A.T. MPPT control in wind energy conversion systems and the application of fractional control (PIα) in pitch wind turbine. Int. J. Model. Identif. Control 2016, 26, 140–151. [Google Scholar] [CrossRef]
- Osintsev, K.; Aliukov, S.; Shishkov, A. Improvement dependability of offshore horizontal-axis wind turbines by applying new mathematical methods for calculation the excess speed in case of wind gusts. Energies 2021, 14, 3085. [Google Scholar] [CrossRef]
- Carlin, P.W.; Laxson, A.S.; Muljadi, E.B. The history and state of the art of variable-speed wind turbine technology. Wind. Energy: Int. J. Prog. Appl. Wind. Power Convers. Technol. 2003, 6, 129–159. [Google Scholar] [CrossRef]
- Joo, Y. Integral sliding mode control for increasing maximum power extraction efficiency of variable-speed wind energy system. Int. J. Electr. Power Energy Syst. 2022, 139, 107958. [Google Scholar]
- Greene, S.; Morrissey, M.; Johnson, S.E. Wind climatology, climate change, and wind energy. Geogr. Compass 2010, 4, 1592–1605. [Google Scholar] [CrossRef]
- Rasmussen, D.; Holloway, T.; Nemet, G. Opportunities and challenges in assessing climate change impacts on wind energy—A critical comparison of wind speed projections in California. Environ. Res. Lett. 2011, 6, 024008. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Santos, C.S. Potential impacts of climate change on European wind energy resource under the CMIP5 future climate projections. Renew. Energy 2017, 101, 29–40. [Google Scholar] [CrossRef]
- Olabi, A.; Abdelkareem, M.A. Renewable energy and climate change. Renew. Sustain. Energy Rev. 2022, 158, 112111. [Google Scholar] [CrossRef]
- Fakhry, M.; Farzaneh, M.R.; Eslamian, S.; Nazari, R. Wind Speed Regionalization Under Climate Change Conditions. In New Developments in Renewable Energy; Arman, H., Yuksel, I., Eds.; IntechOpen: London, UK, 2013. [Google Scholar]
- Nolan, P.; Lynch, P.; McGrath, R.; Semmler, T.; Wang, S. Simulating climate change and its effects on the wind energy resource of Ireland. Wind Energy 2012, 15, 593–608. [Google Scholar] [CrossRef]
- Koletsis, I.; Kotroni, V.; Lagouvardos, K.; Soukissian, T. Assessment of offshore wind speed and power potential over the Mediterranean and the Black Seas under future climate changes. Renew. Sustain. Energy Rev. 2016, 60, 234–245. [Google Scholar] [CrossRef]
- Davy, R.; Gnatiuk, N.; Pettersson, L.; Bobylev, L. Climate change impacts on wind energy potential in the European domain with a focus on the Black Sea. Renew. Sustain. Energy Rev. 2018, 81, 1652–1659. [Google Scholar] [CrossRef]
- Ruffato-Ferreira, V.; da Costa Barreto, R.; Júnior, A.O.; Silva, W.L.; de Berrêdo Viana, D.; do Nascimento, J.A.S.; de Freitas, M.A.V. A foundation for the strategic long-term planning of the renewable energy sector in Brazil: Hydroelectricity and wind energy in the face of climate change scenarios. Renew. Sustain. Energy Rev. 2017, 72, 1124–1137. [Google Scholar] [CrossRef]
- Kim, K.; Kim, B.; Kim, H. A decision-making model for the analysis of offshore wind farm projects under climate uncertainties: A case study of South Korea. Renew. Sustain. Energy Rev. 2018, 94, 853–860. [Google Scholar] [CrossRef]
- Solaun, K.; Cerdá, E. Impacts of climate change on wind energy power–Four wind farms in Spain. Renew. Energy 2020, 145, 1306–1316. [Google Scholar] [CrossRef]
- Hdidouan, D.; Staffell, I. The impact of climate change on the levelised cost of wind energy. Renew. Energy 2017, 101, 575–592. [Google Scholar] [CrossRef]
- Sawant, M.; Thakare, S.; Rao, A.P.; Feijóo-Lorenzo, A.E.; Bokde, N.D. A review on state-of-the-art reviews in wind-turbine-and wind-farm-related topics. Energies 2021, 14, 2041. [Google Scholar] [CrossRef]
- Pfaffel, S.; Faulstich, S.; Rohrig, K. Performance and reliability of wind turbines: A review. Energies 2017, 10, 1904. [Google Scholar] [CrossRef]
- Zhang, Z.; Hackl, C.M.; Kennel, R. Computationally efficient DMPC for three-level NPC back-to-back converters in wind turbine systems with PMSG. IEEE Trans. Power Electron. 2016, 32, 8018–8034. [Google Scholar] [CrossRef]
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.A.; Ekemb, G. Wind turbine condition monitoring: State-of-the-art review, new trends, and future challenges. Energies 2014, 7, 2595–2630. [Google Scholar] [CrossRef]
- Wang, L.; Kolios, A.; Liu, X.; Venetsanos, D.; Rui, C. Reliability of offshore wind turbine support structures: A state-of-the-art review. Renew. Sustain. Energy Rev. 2022, 161, 112250. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Lian, J. Review of integrated installation technologies for offshore wind turbines: Current progress and future development trends. Energy Convers. Manag. 2022, 255, 115319. [Google Scholar] [CrossRef]
- Roy, P.; He, J.; Zhao, T.; Singh, Y. Recent Advances of Wind-Solar Hybrid Renewable Energy Systems for Power Generation: A Review. IEEE Open J. Ind. Electron. Soc. 2022, 3, 81–104. [Google Scholar] [CrossRef]
- Abdul Basit, B.; Nguyen, A.T.; Ryu, S.W.; Park, H.; Jung, J.W. A state-of-the-art comprehensive review of modern control techniques for grid-connected wind turbines and photovoltaic arrays distributed generation systems. IET Renew. Power Gener. 2022. [Google Scholar] [CrossRef]
- Kumar, D.; Chatterjee, K. A review of conventional and advanced MPPT algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2016, 55, 957–970. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Su, M.; Liu, A.; Liu, Y.; Joo, Y.H. A comparison study between two MPPT control methods for a large variable-speed wind turbine under different wind speed characteristics. Energies 2017, 10, 613. [Google Scholar] [CrossRef]
- Ghaffarzadeh, H.; Mehrizi-Sani, A. Review of Control Techniques for Wind Energy Systems. Energies 2020, 13, 6666. [Google Scholar] [CrossRef]
- Salic, T.; Charpentier, J.F.; Benbouzid, M.; Le Boulluec, M. Control strategies for floating offshore wind turbine: Challenges and trends. Electronics 2019, 8, 1185. [Google Scholar] [CrossRef]
- Fakorede, O.; Feger, Z.; Ibrahim, H.; Ilinca, A.; Perron, J.; Masson, C. Ice protection systems for wind turbines in cold climate: Characteristics, comparisons and analysis. Renew. Sustain. Energy Rev. 2016, 65, 662–675. [Google Scholar] [CrossRef]
- Swenson, L.; Gao, L.; Hong, J.; Shen, L. An efficacious model for predicting icing-induced energy loss for wind turbines. Appl. Energy 2022, 305, 117809. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, Z.; Jiang, G.; He, Q.; Xie, P. Detecting Wind Turbine Blade Icing with a Multiscale Long Short-Term Memory Network. Energies 2022, 15, 2864. [Google Scholar] [CrossRef]
- Contreras Montoya, L.T.; Lain, S.; Ilinca, A. A Review on the Estimation of Power Loss Due to Icing in Wind Turbines. Energies 2022, 15, 1083. [Google Scholar] [CrossRef]
- Virtanen, E.A.; Lappalainen, J.; Nurmi, M.; Viitasalo, M.; Tikanmäki, M.; Heinonen, J.; Atlaskin, E.; Kallasvuo, M.; Tikkanen, H.; Moilanen, A. Balancing profitability of energy production, societal impacts and biodiversity in offshore wind farm design. Renew. Sustain. Energy Rev. 2022, 158, 112087. [Google Scholar] [CrossRef]
- Alzayed, M.; Chaoui, H.; Farajpour, Y. Maximum power tracking for a wind energy conversion system using cascade-forward neural networks. IEEE Trans. Sustain. Energy 2021, 12, 2367–2377. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Y.; Li, F.; Jiang, J. Extreme dynamic responses of mw-level wind turbine tower in the strong typhoon considering wind-rain loads. Math. Probl. Eng. 2013, 2013, 512530. [Google Scholar] [CrossRef]
- Ke, S.; Yu, W.; Wang, T.; Ge, Y. Aerodynamic performance and wind-induced effect of large-scale wind turbine system under yaw and wind-rain combination action. Renew. Energy 2019, 136, 235–253. [Google Scholar] [CrossRef]
- Keegan, M.H.; Nash, D.; Stack, M. Modelling rain drop impact on offshore wind turbine blades. In Proceedings of the ASME Turbo Expo 2012, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar]
- Cohan, A.C.; Arastoopour, H. Numerical simulation and analysis of the effect of rain and surface property on wind-turbine airfoil performance. Int. J. Multiph. Flow 2016, 81, 46–53. [Google Scholar] [CrossRef]
- Palanimuthu, K.; Mayilsamy, G.; Lee, S.R.; Jung, S.Y.; Joo, Y.H. Fault Ride-through for PMVG-based Wind Turbine System Using Coordinated Active and Reactive Power Control Strategy. IEEE Trans. Ind. Electron. 2022, 1–11. [Google Scholar] [CrossRef]
- Rahimilarki, R.; Gao, Z.; Jin, N.; Zhang, A. Convolutional neural network fault classification based on time-series analysis for benchmark wind turbine machine. Renew. Energy 2022, 185, 916–931. [Google Scholar] [CrossRef]
- Palanimuthu, K.; Kim, H.S.; Joo, Y.H. TS fuzzy sliding mode control for double-fed induction generator-based wind energy system with a membership function-dependent H∞-approach. Inf. Sci. 2022, 596, 73–92. [Google Scholar] [CrossRef]
- Subramaniyam, R.; Joo, Y.H. Memory-based ISMC design of DFIG-based wind turbine model via T-S fuzzy approach. IET Control Theory Appl. 2021, 15, 348–359. [Google Scholar] [CrossRef]
- Farkas, Z. Considering air density in wind power production. arXiv 2011, arXiv:1103.2198. [Google Scholar]
- Collins, J.; Parkes, J.; Tindal, A. Short term forecasting for utility-scale wind farms—The power model challenge. Wind. Eng. 2009, 33, 247–257. [Google Scholar] [CrossRef]
- Hersbach, H. The ERA5 Atmospheric Reanalysis. In Proceedings of the AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, December 2016; Volume 2016, p. NG33D–01. [Google Scholar]
- Ulazia, A.; Sáenz, J.; Ibarra-Berastegi, G.; González-Rojí, S.J.; Carreno-Madinabeitia, S. Global estimations of wind energy potential considering seasonal air density changes. Energy 2019, 187, 115938. [Google Scholar] [CrossRef]
- Wen, X.; Wang, J.; Fan, Q. Impact of Air Humidity on Wind Power Generator’s Output. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Banda Aceh, Indonesia, 26–27 September 2018; Volume 186, p. 012067. [Google Scholar]
- Thogersen, M. Modelling of the Variation of Air Density with Altitude through Pressure, Humidity and Temperature; EMD International A/S: Aalborg, Denmark, 2005. [Google Scholar]
- Masters, G.M. Renewable and Efficient Electric Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Shelquist, R. Equations-Air Density and Density Altitude. 2009. Available online: https://wahiduddin.net/calc/density_altitude.htm (accessed on 1 September 2022).
- Ashuri, T.; Martins, J.R.; Zaaijer, M.B.; van Kuik, G.A.; van Bussel, G.J. Aeroservoelastic design definition of a 20 MW common research wind turbine model. Wind Energy 2016, 19, 2071–2087. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Yatim, A.; Tan, C.W.; Saidur, R. A review of maximum power point tracking algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2012, 16, 3220–3227. [Google Scholar] [CrossRef]
- Keegan, M.H.; Nash, D.; Stack, M. On erosion issues associated with the leading edge of wind turbine blades. J. Phys. Appl. Phys. 2013, 46, 383001. [Google Scholar] [CrossRef]
- Chou, J.S.; Chiu, C.K.; Huang, I.K.; Chi, K.N. Failure analysis of wind turbine blade under critical wind loads. Eng. Fail. Anal. 2013, 27, 99–118. [Google Scholar] [CrossRef]
- Bartolomé, L.; Teuwen, J. Prospective challenges in the experimentation of the rain erosion on the leading edge of wind turbine blades. Wind Energy 2019, 22, 140–151. [Google Scholar] [CrossRef]
- Wu, Z.; Cao, Y.; Nie, S.; Yang, Y. Effects of rain on vertical axis wind turbine performance. J. Wind. Eng. Ind. Aerodyn. 2017, 170, 128–140. [Google Scholar] [CrossRef]
- Bech, J.I.; Johansen, N.F.J.; Madsen, M.B.; Hannesdóttir, Á.; Hasager, C.B. Experimental study on the effect of drop size in rain erosion test and on lifetime prediction of wind turbine blades. Renew. Energy 2022, 197, 776–789. [Google Scholar] [CrossRef]
- Anh, N.T.; Duc, N.H. A method to analyze power output of vertical-axis wind turbines under rain. Vietnam. J. Sci. Technol. 2018, 56, 761–771. [Google Scholar]
- Anh, N.T.; Duc, N.H. A study on power output of horizontal-axis wind turbines under rain. Vietnam. J. Sci. Technol. 2019, 57, 356. [Google Scholar] [CrossRef]
- Verma, A.S.; Castro, S.G.; Jiang, Z.; Teuwen, J.J. Numerical investigation of rain droplet impact on offshore wind turbine blades under different rainfall conditions: A parametric study. Compos. Struct. 2020, 241, 112096. [Google Scholar] [CrossRef]
- Anh, N.T.; Duc, N.H. Effect Analysis of Performance and Pitch Controller Operation for Wind Turbine under Rain. GMSARN Int. J. 2022, 16, 339–347. [Google Scholar]
- Marshall, J.S. The distribution of raindrops with size. J. Meteor. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Seo, S. Run or walk in the rain?(orthogonal projected area of ellipsoid). IOSR J. Appl. Phys. 2015, 7, 139–150. [Google Scholar]
- Tiwari, R.; Babu, N.R. Recent developments of control strategies for wind energy conversion system. Renew. Sustain. Energy Rev. 2016, 66, 268–285. [Google Scholar] [CrossRef]
- Navarrete, E.C.; Perea, M.T.; Correa, J.J.; Serrano, R.C.; Moreno, G.R. Expert control systems implemented in a pitch control of wind turbine: A review. IEEE Access 2019, 7, 13241–13259. [Google Scholar] [CrossRef]
- Gambier, A. Pitch Control of Three Bladed Large Wind Energy Converters—A Review. Energies 2021, 14, 8083. [Google Scholar] [CrossRef]
- Tang, X.; Yin, M.; Shen, C.; Xu, Y.; Dong, Z.Y.; Zou, Y. Active power control of wind turbine generators via coordinated rotor speed and pitch angle regulation. IEEE Trans. Sustain. Energy 2018, 10, 822–832. [Google Scholar] [CrossRef]
- Njiri, J.G.; Söffker, D. State-of-the-art in wind turbine control: Trends and challenges. Renew. Sustain. Energy Rev. 2016, 60, 377–393. [Google Scholar] [CrossRef]
- Cho, S.; Choi, M.; Gao, Z.; Moan, T. Fault detection and diagnosis of a blade pitch system in a floating wind turbine based on Kalman filters and artificial neural networks. Renew. Energy 2021, 169, 1–13. [Google Scholar] [CrossRef]
- Pan, L.; Wang, X. Variable pitch control on direct-driven PMSG for offshore wind turbine using Repetitive-TS fuzzy PID control. Renew. Energy 2020, 159, 221–237. [Google Scholar] [CrossRef]
- Sierra-Garcia, J.E.; Santos, M.; Pandit, R. Wind turbine pitch reinforcement learning control improved by PID regulator and learning observer. Eng. Appl. Artif. Intell. 2022, 111, 104769. [Google Scholar] [CrossRef]
- Pan, L.; Xiong, Y.; Zhu, Z.; Wang, L. Research on variable pitch control strategy of direct-driven offshore wind turbine using KELM wind speed soft sensor. Renew. Energy 2022, 184, 1002–1017. [Google Scholar] [CrossRef]
- Ossmann, D.; Seiler, P.; Milliren, C.; Danker, A. Field testing of multi-variable individual pitch control on a utility-scale wind turbine. Renew. Energy 2021, 170, 1245–1256. [Google Scholar] [CrossRef]
- Tang, S.; Tian, D.; Wu, X.; Huang, M.; Deng, Y. Wind turbine load reduction based on 2DoF robust individual pitch control. Renew. Energy 2022, 183, 28–40. [Google Scholar] [CrossRef]
- Li, J.; Wang, S. Dual multivariable model-free adaptive individual pitch control for load reduction in wind turbines with actuator faults. Renew. Energy 2021, 174, 293–304. [Google Scholar] [CrossRef]
- Chang-Chien, L.R.; Sun, C.C.; Yeh, Y.J. Modeling of wind farm participation in AGC. IEEE Trans. Power Syst. 2013, 29, 1204–1211. [Google Scholar] [CrossRef]
- Yang, J.; Zheng, S.; Song, D.; Su, M.; Yang, X.; Joo, Y.H. Data-driven modeling for fatigue loads of large-scale wind turbines under active power regulation. Wind Energy 2021, 24, 558–572. [Google Scholar] [CrossRef]
- Chang-Chien, L.R.; Lin, W.T.; Yin, Y.C. Enhancing frequency response control by DFIGs in the high wind penetrated power systems. IEEE Trans. Power Syst. 2010, 26, 710–718. [Google Scholar] [CrossRef]
- Gu, W.; Yin, M.; Chen, Z.; Zou, Y. Active Power Control of Wind Turbine Generators Based on the Maximum Disturbance Range of Nonpitch Regulation. IEEE Trans. Sustain. Energy 2021, 13, 170–181. [Google Scholar] [CrossRef]
- Yang, J.; Fang, L.; Song, D.; Su, M.; Yang, X.; Huang, L.; Joo, Y.H. Review of control strategy of large horizontal-axis wind turbines yaw system. Wind Energy 2021, 24, 97–115. [Google Scholar] [CrossRef]
- Yang, J.; Wang, L.; Song, D.; Huang, C.; Huang, L.; Wang, J. Incorporating environmental impacts into zero-point shifting diagnosis of wind turbines yaw angle. Energy 2022, 238, 121762. [Google Scholar] [CrossRef]
- Sun, J.; Chen, Z.; Yu, H.; Gao, S.; Wang, B.; Ying, Y.; Sun, Y.; Qian, P.; Zhang, D.; Si, Y. Quantitative evaluation of yaw-misalignment and aerodynamic wake induced fatigue loads of offshore Wind turbines. Renew. Energy 2022, 199, 71–86. [Google Scholar] [CrossRef]
- Shu, T.; Song, D.; Joo, Y.H. Decentralised optimisation for large offshore wind farms using a sparsified wake directed graph. Appl. Energy 2022, 306, 117986. [Google Scholar] [CrossRef]
- Ahmad, T.; Basit, A.; Anwar, J.; Coupiac, O.; Kazemtabrizi, B.; Matthews, P.C. Fast processing intelligent wind farm controller for production maximisation. Energies 2019, 12, 544. [Google Scholar] [CrossRef]
- Song, D.; Fan, X.; Yang, J.; Liu, A.; Chen, S.; Joo, Y.H. Power extraction efficiency optimization of horizontal-axis wind turbines through optimizing control parameters of yaw control systems using an intelligent method. Appl. Energy 2018, 224, 267–279. [Google Scholar] [CrossRef]
- Song, D.; Li, Z.; Wang, L.; Jin, F.; Huang, C.; Xia, E.; Rizk-Allah, R.M.; Yang, J.; Su, M.; Joo, Y.H. Energy capture efficiency enhancement of wind turbines via stochastic model predictive yaw control based on intelligent scenarios generation. Appl. Energy 2022, 312, 118773. [Google Scholar] [CrossRef]
- Chu, X. Two degrees of freedom cooperative suspension control for maglev wind yaw system. IEEE/ASME Trans. Mechatronics 2021, 3, 1425–1435. [Google Scholar] [CrossRef]
- Solomin, E.V.; Terekhin, A.A.; Martyanov, A.S.; Shishkov, A.N.; Kovalyov, A.A.; Ismagilov, D.R.; Ryavkin, G.N. Horizontal axis wind turbine yaw differential error reduction approach. Energy Convers. Manag. 2022, 254, 115255. [Google Scholar] [CrossRef]
- Mesemanolis, A.; Mademlis, C. Combined maximum power point and yaw control strategy for a horizontal axis wind turbine. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 1704–1710. [Google Scholar]
- Liu, Z.; Yao, Q.; Ma, B. Optimal Control Strategy of Fatigue-Oriented Wind Turbine Yaw System. In Proceedings of the 16th Annual Conference of China Electrotechnical Society; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1111–1122. [Google Scholar]
- Cossu, C. Wake redirection at higher axial induction. Wind Energy Sci. 2021, 6, 377–388. [Google Scholar] [CrossRef]
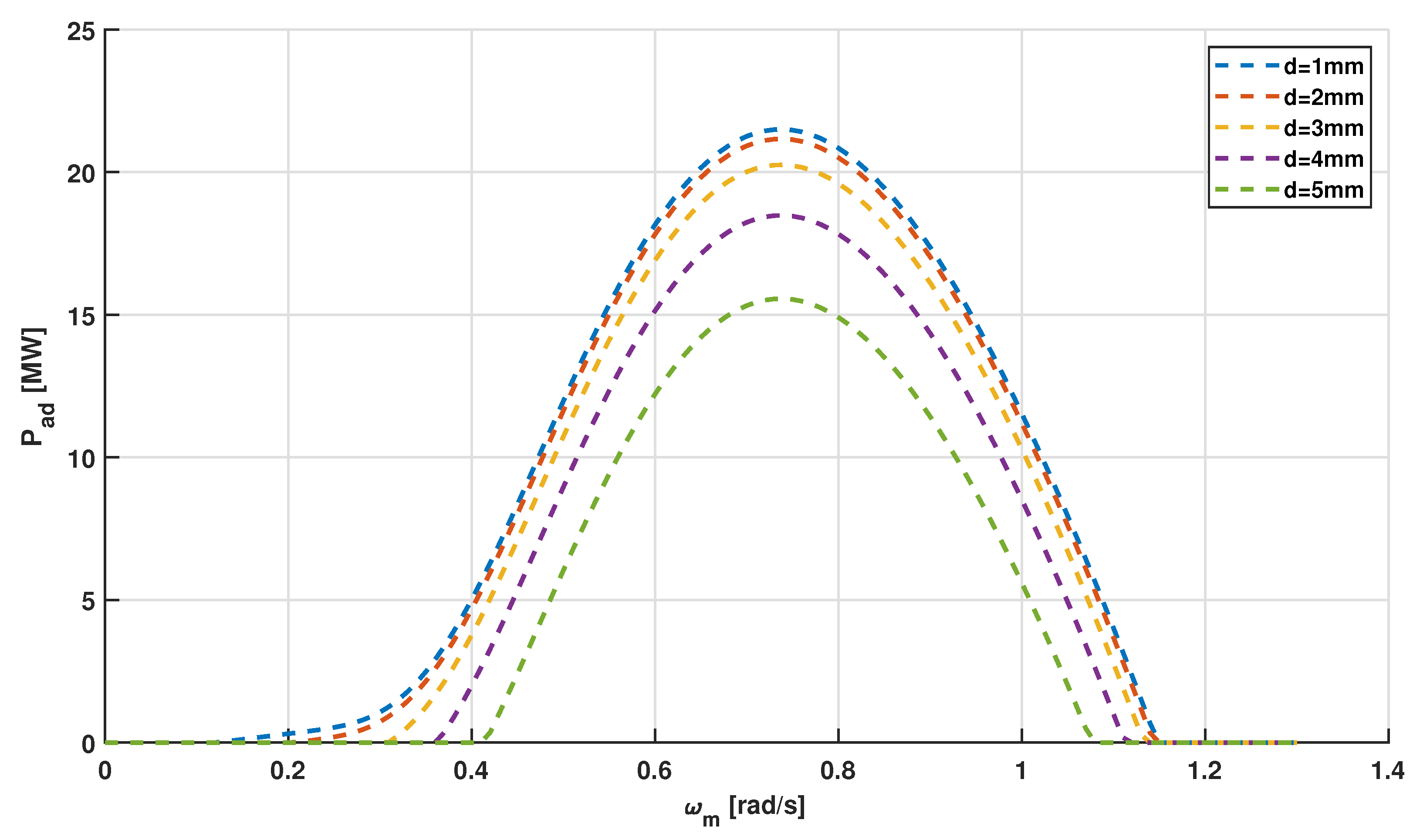
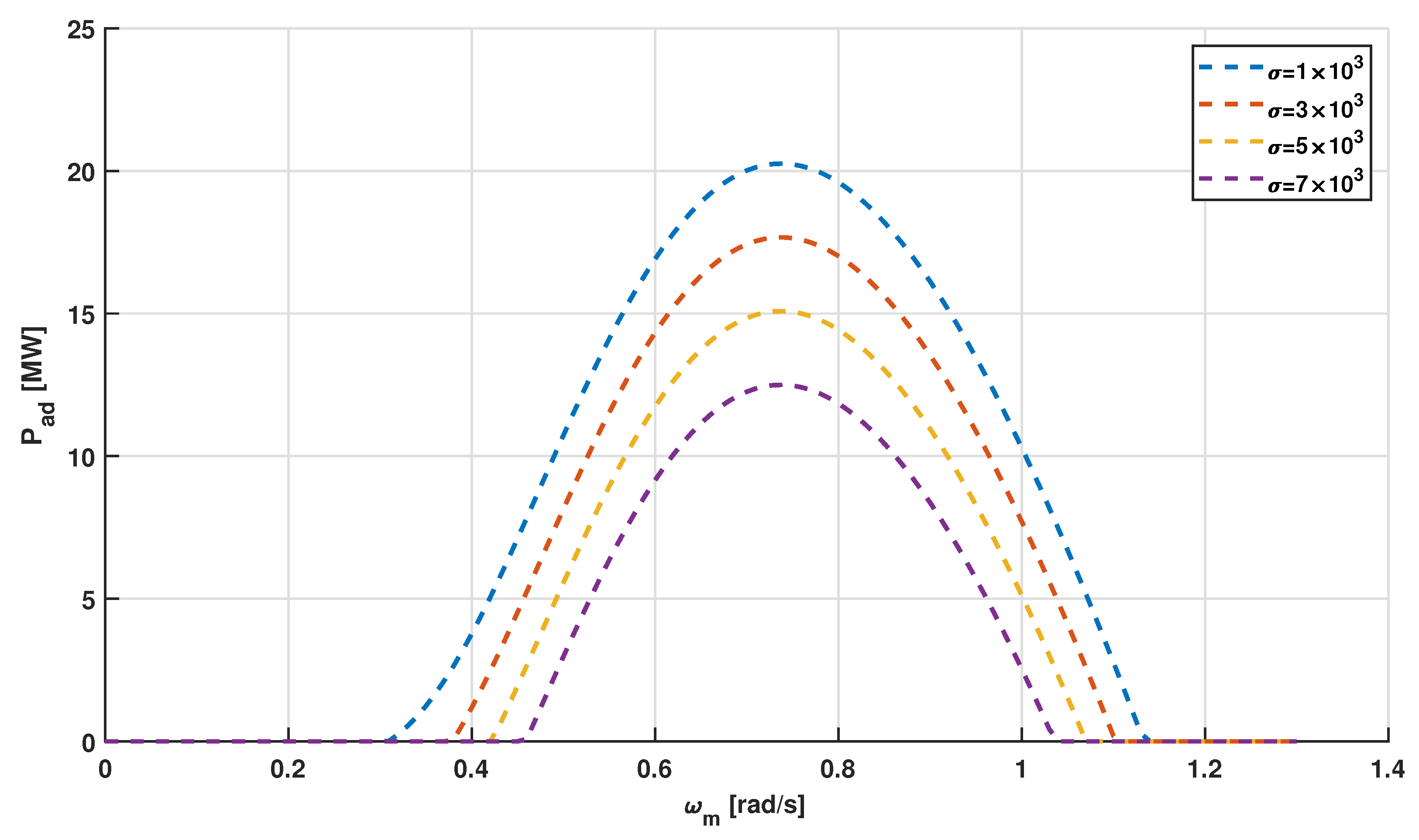
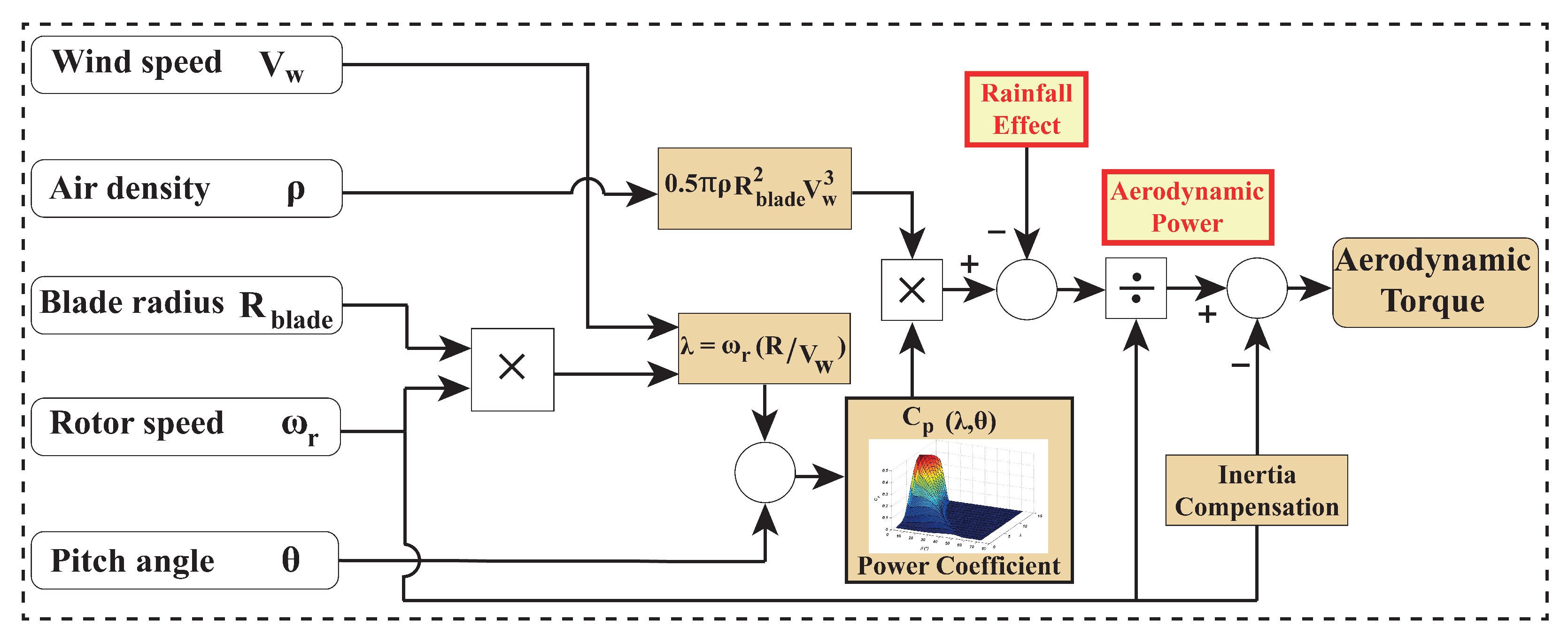
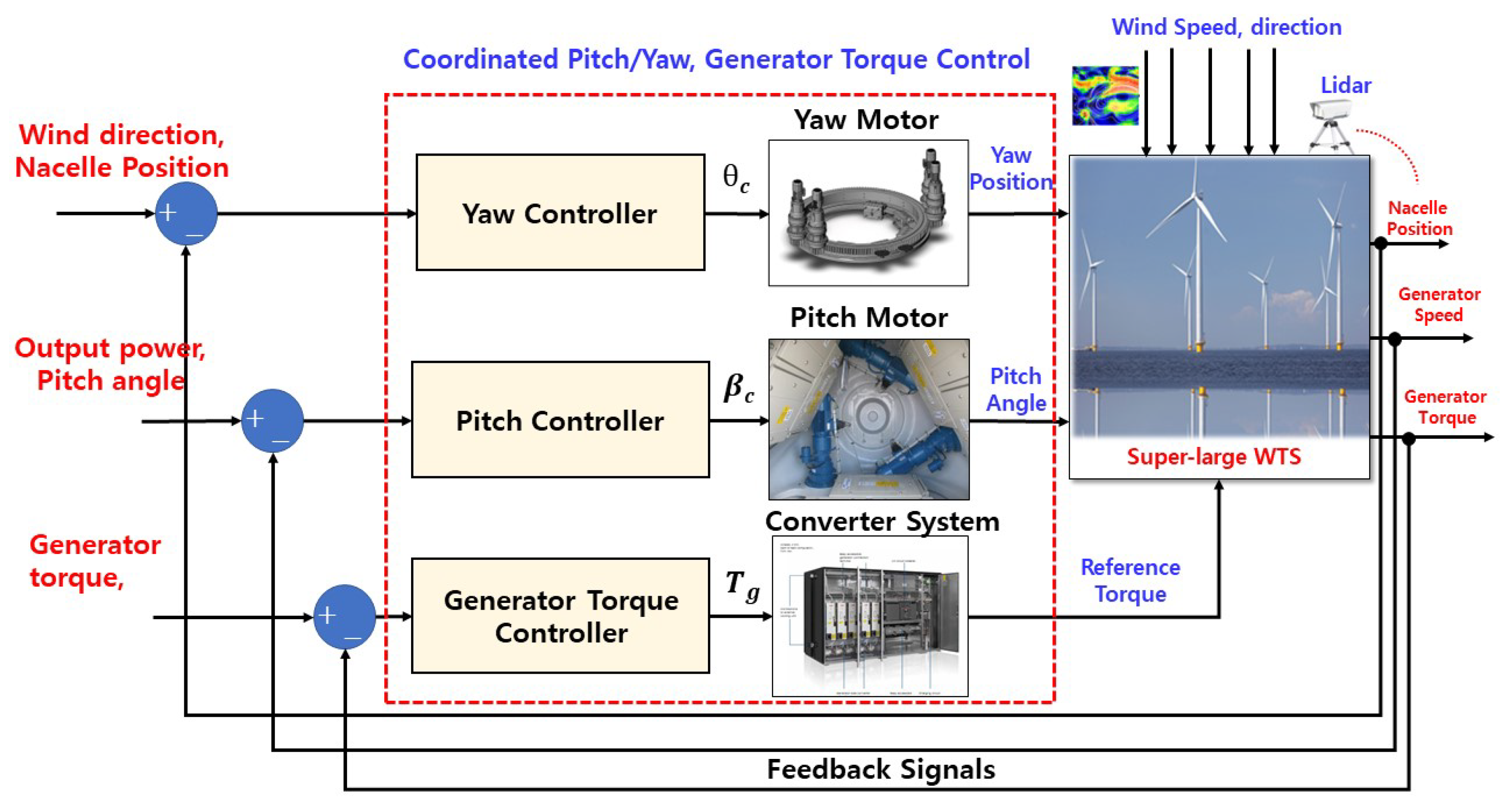
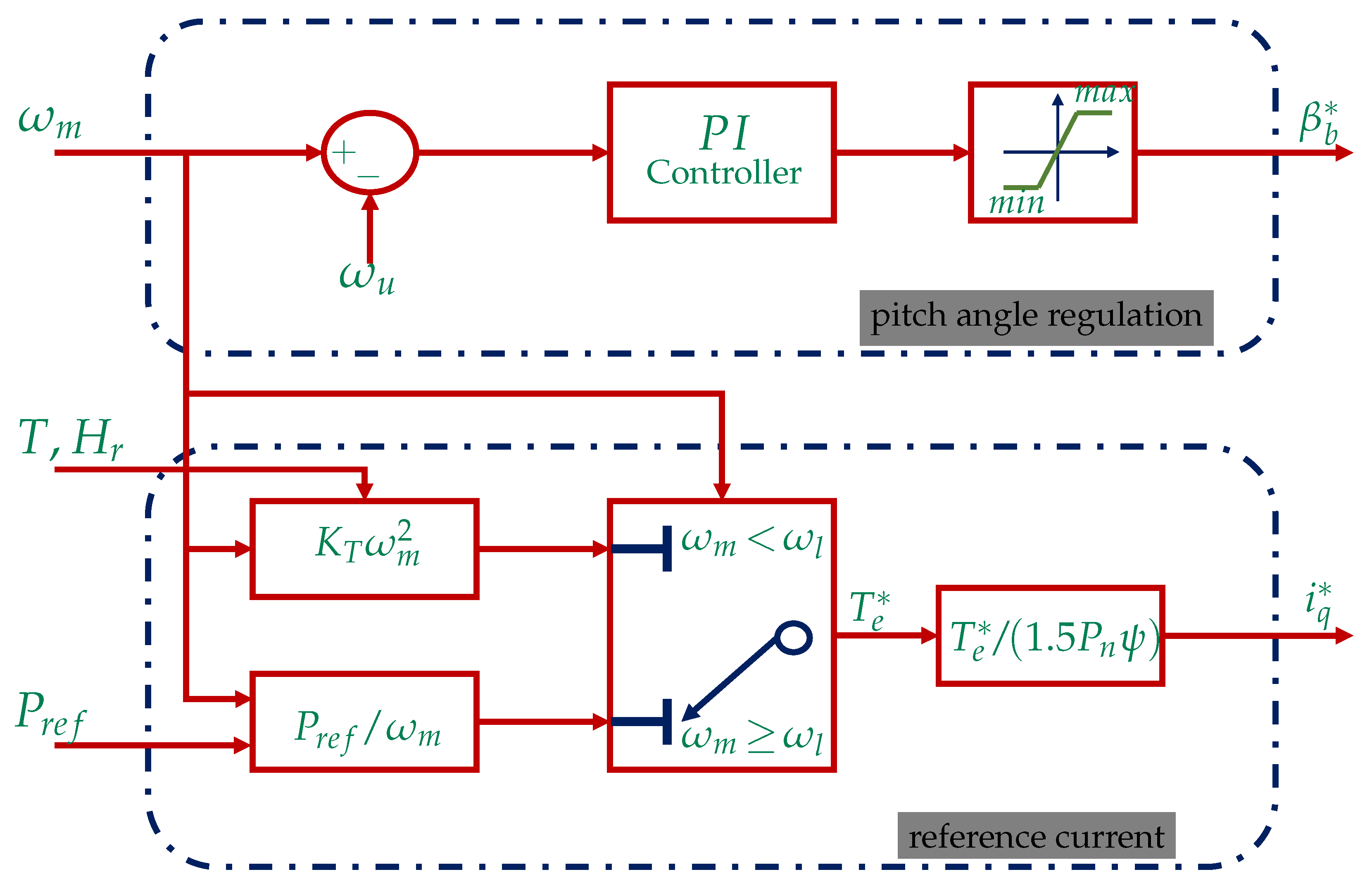
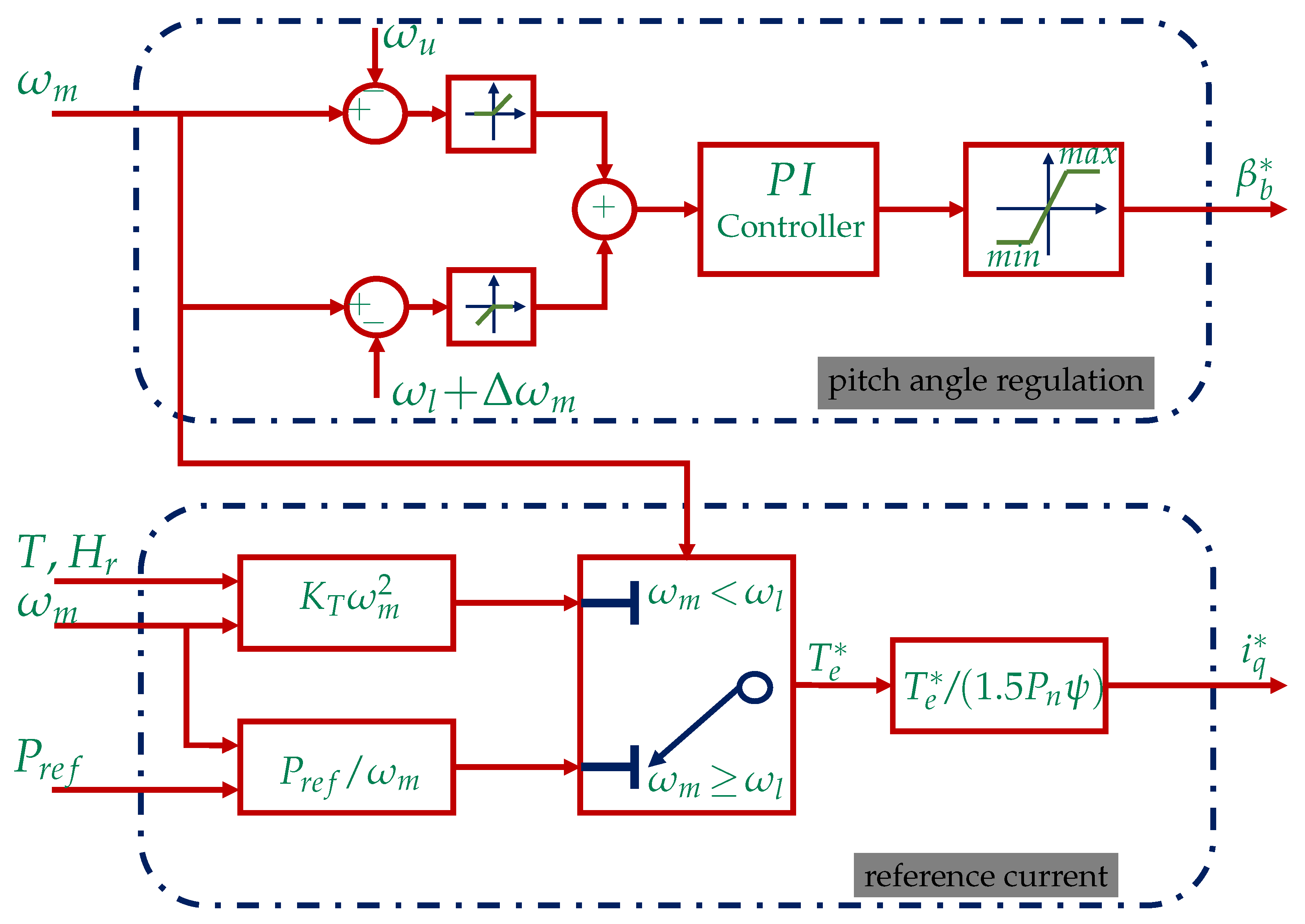
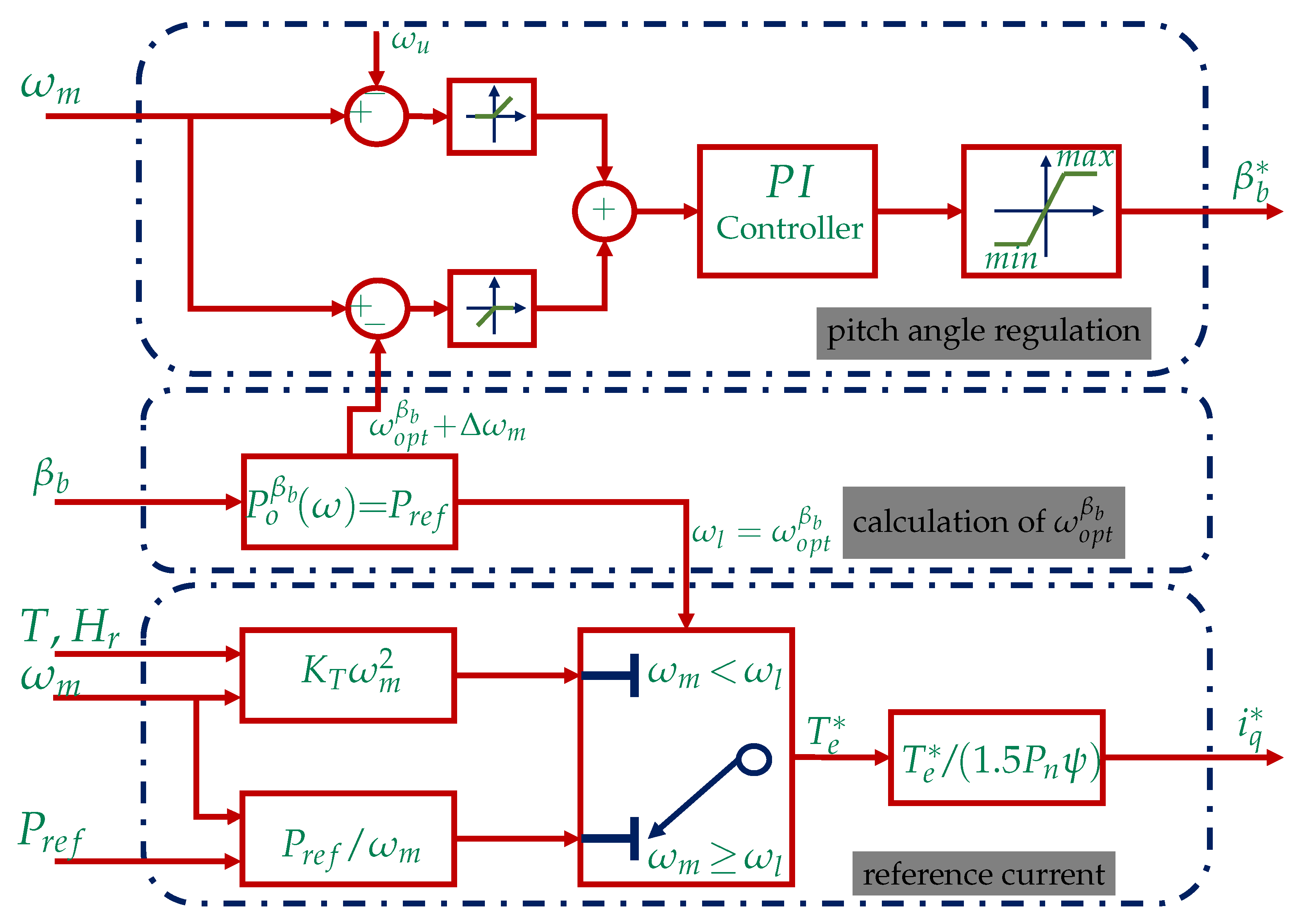
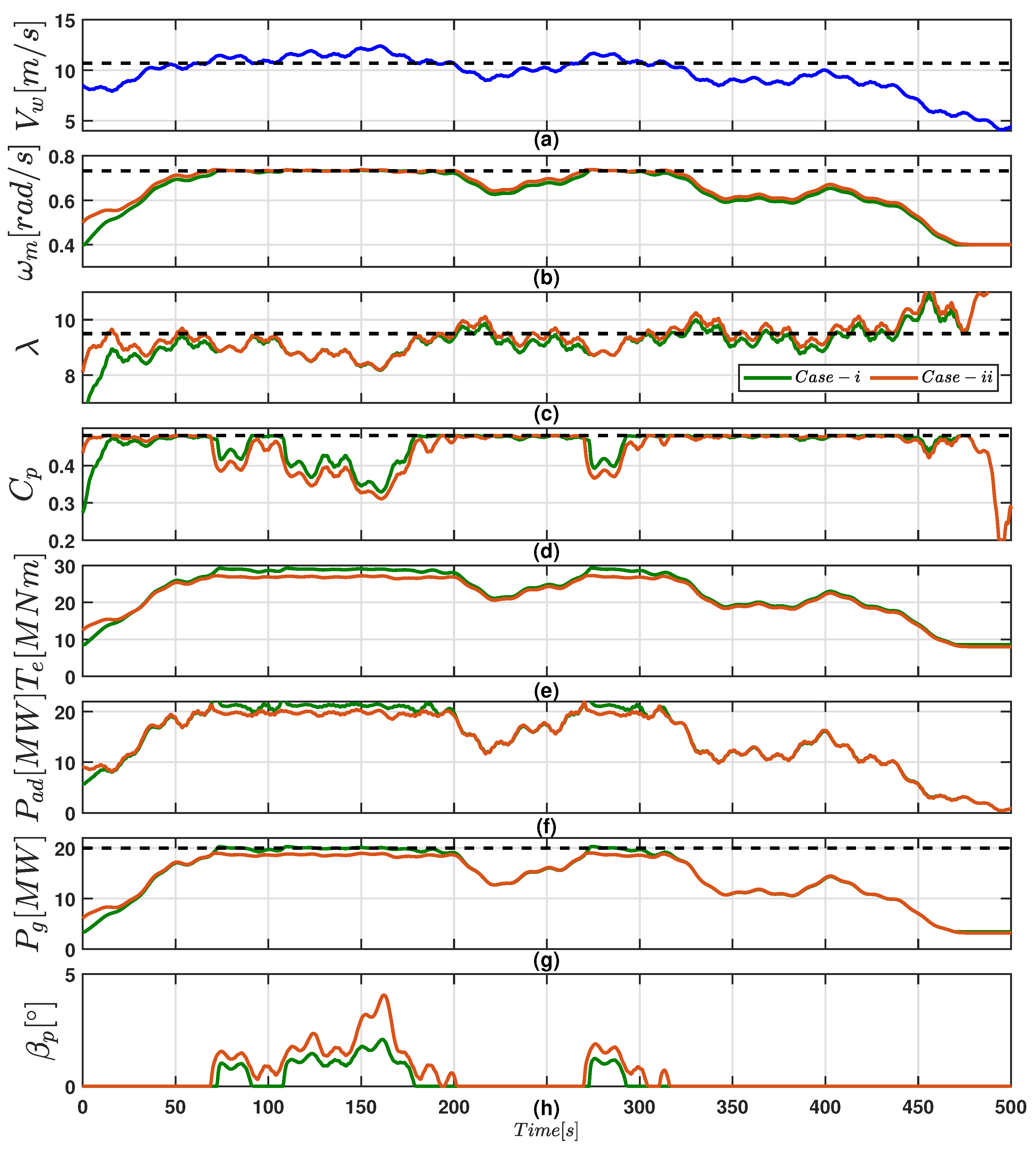
| Parameter | Description | Value |
|---|---|---|
| Grid parameters | ||
| (V) | RMS Grid voltage | 6600 |
| (m) | Filter resistance | 1750 |
| (mH) | Filter inductance | 2.1 |
| Aerodynamic parameters | ||
| (MW) | Rated aerodynamic mechanical power | 21.2 |
| (m) | Rotor blade radius | 138 |
| Optimal tip-speed ratio | 9.5085 | |
| (m/s) | Rated wind speed | 10.715 |
| Maximum power coefficient | 0.48 | |
| (Nm s/rad) | Damping coefficient | 200 |
| J (Mnm) | Net inertia of rotating shaft | 4.872 |
| PMSG parameters | ||
| (MW) | Rated stator power | 20 |
| Stator poles | 160 | |
| (Wb) | Stator magnetic flux | 93 |
| (mH) | Stator inductance | 27.49 |
| (m) | Stator resistance | 44.25 |
| (V) | Induced voltage in RMS | 6800 |
| Classification | Light Rain | Moderate Rain | Heavy Rain | Rainstorm |
|---|---|---|---|---|
| Rain intensity (mm/h) | 2, 5 | 8 | 16 | 32 |
| Classification | Heavy rainstorm | Heavy rainstorm | Heavy rainstorm | Heavy rainstorm |
| (weak) | (moderate) | (strong) | (extreme) | |
| Rain intensity (mm/h) | 64 | 100 | 200 | 709, 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palanimuthu, K.; Mayilsamy, G.; Basheer, A.A.; Lee, S.-R.; Song, D.; Joo, Y.H. A Review of Recent Aerodynamic Power Extraction Challenges in Coordinated Pitch, Yaw, and Torque Control of Large-Scale Wind Turbine Systems. Energies 2022, 15, 8161. https://doi.org/10.3390/en15218161
Palanimuthu K, Mayilsamy G, Basheer AA, Lee S-R, Song D, Joo YH. A Review of Recent Aerodynamic Power Extraction Challenges in Coordinated Pitch, Yaw, and Torque Control of Large-Scale Wind Turbine Systems. Energies. 2022; 15(21):8161. https://doi.org/10.3390/en15218161
Chicago/Turabian StylePalanimuthu, Kumarasamy, Ganesh Mayilsamy, Ameerkhan Abdul Basheer, Seong-Ryong Lee, Dongran Song, and Young Hoon Joo. 2022. "A Review of Recent Aerodynamic Power Extraction Challenges in Coordinated Pitch, Yaw, and Torque Control of Large-Scale Wind Turbine Systems" Energies 15, no. 21: 8161. https://doi.org/10.3390/en15218161
APA StylePalanimuthu, K., Mayilsamy, G., Basheer, A. A., Lee, S.-R., Song, D., & Joo, Y. H. (2022). A Review of Recent Aerodynamic Power Extraction Challenges in Coordinated Pitch, Yaw, and Torque Control of Large-Scale Wind Turbine Systems. Energies, 15(21), 8161. https://doi.org/10.3390/en15218161








