Steady-State Analysis and Optimal Design of an LLC Resonant Converter Considering Internal Loss Resistance
Abstract
1. Introduction
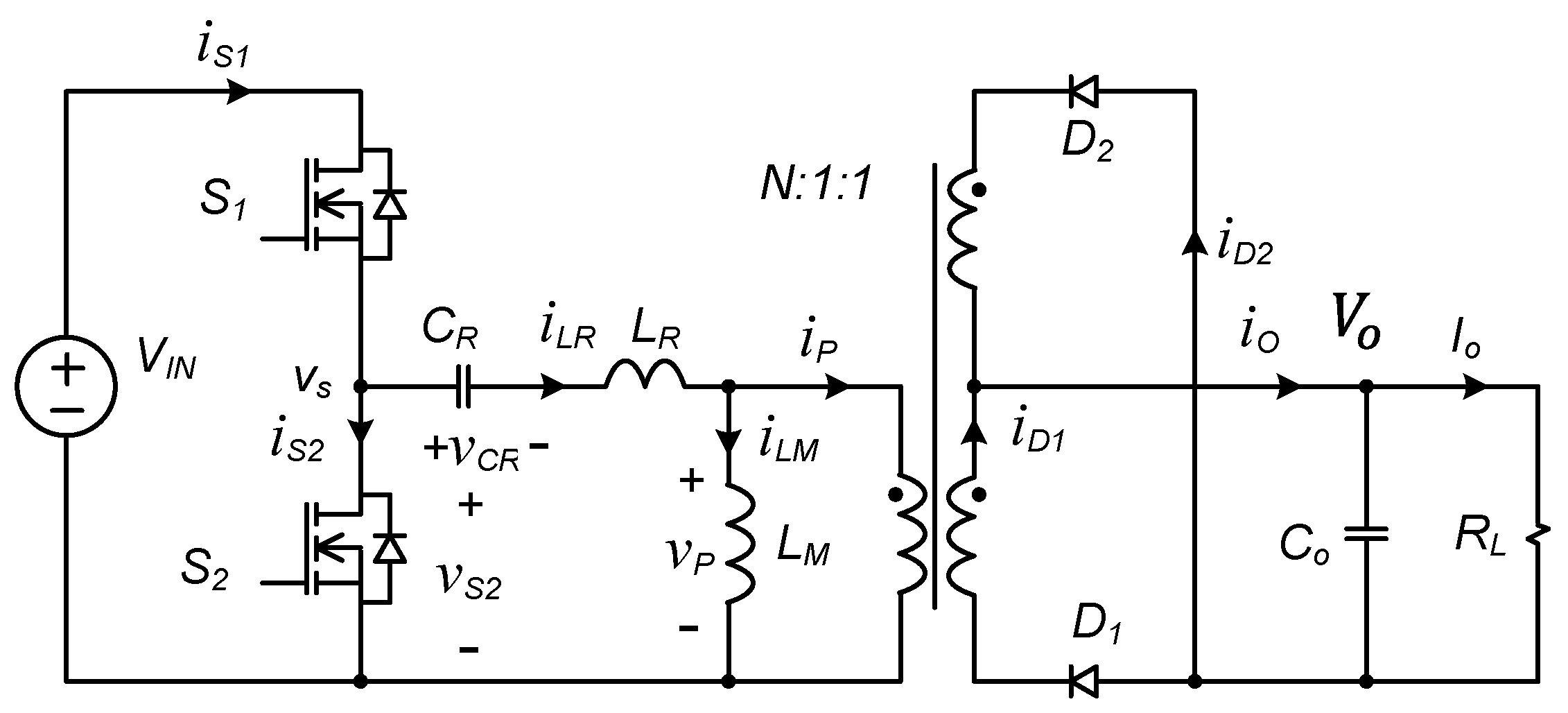
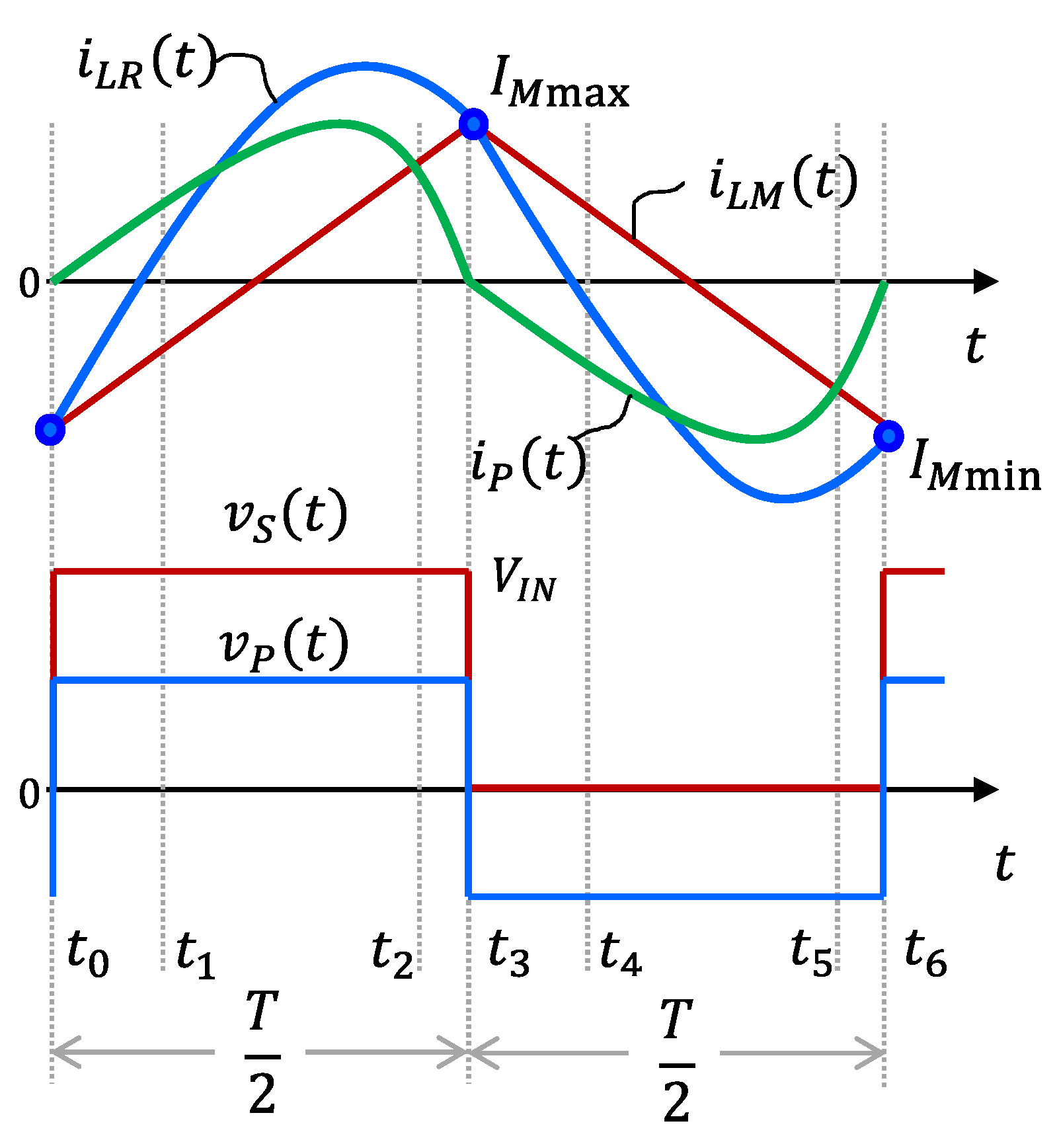
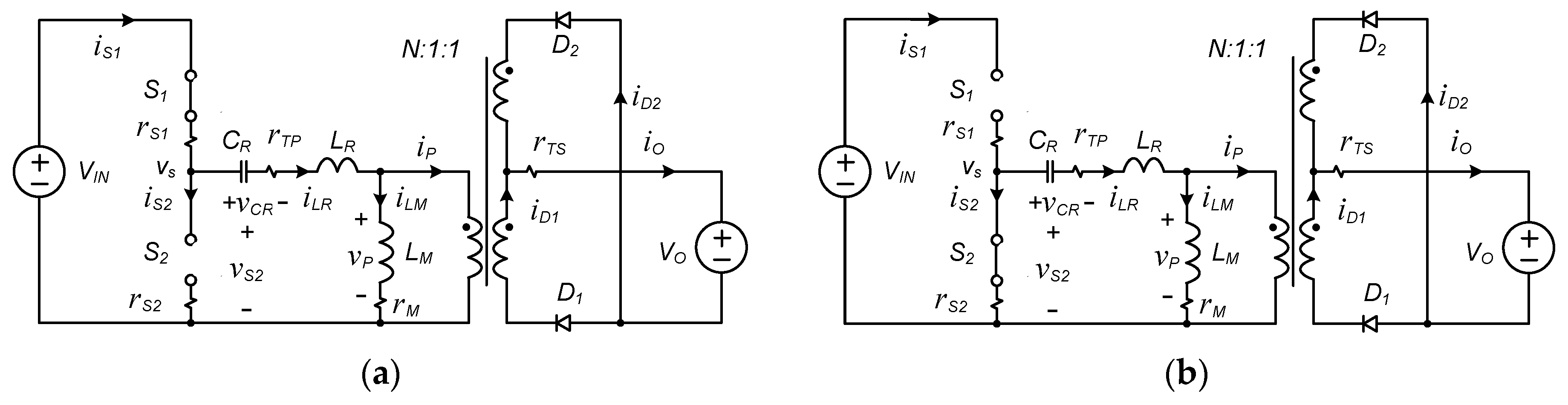
2. Steady-State Analysis of LLC Resonant Converter
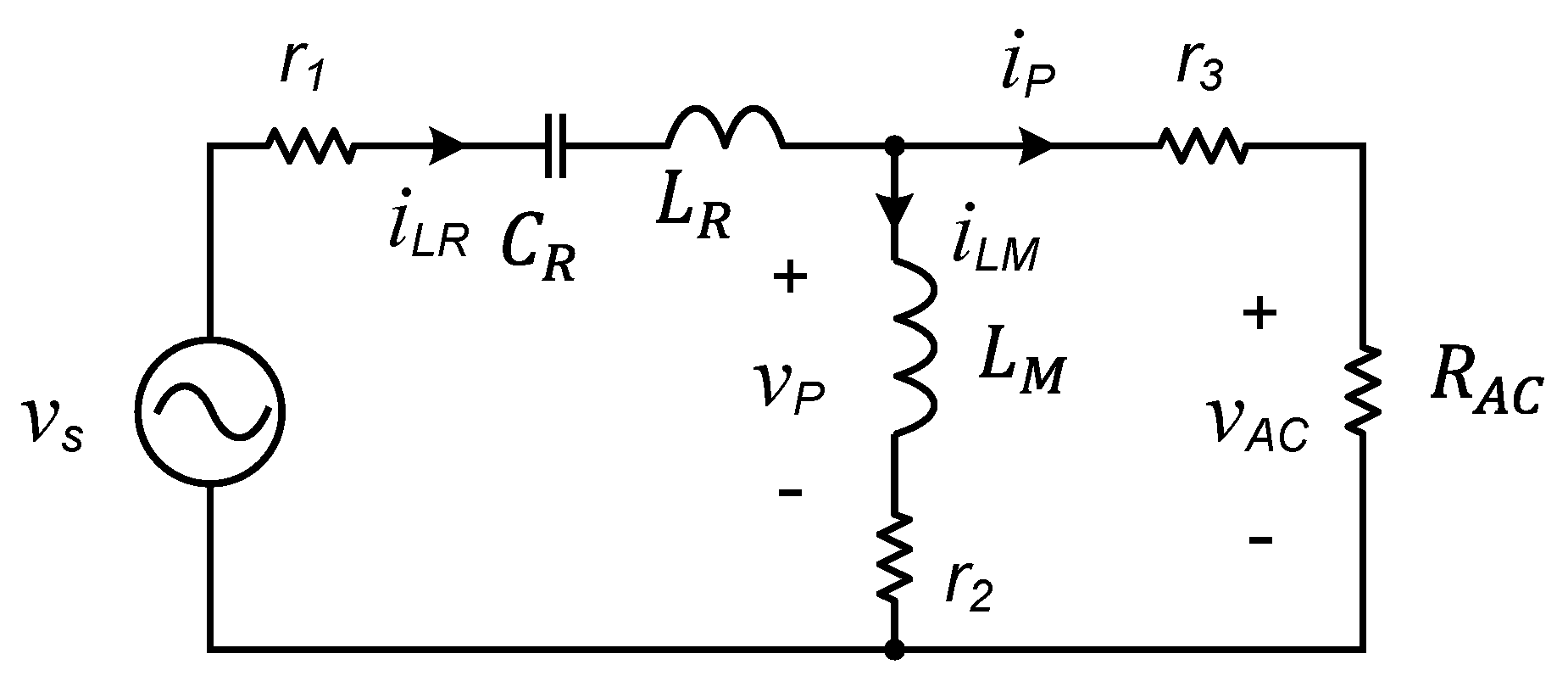
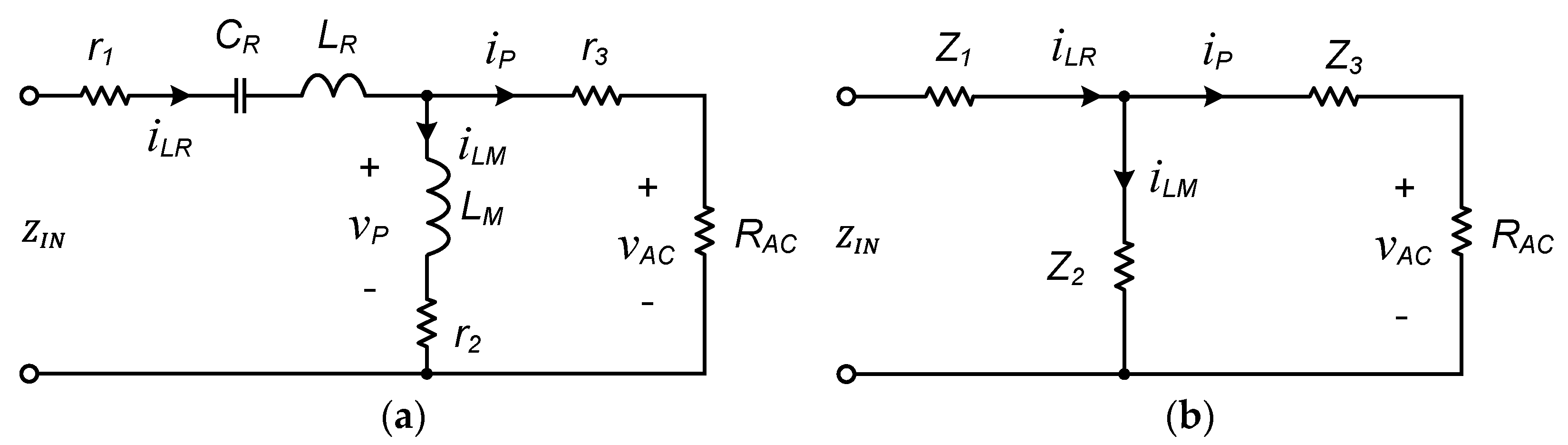
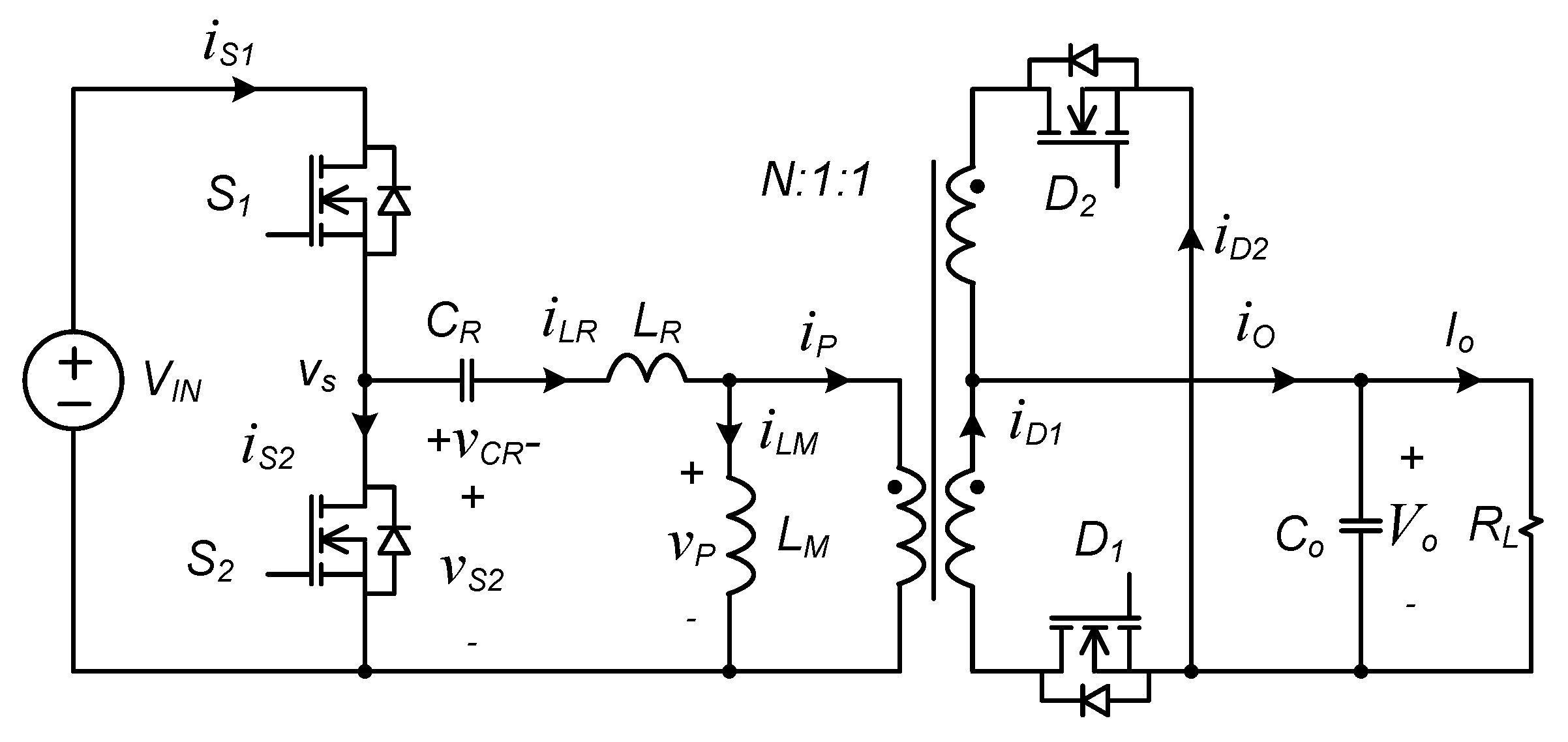
2.1. AC Equivalent Circuit
2.2. DC Conversion Ratio
- denotes the characteristic impedance;
- denotes the magnetizing inductance;
- denotes the resonant inductance;
- denotes the inductance ratio;
- denotes the resonant capacitor;
- denotes the resonant angular frequency;
- denotes the angular normalized frequency;
- denotes the angular switching frequency.
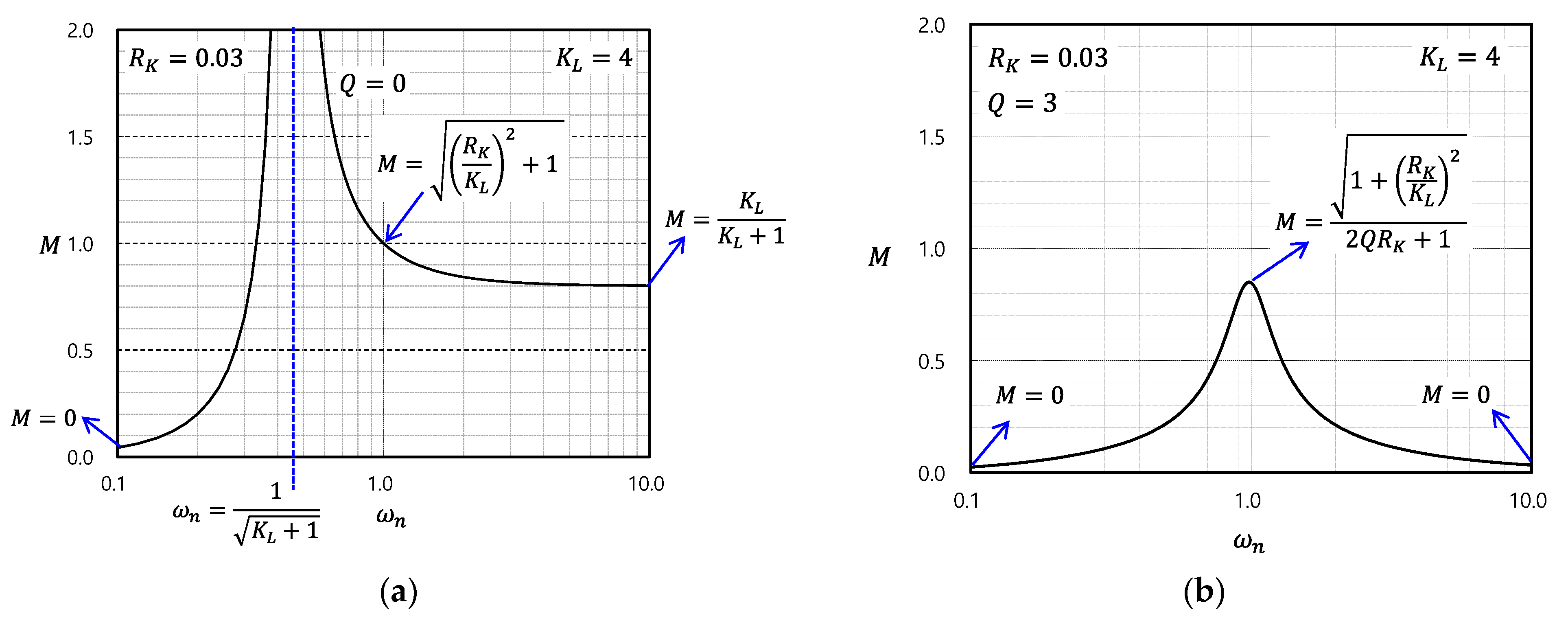
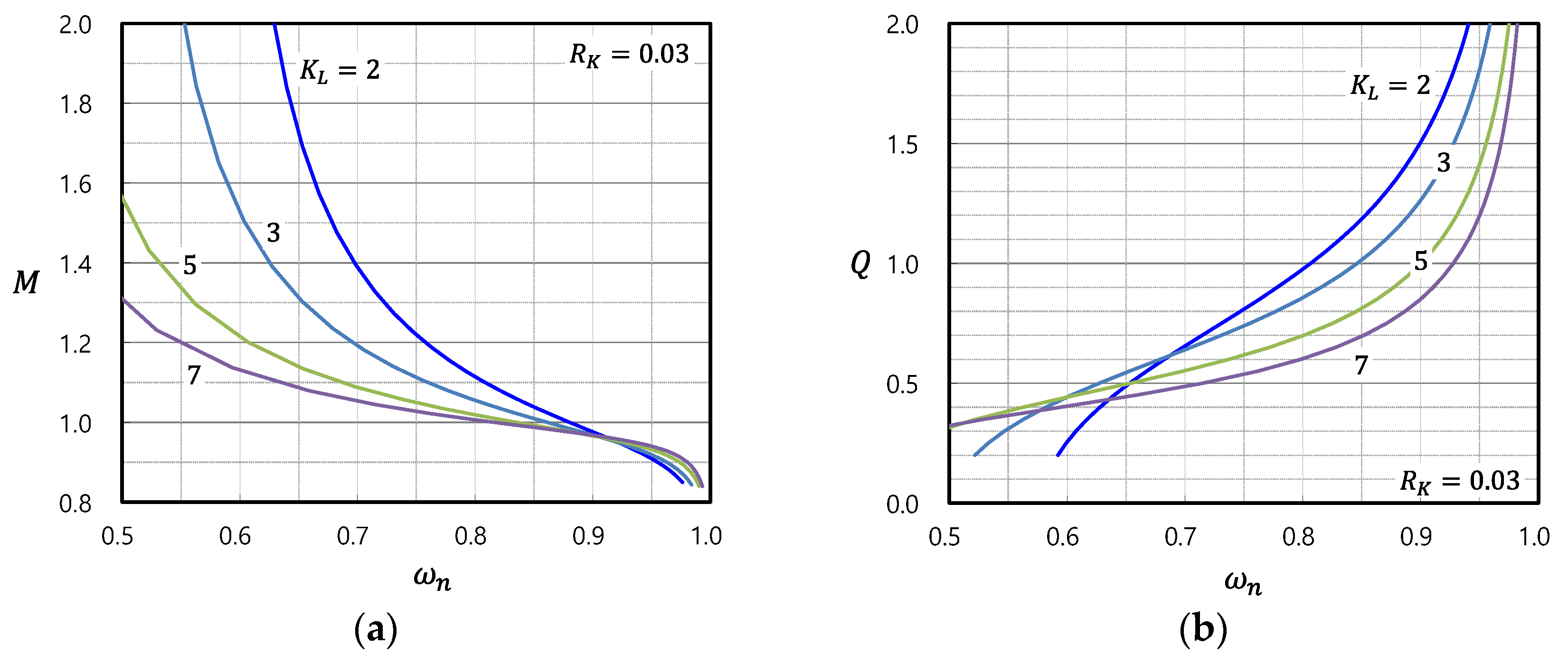
2.3. Frequency Characteristics of Voltage Gain
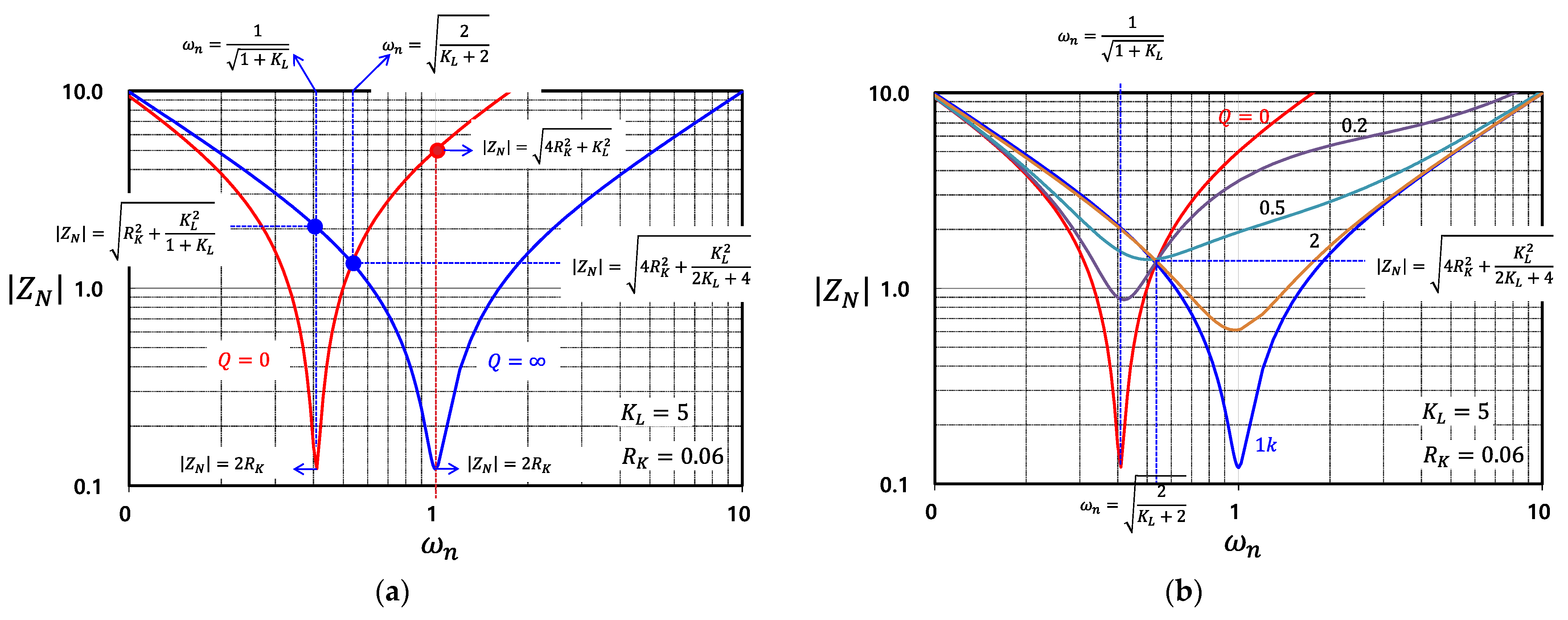
2.4. Input Impedance Characteristics
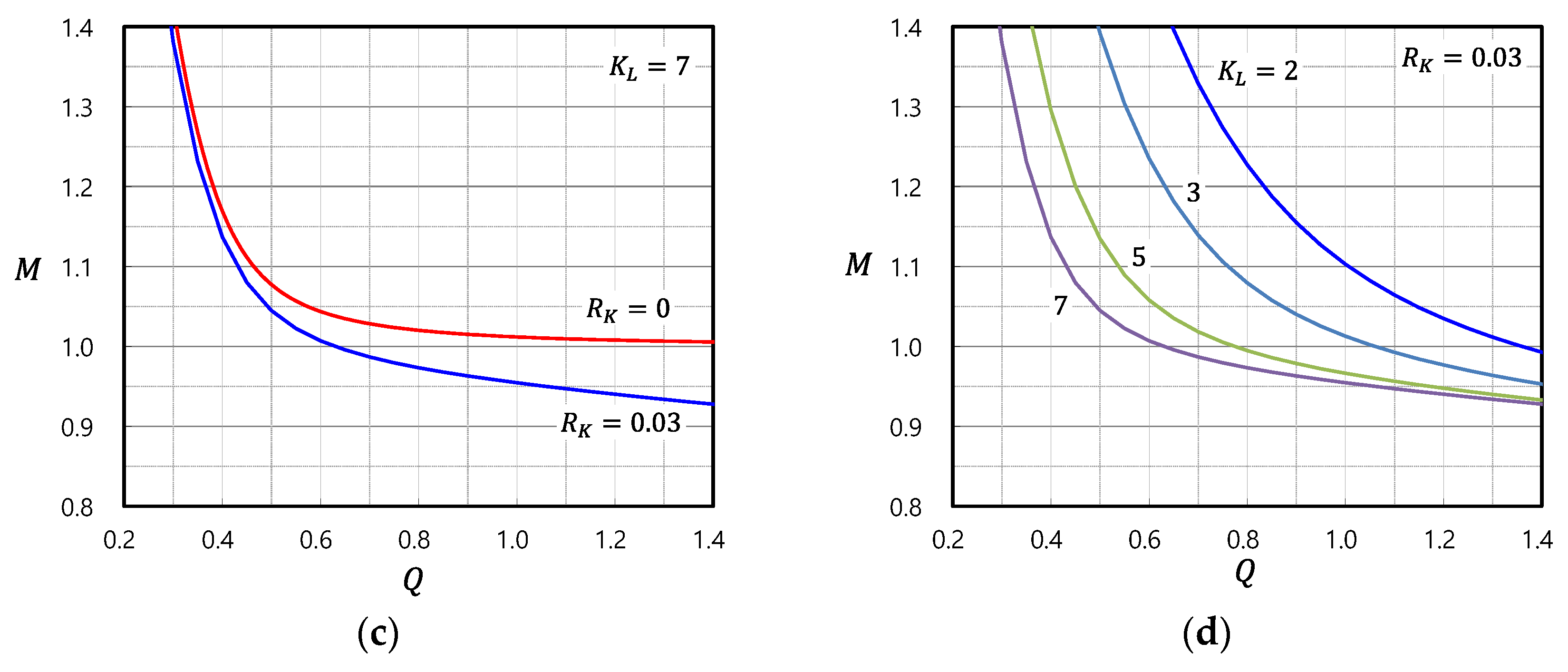
3. Optimal Design of LLC Resonant Converter
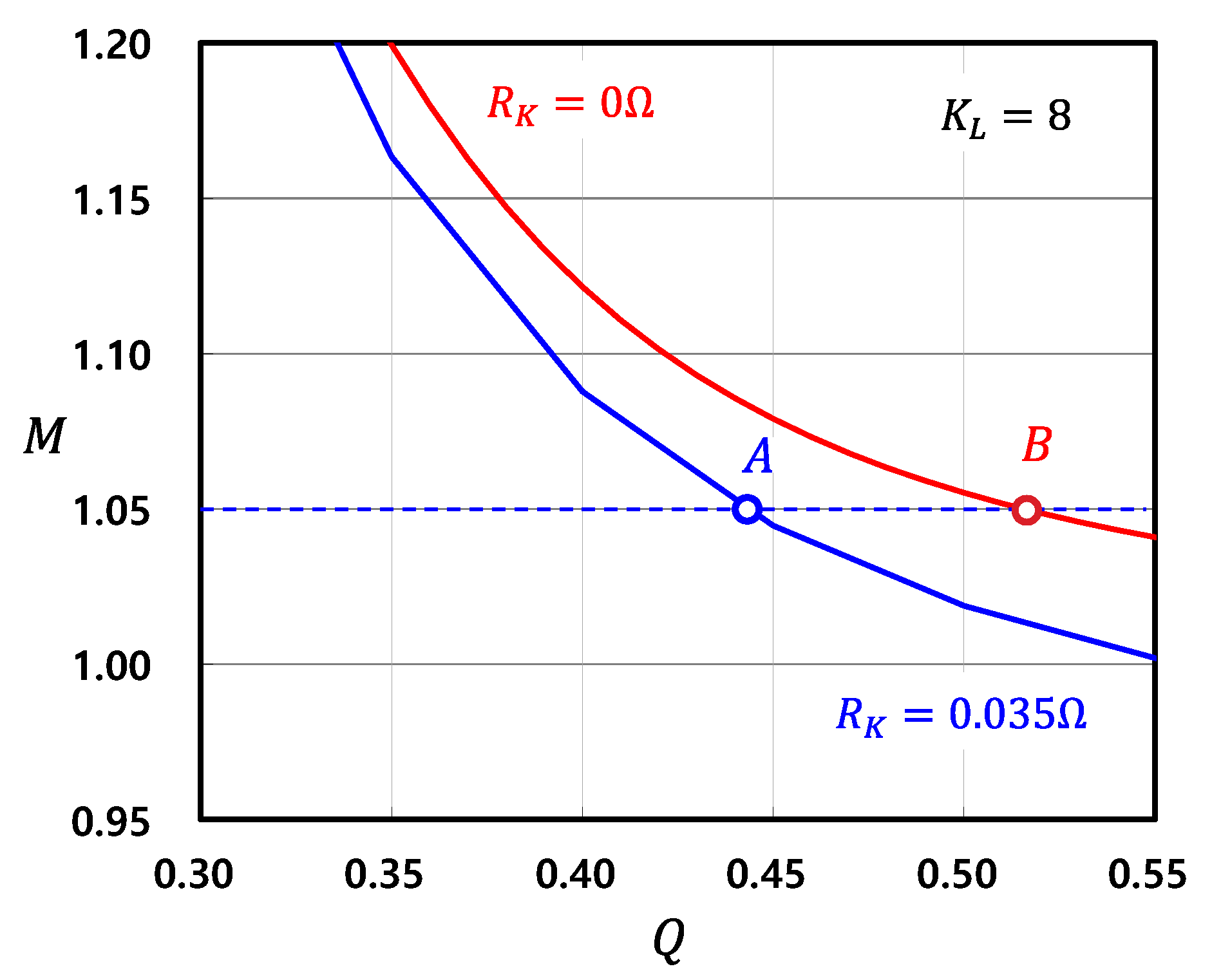
3.1. Optimal Design Process
3.2. Circuit Simulation Results and Comparison
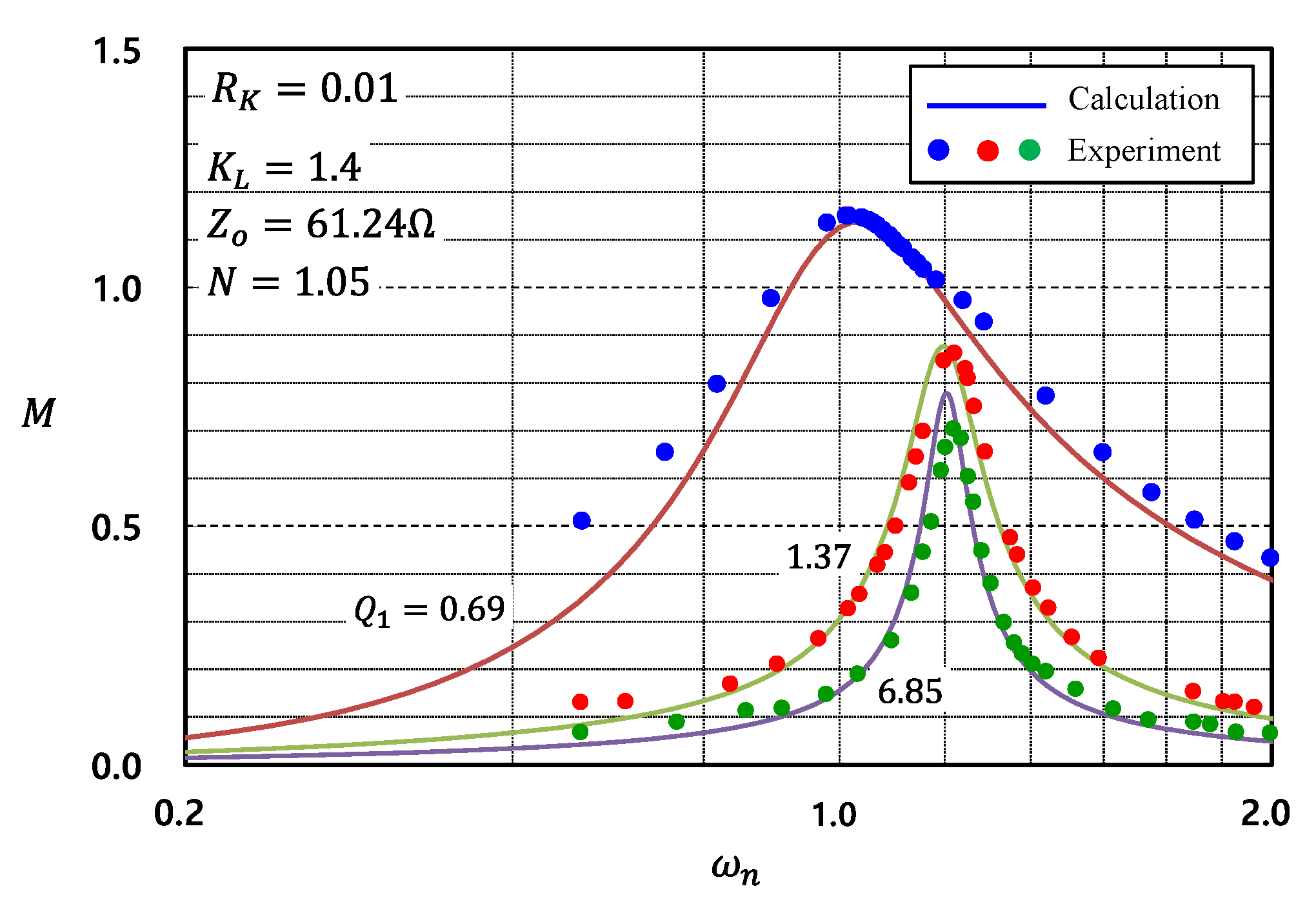
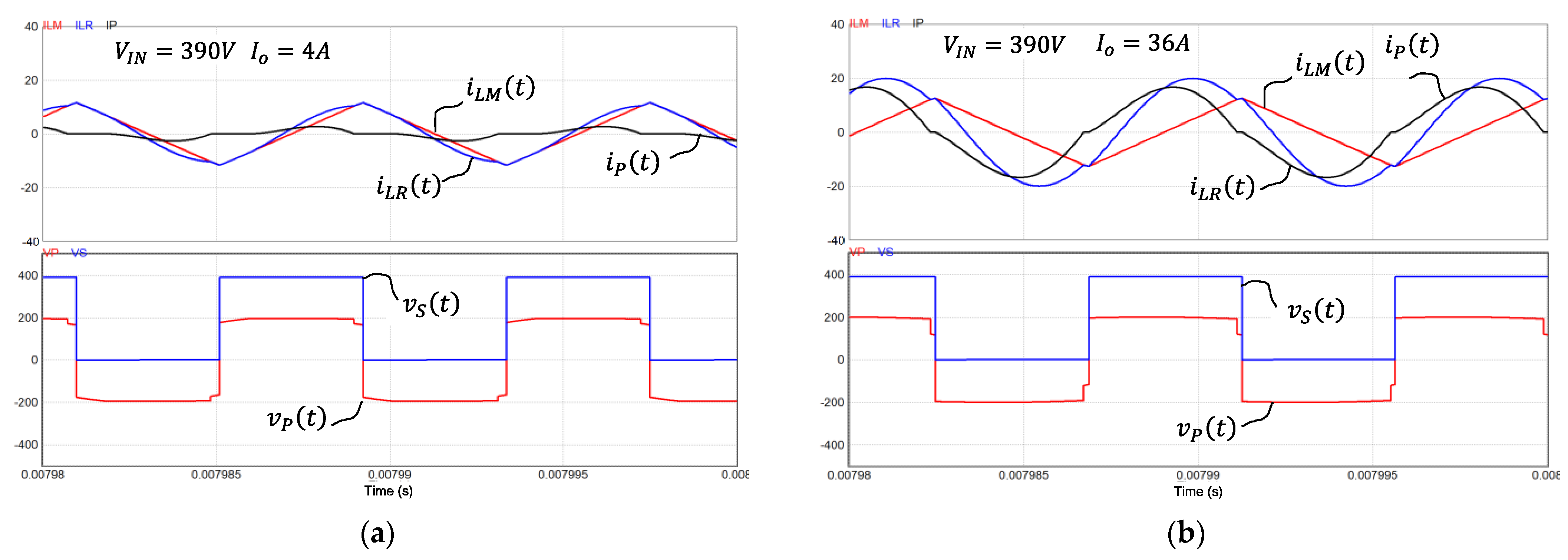
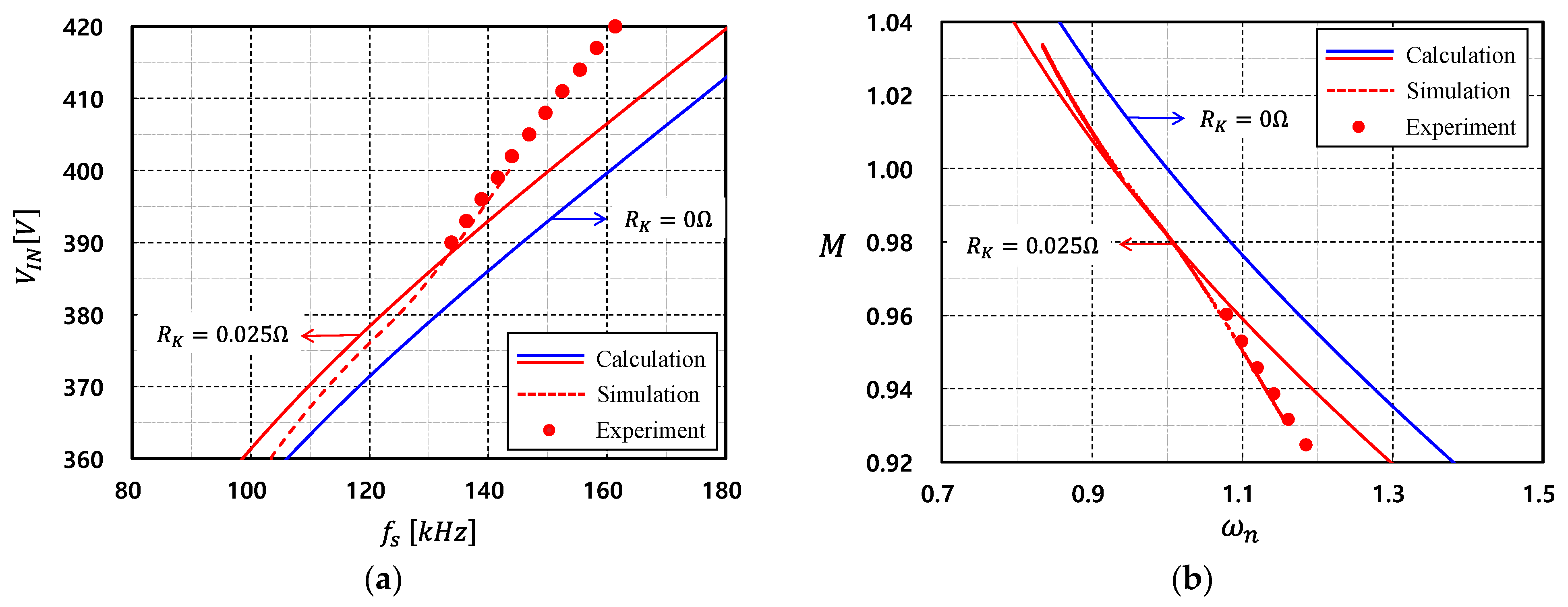
4. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khoobroo, E.; Ashrafinia, B.; Akhbari, M. Optimal design of LLC resonant converter with improved controllability. In Proceedings of the 5th Annual International Power Electronics, Drive Systems and Technologies Conference (PEDSTC 2014), Tehran, Iran, 5–6 February 2014; pp. 396–401. [Google Scholar] [CrossRef]
- Beiranvand, R.; Rashidian, B.; Zolghadri, M.R.; Hossein Alavi, S.M. A Design Procedure for Optimizing the LLC Resonant Converter as a Wide Output Range Voltage Source. IEEE Trans. Power Electron. 2012, 27, 3749–3763. [Google Scholar] [CrossRef]
- Zheng, R.; Liu, B.; Duan, S. Analysis and Parameter Optimization of Start-Up Process for LLC Resonant Converter. IEEE Trans. Power Electron. 2015, 30, 7113–7122. [Google Scholar] [CrossRef]
- Lee, I.O.; Moon, G.W. The k-Q Analysis for an LLC Series Resonant Converter. IEEE Trans. Power Electron. 2013, 29, 13–16. [Google Scholar] [CrossRef]
- Tan, X.; Ruan, X. Equivalence Relations of Resonant Tanks: A New Perspective for Selection and Design of Resonant Converters. IEEE Trans. Ind. Electron. 2016, 63, 2111–2123. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, L.; Wang, H.; Liu, Y.F.; Sen, P.C. An Accurate Design Algorithm for LLC Resonant Converters—Part I. IEEE Trans. Power Electron. 2016, 31, 5435–5447. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, L.; Qiu, Y.; Liu, Y.F.; Sen, P.C. An Accurate Design Algorithm for LLC Resonant Converters—Part II. IEEE Trans. Power Electron. 2016, 31, 5448–5460. [Google Scholar] [CrossRef]
- Fang, X.; Hu, H.; Chen, F.; Somani, U.; Auadisian, E.; Shen, J.; Batarseh, I. Efficiency-Oriented Optimal Design of the LLC Resonant Converter Based on Peak Gain Placement. IEEE Trans. Power Electron. 2013, 28, 2285–2296. [Google Scholar] [CrossRef]
- Beiranvand, R.; Zolghadri, M.R.; Rashidian, B.; Alavi, S.M.H. Optimizing the LLC–LC Resonant Converter Topology for Wide-Output-Voltage and Wide-Output-Load Applications. IEEE Trans. Power Electron. 2011, 26, 3192–3204. [Google Scholar] [CrossRef]
- Fang, Z.; Cai, T.; Duan, S.; Chen, C. Optimal Design Methodology for LLC Resonant Converter in Battery Charging Applications Based on Time-Weighted Average Efficiency. IEEE Trans. Power Electron. 2015, 30, 5469–5483. [Google Scholar] [CrossRef]
- Yu, R.; Ho, G.K.Y.; Pong, B.M.H.; Ling, B.W.K.; Lam, J. Computer-Aided Design and Optimization of High-Efficiency LLC Series Resonant Converter. IEEE Trans. Power Electron. 2012, 27, 3243–3256. [Google Scholar] [CrossRef]
- Li, G.; Xia, J.; Wang, K.; Deng, Y.; He, X.; Wang, Y. Hybrid Modulating of Parallel-series LLC Resonant Converter and Phase Shift Full-Bridege Converter for a Dual-output DC-DC Converter. IEEE Trans. Power Electron. 2019, 7, 833–842. [Google Scholar] [CrossRef]
- Qian, T.; Qian, C. An Adaptive Frequency Optimization Scheme for LLC Converter with Adjustable Energy Transferring Time. IEEE Trans. Power Electron. 2019, 34, 2018–2024. [Google Scholar] [CrossRef]
- Da Silva, R.L.; Borges, V.L.F.; Possamai, C.E.; Barbi, I. Solid-State Transformer for Power Distribution Grid Based on a Hybrid Switched-Capacitor LLC-SRC Converter: Analysis, Design, and Experimentation. IEEE Access 2020, 8, 141182–141207. [Google Scholar] [CrossRef]
- Shafaei, R.; Perez, M.C.G.; Ordonez, M. Planar Transformers in LLC Resonant Converters: High-Frequency Fringing Losses Modeling. IEEE Trans. Power Electron. 2020, 35, 9632–9649. [Google Scholar] [CrossRef]
- Duan, J.; Zhang, D.; Gu, R. Partial-Power Post-Regulated LLC Resonant DC Transformer. IEEE Trans. Ind. Electron. 2022, 69, 7909–7919. [Google Scholar] [CrossRef]
- Glitz, E.S.; Ordonez, M. MOSFET Power Loss Estimation in LLC Resonant Converters: Time Interval Analysis. IEEE Trans. Power Electron. 2019, 34, 11964–11980. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Zheng, T.Q.; Yang, J. A Modified Gain Model and the Corresponding Design Method for an LLC Resonant Converter. IEEE Trans. Power Electron. 2017, 32, 6716–6727. [Google Scholar] [CrossRef]
- Kim, D.K.; Moon, S.; Yeon, C.O.; Moon, G.W. High-Efficiency LLC Resonant Converter with High Voltage Gain Using an Auxiliary LC Resonant Circuit. IEEE Trans. Power Electron. 2016, 31, 6901–6909. [Google Scholar] [CrossRef]
- Xu, H.; Yin, Z.; Zhao, Y.; Huang, Y. Accurate Design of High-Efficiency LLC Resonant Converter with Wide Output Voltage. IEEE Access 2017, 5, 26653–26665. [Google Scholar] [CrossRef]
- Chen, S.Y.; Li, Z.R.; Chen, C.L. Analysis and Design of Single-Stage AC/DC LLC Resonant Converter. IEEE Trans. Ind. Electron. 2012, 59, 1538–1544. [Google Scholar] [CrossRef]
- Fang, X.; Hu, H.; Shen, Z.J.; Batarseh, I. Operation Mode Analysis and Peak Gain Approximation of the LLC Resonant Converter. IEEE Trans. Power Electron. 2012, 27, 1985–1995. [Google Scholar] [CrossRef]
- Ivensky, G.; Bronshtein, S.; Abramovitz, A. Approximate Analysis of Resonant LLC DC-DC Converter. IEEE Trans. Power Electron. 2011, 26, 3274–3284. [Google Scholar] [CrossRef]
- Duan, F.; Xu, M.; Yang, X.; Yao, Y. Canonical Model and Design Methodology for LLC DC/DC Converter with Constant Current Operation Capability under Shorted Load. IEEE Trans. Power Electron. 2016, 31, 6870–6883. [Google Scholar] [CrossRef]
- Jung, J.H.; Kim, H.S.; Ryu, M.H.; Baek, J.W. Design Methodology of Bidirectional CLLC Resonant Converter for High-Frequency Isolation of DC Distribution Systems. IEEE Trans. Power Electron. 2013, 28, 1741–1755. [Google Scholar] [CrossRef]
- Hu, S.; Deng, J.; Mi, C.; Zhang, M. Optimal design of line level control resonant converters in plug-in hybrid electric vehicle battery chargers. IET Electr. Syst. Transp. 2014, 4, 21–28. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, L.; Ma, T. Conduction Loss Analysis and Optimization Design of Full Bridge LLC Resonant Converter. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 2703–2707. [Google Scholar] [CrossRef]
- Yang, C.H.; Liang, T.J.; Chen, K.H.; Li, J.S.; Lee, J.S. Loss analysis of half-bridge LLC resonant converter. In Proceedings of the 2013 1st International Future Energy Electronics Conference (IFEEC), Tainan, Taiwan, 3–6 November 2013; pp. 155–160. [Google Scholar] [CrossRef]
- Zhao, C.; Xinke, W.; Meng, P.; Qian, Z. Optimum design consideration and implementation of a novel synchronous rectified soft-switched phase-shift full-bridge converter for low-output-voltage high-output-current applications. IEEE Trans. Power Electron. 2009, 24, 388–397. [Google Scholar] [CrossRef]
- Beiranvand, R.; Rashidian, B.; Zolghadri, M.; Alavi, S.M. Using LLC resonant converter for designing wide-range voltage source. IEEE Trans. Ind. Electron. 2011, 58, 1746–1756. [Google Scholar] [CrossRef]
- Kim, J.; Moon, G. A new LLC natural resonant converter with narrow switching frequency variation and reduced conduction losses. IEEE Trans. Power Electron. 2014, 29, 4278–4287. [Google Scholar] [CrossRef]
- Jami, M.; Beiranvand, R.; Mohamadian, M.; Ghasemi, M. Optimization the LLC resonant converter for achieving maximum efficiency at a predetermined load value. In Proceedings of the 6th Power Electronics, Drive Systems & Technologies Conference (PEDSTC2015), Tehran, Iran, 3–4 February 2015; pp. 149–155. [Google Scholar] [CrossRef]
- Chen, W.; Xu, M.; Ge, Y.; Guo, Q.; Jiang, T.; Che, X. Parameter Design of High Power LLC Resonant Converter. In Proceedings of the 2022 IEEE 5th International Conference on Electronics Technology (ICET), Chengdu, China, 13–16 May 2022; pp. 421–425. [Google Scholar] [CrossRef]
- Ahn, T.Y. A Study on Steady State Characteristics of LLC Resonant Half Bridge Converter Considering Internal Losses. IKEEE 2018, 22, 985–991. [Google Scholar] [CrossRef]
- Yoon, K.H.; Noh, Y.J.; Phum, S.; Meas, S.; Jang, S.H.; Kim, E.S. LLC resonant converter with wide input voltage and load range at fixed switching frequency. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 1338–1342. [Google Scholar] [CrossRef]
- Yang, B.; Lee, F.C.; Zhang, A.J.; Huang, G. LLC resonant converter for front end DC/DC conversion. In Proceedings of the APEC, Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No.02CH37335), Dallas, TX, USA, 10–14 March 2002; Volume 2, pp. 1108–1112. [Google Scholar] [CrossRef]









| Conditions | ||
|---|---|---|
| Conditions | ||
|---|---|---|
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Input voltage range | 360–400 | V | |
| Nominal input voltage | 380 | V | |
| Output voltage | 54 | V | |
| Maximum output power | 2.0 | kW | |
| Maximum output current | 36 | A | |
| Resonant frequency | 125 | kHz | |
| Inductance ratio | 8 | - |
| Parameter | Symbol | Value | Specifications |
|---|---|---|---|
| Main switch | SiHG73N60E | 650 V, 73 A, 39 mΩ | |
| Resonant capacitor | 2 | ||
| Resonant inductor | 7 | PQ3535 | |
| Resonant inductor | 58 | PQ3535 | |
| Transformer turns ratio | 35:10:10 | PQ3552 | |
| Rectifier switch | IPP051N15N5 | 150 V, 120 A, 5.1 mΩ | |
| Output capacitor | 960 | 120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, J.-S.; Gil, Y.-M.; Ahn, T.-Y. Steady-State Analysis and Optimal Design of an LLC Resonant Converter Considering Internal Loss Resistance. Energies 2022, 15, 8144. https://doi.org/10.3390/en15218144
Yoo J-S, Gil Y-M, Ahn T-Y. Steady-State Analysis and Optimal Design of an LLC Resonant Converter Considering Internal Loss Resistance. Energies. 2022; 15(21):8144. https://doi.org/10.3390/en15218144
Chicago/Turabian StyleYoo, Jeong-Sang, Yong-Man Gil, and Tae-Young Ahn. 2022. "Steady-State Analysis and Optimal Design of an LLC Resonant Converter Considering Internal Loss Resistance" Energies 15, no. 21: 8144. https://doi.org/10.3390/en15218144
APA StyleYoo, J.-S., Gil, Y.-M., & Ahn, T.-Y. (2022). Steady-State Analysis and Optimal Design of an LLC Resonant Converter Considering Internal Loss Resistance. Energies, 15(21), 8144. https://doi.org/10.3390/en15218144





