Abstract
One of the main challenges faced by floor treatment service robots is to compute optimal paths that completely cover a set of target areas. Short paths are of noticeable importance because their length is directly proportional to the energy used by the robot. Such a problem is known to be NP-hard; therefore, efficient algorithms are needed. In particular, computation efficiency is important for mobile robots with limited onboard computation capability. The general problem is known as coverage path planning (CPP). The CPP has several variants for single regions and for disjoint regions. In this research, we are investigating the solutions for disjoint target regions (rooms) that have fixed connection points (doors). In particular, we have found effective simplifications for the cases of rooms with one and two doors, while the challenging case of an unbounded number of rooms can be solved by approximation. As a result, this work presents a divide and conquer strategy (DnCS) to address the problem of finding a path for a sweeping robot that needs to sweep a set of disjoint rooms that are connected by fixed doors and corridors. The strategy divides the problem into computing the sweeping paths for the target rooms and then merges those paths into one solution by optimising the room visiting order. In this strategy, a geometrical approach for room coverage and an undirected rural postman problem optimisation are strategically combined to solve the coverage of the entire area of interest. The strategy has been tested in several synthetic maps and a real scenario showing short computation times and complete coverage.
1. Introduction
Ever since the first robots were given the means to navigate a designated environment, whether it is on the ground, in the air or in water, moving from one position to another has been a topic of scientific interest for several decades. The initial path planning problem consists of finding a path that takes a robot from an initial position to a desired goal while avoiding obstacles in the way. Once a mobile robot was expected to achieve more than just reach a point and navigate over the entire work area, coverage path planning (CPP) drew the attention of researchers to tackle this new challenge. CPP is particularly relevant in areas such as agriculture [1], which uses ground and aerial autonomous robots, lawn mowing, and floor treatment [2]. The CPP can be defined as computing a route for a robot so that a target area will be completely covered [3]. Since the CPP has been demonstrated to be NP-hard, it is essential to provide efficient algorithms that provide feasible solutions; furthermore, in robotics, it is of relevant importance to compute those solutions in a short time using low computational resources. The CPP has several instances that depend on the target area and the kinematic capabilities of the robot [3]; in consequence, there is no general method that can effectively address all of them.
In the area of automated floor treatment intended for commercial indoor use, the IEC 63327:2021 identifies sweeping, scrubbing, wet or dry pick-up, polishing, application of wax and powder-based detergents, sealing products, and shampooing of floors as the operations that can be executed by means of an automatic floor treatment machine. Each of these operations poses a different set of path planning requirements that ultimately impact how to achieve the best coverage.
In this paper, the sweeping coverage path planning problem (S-CPP) is addressed and can be defined as computing a path so that a floor-sweeping differential drive robot intended for commercial use completely covers a target area. A restriction of the problem is that the robot can not go outside the free regions specified on the map. Going deeper, the S-CPP can be classified into two variations: for single regions and for disjoint regions. Single regions are defined by one connected component, convex or non-convex, and with or without obstacles in the interior of the connected component. Some examples are [4,5,6,7,8]. Disjoint regions present areas with more than one component. The robot has to follow arbitrary routes to move between components. This is a less studied area and the works that have been found are the following: [9,10,11,12,13,14]. Methods developed for single regions are not adequate for disjoint scenarios since, by definition, they will try to cover all intermediate areas, while methods for disjoint areas only follow the shortest available path.
A specific instance of the S-CPP is tackled for the purposes of this research, where a set of target rooms is connected by doors and corridors. The rooms have to be swept, but the corridors are defined as transit areas only. In consequence, this problem can be classified as CPP for disjoint regions. As we will discuss in detail in Section 2, this particular problem has not been studied in the literature because previous research has focused on unmanned aerial vehicles, which can travel directly between regions, and the entrance or exit points are not restricted. Our research proposes that the general coverage tour can be modelled as a multi-rural postman problem (multi-RPP), which is an arc routing problem where a special subset of edges must be travelled. Similar modelling has been used to cover multiple terrains with unmanned aerial vehicles (UAVs) [9]. However, as we already mentioned, while the UAVs can enter and exit the terrains at any point, in the proposed application, the entry points are constrained by the doors, so previous solutions cannot be directly applied to this particular use case.
To tackle the S-CPP for disjoint areas, a divide and conquer method is proposed in this paper. First, the map is segmented into rooms and corridors. Then, depending on the room’s shape and door points, a coverage path for each one is computed. Next, to merge the disjoint paths into a single tour, a graph is constructed, and the RPP is solved with an optimisation strategy. The advantage of this strategy is that, even though the problem remains NP-Hard, the instance size is drastically reduced. In the previous grid-based works [10,12], the size of the instance depends on the number of cells. For large floors, the division of the map by the robot footprint might result in hundreds or thousands of positions, so optimising a path for such an instance size could be prohibitive; such fact can be observed in previous works where the maps have a small number of cells [10]. On the other hand, the presented proposal divides the problem into rooms and then optimises for an instance equal to the number of rooms on the map, which should be noticeably smaller. The method has been tested in several synthetic maps and in a real case validating its efficiency and effectiveness. In particular, the computation times are short enough to be implemented in the robot-embedded system—less than 0.03 s.
To summarise, our contribution is the proposition of a divide and conquer strategy for the coverage path planning of disjoint areas that are accessible only through door points. To the best of our knowledge, such a problem has not been addressed in previous literature.
The rest of the paper is presented as follows. Section 2 presents a short review of related work. Section 3 models the problem. Then, Section 4 describes the proposed strategy that divides the problem and computes the path. Section 5 presents the experiments conducted to validate the proposed method. Finally, Section 6 presents the conclusion and future research directions.
2. Related Work
To this day, coverage path planning remains an active area of research as it is applicable for unmanned aerial vehicles (UAVs) [6], autonomous underwater vehicles (AUVs), unmanned ground vehicles (UGVs), autonomous surface vehicles (ASVs) and also planning the path of the end-effector of industrial robots that need to perform surface treatment operations such as milling or laser cleaning. The authors of [15] present a comprehensive review of CPP in robotics using classical and heuristic algorithms; although no specific mention is made of the particular case of sweeping robots, some references are made to general cleaning robots from which it can be identified that reported research is focused on solving the problem of single areas with obstacles [8,16,17,18,19,20,21] or conjoined areas within a delimited squared space [5,22,23,24,25]. A note worth taking from [15] is that the authors conclude that coverage sequence optimisation, regarded as set covering and travelling salesman problems, is necessary to be tackled for the case of complex CPP problems.
On the particular scope of sweeping robots, the authors of [19] introduce a path planning strategy for intelligent sweeping robots focusing on decomposing a single squared area into cells to be travelled, comparing an inward spiral method with a global traversal planner based on the A* algorithm. Complementarily, the authors of [5] present a complete coverage path planning for intelligent sweeping robots, where the problem of excessive decomposition of the target area is highlighted for the cases of complex concave polygons, introducing an optimisation approach that takes into consideration the number of turns to determine an optimal path for a single area based on a combination of the rotating callipers path planning introduced by [26] and a heuristic algorithm.
As such, the general coverage path planning problem is NP-Hard consisting of two parts. The first part involves determining the minimum set of robot positions necessary to cover the region of interest. Karp demonstrated such a problem to be NP-Complete [27]. Still, each position has to be travelled one by one because the number of scrubbing robots is usually smaller than the number of positions. Therefore, a travelling salesman problem (TSP) has to be solved to generate a full path. Although the CPP also arises in 3D domains [28], the scope of this work only contemplates 2D applications.
The CPP problem has been formulated in several ways. In all cases, the complexity remains, but the instance size can be decreased under some assumptions and strategies. One approach is to divide the map into a uniform grid [7,29]; this roughly approximates the target area and allows the formulation of the planning as a TSP problem where all the cells must be visited. The advantage of the grid-based approach is that the shape of the map is not restricted; however, the number of cells is usually large, and consequently, the optimisation requires intensive calculations. Therefore, real-time planning by robots with low computation capabilities is unfeasible.
An alternative is to formulate a geometrical approach where a polygon represents the map, and the path is estimated as a set of sweeping lines or intersection points. This approach requires fewer computation resources, but more assumptions are made. For example, the vehicle executes relatively simple trajectories such as straight lines or Dublin’s curves. For non-convex polygons, the region is split into convex areas [30], and the previous methods can be applied.
Concerning the proposed modelling problem, one of the first works that tackled the coverage path planning as an RPP was the work of Vasquez et al. [9]. In that case, the problem arises in the context of surveying disjoint terrains with an aerial vehicle. That problem differs from the one presented here since the aerial vehicle can enter and exit the region of interest at any point in the polygon. The general RPP has been proven to be NP-Hard [31], and only a special case can be solved in polynomial time [32]. Therefore, the proposed methods for finding feasible solutions include genetic algorithms [33,34], neural networks [35], and heuristics [36], among others.
This work focuses on solving the problem of cleaning coverage sequence optimisation of disjoint areas by planning a path for covering a set of rooms that are connected by fixed door points and transit corridors, which is still an open problem.
3. Problem Modelling
The mobile robot is always in contact with the ground, so the map always specifies the navigable space. In consequence, the region of interest’s map is defined by single, convex or non-convex polygons with or without holes. As with some previous methods [37,38], the polygon is decomposed into smaller regions of interest. In particular, we are interested in a subset of maps designated as room-based interior maps. In these maps, the rooms are defined by convex polygons without holes and are connected by corridors. Figure 1 illustrates some examples of such maps. Thus, the aim is to plan a path for the sweeper robot so that the entire area of all the rooms is cleaned.
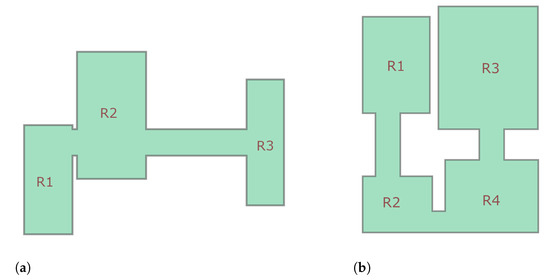
Figure 1.
Examples of room-based interior maps. In these maps, the rooms are described by convex polygons, and they are connected by corridors. (a) Map A with three rooms and two corridors. (b) Map B with four rooms and three corridors.
Formally, the coverage path planning problem for room-based interior maps is stated as follows: Given (i) a set of n rooms, , (ii) a set of door points for each room, where is the door for the room (note that the number of doors, d, may be different for each room) and (iii) a set of corridors that connect the door points, , where each corridor is a tuple that indicates what pair or doors it connects, , compute a path that covers all the rooms in the shortest distance. If the motion primitives are limited to straight lines and rotations in site, the problem is reduced to compute the series of robot workspace positions, , that covers all the rooms in the shortest distance. implicitly contains the visiting order of the rooms and the search pattern for each of them. In addition, the following assumptions are relevant: A room has at least one door, the doors are the unique points that the robot can use to enter or exit from a room, and the cost of a path that covers a room in a given order is the same as covering the same room with the same path in reverse order. Finally, as we will show in the following section, the problem can vary from a TSP to a multi-RPP, and for each case, an appropriate solution is required.
4. Sweeping Coverage Path Planning
Depending on the number of doors for each room, the problem changes. However, when (i) the rooms have only one door, a typical configuration for hotel floors, or (ii) when the rooms have two doors at maximum, creating loops in the graph, we have identified that the problem can be simplified to an exact TSP or to a single uRPP, respectively.
To deal with the cases of one or two doors per room, a divide and conquer strategy is proposed. In this strategy (See Section 4.1), the first target is to decompose the whole problem into small pieces that can be solved by available effective planners. Then, the second target is to combine the small paths into a whole connected cleaning path. To deal with the challenging case of rooms with more than two doors, a deeper study has to be carried out since the optimisation problem grows as a combinatorics problem; nonetheless, an insight into possible solutions is described in Section 4.2.
4.1. Divide and Conquer Strategy
Since the unique points for entering or exiting are defined by the door points, the cost of the path that covers each room is independent of the rest of the tour. This can be corroborated in the problem definition, where the room edges are connected only to door points. An illustration of this fact can be seen in Figure 2a. In such an illustration, the map is composed of three rooms and two corridors. This fact allows us to propose a divide and conquer strategy.
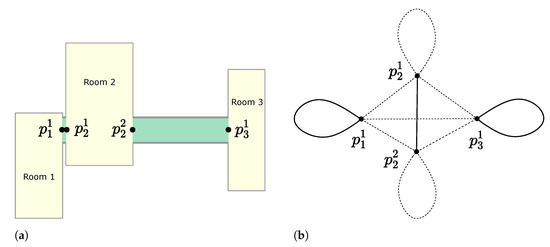
Figure 2.
Example of a segmented map and its corresponding graph used for tour planning. We observe that each room is only accessible by the door points. In the corresponding graph, the door points are converted to vertices, while the movements through rooms and corridors are converted into edges. To cover all the rooms, the edges drawn with continuous lines must be travelled, while the edges drawn with dotted lines to be travelled in the formulation of the rural postman problem are optional. (a) Segmented map and door points. (b) Corresponding graph.
The proposed strategy is summarised in Algorithm 1 and described next. First, the “divide part” of the method is applied, where the map is segmented into rooms and corridors. Line 1 of the algorithm can be automatically achieved by topological map generation [37,39,40] or semantic segmentation [41]. Next, for each room, the door points are computed as the intersection of a perpendicular line that passes through the middle of the door and a polygon eroded by a kernel with a diameter equal to the span of the cleaning area (Line 3). As follows, the coverage pattern is computed using an adaptation of the rotating calipers path planner (RCPP) [26] (Line 4) to this problem. Such adaptation is called RCPPforRoom. The RCPPforRoom receives as input the polygon of the room, the door points and the span of the cleaning area and returns the room cleaning pattern. The proposed adaptation is described separately in Section 4.1.1 because it relies only on computational geometry and keeps the property that it computes the shortest path in the room, as described in [26]. Once a path has been computed for each room, the paths are merged into one full path. Consequently, a complete graph, G, and its adjacency matrix, A, are constructed from the already computed door points and cleaning pattern distances. The path between the remaining door points is calculated by computing the medial axis of the map, converting the medial axis into a temporal graph and estimating the best path with the A* algorithm [42]. An alternative to the A* is the Dijkstra algorithm, as reported in [43]. Finally, the entire trajectory is obtained by finding the shortest travelled tour that satisfies the undirected rural postman problem. To determine the shortest tour, a genetic algorithm (GA) is proposed. The modelling and GA implementation are described in detail in Section 4.1.2.
| Algorithm 1: Divide and conquer sweeping coverage path planner. |
 |
4.1.1. Single Room Path Planning
A room is a segmented region of the map, and it is defined by a convex polygon. See Figure 3 as an example. It is assumed that the rooms are connected to larger rooms or hallways by doors. The doors are represented by single points, with the understanding that the robot is able to access a given space through the door; otherwise, there is no door point. As mentioned before, there is a maximum of two doors per room; this allows us to model the problem as the rural postman problem. The generalisation for an undefined number of doors is left for future work. Since the door points can be used as the entrance or exit from the room, they are simply labelled by an index. Therefore, for a room i, its room doors are and , in case it has two doors. For rooms with one door, the unique point is .
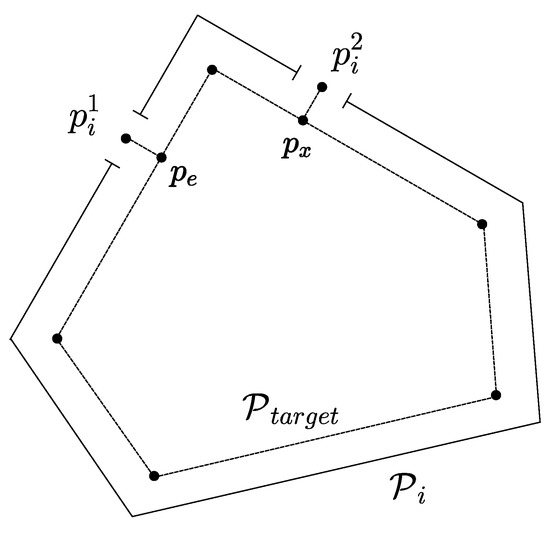
Figure 3.
Illustration of the polygon and points construction for a target room.
To obtain the door points from each room, getDoorPoint function in Algorithm 1, the calculated room polygon and the full map polygon are used. First, the set difference [44] of the room with the intersection of both polygons provides a set of line segments, namely:
where is a segment line that can be defined as follows:
where and are the initial and ending points of the j-th line segment and . Since there are at maximum two doors, the number of segment lines is at most two. Second, for each line segment, the middle point of the segment is computed, and it is taken as the door point, that is:
Once the door points have been computed, the following step is to compute the coverage pattern that cleans each room, i.e., the CPPforRoom function in Algorithm 1. To solve the problem, we adapt the RCPP planner [26], which estimates the optimal edge-vertex path that covers a convex polygon given starting and ending points. The proposed adaption is summarised in Algorithm 2. Given that such an algorithm requires a target convex polygon and two points as input, a new smaller polygon and two inner points are created (lines 1 to 3 of Algorithm 2). The reason is that the RCPP planner considers the edges of the polygon as valid positions. Though, for this use case, that implies that the robot will be in collision with the walls. The smaller polygon, , is computed by negatively offsetting the polygon by a circle with a diameter equal to , in other words, by computing the Minkowski difference [44,45] of with the circle. Next, the starting and ending points, and , are computed as the intersection with the polygon of the perpendicular line to the polygon that passes through the door points. Finally, the RCPP is called, and it returns a path, W, as a sequence of points that the robot has to follow, and the length of such path, l. To complete the path, the door points are appended to W, and the length is updated.
| Algorithm 2:CPPforRoom. Coverage path planning for a single room. |
Data: Room polygon (), door points (), cleaning span () Result: Path (W) 1 ErodePolygon() 2 NearestPoint(); 3 NearestPoint(); 4 RCPP; 5 6 ; 7 return |
4.1.2. Shortest Cleaning Tour
The previous Section 4.1.1 presented the first two parts of the divide and conquer strategy, where the map is segmented into rooms, and for each one, a cleaning pattern is computed. In the following sections, the last part is introduced, where the paths are connected into one single solution by optimising the general tour, namely the description to function GetShortestTour in Algorithm 1. Since we have identified that the problem can be addressed in different forms depending on the number of doors, we present two cases, when all the rooms have only one door and when they have a maximum of two doors.
4.1.3. Rooms of One Door-Solving a TSP
A particular instance of the problem arises when for all rooms, there is only one door. In those cases, given that , the full path computation can be modelled as a travelling salesman problem.
The reasoning behind this idea is the following. First, as we stated before, the optimal cleaning path of the room is independent of the rest of the map. Therefore, in the general graph, G, we can replace the vertices , and, in consequence, the edge , by only one vertex. Let us name the new vertex as (making reference to room i). Second, the reduced general path, , only contains vertices representing rooms, , and the edges that define connections between rooms, . The shape of the reduced graph can vary from a cycle graph to a complete graph depending on the connections in A. Note that is not the dual of G, as proposed in [46], because in this case, the hallways are not converted to vertices. Therefore, assuming that visiting the vertex of each room entrance implies the cleaning of such room, the full path is the one that visits all the vertexes with the shortest distance; in other words, the solution is the Hamiltonian circle in . Note that the full cleaning distance should add up the distances to clean each room.
To solve the TSP in , we apply a genetic algorithm (GA) as reported in [47] whose chromosome is a possible tour. The objective function measures the travelling distance of the possible tour.
4.1.4. Rooms of Two Doors-Solving a RPP
In this section, we propose the solution to the GetShortestTour function of the general strategy when the rooms a maximum of two doors.
Since the path for each room has already been computed [3], the problem can be modelled as an undirected rural postman problem (uRPP). The uRPP is a variation of the Chinese postman problem. It is defined on an undirected graph , where V is a list of vertices and E is a list of edges. Each edge, e, has an associated cost . In particular, the uRPP defines a subset of edges, , that must be part of the whole path. Then, the goal is to determine the least cost tour traversing each edge of at least once [32]. As it has been mentioned, the stated problem to be solved in this work is similar to the problem of covering with a drone a set of disjoint terrains [9]; however, in this problem, the vertices are defined by the door points. Considering the navigation constraints imposed by the doors, set V is composed of the home point and the door points, where the door points are points in the map that the robot has to cross in order to enter to or exit from a room. Namely,
where is the home point and is the door point of the room. Note that for each room, there is at least one door point.
Based on V, a complete graph can be constructed. Therefore, V has vertices, and E has edges. The subset of edges that needs to be travelled, , is defined by the edges that connect two door points of the same polygon; for rooms with a single door, a loop edge is included, see Equation (5).
On the other hand, the corridors or edges that connect door points of different polygons do not belong to . In cases where the corridors must be covered, those should be defined as rooms and connected to the other rooms. See Figure 2 as an example. In such figure, a given map and its corresponding graph are drawn. The edges that represent rooms must be travelled, while the edges that represent corridors are optional.
The cost for an edge, , that does not belong to is computed as the distance between the door points the corridor. Such distance can be computed directly on the map.
If the edge belongs to , then the cost is computed as the cost of the path that covers the associated room. Please see Equation (7).
The presented model defines a graph-based representation of the environment and the problem as a uRPP. The following section presents an efficient method for computing a feasible solution.
Continuing from the graph computed previously, see line 9 of Algorithm 1. The task is to compute a visiting order for the rooms based on the graph, G, and the distance-based adjacency matrix A, GetShortestTour function in Algorithm 1. Such order is specified as a list, , whose elements are the edges to be travelled.
Let us define the cost of a tour as the distance that that robot travels to complete it.
where is the cost of travelling the edge . Therefore, the problem can be stated as an optimisation problem,
s.t.
The first constraint states that the first edge in the tour starts with the home point. The second constraint states that the last point in the tour will be the home point again. The third constraint guarantees that all the rooms will be cleaned. Equation (8) only includes distance, but it can also include additional factors such as effort or time.
4.2. General Case Insight
The general case is for the S-CPP with disjoint rooms, with rooms with more than two doors. Although in practical applications, this scenario is rare, it is theoretically important to consider. The main change is that for the rooms with more than two doors, there is more than one combination to enter and exit the room. Formally, there are
possible ways to enter and exit from a room, where is the number of doors for the i-th room. Note that for , , given that the same door is used as entrance and exit. Based on the previous statement, we can notice that, for each possible combination, a uRPP is defined. Therefore, the multi-uRPP is a generalisation that has
possible instances. One way to apply the proposed method for scenarios with rooms that have more than two doors is to split each room into subareas so that each sub area will have two doors at maximum. Such problem is similar to performing a convex image partitioning [48] with additional constraints.
5. Experiments
To validate the effectiveness and efficiency of the proposed method, the proposed strategy was tested for the environments illustrated in Figure 1; additionally, for comparison purposes, paths were computed using a Countour planner for the same test environment; the performance is summarised in Table 1. The method was implemented in Python using the Shapely Library [49]. For the DnCS-RCPP, we used the author’s Matlab implementation [50]. The experiments were conducted on an i7 machine with 16 GB of RAM.

Table 1.
Results for the proposed maps. Travelling distance in pixels.
5.1. Synthetic Scenarios
In this experiment, we tested the proposed method versus a previous approach in several synthetic environments. In particular, three methods were tested: (i) the DnCS-RCPP as proposed in this paper, (ii) DnCS-Contour, a variation that uses a local contour planner [51] and (iii) the two steps path planner (TSPP) [9], a reported method for coverage path planning of disjoint areas. The summary of the experiments is described in Table 1. Figure 4 shows the computed path for each map obtained by the three methods. As it can be seen, the proposed method is able to compute the required path for the rooms on the tested maps. For map A, the total processing time required was 0.001 s. For map B, the processing time was 0.036, while for the Countour planner, the times were 0.001 and 0.041, respectively. It can be seen that, even though that the RCPP computes shorter paths, those paths might be unfeasible. For example, for map B, the robot must travel through occupied areas. The reason of the TSPP failure is that it considers that the rooms are accessible at any point, while the proposed approach considers the doors as the unique access points. On the other hand, DnCS always provides feasible paths. In addition, DnCS-RCPP provides shorter paths compared with those rendered by the DnCS-Countour planner, the processing times being similar in both cases. As a result, the short computation times show that the proposed method could be implemented in robotics platforms with low computational cost. With respect to the paths, we can observe that the routes are coherent, and the paths are not always oriented with the largest edge; for example, in map B, it is easy to observe that the door points are taken into account in order to decrease the path length.
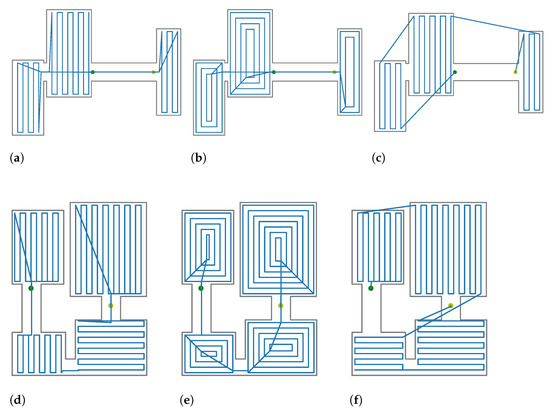
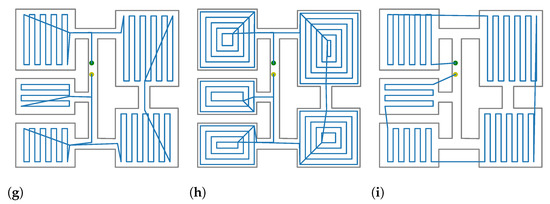
Figure 4.
Comparison of computed paths for the proposed maps. The maps are delimited by a grey line. The computed path is drawn in blue. Starting point is drawn in green. Ending point is drawn in yellow. (a) Map A; DnCS-RCPP. (b) Map A; DnCS-Contour. (c) Map A; TSPP [9] (d) Map B; DnCS-RCPP. (e) Map B; DnC-Contours. (f) Map B; TSPP [9]. (g) Map C; DnCS-RCPP. (h) Map C; DnC-Contours. (i) Map C; TSPP [9].
5.2. Case Study
To illustrate the applicability of the proposed strategy, paths were computed for a real environment. The target map was obtained using SLAM [52] with an Ouster® LIDAR of an office building. The obtained probabilistic grid is displayed in Figure 5a. Such a probabilistic grid was first thresholded and manually cleaned to remove the laser misreadings. Then the contour was found using Suzuki’s algorithm [53]. Then, the contour was converted to a polygon by discarding collinear points. Then the rooms were segmented according to the cleaning needs specified by the final user.
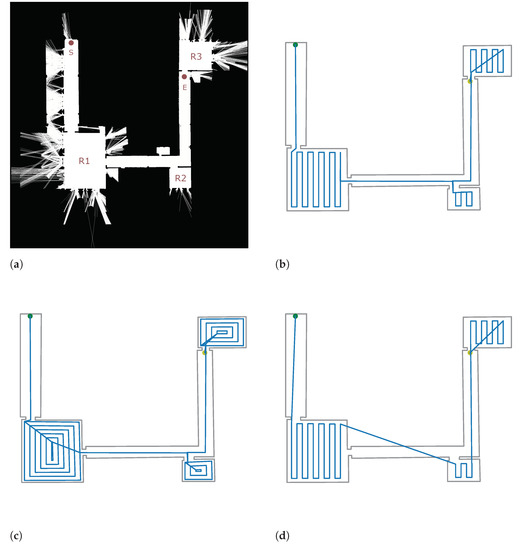
Figure 5.
Case study. The map generated after SLAM and the computed coverage paths are displayed. Robot starting point is drawn in green. Ending point is drawn in yellow. (a) The 2D initial map. Rooms (R1, R2 and R3), starting point (S) and ending point (E) are specified by the final user. (b) Computed path by DnC-RCPP. The map polygon is displayed in grey. The planned route is drawn in blue. (c) Computed path by DnC-Contour. The map polygon is displayed in grey. The planned route is drawn in blue. (d) Computed path by TSPP [9]. The map polygon is displayed in grey. The planned route is drawn in blue.
The polygon was introduced to the proposed planner in order to compute the full path. The computed path is displayed in Figure 5b. As we can see in the figure, the robot moves to the room R1, then it moves to R2, and finally, it reaches the R3. The paths for R1 and R2 are the shortest given that no overlap is produced. For the last room, after cleaning, the robot makes a movement to reach the ending point; therefore, it crosses through the room.
Table 2 summarises the results where the three implemented methods are compared. It is important to highlight that even though the TSPP algorithm seems to provide the shortest path, as can be observed in Figure 5d, the path is not feasible to be executed by a floor-cleaning robot. Conversely, both the DnCS-RCPP (Figure 5b) and the DnCS-Contour (Figure 5c) implementations provide feasible paths, being the DnCS-RCPP the shortest. Regarding the computation time to plan the entire path, the TSPP took over 2.5 times longer than the other two approaches. In conclusion, the method was effective for computing the path in the tested scenario.

Table 2.
Results for the case study. Travelling distance in pixels.
6. Conclusions and Future Work
This paper presents a method based on a divide and conquer strategy to tackle the problem of coverage path planning of large areas to be cleaned using a sweeping robot by extending the applicability of the undirected rural postman problem to cover several rooms connected by corridors. By segmenting a given map into individual rooms and transit corridors and defining the area’s access points, the method divides the problem into room coverage planning and merges the routes by planning a full tour. The room coverage is solved by a geometrical approach, while defining the shortest tour is solved as an optimisation problem using a heuristic algorithm. The results show that the complete coverage paths obtained with the DnCS-RCPP are shorter than those obtained with the Contour planner, providing an excellent alternative to efficiently compute complete coverage paths for sweeping robots when the target area is composed of several rooms. The overall processing time required to obtain suitable paths provides promising results to be considered for implementation on real robotics platforms.
In future works, the generalisation of the method for rooms with more than two possible doors, as well as larger areas such as malls or sports facilities, will be addressed, taking into consideration the kinematic constraints imposed by the mechanical configuration of the autonomous cleaning robot, such as commercial scrubber dryer robots that require a specific turning radius to avoid leaving wet marks or spills on the floor.
Author Contributions
Conceptualisation, J.I.V. and E.A.M.-C.; methodology, J.I.V.; software, J.I.V.; validation, J.I.V.; formal analysis, J.I.V. and E.A.M.-C.; data curation, J.I.V. and E.A.M.-C.; writing–original draft preparation, J.I.V.; writing–review and editing, E.A.M.-C.; project administration, E.A.M.-C.; funding acquisition, E.A.M.-C. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the European Regional Development Fund within the project “Robotic Solutions–True Autonomy for Indoor Autonomous Robots” 1.1.1.1/19/A/141.
Data Availability Statement
Not applicable.
Acknowledgments
The authors wish to thank the Instituto Politécnico Nacional, the Transport and Telecommunication Institute and SIA Robotic Solutions for the opportunity to collaborate together in this research.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CPP | coverage path planning |
| DnCS | divide and conquer strategy |
| GA | genetic algorithm |
| MDPI | multidisciplinary digital publishing institute |
| RPP | rural postman problem |
| RCPP | rotating callipers path planner |
| S-CPP | sweeping coverage path planning problem |
| TSP | travelling salesman problem |
| UAV | unmanned aerial vehicle |
| uRPP | undirected rural postman problem |
References
- Plessen, M.M.G. Partial field coverage based on two path planning patterns. Biosyst. Eng. 2018, 171, 16–29. [Google Scholar] [CrossRef]
- Engelsons, D.; Tiger, M.; Heintz, F. Coverage Path Planning in Large-scale Multi-floor Urban Environments with Applications to Autonomous Road Sweeping. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 3328–3334. [Google Scholar]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Rottmann, N.; Denz, R.; Bruder, R.; Rueckert, E. A Probabilistic Approach for Complete Coverage Path Planning with low-cost Systems. In Proceedings of the 2021 European Conference on Mobile Robots (ECMR), Bonn, Germany, 31 August –3 September 2021; pp. 1–8. [Google Scholar]
- Luo, B.; Huang, Y.; Deng, F.; Li, W.; Yan, Y. Complete Coverage Path Planning for Intelligent Sweeping Robot. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), Dalian, China, 14–16 April 2021; pp. 316–321. [Google Scholar]
- Tang, G.; Tang, C.; Zhou, H.; Claramunt, C.; Men, S. R-DFS: A coverage path planning approach based on region optimal decomposition. Remote Sens. 2021, 13, 1525. [Google Scholar] [CrossRef]
- Cho, S.W.; Park, H.J.; Lee, H.; Shim, D.H.; Kim, S.Y. Coverage path planning for multiple unmanned aerial vehicles in maritime search and rescue operations. Comput. Ind. Eng. 2021, 161, 107612. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, X.; Zhu, S. Combined coverage path planning for autonomous cleaning robots in unstructured environments. In Proceedings of the 2008 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 8271–8276. [Google Scholar]
- Vasquez-Gomez, J.I.; Herrera-Lozada, J.C.; Olguin-Carbajal, M. Coverage Path Planning for Surveying Disjoint Areas. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 899–904. [Google Scholar]
- Khanam, Z.; Saha, S.; Ehsan, S.; Stolkin, R.; Mcdonald-Maier, K. Coverage path planning techniques for inspection of disjoint regions with precedence provision. IEEE Access 2020, 9, 5412–5427. [Google Scholar] [CrossRef]
- Choi, Y.; Choi, Y.; Briceno, S.; Mavris, D.N. Multi-UAS path-planning for a large-scale disjoint disaster management. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 799–807. [Google Scholar]
- Wang, Y.; Kirubarajan, T.; Tharmarasa, R.; Jassemi-Zargani, R.; Kashyap, N. Multiperiod coverage path planning and scheduling for airborne surveillance. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2257–2273. [Google Scholar] [CrossRef]
- Shao, X.X.; Gong, Y.J.; Zhan, Z.H.; Zhang, J. Bipartite Cooperative Coevolution for Energy-Aware Coverage Path Planning of UAVs. IEEE Trans. Artif. Intell. 2022, 3, 29–42. [Google Scholar] [CrossRef]
- Khanam, Z.; McDonald-Maier, K.; Ehsan, S. Near-Optimal Coverage Path Planning of Distributed Regions for Aerial Robots with Energy Constraint. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 1659–1664. [Google Scholar]
- Tan, C.S.; Mohd-Mokhtar, R.; Arshad, M.R. A comprehensive review of coverage path planning in robotics using classical and heuristic algorithms. IEEE Access 2021, 9, 119310–119342. [Google Scholar] [CrossRef]
- Hu, G.; Hu, Z.; Wang, H. Complete coverage path planning for road cleaning robot. In Proceedings of the 2010 International Conference on Networking, Sensing and Control (ICNSC), Chicago, IL, USA, 10–12 April 2010; pp. 643–648. [Google Scholar]
- Dakulović, M.; Horvatić, S.; Petrović, I. Complete coverage D* algorithm for path planning of a floor-cleaning mobile robot. IFAC Proc. Vol. 2011, 44, 5950–5955. [Google Scholar] [CrossRef]
- Choi, S.; Lee, S.; Viet, H.H.; Chung, T. B-theta*: An efficient online coverage algorithm for autonomous cleaning robots. J. Intell. Robot. Syst. 2017, 87, 265–290. [Google Scholar] [CrossRef]
- Zhang, H.; Hong, W.; Chen, M. A Path Planning Strategy for Intelligent Sweeping Robots. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 11–15. [Google Scholar]
- Le, A.V.; Ku, P.C.; Than Tun, T.; Huu Khanh Nhan, N.; Shi, Y.; Mohan, R.E. Realization energy optimization of complete path planning in differential drive based self-reconfigurable floor cleaning robot. Energies 2019, 12, 1136. [Google Scholar] [CrossRef]
- Kyaw, P.T.; Paing, A.; Thu, T.T.; Mohan, R.E.; Le, A.V.; Veerajagadheswar, P. Coverage path planning for decomposition reconfigurable grid-maps using deep reinforcement learning based travelling salesman problem. IEEE Access 2020, 8, 225945–225956. [Google Scholar] [CrossRef]
- Liu, H.; Ma, J.; Huang, W. Sensor-based complete coverage path planning in dynamic environment for cleaning robot. CAAI Trans. Intell. Technol. 2018, 3, 65–72. [Google Scholar] [CrossRef]
- Miao, X.; Lee, J.; Kang, B.Y. Scalable coverage path planning for cleaning robots using rectangular map decomposition on large environments. IEEE Access 2018, 6, 38200–38215. [Google Scholar] [CrossRef]
- Lakshmanan, A.K.; Mohan, R.E.; Ramalingam, B.; Le, A.V.; Veerajagadeshwar, P.; Tiwari, K.; Ilyas, M. Complete coverage path planning using reinforcement learning for tetromino based cleaning and maintenance robot. Autom. Constr. 2020, 112, 103078. [Google Scholar] [CrossRef]
- Muthugala, M.V.J.; Samarakoon, S.B.P.; Elara, M.R. Tradeoff between area coverage and energy usage of a self-reconfigurable floor cleaning robot based on user preference. IEEE Access 2020, 8, 76267–76275. [Google Scholar] [CrossRef]
- Vasquez-Gomez, J.I.; Marciano-Melchor, M.; Valentin, L.; Herrera-Lozada, J.C. Coverage path planning for 2d convex regions. J. Intell. Robot. Syst. 2020, 97, 81–94. [Google Scholar] [CrossRef]
- Karp, R.M. Reducibility among combinatorial problems. In Complexity of Computer Computations; Springer: Berlin/Heidelberg, Germany, 1972; pp. 85–103. [Google Scholar]
- Felsner, K.; Schlachter, K.; Zambal, S. Robotic Coverage Path Planning for Ultrasonic Inspection. Appl. Sci. 2021, 11, 10512. [Google Scholar] [CrossRef]
- Tnunay, H.; Moussa, K.; Hably, A.; Marchand, N. Virtual Leader based Trajectory Generation of UAV Formation for Visual Area Coverage. In Proceedings of the IECON 2021–47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar]
- Mayilvaganam, K.; Shrivastava, A.; Rajagopal, P. An optimal coverage path plan for an autonomous vehicle based on polygon decomposition and ant colony optimisation. Ocean. Eng. 2022, 252, 111101. [Google Scholar] [CrossRef]
- Lenstra, J.K.; Kan, A. On general routing problems. Networks 1976, 6, 273–280. [Google Scholar] [CrossRef]
- Corberán, Á.; Laporte, G. Arc Routing: Problems, Methods, and Applications; SIAM: Philadelphia, PA, USA, 2013. [Google Scholar]
- Xin, J.; Yu, B.; D’Ariano, A.; Wang, H.; Wang, M. Time-dependent rural postman problem: Time-space network formulation and genetic algorithm. Oper. Res. 2022, 22, 2943–2972. [Google Scholar] [CrossRef]
- Kang, M.J.; Han, C.G. Solving the rural postman problem using a genetic algorithm with a graph transformation. In Proceedings of the 1998 ACM Symposium on Applied Computing, Atlanta, GA, USA, 27 February–1 March 1998; pp. 356–360. [Google Scholar]
- Masutti, T.A.; de Castro, L.N. Neuro-immune approach to solve routing problems. Neurocomputing 2009, 72, 2189–2197. [Google Scholar] [CrossRef]
- Pearn, W.; Wu, T. Algorithms for the rural postman problem. Comput. Oper. Res. 1995, 22, 819–828. [Google Scholar] [CrossRef]
- Bormann, R.; Jordan, F.; Li, W.; Hampp, J.; Hägele, M. Room segmentation: Survey, implementation, and analysis. In Proceedings of the 2016 IEEE international conference on robotics and automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1019–1026. [Google Scholar]
- Deng, D.; Jing, W.; Fu, Y.; Huang, Z.; Liu, J.; Shimada, K. Constrained heterogeneous vehicle path planning for large-area coverage. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4113–4120. [Google Scholar]
- Zhou, Y.; Yu, S.; Sun, R.; Sun, Y.; Sun, L. Topological segmentation for indoor environments from grid maps using an improved NJW algorithm. In Proceedings of the 2017 IEEE International Conference on Information and Automation (ICIA), Macao, China, 18–20 July 2017; pp. 142–147. [Google Scholar]
- Lin, Z.; Xiu, C.; Yang, W.; Yang, D. A Graph-Based Topological Maps Generation Method for Indoor Localization. In Proceedings of the 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS), Wuhan, China, 22–23 March 2018; pp. 1–8. [Google Scholar]
- Perez-Gonzalez, A.; Benitez-Montoya, N.; Jaramillo-Duque, A.; Cano-Quintero, J.B. Coverage Path Planning with Semantic Segmentation for UAV in PV Plants. Appl. Sci. 2021, 11, 12093. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Jensen, M.A.F.; Bochtis, D.; Sørensen, C.G.; Blas, M.R.; Lykkegaard, K.L. In-field and inter-field path planning for agricultural transport units. Comput. Ind. Eng. 2012, 63, 1054–1061. [Google Scholar] [CrossRef]
- Mark, d.B.; Otfried, C.; Marc, v.K.; Mark, O. Computational Geometry Algorithms and Applications; Spinger: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Fogel, E.; Setter, O.; Wein, R.; Zucker, G.; Zukerman, B.; Halperin, D. 2D Regularized Boolean Set-Operations. In CGAL User and Reference Manual, 5th ed.; CGAL Editorial Board: Sophia Antipolis, France, 2022. [Google Scholar]
- Xu, A.; Viriyasuthee, C.; Rekleitis, I. Efficient complete coverage of a known arbitrary environment with applications to aerial operations. Auton. Robot. 2014, 36, 365–381. [Google Scholar] [CrossRef]
- Grefenstette, J.; Gopal, R.; Rosmaita, B.; Van Gucht, D. Genetic algorithms for the traveling salesman problem. In Proceedings of the First International Conference on Genetic Algorithms and Their Applications, Sheffield, UK, 12–14 September 1995; Lawrence Erlbaum: Mahwah, NJ, USA; pp. 160–168. [Google Scholar]
- Duan, L.; Lafarge, F. Image partitioning into convex polygons. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3119–3127. [Google Scholar]
- Gillies, S. The Shapely User Manual. 2013. Available online: https://pypi.org/project/Shapely (accessed on 8 August 2022).
- Vasquez, J.I. Optimal Coverage Path Planner Implementation. 2019. Available online: https://github.com/irvingvasquez/ocpp (accessed on 8 August 2022).
- Bormann, R.; Jordan, F.; Hampp, J.; Hägele, M. Indoor coverage path planning: Survey, implementation, analysis. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1718–1725. [Google Scholar]
- Burgard, W.; Fox, D.; Thrun, S. Probabilistic Robotics; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Suzuki, S. Topological structural analysis of digitized binary images by border following. Comput. Vision, Graph. Image Process. 1985, 30, 32–46. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).