Abstract
In this paper, we present an approach for multi-level parallel-in-time (PinT) electromagnetic transient (EMT) simulation. We evaluate the approach in the context of power electronics system-level simulation. While PinT approaches to power electronics simulations based on two-level algorithms have been thoroughly explored in the past, multi-level PinT approaches have not yet been investigated. We use the multigrid-reduction-in-time (MGRIT) method to parallelize a dedicated EMT simulation tool which is capable of switching between different converter models as it operates. The presented approach yields a time-parallel speed-up of up to 10 times compared to the sequential-in-time implementation. We also show that special care has to be taken to synchronize the time grids with the electronic components’ switching periods, indicating that further research into the usage of different models from adequate model hierarchies is necessary.
1. Introduction
In recent years, partly due to the introduction of larger and more complex converter-level solutions, the execution speed of power electronics simulations has become a concern [1,2,3].
To allow for the growing size of analyzed systems, while maintaining a high resolution in the time domain required by switching devices, many simulations employ techniques of parallel computing [4,5,6,7,8,9], such as parallelization of calculations of different components [10,11]. Modern power electronics devices are increasingly penetrating power systems, while requiring even smaller time-steps and, thus, slowing down simulations [12].
Physical systems like these introduce restrictions on the simulation’s time-step and, thus, slow down computation. Within power electronics simulations, the smallest acceptable time-step is often determined by switching frequencies of converter devices. Increasing the complexity of the simulated system results in longer execution times, assuming that the time-step is already set to the largest meaningful value. This issue is usually addressed by exploiting parallelism of the model or in the simulation algorithm in some way and, thus, distributing the computations among multiple computing units. This approach is supported by the fact that speed-up cannot be expected to originate from semi-conductor improvements alone, but rather from improving algorithms and hardware architecture simultaneously [13].
Dynamic simulations, even with a high degree of spatial parallelism, are still inherently bounded by the sequential nature of the time-stepping involved. To address this, even before multicore architectures were the standard, methods for parallelization of the temporal dimensions have been proposed [14], and subsequently, many new techniques have been explored [15]. Based on the Parareal algorithm [16], published in 2001, various sophisticated PinT simulation techniques have been developed. In conjunction with spectral-deferred-correction (SDC) methods [17], which apply an iterative solver to a collocation-like problem [18,19,20,21], hybrid parareal spectral-deferred-correction (SDC) methods were presented in [22,23]. Further developments evolved into the parallel full-approximation scheme in space and time (PFASST) [24]. A somewhat different foundation for parallel-in-time (PinT) methods is provided by multigrid-based methods [25,26]. However, both Parareal and PFASST can be perceived as special cases of the multigrid approach [25], as discussed in [27,28]. Besides the multigrid-reduction-in-time (MGRIT) algorithm [29], space-time multigrid methods [30,31] and multigrid wave-form relaxation methods [32,33] have been developed.
The MGRIT method has been shown to be applicable in high-performance computing environments, where thousands of computing units are available for simulations [34,35].
At the cost of increasing the overall number of computations, speed-up can be achieved given a sufficient number of computing units. This serves as the main motivation to adapt the MGRIT technique developed for the numerical solution of differential equations [29] to the simulation of electronic circuits usually described by differential algebraic systems of equations (DAEs).
Recently, the parareal approach was shown to be applicable to electromagnetic transient (EMT) simulations of power systems [36], DC and AC/DC grids with device-level switch modelling [37,38,39] and simulations of electric vehicles [40]. Further implementations of a two-level approach have been published [41,42], showing the continued interest in parallelization-in-time for power system simulations.
Multi-level approaches have been successfully applied to power system simulations with scheduled event detection [43] and to power delivery networks with non-linear load-models [44].
The multi-level parallel-in-time (PinT) simulation of device-level, switching-model converters has not yet been demonstrated to the authors’ knowledge. Since it promises further speed-up if sufficient computing resources are available, while providing similar levels of accuracy [45], the combination of MGRIT with power electronics simulation and control will be explored in this publication. We focus on the comparison between sequential, two-level, and multi-level versions of the same algorithm, analyzing the influence of further time-parallel levels beyond the first, while exploring the limitations on coarse level time-step size due to interference with the switching periods of the modelled devices.
Section 2 gives an overview of the MGRIT algorithm. Section 3 describes the implemented algorithm and test cases. The resulting simulation data are presented in Section 4 along with a comparison with time-sequential simulation techniques. We show that the presented multi-level approach is able to provide a speed-up of between three and four times compared to two-level versions, and up to 10 times compared to the fully sequential version. Section 5 concludes the article with some summarizing thoughts, and points to opportunities for further research.
2. The Parallel-in-Time (PinT) Approach
The well-researched Parareal algorithm [16] forms the basis of parallel-in-time simulations and can be interpreted as a two-level version of multigrid-reduction-in-time (MGRIT) [46]. The basic idea of Parareal is an iteration between a less accurate, but quick, simulation with long time-steps and calculating the exact solution (on the different time slices in-between) in parallel, which is, in turn, used to update the approximation on the coarse grid. Using the MGRIT algorithm, an existing time-stepping scheme can be modified to be executed in a PinT fashion [29,47]. Recursive application of such a two-level approach leads to multi-level variants of MGRIT [29].
In this chapter, we briefly introduce the PinT-algorithm MGRIT [29,45]. We start with some definitions and then give an overview of the MGRIT scheme, as presented in [29,46].
Assume a given initial value problem (IVP) of the form
where x is an at least once continuously differentiable, complex, vector-valued function of time t, is its initial value at time , and f describes the first derivative of x at time t in terms of and t.
To discretize the simulation interval , choose a time-step for some . With this, we define the fine time grid
We now introduce the propagator , an operator that approximates x at time based on a previous value ,
Starting with the initial condition , and applying the propagator iteratively, we could compute an approximate solution , for , of the system of Equation (1) on the fine time grid . This approximate solution is given by the sequence
The above approach describes a standard (sequential) numerical integration method. For PinT, we now introduce a second coarse time grid with coarse time-step , where for some is the coarsening factor between the two grids. Then, we can express the coarse time-step as and the coarse time grid as
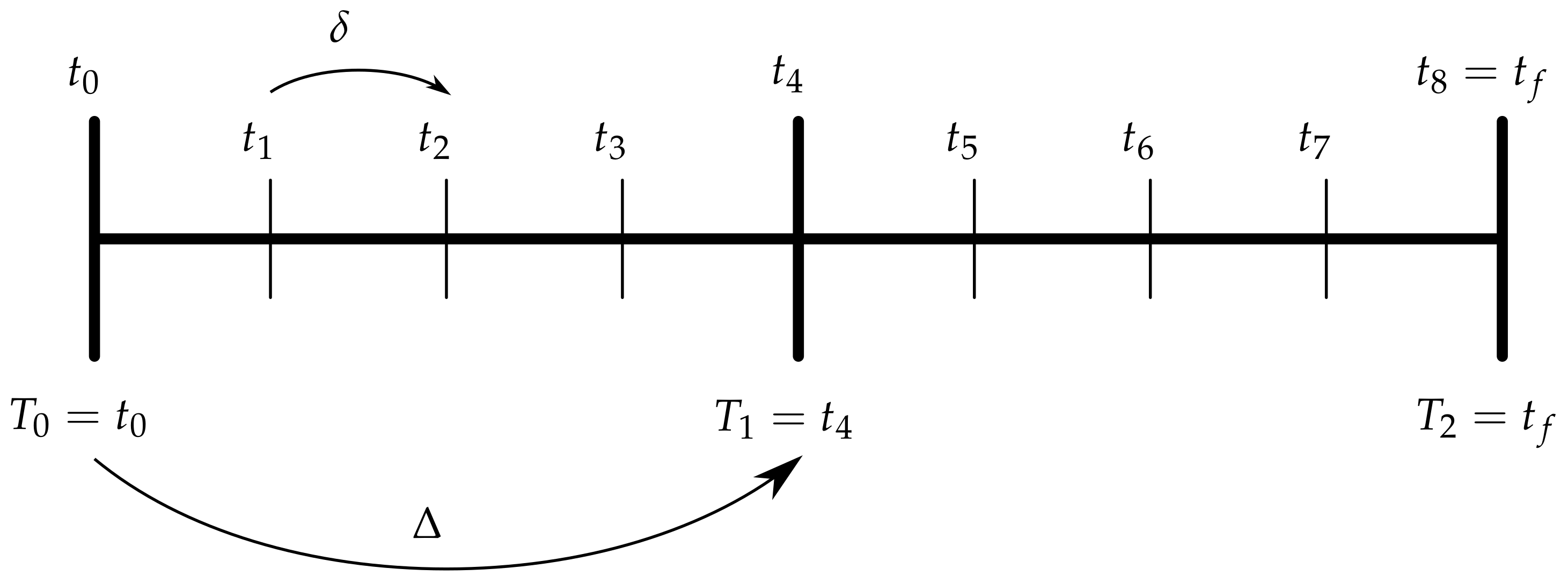
Here, we introduce the notation for denoting points on the coarse time grid. To distinguish the two grids, will be called the fine grid. Time points that are only on the fine grid, , are called F-points. Points on the coarse grid, are called C-points. An illustration of both time grids and the involved notation can be found in Figure 1.
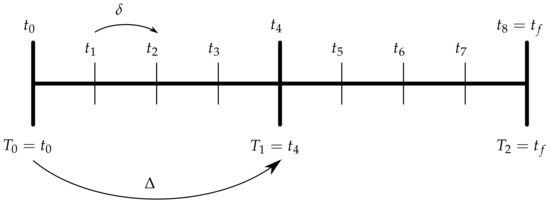
Figure 1.
Visualization of the time interval and notation for two different time grids. Step sizes are (fine grid) and (coarse grid), the coarsening factor is . C-points (F-points) are drawn as long (short) vertical lines which define the time grids ().
Analogous to the fine propagator , we introduce the coarse propagator . It represents an integration algorithm that approximates the solutions on the coarse grid, . Starting with , we can generate the approximate solution on the C-points iteratively:
In principal, parallelism is achieved in the following way: First, the evolution of the initial condition over the coarse grid is computed sequentially, yielding approximations . Then, these serve as initial conditions for the fine-grid propagation on the F-points in the different time slices, , which can be computed independently of one another.
The following paragraph formalizes this general intuition by introducing the MGRIT algorithm.
Multigrid Reduction in Time
This group of algorithms recursively applies a two-level integration scheme to yield a multi-level approach and, thus, allows for a higher degree of parallelism compared to purely parallel-in-space (PinS) approaches [29,46]. For simplicity, we only present the two-level version here. Higher-level versions are easily derived from this by recursively introducing additional time grids (although convergence considerations are more complicated in the multi-level case [48]).
The approximate solution of the initial value problem (IVP) (1) on a given fine time grid with propagator may be written in a more succinct way. Note that , as introduced above, may be a non-linear and explicitly time-dependent function. For simplicity, we restrict ourselves here to linear and time-independent propagators and . Thus, we can rewrite the iterative update given by Equation (2) into one simultaneous linear equation system:
Introducing the coarse time-grid and denoting the cf-times successive application of with , we may rewrite the above equation as
Solving this system yields the solution on the coarse grid as approximated by the fine propagator. Now, replacing each in by the coarse-grid propagator , we gain the coarse-grid approximation:
The classical residual-correction method [49] forms the basis of the multigrid procedure for linear systems of equations [50]. In the following, we present the residual-correction method within MGRIT. Let denote the approximate solution after the l-th iteration, with some initial condition (this may, for example, simply be the initial value at all C-points). By defining the residual of the l-th iteration at the C-points,
the coarse grid correction may be introduced:
This correction is used to update the states at the C-points in an iterative manner:
Plugging Equations (6) and (7) into (8), the update rule becomes
which can be interpreted as a pre-conditioned stationary iteration. The fine-solution term can be computed in parallel, using the results from the preceding coarse solve as initial values.
The -th row of Equation (9), with , corresponds to a given C-point and may be written as
by multiplying Equation (9) with from the left. It is easy to see that the fine-grid approximation is recovered at the C-points if the terms and converge towards each other as l grows.
Algorithm 1 summarizes the procedure for two levels as published in [46]. This two-level version is equivalent to the Parareal approach [16]; recursive application yields a multi-level integration scheme [45]. Note that a (potentially significantly) reduced amount of sequential time-stepping is still needed on the individual levels, at least in between respective C-points or, on the coarsest level, in the process of computing the residual . For a maximally possible amount of levels with coarsening factor , the highest number of successive sequential steps is also two.
| Algorithm 1: 2-level MGRIT algorithm |
| 1: repeat |
| 2: Propagate approximate solution , cf. Equation (3) |
| 3: Compute residual on coarse grid, cf. Equation (6) |
| 4: Solve coarse grid correction problem, cf. Equation (7) |
| 5: Correct approximate solution at C-points, cf. Equation (8) |
| 6: until norm of residual is sufficiently small. |
| 7: Update solution at F-points, cf. Equation (3) |
3. Implementation
In this section, we present the conceptual combination of the resistive companion (RC) method [51] with the MGRIT algorithm. We use the MGRIT implementation from the XBraid software package [52]. For simplicity, we implement only a sequential-in-space version of the RC method, dubbed here resistive companion solver (RCS). This solver implements some features not commonly found in power electronics simulation software: Notably, the representation of the system state (including control logic) accommodates the multi-level nature of the MGRIT approach by allowing for changes of the time-step and other simulation parameters as it operates. This is enabled, in part, by employing physical currents as system variables instead of the current injections resulting from discretizations of differential equations, which are commonly used in fixed time-step implementations of electromagnetic transient (EMT)-solvers. This is depicted, e.g., in Equation (4) of [53], where the current injections are usually calculated in a post-step and used directly for the calculation of the next time-step. Instead, we use the physical current to calculate the required current injection based on the currently applicable time-step length. This proof-of-concept sequential-in-space time-stepping scheme can be replaced with parallelized versions without needing to change the PinT algorithm.
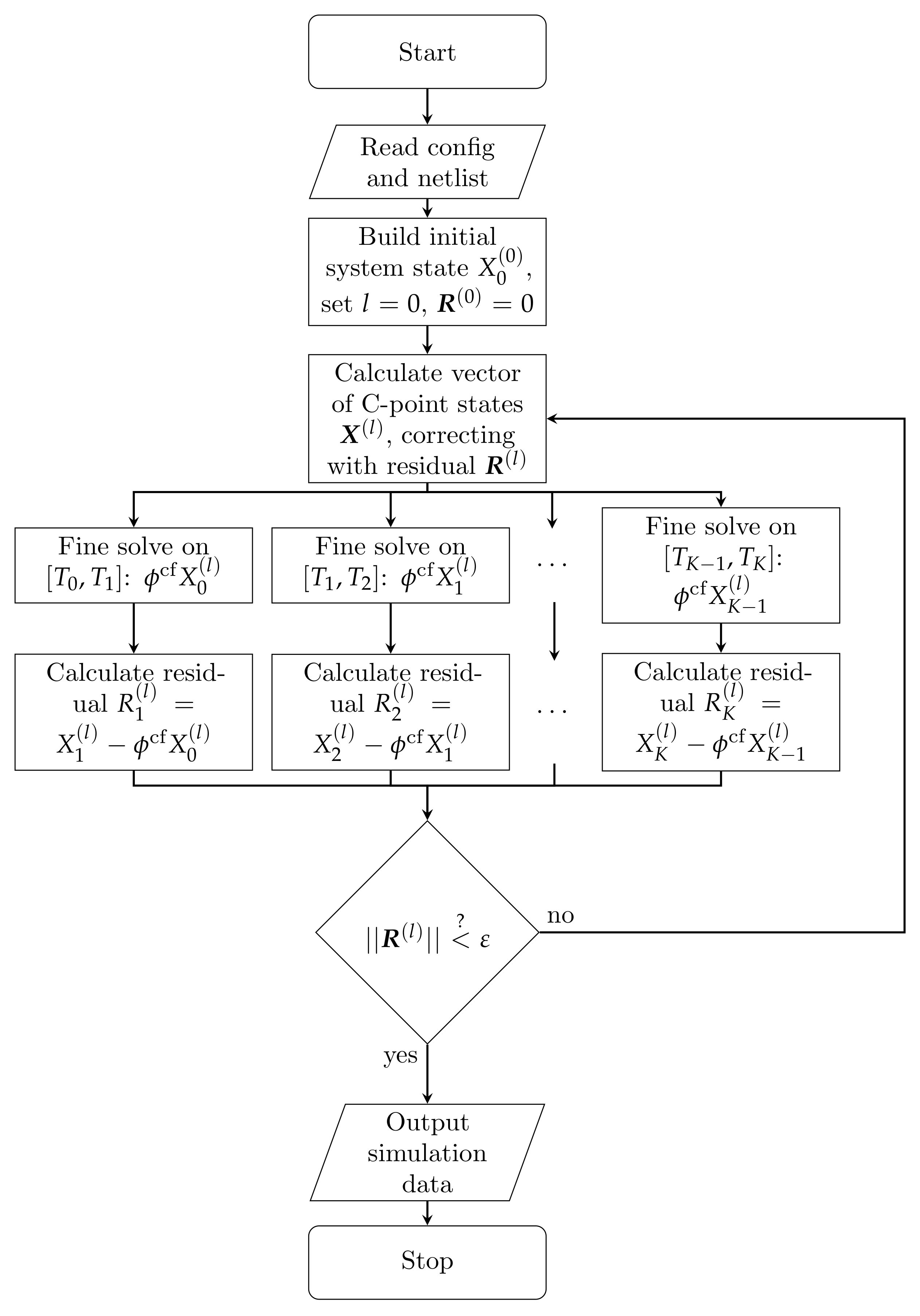
A flowchart of the two-level version of the MGRIT algorithm used in this article is given in Figure 2.
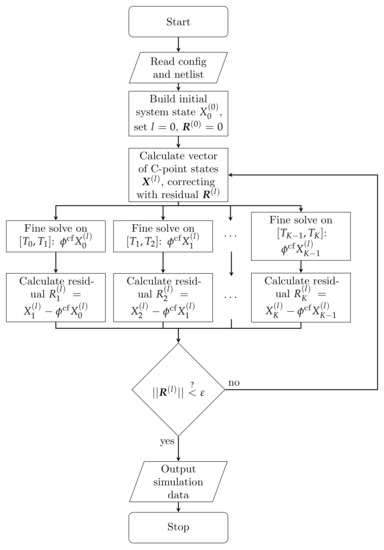
Figure 2.
Execution flowchart of the implemented PinT version of the resistive-companion type solver in the two-level version.
3.1. Special Considerations for the Solver
To keep track of the different parameters, we use a system-state object that contains all independent parameters of the system which are subject to change during the simulation. This includes, but is not limited to, nodal voltages, branch currents, control parameters, such as current and accumulated error, duty cycles, etc. All of these can easily be overwritten at any time to allow for the injections necessary in the algorithm.
Furthermore, special care has to be taken of the controller’s duty cycle. Resolving this duty cycle with an appropriate time-step is necessary to accurately reproduce the controller’s behavior in electromagnetic transient situations. Thus, the coarse step should not be too large.
Note that the combination of methods described here does not lead to a gain in computation speed compared to the sequential implementation for all possible combinations of parameters. The actual speed-up is highly dependent on multiple factors, such as the coarsening factor, number of levels, and the test case itself, as will be shown in Section 4 below. This article aims to provide a proof of concept for simulating power electronics in a multi-level PinT fashion. It exhibits speed-ups of up to 10 times compared to sequential simulation. Theoretically, the potential speed-up is mainly bounded by the number of available processors in the most simple cases.
The resistive companion solver (RCS) developed for this article is implemented in C++ and uses the C++ interface provided by the XBraid software [52]. In order to enable a PinT execution of the sequential RCS utilizing the XBraid package, only a few additional wrapping routines and data structures have to be provided. This allows for direct comparison of the unchanged sequential program and the corresponding MGRIT counterpart. For each MGRIT level, distinct discretization schemes may be used, resulting in a level-dependent propagator . Similarly, different techniques for the matrix decomposition may be invoked on different levels. At the time of writing, three different LU decomposition methods from the Eigen3 library [54] are available; the implementation of further factorization techniques, e.g., iterative solvers, is possible.
As is usual for a resistive companion (RC) approach, the modular implementation allows for dynamically reading in netlist and simulation parameters at runtime. Among the additional parameters needed for PinT execution are the number of different levels, the coarsening factors between the levels, and additional options, such as a halting tolerance for the residual between solutions on different levels.
The setup of the system matrix is performed analogously to classical EMT-type approaches and will not be shown explicitly here. We refer the interested reader to [51] for more details. Note that the use of an implicit method, such as implicit Euler or the implicit midpoint-rule, is recommended, since MGRIT is known to perform better with L-stable methods [55].
3.2. Modeling of Converters
For the converters, both a traditional switching model and an averaged model were implemented. For the latter, each converter is replaced by a number of voltage sources, current sources, and resistors. The parameters of these substitute elements are updated in every time-step to reflect the behavior of the emulated component.
For simplicity, a single proportional-integral (PI) controller is used to control either the output voltage or the output current of the converter. Depending on the switching frequency , the duty cycle is recalculated in periods given by . The control signal is given by . The cumulative error given by the integral is dependent on the history of the system and, thus, needs to be updated properly respecting the used time-step and previously accumulated error. For a given time-step , the integral component is approximated by .
4. Evaluation
In this section, we present a number of test cases and analyze the performance of our PinT solver in comparison with sequential time-stepping. The smaller cases also function as building blocks for a scalable DC-microgrid test case.
All calculations were executed on a machine with two AMD EPYC 7H12 CPUs with 2.60–3.30 GHz clock speed and 64 cores each. For the parallel calculations, if not otherwise indicated, 128 processing units were used independent of the number of coarse intervals. This was due to the overall execution time being lowest with the maximum available processors.
The halting criterion used is a relative tolerance of on the normalized residuum . All given timings are average values from 10 different executions. Standard deviations of all values are below of the given value.
4.1. Pi-Model Line
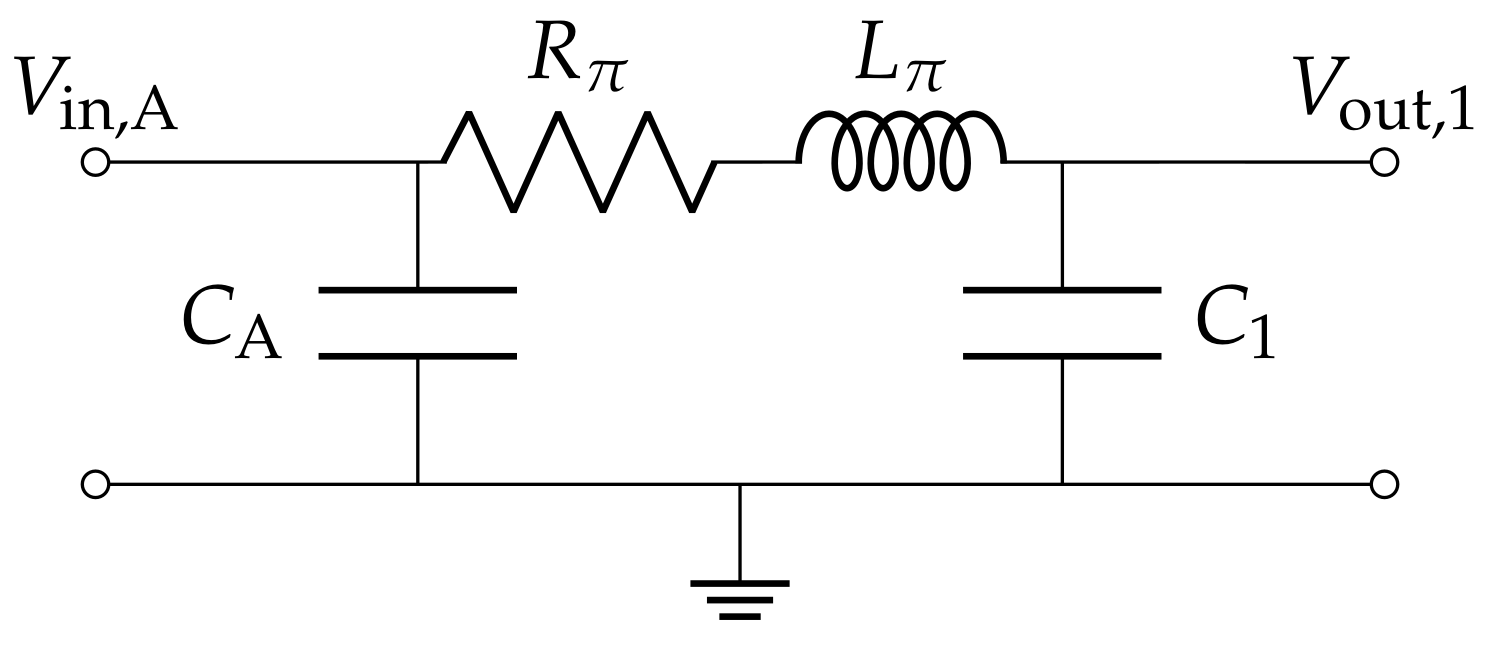
As a first example, we consider a simple pi-model line, as illustrated in Figure 3. Adding a voltage source supplying a voltage (with internal resistance ) on the terminals of capacitor and a resistive load on those of , we obtain a first simple test case. The simulation results in comparison with sequential time-stepping for different simulation lengths , coarsening factors cf, and number of levels are summarized in Table 1. The time-step on the finest level was chosen as s, which was also used for the sequential simulation. Since our model here is equivalent to a system of well-behaved ordinary differential equations (ODEs), the results confirm that, as expected, the MGRIT algorithm converges for all combinations of meta-parameters. While higher numbers of levels and higher coarsening factors lead to an increase in the required number of iterations until convergence, the speed-up seems to be more or less independent as single iterations are faster. For the most effective combination of parameters, a speed-up of about one order of magnitude can be observed.
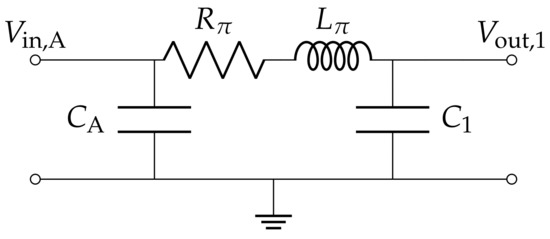
Figure 3.
Schematic of the pi-line. For testing the components individually in a simple test case, voltage source and resistive load were added at the respective terminals.

Table 1.
Runtime of multi-level PinT compared to two-level and sequential time-stepping for the pi-line test case.
4.2. Converter
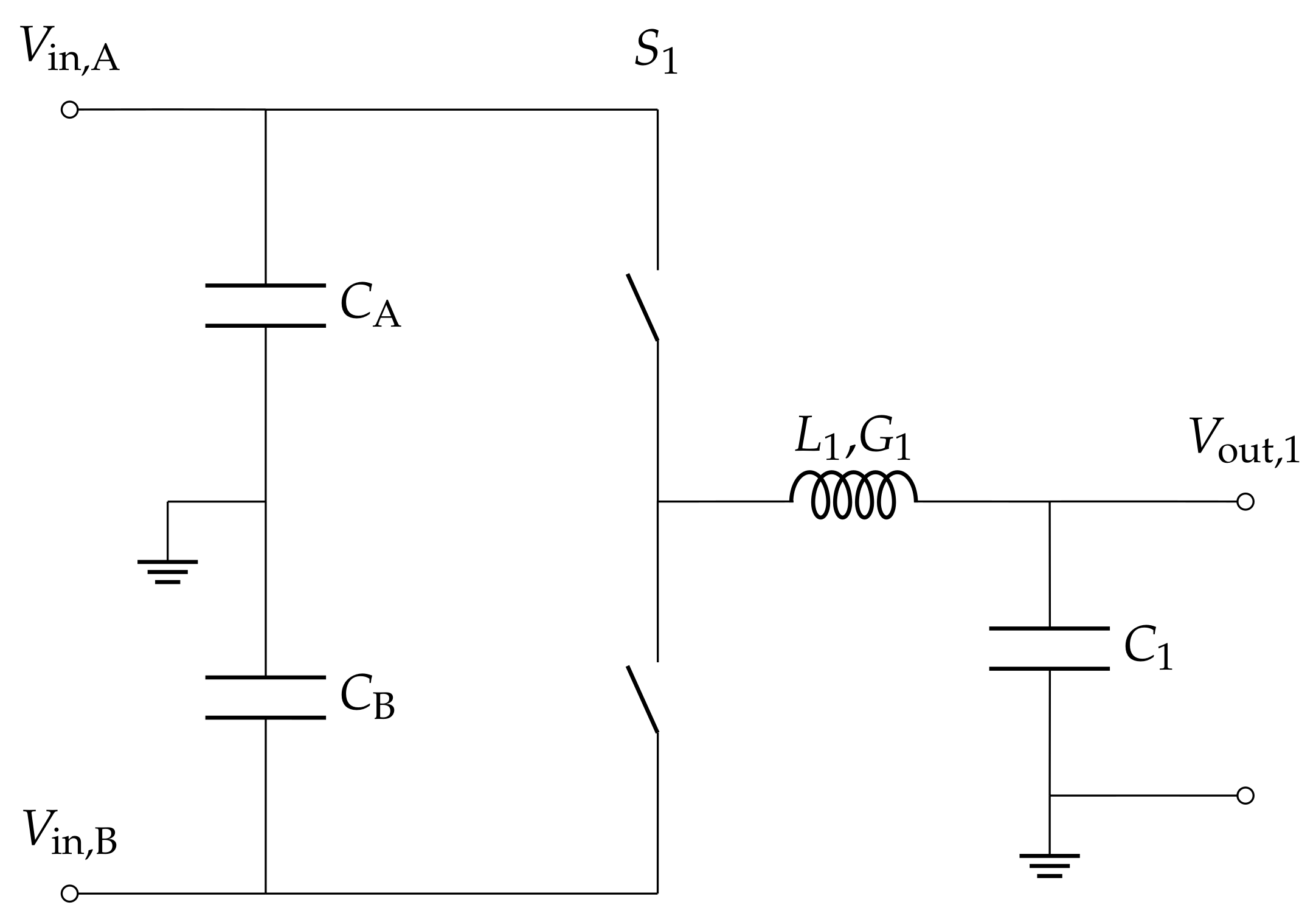
As a second test case, we considered a single leg of a power converter as indicated in Figure 4. We used the latency-based linear multistep compound (LB-LMC) modelling approach [10] to ensure that our results were compatible with parallel-in-space (PinS) execution of individual time steps.
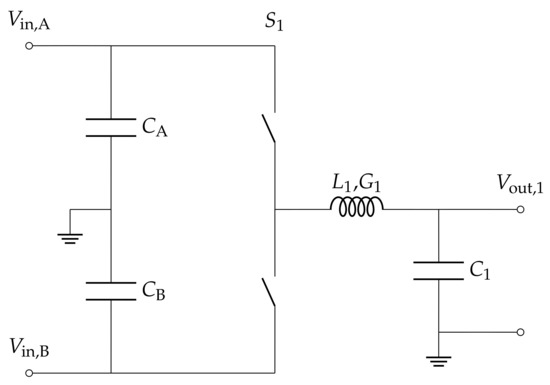
Figure 4.
Schematic of the converter with output LC-filter. For testing the components individually in a simple test case, voltage source and resistive load were added at the respective terminals.
The simulation results in comparison with sequential time-stepping for different simulation lengths , coarsening factors cf, and number of levels are summarized in Table 2. For the converter, we used a time-step of s and a switching frequency of . Again, we see a higher number of iterations for higher coarsening factors and numbers of levels, by which the overall reduction in runtime seems unaffected. The speed-up for the best combination of parameters is about one order of magnitude, as before.

Table 2.
Runtime of multi-level PinT compared to two-level and sequential time-stepping for the converter test case. Deterioration in convergence occurs for cases in which the coarsest time-step and switching period of the converter are not well-aligned.
Due to the switching behavior of the converter, we expect impaired convergence for cases where the maximum time-step is greater than the switching period of the converter or does not align with it. Considering, for example, the case of and , the coarsest time-step would be . The switching period of is not an integer multiple of this time-step, and, thus, the coarsest steps do not align with the switching events. For all combinations of parameters in which the switching period is not an integer multiple of the coarsest time-step, we see that the approximation on the coarse grid is not able to appropriately capture the development of the duty cycle and cumulative error, leading to non-convergence.
4.3. Microgrid
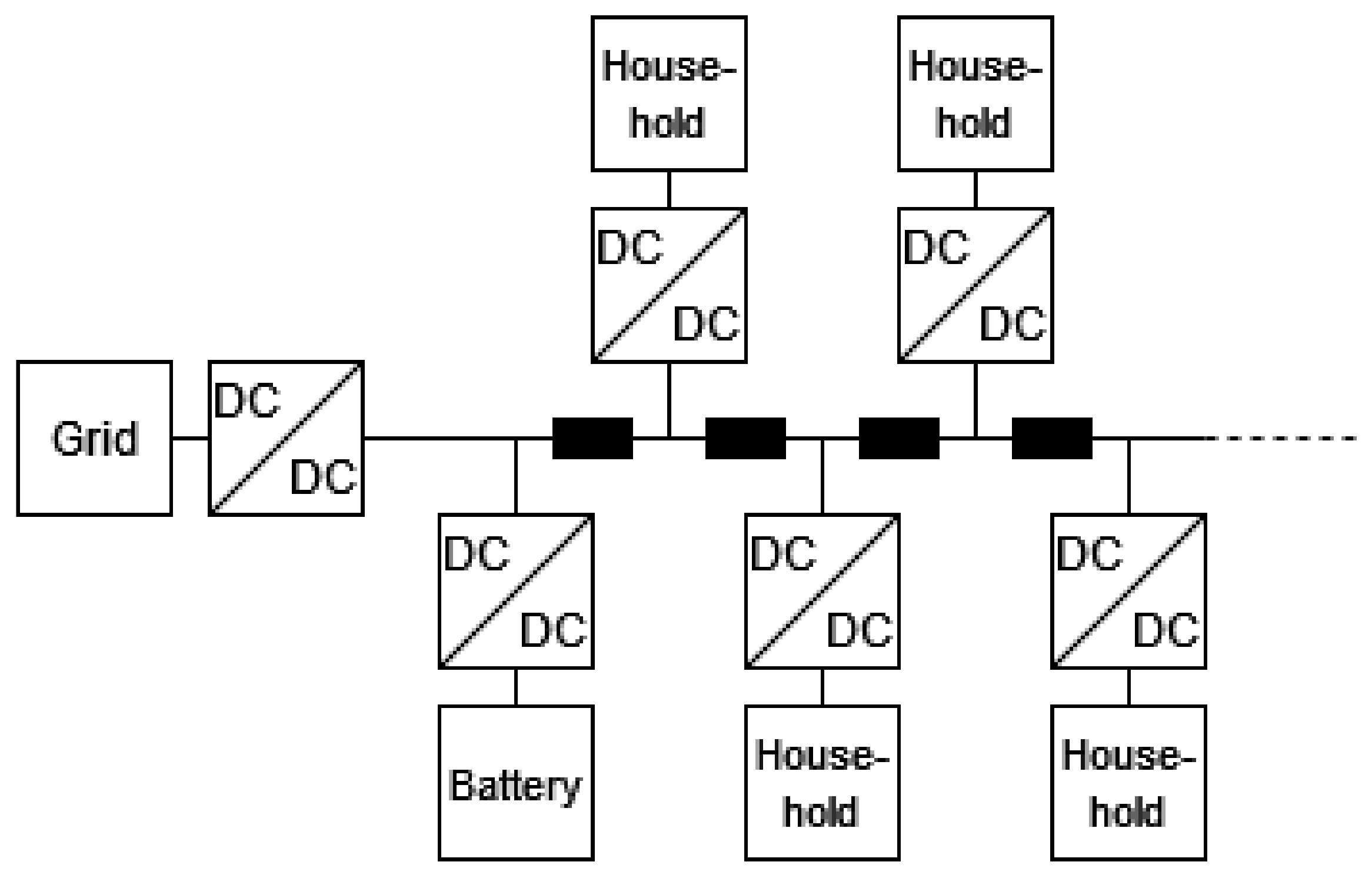
As a final and more comprehensive test case, we consider a residential microgrid. The schematic of the microgrid can be found in Figure 5. The microgrid is structured around a DC bus where household, storage and generation units are interfaced by means of DC/DC converters. The number of household-type elements is not fixed and can be used to scale the computational burden of the test case (cf. Section 4.5). As an example, the electrical current for 16 households, ramping up their consumption over one second, with randomly selected initial times, is shown in Figure 6.
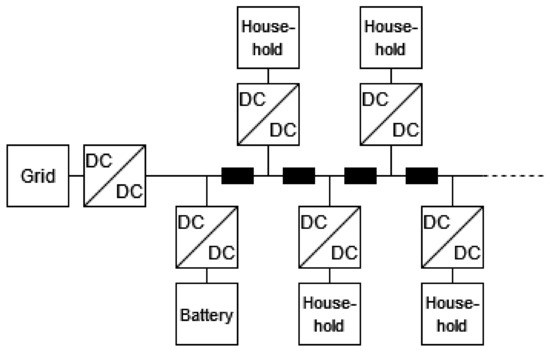
Figure 5.
Schematic of the microgrid. Converters are marked by the label “DC/DC”, while the labels “Grid”, “Battery”, and “Household” represent simple models of the given elements. Black boxes represent a pi-model line, as described in Section 4.1.
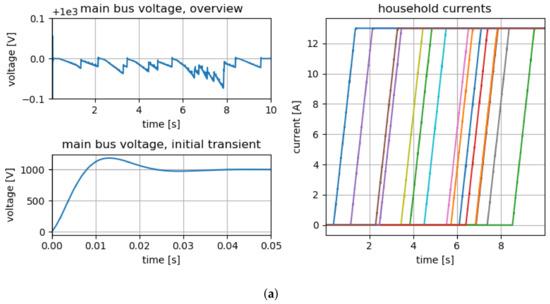
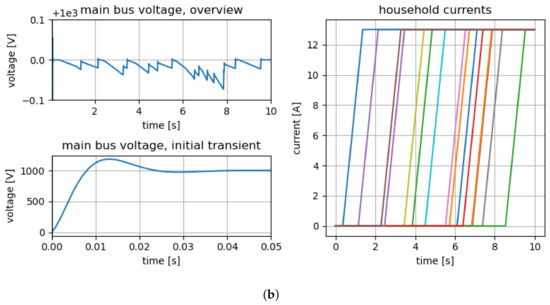
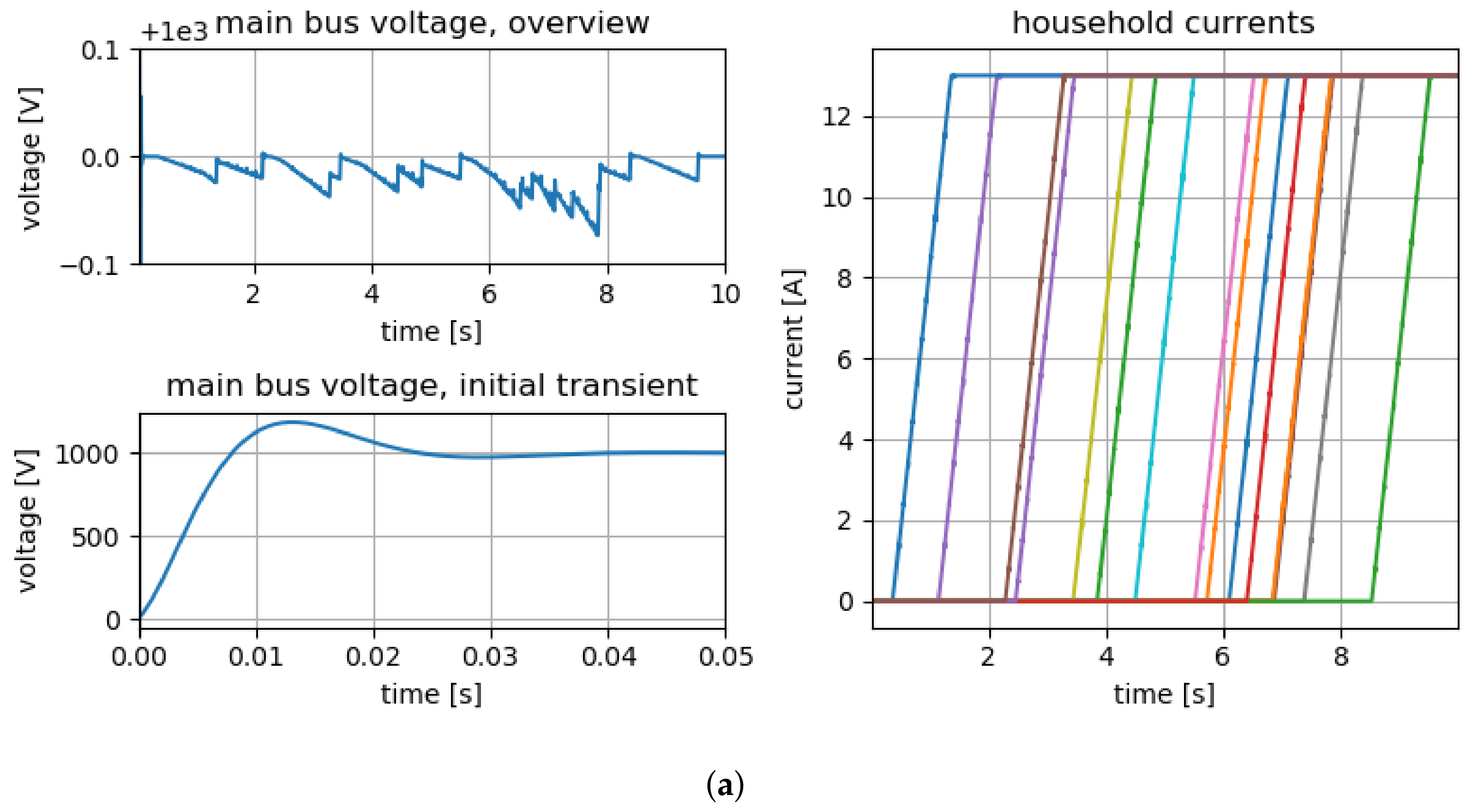
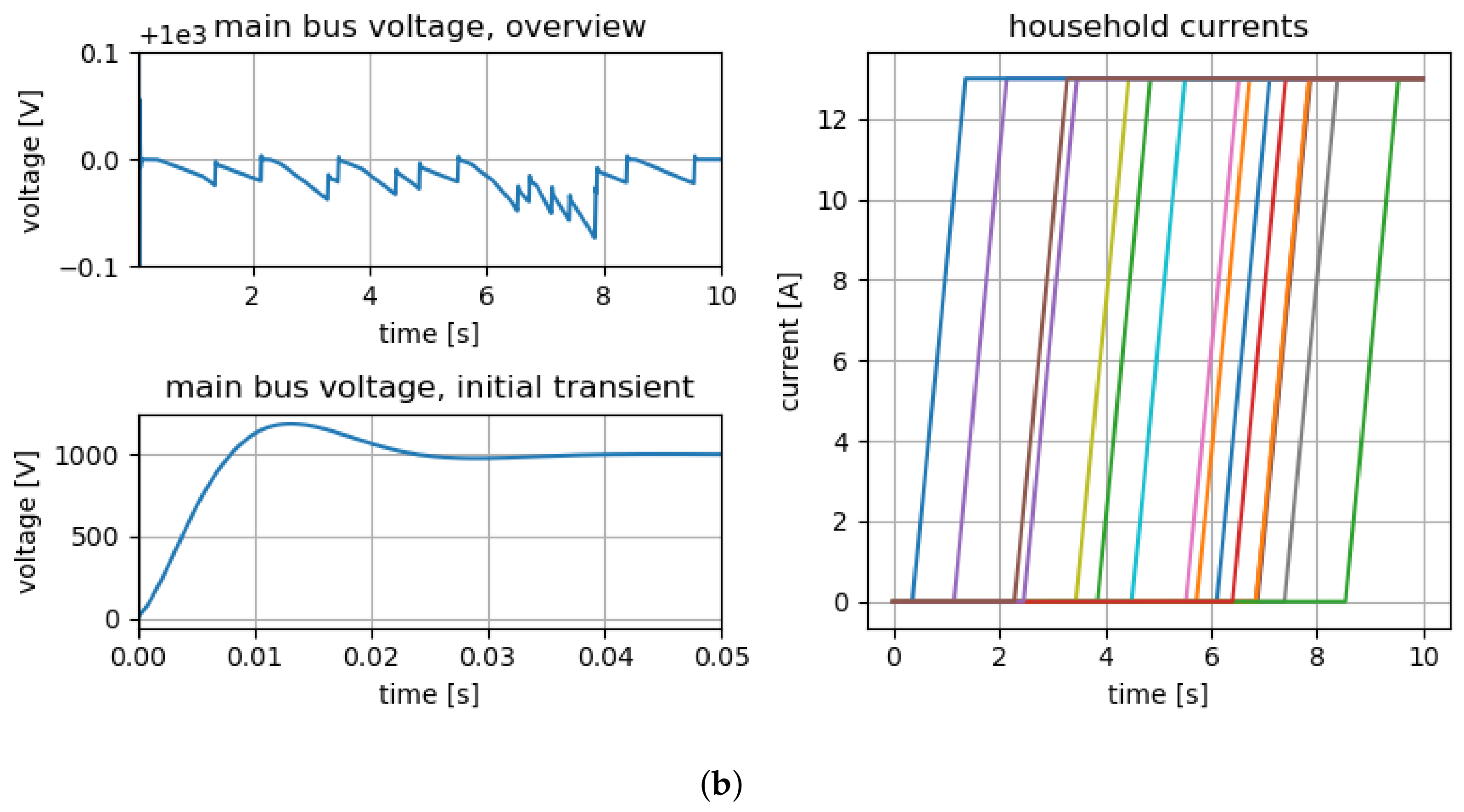
Figure 6.
Simulation results of a 16-household microgrid with ramps in each household for (a) PinT and (b) sequential execution. The simulation was performed with a cold-start (all voltages and currents equal to zero). The initial transient of the main bus voltage is shown in the lower left plots, respectively. The development of the current over the whole simulation interval is shown in the respective upper left plots (note the shift of the abscissa by the target voltage, ). The main bus voltage stays well within an error interval of . The currents in the households are summarized in the right-hand side plots. Each household ramps up its power consumption from zero to over one second, with randomly chosen switch-on times. (a) Results of PinT simulation. Some minor artifacts resulting from iterating only until the chosen error tolerance was reached are visible. (b) Results of sequential simulation for comparison.
The simulation results in comparison with sequential time-stepping for different simulation lengths , coarsening factors cf, and number of levels are summarized in Table 3. As for the single converter, we used a time-step s and a switching frequency . Non-convergence of the residuals is marked with “NC” for the applicable parameter combinations. As with the converter model, the reason for this non-convergence is that, due to the internal switching cycle of the proportional-integral (PI)-controlled converter, some combinations of coarsening factors cf and number of coarse intervals lead to control events that fall between coarse time-grid points and, thus, cannot be calculated correctly on the coarse grids. As in the previous cases, an increase in the required number of iterations for certain parameter combinations does not lead to less speed-up.

Table 3.
Runtime of multi-level PinT compared to two-level and sequential time-stepping for the microgrid test case with four household-type elements. The results summarized here display the expected behavior of no convergence whenever the coarsest time-step does not align with the switching period. On the other hand, when alignment is given, the algorithm converges and, for higher coarsening factors and amounts of levels, speeds up the simulation somewhat.
To test the multi-level capabilities of our approach, a second series of measurements with a much smaller time-step of s and s was performed. While this is not a step size that would usually be used, the results summarized in Table 4 show that higher amounts of coarse levels are not only possible with the right combination of parameters but even lead to better speed-ups. Nevertheless, the problem remains that the coarsest levels have to coincide with the switching intervals. The use of an averaged model of the controlled converter might resolve the issue but this is not within the scope of this article.

Table 4.
Runtimes for sufficiently small time-step to allow convergence in the microgrid test case. Time-steps of this size would usually not be used in applications, but the results prove that better speed-ups are possible if the alignment of coarse step size and switching period is respected.
4.4. Multi-Level Scaling Advantage
The scaling potential of the multi-level approach becomes apparent when reducing the amount of coarse steps to correspond to the number of processing units available, such that the available two-level parallelism is exhausted. When using a two-level approach, the number of processing units that can reasonably be used corresponds to the number of time slices whose fine solution can theoretically be computed in parallel. This means that the number of C-points should correspond to the number of processing units for the optimal two-level speed-up.
A multi-level approach, on the other hand, can enable much more parallelism to exploit any further processing capabilities.
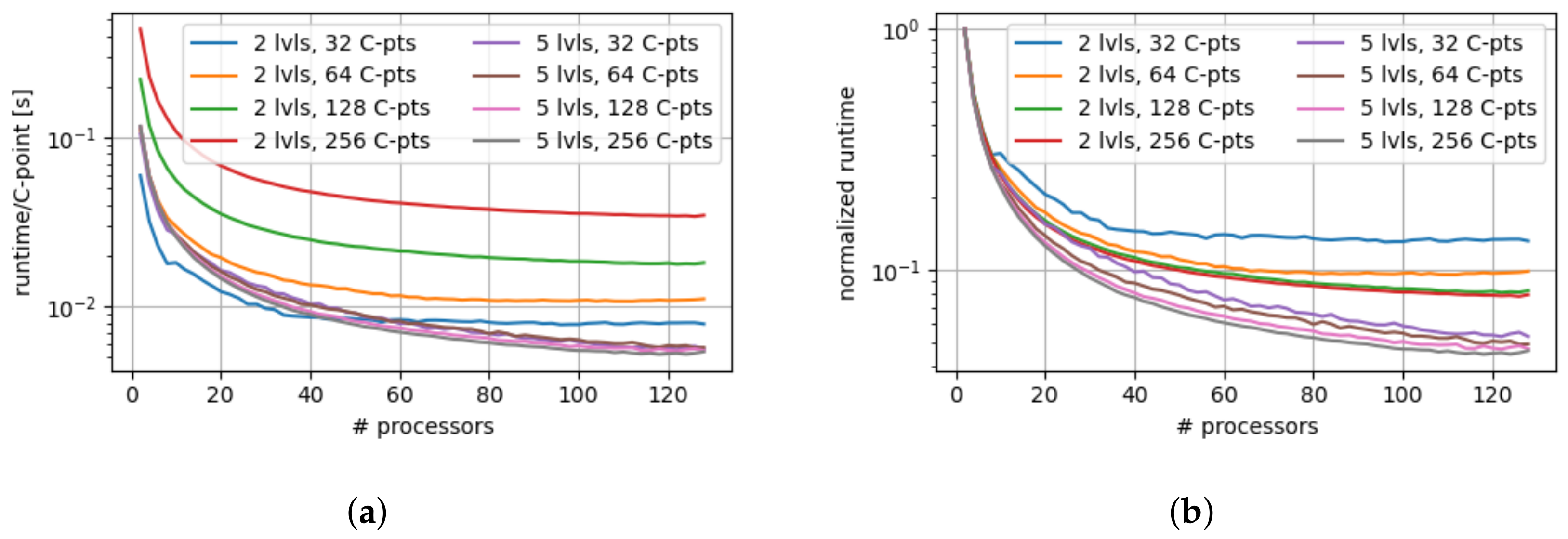
To illustrate this, we solve the microgrid test case with a two-level and a five-level algorithm for simulation durations corresponding to 64, 96, 128, and 256 coarsest time-steps, respectively. In both the two-level and the five-level version, the coarsest step size is chosen to correspond to , while the finest time-step was set to . The two-level version employs a coarsening factor to reach on the coarse level, while the five-level version’s uniform coarsening factor was chosen as , resulting in each level’s step length being twice that of the previous level, and ultimately reaching on the coarsest level. As mentioned above, we expected the speed-up of the two-level version to plateau when the number of processes reached the number of coarse levels. Figure 7a,b demonstrate that this expected behavior does indeed occur, showcasing the increased amount of parallelism that multi-level approaches can offer.
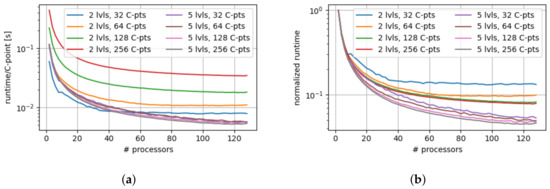
Figure 7.
Multi-level allows for higher rates of parallelism, resulting in more speed-up in case the available resources are already exhausted by a two-level PinT algorithm. The plots illustrate this comparing speed-ups between the two-level and five-level versions of the MGRIT algorithm for 64, 96, 128, and 256 time-steps on the coarsest level. In all cases, a microgrid with four household-type elements was simulated with a coarsest time-step of and a fine time-step of . For the five-level version, three intermediate coarsening levels with uniform coarsening factor were added, resulting in time-steps of . (a) Absolute runtime per coarse step. For all cases, the multi-level version scales better with increasing number of processors. (b) Illustration of speed-up only resulting from adding processors. Relative runtime compared to that of the first datapoint.
4.5. Scalability of the Test Case
Testing the scalability (in space) of our approach, we added varying amounts of household-type elements to the microgrid studied in Section 4.3, connected via pi-model lines, as shown in Figure 5. As meta-parameters, we used differently spaced time grids with a coarsening factor of . The results can be found in Table 5.

Table 5.
Microgrid: Runtime Comparison Between PinT and Sequential Timestepping for Different Grid Sizes.
The percentage speed-up compared to sequential execution remains stable even for much larger grids.
While this indicates the workability of our approach, the execution time itself remains dependent on the grid-size. Different components are still solved sequentially per time-step, leading to increased execution times on a component level and, thus, higher overall execution times. To tackle this, parallelization techniques in space, such as the latency-based linear multistep compound (LB-LMC) approach, are needed. The simultaneous application of both a PinS and a multi-level PinT method will be analyzed in a future publication.
5. Conclusions
Multi-level approaches provide further opportunities for parallelization when the per-step parallelity is already fully exhausted. Application to simulations of converters that are modelled on the switch-level may enable faster-than-real-time simulations of power systems at a level of accuracy that, until now, has only been reached by slower simulation approaches.
In this paper, we have presented a multi-level PinT approach for simulating power electronics devices in DC microgrids. The approach has been shown to provide further parallelization opportunities and, thus, better scaling with processor number than simple two-level approaches, while already reaching speed-ups of up to four times compared to the two-level version when executed with a relatively small number of processing units (cf. Table 2). With the right meta-parameters, which depend upon the simulated case, we were able to reduce the PinT simulation time to between and of the sequential simulation time, as shown in Table 1 and Table 3. Overall, a higher coarsening factor and increased number of levels seem to lead to a higher number of required iterations until the algorithm converges, but, due to faster iterations, an improved speed-up is still possible, as shown, for example, in Table 3.
While a good choice of the meta-parameters can increase performance, a poor choice can also lead to severe deterioration of performance. These cases seem to occur especially when the internal switching cycle and the coarser time-steps are not synchronized, both for small and large numbers of switch-level modelled power-converter devices. The use of averaged models for the coarse propagators may help mitigate these effects and improve convergence. Applicable model hierarchies that enable larger course-level time-steps are, thus, an interesting avenue for future research.
Of course, a pure PinT approach cannot speed up the individual time-steps. In general, PinT approaches are most effectively used together with highly optimized parallel-in-space (PinS) approaches, when the latters’ potential speed-up is already exhausted and further computing resources are available. The scaling study in Section 4.5 showcases that the speed-up via multi-level PinT is relatively independent of the system size, which suggests that any speed-up gained via single-step-based parallel methods will not diminish the additional potential for PinT speed-up. Thus, a combination with the latency-based linear multistep compound (LB-LMC) method of achieving high spatial parallelism represents a promising candidate for future research.
Author Contributions
Conceptualization, J.S. and A.B.; methodology, J.S.; software, J.S. and D.D.; validation, J.S. and D.D.; formal analysis, J.S.; investigation, J.S.; resources, A.B.; writing—original draft preparation, J.S. and D.D.; writing—review and editing, J.S. and A.B.; visualization, J.S.; supervision, A.B.; project administration, A.B.; funding acquisition, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—project number 313504828.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Lin, N.; Dinavahi, V. Dynamic Electro-Magnetic-Thermal Modeling of MMC-Based DC–DC Converter for Real-Time Simulation of MTDC Grid. IEEE Trans. Power Deliv. 2018, 33, 1337–1347. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, C.; Liu, W.; Guo, C. Accelerated Model of Modular Multilevel Converters in PSCAD/EMTDC. IEEE Trans. Power Deliv. 2013, 28, 129–136. [Google Scholar] [CrossRef]
- Montano, F.; Ould-Bachir, T.; David, J.P. An Evaluation of a High-Level Synthesis Approach to the FPGA-Based Submicrosecond Real-Time Simulation of Power Converters. IEEE Trans. Ind. Electron. 2018, 65, 636–644. [Google Scholar] [CrossRef]
- Marti, J.R.; Linares, L.R. Real-time EMTP-based transients simulation. IEEE Trans. Power Syst. 1994, 9, 1309–1317. [Google Scholar] [CrossRef]
- Devaux, O.; Levacher, L.; Huet, O. An advanced and powerful real-time digital transient network analyser. IEEE Trans. Power Deliv. 1998, 13, 421–426. [Google Scholar] [CrossRef]
- Hollman, J.A.; Marti, J.R. Real time network simulation with PC-cluster. IEEE Trans. Power Syst. 2003, 18, 563–569. [Google Scholar] [CrossRef]
- Lok-Fu, P.; Faruque, M.O.; Xin, N.; Dinavahi, V. A versatile cluster-based real-time digital simulator for power engineering research. IEEE Trans. Power Syst. 2006, 21, 455–465. [Google Scholar] [CrossRef]
- Zhou, Z.; Dinavahi, V. Parallel Massive-Thread Electromagnetic Transient Simulation on GPU. IEEE Trans. Power Deliv. 2014, 29, 1045–1053. [Google Scholar] [CrossRef]
- Le-Huy, P.; Woodacre, M.; Guérette, S.; Lemieux, É. Massively Parallel Real-Time Simulation of Very-Large-Scale Power Systems. In Proceedings of the IPST Conference IPST2017, Seoul, Korea, 26–29 June 2017. [Google Scholar]
- Benigni, A.; Monti, A. A parallel approach to real-time simulation of power electronics systems. IEEE Trans. Power Electron. 2014, 30, 5192–5206. [Google Scholar] [CrossRef]
- Razik, L. High-Performance Computing Methods in Large-Scale Power System Simulation. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2020. [Google Scholar]
- Ou, K.; Rao, H.; Cai, Z.; Guo, H.; Lin, X.; Guan, L.; Maguire, T.; Warkentin, B.; Chen, Y. MMC-HVDC Simulation and Testing Based on Real-Time Digital Simulator and Physical Control System. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 1109–1116. [Google Scholar] [CrossRef]
- Leiserson, C.E.; Thompson, N.C.; Emer, J.S.; Kuszmaul, B.C.; Lampson, B.W.; Sanchez, D.; Schardl, T.B. There’s plenty of room at the Top: What will drive computer performance after Moore’s law? Science 2020, 368, eaam9744. [Google Scholar] [CrossRef] [PubMed]
- Nievergelt, J. Parallel methods for integrating ordinary differential equations. Commun. ACM 1964, 7, 731–733. [Google Scholar] [CrossRef]
- Gander, M.J. 50 Years of Time Parallel Time Integration. In Multiple Shooting and Time Domain Decomposition Methods; Carraro, T., Geiger, M., Körkel, S., Rannacher, R., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 69–113. [Google Scholar]
- Lions, J.L. Résolution d’EDP par un schéma en temps “pararéel” A “parareal” in time discretization of PDE’s. CRASM 2001, 332, 661–668. [Google Scholar]
- Dutt, A.; Greengard, L.; Rokhlin, V. Spectral deferred correction methods for ordinary differential equations. BIT Numer. Math. 2000, 40, 241–266. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Thomas, A., Jr. Spectral Methods in Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Vlassenbroeck, J.; Van Dooren, R. A Chebyshev technique for solving nonlinear optimal control problems. IEEE Trans. Autom. Control 1988, 33, 333–340. [Google Scholar] [CrossRef]
- Reddien, G. Collocation at Gauss points as a discretization in optimal control. SIAM J. Control Optim. 1979, 17, 298–306. [Google Scholar] [CrossRef]
- Speck, R.; Ruprecht, D.; Emmett, M.; Minion, M.; Bolten, M.; Krause, R. A multi-level spectral deferred correction method. BIT Numer. Math. 2015, 55, 843–867. [Google Scholar] [CrossRef]
- Minion, M.L.; Williams, S.A. Parareal and spectral deferred corrections. In AIP Conference Proceedings; American Institute of Physics: Melville, NY, USA, 2008; Volume 1048, pp. 388–391. [Google Scholar]
- Minion, M. A hybrid parareal spectral deferred corrections method. Commun. Appl. Math. Comput. Sci. 2011, 5, 265–301. [Google Scholar] [CrossRef]
- Emmett, M.; Minion, M. Toward an efficient parallel in time method for partial differential equations. Commun. Appl. Math. Comput. Sci. 2012, 7, 105–132. [Google Scholar] [CrossRef]
- Trottenberg, U.; Oosterlee, C.W.; Schuller, A. Multigrid; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Hackbusch, W. Parabolic multigrid methods. In Computing Methods in Applied Sciences and Engineering; Glowinski, R., VI, Lions, J.-L., Eds.; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Gander, M.J.; Vandewalle, S. Analysis of the parareal time-parallel time-integration method. SIAM J. Sci. Comput. 2007, 29, 556–578. [Google Scholar] [CrossRef]
- Bolten, M.; Moser, D.; Speck, R. A multigrid perspective on the parallel full approximation scheme in space and time. Numer. Linear Algebra Appl. 2017, 24, e2110. [Google Scholar] [CrossRef]
- Falgout, R.D.; Friedhoff, S.; Kolev, T.V.; MacLachlan, S.P.; Schroder, J.B. Parallel time integration with multigrid. SIAM J. Sci. Comput. 2014, 36, C635–C661. [Google Scholar] [CrossRef]
- Horton, G.; Vandewalle, S. A space-time multigrid method for parabolic partial differential equations. SIAM J. Sci. Comput. 1995, 16, 848–864. [Google Scholar] [CrossRef]
- Gander, M.J.; Neumuller, M. Analysis of a new space-time parallel multigrid algorithm for parabolic problems. SIAM J. Sci. Comput. 2016, 38, A2173–A2208. [Google Scholar] [CrossRef]
- Vandewalle, S.; Van de Velde, E. Space-time concurrent multigrid waveform relaxation. Ann. Numer. Math. 1994, 1, 335–346. [Google Scholar]
- Lubich, C.; Ostermann, A. Multi-grid dynamic iteration for parabolic equations. BIT Numer. Math. 1987, 27, 216–234. [Google Scholar] [CrossRef]
- Falgout, R.D.; Manteuffel, T.A.; O’Neill, B.; Schroder, J.B. Multigrid reduction in time for nonlinear parabolic problems: A case study. SIAM J. Sci. Comput. 2017, 39, S298–S322. [Google Scholar] [CrossRef]
- Friedhoff, S.; Hahne, J.; Schöps, S. Multigrid-reduction-in-time for Eddy Current problems. PAMM 2019, 19, e201900262. [Google Scholar] [CrossRef]
- Cheng, T.; Duan, T.; Dinavahi, V. Parallel-in-Time Object-Oriented Electromagnetic Transient Simulation of Power Systems. IEEE Open Access J. Power Energy 2020, 7, 296–306. [Google Scholar] [CrossRef]
- Pels, A.; Kulchytska-Ruchka, I.; Schöps, S. Parallel-in-Time Simulation of Power Converters Using Multirate PDEs. In Scientific Computing in Electrical Engineering; van Beurden, M., Budko, N., Schilders, W., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 33–41. [Google Scholar]
- Cheng, T.; Lin, N.; Liang, T.; Dinavahi, V. Parallel-in-time-and-space electromagnetic transient simulation of multi-terminal DC grids with device-level switch modelling. IET Gener. Transm. Distrib. 2022, 16, 149–162. [Google Scholar] [CrossRef]
- Cheng, T.; Lin, N.; Dinavahi, V. Hybrid Parallel-in-Time-and-Space Transient Stability Simulation of Large-Scale AC/DC Grids. In IEEE Transactions on Power Systems; IEEE: New York, NY, USA, 2022; p. 1. [Google Scholar] [CrossRef]
- Lyu, C.; Lin, N.; Dinavahi, V. Device-Level Parallel-in-Time Simulation of MMC-Based Energy System for Electric Vehicles. IEEE Trans. Veh. Technol. 2021, 70, 5669–5678. [Google Scholar] [CrossRef]
- Park, B.; Sun, K.; Dimitrovski, A.; Liu, Y.; Simunovic, S. Examination of Semi-Analytical Solution Methods in the Coarse Operator of Parareal Algorithm for Power System Simulation. IEEE Trans. Power Syst. 2021, 36, 5068–5080. [Google Scholar] [CrossRef]
- Cai, M.; Mahseredjian, J.; Kocar, I.; Fu, X.; Haddadi, A. A parallelization-in-time approach for accelerating EMT simulations. Electr. Power Syst. Res. 2021, 197, 107346. [Google Scholar] [CrossRef]
- Schroder, J.B.; Falgout, R.D.; Woodward, C.S.; Top, P.; Lecouvez, M. Parallel-in-time solution of power systems with scheduled events. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Cheng, C.K.; Ho, C.T.; Jia, C.; Wang, X.; Zen, Z.; Zha, X. A Parallel-in-Time Circuit Simulator for Power Delivery Networks with Nonlinear Load Models. In Proceedings of the 2020 IEEE 29th Conference on Electrical Performance of Electronic Packaging and Systems (EPEPS), San Jose, CA, USA, 5–7 October 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Friedhoff, S.; Falgout, R.D.; Kolev, T.V.; MacLachlan, S.P.; Schroder, J.B. A Multigrid-in-Time Algorithm for Solving Evolution Equations in Parallel. In Proceedings of the Sixteenth Copper Mountain Conference on Multigrid Methods, Copper Mountain, CO, USA, 17–22 March 2013. [Google Scholar]
- Dobrev, V.A.; Kolev, T.; Petersson, N.A.; Schroder, J.B. Two-Level Convergence Theory for Multigrid Reduction in Time (MGRIT). SIAM J. Sci. Comput. 2017, 39, S501–S527. [Google Scholar] [CrossRef]
- Günther, S.; Gauger, N.R.; Schroder, J.B. A Non-Intrusive Parallel-in-Time Adjoint Solver with the XBraid Library. Comput. Vis. Sci. 2018, 19, 85–95. [Google Scholar] [CrossRef]
- Hessenthaler, A.; Southworth, B.S.; Nordsletten, D.; Röhrle, O.; Falgout, R.D.; Schroder, J.B. Multilevel convergence analysis of multigrid-reduction-in-time. SIAM J. Sci. Comput. 2020, 42, A771–A796. [Google Scholar] [CrossRef]
- Beilina, L.; Karchevskii, E.; Karchevskii, M. Numerical Linear Algebra: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Hackbusch, W. Multi-Grid Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 4. [Google Scholar]
- Dommel, H.W. Digital computer solution of electromagnetic transients in single-and multiphase networks. In IEEE Transactions on Power Apparatus and Systems; IEEE: New York, NY, USA, 1969; pp. 388–399. [Google Scholar]
- XBraid: Parallel Multigrid in Time. Available online: https://github.com/XBraid/xbraid (accessed on 24 August 2022).
- Wu, B.; Dougal, R.; White, R.E. Resistive companion battery modeling for electric circuit simulations. J. Power Sources 2001, 93, 186–200. [Google Scholar] [CrossRef]
- Guennebaud, G.; Steiner, B.; Larsen, R.M.; Sánchez, A.; Hertzberg, C.; Zhulenev, E.; Goli, M.; Tellenbach, D.; Jacob, B.; Margaritis, K.; et al. Eigen v3. 2010. Available online: http://eigen.tuxfamily.org (accessed on 25 January 2022).
- Friedhoff, S.; Southworth, B.S. On “Optimal” h-independent convergence of Parareal and multigrid-reduction-in-time using Runge-Kutta time integration. Numer. Linear Algebra Appl. 2021, 28, e2301. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).