Abstract
Increasing economic and population growth has led to a rise in electricity consumption. Consequently, electrical utility firms must have a proper energy management strategy in place to improve citizens’ quality of life and ensure an organization’s seamless operation, particularly amid unanticipated circumstances such as coronavirus disease (COVID-19). There is a growing interest in the application of artificial intelligence models to electricity prediction during the COVID-19 pandemic, but the impacts of clustering methods and parameter selection have not been explored. Consequently, this study investigates the impacts of clustering techniques and different significant parameters of the adaptive neuro-fuzzy inference systems (ANFIS) model for predicting electricity consumption during the COVID-19 pandemic using districts of Lagos, Nigeria as a case study. The energy prediction of the dataset was examined in relation to three clustering techniques: grid partitioning (GP), subtractive clustering (SC), fuzzy c-means (FCM), and other key parameters such as clustering radius (CR), input and output membership functions, and the number of clusters. Using renowned statistical metrics, the best sub-models for each clustering technique were selected. The outcome showed that the ANFIS-based FCM technique produced the best results with five clusters, with the Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Coefficient of Variation (RCoV), Coefficient of Variation of the Root Mean Square Error (CVRMSE), and Mean Absolute Percentage Error (MAPE) being 1137.6024, 898.5070, 0.0586, 11.5727, and 9.3122, respectively. The FCM clustering technique is recommended for usage in ANFIS models that employ similar time series data due to its accuracy and speed.
1. Introduction
Electricity is essential for improving one’s quality of life as well as maintaining the efficient running of an organization. The primary responsibility of electric utility companies is to ensure that consumers have uninterrupted access to electricity through the process of generation, transmission, and distribution [1,2]. Hence, understanding energy production and consumption are critical for budgeting production costs, planning for the future, and establishing a production–consumption balance. For instance, the advent of the novel coronavirus disease (COVID-19 or SARS-COV-2) which broke out in China in 2020, has pushed humanity in the direction of a new norm, and adjustment to it is inevitable. In an effort to curb the spread of COVID-19, lockdowns were implemented, social distancing was established, and public meetings were either limited to a small number of individuals or outright forbidden. In response, the lockdowns greatly impacted traveling, social interaction, working, schooling, tourism, and health care and reduced commercial and industrial operations. The effects of these adjustments on everyday life have affected where, when, and how power is utilized, both in areas recovering from the pandemic and during its height [3]. As epidemic prevention and control strategies changed frequently, load forecasting became more imperative [4]. In the wake of the pandemic, Nigeria, like many developing countries, also saw a lockdown. Nigeria, home to more than 200 million people, confirmed its first case of COVID-19 in Lagos State on 27 February 2020 [5]. Due to a variety of factors, Lagos State is prone to the COVID-19 pandemic spreading quickly. These include its substantial population, overburdened infrastructure, and role as a key regional transit hub for air, land, and sea travel [6]. Combining the effects of the pandemic and poor energy conditions adds new hurdles to those already present. Poor access to energy contributes to the high level of poverty in developing countries [7]. For the energy supply to remain stable and for end customers to have improved operations, a realistic energy forecast is essential. As stated in [8], putting policies in place that will accelerate the development of systems that can foresee demand is vital to ensuring energy stability. Taking a closer look at how the COVID-19 pandemic has impacted electricity consumption could provide insight into society’s response to upcoming shocks and extreme events in the future [3].
According to earlier research, developing artificial intelligence technologies based on statistical and mathematical methods has demonstrated possible answers in estimating and forecasting power consumption. There are two basic classifications of prediction methods [4]. The first is the classic approach, which may be exemplified by regression analysis [9], and the time series approach [10]. The second category includes artificial intelligence techniques such as artificial neural networks (ANN) [11], support vector machines (SVM) [12], and gray models (GM) [13]. That said, forecasting methodologies have advanced significantly over time. Non-linear forecasting has garnered greater attention compared to traditional linear models. This is because real-world problems are nonlinear, and only nonlinear forecasting approaches can produce forecasting models that are accurate and dependable [14]. Nonlinear forecasting has the benefit of being robust and able to handle perturbations, which is one of its major advantages. In addition, the use of soft computing techniques has played major roles in different spheres of life [15,16,17].
1.1. Related Work
ANN is a typical example of a nonlinear forecasting model. ANN is a commonly used machine learning (ML) technology that can replicate synaptic behavior between brain neurons by combining many nonlinear parallel processors to perform the learning function [18]. Previous studies have explored the ANN in forecasting the electricity consumption of buildings, university campuses, residences, etc. For instance, an intelligent technique for forecasting the electricity consumption of buildings was performed by Amber et al. [19]. An analysis of five distinct intelligent methodologies was carried out using the historical power consumption of a building, as well as the associated weather data. As stated by the authors, the ANN model performed at its best when compared to other approaches while using the fewest statistical indicators. In [20], an ML model was developed for heating, ventilation, and air conditioning (HVAC) electricity consumption. A feed-forward back-propagation ANN was shown to perform better than a random forest (RF) model, according to the authors. To understand how a residential electricity customer’s power consumption behavior is affected by the price of electricity, a model was developed in [21], using a multi-layer perceptron, and a recurrent model based on a long–short-term memory (LSTM) network.
For enhancing the prediction of energy consumption in residential constructions during the early design phases, Elbeltagi and Wefki [22] developed a system based on ANNs. The authors suggest that the proposed approach reduces technical impediments by integrating and automating commonly available commercial technologies. Chen et al. [23] investigated the forecasting of office building power usage using ANN while partitioning the time horizon for diverse occupancy rates. The proposed ANN model produced a reliable outcome.
Moon et al. [24] conducted a comparative study using diverse combinations of hyperparameters (activation function and number of hidden layers) of neural networks to identify the most efficient parameters for ANN-based energy consumption. The authors reported the optimal performance of the proposed model with five hidden layers and a scaled exponential linear unit (SELU) activation function. Yuan et al. [25] offered an ANN-based prediction model for seasonal hourly electricity consumption for three areas of a university campus using Japan as a case study. For testing, the proposed model generated optimal results with correlation coefficients between 0.95 and 0.99 using feed-forward ANNs trained with Levenberg–Marquardt (LM) back-propagation algorithms.
ANFIS is another modeling technique which amalgamates the ANN with a fuzzy inference system (FIS) to improve the speed, fault tolerance, and addictiveness of the modeling system [26]. In this way, ANFIS has become an accepted tool in forecasting time series and analyzing problems. Numerous fields such as smart grid [27], wind energy [28], agriculture [29], petroleum engineering [30], stock-market [31], and biogas [32], etc. have utilized the ANFIS for forecasting. As compared to other methods, its effectiveness is demonstrated by its superior performance. This is attributable to its special features of harnessing both ANN and FIS. Chen and Lee [33] presented the efficacy of ANFIS in the prediction of power consumption for buildings utilizing multiple ANFIS models with gray relational analysis. An ANFIS-based short-term predictive model for an educational building was carried out in [34]. The suggested model produced accurate prediction under some statistical metrics using a data split of 80%, 10%, and 10% for training, testing, and validation, respectively. Using ANN and ANFIS techniques, Kaysal et al. [35] designed a short-term load forecasting (STLF) model for a small region. The proposed ANFIS model demonstrated the best performance under the RMSE and MAPE statistical metrics. Klimenko et al. [36] worked on the forecasting of electric energy consumption of urban systems using autoregressive integrated moving average (ARIMA), ANN, and ANFIS models. The suggested ANFIS strategy was found to be the most successful in the investigation as a short-term and operational forecasting technique that also uses meteorological parameters. Table 1 shows the summary table of the previous works as discussed and their various contributions.

Table 1.
Summary of the contributions of previous studies.
However, even though ANFIS has been widely employed in the prediction of electricity consumption, earlier research failed to address the impact of clustering techniques and other key parameters that are critical to the operation of the ANFIS model. The choice of clustering techniques must be carried out carefully since clustering strategies have a significant influence on the precision of the model when approximating an output function [38]. Optimal performance and excellent prediction accuracy need carefully chosen clustering approaches and other critical parameters. Failure to select the best clustering approaches and parameters will eventually diminish the model’s accuracy. The performance of ANFIS is hinged on the appropriate parameter selection. In response, this study is aimed at investigating the effect of ANFIS clustering techniques, such as subtractive clustering (SC), grid partitioning (GP), and fuzzy c-means (FCM) in predicting electricity consumption during COVID-19 using Lagos, Nigeria as a case study.
1.2. Contribution and Paper Organization
The main contributions of this study are as follows:
- develop three ANFIS models by employing subtractive clustering, grid partitioning, and fuzzy c-means techniques, respectively.
- develop multiple sub-models by varying different parameters such as the input MF-type, output MF-type, cluster radius, and number of clusters.
- extensively compare overall prediction performances using five prominent performance metrics and computational time.
2. Materials and Methods
2.1. ANFIS Model
Adaptive Neuro-Fuzzy Inference System (ANFIS) was presented by Jang [26] in 1993. It is a unique hybrid model which employs the paired features of neural networks and fuzzy logic in its design. In other words, being an adaptive hybrid multi-layer feedforward network ANFIS harnesses the duo learning capabilities of artificial neural networks (ANN) with fuzzy inference systems (FIS) to mimic the process through which humans make knowledgeable decisions [39]. The ANFIS modeling technique is derived from the Takagi–Sugeno fuzzy system, which consists of antecedents and consequences [40]. The five levels of the ANFIS architectural framework are the fuzzy, product, normalization, defuzzification, and summation layers, which are arranged from layer 1 to layer 5 [26,41]. ANFIS is a hybrid learning methodology that uses back-propagation gradient descent with least squares techniques for optimizing model parameters. The basic ANFIS model uses five layers and fuzzy IF-THEN rules to produce a nonlinear map between input and output, as illustrated in Figure 1. In the first layer, two inputs are received, x and y, and each node’s output is determined by the generalized Gaussian membership function (). These steps are depicted in Equations (1)–(3) [26].
where membership values of are designated as and ; the premise parameter sets are and .
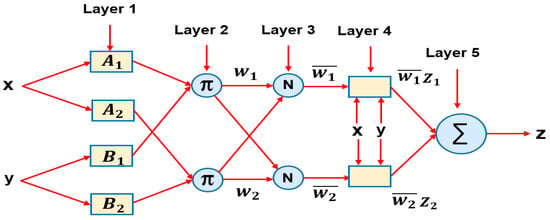
Figure 1.
ANFIS model architecture.
The output of each node in the second layer (the firing strength of a rule) is calculated in the next phase of ANFIS using Equation (4) [26]:
The output of the third layer node is described in Equation (8), which is also known as the normalized firing strength [26]:
The output is computed by the adaptive nodes at Layer 4 using Equation (6) [26]:
where , , and are the consequent parameters of the node . The ANFIS model’s final layer contains just one node, and its output is calculated as follows [26]:
The clustering approach is critical to the ANFIS model’s viability and tractability [41]. The choice of clustering algorithms must be considered carefully since the type of clustering utilized for ANIFS has a significant influence on the model’s accuracy when approximating an output function [38]. Hence, the next session discusses the different types of clustering techniques used in this study. Figure 2 shows the flowchart of the proposed ANFIS model.
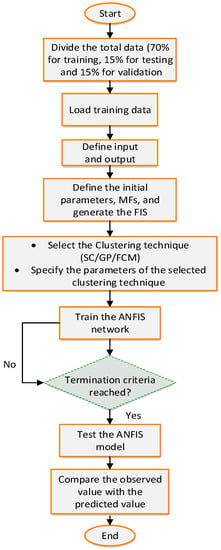
Figure 2.
Flowchart of the proposed ANFIS model.
2.2. Clustering Technique
Organizing data sets into groups and placing them in clusters in such a way that each cluster contains unique objects is known as clustering, and it is a crucial task in data mining and statistical analysis [42]. Clustering is one of the key phenomena in the development of the ANFIS model. In order to allocate MFs and produce the FIS structure from the data, the ANFIS uses clustering algorithms to organize data into comparable fuzzy clusters [40]. The three most widely used clustering techniques are subtractive clustering (SC), grid partitioning (GP), and fuzzy c-means (FCM). Each one of these clustering techniques is explored in this present study to predict energy usage.
2.2.1. Subtractive Clustering (SC)
The SC approach is used when it is unclear how many data distribution centers will be needed. ANFIS-SC is a merger of the ANFIS and SC techniques. This method calculates the likelihood that each data point will develop a cluster center based on the density of the nearby data points and operates under the premise that each data point is a potential cluster center [42]. Suppose that there are data points in an dimensional space and that the data points have been normalized in each dimension, then Equation (8) gives the potential of data point .
where is the Euclidean distance and is given as , can be expressed as a positive constant which is a radius which determines the neighboring data point. Hence, the potential of a data point depends on its proximity to other data points [42]. In clustering data spaces, the radius must be selected carefully because its size determines the number of clusters.
2.2.2. Grid Partitioning (GP)
One of the most important steps is to decide on the ideal amount and types of fuzzy rules [43]. Subtractive clustering is one of several automated techniques available for this purpose. Clustering is achieved by dividing the input space into rectangular subspaces by axis-parallel partition based on a predefined number of MFs and their types per dimension. The number of fuzzy rules and the input have an exponential connection, signifying that the number of fuzzy rules in a system with inputs and MFs for each variable will be [44]. In response, massive computer memory is needed. This is a significant drawback of the GP approach, and this restriction is known as “curse dimensionality [45]”. The performance of the system is influenced by the size of the input, hence an adaptive GP can be employed to optimize the size and location of the fuzzy grid areas [46].
2.2.3. Fuzzy c-Means Clustering (FCM)
The FCM clustering method is a fuzzed variation of the k-means algorithm, which was derived from the traditional Euclidean distance function and incorporates hyperspherical clusters [47]. An estimate of the cluster center serves as the algorithm’s first step. This methodology provides a membership degree to each data point and leads the data centers by regularly updating the centers and the membership of each data point, in contrast to hard clustering methodologies, in which each observation could only directly relate to a single and only one cluster [40,48,49]. In addition to its speed-boosting capability, the FCM offers the advantage that it does not restrict cluster boundaries, which allows objects to belong to more than one group rather than to a single group exclusively [50]. The expression in Equation (9) is utilized to minimize the distance center to each datum for each fuzzy group and vector , = 1, 2 … .
where is the degree of membership, (0, 1), is the weighting exponent, which is any number concerning , is the data points, is the centroid of clusters, and is the number of clusters. Equation (10) indicates the of the data point in the cluster at any iteration.
2.3. Case Study
Lagos State is the commercial center of Nigeria due to its fast urbanization and population growth. Lagos is the most populated metropolis in Africa, with an estimated 20 million residents spread over 3577 km2 [5]. It also has Nigeria’s greatest population density. Geographically, Lagos is located in Southwestern Nigeria (see Figure 3). Located in the south of the Atlantic Ocean, it is bordered by the Atlantic Ocean on the north and east as well as the Ogun State of Nigeria on the west [51]. It is located on latitude 6°27′55.5192″ N and longitude 3°24′23.2128″ E, respectively. There are 20 local government areas (LGA) in it, and 16 of them compose the high-density metropolitan region [52]. The state has two seasons: a rainy season from April to October and a dry season from November to March. This is due to the interaction between the warm, humid marine tropical air mass and the hot, dry continental air mass from the interior [53]. Year-round, the air is quite humid, with monthly maximum average temperatures ranging from 28.6 °C in July/August to 33.7 °C in March [54]. The level of temperature and humidity during the different seasons alters people’s lifestyles and inevitably their energy consumption. The same is true during the pandemic. Consequently, this study utilizes electricity consumption data (during the COVID-19 pandemic) from ten key districts in Lagos (see Figure 3) for model development.
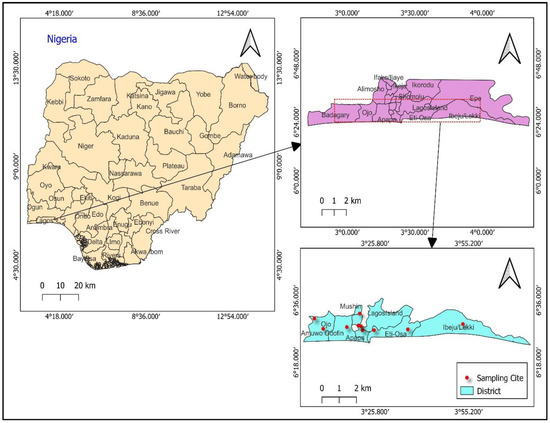
Figure 3.
Map showing the geographical location of the study area.
2.4. Data Collection
This paper investigates the impact of clustering techniques and other essential parameters for estimating the power usage of ten Lagos districts (see Figure 3). The forecasting model was developed using the historical energy data of ten districts in Lagos, which were obtained from Eko Electricity Distribution Company (EKEDC) for the period between 1 January 2019 and 31 December 2020. Similarly, corresponding essential meteorological data for the same period was obtained from the nearby weather stations reported by Visual Crossing Weather Data. The meteorological inputs are maximum temperature, minimum temperature, humidity, and wind speed, respectively. The output of the model is electricity consumption (MWh). The total number of data obtained was divided into training (70%), testing (15%), and validation (15%) for the development of the model. The architectural design of the model is presented in Figure 4. Owing to the fact clustering plays an important role in the operation of ANFIS, a comprehensive comparative study is conducted between the three key clustering techniques while at the same time considering key parameter variations, yielding several sub-models. As depicted in Figure 4, the meteorological data are inputted into each of the models, namely, ANFIS-GP, ANFIS-SC, and ANFIS-FCM, respectively. The output of the model is electricity consumption. In the end, the optimal model is selected.
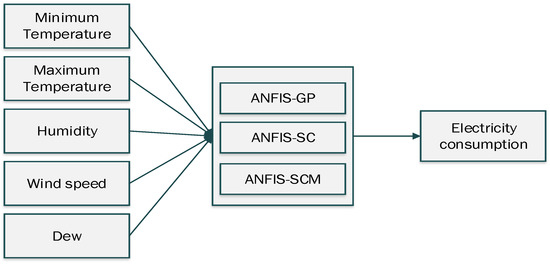
Figure 4.
Architectural design of the proposed models.
2.5. Performance Evaluation
The proposed models utilized a dataset division of 70% for training and 30% for testing. Generally, developed models are often evaluated by applying statistical metrics to determine their accuracy. The developed models were implemented under five performance measures to reveal the models’ correctness between the actual electricity usage and the predicted values. The test data were analyzed according to the same and renowned statistical metrics for a fair comparison and testing of model reliability. Among the performance metrics used are the Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Coefficient of variation (RCoV). In addition, the coefficient of variation of the root mean square error (CVRMSE) and Mean Absolute Percentage Error (MAPE) are also used to compare the performance of the developed models. The reason for this is that they are more understandable than other performance metrics, such as RMSE or MSE because they represent accuracy in per cent terms [24]. We also evaluated the models’ performance based on their computational time (CT). As presented in Table 2, the more closely they approach zero, the more trustworthy the model is, while a negative value denotes an underestimation tendency of the model [1,55,56,57]. The descriptions of the performance metrics are as follows:

Table 2.
Performance evaluation acceptability criteria.
Root mean square error:
Coefficient of variation of the root mean square error:
Mean absolute percentage error:
Mean absolute deviation:
Coefficient of variation:
where is the sample index and and are the actual and predicted values, respectively; is the average of the actual values.
3. Results and Discussion
An overview of the experimental and statistical results is presented and discussed in this section. The models are executed on a Microsoft Windows 10 operating system with an Intel (R) CPU @3.20 GHz and 16 GB of RAM. For a fair comparison, all the sub-models have been implemented using the same platform. Table 3 shows the parameters of the developed models, which include ANFIS-SC, ANFIS-GP, and ANFIS-FCM. The performance analysis of the training and testing phases for the ANFIS-GP model is described in Table 4. In the same vein, Table 5 consists of the results for the ANFIS-SC models while Table 6 is for ANFIS-FCM. The bold fonts in the tables indicate the best results.

Table 3.
Parameter settings for the ANFIS models.

Table 4.
Performance analysis for ANFIS-GP models.

Table 5.
Performance analysis for ANFIS-SC models.

Table 6.
Performance analysis for ANFIS-FCM models.
The membership function (MF) used in the design of the FIS for a GP-based ANFIS is key to its optimal operation [42]. An MF in fuzzy set theory describes the degree of truth (“partial truth instead of TRUE or FALSE, 0 or 1”) of a crisp value in the range 0 to 1 [58]. This assists in the design of practical scenarios that contain ambiguity or have ill-defined issues. In response, multiple MF-types were used to build the ANFIS-GP, featuring five distinct previously defined statistical measures (namely, MAPE, MAE, RCoV, and RMSE) culminating in eight sub-models. Based on the testing phase of the sub-models as depicted in Table 4, the dsig-MF outclassed the other sub-models with the highest accuracy (88.2%), followed by the other sub-models in decreasing order: pi-MF (87.9%), gauss2-MF (87.4%), gbell-MF (linear) (86.9%), trap-MF (86.4581), psig-MF (86.4581%), gbell-MF (constant) (33.8%), and gauss-MF (15.8%). A further point to be noted, as depicted in Table 4, is that linear MF-type output sub-models performed more poorly than constant MF-type output sub-models for the Sugeno-type FIS.
In terms of the MAE under the testing phase, the best performance was obtained from the ANFIS-GP4 by having the minimum (1.0390 × 103) in comparison to other sub-models. However, as depicted in Table 4, the maximum values for the MAE were obtained from ANFIS-GP1 ( = 7.3954 × 103) and ANFIS-GP5 ( = 5.7619 × 103). Similarly, the ANFIS-GP4 maintained its superior performance with the minimum (0.0309), (14.8571), and (1436.2819), respectively. A computational time (CT) evaluation is important for GP due to the computational intensity associated with the large rule base that results in curse dimensionality [42,45]. As presented in Table 4, the maximum CT was delivered by ANFIS-GP7 ( = 46.1492), while the sub-model with the best CT belongs to the ANFIS-GP4 ( = 24.2021). Performance analysis of ANFIS-GP sub-models revealed that ANFIS-GP4 with input MF-type “dsig-MF” and output MF-type “constant” delivered the best overall results.
One common technique for clustering data is the SC algorithm. However, a crucial component that impacts the effectiveness of the clustering results is each cluster’s radius [59,60]. As a result, the impact of the clustering radius (CR) was examined for the ANFIS-SC varying the CR in the range of 0.2–0.4 for different sub-models. The results of the different sub-models with diverse CR values are reported in Table 5. Considering the testing phase, the best sub-model accuracy is demonstrated by ANFIS-SC5 with an accuracy of 89.9%, followed by ANFIS-SC4 (88.3%), ANFIS-SC2 (87%), ANFIS-SC3 (86.8%), and ANFIS-SC1 (39.37%). Additionally, the best performance for the MAE and RCoV statistical metrics was exhibited by the ANFIS-SC5 (MAE = 858.7494; RCoV = 0.0357) compared to the other sub-models. ANFIS-SC5 performed similarly, with the lowest error values for the CVRMSE (12.3323) and RMSE (1182.2446), surpassing other approaches. Nonetheless, ANFIS-SC4 performed somewhat better in terms of CT (13.0126 s) than ANFIS-SC5, which had a CT value of 13.0304 s.
The number of clusters in the FCM plays a key role in its performance. An ANFIS-based FCM model has the challenging task of determining the number of clusters, so determining the number of clusters takes a variety of experiments. In response, a different number of clusters are examined and tested under the five statistical metrics and the CT for the ANFIS-FCM models. ANFIS-FCM3 outperformed other sub-models in terms of accuracy throughout the testing phase (Table 6), achieving an accuracy of 90.7% while using five clusters. Furthermore, the minimal error for the MAE (898.5070) was provided by the ANFIS-FCM3 compared to other sub-models. The ANFIS-FCM3 maintained its ideal performance under the error performance CVRMSE and the RMSE, with 11.5727 and 1137.6024, respectively. However, the ANFIS-FC3 delivered a better performance in terms of CT. The observation of Table 6 suggests that the number of clusters is not necessarily a determining factor for optimal performance. This finding is consistent with that of Wiharto and Suryani [61], who found that increasing the number of clusters may not always result in the best performance and that several experiments may be necessary to determine the number that is best for a proposed model.
Comparison between Optimal Sub-Models
This session evaluates the performance of the optimal sub-models in the three previously stated scenarios. Table 7 displays the comparison of the three best sub-models obtained from earlier analysis. The comparison of the three sub-models is shown in Figure 5a,b. The graph between the actual and predicted electricity consumption for the three optimum sub-models is also shown in Figure 6, Figure 7 and Figure 8, along with the error graphs. Taking the testing phase into account, the results from Table 7 show that the three models provided good results in the prediction of electricity consumption; however, the ANFIS-FCM3, with five clusters, delivered the best model prediction accuracy of 90.7% compared to ANFIS-SC5 (CR = 0.40) with 89.9% and ANFIS-GP4 (dsigMF, constant) with 88.2%. ANFIS-FCM3 (with five clusters) again produced the smallest values for the RMSE (1137.6024) and CVRMSE (11.5727) when compared with the other sub-models. Nevertheless, as shown in Table 7 and Figure 5b, the ANFIS-SC5 (with CR = 0.40) surpassed the other two sub-optimal models in terms of the MAE. Additionally, the ANGIS-GP4 (with dsigMF, constant) demonstrated better results in terms of the RCoV statistical metrics. That said, the ANFIS-FCM3 (with five clusters), maintained its best performance for the CT with the smallest value of 12.6918 s (Figure 5a).

Table 7.
Optimal sub-models comparison.
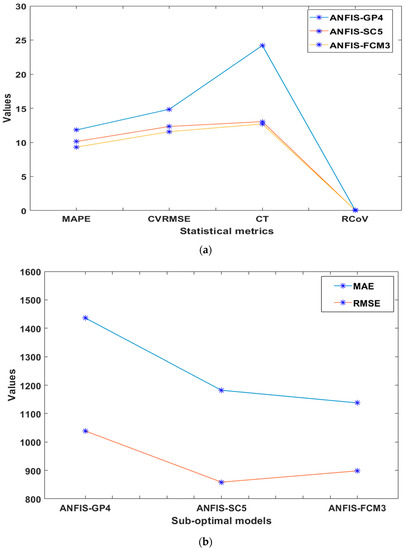
Figure 5.
Graph of statistical metrics for (a) MAPE, RCoV, CVRMSE, and CT (b) MAE and RMSE.
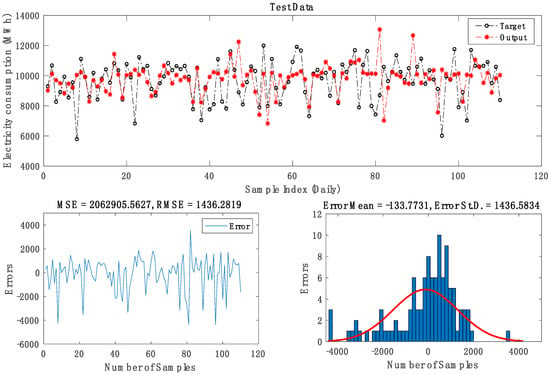
Figure 6.
Optimal ANFIS-GP4 sub-model.
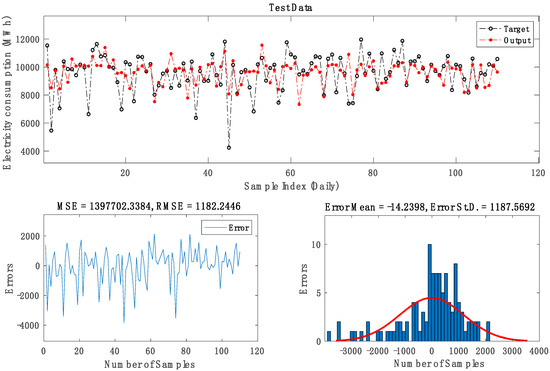
Figure 7.
Optimal ANFIS-SC5 sub-model.
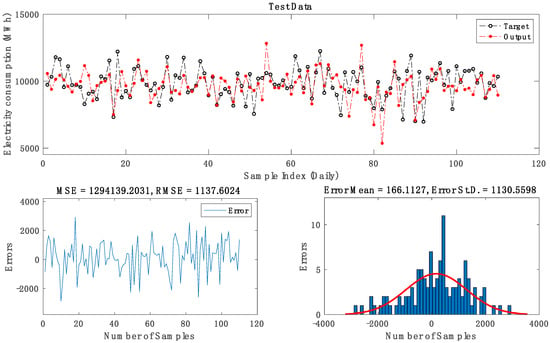
Figure 8.
Optimal ANFIS-FCM3 sub-model.
According to the results, the ANFIS-FCM3 (with five clusters) provided the best performance among the three sub-optimal models. This is similar to the findings that identified the FCM as a recognized clustering approach due to its benefit of resilience to ambiguity and ability to retain significantly more data than any other hard clustering method [62,63]. Table 8 presents the comparison of the best sub-optimal model with related works on electricity consumption prediction. As seen in Table 8, the comparison of the ANFIS-FCM3 is encouraging with a better MAPE, RMSE, and CVRMSE. The present study is also notable for its use of several performance metrics, which provide a good means of estimating model performance.

Table 8.
Comparison of the sub-optimal model with previous works, involving energy usage prediction.
4. Conclusions and Future Work
Energy consumption forecasting is crucial for operational and strategic planning. This is particularly vital in the event of unanticipated occurrences. This study examined the performance of clustering techniques and the ANFIS model parameters in predicting energy consumption during the COVID-19 pandemic, using Lagos Nigeria as a case study. We studied the effects of prominent clustering techniques, such as GP, SC, and FCM, as well as other key parameters, including clustering radius (CR), input and output MFs, and numbers of clusters. The experimental data used comprised five meteorological input variables and electricity consumption as the output. A number of sub-models were obtained after several simulations were performed. The performance evaluation was carried out using well-known statistical metrics: MAPE, MAE, RCoV, CVRMSE, and RMSE. The sub-models with the best performance in each of the stages of the comparative study were ANFIS-GP4, ANFIS-SC5, and ANFIS-FCM3, respectively. Further comparison between the aforementioned sub-models showed that the ANFIS-FCM3 outscored its counterparts with the minimal values of the MAPE (9.3122%), CVRMSE (11.5727), and RMSE (1137.6024). In the same vein, the ANFIS-FCM3 demonstrated the best computation time (CT) with the smallest value of 12.6918 s. The following are some major inferences drawn from this study:
- In comparison to other sub-models, the ANFIS-FCM (with five clusters) is more efficient, with minimal prediction errors and exhibiting an adequate improvement in prediction. Based on the results, it can be concluded that the FCM is found to be a better clustering technique for the ANFIS to model electricity consumption. This is congruent with the findings of Abdulshahed et al. [50], which indicated that, in addition to its speed-boosting capability, the FCM clustering approach has the benefit of not restricting cluster borders, allowing objects to belong to more than one group rather than just one.
- Our study also revealed that the type of the data clustering technique selected as well as other significant parameters have a substantial impact on the accuracy of ANFIS modeling.
- Furthermore, it may not always be the case with ANFIS-FCM that adding more clusters improve performance; hence, it may be essential to conduct multiple experiments to determine the optimal number of clusters for a given model.
- Making strategic energy plans and planning for the future requires knowing how much energy is produced and consumed. The present study will help to provide a reliable energy forecast in ensuring energy supply stability and better operations for end-users, especially during unforeseen eventualities.
The present study considered a medium-term forecast (MTF) based on the data obtained. However, future studies may consider increasing the experimental data and input variables for a more robust model. Although the number of datasets used in this work is not much less than those of other researchers, working with more data would produce more precise results. Further studies may consider enhancing the accuracy of forecasts by using new-generation metaheuristic algorithms.
Author Contributions
Conceptualization, S.O. and A.A.; Funding acquisition, Y.S.; Investigation, A.A.; Methodology, S.O.; Project administration, Y.S.; Resources, A.A.; Software, S.O.; Supervision, Y.S.; Writing—original draft, S.O.; Writing—review and editing, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the South African National Research Foundation under Grant 137951, Grant 141951, and Grant 132797, and in part by the South African National Research Foundation Incentive under Grant 132159.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used this manuscript.
| ANFIS | Adaptive neuro-fuzzy inference systems |
| ANN | Artificial neural networks |
| GP | Grid partitioning |
| SC | Subtractive clustering |
| FCM | Fuzzy c-means |
| CR | Clustering radius |
| RMSE | Root Mean Square Error |
| MR | Multiple Regression |
| DNN | Deep Neural Network |
| GP | Genetic Programing |
| SVM | Support Vector Machine |
| MAE | Mean Absolute Error |
| RCoV | Coefficient of Variation |
| CVRMSE | Coefficient of Variation of the Root Mean Square Error |
| STLF | Short term load forcasting |
| MAPE | Mean Absolute Percentage Error |
| ML | Machine Learning |
| FIS | Fuzzy inference systems |
| SELU | Scaled exponential linear unit |
| LGA | Local government areas |
| GM | Gray models |
| HVAC | Heating, ventilation, and air conditioning |
| LM | Levenberg–Marquardt |
| MF | Membership Function |
| CT | Computational time |
References
- Souhe, F.G.Y.; Mbey, C.F.; Boum, A.T.; Ele, P.; Kakeu, V.J.F. A hybrid model for forecasting the consumption of electrical energy in a smart grid. J. Eng. 2022, 2022, 629–643. [Google Scholar] [CrossRef]
- Oladipo, S.; Sun, Y.; Wang, Z. An enhanced flower pollinated algorithm with a modified fluctuation rate for global optimisation and load frequency control system. IET Renew. Power Gener. 2022, 16, 1220–1245. [Google Scholar] [CrossRef]
- Buechler, E.; Powell, S.; Sun, T.; Astier, N.; Zanocco, C.; Bolorinos, J.; Flora, J.; Boudet, H.; Rajagopal, R. Global changes in electricity consumption during COVID-19. iScience 2022, 25, 103568. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, Y.; Ma, G.; Chen, X.; Fan, J.; Yang, B. Prediction of electricity consumption during epidemic period based on improved particle swarm optimization algorithm. Energy Rep. 2022, 8, 437–446. [Google Scholar] [CrossRef]
- Mogaji, E. Impact of COVID-19 on transportation in Lagos, Nigeria. Transp. Res. Interdiscip. Perspect. 2020, 6, 100154. [Google Scholar] [CrossRef] [PubMed]
- Ebenso, B.; Otu, A. Can Nigeria contain the COVID-19 outbreak using lessons from recent epidemics? Lancet Glob. Health 2020, 8, e770. [Google Scholar] [CrossRef]
- Sanusi, Y.A.; Owoyele, G.S. Energy Poverty and its Spatial Differences in Nigeria: Reversing the Trend. Energy Procedia 2016, 93, 53–60. [Google Scholar] [CrossRef]
- Andrade, J.V.B.; Salles, R.S.; Silva, M.N.S.; Bonatto, B.D. Falling Consumption and Demand for Electricity in South Africa—A Blessing and a Curse. In Proceedings of the 2020 IEEE PES/IAS PowerAfrica, PowerAfrica 2020, Nairobi, Kenya, 25–28 August 2020; Institute of Electrical and Electronics Engineers Inc.: Nairobi, Kenya, 2020; pp. 1–5. [Google Scholar]
- Luan, C.; Pang, X.; Wang, Y.; Liu, L.; You, S. Comprehensive Forecasting Method of Monthly Electricity Consumption Based on Time Series Decomposition and Regression Analysis. In Proceedings of the 2020 2nd International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 23–25 October 2020. [Google Scholar] [CrossRef]
- Dodamani, S.N.; Shetty, V.J.; Magadum, R.B. Short term load forecast based on time series analysis: A case study. In Proceedings of the 2015 International Conference on Technological Advancements in Power and Energy (TAP Energy), Kollam, India, 24–26 June 2015; pp. 299–303. [Google Scholar] [CrossRef]
- Charyloniuk, W.; Chen, M.S. Very short-term load forecasting using artificial neural networks. IEEE Trans. Power Syst. 2000, 15, 263–268. [Google Scholar] [CrossRef]
- Amin, M.A.A.; Hoque, M.A. Comparison of ARIMA and SVM for Short-term Load Forecasting. In Proceedings of the 2019 9th Annual Information Technology, Electromechanical Engineering and Microelectronics Conference (IEMECON), Jaipur, India, 13–15 March 2019; pp. 1–6. [Google Scholar]
- Zhang, Y.; Sun, H.; Guo, Y. Wind power prediction based on pso-svr and grey combination model. IEEE Access 2019, 7, 136254–136267. [Google Scholar] [CrossRef]
- Adedeji, P.A.; Akinlabi, S.; Ajayi, O.; Madushele, N. Non-linear autoregressive neural network (NARNET) with SSA filtering for a university energy consumption forecast. Procedia Manuf. 2019, 33, 176–183. [Google Scholar] [CrossRef]
- Rajamoorthy, R.; Arunachalam, G.; Kasinathan, P.; Devendiran, R.; Ahmadi, P.; Pandiyan, S.; Muthusamy, S.; Panchal, H.; Kazem, H.A.; Sharma, P. A novel intelligent transport system charging scheduling for electric vehicles using Grey Wolf Optimizer and Sail Fish Optimization algorithms. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 3555–3575. [Google Scholar] [CrossRef]
- Jaglan, A.K.; Cheela, V.R.S.; Vinaik, M.; Dubey, B. Environmental Impact Evaluation of University Integrated Waste Management System in India Using Life Cycle Analysis. Sustainability 2022, 14, 8361. [Google Scholar] [CrossRef]
- Sharma, V.; Tripathi, A.K. A systematic review of meta-heuristic algorithms in IoT based application. Array 2022, 14, 100164. [Google Scholar] [CrossRef]
- Xu, A.; Li, R.; Chang, H.; Xu, Y.; Li, X.; Lin, G.; Zhao, Y. Artificial neural network (ANN) modeling for the prediction of odor emission rates from landfill working surface. Waste Manag. 2022, 138, 158–171. [Google Scholar] [CrossRef] [PubMed]
- Amber, K.P.; Ahmad, R.; Aslam, M.W.; Kousar, A.; Usman, M.; Khan, M.S. Intelligent techniques for forecasting electricity consumption of buildings. Energy 2018, 157, 886–893. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Trees vs. Neurons: Comparison between random forest and ANN for high-resolution prediction of building energy consumption. Energy Build. 2017, 147, 77–89. [Google Scholar] [CrossRef]
- Nakabi, T.A.; Toivanen, P. An ANN-based model for learning individual customer behavior in response to electricity prices. Sustain. Energy Grids Netw. 2019, 18, 100212. [Google Scholar] [CrossRef]
- Elbeltagi, E.; Wefki, H. Predicting energy consumption for residential buildings using ANN through parametric modeling. Energy Rep. 2021, 7, 2534–2545. [Google Scholar] [CrossRef]
- Chen, S.; Ren, Y.; Friedrich, D.; Yu, Z.; Yu, J. Prediction of office building electricity demand using artificial neural network by splitting the time horizon for different occupancy rates. Energy AI 2021, 5, 100093. [Google Scholar] [CrossRef]
- Moon, J.; Park, S.; Rho, S.; Hwang, E. A comparative analysis of artificial neural network architectures for building energy consumption forecasting. Int. J. Distrib. Sens. Netw. 2019, 15, 155014771987761. [Google Scholar] [CrossRef]
- Yuan, J.; Farnham, C.; Azuma, C.; Emura, K. Predictive artificial neural network models to forecast the seasonal hourly electricity consumption for a University Campus. Sustain. Cities Soc. 2018, 42, 82–92. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Perveen, G.; Rizwan, M.; Goel, N. An ANFIS-based model for solar energy forecasting and its smart grid application. Eng. Reports 2019, 1, e12070. [Google Scholar] [CrossRef]
- Adedeji, P.A.; Akinlabi, S.A.; Madushele, N.; Olatunji, O.O. Neuro-fuzzy resource forecast in site suitability assessment for wind and solar energy: A mini review. J. Clean. Prod. 2020, 269, 122104. [Google Scholar] [CrossRef]
- Esmaili, M.; Aliniaeifard, S.; Mashal, M.; Vakilian, K.A.; Ghorbanzadeh, P.; Azadegan, B.; Seif, M.; Didaran, F. Assessment of adaptive neuro-fuzzy inference system (ANFIS) to predict production and water productivity of lettuce in response to different light intensities and CO2 concentrations. Agric. Water Manag. 2021, 258, 107201. [Google Scholar] [CrossRef]
- Alrassas, A.M.; Al-Qaness, M.A.A.; Ewees, A.A.; Ren, S.; Elaziz, M.A.; Damaševičius, R.; Krilavičius, T. Optimized ANFIS Model Using Aquila Optimizer for Oil Production Forecasting. Processes 2021, 9, 1194. [Google Scholar] [CrossRef]
- Thakkar, A.; Chaudhari, K. Fusion in stock market prediction: A decade survey on the necessity, recent developments, and potential future directions. Inf. Fusion 2021, 65, 95–107. [Google Scholar] [CrossRef]
- Olatunji, O.O.; Akinlabi, S.; Madushele, N.; Adedeji, P.A. A GA-ANFIS Model for the Prediction of Biomass Elemental Properties. In Trends in Manufacturing and Engineering Management; Springer: Singapore, 2021; pp. 1099–1114. [Google Scholar] [CrossRef]
- Chen, H.Y.; Lee, C.H. Electricity consumption prediction for buildings using multiple adaptive network-based fuzzy inference system models and gray relational analysis. Energy Rep. 2019, 5, 1509–1524. [Google Scholar] [CrossRef]
- Ghenai, C.; Al-Mufti, O.A.A.; Al-Isawi, O.A.M.; Amirah, L.H.L.; Merabet, A. Short-term building electrical load forecasting using adaptive neuro-fuzzy inference system (ANFIS). J. Build. Eng. 2022, 52, 104323. [Google Scholar] [CrossRef]
- Kaysal, A.; Köroglu, S.; Oguz, Y.; Kaysal, K. Artificial Neural Networks and Adaptive Neuro-Fuzzy Inference Systems Approaches to Forecast the Electricity Data for Load Demand, an Analysis of Dinar District Case. In Proceedings of the 2018 2nd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 19–21 October 2018; pp. 1–6. [Google Scholar]
- Klimenko, V.V.; Luferov, V.S.; Stefantsov, A.G. Neuro-fuzzy models for operational forecasting of electric energy consumption of the urban system. AIP Conf. Proc. 2021, 2410, 20010. [Google Scholar] [CrossRef]
- Sharma, P.; Sahoo, B.B.; Said, Z.; Hadiyanto, H.; Nguyen, X.P.; Nižetić, S.; Huang, Z.; Hoang, A.T.; Li, C. Application of machine learning and Box-Behnken design in optimizing engine characteristics operated with a dual-fuel mode of algal biodiesel and waste-derived biogas. Int. J. Hydrogen Energy 2022. [Google Scholar] [CrossRef]
- Adeleke, O.; Akinlabi, S.; Jen, T.C.; Adedeji, P.A.; Dunmade, I. Evolutionary-based neuro-fuzzy modelling of combustion enthalpy of municipal solid waste. Neural Comput. Appl. 2022, 34, 7419–7436. [Google Scholar] [CrossRef]
- Fattahi, H. Adaptive neuro fuzzy inference system based on fuzzy c–means clustering algorithm, a technique for estimation of tbm penetration rate. Iran Univ. Sci. Technol. 2016, 6, 159–171. [Google Scholar]
- Adedeji, P.A.; Akinlabi, S.; Madushele, N.; Olatunji, O.O. Wind turbine power output very short-term forecast: A comparative study of data clustering techniques in a PSO-ANFIS model. J. Clean. Prod. 2020, 254, 120135. [Google Scholar] [CrossRef]
- Adedeji, P.; Madushele, N.; Akinlabi, S. Adaptive Neuro-fuzzy Inference System (ANFIS) for a multi-campus institution energy consumption forecast in South Africa. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Washington, DC, USA, 27–29 September 2018; pp. 950–958. [Google Scholar]
- Adeleke, O.; Akinlabi, S.A.; Jen, T.C.; Dunmade, I. Prediction of municipal solid waste generation: An investigation of the effect of clustering techniques and parameters on ANFIS model performance. Environ. Techology 2020, 43, 1634–1647. [Google Scholar] [CrossRef]
- Pandit, A.; Panda, S. Prediction of earthquake magnitude using soft computing techniques: ANN and ANFIS. Arab. J. Geosci. 2021, 14, 1260. [Google Scholar] [CrossRef]
- Wei, M.; Bai, B.; Sung, A.H.; Liu, Q.; Wang, J.; Cather, M.E. Predicting injection profiles using ANFIS. Inf. Sci. 2007, 177, 4445–4461. [Google Scholar] [CrossRef]
- Narayanan, S.J.; Paramasivam, I.; Bhatt, R.B.; Khalid, M. A Study on the Approximation of Clustered Data to Parameterized Family of Fuzzy Membership Functions for the Induction of Fuzzy Decision Trees. Cybern. Inf. Technol. 2015, 15, 75–96. [Google Scholar] [CrossRef]
- Benmouiza, K.; Cheknane, A. Clustered ANFIS network using fuzzy c-means, subtractive clustering, and grid partitioning for hourly solar radiation forecasting. Theor. Appl. Climatol. 2019, 137, 31–43. [Google Scholar] [CrossRef]
- Küükdeniz, T.; Baray, A.; Ecerkale, K.; Esnaf, Ş. Integrated use of fuzzy c-means and convex programming for capacitated multi-facility location problem. Expert Syst. Appl. 2012, 39, 4306–4314. [Google Scholar] [CrossRef]
- Rezakazemi, M.; Dashti, A.; Asghari, M.; Shirazian, S. H2-selective mixed matrix membranes modeling using ANFIS, PSO-ANFIS, GA-ANFIS. Int. J. Hydrog. Energy 2017, 42, 15211–15225. [Google Scholar] [CrossRef]
- Barak, S.; Sadegh, S.S. Forecasting energy consumption using ensemble ARIMA-ANFIS hybrid algorithm. Int. J. Electr. Power Energy Syst. 2016, 82, 92–104. [Google Scholar] [CrossRef]
- Abdulshahed, A.M.; Longstaff, A.P.; Fletcher, S. The application of ANFIS prediction models for thermal error compensation on CNC machine tools. Appl. Soft Comput. 2015, 27, 158–168. [Google Scholar] [CrossRef]
- Elias, P.; Omojola, A. Case study: The challenges of climate change for Lagos, Nigeria. Curr. Opin. Environ. Sustain. 2015, 13, 74–78. [Google Scholar] [CrossRef]
- Nkeki, N.F.; Ojeh, V.N. Flood risks analysis in a littoral African city: Using geographic information system. In Geographic Information Systems (GIS): Techniques, Applications and Technologies; Nielson, Ed.; Nova Science Publisher: New York, NY, USA, 2014. [Google Scholar]
- Fasona, M.J.; Omojola, A.S.; Odunuga, S.; Tejuoso, O.; Amogu, N. An appraisal of sustainable water management solutions for large cities in developing countries through GIS: The case of Lagos, Nigeria. In Proceedings of the Symposium S2 Held during the 7th IAHS Scientific Assembly, Foz do Iguacu, Brazil, 3–9 April 2005; pp. 49–57. [Google Scholar]
- Ojeh, V.N.; Balogun, A.A.; Okhimamhe, A.A. Urban-Rural Temperature Differences in Lagos. Climate 2016, 4, 29. [Google Scholar] [CrossRef]
- Eminoglu, U.; Turksoy, O. Power curve modeling for wind turbine systems: A comparison study. Int. J. Ambient. Energy 2019, 42, 1912–1921. [Google Scholar] [CrossRef]
- Kwon, Y.; Kwasinski, A.; Kwasinski, A. Solar Irradiance Forecast Using Naïve Bayes Classifier Based on Publicly Available Weather Forecasting Variables. Energies 2019, 12, 1529. [Google Scholar] [CrossRef]
- Ceylan, Z. The impact of COVID-19 on the electricity demand: A case study for Turkey. Int. J. Energy Res. 2021, 45, 13022. [Google Scholar] [CrossRef]
- Talpur, N.; Salleh, M.N.M.; Hussain, K. An investigation of membership functions on performance of ANFIS for solving classification problems. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Melaka, Malaysia, 6–7 May 2017; IOP Publishing: Bristol, UK, 2017; Volume 226, p. 12103. [Google Scholar]
- Shieh, H.-L.; Chang, P.-L.; Lee, C.-N. An efficient method for estimating cluster radius of subtractive clustering based on genetic algorithm. In Proceedings of the 2013 IEEE International Symposium on Consumer Electronics (ISCE), Hsinchu, Taiwan, 3–6 June 2013; pp. 139–140. [Google Scholar]
- Alfarraj, O.; Alkhalaf, S. Optimized automatic generation of fuzzy rules for nonlinear system based on subtractive clustering algorithm for medical image segmentation. J. Med. Imaging Health Inform. 2017, 7, 500–507. [Google Scholar] [CrossRef]
- Wiharto, W.; Suryani, E. The analysis effect of cluster numbers on fuzzy c-means algorithm for blood vessel segmentation of retinal fundus image. In Proceedings of the 2019 International Conference on Information and Communications Technology, ICOIACT 2019, Yogyakarta, Indonesia, 24–25 July 2019; Institute of Electrical and Electronics Engineers Inc.: Yogyakarta, Indonesia; pp. 106–110. [Google Scholar]
- Lu, Y.; Ma, T.; Yin, C.; Xie, X.; Tian, W.; Zhong, S.M. Implementation of the Fuzzy C-Means Clustering Algorithm in Meteorological Data. Int. J. Database Theory Appl. 2013, 6, 1–18. [Google Scholar] [CrossRef]
- Verma, H.; Agrawal, R.K.; Sharan, A. An improved intuitionistic fuzzy c-means clustering algorithm incorporating local information for brain image segmentation. Appl. Soft Comput. 2016, 46, 543–557. [Google Scholar] [CrossRef]
- Cao, L.; Li, Y.; Zhang, J.; Jiang, Y.; Han, Y.; Wei, J. Electrical load prediction of healthcare buildings through single and ensemble learning. Energy Rep. 2020, 6, 2751–2767. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).