Features of Radiative Mixed Convective Heat Transfer on the Slip Flow of Nanofluid Past a Stretching Bended Sheet with Activation Energy and Binary Reaction

Abstract

The current exploration aims to inspect the features of thermal radiation on the buoyancy or mixed convective fluid flow induced by nanofluid through a stretching permeable bended sheet. The impact of activation energy and binary reaction along with slip migration is taken into account to discuss the fine points of water-based alumina nanoparticle flow. The structure of the curved sheet is assumed to be stretchable and the bended texture is coiled within a circular section with radius $R_b$. The similarity technique is utilized to reduce the leading partial differential equations into ordinary differential equations. These reduced equations are then deciphered numerically by employing the bvp4c method. The outcomes of the model were constructed in the form of several figures and bar graphs for the case of opposing and assisting flows with varying distinct embedded control parameters. The results display that the velocity field curves escalate with a higher radius of curvature parameter while temperature and concentration profiles shrink. More precisely, the outcomes show that the temperature distribution profile increases with the increase in nanoparticle’s volume fraction as well as thermal radiation parameter. Meanwhile, the concentration and velocity fields are decelerated with higher impacts of nanoparticle volume fraction. In addition, the heat and mass transfer rates were significantly improved for the higher value of the radiation and Schmidt number. On the other hand, the growing values of the velocity slip factor decrease the shear stress. Furthermore, the results are compared with the previous results in the limiting cases and observed a tremendous harmony.

1. Introduction

In our technologically advanced era, where technology becomes smaller in size as well as exceptional in terms of quality, nanotechnology is a sector that is expanding quickly. To manufacture goods at the molecular and atomic scales for certain industrial uses, materials must undergo specialized treatment. Nanofluid is one of the crucial components of nanotechnology, which is mostly used to successfully address issues in heat transmission. Modern industrial, engineering, and scientific activities, such as those involving nuclear reactions, thermal power plants, and highly developed procedures, face significant challenges in the thermal management of exceedingly sensitive systems. Kerosene oil, alumina, water, ethylene glycol, and other common fluids are combined with solid nanoparticles that range in size from 1 to 100 nm to create a posited nanofluid. These significant developments are a credit to Choi and Eastman’s [1] pioneering work, which introduced the idea of nanofluids. Copper nanoparticles deferral boosts engine oil conduction capability by 40%, see Eastman et al. [2]. This result is mainly attributable to the fact that copper has 3000 times the heat conductivity of engine oil. Ali et al. [3] studied the porous medium and non-Newtonian nanofluid flow over an extending sheet with varying radii of Cu nanoparticles subject to Lorentz forces. The numerical outcomes were calculated in terms of various graphs and tables for the numerous dissimilar distinguished parameters. Vajravelu et al. [4] investigated the numerical examination of the free convection flow of Ag-water and Cu-water nanofluids over a stretching sheet via the Keller box approach. They noticed that when the volume fraction of nanoparticles increased, the thickness of the temperature boundary layer increased, while the velocity boundary layer thickness decreased. Khan et al. [5] explored the significance of zero mass flux, magneto-hydrodynamics, and nanoparticles migration on the dynamics of Sisko fluid induced by a radially stretching and shrinking surface with experiencing the impacts of convective boundary conditions. Additionally, dual (first and second) branch outcomes are found for the phenomenon of the shrinking parameter, while a unique single solution was observed for the case of the stretching parameter. Makinde and Aziz [6] scrutinized the convective boundary condition on the heat and mass transfer boundary layer nanofluid flow past a stretched sheet. The quantitative and graphical data on thermal and concentration boundary layers are discovered in the form of tables and graphs due to the impacts of several comprised parameters. Hashim et al. [7] examined the radiative axisymmetric Carreau nanofluid flow induced by a radially shrinking surface with Lorentz forces. Moreover, they explored the stability examination to check that the first solution was stable and physically trustworthy while the second one was not. The impacts of leading edge accretion or ablation on the time-dependent boundary layer nanofluid flow over a movable surface with multiple solutions were highlighted by Roşca and Pop [8]. It is further revealed that this boundary layer solution differs qualitatively from the Rayleigh and Blasius issues for nanofluids. Khan et al. [9] discussed the radiative-based blood fluid conveying gold nanoparticles over a magnetohydrodynamic movable permeable bended sheet with an irregular heat source/sink. The outcome indicated that requisite gold nanoparticles are useful for medication delivery and movement mechanisms because the nanoparticle volume fraction parameter controls the velocity boundary layer. Meanwhile, Au nanoparticles increase the temperature curves to kill cancer cells. The consequences of thermophoresis and Brownian motion, third-grade fluid parameters, micro-polarity, induced magnetic field, and micro-inertia density on the stream of an electrically conductive nanofluid migration towards an exponentially stretchable sheet was analyzed by Awan et al. [10]. Yu et al. [11] scrutinized the analysis of thermophoretic particle deposition, porous medium, and nanoparticle aggregation on the movement of a bioconvection micropolar fluid comprising titanium dioxide nanoparticles over a stretched sheet subject to a heat source/sink. They discussed the outcomes with and without the appearance of nanoparticle aggregation. Recently, Madhukesh et al. [12] inspected the factor of heat sink/source and Marangoni convection on the chemically reactive transport conveying nanoparticles flow past a stretchable sheet with a significant influence of thermophoretic particle deposition. They concluded that the heat transfer upsurges with the heat source factor and reduces the with heat sink factor.

The inspiration of thermal radiation has an important role in many technical and industrial processes, such as the production of gas turbines, electric power, nuclear power plants, spacecraft, non-destructive testing, reliable equipment design, solar cell panels, propulsion systems, and many others. Furthermore, to produce the desired class of goods in industrial and mechanical processes, it is essential to comprehend the effects of thermal radiation characteristics. The influence of radiative MHD micropolar blood flow induced by a movable permeable curved sheet in the existence of Au nanoparticles with irregular heat sink/source was inspected by Chu et al. [13]. They have found multiple branch outcomes with variation in distinct involved parameters for the case of shrinking and stretching parameters. The analysis of the heat transfer enhancement brought about by a stretchable sheet in Reiner-Philippoff nanofluid flow with experiencing the momentous impact of Lorentz forces and non-linear thermal radiation was explored by Reddy et al. [14]. Furthermore, the heat transfer was higher in non-linear thermal radiation as compared to linear thermal radiation. Shamshuddin et al. [15] explored the significance of erratic heat source/sink, non-linear thermal radiation, and thermophoretic particle deposition of Casson nanofluid on the Riga plate surface with chemical reaction. They have discussed the model for the CuO-water and MgO-water nanofluids. In addition, the temperature behavior uplifts for both nanofluids with rising values of the Casson fluid parameter. Raza et al. [16] investigated the radiative non-Newtonian nanofluid flow inside a converging/diverging channel with drag forces. They utilized that the velocity and temperature field curves augmented with the superior impact of the magnetic and stretching parameters. Recently, Khan et al. [17] discussed the impressions of mass transpiration velocity on radiative wall jets’ heat transfer flow in the presence of SAE50-ZnO nano-lubricants with an extended Darcy-Brinkman porous medium. Initially, the velocity curves decline and then increase closer to the boundary of the wall jet owing to the augmentation in the suction parameter, while the temperature curve shrinks.

Chemical changes play a significant role in a variety of mechanical, chemical, and manufacturing processes. Therefore, to regulate a requisite process, a significant amount of oxygen, often referred to as activation energy, is required. Activation energy is the term used to describe the energy required to start the posited process of the chemical reaction. Svante Arrhenius developed the central concept for this subject in 1889. After these inventions, many new works have been published by distinct well-known researchers; some of the latest studies are summarized in the current paragraph. Kumar et al. [18] explained the impact of magnetite nanofluid and Arrhenius activation energy flowing across a porous rotating disc in a presence of the magnetic field. They used the fourth-order finite difference Noumerov’s technique, in which one of the important findings of the current inquiry is that the species concentration behaviors decrease as Arrhenius activation energy increases. Salahuddin et al. [19] studied the internal energy change and variable thermo-physical properties in a rotating frame towards an exponentially stretching sheet with activation energy. They observed that the temperature field curve enhances with growing values of Arrhenius activation energy and Eckert number. Muhammad Azam and Abbas [20] analyzed the analysis of activation energy for cross radiative nanofluid flow past a melting wedge with viscous dissipation. From the discovery, it is important to note that increasing values of the activation energy parameter boosted nanoparticle concentration and concentration boundary layer thickness. In addition, several more relevant researches work on the subject matter have been published in different journals, see [21,22,23]. Recently, Tayyab et al. [24] inspected the insightful investigation of three-dimensional rotating nanofluid flow when Darcy-Forchheimer law, magneto-hydrodynamics, activation energy, and bioconvection inspirations are significant.

Inspired by the publications mentioned above, this paper reveals the impact of activation energy along with chemical reaction on the mixed convection flow based on nanofluid through a stretchable bended curve with slip effect. The bended curve has been conceived as coiling inside a radius circle of $R_b$. The combination of activation energy along with slip effect has not been investigated yet. The resulting non-linear equations are dealt with using a similarity technique, and equations that have been reframed are used to examine the flow. The bvp4c technique is utilized to acquire the numerical result of the problem. The effects of numerous physical parameters on energy integrity induced by nanofluid have been elaborated in detail.

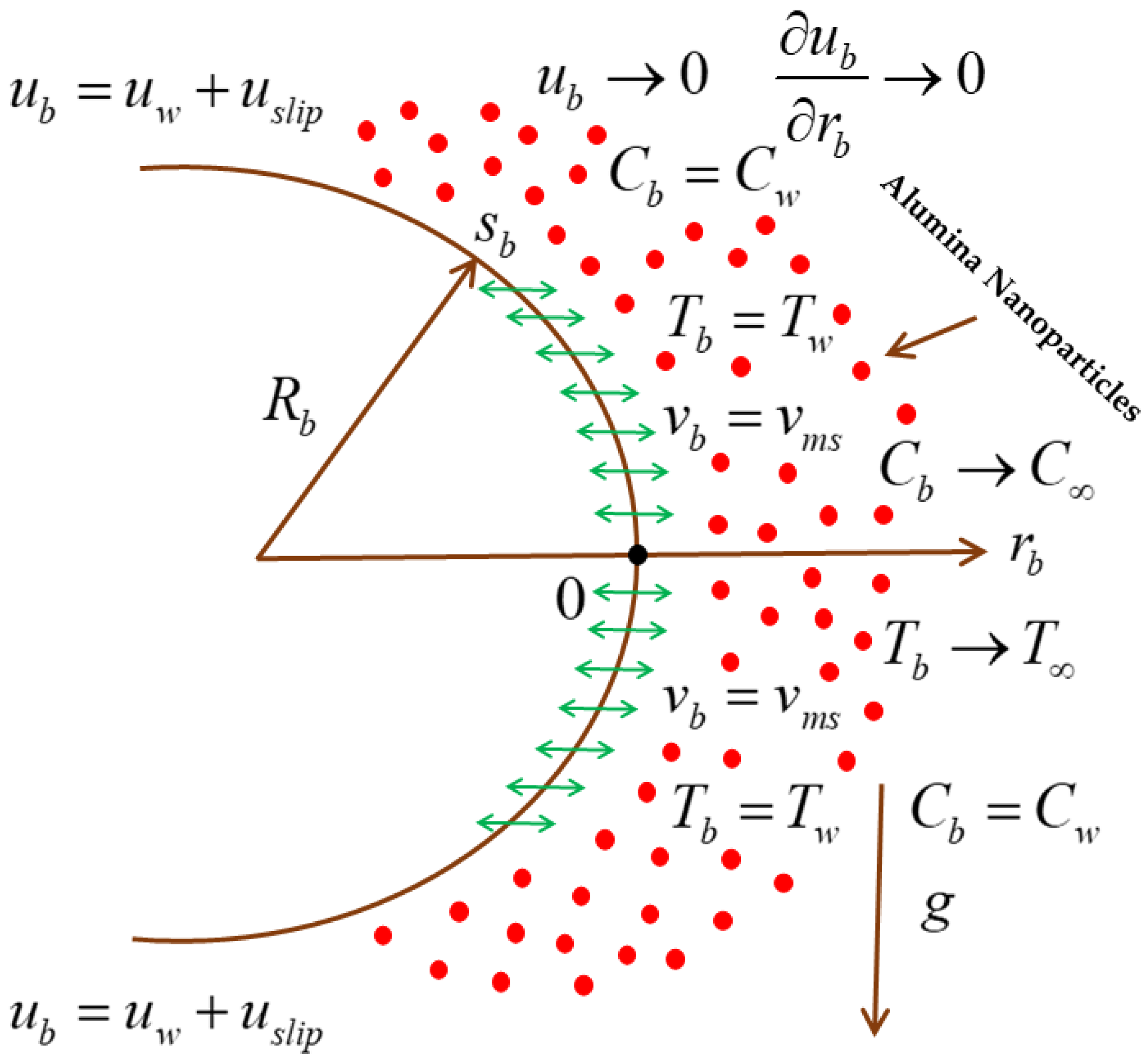
2. Description and Mathematical Modeling of the Problem

Let us consider a 2D mixed convection flow and heat transfer by incorporating the slip effect, Arrhenius activation energy, and binary reaction over a continuous stretching bended permeable sheet with enclosing radiation impact. A sketch of the model is illustrated in Figure 1, where ($r_b,s_b$) are the necessary curvilinear coordinates with a specific radius $R_b$, the radial coordinates $r_b$ and arc length coordinates $s_b$ are taken orthogonal and parallel to the fluid flow directions, respectively, the corresponding key requisite components of velocity are symbolized by $u_b$ and $v_b$, and $q_r^{*}$ symbolically denotes the radiative heat flow term that was induced in the necessary energy equation. Additionally, it is assumed that the wall surface of the bended sheet is stretched as well as slippery, so, mathematically, it is demarcated as $u_b\left(0,s_b\right)=u_w+u_{slip}$, where $u_w=a_0{s}_b$, and $u_{slip}=L\left(\frac{\partial u_b}{\partial r_b}-\frac{u_b}{r_b+R_b}\right)$, and where $a_0>0$ is the positive arbitrary constant and $L$ is the slip characteristic length. Moreover, the mass transpiration velocity of the curved sheet is signified by $v_{ms}$, where $v_{ms}>0$, and $v_{ms}<0$ correspond to the case of suction and injection, respectively. We have also assumed that the temperature and the concentration at the surface of the bended sheet and the external flow (far-field) are symbolized by $T_w$, $C_w$, $T_{\infty }$, and $C_{\infty }$, respectively. The following assumptions are used to further simplify the provided model:

• Incompressible flow;
• Steady flow;
• Buoyancy flow (opposing and assisting flows);
• Permeable bended stretching sheet;
• Slip velocity;
• Nanofluid;
• Boundary-layer approximation;
• Boussinesq approximation.

Under these postulations, the steady leading governing equations in the partial differential equations form are written as follows [9,13]:

$$\frac{\partial }{\partial r_b}\left[\left(r_b+R_b\right)v_b\right]+R_b\frac{\partial u_b}{\partial s_b}=0,$$

(1)

$$\frac{u_b^2}{\left(r_b+R_b\right)}=\frac{1}{{\rho }_{nf}}\frac{\partial p_b}{\partial r_b},$$

(2)

$$\begin{array}{l}\frac{R_b}{\left(r_b+R_b\right)}{u}_b\frac{\partial u_b}{\partial s_b}+v_b\frac{\partial u_b}{\partial r_b}+\frac{u_b{v}_b}{\left(r_b+R_b\right)}=-\frac{1}{{\rho }_{nf}}\frac{R_b}{\left(r_b+R_b\right)}\frac{\partial p_b}{\partial s_b}\\ +\frac{{\mu }_{nf}}{{\rho }_{nf}}\left(\frac{{\partial }^2{u}_b}{\partial r_b^2}+\frac{1}{\left(r_b+R_b\right)}\frac{\partial u_b}{\partial r_b}-\frac{u_b}{{\left(r_b+R_b\right)}^2}\right)+\frac{{\left(\rho \beta \right)}_{nf}}{{\rho }_{nf}}\left(T_b-T_{\infty }\right),\end{array}$$

(3)

$$\begin{array}{l}\frac{R_b}{\left(r_b+R_b\right)}{u}_b\frac{\partial T_b}{\partial s_b}+v_b\frac{\partial T_b}{\partial r_b}=\frac{k_{nf}}{{\left(\rho C_p\right)}_{nf}}\left(\frac{{\partial }^2{T}_b}{\partial r_b^2}+\frac{1}{\left(r_b+R_b\right)}\frac{\partial T_b}{\partial r_b}\right)\\ -\frac{1}{{\left(\rho C_p\right)}_{nf}\left(r_b+R_b\right)}\frac{\partial }{\partial r_b}\left[\left(r_b+R_b\right)q_r^{*}\right],\end{array}$$

(4)

$$\begin{array}{l}\frac{R_b}{\left(r_b+R_b\right)}{u}_b\frac{\partial C_b}{\partial s_b}+v_b\frac{\partial C_b}{\partial r_b}=D_m\left(\frac{{\partial }^2{C}_b}{\partial r_b^2}+\frac{1}{\left(r_b+R_b\right)}\frac{\partial C_b}{\partial r_b}\right)\\ -k_{re}^2{\left(\frac{T_b}{T_{\infty }}\right)}^n\exp \left(-\frac{E_b}{k_f{T}_b}\right)\left(C_b-C_{\infty }\right),\end{array}$$

(5)

with the following suitable boundary conditions:

$$\begin{array}{l}{u}_b=a_0{s}_b+L\left(\frac{\partial u_b}{\partial r_b}-\frac{u_b}{r_b+R_b}\right),v_b=v_{ms},T_b=T_w,C_b=C_w,\mathrm{at}{r}_b=0,\\ u_b\to 0,\frac{\partial u_b}{\partial r_b}\to 0,T_b\to T_{\infty },C_b\to C_{\infty }\mathrm{as}{r}_b\to \infty .\end{array}$$

(6)

where $T_b$ and $C_b$ indicate the temperature and concentration of the nanofluid, $D_m$ identifies the mass diffusion coefficient, $E_b$ indicates the activation energy, and $k_{re}^2$ corresponds to the chemical reaction rate. It is further assumed that the mass transpiration velocity is $v_{ms}=-{\left({\nu }_f{a}_0\right)}^{1/2}{f}_{wa}$, where ${\nu }_f$ signifies the respective kinematic viscosity and $f_{wa}$ is called the mass suction/injection parameter. Additionally, the last term in the energy Equation (4) represents the radiative heat flux $q_r^{*}$. Meanwhile, using the Rosseland estimation, the term is exemplified as follows [25,26,27]:

$$q_r^{*}=-\left(\frac{4{\sigma }_b}{3k_b}\right)\frac{\partial T_b^4}{\partial r_b},$$

(7)

where $k_b$ and ${\sigma }_b$ designate the coefficient of mean proportion and the constant of Stefan–Boltzmann, respectively. Expanding the fourth power of $T_b^4$ at a point $T_{\infty }$ and ignoring the higher order power of terms, we obtain $T_b^4\approx 4T_b{T}_{\infty }^3-3T_{\infty }^4$.

Using the simplified value of $T_b^4$ in Equation (7), we obtain:

$$q_r^{*}=-\left(\frac{16{\sigma }_b{T}_{\infty }^3}{3k_b}\right)\frac{\partial T_b}{\partial r_b}.$$

(8)

Furthermore, the above equations comprised distinct symbols which are used for the present selected nanofluids. These symbols are ${\rho }_{nf}$, $k_{nf}$, ${\mu }_{nf}$, ${\left(\rho C_p\right)}_{nf}$ and ${\left(\rho \beta \right)}_{nf}$, which indicate the specific density, thermal conductivity, viscosity, heat capacitance, and the thermal expansion coefficients of the nanofluids, respectively. The correlations of the nanofluids [17] are given by:

$$\frac{{\mu }_{nf}}{{\mu }_f}=\frac{1}{{\left(1-\phi \right)}^{2.5}},\frac{{\rho }_{nf}}{{\rho }_f}=\phi \left(\frac{{\rho }_{snp}}{{\rho }_f}\right)+\left(1-\phi \right),$$

(9)

$$\frac{{\left(\rho \beta \right)}_{nf}}{{\left(\rho \beta \right)}_f}=\phi \left(\frac{{\left(\rho \beta \right)}_{snp}}{{\left(\rho \beta \right)}_f}\right)+\left(1-\phi \right).$$

(10)

$$\frac{k_{nf}}{k_f}=\frac{k_{snp}+2k_f-2\phi \left(k_f-k_{snp}\right)}{k_{snp}+2k_f+\phi \left(k_f-k_{snp}\right)},$$

(11)

$$\frac{{\left(\rho C_p\right)}_{nf}}{{\left(\rho C_p\right)}_f}=\phi \left(\frac{{\left(\rho C_p\right)}_{snp}}{{\left(\rho C_p\right)}_f}\right)+\left(1-\phi \right).$$

(12)

Thus, Equations (9)–(12) illustrate the physical features of the water-based alumina nanofluids, where $\phi$ implies the nanoparticle solid volume fraction. Moreover, the subscript $snp$ and $f$ are the solid nanoparticles and the base working fluid (H₂O). Generally, the data of the alumina (Al₂O₃) nanoparticles along with the regular-based fluid (H₂O) are given in

Table 1. Physical data of the base water fluid and alumina nanoparticles.

Properties	Alumina (Al2O3)	Water (H2O)
$\beta \times {10}^{-5}\left(1/K\right)$	25.5	21
$k \left(W/mk\right)$	40	0.613
$\rho \left(kg/m^3\right)$	3970	997.1
$c_p\left(J kgK\right)$	765	4179
Pr	-	6.2

(see [28]).

We employed and utilized the following similarity factors to facilitate further study of the given problem at hand. Let:

$$\begin{array}{l}{u}_b=a_{0}s{S}^{\prime }\left(\xi \right),v_b=-\sqrt{a_0{v}_f}\frac{R_b}{r_b+R_b}S\left(\xi \right),\xi =r_b\sqrt{a_0/v_f},\\ G\left(\xi \right)=\frac{T_b-T_{\infty }}{T_w-T_{\infty }},F\left(\xi \right)=\frac{C_b-C_{\infty }}{C_w-C_{\infty }},p={\rho }_f{a}_0^2{s}^{2}P\left(\xi \right).\end{array}$$

(13)

The Equation (1) holds obviously after implementing the similarity factors (13), while the remaining leading governing equations and boundary conditions in the dimensionless version are as follows:

$$P^{\prime }=\frac{S^{{\prime }^2}{\Sigma }_1}{\xi +D_a},$$

(14)

$$\begin{array}{l}\frac{2D_{a}P}{\left(\xi +D_a\right){\Sigma }_1}=\frac{D_a}{\xi +D_a}S{S}^{″}-\frac{D_a}{\xi +D_a}{S}^{{\prime }^2}+\frac{D_a}{{\left(\xi +D_a\right)}^2}S{S}^{\prime }+\left(\frac{{\Sigma }_2}{{\Sigma }_1}\right)\left\{S^{‴}+\frac{S^{″}}{\xi +D_a}-\frac{S^{\prime }}{{\left(\xi +D_a\right)}^2}\right\}\\ +\frac{{\Sigma }_3}{{\Sigma }_1}{\gamma }_{a}G,\end{array}$$

(15)

$$\left({\Sigma }_4+\frac{4}{3}{N}_{rad}\right)\left\{G^{″}+\frac{G^{\prime }}{\xi +D_a}\right\}+{\Sigma }_5\mathrm{Pr}\frac{D_a}{\xi +D_a}{G}^{\prime }S=0,$$

(16)

$$\left\{F^{″}+\frac{F^{\prime }}{\xi +D_a}\right\}+\frac{D_a}{\xi +D_a}S{c}_a{F}^{\prime }S-S{c}_{a}R{c}_a{\left(1+{\delta }_{a}G\right)}^n\exp \left(\frac{-E_a}{1+{\delta }_{a}G}\right)F=0,$$

(17)

with reduce BCs:

$$\begin{array}{l}{S}^{\prime }\left(0\right)=\left(\frac{D_a}{D_a+{\Sigma }_a}\right)\left(1+{\Sigma }_a{S}^{″}\left(0\right)\right),S\left(0\right)=f_{wa},G\left(0\right)=1,F\left(0\right)=1\mathrm{at}\xi =0,\\ S^{\prime }\left(\xi \right)\to 0,S^{″}\left(\xi \right)\to 0,G\left(\xi \right)\to 0,F\left(\xi \right)\to 0\mathrm{as}\xi \to \infty .\end{array}$$

(18)

In which:

$$\begin{gathered} {\Sigma }_1=\frac{{\mu }_{nf}}{{\mu }_f}=\frac{1}{{\left(1-\phi \right)}^{2.5}},{\Sigma }_2=\frac{{\rho }_{nf}}{{\rho }_f}=\phi \left(\frac{{\rho }_{snp}}{{\rho }_f}\right)+\left(1-\phi \right), \\ {\Sigma }_3=\frac{{\left(\rho \beta \right)}_{nf}}{{\left(\rho \beta \right)}_f}=\phi \left(\frac{{\left(\rho \beta \right)}_{snp}}{{\left(\rho \beta \right)}_f}\right)+\left(1-\phi \right),{\Sigma }_4=\frac{k_{nf}}{k_f}=\frac{k_{snp}+2k_f-2\phi \left(k_f-k_{snp}\right)}{k_{snp}+2k_f+\phi \left(k_f-k_{snp}\right)}, \\ {\Sigma }_5=\frac{{\left(\rho C_p\right)}_{nf}}{{\left(\rho C_p\right)}_f}=\phi \left(\frac{{\left(\rho C_p\right)}_{snp}}{{\left(\rho C_p\right)}_f}\right)+\left(1-\phi \right). \end{gathered}$$

Additionally, the above-stated dimensionless equations comprised distinct distinguished constraints, such as the Prandtl number $\mathrm{Pr}={\nu }_f/{\alpha }_f,$ the velocity slip parameter ${\Sigma }_a=L\sqrt{a_0/{\nu }_f}$, the radius of curvature factor $D_a=R_b\sqrt{a_0/{\nu }_f}$, the radiation factor $N_{rad}=4{\sigma }_b{T}_{\infty }^3/k_b{k}_f$, the Schmidt number $S{c}_a={\nu }_f/D_m$, the chemical reaction rate parameter $R{c}_a=k_{re}^2/a_0$, the temperature difference parameter ${\delta }_a=\frac{T_w-T_{\infty }}{T_{\infty }}$, the activation energy parameter $E_a=\frac{E_b}{k_f{T}_{\infty }}$, and the mixed convection factor ${\gamma }_a=\frac{g{\beta }_f\left(T_w-T_{\infty }\right)}{a_0{}^2{s}_b}$, where $a_0$ has dimension ${\left[T\right]}^{-1}$. Moreover, the mixed convection or buoyancy parameter is the ratio of the posited Grashof number $G{r}_s=\frac{g{\beta }_f\left(T_w-T_{\infty }\right)s_b^3}{{\upsilon }_f^2}$ and the local Reynolds number ${\mathrm{Re}}_{s_b}^2={\left(\frac{u_w{s}_b}{{\nu }_f}\right)}^2$.

Now, eliminating the term pressure from Equations (14) and (15), one obtains:

$$\begin{array}{l}{\Sigma }_2{S}^{(4)}+\\ {\Sigma }_1\left\{\frac{D_a}{\xi +D_a}S{S}^{‴}-\frac{D_a}{\xi +D_a}{S}^{\prime }{S}^{″}+\frac{D_a}{{\left(\xi +D_a\right)}^2}S{S}^{″}-\frac{D_a}{{\left(\xi +D_a\right)}^3}S{S}^{\prime }-\frac{D_a}{{\left(\xi +D_a\right)}^2}{S}^{{\prime }^2}\right\}+\\ {\Sigma }_2\left\{\frac{2S^{‴}}{\xi +D_a}+\frac{S^{\prime }}{{\left(\xi +D_a\right)}^3}-\frac{S^{″}}{{\left(\xi +D_a\right)}^2}\right\}+{\Sigma }_3{\gamma }_a\left(G^{\prime }+\frac{G}{\xi +D_a}\right)=0.\end{array}$$

(19)

The pressure term from Equation (15) can easily be rewritten as follows:

$$P=\frac{\left(\xi +D_a\right){\Sigma }_1}{2D_a}\left[\begin{array}{l}\frac{D_a}{\xi +D_a}S{S}^{″}-\frac{D_a}{\xi +D_a}{S}^{\prime }{}^2+\frac{D_a}{{\left(\xi +D_a\right)}^2}S{S}^{\prime }+\left(\frac{{\Sigma }_2}{{\Sigma }_1}\right)\left\{S^{‴}+\frac{S^{″}}{\xi +D_a}-\frac{S^{\prime }}{{\left(\xi +D_a\right)}^2}\right\}\\ +\frac{{\Sigma }_3}{{\Sigma }_1}{\gamma }_{a}G\end{array}\right].$$

(20)

The skin-friction coefficient, the local Nusselt number, and the Sherwood number along the $s_b-$ directions are the relevant physical quantities or gradients, and they are demarcated as:

$$C_{f{s}_b}=\frac{{\tau }_{r_b{s}_b}}{{\rho }_f{u}_w^2},N{u}_{s_b}=\frac{s_b{q}_w}{k_f\left(T_w-T_{\infty }\right)},\mathrm{and}S{h}_{s_b}=\frac{s_b{j}_w}{D_m\left(C_w-C_{\infty }\right)},$$

(21)

where ${\tau }_{r_d{s}_d}$, $q_w$, and $j_w$ correspond to the shear stress, the heat, and mass fluxes, respectively. These terms are mathematically expressed as:

$${\tau }_{r_b{s}_b}={\mu }_{nf}{\left(\frac{\partial u_b}{\partial r_b}-\frac{u_b}{r_b+R_b}\right)}_{r_b=0},q_w=-k_f\left(\frac{k_{nf}}{k_f}+\frac{16{\sigma }_b{T}_{\infty }^3}{3k_f{k}_b}\right){\left.\frac{\partial T_b}{\partial r_b}\right|}_{r_b=0}\mathrm{and}{j}_w=-D_m{\left.\frac{\partial C_b}{\partial r_b}\right|}_{r_b=0},$$

(22)

Initially, to input Equation (22) in the above Equation (21), then employing the similarity transformations, we obtain:

$$\left\{C_{f{s}_b}{\mathrm{Re}}_{s_b}^{1/2}={\Sigma }_1\left(\frac{D_a{S}^{″}\left(0\right)-S^{\prime }\left(0\right)}{D_a}\right),N{u}_{s_b}{\mathrm{Re}}_{s_b}^{-1/2}=-\left({\Sigma }_4+\frac{4}{3}{N}_{rad}\right)G^{\prime }\left(0\right),\right.$$

(23)

and the reduced mass transfer rate as:

$$S{h}_{s_b}{\mathrm{Re}}_{s_b}^{-1/2}=-F^{\prime }\left(0\right).$$

(24)

where the local Reynolds number is signified as ${\mathrm{Re}}_{s_b}=\frac{u_w{s}_b}{{\nu }_f}$.

3. Solution Methodology and Verification of the Code

The structure of the problem is completely bounded by the set of equations with the boundary conditions (16)–(19), which have been numerically simulated using the bvp4c solver, which occupies a well-known finite difference approach that relies on the three-stage Lobatto IIIA formula, see Khan et al. [28] and Shampine et al. [29]. The given technique involves the new notation to transform the higher-order system into first-order ODEs. Let:

$$S=A_1,S^{\prime }=A_2,S^{″}=A_3,S^{‴}=A_4,G=A_5,G^{\prime }=A_6,F=A_7,F^{\prime }=A_8.$$

(25)

Using Equation (25) in the attained similarity Equations (16)–(19), one obtains:

$$\frac{d}{d\xi }\left(\begin{array}{c}{A}_1\\ A_2\\ A_3\\ A_4\\ A_5\\ A_6\\ A_7\\ A_8\end{array}\right)=\left(\begin{array}{l}{A}_2\\ A_3\\ A_4\\ {\Sigma }_2{}^{-1}\left[\begin{array}{l}-{\Sigma }_1\left\{\begin{array}{l}\frac{D_a}{\xi +D_a}{A}_1{A}_4-\frac{D_a}{\xi +D_a}{A}_2{A}_3+\frac{D_a}{{\left(\xi +D_a\right)}^2}{A}_1{A}_3-\\ \frac{D_a}{{\left(\xi +D_a\right)}^3}{A}_1{A}_2-\frac{D_a}{{\left(\xi +D_a\right)}^2}{A}_2{}^2\end{array}\right\}\\ -{\Sigma }_2\left\{\frac{2A_4}{\xi +D_a}+\frac{A_2}{{\left(\xi +D_a\right)}^3}-\frac{A_3}{{\left(\xi +D_a\right)}^2}\right\}-{\Sigma }_3{\gamma }_a\left(A_6+\frac{A_5}{\xi +D_a}\right)\end{array}\right]\\ A_6\\ \left(\frac{-A_6}{\xi +D_a}\right)-\left(\frac{{\Sigma }_5\mathrm{Pr}{\xi }_a}{\left({\Sigma }_4+\frac{4}{3}{N}_{rad}\right)\left(\xi +D_a\right)}\right)A_6{A}_1\\ A_8\\ -\frac{A_8}{\xi +D_a}-\frac{D_a}{\xi +D_a}S{c}_a{A}_8{A}_1+S{c}_{a}R{c}_a{\left(1+{\delta }_a{A}_5\right)}^n\exp \left(\frac{-E_a}{1+{\delta }_a{A}_5}\right)A_7\end{array}\right),$$

(26)

where the initial and infinite boundary conditions are:

$$\begin{array}{l}{A}_2\left(0\right)=\left(\frac{D_a}{D_a+{\Sigma }_a}\right)\left(1+{\Sigma }_a{A}_3\left(0\right)\right),A_1\left(0\right)=f_{wa},A_5\left(0\right)=1,A_7\left(0\right)=1\mathrm{at}\xi =0,\\ A_2\left(\xi \right)\to 0,A_3\left(\xi \right)\to 0,A_5\left(\xi \right)\to 0,A_7\left(\xi \right)\to 0\mathrm{as}\xi \to \infty .\end{array}$$

(27)

The code needs to make an initial guess before starting the simulation. Since there is only one solution possible, the system needs an appropriate starting guess so that the output can satisfy both the convergence criteria and the initial and infinite boundary conditions (27). In addition, we have fixed the error tolerance $\epsilon ={10}^{-6}$ throughout the computation along with the best appropriate finite value $\xi \to \infty$, such as the thickness of the restricted boundary layer $\xi ={\xi }_{\max }=8.0$, where the graphs asymptotically satisfy the criterion of convergence. This procedure is further explained in [30,31,32]. To ensure the reliability, validity, and accuracy of the given code, the current findings were confirmed by making a comparison with previously released data. In this respect,

Table 2. Evaluation of the present outcomes of the skin friction for the distinct value of the radius curvature parameter $D_a$ when ${\Sigma }_a={\gamma }_a=f_{wa}=0$.

${\mathit{D}}_{\mathit{a}}$	Sanni et al. [33]	Zaheer et al. [34]	Present Results
5	1.1507	1.1576	1.1507
10	1.0734	1.0735	1.0734
20	1.0355	1.0356	1.0356
30	1.0235	1.0235	1.0235
40	1.0176	1.0176	1.0175
50	1.0140	1.0141	1.0141
100	1.0070	1.0070	1.0070
200	1.0036	1.0036	1.0035
1000	1.0008	1.0008	1.0008
$\infty$	1.0000	1.0000	1.0000

highlights the authentication of the shear stress values for the limiting situation of stretching bended sheet when ${\Sigma }_a={\gamma }_a=0$ and $f_{wa}=0$ with dissimilar values of the radius curvature parameter, and the comparison demonstrates a perfect sound. Hence, the current outcomes are satisfactory and accurate.

4. Discussion of the Results

This section demonstrates the complete physical discussions of the acquired outcomes for the case of assisting flow (ASF) as well as opposing flow (OPF). The procedure of the scheme has been discussed in depth in Section 3, so no need to repeat it here. In contrast, Table 1 represents the base water fluid and alumina nanoparticle physical data, while the comparison of the current results and the old published work is excellently matched and consequently numerically illustrated in Table 2. In addition, the given problem set of similarity equations comprised dissimilar influential constraints. The impression of these factors on the velocity, temperature, and concentration profiles of the (water/alumina) nanofluid for the case of assisting and opposing flows are graphically depicted in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, respectively, while the gradient (shear stress, heat transfer, and mass transfer rates) profiles with variation in these factors are shown in terms of several bar graphs. Different colors were used in all the graphs to differentiate the case of ASF as well as OPF.

4.1. Interpretation of Velocity Profiles

Figure 2 and Figure 3 demonstrate the velocity curves of the (water/alumina) nanofluid for the case of ASF and OPF with the varying values of the radius of curvature parameter $D_a$, and the nanoparticle volume fraction $\phi$, respectively. Both solution graphs asymptotically converged and satisfied the infinite boundary conditions (18) for the case of ASF as well as for the case of OPF. In addition, the outcomes reveal that the curve of velocity enhances for both phenomena (ASF and OPF) due to the larger impacts of $D_a$, while it declines with nanoparticle volume fraction. However, the momentum boundary layer thickness escalates and decelerates with the respective superior values of the radius of curvature parameter and the nanoparticles volume fraction. Generally, the greater radius is caused by the radius of curvature parameter inclination, and if the liquid travels faster over the bended sheet, the gradient of velocity is increased. On the other hand, the influence of the velocity slip factor on velocity curves of the water-based alumina nanoparticle flows for the case of ASF and OPF is exemplified in Figure 4. With rising values of the slip factor, the curves of the velocity profile shrinkage for both phenomena. This behavior of the motion is noticed due to the fact that the higher slip factor can create resistance in the fluid motion particles, as a consequence, the MBLT (momentum boundary layer thickness) and velocity curves reduce. Furthermore, the gap in the existing graph for both solution curves is slightly smaller as compared to the aforementioned two plots.

Figure 2. Velocity profile for the case of ASF and OPF due to variations in the values of $D_a$.

Figure 2. Velocity profile for the case of ASF and OPF due to variations in the values of $D_a$.

Figure 3. Velocity profile for the case of ASF and OPF due to variations in the values of $\phi$.

Figure 3. Velocity profile for the case of ASF and OPF due to variations in the values of $\phi$.

Figure 4. Velocity profile for the case of ASF and OPF due to variations in the values of ${\Sigma }_a$.

Figure 4. Velocity profile for the case of ASF and OPF due to variations in the values of ${\Sigma }_a$.

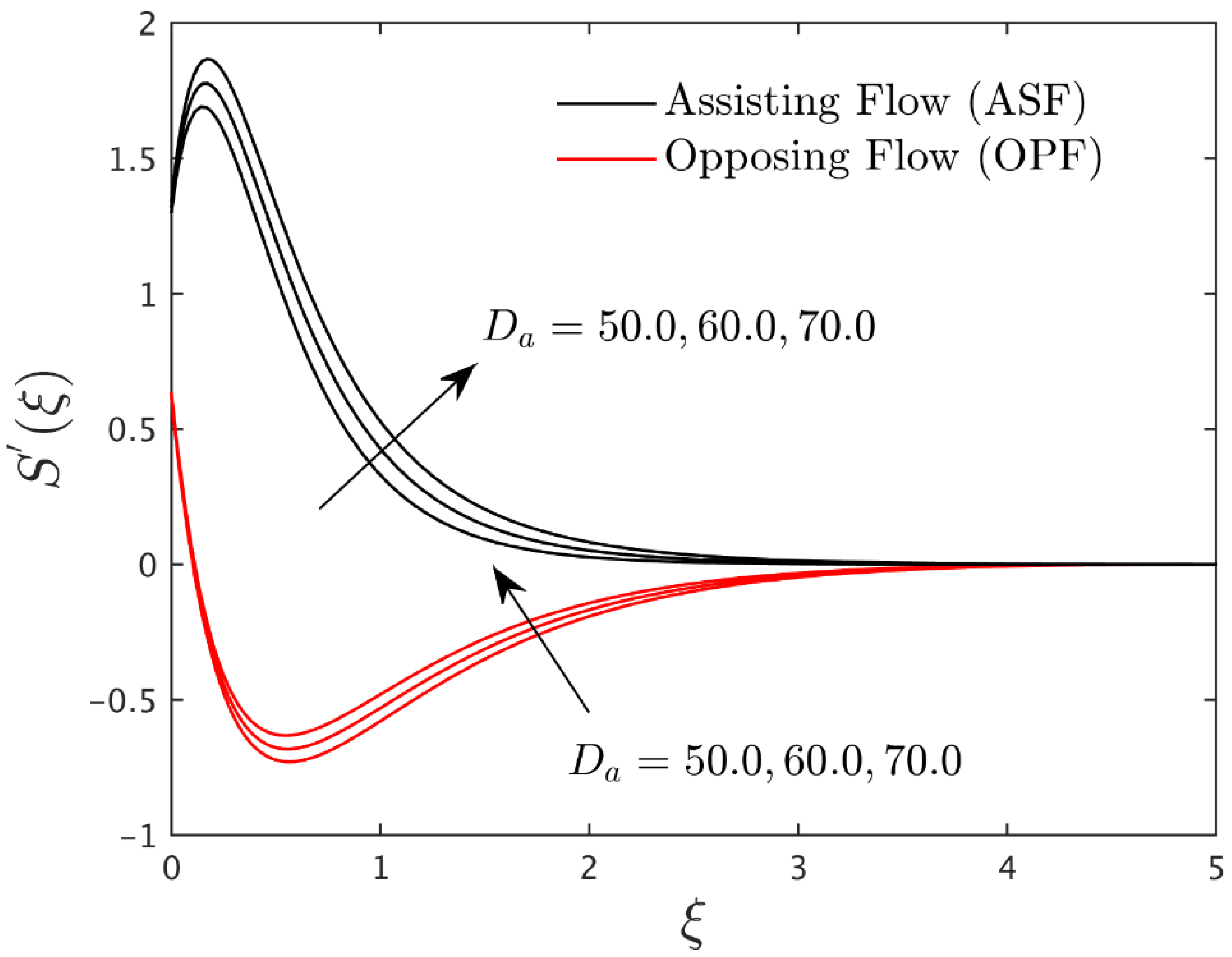
4.2. Interpretation of Temperature Profiles

The effect of the radius of curvature parameter $D_a$, and the nanoparticle volume fraction on the temperature profile of the (water/alumina) nanofluid for the case of ASF and OPF are graphically revealed in Figure 5 and Figure 6, respectively. With variations in $D_a$, the temperature profile abruptly decreases in the case of ASF as well as OFP, while it is enhanced due to the larger values of $\phi$ in both cases. Additionally, from Figure 5, it can be seen that the gap in the choice of ASF solution curves is higher than the gap of the solution curves for the choice of OPF. Meanwhile, for the higher impact of nanoparticle volume fraction, the temperature profile for both choices of ${\gamma }_a$ are closer, and therefore, it is difficult to differentiate it in the current form (see Figure 6). Hence, we have zoomed in at a specific portion of the graph and exposed the gap for each distinct value of $\phi$ (see in the small zooming windows) of the plots. From a physical point of view, a higher nanoparticle volume fraction improves the quantity of thermal conductivity. In this higher thermal conductivity respect, the temperature profile and the thickness of the thermal boundary layer boosted for both positive and negative selected values of the buoyancy parameter. Figure 7 displays the effect of radiation parameter $N_{rad}$ on the temperature solution curves of the water-based alumina nanoparticles flow. Solutions are constructed for both ASF and OPF. Therefore, the temperature solution curves are augmented with a higher influence of radiation parameter. In a general scenario, the higher impacts of radiation produce a substantial quantity of heating to the alumina nanoparticles that enlarges the temperature profile of the bended sheet flow.

Figure 5. Temperature profile for the case of ASF and OPF due to variations in the values of $D_a$.

Figure 5. Temperature profile for the case of ASF and OPF due to variations in the values of $D_a$.

Figure 6. Temperature profile for the case of ASF and OPF due to variations in the values of $\phi$.

Figure 6. Temperature profile for the case of ASF and OPF due to variations in the values of $\phi$.

Figure 7. Temperature profile for the case of ASF and OPF due to variations in the values of $N_{rad}$.

Figure 7. Temperature profile for the case of ASF and OPF due to variations in the values of $N_{rad}$.

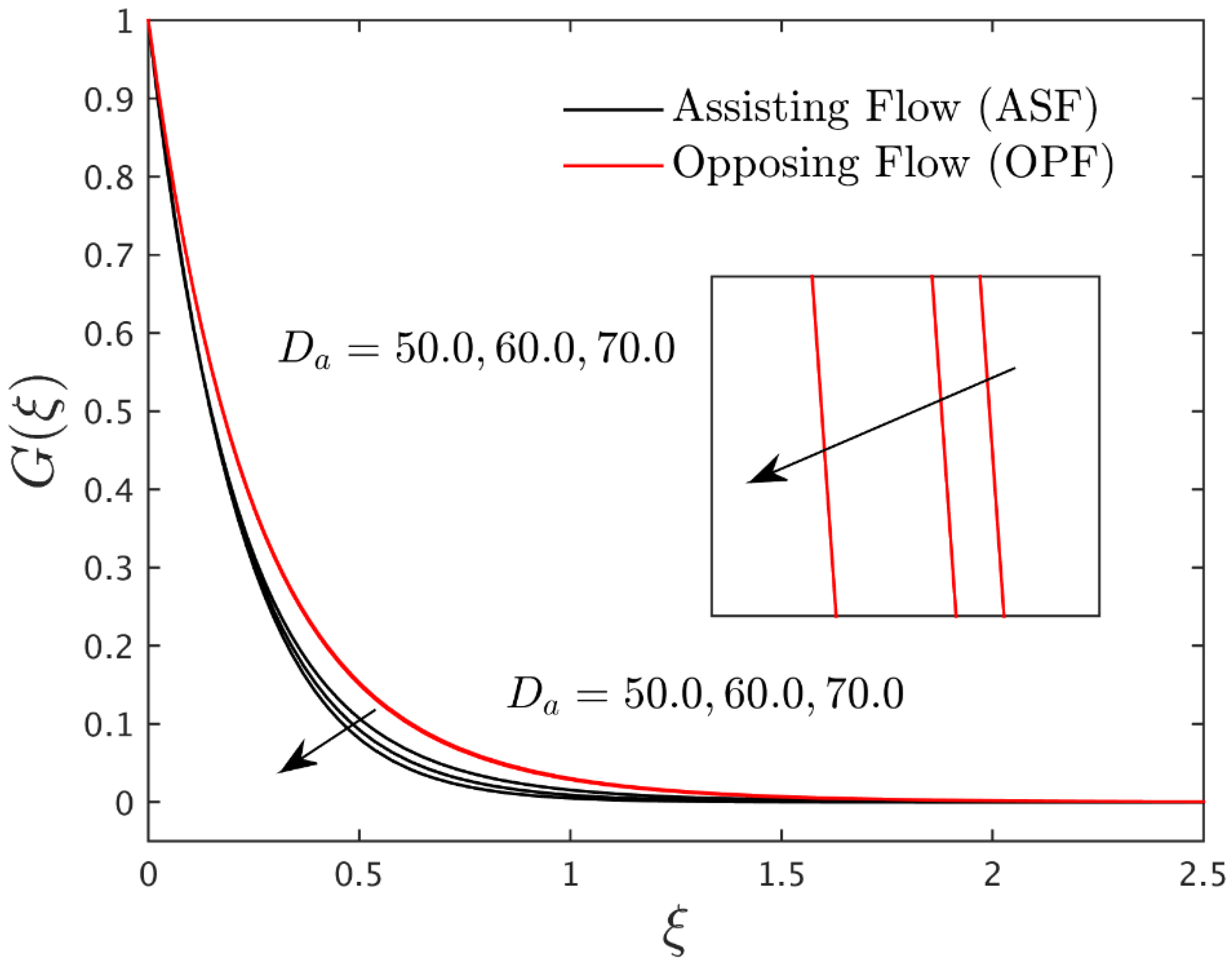
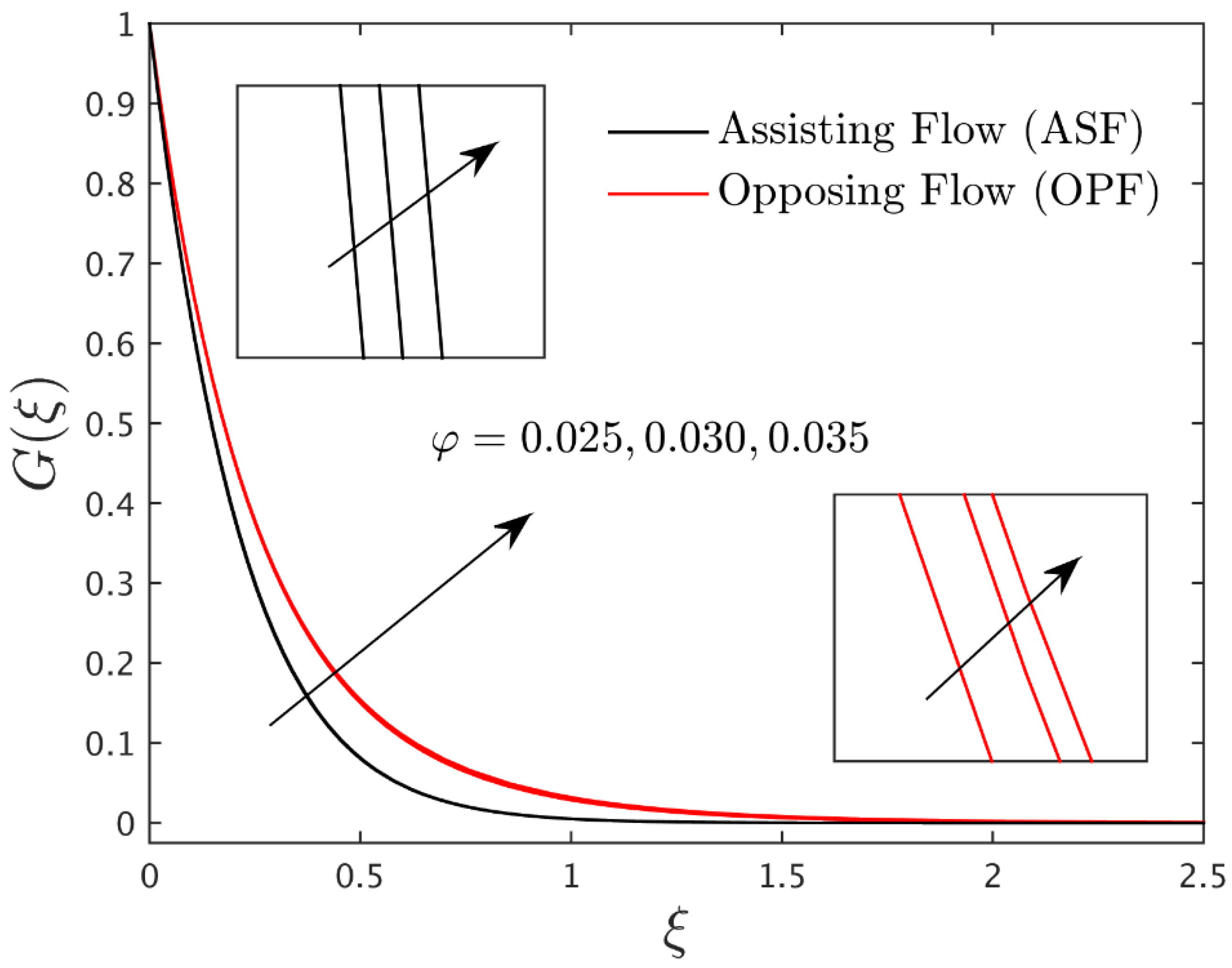
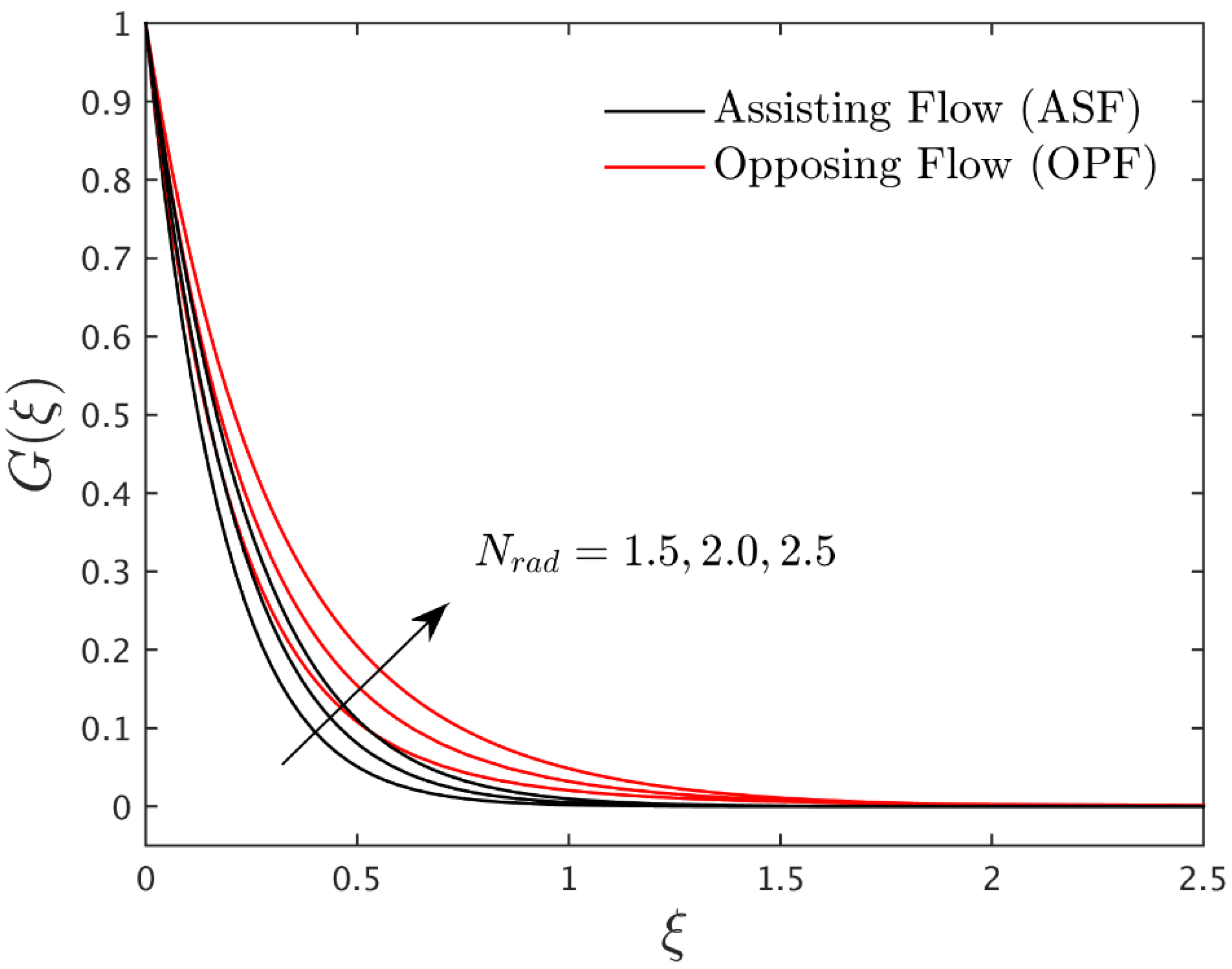
4.3. Interpretation of Concentration Profiles

Figure 8, Figure 9 and Figure 10 display the concentration profiles of the water-based alumina nanoparticles flow in the case of ASF and OPF with variation in the radius of curvature parameter $D_a$, nanoparticle volume fraction $\phi$, and the Schmidt number $S{c}_a$, respectively. From all the graphs, it is discovered that the concentration curves and the thickness of the concentration boundary layer decline as the radius of curvature parameter $D_a$, nanoparticle volume fraction $\phi$, and the Schmidt number $S{c}_a$ rises. In Figure 8, the outcomes look better gap-wise as compared to the outcomes bounded in Figure 9 and Figure 10, respectively. Finally, in the last graph, the solution behavior is noticed due to the higher impact of the Schmidt number. It is the ratio of the mass-momentum transfer rate. It is found that increasing the heat to mass diffusion ratio causes the former diffusion (mass diffusivity) to replace the latter (momentum diffusivity), which results in a reduction in the mass distribution or concentration profile.

Figure 8. Concentration profile for the case of ASF and OPF due to variations in the values of $D_a$.

Figure 8. Concentration profile for the case of ASF and OPF due to variations in the values of $D_a$.

Figure 9. Concentration profile for the case of ASF and OPF due to variations in the values of $\phi$.

Figure 9. Concentration profile for the case of ASF and OPF due to variations in the values of $\phi$.

Figure 10. Concentration profile for the case of ASF and OPF due to variations in the values of $S{c}_a$.

Figure 10. Concentration profile for the case of ASF and OPF due to variations in the values of $S{c}_a$.

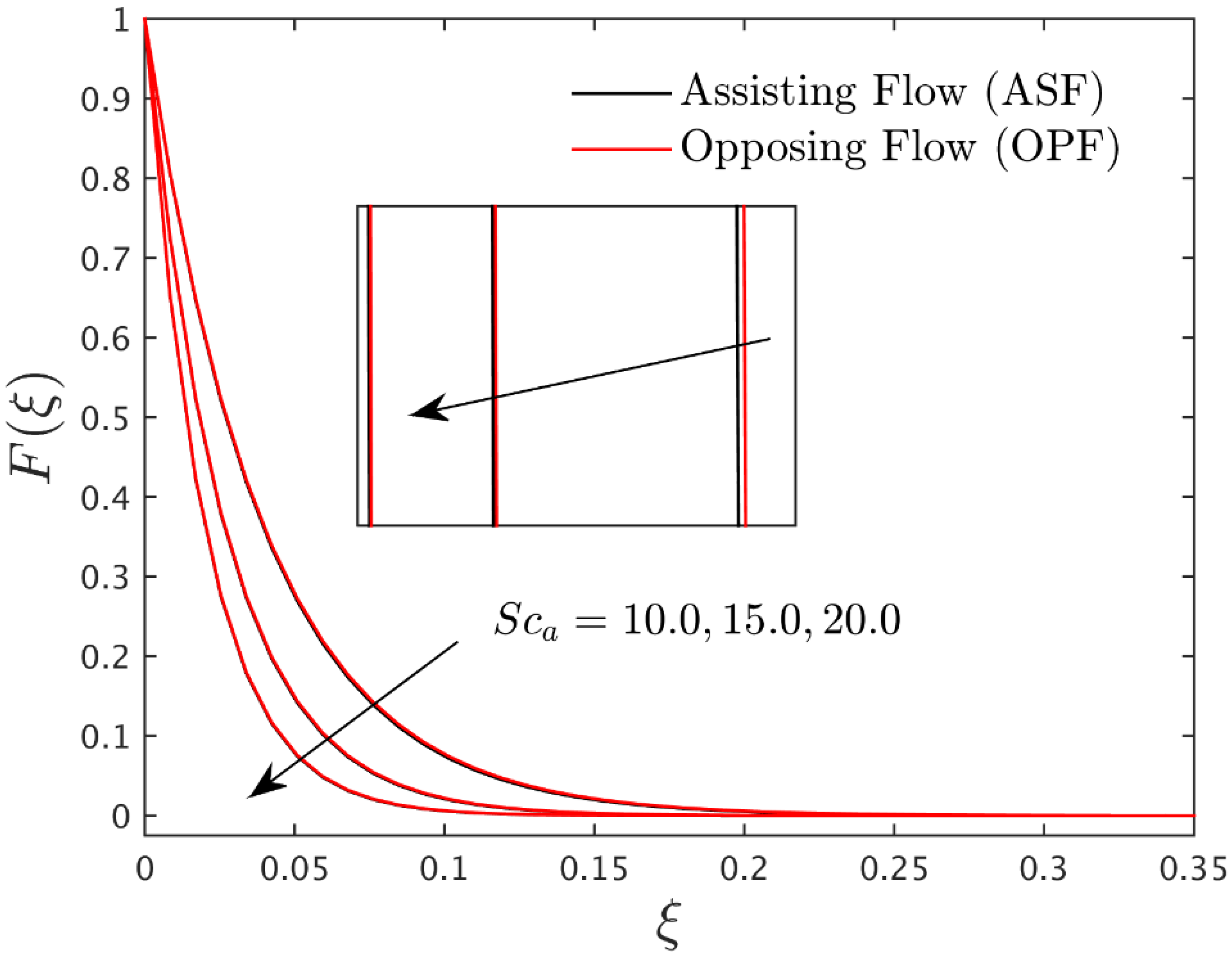
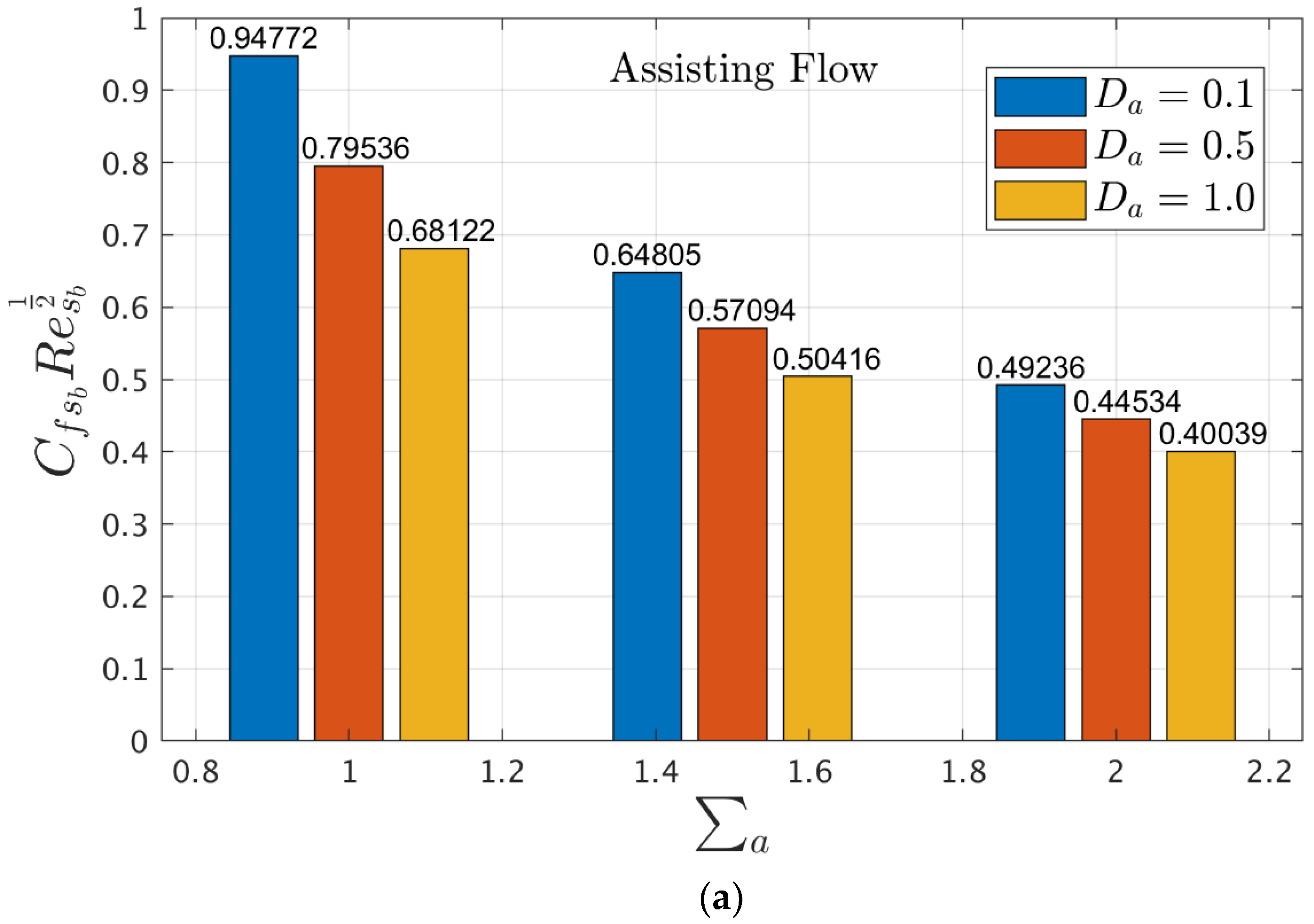
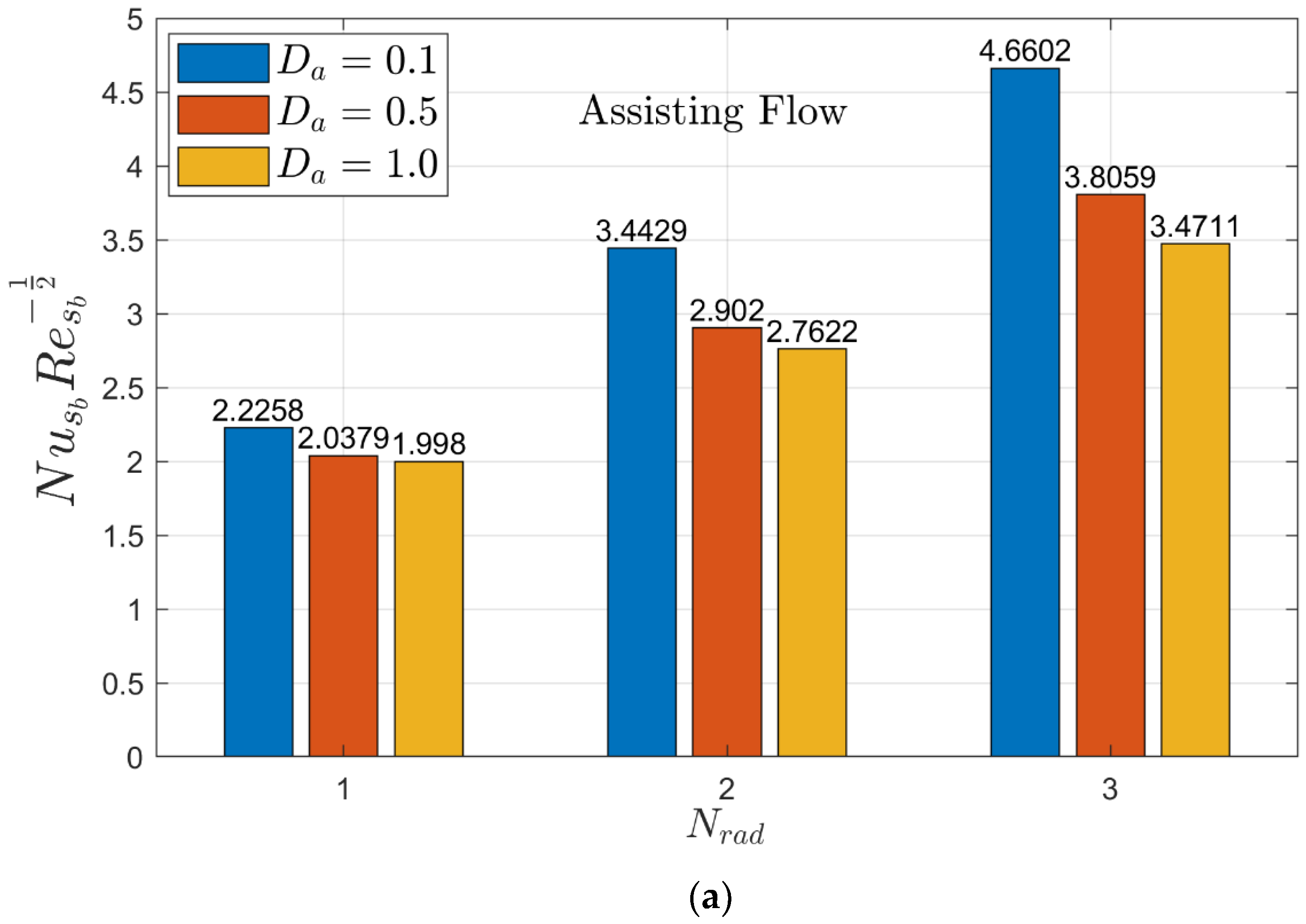
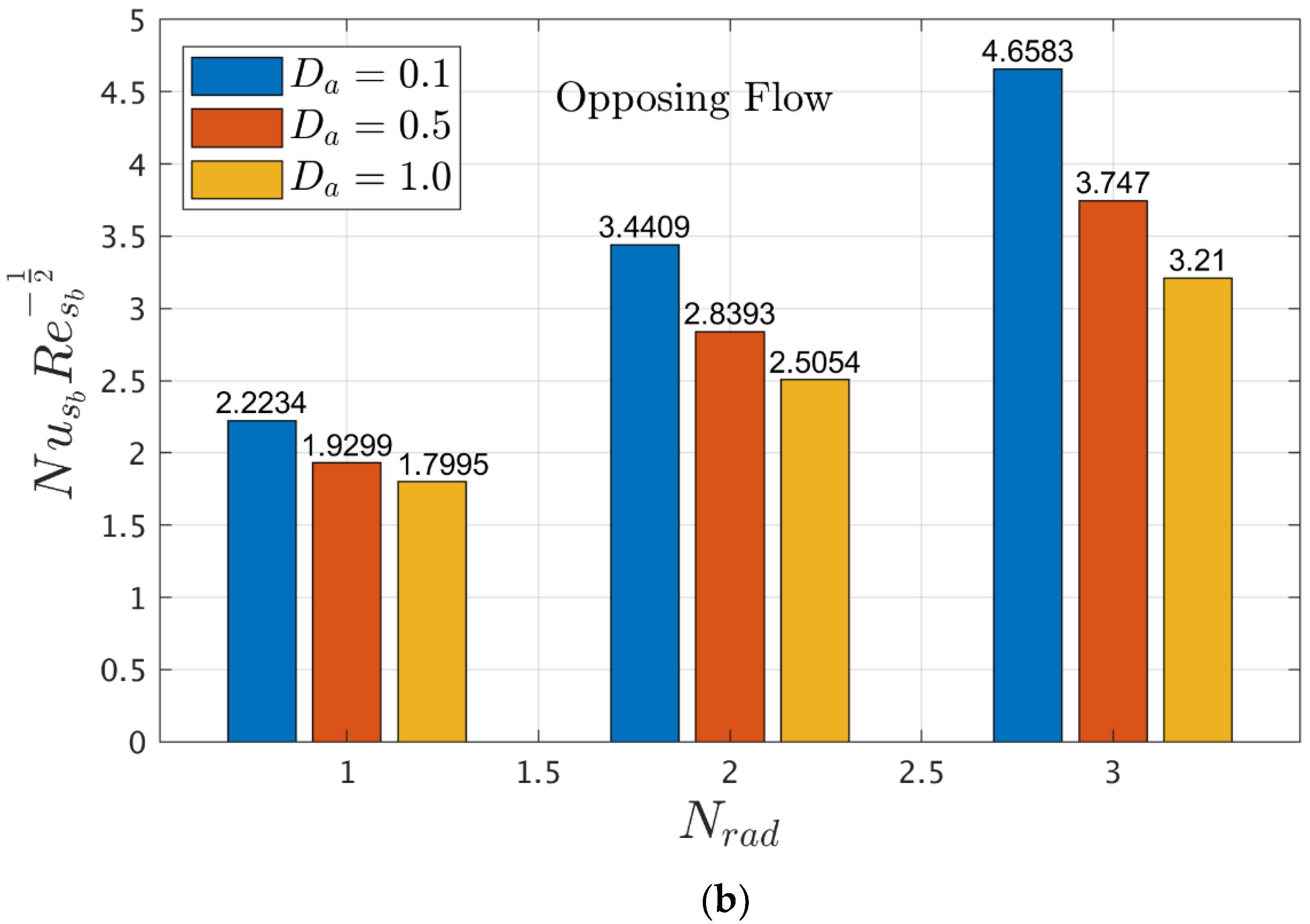
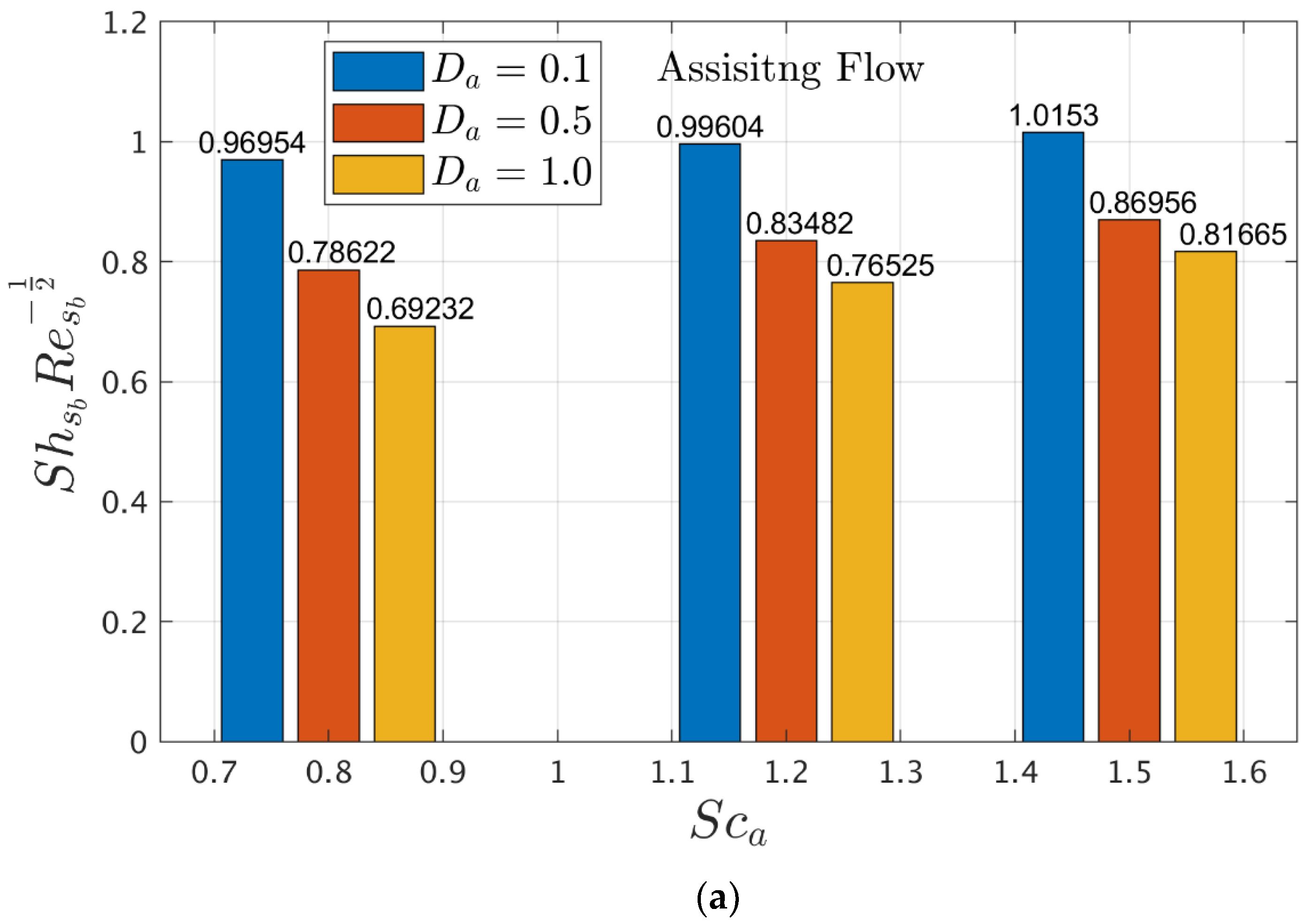
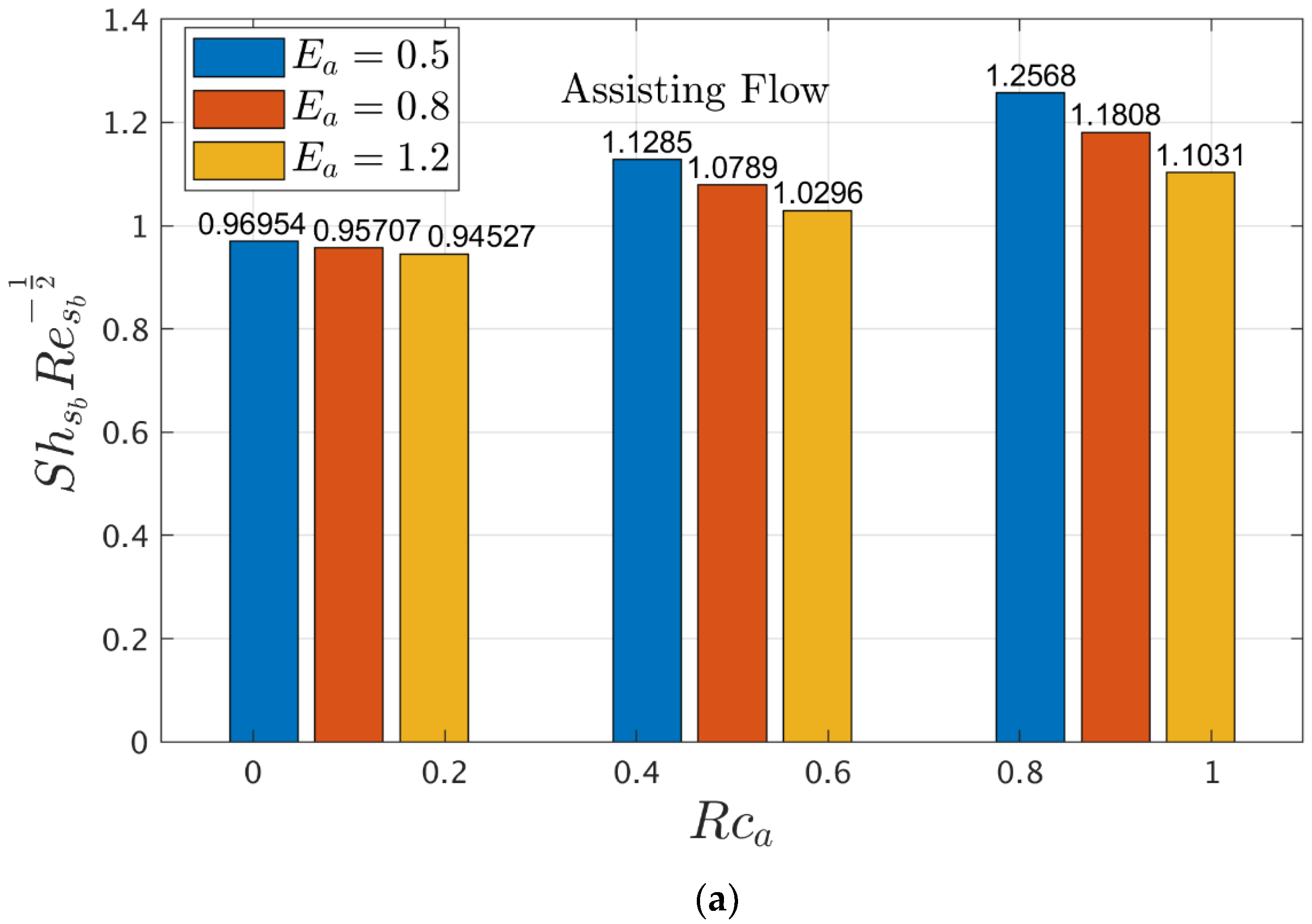
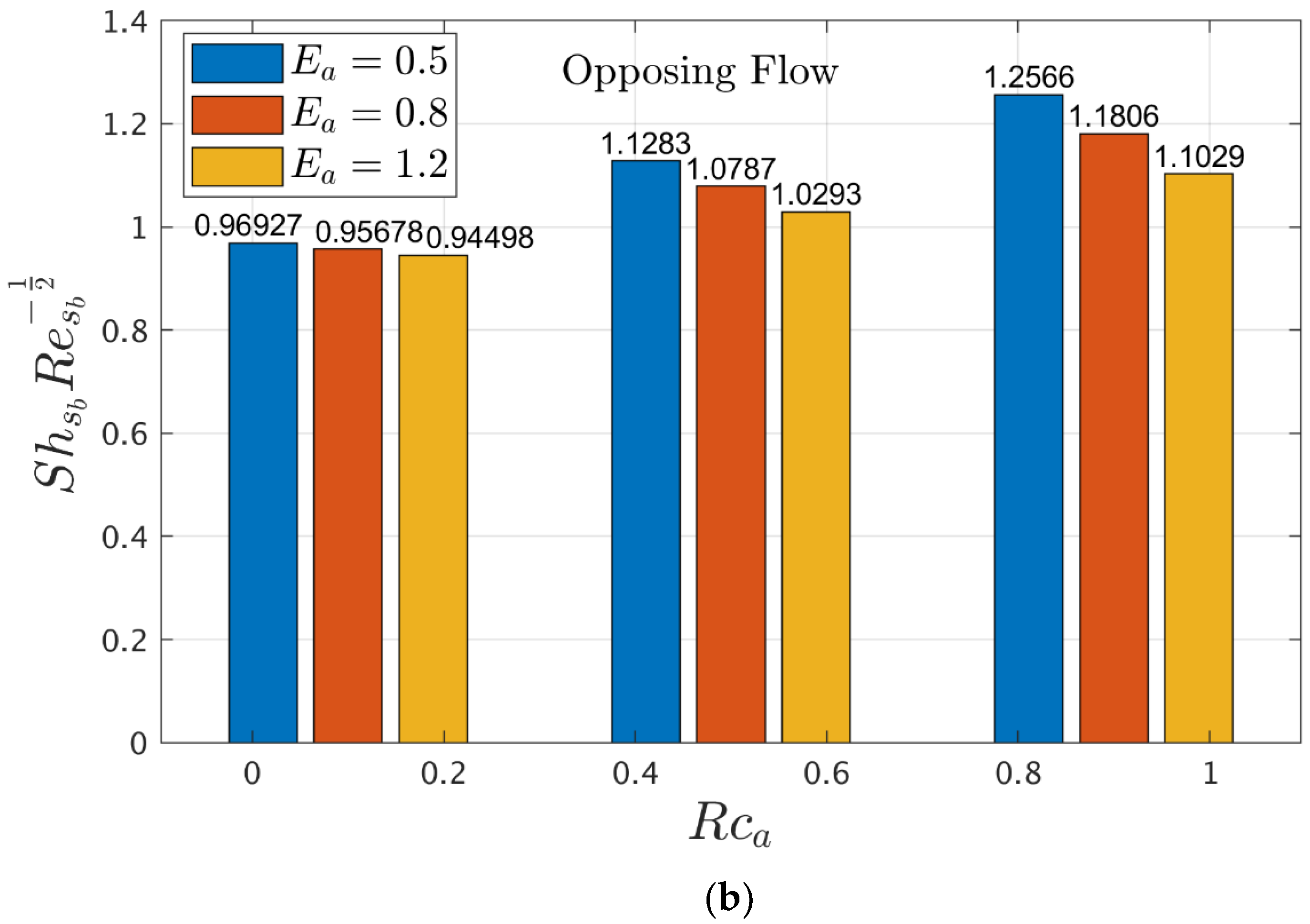
4.4. Interpretation of Gradients in Terms of Bar Graphs

The present portion of the work demonstrates the important engineering factors such as shear stress, heat, and mass transfer rates in terms of the various bar graphs for the case of ASF and OPF. The radius of curvature parameter $D_a$, velocity slip parameter ${\Sigma }_a$, radiation parameter $N_{rad}$, Schmidt number $S{c}_a$, reaction rate parameter $R{c}_a$, and activation energy parameter $E_a$ on the gradients (shear stress, heat, and mass transfer rates) are illustrated in the form of bar graphs (see Figure 11a,b, Figure 12a,b, Figure 13a,b and Figure 14a,b), respectively. Figure 11a,b portrays the variation of $C_{f{s}_b}{\mathrm{Re}}_{s_b}^{1/2}$ against velocity slip parameter ${\Sigma }_a$ for various radius values of curvature parameter for the case of ASF and OPF. It can be seen from the figure that the surface drag force is less in the ASF case than in the case of OPF for escalating values of ${\Sigma }_a$. This is because an increase in ${\Sigma }_a$ might serve as a barrier in the liquid flow particles, reducing the thickness of the momentum boundary layer and velocity gradients. In addition, it is worth mentioning that the shear stress decreases up to 31.62% and 31.63%, respectively, for ASF and OPF due to continuous enhancement in the values of the velocity slip parameter. However, the shear stress reduces more for the case of ASF, which is around 16.08%. Meanwhile, for the case of OPF, it is decreases by 13.63%. In other words, improvement in $D_a$ will result in a higher radius of the sheet which allows the fluid to flow faster. This results in lower surface drag force. In addition, if any parameter increases the velocity, which ultimately reduces the skin friction due to the inverse relation between the velocity and the skin friction. Figure 12a,b shows the variation in the rate of heat transfer against the radiation parameter for numerous values of $D_a$. The rate of thermal distribution enhances with escalating values of $N_{rad}$ and $D_a$. Improvement in $N_{rad}$ will gradually improve the thermal distribution rate due to the presence of Rosseland’s diffusion approximation and a larger value of $D_a$ allows the fluid to distribute the heat efficiently in the system. From the figure, it is noticed that the rate of heat distribution was increased up to 54.68% for the case of ASF and 54.76% for the case of OPF, owing to the larger values of the radiation parameter. Percentage wise, the enhancement is more for the case of OPF as compared to the case of ASF. Figure 13a,b displays the rate of mass transfer versus $S{c}_a$ with different values of $D_a$ for both ASF and OPF. The rate of mass transfer declines for escalating values of $D_a$ and $S{c}_a$. Improvement in $S{c}_a$ (mass diffusion ratio momentum diffusivity) and $D_a$ (leading to larger radius) will gradually decline the rate of mass transfer. Figure 14a,b demonstrates the impact of mass distribution rate versus reaction rate parameter $R{c}_a$, for distinct values of the activation energy parameter. The mass distribution enhances due to the appearance of the Arrhenius function factor in the activation energy parameter but gradually declines due to improvement in the reaction rate parameter. It can also be seen from Figure 13a,b and Figure 14a,b that the mass distribution rate is more in the case of ASF than in the OPF phenomenon. Furthermore, the rate of mass transfer upsurges up to 2.73% and 16.40% for the case of ASF due to the larger values of $S{c}_a$ and $R{c}_a$, respectively, but it declines with $D_a$ and $E_a$, up to 18.9% and 1.29%, respectively. However, the rate of mass transfer for the case of OPF decreases up to 19.76% and 1.30% due to the superior values of $D_a$ and $E_a$, respectively, while it increases at around 2.72% for the larger values of $S{c}_a$ and 16.41% with higher impacts of $R{c}_a$.

5. Final Remarks

In the present paper, the radiative impact on the mixed convective flow with heat and mass transfer over a stretching permeable bended sheet comprising water-based alumina nanoparticles with slip effect has been explored. Additionally, the analysis of Arrhenius activation energy and binary chemical reaction has also been implemented in the contemporary curved surface geometry. Initially, the problem was captured in the form of PDEs and then shifted to ODEs via exercising the similarity variables. Furthermore, the problem was numerically solved by a finite difference-based technique, namely bvp4c in MATLAB. Numerical outcomes for the case of ASF and OPF of the associated parameters were also examined and plotted for the velocity, temperature, and concentration profiles while the gradients’ (shear stress, heat, and mass transfer rates) behaviors were shown through several bar graphs. Furthermore, the outcomes obtained were consistent for the limiting case with the ones in the literature. The key points are given below:

• The velocity profile enhances for both ASF and OPF due to the higher impact of the radius curvature parameter; however, for the temperature and concentration profiles, a decreasing behavior is noticed.
• For increasing values of nanoparticle volume fraction, the temperature profile escalates, while velocity and concentration profiles decelerate for ASF and OPF.
• For ASF as well as OPF, the temperature profile significantly increases by incorporating the radiation parameter.
• With rising impact of the slip parameter, the shear stress output is smaller for the case of ASF as compared to the OPF.
• The heat transport rate improves by increasing the radiation parameter and radius of curvature parameter.
• The Arrhenius function factor, which appears in the activation energy parameter, causes the mass distribution to improve. However, as the reaction rate parameter improves, the mass distribution steadily decreases.