A Hybrid Model for GRU Ultra-Short-Term Wind Speed Prediction Based on Tsfresh and Sparse PCA
Abstract
1. Introduction
- A new short-term wind speed hybrid prediction model was proposed;
- A detailed comparison of the performance and computation time of the proposed model with neural network models and statistical models was made;
- It was verified that the feature expansion approach was superior to the approach using data features related to wind speed in the point prediction of univariate wind speed time series data.
2. Materials and Methods
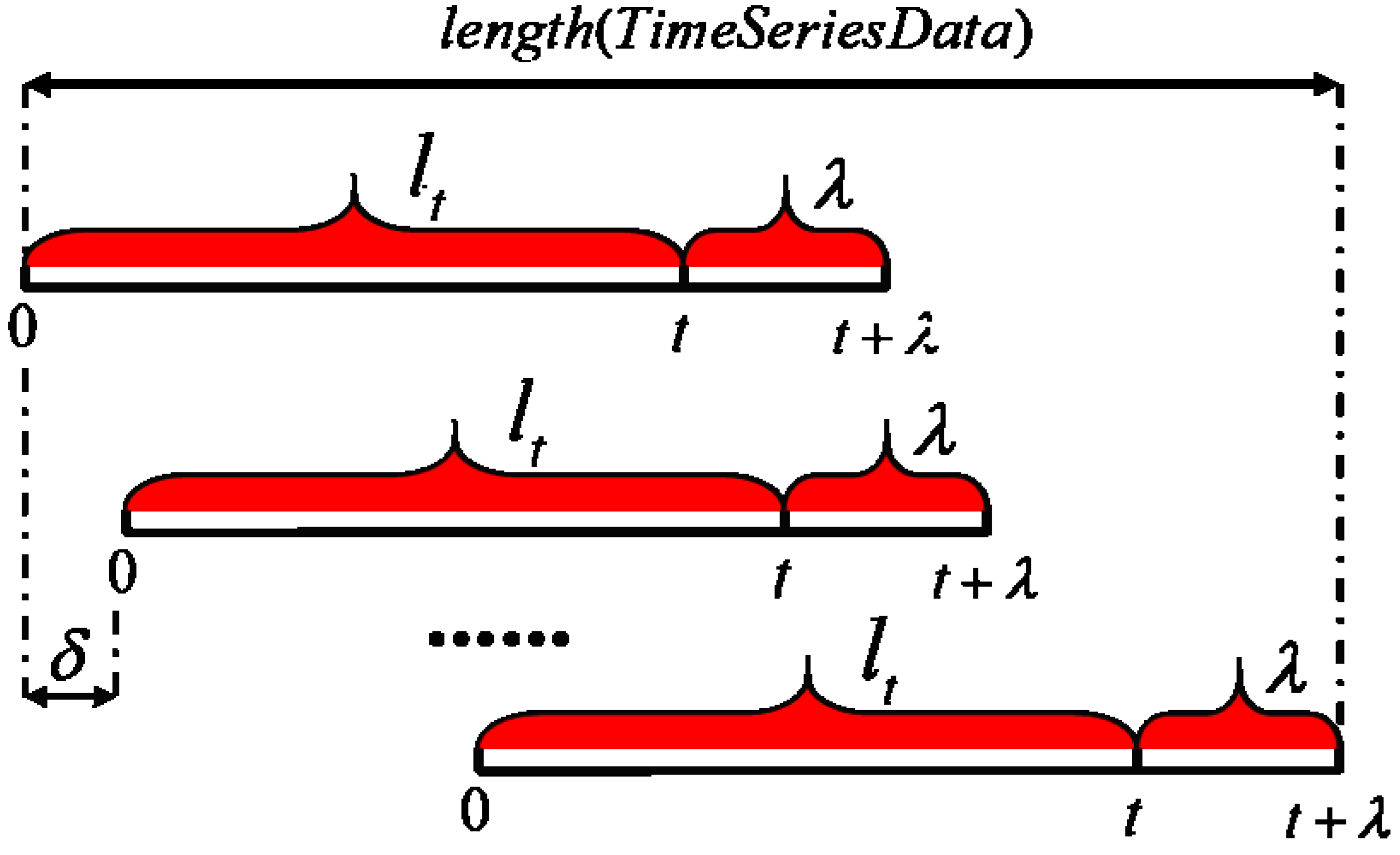
2.1. Tsfresh-Time Series Feature Extraction
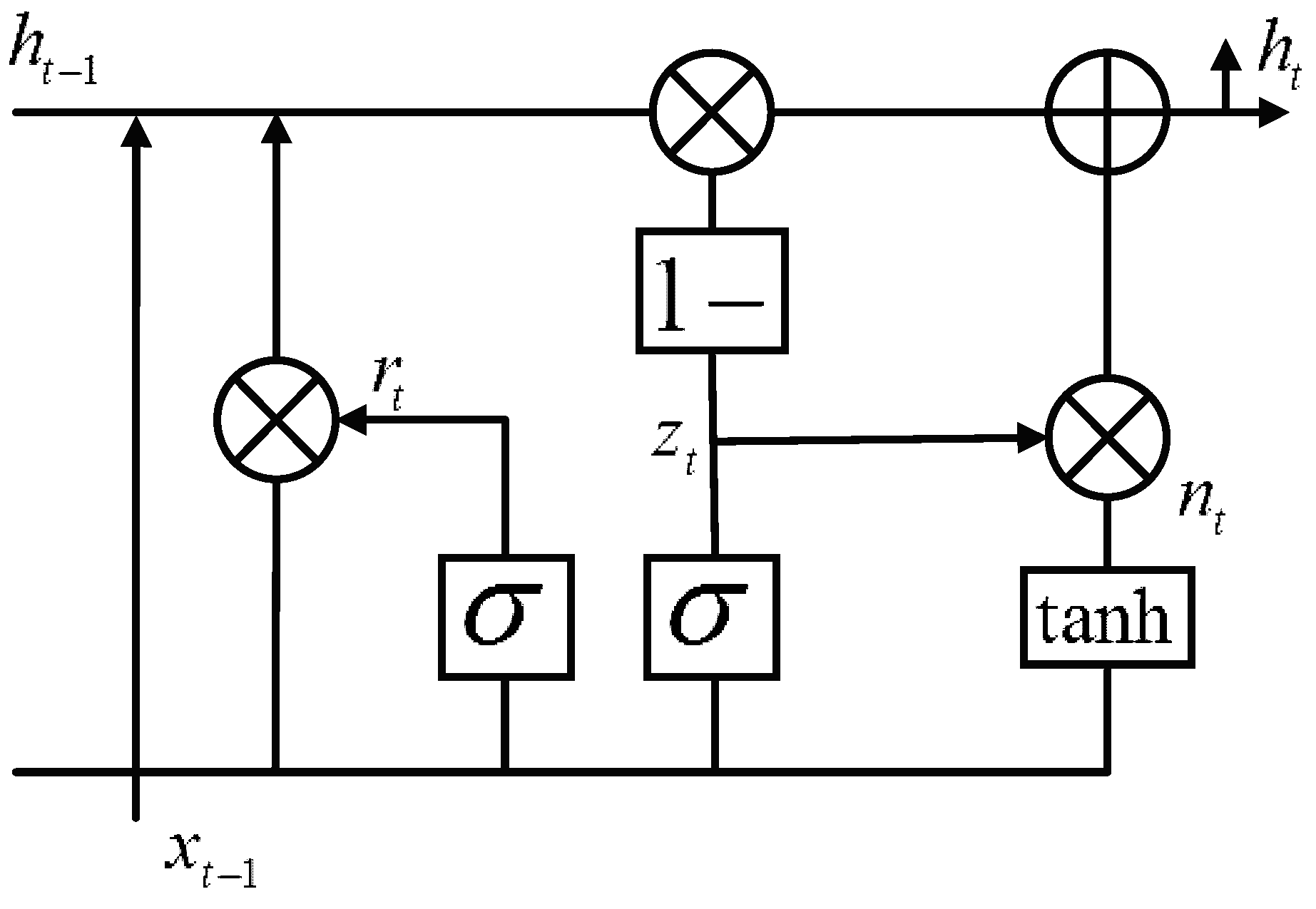
2.2. GRU
- Firstly, we defined Wir, Whr, Wiz, Whz, Win, and Whn as the weight matrices for the different phases, and bir, bhr, biz, bhz, bin, and bhn were the bias terms.
- The GRU reset gate rt was introduced through the reset gate calculated using the equation:
- 3.
- The update gate zt controlled the amount of information forgotten by the hidden layer at the previous moment:
- 4.
- The hidden state ht carried the information of the current cell and passed it down to the network, and the last output value was chosen among nt and ht:
2.3. Sparse PCA
- A starts from the first k ordinary principal components V [1: p, 1:k] (p→∞);
- Given A as:
- 3.
- Given B as:
- 4.
- Repeat steps 2 and 3 above until convergence.
- 5.
- Finally, standardization:
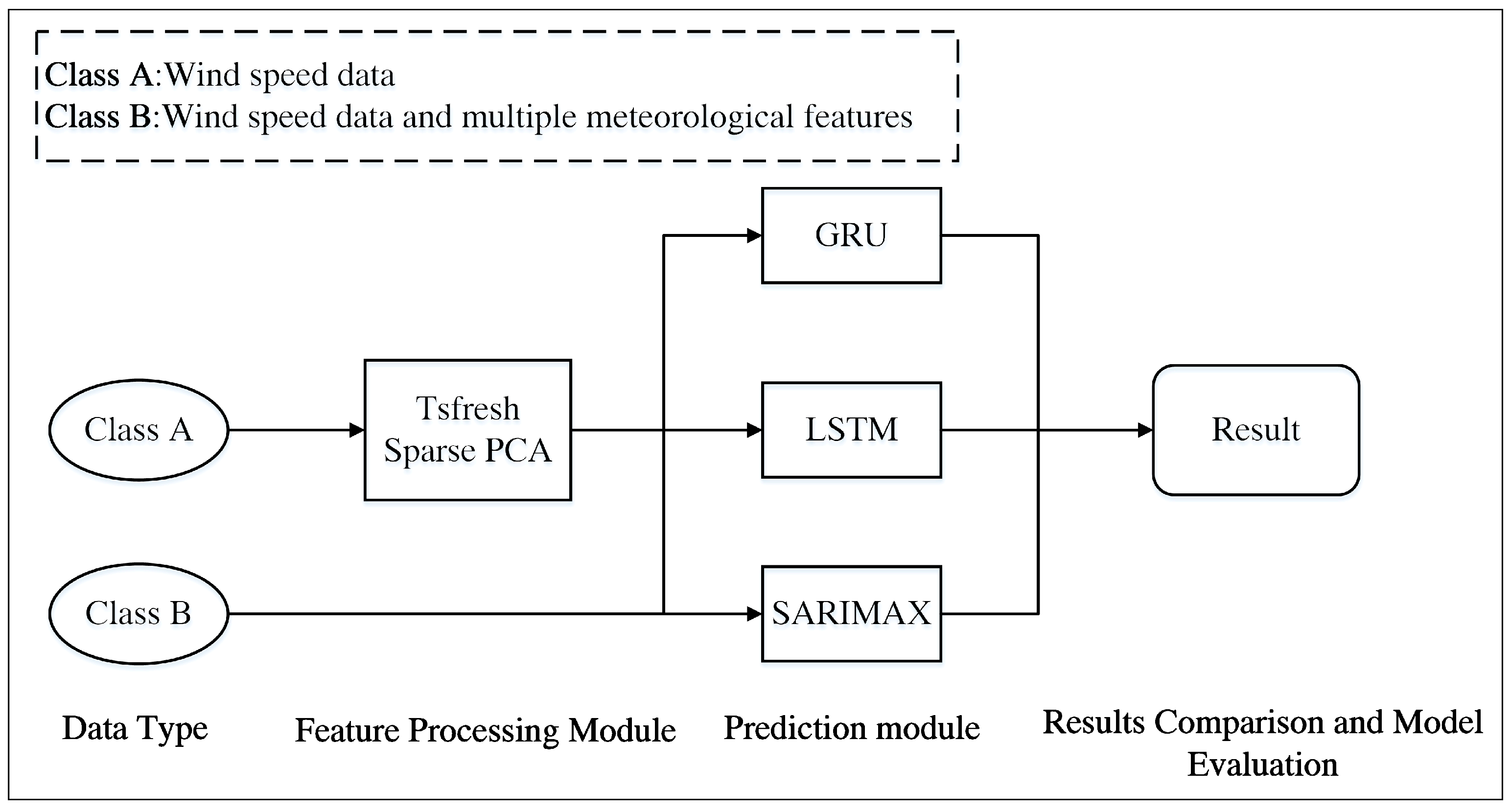
3. Realization of Prediction Model
- All data were sliced and normalized.
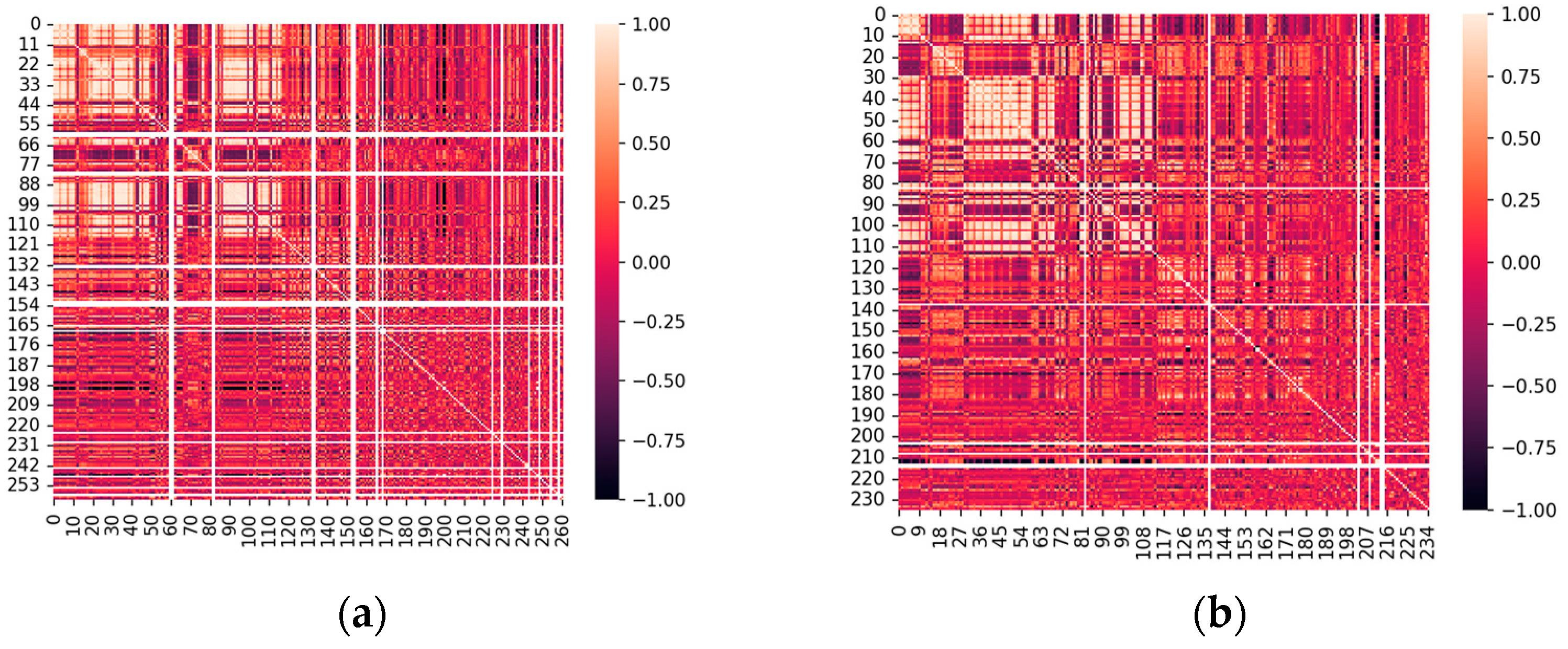
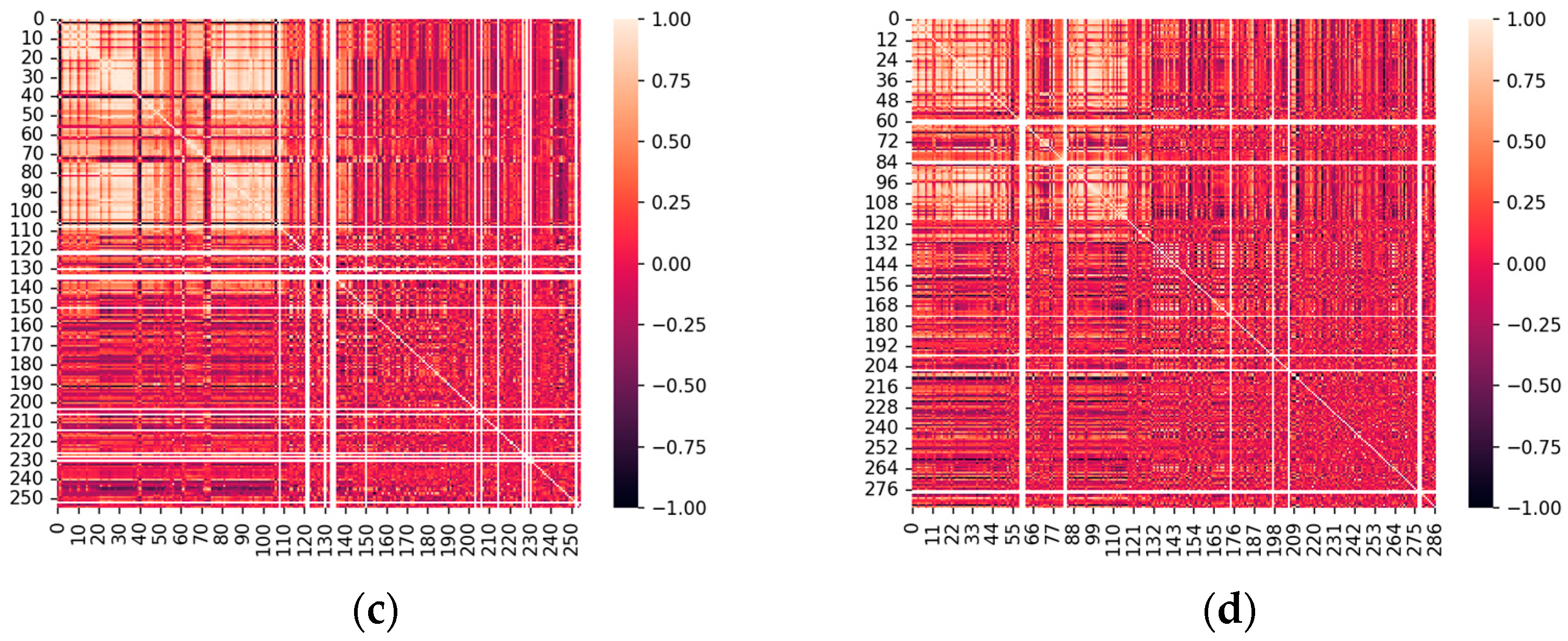
- Data feature processing included feature extraction and feature selection, with Tsfresh in charge of feature extraction and Sparse PCA in charge of feature selection.
- GRU accepted the input data for data fitting to obtain the predicted values and calculated the error based on the predicted and true values.
- The weights of the layers of the GRU network were updated based on the BPTT algorithm [27].
- After setting the number of training steps, steps 3 and 4 were repeated, and the Adam optimization algorithm was used to calculate the update steps until the loss function was minimized.
- After the network was trained, the wind speed was predicted for each minute of the next hour.
- Error analysis was carried out to evaluate the model performance.
4. Case Analysis
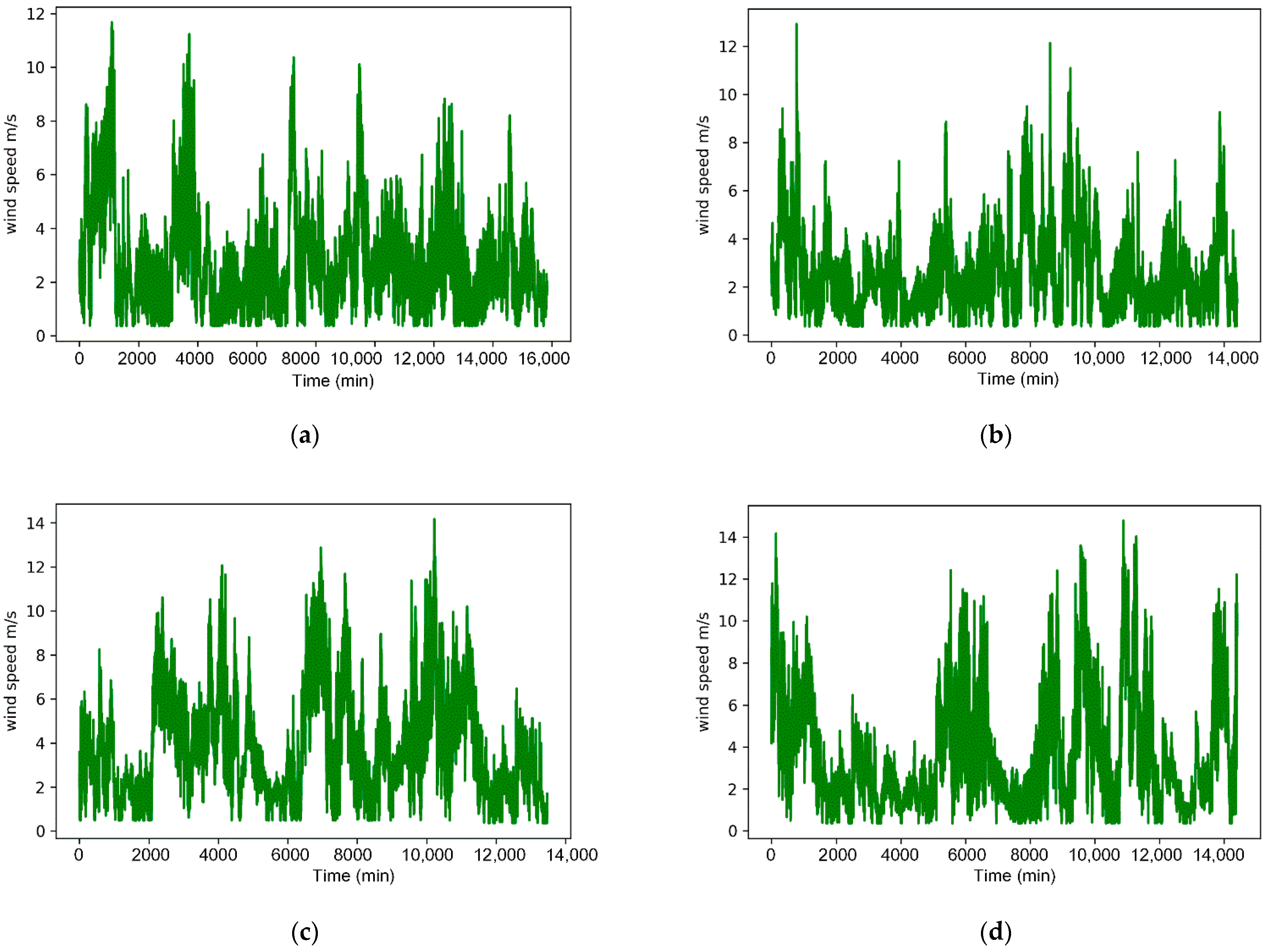
4.1. Experimental Data
4.2. Feature Processing Result
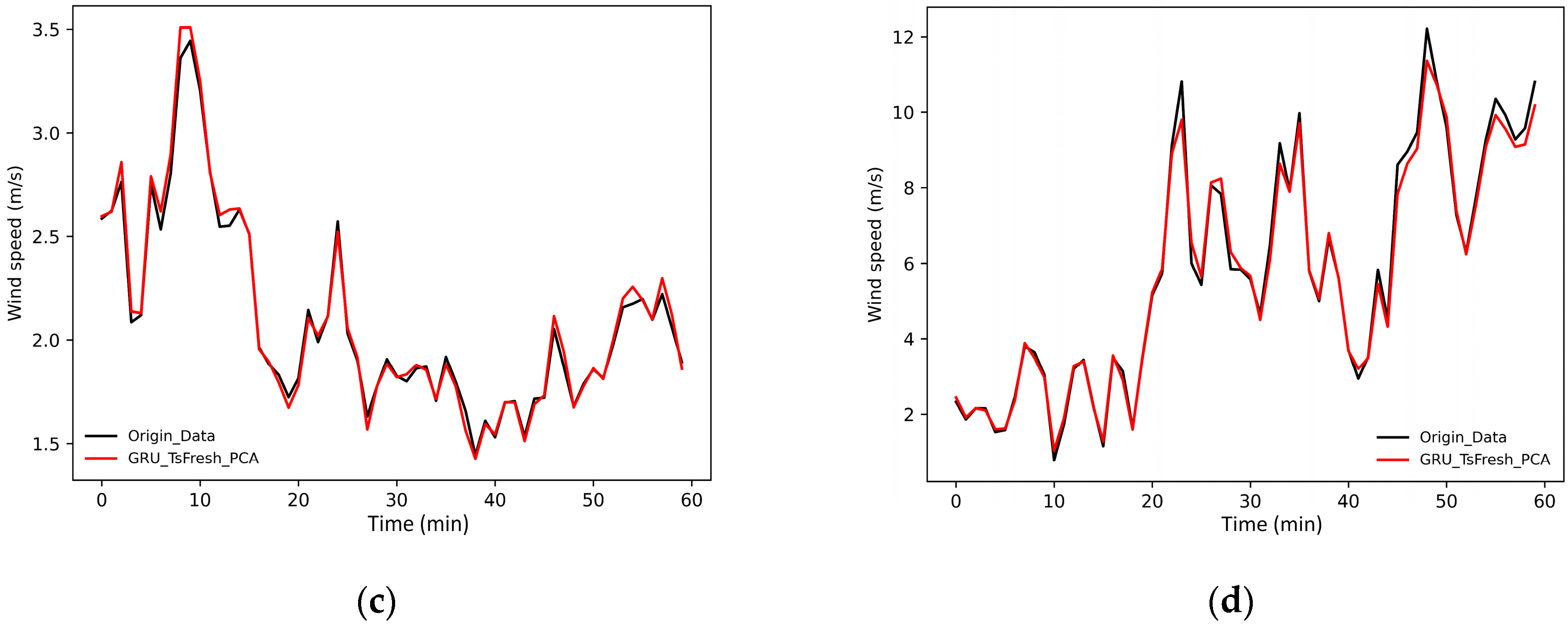
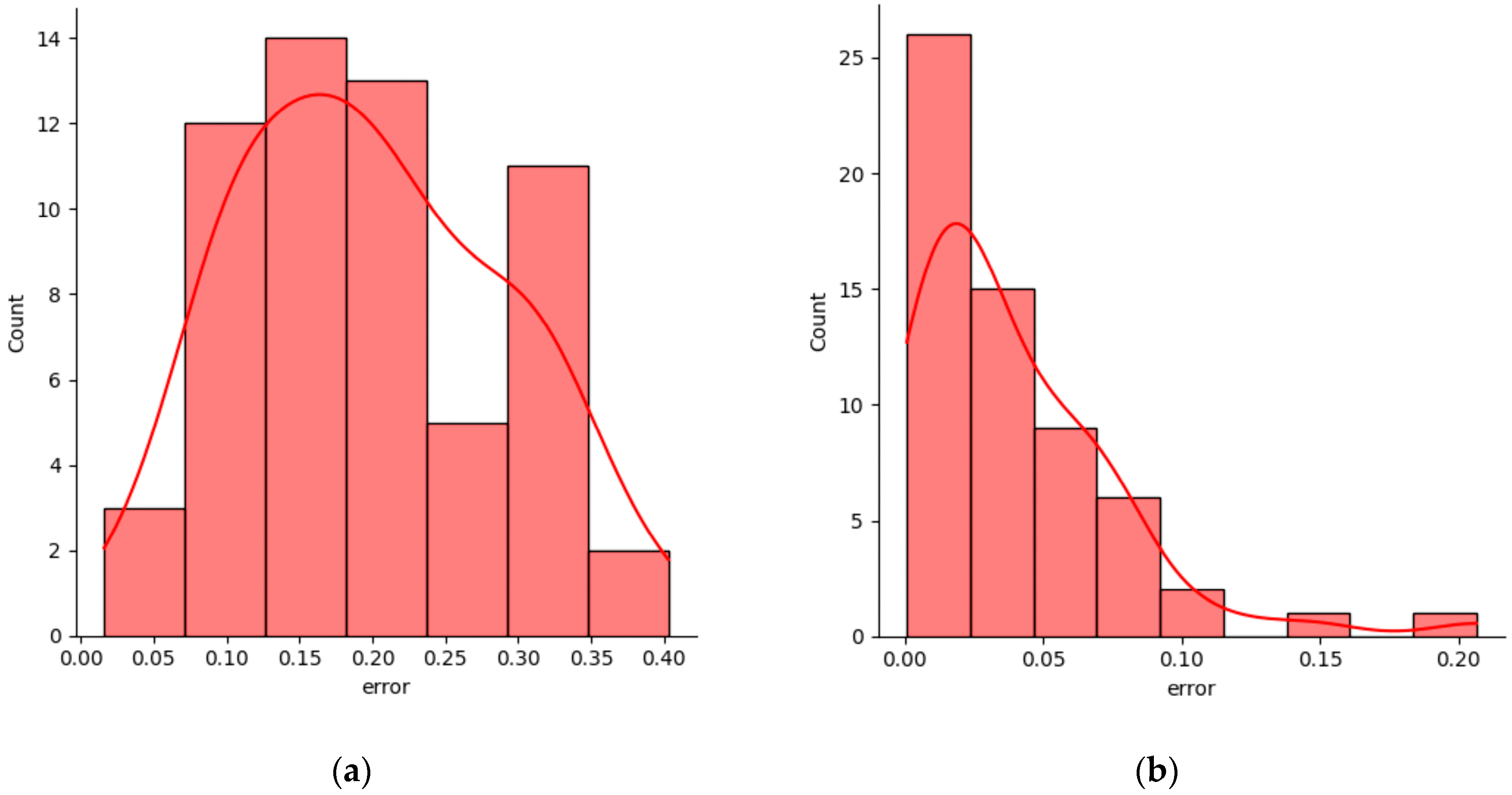
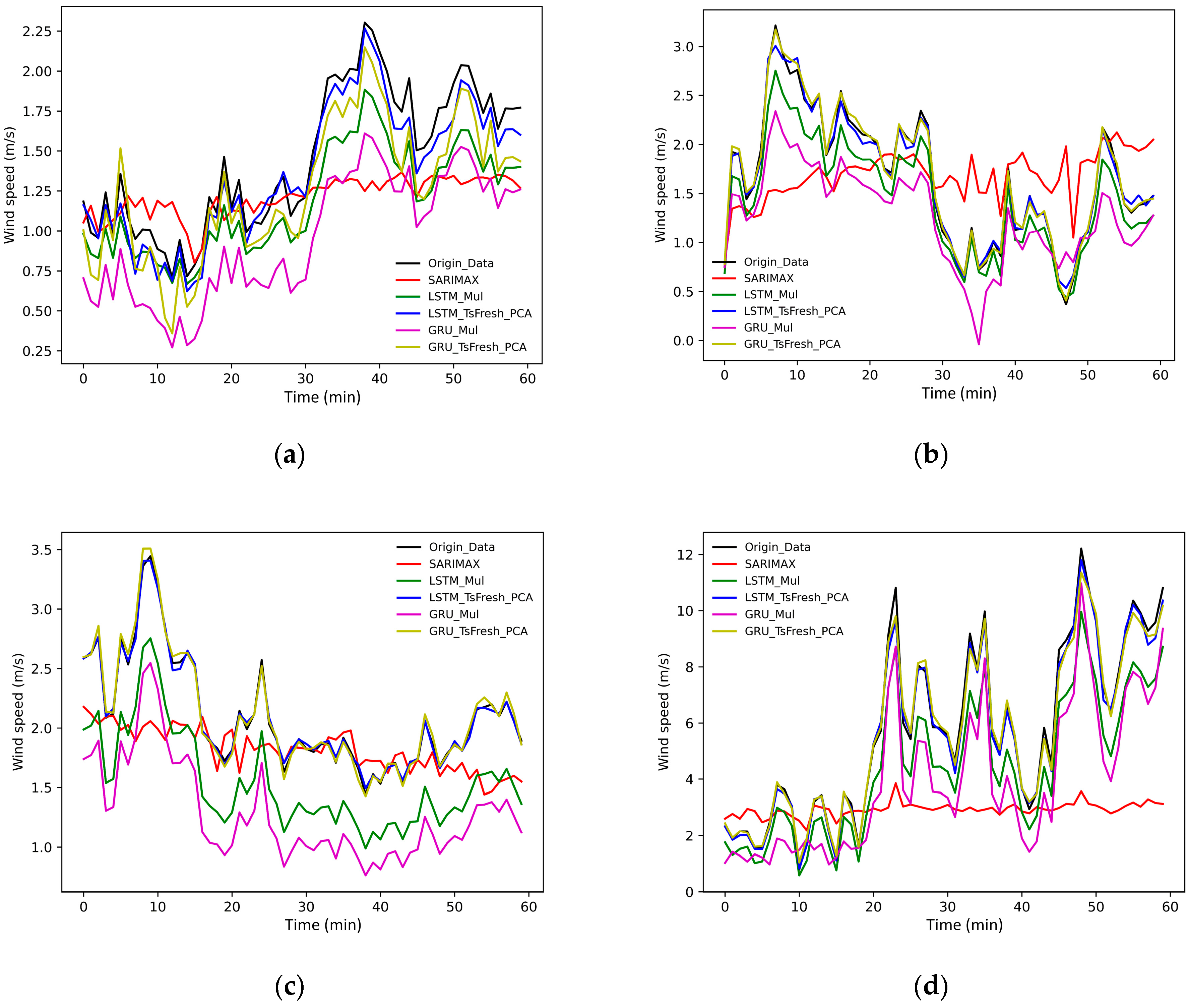
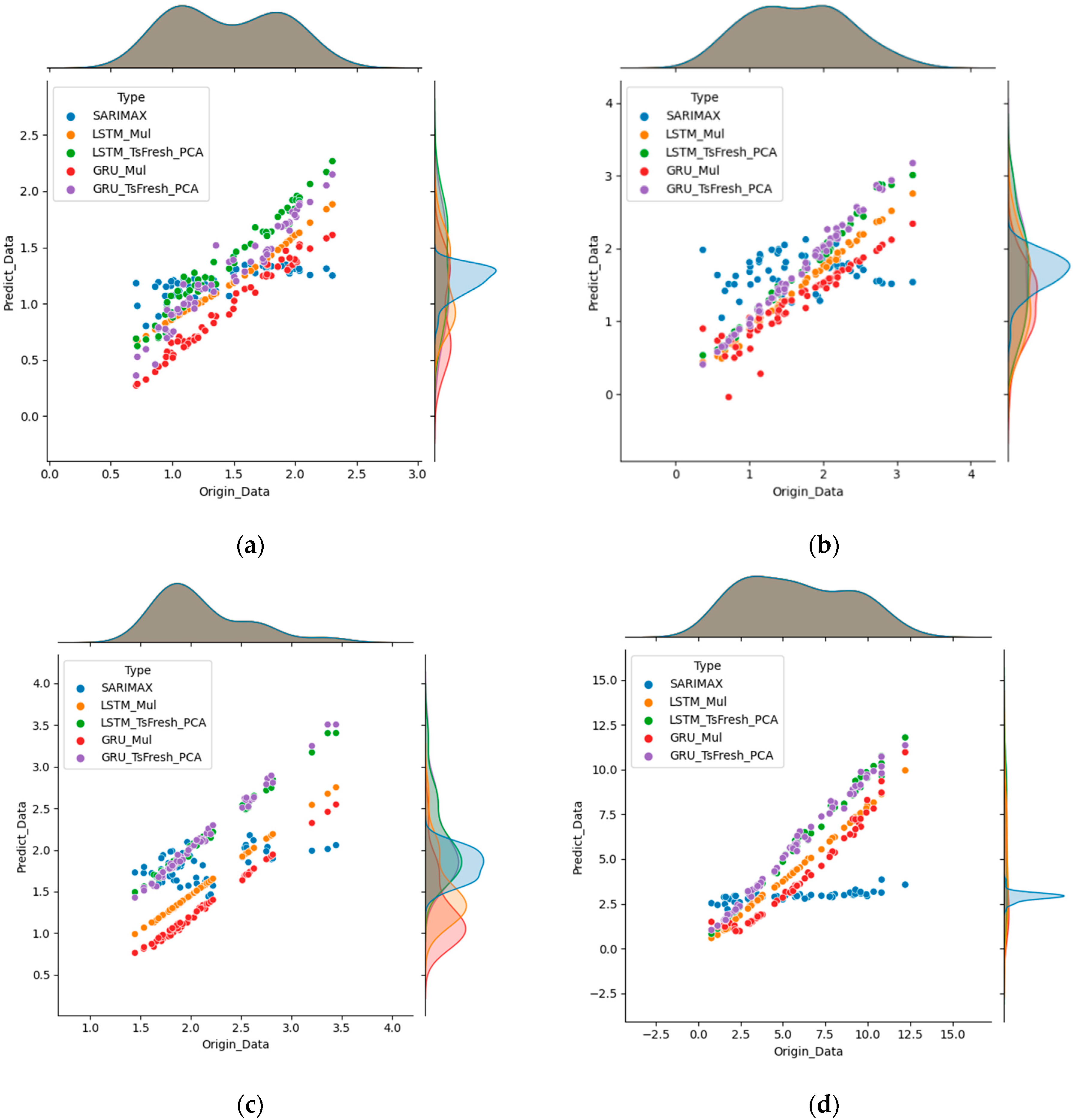
4.3. Analysis of Hybrid Model Prediction Results
4.4. Comparison of Prediction Results of Different Models
4.4.1. Description of the Control Experiment
4.4.2. Controlled Experimental Evaluation
- (1)
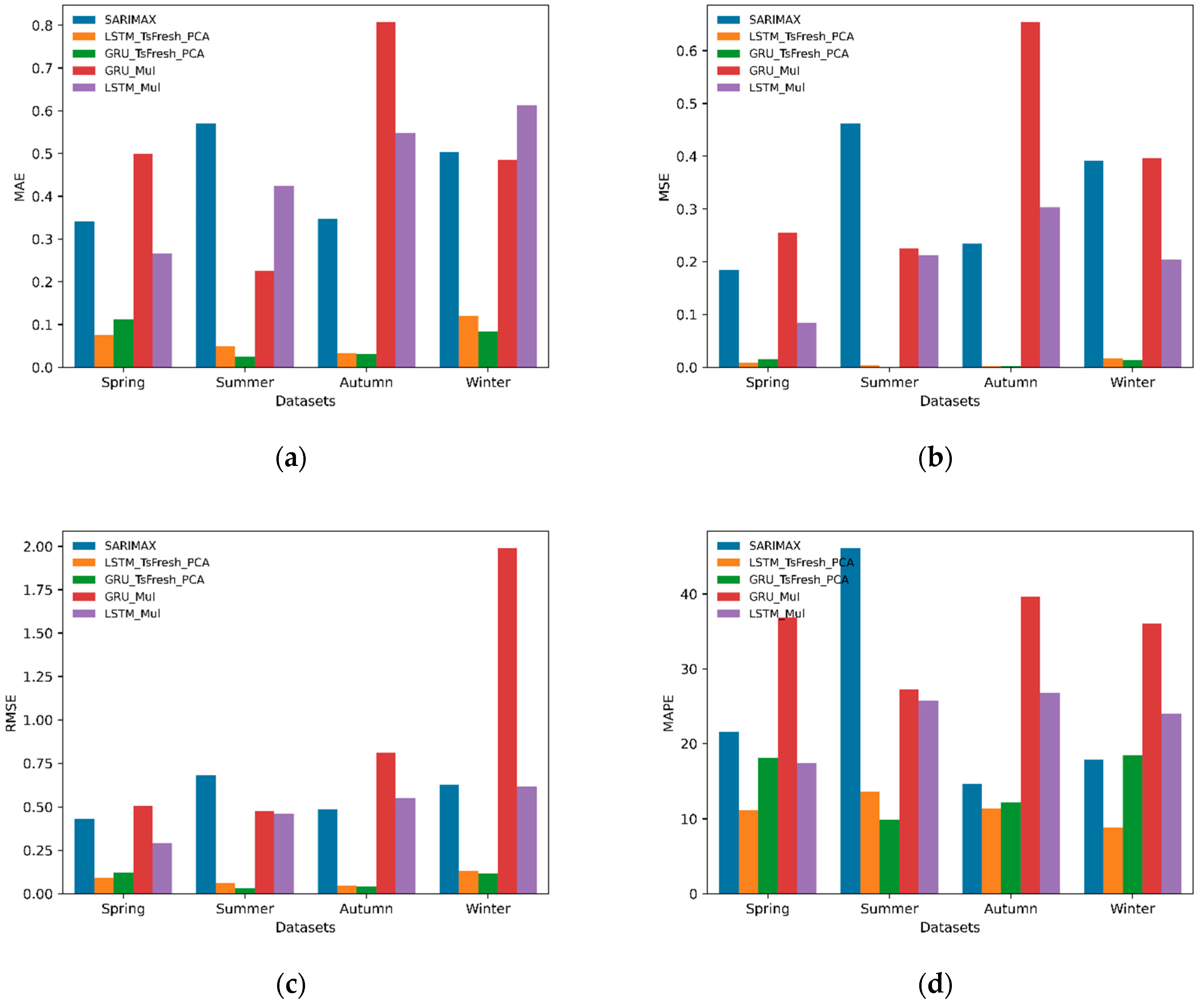
- Comparing the values of the single model and neural network model on the metrics MSE, MAE, RMSE, and MAPE, it was observed that the neural network model achieved superior performance on the four metrics, which indicated that the neural network could contribute to improving the model prediction. Taking the summer dataset as an example, the MAE of the SARIMAX model was 0.57048, and the MAE of the four neural network models were 0.4237, 0.2248, 0.0492, and 0.0238, respectively. The same situation occurred for MSE, RMSE, and MAPE. Similarly, the law continued to be maintained for the other three data sets.
- (2)
- In the neural network model, the neural network with the feature extraction module performed better than the neural network model using only 12 types of climate data as feature data. Taking the summer dataset as an example, the MAE of the SARIMAX model was 0.57048, and the MAE of the four neural network models were 0.4237, 0.2248, 0.0492, and 0.0238, respectively. The same situation was observed for MSE, RMSE, and MAPE. Similarly, the law continued to be maintained for the other three data sets.
- (3)
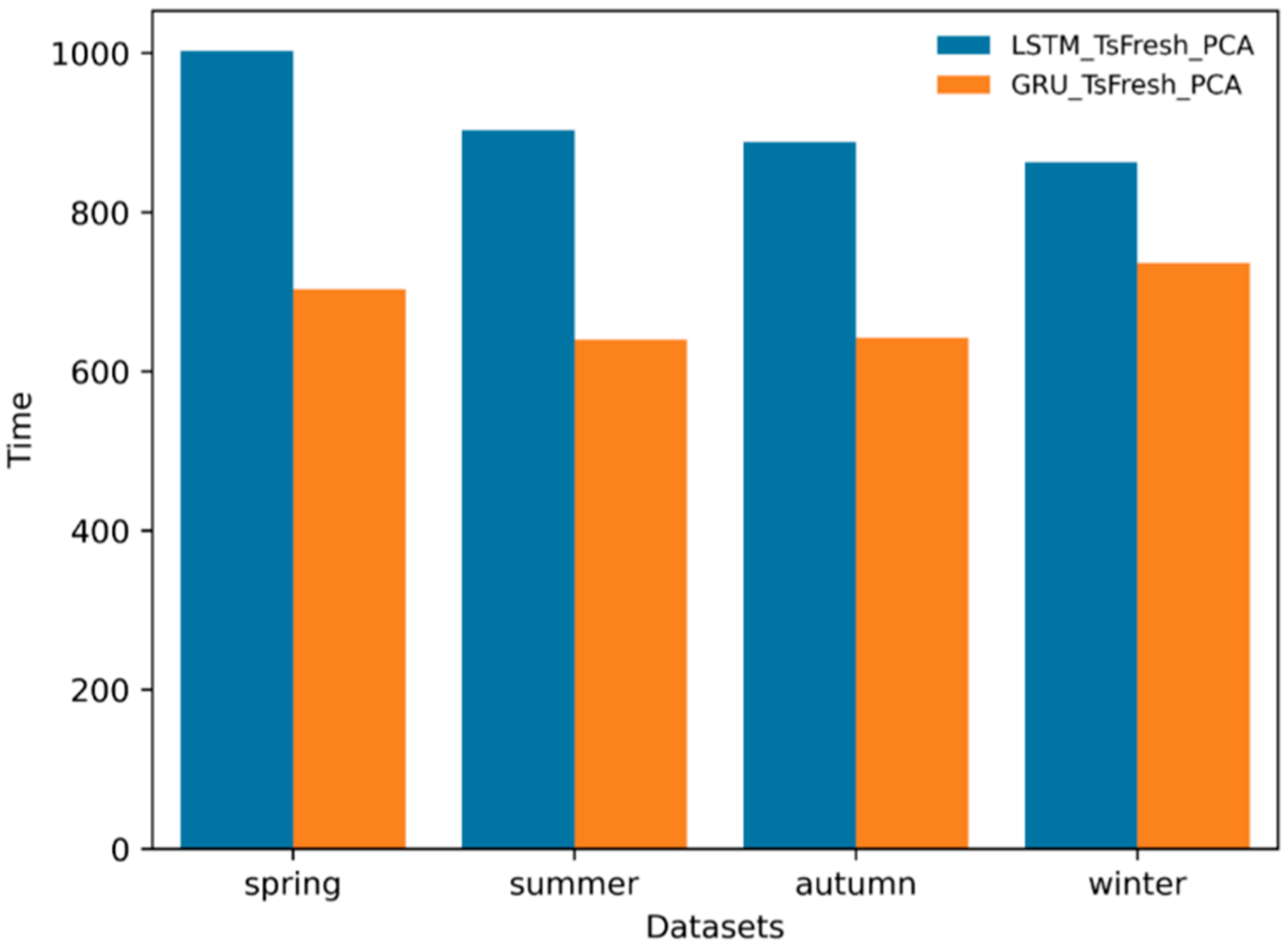
- Among the proposed hybrid models, the GRU_Tsfresh_PCA model had better predictive power than the LSTM_Tsfresh_PCA model in the summer, autumn, and winter datasets. In the spring dataset, the prediction accuracy of the two models was the same. Taking the winter dataset as an example, the GRU_Tsfresh_PCA model decreased 17.42% in MSE, 30.42% in MAE, 9.1% in RMSE, and 1.8% in MAPE compared with the LSTM_Tsfresh_PCA model.
4.4.3. Visual Analysis of the Prediction Results
5. Conclusions
- (1)
- The proposed model GRU_Tsfresh_PCA had the best prediction results.
- (2)
- Experimentally, it was demonstrated that the GRU network outperformed the LSTM network under the same computational conditions after the wind speed data were processed by features.
- (3)
- The experimental results showed that the feature expansion could not only fit the existing meteorological features, but also fit the feature data more suitable for wind speed prediction than using the meteorological feature data related to the original wind speed data directly. These data were not directly obtained in reality.
- (4)
- In summary, the proposed method in this paper could be expected to have good application prospects in the future because of its low computational cost and good prediction performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Balat, M. A review of modern wind turbine technology. Energy Sources Part A 2009, 31, 1561–1572. [Google Scholar] [CrossRef]
- Bhadane, K.V.; Ballal, M.S.; Moharil, R.M. Investigation for causes of poor power quality in grid connected wind energy-A review. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
- Khadem, S.K.; Basu, M.; Conlon, M. Power quality in grid connected renewable energy systems: Role of custom power devices. Renew. Energy Power Qual. J. 2010, 1, 878–881. [Google Scholar] [CrossRef]
- Li, N.; He, F.; Ma, W. Wind power prediction based on extreme learning machine with kernel mean p-power error loss. Energies 2019, 12, 673. [Google Scholar] [CrossRef]
- Giebel, G.; Kariniotakis, G. Best practice in short-term forecasting—A users guide. In Proceedings of the CD-Rom Proceedings European Wind Energy Conference, London, UK, 7 May 2007. [Google Scholar]
- Aburiyana, G.; El-Hawary, M.E. An overview of forecasting techniques for load, wind and solar powers. In Proceedings of the 2017 IEEE Electrical Power and Energy Conference (EPEC), Saskatoon, SK, Canada, 22–25 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–7. [Google Scholar]
- Mosaico, G.; Saviozzi, M. A hybrid methodology for the day-ahead PV forecasting exploiting a Clear Sky Model or Artificial Neural Networks. In Proceedings of the IEEE EUROCON 2019—18th International Conference on Smart Technologies, Novi Sad, Serbia, 1–4 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Chen, J.F.; Wang, W.M.; Huang, C.M. Analysis of an adaptive time-series autoregressive moving-average (ARMA) model for short-term load forecasting. Electr. Power Syst. Res. 1995, 34, 187–196. [Google Scholar] [CrossRef]
- Jeong, K.; Koo, C.; Hong, T. An estimation model for determining the annual energy cost budget in educational facilities using SARIMA (seasonal autoregressive integrated moving average) and ANN (artificial neural network). Energy 2014, 71, 71–79. [Google Scholar] [CrossRef]
- Tyass, I.; Bellat, A.; Raihani, A.; Mansouri, K.; Khalili, T. Wind Speed Prediction Based on Seasonal ARIMA model. E3S Web Conf. EDP Sci. 2022, 336, 00034. [Google Scholar] [CrossRef]
- Kritharas, P. Developing a SARIMAX Model for Monthly Wind Speed Forecasting in the UK. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2014. [Google Scholar]
- Lydia, M.; Kumar, S.S.; Selvakumar, A.I.; Kumar, G.E.P. Linear and non-linear autoregressive models for short-term wind speed forecasting. Energy Convers. Manag. 2016, 112, 115–124. [Google Scholar] [CrossRef]
- Duan, J.; Zuo, H.; Bai, Y.; Duan, J.; Chang, M.; Chen, B. Short-term wind speed forecasting using recurrent neural networks with error correction. Energy 2021, 217, 119397. [Google Scholar] [CrossRef]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Zhu, Q.; Chen, J.; Shi, D.; Zhu, L.; Bai, X.; Duan, X.; Liu, Y. Learning temporal and spatial correlations jointly: A unified framework for wind speed prediction. IEEE Trans. Sustain. Energy 2019, 11, 509–523. [Google Scholar] [CrossRef]
- Liu, M.; Qiu, P.; Wei, K. Research on wind speed prediction of wind power system based on GRU deep learning. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Changsha, China, 8–10 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1699–1703. [Google Scholar]
- Li, C.; Tang, G.; Xue, X.; Saeed, A.; Hu, X. Short-term wind speed interval prediction based on ensemble GRU model. IEEE Trans. Sustain. Energy 2019, 11, 1370–1380. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, C.; Li, J.; Sun, B.; Yang, J.; Arpino, F. A hybrid method for ultrashort-term wind power prediction considering meteorological features and seasonal information. Math. Probl. Eng. 2020, 2020, 1795486. [Google Scholar] [CrossRef]
- Jung, J.; Broadwater, R.P. Current status and future advances for wind speed and power forecasting. Renew. Sustain. Energy Rev. 2014, 31, 762–777. [Google Scholar] [CrossRef]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. In Data Classification: Algorithms and Applications; Chapman and Hall: New York, NY, USA, 2014; p. 37. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Christ, M.; Braun, N.; Neuffer, J.; Kempa-Liehr, A.W. Time series feature extraction on basis of scalable hypothesis tests (Tsfresh—A python package). Neurocomputing 2018, 307, 72–77. [Google Scholar] [CrossRef]
- Zhou, G.B.; Wu, J.; Zhang, C.L.; Zhou, Z.H. Minimal gated unit for recurrent neural networks. Int. J. Autom. Comput. 2016, 13, 226–234. [Google Scholar] [CrossRef]
- Rana, R. Gated recurrent unit (GRU) for emotion classification from noisy speech. arXiv 2016, arXiv:1612.07778. [Google Scholar]
- Cai, T.T.; Ma, Z.; Wu, Y. Sparse PCA: Optimal rates and adaptive estimation. Ann. Stat. 2013, 41, 3074–3110. [Google Scholar] [CrossRef]
- Guo, J. Backpropagation through Time, Harbin Institute of Technology: Harbin, China, 2013; Volume 40, 1–6, unpublished work.
- Jager, D.; Andreas, A. NREL National Wind Technology Center (NWTC): M2 Tower; Boulder, Colorado (Data); National Renewable Energy Lab. (NREL): Golden, CO, USA, 1996.



| Forecast Content | Time Horizon | Application |
|---|---|---|
| ultra-short-term | ≤1 h | Real-time grid operation, equipment monitoring, etc. |
| short-term | ≤8 h | Load dispatch planning, load rationalization decision and power market operation guarantee, etc. |
| medium-term | ≤24 h | Reserve demand decision, etc. |
| long-term | >24 h | Wind farm design, optimization of operation cost, etc. |
| Dataset | Samples | Length | Mathematical Statistical Indicators | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Mean | Std | Median | Skew | Kurtosis | |||
| spring | all | 15,840 | 11.68 | 0.36 | 2.76 | 1.78 | 2.32 | 1.29 | 1.67 |
| train | 11,880 | 11.68 | 0.36 | 2.86 | 1.87 | 2.39 | 1.22 | 1.33 | |
| validation | 3240 | 8.83 | 0.36 | 2.45 | 1.4 | 2.2 | 1.17 | 1.69 | |
| test | 720 | 2.3 | 0.71 | 1.45 | 0.44 | 1.4 | 0.11 | −1.3 | |
| summer | all | 14,400 | 12.92 | 0.36 | 2.61 | 1.65 | 2.21 | 1.33 | 2 |
| train | 10,800 | 12.92 | 0.36 | 2.7 | 1.74 | 2.28 | 1.25 | 1.59 | |
| validation | 3540 | 9.26 | 0.36 | 2.36 | 1.34 | 2.08 | 1.48 | 3.02 | |
| test | 60 | 3.21 | 0.37 | 1.66 | 0.67 | 1.64 | 0.16 | −0.7 | |
| autumn | all | 13,476 | 14.17 | 0.36 | 3.86 | 2.35 | 3.36 | 0.8 | 0.07 |
| train | 10,107 | 12.87 | 0.48 | 3.93 | 2.33 | 3.49 | 0.76 | −0.05 | |
| validation | 3309 | 14.17 | 0.36 | 3.7 | 2.42 | 3.08 | 0.95 | 0.46 | |
| test | 60 | 1.69 | 0.36 | 0.67 | 0.34 | 0.57 | 0.99 | 0.35 | |
| winter | all | 14,400 | 14.78 | 0.36 | 3.64 | 2.59 | 2.81 | 1.13 | 0.72 |
| train | 10,800 | 14.17 | 0.36 | 3.5 | 2.43 | 2.71 | 1.11 | 0.72 | |
| validation | 3540 | 14.78 | 0.36 | 4.04 | 2.96 | 3.1 | 1.03 | 2.53 | |
| test | 60 | 12.21 | 0.77 | 5.77 | 3.09 | 5.66 | 0.23 | −1.14 | |
| Datasets | Number_Tsfresh | Number Sparse PCA |
|---|---|---|
| spring | 789 | 253 |
| summer | 789 | 234 |
| autumn | 789 | 250 |
| winter | 789 | 286 |
| Model Name | Module Composition | Data Type |
|---|---|---|
| SARIMAX Model | SARIMAX | Class A |
| LSTM_Tsfresh_PCA Model | Tsfresh, Sparse PCA, LSTM Network | Class A & Class B |
| GRU_Tsfresh_PCA Model | Tsfresh, Sparse PCA, GRU Network | Class A & Class B |
| LSTM_Mul Model | LSTM Network | Class A & Class B |
| GRU_Mul Model | GRU Network | Class A & Class B |
| Datasets | Data Type | Model Name | MSE | MAE | RMSE | MAPE |
|---|---|---|---|---|---|---|
| spring | Class A | SARIMAX | 0.18415 | 0.34181 | 0.42913 | 21.5437 |
| Class B | LSTM_Tsfresh_PCA | 0.00799 | 0.07536 | 0.08941 | 11.1132 | |
| Class B | GRU_Tsfresh_PCA | 0.01497 | 0.11156 | 0.12236 | 18.0979 | |
| Class A | GRU_Mul | 0.25500 | 0.49914 | 0.50498 | 36.8452 | |
| Class A | LSTM_Mul | 0.08446 | 0.26586 | 0.29063 | 17.4014 | |
| summer | Class A | SARIMAX | 0.4618 | 0.57048 | 0.67962 | 46.122 |
| Class B | LSTM_Tsfresh_PCA | 0.00359 | 0.04922 | 0.05996 | 13.6168 | |
| Class B | GRU_Tsfresh_PCA | 0.00108 | 0.02384 | 0.0329 | 9.8534 | |
| Class A | GRU_Mul | 0.22479 | 0.22479 | 0.47412 | 27.2866 | |
| Class A | LSTM_Mul | 0.21244 | 0.42376 | 0.46091 | 25.7521 | |
| autumn | Class A | SARIMAX | 0.23448 | 0.34644 | 0.48424 | 14.6314 |
| Class B | LSTM_Tsfresh_PCA | 0.00199 | 0.03317 | 0.04467 | 11.3925 | |
| Class B | GRU_Tsfresh_PCA | 0.00184 | 0.03148 | 0.04294 | 12.1422 | |
| Class A | GRU_Mul | 0.65398 | 0.80724 | 0.80869 | 39.6676 | |
| Class A | LSTM_Mul | 0.30338 | 0.54856 | 0.55079 | 26.7687 | |
| winter | Class A | SARIMAX | 0.39196 | 0.50293 | 0.62606 | 17.906 |
| Class B | LSTM_Tsfresh_PCA | 0.01699 | 0.11946 | 0.13033 | 8.7932 | |
| Class B | GRU_Tsfresh_PCA | 0.01403 | 0.08312 | 0.11846 | 18.4467 | |
| Class A | GRU_Mul | 0.39577 | 0.48542 | 1.9894 | 36.0289 | |
| Class A | LSTM_Mul | 0.20425 | 0.61302 | 0.61429 | 23.9961 |
| Datasets | Model Name | PMSE(%) | PMAE(%) | PRMSE(%) | PMAPE(%) |
|---|---|---|---|---|---|
| spring | SARIMAX | 0.918708 | 0.67362 | 0.714865 | 0.159945 |
| LSTM_Tsfresh_PCA | −0.87359 | −0.48036 | −0.36853 | −0.6285 | |
| GRU_Mul | 0.941294 | 0.776496 | 0.757693 | 0.508813 | |
| LSTM_Mul | 0.822756 | 0.580381 | 0.578984 | −0.04003 | |
| summer | SARIMAX | 0.997661 | 0.958211 | 0.951591 | 0.786362 |
| LSTM_Tsfresh_PCA | 0.699164 | 0.515644 | 0.451301 | 0.276379 | |
| GRU_Mul | 0.995196 | 0.893945 | 0.930608 | 0.638892 | |
| LSTM_Mul | 0.994916 | 0.943742 | 0.928619 | 0.617375 | |
| autumn | SARIMAX | 0.992153 | 0.909133 | 0.911325 | 0.909133 |
| LSTM_Tsfresh_PCA | 0.075377 | 0.05095 | 0.05095 | 0.05095 | |
| GRU_Mul | 0.997186 | 0.961003 | 0.961003 | 0.961003 | |
| LSTM_Mul | 0.993935 | 0.942613 | 0.942613 | 0.942613 | |
| winter | SARIMAX | 0.964206 | 0.834728 | 0.834728 | 0.834728 |
| LSTM_Tsfresh_PCA | 0.17422 | 0.304202 | 0.304202 | 0.304202 | |
| GRU_Mul | 0.96455 | 0.828767 | 0.828767 | 0.828767 | |
| LSTM_Mul | 0.93131 | 0.864409 | 0.864409 | 0.864409 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Gui, R. A Hybrid Model for GRU Ultra-Short-Term Wind Speed Prediction Based on Tsfresh and Sparse PCA. Energies 2022, 15, 7567. https://doi.org/10.3390/en15207567
Wang Y, Gui R. A Hybrid Model for GRU Ultra-Short-Term Wind Speed Prediction Based on Tsfresh and Sparse PCA. Energies. 2022; 15(20):7567. https://doi.org/10.3390/en15207567
Chicago/Turabian StyleWang, Yaqi, and Renzhou Gui. 2022. "A Hybrid Model for GRU Ultra-Short-Term Wind Speed Prediction Based on Tsfresh and Sparse PCA" Energies 15, no. 20: 7567. https://doi.org/10.3390/en15207567
APA StyleWang, Y., & Gui, R. (2022). A Hybrid Model for GRU Ultra-Short-Term Wind Speed Prediction Based on Tsfresh and Sparse PCA. Energies, 15(20), 7567. https://doi.org/10.3390/en15207567






