Evaluation Methods of Salt Pillar Stability of Salt Cavern Energy Storage
Abstract
1. Introduction
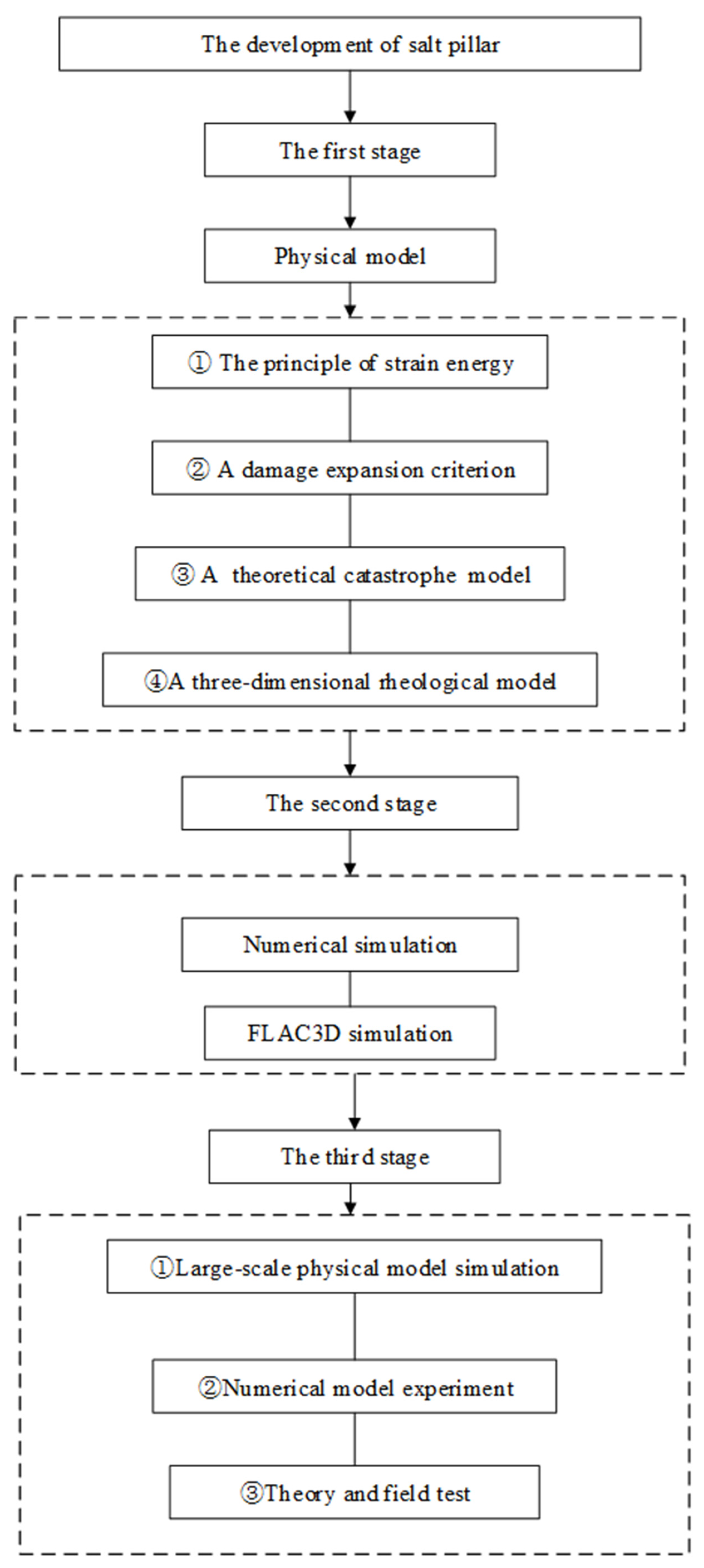
- The first stage: the phase of the investigation of basic mechanical properties of the pillar and the development and application of models. During this stage, one mainly builds physical models for experimental simulation, and then explores the mechanics and other related properties of the salt pillar;
- The second stage: the phase of combining computer simulation and traditional analysis. This stage involves the analysis of the numerical model and the mechanical parameters to ensure the stability of the pillars between salt caverns;
- The third stage: the comprehensive research phase of calculation analysis and large-scale experiments. This stage involves the comprehensive analysis of the adequate width and stability of the pillar through the numerical analyses combined with the large-scale physical model.
2. Analysis of Destabilization Damage of Salt Pillar under the Action of Ground Stress
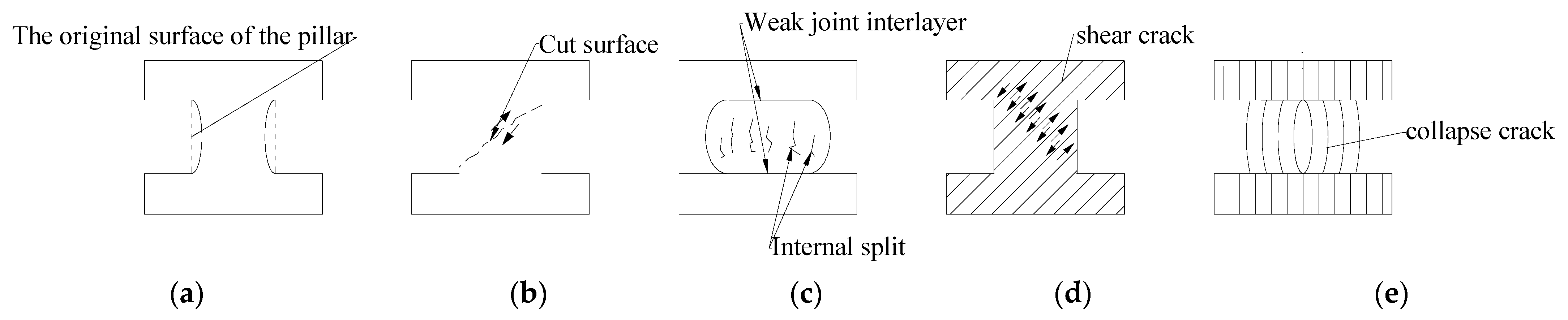
2.1. Macroscopic Manifestations of Salt Pillar Instability
2.2. Microscopic Manifestations of Salt Pillar Instability
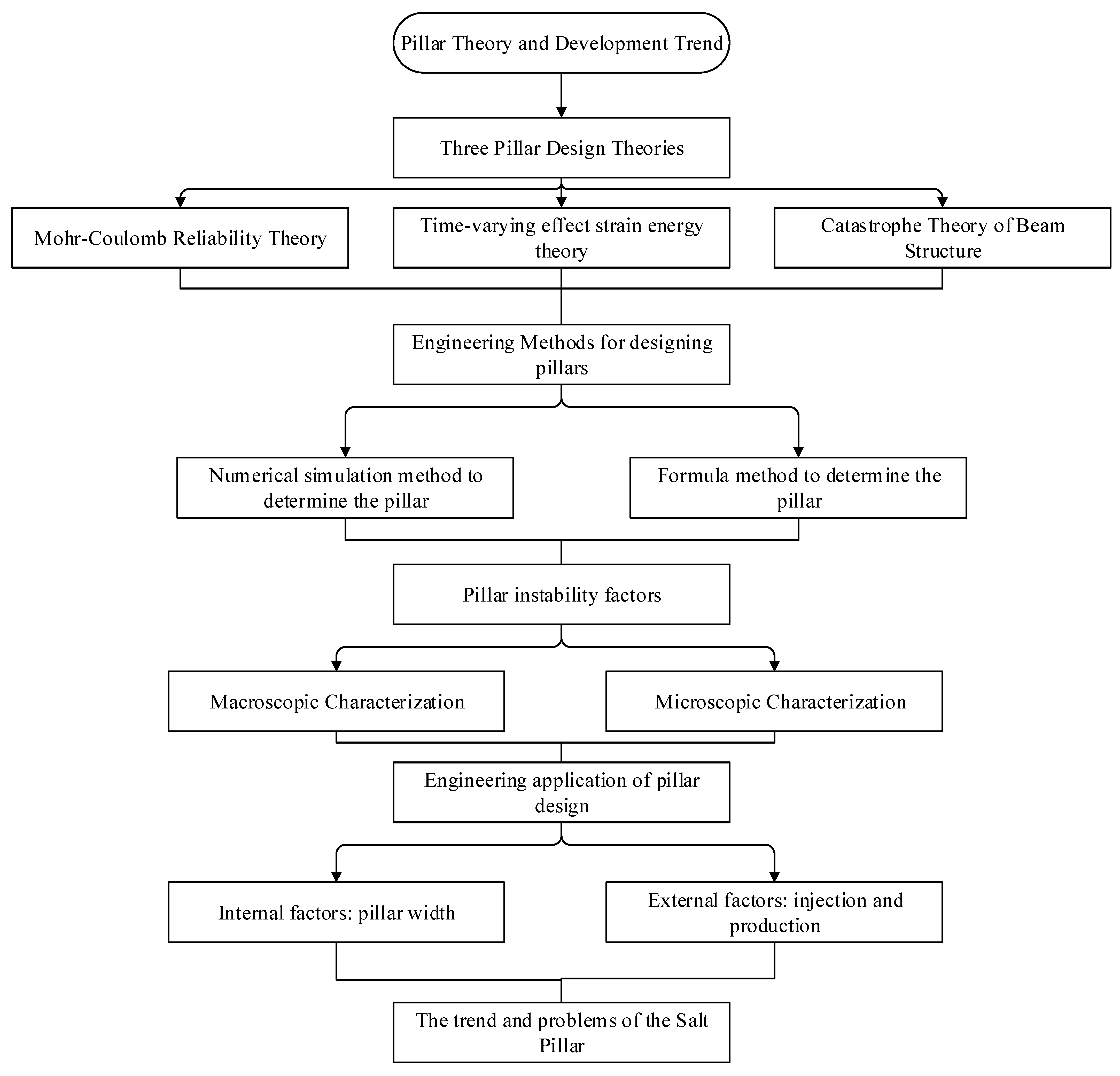
3. Basic Theory of Salt Pillar and Design Methods
3.1. Basic Theory of Salt Pillar
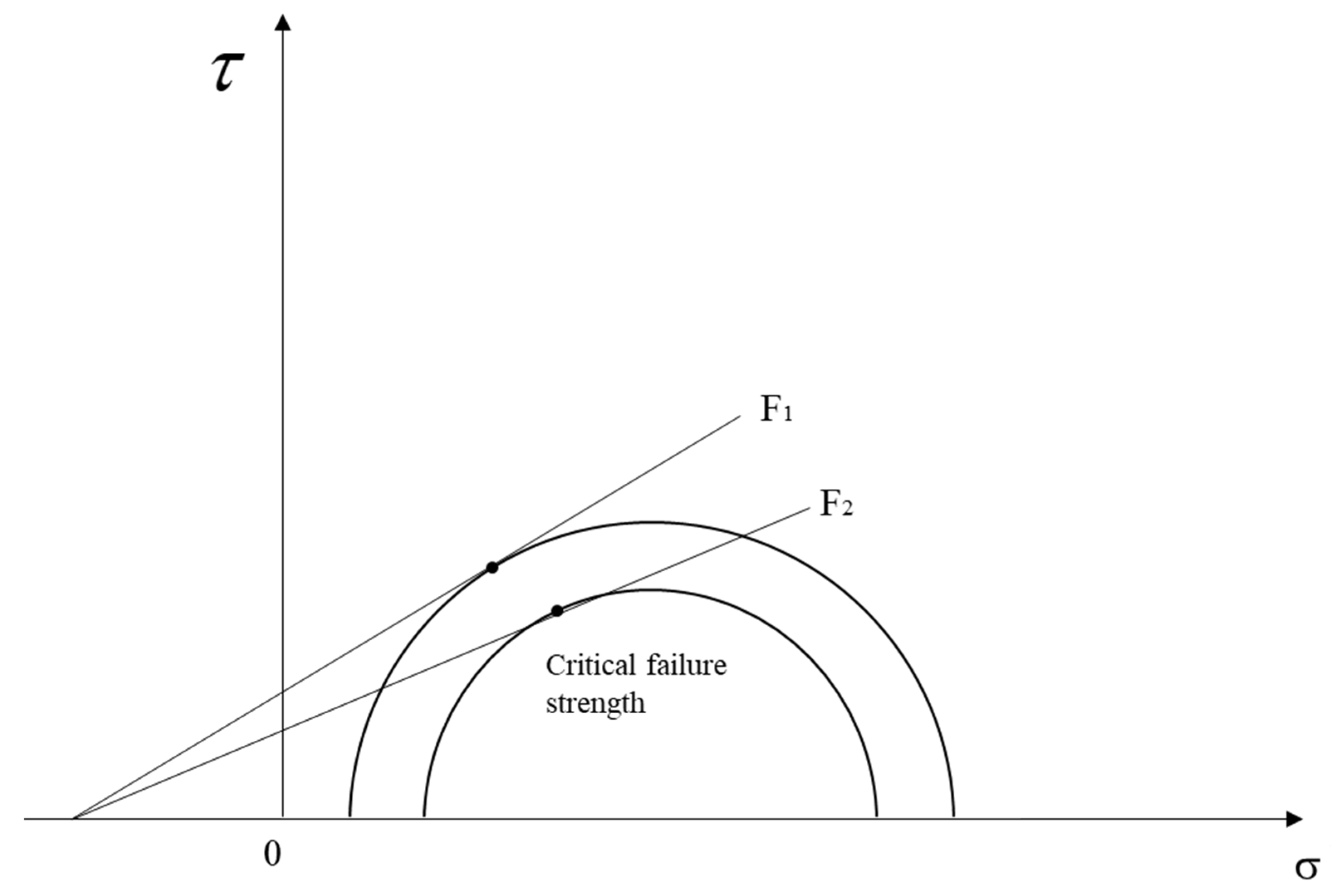
3.1.1. The Mohr–Coulomb Criterion of Salt Pillar
3.1.2. The Strain Energy Theory of Salt Pillar
3.1.3. The Catastrophe Theory of Salt Pillar
3.2. Salt Pillar Design Method
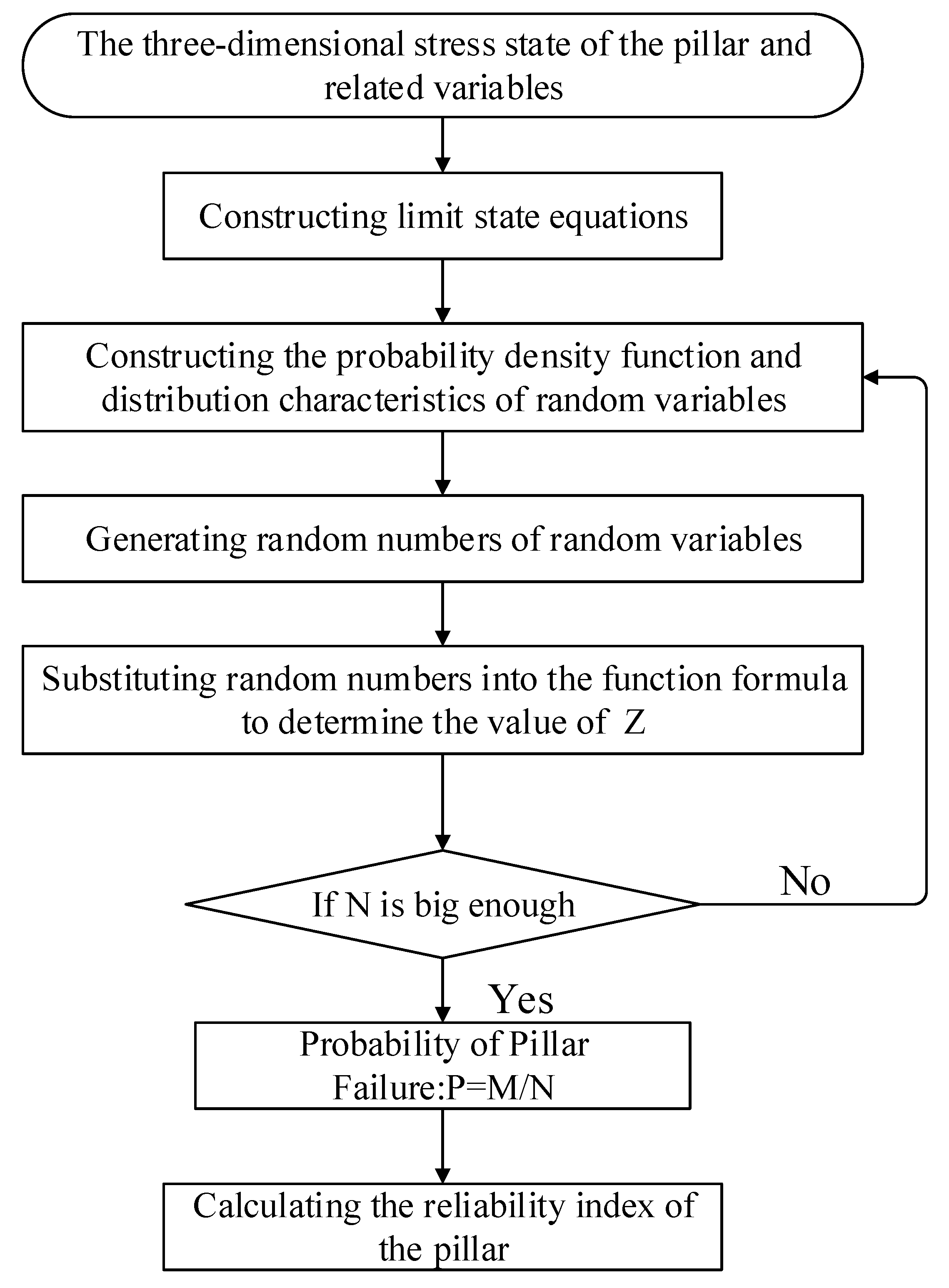
3.2.1. Equation Method of Designing Salt Pillars
3.2.2. Numerical Simulation Method for Designing Salt Pillars
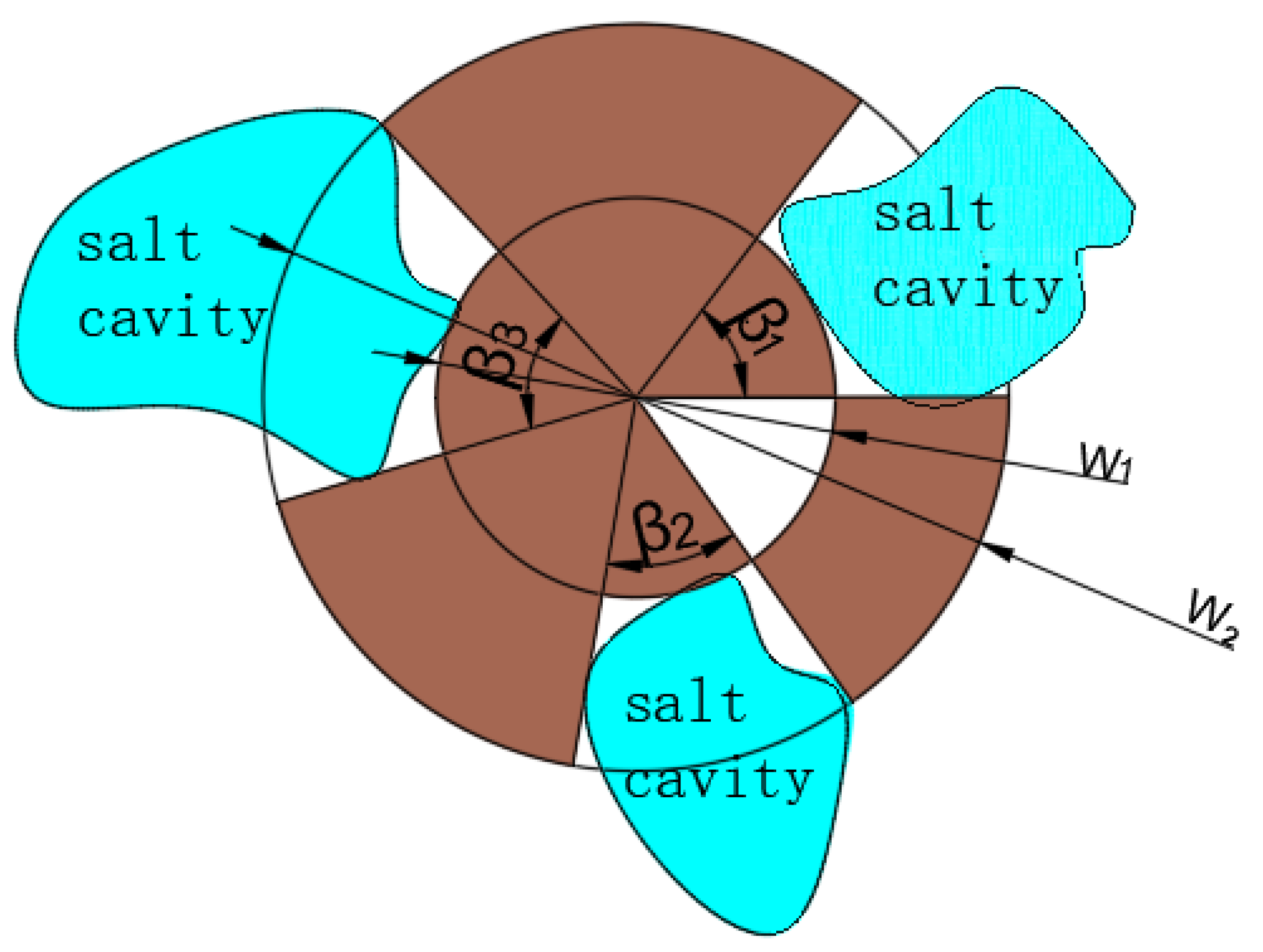
Double-Cavern Model
The Group Model
The Cusp Displacement Catastrophe Model
- IF > 0, the pillar is stable;
- IF = 0, the pillar is prone to instability;
- IF < 0, the pillar is unstable.
4. The Factors That Influence the Salt Pillar Design
4.1. The Width of the Salt Pillar
4.2. The Salt Pillar Injection–Withdrawal Process
5. Characteristics and Development Trends of Existing Theories
6. Conclusions
- The salt pillar stability should consider the mechanical properties of salt rock in different areas. Safe pillars are an important design factor for the safe and stable operation of gas storages. Therefore, it is necessary to constantly explore the current state of China’s salt rock and field conditions in the design of safe pillars. Establishing a database of mechanical properties of salt rock in different regions of China and realizing an engineering classification of salt rock is urgent. Conducting targeted research on salt pillars according to the salt rock conditions in the area is necessary.
- From a comprehensive analysis point of view, many theories need to be improved in the field of gas storage pillar research. The research methods of coal pillar theory can contribute to the salt pillar development. It is necessary to continuously increase the intensity of basic research on salt pillars, to make breakthroughs in the mechanism and retention of pillars.
- In the actual engineering application of safe pillars, a pillar maintenance method must be compatible with the actual engineering case. Firstly, a comprehensive evaluation model and pillar design systematic methods is established, and the main factors according to specific geological conditions are chosen. Next, related experiments should be carried out according to the precise factors. During the experimental period, the difference in the mechanical properties of the salt rock should be considered. Finally, a suitable salt pillar design scheme should be chosen according to experimental results.
- The salt pillars numerical simulation should be systematic, large-scale, and integrated. Additionally, a comprehensive integrated system of salt cavern gas storage and safe pillars determination also needs to be developed. New experimental instruments and equipment, which can be verified automatically, to evaluate pillars need to be explored.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ran, L.N. Development status and trends of underground gas storage in the world. In Proceedings of the 2016 National Natural Gas Academic Annual Conference, Yinchuan, China, 28 September 2016. [Google Scholar]
- Ding, G.S.; Xie, P. Current status and development prospects of underground gas storage in China. Nat. Gas Ind. 2006, 6, 111–113+70. [Google Scholar]
- Zhang, N.; Liu, W.; Zhang, Y. Microscopic Pore Structure of Surrounding Rock for Underground Strategic Petroleum Reserve (SPR) Caverns in Bedded Rock Salt. Energies 2020, 13, 1565. [Google Scholar] [CrossRef]
- Jing, W.J.; Yang, C.H.; Chen, F. Risk assessment of underground salt rock oil/gas storage based on accident statistical analysis. Rock Soil Mech. 2011, 32, 1787–1793. [Google Scholar]
- Yang, Q.; Pan, Y.W.; Deng, J.Q. Critical spacing and damage analysis of underground salt rock storage group. Chin. J. Rock Mech. Eng. 2012, 31, 1729–1736. [Google Scholar]
- Yang, C.H. Research on key mechanical problems in deep petroleum storage in layered salt rock mass. In Proceedings of the Academic Conference of the Chinese Society of Mechanics’2005, Beijing, China, 26 August 2005. [Google Scholar]
- Junthong, P.; Khamrat, S.; Sartkaew, S.; Fuenkajorn, K. Determination of time-dependent strengths of salt pillars based on strain energy principle. Int. J. Min. Sci. Technol. 2019, 29, 273–279. [Google Scholar] [CrossRef]
- Devries, K.L. Laboratory Testing in Support of a Bedded Salt Failure Criterion. In Proceedings of the Solution Mining Research Institute Fall Meeting 2003, Washington, DC, USA, 11–12 December 2012. [Google Scholar]
- Ren, S.; Jiang, D.Y.; Liu, X.R. Catastrophe theory analysis of pillar stability between rock salt cavern well groups. China Min. 2004, 1, 71–73. [Google Scholar]
- Zhang, Q.Y.; Duan, K.; Xiang, W. Three-dimensional rheological model test study on operation stability of deeply layered salt rock underground gas storage group affected by extreme risk factors. Chin. J. Rock Mech. Eng. 2012, 31, 1766–1775. [Google Scholar]
- Zhang, Q.Y.; Duan, K.; Jiao, Y. Physical model test and numerical simulation for the stability analysis of deep gas storage cavern group located in bedded rock salt formation. Int. J. Rock Mech. Min. Sci. 2017, 94, 43–54. [Google Scholar] [CrossRef]
- Wang, H.; Cao, H.; Yu, S.B.; Qin, X.S.; Yuan, Y. Limit equilibrium method for the design of underground mining pillars in salt mines. China Min. Ind. 2016, 25, 267–269. [Google Scholar]
- Liu, M.Y.; Chi, X.W.; Zhang, Y.L. Reliability design of pillar structure. J. Wuhan Univ. Technol. 1998, 1, 54–56. [Google Scholar]
- Liu, M.Y.; Xu, C.Y. Stability analysis of pillars in underground goaf. Min. Metall. Eng. 2000, 1, 19–22. [Google Scholar]
- Beckenham, R.F.; Urai, J.L. Pillar deformation-induced surface subsidence in the Hengelo brine field. In The Mechanical Behavior of Salt–Understanding of THMC Processes in Salt; CRC Press: Leiden, The Netherlands, 2007. [Google Scholar]
- Mo, J.; Liang, W.G.; Zhao, Y.S.; Yang, H.J.; Qu, D.A. Study on the influence of pillar width on the operation stability of gas storage. J. Taiyuan Univ. Technol. 2009, 40, 279–282. [Google Scholar]
- Liu, J.; Song, J.; Zhang, Q.Y.; Zhang, W.Q.; Jia, C.; Li, S.C.; Yang, C.H. Numerical calculation and analysis of the interval between salt rock underground gas storage groups. Chin. J. Rock Mech. Eng. 2011, 30, 3413–3420. [Google Scholar]
- Wang, T.T.; Yan, X.Z.; Yang, H.L.; Yang, X.J. Research on pillar stability between multi-layered salt cavern gas storage groups. Acta China Coal Soc. 2011, 36, 790–795. [Google Scholar]
- Wu, W.; Hou, Z.M.; Yang, C.H. Research on the Stability Evaluation Criteria of Underground Energy (Oil and Natural Gas) Storage in Salt Rock. Chin. J. Rock Mech. Eng. 2005, 14, 2497–2505. [Google Scholar]
- Wang, T.T. Stability analysis of the pillars between bedded salt cavern gas storages by cusp catastrophe model. Sci. China Technol. Sci. 2011, 54, 1615–1623. [Google Scholar] [CrossRef]
- Wu, Z.D.; Wang, Y.; Zhang, M.; Li, Z.J. Research on pillar design and safety of salt cavern gas storage. In Proceedings of the 2018 National Natural Gas Conference, Fuzhou, China, 14 November 2018. [Google Scholar]
- Wang, T.; Yang, C.; Yan, X.; Li, Y.; Liu, W.; Liang, C.; Li, J. Dynamic response of underground gas storage salt cavern under seismic loads. Tunn. Undergr. Space Technol. 2014, 43, 241–252. [Google Scholar] [CrossRef]
- Zhao, S.; Fang, X.L.; Liu, W.; Yan, X.Z.; Han, L.L. Pillar stability of underground salt cavern gas storage based on reliability theory. Oil Gas Storage Transp. 2014, 33, 839–843. [Google Scholar]
- Uri, L.; Ňup Rek, R. Numerical Analysis of the Stability of Lignite Pillars. Procedia Eng. 2017, 191, 310–316. [Google Scholar]
- Li, Z.J. Analysis and Application of Pillar Stability of Deep Salt Rock Gas Storage; Shandong University: Shandong, China, 2018. [Google Scholar]
- Fu, X.F. Stability analysis of Huangchang salt cavern underground gas storage in Jianghan Basin. J. Shanxi Datong Univ. (Nat. Sci. Ed.) 2020, 36, 73–75. [Google Scholar]
- Song, W.D.; Cao, S.; Fu, J.X.; Jiang, G.J.; Wu, F. Sensitivity analysis, and application study of factors affecting pillar stability. Rock Soil Mech. 2014, 35, 271–277. [Google Scholar]
- Zhang, N.; Shi, X.; Zhang, Y.; Shan, P. Tightness Analysis of Underground Natural Gas and Oil Storage Caverns with Limit Pillar Widths in Bedded Rock Salt. IEEE Access 2020, 8, 12130–12145. [Google Scholar] [CrossRef]
- Baryakh, A.A.; Asanov, V.A.; Toksarov, V.N.; Gilev, M.V. Evaluating the residual life of salt pillars. J. Min. Sci. 1998, 34, 14–20. [Google Scholar] [CrossRef]
- Van Sambeek, L.L. Salt Pillar Design Equation; Series on rock and soil mechanics; Trans Tech Publications: Clausthal-Zellerfeld, Germany, 1998; pp. 495–508. [Google Scholar]
- Yang, C.; Wang, T.; Li, J.; Ma, H.; Shi, X.; Daemen, J.J.K. Feasibility analysis of using closely spaced caverns in bedded rock salt for underground gas storage: A case study. Environ. Earth Sci. 2016, 75, 1138. [Google Scholar] [CrossRef]
- Staudtmeister, K.; Rokahr, R.B. Rock mechanical design of storage caverns for natural gas in rock salt mass. Int. J. Rock Mech. Min. Sci. 1997, 34, 300. [Google Scholar] [CrossRef]
- Yin, S.H.; Wu, A.X.; Li, X.W. Orthogonal range analysis of sensitivity to factors affecting pillar stability. J. China Coal Soc. 2012, 37, 48–52. [Google Scholar]
- Zhurkov, S.N. Kinetic concept of the strength of solids. Int. J. Fract. 1984, 26, 295–307. [Google Scholar] [CrossRef]
- Guo, K.Y. Study on the Creep Characteristics of Salt Rock; Chongqing University: Chongqing, China, 2004. [Google Scholar]
- Zhang, S.Z. Analysis of the Roof-Pillar Stability of the 1# Copper Mine with the Room-Pillar Method in the Dahongshan Iron Mine; Kunming University of Science and Technology: Kunming, China, 2014. [Google Scholar]
- Wang, X.S. Study on Stability of Salt Rock Gas Storage during Operation Period; Chongqing University: Chongqing, China, 2009. [Google Scholar]
- Gong, J.W.; Cui, J.J.; Xi, X.W.; Lin, K. FLAC numerical simulation software and its application in geology. Tecton. Metallog. 2002, 3, 321–325. [Google Scholar]
- Xue, H.; Han, C.Y.; Xiao, B.Y.; Yan, A.H.; Li, X.M. Stability analysis of salt cavern double reservoir cavern with reasonable pillar width. Oil Gas Storage Transp. 2021, 40, 753–760. [Google Scholar]
- Zhao, K.L. Study on the Availability of Underground Salt Rock Gas Storage in the Process of Gas Injection and Production; Graduate University of Chinese Academy of Sciences (Wuhan Institute of Rock and Soil Mechanics): Wuhan, China, 2009; p. 672. [Google Scholar]




| Writer | Theory | Research Point |
|---|---|---|
| Prapasiri [7] | the principle of strain energy | the strength of the salt pillar |
| Kerry L. De [8] | a damage expansion criterion | the strength of the salt pillar |
| Ren [9] | a catastrophic theoretical model | the pillar instability |
| Zhang [11] | a three-dimensional rheological model | the deformation characteristics of salt pillar |
| Wang [12] | limit balance method | limit width of the pillar |
| Liu [13,14] | the mass mechanical parameters and external loads | the stability of the salt pillar |
| Bekendam [15] | the subsidence rate map | the impact of the salt pillar |
| Theory Name | Advantages | Disadvantages | Practical Application Conditions |
|---|---|---|---|
| The Mohr–Coulomb criterion | Implemented quantitative analysis of salt pillar design and probabilistic-based algorithms | The size of the random variables used lacks corresponding definition criteria | This method is advantageous when the design of the pillar where it is located has a large number of variables, and the data has a large randomness. |
| The strain energy theory | This theory, based on the time-varying effect of salt rock design, has more applicability than the traditional strength criterion | The shape effect and end effect of the salt pillar are ignored and need to be experimentally determined | This method is used when the creep deformation of the designed salt pillar is large, and sufficient experimental time is available to conduct it. |
| The catastrophe theory | Simple model, easy force analysis, and salt pillar design depends on internal energy | Complex geological conditions of the salt pillar does not meet this requirement | This method is applicable if the geological conditions are simple and the strength of the pillar and roof is known |
| Writer | Research Point | Software |
|---|---|---|
| Mo [16] | the influence of pillar width | FLAC3D |
| Wang [18] | the influence of pillar width, internal pressure, buried depth | FLAC3D |
| Wu [19] | the stability rating standard | FLAC3D |
| Wang [22] | a dynamic elastoplastic model | FLAC3D |
| Zhao [23] | the stable failure function | FLAC3D |
| Lukas [24] | the influence of bolt support | FLAC3D |
| Theory Name | Specific Method | Method Description | Advantages | Disadvantages | Instructions |
|---|---|---|---|---|---|
| Equation method | (1) Mohr–Coulomb criterion | The gas caverns spacing must be such that the stress in the middle part of the pillar is less than the strength of the salt rock during operation | It is simple to use the pillar safety factor as an indicator of pillar design by specifying only the compressive strength and positive stress to which the pillar is subjected | The method differs to a certain extent from the specific actual project, and the salt pillar design is too large, wasting salt rock resources | This design method is used as the most traditional way of designing mineral pillars, analyzing the minimum width of the salt pillar design process from a mechanical point of view and formula. |
| (2) Point safety factor method | Ratio of the value of the ultimate damage state that may be reached at a point of the column to the actual value of the stress state at that point | Establishing a design method for salt pillars based on the stress action point of pillar damage | There may be some gaps in the actual situation | This method is an innovation of the traditional Mohr–Coulomb criterion, which considers the strength of the action at a point of salt pillar rupture. | |
| (3) Damage expansion criterion | Formulation based on the second invariant of the plastic mechanics partial stress tensor | A theory based on the occurrence of plastic expansion of rocks, which is consistent with the properties of rocks | The criteria for damage expansion of the salt pillar need to be obtained experimentally, etc. | Expansion of the criteria for the design of salt pillars based on the plasticity theory formula method | |
| Numerical simulation | (1) Double-cavern model | Salt pillar design method based on the establishment of two caverns | Simulation of the plastic zone and displacement variation of the salt pillar at different widths | May be different from the actual situation force, influenced by the mesh division | Stability analysis of salt pillar design based on finite difference method |
| (2) The group model | Salt pillar design method based on the establishment of three caverns | Simulation of the plastic zone and displacement variation of the salt pillar at different widths | Influenced by the mesh division | Stability analysis of salt pillar design based on finite difference method | |
| (3) The cusp displacement catastrophe model | Analysis by finite unit strength reduction method | Salt pillar design by discount factor is simpler and meets safety pillar criteria | There may be discrepancies with the actual project | The idea based on the discount-subtraction method can simplify the complexity of the numerical simulation process |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, H.; Wei, X.; Shi, X.; Liang, X.; Bai, W.; Ge, L. Evaluation Methods of Salt Pillar Stability of Salt Cavern Energy Storage. Energies 2022, 15, 7570. https://doi.org/10.3390/en15207570
Ma H, Wei X, Shi X, Liang X, Bai W, Ge L. Evaluation Methods of Salt Pillar Stability of Salt Cavern Energy Storage. Energies. 2022; 15(20):7570. https://doi.org/10.3390/en15207570
Chicago/Turabian StyleMa, Hongling, Xinxing Wei, Xilin Shi, Xiaopeng Liang, Weizheng Bai, and Lingzhi Ge. 2022. "Evaluation Methods of Salt Pillar Stability of Salt Cavern Energy Storage" Energies 15, no. 20: 7570. https://doi.org/10.3390/en15207570
APA StyleMa, H., Wei, X., Shi, X., Liang, X., Bai, W., & Ge, L. (2022). Evaluation Methods of Salt Pillar Stability of Salt Cavern Energy Storage. Energies, 15(20), 7570. https://doi.org/10.3390/en15207570






