A Recent Advance on Partial Evaporating Organic Rankine Cycle: Experimental Results on an Axial Turbine
Abstract
1. Introduction
- Fouling reduces the performance of the heat exchangers and therefore the heat source received by the ORC. Moreover, geothermal waters, which as explained before is a very important heat source for ORC systems, contain many fouling and corrosion ions. Thus, ions cause serious problems of fouling and corrosion [4,5,6]. Similar problems occur with industrial waste heat. The degradation of the heat exchanger performance could prevent the working fluid from completely evaporating and thus cause liquid droplets in the turbine which could lead to its erosion [7,8]. As an illustration, the economic cost of fouling in heat exchangers is estimated as USD 14 billion per year in 2014 in the United States of America [9,10].
- The partial-load behavior of ORC systems is generally considered as satisfactory, compared to other thermodynamic cycles [1]. However, in large off-design conditions of a “normal” ORC system submitted to a large deviation of the heat source, partial evaporation can occur, leading to a two-phase condition at the turbine inlet. Generally, this behavior is forbidden and ORC production must be reduced or even stopped if the risk of a two-phase condition arises.
2. Experimental Test Bench
2.1. ORC Loop
2.2. Fluid Candidates
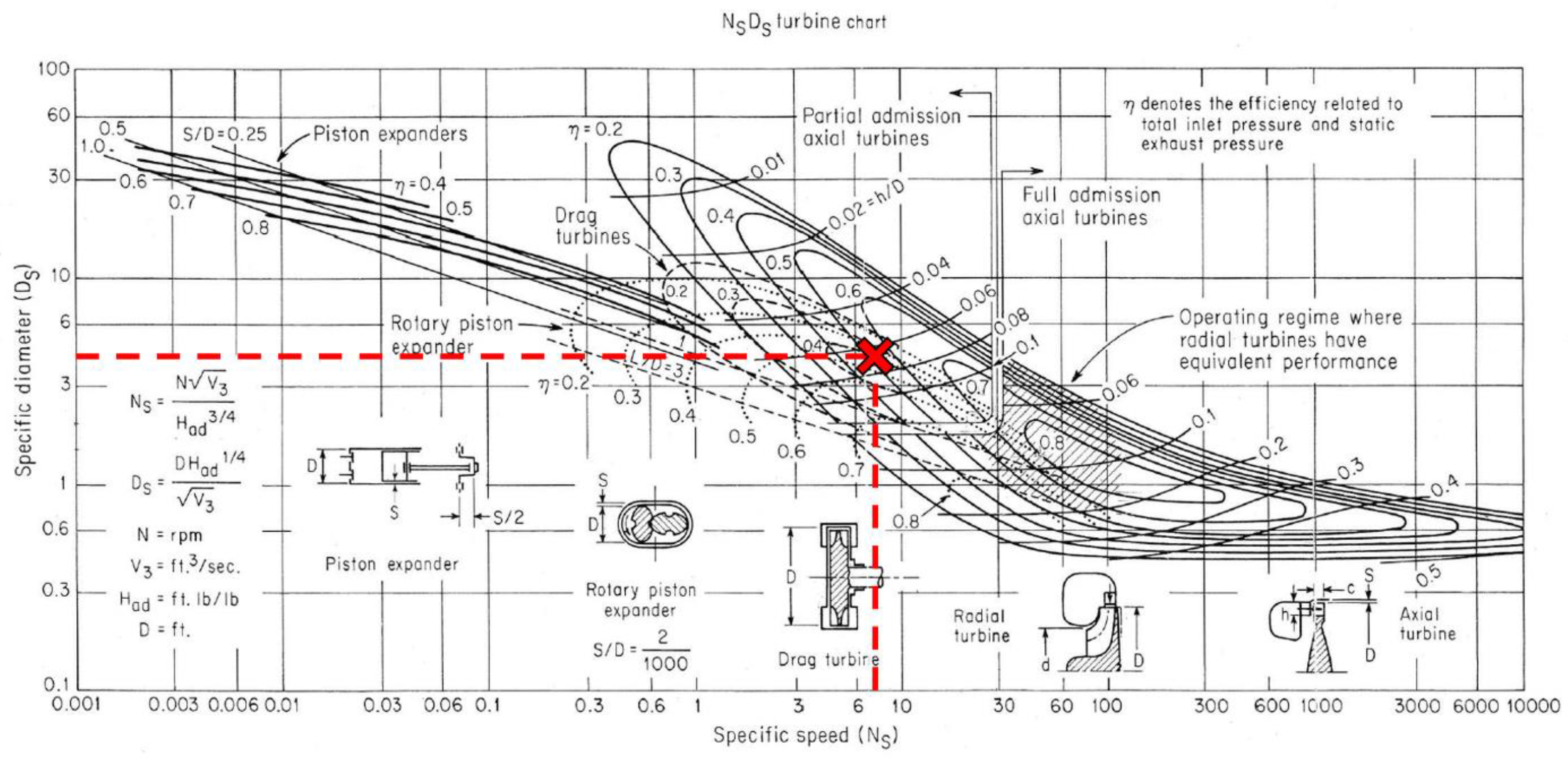
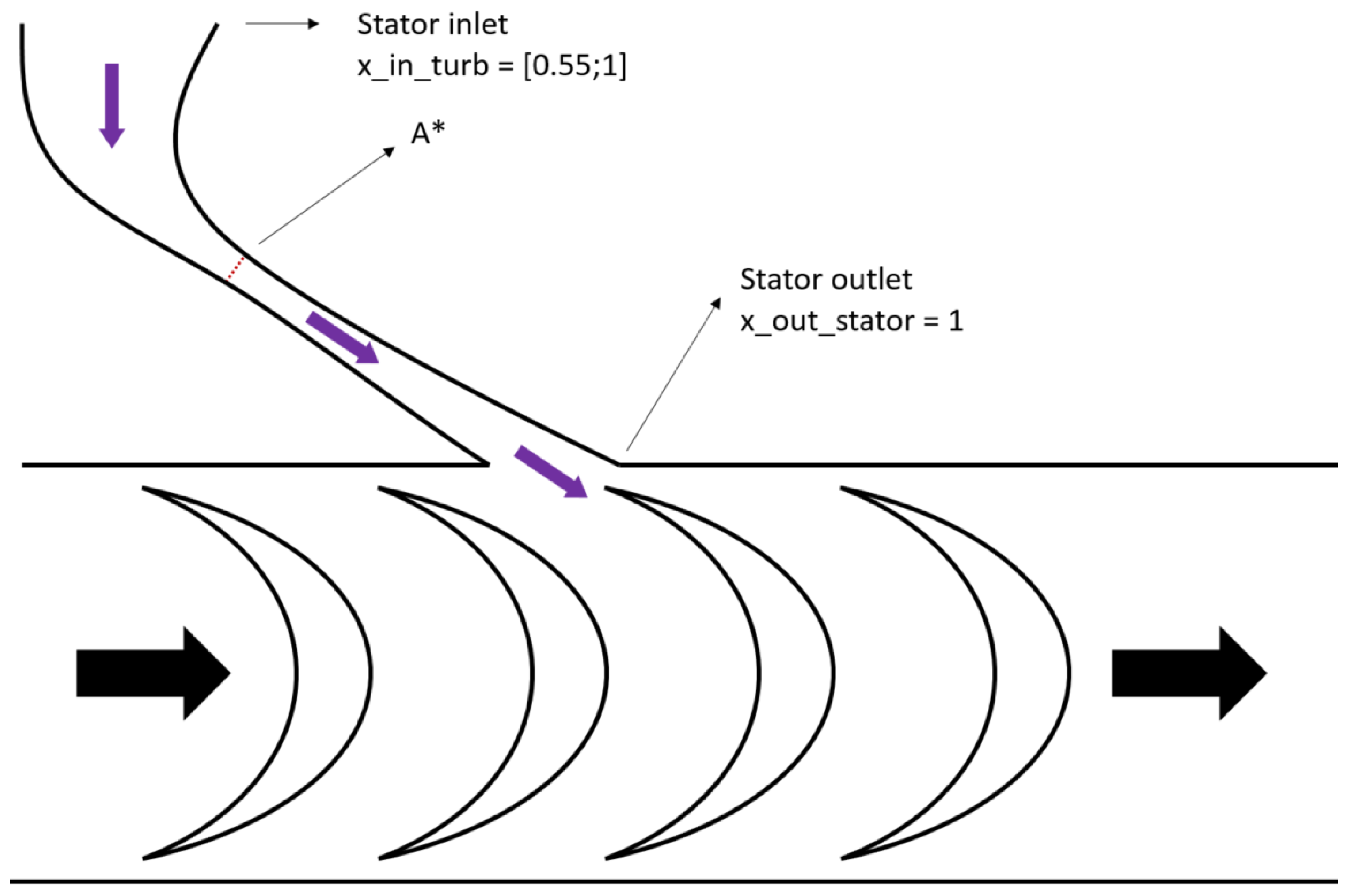
2.3. Partial Admission Micro Axial Turbine
2.4. Test Campaigns
3. Results and Preliminary Analysis of the First Campaign
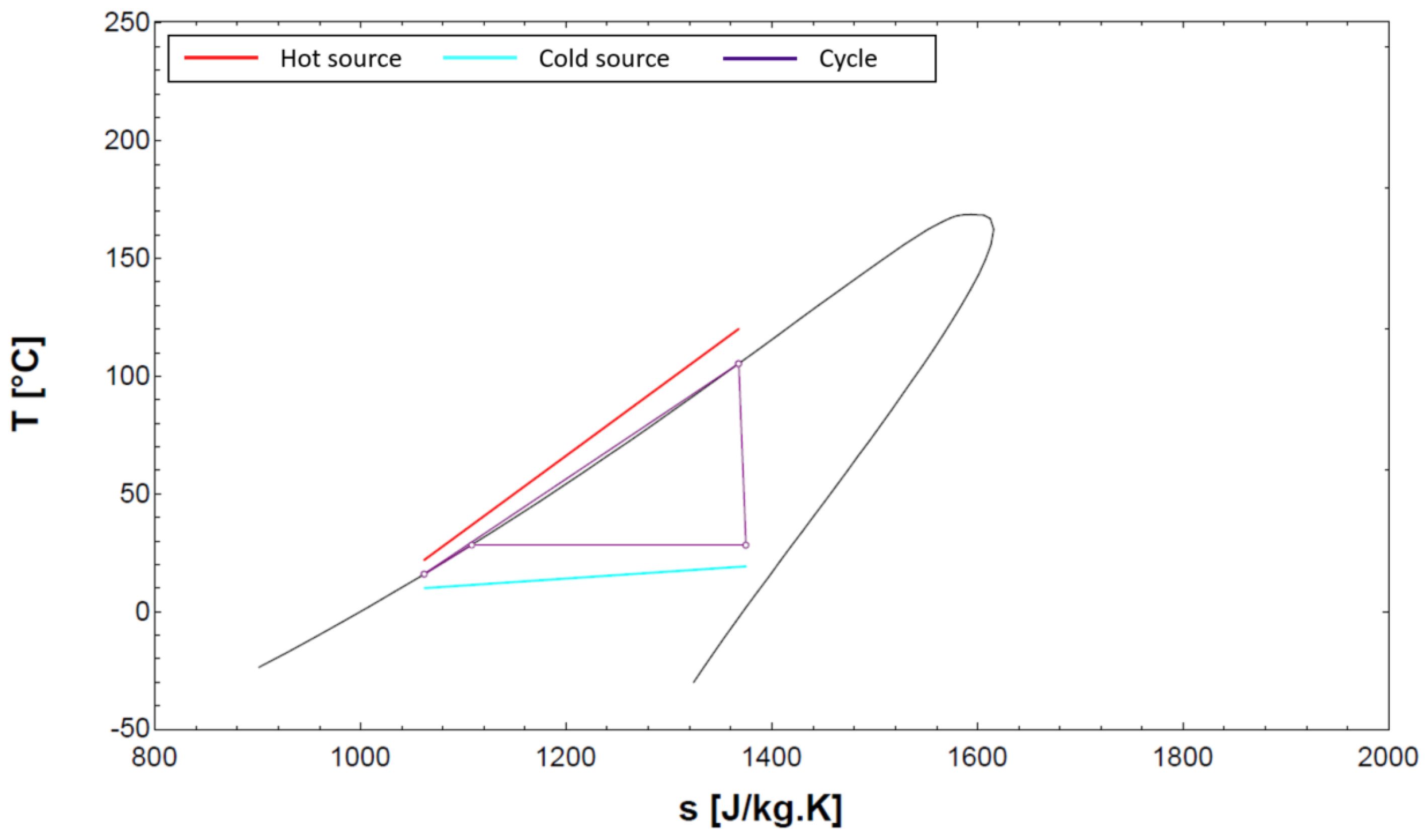
3.1. Nominal Working Point
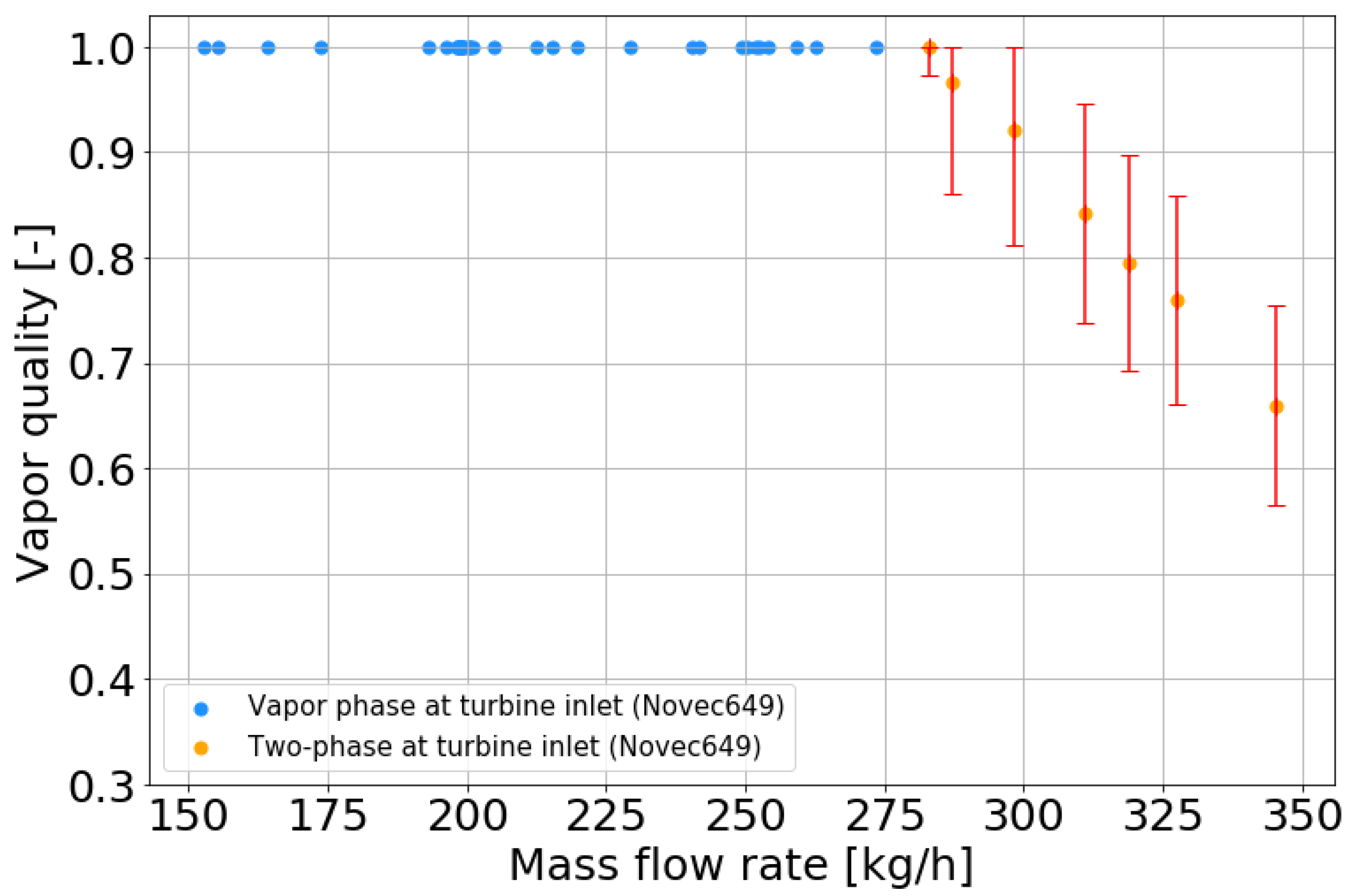
3.2. Vapor Quality Estimation
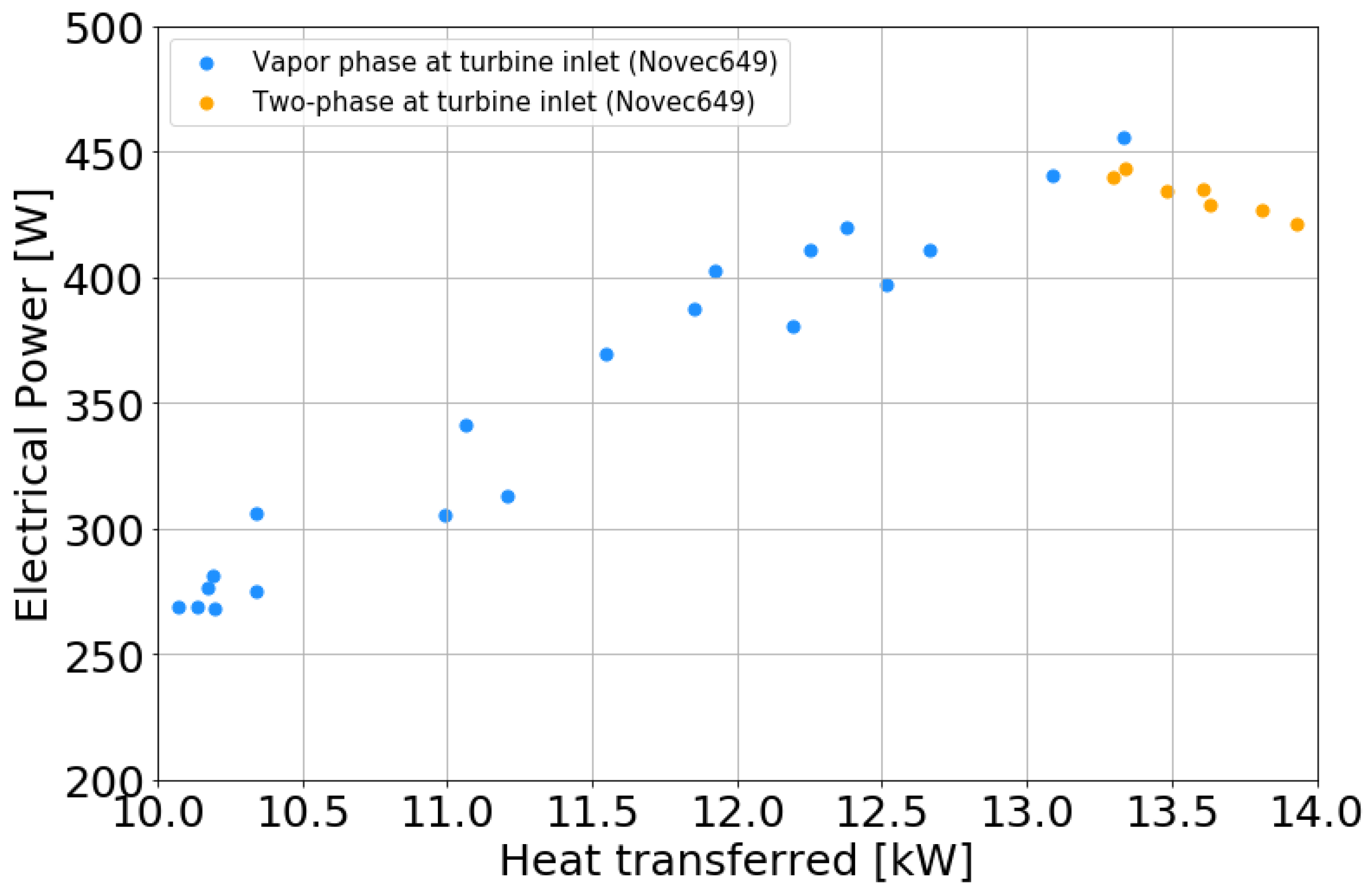
3.3. Electrical Production
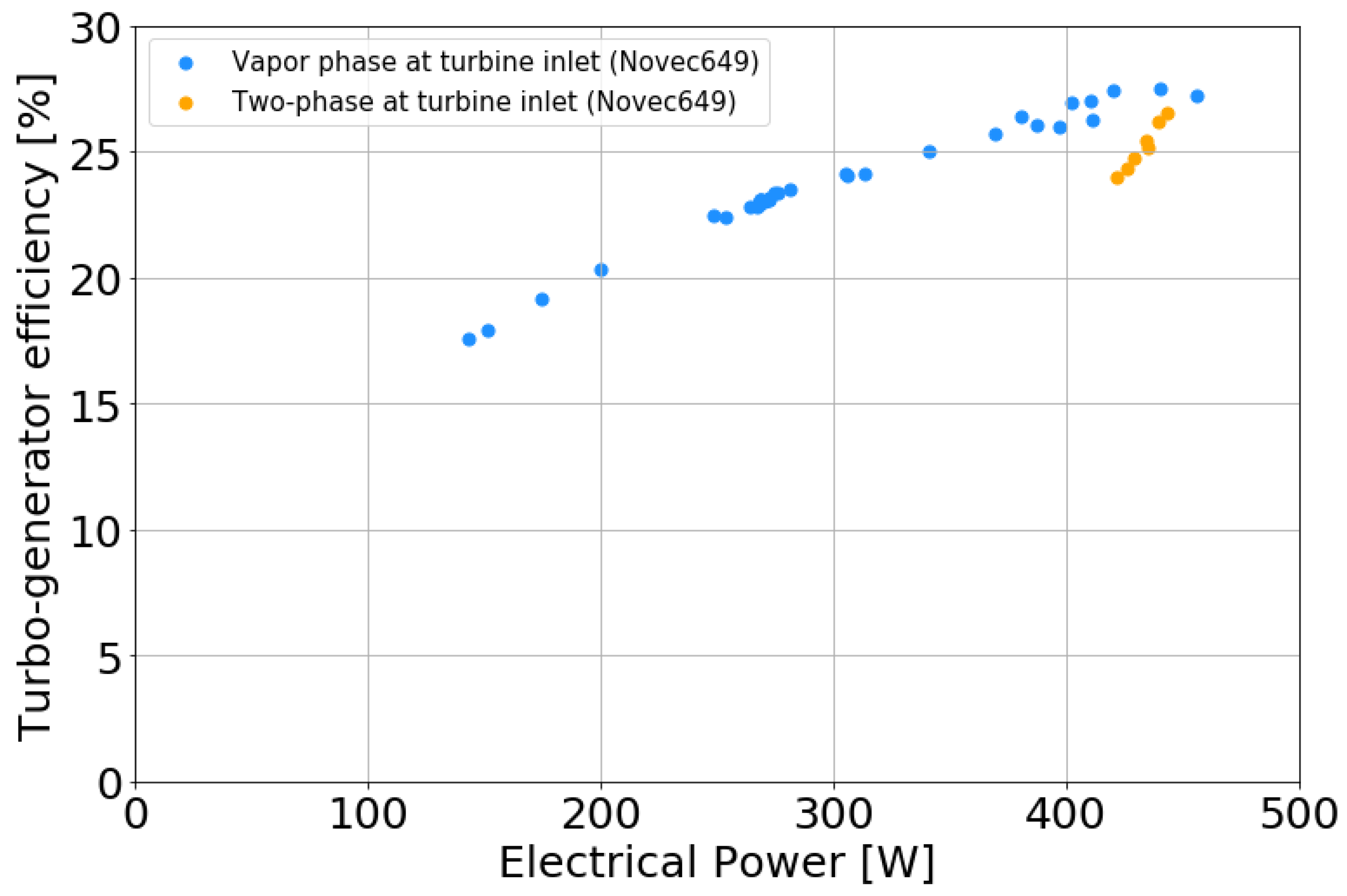
3.4. Efficiency
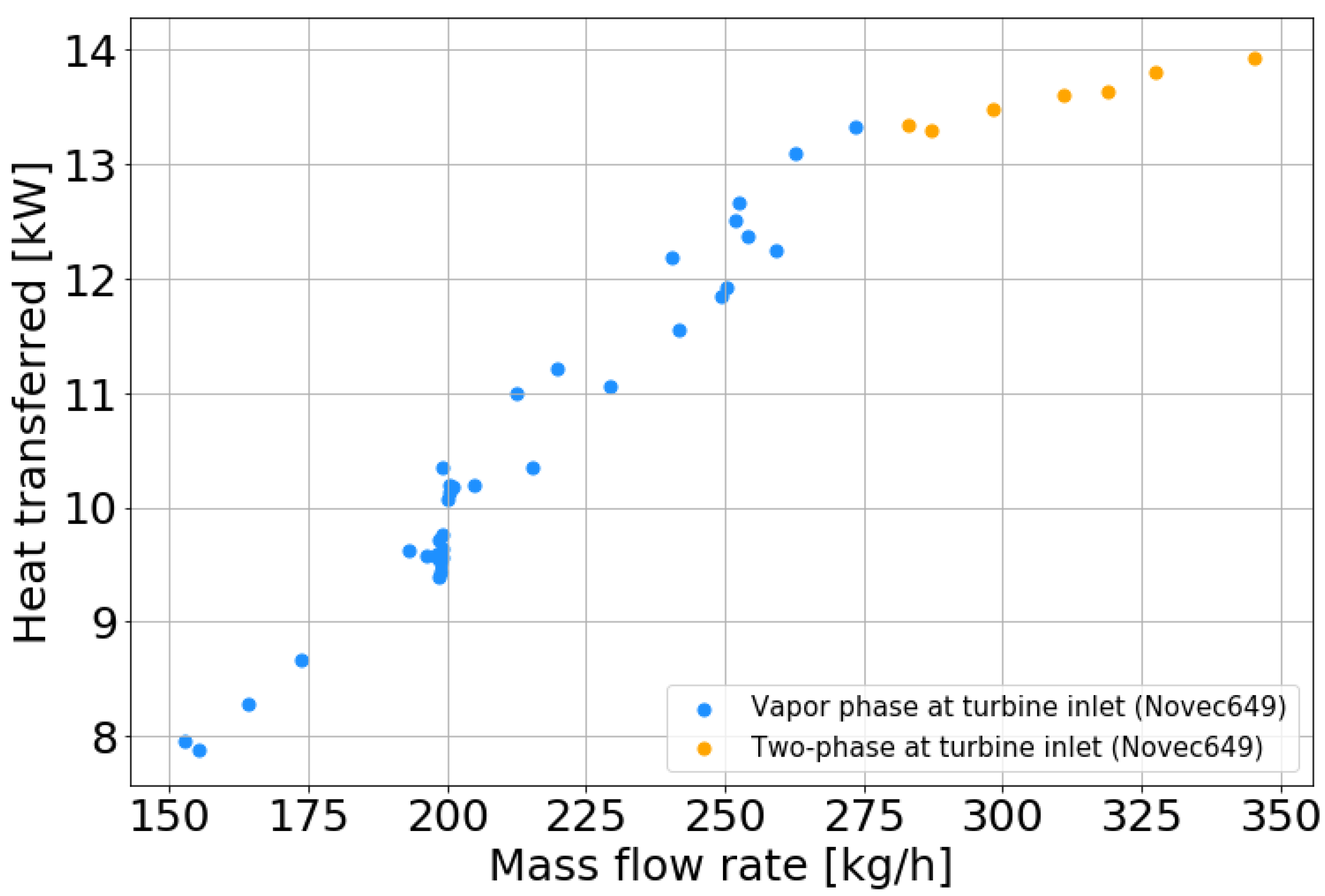
3.5. Vapor Mass Flow
4. Results and Analysis of All Tests
4.1. Mass Flow Rate Model: One-Phase, Two-Phase and Multi-Fluid Aspect
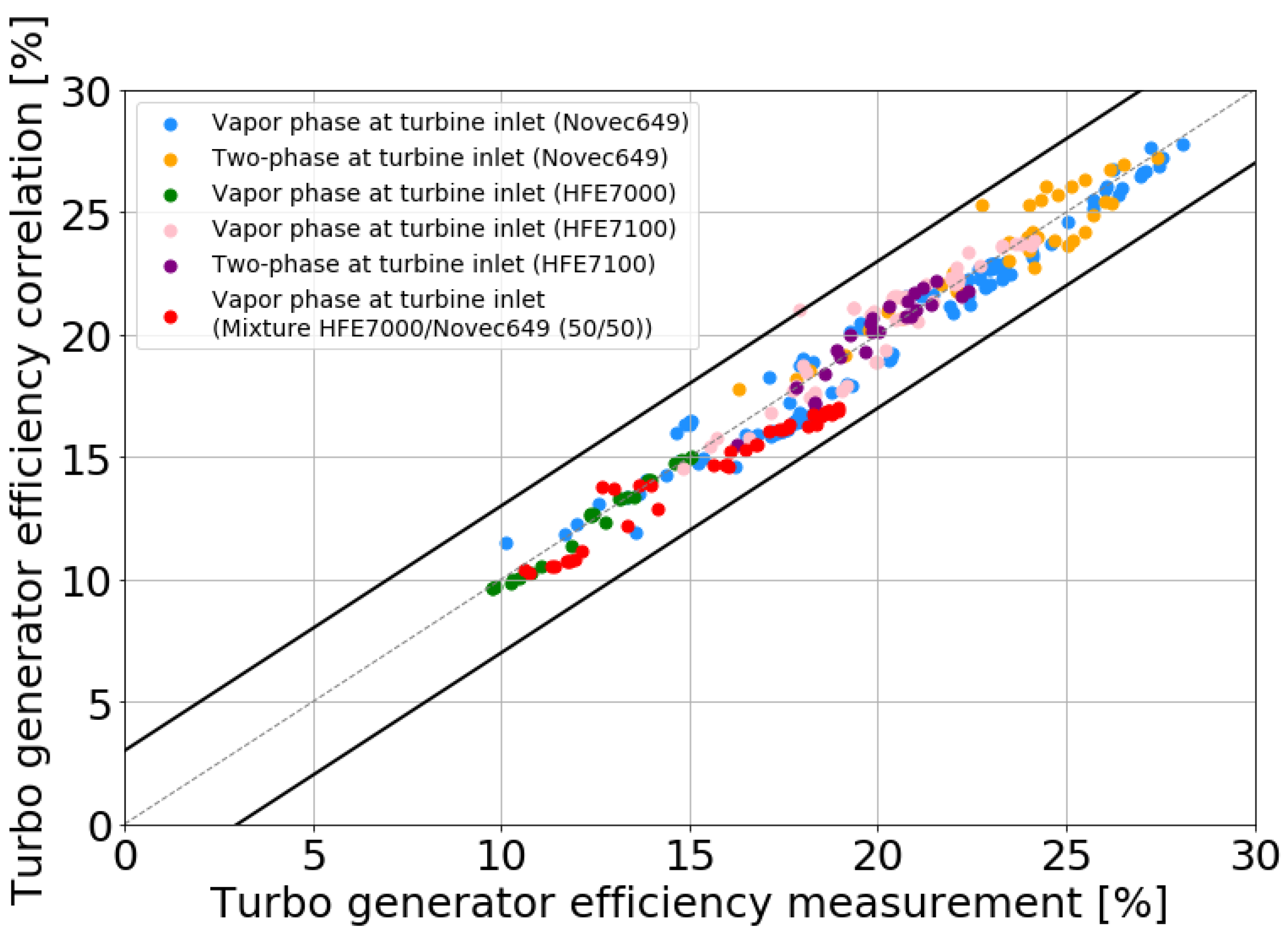
4.2. Efficiency Analysis
4.2.1. Single-Phase Condition at Turbine Inlet
4.2.2. Two-Phase Condition at Turbine Inlet
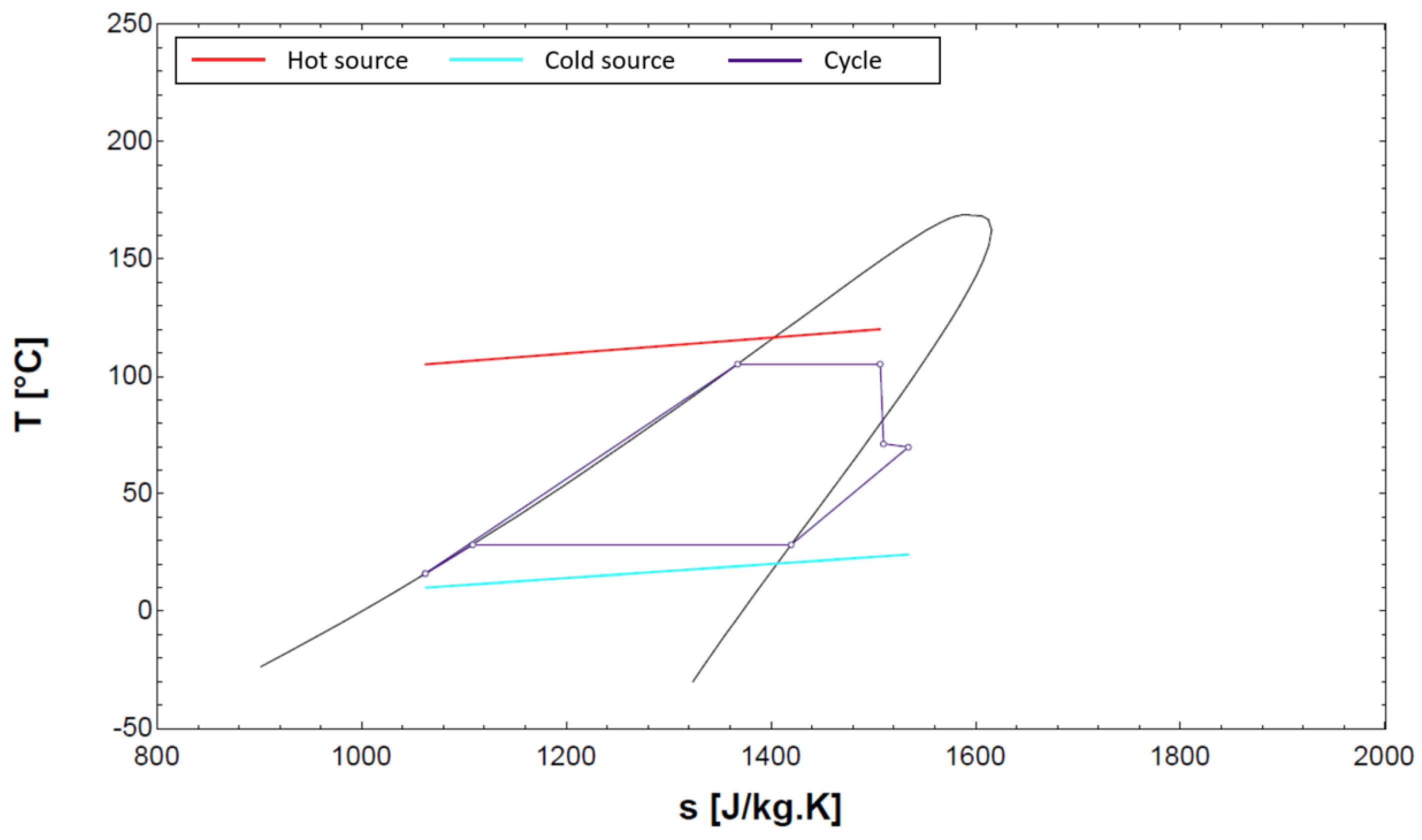
4.3. Two-Phase Expansion
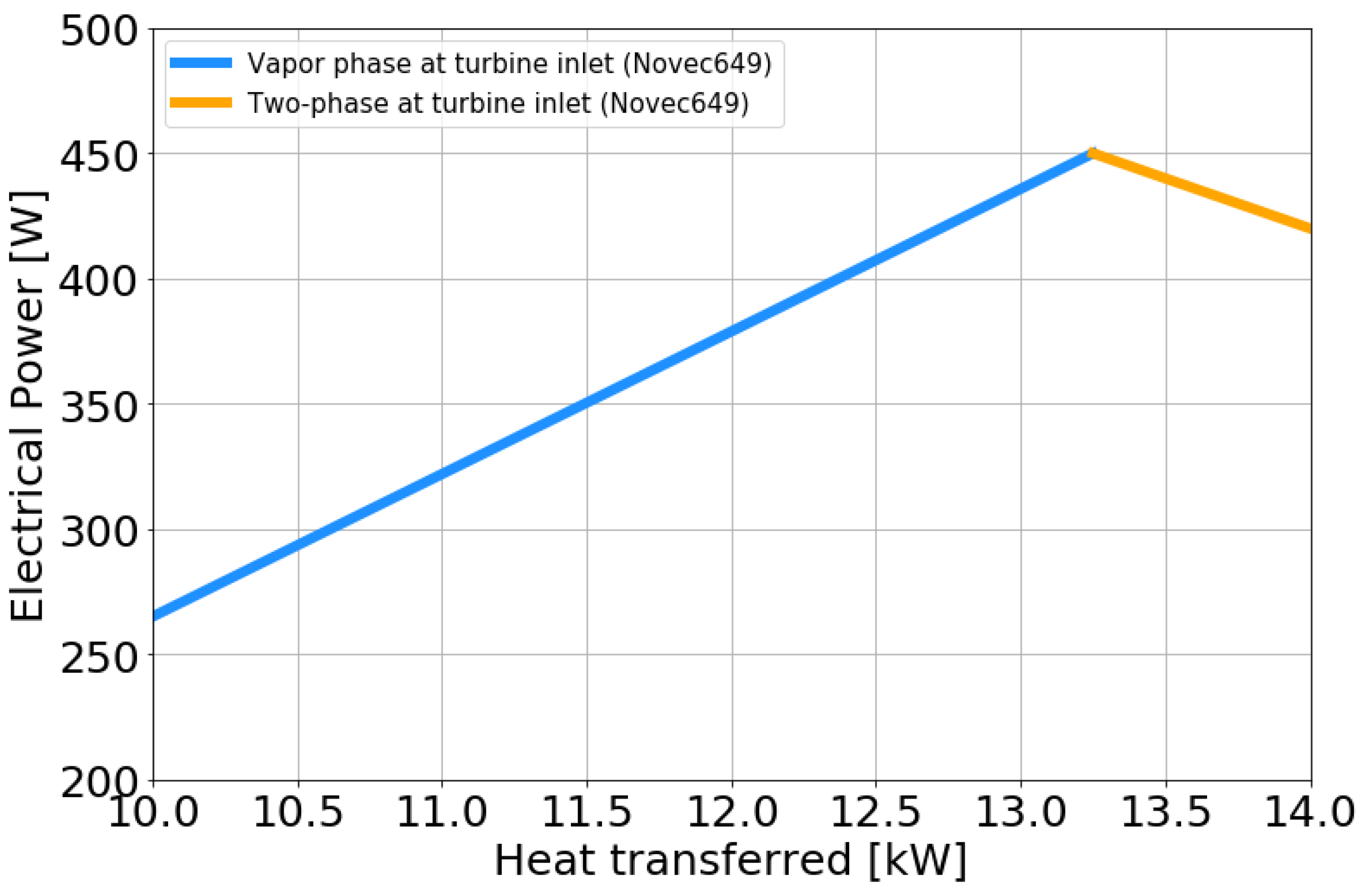
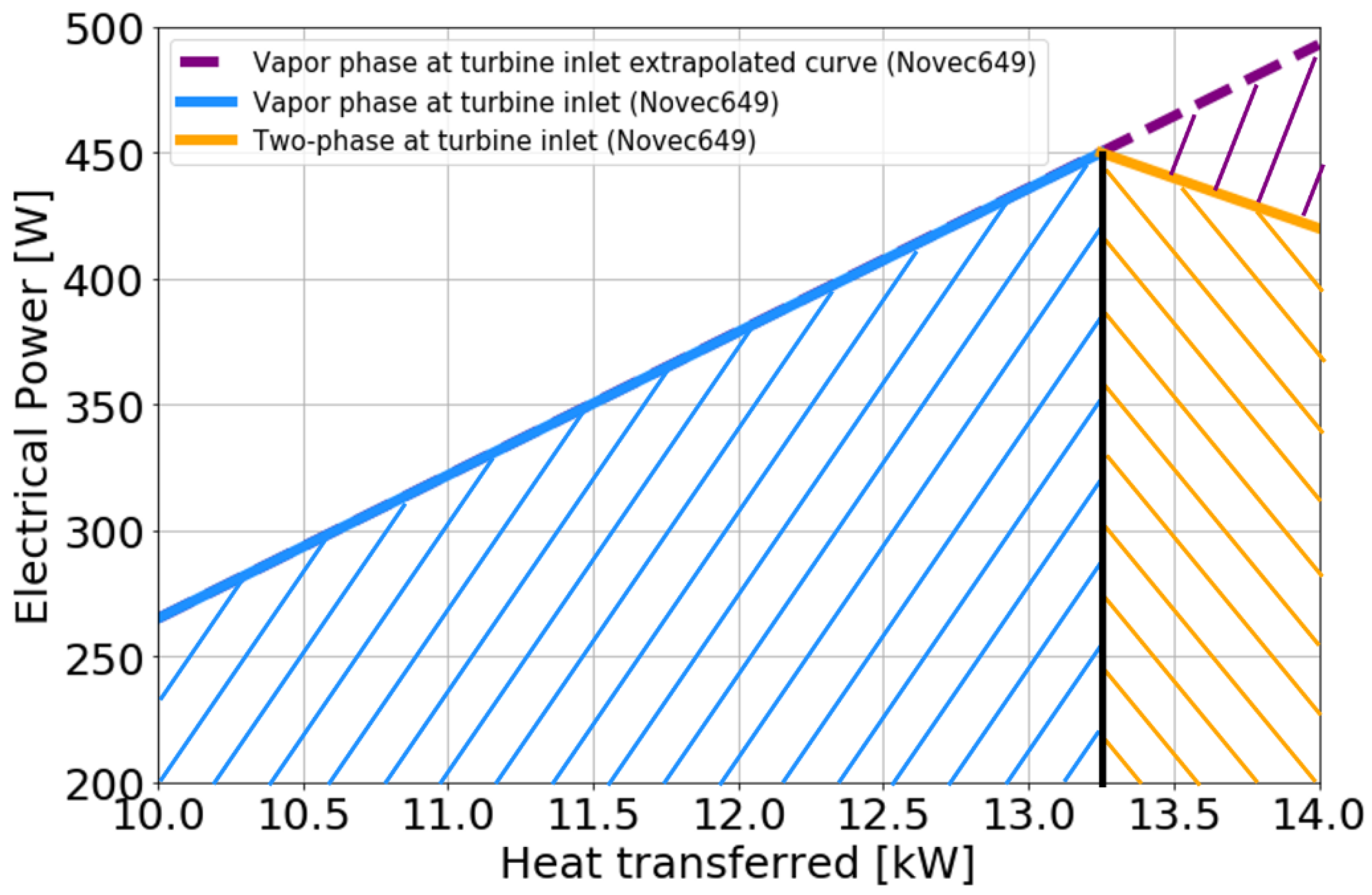
- Case 1: The turbine is only designed for single-phase operation. In this situation, only the blue part of Figure 20 makes electricity production possible and the maximum heat transferred at the evaporator is of about 13.3 kW.
- Case 2: The turbine is designed for a single-phase and two-phase operation (case studied in this article). In this situation, the electrical production zone in Figure 20 corresponds to the orange and blue zones, and the maximum heat transferred at the evaporator is of about 14kW.
- Case 3: The turbine is designed for a single-phase operation and the evaporator is redesigned to be of a larger size. In this situation, the electric production zone in Figure 20 corresponds to the orange zone, the blue zone and the purple zone, and the maximum heat transferred at the evaporator is of about 14kW. The single-phase production line of this case corresponds to the continuity of the turbine production line studied in this article.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | Subscripts | |||
| Critical section stator | (m2) | elec | Electric | |
| c | Speed of sound | (m. s−1) | evap | Evaporator |
| Enthalpy difference | (J.kg−1) | hs | Hot source | |
| D | Diameter | (m) | in | Input |
| Ds | Specific diameter | (-) | is | Isentropic |
| η | Efficiency | (-) | lh | Latent heat |
| γ | Polytropic exponent | (-) | liq | Liquid |
| Mass flow rate | (kg.s−1) | out | Output | |
| N | Rotation speed | (tr.min−1) | rota | Rotation |
| Ns | Specific speed | (-) | sh | Sensible heat |
| Pressure Ratio | (-) | tot | Total | |
| P | Pressure | (Pa) | tg | Turbo-generator |
| Thermal power | (W) | turb | Turbine | |
| q | Volume flow | (m3. s−1) | vap | Vapor |
| Density | (kg. m−3) | wf | Working fluid | |
| Turbine electrical power | (W) | |||
| Vapor quality | (-) | |||
References
- Astolfi, M. 3—Technical options for Organic Rankine Cycle systems. In Organic Rankine Cycle (ORC) Power Systems; Macchi, E., Astolfi, M., Eds.; Woodhead Publishing: Sawston, UK, 2017; pp. 67–89. ISBN 978-0-08-100510-1. [Google Scholar]
- Obi, J.B. State of Art on ORC Applications for Waste Heat Recovery and Micro-cogeneration for Installations up to 100kWe. Energy Procedia 2015, 82, 994–1001. [Google Scholar] [CrossRef][Green Version]
- Wieland, C.; Dawo, F.; Schifflechner, C.; Astolfi, M. Market report on organic rankine cycle power systems: Recent developments and outlook. In Proceedings of the 6th International Seminar on ORC Power Systems, Munich, Germany, 11–13 October 2021; Volume 10, pp. 11–13. [Google Scholar]
- Wang, G.G.; Zhu, L.Q.; Liu, H.C.; Li, W.P. Galvanic corrosion of Ni–Cu–Al composite coating and its anti-fouling property for metal pipeline in simulated geothermal water. Surf. Coat. Technol. 2012, 206, 3728–3732. [Google Scholar] [CrossRef]
- Cheng, Y.H.; Zou, Y.; Cheng, L.; Liu, W. Effect of the microstructure on the properties of Ni–P deposits on heat transfer surface. Surf. Coat. Technol. 2009, 203, 1559–1564. [Google Scholar] [CrossRef]
- Wu, K.; Zhu, L.; Li, W.; Liu, H. Effect of Ca2+and Mg2+ on corrosion and scaling of galvanized steel pipe in simulated geothermal water. Corros. Sci. 2010, 52, 2244–2249. [Google Scholar] [CrossRef]
- Stijepovic, M.Z.; Linke, P.; Papadopoulos, A.I.; Grujic, A.S. On the role of working fluid properties in Organic Rankine Cycle performance. Appl. Therm. Eng. 2012, 36, 406–413. [Google Scholar] [CrossRef]
- Staniša, B.; Ivušić, V. Erosion behaviour and mechanisms for steam turbine rotor blades. Wear 1995, 186–187, 395–400. [Google Scholar] [CrossRef]
- Hou, T.K.; Kazi, S.N.; Mahat, A.B.; Teng, C.B.; Al-Shamma’a, A.; Shaw, A. Industrial Heat Exchanger: Operation and Maintenance to Minimize Fouling and Corrosion. In Heat Exchangers—Advanced Features and Applications; Murshed, S.M.S., Lopes, M.M., Eds.; IntechOpen: London, UK, 2017; ISBN 978-953-51-3091-8. [Google Scholar]
- Sheriff, M.Z.; Karim, M.N.; Kravaris, C.; Nounou, H.N.; Nounou, M.N. An operating economics-driven perspective on monitoring and maintenance in multiple operating regimes: Application to monitor fouling in heat exchangers. Chem. Eng. Res. Des. 2022, 184, 233–245. [Google Scholar] [CrossRef]
- Joy, J.; Kochunni, S.K.; Chowdhury, K. Size reduction and enhanced power generation in ORC by vaporizing LNG at high supercritical pressure irrespective of delivery pressure. Energy 2022, 260, 124922. [Google Scholar] [CrossRef]
- Desai, N.B.; Tammone, C.; Haglind, F. Comparative analysis of two-phase expansion and sub-critical organic Rankine cycle systems for solar and geothermal applications. In Proceedings of the 35th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Copenhagen, Denmark, 3–7 July 2022. [Google Scholar]
- White, M.T. Cycle and turbine optimisation for an ORC operating with two-phase expansion. Appl. Therm. Eng. 2021, 192, 116852. [Google Scholar] [CrossRef]
- Lai, N.A.; Fischer, J. Efficiencies of power flash cycles. Energy 2012, 44, 1017–1027. [Google Scholar] [CrossRef]
- Ortego Sampedro, E.; Breque, F.; Nemer, M. Two-phase nozzles performances CFD modeling for low-grade heat to power generation: Mass transfer models assessment and a novel transitional formulation. Therm. Sci. Eng. Prog. 2022, 27, 101139. [Google Scholar] [CrossRef]
- Smith, I.K. Development of the Trilateral Flash Cycle System: Part 1: Fundamental Considerations. Proc. Inst. Mech. Eng. Part J. Power Energy 1993, 207, 179–194. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Rana, S.; Ahmadi, M.; Date, A.; Akbarzadeh, A. Trilateral Flash Cycle (TFC): A promising thermodynamic cycle for low grade heat to power generation. Energy Procedia 2019, 160, 208–214. [Google Scholar] [CrossRef]
- Öhman, H.; Lundqvist, P. Experimental investigation of a Lysholm Turbine operating with superheated, saturated and 2-phase inlet conditions. Appl. Therm. Eng. 2013, 50, 1211–1218. [Google Scholar] [CrossRef]
- Bianchi, G.; McGinty, R.; Oliver, D.; Brightman, D.; Zaher, O.; Tassou, S.A.; Miller, J.; Jouhara, H. Development and analysis of a packaged Trilateral Flash Cycle system for low grade heat to power conversion applications. Therm. Sci. Eng. Prog. 2017, 4, 113–121. [Google Scholar] [CrossRef]
- Xia, G.-D.; Zhang, Y.-Q.; Wu, Y.-T.; Ma, C.-F.; Ji, W.-N.; Liu, S.-W.; Guo, H. Experimental study on the performance of single-screw expander with different inlet vapor dryness. Appl. Therm. Eng. 2015, 87, 34–40. [Google Scholar] [CrossRef]
- Papes, I.; Degroote, J.; Vierendeels, J. New insights in twin screw expander performance for small scale ORC systems from 3D CFD analysis. Appl. Therm. Eng. 2015, 91, 535–546. [Google Scholar] [CrossRef]
- Read, M.; Smith, I.; Stosic, N. Optimisation of Screw Expanders for Power Recovery From Low Grade Heat Sources. Energy Technol. Policy 2013, 1, 131–142. [Google Scholar]
- Tang, H.; Wu, H.; Wang, X.; Xing, Z. Performance study of a twin-screw expander used in a geothermal organic Rankine cycle power generator. Energy 2015, 90, 631–642. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, D.; Gao, N.; Zhu, T.; Xie, F. Experimental testing and numerical simulation of scroll expander in a small scale organic Rankine cycle system. Appl. Therm. Eng. 2015, 87, 529–537. [Google Scholar] [CrossRef]
- Liu, Z.; Tian, G.; Wei, M.; Song, P.; Lu, Y.; Ashby, G.; Roskilly, A.P. Modellingand Optimisation on Scroll Expander for Waste Heat Recovery Organic Rankine Cycle. Energy Procedia 2015, 75, 1603–1608. [Google Scholar] [CrossRef]
- Fischer, J. Comparison of trilateral cycles and organic Rankine cycles. Energy 2011, 36, 6208–6219. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Rana, S.; Ahmadi, M.; Date, A.; Akbarzadeh, A. Experimental study on the prospect of low-temperature heat to power generation using Trilateral Flash Cycle (TFC). Appl. Therm. Eng. 2020, 172, 115139. [Google Scholar] [CrossRef]
- Dawo, F.; Buhr, J.; Wieland, C.; Hartmut, S. Experimental Investigation of the Partially Evaporated Organic Rankine Cycle for Various Heat Source Conditions. In Proceedings of the 6th International Seminar on ORC Power Systems, Munich, Germany, 11–13 October 2021. [Google Scholar]
- Lecompte, S.; Huisseune, H.; van den Broek, M.; De Paepe, M. Methodical thermodynamic analysis and regression models of organic Rankine cycle architectures for waste heat recovery. Energy 2015, 87, 60–76. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, F.; Yu, L. Performance analysis of the partial evaporating organic Rankine cycle (PEORC) using zeotropic mixtures. Energy Convers. Manag. 2016, 129, 89–99. [Google Scholar] [CrossRef]
- Elliot, D.G. Theory and Tests of Two-Phase Turbines; Jet Propulsion Lab.: Pasadena, CA, USA; National Aeronautics and Space Administration: Washington, DC, USA, 1982.
- Macchi, E.; Astolfi, M. 9-Axial flow turbines for Organic Rankine Cycle applications. In Organic Rankine Cycle (ORC) Power Systems; Macchi, E., Astolfi, M., Eds.; Woodhead Publishing: Sawston, UK, 2017; pp. 299–319. ISBN 978-0-08-100510-1. [Google Scholar]
- 3MTM NovecTM 649 Engineering Fluid. Available online: https://multimedia.3m.com/mws/media/569865O/3m-novec-engineered-fluid-649.pdf (accessed on 7 January 2022).
- Proposal for a Regulation of the European Parliament and of the Council on Fluorinated Greenhouse Gases, COM(2012) 643 Final, 11 July 2012.
- UNFCCC. UN Framwork Convention on Climate Change, Kyoto Protocol Reference Manual on Accounting of Emissions and Assigned Amount, Working Papers; UN Framwork Convention on Climate Change: New York, NY, USA, 2009. [Google Scholar]
- Blondel, Q. Etude et Optimisation Énergétique des Mélanges Zéotropes Pour Les Cycles Thermodynamiques de Rankine; Université Grenoble Alpes: Grenoble, France, 2021. [Google Scholar]
- Scaccabarozzi, R.; Tavano, M.; Invernizzi, C.M.; Martelli, E. Comparison of working fluids and cycle optimization for heat recovery ORCs from large internal combustion engines. Energy 2018, 158, 396–416. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Wang, L.; Bu, X. Thermodynamic Analysis of Organic Rankine Cycle with Hydrofluoroethers as Working Fluids. Energy Procedia 2017, 105, 1889–1894. [Google Scholar] [CrossRef]
- Kaczmarczyk, T.; Zywica, G.; Ihnatowicz, E. Experimental Investigation of a Radial Microturbine in Organic Rankine Cycle System With Hfe7100 as Working Fluid. In Proceedings of the 3rd International Seminar on ORC Power Systems, Brussel, Belgium, 12–14 October 2015. [Google Scholar]
- Blondel, Q.; Tauveron, N.; Caney, N.; Voeltzel, N. Experimental study and optimization of the Organic Rankine Cycle with pure NovecTM649 and zeotropic mixture NovecTM649/HFE7000 as working fluid. Appl. Sci. Switz. 2019, 9, 1865. [Google Scholar] [CrossRef]
- Krempus, D.; Bahamonde, S. On Mixtures as Working Fluids for Air-cooled ORC Bottoming Power Plants of Gas Turbines. In Proceedings of the 6th International Seminar on ORC Power Systems, Munich, Germany, 11–13 October 2021. [Google Scholar]
- EES: Engineering Equation Solver. F-Chart Software: Engineering Software. Available online: https://fchartsoftware.com/ees/ (accessed on 12 July 2021).
- Sherena.johnson@nist.gov, ‘REFPROP’, NIST, 18 April 2013. Available online: https://www.nist.gov/srd/refprop (accessed on 12 July 2021).
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Weiß, A.P.; Popp, T.; Müller, J.; Hauer, J.; Brüggemann, D.; Preißinger, M. Experimental characterization and comparison of an axial and a cantilever micro-turbine for small-scale Organic Rankine Cycle. Appl. Therm. Eng. 2018, 140, 235–244. [Google Scholar] [CrossRef]
- Balje´, O.E. A Study on Design Criteria and Matching of Turbomachines: Part A—Similarity Relations and Design Criteria of Turbines. J. Eng. Power 1962, 84, 83–102. [Google Scholar] [CrossRef]
- Wet Steam Turbines for Nuclear Power Plants By Alexander S Leyzerovich. Technical Books Pdf | Download Free PDF Books, Notes, and Study Material. Available online: https://www.technicalbookspdf.com/wet-steam-turbines-for-nuclear-power-plants-by-alexander-s-leyzerovich/ (accessed on 24 July 2022).
- Nederstigt, P. Real Gas Thermodynamics: And the Isentropic Behavior of Substances; Delft University of Technology: Delft, The Netherlands, 2017. [Google Scholar]
- Galuppo, F. Design, Optimization and Control by Condensation Pressure Manipulation of an ORC Based Waste Heat Recovery System in Heavy-Duty Trucks; Université de Lyon: Lyon, France, 2021. [Google Scholar]









| Variable | Equipment | Range | Uncertainty |
|---|---|---|---|
| Electrical power | Wattmeter | 0–3250 W | ±0.3% |
| Volume flow (hot source) | EFM | 0–3500 L/h | ±0.23% |
| Volume flow (cold source) | EFM | 0–2500 L/h | ±0.33% |
| Mass flow rate (working fluid) | Coriolis | 50–500 kg/h | ±0.30% |
| Temperature | Thermocouple Type-T | −200–200 °C | ±0.1 °C |
| Pressure | APS | 0–7 bar | ±1% |
| Properties | Novec649TM | HFE7000 | HFE7100 | Blend 50% Novec649TM– 50%HFE7000 |
|---|---|---|---|---|
| Fluid type | Dry | Dry | Dry | Dry |
| Fluid class | Fluoroketone | Hydrofluoroether | Hydrofluoroether | - |
| Formula | CF3CF2C(O)CF(CF3)2 | C3F7OCH3 | C4F9OCH3 | - |
| Critical temperature (°C) | 169 | 165 | 195 | 162 |
| Critical pressure (bar) | 18.7 | 24.8 | 22.3 | 22 |
| Normal glide | 0 | 0 | 0 | 2 |
| ODP | 0 | 0 | 0 | 0 |
| GWP | 1 | 530 | 320 | 266 |
| Flammability | No | No | No | No |
| Toxicity | Null | Low | Low | Low |
| Variable Parameter | Variation Range | |
|---|---|---|
| Heat source | Inlet temperature | 110 °C |
| Flow rate | 2000–3500 L.h−1 | |
| Cooling source | Inlet temperature | 13 °C |
| Flow rate | 1000–2500 L.h−1 | |
| Working fluid | Fluid type (number of tests) | Novec649TM (42) |
| Flow rate | 0.03–0.09 kg.s−1 | |
| Variable Parameter | Variation Range | |
|---|---|---|
| Heat source | Inlet temperature | 90–110 °C |
| Flow rate | 200–3500 L.h−1 | |
| Cooling source | Inlet temperature | 13–35 °C |
| Flow rate | 250–2500 L.h−1 | |
| Working fluid | Fluid type (number of tests) | Novec649TM (106) HFE7000 (28) HFE7100 (75) 50%Novec649–50%HFE7000 (40) |
| Flow rate | 0.03–0.09 kg.s−1 | |
| Parameters | Data | |
|---|---|---|
| Fluid | Novec649TM | [-] |
| Mass flow rate | 0.076 | [kg.s−1] |
| Inlet temperature | 108.2 | [°C] |
| Inlet pressure | 5.30 | [bar] |
| Outlet pressure | 0.44 | [bar] |
| Rotation speed | 9750 | [RPM] |
| Blue Zone Production (Figure 20) | Orange Zone Production (Figure 20) | Purple Zone Production (Figure 20) | Average Production between 10 and 13.3 kW Hot Source | Average Production between 13.3 and 14 kW Hot Source | Average Production between 10and 14 kW Hot Source | |
|---|---|---|---|---|---|---|
| [-] | [-] | [-] | [W] | [W] | [W] | |
| Case 1 | Ok | No | No | 355 | 0 | 293 |
| Case 2 | OK | Ok | No | 355 | 435 | 369 |
| Case 3 | Ok | Ok | Ok | 355 | 475 | 376 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lhermet, G.; Tauveron, N.; Caney, N.; Blondel, Q.; Morin, F. A Recent Advance on Partial Evaporating Organic Rankine Cycle: Experimental Results on an Axial Turbine. Energies 2022, 15, 7559. https://doi.org/10.3390/en15207559
Lhermet G, Tauveron N, Caney N, Blondel Q, Morin F. A Recent Advance on Partial Evaporating Organic Rankine Cycle: Experimental Results on an Axial Turbine. Energies. 2022; 15(20):7559. https://doi.org/10.3390/en15207559
Chicago/Turabian StyleLhermet, Guillaume, Nicolas Tauveron, Nadia Caney, Quentin Blondel, and Franck Morin. 2022. "A Recent Advance on Partial Evaporating Organic Rankine Cycle: Experimental Results on an Axial Turbine" Energies 15, no. 20: 7559. https://doi.org/10.3390/en15207559
APA StyleLhermet, G., Tauveron, N., Caney, N., Blondel, Q., & Morin, F. (2022). A Recent Advance on Partial Evaporating Organic Rankine Cycle: Experimental Results on an Axial Turbine. Energies, 15(20), 7559. https://doi.org/10.3390/en15207559






