Numerical Analysis of a Horizontal Pressure Differential Wave Energy Converter
Abstract
1. Introduction
2. Numerical Modeling
2.1. Continuity, Momentum, and Volume Fraction
- Laminar flow
- Regular gravity waves
- Shallow water
- Two-dimensional geometry
Boundary Conditions
2.2. Performance Assessment
2.3. Pressure Resource
3. Results and Discussion
3.1. Model Setup and Validation
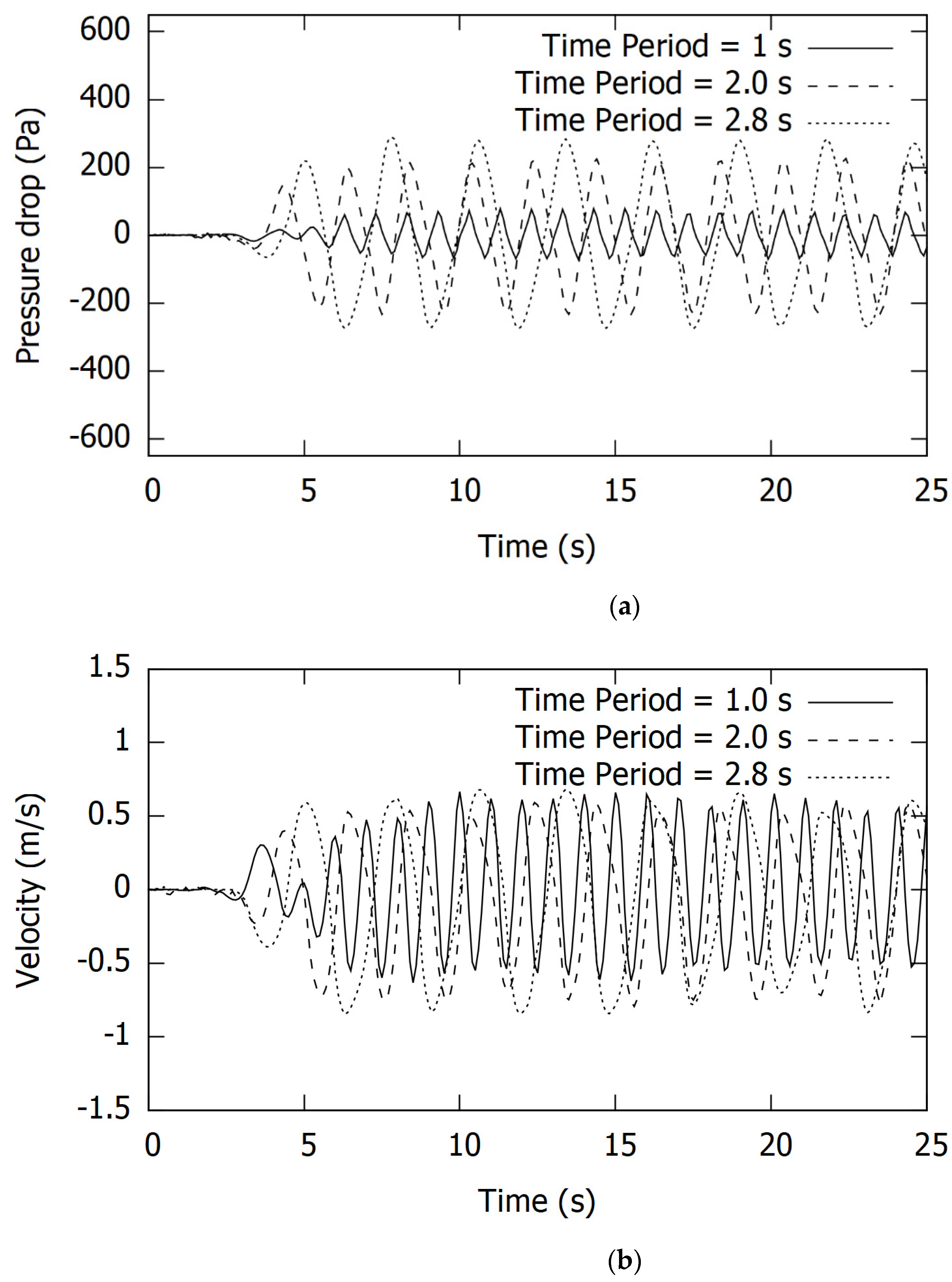
3.2. Flow Dynamics in the Wave Energy Extraction Device
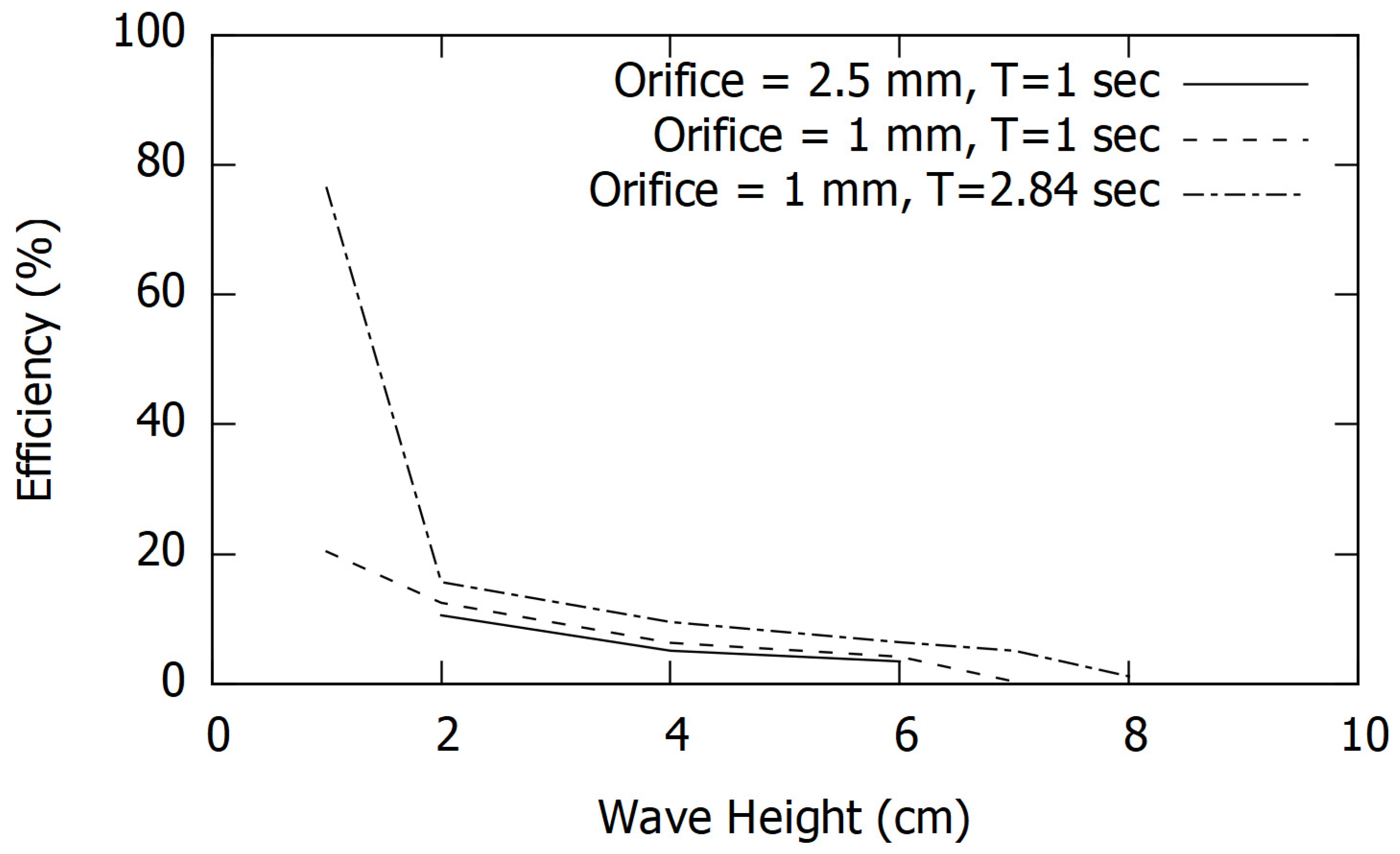
3.3. Performance Characteristics
4. Conclusions
- The CFD model used for simulating the wave conditions has been successfully validated against free surface elevation data from the published literature.
- The concept of a differential pressure-driven wave energy device has been proven by numerical simulation.
- Simulation results show that the efficiency of the device decreases with the wave height but increases significantly with the wave time period.
- A higher power take-off (PTO) damping also increases the efficiency of the device.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Falcao, A.F.d. Wave Energy Utilization: A review of the technologies. Renw. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Guedes Soares, C.; Bhattacharjee, J.; Tello, M.; Pietra, L. Review and classification of wave energy converters. In Maritime Engineering and Technology; Soares, C.G., Sutulo, Y.G.S., Santos, T.A., Eds.; Taylor and Francis Group: London, UK, 2012; pp. 585–594. [Google Scholar]
- Falnes, J. A review of wave energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef]
- Mustapa, M.A.; Yaakob, O.B.; Ahmed, Y.M.; Rheem, C.K.; Koh, K.K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- McNatt, J.C.; Ozkan-Haller, H.T.; Morrow, M.; Delos-Reyes, M. Preliminary Modelling Analsys of a Horizontal Pressure Differential Wave Energy Converter. J. Offshore Mech. Arct. Eng. 2014, 136, 011901. [Google Scholar] [CrossRef]
- Simon, M.J. Wave-Energy Extraction by a Submerged Cylindrical Resonant Duct. J. Fluid Mech. 1981, 36, 159–187. [Google Scholar] [CrossRef]
- Graw, K. Shore Protection and Electricity by Submerged Plate Wave Energy Converter. In Proceedings of the European Wave Energy Symposium, Edinburgh, UK, 21–24 July 1993; pp. 379–384. [Google Scholar]
- Orer, G.; Ozdamar, A. An Experimental Study on the Efficiency of the Submerged Plate Wave Energy Converter. Renew. Energy 2007, 32, 1317–1327. [Google Scholar] [CrossRef]
- Babarit, F.; Wendt, Y.-H.; Yu, J.; Weber. Investigation on the energy absorption performance of a fixed-bottom pressure-differential wave energy converter. Appl. Ocean. Energy 2017, 65, 90–101. [Google Scholar] [CrossRef]
- Schonborn, A. A harmonic pressure differential wave energy converter. Int. J. Mar. Energy 2017, 19, 47–54. [Google Scholar] [CrossRef]
- Windt, J.; Davidson, P.; Schmitt, J.V.; Ringwood. On the assessment of numerical wave makers in CFD simulations. J. Mar. Sci. Eng. 2019, 7, 47. [Google Scholar] [CrossRef]
- Rezanejad, K.; Gadelho, J.F.M.; Soares, C.G. Hydrodynamic analysis of an oscillating water column wave energy converter in the stepped bottom condition using CFD. Renew. Energy 2019, 135, 1241–1259. [Google Scholar] [CrossRef]
- Dai, S.; Day, S.; Yuan, Z.; Wang, H. Investigation on the hydrodynamic scaling effect of an OWC type wave energy device using experiment and CFD simulation. Renew. Energy 2019, 142, 184–194. [Google Scholar] [CrossRef]
- Kamath, A.; Bihs, H.; Arntsen, Ø.A. Numerical modeling of power take-off damping in an oscillating water column device. Int. J. Mar. Energy 2015, 10, 1–16. [Google Scholar] [CrossRef]
- Monino, A.; Medina-Lopez, E.; Clavero, M.; Benslimane, S. Numerical Simulation of a simple OWC problem for turbine performance. Int. J. Mar. Energy 2017, 20, 17–32. [Google Scholar] [CrossRef]
- Shah, I.; Kim, S.W.; Kim, K.; Doh, Y.H.; Choi, K.H. Experimental and numerical analysis of Y-shaped split and recombination micro-mixer with different mixing units. Chem. Eng. J. 2019, 358, 691–706. [Google Scholar] [CrossRef]
- Hasan, N.; Tibba, I.G.S.; Mosisa, F.T.; Daniel, A. Ground tunnel as renewable energy utilization of ground energy as a source and sink for building heating and cooling. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2018; p. 020005. [Google Scholar] [CrossRef]
- Wang, D.X.; Sun, J.W.; Gui, J.S.; Ma, Z.; Ning, D.Z.; Fang, K.Z. A numerical piston-type wave-maker toolbox for the open-source library OpenFOAM. J. Hydrodyn. 2019, 31, 800–813. [Google Scholar] [CrossRef]
- Sheng, W.; Alcorn, R.; Lewis, A. Assessment of primary energy conversions of oscillating water columns, I. Hydrodynamics Analysis. J. Renew. Sustain. Energy 2014, 6, 053113. [Google Scholar] [CrossRef]
- Colling, J.K.; Jafari Kang, S.; Dehdashti, E.; Husain, S.; Masoud, H.; Parker, G. Free-Decay Heave Motion of a Spherical Buoy. Fluids 2022, 7, 188. [Google Scholar] [CrossRef]

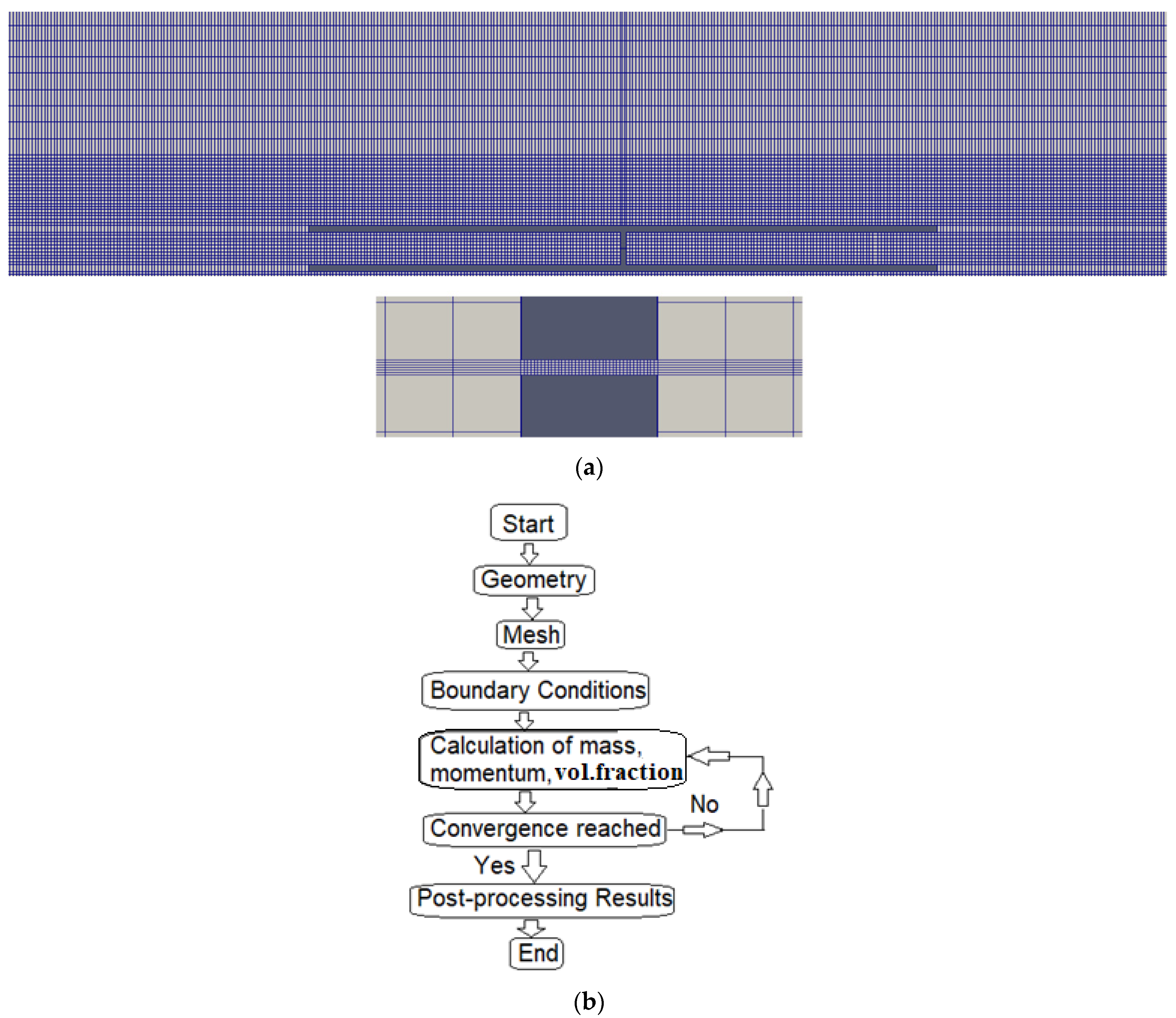


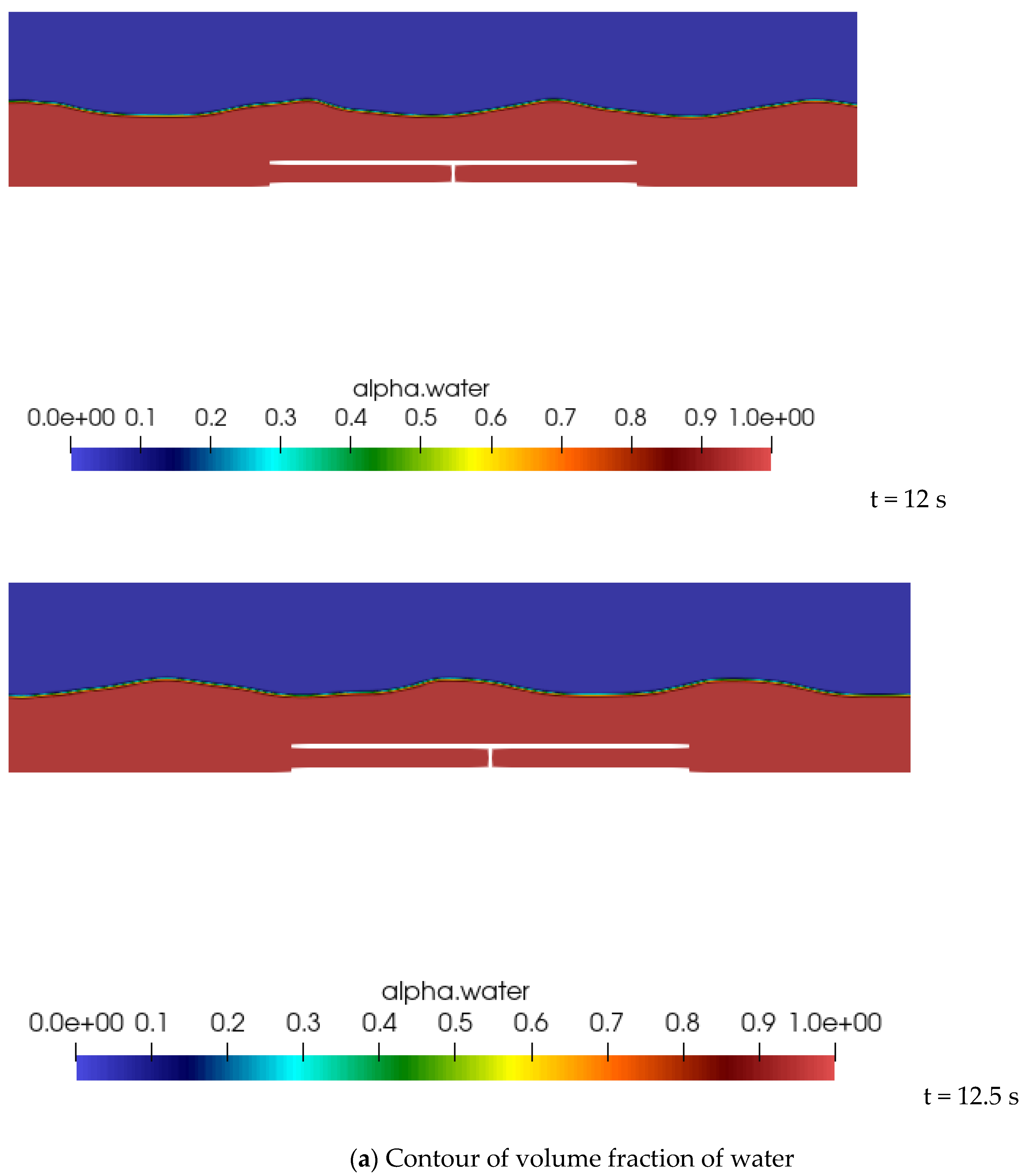
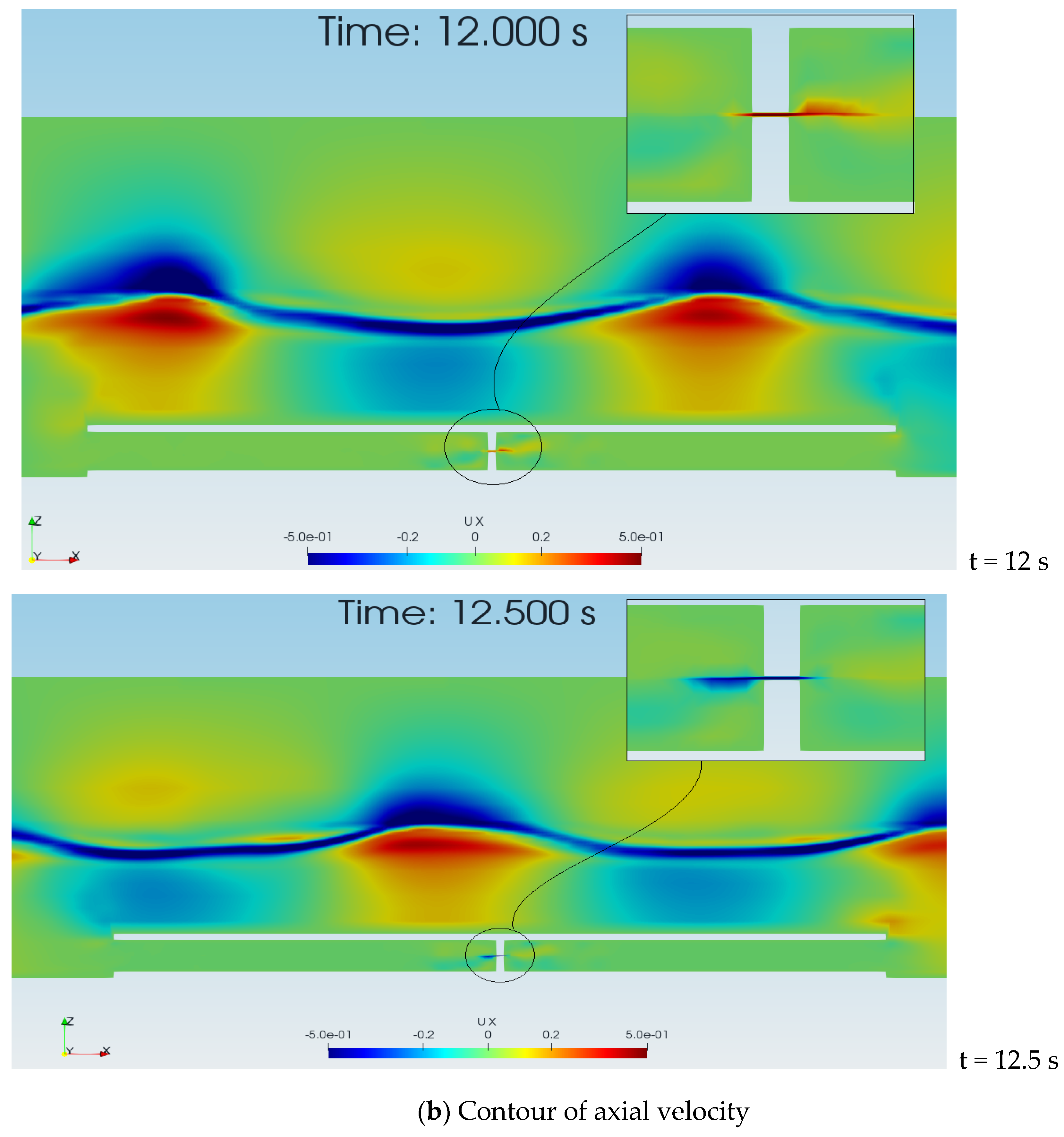
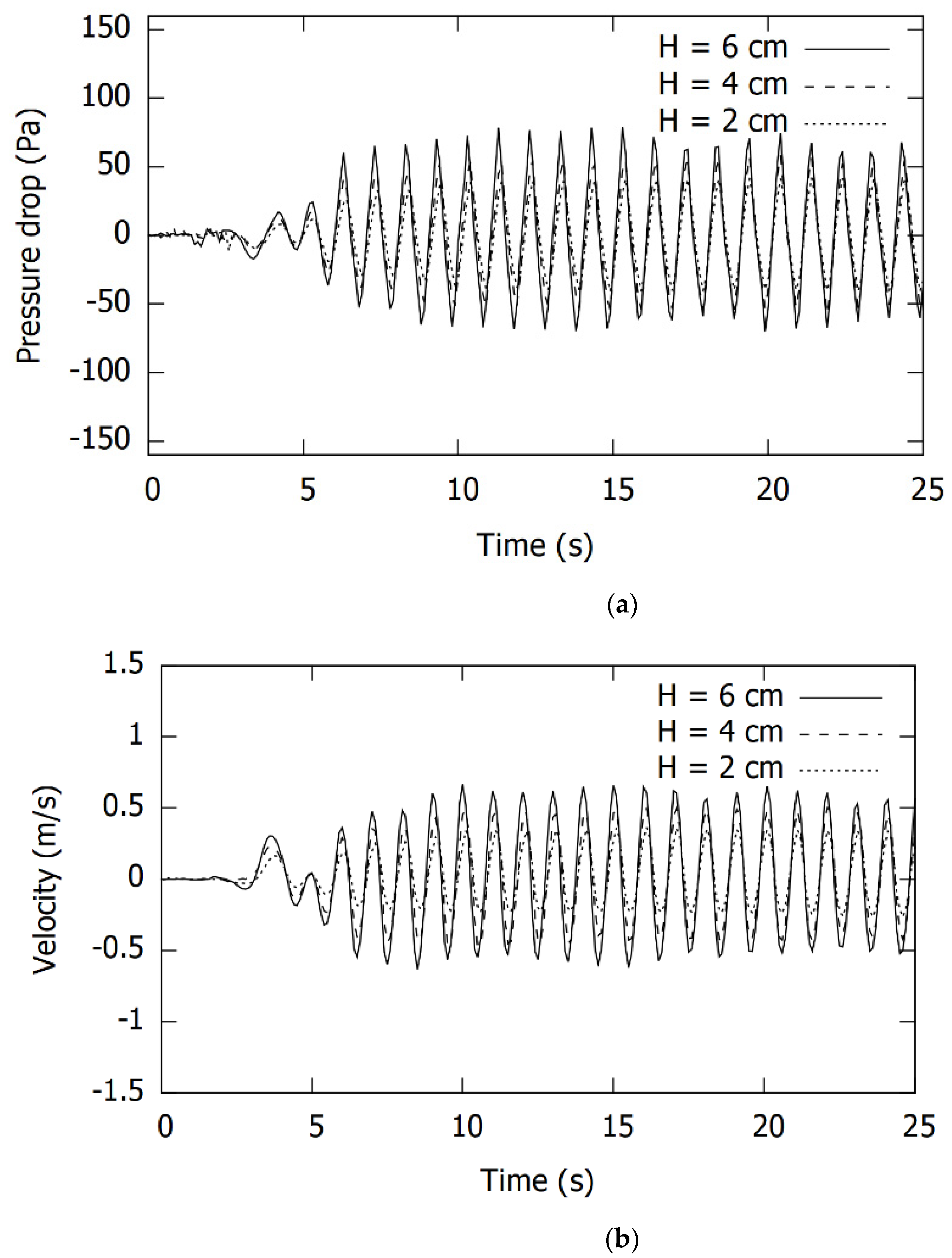

| Length (m) | 10 m |
|---|---|
| Diameter (m) | 0.1 m |
| Orifice opening (mm) | 1 mm, 2.5 mm |
| Mesh Elements | (Normalized Surface Elevation)CFD/(Normalized Surface Elevation)Expt |
|---|---|
| 31,500 | 1.2 |
| 42,000 | 1.15 |
| 112,500 | 1.12 |
| 375,000 | 1.08 |
| 450,000 | 1.04 |
| 860,000 | 1.02 |
| 1,120,000 | 1.005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Renganathan, M.; Hossain, M. Numerical Analysis of a Horizontal Pressure Differential Wave Energy Converter. Energies 2022, 15, 7513. https://doi.org/10.3390/en15207513
Renganathan M, Hossain M. Numerical Analysis of a Horizontal Pressure Differential Wave Energy Converter. Energies. 2022; 15(20):7513. https://doi.org/10.3390/en15207513
Chicago/Turabian StyleRenganathan, Manimaran, and Mamdud Hossain. 2022. "Numerical Analysis of a Horizontal Pressure Differential Wave Energy Converter" Energies 15, no. 20: 7513. https://doi.org/10.3390/en15207513
APA StyleRenganathan, M., & Hossain, M. (2022). Numerical Analysis of a Horizontal Pressure Differential Wave Energy Converter. Energies, 15(20), 7513. https://doi.org/10.3390/en15207513







