LCOE-Based Optimization for the Design of Small Run-of-River Hydropower Plants
Abstract
1. Introduction
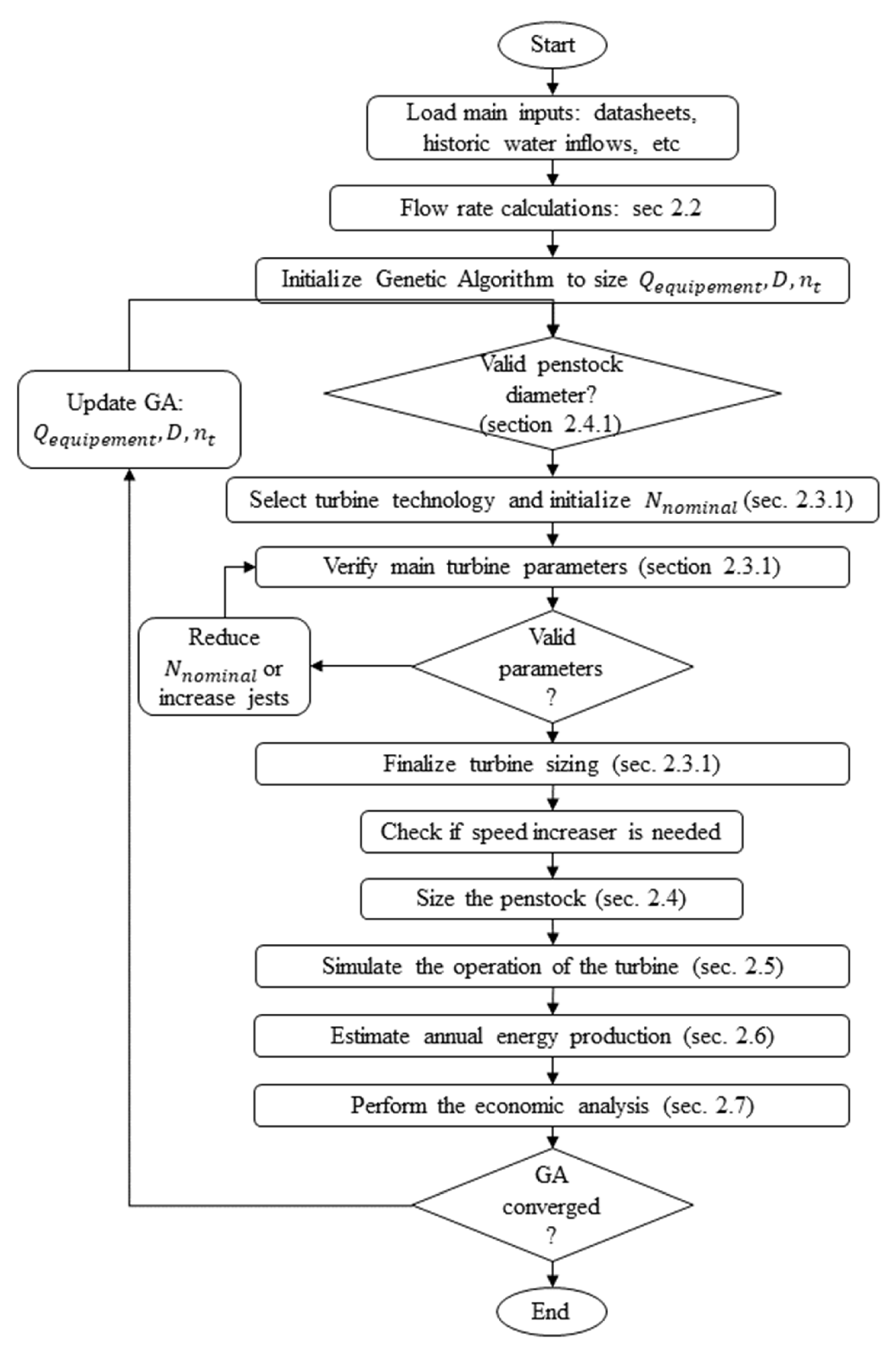
2. Materials and Methods: Description of the Developed Model
2.1. The Design Procedure
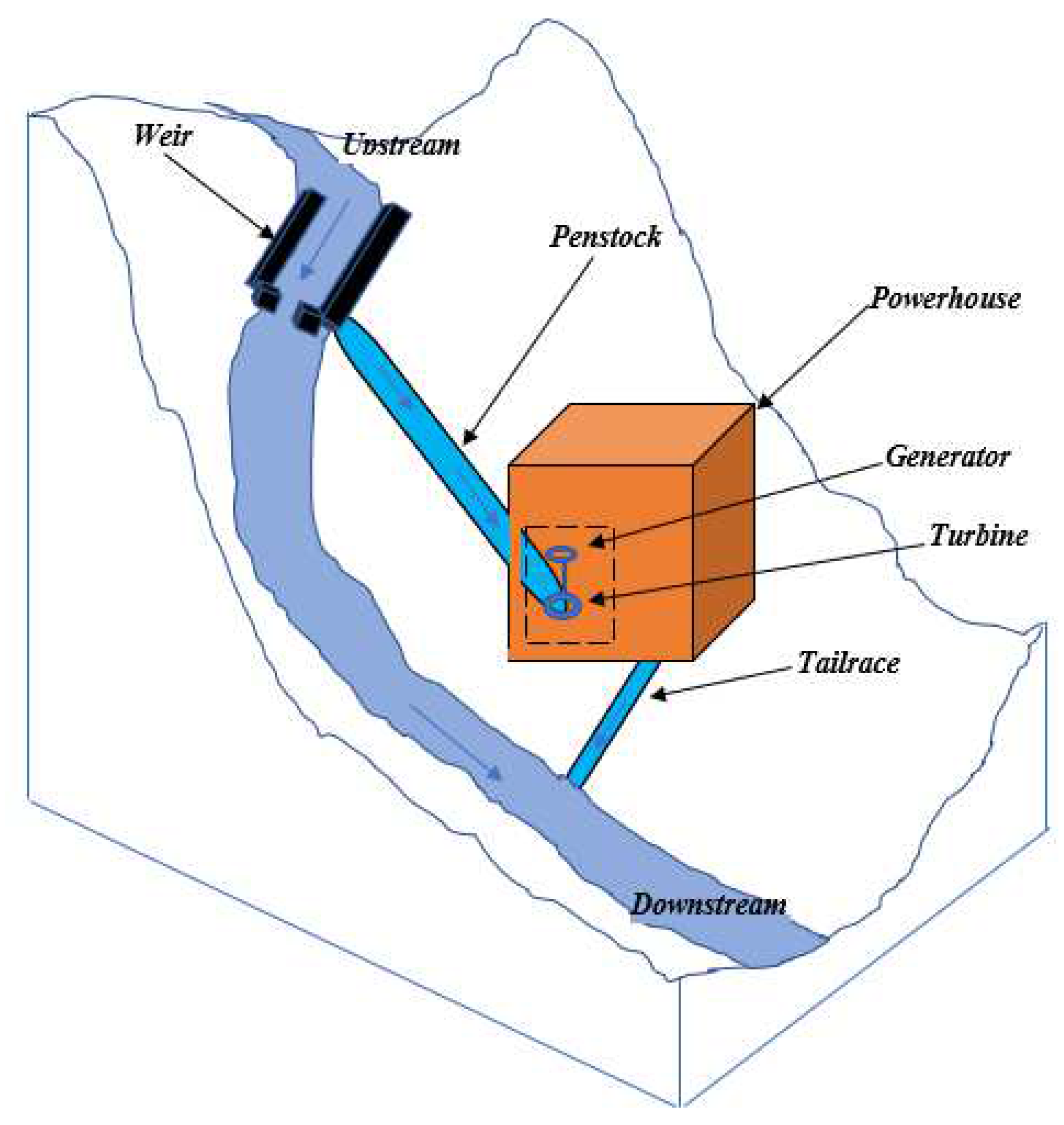
- Penstocks are buried only if a minimum of rock excavation is required [41]. However, since excavation leads to additional costs, this study assumes that penstocks are installed over the ground, hence leading to a positive suction head;
- The plant is connected to an existing electrical network and, hence, all the electricity produced is actually sold;
- The power plant is always in operation: no fault occurs, and as multiple turbines are installed, it is assumed that the maintenance plan can be performed without interruptions;
- Line losses are neglected;
- In order to generalize the model, the penstock configuration and its singularities are understood as sufficiently close to those of the 21 power plants that allowed Singhal MK and Arun Kumar [23] to develop a relationship between total head losses and friction losses: this formula allows one to calculate total head losses from friction losses, penstock length, and gross head and was found to be usable for hydropower projects due to the correlation coefficient of the relation obtained being 0.837, which is within the authorized limit;
- The deviation of the watercourse is made from a weir that does not allow considerable storage, as the role of the retaining structure is only to keep the level constant so as to ensure that the water intake and penstock are always supplied [41]. Additionally, that it is set up with what is necessary for the normal operation of the power plant, for example, it should be able to prevent the entry of suspended sediments;
- The topography of the site is appropriate for the production of hydroelectricity;
- The gross head is constant and that when dealing with low head schemes (2–30 m), since this assumption is no longer verified, an average value of the gross head measured is used;
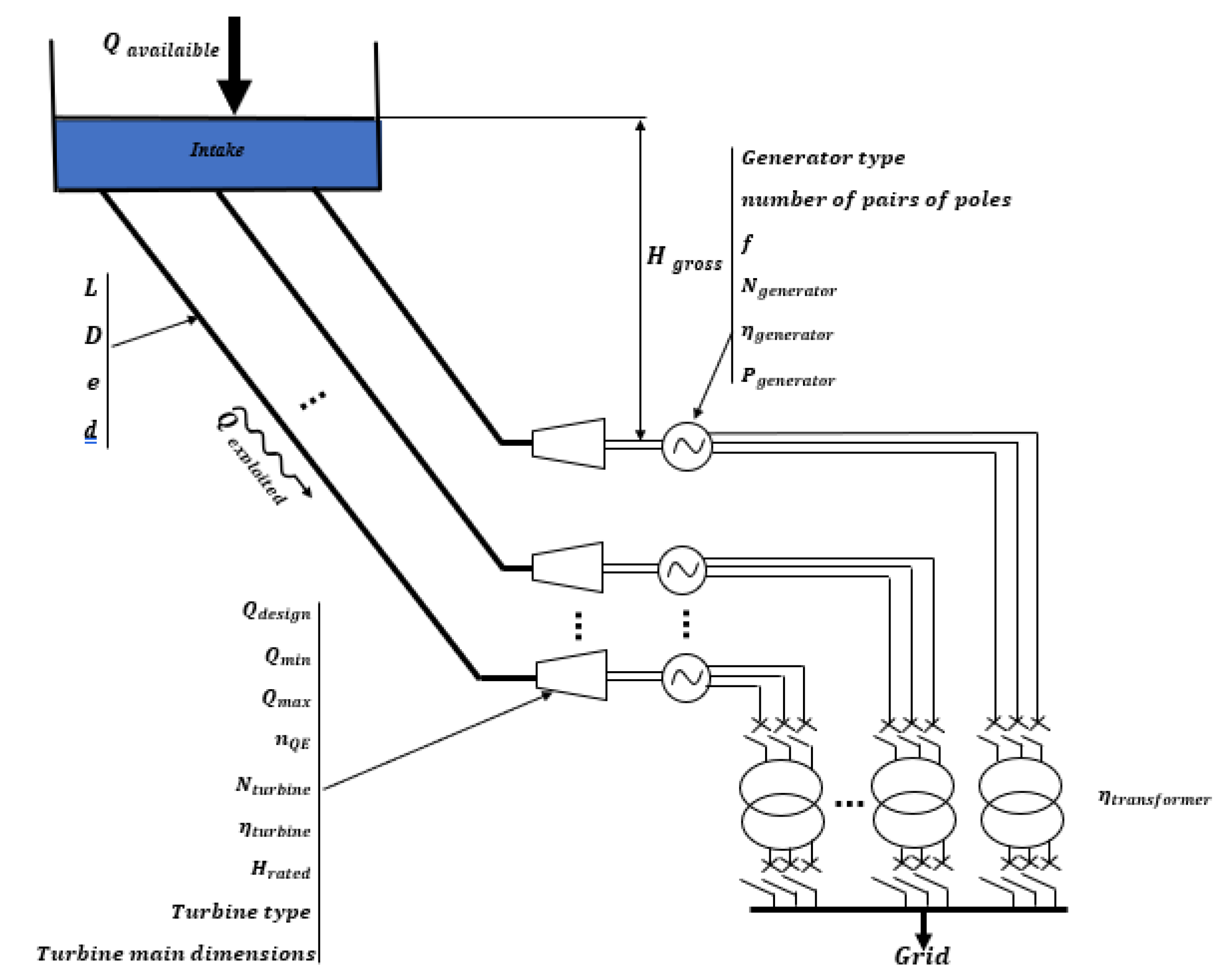
- The numerical model focuses on small run-of-river hydropower plants with a capacity between 500 kW and 10 MW, therefore having low- and high-head projects (3–20 m and above 100 m) and for a configuration where the intake is directly linked to the penstock, as shown in Figure 1.
- Design of the penstock: calculation of its diameter, its thickness, and its aeration pipe diameter;
- Determination of the optimal number of turbines;
- Optimal selection of turbine: turbine type, admissible suction head, design flow rate, rated head, rated power, rotational speed, specific speed, and main dimensions of the turbine wheels;
- Choice of generator: type of generator, frequency, number of pairs of poles, rated power, and rotation speed;
- Choice of whether or not to use a speed increaser between the turbine and the generator;
- Estimate of the annual energy produced;
- Estimation of the investment, operating, and maintenance costs of the project over its lifetime;
- Calculation of economic criteria: LCC, LCOE, Net Present Value, and return on investment time;
- Choice of the technical solution with the best LCOE;
- Simulation of the operating mode of the sized run-of-river plant equipment (penstocks, turbines, and generators), thus making it possible to estimate the average daily flow rates driving each turbine; the number of turbines used each day of the year; the average daily speeds of water in the penstock; friction; singular and total average daily head losses in the penstock; the average daily net heads; and average daily energies produced.
2.2. Definition of the Flow Rate of the Equipment
2.3. Selection of Turbine and Generator Technology
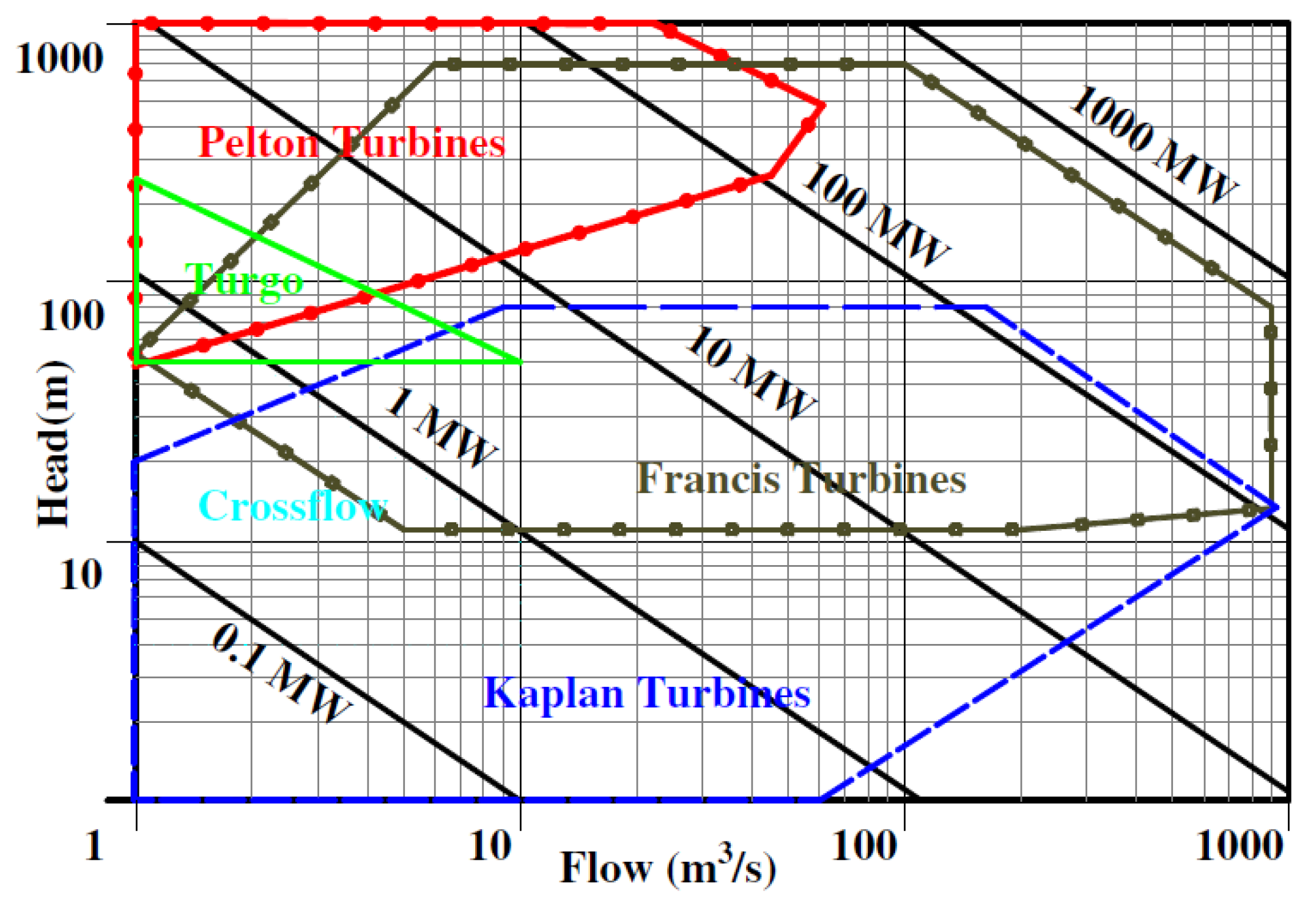
2.3.1. Turbine Case
- Pelton turbines
- Francis turbines
- Kaplan turbines
2.3.2. Generator Case
2.4. Design of the Penstock
2.4.1. Calculation of the Penstock Diameter
2.4.2. Calculation of the Penstock Thickness
- Proposal of a first estimate of e
- Calculate c, hmax, and emin
- Compare e and emin: if e < emin, then start again with a larger value of e and e > emin. Attempt to make e equal to the available wall thickness that is closest to emin, above or below, and repeat the calculation.
- Repeat the two previous steps until the minimum available wall thickness is made to be greater than emin
- e should be increased by 1.5 mm while dealing with mild steel pipes in order to take into consideration corrosion effects.
2.4.3. Calculation of the Air Vent Pipe Diameter
2.5. Turbine Operation Model
- In the first case (1), no turbine is in operation;
- In case (2), a turbine is in operation, and this is all the exploitable flow that is used;
- In case (3), (x + 1) turbines operate such that with 0 y and (x + 1), which is the natural number directly greater than (), if or x turbines operate such that if ;
- In case (4), all the turbines are in rated operation, each of them exploiting the maximum flow that it can turbinate and the rest of the water flow being lost;
- In case (5), no turbine is operating.
2.6. Annual Energy Production Estimation
2.7. Economic Analysis
2.7.1. Cost Estimate Model
- For a low-head project (3–20 m) [33]
- For a high-head project (more than 100 m) [32]
- The price for structural steel (including fabrication, transportation to site, and erection) is 75,000 Indian Rupee/MT;
- The price for M20 grade concrete work in plain cement concrete as well as in reinforced cement concrete, including shuttering, mixing, placing in position, compacting, and curing is 3640 Indian Rupee/m3;
- The price for reinforcement steel bars of iron 500 grade, including cutting, bending, binding, and placing in position is 55,000 Indian Rupee/MT;
- The price for earthwork in excavation with all leads and lifts in ordinary soil is 265 Indian Rupee/m3;
- The price for earthwork in excavation with all leads and lifts in soft rock, where blasting is not required is 330 Indian Rupee/m3;
- The price for earthwork in excavation with all leads and lifts in hard rock, including blasting is 550 Indian Rupee/m3.
2.7.2. Economic Criteria Calculation
- Life Cycle Cost (LCC)
- Levelized Cost of Energy (LCOE)
- Net Present Value (NPV)
- Return on investment time
2.8. Optimization Method
3. Case Study
4. Results
4.1. Optimal Design of the System
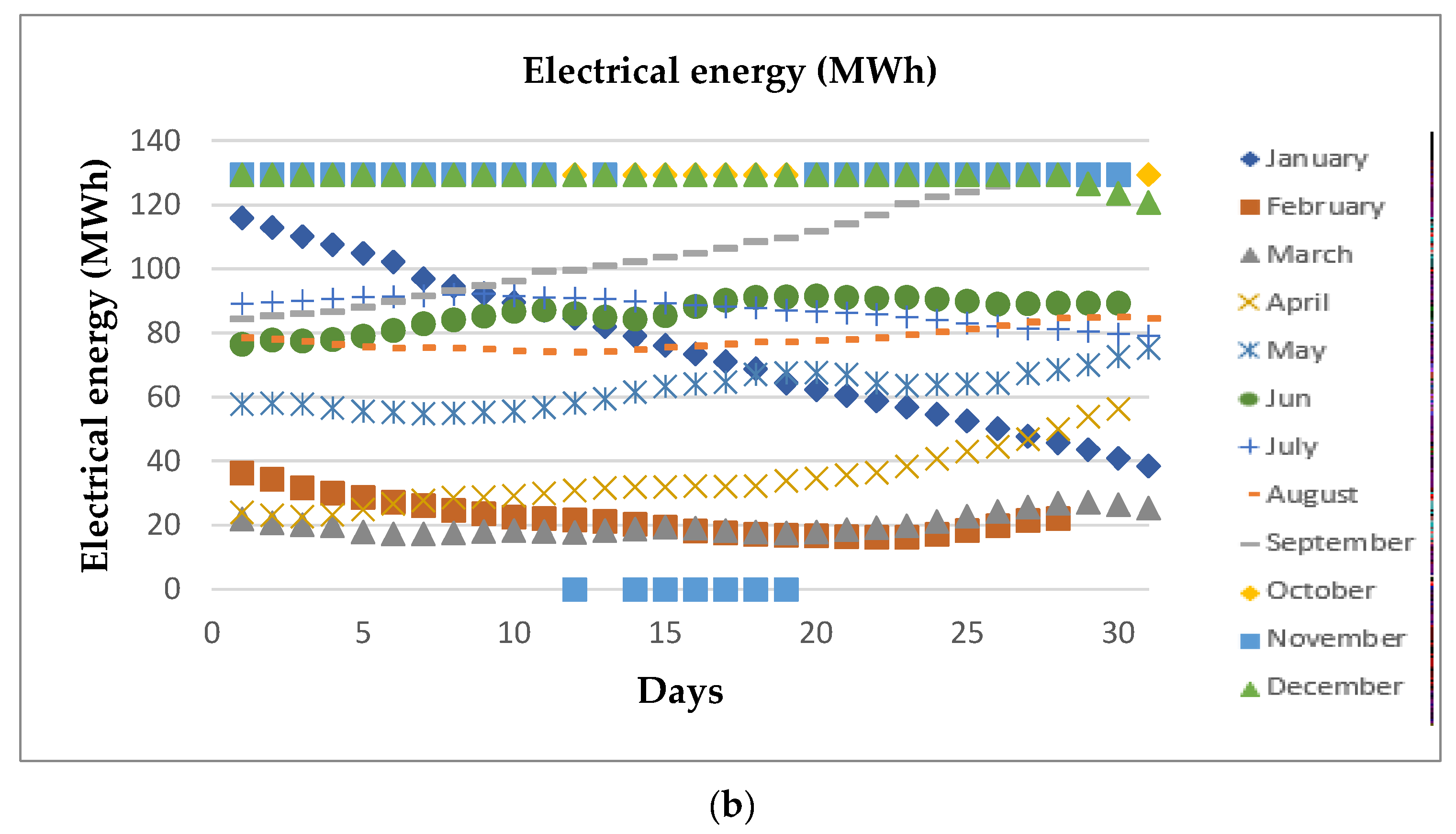
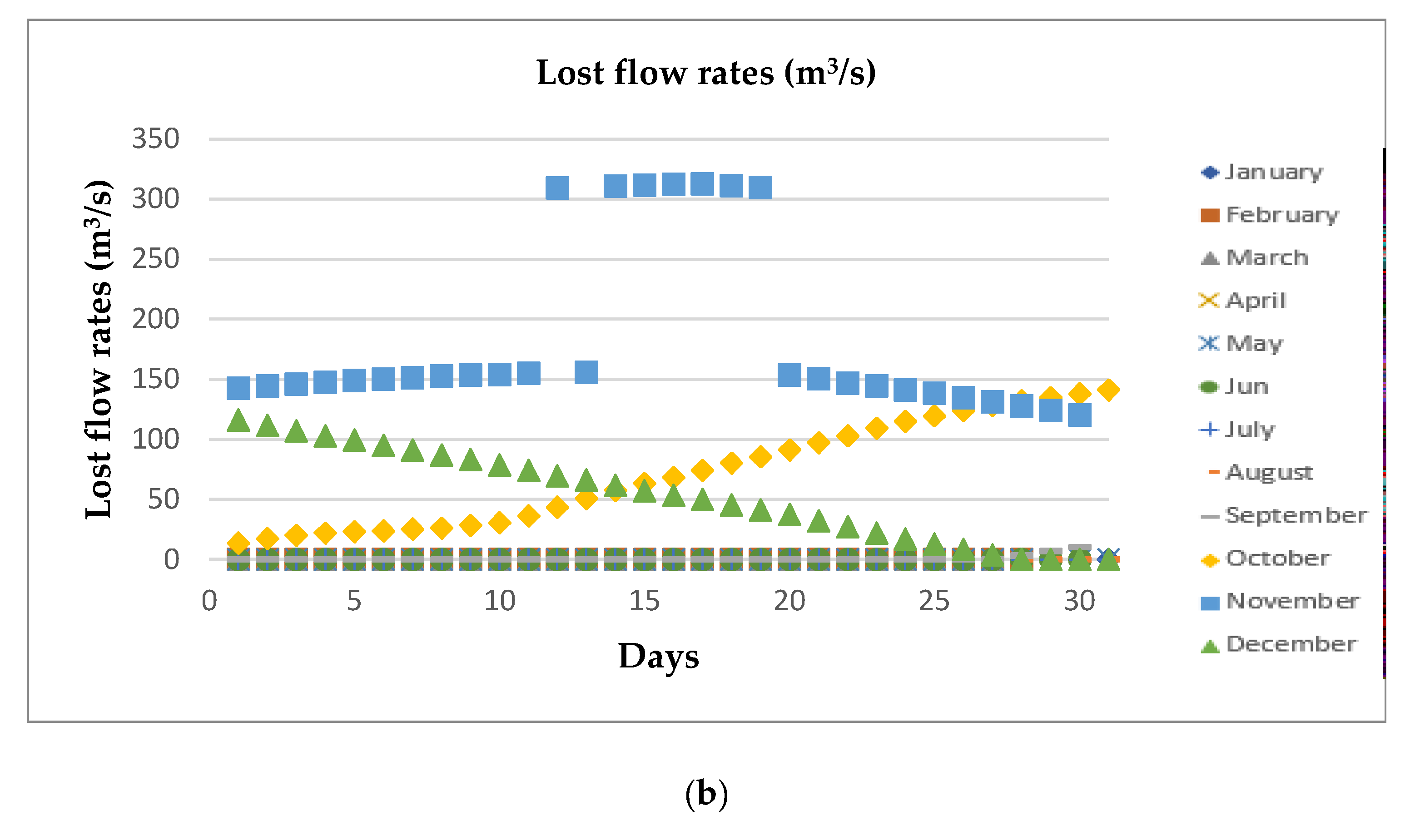
4.2. Optimal System Operation over the Year
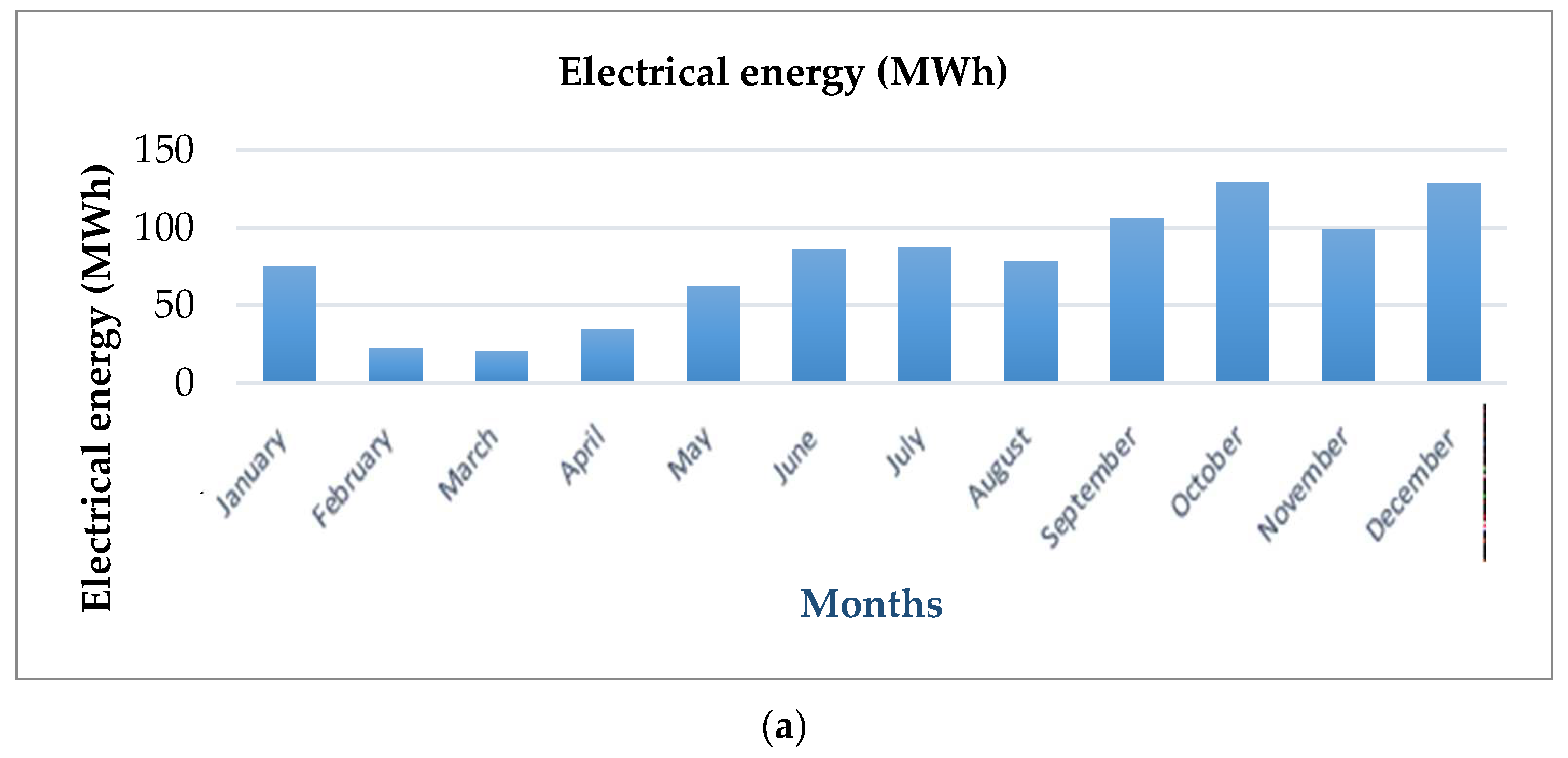
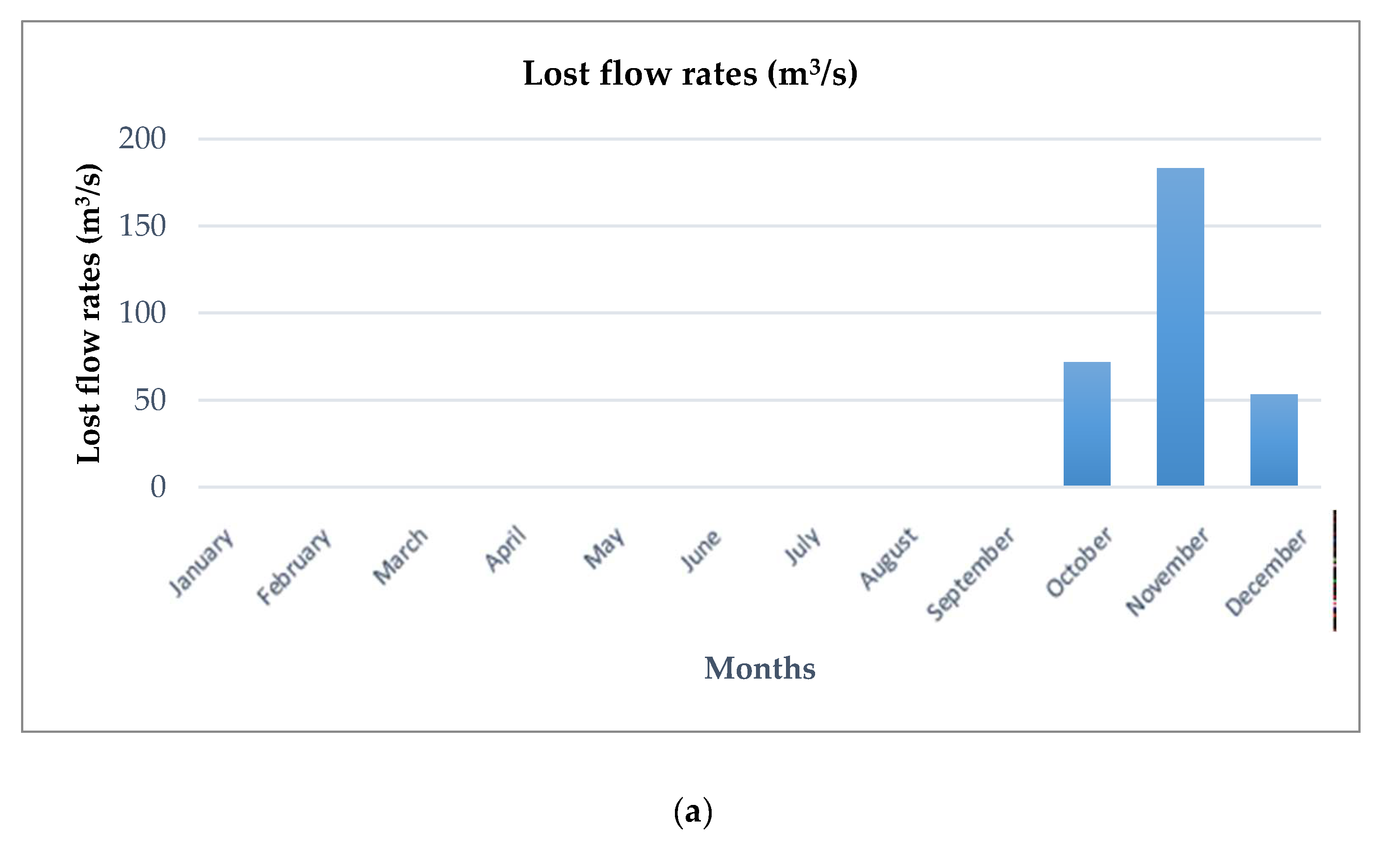
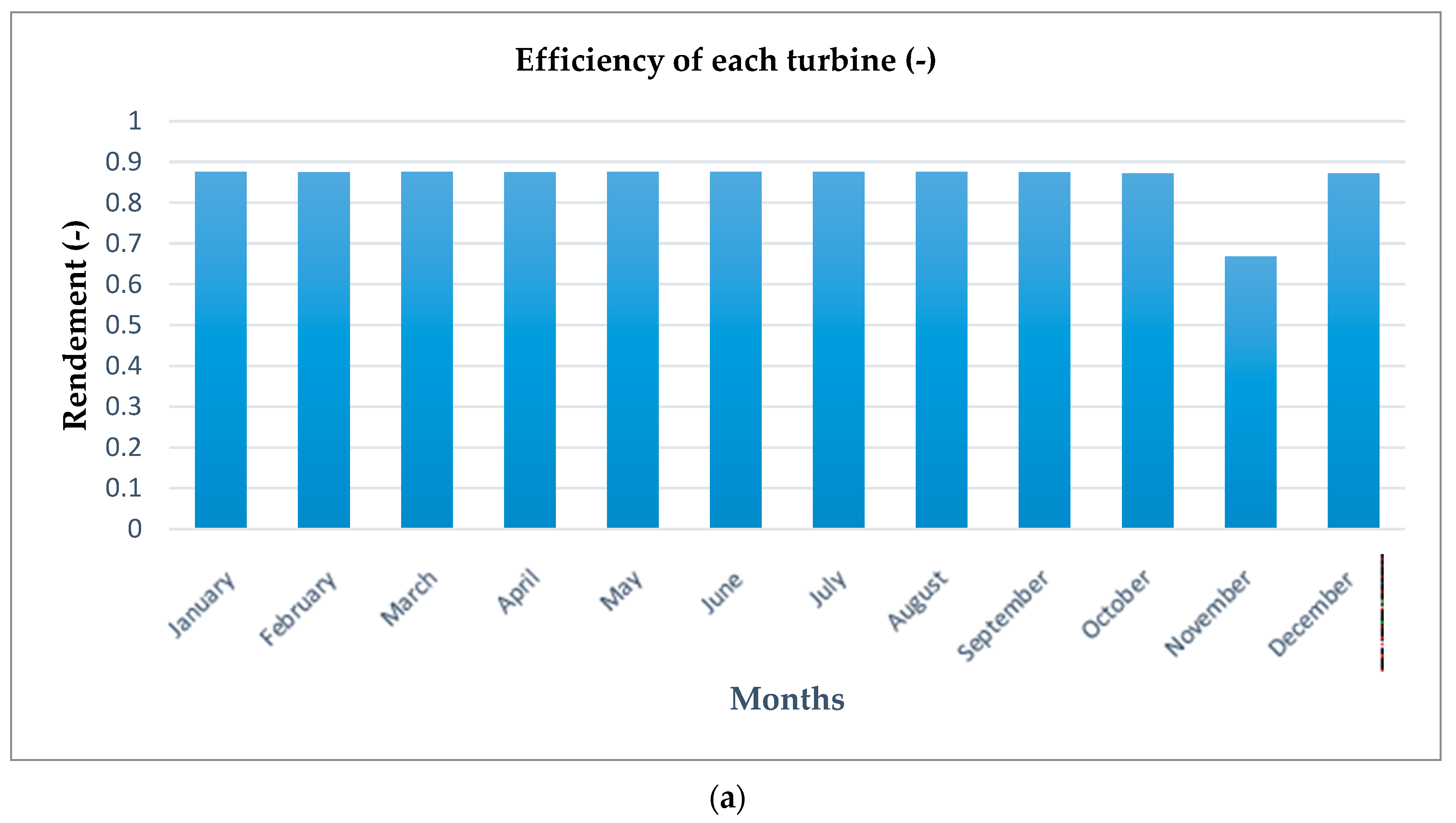
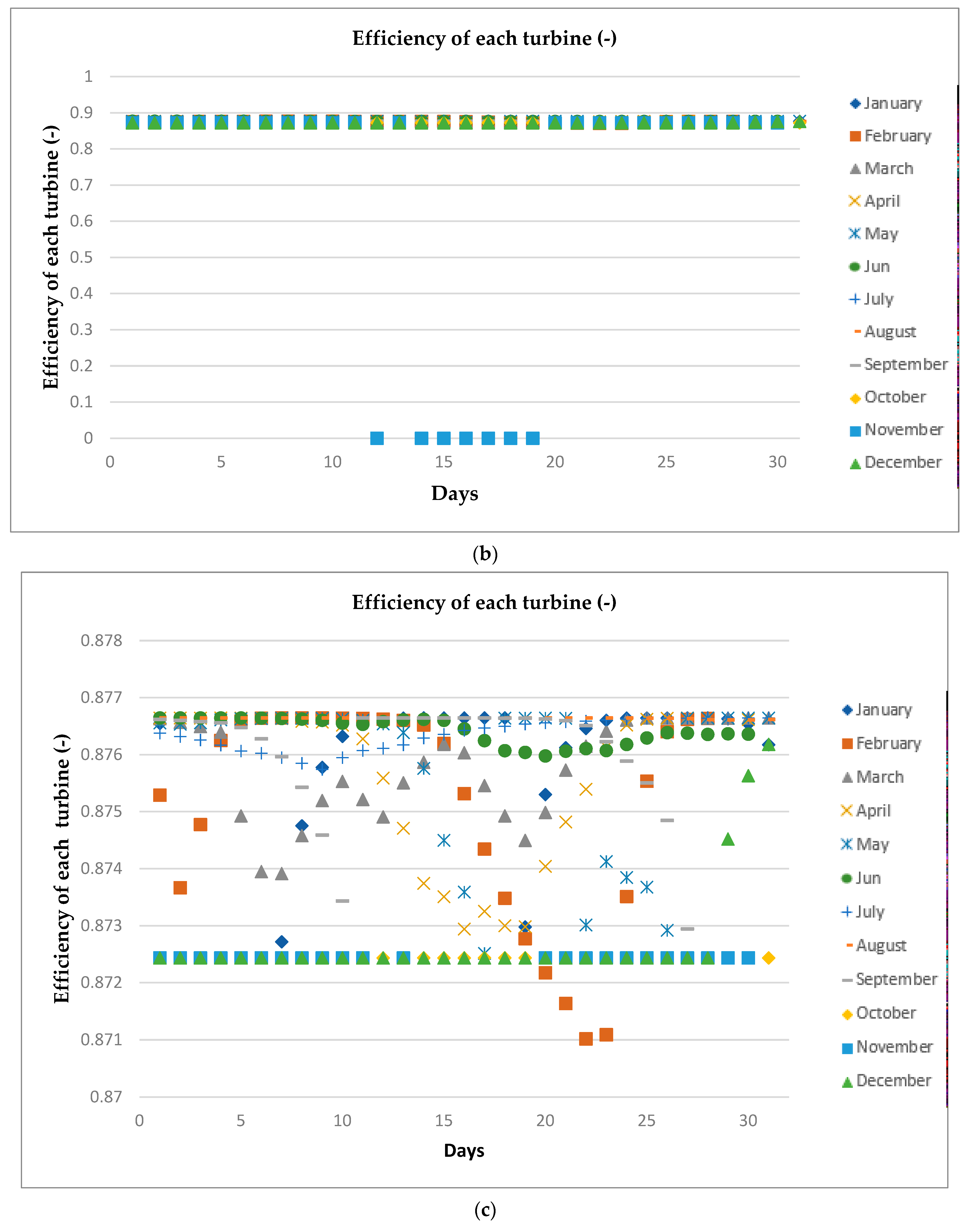
4.3. Analysis of the Energy Efficiency of the Optimal System
4.4. Economic Analysis of the Optimal System
5. Conclusions and Future Scope
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Safarian, S.; Unnborsson, R.; Ritcher, C. A review of biomass gasification modelling. Renew. Sustain. Energy Rev. 2019, 110, 378–391. [Google Scholar] [CrossRef]
- Hydropower Status Report, Sector Trends and Insights 2019. Available online: www.hydropower.org (accessed on 15 March 2021).
- Breeze, P. Power Generation Technologie; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Skoulikaris, C. Run-Of-River Small Hydropower Plants as Hydro-Resilience Assets against Climate change. Sustainability 2021, 13, 14001. [Google Scholar] [CrossRef]
- Borkowski, D.; Cholewa, D.; Korzen, A. Run-of-the-River Hydro-PV Battery Hybrid System as an Energy Supplier for Local Loads. Energies 2021, 14, 5160. [Google Scholar] [CrossRef]
- Kumar, D.; Katoch, S. Sustainability indicators for run of the river (RoR) hydropower projects in hydro rich regions of India. Renew. Sustain. Energy Rev. 2014, 35, 101–108. [Google Scholar] [CrossRef]
- Goodland, R. Environmental sustainability and the power sector. Impact Assess. 2012, 12, 409–470. [Google Scholar] [CrossRef]
- Korkovelos, A.; Mentis, D.; Siyal, H.; Arderne, C.; Rogner, H.; Bazilian, M.; Howells, M.; Beck, H.; Roo, D. A Geospatial Assessment of Small-Scale Hydropower Potential in Sub-Saharan Africa. Energies 2018, 11, 3100. [Google Scholar] [CrossRef]
- Haddad, O.; Moradi-Jalal, M. Design–operation optimisation of run-of-river powerplants. Water Manag. 2011, 164, 463–475. [Google Scholar]
- Vougioukli, A.; Didaskalou, E.; Georgakellos, D. Financial Appraisal of Small Hydro-Power Considering the Cradle-to-Grave Environmental Cost: A Case from Greece. Energies 2017, 10, 430. [Google Scholar] [CrossRef]
- Okot, D. Review of small hydropower technology. Renew. Sustain. Energy Rev. 2013, 26, 515–520. [Google Scholar] [CrossRef]
- Paish, O. Small hydro power: Technology and current status. Renew. Sustain. Energy Rev. 2002, 6, 537–556. [Google Scholar] [CrossRef]
- Karlis, D.; Papadopoulos, P. A systematic assessment of the technical feasibility and economic viability of small hydroelectric system installations. Renew. Energy 2000, 20, 253–262. [Google Scholar] [CrossRef]
- ONUDI Rapport Mondial sur le Développement de la Petite Hydraulique 2019. Available online: www.unido.org (accessed on 1 October 2021).
- Jasper, A.; Veysel, Y. A toolbox for the optimal design of run-of-river hydropower plants. Environ. Model. Softw. 2019, 111, 134–152. [Google Scholar]
- Tsuanyo, D.; Azoumah, Y.; Aussel, D.; Neveu, P. Modeling and optimization of batteryless hybrid PV (photovoltaic)/Diesel systems for off-grid applications. Energy 2015, 86, 152–163. [Google Scholar] [CrossRef]
- Tapia, C.; Gutiérrez, R.; Millan, G. An Evolutionary Computational Approach for Designing Micro Hydro Power Plants. Energies 2019, 12, 878. [Google Scholar] [CrossRef]
- Panagiotis, I.; Konstantinos, L. Optimizing Current and Future Hydroelectric Energy Production and Water Uses of Complex Multi-Reservoir System in the Aliakmon River, Greece. Energies 2020, 13, 6499. [Google Scholar]
- Anagnostopoulos, J.; Papantonis, D. Application of evolutionary algorithms for the optimal design of a small hydroelectric power plant. In Proceedings of the HYDRO 2004: A New Era for Hydropower, Porto, Portugal, 18–21 October 2004; Available online: www.researchgate.net (accessed on 10 March 2021).
- Anagnostopoulos, J.; Papantonis, D. Optimal sizing of a run-of-river small hydropower plant. Energy Convers. Manag. 2007, 48, 2663–2670. [Google Scholar] [CrossRef]
- Getachew, E.; Miroslav, M.; Juan, C.; Franca, J. Optimization of Run-of-River Hydropower Plant Capacity. Water Power Dam Constr. 2018, 1–10. Available online: www.researchgate.net (accessed on 22 March 2020).
- Ibrahim, M.; Imam, Y.; Ghanem, A. Optimal Planning and Design of Run-of-river Hydroelectric Power Projects. Renew. Energy 2019, 141, 858–873. [Google Scholar] [CrossRef]
- Kumar, A.; Singhal, M. Optimum Design of Penstock for Hydro Projects. Int. J. Energy Power Eng. 2015, 4, 216–226. [Google Scholar]
- Chinyere, A.; Obasih, R.; Ojo, E.; Okonkwo, C.; Mafiana, E. Technical Details for the Design of a Penstock for Kuchigoro Small Hydro Project. Am. J. Renew. Sustain. Energy 2017, 3, 27–35. [Google Scholar]
- Alexander, K.; Giddens, E. Optimum penstocks for low head microhydro schemes. Renew. Energy 2008, 33, 507–519. [Google Scholar] [CrossRef]
- Voros, N.; Kiranousdis, C.; Maroulis, Z. Short-cut design of small hydroelectric plants. Renew. Energy 2000, 19, 545–563. [Google Scholar] [CrossRef]
- Munir, M.; Shakir, A.; Khan, M. Optimal Sizing of Low Head Hydropower Plant- A Case Study of Hydropower Project at Head of UCC (Lower) at Bambanwala. Pak. J. Engg. Appl. Sci. 2015, 16, 73–83. [Google Scholar]
- Adejumobi, I.; Shobayo, D. Optimal selection of hydraulic turbines for small hydroelectric power generation—A case study of Opeki river, South Western Nigeria. Niger. J. Technol. 2015, 34, 530–537. [Google Scholar] [CrossRef]
- Sangal, S.; Garg, A.; Kumar, D. Review of Optimal Selection of Turbines for Hydroelectric Projects. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 424–430. [Google Scholar]
- Mishra, S.; Singal, K.; Khatod, D. A review on electromechanical equipment applicable to small hydropower plants. Int. J. Energy Res. 2012, 5, 553–571. [Google Scholar] [CrossRef]
- Mishra, S.; Singal, K.; Khatod, D. Approach for Cost Determination of Electro-Mechanical Equipment in RoR Projects. Smart Grid Renew. Energy 2011, 2, 63–67. [Google Scholar] [CrossRef]
- Mishra, S.; Singal, K.; Khatod, D. Cost Optimization of High Head Run of River Small Hydropower Projects. In Application of Geographical Information Systems and Soft Compuation Techniques in Water and Water Based Renewable Energy Problems; Springer: Singapore, 2018; pp. 141–166. [Google Scholar] [CrossRef]
- Singal, K.; Saini, P.; Raghuvanshi, S. Analysis for cost estimation of low head run-of-river small hydropower schemes. Energy Sustain. Dev. 2010, 14, 117–126. [Google Scholar] [CrossRef]
- Ogayar, B.; Vidal, P. Cost determination of the electro-mechanical equipment of a small hydro-power plant. Renew. Energy 2009, 34, 6–13. [Google Scholar] [CrossRef]
- Singal, K.; Saini, P.; Raghuvanshi, S. Cost Optimisation Based on Electro-Mechanical Equipment of Canal Based Low Head Small Hydropower Scheme. Open Renew. Energy J. 2008, 1, 26–35. [Google Scholar]
- Singal, K.; Saini, P. Analytical Approach for Cost Estimation of Low Head Small Hydropower Schemes. In Proceedings of the International Conference on Small Hydropower-Hydro Sri Lanka, New Delhi, India, 22–24 October 2007. [Google Scholar]
- Aggidis, G.; Luchinskaya, E.; Rothschild, R.; Howard, D. The costs of small-scale hydro power production: Impact on the development of existing potential. Renew. Energy 2010, 35, 2632–2638. [Google Scholar] [CrossRef]
- Najmaii, M.; Movaghar, A. Optimal Design of Run-of-River Power Plants. Water Resour. Res. 1992, 28, 991–997. [Google Scholar] [CrossRef]
- Santolin, A.; Gavazzini, G.; Pavesi, G.; Rossetti, A. Techno-economical method for the capacity sizing of a small hydropower plant. Energy Convers. Manag. 2011, 52, 2533–2541. [Google Scholar] [CrossRef]
- Patro, E.; Kishore, T.; Haghighi, A. Levelized Cost of Electricity Generation by Small Hydropower Projects under Clean Development Mechanism in India. Energies 2022, 15, 1473. [Google Scholar] [CrossRef]
- ESHA Guide on How to Develop a Small Hydropower Plant. 2004. Available online: www.canyonhydro.org (accessed on 17 March 2019).
- Pigueron, Y.; Dubas, M. Guide pour l’étude sommaire de petites centrales hydrauliques, Hes.so 2009. Available online: www.vs.ch (accessed on 17 March 2019).
- Martin, J.; Tchouate, H. La Filière Hydroélectrique: Aspects Technologiques et Environnementaux; Université Catholique de Louvain-GEB: Louvain, Belgique, 2003. [Google Scholar]
- Hänggi, P.; Weingartner, R. Variations in discharge volumes for hydropower generation in Switzerland. Water Resour. Manag. 2012, 26, 1231–1252. [Google Scholar] [CrossRef]
- Ye, L.; Ding, W.; Zeng, X.; Xin, Z.; Wu, J.; Zhang, C. Inherent Relationship between Flow Duration Curves at Different Time Scales: A Perspective on Monthly Flow Data Utilization in Daily Flow Duration Curve Estimation. Water 2018, 10, 1008. [Google Scholar] [CrossRef]
- Chen, J.; Yang, H.; Liu, C.; Lau, C.; Lo, M. A novel vertical axis water turbine for power generation from water pipelines. Energy 2013, 54, 184–193. [Google Scholar] [CrossRef]
- Ramos, H. Guidelines for Design of Small Hydropower Plants, Belfast, North Ireland. WREAN (West. Reg. Energy Agency Netw.) DED (Dep. Econ. Dev.). 2000. Available online: www.civil.ist.utl.pt (accessed on 18 March 2020).
- Parish, O.; Fraenkel, P.; Bokalders, V. Micro-Hydro Power A Guide for Development Workers; Practical Action Publishing: Rugby, UK, 1991. [Google Scholar]
- Jantasuto, O. Review of small hydropower system. Int. J. Adv. Cult. Technol. 2015, 3, 101–112. [Google Scholar] [CrossRef][Green Version]
- RetScreen International Clean Energy Project Analysis, 2001–2004. Available online: www.ieahydro.org (accessed on 17 March 2019).
- Kishore, T.S.; Patro, E.R.; Harish, V.S.K.V.; Haghighi, A.T. A Comprehensive Study on the Recent Progress and Trends in Development of Small Hydropower Projects. Energies 2021, 14, 2882. [Google Scholar] [CrossRef]
- Tsuanyo, D.; Approches Technico-Economiques D’optimisation des Systèmes Energétiques Décentralisés: Cas des Systèmes Hybrides PV/Diesel. Ph.D. Thesis, Universite de Perpignan via Domitia, 2015. Available online: www.theses.fr (accessed on 15 April 2020).
- Irena Renewable Power Generation Costs in 2014. Available online: www.irena.org (accessed on 25 October 2020).
- Audry, S. Hydrological Data, Nyong, Cameroon [Data set]. Theia. 2012. Available online: https://mtropics.obs-mip.fr/products/?uuid=5dc044eb-b8a6-bce2-0e88-e3e97ec0ac87 (accessed on 2 October 2021).
- Available online: www.infociments.fr (accessed on 2 October 2021).
- Available online: www.4.ac-nancy-metz.fr (accessed on 2 October 2021).
- The World’s Trusted Currency Authority. Available online: www.xe.com (accessed on 2 October 2021).
- Kengne, S.; Hamandjoda, O.; Nganhou, J. Methodology of Feasibility Studies of Micro-Hydro power plants in Cameroon: Case of the Micro-hydro of KEMKEN. Energy Procedia 2017, 119, 17–28. [Google Scholar] [CrossRef]
- Available online: www.process.free.fr (accessed on 2 October 2021).
- Ahenkorah, A.; Caceres, R. Jean-Michel Hydropower. In IPCC Special Report on Renewable Energy Sources and Climate Change Mitigation; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2011. [Google Scholar]
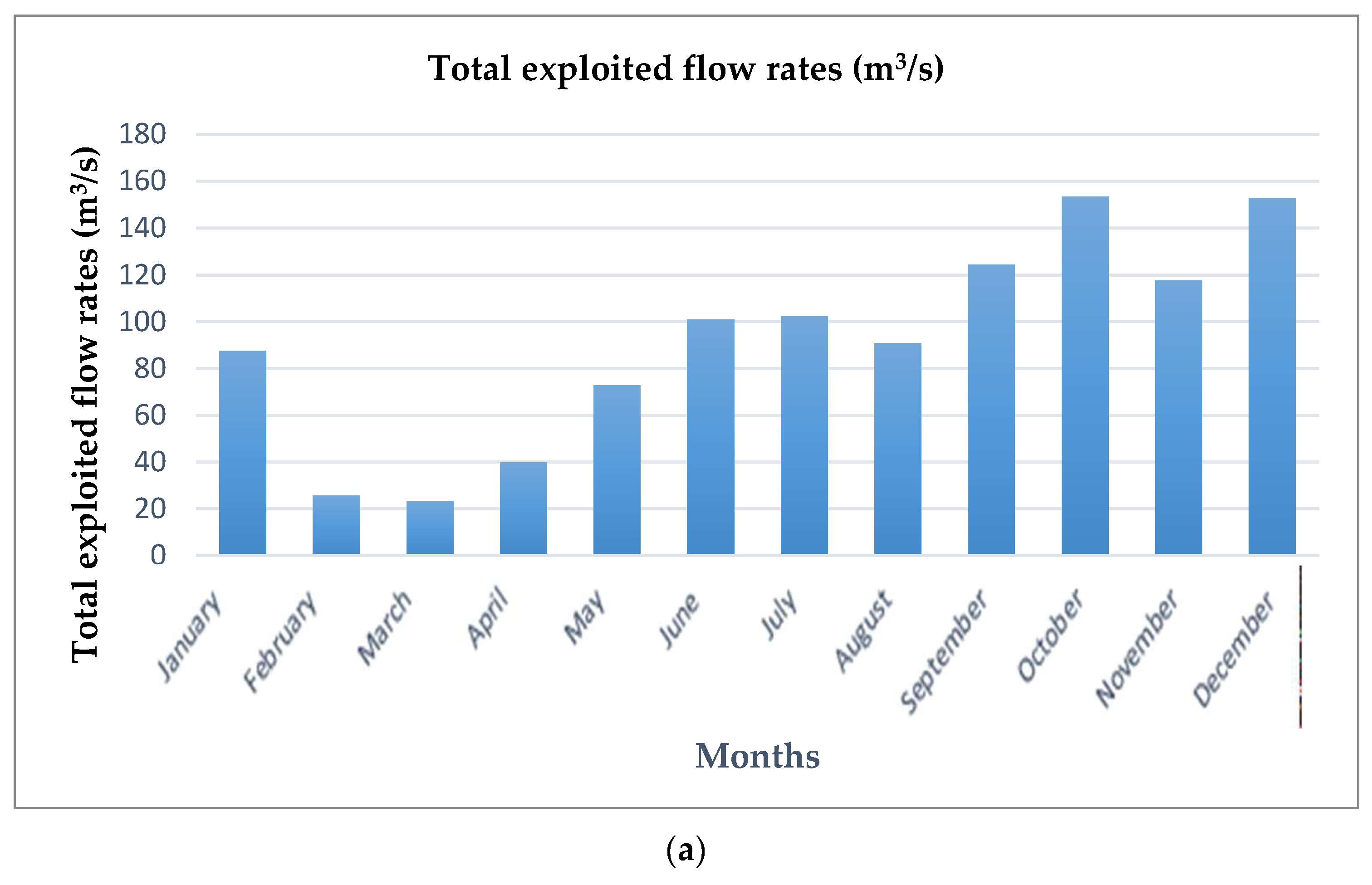
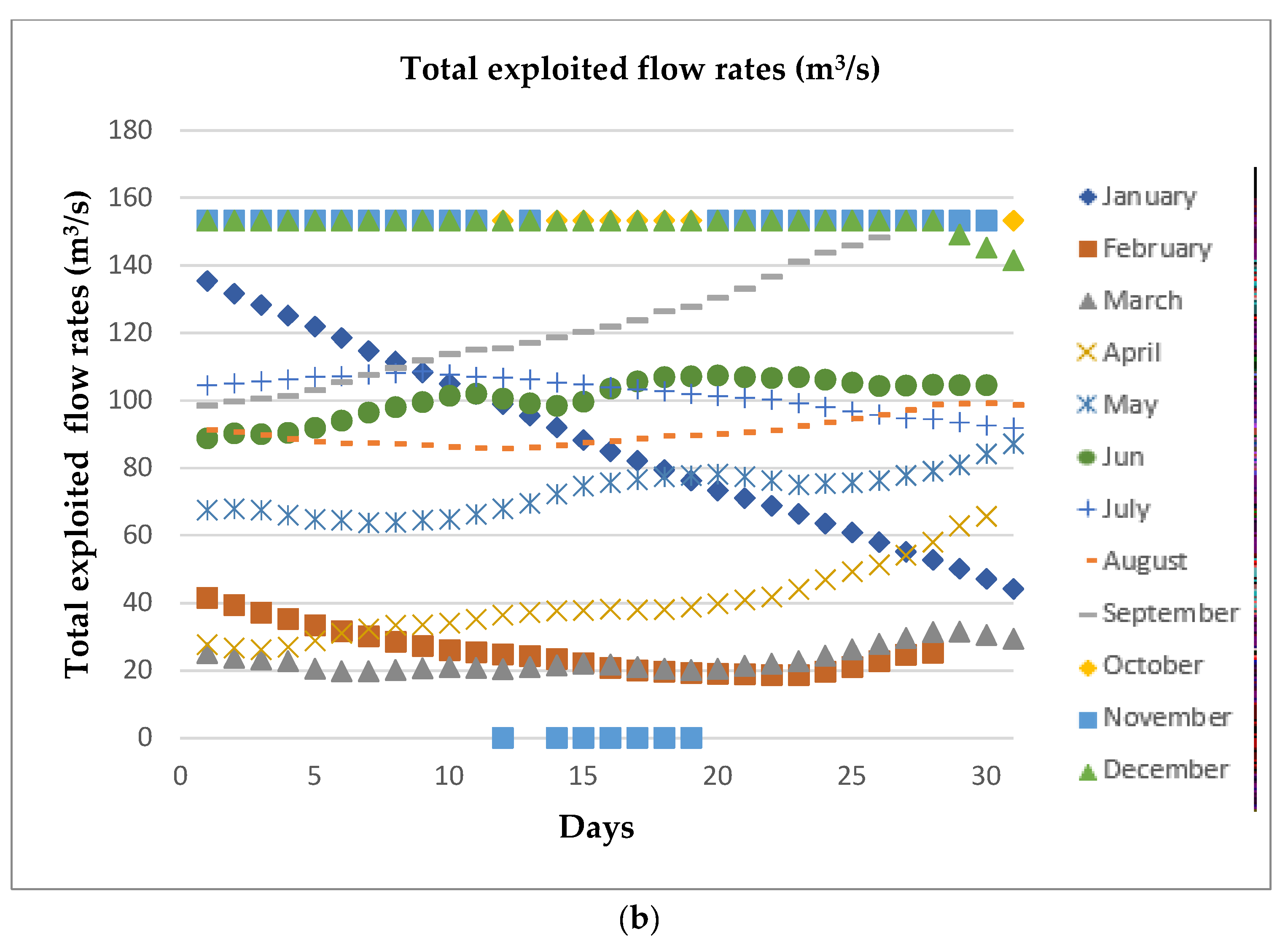
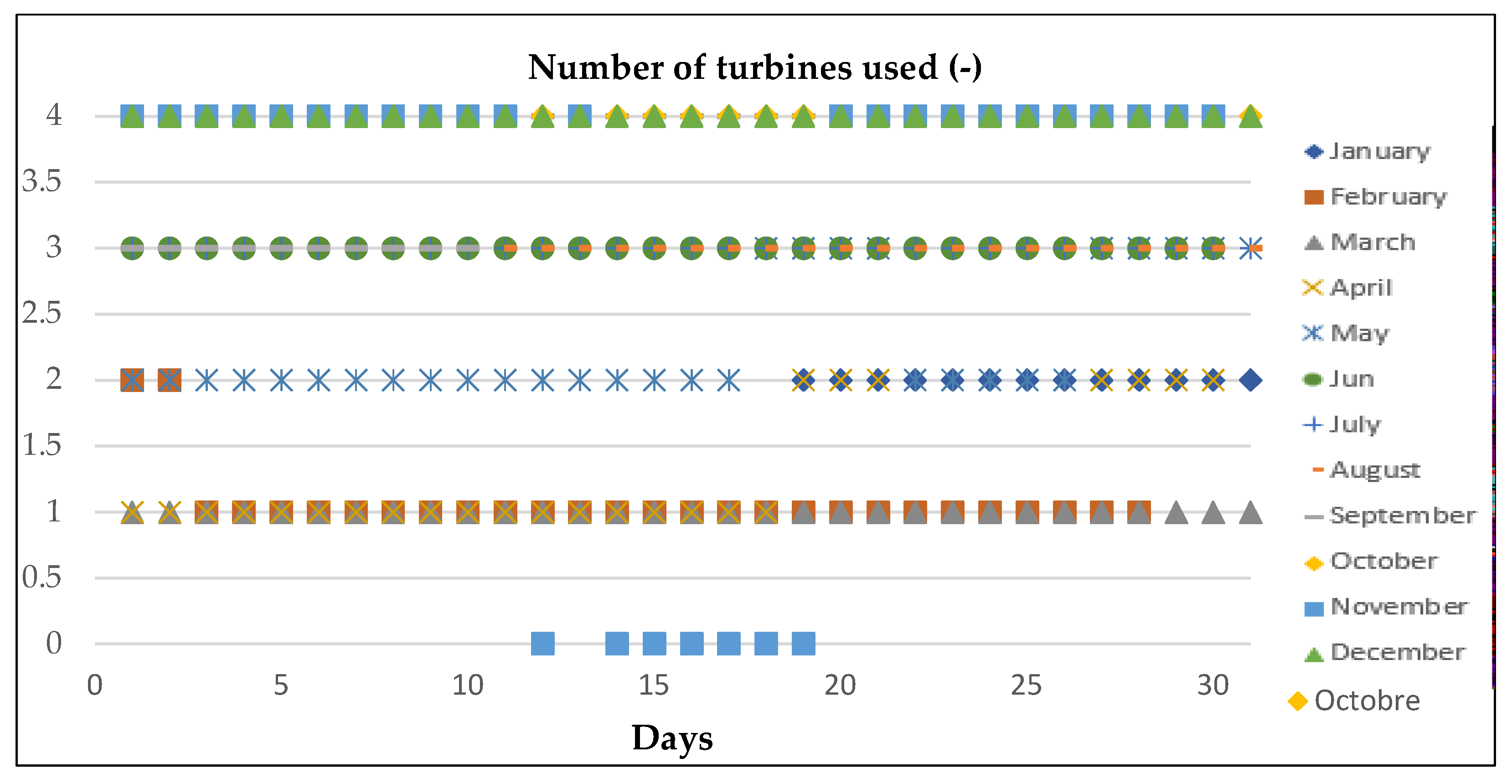
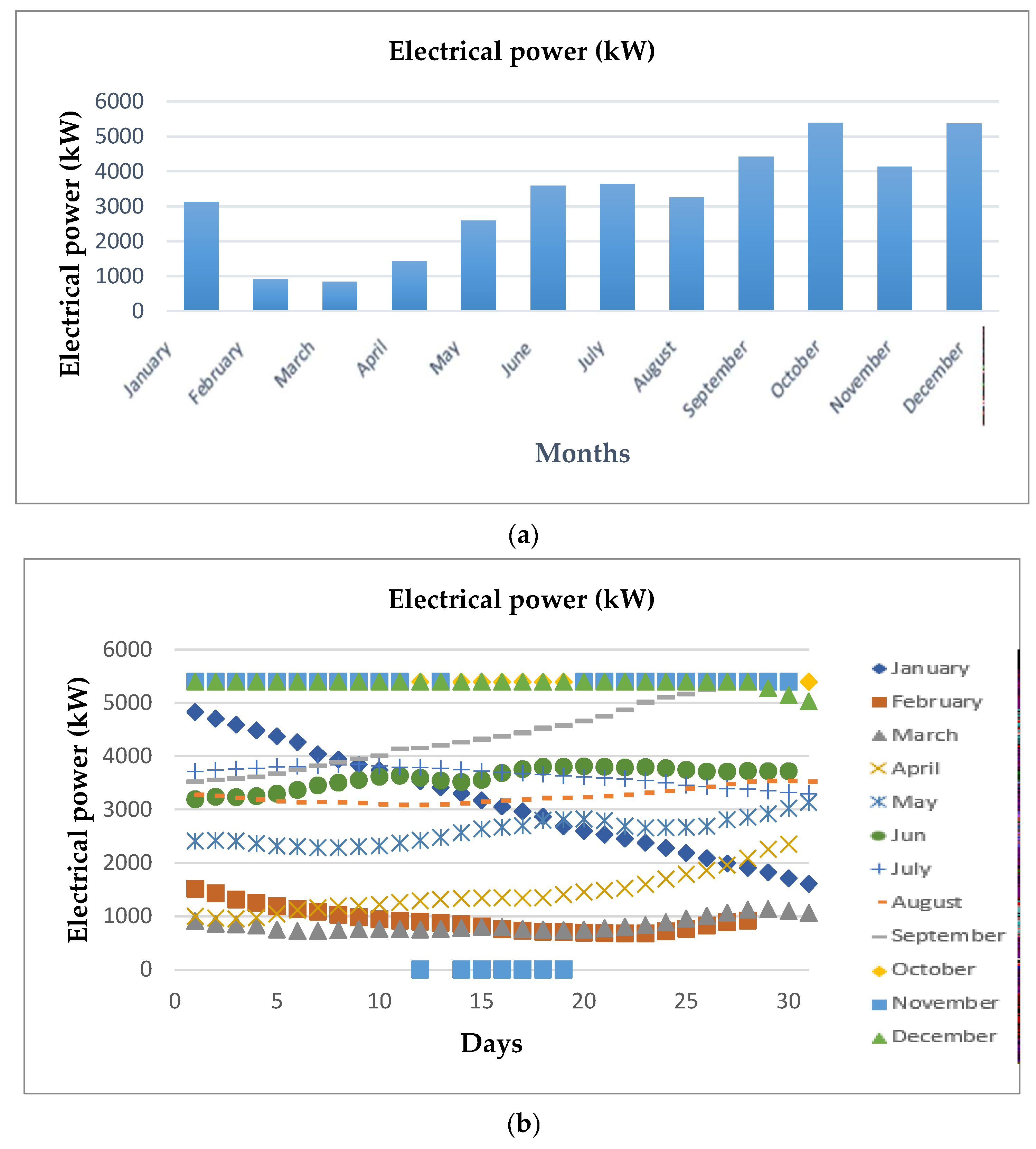
| Turbine Type | Acceptance of Flow Variation | Acceptance of Head Variation |
|---|---|---|
| Pelton | High | Low |
| Francis | Medium | Low |
| Kaplan double regulated | High | High |
| Kaplan single regulated | High | Medium |
| Propeller | Low | Low |
| Type of Turbine | Range |
|---|---|
| Pelton one nozzle | 0.005 ≤ ≤ 0.025 |
| Pelton n nozzles | 0.005 n0.5 ≤ ≤ 0.025 n0.5 |
| Francis | 0.05 ≤ ≤ 0.33 |
| Kaplan, propellers, bulbs | 0.19 ≤ ≤ 1.55 |
| Number of Poles | Speed for a Frequency of 50 Hz (rpm) |
|---|---|
| 2 | 3000 |
| 4 | 1500 |
| 6 | 1000 |
| 8 | 750 |
| 10 | 600 |
| 12 | 500 |
| 14 | 428 |
| 16 | 375 |
| 18 | 333 |
| 20 | 300 |
| 22 | 272 |
| 24 | 250 |
| 26 | 231 |
| 28 | 214 |
| Turbine Type | Best Efficiency |
|---|---|
| Kaplan single regulated | 0.91 |
| Kaplan double regulated | 0.93 |
| Francis | 0.94 |
| Pelton n nozzles | 0.9 |
| Pelton 1 nozzle | 0.89 |
| Turgo | 0.85 |
| Rated Power | Best Efficiency |
|---|---|
| 10 | 0.91 |
| 50 | 0.94 |
| 100 | 0.95 |
| 250 | 0.955 |
| 500 | 0.96 |
| 1000 | 0.97 |
| Head (m) | Maximum Speed (m/s) |
|---|---|
| Low head (50 < H) | 2–3 |
| Medium head (50 ≤ H ≤ 250) | 3–4 |
| High head (H > 250) | 4–5 |
| No. | Civil Works Components | Items | ||||
|---|---|---|---|---|---|---|
| Earth Work in Excavation (m3), E/W | Concreting (m3), Conc. | Reinforcement Steel (MT), RS | Structural Steel/Material (MT), SS | |||
| 1 | Diversion weir | |||||
| 2 | Penstock (per meter) | PVC pipe | ||||
| GRP pipe | ||||||
| HDPE pipe | ||||||
| Steel pipe | ||||||
| 3 | Tail race channel (per meter) | - | ||||
| 4 | Powerhouse building | Pelton/Turgo impulse | ||||
| Francis | ||||||
| No. | Type of Equipment | Coefficients in Cost Correlation | |||
|---|---|---|---|---|---|
| 1 | Turbine with governing system (TG) | Pelton | 117,313 | −0.03 | −0.39 |
| Turgo impulse | 145,121 | −0.12 | −0.24 | ||
| Francis | 125,354 | −0.01 | −0.38 | ||
| 2 | Generator with excitation system or capacitor bank (GE). | Induction | 130,262 | −0.19 | −0.22 |
| Synchronous | 143,660 | −0.18 | −0.21 | ||
| 3 | Auxiliaries | 21,846 | −0.19 | −0.22 | |
| 4 | Transformer | 221 | 0.11 | 0.01 | |
| 5 | Switchyard | 1.82 | 0.17 | 0.93 | |
| Economic and Technical Parameters | Symbol | Value |
|---|---|---|
| Roughness height for welded steel | 0.6 mm [41] | |
| Density of welded steel | 7.9 ton/m3 (7.7–8 ton/m3) [55] | |
| Kinematic viscosity of water (at 26 °C, average temperature of Mbalmayo over the year) | 0.878 × 10−6 m2/s [56] | |
| Density of water | 1000 kg/m3 | |
| Gravitational acceleration | 9.81 m/s2 | |
| Flow velocity of water at the outlet of the turbine | 2 m/s [41] | |
| Bulk modulus of water | 2.1 × 109 N/mm2 [41] | |
| Young’s Modulus of Elasticity for welded steel | 2.06 × 1011 N/m2 [41] | |
| Ultimate tensile strength of welded steel | 400 × 106 N/mm2 [41] | |
| Energy price | 0.1 USD/kWh | |
| Operation and Maintenance cost coefficient | 2.5 % [53] | |
| Indian rupee/ USD exchange rate | 0.0136333 [57] | |
| Percentage of non-operated interannual flow | 10% [41] | |
| Project lifespan | 50 years | |
| Lifespan of civil works components | 50 years | |
| Lifespan of electromechanical equipment | 25 years | |
| Generator efficiency | Table 5 [41] | |
| Average efficiency of the generator | 0.9 | |
| Turbine efficiency | Table 4 [41] | |
| Speed increaser efficiency | 0.97 [41] | |
| Transformer efficiency | 0.98 [49] | |
| Discount rate | 12.5 % [58] | |
| Atmospheric pressure | 10.3 mCE (101 000 Pa) [41] | |
| Vapor pressure of water (at 26 °C, average temperature of Mbalmayo over the year) | 0.34 mCE (3 360 Pa) [59] |
| Characteristics of the Turbine | |
|---|---|
| Turbine type | KAPLAN double regulated |
| Design flow rate (m3/s) | 38.35 |
| Specific speed (-) | 1.21 |
| Rotational speed (rpm) | 210 |
| Rated head (m) | 4.8 |
| Maximal suction head (m) | 0.34 |
| The runner outer diametert (m) | 2.4 |
| The runner hub diametert (m) | 0.79 |
| Best efficiency (-) | 0.93 |
| Rated power (MW) | 1.68 |
| Number of turbines (-) | 4 |
| Minimal flow rate (m3/s) | 5.75 |
| Maximal flow rate (m3/s) | 38.35 |
| Characteristics of the Generator | |
|---|---|
| Generator type | Asynchronous |
| Number of poles | 8 |
| Frequency (Hz) | 50 |
| Rotational speed (rpm) | 750 |
| Best efficiency (-) | 0.97 |
| Rated power (MW) | 1.58 |
| Characteristics of the Penstock | |
|---|---|
| Optimal diameter of the penstock (m) | 4.1 |
| Minimal thickness of the penstock (mm) | 19.04 |
| Length of the penstock (m) | 97.62 |
| Air vent pipe diameter of the penstock (cm) | 55.36 |
| Maximal total head losses in the penstock (m) | 0.2 |
| Maximal friction losses in the penstock (m) | 0.133 |
| Maximal singular losses in the penstock (m) | 0.067 |
| Maximal speed of water in the penstock (m/s) | 2.9 |
| Average speed of water in the penstock (m/s) | 2.4 |
| Surge head in the penstock (m) | 353.88 |
| Total head in the penstock (m) | 358.88 |
| Wave speed (m/s) | 1447.46 |
| Other Characteristics of the Project | |
|---|---|
| Flow rate of equipment (m3/s) | 153.41 |
| Gross head (m) | 5 |
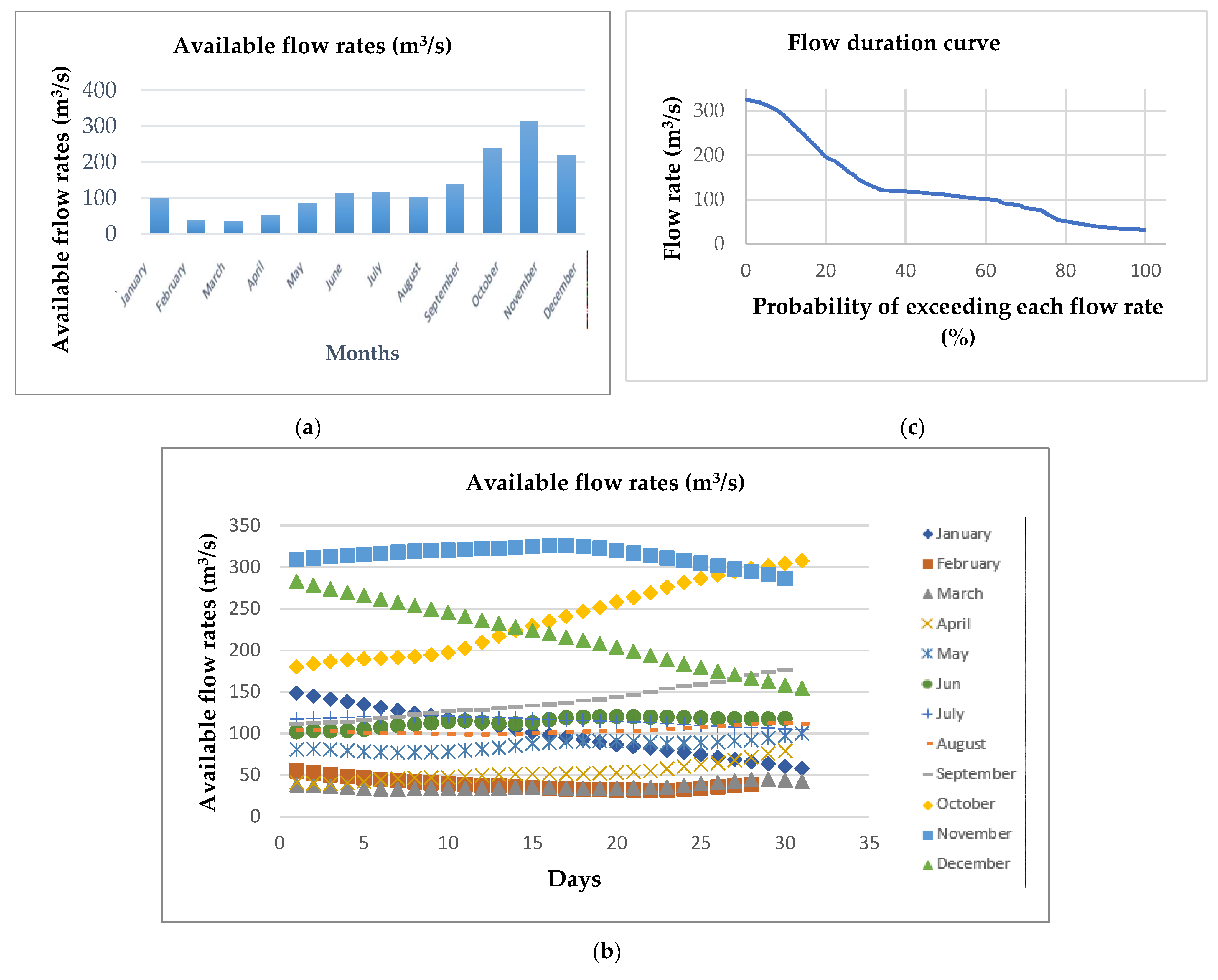
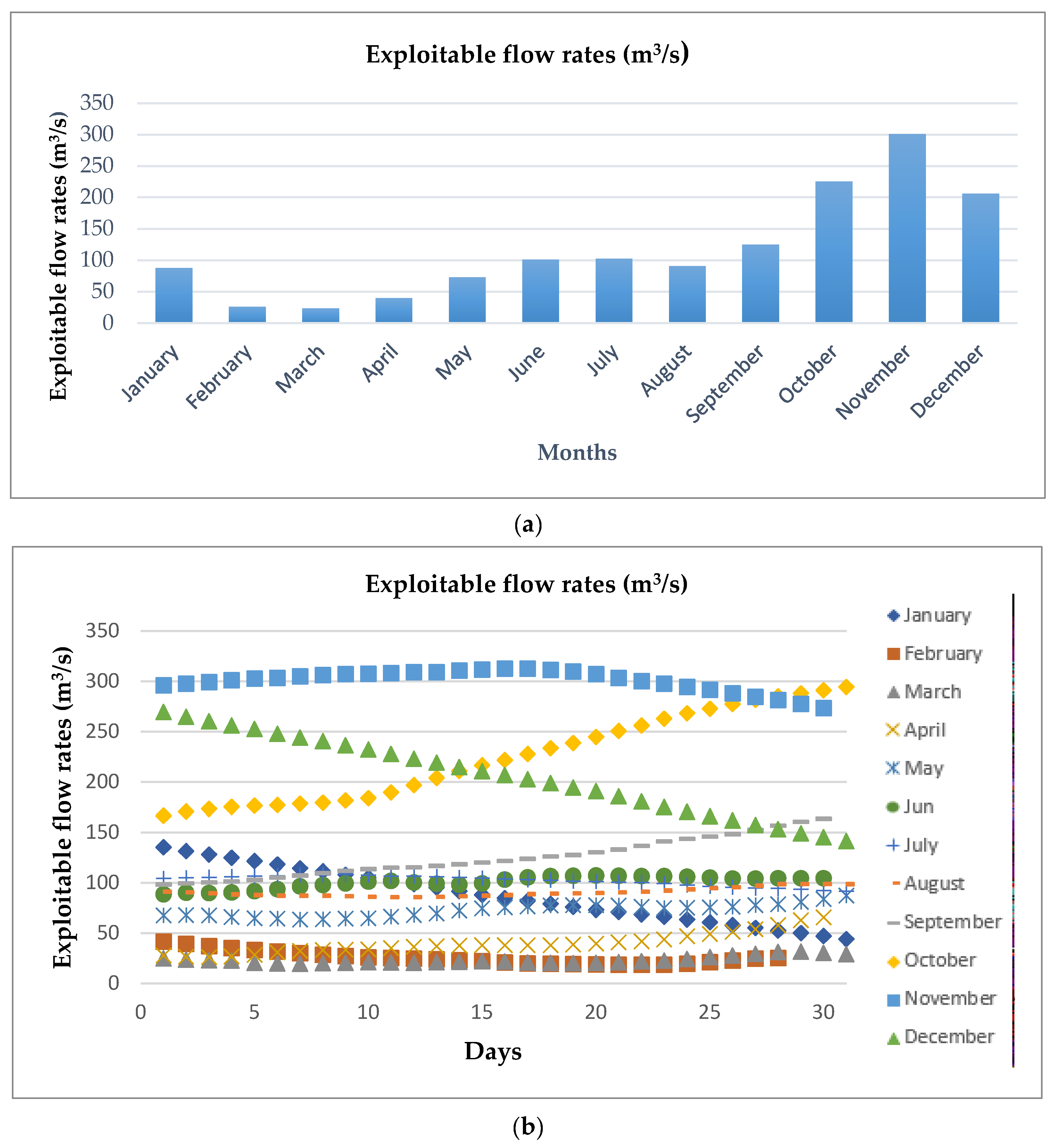
| Average available flow rate over the year (m3/s) | 130.13 |
| Residual flow rate (m3/s) | 13.01 |
| Average exploitable flow rate over the year (m3/s) | 117.11 |
| Safety flow rate (m3/s) | 309.17 |
| Energy Criteria | |
|---|---|
| Total installed capacity (MW) | 6.32 |
| Productible (GWh) | 28.42 |
| Water exploitation Index (%) | 78.04 |
| Energy production Index (%) | 56.47 |
| Average efficiency of the turbines over the year (-) | 0.88 |
| Load Index (%) | 51.32 |
| Economic Criteria | |
|---|---|
| LCC (MUSD) | 11.37 |
| LCOE (USD/kWh) | 0.0502 |
| Net Present Value (MUSD) | 11.30 |
| Payback period (years) | 5 years 2 months |
| Cost of civil works (MUSD) | 2.13 |
| Cost of electromechanical equipment (MUSD) | 3.13 |
| Miscellaneous and indirect cost (MUSD) | 1.09 |
| Initial investment cost (MUSD) | 5.94 |
| Replacement cost over the lifetime project (MUSD) | 3.54 |
| Total investment cost over the lifetime project (MUSD) | 9.48 |
| Operation and Maintenance cost per year (MUSD) | 0.237 |
| No. | Investment Cost (IC) (USD2005/kW) | O&M Cost (% of IC) | Capacity Factor (%) | Lifetime (Years) | Discount Rate (%) | LCOE (cents/kWh) | Comments |
|---|---|---|---|---|---|---|---|
| 1 | ˂500–6200 Median 1650 90% below 3250 | 41–61 | 2155 Projects in USA 43,000 MW in total Annual Capacity factor (except Rhode Island) | ||||
| 2 | ˂500–4500 Median 1000 90% below 1700 | 55–60 | 250 Projects for commissioning 2002–2020 Total Capacity 202,000 MW Worldwide but mostly Asia and Europe | ||||
| 3 | 1000–3500 700–8000 | 35–60 20–90 | 2–10 2–12 | Large Hydro Small Hydro (˂10 MW) (Not explicitly stated as levelized cost in report) | |||
| 4 | 2184 | 2.5 | 45 | 40 | 10 | 7.1 | |
| 5 | 1000–5500 2500–7000 | 2.2–3 | 10 10 | 3–12 5.6–14 | Large Hydro Small Hydro | ||
| 6 | 2880 in 2010 | 4 | 45 | 40 | 10 | 10.4 | |
| 7 | 2440 | 6 | 7.3 | Study applies to Germany only | |||
| 8 | 1000–5500 | 4 | 33 | 30 | 9.8 | Indicative average LCOE year 2000 | |
| 9 | 750–19,000 in 2010 (1278 average) | 51 | 80 80 | 2.3–45.9 4.8 | Range for 13 projects from 0.3 to 18,000 MW Weighted average for all projects | ||
| 10 | 5–12 3–5 5–40 | Small Hydro (˂10 MW) Large Hydro (˃10 MW) Off-Grid (˂1 MW) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amougou, C.B.; Tsuanyo, D.; Fioriti, D.; Kenfack, J.; Aziz, A.; Elé Abiama, P. LCOE-Based Optimization for the Design of Small Run-of-River Hydropower Plants. Energies 2022, 15, 7507. https://doi.org/10.3390/en15207507
Amougou CB, Tsuanyo D, Fioriti D, Kenfack J, Aziz A, Elé Abiama P. LCOE-Based Optimization for the Design of Small Run-of-River Hydropower Plants. Energies. 2022; 15(20):7507. https://doi.org/10.3390/en15207507
Chicago/Turabian StyleAmougou, Claude Boris, David Tsuanyo, Davide Fioriti, Joseph Kenfack, Abdoul Aziz, and Patrice Elé Abiama. 2022. "LCOE-Based Optimization for the Design of Small Run-of-River Hydropower Plants" Energies 15, no. 20: 7507. https://doi.org/10.3390/en15207507
APA StyleAmougou, C. B., Tsuanyo, D., Fioriti, D., Kenfack, J., Aziz, A., & Elé Abiama, P. (2022). LCOE-Based Optimization for the Design of Small Run-of-River Hydropower Plants. Energies, 15(20), 7507. https://doi.org/10.3390/en15207507







