Abstract
This article is dedicated to providing a detailed review concerning the SPH-based hydrodynamic simulations for ocean energy devices (OEDs). Attention is particularly focused on three topics that are tightly related to the concerning field, covering (1) SPH-based numerical fluid tanks, (2) multi-physics SPH techniques towards simulating OEDs, and finally (3) computational efficiency and capacity. In addition, the striking challenges of the SPH method with respect to simulating OEDs are elaborated, and the future prospects of the SPH method for the concerning topics are also provided.
Keywords:
smoothed particle hydrodynamics; ocean energy devices; floating wind turbines; wave energy converters; tidal current turbines; unified particle generator; numerical fluid tanks; particle shifting techniques; tensile instability control; multi-physics SPH simulations; multibody dynamics; fluid-structure interactions; hydroelasticity; multiphase flows; air-entrainment; parallel computing; multi-resolution; open-source SPH packages 1. Introduction
During the past several decades, renewable energy has become the most significant resource for human activities because of the worldwide awareness of the depletion of traditional fossil fuels as well as their harmful impacts on human’s living environment [1]. Among various types of renewable energy, ocean energy has been regarded as the preferred one to tackle the dilemma of humans owing to its abundant storage and, more importantly, its very low carbon dioxide emissions [2]. Since the capture and exploitation of ocean energy started to receive attention by the scientific and industrial communities [3], the technologies for harnessing ocean energy have been investigated and developed significantly to meet the energy market, which considerably fosters the invention of diverse Ocean Energy Devices (OEDs) ranging from small-scale isolated apparatus [4] to large-scale Integrated Energy Harvesting Systems (IEHSs) [5,6]. Generally speaking, as shown in Figure 1, the classification of OEDs can be mainly categorized by their energy resource, i.e., winds (e.g., Floating Wind Turbines, FWTs) [7,8,9,10], waves (e.g., Wave Energy Converters, WECs) [11,12,13], currents (e.g., Tidal Current Turbines, TCTs) [14,15,16], and multi-resource (see e.g., [6]). As pointed out by Said and Ringwood [17], ordinary OEDs consist of four phases to converting ocean energy to electricity (see also Figure 2), namely, absorption, transmission, generation, and conditioning. Among them, the absorption and transmission phases are typically characterized by Fluid–Structure Interaction (FSI), whereas the generation and conditioning phases mainly involve control strategies. Each phase has its scientific problems, and the present work is particularly devoted to the FSIs phases as illustrated in Figure 2. For the control problems, the readers can refer to [18].
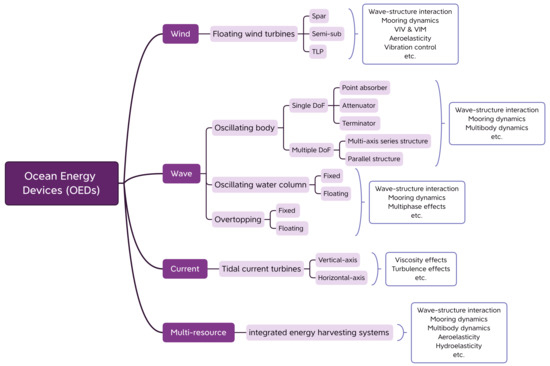
Figure 1.
A popular classification of various OEDs (inspired from [13]) and the typical hydrodynamic problems associated with them.
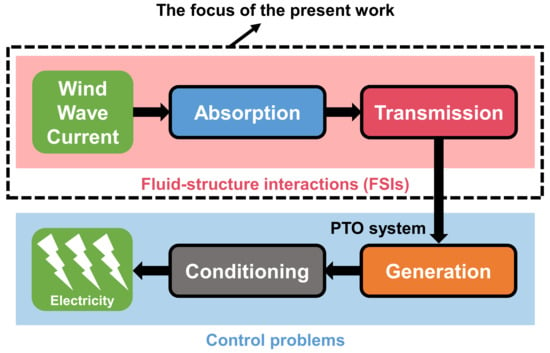
Figure 2.
The working pipeline of a generic OED (adapted from [17]), and the focus of the present study.
In fact, all of the aforementioned OEDs (see also Figure 1) can be treated as a special group of general nearshore/offshore structures that are widely employed in coastal and ocean engineering for diverse human activities, while there are several differences between OEDs and those traditional ones (e.g., vessels and platforms) from the hydrodynamic point of view. For example, traditional floating structures usually require minimum motion response during their working stage to guarantee the safety of both the staff and apparatuses, whereas for the sake of efficiently converting the mechanical energy of fluids to electricity by the Power Take-Off (PTO) system of them [19], OEDs are often expected to possess maximum motion responses in a diverse sea environment, e.g., working at a resonance status (see, e.g., [20,21,22]). Another example is that the aeroelasticity always imposes negligible effects on traditional offshore structures, while this is not the case when evaluating the working performance of FWTs, on which the coupling between flexible blades and air has strong nonlinear effects [23,24,25], thereby affecting their ability for generating electricity. In addition to these differences, those hydrodynamic problems originating from traditional offshore structures also widely exist in OEDs, e.g., hydroelasticity (see, e.g., [5,26,27]), wave slamming (see, e.g., [28,29]), Vortex-Induced Vibration/Motion (VIV and VIM) (see, e.g., [30,31,32]), multibody interactions (see, e.g., [33,34]), vibration control (see, e.g., [35,36]), viscosity and turbulence effects (see, e.g., [37,38,39,40]), and mooring dynamics (see e.g., [41,42]). Therefore, the hydrodynamic problems regarding OEDs are typically characterized by strongly nonlinear multi-physics coupling, which is, to a large extent, even more complicated than that of traditional coastal and ocean engineering structures. Because of the complexity and nonlinearity, during the past decades, the hydrodynamic performance of various OEDs has been considerably investigated to obtain the best ability of power generation under diverse real-sea environments (see, e.g., [7,9,13,15,16,19]).
Similar to other ocean engineering structures, the methodologies to investigate the hydrodynamic performance of OEDs can be mainly categorized into three types, i.e., a theoretical method (also named an analytical or semi-analytical method), an experimental method, and a numerical method. In terms of the theoretical method, it mainly relies on potential flow theory where linearized (or nonlinearized), incompressible, irrotational, and inviscid assumptions are always adopted (see, e.g., [19,43,44]). Nonetheless, as mentioned above, the concerning field is featured by strong nonlinearity and multi-physics coupling, so that the theoretical method seems a less ideal tool when considering complex working conditions, for example, large body motion (e.g., Oscillating Wave Surge Converters (OWSCs) [45,46]), multiphase flows (e.g., FWTs and Oscillating Water Columns (OWCs) converter), viscosity, and turbulence (e.g., FWTs and TCTs). In terms of the experimental method, it can be further divided into real-sea tests (see, e.g., [47,48]) and model tests (see, e.g., [49,50,51]). There is no doubt that a full-scale experiment is one of the best measures to evaluate the hydrodynamic performance of OEDs because it can reproduce the realistic working environment without any simplifications and scaling effects. However, full-scale tests are always very expensive, and the processing of the prototype of OEDs is not trivial. As a consequence, model tests are preferred by the engineering communities because of their relatively lower costs and higher feasibility. Notwithstanding, the reliability of model tests is particularly constrained by scaling effects since it is impossible to simultaneously satisfy the Froude and Reynolds similarity in a laboratory experiment (see, e.g., [52,53,54]). On the other hand, although model tests are cheaper than full-scale tests, it remains expensive compared with other methods. Therefore, the last one (i.e., the numerical method) is preferred at the pre-design stage of OEDs.
The numerical method is also known as Computational Fluid Dynamics (CFD) in the literature; it has been boosting during the past decades owing to the prosperous semiconductor industry that fosters the development of computer hardware. Although extensive CFD tools have been developed on both open-source platforms and commercial packages, only three types of CFD have been widely adopted for simulating OEDs, i.e., the Potential Flow (PF) solver, the Reynolds Averaged Navier–Stokes (RANS) solver, and the meshfree solver (see also Figure 3). Among them, PF, usually implemented by the Boundary Element (BE) approach, is the most computationally efficient one because it only requires a boundary grid on the OEDs surfaces. However, due to the linearized, irrotational, and inviscid hypotheses, PF is not suitable to be applied to violent free-surface breaking or viscosity-dominated problems. In order to deal with the deficiencies of PF, RANS was thereby developed by modeling the turbulence effects using the time-averaging approach, retaining the fully nonlinear characteristics of the Navier–Stokes equation. There is no doubt that RANS possesses better accuracy and applicability than PF because of its nonlinearity and viscosity consideration, whereas its computational cost is considerably greater than PF. Despite its remarkable advantages and successful applications in designing OEDs (see, e.g., [55,56,57,58,59]), RANS undergo several striking issues in some circumstances caused by its Eulerian nature. Among them, the two most challenging issues are (1) the accurate capture of highly distorted topological deformations and (2) the prevention of the over-dissipation of dynamic multiphase interfaces (or fluid jets and droplets). In terms of the former, for example, when multibody dynamics systems are involved, it is difficult to simulate such complicated coupling behaviors via mesh methods, although this could be realized by using the numerical technique known as the Overset Mesh. However, the flow information should be interpolated via the interfaces between the overset region and the background region, which could result in some discontinuities of the field quantities and could thus reduce the numerical accuracy and stability. Another drawback is that in those regions characterized by violent free-surface evolutions, e.g., wave breaking/slamming in the vicinity of OEDs (see Figure 20), mesh methods could provide inaccurate numerical results caused by their over-dissipation characteristic (i.e., mass non-conservation). Considering the aforementioned two deficiencies, it is in favor of using the meshfree method to remove the dilemma.
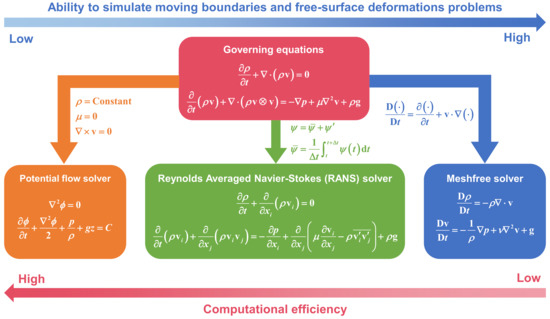
Figure 3.
A brief comparison of the most popular numerical methods for simulating OEDs. For more details regarding these governing equations, the readers can refer to the textbooks [60,61,62].
The meshfree method has been considerably investigated and developed during the past decades owing to their distinct superiorities compared with mesh methods, e.g., easy-to-model moving boundaries and capture free-surface fragmentation. Among them, the Smoothed Particle Hydrodynamics (SPH) method is one of the most promising truly meshfree methods. The SPH method was initially proposed for astronomy simulations in 1977 by Gingold and Monaghan [63] and Lucy [64]. Since the very early years of the 1990s, the SPH method began to be applied to violent free-surface evolutions due to its Lagrangian nature that is inherent to be suitable for such problems. Especially, after the pioneering work conducted by Monaghan in 1994 [65], the SPH method has witnessed its surprising advances in tackling coastal and ocean engineering problems, of course for OEDs simulations as well. Although extensive literature regarding simulating OEDs using the SPH method was published during the past decades, to the best knowledge of the authors, it still lacks an effort dedicated to providing a detailed review of this field. Note that although several reviews have been focused on the SPH applications towards coastal and ocean engineering (see, e.g., [66,67]), free-surface flows (see, e.g., [68,69,70,71,72]), multiphase flows (see e.g., [73]), FSI problems (see, e.g., [74,75,76,77]), and diverse industrial applications (see, e.g., [78,79,80,81,82,83]), these works paid little attention to OEDs, for which several hydrodynamic problems are quite different from traditional nearshore/offshore structures and thereby deserve energy engineers and SPH practitioners’ attention. Therefore, in contrast to the previous reviews, this study aimed at offering the state-of-the-art progress with regard to various advanced SPH techniques in the hydrodynamic predictions of OEDs towards industrial applications, and the attention of the present work is particularly focused on the following topics (see Figure 4 for more details)
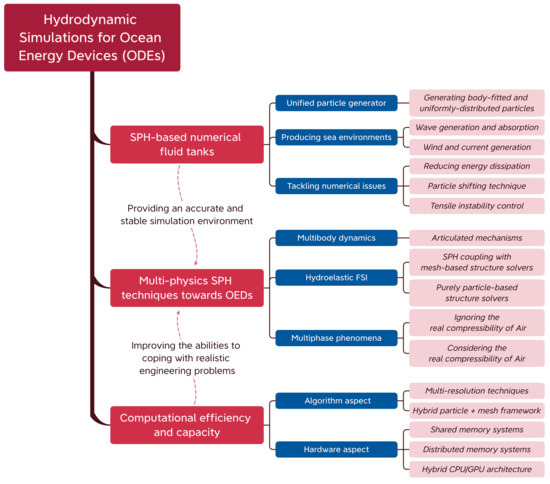
Figure 4.
The outline of the present article.
- 1.
- SPH-based numerical fluid tanks.
- 2.
- Multi-physics SPH techniques for simulating OEDs.
- 3.
- Computational efficiency and capacity.
The remainder of the article is organized as follows. In Section 2, the governing equations of the fluid and the fundamental concepts of the SPH method are briefly recalled. In Section 3, the latest development of SPH-based numerical fluid (including wind, wave, and current) tanks are reviewed. In addition to that, the attention of this section is also focused on how to accurately deal with the numerical issues including (1) disordered particle distribution, (2) tensile instability, and (3) the over-attenuation of wave propagation. Section 4, Section 5 and Section 6 are devoted to stating the up-to-date multi-physics SPH techniques towards simulating OEDs, including (1) the multibody dynamics with a mooring system, (2) hydroelastic FSIs, and (3) multiphase flows. Subsequently, in Section 7, how to improve computational efficiency and capacity via diverse techniques from the algorithm and hardware aspects are discussed, which are significant for simulating OEDs because such a type of SPH simulations is usually characterized by a huge computational domain and a substantial total particle number. Finally, conclusions and future prospects of the concerning topics are illustrated in the last part of the article.
2. A Brief Recall of the SPH Method for Simulating Hydrodynamic Problems Related to OEDs
In order to ensure the completeness of the article, in this section, we offer a brief recall with respect to the governing equations of the fluid and the fundamental concepts of the SPH method; for a comprehensive description of the methodology, the readers can refer to classical textbooks (see, e.g., [62,84]).
2.1. Governing Equations: Weakly Compressible and Truly Incompressible Hypotheses
2.1.1. Weakly Compressible Hypotheses
In the weakly compressible hypotheses, the pressure and density of the fluid can be decoupled via a stiff Equation of State (EoS). Therefore, the governing equations of the fluid can be written as the following Lagrangian formalism (see, e.g., [79,85]).
represents the Lagrangian/material derivative, and the subscript 0 denotes the reference value of the acted variable. , p, , and denote the density, pressure, kinematic viscosity, and velocity vector of the fluid, respectively. signifies gravitational acceleration. stands for the polytropic coefficient, which is usually adopted as and for water and air (see, e.g., [86,87]), respectively. signifies the reference density at rest. is a pseudo sound speed, which is normally adopted as 10 times higher than the anticipated maximum fluid velocity, , for the sake of reducing the density variation down to 1%, i.e., [85]. Note that if the value of is set to 1, the EoS can be simplified to . This simplification was firstly used by Morris et al. [88], showing more stability within the WCSPH framework.
One of the greatest superiorities of WCSPH is its fully explicit property in time, which means that the velocity, position, and density of fluid particles can be updated straightforwardly via
and
where denotes the position vector of the fluid and the time step. The superscript of n and denote the n-th and -th time steps, respectively. Finally, the pressure can be obtained by the EoS through the updated density. Practically, to ensure numerical stability, the predictor-corrector method or Roung–Kutta time integrations are often adopted (see more details in Section 2.3).
2.1.2. Truly Incompressible Hypotheses
Conversely, the governing equations for the truly incompressible fluid become
To enforce incompressibility and solve the Pressure Poisson Equation (PPE), the procedure proposed by Cummins and Rudman [89] has been generally adopted in the SPH community (see, e.g., [90,91,92,93]), which was inspired by Chorin’s projection method [94] with an adapted form. This method consists of two steps, i.e., the prediction and correction steps. The prediction step is to calculate the intermediate velocity, , based on the viscosity and gravity forces via
Subsequently, the correction step can be implemented based on the pressure force via
Finally, the intermediate velocity can be projected on the divergence-free space by writing the divergence of Equation (6), which yields the following PPE
where signifies the Laplacian operator. Once the pressure is obtained from PPE, the velocity and position at the -th step can be updated via
2.1.3. Weakly Compressible or Truly Incompressible: The Best Choice towards OEDs Simulations
Traditionally speaking, in the early years, SPH practitioners were in favor of using ISPH rather than WCSPH for coastal and ocean engineering simulations owing to its inherent noise-free characteristic. For example, in 2008, Lee et al. [91] carried out a detailed investigation on the differences between WCSPH and ISPH. It was concluded that ISPH can provide much smoother velocity and pressure fields than WCSPH in every case they implemented; these were also proved and supported by other researchers (see, e.g., [95,96]).
To reduce the spurious numerical noise of WCSPH, several measures have been proposed over the years. The related pioneering work can be traced back to Monaghan and Gingold [97], where an artificial viscosity term based on a Neumann–Richtmeyer viscosity was proposed to alleviate the oscillations induced by shock waves. The next breakthrough corresponds to Colagrossi and Landrini [86], where a Mean Least Square (MLS) integral interpretation was introduced to filter the oscillating density field. Although this scheme can provide good results, it cannot be applied to long-term simulations because the hydrostatic component of the fluid system is nonphysically filtered, leading to the non-conservation of total fluid volume [98,99]. Further, Molteni and Colagrossi [100] proposed to use a numerical diffusive term inside the continuity equation; this term can give good results but fails also to produce the hydrostatic solution. Consequently, the authors deactivated the diffusive term when the pressure is below the hydrostatic solution, which weakens the effectiveness of the diffusive term. Fortunately, this issue was successfully resolved by Antuono et al. [98] in 2010, resulting in the -SPH model that produces an excellent density/pressure solution in most cases; this work was further extended to violent free-surface flows by Marrone et al. [101] in 2011. There is no doubt that after being proposed, the -SPH model almost became the standard form for WCSPH; these works were also awarded with the Monaghan Prize in 2018 by SPH Research and Engineering International Community (SPHERIC)) for their outstanding contributions to the SPH community [102].
Although ISPH shows better performance in tackling incompressible flow problems, three issues pose some limitations in simulating OEDs. Firstly, ISPH must solve PPE that is implicit in time, which is not straightforward to code compared with WCSPH. Secondly, ISPH demands the explicit detection of the free-surface to impose the dynamic free-surface boundary condition that is implicitly fulfilled in WCSPH (see, e.g., [103]). Finally, the most striking one is that ISPH is hard to be applied to a large-scale simulation accelerated by the Graphics Processing Units (GPUs) parallelization, especially for the 3D simulations towards realistic industrial applications (see, e.g., [104]). The root is that the required memory of ISPH will be largely occupied by storing the exponentially increasing elements of the PPE matrix as the total particle number increased. In other words, the computational capacity of ISPH could be far smaller than WCSPH when the GPU parallelization is employed. Nonetheless, WCSPH is free from this issue because its required memory grows linearly as the increase in total particle number due to the fully explicit property in time. Therefore, only a few efforts have been dedicated to implementing ISPH on GPU (see, e.g., [104,105,106]).
It should be kept in mind that the simulations of OEDs usually involve the FSI process between water waves and complex structures (even an array of OEDs), which usually requires (1) a huge computational domain to prevent possible nonphysical reflected waves from borders and (2) sufficiently refined particle resolution to accurately capture the spatiotemporal free-surface evolutions, meaning that the total particle number could be substantial in such a type of SPH simulations. From this point of view, WCSPH is now more feasible than ISPH considering the balance between numerical accuracy and computational efficiency/capacity. This is why the present popular GPU-based open-source SPH solvers (e.g., DualSPHysics [107] and GPUSPH [108]) have adopted WCSPH rather than ISPH as their solver framework. Therefore, in the following discussions, attention is particularly focused on WCSPH; for classical literature regarding ISPH, the readers can refer to [89,90,92,93].
2.2. The Fundamental Concepts of SPH
2.2.1. Kernel and Particle Approximations
In the SPH method, the discrete governing equations can be constructed following two steps, i.e., the kernel approximation and particle approximation (see, e.g., [75,78]). The kernel approximation aims to evaluate field qualities and their spatial derivative (i.e., gradient and divergence) via the kernel function as
where and represent the generic scalar and vector functions, respectively. and stand for the targeted position and its neighboring points, respectively. signifies the kernel function to approximate the reciprocal contribution between two points of interest with h being the smoothing length. denotes the infinitesimal integral element. Note that owing to the compact support property of the kernel function, the integrals of Equations (9)–(11) vanish in those regions beyond the support domain denoted by .
Considering the kernel property of
Equations (13) and (14) are preferred by SPH practitioners since this formalism could somewhat reduce the kernel truncation on boundaries. In order to transform the kernel approximation into the particle approximation, the computational domain should be discretized into several particles that carry all field quantities of the flow region. Note that a lumped volume defined as is imposed to each particle at every time step with being the invariant particle mass of the i-th particle given at the initialization; this means that these particles do not have a fixed volume (or shape) and therefore could trigger the particle Lagrangian structures behaving as the particle clumping and clustering phenomenon during an SPH simulation; this will be further discussed in Section 3.3.1.
Subsequently, by summing up the overall neighboring particles within the support radius of the i-th particle, Equations (9), (13), and (14) can be rewritten from the continuous form to the discrete form as
respectively, where the subscripts i and j refer to the targeted particle and its neighboring particles, respectively. The subscript i in denotes that the acted variable is evaluated with respect to the i-th particle. is adopted hereafter for brevity.
2.2.2. Discrete Governing Equations: The WCSPH Model
According to Equations (15)–(17), system (1) can thereby be converted into the following popular WCSPH formalism
where and stand for the density diffusive term and the viscosity term, respectively. and denote the anticipated maximum velocity and pressure in the flow domain, respectively. As discussed in Section 2.1.3, the most popular density diffusive term is the -term given as [98]
where refers to the renomalized density gradient [109] that can recover the particle consistency in the vicinity of boundaries. For more details regarding the -term, the readers can refer to [98,101].
Regarding the viscosity term, as suggested by Monaghan and Gingold [97], when an inviscid fluid assumption is adopted, an artificial viscosity term should be employed to improve the robustness of an SPH simulation. On the contrary, when considering the physical viscosity (e.g., foil hydrodynamics), the artificial viscosity can be directly converted into the physical one because the former is equivalent to a Neumann–Richtmeyer viscosity [85,97]. can be written as
where with n being the dimension of the simulation. is given as
where is expected to prevent a zero denominator.
In addition to the -SPH model, another popular WCSPH model is the Riemann-SPH that employs a Riemann solver into the governing equations to stabilize the calculation and alleviate the nonphysical pressure noise. The governing equations of the Riemann-SPH model can be written as (see, e.g., [110])
where and are the solutions of an inter-particle Riemann problem along with the vector pointing from the i-th particle to the j-th particle (see, e.g., [111,112]). The Riemann-SPH solver can provide accurate pressure field comparable to the -SPH model; therefore, in the present SPH community, both the -SPH and Riemann-SPH have been widely employed to solve engineering problems [113,114]. Typical examples are DualSPHysics with -SPH [107], SPHinXsys [112] and Nextflow Software [115] with Riemann-SPH.
2.3. Time Integration
Regarding time integration, several schemes are available in the SPH literature such as the Verlet or Symplectic schemes (see, e.g., [107,112]), the 4th-order-Runge–Kutta (RK4) scheme (see, e.g., [99,116]), and the prediction-correction scheme (see, e.g., [117]). No matter which time-integration scheme is adopted, the time step, , should be determined by the Courant–Friedrich–Levy (CFL) condition as (see, e.g., [112,118,119,120]).
where denotes the kinematic viscosity of the fluid. Note that the value of CFL can be up to in RK4 because of its high-order accurate property, while in other second-order accurate schemes, this value has been usually adopted as to stabilize the simulation. For instance, in DualSPHysics the default value of CFL is 0.3 [107], and in SPHinXsys the default values of CFL are 0.25 and 0.6 for the advection criterion and the acoustic criterion [112], respectively, whereas in those simulations adopting RK4, the value of CFL has been usually adopted as 1.0∼1.25 (see, e.g., [118,119]). From this point of view, although RK4 requires more sub-steps for each time step, its computational costs would not increase apparently due to the larger value of CFL.
2.4. Boundary Conditions
2.4.1. Free-Surface Boundary Condition
In the context of OEDs simulations using WCSPH, the most important two boundary conditions are the (1) free-surface boundary and (2) wall boundary for most cases. In terms of the free-surface boundary, it can be further categorized into the Kinematic and Dynamic Free-surface Boundary Condition, i.e., KFSBC and DFSBC, respectively. Because the SPH method is a purely Lagrangian numerical scheme, KFSBC is naturally satisfied without any extra requirements. Furthermore, it has been demonstrated by Colagrossi et al. [103] that in the WCSPH scenario, DFSBC can also be implicitly satisfied because and in the free-surface. However, the authors have also pointed out that the formalism of SPH operators imposes significant effects on the convergence properties for simulating free-surface problems (for more details, the readers can refer to [103]). Therefore, only the wall boundary should be taken into account by SPH practitioners in WCSPH simulations.
2.4.2. Wall Boundary Condition
Generally speaking, in the SPH framework, the wall boundary condition can be enforced by two methods. One way is to distribute particles on wall surfaces to complete the kernel support near the boundary, which is the most popular method in the present SPH community. For example, the technique named Fixed Ghost Particle proposed by Adami et al. [121] was adopted in SPHinXsys or Dynamic Boundary Condition by Crespo et al. [122,123] in DualSPHysics. Another method is based on the normal-flux method that discretizes physical walls into several segments, i.e., line elements in 2D and triangle elements in 3D; this method was adopted by several commercial SPH packages, such as Nextflow Software [115] and Dive Solution [124]. It should be highlighted here that which method is the best choice for simulating OEDs is still an open topic for the SPH community because both of the two methods have their superiorities. In terms of the normal-flux method, it could save a significant amount of time in the pre-process stage because the only required file is just geometry data (e.g., STL-format file); this method facilitates accurately modeling arbitrarily complex 3D structures as proved by Chiron et al. [125]. On the contrary, the particle-based wall boundary is strongly limited by the particle generation because it is hard to obtain high-quality particles needed by SPH simulations, whereas it facilitates the generality and extendibility of SPH codes because the solver can be developed in a unified Lagrangian particle framework. Besides, a particle-based wall boundary can be implemented without any extra requirements to tackle the fluid–structure interfaces, improving the numerical accuracy and stability for SPH simulations.
There is no doubt that compared with generating high-quality particles on body surfaces, creating grids for complex 3D structures is more easy-to-realize because there have been substantial open-source (e.g., OpenFoam [126] and TetGen [127]) and commercial (e.g., Altair Hypermesh and ANSYS ICEM) packages that can cope well with this. Therefore, in this subsection, attention is particularly focused on several feasible methods to generate body-fitted and uniformly distributed particles, which is the most important pre-process technique for simulating OEDs when a unified particle framework is considered.
It is evident that creating body-fitted and uniformly distributed particles on body surfaces is not trivial for SPH practitioners. The pioneering work for proposing a generic-purpose particle-generating technique can be traced back to Colagrossi et al. [128], where the Particle-Packing Algorithm (PPA) was elaborated. As demonstrated by the authors, PPA can be embedded without difficulty into whatever WCSPH or ISPH codes since the algorithm is proposed directly based on some intrinsic features of the SPH method (see [128] for more details). Nevertheless, to the best knowledge of the authors, there has been no user-friendly open-source particle generator developed based on PPA. Another accessible particle-generating technique is the CAD-BPG that has been proposed by Zhu et al. [129] in 2021. In this technique, to achieve body-fitted and uniformly distributed particles on wall surfaces, a physics-driven relaxation process governed by a transport-velocity is employed to characterize the particle evolutions; this procedure is now integrated on the latest version of SPHinXsys [112], showing excellent ability and user-friendly properties for creating body-fitted particles for arbitrarily complex 3D structures. Figure 5 displays the general procedure for creating body-fitted particles for a semi-submersible FWT using the CAD-BPG solvers, while in Figure 6 several zoom-in views of the output FWT’s particles are illustrated to demonstrate the high-quality particle distribution provided by the particle generator. One can see that the solver is easy to use, and the resulting particles show a quite homogeneous characteristic that facilitates the numerical accuracy and stability of SPH simulations. Of course, the solver can also be applied to arbitrarily complex 2D structures; a typical example for a 2D hydrofoil is shown in Figure 7. Note that for generating 2D particles, instead of using a 3D STL file, the required file is a dat file containing the coordinate information of the border of the targeted 2D body (for more details, the readers can refer to the tutorial documents of SPHinXsys).
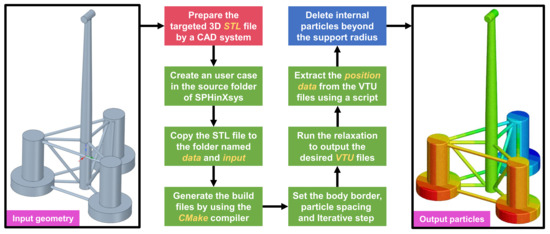
Figure 5.
The pipeline of CAD-BPG: an example for generating the body-fitted and uniformly distributed particles of a semi-submersible FWT.
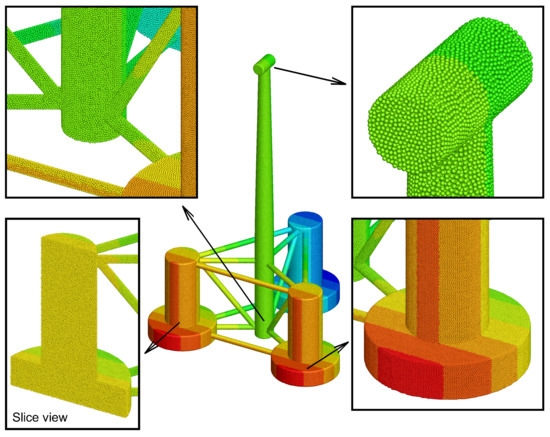
Figure 6.
The zoom-in view of the FWT’s particles. The color represents the x-axis position.
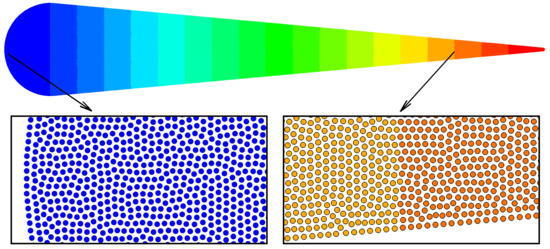
Figure 7.
The body-fitted and uniformly distributed 2D particles generated by the CAD-BPG solver: an example of a 2D hydrofoil. The color represents the x-axis position.
Of course, to simulate OEDs, other boundary conditions such as the wavemaker boundary for generating water waves and the inlet/outlet boundary for generating winds and currents are also very important, which will be further discussed in Section 3.
3. Numerical Fluid Tank Based on SPH for Simulating Hydrodynamic Problems Related to OEDs
In the context of coastal and ocean engineering, establishing accurate and robust numerical fluid tanks (NFTs) to generate targeted waves, currents, and winds is the most significant prerequisite for FSIs simulations. As discussed in Section 1, traditional Eulerian mesh-based NFTs, e.g., Finite Volume (FV) and Finite Difference (FD), are mature algorithmically, and this type of NFTs can be efficiently established by either using commercial packages (e.g., Siemens STAR-CCM+ and ANSYS Fluent) or open-source codes (e.g., OpenFoam [126]). Notwithstanding, because of their inherent Eulerian nature, mesh-based NFTs usually suffer from some unwanted numerical issues, e.g., the non-conservation of total fluid mass and the over-dissipation of multiphase interfaces. For example, the air–water interfaces are prone to be violently blurred when the mesh resolution of the multiphase interfaces is insufficient, although this could be partly prevented by implementing the Adaptive Mesh Refinement (AMR) technique that refines the mesh resolution in the proximity of multiphase interfaces and consequently provides better sharpness of the phase borders. Nonetheless, as a truly meshless method, SPH is totally free from the aforementioned issues thanks to its Lagrangian characteristic. In fact, Christian et al. [130] have already provided a comprehensive review regarding the high-fidelity numerical wave tanks (NWTs) towards WECs mainly focusing attention on various mesh methods. Differing from that work, in this section, attention is particularly concentrated on how to accurately generate not only water waves but also winds and currents by using the SPH method. Furthermore, several feasible and effective strategies to remove some numerical issues are elaborated, including the over-dissipation of wave energy, anisotropic particle distribution, and tensile instability.
3.1. Wave Tank
3.1.1. Wave Generation
In terms of OEDs, especially for WECs and FWTs, wave excitations are the most critical environmental loads during working. Therefore, an accurate and robust NWT is the base of any numerical method aiming at coastal and ocean engineering purposes. Generally speaking, as outlined by Higuera et al. [131], the numerical wave-generation methods can be categorized into three types, i.e., an internal method, a static-boundary method, and a moving boundary method.
The internal method is also known as the internal wavemaker, which was proposed to add an artificial source term into the continuity/momentum equations to mimic a wavemaker. The superiority of the internal method is avoiding undesired wave reflections from the wave-making boundary [132], whereas it could lead to extra computational costs because of the need of extending the flow domain [67]. For the typical examples of this method using SPH simulations, the readers can refer to [132,133].
In terms of the static boundary, its main idea is to straightforwardly implement Dirichlet conditions for the wave-generation boundary. In this method, the wave-making boundary is handled by different analytical wave theories, giving the anticipated velocity and free-surface elevations to produce the targeted incoming waves [131]. It is evident that this method is naturally suitable for Eulerian mesh-based solvers, whereas in the Lagrangian meshfree framework it is hard to be implemented because the particle position evolves according to the governing equations as time integration. Therefore, scarce attempts have been devoted to this method within the SPH framework, although it is widely applied in mesh-based solvers such as the PF and RANS models.
As can be seen, the aforementioned methods are purely based on a numerical aspect to generate water waves, while the final approach, i.e., the moving boundary method, directly produces water waves via a realistic boundary motion just as the actual wavemaker machines in laboratory experiments. This method, indeed, has been not so common for Eulerian mesh-based solvers since it requires large mesh deformation, which is one of the striking weaknesses of Eulerian methods. However, in meshless approaches such as the SPH method, the implementation of the moving boundary is straightforward without any extra requirements [134]. Therefore, this method is strongly recommended in the SPH simulation of the wave–structure interactions for OEDs; this method has also been adopted by several open-source SPH solvers such as DualSPHysics [107,134] and SPHinXsys [112,135]. Note that for the sake of brevity, in the following discussion, the term of wavemaker especially denotes the moving-boundary method.
The earliest work to use the wavemaker for generating water waves within the SPH framework could be traced back to Monaghan in 1994 [65], where a piston-type wave paddle was employed to produce several water waves. After that, various numerical techniques for producing different types of water waves were investigated, e.g., piston-type [134] and plunger-type [136,137]. For example, Altomare et al. [134] conducted a comprehensive investigation on regular and irregular water-waves generation using a piston-type wavemaker. Sun et al. [138] produced the focusing waves (or freak waves) also using a piston-type wavemaker to study the wave–structure interactions. He et al. [136] realized the solitary-waves generation by employing a plunger-type wavemaker. For a brief summary, the moving-boundary method is now mature for generating various types of water waves, ranging from regular to irregular waves and from linear to nonlinear waves. Therefore, it is recommended for simulating OEDs on account of its higher applicability and versatility compared with other wave-making methods.
3.1.2. Wave Absorption
The wave absorption also plays an important role in NWTs because NWTs are always constructed with limited overall length and width to reduce computational costs, which could trigger wave reflections from the wall boundaries or wave paddles and thereby could largely reduce the quality of the generated water waves. Hence, numerical techniques are needed to tackle the wave reflections.
Traditionally, passive absorbers are the most common techniques for wave absorption, which can be implemented by two methods. One consists of placing a sloping bottom or porous structures in front of the boundaries of interest where large wave reflections could exist; this method is similar to those used in physical tests. However, this type of absorption system is usually very sensitive to specific wave parameters, lacking versatility for different types of water waves. Another method is more simple but effective, i.e., implementing a damping zone into the computational domain. In this damping region, the particle kinetic energy can be dissipated rapidly by different mechanisms, e.g., improving viscosity or reducing velocity. For instance, in the SPH simulations conducted by Sun et al. [138], a viscosity damping zone in front of the end boundary of the tank was built by increasing the artificial viscosity coefficient of the zone. Another example is that Lind et al. [92] employed a velocity damping zone to dissipate the wave energy at the end of a wave tank by an exponentially decaying scheme.
Although passive absorbers show remarkable convenience and performance in practical applications due to their simplicity, it could be not enough when a long-term SPH simulation of wave–structure interactions is performed. The main reason is that in such a simulation, the water waves could be reflected towards the wave paddle and thereby contaminate the SPH results. Consequently, another method, i.e., active absorbers was proposed to tackle this issue. There are various techniques available for this method depending on the feedback of specific field quantities, for example, the free-surface elevations in front of the wavemaker or the force acting on the wavemaker. One typical attempt corresponds to DualSPHysics [107], where the active absorbers have been implemented by using the free-surface evolutions at the wavemaker position as the feedback [134].
On the whole, when a short-term SPH simulation involving water waves is performed, both the passive and active absorbers can be employed. On the contrary, it is in favor of implementing active absorbers to achieve the best quality of wave generation [134].
3.1.3. Wave Energy Attenuation
When an NWT is established by traditional SPH models, it could undergo some numerical issues that strongly limit the applicability of the SPH method. One of the most striking issues is the over-attenuation of wave energy. The wave energy attenuation, behaving as the wave height decaying rapidly within a few wavelengths for progressive waves, has been a serious numerical issue that has to be faced by SPH practitioners when the SPH method is carried out for long-distance wave-propagation problems. The mechanism of such a phenomenon was investigated comprehensively by Colagrossi et al. [139] in 2013, where it was demonstrated that traditional WCSPH possesses the ability to accurately predict the attenuation process of viscous standing waves. However, to realize that it requires the number of neighbors per particle is sufficiently large, and this number should be gradually increased to achieve convergence towards theoretical solutions. In addition, it was also suggested that a higher number of neighbors is required for a larger Reynolds number. Notwithstanding, in practical applications, the number of neighbors per particle cannot be increased as desired because of the unbearable boosting computational costs.
Fortunately, this issue has been successfully resolved by Zago et al. [140] in 2021. In that work, an improved Kernel Gradient Correction (KGC) was imposed to the momentum equation to handle the dissipation issue. Compared with those traditional schemes (see, e.g., [109,141,142,143]), the improved KGC overcomes the non-reciprocity of inter-particle interactions by a symmetrized correction that guarantees the momentum conservation. As demonstrated by Zago et al. [140], the improved KGC shows excellent performance to prevent the wave attenuation with bearable computational costs. This work is a breakthrough corresponding to the industrial SPH applications towards realistic coastal and ocean engineering because it significantly makes the long-term and long-distance water waves simulations realizable.
3.2. Current and Wind Tunnels
In addition to the wave-generation and absorption techniques discussed above, it is also significant to build accurate and robust current and wind tunnels within the SPH framework to simulate the hydrodynamic performance of TCTs and FWTs, for which the working turbines are always fully immersed in the air (i.e., FWTs) or water (i.e., TCTs), respectively. However, because the SPH method is a purely Lagrangian meshless method, it is not trivial to model the inlet/outlet boundary conditions that are very straightforward to be implemented in mesh-based solvers. The main reason is that it is imperative to maintain the flow consistency by avoiding that all the fluid particles move out of the flow domain during simulations. To this end, various inlet/outlet boundary techniques have been proposed during the past two decades. The pioneering work related to the velocity inlet/outlet boundary conditions was conducted by Lastiwka et al. [144] and was further extended by other SPH practitioners (see, e.g., [145,146,147]). Generally, the fundamental principles of these approaches share the same characteristics with some special modifications depending on specific problems.
In order to clearly state the generic mechanism of the inlet/outlet boundary conditions, herein one of the most popular versions presented by Federico et al. [145] is illustrated. Figure 8 shows the bird view of a typical current/wind tunnel. One can see that the flow domain is divided into three parts prior to the simulation. At the inlet domain, the anticipated field quantities such as velocity and pressure are compulsorily assigned to the inlet particles. During time integration, these particles update their physical positions according to the time integration of velocity and do not participate in the SPH calculation. When the inlet particles are beyond the limit of the inlet domain (i.e., Border 1), they immediately become common SPH particles and then participate in the SPH calculation at the following time steps. Conversely, when the SPH particles run out of the limit of the SPH domain (i.e., Border 2), they will be immediately converted into the outlet particles and thereby free again from the SPH calculation. Finally, when a particle runs out of the outlet domain, it will be removed from the computational domain and then supplied into the candidate particle set that will be reused for creating inlet particles.
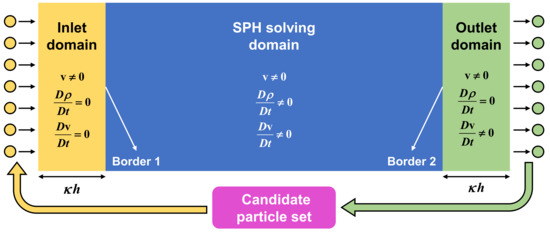
Figure 8.
The schematic diagram of inlet/outlet boundary conditions implemented in particle-based methods (e.g., SPH).
3.3. Numerical Issues Existing in NFTs
The same as other CFD tools, the SPH method has also been bothered by several numerical issues that could strongly limit its versatile applicability for different engineering problems. Among them, the most serious issues are the anisotropic particle distribution and tensile instability. The former could significantly reduce the particle consistency and thus the accuracy and stability of SPH simulations (see, e.g., [78]), while the latter could lead to numerical voids in those fluid domains characterized by strong negative pressures. In fact, these two numerical issues are inherent deficiencies regarding the SPH method. This section aims at providing the latest advanced SPH techniques to cope with them; these techniques are imperative to build an accurate, robust, and versatile NFT for simulating OEDs.
3.3.1. Disordered Particle Distribution: Using Particle-Shifting Techniques
As a purely Lagrangian meshless method, traditional SPH models undergo the particle Lagrangian structures [148] that are characterized by serious particle clustering and clumping. The root of the Lagrangian particle structures can be attributed to the fact that the volume of each particle is simply obtained via the relation of during the time integration, providing no information regarding their volume shapes. As a consequence, whatever the initial distribution of particles, their volume shapes could be strongly stretched or compressed during flow evolutions since each particle must move along with the streamline they belong to; this results in the anisotropic deformations of the volumes macroscopically behaving as the strongly disordered particle pattern (see Figure 9a–c). As pointed out by Liu et al. [78], the regularity of a particle distribution significantly affects the order of particle consistency and thus the numerical accuracy and stability (see also the discussions provided by Antuono et al. [149]). Fortunately, this issue has been successfully resolved by the numerical technique known as the Particle-Shifting Techniques (PSTs) [92,150], which compulsorily shifts fluid particles from their streamlines to a new position according to some principles and thereby offers a homogeneous particle pattern as desired (see Figure 9d). Regarding the shifting principles, the most popular version is to reposition fluid particles from high-concentration regions to low-concentration regions on the basis of Fick’s diffusion law, which therefore forms the Fickian-based PST, which was firstly proposed by Lind et al. in 2012 [92]. The main idea of Lind’s PST can be mathematically written as
where is a diffusion coefficient that determines the magnitude of the shifting, which should satisfy several stability conditions as pointed out by Lind et al. [92]. Note that as reported by Sun et al. [118], in the WCSPH framework, the value of should be determined with a weakly compressible consideration. represents the particle concentration and usually comes from the sum of the kernel function, i.e.
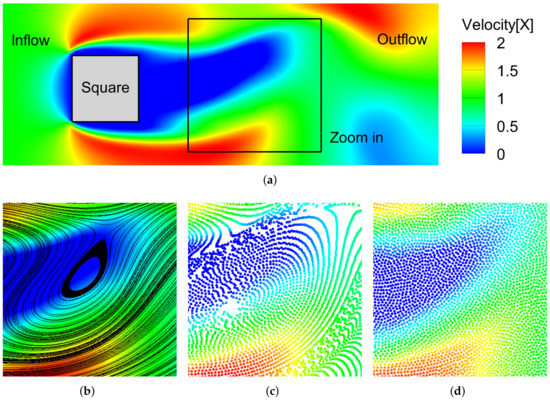
Figure 9.
A uniform incoming flow crossing a square. The numerical results of panel (a,b) are obtained using an FV solver, while that of panel (c,d) are simulated via an SPH solver without and with PST, respectively. (a) FV result of the velocity field in the x-axis direction (Unit: m/s). (b) Streamlines via an FV solver. (c) SPH result without PST. (d) SPH result with PST.
After this pioneering work, PST has been further developed by the SPH community and applied to diverse problems, forming various PST variants in both the weakly compressible and truly incompressible senses (see e.g., [93,118,148,151,152,153,154,155,156,157,158,159]). It is undeniable that PSTs can offer uniform particle distribution (i.e., better quality of particle distribution—see also Figure 10) and thus improve the numerical accuracy and stability of SPH simulations. Notwithstanding, it should be underlined that although the original version of PST and its variants show remarkable ability to cope with several challenging problems, their physical rationality could pose some limitations when being applied to realistic engineering problems. For instance, as reported by the extensive SPH literature (see, e.g., [155,157,158,160]), several versions of PST (see, e.g., [118,156]) could trigger the volume-non-conservation issue in simulating violent free-surface flows with long-term duration. This is caused by the fact that in these PST variants, after being repositioned, the particle positions are still updated according to an unchanged velocity field (i.e., non-Lagrangian transport velocity), which is nonphysical from a rigorous point of view. As a consequence, the accumulating errors on the potential energy gradually lead to the over-expansion (or over-compression when being subjected to negative pressures) of total fluid volume during simulations.
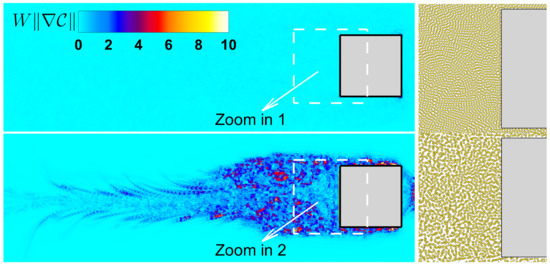
Figure 10.
The quality of particle distribution with (top panel) and without (bottom panel) PST. is closer to zero when the particle distribution is more uniform. For more details regarding the simulation configurations, the readers can refer to [119].
Therefore, the SPH community have been struggling for making PST more physical in different ways, such as integrating the shifting velocity, , into the governing equations (see, e.g., [155,158]) and using a fully Arbitrary-Lagrangian-Eulerian (ALE) framework (see, e.g., [148,161]); these variants strongly improve the rationality and interpretability of PSTs through rigorous mathematical considerations, although they require modifying the existing codes to a large extent because of the more complex formalism of the governing equations. In addition to that, there have been simpler measures such as locally deactivating shifting when the fluid suffers from the volume-non-conservation issue [157] or introducing a corrective cohesion force to adaptively compensate the over-expansion/compression [160]. On the whole, as a simple and powerful SPH technique, PSTs should be taken into account for simulating OEDs to improve the accuracy and stability of the simulation. Notwithstanding, which version of PSTs is the best choice for the concerning topic remains an open topic that needs to be further investigated in the future.
It should be underlined here that in addition to adopting PST, another effective measure to improve the numerical accuracy and robustness of SPH simulations is to implement high-order corrected scheme (see, e.g., [109,141,142,143,162,163]), which is a conventional method in the SPH community and can apparently recover the particle consistency in the case with anisotropic particle pattern (even kernel truncation) [78]. For more discussions corresponding to this topic, the readers can refer to [78,82].
3.3.2. SPH Techniques to Prevent Tensile Instability
It is well known that when a body is subjected to current or wind excitations, the flow field past the body could be characterized by negative pressures induced by the continuous vortex shedding from the edge of the body. A typical example is flows passing a hydrofoil, which is very common when simulating the hydrodynamic performance of the blades installed on FWTs and TCTs. In this circumstance, vortex structures would be continuously discharged from the leading edge of the hydrofoil. This phenomenon can be excellently simulated using mesh methods that are inherently suitable for coping with such problems. However, in the context of SPH, the Tensile Instability (TI) is one of the most critical numerical issues that could destroy the SPH simulation in total when negative pressures are involved. Macroscopically, when TI occurs, the SPH particles could clump/cluster together and thereby trigger spurious flow voids in the flow field. On the contrary, from the microscopical point of view, as pointed out very recently by Lyu et al. [119], the occurrence of TI is indeed caused by the errors of the particle approximation of the kernel gradient. In other words, TI is an inherent deficiency of SPH, and it cannot be removed even by refining particle resolution (see [119] for more details). Therefore, special techniques are needed to tackle the issue. At present, the most effective method to deal with TI is the technique named Tensile Instability Control (TIC) proposed by Sun et al. in 2018 [164]. The principle of TIC can be expressed as
where denotes the free-surface particles. The subscripts i and j refer to the targeted particle and its neighboring particle within the support radius, respectively. As demonstrated by Sun et al. [164], the incorporation with TIC can cope with several challenging problems (see, e.g., Figure 11) that are almost impossible to be successfully simulated using traditional SPH models (see, e.g., [164,165]).
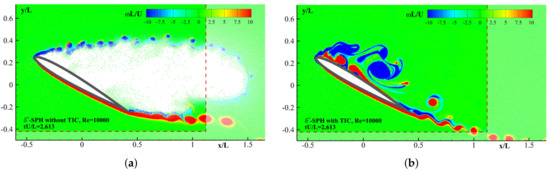
Figure 11.
Direct SPH simulation of viscous flow around a foil at Re = 10,000 without (a) and with (b) TIC. The flow void is induced when TIC is not used. For more details regarding the simulation configurations, the readers can refer to [164].
It is worth noting that in addition to TIC, another effective measure is to add a background pressure (BP) for the whole computational domain; this measure is very popular in the early years because of its easy-to-realize and effective properties. Nevertheless, this measure cannot be directly implemented to those problems where a free-surface exists since in the WCSPH context DFSBC is implicitly fulfilled [103]. In fact, several SPH practitioners have attempted to extend the BP technique to free-surface problems (see, e.g., [166]), whereas it has been proved that TIC possesses better accuracy and stability than the BP technique, at least for the hydrodynamic loads acting on body surfaces [119]. In the context of simulating OEDs, the phenomena involving negative pressures are very common (e.g., vortex shedding for hydrofoils and VIV and VIM problems), and therefore TIC should be employed to prevent the numerical fluid voids that drastically reduce the accuracy and stability of SPH simulations.
4. Multibody Coupling and Mooring Hydrodynamics
Because most of OEDs exploit ocean energy via transmitting mechanical energy into PTO systems, joints/sliders (hereafter referred to as Mechanical Constraint Structures, MCSs) are very common and important in such a process for energy transmission. MCSs can provide kinematic constraints between several objects, allowing that the transmission system of OEDs can more flexibly transmit the mechanical energy of fluids into electricity. For instance, Figure 12a shows the famous attenuator-type WEC named Pelamis [47,167], which consists of four tubular sections connected by three hinged modules that can move relatively to each other. Figure 12b displays another attenuator-type WEC called WaveStar [168], which absorbs wave energy through several partially submerged buoys installed on either longitudinal side of the device. In addition, various OEDs such as FWTs always consist of a main-body module and a mooring system to stabilize the device motion just as those conventional vessels and platforms. Figure 13 illustrates different mooring systems of several types of FWTs, from left to right being the TLP type, the Spar type, and the semi-submersible type, respectively. From the above-shown figures, it is clear that the multibody coupling and mooring dynamics are very important for evaluating the power-generation ability of OEDs. In the early years, although extensive efforts have been devoted to investigating different types of OEDs such as position-fixed WECs (see, e.g., [169,170]) or moving/floating WECs (see, e.g., [171,172,173]), these investigations were conducted without the multibody and mooring dynamics considerations. The SPH community has been pursuing feasible and user-friendly solutions to cope with such complex problems.

Figure 12.
Typical articulated systems installed on different WECs. (a) Pelamis WEC [47]. (b) WaveStar WEC [168].
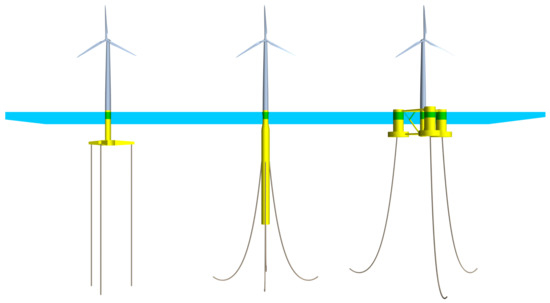
Figure 13.
Typical mooring systems installed on different FWTs with TLP type (left), Spar type (middle), and semi-submersible type (right).
Historically, several popular commercial solvers based on the BE approach such as ANSYS AQWA and DNV SESAM have already provided corresponding modules (including both MCSs and mooring solvers) to tackle such problems. Nevertheless, as discussed in Section 1, these packages are incapable of capturing the nonlinearity behaviors of free-surface evolutions and are hard to be integrated into the SPH solver due to their closed-source property (for more details regarding the BE applications in simulating OEDs, the readers can refer to [174]). On the other hand, extensive efforts have been devoted to coupling FSI solvers with mooring dynamics solvers through different strategies. For instance, the open-source solver MoorDyn has been coupled with the WEC-Sim package (an open-source BE solver based on Matlab) as its mooring module [175]. Another typical example is the OpenFoam solver, which has been further developed by several researchers by integrating in-house mooring modules for the simulations of several traditional ocean engineering structures (see, e.g., [176,177,178,179]), and OEDs such as FWTs as well (see, e.g., [180,181]). However, to the best knowledge of the authors, these existing open-source solvers still lack the ability to cope with an arbitrary number of jointed objects.
At present, the SPH community has been also struggling for developing an “FSI + MCSs + Mooring” coupling solver through different strategies, among which two breakthroughs, as shown in Table 1, have been achieved by DualSPHysics developers and SPHinXsys developers via “DualSPHysics + Project Chrono + MoorDyn” and “SPHinXsys + Simbody” strategies, respectively. Considering their easy accessibility, user-friendly pipeline, good balance between accuracy and efficiency, and more importantly, high feasibility towards simulating OEDs, in this section only these two combinations are involved.

Table 1.
A comparison of the coupling strategies adopted by DualSPHysics and SPHinXsys.
4.1. DualSPHysics’ Solution: Incorporating with Project Chrono and MoorDyn
DualSPHysics is an open-source package devoted to solving the Navier–Stokes equation based on WCSPH, which was initially released in 2011 with the purpose of coping with coastal engineering problems [107]. Thanks to its accuracy and robustness characteristics, DualSPHysics has been significantly improved towards more complicated multi-physics problems by the SPH practitioners and its developers during the past decade (for more details regarding the latest developments of DualSPHysics, the readers can refer to [120]). As pointed out by its developers, the successful coupling with other solvers has been a milestone in the development of DualSPHysics [120]. Among them, the combination of “DualSPHysics + Project Chrono + MoorDyn” is the most significant achievement, which makes DualSPHysics the most powerful toolkit at present for simulating OEDs with articulated and moored structures.
Project Chrono is an open-source multi-physics platform with excellent abilities to simulate collisions and mechanical restrictions such as sliders, springs, and hinges. One of the most striking superiorities of Project Chrono is that this solver can be coupled with DualSPHysics within a unified meshfree framework to cope with complex articulated systems. The flow chart of the coupling process between DualSPHysics and Project Chrono is illustrated in Figure 14. Regarding the mooring dynamics, in fact, several efforts have been dedicated to this topic within the DualSPHysics framework. For instance, inspired by the quasi-static approach proposed by Faltinsen [60], in 2016, Barreiro et al. [185] modeled the mooring system via continuous ropes and wires described by the catenary function. This method was also adopted to simulate floating OWCs moored to the seabed by Crespo et al. in 2017 [186]. However, in that model, only the tension of the mooring lines can be properly solved with the hydrodynamics and the inertial and axial elasticity of the mooring lines being neglected. Fortunately, in 2019, the MoorDyn solver has been successfully coupled with DualSPHysics by Domínguez et al. [187], significantly improving the abilities of DualSPHysics towards simulating moored structures. Since then, this strategy has been widely applied to various mooring systems such as floating breakwaters and WECs (see, e.g., [188,189]). The flow chart of the coupling process between DualSPHysics and MoorDyn is illustrated in Figure 15.
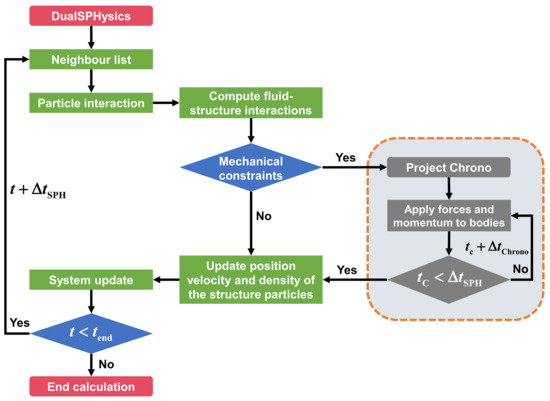
Figure 14.
The flow chart of the coupling process between DualSPHysics and Project Chrono (adapted from [120]).
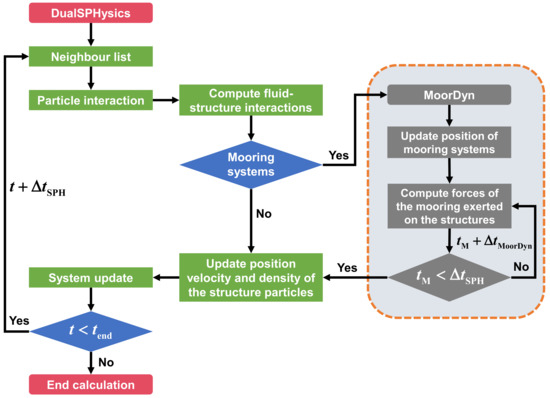
Figure 15.
The flow chart of the coupling process between DualSPHysics and MoorDyn (adapted from [120]).
Typical simulation results of DualSPHysics’ multi-solvers coupling strategy are illustrated in Figure 16. In Figure 16a, the snapshot of a working Pelamis WEC solved by “DualSPHysics + Project Chrono” strategy is shown. The PTO system of Pelamis consists of several hinged cylinders connected to each other, which involves complex relative motion of different parts during working and thus needs a multibody dynamics solver to cope with. In Figure 16b, a mooring semi-submersible FWT under regular wave excitations is displayed, which is simulated through a “DualSPHysics + MoorDyn” strategy. Of course, DualSPHysics can also be employed to investigate other types of OEDs such as point absorbers (see, e.g., [190,191,192]) and OWSCs (see, e.g., [193]). From these discussions, it is clear that the latest version of DualSPHysics (i.e., v5.0) has become a reliable and powerful toolkit for simulating OEDs. It is worth noting that because DualSPHysics is an open-source platform, it can be efficiently coupled with other solvers. For instance, Cui et al. [194] have successfully coupled DualSPHysics with another open-source mooring solver Mooring Analysis Program (MAP++) provided by the National Renewable Energy Laboratory (NREL). This coupling solver has been applied to investigate the hydrodynamic performance of a new-type breakwater, and good numerical results were obtained compared with experimental data.
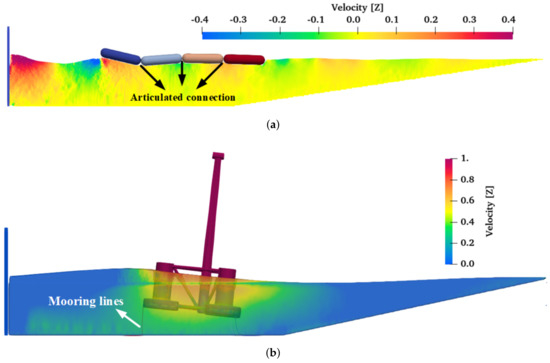
Figure 16.
Typical simulation results of the coupling strategy of DualSPHysics [120]. (a) Pelamis by “DualSPHysics + Project Chrono.” (b) Semi-submersible FWT by “DualSPHysics + MoorDyn.”
4.2. SPHinXsys’ Solution: Incorporating with Simbody
In addition to DualSPHysics, another alternative SPH toolkit to simulate OEDs is SPHinXsys coupling with Simbody. Differing from DualSPHysics that aims at simulating coastal engineering problems, SPHinXsys has been initially developed for the sake of providing a generic C++ Application Programming Interface (API) with high flexibility for domain-specific problems, including fluid dynamics [135], solid mechanics [195], electromechanics, thermodynamics, and reaction–diffusion flows [112]. SPHinXsys is also capable of simulating multibody dynamics problems via incorporating with Simbody. Simbody, firstly released by Stanford University, is an open-source multibody mechanics library towards mechanical, neuromuscular, prosthetic, and biomolecular simulations, which has been intended as a free-access package that can be employed to incorporate robust, high-efficiency multibody dynamics into a broad range of domain-specific end-user applications [184]. Figure 17 displays the snapshot of a seabed-mounted bottom-hinged OWSC subjected to regular wave excitations, which has been recently investigated and reported by Zhang et al. [135] using the “SPHinXsys + Simbody” strategy. Despite this, a mooring-dynamics module has not been officially provided by the solver’s developers, while this can be efficiently realized by users, just as what was done by DualSPHysics’ developers, through incorporating with any open-source mooring dynamics solvers such as MoorDyn and MAP++.
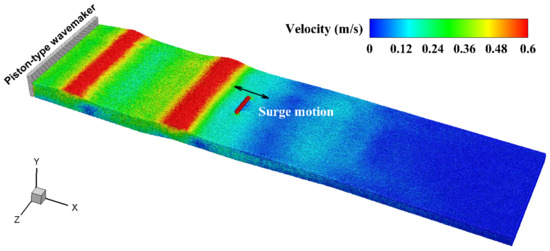
Figure 17.
The snapshot of a working OWSC solved by the “SPHinXsys + Simbody” strategy. Note that this snapshot is adapted from [135] with its author’s kind permission.
It is worth noting that owing to the merits of the Object Oriented Programming (OOP) property, the aforementioned open-source solvers (i.e., Project Chrono, Simbody, and MoorDyn) can be coupled easily with either other open-source SPH solvers or SPH practitioners’ in-house solvers. For example, Wei et al. [196] have successfully coupled the open-source SPH solver GPUSPH with Project Chrono to simulate the hydrodynamic performance of an OWSC. Nevertheless, the strategies provided by DualSPHysics’ and SPHinXsys’ developers are still strongly recommended because of their freely accessible properties; at least, these two solutions are now the most user-friendly resolutions to cope with such problems for those engineers who want to be an SPH user rather than an SPH developer.
5. Hydroelastic Effects in Hydrodynamic Problems Related to OEDs
5.1. The Origin of the Flexibility of OEDs
As for those small-scale OEDs, the hydroelasticity is negligible, whereas it plays an important role when considering the FSI process for a large-scale structure such as IEHSs that has become more and more popular in recent years (see, e.g., [5]). The typical characteristic length of IEHSs could be up to a few hundred meters, or even kilometers, while conventional platforms are usually below ~150 m. In this circumstance, the flexibility of the system cannot be neglected. Generally speaking, the flexibility of IEHSs appears in two forms: (1) the flexibility of the connector components between different system modules (see, e.g., [27] and Figure 18b) and (2) elastic deformations of the whole system (see, e.g., [27] and Figure 18c). In terms of the former, more precisely speaking, when an IEHS is linked by flexible connectors, the whole system cannot be regarded as a rigid body just as a traditional vessel/platform (see Figure 18a) because there are relative motions between different parts of the system (see Figure 18b). In fact, such a type of flexibility is always referred to as multibody dynamics, for which the readers can refer to Section 4 for more details; this section will focus on another type of flexibility, i.e., hydroelasticity (see Figure 18c).
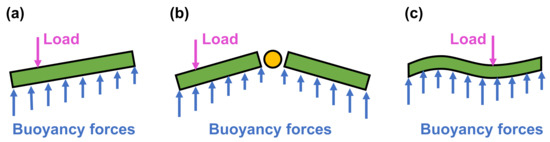
Figure 18.
Typical structure responses of ocean engineering structures with rigid body (a), connected body (b), and flexible body (c) (adapted from [6]). Panels (b,c) represent the flexible deformations caused by the connectors and the structures themselves, respectively.
Hydroelasticity, one of the most challenging topics in ocean engineering, has attracted long-lasting attention from both the scientific and industrial communities. In fact, in the early years, little attention was paid to hydroelasticity because, at that time, the characteristic length of almost all ocean engineering structures was below ~150 m. Nevertheless, as the increasing demands of human activities, Very Large Floating Structures (VLFSs) appeared, such as floating runways, floating cities, and of course IEHSs as well (see, e.g., [197,198]). In this circumstance, the elastic deformations of IEHSs must be taken into account when the characteristic length of the IEHSs exceeds the wavelength [198]. On the other hand, in the last decade, there has been growing attention towards flexible-body WECs enabled by rubber-like elastomeric composite membrane materials [199], which also introduces elasticity into the system. Therefore, an SPH solver handling the hydroelastic FSI processes has been required to meet such demands. Recently, Gotoh et al. [77] have offered a comprehensive review for the latest development of different types of a particle-based hydroelastic FSI solver in ocean engineering; the readers can refer to that work for more details. Differing from that study, this section is not to provide the advancements of hydroelastic FSI solver within the SPH framework but to highlight the most challenging problems in modeling the hydroelastic interactions regarding OEDs.
5.2. Coupling Methods between SPH and Other Structure Solvers
In the context of SPH, two mature coupling paradigms are widely adopted to simulate the hydroelastic interactions. One typical method is to use the particle-mesh coupling strategy where the SPH solver is usually adopted for the fluid portion, while the mesh solver is adopted for the structure portion. Regarding this coupling measure, extensive works can be found in the literature, such as SPH-FE (Finite Element) (see, e.g., [200,201,202,203,204]), the Smoothed Point Interpolation Method (SPH-SPIM) (see, e.g., [205,206]), and MPS-FE (see, e.g., [76,207,208,209]). Another method is totally based on Lagrangian particles either for the fluid solver or the structure solver, e.g., SPH-TLSPH (Total Lagrangian SPH) (see, e.g., [210,211,212,213,214]), the Reproducing Kernel Particle Method (SPH-RKPM) (see e.g., [215,216]), and SPH-PD (Peridynamics) (see, e.g., [217,218,219,220]). In the context of simulating OEDs, which coupling paradigm is the best choice for realistic engineering applications is still an open topic that needs to be further investigated by the SPH community. As pointed out by Gotoh et al. [77], an entirely Lagrangian meshfree framework would bring about several distinct superiorities including higher flexibility, extendibility, generality, and reliability. Despite these, it should be highlighted here that for the realistic engineering problems regarding OEDs that usually involve complex 3D structures (both for external surface and internal skeleton), generating body-fitted and uniformly distributed particles for that is quite challenging even using the particle generator provided by SPHinXsys. On the contrary, there have been various mature grid generators, e.g., ANSYS ICEM, Dassault ABAQUS, and Altair Hypermesh, that can be directly employed to create a set of high-quality body-fitted grids even for very complex 3D structures. From this point of view, in the context of simulating OEDs towards realistic engineering problems, the particle-mesh coupling strategy seems a competitive method to cope with such problems. Notwithstanding, because of the inherent discrepancies of the particle method and the mesh method, how to accurately exchange field information between the fluid–structure interface is a quite challenging problem; this drastically affects the accuracy and stability of a particle-mesh coupling solver, whereas the entirely Lagrangian particle method is free from this issue because both the fluid and structure portions can be solved in a unified framework.
Unfortunately, in the majority of the existing literature, each coupling strategy have been only applied to simple benchmarks, for instance, dam-breaking flows impacting on an elastic plate (see, e.g., [195,210,211,214,221]), sloshing flows bending an elastic baffle (see, e.g., [214,222,223,224]) and the water entry problem for an elastic wedge (see, e.g., [222,223,225,226]). Little attention has been focused on realistic engineering applications for complex 3D structures. Besides, as mentioned above, IEHSs are not only featured by elastic deformations but also by the coupled multibody dynamics between different floating modules; in this sense, a “hydroelasticity-multibody” coupling FSI solver is required for such problems. On the whole, these remain challenging topics needed to be overcome by the SPH community in the future.
6. Multiphase Effects in Hydrodynamic Problems Related to OEDs
Multiphase flows are common phenomena that widely exist in various engineering problems. Different from other industries such as chemistry, and manufacturing where multi-component fluids exist (always more than three components), for most cases regarding ocean engineering, the multiphase problems only involve air and water, which are also the most common fluid media in the OEDs scenario. Note that cavitating flows are not considered herein because there is no mature SPH model of cavitation until now, although this phenomenon has been considerably investigated by mesh-based solvers (see, e.g., [227,228,229,230]). It should be underlined here that this section is not to provide a comprehensive review of the last development of multiphase SPH models but to discuss those multiphase problems regarding OEDs and the existing efforts provided by the SPH community.
In fact, compared with the interface-tracking techniques needed in Eulerian mesh-based solvers (see, e.g., [231,232,233]), multiphase simulations can be more straightforwardly realized in the SPH context, but some numerical issues should be tackled. The most striking one is the density discontinuity at the air–water interface. Colagrossi and Landrini [86] made the pioneering work for simulating air–water multiphase flows at realistic density ratios by rewriting the differential operators of gradient and divergence to minimize the errors caused by the significant density gradient at the interface. After that, several advancements have been made by the SPH community in these years (see, e.g., [234,235,236,237,238,239]). Despite these successes, in the context of simulating OEDs, several issues deserve our attention and will be discussed in the following.
6.1. Multiphase Effects in the OWCs
One typical example corresponding to OEDs for multiphase flows is the Oscillating Water Columns (OWCs). As shown in Figure 19, the main idea of an OWC is to drive an air turbine by exploiting the oscillating air pressures from a periodically moving water level. When a single-phase SPH model is applied to simulate such a problem, some numerical techniques are required to reduce the errors caused by the ignorance of pneumatic effects. One widely adopted method is to make the top of the OWC opening, which means that the pressure of the pneumatic parts is equal to the atmospheric pressure (see, e.g., [240]). As pointed out by Crespo et al. [186], this method makes the pneumatic effects of the problem negligible. Of course, the air chamber can be also closed when the total height of the air chamber is greatly higher than the internal water level (see, e.g., [169]). Another feasible and more accurate approach, as reported by Quartier et al. [241], is to place a cover floating on the top of the water level inside the OWC chamber, which can numerically replace the PTO system by implementing appropriate external forces on the cover (i.e., enforcing artificial damping to the flow system). The results indicate that considering the “air effects” possesses better accuracy than using single-phase SPH models as implemented in [169,186]. Nevertheless, it should be highlighted that the “air-effects” considered by Quartier et al. [241] is only a simplified model because the air pressures inside the OWC chamber are obtained by theoretical formulas, and then it was converted just like equivalent damping to the floating cover. Therefore, such a simplification is only a compromise to achieve a balance between numerical accuracy and efficiency, which is, however, hard to accurately reproduce the real working conditions of the whole OWC, especially for the flow information of the air chamber. Hence, a multiphase SPH model is needed when conducting a comprehensive simulation of OWCs.
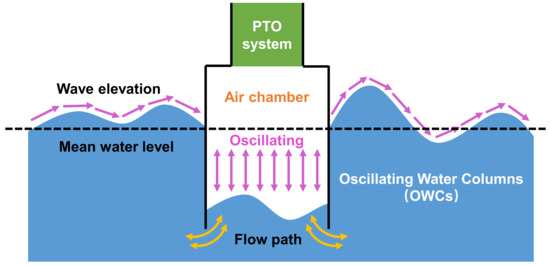
Figure 19.
The schematic diagram of a well-type OWC.
6.2. Air-Cushioning Effects in the Wave Slamming on OEDs
In addition to that, another significant phenomenon associated with multiphase effects is the air-cushioning/entrainment effects, which usually occur during a slamming process. Slamming, characterized by strong nonlinear interactions between fluid and structure, has been considerably investigated for a long time because of its tight relevance to the hydrodynamics of vessels, platforms, and OEDs as well. In terms of OEDs, it is worth noting that these devices, especially for WECs, usually work in harsh sea environments because it facilitates their abilities to energy harvesting. In other words, WECs are in favor of possessing the largest motion responses possible to generate electricity, which is quite different from conventional offshore structures that always require small motion responses in different working conditions. Therefore, from this point of view, slamming could play a more relevant role in the hydrodynamic performance of WECs than other types of ocean engineering structures.
Generally speaking, slamming appears in two forms according to the type of interaction process, i.e., active slamming and passive slamming. The passive slamming can be widely observed in ocean and coastal engineering such as water waves impacting on fixed/floating offshore platforms (see, e.g., [28]) or a tsunami rushing seafront buildings (see, e.g., [242]). In terms of the active slamming, typical cases are water entry/exit problems (e.g., bow flare and missile), seaplane ditching [83], and so on. It is clear that in terms of OEDs, both active slamming and passive slamming exist. First, for all types of WECs and FWTs, the water waves are prone to break on the site of these devices (i.e., passive slamming); therefore, the wave loads induced by the water jets and droplets should be taken into account in the pre-design stage. On the other hand, as highlighted by Sun et al. [138] where freak waves impacting on a fixed offshore structure was investigated, the air pocket/bubble plays a significant role in evaluating the slamming loads because it acts as a buffer between the water and structure surface, and thus excessive impulse peaks can be avoided. In other words, when the air phase is neglected in simulating the wave–structure interactions, the simulated impinging pressures could manifest large oscillation with significant peak values due to the absence of the air-cushioning effects. In the OEDs scenario, both the water jets/droplets and air-entrainment exist. One typical example is illustrated in Figure 20a, in which the experimental snapshot of a flap-type WEC is depicted. As can be seen, the device can drastically slam onto the free-surface in harsh sea environments (i.e., active slamming), leading to the serious free-surface breaking and air-entrainment as highlighted in the experimental snapshot; these strongly nonlinear phenomena could render considerable impulse loads acting on the devices (see, e.g., [45,46]). In this sense, a multiphase SPH model is imperative for such problems.
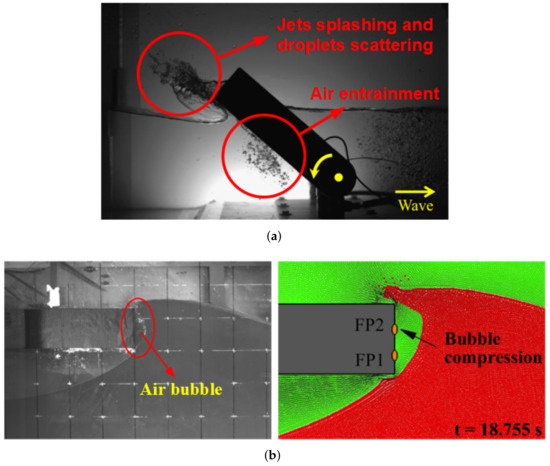
Figure 20.
Typical air-entrainment phenomena in ocean engineering. (a.) OWSC slamming onto free-surface (adapted from [46]). (b) Freak wave slamming on structures (adapted from [138]).
Although the SPH method has achieved significant improvement for modeling multiphase problems, the expensive computational costs are another obstacle that blocks multiphase SPH models from being widely applied towards realistic industrial problems. It is well known that the time step for a multiphase SPH simulation should be governed by the relation of (see, e.g., [86,236]), where the subscripts a and w denotes the air and water phases, respectively. This indicates that the time step depends on the square root of the density ratio , which makes the computational cost unbearable for the multiphase SPH simulation involving a high density ratio (e.g., air-water flows), especially for those large-scale 3D problems. In recent years, some efforts have been devoted to alleviating this. For instance, Lyu et al. [87] have carried out an investigation regarding the wedge-water-entry problems with different density ratios, demonstrating that when the density ratio satisfies , the hydrodynamic characteristics of the wedge are almost the same as the case of the realistic density ratio (i.e., ), which implies that reducing the density ratio down to 100 could be a feasible method to accelerate the multiphase simulation for OEDs. Nevertheless, it should be underlined that this conclusion is obtained based on the cavity dynamics of the wedge, and whether or not it is suitable for simulating other FSI problems needs to be further investigated in the future. In addition to that, another important routine is to implement multi-resolution techniques or parallel computing, which will be elaborated in the next section.
7. Techniques to Improve Numerical Efficiency in SPH Simulations of Hydrodynamic Problems Related to OEDs
Although the SPH method possesses remarkable abilities to deal with multi-physics problems, its computational costs are expensive compared with the mesh methods for the same problem scale. In this subsection, several accelerating techniques for SPH simulations are elaborated from both the algorithm and hardware aspects.
7.1. Multi-Particle-Resolution Techniques
Multi-resolution techniques are not a new topic in the SPH community, which is particularly important to improve the computational efficiency for SPH simulations when the size of the flow domain is very large. During the past two decades, extensive efforts have been devoted to developing various multi-resolution schemes. In these schemes, the regions of interest can be refined with a more concentrated particle distribution. In recent years, several adaptive refinement techniques have been proposed, e.g., Adaptive Particle Refinement (APR) (see, e.g., [243,244]), Adaptive Spatial Refinement (ASR) (see, e.g., [245,246]), Volume Adaptive Scheme (VAS) (see, e.g., [237,238]), and other variants (see, e.g., [247]). As stated in Section 1, the hydrodynamic problems related to OEDs are particularly characterized by moving boundaries and violent free-surface evolutions; therefore, in this subsection, only two adaptive refinement techniques that are very suitable for the concerning topic will be introduced, i.e., APR and ASR. The former is an ideal tool for the moving boundaries problems where the refinement regions can move following the targeted bodies (i.e., OEDs). In terms of the latter, it is very suitable for free-surface and multiphase interface evolutions because these areas can be adaptively refined in this method.
7.1.1. Chiron’s APR Technique
This method was first proposed by Barcarolo et al. [243] and was further improved by Chiron et al. [244] via numerical accuracy, efficiency, and robustness considerations. The main idea of this method is illustrated by a 2D case as shown in Figure 21. As can be seen, when a parent particle (blue color) is detected as the particle to be refined, four children particles (red color) will be created (i.e., particle splitting) with the mass and volume , where the subscripts c and p denote the children and parent particles, respectively. Then, other physical quantities of the children particles such as density, pressure, and velocity are directly inherited from the parent particle to avoid field discontinuities. After splitting, the parent particle will be deactivated (gray color) and thereby excluded from the SPH calculation in the following time integration. In order to exchange flow information between different resolution levels, a transition region is required. As can be observed, in the transition region, the status of the parent particles and children particles is converse with respect to the refined level, i.e., the parent particles remain active, whereas the children particles are deactivated in this area. During time integration, the children particles in the transition region are free from the SPH calculation, while the field quantities of them should be interpolated from their neighboring particles via Shepard interpretation. Note that the only function of these deactivated children particles is to avoid the kernel truncation of the active children particles. Besides, it is also worth noting that although the deactivated particles are free from the SPH calculation, their position should be updated according to their physical velocity at each time step.
Figure 21.
The schematic diagram of Chiron’s APR [244].
One can see that this method is very flexible to implement position-changing particle refinement because the refinement region can be directly updated according to the motion of OEDs, which is very suitable for obtaining the near-field flow information for OEDs in different sea environments. Herein, we show two typical attempts related to the practical application of APR towards ocean engineering problems. The first example is reported by Sun et al. [248] where the wave–structure interactions were simulated by a single-phase SPH model with APR (see Figure 22); the same procedure can be straightforwardly extended to simulating OEDs without any obstacles. One can see from Figure 22 that the pressure field between different resolution levels is excellently distributed without any discontinuities. Another example is associated with the water-entry problem of a wedge simulated by a multiphase SPH model with APR [87]. As shown in Figure 23a, the SPH results are in good agreement with the experimental snapshots. Furthermore, one can see from Figure 23b that both the Worthington jets and rising bubbles were accurately captured without any disturbances/discontinuities even at the multi-resolution interfaces. From the above discussions, it is clear that APR is an accurate and robust tool to model the problems where the position of the objects of interest is dynamically changing.
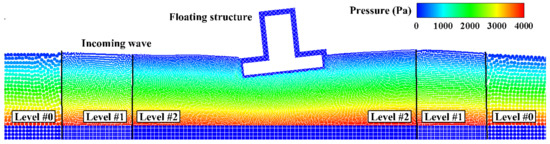
Figure 22.
Wave–structure interactions simulated via a single-phase SPH model with APR [248].
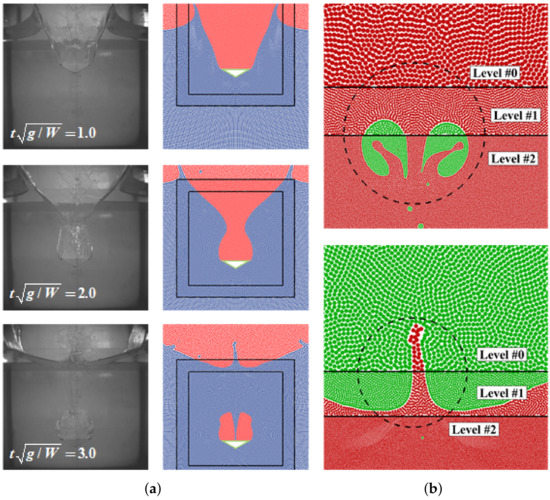
Figure 23.
The water-entry process of a wedge simulated via a multiphase SPH model with APR, where is a nondimensional time variable. (a) The comparison between the experimental snapshots [249] and SPH results [87]. (b) The local flow field of the rising bubbles and Worthington jet.
7.1.2. Yang’s ASR Technique
ASR was originally proposed by Yang et al. [245] in 2019 for simulating multiphase flows and was further extended to free-surface flows in 2021 [246]. Differing from APR, the main idea of ASR is to refine particle resolution according to the distance to the free-surface through particle splitting and merging. In order to further elaborate the principle of ASR, in Figure 24, a 2D scenario is displayed. One can see that in ASR, the computational domain is divided into several particle bands that are parallel to the free-surface (see Figure 24a), where S refers to the reference particle spacing and K is the ratio of the kernel width to the particle spacing. With the purpose of determining whether the mass of a targeted particle is larger than the threshold for splitting or smaller than that for merging, a reference mass should be assigned for each particle as , where d stands for the dimension of the problem. Subsequently, the ratio of the mass of a targeted particle to its reference mass is defined as . When the value of is larger than the critical value of splitting, i.e., , the particle is split into two smaller children particles (see Figure 24b). On the contrary, when the value of is smaller than the critical value of merging, i.e., , the particle is merged with its nearest neighboring particle (see Figure 24c). Finally, for the sake of the mass and momentum conservation, the masses and velocities of the two split particles were computed by and , whereas for the merged particle, it reads and .
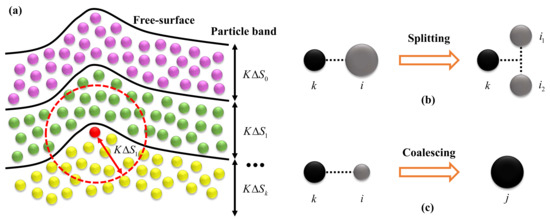
Figure 24.
The schematic diagram of Yang’s ASR [246]. (a) Several particle bands to characterize the distance to the free-surface particles. (b) The principle of particle splitting. (c) The principle of particle coalescing.
Figure 25 illustrates a typical application of ASR where a dam-break problem is simulated [246]. It can be observed that the particle resolution is well refined with the free-surface region being the finest and the inner area the coarsest. From the comparison with the experimental snapshots, it can be concluded that ASR possesses satisfactory accuracy in solving free-surface problems. It is apparent that in the OEDs scenario, the most ideal strategy is to implement APR for the near-field around OEDs, while implementing ASR for the whole computational domain to accurately capture the free-surface evolutions; this can exploit both the advantage of APR and ASR and therefore achieves the best balance between numerical accuracy and efficiency. However, to the best knowledge of the authors, relevant efforts towards such a simulation remain absent and thereby need to be taken into account in the future by the SPH practitioners concerning OEDs simulations.

Figure 25.
Dam-breaking flows simulated via a single-phase SPH model with ASR [246].
7.2. SPH Coupling with Other Efficient Numerical Methods
As aforementioned, APR/ASR techniques shows obvious advantages to improve the computational efficiency for SPH simulations because those regions characterized by strong nonlinear behaviors can be locally refined without field discontinuities. Nevertheless, it should be underlined that the coarsest level of APR/ASR could be dominated by other factors, implying that the particle resolution of the coarsest level cannot be tuned arbitrarily without any restrictions. One typical case, for example, is that when simulating the wave–structure interactions of FWTs or WECs using APR techniques, in order to improve the quality of generated water waves, the particle resolution of the coarsest level should be at least 5~10 particles per wave height [134], which, however, significantly boosts the computational costs owing to the considerable total particle number. In other words, although the technique of APR can improve the computational efficiency to some extent, the computational costs could still be considerable because the particle resolution in the far-field should be adequately fine to capture the incoming water waves. Another typical case is that when simulating the hydrodynamic performance of TCTs, the inflow and outflow particles far away from the device are “useless” because their only function is to maintain the flow consistency of the computational domain. Therefore, it is possible to improve the computational efficiency from another paradigm by replacing the far-field topologies from Lagrangian particles with Eulerian meshes.
In fact, SPH-solver coupling with other methods has been defined as one of the grand challenges for the SPH community by SPHERIC in 2020 [102]. To date, the SPH-DEM solver for fluid-granule problems (see, e.g., [250,251,252,253,254]) and SPH-FE/TLSPH solvers (see, e.g., [200,201,202,203,204,210,211,212,213,214]) for the fluid–solid problem are relatively mature, whereas for fluid simulations, the “SPH+X” coupling solver is still an open topic that has been attracting more and more attention from the SPH community. As discussed in Section 1, the potential-flow theory and the RANS approach are two popular mesh-based methods for simulating OEDs; it is thus naturally the best method to couple these two schemes with the SPH method.
For instance, Serván-Camas et al. [255] studied the coupled sloshing-seakeeping problems by using an SPH-FE solver, in which the far-field solution was solved by the diffraction–radiation problem using FE. However, there are several challenging issues for this type of coupling method. For example, exchanging flow information at the SPH-FE interface is not straightforward because it requires reconciling the irrotational and inviscid solution as it transitions into the SPH region (vice versa). A feasible method to tackle this issue is to implement a buffer to provide a smooth transition between the SPH and FE results. Another more natural way is to solve the fully nonlinear Navier–Stokes equation for the mesh portion. As a mature mesh method, FV has been successfully coupled with SPH by Marrone et al. [256] in a 2D context. In their numerical scheme, as displayed in Figure 26, the computational domain is divided into three sub-regions that are defined as a “pure SPH forcing domain,” an “SPH-FV blending domain,” and a “pure FV forcing domain,” respectively. In the pure SPH forcing domain, the fluid is totally computed by the SPH algorithm so that any numerical issues regarding multiphase interface tracking and mass conservation can be avoided. On the contrary, in the pure FV forcing domain where the flow is almost constant or periodically evolving, the field information is totally solved by the FV algorithm, and consequently, the computational efficiency can be apparently improved. In terms of the SPH-FV blending domain, it works as a flow information exchanger between SPH and FV in which the Lagrangian equations are modified to a new formalism. In this transition domain, when a point approaches the pure SPH forcing domain, the solution will gradually go back to the fully Lagrangian solution. Conversely, when a point approaches the pure FV forcing domain, the SPH solution will recover to the fully Eulerian solution. Therefore, the field quantities can be continuous at the SPH-FV interfaces even when violent phenomena such as shock waves are involved. This work was further improved by Chiron et al. [257] in 2018 by allowing net mass transferring between the SPH and FV domain and free-surface crossing the overlapping domain, which makes the coupling scheme more suitable for simulating wave–structure-interaction problems. Note that in addition to FV, SPH-FD coupling is also a feasible strategy (see, e.g., [258,259]).
Figure 26.
The schematic diagram of the SPH-FV coupling strategy proposed by Marrone et al. [256].
In the OEDs scenario, the coupled SPH-FV framework is very suitable for the wave–structure interactions because such a type of simulations is usually characterized by a huge computational domain and violent free-surface evolutions in the vicinity of OEDs. In this sense, it is possible to build a hybrid NWT where the flow information in the proximity of OEDs is solved by the SPH solver incorporating with APR and the far-field by the FV solver with multi-resolution meshes. This strategy has been successfully realized very recently by Di Mascio et al. [260] in which the algorithms of Marrone et al. [256] and Chiron et al. [257] have been further extended for solving multi-scale 3D free-surface flows; this work provides an excellent reference for those SPH practitioners devoting to OEDs simulations.
7.3. High-Performance Parallel Computing
In the previous subsection, we offered a detailed review of several accelerating techniques from the algorithm aspect. On the contrary, in this subsection, hardware-based accelerating techniques are discussed.
7.3.1. Accelerating SPH Simulation with Central Processing Units (CPUs)
Generally speaking, CPU acceleration can be categorized into two types as their parallelization paradigm, i.e., Shared Memory Systems (SMSs) and Distributed Memory Systems (DMSs). One typical technique related to SMSs is Open Multi-Processing (OpenMP), which can be implemented without difficulty by incorporating with the Single Instruction Multiple Data (SIMD) style of modern CPUs. The SIMD style allows data parallelism by performing the same instruction to all available threads of a processor simultaneously. It is reported that the implementation of OpenMP-based parallelization is very straightforward and only requires slight modifications of existing codes, which are adopted widely by the SPH community (see, e.g., [119,261,262,263]). For instance, DualSPHysics adopted OpenMP as the strategy of CPUs acceleration [107]. Nonetheless, the speedup of OpenMP could be limited caused by the increasing costs of the overhead of data communication from the shared memory to threads (see, e.g., [262,264]). Another typical SMSs framework is Intel’s Thread Building Blocks (TBB) that was developed by the C++ language for parallel programming on multi-core processors. Compared with OpenMP, the most apparent superiority of TBB is that it provides a better balance between the workload and available processing cores for the sake of increasing core utilization (see, e.g., [265]). However, TBB requires cumbersome reconstruction of existing codes so that this framework is more applicable to build a new solver rather than to modify existing codes. To the best knowledge of authors, to date among various open-source SPH packages, only SPHinXsys adopted TBB as the framework of CPUs acceleration [112].
Although SMSs show apparent superiority in accelerating SPH simulations in practical applications, it only accesses their local memory during simulations [261]. In other words, SMSs are preferred to be considered in small- or medium-scale problems because the computational capacity of a single-node computer system is limited. When dealing with large-scale problems, for example, when the order of magnitude of the total particle number reaches ∼ or even higher, another parallelization paradigm, i.e., DMSs, is a more reasonable way to tackle such situations (see, e.g., [266]). At present, the most popular DMSs framework is the Massage Passing Interface (MPI). Differing from OpenMP where the data decomposition is used, in MPI, the key idea is to geometrically decompose the whole computational domain into several sub-regions and then attribute them to a task (processor). The computational efficiency of MPI is largely determined by whether or not there is an identical workload on each employed processor in simulations. As pointed out by Oger et al. [266], the best strategy to balance the workload is of course to measure the actual CPU time of every processor used and to re-act on the sub-region size until a homogeneous workload is achieved. Notwithstanding, this is hard to be realized when the simulations are characterized by fluid fragmentation for which water droplets and jets occur. In addition to the workload, another drawback of MPI is the expensive cost to build a massive multi-processor cluster that is less accessible for ordinary SPH practitioners. Despite this, the superiorities of MPI are evident; the most important one is that MPI can realize large-scale SPH simulations by employing substantial processors up to thousands and even tens of thousands as reported in [264,266,267].
7.3.2. Accelerating SPH Simulation with Graphics Processing Units (GPUs)
In the last decade, Compute Unified Device Architecture (CUDA) programming has witnessed its prosperous developments in the scientific computing community owing to its better ability for data parallelization than the conventional CPU-based paradigm. The pioneering work of illustrating the superiorities of GPUs to SPH simulations can be traced back to Harada et al. [268] in 2007 before the occurrence of CUDA. Since then, GPUs have been widely adopted in the SPH community because the simulation process can be now implemented in GPUs entirely and thus significantly reducing the cost regarding data transfer between CPUs and GPUs (see, e.g., [269,270]). Compared with other SMSs frameworks, CUDA possesses definite superiority in terms of computational efficiency (the speedup of up to two orders of magnitude over using a single-node CPU [269]). More importantly, GPUs are cheaper and more accessible than massive heterogeneous clusters for ordinary SPH practitioners. A brief comparison of the superiorities and limitations between different parallelization frameworks is outlined in Table 2.

Table 2.
The superiority and limitation of different parallelization frameworks.
At present, multiple open-source codes using GPUs parallelization exist, such as DualSPHysics (CUDA) [107,120], AQUAgpusph (OpenCL) [271], GPUSPH (CUDA) [108] and PySPH (CUDA) [272] (see Table 3 for more details). These packages can be conveniently coupled with other open-source code, providing powerful tools for the SPH community to simulate OEDs. For example, Wei et al. [196] coupled Project Chrono with GPUSPH to investigate different types of WECs, demonstrating that the combination of GPUSPH + Project Chrono is a reliable tool for modeling WECs in directional nonlinear sea states. As the most-popular open-source package, DualSPHysics has been also widely employed to simulate OEDs using GPU-accelerating, such as OWCs (see, e.g., [186]), OWSCs (see, e.g., [188,193]), and point-absorbers (see, e.g., [190,191]), showing remarkable ability to cope with fluid–mechanism interaction problems in a user-friendly form. Notwithstanding, GPU technology has its deficiencies. When simulating the realistic large-scale engineering problems for OEDs, the memory restricts the maximum total number of particles. To go beyond this limit, the most-effective measure is to build a multi-GPU framework to extend the computational capacity (see, e.g., [273,274,275,276]). Overall, GPU computing is a milestone in the development of the SPH method, and it will definitely be the most-important method to accelerate the SPH simulations towards OEDs in the future.

Table 3.
The parallelization framework for different open-source packages.
8. Conclusions and Prospects
This article presented the latest developments of SPH techniques for simulating OEDs. Attention was particularly concentrated on three topics, i.e., (1) SPH-based numerical fluid tanks, (2) multi-physics SPH techniques for simulating OEDs, and (3) computational efficiency and capacity of SPH simulations for industrial applications.
It is concluded that at present, the existing SPH techniques can provide a reliable framework for simulating OEDs from the pre-process phase for particle generation to the calculation phase for coupling with multi-physics solvers until the post-process phase using particle-to-mesh interpretation techniques (see, e.g., [214]). Notwithstanding, several challenging problems, especially the considerable computational costs of 3D SPH simulations and the relatively low convergence rate (usually between 1 and 2), are still needed to be further tackled by the SPH community in the future studies, which are listed as follows.
- High-order accurate SPH models;
- Coupled hydroelasticity-multibody FSI solver;
- Multiphase SPH models of high fidelity and efficiency considering real compressibility;
- Accurate and robust multi-scale particle-mesh coupling solver;
- Turbulence and cavitation modeling in the SPH framework.
Author Contributions
Conceptualization, P.-N.S. and H.-G.L.; methodology, P.-N.S. and H.-G.L.; software, P.-N.S. and H.-G.L.; validation, H.-G.L.; formal analysis, H.-G.L.; investigation, H.-G.L., X.-T.H., and S.-Y.Z.; resources, P.-N.S.; data curation, H.-G.L.; writing—original draft preparation, H.-G.L.; writing—review and editing, P.-N.S., X.-T.H., S.-Y.Z., Y.-X.P., T.J., and C.-N.J.; visualization, H.-G.L.; supervision, P.-N.S.; project administration, P.-N.S.; funding acquisition, P.-N.S. and C.-N.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Key Laboratory of Hydraulic Engineering Simulation and Safety (Tianjin University) with grant number HESS-1905; the National Natural Science Foundation of China with grant numbers 51779109, 12002404 and 52171329; the Project of Research and Development Plan in Key Areas of Guangdong Province with grant number 2020B1111010002; the Open Fund of State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology with grant number LP2017; and the Natural Science Foundation of Guangdong Province of China with grant number 2019A1515011405.
Acknowledgments
The authors would like to thank Chi Zhang in the Technical University of Munich and Xiufeng Yang in the Beijing Institute of Technology for their kind assistance during the writing of this article. The two open-source SPH packages (DualSPHysics and SPHinXsys) are also particularly acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SPH | Smoothed Particle Hydrodynamics |
| CFD | Computational Fluid Dynamics |
| PF | Potential Flow |
| BE | Boundary Element |
| RANS | Reynolds Average Navier Stokes |
| SPHERIC | SPH rEsearch and engineeRing International Community |
| KFSBC | Kinematic Free-surface Boundary Condition |
| DFSBC | Dynamic Free-surface Boundary Condition |
| FV | Finite Volume |
| FD | Finite Differece |
| TI | Tensile Instability |
| PD | Peridynamics |
| VLFS(s) | Very Large Floating Structure(s) |
| MCS(s) | Mechanical Constraint Structure(s) |
| AMR | Adaptive Mesh Refinement |
| ALE | Arbitrary Lagrangian Eulerian |
| KGC | Kernel Gradient Correction |
| DBC | Dynamic Boundary Condition |
| PPA | Particle Packing Algorithm |
| NFT(s) | Numerical Fluid Tank(s) |
| NWT(s) | Numerical Wave Tank(s) |
| MCS(s) | Mechanical Constraint Structure(s) |
| ISPH | Incompressible Smoothed Particle Hydrodynamics |
| WCSPH | Weakly Compressible Smoothed Particle Hydrodynamics |
| TLSPH | Total Lagrangian Smoothed Particle Hydrodynamics |
| RKPM | Reproducing Kernel Particle Method |
| SPIM | Smoothed Point Interpolation Method |
| FSI(s) | Fluid–structure Interaction(s) |
| PTO | Power Take-Off |
| IEHSs(s) | Integrated Energy Harvesting System(s) |
| OED(s) | Ocean Energy Device(s) |
| FWT(s) | Floating Wind Turbine(s) |
| WEC(s) | Wave Energy Converter(s) |
| TCT(s) | Tidal Current Turbine(s) |
| OWC(s) | Oscillating Water Column(s) |
| OWSC(s) | Oscillating Wave Surge Converter(s) |
| VLFS(s) | Very Large Floating Structure(s) |
| SPH | Smoothed Particle Hydrodynamics |
| PST(s) | Particle Shifting Technique(s) |
| TIC | Tensile Instability Control |
| TBB | Thread Building Blocks |
| OpenMP | Open Multi-Processing |
| MPI | Massage Passing Interface |
| CUDA | Compute Unified Device Architecture |
| APR | Adaptive Particle Refinement |
| ASR | Adaptive Spatial Refinement |
| VAS | Volume Adaptive Scheme |
| CPU(s) | Central Processing Unit(s) |
| GPU(s) | Graphics Processing Unit(s) |
| SMS(s) | Shared Memory System(s) |
| DMS(s) | Distributed Memory System(s) |
| EoS | Equation of State |
| VIV&VIM | Vortex-Induced Vibration/Motion |
References
- Ammari, C.; Belatrache, D.; Touhami, B.; Makhloufi, S. Sizing, optimization, control and energy management of hybrid renewable energy system—A review. Energy Built Environ. 2021, in press. [Google Scholar] [CrossRef]
- Melikoglu, M. Current status and future of ocean energy sources: A global review. Ocean Eng. 2018, 148, 563–573. [Google Scholar] [CrossRef]
- Salter, S.H. Wave power. Nature 1974, 249, 720–724. [Google Scholar] [CrossRef]
- Khan, N.; Kalair, A.; Abas, N.; Haider, A. Review of ocean tidal, wave and thermal energy technologies. Renew. Sustain. Energy Rev. 2017, 72, 590–604. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, S.; Lu, D.; Tian, X. Numerical investigation of the dynamic response and power capture performance of a VLFS with a wave energy conversion unit. Eng. Struct. 2019, 195, 62–83. [Google Scholar] [CrossRef]
- Nguyen, H.P.; Wang, C.M.; Tay, Z.Y.; Luong, V.H. Wave energy converter and large floating platform integration: A review. Ocean Eng. 2020, 213, 107768. [Google Scholar] [CrossRef]
- Cevasco, D.; Koukoura, S.; Kolios, A.J. Reliability, availability, maintainability data review for the identification of trends in offshore wind energy applications. Renew. Sustain. Energy Rev. 2021, 136, 110414. [Google Scholar] [CrossRef]
- Ren, Z.; Verma, A.S.; Li, Y.; Teuwen, J.J.E.; Jiang, Z. Offshore wind turbine operations and maintenance: A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 144, 110886. [Google Scholar] [CrossRef]
- Rinaldi, G.; Thies, P.R.; Johanning, L. Current Status and Future Trends in the Operation and Maintenance of Offshore Wind Turbines: A Review. Energies 2021, 14, 2484. [Google Scholar] [CrossRef]
- Jiang, Z. Installation of offshore wind turbines: A technical review. Renew. Sustain. Energy Rev. 2021, 139, 110576. [Google Scholar] [CrossRef]
- Santhosh, N.; Baskaran, V.; Amarkarthik, A. A review on front end conversion in ocean wave energy converters. Front. Energy 2015, 9, 297–310. [Google Scholar] [CrossRef]
- Ahamed, R.; McKee, K.; Howard, I. Advancements of wave energy converters based on power take off (PTO) systems: A review. Ocean Eng. 2020, 204, 107248. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Sun, W.; Li, J. Ocean wave energy converters: Technical principle, device realization, and performance evaluation. Renew. Sustain. Energy Rev. 2021, 141, 110764. [Google Scholar] [CrossRef]
- Qian, P.; Feng, B.; Liu, H.; Tian, X.; Si, Y.; Zhang, D. Review on configuration and control methods of tidal current turbines. Renew. Sustain. Energy Rev. 2019, 108, 125–139. [Google Scholar] [CrossRef]
- Nachtane, M.; Tarfaoui, M.; Goda, I.; Rouway, M. A review on the technologies, design considerations and numerical models of tidal current turbines. Renew. Energy 2020, 157, 1274–1288. [Google Scholar] [CrossRef]
- Chowdhury, M.S.; Rahman, K.S.; Selvanathan, V.; Nuthammachot, N.; Suklueng, M.; Mostafaeipour, A.; Habib, A.; Akhtaruzzaman, M.; Amin, N.; Techato, K. Current trends and prospects of tidal energy technology. Environ. Dev. Sustain. 2021, 23, 8179–8194. [Google Scholar] [CrossRef]
- Said, H.A.; Ringwood, J.V. Grid integration aspects of wave energy—Overview and perspectives. IET Renew. Power Gener. 2021, 15, 3045–3064. [Google Scholar] [CrossRef]
- Ozkop, E.; Altas, I.H. Control, power and electrical components in wave energy conversion systems: A review of the technologies. Renew. Sustain. Energy Rev. 2017, 67, 106–115. [Google Scholar] [CrossRef]
- Penalba, M.; Giorgi, G.; Ringwood, J.V. Mathematical modelling of wave energy converters: A review of nonlinear approaches. Renew. Sustain. Energy Rev. 2017, 78, 1188–1207. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Zhou, B.; Zhang, L.; Li, C.; Zang, J.; Zheng, X.; Xu, J.; Zhang, W. Experimental and numerical study on a novel dual-resonance wave energy converter with a built-in power take-off system. Energy 2018, 165, 1008–1020. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, B.; Zang, J.; Vogel, C.; Fan, T.; Chen, C. Effects of narrow gap wave resonance on a dual-floater WEC-breakwater hybrid system. Ocean Eng. 2021, 225, 108762. [Google Scholar] [CrossRef]
- Cheng, Y.; Xi, C.; Dai, S.; Ji, C.; Collu, M.; Li, M.; Yuan, Z.; Incecik, A. Wave energy extraction and hydroelastic response reduction of modular floating breakwaters as array wave energy converters integrated into a very large floating structure. Appl. Energy 2022, 306, 117953. [Google Scholar] [CrossRef]
- Hansen, M.O.L.; Sørensen, J.N.; Voutsinas, S.; Sørensen, N.; Madsen, H.A. State of the art in wind turbine aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2006, 42, 285–330. [Google Scholar] [CrossRef]
- Zhang, P.; Huang, S. Review of aeroelasticity for wind turbine: Current status, research focus and future perspectives. Front. Energy 2011, 5, 419–434. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Kolios, A. State of the art in the aeroelasticity of wind turbine blades: Aeroelastic modelling. Renew. Sustain. Energy Rev. 2016, 64, 195–210. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Tian, X.; Lu, W.; Zhang, X. Combined effects of raft length ratio and structural flexibility on power capture performance of an interconnected-two-raft wave energy converter. Ocean Eng. 2019, 177, 12–28. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, D.; Guo, F.; Gao, Y.; Sun, Y. The maximum wave energy conversion by two interconnected floaters: Effects of structural flexibility. Appl. Ocean Res. 2018, 71, 34–47. [Google Scholar] [CrossRef]
- Dias, F.; Ghidaglia, J.M. Slamming: Recent Progress in the Evaluation of Impact Pressures. Annu. Rev. Fluid Mech. 2018, 50, 243–273. [Google Scholar] [CrossRef]
- Saincher, S.; Banerjee, J. Influence of wave breaking on the hydrodynamics of wave energy converters: A review. Renew. Sustain. Energy Rev. 2016, 58, 704–717. [Google Scholar] [CrossRef]
- Sun, H.; Kim, E.S.; Nowakowski, G.; Mauer, E.; Bernitsas, M.M. Effect of mass-ratio, damping, and stiffness on optimal hydrokinetic energy conversion of a single, rough cylinder in flow induced motions. Renew. Energy 2016, 99, 936–959. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Mao, Z.; Song, B.; Ding, W.; Tian, W. Numerical investigation on effect of damping-ratio and mass-ratio on energy harnessing of a square cylinder in FIM. Energy 2018, 144, 218–231. [Google Scholar] [CrossRef]
- Kim, E.S.; Sun, H.; Park, H.; Shin, S.-c.; Chae, E.J.; Ouderkirk, R.; Bernitsas, M.M. Development of an alternating lift converter utilizing flow-induced oscillations to harness horizontal hydrokinetic energy. Renew. Sustain. Energy Rev. 2021, 145, 111094. [Google Scholar] [CrossRef]
- Yang, S.; Chen, H.; Ji, Z.; Li, H.; Xiang, X. Modelling and analysis of inertia self-tuning phase control strategy for a floating multi-body wave energy converter. IET Renew. Power Gener. 2021, 15, 3126–3137. [Google Scholar] [CrossRef]
- Zhang, Y.; Zang, W.; Zheng, J.; Cappietti, L.; Zhang, J.; Zheng, Y.; Fernandez-Rodriguez, E. The influence of waves propagating with the current on the wake of a tidal stream turbine. Appl. Energy 2021, 290, 116729. [Google Scholar] [CrossRef]
- Rahman, M.; Ong, Z.C.; Chong, W.T.; Julai, S.; Khoo, S.Y. Performance enhancement of wind turbine systems with vibration control: A review. Renew. Sustain. Energy Rev. 2015, 51, 43–54. [Google Scholar] [CrossRef]
- Zuo, H.; Bi, K.; Hao, H. A state-of-the-art review on the vibration mitigation of wind turbines. Renew. Sustain. Energy Rev. 2020, 121, 109710. [Google Scholar] [CrossRef]
- Sentchev, A.; Thiébaut, M.; Schmitt, F.G. Impact of turbulence on power production by a free-stream tidal turbine in real sea conditions. Renew. Energy 2020, 147, 1932–1940. [Google Scholar] [CrossRef]
- Ahmadi, M.H.B.; Yang, Z. The evolution of turbulence characteristics in the wake of a horizontal axis tidal stream turbine. Renew. Energy 2020, 151, 1008–1015. [Google Scholar] [CrossRef]
- Ebdon, T.; Allmark, M.J.; O Doherty, D.M.; Mason-Jones, A.; O Doherty, T.; Germain, G.; Gaurier, B. The impact of turbulence and turbine operating condition on the wakes of tidal turbines. Renew. Energy 2021, 165, 96–116. [Google Scholar] [CrossRef]
- Neunaber, I.; Hölling, M.; Whale, J.; Peinke, J. Comparison of the turbulence in the wakes of an actuator disc and a model wind turbine by higher order statistics: A wind tunnel study. Renew. Energy 2021, 179, 1650–1662. [Google Scholar] [CrossRef]
- Davidson, J.; Ringwood, J.V. Mathematical Modelling of Mooring Systems for Wave Energy Converters—A Review. Energies 2017, 10, 666. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Wang, S.; Guedes Soares, C. Review of mooring design for floating wave energy converters. Renew. Sustain. Energy Rev. 2019, 111, 595–621. [Google Scholar] [CrossRef]
- Koh, H.J.; Ruy, W.S.; Cho, I.H.; Kweon, H.M. Multi-objective optimum design of a buoy for the resonant-type wave energy converter. J. Mar. Sci. Technol. 2015, 20, 53–63. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Liu, H.X.; Zhang, L.; Zhang, W.C.; Ma, Q.W. Study on the performance analysis and optimization of funnel concept in wave-energy conversion. J. Mar. Sci. Technol. 2018, 23, 696–705. [Google Scholar] [CrossRef]
- Wei, Y.; Rafiee, A.; Henry, A.; Dias, F. Wave interaction with an oscillating wave surge converter, Part I: Viscous effects. Ocean Eng. 2015, 104, 185–203. [Google Scholar] [CrossRef]
- Wei, Y.; Abadie, T.; Henry, A.; Dias, F. Wave interaction with an Oscillating Wave Surge Converter. Part II: Slamming. Ocean Eng. 2016, 113, 319–334. [Google Scholar] [CrossRef]
- Henderson, R. Design, simulation, and testing of a novel hydraulic power take-off system for the Pelamis wave energy converter. Renew. Energy 2006, 31, 271–283. [Google Scholar] [CrossRef]
- Kofoed, J.P.; Frigaard, P.; Friis-Madsen, E.; Sørensen, H.C. Prototype testing of the wave energy converter wave dragon. Renew. Energy 2006, 31, 181–189. [Google Scholar] [CrossRef] [Green Version]
- Ning, D.; Zhao, X.; Göteman, M.; Kang, H. Hydrodynamic performance of a pile-restrained WEC-type floating breakwater: An experimental study. Renew. Energy 2016, 95, 531–541. [Google Scholar] [CrossRef]
- Chen, L.; Hashim, R.; Othman, F.; Motamedi, S. Experimental study on scour profile of pile-supported horizontal axis tidal current turbine. Renew. Energy 2017, 114, 744–754. [Google Scholar] [CrossRef]
- Xu, X.; Day, S. Experimental investigation on dynamic responses of a spar-type offshore floating wind turbine and its mooring system behaviour. Ocean Eng. 2021, 236, 109488. [Google Scholar] [CrossRef]
- Windt, C.; Davidson, J.; Ringwood, J.V. Numerical analysis of the hydrodynamic scaling effects for the Wavestar wave energy converter. J. Fluids Struct. 2021, 105, 103328. [Google Scholar] [CrossRef]
- Palm, J.; Eskilsson, C.; Bergdahl, L.; Bensow, R.E. Assessment of Scale Effects, Viscous Forces and Induced Drag on a Point-Absorbing Wave Energy Converter by CFD Simulations. J. Mar. Sci. Eng. 2018, 6, 124. [Google Scholar] [CrossRef] [Green Version]
- Dai, S.; Day, S.; Yuan, Z.; Wang, H. Investigation on the hydrodynamic scaling effect of an OWC type wave energy device using experiment and CFD simulation. Renew. Energy 2019, 142, 184–194. [Google Scholar] [CrossRef]
- Ransley, E.; Greaves, D.; Raby, A.; Simmonds, D.; Hann, M. Survivability of wave energy converters using CFD. Renew. Energy 2017, 109, 235–247. [Google Scholar] [CrossRef] [Green Version]
- Nuernberg, M.; Tao, L. Three dimensional tidal turbine array simulations using OpenFOAM with dynamic mesh. Ocean Eng. 2018, 147, 629–646. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Hu, Z.; Wan, D.; Xiao, Q. Comparisons of the dynamical characteristics of a semi-submersible floating offshore wind turbine based on two different blade concepts. Ocean Eng. 2018, 153, 305–318. [Google Scholar] [CrossRef] [Green Version]
- Fertahi, E.D.; Bouhal, T.; Rajad, O.; Kousksou, T.; Arid, A.; El Rhafiki, T.; Jamil, A.; Benbassou, A. CFD performance enhancement of a low cut-in speed current Vertical Tidal Turbine through the nested hybridization of Savonius and Darrieus. Energy Convers. Manag. 2018, 169, 266–278. [Google Scholar] [CrossRef]
- Cheng, P.; Huang, Y.; Wan, D. A numerical model for fully coupled aero-hydrodynamic analysis of floating offshore wind turbine. Ocean Eng. 2019, 173, 183–196. [Google Scholar] [CrossRef]
- Faltinsen, O. Sea Loads on Ships and Offshore Structures (Cambridge Ocean Technology Series); Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Prentice Hall: Harlow, UK, 2007. [Google Scholar]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific Publishing Company: Singapore, 2003. [Google Scholar]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astrophys. J. 1977, 8, 1013–1024. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Gotoh, H.; Khayyer, A. On the state-of-the-art of particle methods for coastal and ocean engineering. Coast. Eng. J. 2018, 60, 79–103. [Google Scholar] [CrossRef]
- Luo, M.; Khayyer, A.; Lin, P. Particle methods in ocean and coastal engineering. Appl. Ocean Res. 2021, 114, 102734. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M.; Rogers, B.D.; Violeau, D.; Grassa, J.M.; Crespo, A.J.C. Foreword: SPH for free-surface flows. J. Hydraul. Res. 2010, 48, 3–5. [Google Scholar] [CrossRef]
- Violeau, D.; Rogers, B.D. Smoothed particle hydrodynamics (SPH) for free-surface flows: Past, present and future. J. Hydraul. Res. 2015, 54, 1–26. [Google Scholar] [CrossRef]
- Ren, L.; Wang, X.; Zhang, Y.; Gu, S. SPH method-based study on energy dissipation characteristics of stepped spillway. Water Resour. Hydropower Eng. 2017, 48, 113–117. [Google Scholar]
- Sun, P.; Zhang, A.M.; Marrone, S.; Ming, F. An accurate and efficient SPH modeling of the water entry of circular cylinders. Appl. Ocean Res. 2018, 72, 60–75. [Google Scholar] [CrossRef]
- He, F.; Zhang, H.; Huang, C.; Liu, M. Numerical investigation of the solitary wave breaking over a slope by using the finite particle method. Coast. Eng. 2020, 156, 103617. [Google Scholar] [CrossRef]
- Wang, Z.B.; Chen, R.; Wang, H.; Liao, Q.; Zhu, X.; Li, S.Z. An overview of smoothed particle hydrodynamics for simulating multiphase flow. Appl. Math. Model. 2016, 40, 9625–9655. [Google Scholar] [CrossRef]
- Zhang, A.m.; Sun, P.n.; Ming, F.r.; Colagrossi, A. Smoothed particle hydrodynamics and its applications in fluid-structure interactions. J. Hydrodyn. Ser. B 2017, 29, 187–216. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Z. Smoothed particle hydrodynamics (SPH) for modeling fluid-structure interactions. Sci. China Phys. Mech. Astron. 2019, 62, 984701. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, W.; Wan, D. Partitioned MPS-FEM method for free-surface flows interacting with deformable structures. Appl. Ocean Res. 2021, 114, 102775. [Google Scholar] [CrossRef]
- Gotoh, H.; Khayyer, A.; Shimizu, Y. Entirely Lagrangian meshfree computational methods for hydroelastic fluid-structure interactions in ocean engineering—Reliability, adaptivity and generality. Appl. Ocean Res. 2021, 115, 102822. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An Overview and Recent Developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Monaghan, J.J. Smoothed Particle Hydrodynamics and Its Diverse Applications. Annu. Rev. Fluid Mech. 2012, 44, 323–346. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Zhang, H.; Qu, X. SPH method-based study on numerical simulation of jet flow. Water Resour. Hydropower Eng. 2017, 48, 82–85. [Google Scholar]
- Ye, T.; Pan, D.; Huang, C.; Liu, M. Smoothed particle hydrodynamics (SPH) for complex fluid flows: Recent developments in methodology and applications. Phys. Fluids 2019, 31, 11301. [Google Scholar] [CrossRef]
- Oger, G.; Vergnaud, A.; Bouscasse, B.; Ohana, J.; Zarim, M.A.; De Leffe, M.; Bannier, A.; Chiron, L.; Jus, Y.; Garnier, M.; et al. Simulations of helicopter ditching using smoothed particle hydrodynamics. J. Hydrodyn. 2020, 32, 653–663. [Google Scholar] [CrossRef]
- Violeau, D. Fluid Mechanics and the SPH Method: Theory and Applications; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Lyu, H.G.; Deng, R.; Sun, P.N.; Miao, J.M. Study on the wedge penetrating fluid interfaces characterized by different density-ratios: Numerical investigations with a multi-phase SPH model. Ocean Eng. 2021, 237, 109538. [Google Scholar] [CrossRef]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling Low Reynolds Number Incompressible Flows Using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Cummins, S.J.; Rudman, M. An SPH Projection Method. J. Comput. Phys. 1999, 152, 584–607. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Shao, S.D. Corrected Incompressible SPH method for accurate water-surface tracking in breaking waves. Coast. Eng. 2008, 55, 236–250. [Google Scholar] [CrossRef] [Green Version]
- Lee, E.S.; Moulinec, C.; Xu, R.; Violeau, D.; Laurence, D.; Stansby, P. Comparisons of weakly compressible and truly incompressible algorithms for the SPH mesh free particle method. J. Comput. Phys. 2008, 227, 8417–8436. [Google Scholar] [CrossRef]
- Lind, S.J.; Xu, R.; Stansby, P.K.; Rogers, B.D. Incompressible smoothed particle hydrodynamics for free-surface flows: A generalised diffusion-based algorithm for stability and validations for impulsive flows and propagating waves. J. Comput. Phys. 2012, 231, 1499–1523. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Shimizu, Y. Comparative study on accuracy and conservation properties of two particle regularization schemes and proposal of an optimized particle shifting scheme in ISPH context. J. Comput. Phys. 2017, 332, 236–256. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical solution of the navier-stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Shao, S. Enhanced predictions of wave impact pressure by improved incompressible SPH methods. Appl. Ocean Res. 2009, 31, 111–131. [Google Scholar] [CrossRef] [Green Version]
- Khayyer, A.; Gotoh, H. A higher order Laplacian model for enhancement and stabilization of pressure calculation by the MPS method. Appl. Ocean Res. 2010, 32, 124–131. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Gingold, R.A. Shock simulation by the particle method SPH. J. Comput. Phys. 1983, 52, 374–389. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S.; Molteni, D. Free-surface flows solved by means of SPH schemes with numerical diffusive terms. Comput. Phys. Commun. 2010, 181, 532–549. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical diffusive terms in weakly-compressible SPH schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Molteni, D.; Colagrossi, A. A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH. Comput. Phys. Commun. 2009, 180, 861–872. [Google Scholar] [CrossRef]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touzé, D.; Graziani, G. δ-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Vacondio, R.; Altomare, C.; De Leffe, M.; Hu, X.; Le Touzé, D.; Lind, S.; Marongiu, J.C.; Marrone, S.; Rogers, B.D.; Souto-Iglesias, A. Grand challenges for Smoothed Particle Hydrodynamics numerical schemes. Comput. Part. Mech. 2020, 8, 575–588. [Google Scholar] [CrossRef]
- Colagrossi, A.; Antuono, M.; Le Touzé, D. Theoretical considerations on the free-surface role in the smoothed-particle-hydrodynamics model. Phys. Review. E Stat. Nonlinear Soft Matter Phys. 2009, 79, 056701. [Google Scholar] [CrossRef] [PubMed]
- Chow, A.D.; Rogers, B.D.; Lind, S.J.; Stansby, P.K. Incompressible SPH (ISPH) with fast Poisson solver on a GPU. Comput. Phys. Commun. 2018, 226, 81–103. [Google Scholar] [CrossRef]
- Qiu, L.C. OpenCL-Based GPU Acceleration of ISPH Simulation for Incompressible Flows. Appl. Mech. Mater. 2014, 444–445, 380–384. [Google Scholar] [CrossRef]
- Chow, A.D.; Rogers, B.D.; Lind, S.J.; Stansby, P.K. Numerical wave basin using incompressible smoothed particle hydrodynamics (ISPH) on a single GPU with vertical cylinder test cases. Comput. Fluids 2019, 179, 543–562. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Domínguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Bilotta, G.; Hérault, A.; Cappello, A.; Ganci, G.; Del Negro, C. GPUSPH: A Smoothed Particle Hydrodynamics model for the thermal and rheological evolution of lava flows. Geol. Soc. Lond. Spec. Publ. 2016, 426, 387–408. [Google Scholar] [CrossRef]
- Randles, P.W.; Libersky, L.D. Smoothed Particle Hydrodynamics: Some recent improvements and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 375–408. [Google Scholar] [CrossRef]
- VILA, J.P. On particle weighted methods and smooth particle hydrodynamics. Math. Model. Methods Appl. Sci. 1999, 09, 161–209. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, X.Y.; Adams, N.A. A weakly compressible SPH method based on a low-dissipation Riemann solver. J. Comput. Phys. 2017, 335, 605–620. [Google Scholar] [CrossRef]
- Zhang, C.; Rezavand, M.; Zhu, Y.; Yu, Y.; Wu, D.; Zhang, W.; Wang, J.; Hu, X. SPHinXsys: An open-source multi-physics and multi-resolution library based on smoothed particle hydrodynamics. Comput. Phys. Commun. 2021, 267, 108066. [Google Scholar] [CrossRef]
- Meng, Z.F.; Zhang, A.M.; Wang, P.P.; Ming, F.R. A shock-capturing scheme with a novel limiter for compressible flows solved by smoothed particle hydrodynamics. Comput. Methods Appl. Mech. Eng. 2021, 386, 114082. [Google Scholar] [CrossRef]
- Meng, Z.F.; Ming, F.R.; Wang, P.P.; Zhang, A.M. Numerical simulation of water entry problems considering air effect using a multiphase Riemann-SPH model. Adv. Aerodyn. 2021, 3, 1–16. [Google Scholar]
- The NextFlow Software. Available online: https://www.nextflow-software.com/ (accessed on 25 November 2021).
- Sun, P.; Ming, F.; Zhang, A. Numerical simulation of interactions between free surface and rigid body using a robust SPH method. Ocean Eng. 2015, 98, 32–49. [Google Scholar] [CrossRef]
- Ming, F.R.; Sun, P.N.; Zhang, A.M. Numerical investigation of rising bubbles bursting at a free surface through a multiphase SPH model. Meccanica 2017, 52, 2665–2684. [Google Scholar] [CrossRef]
- Sun, P.N.; Colagrossi, A.; Marrone, S.; Zhang, A.M. The deltaplus-SPH model: Simple procedures for a further improvement of the SPH scheme. Comput. Methods Appl. Mech. Eng. 2017, 315, 25–49. [Google Scholar] [CrossRef]
- Lyu, H.G.; Sun, P.N.; Huang, X.T.; Chen, S.H.; Zhang, A.M. On removing the numerical instability induced by negative pressures in SPH simulations of typical fluid–structure interaction problems in ocean engineering. Appl. Ocean Res. 2021, 117, 102938. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Fourtakas, G.; Altomare, C.; Canelas, R.B.; Tafuni, A.; García-Feal, O.; Martínez-Estévez, I.; Mokos, A.; Vacondio, R.; Crespo, A.J.C.; et al. DualSPHysics: From fluid dynamics to multiphysics problems. Comput. Part. Mech. 2021, 8, 1–29. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.; Adams, N. A generalized wall boundary condition for smoothed particle hydrodynamics. J. Comput. Phys. 2012, 231, 7057–7075. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Gómez-Gesteira, M.; Dalrymple, R.A. Boundary Conditions Generated by Dynamic Particles in SPH Methods. Comput. Mater. Contin. 2007, 5, 173–184. [Google Scholar]
- English, A.; Domínguez, J.M.; Vacondio, R.; Crespo, A.J.C.; Stansby, P.K.; Lind, S.J.; Chiapponi, L.; Gómez-Gesteira, M. Modified dynamic boundary conditions (mDBC) for general-purpose smoothed particle hydrodynamics (SPH): Application to tank sloshing, dam break and fish pass problems. Comput. Part. Mech. 2021, 8, 1–15. [Google Scholar] [CrossRef]
- The Dive Solution. Available online: https://www.dive-solutions.de/ (accessed on 25 November 2021).
- Chiron, L.; de Leffe, M.; Oger, G.; Le Touzé, D. Fast and accurate SPH modelling of 3D complex wall boundaries in viscous and non viscous flows. Comput. Phys. Commun. 2019, 234, 93–111. [Google Scholar] [CrossRef]
- Jasak, H. OpenFOAM: Open source CFD in research and industry. Int. J. Nav. Archit. Ocean Eng. 2009, 1, 89–94. [Google Scholar] [CrossRef] [Green Version]
- Si, H. TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator. ACM Trans. Math. Softw. 2015, 41, 1–36. [Google Scholar] [CrossRef]
- Colagrossi, A.; Bouscasse, B.; Antuono, M.; Marrone, S. Particle packing algorithm for SPH schemes. Comput. Phys. Commun. 2012, 183, 1641–1653. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Zhang, C.; Yu, Y.; Hu, X. A CAD-compatible body-fitted particle generator for arbitrarily complex geometry and its application to wave-structure interaction. J. Hydrodyn. 2021, 33, 195–206. [Google Scholar] [CrossRef]
- Windt, C.; Davidson, J.; Ringwood, J.V. High-fidelity numerical modelling of ocean wave energy systems: A review of computational fluid dynamics-based numerical wave tanks. Renew. Sustain. Energy Rev. 2018, 93, 610–630. [Google Scholar] [CrossRef] [Green Version]
- Higuera, P.; Losada, I.J.; Lara, J.L. Three-dimensional numerical wave generation with moving boundaries. Coast. Eng. 2015, 101, 35–47. [Google Scholar] [CrossRef]
- Liu, X.; Lin, P.; Shao, S. ISPH wave simulation by using an internal wave maker. Coast. Eng. 2015, 95, 160–170. [Google Scholar] [CrossRef] [Green Version]
- Wen, H.; Ren, B. A non-reflective spectral wave maker for SPH modeling of nonlinear wave motion. Wave Motion 2018, 79, 112–128. [Google Scholar] [CrossRef]
- Altomare, C.; Domínguez, J.M.; Crespo, A.J.C.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-crested wave generation and absorption for SPH-based DualSPHysics model. Coast. Eng. 2017, 127, 37–54. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, Y.; Dias, F.; Hu, X. An efficient fully Lagrangian solver for modeling wave interaction with oscillating wave surge converter. Ocean Eng. 2021, 236, 109540. [Google Scholar] [CrossRef]
- He, M.; Khayyer, A.; Gao, X.; Xu, W.; Liu, B. Theoretical method for generating solitary waves using plunger-type wavemakers and its Smoothed Particle Hydrodynamics validation. Appl. Ocean Res. 2021, 106, 102414. [Google Scholar] [CrossRef]
- Yim, S.C.; Yuk, D.; Panizzo, A.; Di Risio, M.; Liu, P.L.F. Numerical Simulations of Wave Generation by a Vertical Plunger Using RANS and SPH Models. J. Waterw. Port, Coastal Ocean Eng. 2008, 134, 143–159. [Google Scholar] [CrossRef] [Green Version]
- Sun, P.N.; Luo, M.; Le Touzé, D.; Zhang, A.M. The suction effect during freak wave slamming on a fixed platform deck: Smoothed particle hydrodynamics simulation and experimental study. Phys. Fluids 2019, 31, 117108. [Google Scholar] [CrossRef]
- Colagrossi, A.; Souto-Iglesias, A.; Antuono, M.; Marrone, S. Smoothed-particle-hydrodynamics modeling of dissipation mechanisms in gravity waves. Phys. Rev. E 2013, 87, 023302. [Google Scholar] [CrossRef]
- Zago, V.; Schulze, L.J.; Bilotta, G.; Almashan, N.; Dalrymple, R.A. Overcoming excessive numerical dissipation in SPH modeling of water waves. Coast. Eng. 2021, 170, 104018. [Google Scholar] [CrossRef]
- Chen, J.K.; Beraun, J.E.; Carney, T.C. A corrective smoothed particle method for boundary value problems in heat conduction. Int. J. Numer. Methods Eng. 1999, 46, 231–252. [Google Scholar] [CrossRef]
- Bonet, J.; Lok, T.S.L. Variational and momentum preservation aspects of Smooth Particle Hydrodynamic formulations. Comput. Methods Appl. Mech. Eng. 1999, 180, 97–115. [Google Scholar] [CrossRef]
- Huang, C.; Lei, J.M.; Liu, M.B.; Peng, X.Y. A kernel gradient free (KGF) SPH method. Int. J. Numer. Methods Fluids 2015, 78, 691–707. [Google Scholar] [CrossRef]
- Lastiwka, M.; Basa, M.; Quinlan, N.J. Permeable and non-reflecting boundary conditions in SPH. Int. J. Numer. Methods Fluids 2009, 61, 709–724. [Google Scholar] [CrossRef] [Green Version]
- Federico, I.; Marrone, S.; Colagrossi, A.; Aristodemo, F.; Antuono, M. Simulating 2D open-channel flows through an SPH model. Eur. J. Mech. B Fluids 2012, 34, 35–46. [Google Scholar] [CrossRef]
- Vacondio, R.; Rogers, B.D.; Stansby, P.K.; Mignosa, P. SPH Modeling of Shallow Flow with Open Boundaries for Practical Flood Simulation. J. Hydraul. Eng. 2012, 138, 530–541. [Google Scholar] [CrossRef]
- Khorasanizade, S.; Sousa, J.M.M. An innovative open boundary treatment for incompressible SPH. Int. J. Numer. Methods Fluids 2016, 80, 161–180. [Google Scholar] [CrossRef]
- Oger, G.; Marrone, S.; Le Touzé, D.; de Leffe, M. SPH accuracy improvement through the combination of a quasi-Lagrangian shifting transport velocity and consistent ALE formalisms. J. Comput. Phys. 2016, 313, 76–98. [Google Scholar] [CrossRef]
- Antuono, M.; Bouscasse, B.; Colagrossi, A.; Marrone, S. A measure of spatial disorder in particle methods. Comput. Phys. Commun. 2014, 185, 2609–2621. [Google Scholar] [CrossRef]
- Xu, R.; Stansby, P.; Laurence, D. Accuracy and stability in incompressible SPH (ISPH) based on the projection method and a new approach. J. Comput. Phys. 2009, 228, 6703–6725. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.Y.; Adams, N.A. A transport-velocity formulation for smoothed particle hydrodynamics. J. Comput. Phys. 2013, 241, 292–307. [Google Scholar] [CrossRef]
- Mokos, A.; Rogers, B.D.; Stansby, P.K. A multi-phase particle shifting algorithm for SPH simulations of violent hydrodynamics with a large number of particles. J. Hydraul. Res. 2016, 55, 143–162. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Zhang, D.H.; Shi, Y.X.; Si, Y.L.; Huang, B. Coupled finite particle method with a modified particle shifting technology. Int. J. Numer. Methods Eng. 2018, 113, 179–207. [Google Scholar] [CrossRef]
- Huang, C.; Long, T.; Li, S.M.; Liu, M.B. A kernel gradient-free SPH method with iterative particle shifting technology for modeling low-Reynolds flows around airfoils. Eng. Anal. Bound. Elem. 2019, 106, 571–587. [Google Scholar] [CrossRef]
- Sun, P.N.; Colagrossi, A.; Marrone, S.; Antuono, M.; Zhang, A.M. A consistent approach to particle shifting in the δ-Plus-SPH model. Comput. Methods Appl. Mech. Eng. 2019, 348, 912–934. [Google Scholar] [CrossRef]
- Wang, P.P.; Meng, Z.F.; Zhang, A.M.; Ming, F.R.; Sun, P.N. Improved particle shifting technology and optimized free-surface detection method for free-surface flows in smoothed particle hydrodynamics. Comput. Methods Appl. Mech. Eng. 2019, 357, 112580. [Google Scholar] [CrossRef]
- Krimi, A.; Jandaghian, M.; Shakibaeinia, A. A WCSPH Particle Shifting Strategy for Simulating Violent Free Surface Flows. Water 2020, 12, 3189. [Google Scholar] [CrossRef]
- Jandaghian, M.; Krimi, A.; Zarrati, A.R.; Shakibaeinia, A. Enhanced weakly-compressible MPS method for violent free-surface flows: Role of particle regularization techniques. J. Comput. Phys. 2021, 434, 110202. [Google Scholar] [CrossRef]
- Jiang, T.; Ren, J.; Yuan, J.; Zhou, W.; Wang, D.S. A least-squares particle model with other techniques for 2D viscoelastic fluid/free surface flow. J. Comput. Phys. 2020, 407, 109255. [Google Scholar] [CrossRef]
- Lyu, H.G.; Sun, P.N. Further enhancement of the particle shifting technique: Towards better volume conservation and particle distribution in SPH simulations of violent free-surface flows. Appl. Math. Model. 2022, 101, 214–238. [Google Scholar] [CrossRef]
- Antuono, M.; Sun, P.N.; Marrone, S.; Colagrossi, A. The δ-ALE-SPH model: An arbitrary Lagrangian-Eulerian framework for the δ-SPH model with particle shifting technique. Comput. Fluids 2021, 216, 104806. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 2006, 56, 19–36. [Google Scholar] [CrossRef]
- Wang, P.P.; Zhang, A.M.; Meng, Z.F.; Ming, F.R.; Fang, X.L. A new type of WENO scheme in SPH for compressible flows with discontinuities. Comput. Methods Appl. Mech. Eng. 2021, 381, 113770. [Google Scholar] [CrossRef]
- Sun, P.N.; Colagrossi, A.; Marrone, S.; Antuono, M.; Zhang, A.M. Multi-resolution Delta-plus-SPH with tensile instability control: Towards high Reynolds number flows. Comput. Phys. Commun. 2018, 224, 63–80. [Google Scholar] [CrossRef]
- Antuono, M.; Marrone, S.; Di Mascio, A.; Colagrossi, A. Smoothed particle hydrodynamics method from a large eddy simulation perspective. Generalization to a quasi-Lagrangian model. Phys. Fluids 2021, 33, 015102. [Google Scholar] [CrossRef]
- Moghimi, M.H.; Quinlan, N.J. Application of background pressure with kinematic criterion for free surface extension to suppress non-physical voids in the finite volume particle method. Eng. Anal. Bound. Elem. 2019, 106, 126–138. [Google Scholar] [CrossRef] [Green Version]
- Dalton, G.; Alcorn, R.; Lewis, T. Case study feasibility analysis of the Pelamis wave energy convertor in Ireland, Portugal and North America. Renew. Energy 2010, 35, 443–455. [Google Scholar] [CrossRef]
- Hansen, R.H.; Kramer, M.M.; Vidal, E. Discrete Displacement Hydraulic Power Take-Off System for the Wavestar Wave Energy Converter. Energies 2013, 6, 4001–4044. [Google Scholar] [CrossRef]
- Wen, H.; Ren, B.; Yu, X. An improved SPH model for turbulent hydrodynamics of a 2D oscillating water chamber. Ocean Eng. 2018, 150, 152–166. [Google Scholar] [CrossRef]
- Madhi, F.; Yeung, R.W. On survivability of asymmetric wave-energy converters in extreme waves. Renew. Energy 2018, 119, 891–909. [Google Scholar] [CrossRef]
- Yeylaghi, S.; Moa, B.; Oshkai, P.; Buckham, B.; Crawford, C. ISPH modelling of an oscillating wave surge converter using an OpenMP-based parallel approach. J. Ocean Eng. Mar. Energy 2016, 2, 301–312. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.H.; Shi, Y.X.; Huang, C.; Si, Y.L.; Huang, B.; Li, W. SPH method with applications of oscillating wave surge converter. Ocean Eng. 2018, 152, 273–285. [Google Scholar] [CrossRef]
- Marrone, S.; Colagrossi, A.; Baudry, V.; Le Touzé, D. Extreme wave impacts on a wave energy converter: Load prediction through a SPH model. Coast. Eng. J. 2019, 61, 63–77. [Google Scholar] [CrossRef]
- Papillon, L.; Costello, R.; Ringwood, J.V. Boundary element and integral methods in potential flow theory: A review with a focus on wave energy applications. J. Ocean Eng. Mar. Energy 2020, 6, 303–337. [Google Scholar] [CrossRef]
- Sirnivas, S.; Yu, Y.H.; Hall, M.; Bosma, B. Coupled Mooring. Analyses for the WEC-Sim Wave Energy Converter Design Tool, Volume 6: Ocean Space Utilization; Ocean Renewable Energy. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Liu, Y.C.; Peng, Y.; Wan, D.C. Numerical Investigation on Interaction between a Semi-Submersible Platform and Its Mooring System, Volume 7: Ocean Engineering. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar]
- Palm, J.; Eskilsson, C.; Paredes, G.M.; Bergdahl, L. Coupled mooring analysis for floating wave energy converters using CFD: Formulation and validation. Int. J. Mar. Energy 2016, 16, 83–99. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.H.; Zhao, W.W.; Wan, D.C. Development of naoe-FOAM-SJTU solver based on OpenFOAM for marine hydrodynamics. J. Hydrodyn. 2019, 31, 1–20. [Google Scholar] [CrossRef]
- He, J.W.; Wan, D.C.; Hu, Z.Q. CFD Simulations of Helical Strakes Reducing Vortex Induced Motion of a Semi-Submersible, Volume 2: CFD and FSI. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C.; Wan, D. Establishing a fully coupled CFD analysis tool for floating offshore wind turbines. Renew. Energy 2017, 112, 280–301. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Xiao, Q. Development of a fully coupled aero-hydro-mooring-elastic tool for floating offshore wind turbines. J. Hydrodyn. 2019, 31, 21–33. [Google Scholar] [CrossRef] [Green Version]
- The MoorDyn Solver. Available online: https://github.com/mattEhall/MoorDyn (accessed on 25 November 2021).
- Tasora, A.; Anitescu, M. A matrix-free cone complementarity approach for solving large-scale, nonsmooth, rigid body dynamics. Comput. Methods Appl. Mech. Eng. 2011, 200, 439–453. [Google Scholar] [CrossRef] [Green Version]
- Sherman, M.A.; Seth, A.; Delp, S.L. Simbody: Multibody dynamics for biomedical research. Procedia IUTAM 2011, 2, 241–261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barreiro, A.; Crespo, A.J.C.; Dominguez, J.M.; Garcia-Feal, O.; Zabala, I.; Gomez-Gesteira, M. Quasi-static mooring solver implemented in SPH. J. Ocean Eng. Mar. Energy 2016, 2, 381–396. [Google Scholar] [CrossRef] [Green Version]
- Crespo, A.; Altomare, C.; Domínguez, J.; González-Cao, J.; Gómez-Gesteira, M. Towards simulating floating offshore oscillating water column converters with Smoothed Particle Hydrodynamics. Coast. Eng. 2017, 126, 11–26. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.C.; Hall, M.; Altomare, C.; Wu, M.; Stratigaki, V.; Troch, P.; Cappietti, L.; Gómez-Gesteira, M. SPH simulation of floating structures with moorings. Coast. Eng. 2019, 153, 103560. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y. Numerical studies of submerged moored box-type floating breakwaters with different shapes of cross-sections using SPH. Coast. Eng. 2020, 158, 103687. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y. Numerical investigations and optimizations of typical submerged box-type floating breakwaters using SPH. Ocean Eng. 2020, 209, 107475. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.J.C.; Tagliafierro, B.; Altomare, C.; Domínguez, J.M.; Gómez-Gesteira, M.; Viccione, G. Efficiency and survivability analysis of a point-absorber wave energy converter using DualSPHysics. Renew. Energy 2020, 162, 1763–1776. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.J.C.; Coe, R.G.; Tagliafierro, B.; Domínguez, J.M.; Bacelli, G.; Gómez-Gesteira, M. Modelling a Heaving Point-Absorber with a Closed-Loop Control System Using the DualSPHysics Code. Energies 2021, 14, 760. [Google Scholar] [CrossRef]
- Quartier, N.; Ropero-Giralda, P.M.; Domínguez, J.;; Stratigaki, V.;; Troch, P. Influence of the Drag Force on the Average Absorbed Power of Heaving Wave Energy Converters Using Smoothed Particle Hydrodynamics. Water 2021, 13, 384. [Google Scholar] [CrossRef]
- Brito, M.; Canelas, R.B.; García-Feal, O.; Domínguez, J.M.; Crespo, A.J.C.; Ferreira, R.M.L.; Neves, M.G.; Teixeira, L. A numerical tool for modelling oscillating wave surge converter with nonlinear mechanical constraints. Renew. Energy 2020, 146, 2024–2043. [Google Scholar] [CrossRef]
- Cui, J.; Chen, X.; Sun, P. Numerical investigation on the hydrodynamic performance of a new designed breakwater using smoothed particle hydrodynamic method. Eng. Anal. Bound. Elem. 2021, 130, 379–403. [Google Scholar] [CrossRef]
- Zhang, C.; Rezavand, M.; Hu, X. A multi-resolution SPH method for fluid-structure interactions. J. Comput. Phys. 2021, 429, 110028. [Google Scholar] [CrossRef]
- Wei, Z.; Edge, B.L.; Dalrymple, R.A.; Hérault, A. Modeling of wave energy converters by GPUSPH and Project Chrono. Ocean Eng. 2019, 183, 332–349. [Google Scholar] [CrossRef]
- Wang, C.; Tay, Z.Y.; Takagi, K.; Utsunomiya, T. Literature Review of Methods for Mitigating Hydroelastic Response of VLFS Under Wave Action. Appl. Mech. Rev. 2010, 63, 030802. [Google Scholar] [CrossRef]
- Ding, J.; Wu, Y.; Xie, Z.; Yang, W.; Wang, S.; Yu, J.; Yu, T. Overview: Research on hydroelastic responses of VLFS in complex environments. Mar. Struct. 2021, 78, 102978. [Google Scholar] [CrossRef]
- Collins, I.; Hossain, M.; Dettmer, W.; Masters, I. Flexible membrane structures for wave energy harvesting: A review of the developments, materials and computational modelling approaches. Renew. Sustain. Energy Rev. 2021, 151, 111478. [Google Scholar] [CrossRef]
- Long, T.; Huang, C.; Hu, D.; Liu, M. Coupling edge-based smoothed finite element method with smoothed particle hydrodynamics for fluid structure interaction problems. Ocean Eng. 2021, 225, 108772. [Google Scholar] [CrossRef]
- Yang, Q.; Jones, V.; McCue, L. Free-surface flow interactions with deformable structures using an SPH–FEM model. Ocean Eng. 2012, 55, 136–147. [Google Scholar] [CrossRef]
- Ming, F.; Zhang, A.; Xue, Y.; Wang, S. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions. Ocean Eng. 2016, 117, 359–382. [Google Scholar] [CrossRef]
- Long, T.; Hu, D.; Wan, D.; Zhuang, C.; Yang, G. An arbitrary boundary with ghost particles incorporated in coupled FEM–SPH model for FSI problems. J. Comput. Phys. 2017, 350, 166–183. [Google Scholar] [CrossRef]
- Zhang, N.; Yan, S.; Zheng, X.; Ma, Q. A 3D Hybrid Model Coupling SPH and QALE-FEM for Simulating Nonlinear Wave-structure Interaction. Int. J. Offshore Polar Eng. 2020, 30, 11–19. [Google Scholar] [CrossRef]
- Hu, T.; Wang, S.; Zhang, G.; Sun, Z.; Zhou, B. Numerical simulations of sloshing flows with an elastic baffle using a SPH-SPIM coupled method. Appl. Ocean Res. 2019, 93, 101950. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, T.; Sun, Z.; Wang, S.; Shi, S.; Zhang, Z. A δSPH–SPIM coupled method for fluid–structure interaction problems. J. Fluids Struct. 2021, 101, 103210. [Google Scholar] [CrossRef]
- Rao, C.p.; Wan, D.c. Numerical study of the wave-induced slamming force on the elastic plate based on MPS-FEM coupled method. J. Hydrodyn. 2018, 30, 70–78. [Google Scholar] [CrossRef]
- Zheng, H.; Shioya, R. Verifications for Large-Scale Parallel Simulations of 3D Fluid–Structure Interaction Using Moving Particle Simulation (MPS) and Finite Element Method (FEM). Int. J. Comput. Methods 2019, 16, 1840014. [Google Scholar] [CrossRef]
- Zhang, Y.; Wan, D. MPS-FEM Coupled Method for Fluid–Structure Interaction in 3D Dam-Break Flows. Int. J. Comput. Methods 2019, 16, 1846009. [Google Scholar] [CrossRef]
- He, J.; Tofighi, N.; Yildiz, M.; Lei, J.; Suleman, A. A coupled WC-TL SPH method for simulation of hydroelastic problems. Int. J. Comput. Fluid Dyn. 2017, 31, 174–187. [Google Scholar] [CrossRef]
- Sun, P.N.; Le Touzé, D.; Zhang, A.M. Study of a complex fluid-structure dam-breaking benchmark problem using a multi-phase SPH method with APR. Eng. Anal. Bound. Elem. 2019, 104, 240–258. [Google Scholar] [CrossRef]
- Zhan, L.; Peng, C.; Zhang, B.; Wu, W. A stabilized TL–WC SPH approach with GPU acceleration for three-dimensional fluid–structure interaction. J. Fluids Struct. 2019, 86, 329–353. [Google Scholar] [CrossRef]
- Islam, M.R.I.; Peng, C. A Total Lagrangian SPH method for modelling damage and failure in solids. Int. J. Mech. Sci. 2019, 157–158, 498–511. [Google Scholar] [CrossRef] [Green Version]
- Sun, P.N.; Le Touzé, D.; Oger, G.; Zhang, A.M. An accurate FSI-SPH modeling of challenging fluid-structure interaction problems in two and three dimensions. Ocean Eng. 2021, 221, 108552. [Google Scholar] [CrossRef]
- Peng, Y.X.; Zhang, A.M.; Ming, F.R. Numerical simulation of structural damage subjected to the near-field underwater explosion based on SPH and RKPM. Ocean Eng. 2021, 222, 108576. [Google Scholar] [CrossRef]
- Peng, Y.X.; Zhang, A.M.; Wang, S.P. Coupling of WCSPH and RKPM for the simulation of incompressible fluid–structure interactions. J. Fluids Struct. 2021, 102, 103254. [Google Scholar] [CrossRef]
- Ren, B.; Fan, H.; Bergel, G.L.; Regueiro, R.A.; Lai, X.; Li, S. A peridynamics–SPH coupling approach to simulate soil fragmentation induced by shock waves. Comput. Mech. 2015, 55, 287–302. [Google Scholar] [CrossRef]
- Fan, H.; Bergel, G.L.; Li, S. A hybrid peridynamics–SPH simulation of soil fragmentation by blast loads of buried explosive. Int. J. Impact Eng. 2016, 87, 14–27. [Google Scholar] [CrossRef] [Green Version]
- Fan, H.; Li, S. A Peridynamics-SPH modeling and simulation of blast fragmentation of soil under buried explosive loads. Comput. Methods Appl. Mech. Eng. 2017, 318, 349–381. [Google Scholar] [CrossRef]
- Sun, W.K.; Zhang, L.W.; Liew, K. A smoothed particle hydrodynamics–peridynamics coupling strategy for modeling fluid–structure interaction problems. Comput. Methods Appl. Mech. Eng. 2020, 371, 113298. [Google Scholar] [CrossRef]
- O Connor, J.; Rogers, B.D. A fluid–structure interaction model for free-surface flows and flexible structures using smoothed particle hydrodynamics on a GPU. J. Fluids Struct. 2021, 104, 103312. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Falahaty, H.; Shimizu, Y. An enhanced ISPH–SPH coupled method for simulation of incompressible fluid–elastic structure interactions. Comput. Phys. Commun. 2018, 232, 139–164. [Google Scholar] [CrossRef]
- Khayyer, A.; Tsuruta, N.; Shimizu, Y.; Gotoh, H. Multi-resolution MPS for incompressible fluid-elastic structure interactions in ocean engineering. Appl. Ocean Res. 2019, 82, 397–414. [Google Scholar] [CrossRef]
- Khayyer, A.; Shimizu, Y.; Gotoh, H.; Hattori, S. Multi-resolution ISPH-SPH for accurate and efficient simulation of hydroelastic fluid-structure interactions in ocean engineering. Ocean Eng. 2021, 226, 108652. [Google Scholar] [CrossRef]
- Panciroli, R.; Abrate, S.; Minak, G.; Zucchelli, A. Hydroelasticity in water-entry problems: Comparison between experimental and SPH results. Compos. Struct. 2012, 94, 532–539. [Google Scholar] [CrossRef]
- Khayyer, A.; Shimizu, Y.; Gotoh, H.; Nagashima, K. A coupled incompressible SPH-Hamiltonian SPH solver for hydroelastic FSI corresponding to composite structures. Appl. Math. Model. 2021, 94, 242–271. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.; Wu, Y.; Peng, X.; Duan, Y. Numerical analysis of unsteady cavitating turbulent flow and shedding horse-shoe vortex structure around a twisted hydrofoil. Int. J. Multiph. Flow 2013, 51, 33–43. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.w.; Ji, B.; Tsujimoto, Y. A review of cavitation in hydraulic machinery. J. Hydrodyn. 2016, 28, 335–358. [Google Scholar] [CrossRef]
- Long, X.; Cheng, H.; Ji, B.; Arndt, R.E.; Peng, X. Large eddy simulation and Euler–Lagrangian coupling investigation of the transient cavitating turbulent flow around a twisted hydrofoil. Int. J. Multiph. Flow 2018, 100, 41–56. [Google Scholar] [CrossRef]
- Cheng, H.; Bai, X.; Long, X.; Ji, B.; Peng, X.; Farhat, M. Large eddy simulation of the tip-leakage cavitating flow with an insight on how cavitation influences vorticity and turbulence. Appl. Math. Model. 2020, 77, 788–809. [Google Scholar] [CrossRef]
- Van Paepegem, W.; Blommaert, C.; De Baere, I.; Degrieck, J.; De Backer, G.; De Rouck, J.; Degroote, J.; Vierendeels, J.; Matthys, S.; Taerwe, L. Slamming wave impact of a composite buoy for wave energy applications: Design and large-scale testing. Polym. Compos. 2011, 32, 700–713. [Google Scholar] [CrossRef]
- Martínez-Ferrer, P.J.; Qian, L.; Causon, D.M.; Mingham, C.G.; Ma, Z. Numerical Simulation of Wave Slamming on a Flap-Type Oscillating Wave Energy Device. Int. J. Offshore Polar Eng. 2018, 28, 65–71. [Google Scholar] [CrossRef]
- Renzi, E.; Wei, Y.; Dias, F. The pressure impulse of wave slamming on an oscillating wave energy converter. J. Fluids Struct. 2018, 82, 258–271. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.Y.; Adams, N.A. A multi-phase SPH method for macroscopic and mesoscopic flows. J. Comput. Phys. 2006, 213, 844–861. [Google Scholar] [CrossRef]
- Grenier, N.; Antuono, M.; Colagrossi, A.; Le Touzé, D.; Alessandrini, B. An Hamiltonian interface SPH formulation for multi-fluid and free surface flows. J. Comput. Phys. 2009, 228, 8380–8393. [Google Scholar] [CrossRef]
- Hammani, I.; Marrone, S.; Colagrossi, A.; Oger, G.; Le Touzé, D. Detailed study on the extension of the δ-SPH model to multi-phase flow. Comput. Methods Appl. Mech. Eng. 2020, 368, 113189. [Google Scholar] [CrossRef]
- Sun, P.N.; Le Touzé, D.; Oger, G.; Zhang, A.M. An accurate SPH Volume Adaptive Scheme for modeling strongly-compressible multiphase flows. Part 1: Numerical scheme and validations with basic 1D and 2D benchmarks. J. Comput. Phys. 2020, 426, 109937. [Google Scholar] [CrossRef]
- Sun, P.N.; Le Touzé, D.; Oger, G.; Zhang, A.M. An accurate SPH Volume Adaptive Scheme for modeling strongly-compressible multiphase flows. Part 2: Extension of the scheme to cylindrical coordinates and simulations of 3D axisymmetric problems with experimental validations. J. Comput. Phys. 2020, 426, 109936. [Google Scholar] [CrossRef]
- Jiang, T.; Li, Y.; Sun, P.N.; Ren, J.L.; Li, Q.; Yuan, J.Y. A corrected WCSPH scheme with improved interface treatments for the viscous/viscoelastic two-phase flows. Comput. Part. Mech. 2021, 8, 1–21. [Google Scholar] [CrossRef]
- Zhu, G.; Graham, D.; Zheng, S.; Hughes, J.; Greaves, D. Hydrodynamics of onshore oscillating water column devices: A numerical study using smoothed particle hydrodynamics. Ocean Eng. 2020, 218, 108226. [Google Scholar] [CrossRef]
- Quartier, N.; Crespo, A.J.C.; Domínguez, J.M.; Stratigaki, V.; Troch, P. Efficient response of an onshore Oscillating Water Column Wave Energy Converter using a one-phase SPH model coupled with a multiphysics library. Appl. Ocean Res. 2021, 115, 102856. [Google Scholar] [CrossRef]
- Sarfaraz, M.; Pak, A. SPH numerical simulation of tsunami wave forces impinged on bridge superstructures. Coast. Eng. 2017, 121, 145–157. [Google Scholar] [CrossRef]
- Barcarolo, D.A.; Le Touzé, D.; Oger, G.; de Vuyst, F. Adaptive particle refinement and derefinement applied to the smoothed particle hydrodynamics method. J. Comput. Phys. 2014, 273, 640–657. [Google Scholar] [CrossRef]
- Chiron, L.; Oger, G.; de Leffe, M.; Le Touzé, D. Analysis and improvements of Adaptive Particle Refinement (APR) through CPU time, accuracy and robustness considerations. J. Comput. Phys. 2018, 354, 552–575. [Google Scholar] [CrossRef]
- Yang, X.; Kong, S.C. Adaptive resolution for multiphase smoothed particle hydrodynamics. Comput. Phys. Commun. 2019, 239, 112–125. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Kong, S.C.; Liu, M.; Liu, Q. Smoothed particle hydrodynamics with adaptive spatial resolution (SPH-ASR) for free surface flows. J. Comput. Phys. 2021, 443, 110539. [Google Scholar] [CrossRef]
- Hu, W.; Guo, G.; Hu, X.; Negrut, D.; Xu, Z.; Pan, W. A consistent spatially adaptive smoothed particle hydrodynamics method for fluid–structure interactions. Comput. Methods Appl. Mech. Eng. 2019, 347, 402–424. [Google Scholar] [CrossRef] [Green Version]
- Sun, P.N.; Colagrossi, A.; Marrone, S.; Zhang, A.M. Nonlinear water wave interactions with floating bodies using the δplus-SPH model. In Proceedings of the 32th International Workshop on Water Waves and Floating Bodies (IWWWFB), Dalian, China, 23–26 April 2017. [Google Scholar]
- Gong, K.; Shao, S.; Liu, H.; Wang, B.; Tan, S.K. Two-phase SPH simulation of fluid–structure interactions. J. Fluids Struct. 2016, 65, 155–179. [Google Scholar] [CrossRef] [Green Version]
- Markauskas, D.; Kruggel-Emden, H.; Sivanesapillai, R.; Steeb, H. Comparative study on mesh-based and mesh-less coupled CFD-DEM methods to model particle-laden flow. Powder Technol. 2017, 305, 78–88. [Google Scholar] [CrossRef] [Green Version]
- Markauskas, D.; Kruggel-Emden, H. Coupled DEM-SPH simulations of wet continuous screening. Adv. Powder Technol. 2019, 30, 2997–3009. [Google Scholar] [CrossRef]
- Xu, W.J.; Dong, X.Y.; Ding, W.T. Analysis of fluid-particle interaction in granular materials using coupled SPH-DEM method. Powder Technol. 2019, 353, 459–472. [Google Scholar] [CrossRef]
- Peng, C.; Zhan, L.; Wu, W.; Zhang, B. A fully resolved SPH-DEM method for heterogeneous suspensions with arbitrary particle shape. Powder Technol. 2021, 387, 509–526. [Google Scholar] [CrossRef]
- Ng, K.C.; Alexiadis, A.; Chen, H.; Sheu, T.W.H. Numerical computation of fluid–solid mixture flow using the SPH–VCPM–DEM method. J. Fluids Struct. 2021, 106, 103369. [Google Scholar] [CrossRef]
- Serván-Camas, B.; Cercós-Pita, J.; Colom-Cobb, J.; García-Espinosa, J.; Souto-Iglesias, A. Time domain simulation of coupled sloshing–seakeeping problems by SPH–FEM coupling. Ocean Eng. 2016, 123, 383–396. [Google Scholar] [CrossRef] [Green Version]
- Marrone, S.; Di Mascio, A.; Le Touzé, D. Coupling of Smoothed Particle Hydrodynamics with Finite Volume method for free-surface flows. J. Comput. Phys. 2016, 310, 161–180. [Google Scholar] [CrossRef]
- Chiron, L.; Marrone, S.; Di Mascio, A.; Le Touzé, D. Coupled SPH–FV method with net vorticity and mass transfer. J. Comput. Phys. 2018, 364, 111–136. [Google Scholar] [CrossRef]
- Bai, B.; Rao, D.; Xu, T.; Chen, P. SPH-FDM boundary for the analysis of thermal process in homogeneous media with a discontinuous interface. Int. J. Heat Mass Transf. 2018, 117, 517–526. [Google Scholar] [CrossRef]
- Huang, C.; Long, T.; Liu, M.B. Coupling finite difference method with finite particle method for modeling viscous incompressible flows. Int. J. Numer. Methods Fluids 2019, 90, 564–583. [Google Scholar] [CrossRef]
- Di Mascio, A.; Marrone, S.; Colagrossi, A.; Chiron, L.; Le Touzé, D. SPH–FV coupling algorithm for solving multi-scale three-dimensional free-surface flows. Appl. Ocean Res. 2021, 115, 102846. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.C.; Gómez-Gesteira, M. Optimization strategies for CPU and GPU implementations of a smoothed particle hydrodynamics method. Comput. Phys. Commun. 2013, 184, 617–627. [Google Scholar] [CrossRef]
- Luo, M.; Koh, C. Shared-Memory parallelization of consistent particle method for violent wave impact problems. Appl. Ocean Res. 2017, 69, 87–99. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Tian, L.; Rubinato, M.; Gu, S.; Yu, T.; Xu, Z.; Cao, P.; Wang, X.; Zhao, Q. A New Parallel Framework of SPH-SWE for Dam Break Simulation Based on OpenMP. Water 2020, 12, 1395. [Google Scholar] [CrossRef]
- Cui, X.; Habashi, W.G.; Casseau, V. MPI Parallelisation of 3D Multiphase Smoothed Particle Hydrodynamics. Int. J. Comput. Fluid Dyn. 2020, 34, 610–621. [Google Scholar] [CrossRef]
- Olivier, S.L.; Prins, J.F. Comparison of OpenMP 3.0 and Other Task Parallel Frameworks on Unbalanced Task Graphs. Int. J. Parallel Program. 2010, 38, 341–360. [Google Scholar] [CrossRef] [Green Version]
- Oger, G.; Le Touzé, D.; Guibert, D.; de Leffe, M.; Biddiscombe, J.; Soumagne, J.; Piccinali, J.G. On distributed memory MPI-based parallelization of SPH codes in massive HPC context. Comput. Phys. Commun. 2016, 200, 1–14. [Google Scholar] [CrossRef]
- Yang, E.; Bui, H.H.; De Sterck, H.; Nguyen, G.D.; Bouazza, A. A scalable parallel computing SPH framework for predictions of geophysical granular flows. Comput. Geotech. 2020, 121, 103474. [Google Scholar] [CrossRef]
- Harada, T.; Koshizuka, S.; Kawaguchi, Y. Smotthed Particle Hydrodynamics on GPUs. In Proceedings of the Computer Graphics International 2007, Petropolis, Brazil, 30 May–2 June 2007. [Google Scholar]
- Crespo, A.C.; Dominguez, J.M.; Barreiro, A.; Gómez-Gesteira, M.; Rogers, B.D. GPUs, a New Tool of Acceleration in CFD: Efficiency and Reliability on Smoothed Particle Hydrodynamics Methods. PLoS ONE 2011, 6, e20685. [Google Scholar] [CrossRef]
- Hérault, A.; Bilotta, G.; Dalrymple, R.A. SPH on GPU with CUDA. J. Hydraul. Res. 2010, 48, 74–79. [Google Scholar] [CrossRef]
- Cercos-Pita, J.L. AQUAgpusph, a new free 3D SPH solver accelerated with OpenCL. Comput. Phys. Commun. 2015, 192, 295–312. [Google Scholar] [CrossRef]
- Ramachandran, P.; Bhosale, A.; Puri, K.; Negi, P.; Muta, A.; Dinesh, A.; Menon, D.; Govind, R.; Sanka, S.; Sebastian, A.S.; et al. PySPH: A Python-based Framework for Smoothed Particle Hydrodynamics. ACM Trans. Math. Softw. 2021, 47. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.C.; Valdez-Balderas, D.; Rogers, B.D.; Gómez-Gesteira, M. New multi-GPU implementation for smoothed particle hydrodynamics on heterogeneous clusters. Comput. Phys. Commun. 2013, 184, 1848–1860. [Google Scholar] [CrossRef]
- Valdez-Balderas, D.; Domínguez, J.M.; Rogers, B.D.; Crespo, A.J.C. Towards accelerating smoothed particle hydrodynamics simulations for free-surface flows on multi-GPU clusters. J. Parallel Distrib. Comput. 2013, 73, 1483–1493. [Google Scholar] [CrossRef] [Green Version]
- Ji, Z.; Xu, F.; Takahashi, A.; Sun, Y. Large scale water entry simulation with smoothed particle hydrodynamics on single- and multi-GPU systems. Comput. Phys. Commun. 2016, 209, 1–12. [Google Scholar] [CrossRef]
- Morikawa, D.; Senadheera, H.; Asai, M. Explicit incompressible smoothed particle hydrodynamics in a multi-GPU environment for large-scale simulations. Comput. Part. Mech. 2021, 8, 493–510. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).