Statistical Investigation of Climate Change Effects on the Utilization of the Sediment Heat Energy
Abstract
:1. Introduction
- (1)
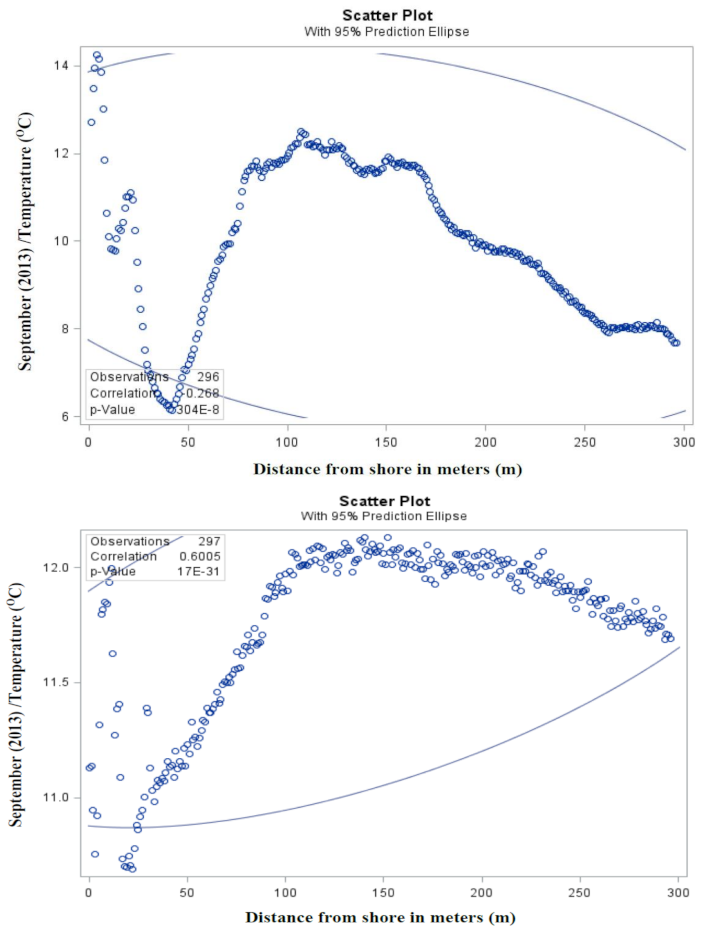
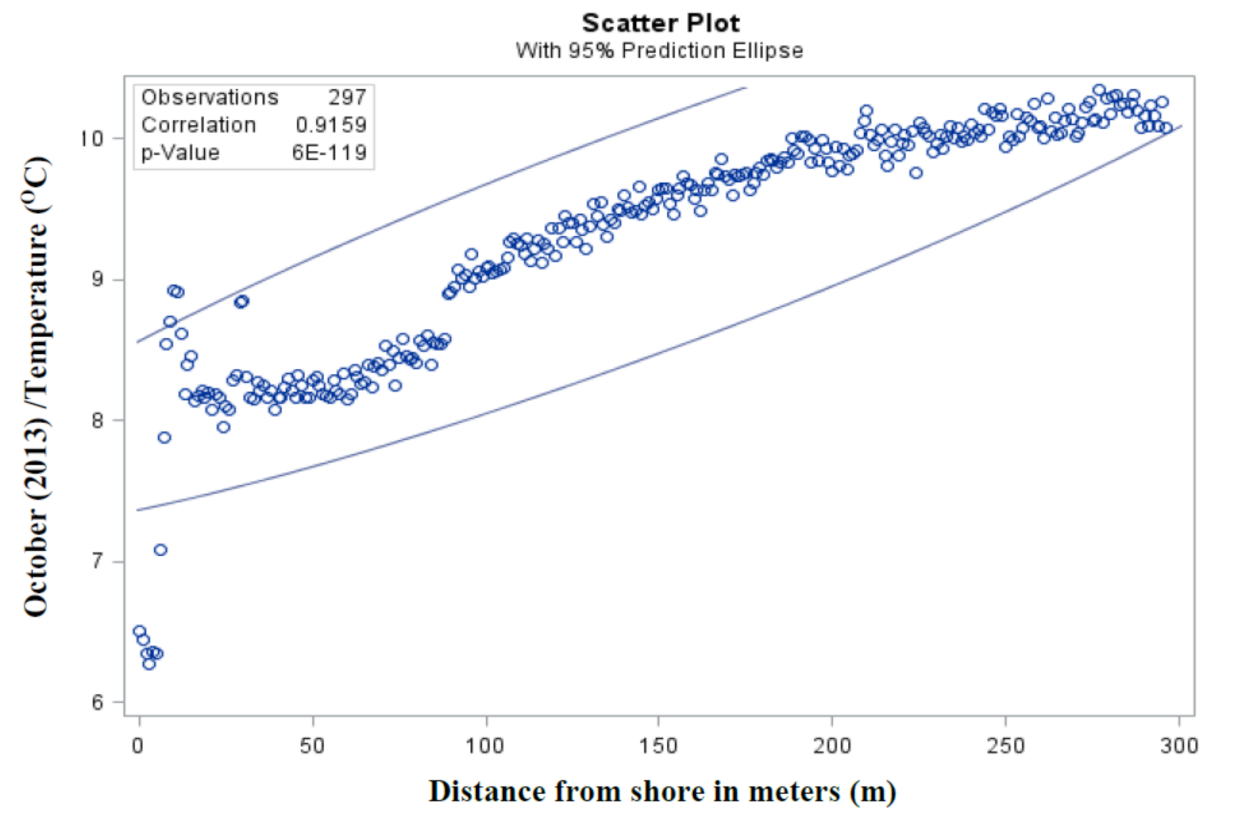
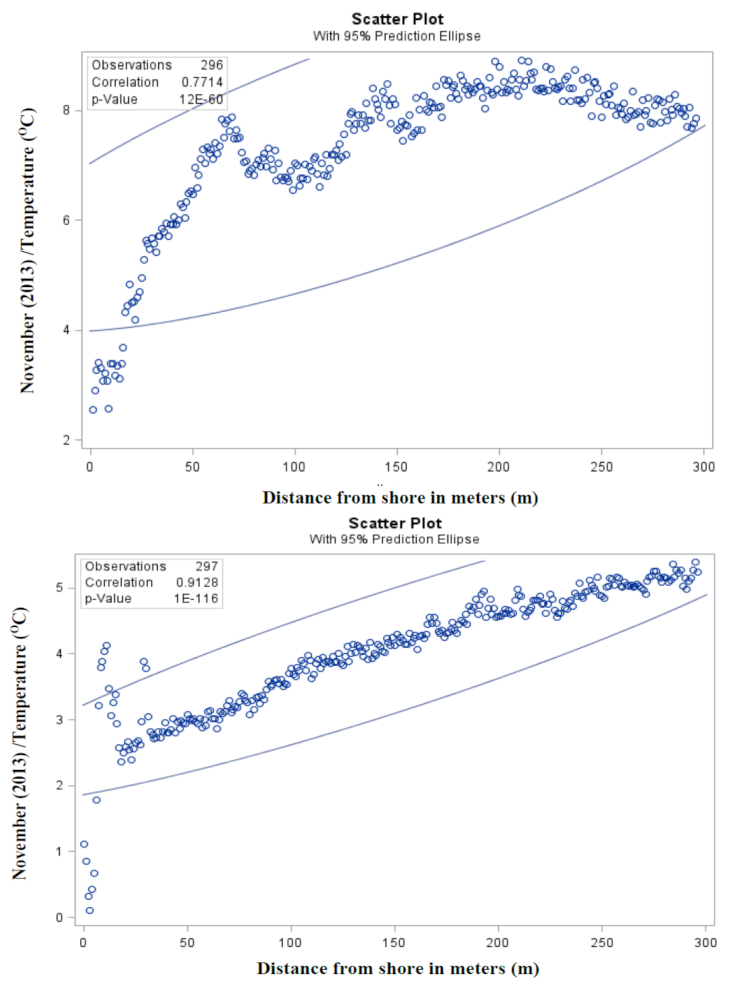
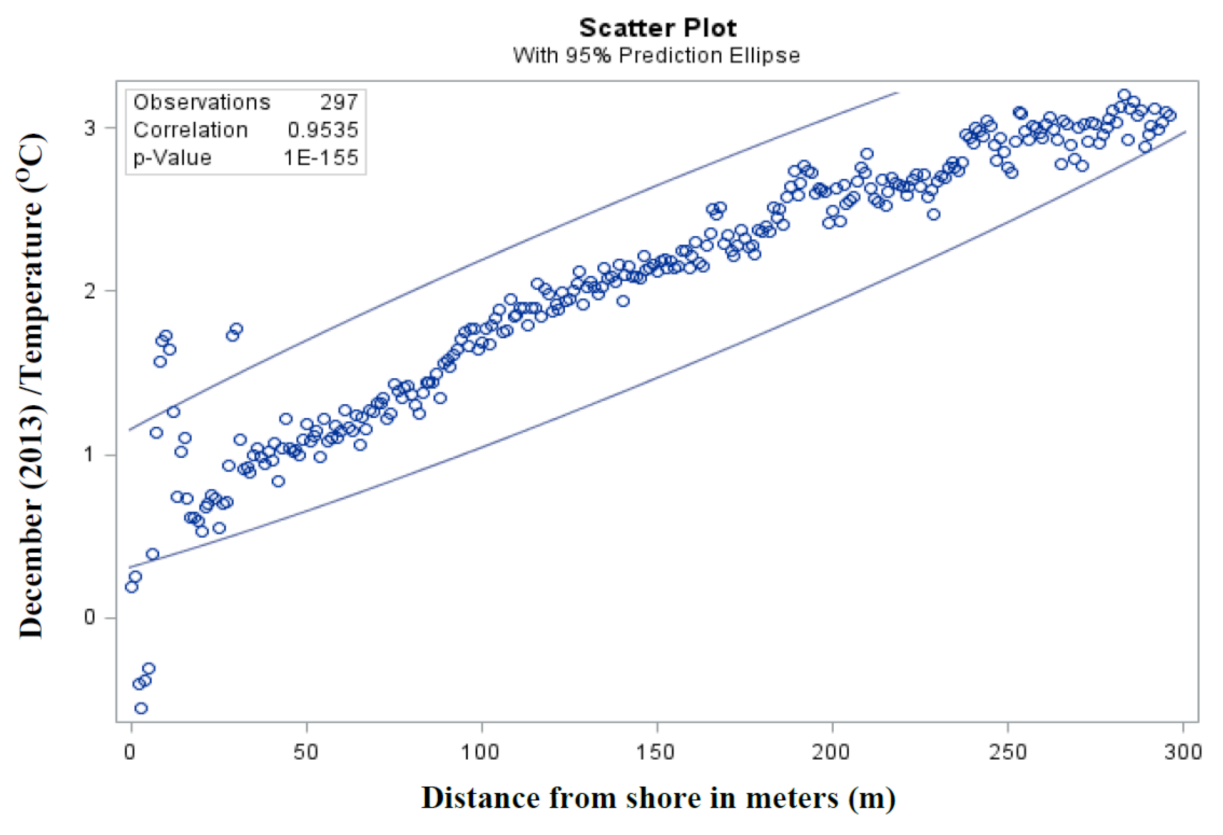
- Is there a correlation between different months vs. the distance from shore in sediment temperature? At what distance is the maximum sediment heat energy production possible?
- (2)
- Can climate change be advantageous for using sediment heat energy?
- (3)
- What are the benefits for using sediment heat energy if weather temperatures become warmer in summer and winter?
2. Materials and Methods
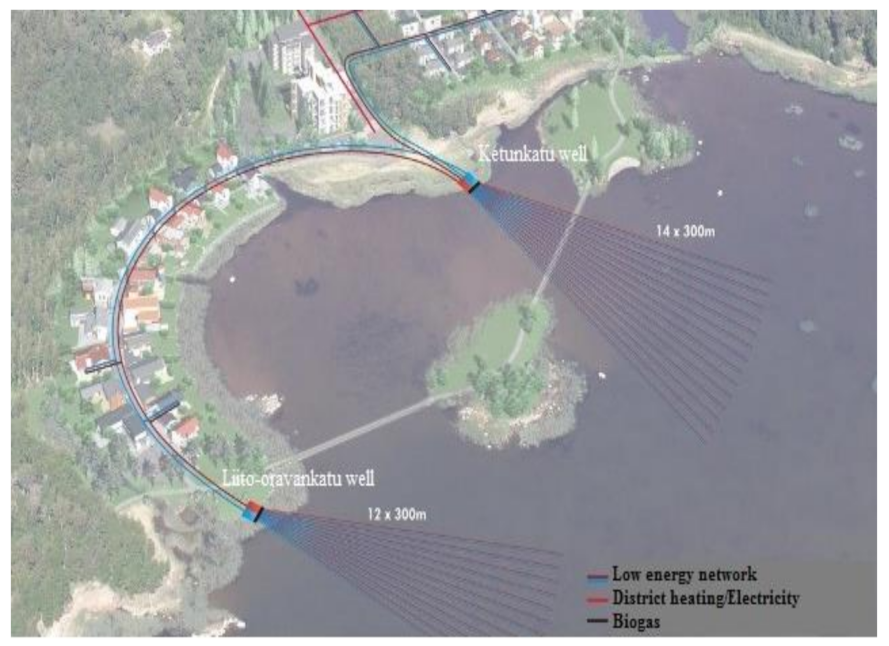
2.1. Data Collection Sites, Method, Descriptions and Validations
2.2. General Statistical Analysis Method
- (1)
- Decide specific points of interest;
- (2)
- Formulate several hypotheses;
- (3)
- Design and choose the necessary data and parameters for analyses;
- (4)
- Collect dummy data to form approximate values based on what was expected to be obtained—some of our original data were used as dummy data during this analysis;
- (5)
- Select appropriate tests;
- (6)
- Carry out the test(s) using the dummy data;
- (7)
- If there are problems, go back to step 3 (or 2); otherwise, proceed to use real data;
- (8)
- Carry out the test(s) using the real data and report the findings and/or return to step 2.
3. Results
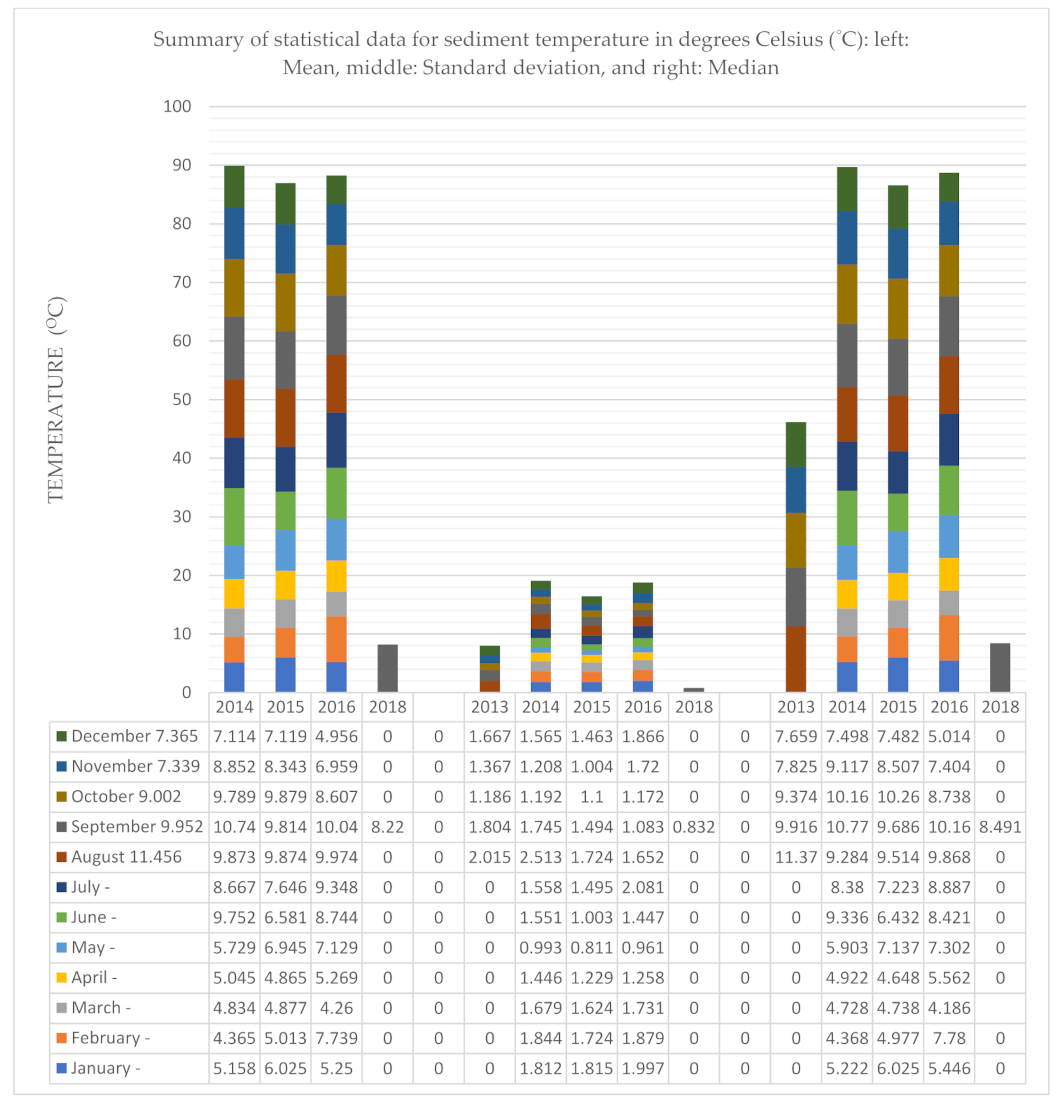
3.1. Summary of Statistics
3.2. Dependency Analysis
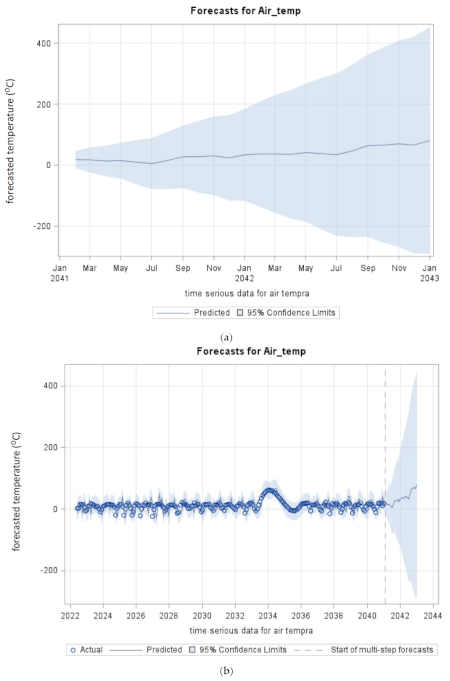
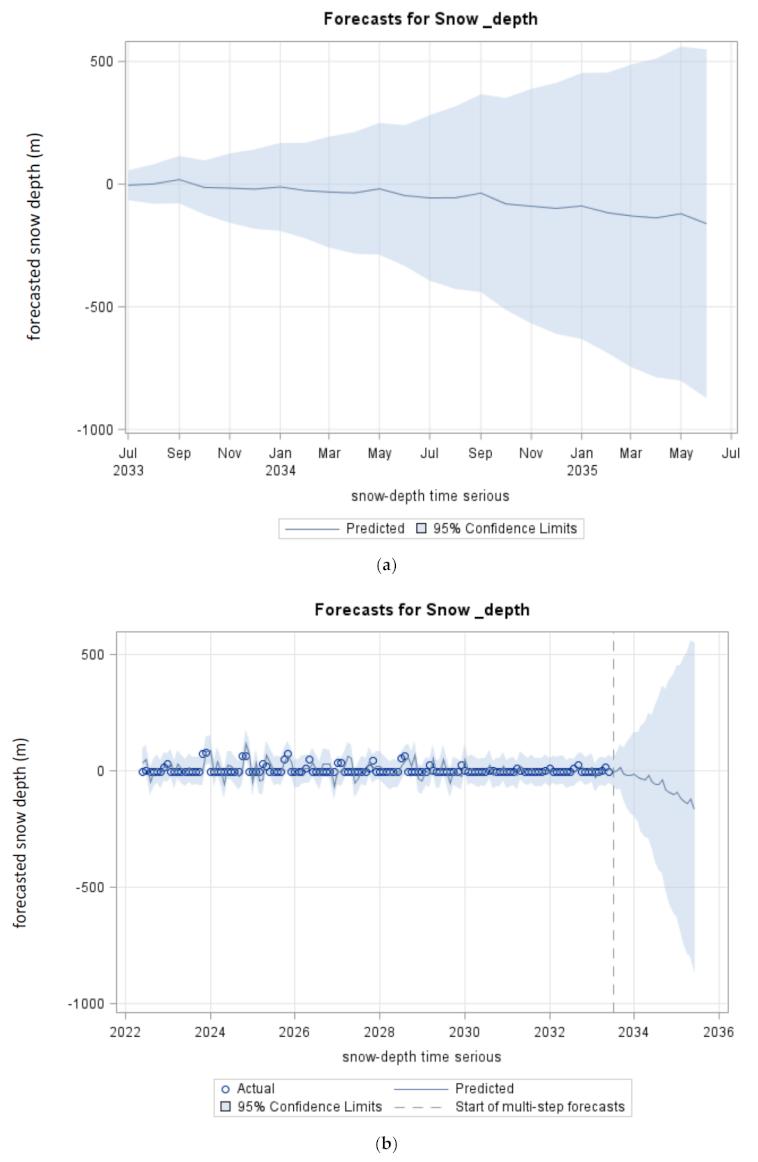
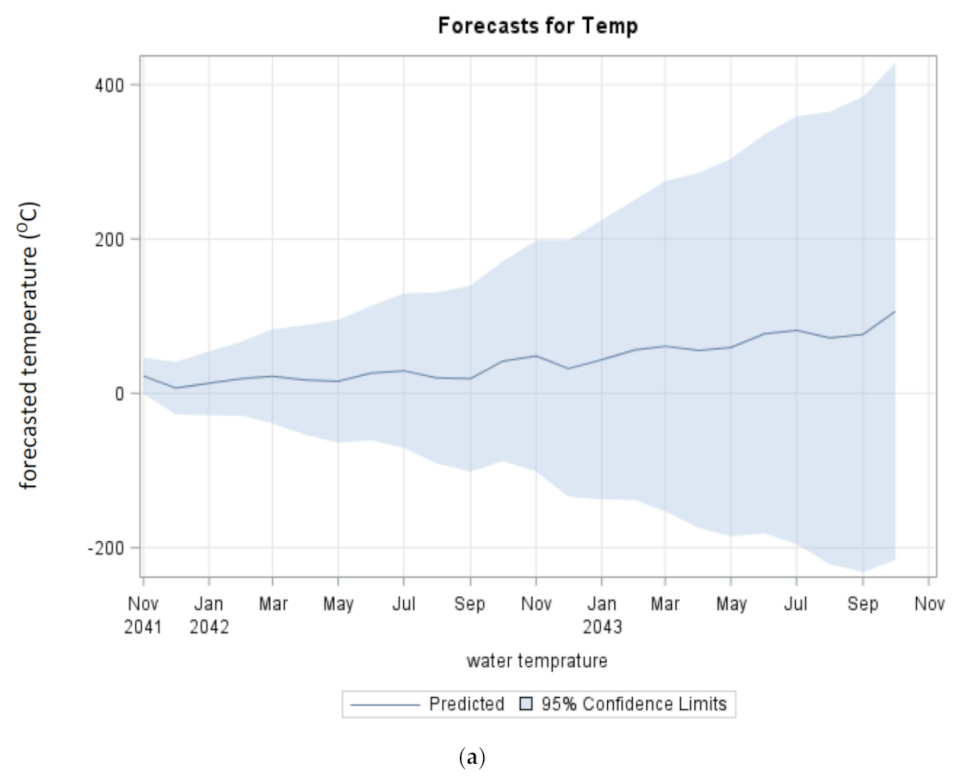
3.3. ARIMA Modeling Forecast
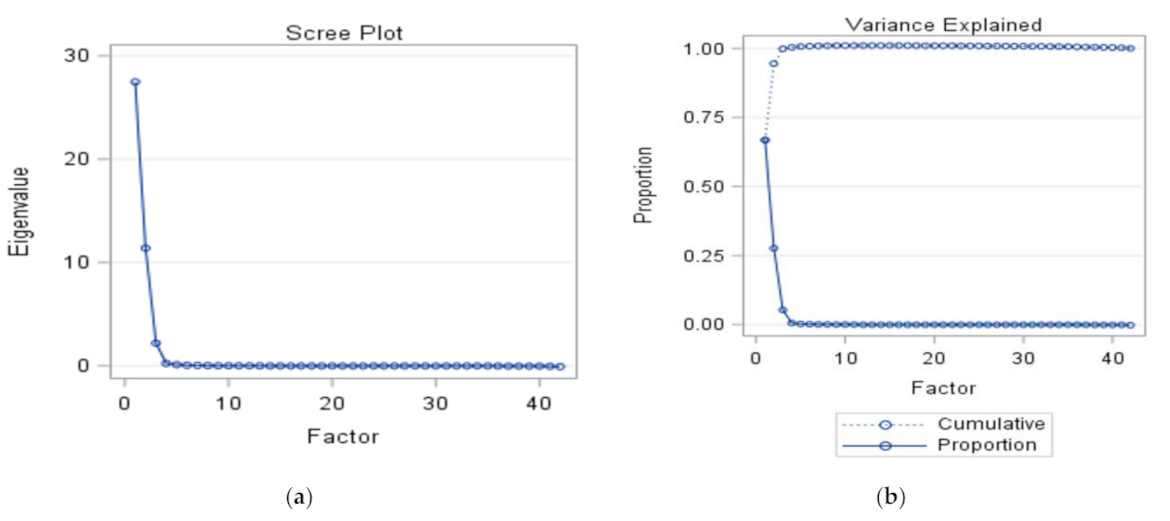
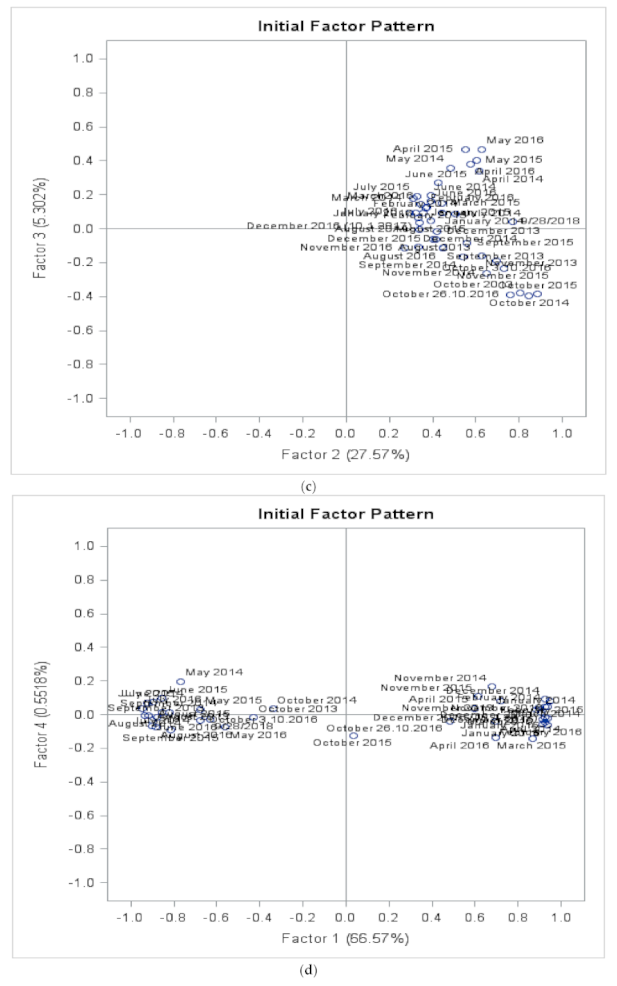
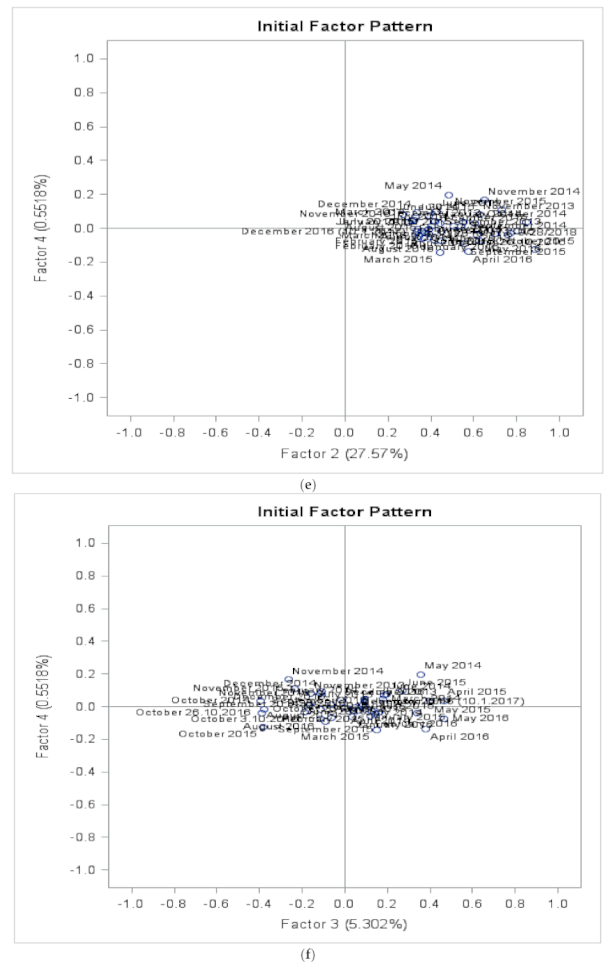
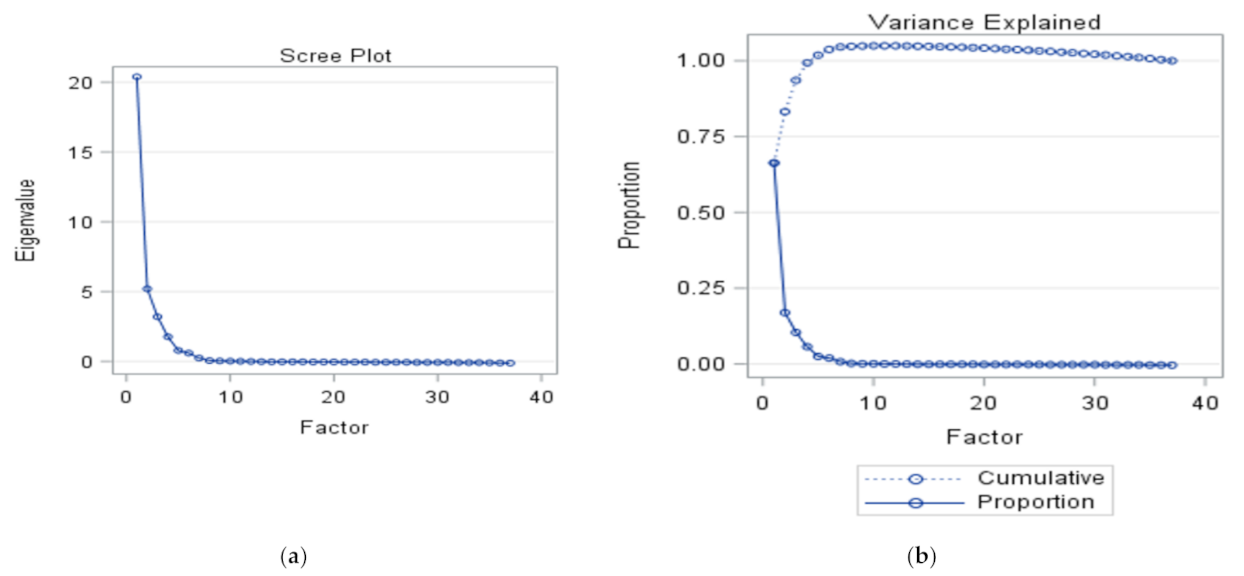
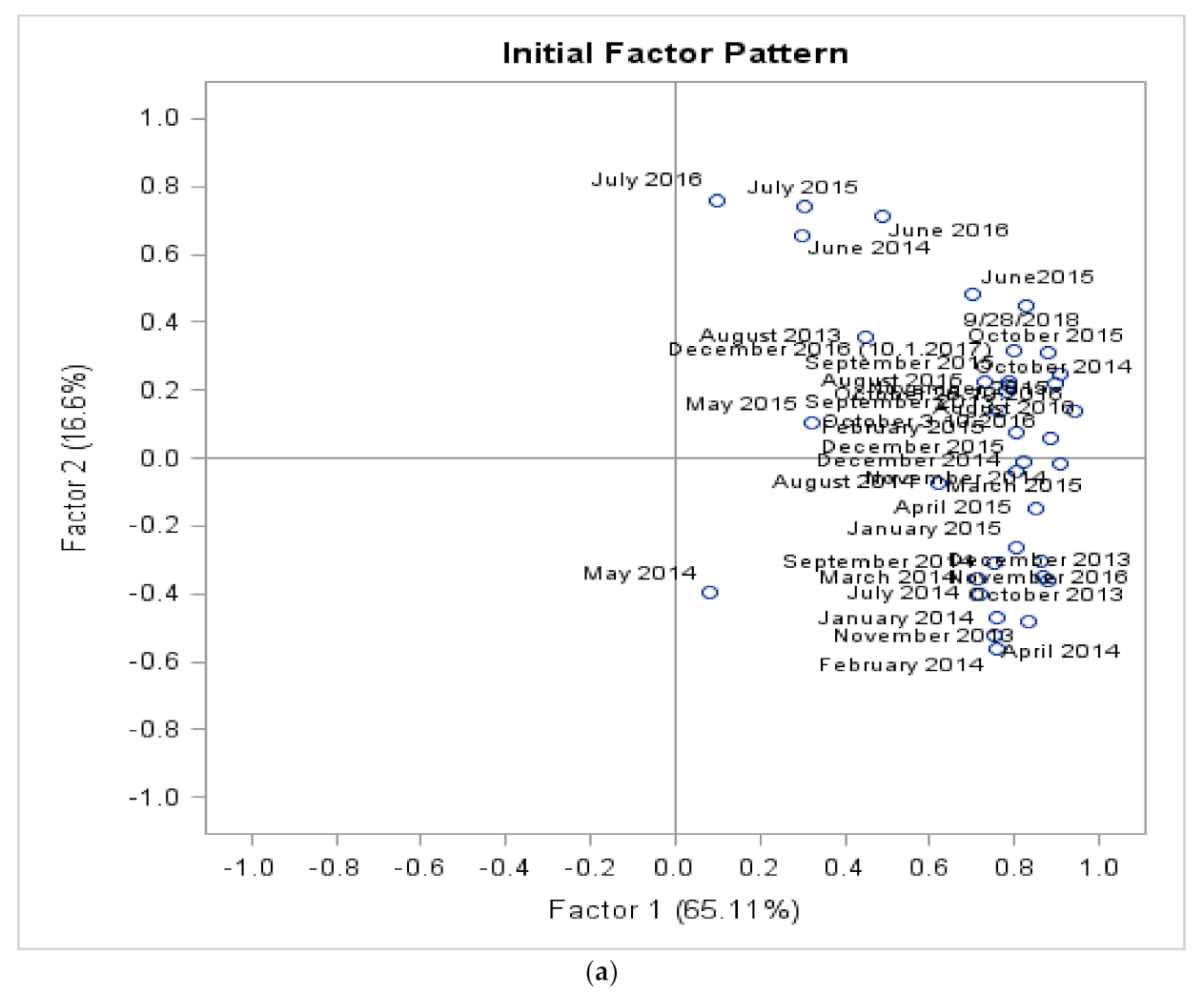
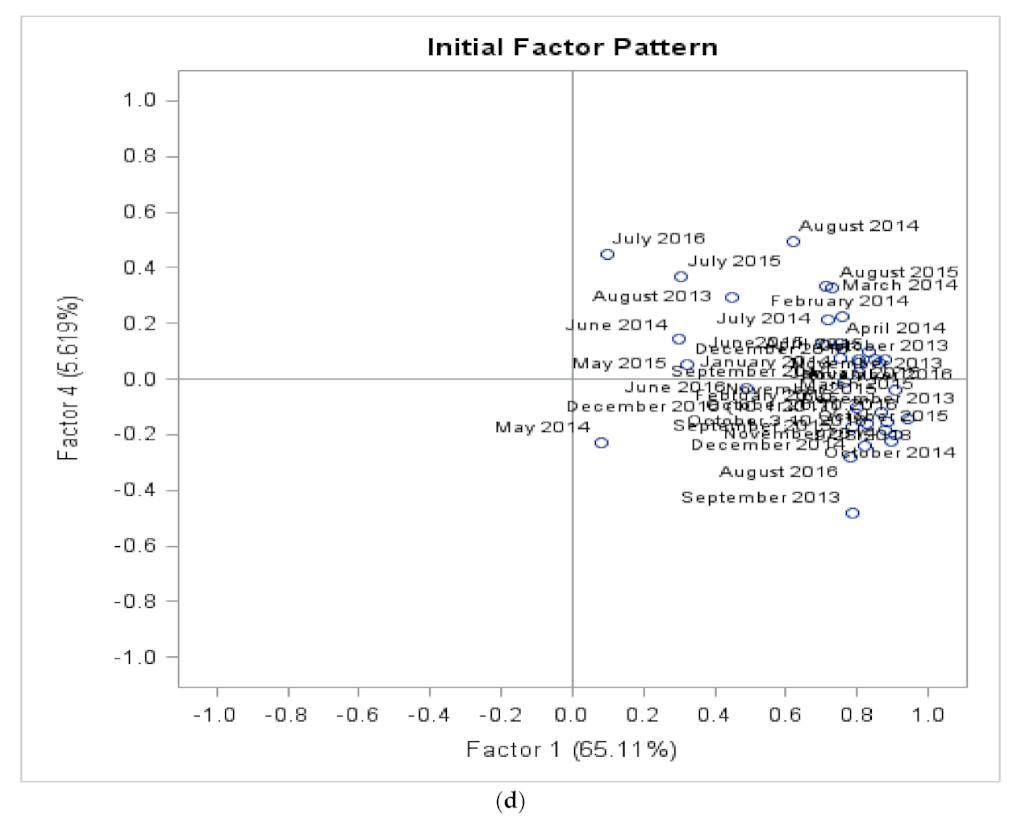
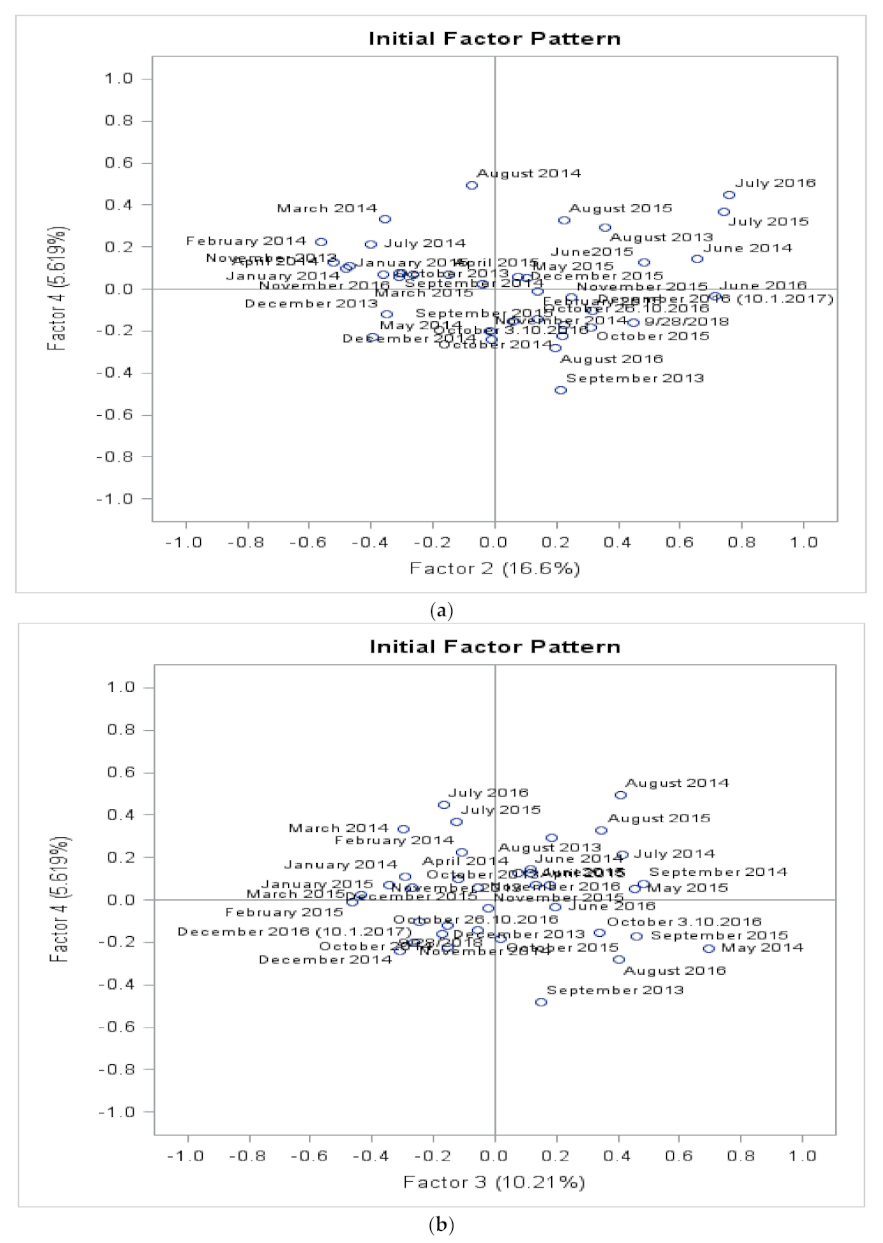
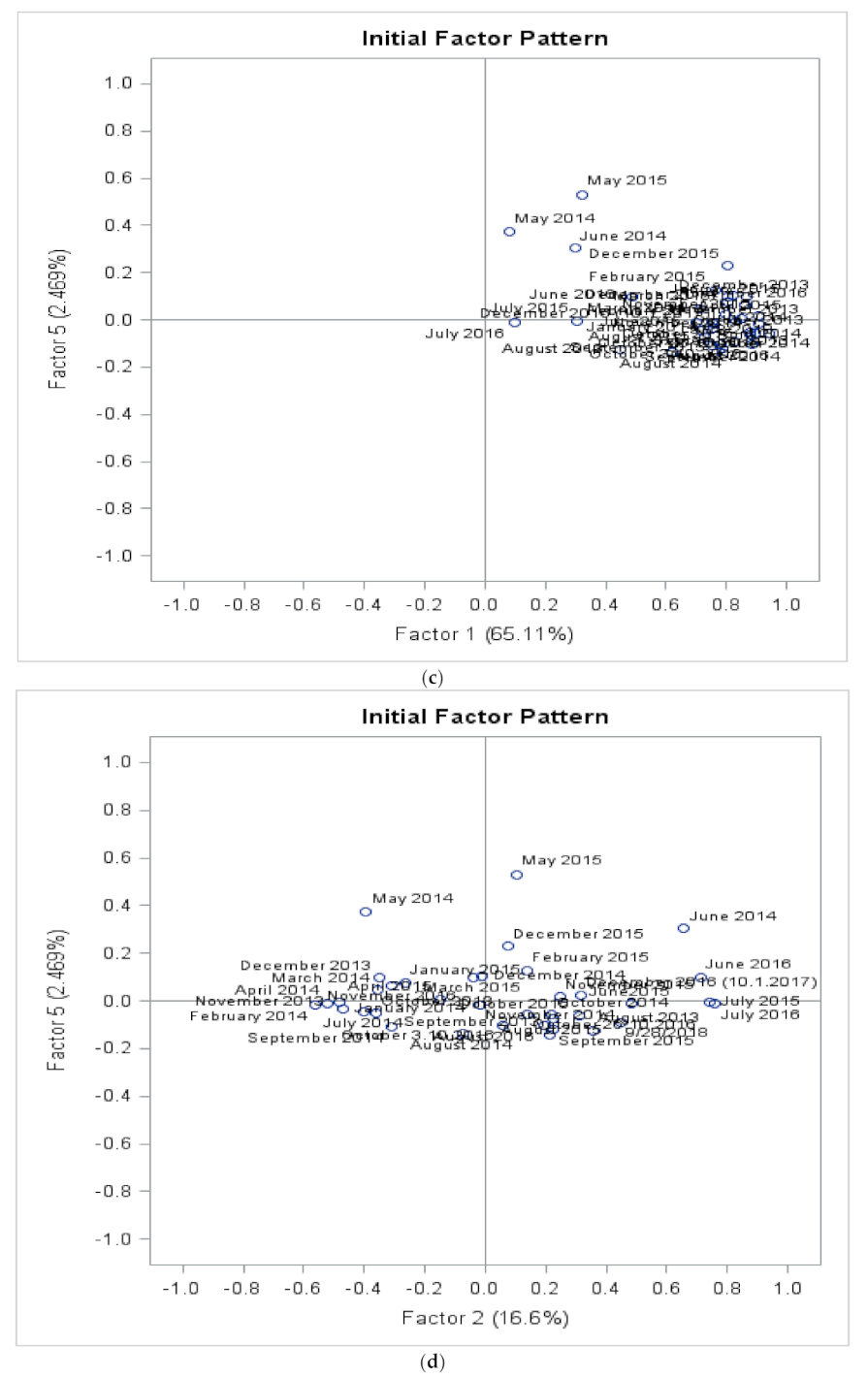
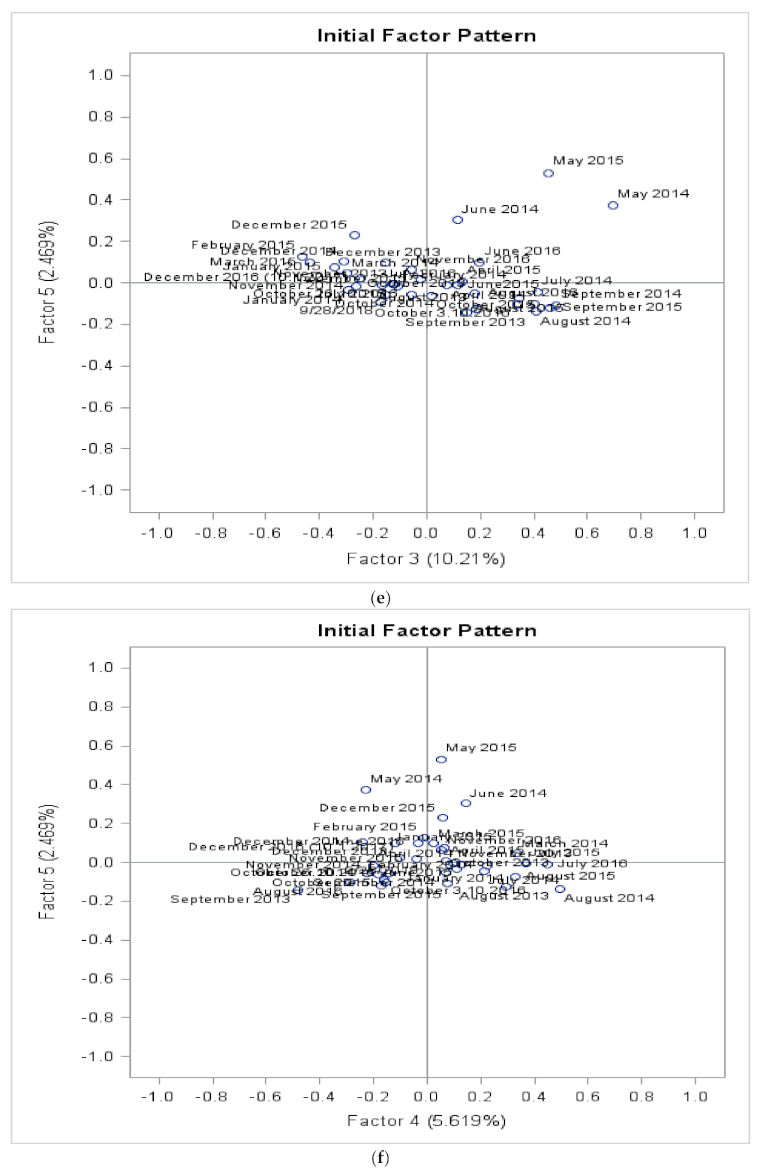
3.4. Validations by Factor Analysis
3.4.1. Validations by Factor Analysis for City of Vaasa at Suvilahti, Ketunkatu Site Data
3.4.2. Validations by Factor Analysis for the Suvilahti, Liito-Oravankatu Site Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ARIMA | Autoregression Integrated Moving Average |
| DTS | Distributed Temperature Sensing |
| FMI | Finnish Meteorological Institute |
| ELY-keskus | Center for Economic Development, Transport, and the Environment |
| IPCC | Intergovernmental Panel on Climate Change |
| Pt100s | The most common Platinum resistance thermometer |
| SAS | Statistical Analysis Software (Enterprise Guide 7.1) |
References
- Hiltunen, E.; Martinkauppi, J.B.; Mäkiranta, A.; Rinta-Luoma, J.; Syrjälä, T. Seasonal temperature variation in heat collection liquid used in renewable, carbon-free heat production from urban and rural water areas. Agron. Res. 2015, 13, 485–493. [Google Scholar]
- Likens, G.E.; Johnson, N.M. Measurement and analysis of the annual heat budget for the sediment in two Wisconsin lakes. Limnol. Oceanogr. 1969, 14, 115–135. [Google Scholar] [CrossRef]
- Oceanography 101 (Miracosta). (15 February 2021). Available online: https://geo.libretexts.org/@go/page/9666 (accessed on 18 July 2021).
- Savola, A. Fluid Flow Modeling Inside Heat Collection Pipes with Finite Element Method. Master’s thesis, University of Vaasa, Vaasa, Finland, 2012. [Google Scholar]
- Mäkiranta, A. Distributed Temperature Sensing Method–Usability in Asphalt and Sediment Heat Measurement. Master’s thesis, University of Vaasa, Vaasa, Finland, 2013. [Google Scholar]
- Ukil, A.; Braendle, H.; Krippner, P. Distributed temperature sensing: Review of technology and applications. IEEE Sens. J. 2012, 12, 885–892. [Google Scholar] [CrossRef] [Green Version]
- Wilcock, W.S.D.; Kauffman, P.C. Development of a seawater battery for deep-water applications. J. Power Sources 1997, 66, 71–75. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, D.; Richard, P.; Li, X. A geochemical record of environmental changes in sediments from Sishili Bay, northern Yellow Sea, China: Anthropogenic influence on organic matter sources and composition over the last 100 years. Mar. Pollut. Bull. 2013, 77, 227–236. [Google Scholar] [CrossRef]
- Reimers, C.R.; Tender, L.M.; Fertig, S.; Wang, W. Harvesting energy from the marine sediment-water interface. Environ. Sci. Technol. 2001, 35, 192–195. [Google Scholar] [CrossRef] [PubMed]
- Hiltunen, E.; Martinkauppi, J.B.; Zhu, L.; Mäkiranta, A.; Lieskoski, M.; Rinta-Luoma, J. Renewable, carbon-free heat production from urban and rural water areas. J. Clean. Prod. 2015, 153, 379–404. [Google Scholar] [CrossRef]
- Mäkiranta, A.; Martinkauppi, J.B.; Hiltunen, E. Seabed sediment—A natural seasonal heat storage feasibility study. Agron. Res. 2017, 15 (Suppl. S1), 1101–1106. [Google Scholar]
- Mäkiranta, A.; Martinkauppi, J.B.; Hiltunen, E. Correlation between temperature of air, heat carrier liquid and seabed sediment in renewable low energy network. Agron. Res. 2016, 14 (Suppl. S1), 1191–1199. [Google Scholar]
- Mäkiranta, A.; Martinkauppi, B.; Hiltunen, E.; Lieskoski, M. Seabed sediment as an annually renewable heat source. Appl. Sci. 2018, 8, 290. [Google Scholar] [CrossRef] [Green Version]
- Sebok, E.; Müller, S. The effect of sediment thermal conductivity on vertical groundwater flux estimates. Hydrol. Earth Syst. Sci. 2019, 23, 3305–3317. [Google Scholar] [CrossRef] [Green Version]
- Goto, S.; Yamano, M.; Morita, S.; Kanamatsu, T.; Hachikubo, A.; Kataoka, S.; Tanahashi, M.; Matsumoto, R. Physical and thermal properties of mud-dominant sediment from the Joetsu Basin in the eastern margin of the Japan Sea. Mar. Geophys. Res. 2017, 38, 393–407. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Ma, J. Temperature Rise of Seawater Simulation under the Influence of Sediment-Water Heat Exchange. Water 2018, 10, 656. [Google Scholar] [CrossRef] [Green Version]
- Golosov, S.; Kirillin, G. A parameterized model of heat storage by lake sediments. In Environmental Modeling and Software; Elsevier: Amsterdam, The Netherlands, 2010; Volume 25, pp. 793–801. [Google Scholar] [CrossRef]
- Pivato, M.; Carniello, L.; Gardner, J.; Silvestri, S.; Marani, M. Water and sediment temperature dynamics in shallow tidal environments: The role of the heat flux at the sediment-water interface. Adv. Water Resour. 2018, 113, 126–140. [Google Scholar] [CrossRef]
- Hamilton, D.P.; Magee, M.R.; Wu, C.H.; Kratz, T.K. Ice cover and thermal regime in a dimictic seepage lake under climate change. Inland Waters 2018, 8, 381–398. [Google Scholar] [CrossRef]
- Ellis, C.R.; Stefan, H.G.; Gu, R. Water temperature dynamics and heat transfer beneath the ice cover of a lake. Limnol. Oceanogr. 1991, 36, 324–335. [Google Scholar] [CrossRef]
- Smith, P.N. Observations and simulations of water-sediment heat exchange in a shallow coastal lagoon. Estuaries 2002, 25, 483–487. [Google Scholar] [CrossRef]
- Tsay, T.-K.; Ruggaber, G.J.; Effler, S.W.; Driscoll, C.T. Thermal Stratification modeling of lakes with sediment heat flux. J. Hydraul. Eng. 1992, 118, 407–419. [Google Scholar] [CrossRef]
- Meyers, L.S.; Gamst, G.; Guarino, A.J. Data Analysis Using SAS Enterprise Guide; Cambridge University Press: Cambridge, UK, 2009; ISBN -13. [Google Scholar]
- Dytham, C. Choosing and Using Statistics—A Biologist’s Guide, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-1-4443-2843-1. [Google Scholar]
- IPCC. Climate Change 2021: The Physical Science Basis. In Proceedings of the Contribution of Working Group— I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC AR6 WGI), 2021. Available online: https://www.ipcc (accessed on 31 July 2021).
- Drucker-Godard, C.; Ehlinger, S.; Grenier, C. Validity and Reliability. In Doing Management Research; SAGE Publication Ltd.: London, UK, 2011; pp. 196–220. [Google Scholar] [CrossRef]
- Kim, T.W.; Cho, Y.K. Calculation of heat flux in a macrotidal flat using FVCOM. J. Geophys. Res. Ocean. 2011, 116, 869–881. [Google Scholar] [CrossRef] [Green Version]
- Rinehimer, J.P.; Thomson, J.T. Observations and modeling of heat fluxes on tidal flats. J. Geophys. Res. Ocean. 2014, 119, 133–146. [Google Scholar] [CrossRef]
- Guarini, J.M.; Blanchard, G.F.; Gros, P.; Harrison, S.J. Modelling the mud surface temperature on intertidal flats to investigate the spatio-temporal dynamics of the benthic microalgal photosynthetic capacity. Mar. Ecol. Prog. Ser. 1997, 153, 25–36. [Google Scholar] [CrossRef]
- Fang, X.; Stefan, H.G. Temperature variability in lake sediments. Water Resour. Res. 1997, 34, 717–729. [Google Scholar] [CrossRef]









| Pearson’s Correlation for Month Temperature vs. Distance | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distance | Distance | Distance | Distance | Distance | Distance | Distance | |||||||
| distance | 1 | 14 January | 0.83502 | 14 July | −0.23757 | 15 January | 0.83798 | 15 July | −0.36584 | 16 January | 0.78473 | 16 July | −0.40112 |
| <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | ||||||||
| 297 | 297 | 297 | 297 | 297 | 297 | 297 | |||||||
| 13 August | −0.06398 | 14 February | 0.85858 | 14 August | −0.4735 | 15 February | 0.84782 | 15 August | −0.45013 | 16 February | 0.82599 | August | −0.36077 |
| 0.2717 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | |||||||
| 297 | 297 | 297 | 297 | 297 | 297 | 297 | |||||||
| 13 September | −0.26751 | 14 March | 0.88269 | 14 September | −0.33784 | 15 March | 0.861 | 15 September | −0.3517 | 16 March | 0.85545 | 3 October 2016 | −0.06442 |
| <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | 0.2684 | |||||||
| 296 | 297 | 297 | 297 | 297 | 297 | 297 | |||||||
| 13 October | 0.2583 | 14 April | 0.88997 | 14 October | 0.07311 | 14 April | 0.92268 | 15 October | 0.23263 | 16 April | 0.78695 | 26 October 2016 | 0.56589 |
| <0.0001 | <0.0001 | 0.209 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | |||||||
| 296 | 297 | 297 | 297 | 297 | 214 | 297 | |||||||
| 13 November | 0.77142 | 13 May | 0.36606 | 14 November | 0.67664 | 15 May | 0.60669 | November 15 | 0.66131 | 16 May | 0.58907 | 16 November | 0.78826 |
| <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | |||||||
| 296 | 297 | 297 | 297 | 297 | 297 | 297 | |||||||
| 13 December | 0.81126 | 14 June | −0.21912 | 14 December | 0.79345 | 15 June | −0.06697 | 15 December | 0.78921 | 16 June | −0.18148 | December 2016 (10 January 2017) | 0.83927 |
| <0.0001 | 0.0001 | <0.0001 | 0.2499 | <0.0001 | 0.0017 | <0.0001 | |||||||
| 296 | 297 | 297 | 297 | 297 | 297 | 297 | |||||||
| 28 September 2018 | 0.35938 | ||||||||||||
| <0.0001 | |||||||||||||
| 297 | |||||||||||||
| Pearson’s Correlation for Month Temperature vs. Distance | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Distance | Distance | Distance | Distance | Distance | Distance | Distance | |||||
| distance | 1 | 14 January | 0.83861 | 14 July | 0.66525 | 15 January | 0.94156 | 15 July | −0.61598 | 16 June | 0.62211 |
| <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | |||||||
| 297 | 297 | 297 | 297 | 297 | 297 | ||||||
| 13 August | −0.68564 | 14 February | 0.91661 | 14 August | −0.91378 | 15 February | 0.95283 | 15 August | −0.38679 | 16 July | −0.88149 |
| <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | ||||||
| 297 | 297 | 297 | 297 | 297 | 297 | ||||||
| 13 September | 0.60053 | 14 March | 0.9571 | 14 September | 0.56162 | 15 March | 0.94234 | 15 September | 0.70828 | 16 August | 0.66973 |
| <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | ||||||
| 297 | 297 | 297 | 297 | 297 | 297 | ||||||
| 13 October | 0.9159 | 14 April | 0.93862 | 14 October | 0.92784 | 15 April | 0.96703 | 15 October | 0.93696 | 3 October 2016 | 0.9117 |
| <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | ||||||
| 297 | 297 | 297 | 297 | 297 | 297 | ||||||
| 13 November | 0.91276 | 14 May | 0.78181 | 14 November | 0.95282 | 15 May | 0.87094 | 15 November | 0.95067 | 26 October 2016 | 0.94707 |
| <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | ||||||
| 297 | 297 | 297 | 297 | 297 | 297 | ||||||
| 13 December | 0.95347 | 14 June | −0.67468 | 14 December | 0.96502 | 15 June | 0.80705 | 15 December | 0.96568 | 16 November | 0.95512 |
| <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | ||||||
| 297 | 297 | 297 | 297 | 297 | 297 | ||||||
| December 2016 (10 January 2017) | 0.96501 | ||||||||||
| <0.0001 | |||||||||||
| 297 | |||||||||||
| 28 September 2018 | 0.89186 | ||||||||||
| <0.0001 | |||||||||||
| 297 | |||||||||||
| Input Data Type | Raw Data | ||
|---|---|---|---|
| Number of Records Read | 298 | ||
| Number of Records Used | 213 | ||
| N for Significance Tests | 213 | ||
| Variance Explained by Each Factor | |||
| Factor 1 | Factor 2 | Factor 3 | Factor 4 |
| 27.479995 | 11.382338 | 2.188676 | 0.227792 |
| Input Data Type | Raw Data | |||
|---|---|---|---|---|
| Number of Records Read | 298 | |||
| Number of Records Used | 297 | |||
| N for Significance Tests | 297 | |||
| Variance Explained by Each Factor | ||||
| Factor 1 | Factor 2 | Factor 3 | Factor 4 | Factor 5 |
| 20.390920 | 5.198181 | 3.196084 | 1.759724 | 0.773356 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Girgibo, N.; Mäkiranta, A.; Lü, X.; Hiltunen, E. Statistical Investigation of Climate Change Effects on the Utilization of the Sediment Heat Energy. Energies 2022, 15, 435. https://doi.org/10.3390/en15020435
Girgibo N, Mäkiranta A, Lü X, Hiltunen E. Statistical Investigation of Climate Change Effects on the Utilization of the Sediment Heat Energy. Energies. 2022; 15(2):435. https://doi.org/10.3390/en15020435
Chicago/Turabian StyleGirgibo, Nebiyu, Anne Mäkiranta, Xiaoshu Lü, and Erkki Hiltunen. 2022. "Statistical Investigation of Climate Change Effects on the Utilization of the Sediment Heat Energy" Energies 15, no. 2: 435. https://doi.org/10.3390/en15020435
APA StyleGirgibo, N., Mäkiranta, A., Lü, X., & Hiltunen, E. (2022). Statistical Investigation of Climate Change Effects on the Utilization of the Sediment Heat Energy. Energies, 15(2), 435. https://doi.org/10.3390/en15020435







