Abstract
This paper presents original concepts of control systems for an electrical drive with an elastic mechanical coupling between the motor and the driven mechanism. The synthesis procedure of the speed controller uses a proposed quality index (cost function) of system operation ensures the minimization of both tracking errors and torsional vibrations. Proper selection of the cost function focusses more on the reduction of torsional vibrations due to their negative influence on the drive’s mechanical coupling vitality. The omission of the plant identification of an adaptive fuzzy controller was proposed. Two types of fuzzy controllers were analyzed, namely with type I and type II fuzzy membership functions. The novelty of the presented approach is in the application of a Petri transition layer in a type II fuzzy controller which reduces the numerical complexity in case of a large number of complicated type II fuzzy sets. The presented simulation and experimental results prove that the best dumping of mechanical vibrations ensures the adaptive fuzzy controller with type II functions and a Petri transition layer.
1. Introduction
The demand for the productivity of technological processes is still growing. This goal can be achieved by increasing the speed of the industrial lines. The primary devices which are moving modern processes are electrical motors. They provide driving torque from electrical motors to load machines through different transmission systems, such as mechanical shafts, belts or chains. However, due to the finite stiffens of those elements, the undesirable phenomena can be excited. The major problem of such systems, which limit their performance, are torsional vibrations [1,2,3,4].
Torsional vibrations were first recognized in big industrial drives, a typical example being rolling mill drives, in which the mechanical connection may be as long as ten meters and the driving motor and load machines possess large inertia. A similar problem is evident in conveyer belt drive. The elasticity of the belt causes several problems in industrial applications. Another traditional example are cage-hoist drives, but torsional vibrations were investigated in paper and textile industries [1,2,3,4].
The characteristic feature of the above-mentioned applications is a low frequency of torsional vibrations. Due to the progress of modern power electronics, microprocessor techniques which allows forcing the driving torque of the motor practically without delay (as compared to the time constant of the driving elements) the torsional vibrations are recognized nowadays in almost all modern drive systems, for instance micro-electromechanical systems, robot-arm drives, CNC-tools, deep space antenna systems, drives in electrical cars, windmills and others [3,4,5]. Up until the present moment, different control approaches developed in order to suppress torsional vibrations can be divided into two main frameworks.
The first one includes all methodologies based on the application of additional mechanical dampers. These approaches, applied in electrical car or robot arm drives have the following drawbacks. Firstly, their use increases the total cost of the mechanism. Secondly, the mechanical dampers require some space, which is not always available. Furthermore, the additional elements affect the reliability of the system; therefore this approach is not preferable in modern systems.
The second framework involves all concepts based on control theory. The main advantage of this approach is the fact that only the control program is modified, while the mechanical parts of the drives remain identical. This framework can be divided into the following groups.
The concept based on the linear control theory constitutes the first one. The most basic methodology is the application of the standard PI controller. However, due to the fact that the closed-loop system is a fourth-order and there are (in PI) only two parameters, the independent location of the closed-loop poles of the system is not possible. This means that in this system the performance limitations are visible [6,7,8,9]. In [6], the analysis of the influence of the closed-loop poles’ location on the drive performance is presented. The following configurations of poles are considered: with an identical resonant pulsation, damping and real part. The mathematical formulas which allow assigning the poles in the selected position are provided. It is shown that oscillations are reduced effectively when poles of the system have an identical real part. The more detailed analysis of such methodology is provided in [7]. In this paper, the relationship between individual closed-loop poles is shown. The author set the position of the one pair of poles, the location of other pair comes from design requirements and limitations. This extends the possible location of poles presented in [7], which can result in a better performance of the drive. The most detailed analysis of such a system is presented in [8]. The authors investigate three above-mentioned positions of the system closed-loop poles. They claim that the most effective strategy is based on the identical pulsation and damping assignment. The application of the d-decomposition technique to the analysis of the drive performance is presented in [9]. This technique allows to determine the stable region of the work as a function of changes of particular parameters of the control structure (plant as well as controller coefficients). Furthermore, additional delays (caused by the torque control loop and speed sensor) can be included in the formal analysis. The optimal gains of the controller can be selected on the basis of the gain and phase margin of the system.
In order to improve the features of the structure with a PI controller, different approaches have been proposed. The most popular one is based on inserting one or two additional feedbacks to the structure, which increases the number of the control parameters and allow to shift the system poles to the desired position. According to the literature, one of the most popular is a system with one additional feedback from the shaft torque. In [10] the nine possible additional feedbacks are analyzed. It is shown that all systems can be divided into three major groups with identical performance. Another approach visible in the literature is based on the application of the state controller [11,12,13]. Usually, systems with an additional integration term, located in the main path are considered. Given that the state controller allows one to locate the closed-loop poles independently, the desired performance can be achieved. The main problem connected with the state-controller is the location of closed-loop poles, the problem of estimation of the non-measurable variable, and limitations of the internal states (e.g., shaft torque) of the system. In order to improve the system performance, in [11] the advanced estimation technique based on the MHE (moving horizon estimator) algorithm is proposed. The increased accuracy of the estimator ensures more efficient works of the state-controller. In [12] the auto-tuning methodology based on the Artificial Bee Colony is described. The gains of the state controller are selected using user-defined optimization function. It allows obtaining optimal performances for the specified criteria. The state controller is proposed in [13] for a system with an additional internal delay. This element increases the order of the system, but the extended analysis allows to obtain better performance.
A methodology that allows to locate poles independently and at the same time neglects the effect of the load (disturbance) torque is Forced Dynamic Control. This control method was proposed by S. Dodds in [14]. The future modification of this strategy was discussed in [15]. In this paper, the control of the two-mass system with the additional limitation of electromagnetic and shaft torque is considered. There are also other methodologies based on linear control theory, however, they are less popular.
The suppression of the torsional oscillations with the help of a disturbance observer(s) is quite a popular approach. The concept is based on the estimation of the torsional torque (which is treated as a disturbance) and feeding it back to the control structure. In [16] a slow RRC (Resonance Ratio Control) is proposed. The methodology which allows selecting the controller parameters is described. In order to reduce noises in the estimated torsional torque, a low pass filter is proposed. The application of the RRC to pushing control of flexible manipulator is introduced in [17]. The proposed algorithm includes three modes: approaching, touching and pushing. In the first mode RRC is used to damp torsional vibrations. The drive system with a backlash is investigated in [18]. An additional compensator working together with a returnable speed controller is proposed. A similar problem is considered in [19]. Here, the load side encoder improves the performance of the drive. In [20] control strategies for a humanoid manipulator is proposed. Torsional vibrations are suppressed with the help of the RRC strategy. In order to improve the robustness of the system, additional motor side and arm side disturbance observers are implemented. The double disturbance compensation schemes are investigated in [21]. The experiments performed on a two-joint robot confirmed the effectiveness of the proposed approach.
The second group encompasses concepts based on advanced control strategies. In this group Model Predictive Control (MPC) can be included [22,23,24]. In general, MPC relies on the shifted time window, where the future behaviour of the plant is predicted. Then drawing on the specified cost function, the optimisation process is applied in order to select the suitable control signal. Thus, MPC can be treated as an optimal-control strategy. The input and output constraints problem is taken directly in the MPC during the design of the control algorithm, which is seen as a significant advantage of the MPC. The main drawback of this strategy is large computational effort. For this reason, this strategy was originally implemented in systems with a big time constant (petrochemical industry). Due to the increase in the computational power of microprocessors nowadays, it is also implemented in systems with short sampling times, such as power electronics and electrical drives. The explicit MPC-based speed control structure is investigated in [22]. The system is tested under different conditions, including the limitation of the torsional torque. An example of a position control structure for the drive with a flexible link is presented in [23]. The optimization problem is solved offline in order to reduce the computational effort in the real-time implementation. The limitation of the shaft torque problem is described in detail in [24]. The authors proposed an optimal ratio between different limitations used in the two-mass drive. This strategy improves the drive performance under limitations. The application of the MPC to drive a system with a backlash is presented in [25]. The prediction of the limit cycle with the help of describing function method is implemented.
Another control structure within the second group of strategies is the sliding-mode control (SMC). This strategy is said to be robust against parameter variations and external disturbances. Two kinds of work can be distinguished here, namely reaching and sliding phases. At the start, the system moves using the reaching phase. During this time the system is sensitive to disturbances. In contrast, after obtaining the sliding phase the system becomes robust against disturbances. The application of the sliding-mode control in electrical drives is presented in [26]. The parameters of the control structure are derived on the basis of the Lyapunov theory. Despite external perturbations, the system’s performance is satisfactory. There are also less popular approaches reported in the literature.
Adaptive systems can be distinguished as a third group. In general, two types of adaptive control are mentioned in the literature [27,28,29,30,31,32,33,34,35,36]. The first one is called indirect adaptive control. In these systems an additional block is visible [27]. Its goal is to estimate the value of the changeable parameters of the system. Then, this value is used to retune the controller’s parameters. The main problem in this control structure is the stability and accuracy of the implemented estimation algorithm. Its incorrect work can lead even to control structure instability. In the following papers using this methodology with reference to the two-mass system have been presented [27]. The structure with a PI controller and additional feedbacks is proposed in the paper. The unscented Kalman filter is used in order to estimate the states of the plant as well as the changeable time constant. According to this estimated value, the control structure parameters are retuned online in every iteration.
The second approach is called direct adaptive control, in which the parameters of the controller are changed directly, due to the changes of the tracking error (specified as output between the desired trajectory and real output of the plant) [28,29,30,31,32,33,34,35,36,37,38]. For linear systems the suitable solution could be a classical PI controller. However, in the presence of additional non-linearities and changes of the system parameters a more advanced controller should be used in this structure. In [28] an application of the fuzzy logic controller is described. The authors report good performance of the control structure, yet they describe the learning time as being relatively long. In order to eliminate this drawback, the fuzzy sliding-mode controller has been proposed in [29], since it allows a faster adaptation process and makes the control system more robust to additional disturbances. The control of a nonlinear two-mass system (mechanical hysteresis, frictions) with the help of an adaptive sliding-mode controller is proposed in [30]. Despite nonlinearities, the system is able to damp vibrations effectively. The control of the two-mass system with nonlinear stiffness and damping using a PI controller is presented in [31]. The procedure is based on the backstepping scheme. The authors report good results. The backstepping adaptive control is implemented for a wind turbine [32]. It improves the efficiency of the generated power.
In the literature, different types of controllers are proposed. In [33,34,35,36,37] NN (neural networks) based approaches are implemented. A comparison of four different types of NN controllers is presented in [34]. The problems related to the selection of the initial parameters and learning factors in an adaptation algorithm are discussed. In [35], the drive system with low and high values of resonance modes is considered. In order to damp high-frequency oscillations filter is used. The vibrations generated by low mode is damped with the help of a NN controller. The adaptive controller with the reinforcement learning method is introduced in [36]. The issues connected with the stability of the control structure are also discussed here. The application of the adaptive NN with additional recurrences is presented in [37]. The structure of the NN is inspired by the Elman model. Another visible path are fuzzy systems, these are used not only for motors but also for the stability of energy systems [39,40], and others [41].
The application of a Petri layer with fuzzy type I membership functions is shown in [38]. Not only does it ensure good performance of the system, but it also reduces the numerical complexity of the algorithm.
The main goal of the paper is to present issues related to the application of the adaptive control structure with fuzzy controller based on two types of fuzzy sets. In order to reduce the numerical complexity introduced by the type II fuzzy sets, Petri nets are implemented in the considered fuzzy controller. This drastically reduces the numerical burden of the proposed algorithm and allows real-time implementation on relatively cheap microprocessor. In order to show advantages of the proposed controller comparative studies with fuzzy controller based on I-type sets is also implemented. The designed control structure is tested in a non-linear system. It is shown that the torsional vibrations are the most effectively damped in the control structure with a controller based on the II-type fuzzy sets.
The paper is divided into six sections. After an introduction, where the motivation and brief literature survey is introduced, the mathematical model of the drive is presented. Then the control structure is described in detail. Afterward, selected simulation results are shown. Finally, some concluding remarks are formulated.
2. Adaptive Neuro-Fuzzy Controller with Petri Transition Layer
For this research two input controller has been modelled using the MathWorks Inc. MATLAB Simulink (Natick, MA, USA) environment, of course it can easily be extended to more inputs [38,42]. Input variables can be selected in accordance with the will of the designer. Neuro-fuzzy inference system consists of six basic layers [38,42], and Transition Petri Layer (TPL) implemented between the first and second layer. A schematic diagram of the controller with possible Petri layers is presented in Figure 1. Layers of the controller are presented below.
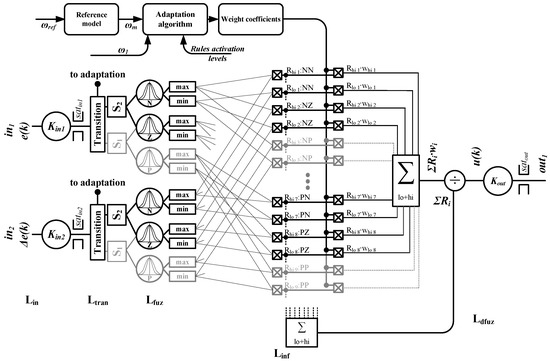
Figure 1.
Schematic diagram of the controller with Petri transition layers.
2.1. Input Layer
The first layer (Lin), scales inputs are as shown in Equation (1). The considered range of each variable is limited (satin_k = 1). Scaling coefficients (Kin_k) fits input signal to the desired limited range of the expected value. It is easy to choose Kin1, as the error signal is difference between desired and measured values. The scaling factor for other inputs should be based on maximum values that may occur at certain inputs that should be treated as “big”. For Kin1 = 1 that would mean error of the nominal value or bigger is considered big, for Kin2 = 1.5 × 10−3 that would be the maximum value of the derivative that would occur for an object defined as (6) [43].
where: ink = [e(k), Δe(k), Σe(k), u(k − 1), …].
Lin = max[min[(Kin_k ⋅ ink), satin_k], − satin_k]
2.2. Transition Petri Layer
The second layer (TPL) identifies the sub-scope of the input value, in which the signal is currently located. This layer allows one to select the corresponding rules and included in them membership functions based on the identified sub-scope of the control function. Only weight coefficients incorporated in the active rules are being adapted in the current iteration. It is dictated by the desire to reduce the numerical complexity of the algorithm with a large number of II-type fuzzy sets. TPL influences the algorithm output value in the same way as the Concurrent Petri layer, but additionally offers smaller computational cost, in Figure 2 the consequences of TPL application in neuro-fuzzy system with three type II Gaussian membership functions for each of two inputs is presented. For any given time, for each input only two instead of four membership functions are active, that causes the need for the analysis of only a quarter of plane. Given that in each iteration only four (22) out of nine (32) rules need to be analyzed. Assuming we would have the lr membership functions and lw inputs, there would be a need for the determination 2lw instead lrlw rules, the same is the case with the adaptation of weights. For three inputs and five membership functions per each input using a transition layer that activates only two functions per input, we have 23 instead of 53 rules that are calculated in each iteration.
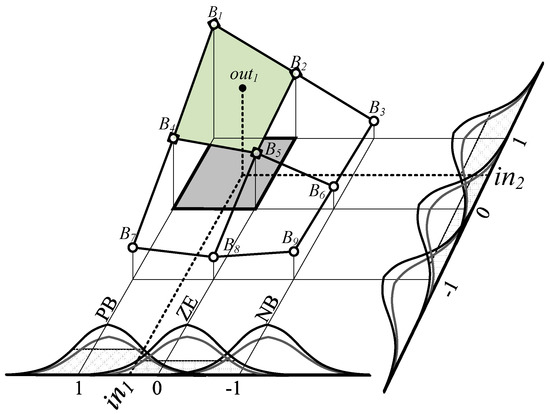
Figure 2.
Control plane for two inputs controller with Gaussian type II membership functions with TPL.
What is important, Gaussian functions medium is infinite, that means for any input each function is active at the non-zero level. TPL application will influence the output value of the whole system causing omission of the least active functions.
2.3. Fuzzyfication Layer
There are various types and shapes [38,39,40,41,42] of membership functions (MF) used at the fuzzyfication layer. In this paper the type II Gaussian MF with uncertain standard deviation [43,44,45] has been proposed. The standard type I Gaussian function is defined by Formula (2). Using type II fuzzy membership functions, for each input value, the output value is described as range. As Figure 3 shows, the output range of the II type membership function is limited by the maximum and minimum value of possible outputs. Thus, for the whole input value range, the output is limited by the values defined by upper and lower boundaries of Gaussian function. The standard deviation is different and the centre () of both functions is same. Therefore the output of fuzzyfication layer is a matrix of n × m × 2 (2: lower and upper boundaries of type II MF).
marking in a formula: i—input index, j—the MF index (for TPL function identified by the layer as one of the most active), k—number of input, n—inputs count (here 3), m—membership functions corresponding to the sector identified by the TPL or the number of membership function corresponding to the input for the controller without TPL.
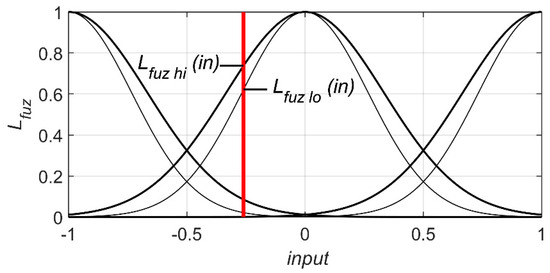
Figure 3.
Type-II fuzzy membership functions.
2.4. Inference Layer
This layer determines the firing levels of individual rules multiplied by the connected weights. Rule base consists of expressions like [38,42]:
Rn: IF e(k) IS Lfuz j1 i1 (e(k)) & Δe(k) IS Lfuz j2 i2 (Δe(k)) THAN y = Rn
In the work t-norm prod was used (3).
where n and m are analogous, as in the fuzzyfication layer, the number of inputs and the number of membership functions for the controller, yet here number of rules is doubled by the fact of existence of the upper and lower bound of the function.
2.5. Defuzyfication Layer
The defuzyfication layer (Ldfuz) calculates the output of the system. For this research standard singleton defuzyfication algorithm has been implemented, the algorithm is described by the Formula (4). In fact, the singleton defuzyfication should be made for both upper and lower boundaries, and then whole output should be calculated for example as the weight of these values, but in proposed solution output is weighted average of lower and upper boundaries singletons.
2.6. Adaptation Algorithm
Equation (5) shows how each weight coefficient is being changed in each iteration:
where: em = ωmod − ω1 reference model tracking error. An inertial second order object has been used as the reference model (6) with parameters ωr = 30, ξ = 1:
In each iteration, adapted weight coefficients are changed by a values dependent on the current model tracking error. Only coefficients corresponding to active rules are adapted proportionally to the level of corresponding rule activation. Weight coefficients should be limited in such a way as to allow to reach the maximum desired output signal value. A description of the control structure with reference model is also presented in [46,47,48,49]. The adaptation parameters (kem, kΔm) are tuned using algorithm described in Section 4.1.
3. Two Mass System—SimPowerSystem Model
The standard cascade structure has been used in the study [50,51,52,53]. The electromagnetic torque is controlled using current controller. For the outer control loop the dynamic of the torque control can be represented by equivalent first-order transfer function with a small time constant. The speed control loop includes mechanical part of the drive (two-mass system with nonlinearities) speed sensor with a neglectable dynamic and speed controller.
In this paper, the system with two separately excited DC motors connected by means of a flexible shaft has been modelled in the MathWorks Inc. MATLAB Simulink (Natick, MA, USA) environment using SimPowerSystems library. The first motor is working as a drive and is controlled using cascade control structure. The second motor works as a generator which energy is wasted at the resistance. Assuming constant excitation of both machines each of them can be described by Equations (7) and (8).
where: Tem—electromagnetic time constant, T1—mechanical time constant of the machine, τL—load torque, ia—armature current, Kt—gain factor of the motor, ua—armature voltage, Ψf—excitation flux
The mentioned cascade control system is shown in the Figure 4 contains two control loops. The inner loop contains electromagnetic part of the motor, the current controller and current measurement. Its purpose is to compensate electromagnetic time constant (Tem). The classical PI controller initially tuned with symmetry criterion is used as current controller. The outer loop—speed control loop—contains speed controller and speed measurement system. Its purpose is to compensate the mechanical time constant (T1)—the biggest time constant in the system. During research, in the first step the classical PI speed controller has been used. Afterwards this speed controller is substituted by proposed fuzzy adaptive controllers.
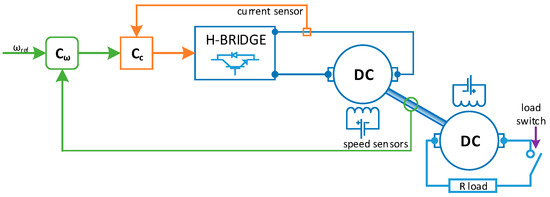
Figure 4.
Control system scheme.
Both DC machines are connected via a long shaft wherein elasticity of the shaft is non-negligible. The block diagram is presented in the Figure 5. Mathematical description includes Equations (9)–(11).
where: ω2—load speed, τe—electromagnetic torque, τs—shaft (torsional) torque, Kc—stiffness constant, D—damping factor of the shaft, τf1, τf2—friction torque of motor and load.
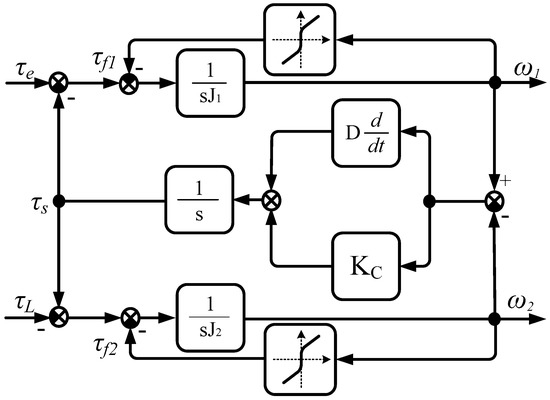
Figure 5.
Block diagram of mechanical part of driver system with elastic coupling and friction.
4. Simulations
The MathWorks Inc. MATLAB (Natick, MA, USA) simulations scenario looks as follows. Firstly the well-known adaptive Mamdani fuzzy controller, then the same controller with Petri layer and type II MF has been created and modelled. Each controller was tuned using PSO. Only the best outcomes were presented, along with optimization process. Tuning process included rng(‘default’) was used to ensure reproducibility. Seven iterations of PSO with variable boundaries for each controller were realized. The chosen simulation outcomes are presented along with comments. To provide a better comparison, a classical PI controller tuned using symmetry criterion (Sym), taking into account flexible connection [54] (Flex), has been shown.
The trajectory used for the simulations is as follows. Reversible speed reference signal of frequency 0.5 Hz and amplitude 0.25 rated value and step change of rated load torque was applied in time 1.5 s. The limited dynamics origins in the usage of the reference model for the adaptation algorithm is shown in (6). This model was also used as filter for the linear controller so the comparison is fair.
4.1. Optimization Process
As an optimization algorithm the Particle Swarm Optimization (PSO) [55,56,57] was used. The swarm size was set as 20. Function tolerance 1 × 10−4. Inertia Range [0.1, 1.5]. Initial swarm span (default) 2000, max iterations (200) was never reached. The maximum number of stall iterations (5), combined with function tolerance were always the reason to stop the algorithm. There were no time constraints. The minimum adaptive neighbourhood size is 0.25. Self-adjustment as well social adjustment of weight was 1.49. Other not-mentioned options are set as default. All the above options are common for all optimizations. The search boundaries and number of optimized variables are only variable parameters.
4.2. The Cost Functions for Optimization
The function (y1) contains sum of two logarithmic expressions. The first part is responsible for proper tracking of reference speed. The second part ensures minimization of damping of torsional vibrations. ISE criterion supports the minimization of higher amplitudes of signals at the expense of weaker minimization of low amplitudes of respectively tracking error and torsional vibrations. The logarithm and multiplication (103 in nominator) allow us to adjust the levels of importance of tracking error (which values is generally bigger) and torsional vibrations causing difference in motor and load speed (ω1−2) effectively the used cost function allows obtaining good tracking with minimized torsional vibrations.
4.3. Simulation Transients
In the figures three types of transients has been presented. In the first transient reference speed versus motor and load speed are presented. In the second transient tracking error of motor speed are shown. The last transient presents the difference between motor and load speed, which is associated with torsional torque. Underneath, the chosen fragments can be found.
The classical PI controller tuned with the symmetry criterion (Sym) and taking into account the flexible connection (Flex) criterion [54] was treated as a reference point.
4.4. Adaptive Fuzzy Controller with Type I Fuzzy Sets
In this section adaptive fuzzy controller with type I fuzzy sets is presented. Tuning process of fuzzy controller is described in Section 4.1 and Section 4.2. Chosen outcomes are presented along with reference transients.
Figure 6, Figure 7 and Figure 8 show the waveforms for the system with a fuzzy controller with type I functions and a classic PI controller tuned in accordance with the methods mentioned earlier. Not surprisingly, each chip worked. However, when analyzing the differences between them, one can notice the potential advantages of more and more complex control systems. In the case of the Flex type settings, it is necessary to know the time constants of the drive. In the case of the PI controller, it is not necessary to know the connection time constant, only the drive. In the case of an adaptive fuzzy controller there is no need to know the drive parameters, although of course it is helpful [58]. Figure 9, Figure 10 and Figure 11 show the zoomed trajectory fragment at the moment of switching the load on at the time of 1.5 s. Figure 12, Figure 13 and Figure 14 show a full relapse. Figure 15 is the flow of the optimization process leading to obtaining the settings corresponding to the presented waveforms.
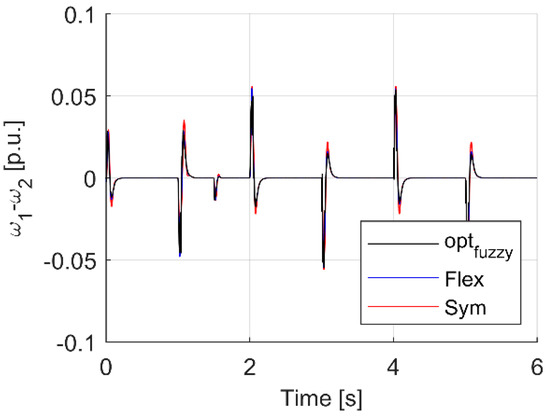
Figure 6.
Transients of difference between motor and load speed for analyzed controller cases.
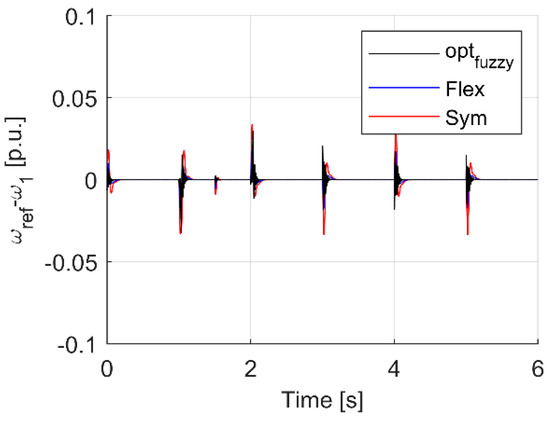
Figure 7.
Transients of difference between motor and reference speed for analyzed controller cases.
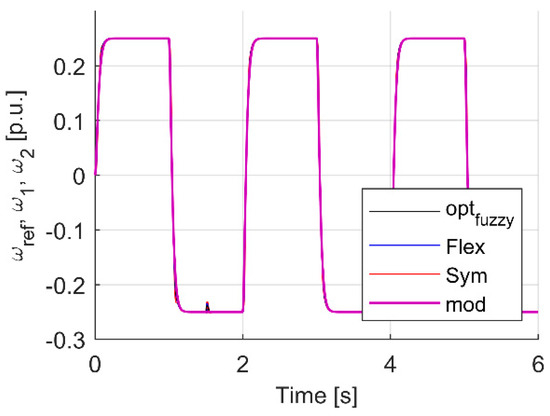
Figure 8.
Transients of motor, load and reference speed for analyzed controller cases.
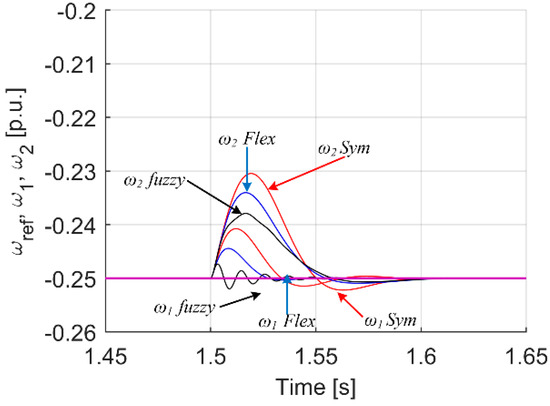
Figure 9.
Transients of difference between motor, load and reference speed under torque load change.
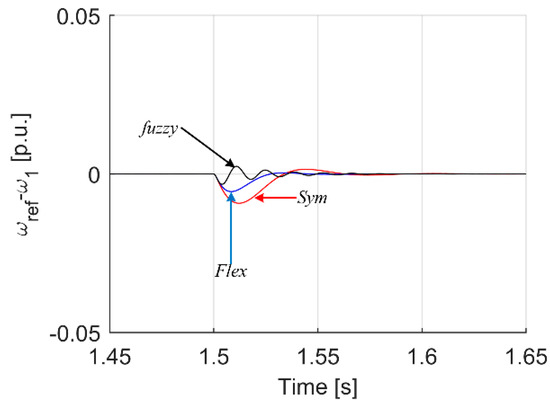
Figure 10.
Transients of difference between motor and reference speed under torque load change.
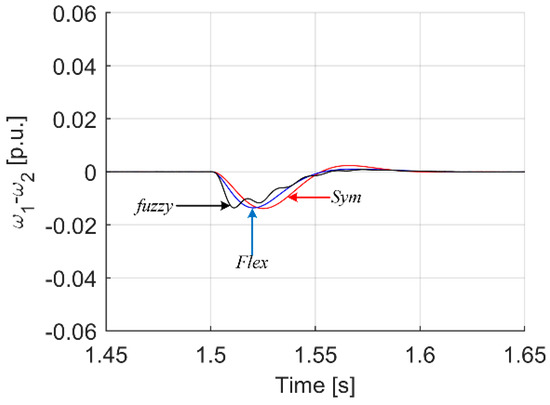
Figure 11.
Transients of difference between motor and load speed under load occurrence.
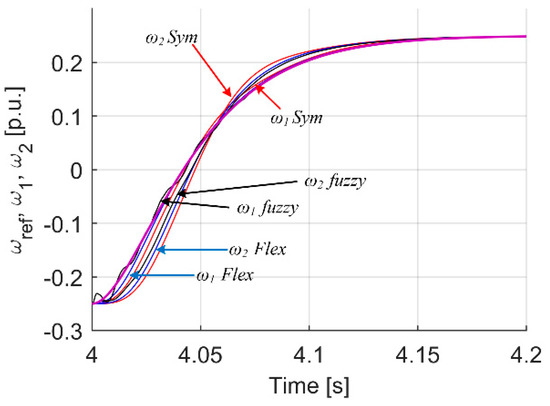
Figure 12.
Transients of motor, load and reference speed for analyzed controller cases.
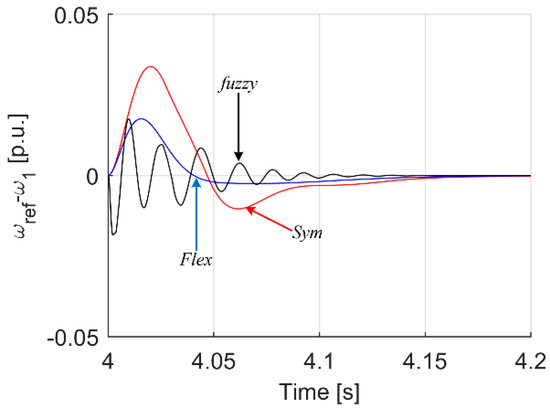
Figure 13.
Transients of difference between motor and reference speed for analyzed controller cases.
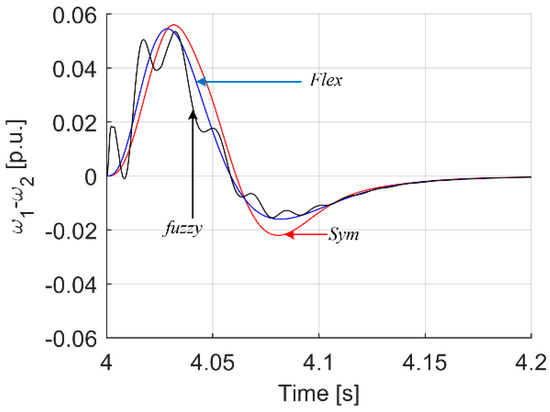
Figure 14.
Transients of motor, load and reference speed for analyzed controller cases.
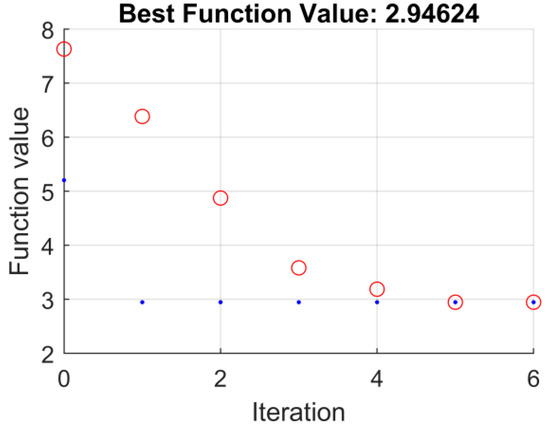
Figure 15.
Adaptation process for the controller with type I functions.
As can be seen in Figure 9, the PI controller tuned in accordance with the symmetry criterion gives the highest value of the speed error at the moment of switching the load on, additionally the response is characterized by swing. In the case of Flex (blue) settings, a significant improvement can be seen, however, the use of a fuzzy controller with type I membership functions gives an even better quality of response. The oscillatory nature of the speed response ω1 appears, however, in the load speed ω2, there are no oscillations. This is confirmed by the analysis of the error ω1.
Looking at Figure 11, it can be seen that the smallest maximum difference between the speed ω1 and ω2 is given by the Flex tuning of the PI controller. A slightly larger difference is offered by the fuzzy regulator, and the smallest, although the differences are minimal, is provided by the tuned Flex regulator. Later in Figure 12, Figure 13 and Figure 14, the transients involved by change of reference speed are shown. Here, too, we can see analogous behavior of a bend, but the time of the dynamic state is relatively longer, so the real differences between the systems are also slightly more significant.
4.5. Adaptive Fuzzy Controller with Type II Fuzzy Sets and Petri Transition Layer
In this section adaptive fuzzy controller with type II fuzzy sets performance is presented. Before mentioned classical PI controller is treated as a reference. Tuning process of fuzzy controller is described in Section 4.1 and Section 4.2. The chosen outcomes are presented along with reference transients.
Analyzing the waveforms in Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23 and Figure 24, it can be seen that also in this case the system with a fuzzy controller with type II functions—turns out to be the best in many respects. Most importantly, the parameter which was the most important in the course of tuning, i.e., the minimization of torsional vibrations, which is manifested by the difference between the drive speed and the actual load speed, is the smallest (Figure 23 and Figure 24) for the case of a fuzzy controller with type II membership functions.
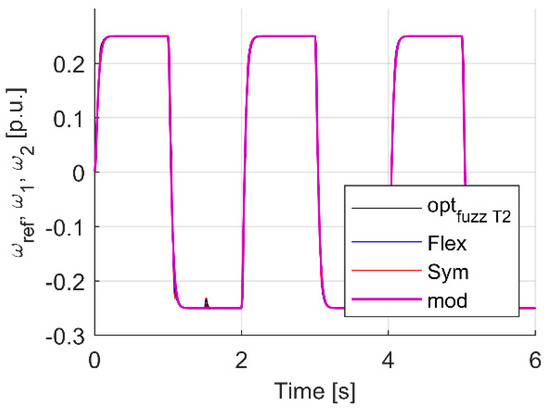
Figure 16.
Transients of motor, load and reference speed for analyzed controller cases.
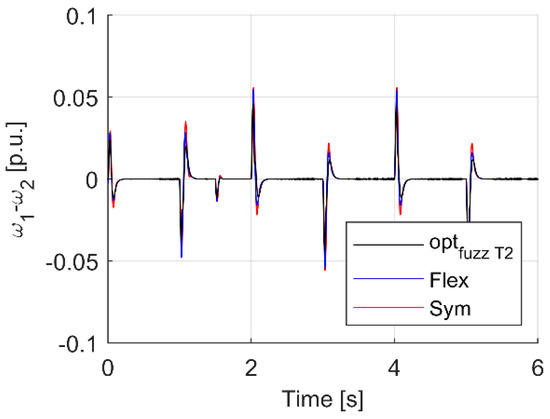
Figure 17.
Transients of difference between motor and load speed for analyzed controller cases.
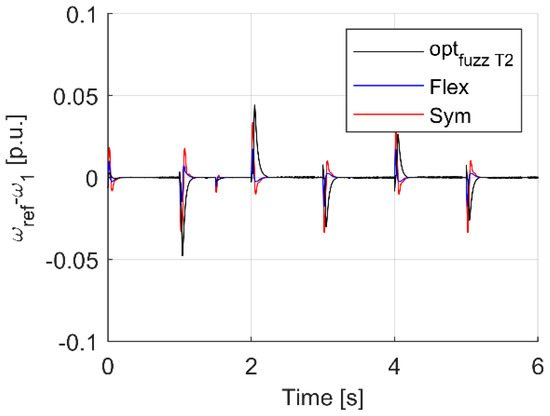
Figure 18.
Transients of difference between motor and reference speed for analyzed controller cases.
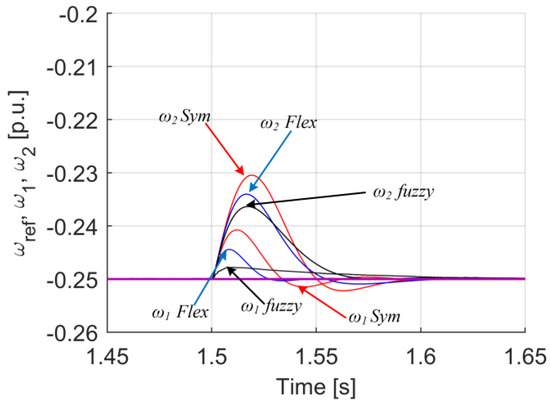
Figure 19.
Transients of motor, load and reference speed for analyzed controller cases.
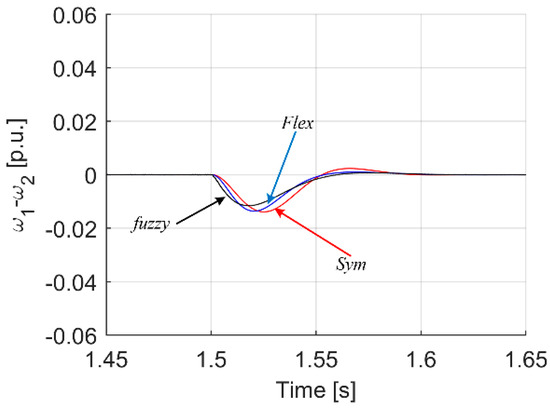
Figure 20.
Transients of difference between motor and load speed for analyzed controller cases—zoom.
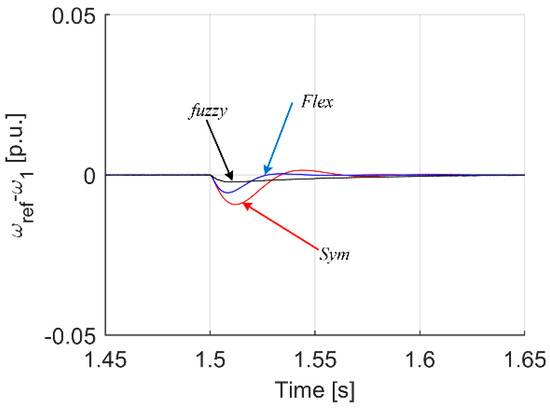
Figure 21.
Transients of difference between motor and reference speed for analyzed controller cases.
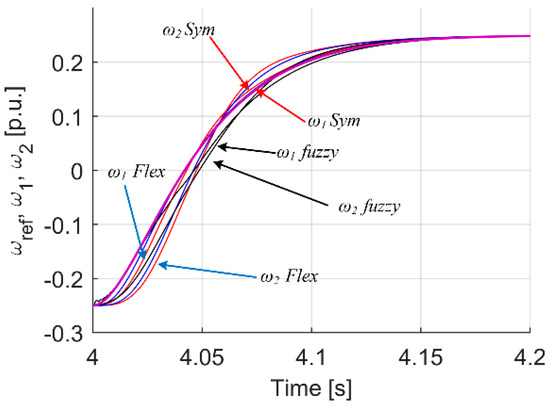
Figure 22.
Transients of motor, load and reference speed for case of reference speed change.
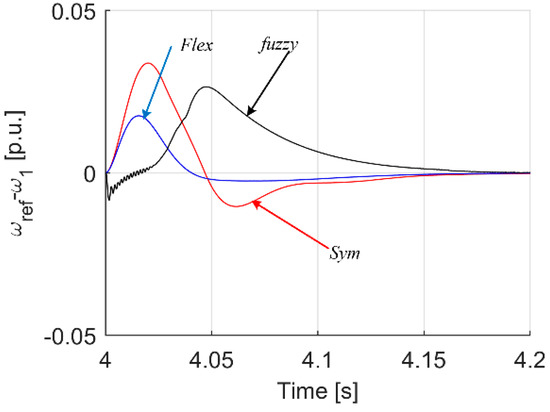
Figure 23.
Transients of difference between motor and load speed for case of reference speed change.
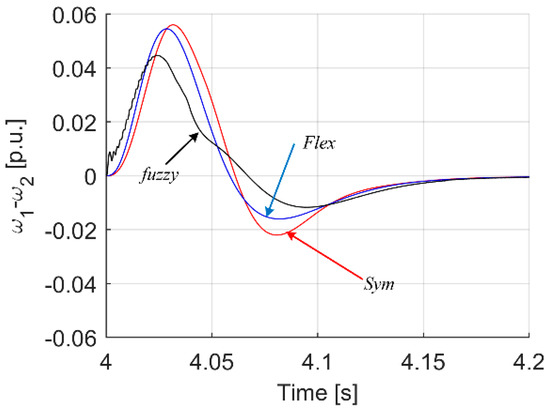
Figure 24.
Transients of difference between motor and reference speed for case of reference speed change.
To be clear, Figure 15 and Figure 25 show the process of adaptation. At the same time, as mentioned in Section 4.2 for each system, a series of adaptations with different scopes of variable searches. It should be noted, however, that each of the sets (specific constraints and specific cost function) were run for both algorithms. Moreover, the reproducibility function allows to guarantee the fairness of such a comparison (each algorithm was optimized for the same parameters). As a result, it turned out that the best quality was obtained with the optimization of the fuzzy controller with the first type functions for constraints kem (0–10) kΔm (0–20) while for the controller with type II functions for constraints were kem (0–10) kΔm (0–10).
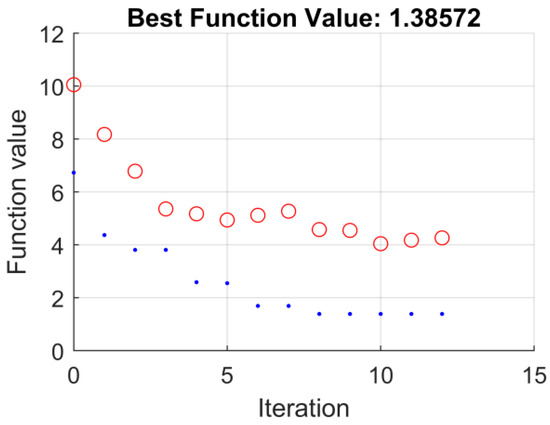
Figure 25.
Adaptation process for the controller with type II functions.
For this controller, which is the main goal of this paper, similar transients like in earlier analysis are presented. First, the analyzed controller with type II functions is presented against the background of—as before—the classical PI controller. Then, in Figure 26, Figure 27 and Figure 28, a comparison of the fuzzy controller with the functions of type I and type II is presented. Two best sets for each type. Colour blue are type II controllers, colour red are type I controllers. As it is seen in Figure 26 both system offers very good trajectory tracking. However, the transient of the difference between machine and load speed (Figure 27) shows a smaller and less rippled trajectory of motor speed for type II fuzzy sets as membership functions. Additionally, speed tracking under load occurrence (Figure 28) is better for type II fs, at the cost of slightly bigger error but fewer ripples during reversion.
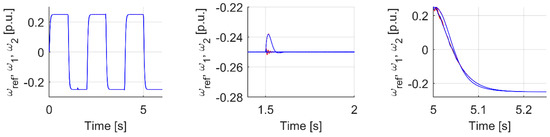
Figure 26.
Transients of motor, load and reference speed for analyzed controller cases.
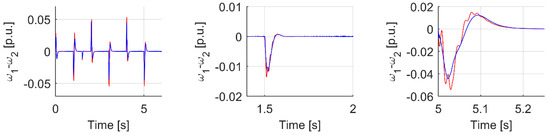
Figure 27.
Transients of difference between motor and load speed for analyzed controller cases.
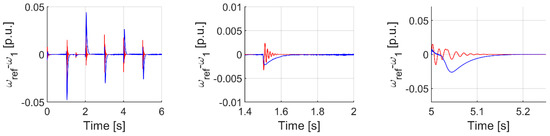
Figure 28.
Transients of difference between motor and reference speed for analyzed controller cases.
In Table 1, the numerical quality indicators have been compiled. The first line is the proposed (14) cost function for optimization process. As it is seen, fuzzy systems, both with type I and II fuzzy MF offer better quality of tracking combined with twisting torque minimization. It is not a surprise, since in general analyzed system is nonlinear, and fuzzy system offers such nonlinear control strategy whereas classical PI controller, even taking flexibility into account is still linear type of control.

Table 1.
The comparison of numerical quality indicators for different controllers.
The second and third line are the maximal differences between the machine and load speed in dynamic state (change of reference speed) and under load occurrence. Again, type II fuzzy sets are better. What is important, however, is that the type I fuzzy system offers a worse quality of this indicator than the PI controller with settings taking flexibility into account.
The last two lines present maximal values of the tracking error of the machine. In this approach better quality of the type II controller is obtained, yet the error of (ωref − ω1) in dynamic states is higher.
5. Experimental Verification
Experimental studies have been carried out on a laboratory system consisting of two DC machines. The first DC motor is supplied by transistor H-bridge. Control is performed by a computer equipped with a DSpace 1103 card. The speed control circuit is sampled at 2 kHz frequency, current loop works at 11 kHz frequency. Due to coupling both DC machines by elastic shaft the drive can be treated as a two-mass system. The block diagram of the test system is shown in Figure 29. The speed is measured using high-quality industrial encoders (Kübler, 5 k imp/rev). Two reversible trajectories were tested, with constant and changeable load torque.
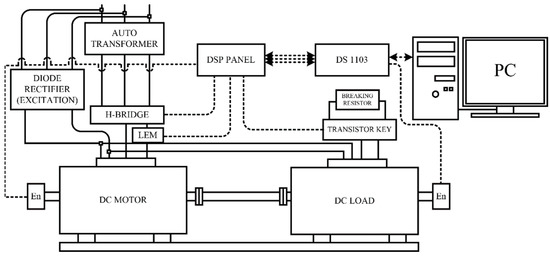
Figure 29.
Block diagram of the experimental system.
The main data of the motor and drive (both motors are the same) are: nominal power PN = 0.5 kW, nominal speed nN = 1450 rev/min, nominal current IN = 3.15 A, nominal voltage UN = 220 V, moment of inertia JN = 0.0044 kg∙m2. Machines are connected with a steel shaft: length l = 60 cm, diameter Φ = 8 mm.
As it is seen in Figure 30 and Figure 31 load speed and motor speed accurately are following reference signal. What is more, the torsional vibrations are very small. In fact, they are at platform noise levels. That is why only chosen cases were presented. If we would like to describe them numerically for the case presented in Figure 30 ISE(ωref − ω1) = 2.6767, ISE(ω1 − ω2) = 0.5812 and criterion (14) = 4.1672. For the 31st fig case it would be ISE(ωref − ω1) = 1.1155, ISE(ω1 − ω2) = 0.2057 and criterion (14) = 2.7725. Having in mind the trajectory parameters, these are considered as very good outcomes.
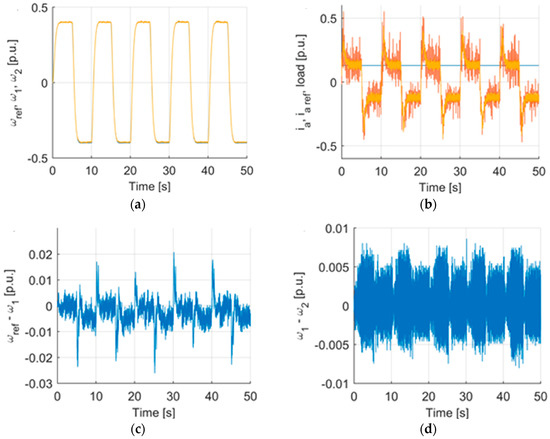
Figure 30.
Experimental transients of the system with type II fuzzy controller with Petri layer. Reference (blue), motor (yellow) and load (orange) speed (a), reference (orange), measured (yellow) armature current and load level (blue) (b), tracking error for motor speed (c), difference between machine and load (d). Case with constant load.
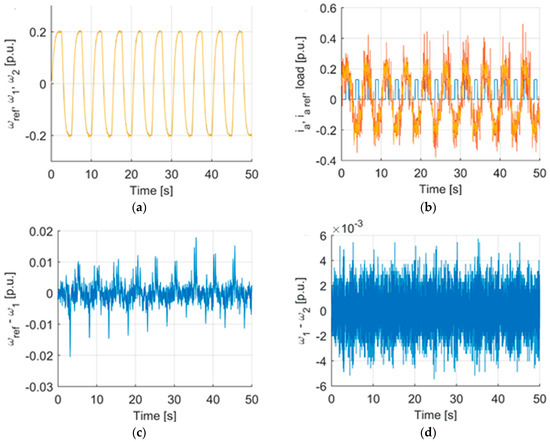
Figure 31.
Experimental transients of the system with type II fuzzy controller with Petri layer. Reference (blue), motor (yellow) and load (orange) speed (a), reference (orange), measured (yellow) armature current and load level (blue) (b), tracking error for motor speed (c), difference between machine and load (d). Case with variable load.
6. Conclusions
This paper presents an original concept of an electrical drive control system with an elastic mechanical coupling between the motor and the driven mechanism. As it is known, unlimited torsional vibrations or torsional momentum may cause the damage to the shaft or non-plastic deformation. Even if it is not a shaft fracture, twisting in its structure significantly weakens the strength over time and thus eventually causes the shaft to break. Therefore, from the strength point of view, the torque values involved by torsional vibrations should be limited.
For this purpose two types of fuzzy controllers with type I and type II fuzzy membership functions have been analyzed. A system quality indicator taking vibrations into account has been proposed in the speed controller synthesis procedure. An important novelty in the presented approach is the use of a transition Petri layer in the type II fuzzy controller to reduce the numerical complexity. When dealing with a large number of complex type II fuzzy sets. Reducing computational complexity as well as the processing time of numerical procedures on a microprocessor chip allows the implementation on a low-cost platform. The simulation and experimental results presented show that the best damping of mechanical vibrations is provided by an adaptive fuzzy controller with type II functions and with a transition Petri layer. The proposed algorithm also has an advantage due to the adaptive nature of the controller, which allowed one to start the control process without drive parameter identification. The theoretical considerations were supported by simulation results, and tested on-site. Continued development work is planned with multi-mass objects, as well as the implementation of the algorithm in a cheaper industrial platform.
Author Contributions
Conceptualization, P.D., K.S.; methodology, P.D., K.S.; software, P.D.; validation, K.S., K.Z. and T.P.; formal analysis, P.D., K.S., K.Z. and T.P.; investigation, P.D., K.S., K.Z. and T.P.; resources, P.D., K.S., K.Z. and T.P.; data curation, P.D., K.S., K.Z. and T.P.; writing—original draft preparation, P.D. and K.S.; writing—review and editing, K.Z. and T.P.; visualization, P.D., K.S., K.Z. and T.P.; supervision, K.S. and K.Z.; project administration, T.P.; funding acquisition, K.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ohnishi, K.; Katsura, S.; Shimono, T. Motion control for real-world haptics. IEEE Ind. Electron. Mag. 2010, 4, 16–19. [Google Scholar] [CrossRef]
- Inoue, Y.; Katsura, S. Spatial disturbance suppression of a flexible system based on wave model. IEEJ J. Ind. Appl. 2018, 7, 236–243. [Google Scholar] [CrossRef] [Green Version]
- Łuczak, D. Nonlinear Identification with Constraints in Frequency Domain of Electric Direct Drive with Multi-Resonant Mechanical Part. Energies 2021, 14, 7190. [Google Scholar] [CrossRef]
- Li, P.; Wang, L.; Zhong, B.; Zhang, M. Linear Active Disturbance Rejection Control for Two-mass Systems via Singular Perturbation Approach. IEEE Ind. Inform. 2021; in press. [Google Scholar] [CrossRef]
- Lozynskyy, A.; Chaban, A.; Perzyński, T.; Szafraniec, A.; Kasha, L. Application of Fractional-Order Calculus to Improve the Mathematical Model of a Two-Mass System with a Long Shaft. Energies 2021, 14, 1854. [Google Scholar] [CrossRef]
- Zhang, G.; Furusho, J. Speed control of two—Inertia system by PI/PID control. IEEE Trans. Ind. Electron. 2000, 47, 603–609. [Google Scholar] [CrossRef]
- Goubej, M. Fundamental performance limitations in PID controlled elastic two-mass systems. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Banff, AB, Canada, 12–15 July 2016; pp. 828–833. [Google Scholar]
- Li, X.; Shang, D.; Li, H.; Li, F. Resonant Suppression Method Based on PI control for Serial Manipulator Servo Drive System. Sci. Prog. 2020, 103, 1–39. [Google Scholar] [CrossRef]
- Nalepa, R.; Najdek, K.; Wróbel, K.; Szabat, K. Application of D-Decomposition Technique to Selection of Controller Parameters for a Two-Mass Drive System. Energies 2020, 13, 6614. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T. Vibration suppression in two-mass drive system using PI speed controller and additional feedbacks—Comparative study. IEEE Trans. Ind. Electron. 2007, 54, 1193–1206. [Google Scholar] [CrossRef]
- Serkies, P. Estimation of state variables of the drive system with elastic joint using moving horizon estimation (MHE). Bull. Pol. Acad. Sci. Tech. Sci. 2019, 67, 883–892. [Google Scholar]
- Szczepański, R.; Kamiński, M.; Tarczewski, T. Auto-tuning process of state feedback speed controller applied for two-mass system. Energies 2020, 13, 3067. [Google Scholar] [CrossRef]
- Sakaino, S.; Kitamura, T.; Mizukami, N.; Tsuji, T. High-Precision Control for Functional Electrical Stimulation Utilizing a High-Resolution Encoder. IEEJ J. Ind. Appl. 2021, 10, 124–133. [Google Scholar] [CrossRef]
- Dodds, S.J.; Szabat, K. Forced dynamic control of electric drives with vibration modes in the mechanical load. In Proceedings of the 12th International Power Electronics and Motion Control Conference, Portoroz, Slovenia, 30 August–1 September 2006; pp. 1245–1250. [Google Scholar]
- Serkies, P.; Szabat, K. Effective damping of the torsional vibrations of the drive system with an elastic joint based on the forced dynamic control algorithms. J. Vib. Control. 2019, 25, 2225–2236. [Google Scholar] [CrossRef]
- Hori, Y.; Sawada, H.; Chun, Y. Slow resonance ratio control for vibration suppression and disturbance rejection in torsional system. IEEE Trans. Ind. Electron. 1999, 46, 162–168. [Google Scholar] [CrossRef]
- Katsura, S.; Suzuki, J.; Ohnishi, K. Pushing operation by flexible manipulator taking environmental information into account. IEEE Trans. Ind. Electron. 2006, 53, 1688–1697. [Google Scholar] [CrossRef]
- Yang, M.; Wang, C.; Xu, D.; Zheng, W.; Lang, X. Shaft Torque Limiting Control Using Shaft Torque Compensator for Two-Inertia Elastic System with Backlash. IEEE/ASME Trans. Mechatron. 2016, 21, 2902–2911. [Google Scholar] [CrossRef]
- Yamada, S.; Fujimoto, H. Precise joint torque control method for two-inertia system with backlash using load-side encoder. IEEJ J. Ind. Appl. 2019, 8, 75–83. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Cui, S.; Liu, Y.; Ren, Y.; Sun, Y. Design and Vibration Suppression Control of a Modular Elastic Joint. Sensors 2018, 18, 1869. [Google Scholar] [CrossRef] [Green Version]
- Trung, T.V.; Iwasaki, M. Double-Disturbance Compensation Design for Full-Closed Cascade Control of Flexible Robots. In Proceedings of the IEEE International Conference on Mechatronics (ICM), Kashiwa, Japan, 7–9 March 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Cychowski, M.T.; Szabat, K. Efficient real-time model predictive control of the drive system with elastic transmission. IET Control. Theory Appl. 2010, 4, 37–49. [Google Scholar] [CrossRef]
- Serkies, P.J.; Szabat, K. Application of the MPC to the position control of the two-mass drive system. IEEE Trans. Ind. Electron. 2013, 60, 3679–3688. [Google Scholar] [CrossRef]
- Wang, C.; Yang, M.; Zheng, W.; Long, J.; Xu, D. Vibration Suppression with Shaft Torque Limitation Using Explicit MPC-PI Switching Control in Elastic Drive Systems. IEEE Trans. Ind. Electron. 2015, 62, 6855–6867. [Google Scholar] [CrossRef]
- Wang, C.; Yang, M.; Zheng, W.; Hu, K.; Xu, D. Analysis and Suppression of Limit Cycle Oscillation for Transmission System with Backlash Nonlinearity. IEEE Trans. Ind. Electron. 2017, 64, 9261–9270. [Google Scholar] [CrossRef]
- Amirkhani, S.; Mobayen, S.; Iliaee, N.; Boubaker, O.; Hosseinnia, S.H. Fast terminal sliding mode tracking control of nonlinear uncertain mass–spring system with experimental verifications. Int. J. Adv. Robot. Syst. 2019, 16, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Szabat, K.; Wróbel, K.; Dróżdż, K.; Janiszewski, D.; Pajchrowski, T.; Wójcik, A. A fuzzy unscented Kalman filter in the adaptive control system of a drive system with a flexible joint. Energies 2020, 13, 2056. [Google Scholar] [CrossRef] [Green Version]
- Orlowska-Kowalska, T.; Szabat, K. Control of the drive system with stiff and elastic couplings using adaptive neuro-fuzzy approach. IEEE Trans. Ind. Electron. 2007, 54, 228–240. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Szabat, K. Adaptive fuzzy sliding mode control of a drive system with flexible joint. In Proceedings of the IECON 32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 994–999. [Google Scholar]
- Wróbel, K. Fuzzy Adaptive Control of Nonlinear Two-Mass System. Power Electron. Drives 2016, 1, 133–146. [Google Scholar] [CrossRef]
- Kabziński, J.; Mosiołek, P. Integrated, Multi-Approach, Adaptive Control of Two-Mass Drive with Nonlinear Damping and Stiffness. Energies 2021, 14, 5475. [Google Scholar] [CrossRef]
- Kaminski, M.; Orlowska-Kowalska, T. Adaptive neural speed controllers applied for a drive system with an elastic mechanical coupling—A comparative study. Eng. Appl. Artif. Intell. 2015, 45, 152–167. [Google Scholar] [CrossRef]
- Gaidi, A.; Lehouche, H.; Belkacemi, S.; Tahraoui, S.; Loucif, M.; Guenounou, O. Adaptive backstepping control of wind turbine two mass model. In Proceedings of the 6th International Conference on Systems and Control (ICSC), Banta, Algeria, 7–9 May 2017; pp. 168–172. [Google Scholar]
- Tran Anh, D.; Nguyen Trong, T. Adaptive Controller of the Major Functions for Controlling a Drive System with Elastic Couplings. Energies 2018, 11, 531. [Google Scholar] [CrossRef] [Green Version]
- Brock, S.; Luczak, D.; Nowopolski, K.; Pajchrowski, T.; Zawirski, K. Two approaches to speed control for multi-mass system with variable mechanical parameters. IEEE Trans. Ind. Electron. 2016, 64, 3338–3347. [Google Scholar] [CrossRef]
- Pajchrowski, T.; Siwek, P.; Wójcik, A. Adaptive controller design for electric drive with variable parameters by Reinforcement Learning method. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 1019–1030. [Google Scholar]
- Kamiński, M.; Szabat, K. Adaptive Control Structure with Neural Data Processing Applied for Electrical Drive with Elastic Shaft. Energies 2021, 14, 3389. [Google Scholar] [CrossRef]
- Derugo, P.; Szabat, K. Adaptive neuro-fuzzy PID controller for nonlinear drive system. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2015, 34, 792–807. [Google Scholar] [CrossRef]
- Samonto, S.; Kar, S.; Pal, S.; Atan, O.; Sekh, A.A. Fuzzy logic controller aided expert relaying mechanism system. J. Frankl. Inst. 2021, 358, 7447–7467. [Google Scholar] [CrossRef]
- Samonto, S.; Kar, S.; Pal, S.; Sekh, A.A. Fuzzy logic based multistage relaying model for cascaded intelligent fault protection scheme. Electr. Power Syst. Res. 2020, 184, 106341. [Google Scholar] [CrossRef]
- Precup, R.E.; Hellendoorn, H. A survey on industrial applications of fuzzy control. Comput. Ind. 2011, 62, 213–226. [Google Scholar] [CrossRef]
- Derugo, P. Adaptive neuro fuzzy PID type II DC shunt motor speed controller with Petri Transition layer. In Proceedings of the IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 395–400. [Google Scholar]
- Castillo, O.; Melin, P.; Kacprzyk, J.; Pedrycz, W. Type-2 fuzzy logic: Theory and applications. In Proceedings of the IEEE International Conference on Granular Computing, Fremont, CA, USA, 2–4 November 2007; p. 145. [Google Scholar]
- Mendel, J.M.; John, R.B. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Karnik, N.N.; Mendel, J.M.; Liang, Q. Type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 1999, 7, 643–658. [Google Scholar] [CrossRef] [Green Version]
- Chai, Y.; Jia, L.; Zhang, Z. Mamdani model based adaptive neural fuzzy inference system and its application. Int. J. Comput. Intell. 2009, 5, 22–29. [Google Scholar]
- Liao, Q.; Li, N.; Li, S. Type-II T-S fuzzy model-based predictive control. In Proceedings of the 48th IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 4193–4198. [Google Scholar] [CrossRef]
- Wai, R.J.; Chu, C.C. Robust petri fuzzy-neural-network control for linear induction motor drive. IEEE Trans. Ind. Electron. 2007, 54, 177–189. [Google Scholar] [CrossRef]
- Szczepanski, R.; Tarczewski, T.; Grzesiak, L.M. Application of optimization algorithms to adaptive motion control for repetitive process. ISA Trans. 2021, 115, 192–205. [Google Scholar] [CrossRef]
- Derugo, P.; Szabat, K. Implementation of the low computational cost fuzzy PID controller for two-mass drive system. In Proceedings of the IEEE 16th International Power Electronics and Motion Control. Conference and Exposition, Antalya, Turkey, 21–24 September 2014; pp. 564–568. [Google Scholar]
- Orlowska-Kowalska, T.; Szabat, K. Optimization of fuzzy-logic speed controller for DC drive system with elastic joints. IEEE Trans. Ind. Appl. 2004, 40, 1138–1144. [Google Scholar] [CrossRef]
- Kamarudin, M.N.; Rozali, S.M. Simulink implementation of digital cascade control DC motor model—A didactic approach. In Proceedings of the IEEE 2nd International Power and Energy Conference, Johor Bahru, Malaysia, 1–3 December 2008; pp. 1043–1048. [Google Scholar]
- Rosić, M.; Antić, S.; Bjekić, M.; Vujičić, V. Educational laboratory setup of DC motor cascade control based on dSPACE1104 platform. Zb. Međunarodne Konf. Obnov. Izvorima Električne Energ. MKOIEE 2017, 5, 213–222. [Google Scholar]
- Szabat, K.; Orłowska-Kowalska, T.; Kowalski, C.T. Wybrane zagadnienia sterowania układu napędowego z połączeniem sprężystym. Masz. Elektr. Zesz. Probl. 2005, 71, 155–160. [Google Scholar]
- Kennedy, J.; Russell, E. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4. [Google Scholar]
- Kabziński, J.; Kacerka, J. Optimization of Polytopic System Eigenvalues by Swarm of Particles. In Proceedings of the International Conference on Artificial Intelligence: Methodology, Systems, and Applications, Los Angeles, CA, USA, 20–22 February 1995; pp. 178–185. [Google Scholar]
- Bansal, J.C. Particle Swarm Optimization, Evolutionary and Swarm Intelligence Algorithms; Springer: Cham, Switzerland, 2019; pp. 11–23. [Google Scholar]
- Derugo, P.; Żychlewicz, M. Reproduction of the control plane as a method of selection of settings for an adaptive fuzzy controller with Petri layer. Arch. Electr. Eng. 2020, 69, 609–624. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).