Numerical Simulation of Bridging Ball Plugging Mechanism in Fractured-Vuggy Carbonate Reservoirs

Abstract

Pores, fractures, caves, and other storage spaces are commonly distributed in fractured-vuggy carbonate reservoirs. During the drilling process, more than half of all drill-in fluid loss issues are caused by developed caves. Cave scales range from centimeters to meters, making leak prevention increasingly difficult through the use of traditional technologies. Currently, there is still high demand for the understanding of feasible loss control techniques, especially in fractured-vuggy carbonate reservoirs. Multistage Bridge Plugging (MBP) technology has facilitated pioneering experiments in many oilfields, but the success rate of plugging is less than 50%, and the effects of plugging are uncontrollable and difficult to predict. This is due to a lack of clarity regarding the plugging mechanism and the key controlling factors. In this study, we used the Discrete Element Method (DEM) simulation method to investigate the controlling factors of MBP technology, and analyzed its applicable conditions. We found that the prerequisite for the success of MBP is the presence of a constricted throat near the wellbore when drilling the well hole; the first-stage bridging ball is the key to the success of MBP. Larger ball radius, cave inclination and initial flow rate, and lower ball velocity are beneficial to the first-stage bridging. All discussion in this research is based on the ideal situation. However, the cave pattern is difficult to describe using several models, let alone by one ideal model. With the progress of seismic fine description technology and mud logging, more accurate characterization of caves in carbonate reservoirs will help to accurately formulate the plugging scheme and greatly improve the success rate of plugging technology. Additionally, the engineering risks of this technology, such as plugging the coiled tubing, need to be further studied.

1. Introduction

Oil and gas are one of the main energy types supporting the daily lives of human beings. These fossil fuels can be found in different reservoir types with different petrophysical properties [1]. Carbonate reservoirs usually include karst caves, fractures, and pores, which can furtherly develop as high-quality oil and gas reservoirs [2]. However, considerable drill-in fluid loss may happen in these spaces, sometimes preventing the completion of wells or even causing them to be scrapped [3]. Even if completion is successful, lost drilling fluid can still induce reservoir damage and affect drilling efficiency [4,5]. Cave scales range from centimeters to meters. Statistics on the single-well drill-in fluid loss in the Ordovician–Cambrian reservoirs in X block of the Tarim Basin of western China (

Table 1. The leakage characteristics in Ordovician–Cambrian reservoirs, X block of Tarim Basin.

Total Wells	Leaky Wells/Total Wells (%)	Min Leakage (m3)	Max Leakage (m3)	Return Loss Wells /Leaky Wells (%)	Drilling Open Caves in Single Wells /Leaky Wells (%)
82	52.4	1.5	1338.0	53.4	62.8

) showed that more than half of the single wells leaked while drilling, and half of the wells leaked due to the development of caves. After drilling open the caves, the leakage rate was high, and the amount of leakage was large, seriously affecting the oilfield’s production efficiency.

There are two key points affecting the loss circulation control of fractured-vuggy carbonate reservoirs: proper invasion and effective plugging of LCMs (lost circulation materials) [6,7,8]. Excessive invasion leads to severe reservoir damage, which, in turn, affects oil and gas production efficiency. Unstable plugging zones will be created by shallow plugging, which easily break during subsequent drilling [9,10]. There are a number of difficulties related to the effective plugging of fractured-vuggy carbonate reservoirs. The most critical problem is that the leakage channel of this type of reservoir is too large, and the LCMs cannot bridge the leakage channel [11]. Consequently, the formation of fluids in the vugs will cause dilution of the LCMs. The settlement and retention of LCMs in a horizontal wellbore is also an important factor [12]. Due to the large depth of the reservoir and the small size of the wellbore, there are engineering risks. The leakage and overflow often occur in the same layer. In traditional research, the following techniques are mainly used to solve the leakage of fractured-vuggy carbonate reservoirs: pure water drilling, rapidly solidifying water-based drilling fluids, inert LCMs plugging, concrete or bag-plugging tools, bypassing the drilling fluid loss layer, and refracting [13,14,15]. However, in the ultra-deep and ultra-high pressure underground environment of western China, the above technologies are not applicable due to factors such as engineering risks and reservoir protection.

In recent years, multistage bridge plugging (MBP) technology has facilitated pioneering experiments in many oilfields. The idea is to adopt multistage bridges. The first stage of bridging uses a bridging ball to change a big cave into small pores; the second stage of bridging involves the addition of relatively small acid-soluble particles and fibers, etc. into the small pores for further plugging. This technology is widely used in oil and gas fields in western China, but the success rate of plugging is less than 50%, and the plugging effect is uncontrollable and difficult to predict. The reason is that the plugging mechanism of this technology and the key factors influencing the success of plugging are not clear.

MBP technology essentially belongs to the category of particle bridging and plugging. At present, there are in-depth studies on the bridging laws of pores or fractures, but the bridging laws of fractured-vuggy reservoirs and the pore structure of plugging layers have not yet ascertained. In porous media cases, the commonly used plugging material bridging design rules are “1/3 bridging theory” [16], “ideal filling d_1/2 theory” [17], “D90 rule” [18], “shield temporary plugging theory” [19], and other plugging particle screening and grading schemes through experiments proposed by scholars [20,21,22]. For regular fractures, some bridging theories have also been proposed through experiments and computational fluid dynamics (CFD)-discrete element (DEM) coupled numerical simulations [23,24,25]. Additionally, the connection between pores and fractures should be considered especially in the particle size/fracture width aspects [15,26,27,28,29]. For natural fractures in the well, Feng et al. and Zhu et al. [6,30,31,32] used fracture reconstruction technology combined with discrete element numerical simulation analysis, and believed that particle bridging mainly comprises single-double particles bridging. When the particle diameter D90 is 1–2 times the average fracture width, the plugging layer is distributed in discontinuous islands. For fractured vugs, there is missing a set of feasible loss control technologies and related theories, mainly because the size, shape, complexity, filling condition, and connection with the wellbore cannot be accurately described or predicted.

One key of MBP is to plug the first-stage plugging layer, the study of the pore structure of which is the critical factor that determines the success rate of MBP. The previous research mainly focused on the pressure-bearing capacity, permeability, and the recoverability of the plugging layer [19,33,34]. In recent years, the mesostructure of the plugging layer has begun to attract researchers’ attention. CT, NMR, and photo-elastic experiments have been applied to analyze the force chain structure and pore structure of the plugging layer [10,35,36], but the research has not been in-depth.

Due to the strict requirements of scale and environmental conditions in fractured-vuggy reservoirs, it is difficult to visualize and quantitatively analyze the particle bridging mechanism from the particle scale. However, the discrete element method (DEM) can make up for this deficiency. Since the DEM was proposed by Cundall and Strack [37], it has become an effective tool for studying the microstructure of granular media. The DEM is directly based on the Newton’s second law; the simulation results can reflect the evolution information of the mesoscopic structure in the particle system. It is widely used in geotechnical mechanics, grain storage, and particle transportation [22,38,39]. In fracture plugging research, the DEM is an important method to reveal and explore the formation process and stability evolution of the mesostructure in the plugging layer. Moreover, the DEM can be coupled with the computational fluid dynamics method (CFD-DEM) to carry out research on the formation process of the plugging layer [8].

Therefore, our focus is on the MBP technology of drilling fluid loss in the drilling process of fractured-vuggy carbonate reservoirs; this study uses DEM to analyze the plugging mechanism and influencing factors of MBP. The structure of the paper is as follows: The second part of the paper is based on the study of geological and leakage characteristics of fractured-vuggy carbonate reservoirs; it contains an analysis of the necessary geological conditions for dealing with the leakage of cavernous reservoirs. The third part mainly introduces the design thought process for the MBP technology, analyzes the factors that affect the effects of MBP, and introduces the DEM simulation method, parameter setting, etc. The fourth part mainly introduces the numerical simulation results, and analyzes the mechanism of MBP technology and its influencing factors.

2. Background of MBP Technology

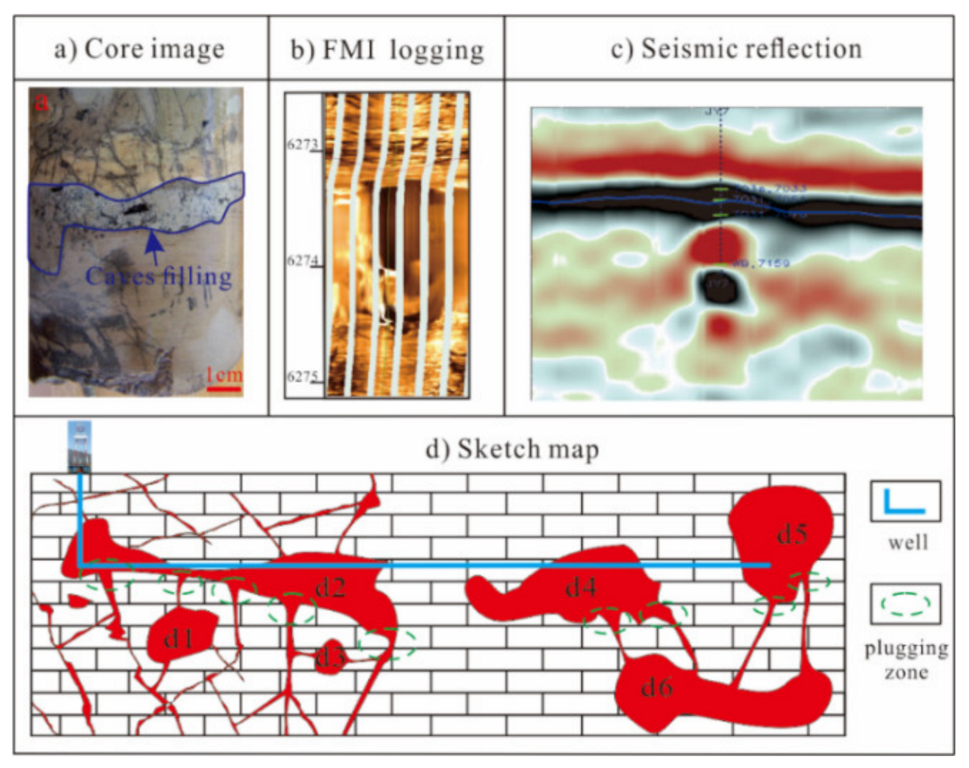
2.1. Geological and Leakage Characteristics of Reservoirs

Carbonate reservoirs are mainly controlled by diagenesis. Early diagenesis destroys the original pores, and the dissolution pores, caves and fractures formed by various diagenesis processes become important reservoir spaces. Among them, caves are the most important reservoir spaces in carbonate reservoirs, which are mostly half-filled or completely filled with mud or collapsed breccia, and are the object of this paper. As the scale ranges from centimeter to meter, the size of some caves is much larger than the size of the cores, causing the drilling extraction rate to be lower. Figure 1 shows the core, log, and seismic reflection profile of a cave: The local characteristics of the cave and the characteristics of the cave fillings can be obtained from the completely filled cave core (Figure 1a). It appears as dark patches on the FMI log (Figure 1b) and beadlike bright reflections on the seismic reflection profile (Figure 1c). Based on shape, connectivity, and interaction with the wellbore, caves can be broadly classified into the following types. (1) Upper cave and lower throat type, where the cave only has throats connected with other fractures and caves on its lower part (Figure 1d4,d5). (2) Lower cave and upper throat type, where the cave only has throats with other fractures and caves on its upper part (Figure 1d6). (3) Cave with throats in the upper and lower parts, with no throat in the horizontal direction (Figure 1d1). (4) Cave with throats in the landscape direction, but no throats in portrait direction (Figure 1d3); and (5) A higher-coordinating structure, for which there are many throats around the cave, connected with other fractures and caves (Figure 1d2).

However, regardless of the type of cave assemblage, there is a key point in the treatment of leakage in cave-type carbonate reservoirs: to form a stable bridge in the caves. No matter how much plugging material is invested, effective plugging cannot be formed for a meter-scale cave. For example, in Figure 1d, if the plugging materials are not effective in plugging at the green dashed line, the plugging materials may settle after they enter cave d6, leading to plugging failure. As a result, leakage treatment for the fractured-vuggy carbonate reservoirs should be plugged at the throat closest to the wellbore by the green dashed line in Figure 1d.

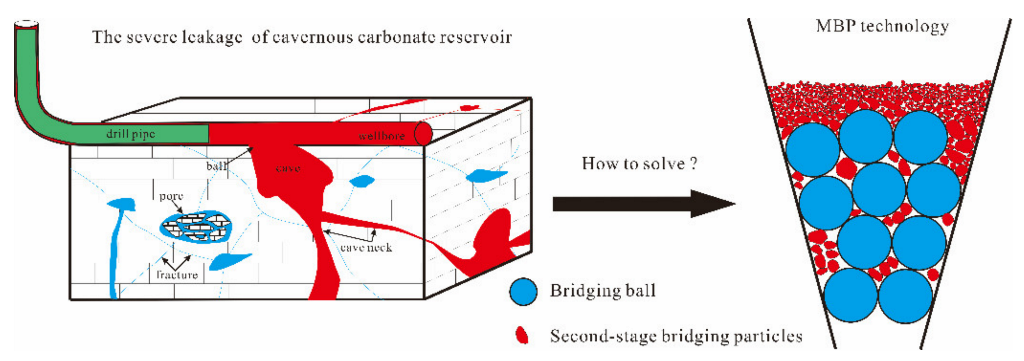
2.2. MBP Technology Theory

The basic idea of the MBP technology is that balls and different scales of particles successively form multiple stages of the bridging structure, and the technology is implemented in two steps (Figure 2). (1) For first-stage bridging, different sizes of bridging ball are casted into the continuous oil pipes, accumulating in the target leakage segment to make a large cave into small pores and form porous media. (2) For second-stage bridging, smaller (compared with bridging ball) acid-soluble particles, fiber, and elastic particles are injected into the leakage segment to further bridge, fill, and compact the porous media. Ultimately, that makes the leakage segment a plugged formation with high-pressure capacity. The key of this technology is whether the bridge ball can form the first stage bridge at the cave throat near the wellbore. Routine experience shows that when people pass through an entrance, they can move smoothly if they move in an orderly manner, in which the traffic is related to the speed and density of the crowd. However, when the entrance is crowded, traffic will be reduced. If the vehicles running on a road keep a certain distance from one another, the traffic flow is smooth. If passing a narrow neck, the density of the vehicles will increase to form a traffic jam, and the traffic flow will immediately decrease. Therefore, this technology has a theoretical basis for success.

First-stage bridging is essentially spherical random packing problems (in this research, all packing problems are considered under three-dimensional conditions), due to the fact that the particle collision, springback, interaction between particles, impact of the container walls during actual packing, the corresponding local structures, and arrangements packed randomly by the spheres are diverse and complex. Different packing densities correspond to a large number of possible arrangements. Generally, a random packing density is mainly affected by the following factors:

Wall effect. The wall effect is relevant to the ratio of the vessel diameter to the sphere diameter. The wall effect consists of two points, the first of which is the relatively high void fraction due to the difference in radius of curvature between the wall and the sphere, and the second of which is the partial ordering in random packing near the solid surface.

Particle shape. According to Ulam’s conjecture, in all convex bodies whose shapes are close to the ball, the random packing density of the sphere is the lowest, which is consistent with the results of the currently known research [40].

Packing speed. The greater the packing speed is, the greater the void fraction becomes. Academic circles have come basically to the same conclusion about the packing density of the isosphere. The random close packing density of the isosphere is approximately 0.64, but it has not been strictly mathematically deduced [41]. The random loose packing density is 0.56, and the regular dense packing density is about 0.74.

Smith obtained the relationship between the average void fraction $\phi$ and the average coordination number $Z$ by plumb packing experiments during the random packing [42]:

$$\phi =\frac{0.414Z-6.527}{0.414Z-10.968}$$

(1)

The experiments also show that the packing density of the sphere increases with the increase of the ratio of vessel diameter to sphere diameter when the ratio is less than 10. When the ratio exceeds 10, the packing density approaches the constant of 0.64. In the work of MBP, the ratio of cave neck diameter to bridging ball diameter is usually smaller than 10, but the ratio above the cave waist is usually greater than 10, therefore, the porosity of the formed porous medium by first-stage bridging near the neck should be slightly higher than that of the waist of the cave. However, the packing density of the first-stage bridging should be greater than the random loose packing (RLP) of 0.56. In other words, if the main arrangement of the bridging balls is between the cubic sparse pack and face-centered cubic pack (or hexagonal close pack), the maximum pore throat radius of porous media formed by first-stage bridging is 0.414 r_b (cubic loose pack, Figure 3a, r_b representing the diameter of the bridging ball) and the minimum pore throat radius is 0.155r_b (face-centered cubic or hexagonal close pack, in Figure 3b). If the bridging ball is in direct contact with the wall, the pore throat radius of the porous medium formed at this time should be between 0.155 and 0.414 r_b.

According to the study of funnel flow and traffic flow in the literature, the key factors affecting the first-stage bridging are the cave neck diameter, dip angle, and the flow rate and speed of the bridging ball. In this work, the impact factors and mechanism of first-stage bridging are analyzed through DEM simulation.

3. Method

At present, there is still not enough theoretical research on the static and dynamic characteristics of granular materials; research on the behavior of granular materials mainly focuses on DEM simulation and experimental aspects. The BALL program, developed by Cundall and Strack [37], for a two-dimensional circular block is the beginning of a DEM. The results of numerical simulations are in good agreement with experimental results obtained using photoelastic techniques, verifying the reliability of the DEM, as studying the behavior of discrete particles can potentially offer new ways to solve this problem. At present, the commonly used DEM softwares are PFC, EDEM, UDEC, etc. All DEM simulations in this research were carried out on the software EDEM 2.7, developed by DEM Solution Ltd.

3.1. Contact Model

The modeling approaches can be roughly divided into two groups: soft-particle and hard-particle models. In a hard-particle model, the interaction forces are assumed to be impulsive, hence, the particles only exchange momentum by means of collisions. A characteristic feature of a hard-sphere simulation is that a sequence of collisions is processed one collision at a time, assuming instantaneous collisions. An important feature of our hard-particle model is that simulations can be performed with realistic values for the key parameters (restitution and friction coefficients), whereas, in soft-particle approaches, softer normal interactions have to be assumed [43]. In Cundall and Strack’s distinct-element method, the interparticle contact forces are calculated based on simple mechanical models, such as springs, dashpots, and friction sliders. A characteristic feature of the soft-particle models is that they are capable of handling multiple particle contacts, which is of importance when modeling quasistatic systems, and a very small time step (<10⁻⁶ s) is required. Regardless of particle surface deformation, the contact force is calculated based on the normal overlap, the tangential displacement of the particles, and the calculation of the contact strength without load history. The calculation of the strength is suitable for the numerical calculation of engineering problems. The soft-particle contact model is adopted by EDEM.

The problem of contact between particles is widespread in nature. The ideal case is the contact between smooth and elastic spherical bodies, and this problem can be found in the classical elasticity theory. The contact model is to link the amount of overlap, the physical properties of contact particles, the impact velocity, and the contact information before this step together by a pair of equal and opposite forces, and to calculate the resultant force on the particles. Then, the acceleration is calculated by Newton’s second law, and the particle velocity and displacement are updated [44].

Mindlin [9] conducted an in-depth discussion of this issue and proposed that the friction coefficient can be used to consider the particle surface roughness. He derived the normal contact stress and tangential stress distribution and formally put forward the concept of contact stiffness. According to the basic characteristics of the bridging ball, the contact model between the bridging balls can meet the Hertz–Mindlin nonslip model, in which the interparticle normal force $F_{\mathrm{n}}$ is assumed:

$$F_{\mathrm{n}}=\frac{4}{3}{E}^{*}{(r^{*})}^{\frac{1}{2}}{\alpha }^{\frac{3}{2}}$$

(2)

In Equation (2), $E^{*}$ is the equivalent elastic modulus, $r^{*}$ is the equivalent particle radius, and α is the normal overlap amount.

Normal damping force $F_n^{\mathrm{d}}$ between contact particles is:

$$F_n^d=-2\sqrt{\frac{5}{6}}\beta \sqrt{S_n{m}^{*}}{\overrightarrow{\nu }}_n^{rel}$$

(3)

In Equation (3), $m^{*}$ is the equivalent mass, and ${\overrightarrow{\nu }}_n^{rel}$ is the normal component of the relative velocity. The coefficient $\beta$ and the normal stiffness $S_n$ are related to the recovery coefficient $e$ and can be obtained from the following two equations:

$$\beta =\frac{\ln e}{\sqrt{{\ln }^{2}e}+{\pi }^2}$$

(4)

$$S_{\mathrm{n}}=2E^{*}\sqrt{r^{*}\alpha }$$

(5)

Tangential force ${\overrightarrow{F}}_t$ between particles can be obtained by the following formula:

$${\overrightarrow{F}}_t=-S_t\overrightarrow{\delta }$$

(6)

In Equation (6), $\overrightarrow{\delta }$ is the tangential overlap amount, and $S_t$ is tangential stiffness.

Tangential damping force $F_t^d$ between particles can be obtained by the following formula:

$$F_t^d=-2\sqrt{\frac{5}{6}}\beta \sqrt{S_t{m}^{*}}{\overrightarrow{\nu }}_t^{rel}$$

(7)

In Equation (7), ${\overrightarrow{\nu }}_t^{rel}$ is the tangential relative speed.

Tangential force is related to friction ${\mu }_s{F}_n$; here, ${\mu }_s$ is the static friction factor.

The rolling friction in the simulation is important, and it can be described by the torque on the contact surface, namely:

$$T_i=-{\mu }_r{F}_n{r}_i{\omega }_i$$

(8)

In Equation (8), ${\mu }_r$ is the rolling friction coefficient, $r_i$ is the distance from the centroid to the contact point, and ${\omega }_i$ is the unit angular velocity vector of the object at the contact point.

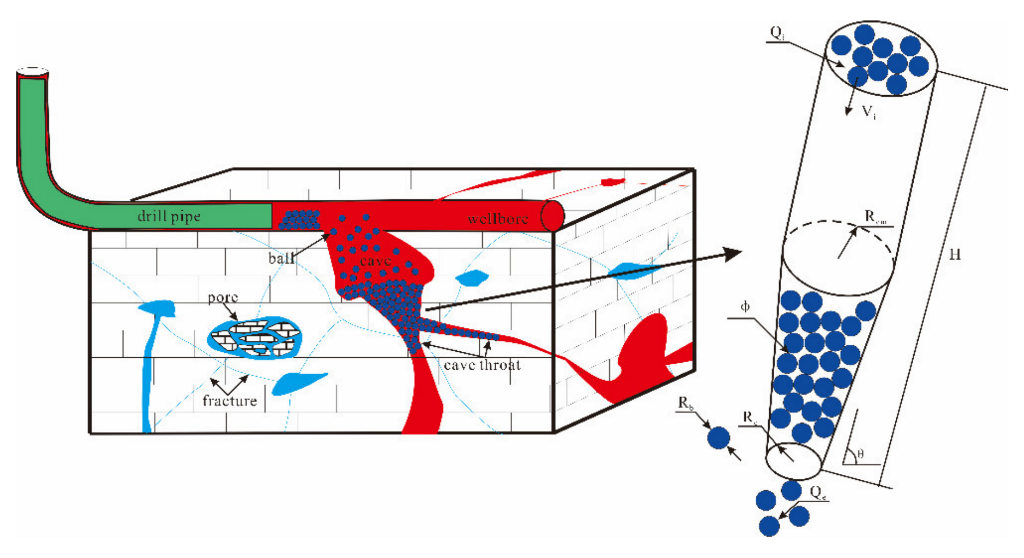
3.2. Geometry and Simulation Parameters

In the process of drilling fluid loss, the drilling fluid replenishment speed in the wellbore is less than the drill-in fluid loss speed, causing the wellbore pressure and formation pressure to be in a nearly balanced state. In this near-balance system, the drag force caused by the fluid flow is not the key factor affecting the bridging-ball migration. The shape and size of the cave, initial flow rate, and speed of the bridging ball are the key factors affecting the first-stage bridging. Therefore, the model and parameters are designed according to the following scheme:

The computational domain is a three-dimensional model that idealizes a cave model into a frustum-shaped, non-closed upper and lower model. The diameter of the model decreases from the top to the bottom to simulate the necking of the cave. When casting balls begins, many bridging balls accumulate in the borehole and fall into the cave and bridge at the cave neck. To explain the mechanism and scope of application of MBP technology, some concepts are defined to describe the geometric parameters of the model and the MBP process (Figure 4).

(1) Cave neck radius R_c: the radius of the cave neck, in mm. (2) Bridging ball radius r_b: the size of the bridging ball used for MBP, in mm. (3) Cave dip angle θ: the angle between the horizontal axis and central axis of an ideal cave, in rad. (4) Bridging ball flow rate Q_e at cave neck: the flow rate of bridging ball that flow out from the cave neck, in pcs/s; (5) Initial flow rate Q_i of bridging ball: the flow rate for the bridging ball entering from the cave inlet, in pcs/s. (6) Initial velocity of the bridging ball V_i: the initial velocity for the bridging ball entering from the cave inlet, in m/s. (7) Number of critical bridging ball N_c: the minimum consumption of bridging ball for successful first-stage bridging, in numbers. (8) Critical initial flow rate: the initial flow rate at which first-stage bridging probability of success is higher than 90% (simulated 50 times), in pcs/s. (9) Porosity of first-stage bridging layer φ: the ratio of the void space in the cave to the cave space, in %.

As described above, in the DEM based on the Hertz–Mindlin nonslip contact model, the particle density, particle distribution, Poisson’s ratio, shear modulus, coefficient of restitution of particle–particle and particle–wall, sliding friction coefficient, and rolling friction coefficient are the key parameters that affect the simulation results. As discussed earlier, the basic parameters of particle density and diameter are fixed in the simulation process, assuming that the particles are rigid bodies in the DEM. The relationship between Poisson’s ratio and elastic modulus is:

$$G=\frac{E}{2(1+\upsilon )}$$

(9)

In Equation (9), $G$ is the shear modulus of the particles, $\upsilon$ is the Poisson’s ratio of the particles, and $E$ is the Young’s modulus of the particles. Poisson’s ratio also affects the equivalent elastic modulus, which, in turn, affects the normal force and the normal damping force. Similarly, the change of the shear modulus will lead to the change of the normal force and the tangential force, so the impact of the whole contact model is complex. This article gives the shear modulus and Poisson’s ratio when setting the simulation parameters. These parameters do not change in the simulation.

As shown in Equations (3)–(5), the coefficient of restitution affects the normal damping force. When the coefficient of restitution is 1, the normal damping force is 0, and the collision is completely elastic. The smaller particle contact force, the higher calculation efficiency, and the smaller coefficient of restitution can increase the normal damping force, thus improving the efficiency. In addition, the coefficient of restitution will also affect the frictional energy consumption. After comprehensive consideration, the particle size, the cave model size, and the results of the tuning parameters used in the DEM simulation are shown in

Table 2. Parameters used in the DEM simulation.

Parameters	Value (Varying Range)
Cave geometry parameters
Dip angle θ (rad)	90 (15~90)
Cave neck radius Rc (mm)	38 (≥38)
Height H (mm)	300 (300~900)
Cave maximum radius Rcm (mm)	120
ball properties
Ball radius Rb (mm)	8.44 (6.33~19)
Ball initial velocity Vi (m/s)	0 (0~3.2)
Ball initial flow rate Qi (numbers per seconds)	200 (100~400)
Ball density ρb (kg/m3)	1800
Shear Modulus (Pa)	9.09 × 108
Poisson ratio (–)	0.25
Cave properties
Shear Modulus (Pa)	1 × 1010
Poisson ratio (–)	0.25
Interaction parameters
Coefficient of restitution ebb = ebc (–)	0.8
Friction coefficient
Sliding μs, bb = μs, bc (–)	0.5
rolling μr, bb = μr, bc (–)	0.01

.

4. Results and Discussion

As mentioned earlier, if you bridge balls one by one across the neck of the cave, effective bridging is always impossible, as long as the size of the balls is smaller than the radius of the neck. The basic condition under which bridging occurs specifies that the flow of bridging is reduced only when the flow of bridging changes from sparse to dense.

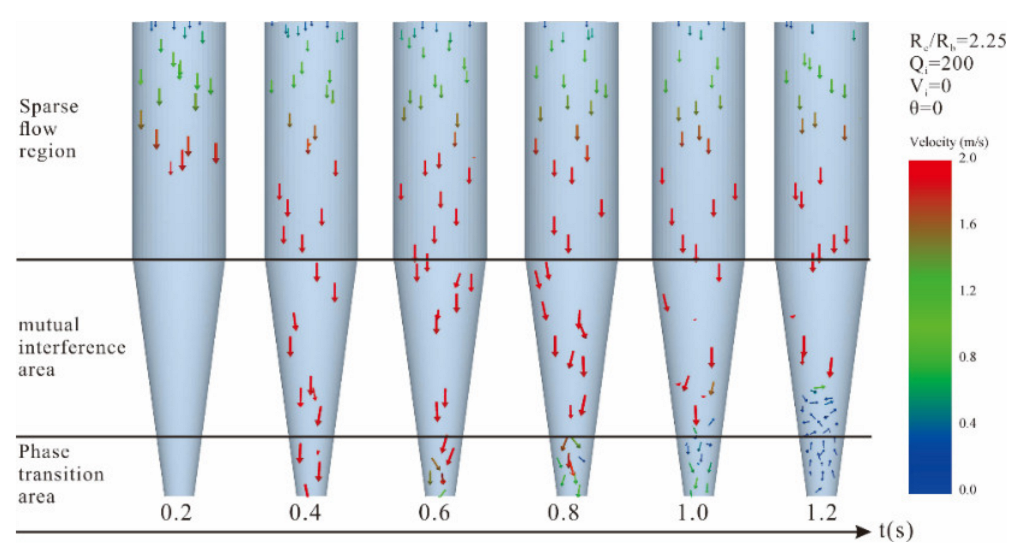
4.1. Flow Characteristics

A granular flow rate depends on particle velocity and flow rate. Sparse flow refers to the free-flow behavior between particles, and the dense flow refers to particle-interactive flow behavior. There is sparse flow of particles in the low degree of interference, but the particle flow rate in dense flow is greatly reduced due to the particle friction, collision, and arching. As granular material flows, the flow rate $Q$ is proportional to particle density $\rho$, velocity $V$, and the flow cross-section $S$. The flow rate in three-dimensional space should take the average value of a columnar body, which is:

$$Q=\rho VS=\frac{{\displaystyle \sum {(\mathrm{m}}_i({\overrightarrow{V}}_i\cdot \overrightarrow{l}))}}{l}$$

(10)

In Equation (10), ${\mathrm{m}}_i$ is the mass of the particle (No.: $i$), ${\overrightarrow{V}}_i$ is the velocity (vector) of the particle (No.: $i$), ${\overrightarrow{V}}_i\cdot \overrightarrow{l}$ is the component (scalar) of the velocity in the axial direction of the cylinder, and $l$ is the axial length of the cylinder.

For MBP technology, the cave shape, borehole conditions, and construction methods are different, so the bridging rules have new differences. Figure 5 shows the mean velocity vector profile of the bridging ball during the MBP process. There are obviously three areas in the vertical direction. The first area is a sparse flow region in which balls do not interfere with each other. There is almost no collision between the balls in this region, and only the vertical velocity increases. As the wall surface is vertical, the bridging ball does not collide with the walls, energy loss and ball speed does not change. The second area is the mutual interference area for balls, in which, because of the collision between the ball and the cave, the ball energy loss, and the change in direction of movement caused by the cave contraction, interference occurs between balls, exacerbating the energy between the balls, and the ball movement becomes complex. The third area is a phase transition area in which further contraction of the cave diameter causes more-frequent ball–ball and ball–cave collisions, frequent energy exchange between balls, and severe energy loss of balls, which, in turn, causes the ball bridging in the caves.

Figure 6 shows the variation of the flow rate of the bridging ball in the area (the phase transition area in Figure 5) over time under the same initial flow rate Q_i and different R_c/r_b. Combined with Figure 5, the analysis shows that the first-stage bridging in time can be divided into four phases (in some curves, there may be one or two phases missing). The first phase is the transition from sparse flow to dense flow, and the flow rate of a bridging ball at the cave neck increases rapidly with time until it reaches the maximum value. The duration of this phase has little to do with R_c/r_b. The end time of the first phase in Figure 6 is 0.35 s or so. However, the maximum value of Q_e is related to the R_c/r_b value. As the R_c/r_b value increases, the maximum value of Q_e also increases. Additionally, the maximum value of Q_e does not change significantly after R_c/r_b > 2. This phase corresponds to t = 0.2 s and t = 0.4 s in Figure 5. At t = 0.4 s, although the velocity of a single ball decreased due to energy loss, the number of bridging balls increases, so the ball can still maintain a relatively fast flow rate with high efficiency from the cave neck, out. The second phase is the transition from dense flow to jamming flow, where outlet flow rate does not change significantly, and the duration of this phase is related to R_c/r_b. As the R_c/r_b increases, the longer the duration of this phase lasts. This phase corresponds to t = 0.6 s and t = 0.8 s in Figure 5. At the beginning of this phase, the velocity of a single ball decreased significantly at the cave neck, but the number of bridging balls further increased. As a result, the ball flow rate did not drop rapidly, and the ball flow out of the cave was also more efficient. However, with the further increase of time, the ball speed further decreased, and the number of balls further increased. Jamming occurred and entered into the third phase. The third phase is the transition from soft jamming flow to deep jamming flow, corresponding to t = 1 s and t = 1.2 s in Figure 5. The bridging structure is not stable at this stage, and the strong chain is still breaking and reforming. At this phase, a portion of the balls at the cave neck had a velocity of 0, but due to the instability of the bridging structure, the flow occurred again. However, with the decrease of the system energy, the bridging structure is gradually stabilized, and the outlet flow rate obviously decreases gradually from the maximum value to 0, until the ball successfully achieved bridging. The fourth phase is the readjustment phase. After the stable bridging structure is formed, the already strong chain strength of the bridging structure is damaged again due to the weight increased of the overlying balls and the positive pressure difference in the cave, and then the new strong chain formed, or the bridging structure is destroyed. This phase in Figure 5 does not correspond to the object. As shown above, the first-stage bridging is a continuous adjustment process, as the balls in the cave continue to increase, the bridging structure is always changing, until it tends to a more stable chain system or causes the bridging structure to collapse (Figure 7).

A granular system has inherent unique properties, such as heterogeneity, discontinuity, randomness, and due to the different initial conditions (such as the formation location) of the granular material, the whole system also causes great differences. In the case of the same model, only the initial position of the ball is changed, and the change of the Q_e in Figure 8 with time is obtained. If the Q_i, R_c/r_b, the V_i, and other conditions are the same, the change in the position of the bridging ball in the formation causes a difference between the second phase and third phase, as mentioned above. As the ball collision intensifies, the exchange and dissipation of energy between balls is frequent, and the butterfly effect caused by the change of the initial position of the balls is more serious. The obvious similarities can be observed from four curves in Figure 8, indicating that, although the system has strong complexity and randomness, the whole law remains similar, still complies with the basic principles of statistical mechanics, and can be accurate with fewer parameters.

The flow of the ball in the cave is related to the cave shape, the ball velocity, the Q_i, and Rc/rb. It is carefully observed that the flow states of ball in the cave can be divided into the following categories (Figure 9). The first is wall flow. When the ball flow is small with a large cave dip angle, the ball can flow along the wall in a smooth and orderly way. The second is climbing flow. When the cave dip angle is larger, the ball movement in front is slower than the ball behind; the following behind ball will climb from the head of the front ball to the top. The third is parabolic flow. When the ball enters the inlet of the cave, due to the large cave dip angle, the ball under the action of gravity flows in a parabolic way. The fourth is leaping flow, because repeated collisions with the cave wall lead to changes in the direction of motion, the ball jumps in an oblique way, and this situation generally requires the ball to have greater kinetic energy. The fifth category is spiral flow. When the ball moves faster and there is less interference between the bridging balls, the ball will drop in a spiral way along the wall surface.

4.2. Influence Factors of Ball Bridging

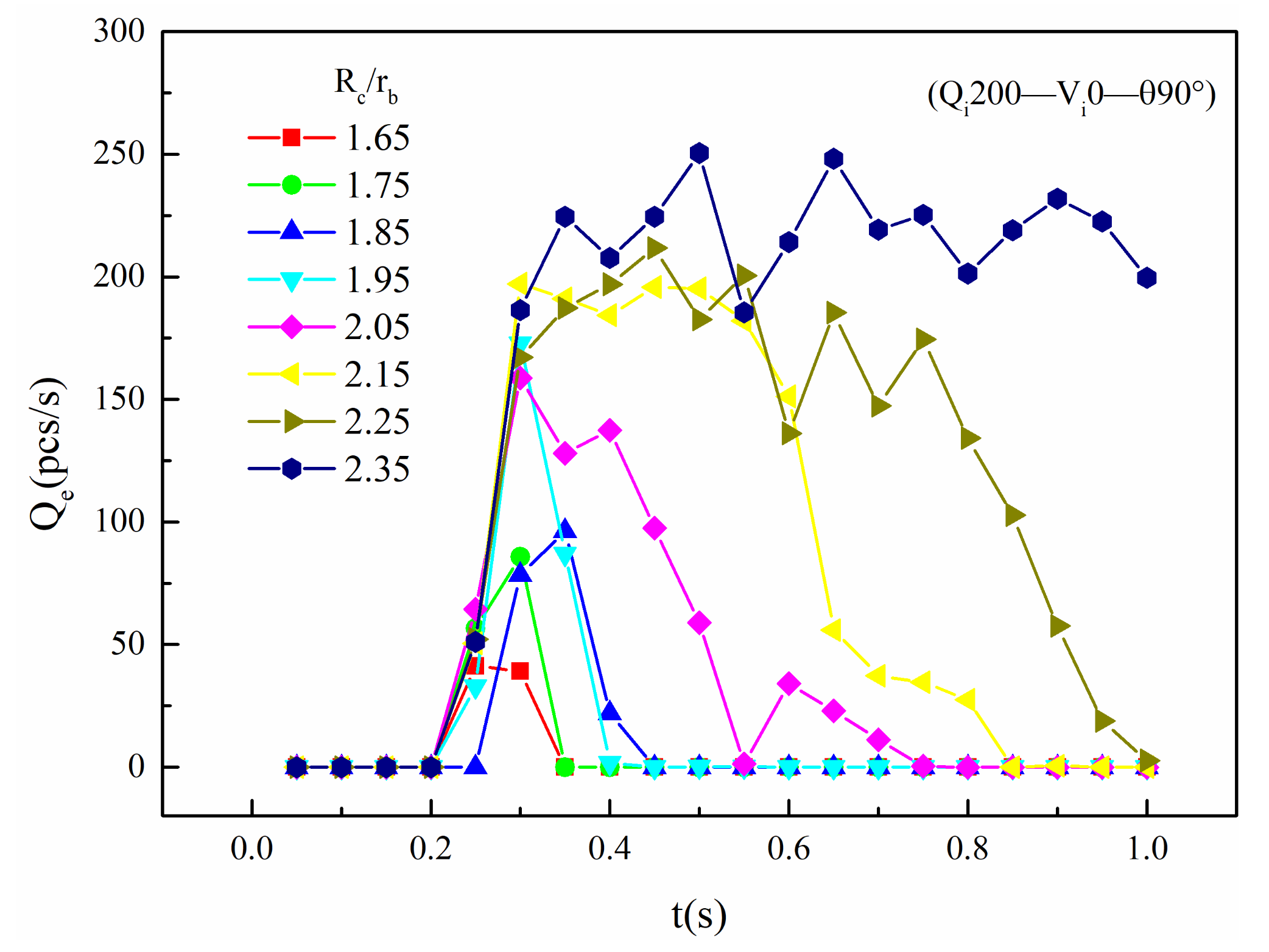
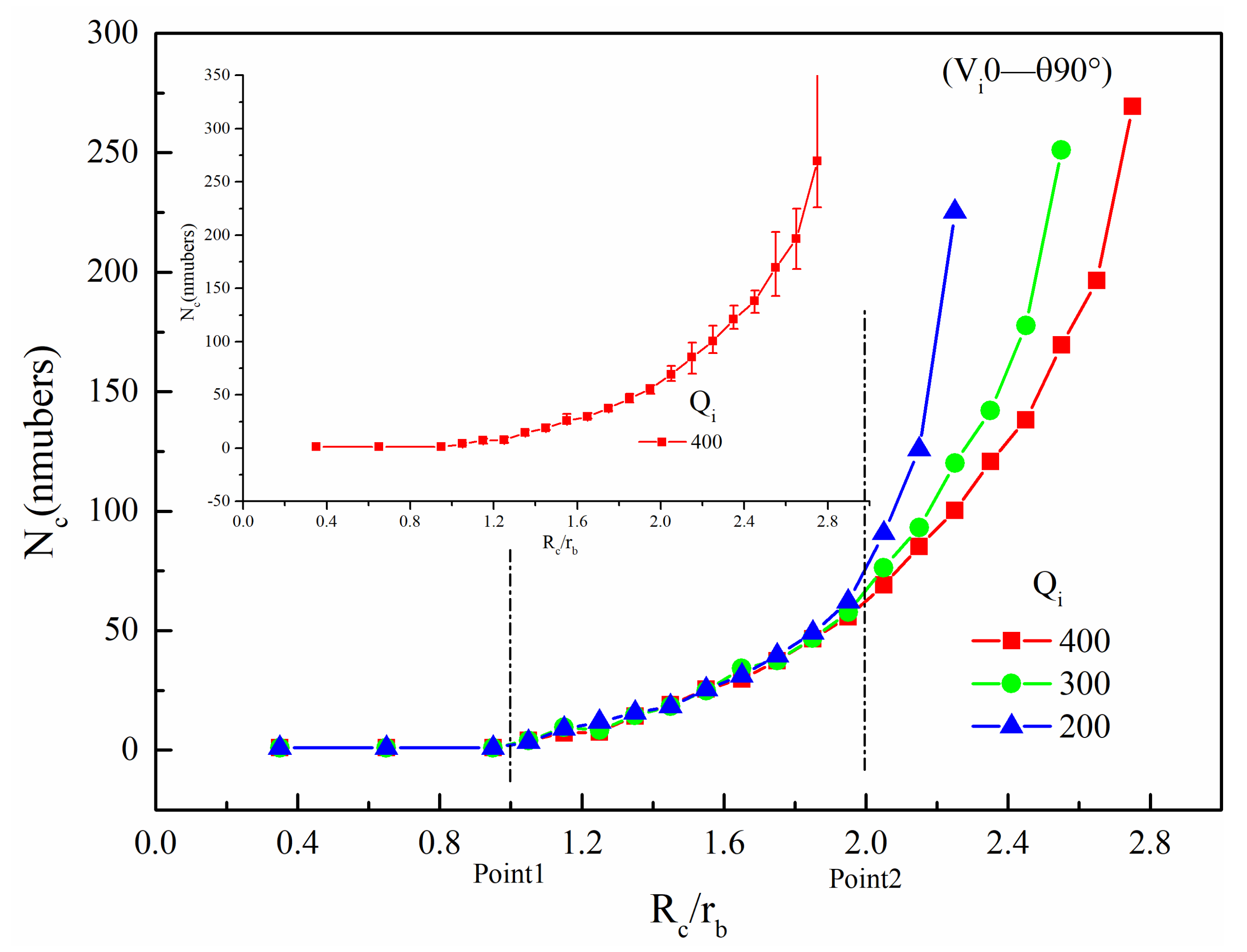
4.2.1. Effect of R_c/r_b

As mentioned earlier, the ball flow has randomness due to the ball’s initial position, so the N_c shows a range of fluctuations. The N_c can be obtained under different R_c/r_b conditions (Figure 10). The fluctuation range of N_c increases with the increase of R_c/r_b, but the fluctuation range is always maintained at within 25% of the average (50 times the simulations).

The results also show that the larger R_c/r_b, the greater the average N_c. The average N_c and R_c/r_b showed a clear three-section relationship. Three sections are separated by two points. The first point is R_c/r_b = 1, and the second point is the maximum of curve curvature. When R_c/r_b < 1, if the bridging ball enters into the cave it can form an effective bridging. When 1 ≤ R_c/r_b < second point, the average N_c increases with the increase of R_c/r_b, but the growth rate is gentle. When the second point ≤ R_c/r_b, the average N_c increases sharply with the increase of R_c/r_b, and the growth rate is accelerated. That is to say, before R_c/R_b < second point, the whole ball-bridging system is more stable, and slight changes of one variable will not cause a significant impact on the entire bridging system. After the second point, a slight change of a variable may cause a drastic change in the system. It is also shown in Figure 10 that as the Q_i increases, the curves gradually shift to the right. The specific changes will be discussed in detail, later.

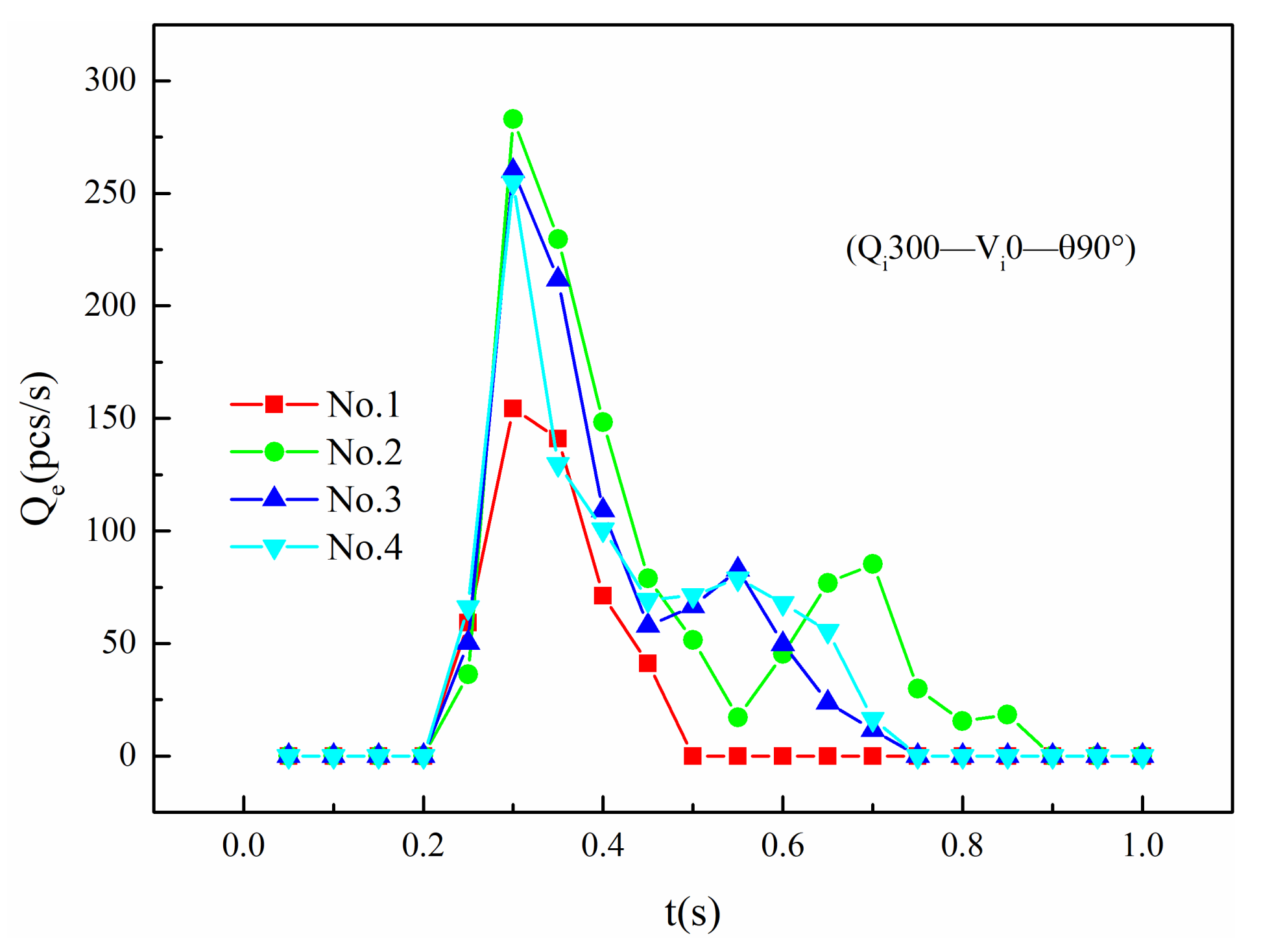
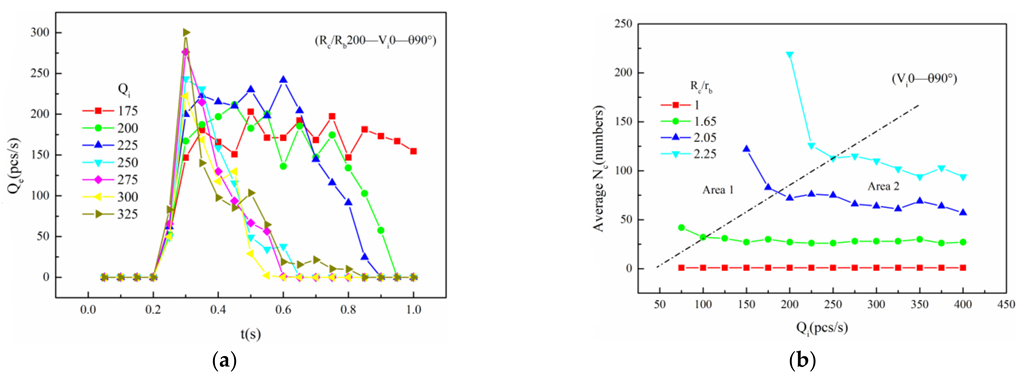
4.2.2. Effect of Q_i

From this analysis, it can be found that the Q_i also has a significant effect on bridging results. Figure 11a shows the changing rule of the Q_e with time by changing Q_i when R_c/r_b is fixed (R_c/r_b = 2.25). Although the Q_i increases, the maximum value of Q_e has not significantly increased; it is between 200 and 300 pcs/s. It is observed that, as the Q_i increases, the time required for successful bridging decreases, but after the Q_i > 250 pcs/s, either (a) the curve shape or the cumulative time from in a sparse flow to in a jammed flow or (b) the maximum Q_e has no significant changes. When the Q_i < 190 pcs/s, no matter how many bridging balls are used to bridge, it is impossible to achieve successful bridging. There is a critical Q_i for ball bridging, and the bridging can only be successful when the Q_i is greater than this value.

Figure 11b shows the relationship between the average N_c and the Q_i under different R_c/r_b conditions. The effect of Q_i on bridging results can be divided into two distinct areas. Area 1 is the severely affected area, where an increase of the Q_i results in a significant decrease of the average N_c. Area 2 is the light-impact area, where the average N_c does not change drastically with the change in Q_i.

The ball bridging is affected by the synergistic effect of R_c/r_b and the Q_i. To illustrate this synergy better, the critical Q_i change under different R_c/r_b conditions is analyzed in Figure 12. When R_c/r_b < 1, as long as the ball that entered into the cave can form a stable bridging, the Q_i is not related to R_c/r_b. When 1 < R_c/r_b < 2, as R_c/r_b increases, the critical Q_i also softly increases, but the area with R_c/r_b > 1.5 increases faster than R_c/R_b < 1.5. When R_c/r_b > 2, the critical Q_i increases sharply with the increase of R_c/r_b. When R_c/r_b = 2.5, the critical Q_i > 400 pcs/s is required.

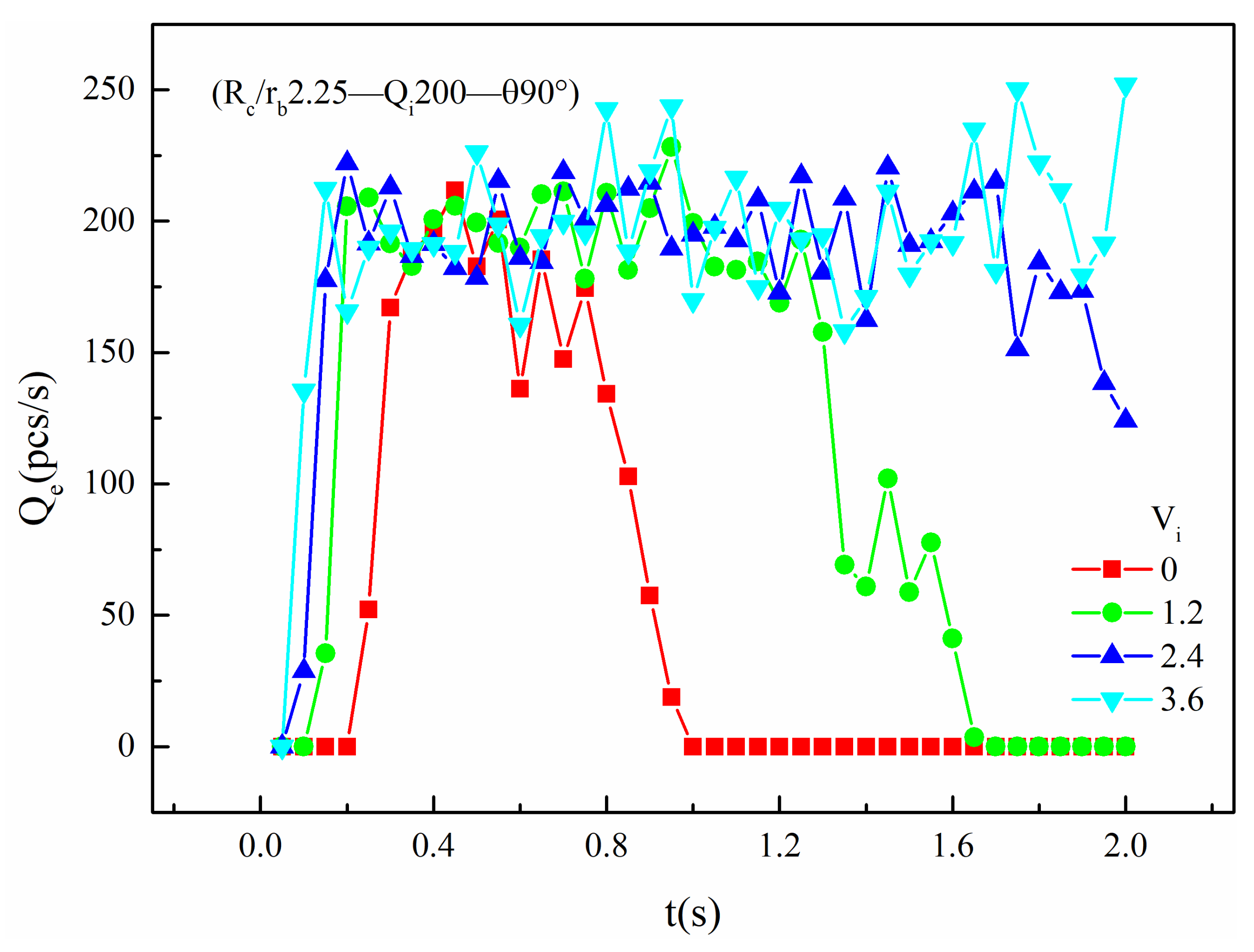
4.2.3. Effect of V_i

As mentioned above, the change of the Q_e is the key factor that causes the jamming. The flow rate of the ball is also directly related to the velocity. Figure 13 shows the Q_e versus time with different V_i. As the V_i increases, the cumulative time required for successful bridging is longer. When the ball speed reached a certain level, it has been unable to bridge, and the Q_e has always maintained a high level. This is because when the velocity of the ball increases, the efficiency of the ball passing through the cave neck increases, and the interference between the balls is reduced. At the same time, due to the large velocity of the ball, the kinetic energy of the granular system is also high. It also takes a longer time and becomes more difficult for the system to dissipate higher energy. When the height of the cave is added, it can be equivalently considered as increasing the initial velocity and initial energy of the balls, and successful bridging is more difficult. If the fluid is in a low-pressure gradient from the cave inlet to the cave neck, the effect of fluid flow on the ball can be neglected. An increase of the fluid density or viscosity can effectively increase the buoyancy and reduce the velocity and kinetic energy of the ball, making ball bridging easier.

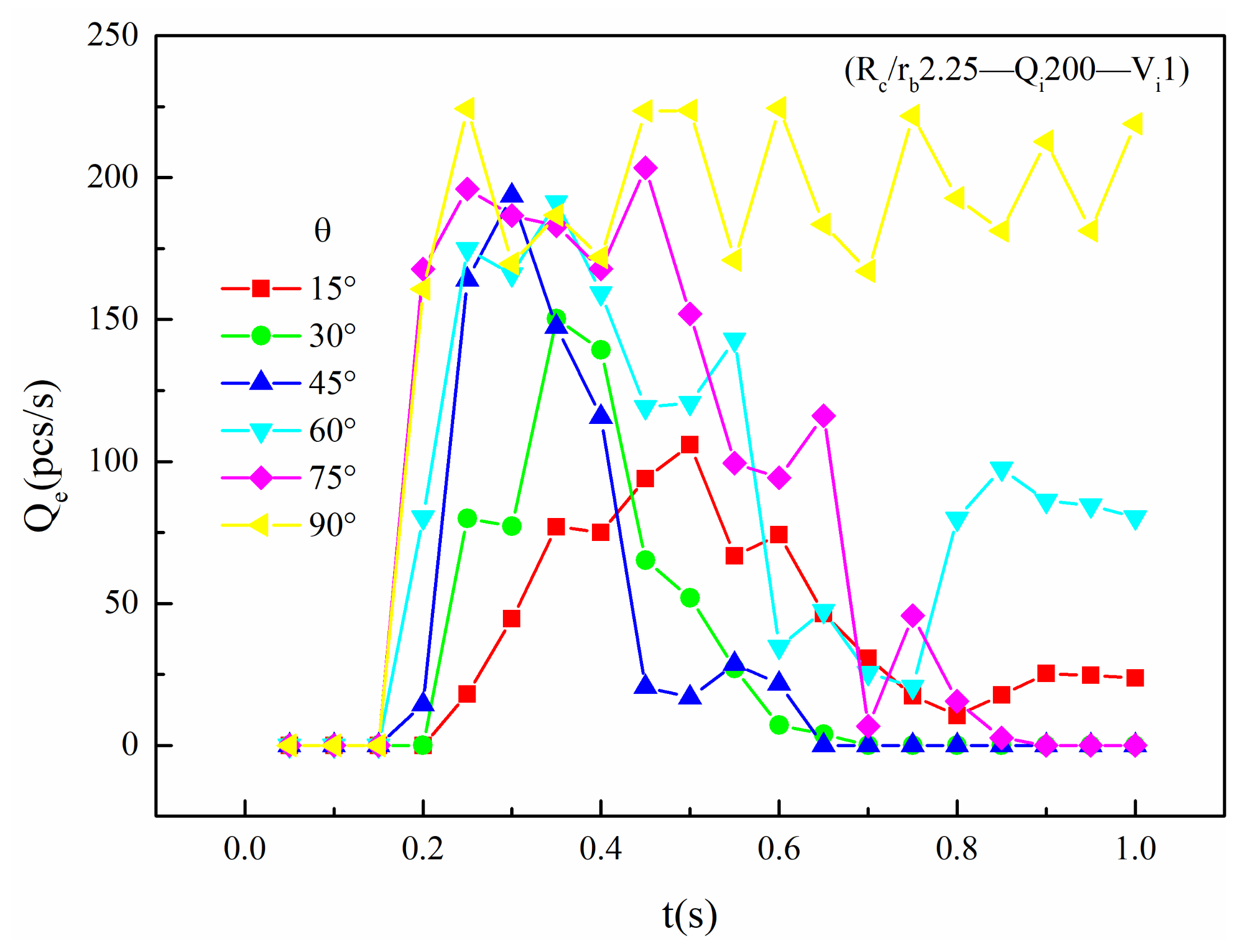
4.2.4. Effect of θ

The bridging effects are different for different dip angles θ. Figure 14 shows the relationship between the Q_e and the time at different θ. The following rules can be found. (1) When the θ is low (<20°), the balls are in a wall flow state. At this time, although two balls still sometimes contact closely, there is always space for the balls in the upper part of the cave; the ball-bridging structure cannot form a strong force chain, so the bridging is difficult. (2) As the θ increases (20°–75°), the balls gradually change from a wall flow into a leaping flow or spiral flow, and the Q_e can further increase. At this time, the stability of the bridging structure is still weak. (3) As the θ further increases (75°–90°), the movement of the balls between the upper and lower of the cave space is nearly the same, and the bridging structure tends to be stable. However, because the balls flow more smoothly, the time required for bridging also increases.

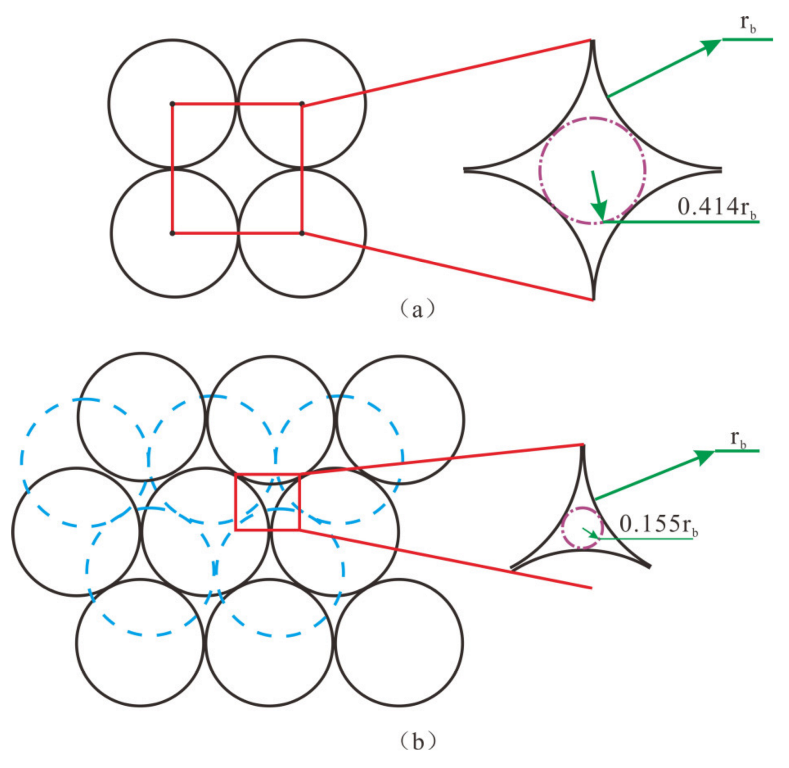
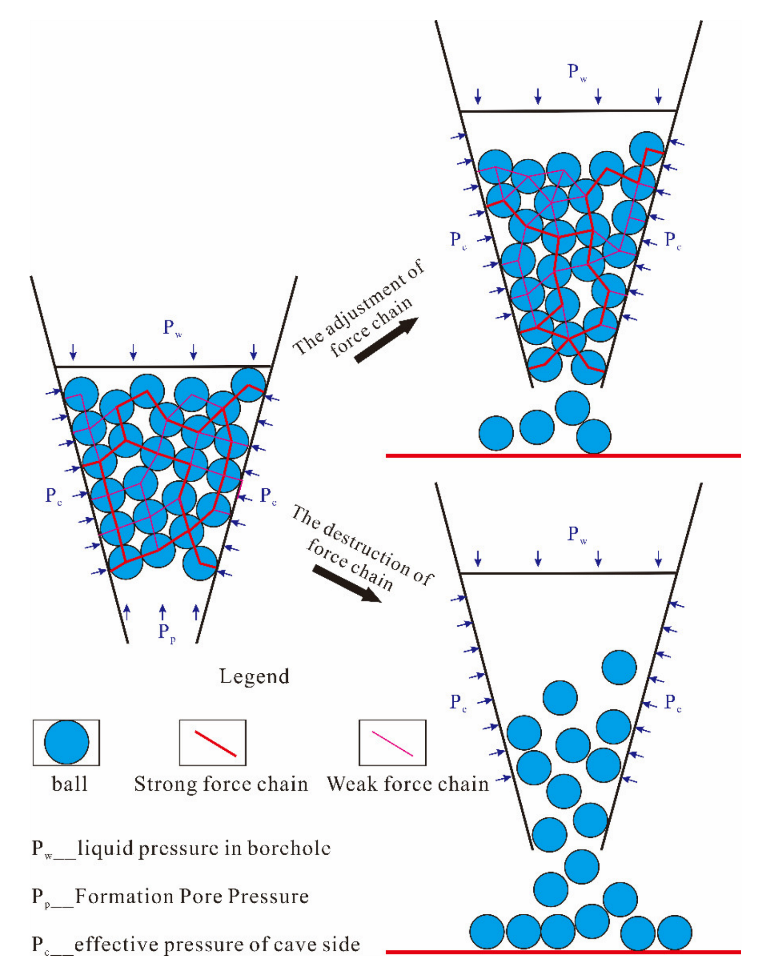
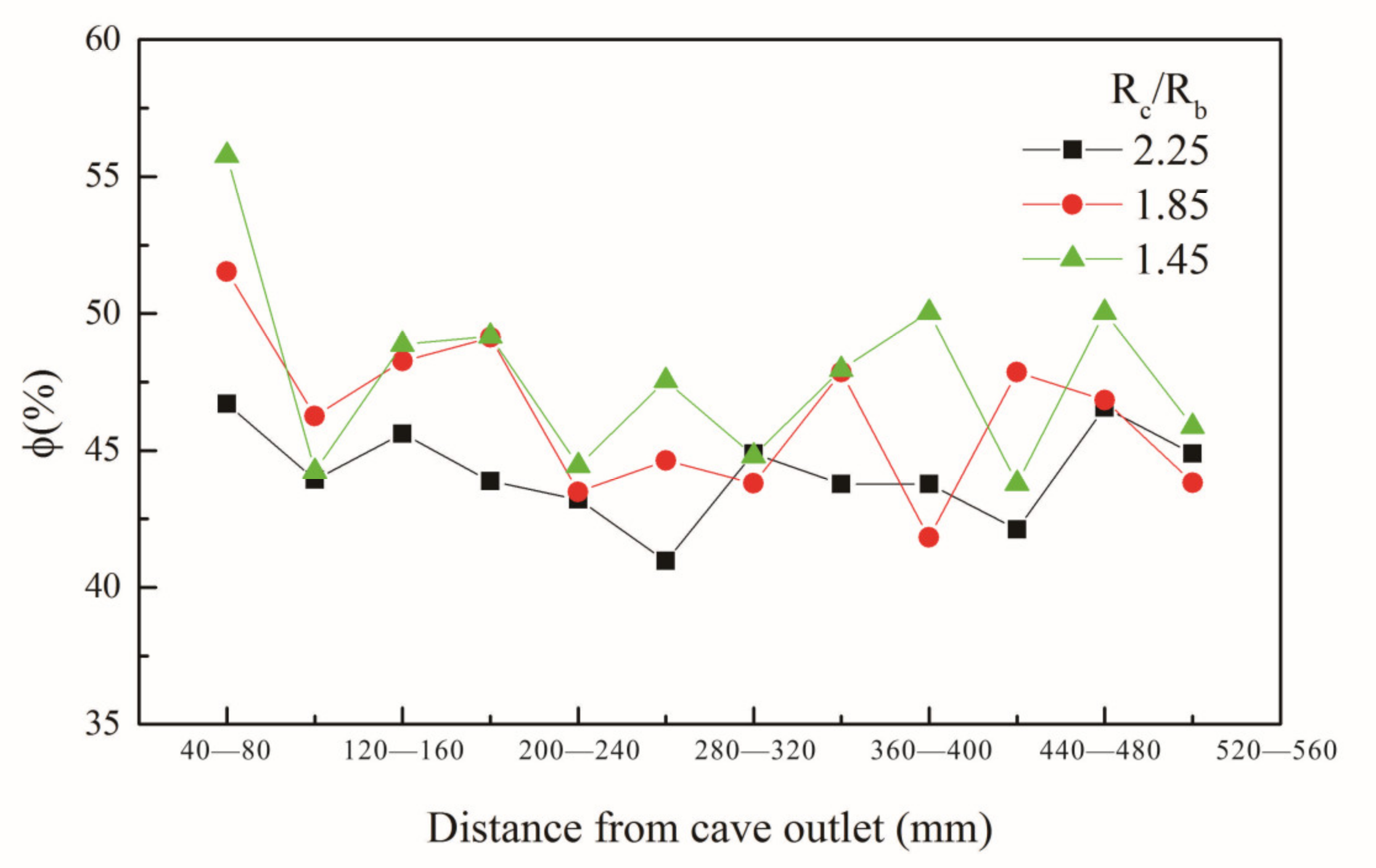
4.3. The Porous Medium Formed in the First-Stage Bridging

Figure 15 shows the vertical variation of the porosity of the porous medium formed in first-stage bridging under different R_c/r_b values. The porosity ranging from 40% to 55% is not significantly different along the axial direction of the cave. However, the smaller the R_c/r_b, the lower the porosity. This is because when R_c/r_b is small, the void space formed between the balls and the wall will be minimal. This is consistent with previous studies on equivalent sphere packing. That is, the pore throat radius of the porous media formed by the first-stage bridging should be 0.155~0.414 r_b, and the porosity of the porous media formed by the first-stage bridging is at least 0.37, providing the basis for screening diameter of the second-stage-bridging acid-soluble particles.

4.4. Discussion

The applicable conditions of MBP technology are:

(1)

Limited by the cave morphology of fracture-vugs in carbonate reservoirs, MBP technology is more likely to achieve effective plugging for caves with throats or high filling degrees near the wellbore. As for the lower cave and the upper throat type, the bridging ball cannot enter the cave neck at a large flow rate.

(2)

Limited by the borehole size, there is an upper limit on the diameter of the plug ball that coiled tubing can inject into the leaking zone. At the same time, there is an upper limit on the diameter of the cave neck that can be effectively plugged due to the limitation of initial flow Qi of the bridging ball. When the actual cave neck diameter exceeds this upper limit, MBP technology will fail.

(3)

All discussion in this research is based on the ideal situation. However, the cave pattern is difficult to describe by using several models, let alone by one ideal model. With the progress of seismic fine description technology, more accurate characterization of caves in carbonate reservoirs, or judging the types of caves by the experience of loss in the drilling process, will help to accurately formulate the plugging scheme and greatly improve the success rate of plugging technology.

(4)

MBP technology makes it possible to deal with the large loss in leakage pathways, but it is limited by the borehole size. The effective diameter of the bridging balls used in operations are limited by continuous oil piping, which means that the diameter of the cave neck that can be effectively plugged has an upper limit. Of course, MBP technology can be applied to plug while drilling. In plugging while drilling, MBP technology is limited by the size of the water eye of the drill bit. In order to avoid engineering risks, the size of the first-stage bridging particles should be less than 1/5 of the diameter of the water eye.

(5)

However, the bridging effect of multiscale mixing of bridging balls is better than single-scale bridging balls. Bridging balls with irregular surface morphology can bridge more easily, enabling the bridging structure to be more stable. In order to avoid particle settling and ensure migration in severe leakage and complex wellbore environments, a lighter and tougher material, with a density far smaller than 1.8 g/cm³, can be used to manufacture the bridging ball.

5. Conclusions

This paper points out a design idea and plugging mechanism for multistage bridging plugging (MBP) technology, which is a cave plugging technology for fractured-vuggy carbonate reservoirs, and analyzes the mechanism and influencing factors of MBP technology through DEM simulation. The following conclusions are drawn:

(1)

The prerequisite for the success of MBP is the presence of a constricted neck near the wellbore that connects with the drilled open caves in the process of well drilling loss. The first-stage bridging is the key to the success of MBP.

(2)

There are mainly five flow modes in different caves, and the formation of stable bridge goes through four stages: the sparse flow to the dense flow stage, the dense flow to the the jamming stage, the soft jamming flow to the deep jamming flow stage, and the readjustment stage.

(3)

The effect of the first-stage bridging takes into account the influence of the cave neck radius, the cave dip angle, the size and the velocity of the bridging ball, etc. (a) With the increase of R_c/r_b, the N_c also increases. When R_c/r_b > 2, the growth rate becomes faster. (b) With the increase of R_c/r_b, the critical Qi also increases. After R_c/r_b > 2, the critical Q_i also increases rapidly. (c) The faster the velocity of the bridging ball, the larger the kinetic energy of the ball becomes, the higher the efficiency through the cave neck becomes, and the more difficult the bridging will be. (d) The cave dip angle mainly affects the manner of ball movement; it is easier to bridge between 75° and 90°, and the bridging is also the most stability.