The Performance of the High-Current Transformer during Operation in the Wide Frequencies Range
Abstract
:1. Introduction
- determination of the wideband performance of the tested HCT and identification of the most favourable connection of sections of secondary and primary windings,
- designation of the factors limiting the wideband operation of the inductive HCT with analysis of the influence of inductance and resistance of the load,
- proposition of the improvements to the construction of the tested inductive HCT to increase its distorted output current RMS value,
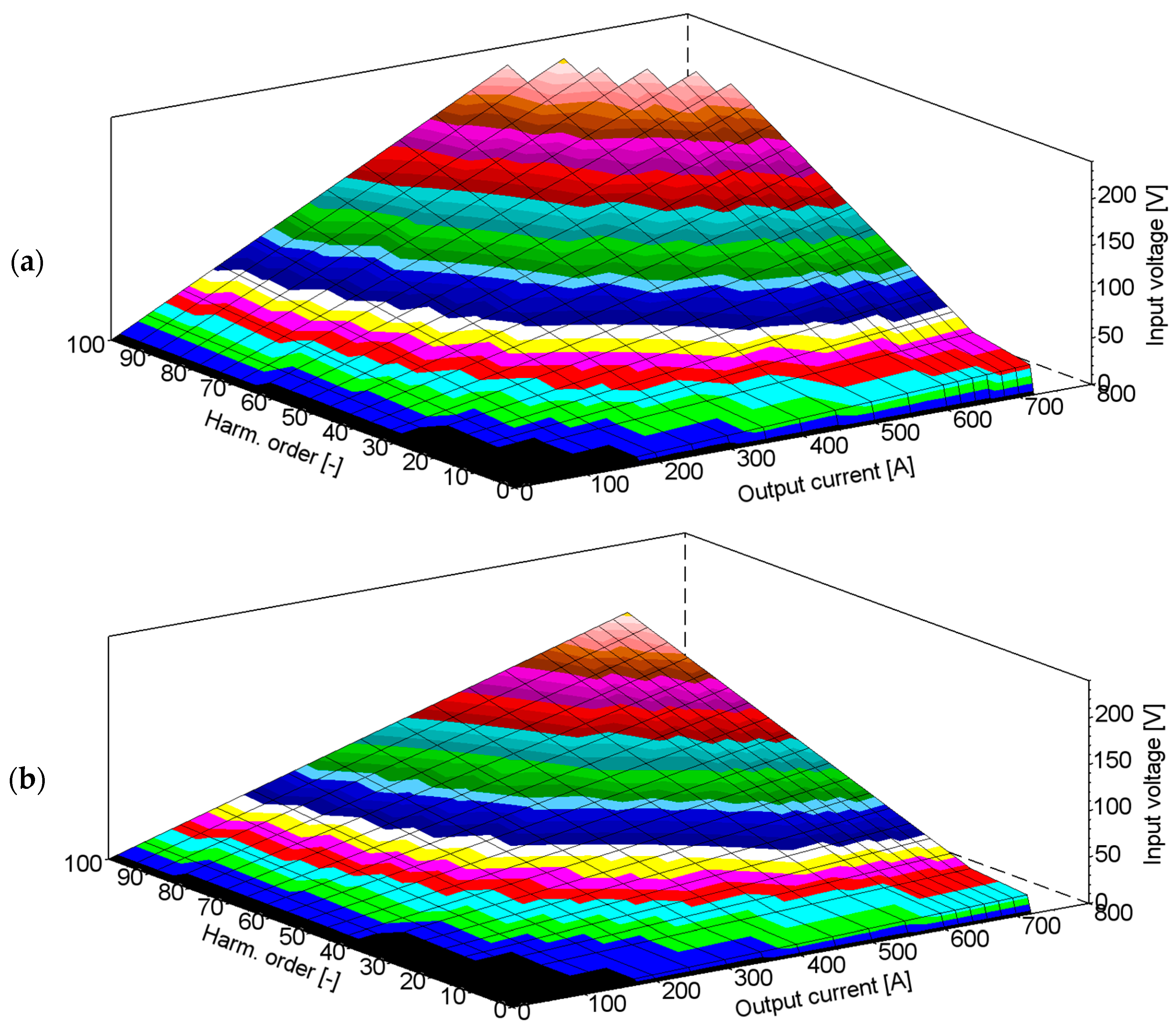
- presentation of the relationship between the RMS value of the distorted output current with a given harmonic order and required RMS value of the input primary voltage,
- designation of the negligibility of the influence of windings resistance and magnetic core excitation current on the wideband performance of the tested inductive HCT.
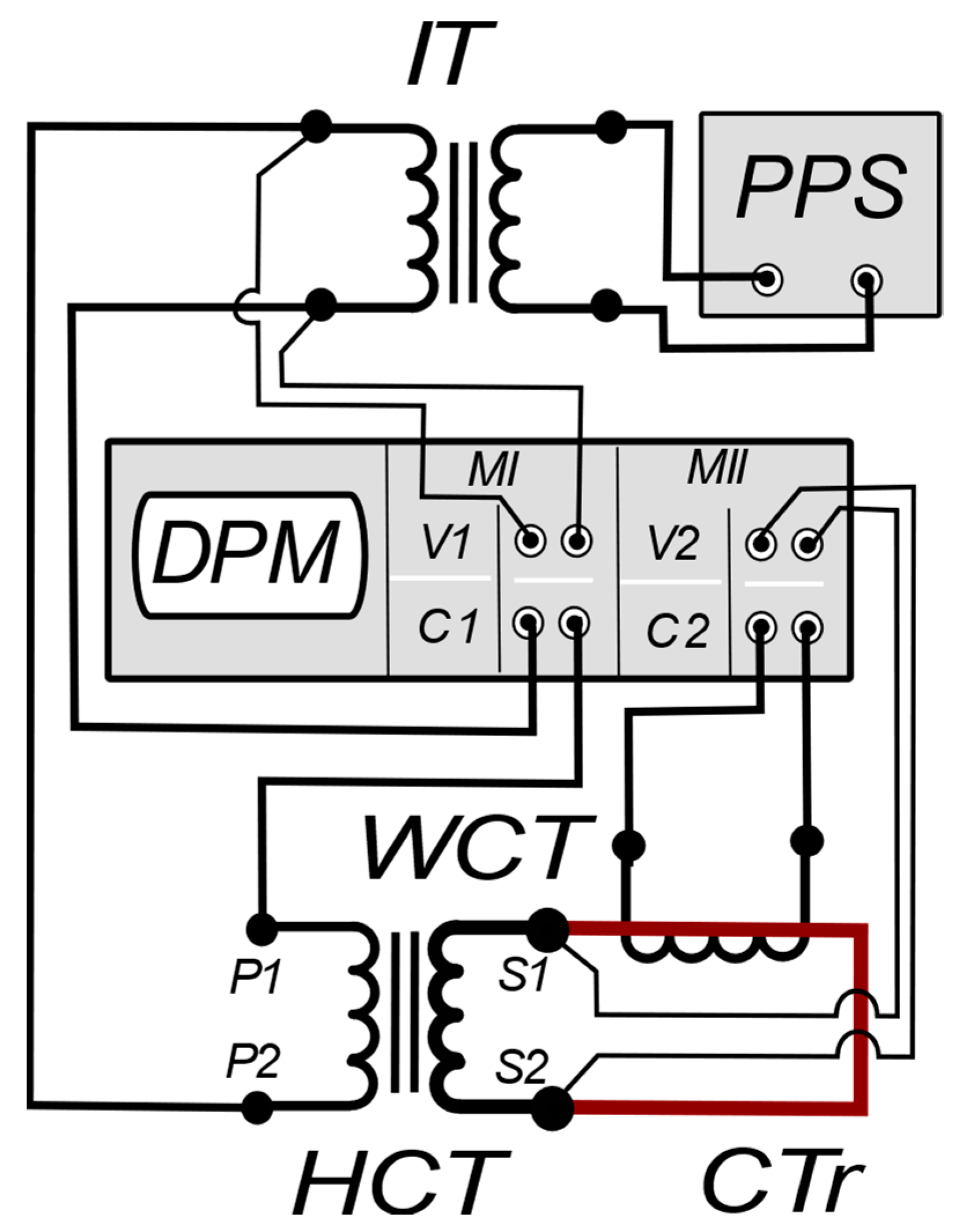
2. The Measuring Circuit and the Tested High-Current Transformer
- PPS—programmable power supply system,
- DPM—digital power meter,
- WCT—wideband current transformer,
- HCT—high-current transformer,
- CTr—current track,
- MI/MII—I/II measuring module of the DPM,
- V1/V2—1/2 voltage input,
- C1/C2—1/2 current input,
- P1/P2—terminals of the primary winding of the HCT,
- S1/S2—terminals of the secondary winding of the HCT.
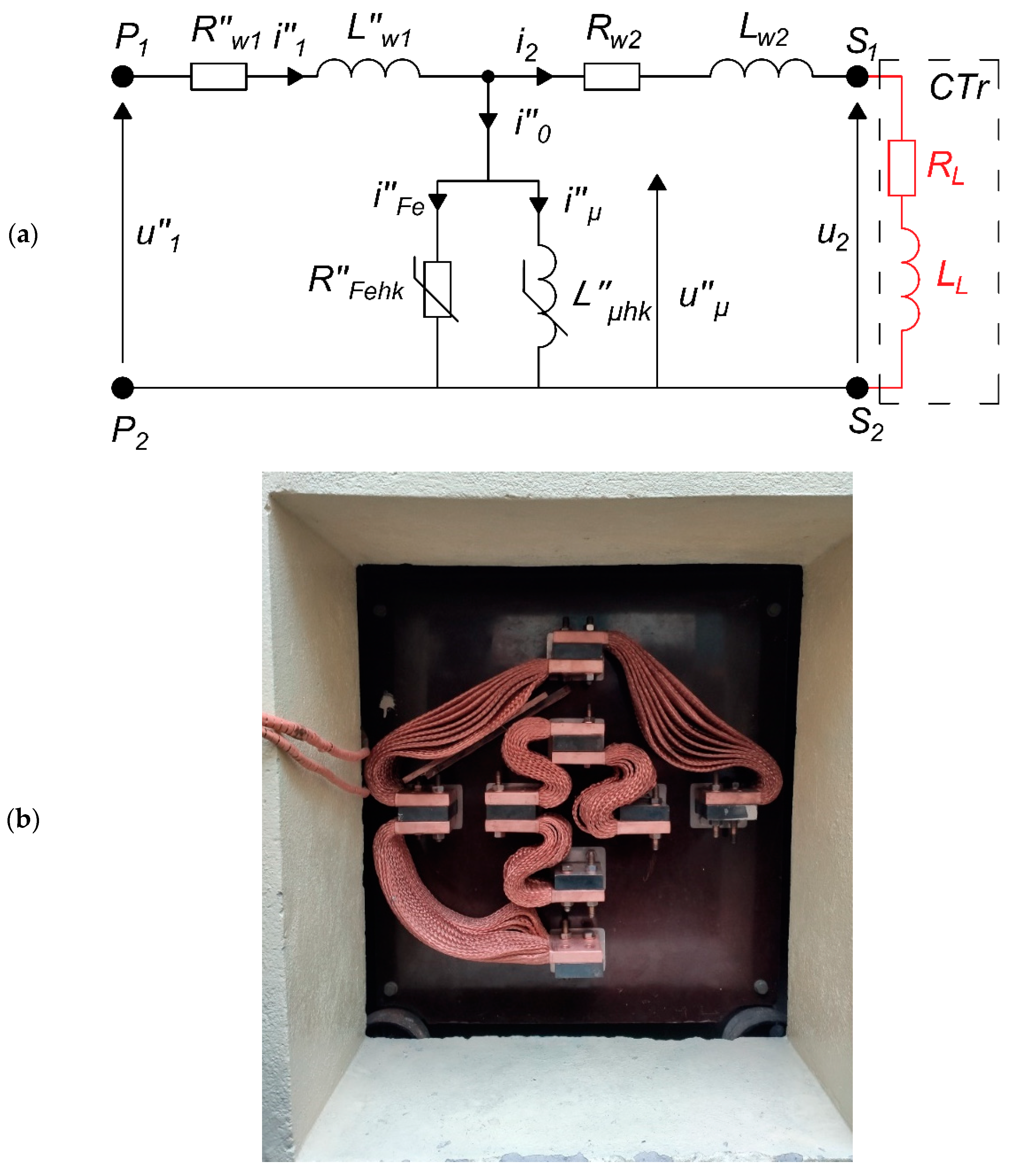
- R″w1—resistance of the primary winding,
- L″w1—leakage inductance of the primary winding,
- Rw2—resistance of the secondary winding,
- Lw2—leakage inductance of the secondary winding,
- RL—resistance of the load associated with the current track,
- LL—inductance of the load associated with the current track,
- R″Fehk—resistance associated with active power losses of the magnetic core,
- L″μhk—mutual inductance of the HCT’s windings,
- i″1—instantaneous current of the HCT’s primary winding,
- i″0—instantaneous excitation current of the HCT’s magnetic core,
- i″μ—instantaneous reactive component of the excitation current,
- i″Fe—instantaneous active component of the excitation current,
- i2—instantaneous current of the HCT’s secondary winding,
- u″1—instantaneous voltage of the HCT’s primary winding,
- u″μ—instantaneous voltage associated with mutual inductance of the HCT’s windings,
- u2—instantaneous voltage of the HCT’s secondary winding.
- hk—the order of higher harmonic component and
- h1—the main component.
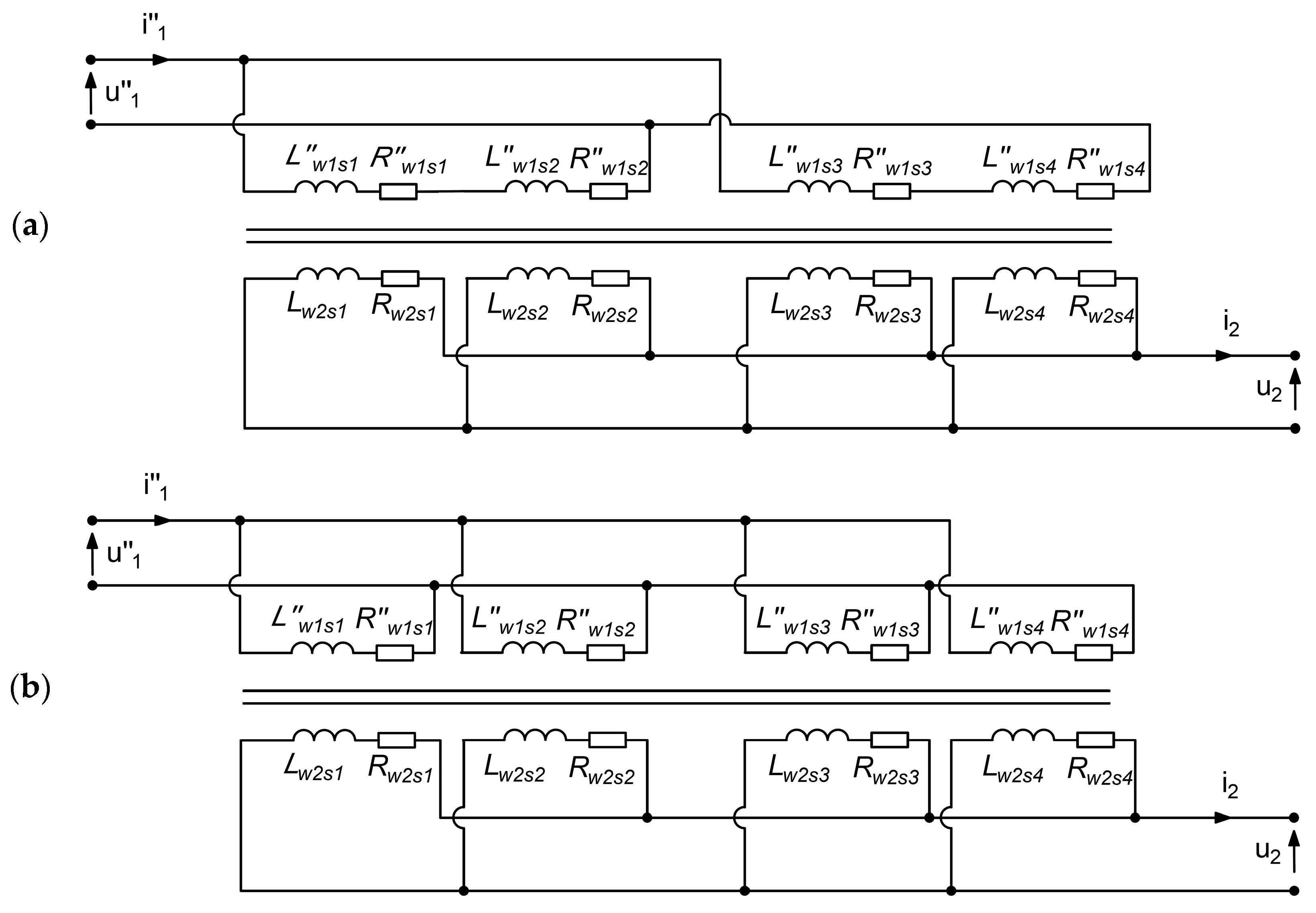
- R″w1s1/R″w1s2/R″w1s3/R″w1s4—resistance of each section of the primary winding,
- L″w1s1/L″w1s2/L″w1s3/L″w1s4—leakage inductance of each section of the primary winding,
- Rw2s1/Rw2s2/Rw2s3/Rw2s4—resistance of each section of the secondary winding,
- Lw2s1/Lw2s2/Lw2s3/Lw2s4—leakage inductance of each section of the primary winding.
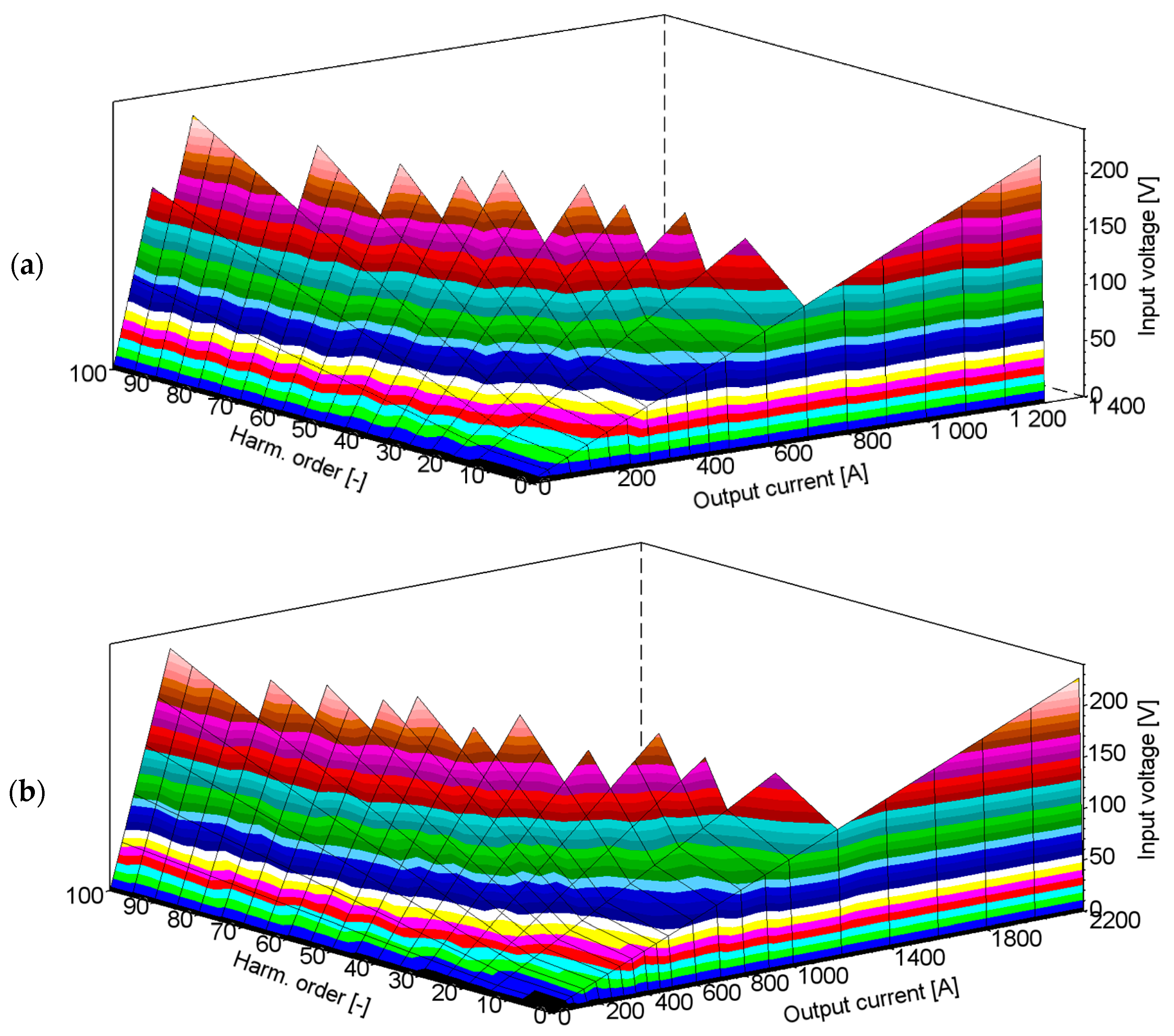
3. Measurement of the HCT’s Transformation Performance in the Wide Frequencies Range
- n—current ratio equal to turns ratio.
4. Calculation of the HCT’s Transformation Performance in the Wide Frequencies Range
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stano, E.; Kaczmarek, P.; Kaczmarek, M. Why Should We Test the Wideband Transformation Accuracy of Inductive Current Transformers? Energies 2022, 15, 5737. [Google Scholar] [CrossRef]
- Stano, E.; Kaczmarek, P.; Kaczmarek, M. Understanding the Frequency Characteristics of Current Error and Phase Displacement of the Corrected Inductive Current Transformer. Energies 2022, 15, 5436. [Google Scholar] [CrossRef]
- Crotti, G.; Chen, Y.; Çayci, H.; D’Avanzo, G.; Landi, C.; Letizia, P.S.; Luiso, M.; Mohns, E.; Muñoz, F.; Styblikova, R.; et al. How Instrument Transformers Influence Power Quality Measurements: A Proposal of Accuracy Verification Tests. Sensors 2022, 22, 5847. [Google Scholar] [CrossRef] [PubMed]
- Crotti, G.; Delle Femine, A.; Gallo, D.; Giordano, D.; Landi, C.; Letizia, P.S.; Luiso, M. Calibration of Current Transformers in distorted conditions. J. Phys. Conf. Ser. 2018, 1065, 052033. [Google Scholar] [CrossRef]
- Cristaldi, L.; Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. A Low-Cost Generator for Testing and Calibrating Current Transformers. IEEE Trans. Instrum. Meas. 2019, 68, 2792–2799. [Google Scholar] [CrossRef]
- Kaczmarek, M.; Szczęsny, A.; Stano, E. Operation of the Electronic Current Transformer for Transformation of Distorted Current Higher Harmonics. Energies 2022, 15, 4368. [Google Scholar] [CrossRef]
- Kaczmarek, M.; Stano, E. The Influence of the 3rd Harmonic of the Distorted Primary Current on the Self-Generation of the Inductive Current Transformers. IEEE Access 2022, 10, 55876–55887. [Google Scholar] [CrossRef]
- Stano, E.; Kaczmarek, M. Wideband self-calibration method of inductive cts and verification of determined values of current and phase errors at harmonics for transformation of distorted current. Sensors 2020, 20, 2167. [Google Scholar] [CrossRef]
- Kaczmarek, M.; Stano, E. Nonlinearity of Magnetic Core in Evaluation of Current and Phase Errors of Transformation of Higher Harmonics of Distorted Current by Inductive Current Transformers. IEEE Access 2020, 8, 118885–118898. [Google Scholar] [CrossRef]
- Kaczmarek, M. Estimation of the inductive current transformer derating for operation with distorted currents. Bull. Polish Acad. Sci. Technol. Sci. 2014, 62, 363–366. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarek, M. Wide frequency operation of the inductive current transformer with Ni80Fe20 toroidal core. Electr. Power Compon. Syst. 2014, 42, 1087–1094. [Google Scholar] [CrossRef]
- Ghaderi, A.; Mingotti, A.; Peretto, L.; Tinarelli, R. Procedure for ratio error and phase displacement prediction of inductive current transformers at different operating conditions. In Proceedings of the I2MTC 2020—International Instrumentation and Measurement Technology Conference, Dubrovnik, Croatia, 25–28 May 2020. [Google Scholar]
- Mingotti, A.; Peretto, L.; Bartolomei, L.; Cavaliere, D.; Tinarelli, R. Are inductive current transformers performance really affected by actual distorted network conditions? An experimental case study. Sensors 2020, 20, 927. [Google Scholar] [CrossRef] [PubMed]
- Murray, R.; De Kock, J. Instrument transformers influence on harmonic measurements for grid code compliance. In Proceedings of the 2018 IEEE 4th Global Electromagnetic Compatibility Conference (GEMCCON), Stellenbosch, South Africa, 7–9 November 2018. [Google Scholar]
- Dirik, H.; Duran, I.U.; Gezegin, C. A Computation and Metering Method for Harmonic Emissions of Individual Consumers. IEEE Trans. Instrum. Meas. 2019, 68, 412–420. [Google Scholar] [CrossRef]
- Zobaa, A.F.; Abdel Aleem, S.H.E. A new approach for harmonic distortion minimization in power systems supplying nonlinear loads. IEEE Trans. Ind. Inform. 2014, 10, 1401–1412. [Google Scholar] [CrossRef]
- Yang, T.; Pen, H.; Wang, D.; Wang, Z. Harmonic analysis in integrated energy system based on compressed sensing. Appl. Energy 2016, 165, 583–591. [Google Scholar] [CrossRef]
- Vieira, D.; Shayani, R.A.; De Oliveira, M.A.G. Reactive Power Billing under Nonsinusoidal Conditions for Low-Voltage Systems. IEEE Trans. Instrum. Meas. 2017, 66, 2004–2011. [Google Scholar] [CrossRef]
- Liang, X. Emerging Power Quality Challenges Due to Integration of Renewable Energy Sources. IEEE Trans. Ind. Appl. 2017, 53, 855–866. [Google Scholar] [CrossRef]
- Hossain, E.; Tur, M.R.; Padmanaban, S.; Ay, S.; Khan, I. Analysis and Mitigation of Power Quality Issues in Distributed Generation Systems Using Custom Power Devices. IEEE Access 2018, 6, 16816–16833. [Google Scholar] [CrossRef]
- da Silva, R.P.B.; Quadros, R.; Shaker, H.R.; da Silva, L.C.P. Effects of mixed electronic loads on the electrical energy systems considering different loading conditions with focus on power quality and billing issues. Appl. Energy 2020, 277, 115558. [Google Scholar] [CrossRef]
- Cataliotti, A.; Cosentino, V.; Crotti, G.; Giordano, D.; Modarres, M.; Di Cara, D.; Tinè, G.; Gallo, D.; Landi, C.; Luiso, M. Metrological performances of voltage and current instrument transformers in harmonics measurements. In Proceedings of the I2MTC 2018—2018 IEEE International Instrumentation and Measurement Technology Conference: Discovering New Horizons in Instrumentation and Measurement, Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar]
- Kaczmarek, M.; Kaczmarek, P. Comparison of the wideband power sources used to supply step-up current transformers for generation of distorted currents. Energies 2020, 13, 1849. [Google Scholar] [CrossRef]
- Brodecki, D.; Stano, E.; Andrychowicz, M.; Kaczmarek, P. Emc of wideband power sources. Energies 2021, 14, 1457. [Google Scholar] [CrossRef]
- Collin, A.J.; Femine, A.D.; Gallo, D.; Langella, R.; Luiso, M. Compensation of current transformers’ nonlinearities by tensor linearization. IEEE Trans. Instrum. Meas. 2019, 68, 3841–3849. [Google Scholar] [CrossRef]
- D’Avanzo, G.; Delle Femine, A.; Gallo, D.; Landi, C.; Luiso, M. Impact of inductive current transformers on synchrophasor measurement in presence of modulations. Meas. J. Int. Meas. Confed. 2020, 155, 107535. [Google Scholar] [CrossRef]
- Laurano, C.; Toscani, S.; Zanoni, M. A simple method for compensating harmonic distortion in current transformers: Experimental validation. Sensors 2021, 21, 2907. [Google Scholar] [CrossRef]
- Liang, C.T.; Chen, K.L.; Tsai, Y.P.; Chen, N. New electronic current transformer with a self-contained power supply. IEEE Trans. Power Deliv. 2015, 30, 184–192. [Google Scholar] [CrossRef]
- McNeill, N.; Dymond, H.; Mellor, P.H. High-fidelity low-cost electronic current sensor for utility power metering. IEEE Trans. Power Deliv. 2011, 26, 2309–2317. [Google Scholar] [CrossRef]
- Tong, Y.; Liu, B.; Abu-Siada, A.; Li, Z.; Li, C.; Zhu, B. Research on calibration technology for electronic current transformers. In Proceedings of the 2018 Condition Monitoring and Diagnosis (CMD), Perth, WA, Australia, 23–26 September 2018; pp. 1–5. [Google Scholar]
- Huang, G.J.; Chen, N.; Chen, K.L. Self-calibration method for coreless Hall effect current transformer. In Proceedings of the IEEE Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Kaczmarek, M.; Stano, E. Proposal for extension of routine tests of the inductive current transformers to evaluation of transformation accuracy of higher harmonics. Int. J. Electr. Power Energy Syst. 2019, 113, 842–849. [Google Scholar] [CrossRef]
- Kaczmarek, M.L.; Stano, E. Application of the inductive high current testing transformer for supplying of the measuring circuit with distorted current. IET Electr. Power Appl. 2019, 13, 1310–1317. [Google Scholar] [CrossRef]





| Configuration of the Sections of the Primary Winding | Configuration of the Sections of the Secondary Winding | Current Ratio | RL [mΩ] | LL [μH] | Measured Max Current with 10% of 100th Harm. [A] | Calculated Max Current with 10% of 100th Harm. [A] |
|---|---|---|---|---|---|---|
| serial | serial | 36 | 0.3 | 3.0 | 350 | 380 |
| 0.2 | 1.5 | 490 | 520 | |||
| serial-parallel | 72 | 0.3 | 3.0 | 270 | 260 | |
| 0.2 | 1.5 | 455 | 430 | |||
| parallel | 144 | 0.3 | 3.0 | 145 | 150 | |
| 0.2 | 1.5 | 255 | 270 | |||
| serial-parallel | serial | 18 | 0.3 | 3.0 | 360 | 360 |
| 0.2 | 1.5 | 360 | 360 | |||
| serial-parallel | 36 | 0.3 | 3.0 | 535 | 520 | |
| 0.2 | 1.5 | 720 | 720 | |||
| parallel | 72 | 0.3 | 3.0 | 290 | 300 | |
| 0.2 | 1.5 | 510 | 540 | |||
| parallel | serial | 9 | 0.3 | 3.0 | 180 | 180 |
| 0.2 | 1.5 | 180 | 180 | |||
| serial-parallel | 18 | 0.3 | 3.0 | 360 | 360 | |
| 0.2 | 1.5 | 360 | 360 | |||
| parallel | 36 | 0.3 | 3.0 | 570 | 590 | |
| 0.2 | 1.5 | 720 | 720 |
| Configuration of the Sections of the Primary Winding | Configuration of the Sections of the Secondary Winding | Current Ratio [–] | Rw1 [mΩ] | Lw1 [μH] | Rw2 [mΩ] | Lw2 [μH] | RL [mΩ] | LL [μH] | Max Harm. Order for 1000 A | Max Current with 10% of 100th Harmonic [A] |
|---|---|---|---|---|---|---|---|---|---|---|
| serial | serial | 36 | 0.17 | 0.61 | 0.64 | 1.75 | 0.3 | 3.0 | 37th | 380 |
| 1.5 | 52th | 520 | ||||||||
| 6.0 | 24th | 240 | ||||||||
| 3.0 | 3.0 | 37th | 380 | |||||||
| serial-parallel | 72 | 0.04 | 0.15 | 0.24 | 0.70 | 0.3 | 3.0 | 26th | 260 | |
| 1.5 | 43th | 430 | ||||||||
| 6.0 | 14th | 150 | ||||||||
| 3.0 | 3.0 | 26th | 260 | |||||||
| parallel | 144 | 0.01 | 0.04 | 0.14 | 0.32 | 0.3 | 3.0 | 15th | 150 | |
| 1.5 | 27th | 270 | ||||||||
| 6.0 | 8th | 80 | ||||||||
| 3.0 | 3.0 | 14th | 150 | |||||||
| serial-parallel | serial | 18 | 0.13 | 0.82 | 0.64 | 1.75 | 0.3 | 3.0 | 72th | 720 |
| 1.5 | 99th | 990 | ||||||||
| 6.0 | 47th | 470 | ||||||||
| 3.0 | 3.0 | 72th | 720 | |||||||
| serial-parallel | 36 | 0.03 | 0.20 | 0.24 | 0.70 | 0.3 | 3.0 | 52th | 520 | |
| 1.5 | 84th | 840 | ||||||||
| 6.0 | 29th | 290 | ||||||||
| 3.0 | 3.0 | 52th | 520 | |||||||
| parallel | 72 | 0.01 | 0.05 | 0.14 | 0.32 | 0.3 | 3.0 | 30th | 300 | |
| 1.5 | 54th | 540 | ||||||||
| 6.0 | 16th | 160 | ||||||||
| 3.0 | 3.0 | 30th | 300 | |||||||
| parallel | serial | 9 | 0.07 | 1.41 | 0.64 | 1.75 | 0.3 | 3.0 | 132th | 1030 |
| 1.5 | 175th | 1030 | ||||||||
| 6.0 | 88th | 880 | ||||||||
| 3.0 | 3.0 | 132th | 1026 | |||||||
| serial-parallel | 18 | 0.02 | 0.35 | 0.24 | 0.70 | 0.3 | 3.0 | 100th | 1000 | |
| 1.5 | 158th | 1580 | ||||||||
| 6.0 | 57th | 570 | ||||||||
| 3.0 | 3.0 | 100th | 1000 | |||||||
| parallel | 36 | 0.005 | 0.09 | 0.14 | 0.32 | 0.3 | 3.0 | 60th | 600 | |
| 1.5 | 106th | 1060 | ||||||||
| 6.0 | 32th | 320 | ||||||||
| 3.0 | 3.0 | 60th | 600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaczmarek, M.; Kaczmarek, P.; Stano, E. The Performance of the High-Current Transformer during Operation in the Wide Frequencies Range. Energies 2022, 15, 7208. https://doi.org/10.3390/en15197208
Kaczmarek M, Kaczmarek P, Stano E. The Performance of the High-Current Transformer during Operation in the Wide Frequencies Range. Energies. 2022; 15(19):7208. https://doi.org/10.3390/en15197208
Chicago/Turabian StyleKaczmarek, Michal, Piotr Kaczmarek, and Ernest Stano. 2022. "The Performance of the High-Current Transformer during Operation in the Wide Frequencies Range" Energies 15, no. 19: 7208. https://doi.org/10.3390/en15197208
APA StyleKaczmarek, M., Kaczmarek, P., & Stano, E. (2022). The Performance of the High-Current Transformer during Operation in the Wide Frequencies Range. Energies, 15(19), 7208. https://doi.org/10.3390/en15197208








