Secondary Voltage Collaborative Control of Distributed Energy System via Multi-Agent Reinforcement Learning
Abstract
:1. Introduction
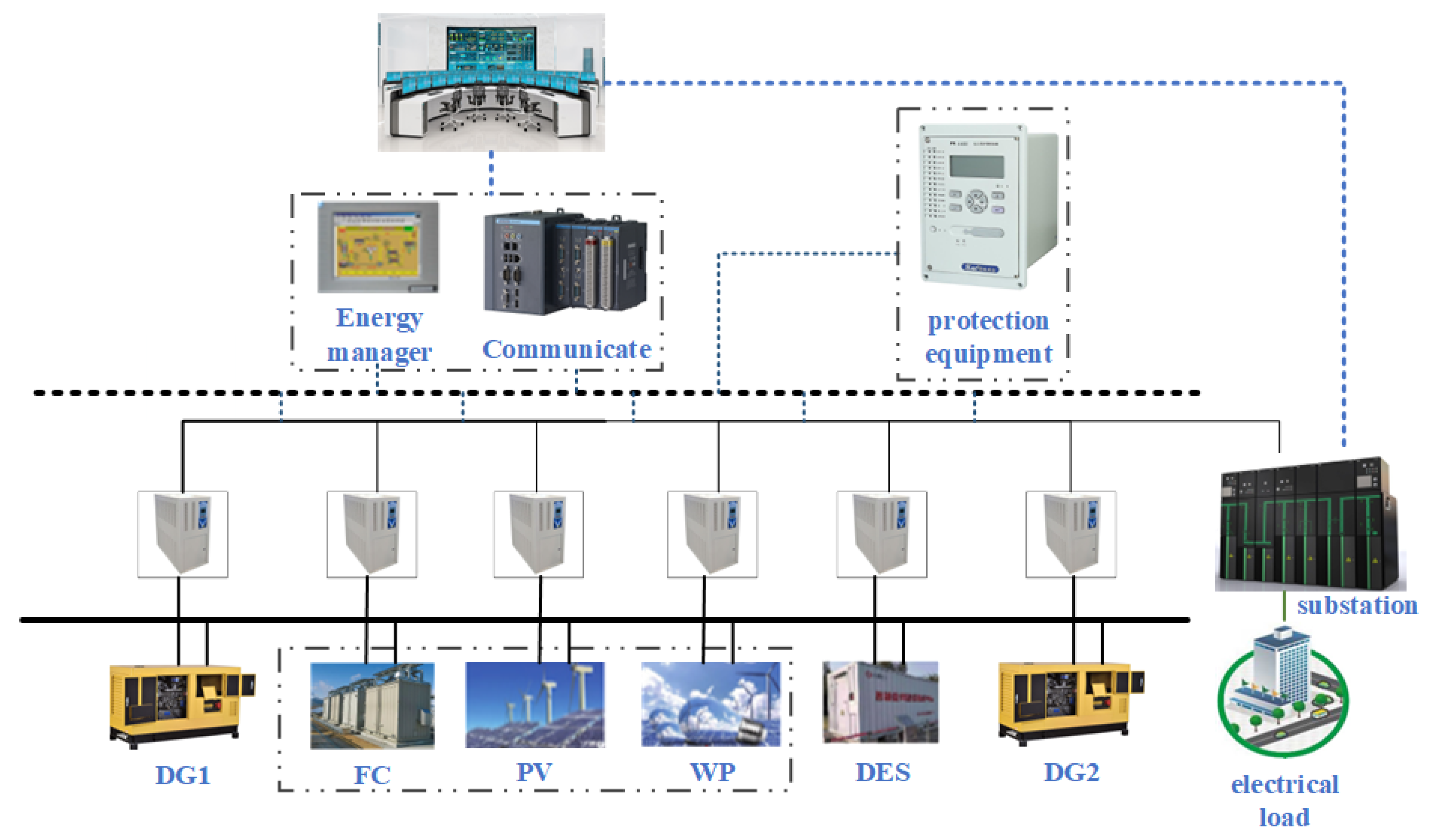
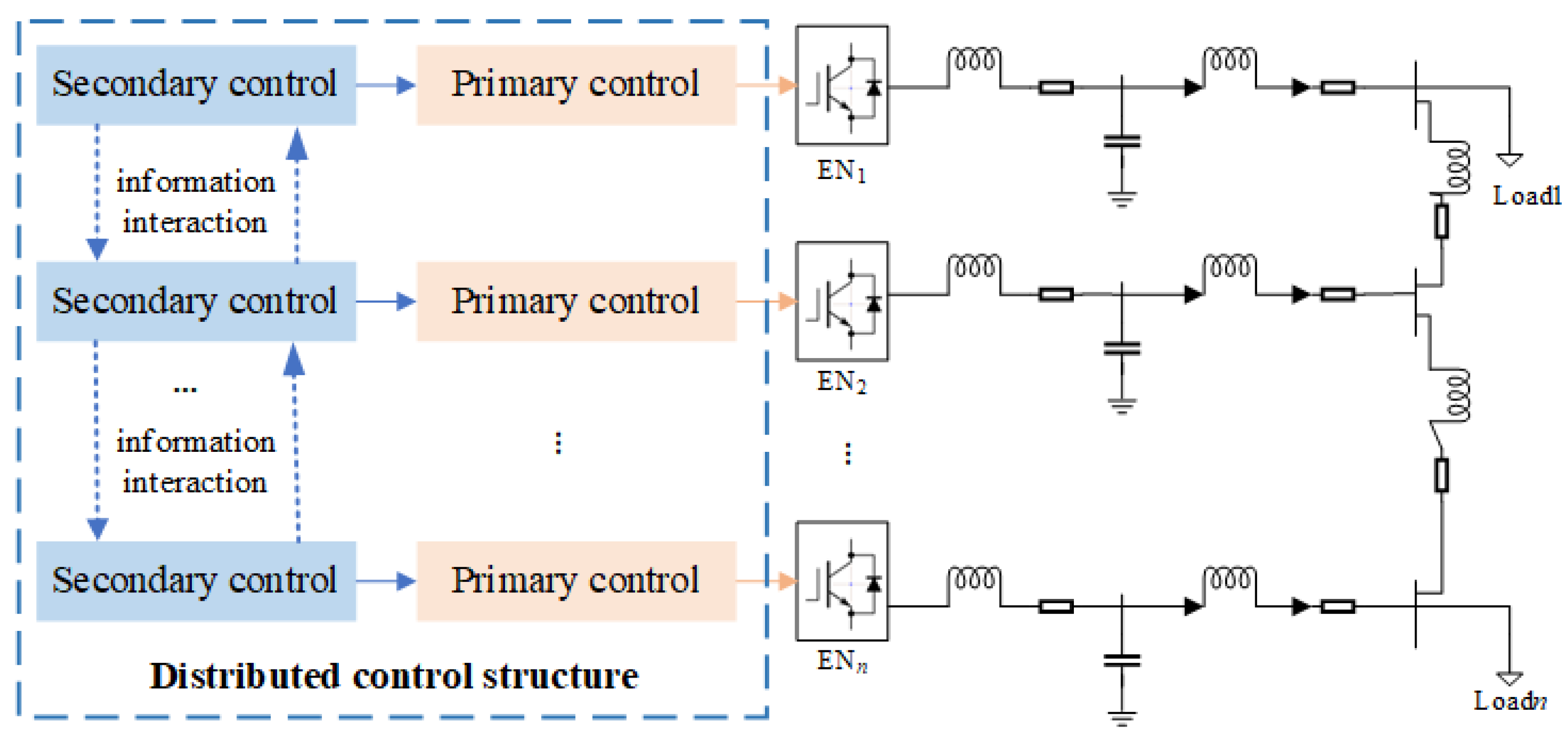
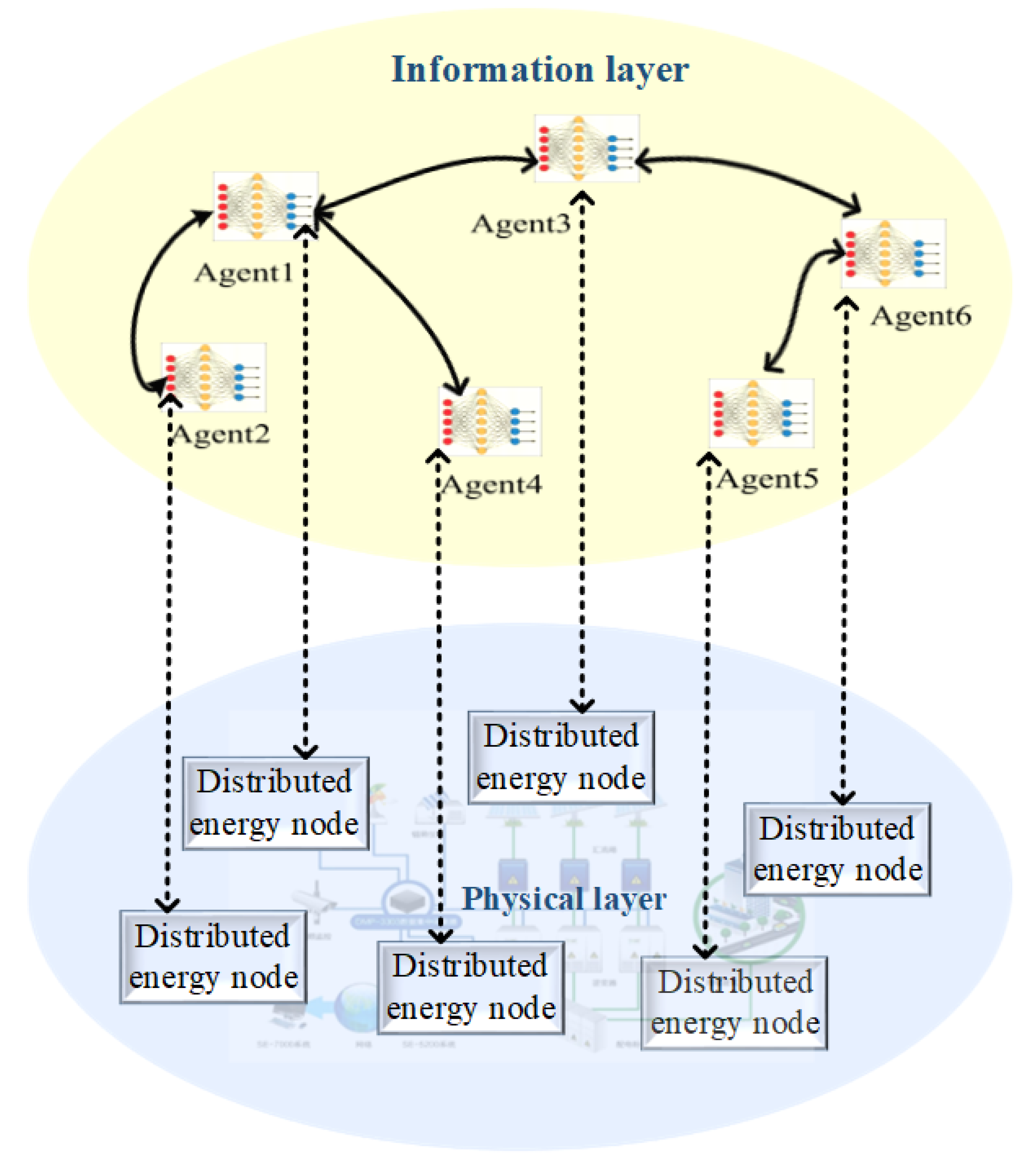
2. Distributed Energy System
3. MA2C-Attention Algorithm
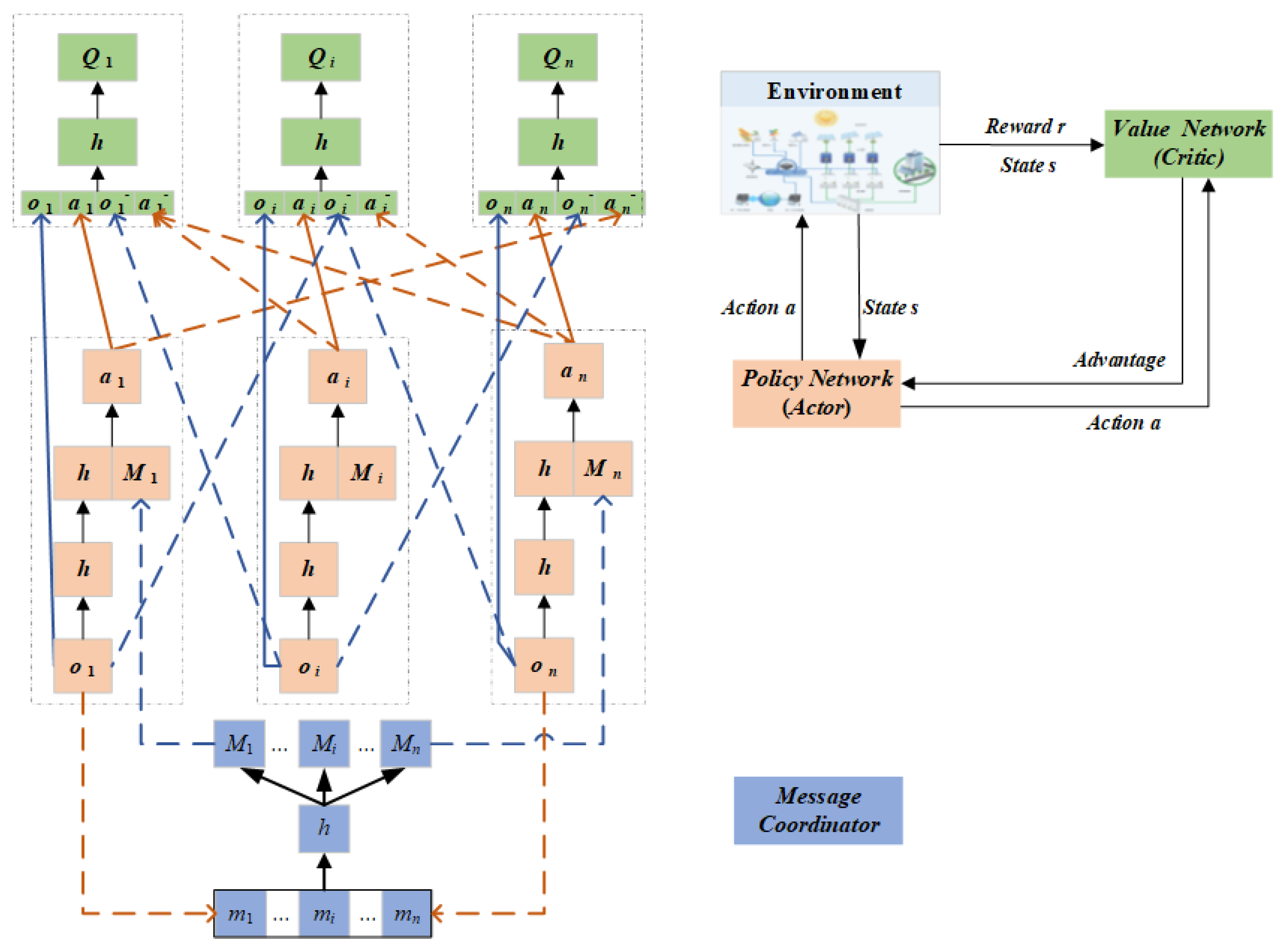
3.1. Multi-Agent Advantage Actor-Critic
3.2. MA2C-Attention Algorithm
| Algorithm 1 MA2C-Attention algorithm |
Input:, , , , L, S Output:,
end
end
end end
end
end |
4. Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X. Discussion on Problems Realated to Development of the Distributed Energy System. Electr. Power Technol. Econ. 2007, 19, 6–8. [Google Scholar]
- González-Torres, M.; Pérez-Lombard, L.; Coronel, J.F.; Maestre, I.R.; Yan, D. A review on buildings energy information: Trends, end-uses, fuels and drivers. Energy Rep. 2022, 8, 626–637. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, W.; Huang, Y.; Li, P.; Dong, L. Simultaneous optimization of renewable energy and energy storage capacity with the hierarchical control. CSEE J. Power Energy Syst. 2022, 8, 95–104. [Google Scholar]
- Huang, X.; Liu, Y.; Liao, Y.; Jiang, Z.; He, J.; Li, Y. Modeling of distributed energy system with multiple energy complementation. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–6. [Google Scholar]
- Li, X.; Ma, R.; Yan, N.; Wang, S.; Hui, D. Research on Optimal Scheduling Method of Hybrid Energy Storage System Considering Health State of Echelon-Use Lithium-Ion Battery. IEEE Trans. Appl. Supercond. 2021, 31, 1–4. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Yan, N.; Ma, R. Cooperative Dispatch of Distributed Energy Storage in Distribution Network With PV Generation Systems. IEEE Trans. Appl. Supercond. 2021, 31, 1–4. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Liu, J.; Xiang, Y.; Yuan, X. Optimal planning of AC-DC hybrid transmission and distributed energy resource system: Review and prospects. CSEE J. Power Energy Syst. 2019, 5, 409–422. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Gooi, H.B.; Jian, Y.; Xin, H.; Jiang, X.; Pan, J. Distributed Robust Energy Management of a Multimicrogrid System in the Real-Time Energy Market. IEEE Trans. Sustain. Energy 2019, 10, 396–406. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Incentivizing Energy Trading for Interconnected Microgrids. IEEE Trans. Smart Grid 2018, 9, 2647–2657. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, K.; Li, H.; Coelho, E.A.A.; Guerrero, J.M. MAS-Based Distributed Coordinated Control and Optimization in Microgrid and Microgrid Clusters: A Comprehensive Overview. IEEE Trans. Power Electron. 2018, 33, 6488–6508. [Google Scholar] [CrossRef]
- Kovaltchouk, T.; Blavette, A.; Aubry, J.; Ahmed, H.B.; Multon, B. Comparison Between Centralized and Decentralized Storage Energy Management for Direct Wave Energy Converter Farm. IEEE Trans. Energy Convers. 2016, 31, 1051–1058. [Google Scholar] [CrossRef]
- Mu, C.; Tang, Y.; He, H. Improved Sliding Mode Design for Load Frequency Control of Power System Integrated an Adaptive Learning Strategy. IEEE Trans. Ind. Electron. 2017, 64, 6742–6751. [Google Scholar] [CrossRef]
- Mu, C.; Liu, W.; Xu, W. Hierarchically Adaptive Frequency Control for an EV-Integrated Smart Grid With Renewable Energy. IEEE Trans. Ind. Inform. 2018, 14, 4254–4263. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Gao, W.; Zheng, X.; Yang, L.; Hao, J.; Dai, X. Distributed electrical energy systems: Needs, concepts, approaches and vision. Acta Autom. Sin. 2017, 43, 1544–1554. [Google Scholar]
- Yu, X.; Jiang, Z.; Zhang, Y. Control of Parallel Inverter-Interfaced Distributed Energy Resources. In Proceedings of the 2008 IEEE Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008; pp. 1–8. [Google Scholar]
- Gholami, S.; Aldeen, M.; Saha, S. Control Strategy for Dispatchable Distributed Energy Resources in Islanded Microgrids. IEEE Trans. Power Syst. 2018, 33, 141–152. [Google Scholar] [CrossRef]
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison Between Traditional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Eddy, Y.S.; Gooi, H.B.; Chen, S.X. Multi-Agent System for Distributed Management of Microgrids. IEEE Trans. Power Syst. 2015, 30, 24–34. [Google Scholar] [CrossRef]
- Zhao, T.; Ding, Z. Distributed Finite-Time Optimal Resource Management for Microgrids Based on Multi-Agent Framework. IEEE Trans. Ind. Electron. 2018, 65, 6571–6580. [Google Scholar] [CrossRef]
- Singh, V.P.; Kishor, N.; Samuel, P. Distributed Multi-Agent System-Based Load Frequency Control for Multi-Area Power System in Smart Grid. IEEE Trans. Ind. Electron. 2017, 64, 5151–5160. [Google Scholar] [CrossRef]
- Colson, C.M.; Nehrir, M.H. Comprehensive Real-Time Microgrid Power Management and Control With Distributed Agents. IEEE Trans. Smart Grid 2013, 4, 617–627. [Google Scholar] [CrossRef]
- Mu, C.; Zhang, Y.; Jia, H.; He, H. Energy-Storage-Based Intelligent Frequency Control of Microgrid With Stochastic Model Uncertainties. IEEE Trans. Smart Grid 2020, 11, 1748–1758. [Google Scholar] [CrossRef]
- Ju, L.; Zhang, Q.; Tan, Z.; Wang, W.; He, X.; Zhang, Z. Multi-agent-system-based coupling control optimization model formicro-grid group intelligent scheduling considering autonomy-cooperative operation strategy. Energy 2018, 157, 1035–1052. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Cooperative Multi-Agent Control of Heterogeneous Storage Devices Distributed in a DC Microgrid. IEEE Trans. Power Syst. 2016, 31, 2974–2986. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, W.; Yu, N. Consensus Multi-Agent Reinforcement Learning for Volt-VAR Control in Power Distribution Networks. IEEE Trans. Smart Grid 2021, 12, 3594–3604. [Google Scholar] [CrossRef]
- Liu, W.; Gu, W.; Sheng, W.; Meng, X.; Wu, Z.; Chen, W. Decentralized Multi-Agent System-Based Cooperative Frequency Control for Autonomous Microgrids With Communication Constraints. IEEE Trans. Sustain. Energy 2014, 5, 446–456. [Google Scholar] [CrossRef]
- Mu, C.; Peng, J.; Tang, Y. Learning-based control for discrete-time constrained nonzero-sum games. CAAI Trans. Intel. Technol. 2020, 6, 203–213. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep Reinforcement Learning for Multiagent Systems: A Review of Challenges, Solutions, and Applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.; Liu, H.; Zhang, T.; Basar, T. Fully Decentralized Multi-Agent Reinforcement Learning with Networked Agents. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 5872–5881. [Google Scholar]
- Sun, C.; Mu, C. Important Scientific Problems of Multi-Agent Deep Reinforcement Learning. Acta Autom. Sin. 2020, 46, 1301–1312. [Google Scholar]
- Wang, J.; Xu, W.; Gu, Y.; Song, W.; Green, T.C. Multi-agent reinforcement learning for active voltage control on power distribution networks. Adv. Neural Inf. Process. Syst. 2021, 34, 3271–3284. [Google Scholar]
- Mao, H.; Zhang, Z.; Xiao, Z.; Gong, Z.; Ni, Y. Learning agent communication under limited bandwidth by message pruning. In Proceedings of the AAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5142–5149. [Google Scholar]
- Sukhbaatar, S.; Fergus, R. Learning multiagent communication with backpropagation. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29. [Google Scholar]
- Chen, D.; Chen, K.; Li, Z.; Chu, T.; Yao, R.; Qiu, F.; Lin, K. PowerNet: Multi-Agent Deep Reinforcement Learning for Scalable Powergrid Control. IEEE Trans. Power Syst. 2022, 37, 1007–1017. [Google Scholar] [CrossRef]
- Chu, T.; Wang, J.; Codecà, L.; Li, Z. Multi-Agent Deep Reinforcement Learning for Large-Scale Traffic Signal Control. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1086–1095. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Tampuu, A.; Matiisen, T.; Kodelja, D.; Kuzovkin, I.; Korjus, K.; Aru, J.; Aru, J.; Vicente, R. Multiagent cooperation and competition with deep reinforcement learning. PLoS ONE 2017, 12, e0172395. [Google Scholar] [CrossRef] [PubMed]
- Mao, H.; Zhang, Z.; Xiao, Z.; Gong, Z.; Ni, Y. Learning multi-agent communication with double attentional deep reinforcement learning. Auton. Agents Multi-Agent Syst. 2020, 34, 1–34. [Google Scholar] [CrossRef]
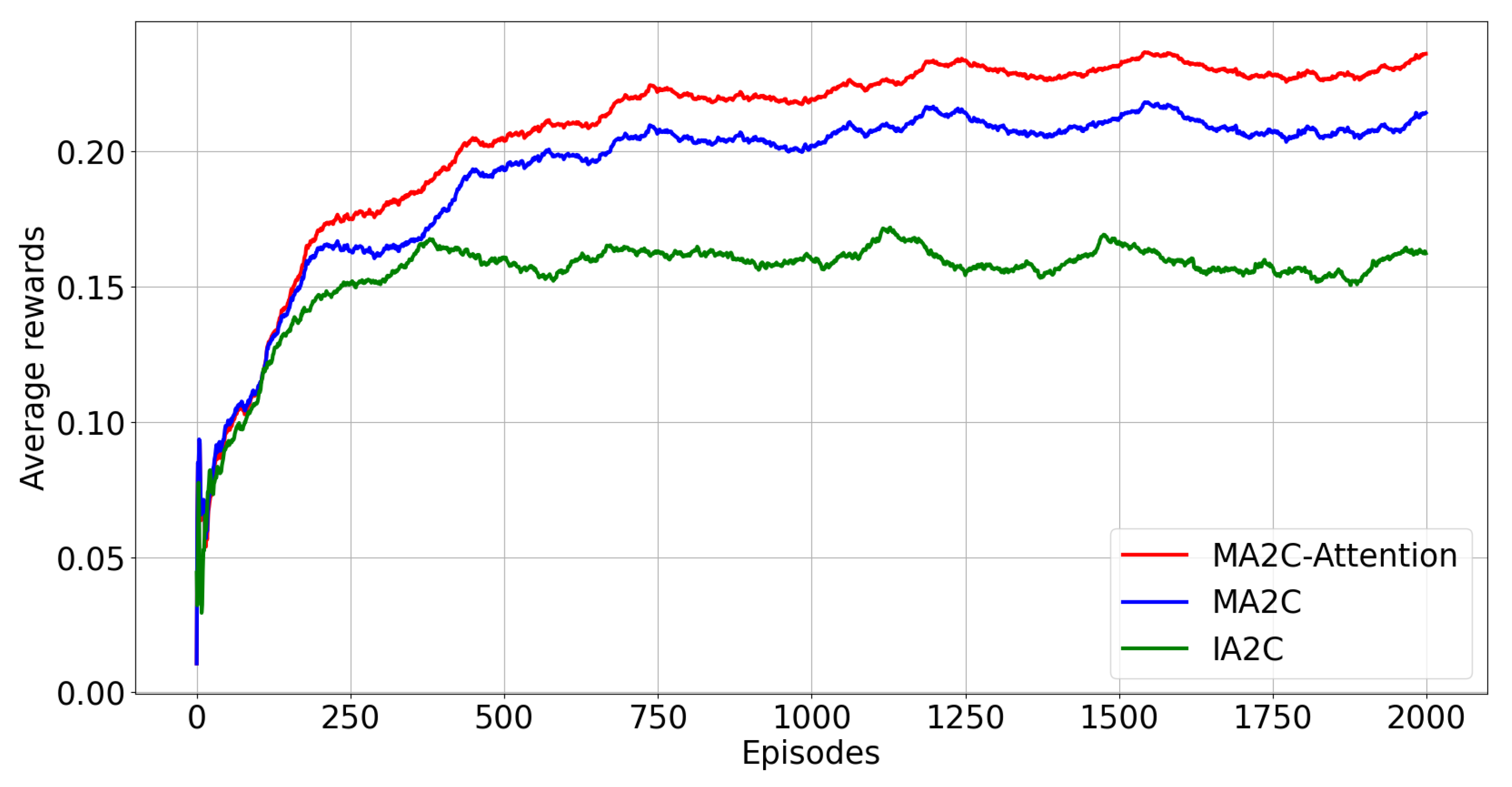
| Random Seeds | MA2C-Attention | MA2C | IA2C |
|---|---|---|---|
| Case 1 | 0.27 | 0.26 | 0.178 |
| Case 2 | 0.25 | 0.25 | 0.112 |
| Case 3 | 0.26 | 0.25 | 0.194 |
| Case 4 | 0.27 | 0.26 | 0.177 |
| Case 5 | 0.27 | 0.25 | 0.175 |
| Average reward | 0.264 | 0.25 | 0.167 |
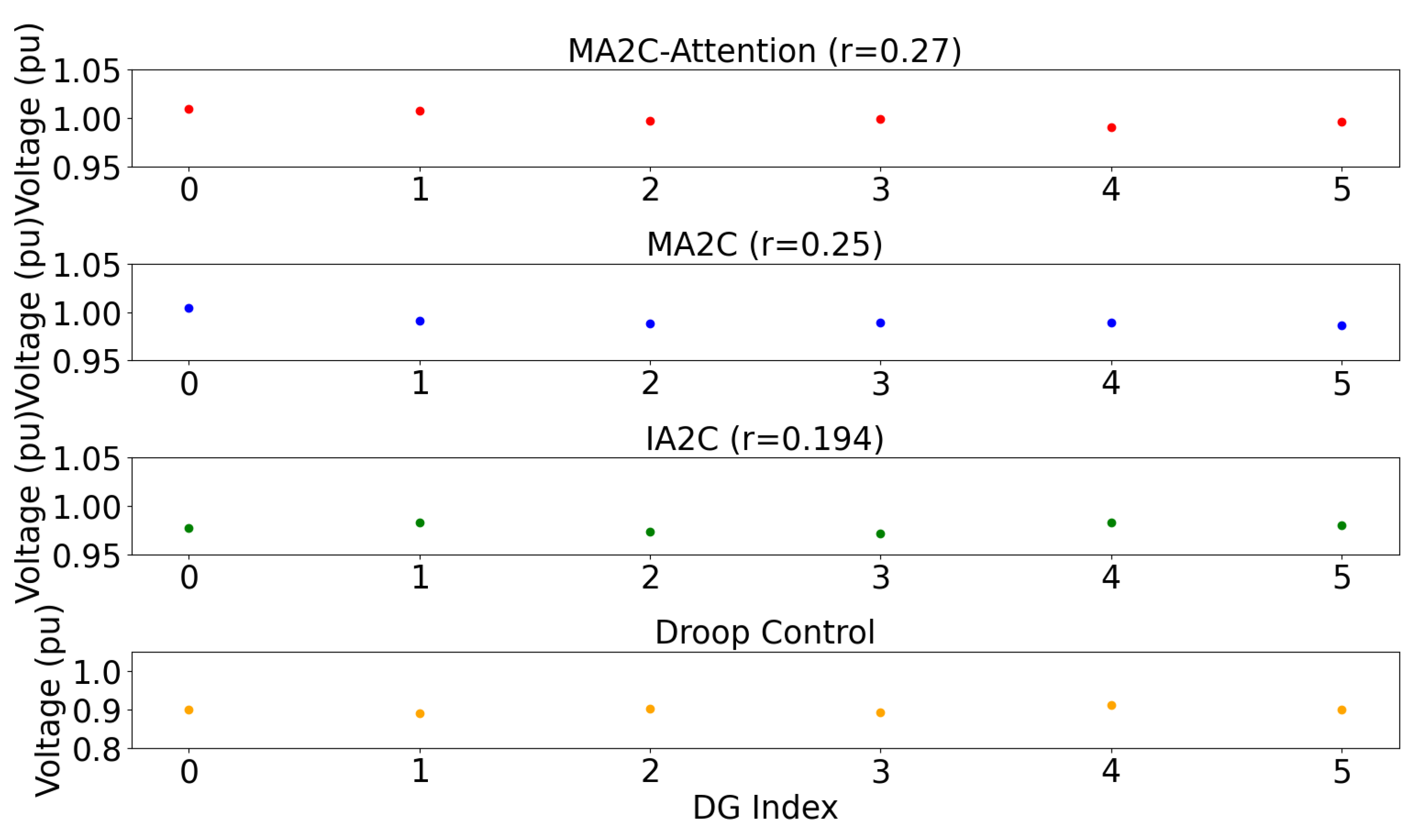
| Method | MA2C-Attention | MA2C | IA2C | Droop Control |
|---|---|---|---|---|
| Agent 1 | 1.00975192 | 1.00467732 | 0.97759587 | 0.9 |
| Agent 2 | 1.00788861 | 0.9908174 | 0.98287053 | 0.89002 |
| Agent 3 | 0.99718829 | 0.9887299 | 0.97389743 | 0.90125 |
| Agent 4 | 0.99951272 | 0.9894690 | 0.97161282 | 0.89234 |
| Agent 5 | 0.99088914 | 0.9894690 | 0.98344116 | 0.91232 |
| Agent 6 | 0.99591974 | 0.9862523 | 0.9800902 | 0.90023 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Ma, S.; Xu, N.; Xiang, T.; Han, X.; Mu, C.; Jin, Y. Secondary Voltage Collaborative Control of Distributed Energy System via Multi-Agent Reinforcement Learning. Energies 2022, 15, 7047. https://doi.org/10.3390/en15197047
Wang T, Ma S, Xu N, Xiang T, Han X, Mu C, Jin Y. Secondary Voltage Collaborative Control of Distributed Energy System via Multi-Agent Reinforcement Learning. Energies. 2022; 15(19):7047. https://doi.org/10.3390/en15197047
Chicago/Turabian StyleWang, Tianhao, Shiqian Ma, Na Xu, Tianchun Xiang, Xiaoyun Han, Chaoxu Mu, and Yao Jin. 2022. "Secondary Voltage Collaborative Control of Distributed Energy System via Multi-Agent Reinforcement Learning" Energies 15, no. 19: 7047. https://doi.org/10.3390/en15197047
APA StyleWang, T., Ma, S., Xu, N., Xiang, T., Han, X., Mu, C., & Jin, Y. (2022). Secondary Voltage Collaborative Control of Distributed Energy System via Multi-Agent Reinforcement Learning. Energies, 15(19), 7047. https://doi.org/10.3390/en15197047





