Solar Radiation Forecasting Using Machine Learning and Ensemble Feature Selection
Abstract
:1. Introduction
- Comparing the performance of different state-of-the-art ML algorithms, including the CatBoost algorithm, which presents fewer applications in solar radiation forecasting to the best of the authors’ knowledge;
- Proposing an ensemble feature selection method to select the most significant endogenous and exogenous variables and their delay values, integrating different ML algorithms.
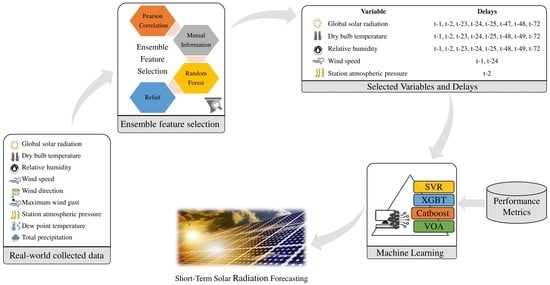
2. Proposed Methodology
2.1. Data Description
2.2. Pre-Processing
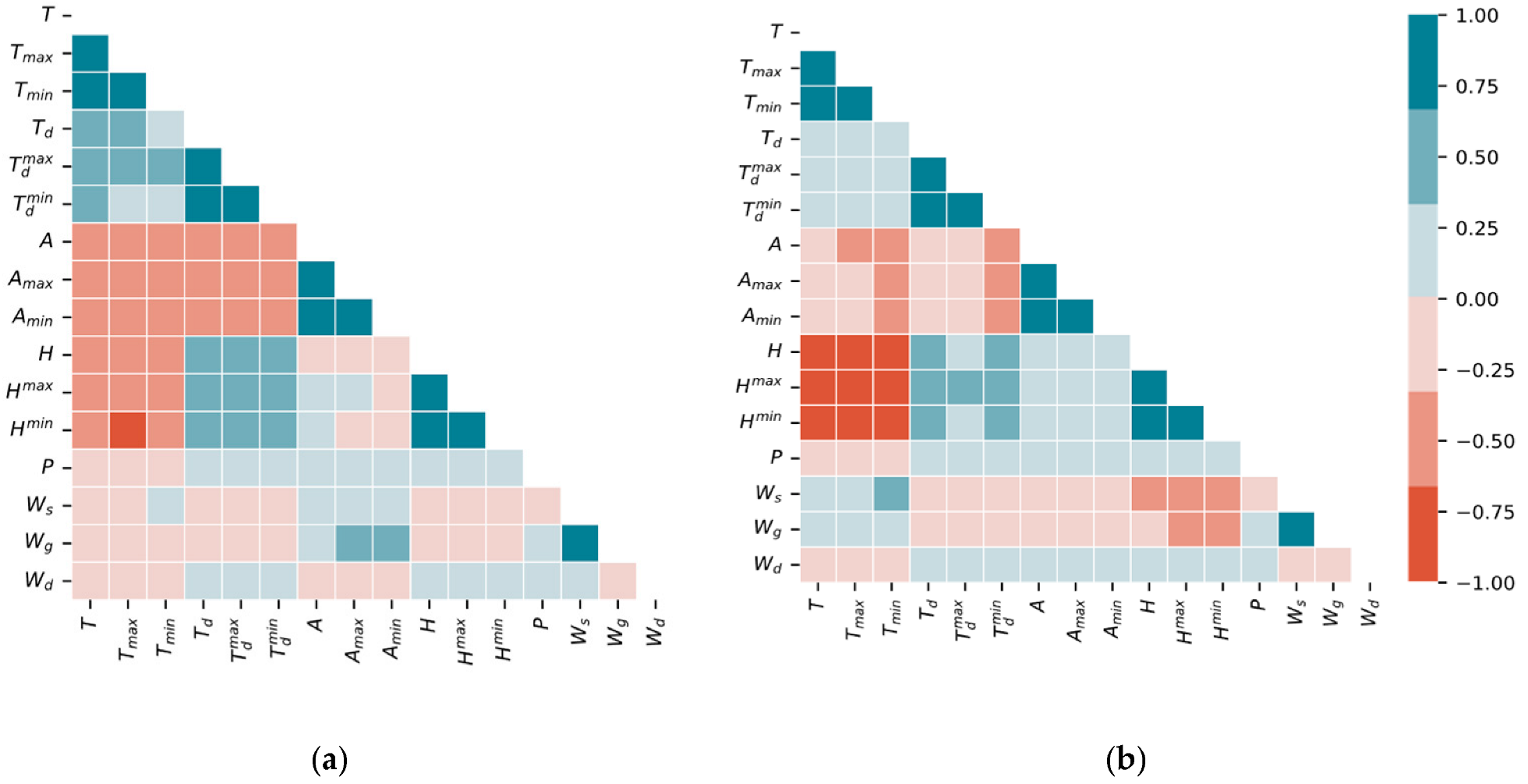
2.3. Ensemble Feature Selection
3. Machine Learning Algorithms
3.1. Support Vector Regression (SVR)
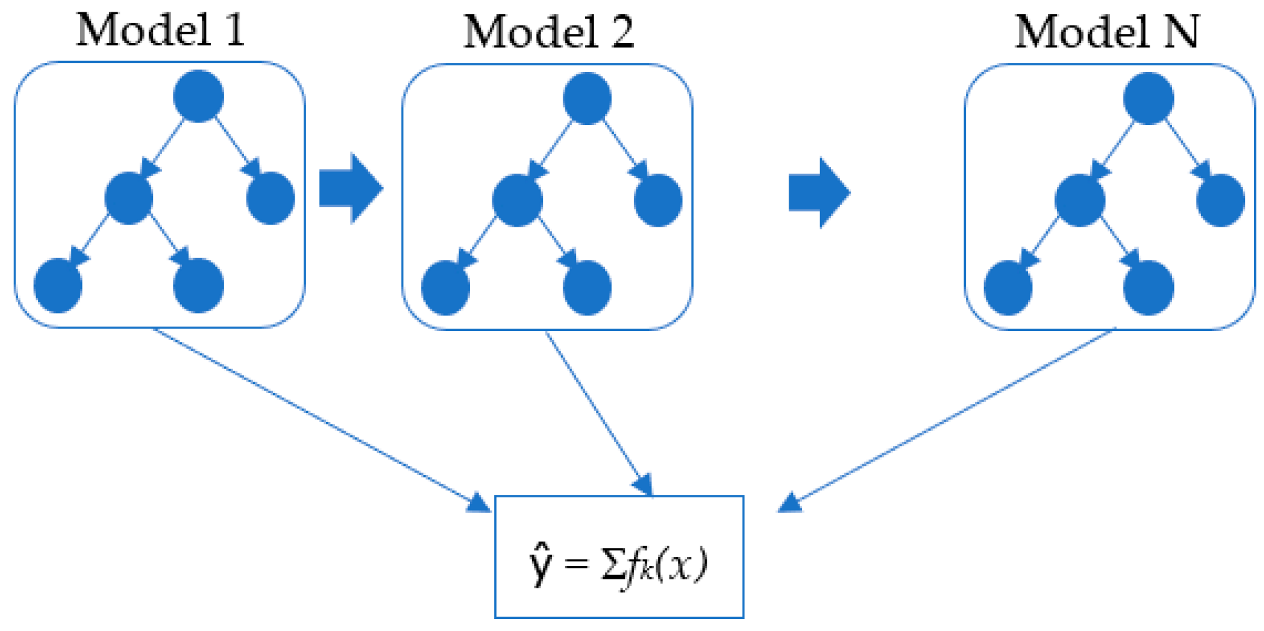
3.2. Extreme Gradient Boosting (XGBT)
3.3. Categorical Boosting (CatBoost)
3.4. Voting Average (VOA)
4. Performance Metrics
5. Results and Discussion
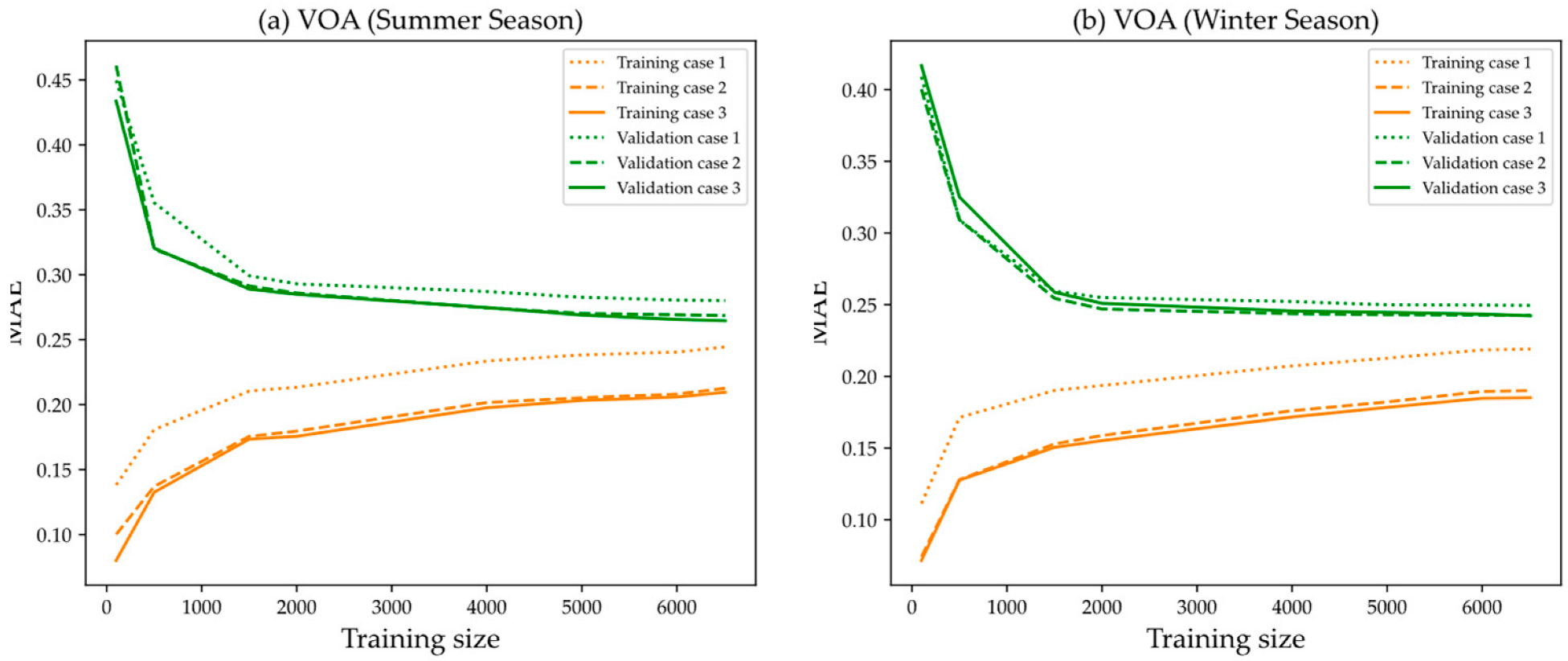
5.1. Impact of Feature Selection of Variables and Delays
- Case 1: The forecasting model is trained using only endogenous inputs, which is the solar radiation and its 10 past observations;
- Case 2: The forecasting model is trained using both endogenous and exogenous inputs (solar radiation and other meteorological data), and their past observations are selected using the Pearson correlation coefficient;
- Case 3: The forecasting model is trained using both endogenous and exogenous inputs, selected using the proposed ensemble feature selection.
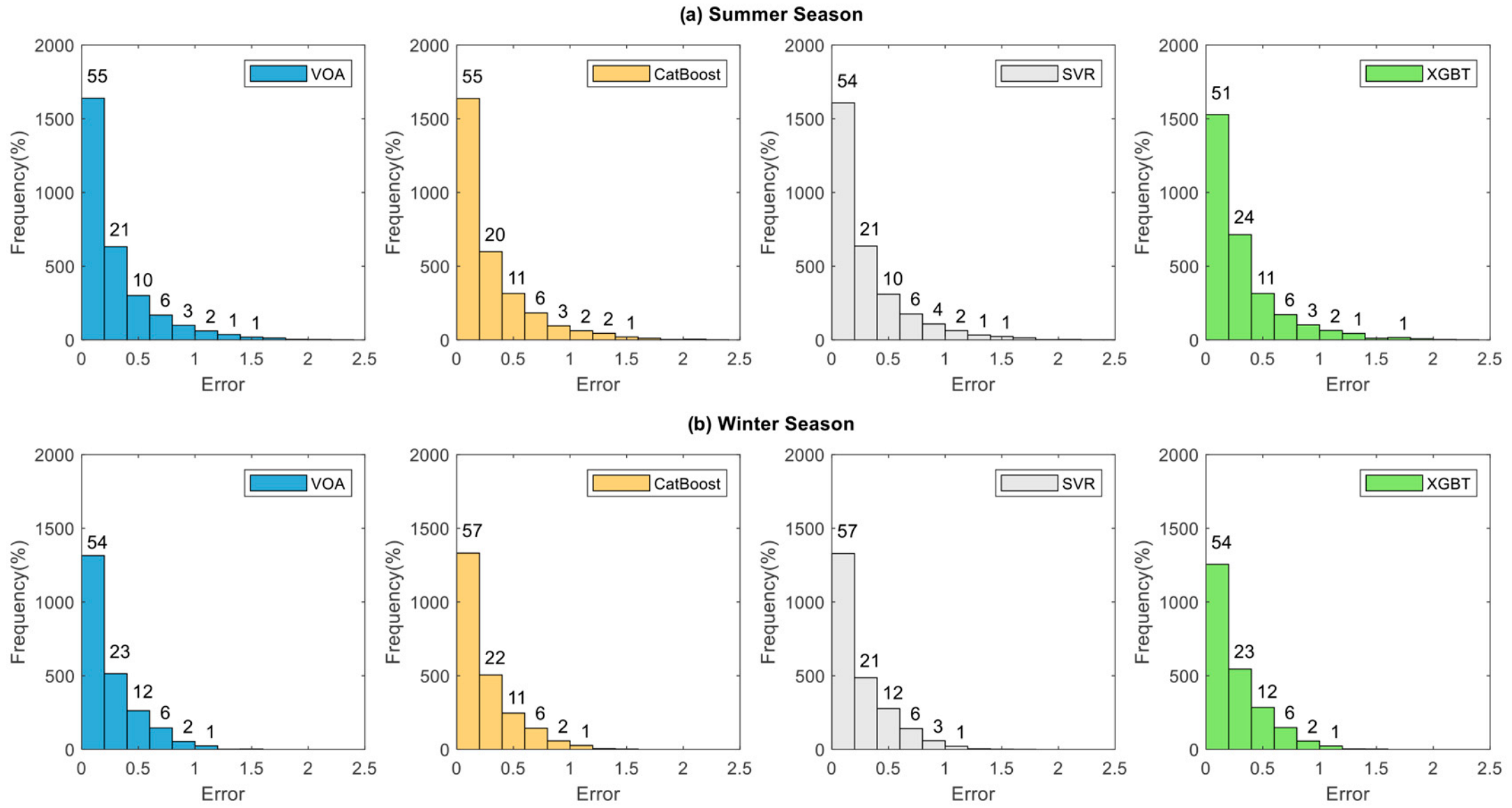
5.2. Forecasting Accuracy of Machine Learning Algorithms
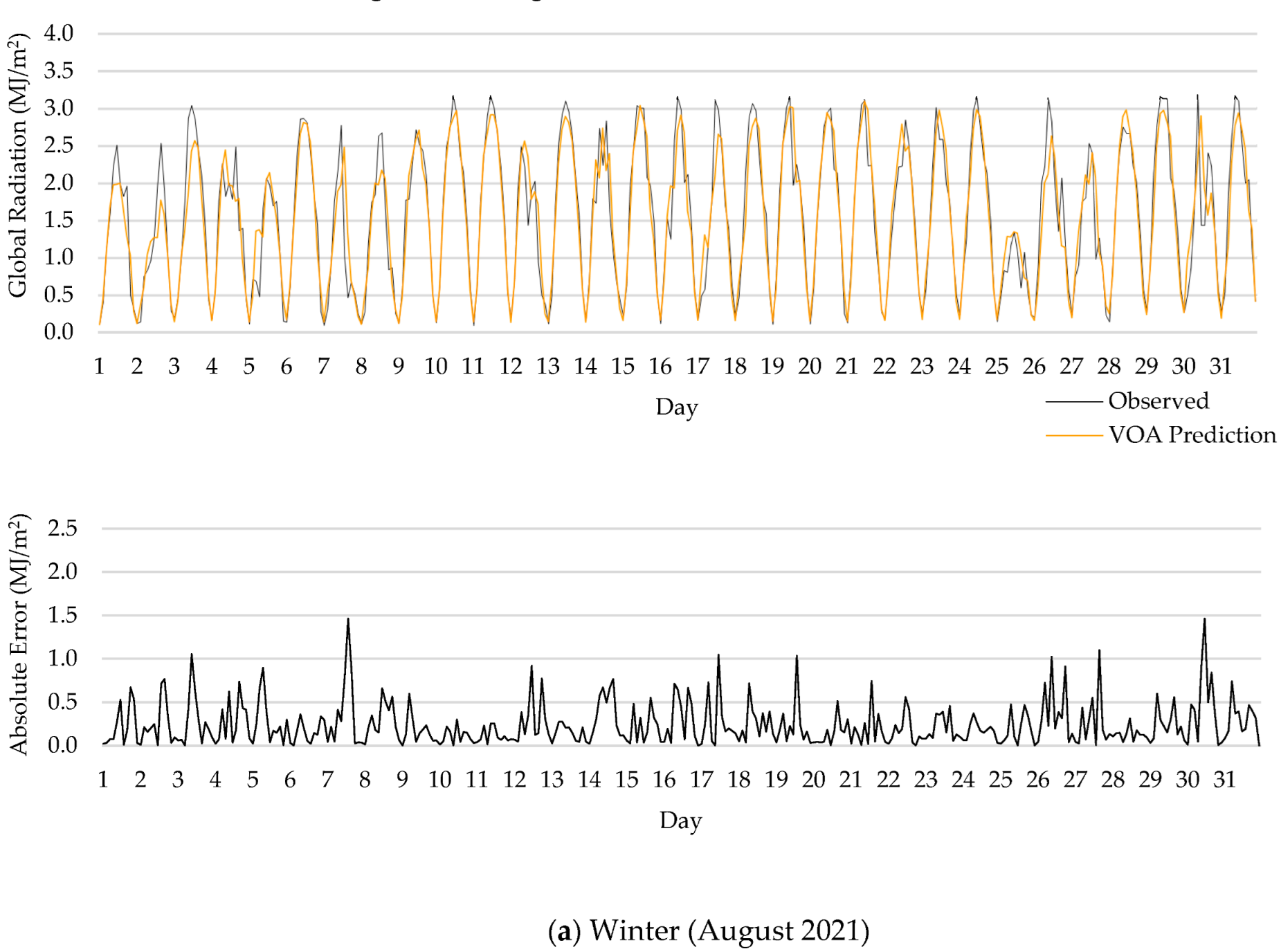
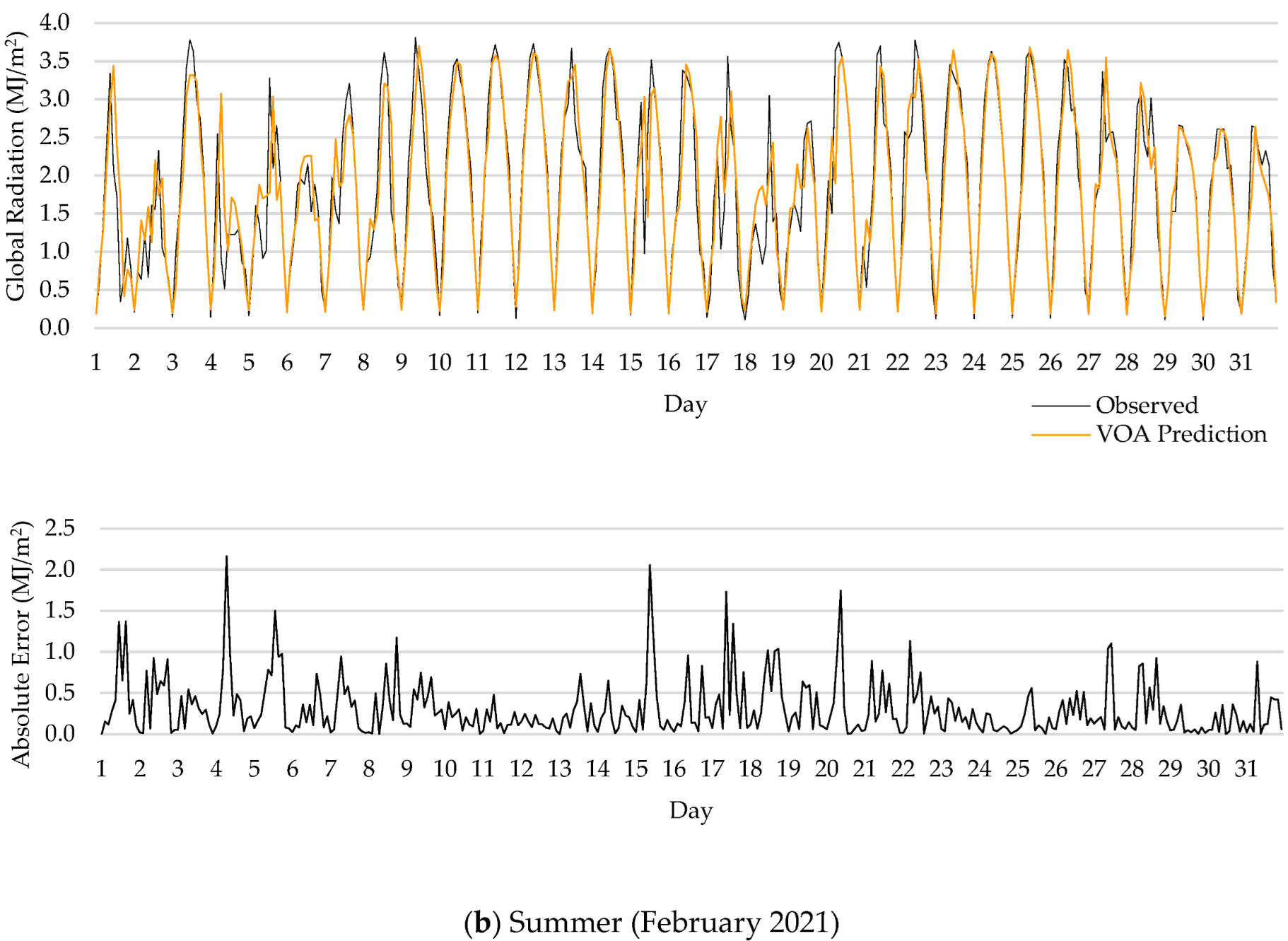
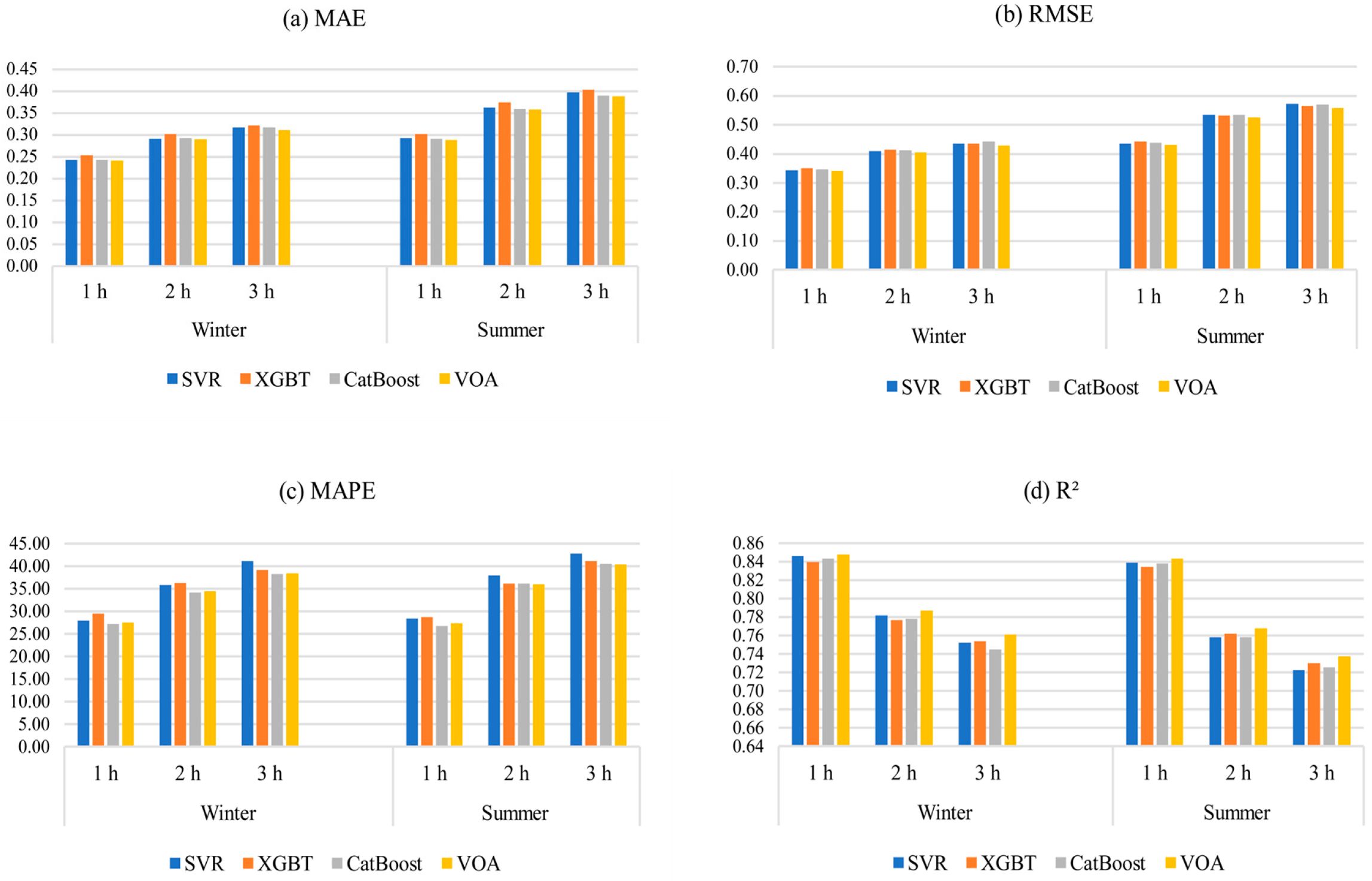
5.3. Results for Different Temporal Scales
6. Conclusions
- The proposed ensemble feature selection outperformed the other two cases analyzed, one using only endogenous variables as inputs and the other using endogenous and exogenous variables as inputs, selected with Pearson’s correlation coefficient;
- As the prediction horizon increased, the error distribution tail became fatter and the range of error values increased;
- All investigated machine learning models revealed acceptable forecasting performance. Among all algorithms, VOA offered the best predictive performance, outperforming other models in every prediction horizon, except for MAPE, wherein Catboost had the lowest error for all forecasting horizons;
- All algorithms have an acceptable testing speed for real-world applications, with an average execution computational time of 11 s. XGBT had a lower training speed, and VOA had a higher training speed.
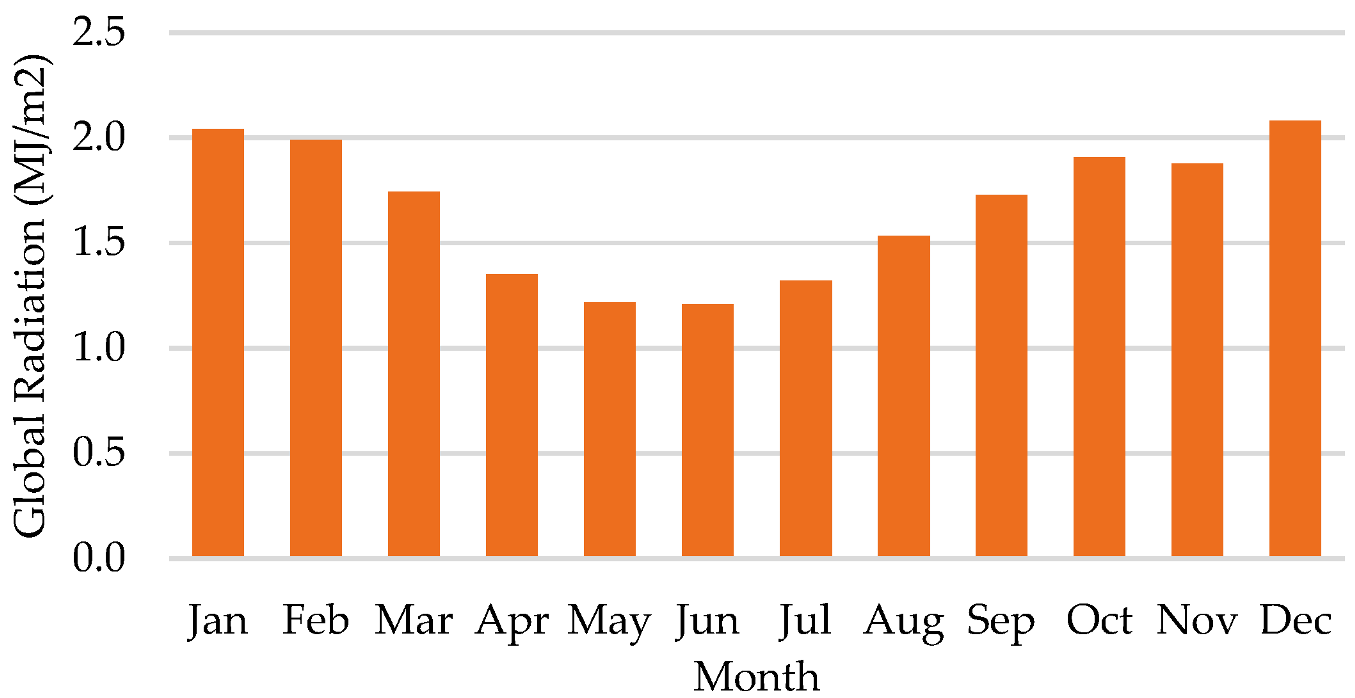
- One interesting finding of this research was that forecasting error was larger in summer than in winter, since the algorithms used are sensitive to the database.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IRENA. Renewable Capacity Highlights 2022. Available online: https://www.irena.org/publications/2022/Apr/Renewable-Capacity-Statistics-2022 (accessed on 20 April 2022).
- Liu, C.; Li, M.; Yu, Y.; Wu, Z.; Gong, H.; Cheng, F. A Review of Multitemporal and Multispatial Scales Photovoltaic Forecasting Methods. IEEE Access 2022, 10, 35073–35093. [Google Scholar] [CrossRef]
- Larson, V.E. Forecasting Solar Irradiance with Numerical Weather Prediction Models. In Solar Energy Forecasting and Resource Assessment; Academic Press: Boston, MA, USA, 2013; pp. 299–318. [Google Scholar]
- Colak, I.; Yesilbudak, M.; Genc, N.; Bayindir, R. Multi-Period Prediction of Solar Radiation Using ARMA and ARIMA Models. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), IEEE, Miami, FL, USA, 9–11 December 2015; pp. 1045–1049. [Google Scholar]
- Huang, J.; Korolkiewicz, M.; Agrawal, M.; Boland, J. Forecasting Solar Radiation on an Hourly Time Scale Using a Coupled AutoRegressive and Dynamical System (CARDS) Model. Solar Energy 2013, 87, 136–149. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S.S. Solar Radiation Prediction Using Artificial Neural Network Techniques: A Review. Renew. Sustain. Energy Rev. 2014, 33, 772–781. [Google Scholar] [CrossRef]
- Kumar, R.; Aggarwal, R.K.; Sharma, J.D. Comparison of Regression and Artificial Neural Network Models for Estimation of Global Solar Radiations. Renew. Sustain. Energy Rev. 2015, 52, 1294–1299. [Google Scholar] [CrossRef]
- Pedro, H.T.C.; Coimbra, C.F.M. Assessment of Forecasting Techniques for Solar Power Production with No Exogenous Inputs. Sol. Energy 2012, 86, 2017–2028. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, D.; Reindl, T.; Walsh, W.M. A Novel Hybrid Approach Based on Self-Organizing Maps, Support Vector Regression and Particle Swarm Optimization to Forecast Solar Irradiance. Energy 2015, 82, 570–577. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine Learning Methods for Solar Radiation Forecasting: A Review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Rodríguez, F.; Azcárate, I.; Vadillo, J.; Galarza, A. Forecasting Intra-Hour Solar Photovoltaic Energy by Assembling Wavelet Based Time-Frequency Analysis with Deep Learning Neural Networks. Int. J. Electr. Power Energy Syst. 2022, 137, 107777. [Google Scholar] [CrossRef]
- Elizabeth Michael, N.; Mishra, M.; Hasan, S.; Al-Durra, A. Short-Term Solar Power Predicting Model Based on Multi-Step CNN Stacked LSTM Technique. Energies 2022, 15, 2150. [Google Scholar] [CrossRef]
- Boubaker, S.; Benghanem, M.; Mellit, A.; Lefza, A.; Kahouli, O.; Kolsi, L. Deep Neural Networks for Predicting Solar Radiation at Hail Region, Saudi Arabia. IEEE Access 2021, 9, 36719–36729. [Google Scholar] [CrossRef]
- Wentz, V.H.; Maciel, J.N.; Gimenez Ledesma, J.J.; Ando Junior, O.H. Solar Irradiance Forecasting to Short-Term PV Power: Accuracy Comparison of ANN and LSTM Models. Energies 2022, 15, 2457. [Google Scholar] [CrossRef]
- Massaoudi, M.; Abu-Rub, H.; Refaat, S.S.; Trabelsi, M.; Chihi, I.; Oueslati, F.S. Enhanced Deep Belief Network Based on Ensemble Learning and Tree-Structured of Parzen Estimators: An Optimal Photovoltaic Power Forecasting Method. IEEE Access 2021, 9, 150330–150344. [Google Scholar] [CrossRef]
- Mahmud, K.; Azam, S.; Karim, A.; Zobaed, S.; Shanmugam, B.; Mathur, D. Machine Learning Based PV Power Generation Forecasting in Alice Springs. IEEE Access 2021, 9, 46117–46128. [Google Scholar] [CrossRef]
- Castangia, M.; Aliberti, A.; Bottaccioli, L.; Macii, E.; Patti, E. A Compound of Feature Selection Techniques to Improve Solar Radiation Forecasting. Expert Syst. Appl. 2021, 178, 114979. [Google Scholar] [CrossRef]
- Tao, C.; Lu, J.; Lang, J.; Peng, X.; Cheng, K.; Duan, S. Short-Term Forecasting of Photovoltaic Power Generation Based on Feature Selection and Bias Compensation–LSTM Network. Energies 2021, 14, 3086. [Google Scholar] [CrossRef]
- Surakhi, O.; Zaidan, M.A.; Fung, P.L.; Hossein Motlagh, N.; Serhan, S.; AlKhanafseh, M.; Ghoniem, R.M.; Hussein, T. Time-Lag Selection for Time-Series Forecasting Using Neural Network and Heuristic Algorithm. Electronics 2021, 10, 2518. [Google Scholar] [CrossRef]
- INMET. Instituto Nacional de Meteorologia. Available online: https://portal.inmet.gov.br/ (accessed on 23 October 2021).
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques, 3rd ed.; Elsevier Inc.: Waltham, MA, USA, 2012. [Google Scholar]
- Mera-Gaona, M.; López, D.M.; Vargas-Canas, R.; Neumann, U. Framework for the Ensemble of Feature Selection Methods. Appl. Sci. 2021, 11, 8122. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L. A Practical Approach to Feature Selection. Mach. Learn. Proc. 1992, 1992, 249–256. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms, 1st ed.; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3 December 2018. [Google Scholar]
- An, K.; Meng, J. Voting-Averaged Combination Method for Regressor Ensemble. In Advanced Intelligent Computing Theories and Applications; Huang, D.S., Zhao, Z., Bevilacqua, V., Figueroa, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6215, pp. 540–546. [Google Scholar]
- Agrawal, T. Hyperparameter Optimization Using Scikit-Learn. In Hyperparameter Optimization in Machine Learning; Apress: Berkeley, CA, USA, 2021; pp. 31–51. ISBN 978-1-4842-6578-9. [Google Scholar]




| Data | Abbreviation | Unity |
|---|---|---|
| Hour | H | hour |
| Global solar radiation | R | MJ/m2 |
| Maximum wind gust | Wg | m/s |
| Wind speed | Ws | m/s |
| Wind direction | Wd | ° |
| Dry bulb temperature | T | °C |
| Hourly maximum temperature | Tmax | °C |
| Hourly minimum temperature | Tmin | °C |
| Dew point temperature | Td | °C |
| Hourly maximum dew point temperature | Tdmax | °C |
| Hourly minimum dew point temperature | Tdmin | °C |
| Total precipitation | P | mm |
| Station atmospheric pressure | A | mb |
| Hourly maximum atmospheric pressure | Amax | mb |
| Hourly minimum atmospheric pressure | Amin | mb |
| Relative humidity | H | % |
| Hourly maximum relative humidity | Hmax | % |
| Hourly minimum relative humidity | Hmin | % |
| Variable | Mean | Standard Deviation | Min | Max |
|---|---|---|---|---|
| H | 12.0 | 3.1623 | 7.0 | 17.0 |
| R | 1.6533 | 1.0462 | 0.0009 | 4.15 |
| Wg | 5.6651 | 1.7302 | 0.6000 | 10.6 |
| Ws | 1.6069 | 0.5372 | 0.1 | 3.0 |
| Wd | 130.8017 | 59.7526 | 1.0 | 360.0 |
| T | 27.3608 | 2.4069 | 20.4 | 34.2 |
| Tmax | 28.1414 | 2.5181 | 20.8 | 35.8 |
| Tmin | 26.5007 | 2.3708 | 19.9 | 32.4 |
| Td | 21.5368 | 1.4812 | 16.8 | 25.5 |
| Tdmax | 22.2897 | 1.4708 | 17.3 | 26.0 |
| Tdmin | 20.8531 | 1.4820 | 16.3 | 25.1 |
| P | 0.2041 | 1.3419 | 0.0 | 50.4 |
| A | 1009.4062 | 2.9636 | 1001.6 | 1017.7 |
| Amax | 1009.7137 | 2.9276 | 1001.9 | 1018.1 |
| Amin | 1009.2102 | 2.9265 | 1001.4 | 1017.5 |
| H | 71.3240 | 10.4711 | 45.0 | 96.0 |
| Hmax | 75.0566 | 10.1359 | 52.0 | 97.0 |
| Hmin | 68.1149 | 11.0133 | 38.0 | 96.0 |
| Winter | |
| Variable | Delays |
| Global solar radiation | t − 1, t − 2, t − 23, t − 24, t − 25, t − 47, t − 48, t − 72 |
| Dry bulb temperature | t − 1, t − 2, t − 23, t − 24, t − 25, t − 48, t − 49, t − 72 |
| Relative humidity | t − 1, t − 2, t − 23, t − 24, t − 25, t − 48, t − 49, t − 72 |
| Wind speed | t − 1, t − 24 |
| Atmospheric pressure | t − 2 |
| Hour, day, month | - |
| Summer | |
| Variable | Delays |
| Global solar radiation | t − 1, t − 2, t − 23, t − 24, t − 25, t − 47, t − 48, t − 72 |
| Dry bulb temperature | t − 1, t − 2, t − 23, t − 24, t − 25, t − 48, t − 49, t − 72 |
| Relative humidity | t − 1, t − 2, t − 23, t − 24, t − 25, t − 48, t − 49, t − 72 |
| Wind speed | t − 1, t − 2 |
| Atmospheric pressure | t − 3 |
| Hour, day, month | - |
| Algorithm | Hyperparameter | |
|---|---|---|
| Winter | Summer | |
| SVR | regularization C = 10, ε = 0.01, γ = auto, kernel function K = RBF | Regularization C = 100, ε = 0.001, γ = auto, kernel function K = RBF |
| XGBT | learning rate = 0.1, max. depth = 5, number of estimators = 80, subsample = 0.9 | learning rate = 0.1, max. depth = 5, number of estimators = 100, subsample = 0.8 |
| CatBoost | depth = 6, L2 regularization = 10, learning rate = 0.05, iterations = 2000 | depth = 6, L2 regularization = 10, learning rate = 0.05, iterations = 2000 |
| VOA | XGBT (learning rate = 0.1, max. depth = 5, number of estimators = 80, subsample = 0.9) CatBoost (depth = 6, L2 regularization = 10, learning rate = 0.05, iterations = 2000) SVR (regularization C = 10, ε = 0.01, γ = auto, kernel function K = RBF) | XGBT (learning rate = 0.1, max. depth = 5, number of estimators = 100, subsample = 0.8) CatBoost (depth = 6, L2 regularization = 10, learning rate = 0.05, iterations = 2000) SVR (regularization C = 100, ε = 0.001, γ = auto, kernel function K = RBF) |
| Winter | ||||
| Input Set | MAE | RMSE | MAPE | R2 |
| Case 1: endogenous | 0.2591 | 0.3532 | 34.1955 | 0.8377 |
| Case 2: end + exog (Pearson coefficient) | 0.2521 | 0.3439 | 32.8627 | 0.8460 |
| Case 3: endo + exog (ensemble selection) | 0.2537 | 0.3431 | 31.8928 | 0.8468 |
| Summer | ||||
| Input Set | MAE | RMSE | MAPE | R2 |
| Case 1: endogenous | 0.3153 | 0.4536 | 35.4139 | 0.8261 |
| Case 2: end + exog (Pearson correlation) | 0.3017 | 0.4358 | 31.1411 | 0.8395 |
| Case 3: endogenous and exogenous | 0.303 | 0.4326 | 30.6106 | 0.8417 |
| Winter | ||||
|---|---|---|---|---|
| SVR | XGBT | CatBoost | VOA | |
| MAE | 0.2430 | 0.2534 | 0.2426 | 0.2417 |
| RMSE | 0.3433 | 0.3507 | 0.3470 | 0.3418 |
| MAPE | 28.0122 | 29.5350 | 27.2163 | 27.4862 |
| R2 | 0.8466 | 0.8399 | 0.8433 | 0.8480 |
| SK | 0.1336 | 0.0880 | 0.0994 | 0.1039 |
| K | −1.1632 | −1.1829 | −1.2022 | −1.1877 |
| Summer | ||||
| SVR | XGBT | CatBoost | VOA | |
| MAE | 0.2922 | 0.3009 | 0.2905 | 0.2877 |
| RMSE | 0.4366 | 0.4426 | 0.4373 | 0.4309 |
| MAPE | 28.3590 | 28.6951 | 26.8127 | 27.3177 |
| R2 | 0.8389 | 0.8344 | 0.8383 | 0.8430 |
| SK | 0.0462 | 0.0332 | 0.0338 | 0.0360 |
| K | 0.2922 | −1.1663 | −1.1551 | −1.1563 |
| Learning Speed (s) | ||||
| SVR | XGBT | CatBoost | VOA | |
| Summer | 63.09 | 2.85 | 13.08 | 183.93 |
| Winter | 9.73 | 1.75 | 9.81 | 14.76 |
| Testing Speed (s) | ||||
| Summer | 36.99 | 1.44 | 13.35 | 13.14 |
| Winter | 4.91 | 1.17 | 10.27 | 10.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solano, E.S.; Dehghanian, P.; Affonso, C.M. Solar Radiation Forecasting Using Machine Learning and Ensemble Feature Selection. Energies 2022, 15, 7049. https://doi.org/10.3390/en15197049
Solano ES, Dehghanian P, Affonso CM. Solar Radiation Forecasting Using Machine Learning and Ensemble Feature Selection. Energies. 2022; 15(19):7049. https://doi.org/10.3390/en15197049
Chicago/Turabian StyleSolano, Edna S., Payman Dehghanian, and Carolina M. Affonso. 2022. "Solar Radiation Forecasting Using Machine Learning and Ensemble Feature Selection" Energies 15, no. 19: 7049. https://doi.org/10.3390/en15197049
APA StyleSolano, E. S., Dehghanian, P., & Affonso, C. M. (2022). Solar Radiation Forecasting Using Machine Learning and Ensemble Feature Selection. Energies, 15(19), 7049. https://doi.org/10.3390/en15197049