A Novel Synchrophasor Estimation Based on Enhanced All-Phase DFT with Iterative Compensation and Its Implementation
Abstract
1. Introduction
2. Principle of All-Phase DFT Spectrum Analysis
2.1. Theoretical Background
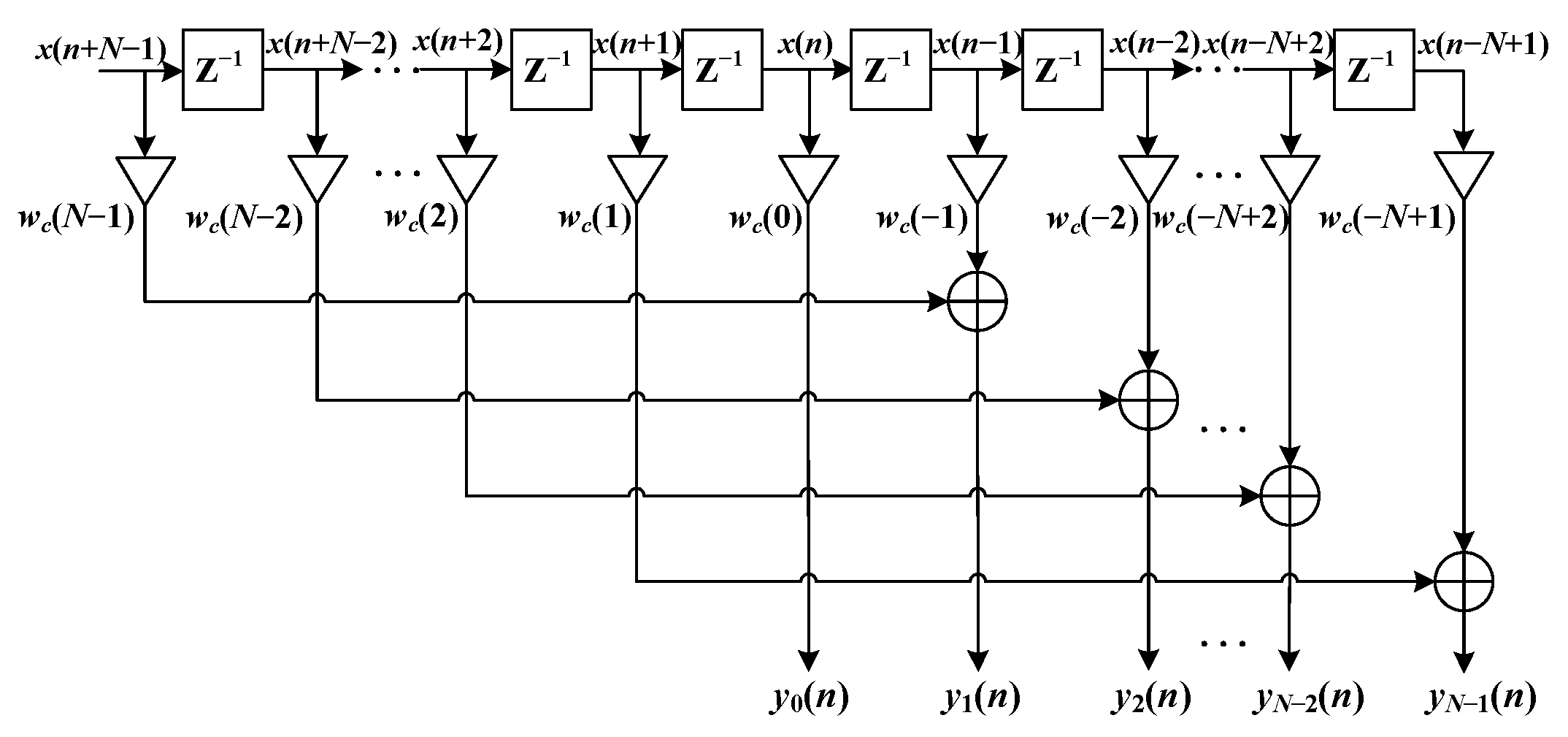
2.2. Traditional apDFT Algorithm Formulation
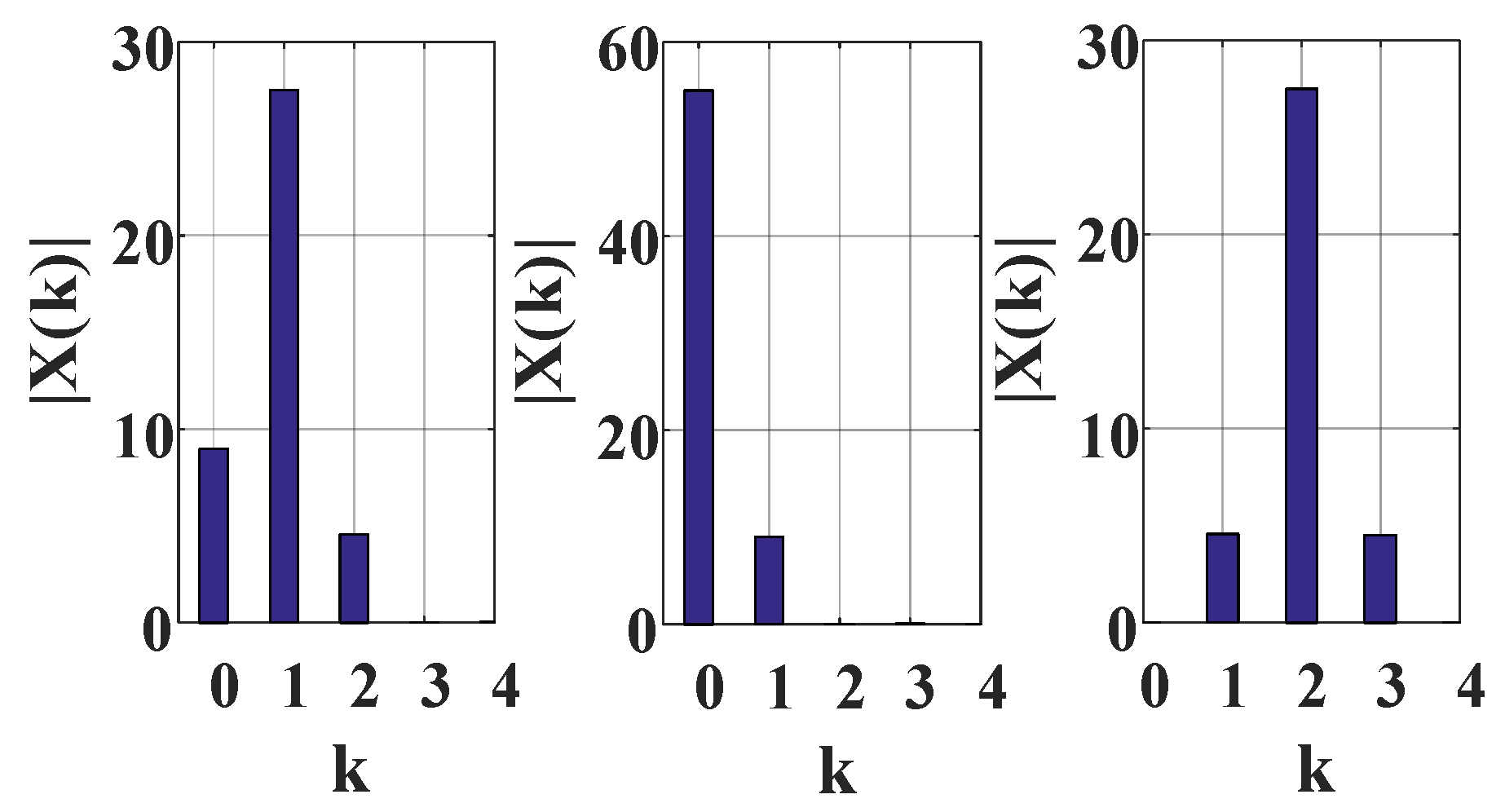
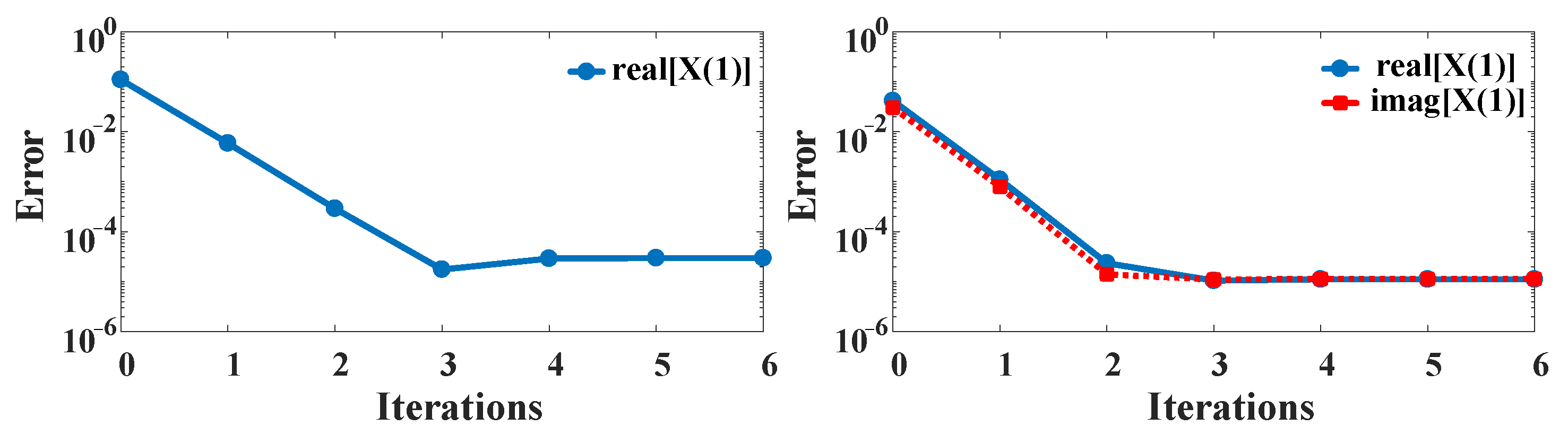
3. Proposed Enhanced-ApDFT
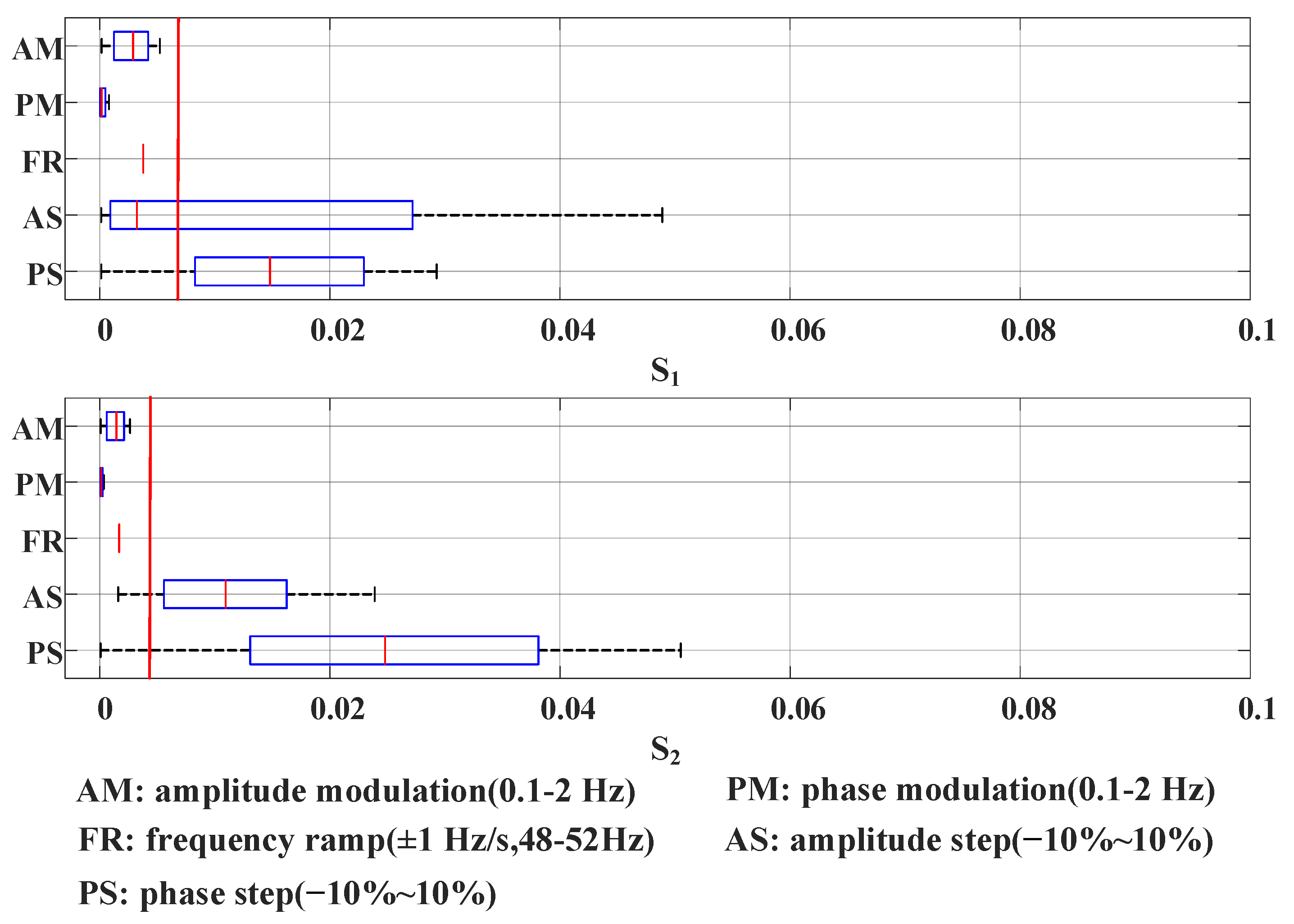
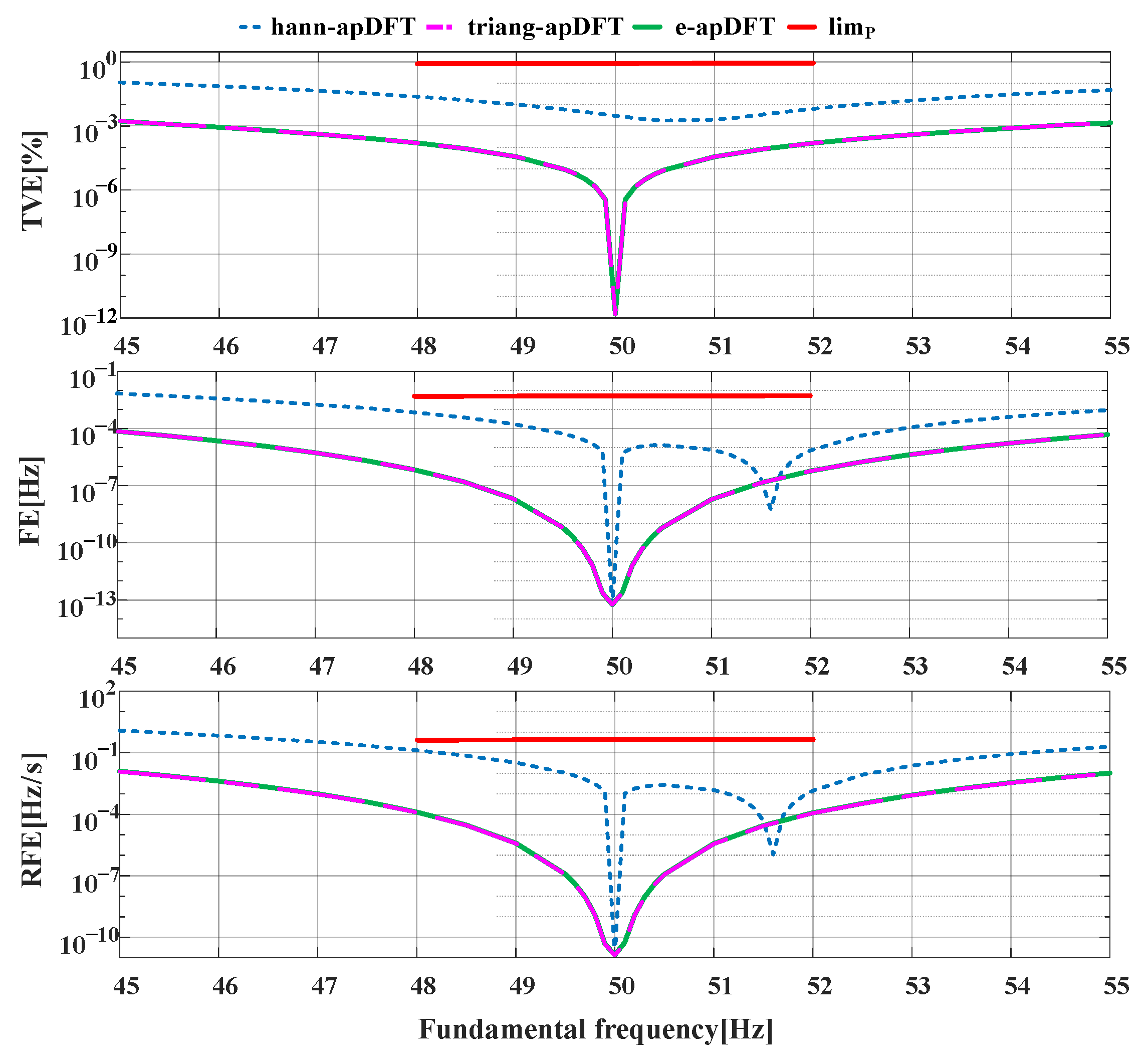
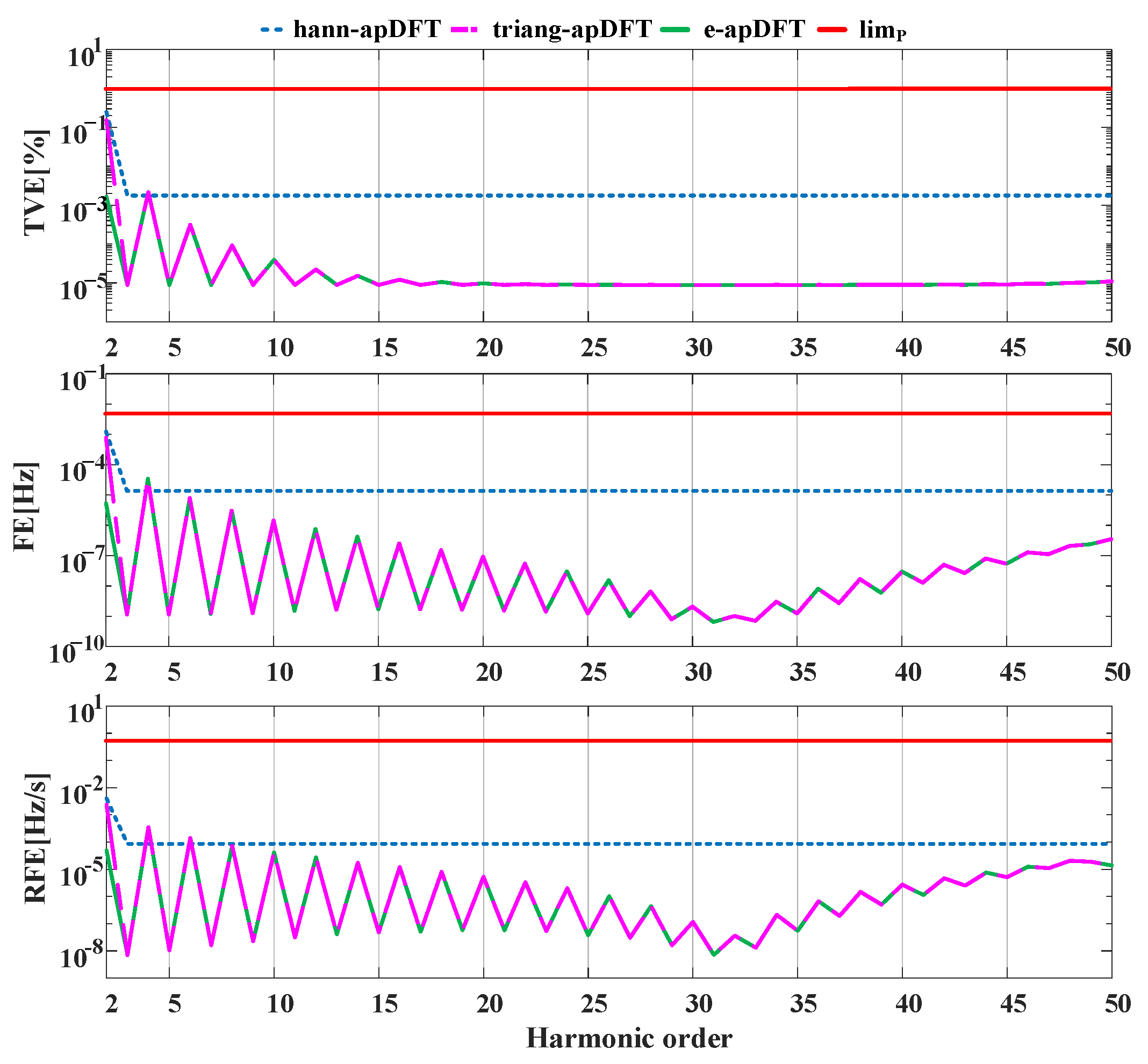
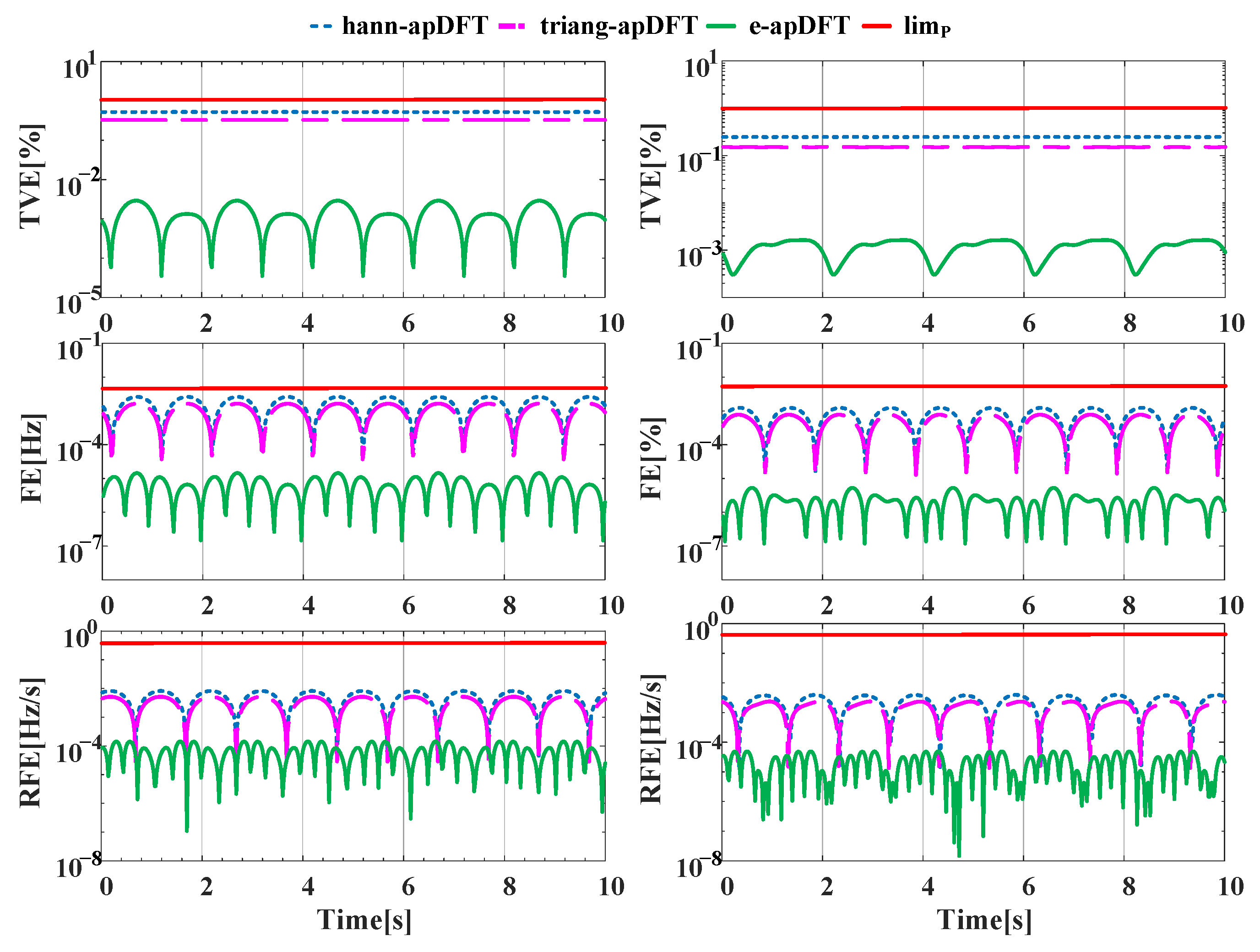
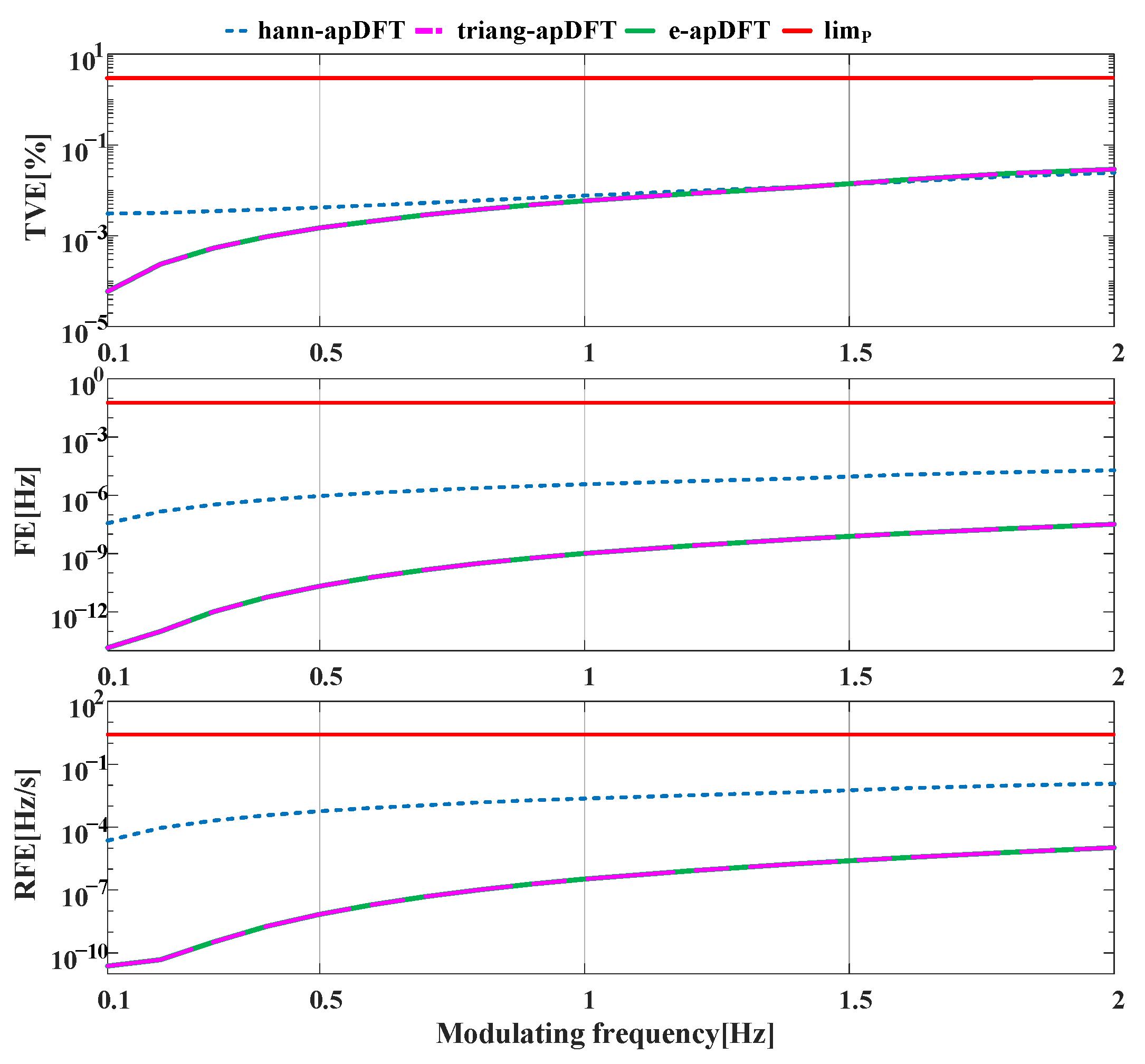
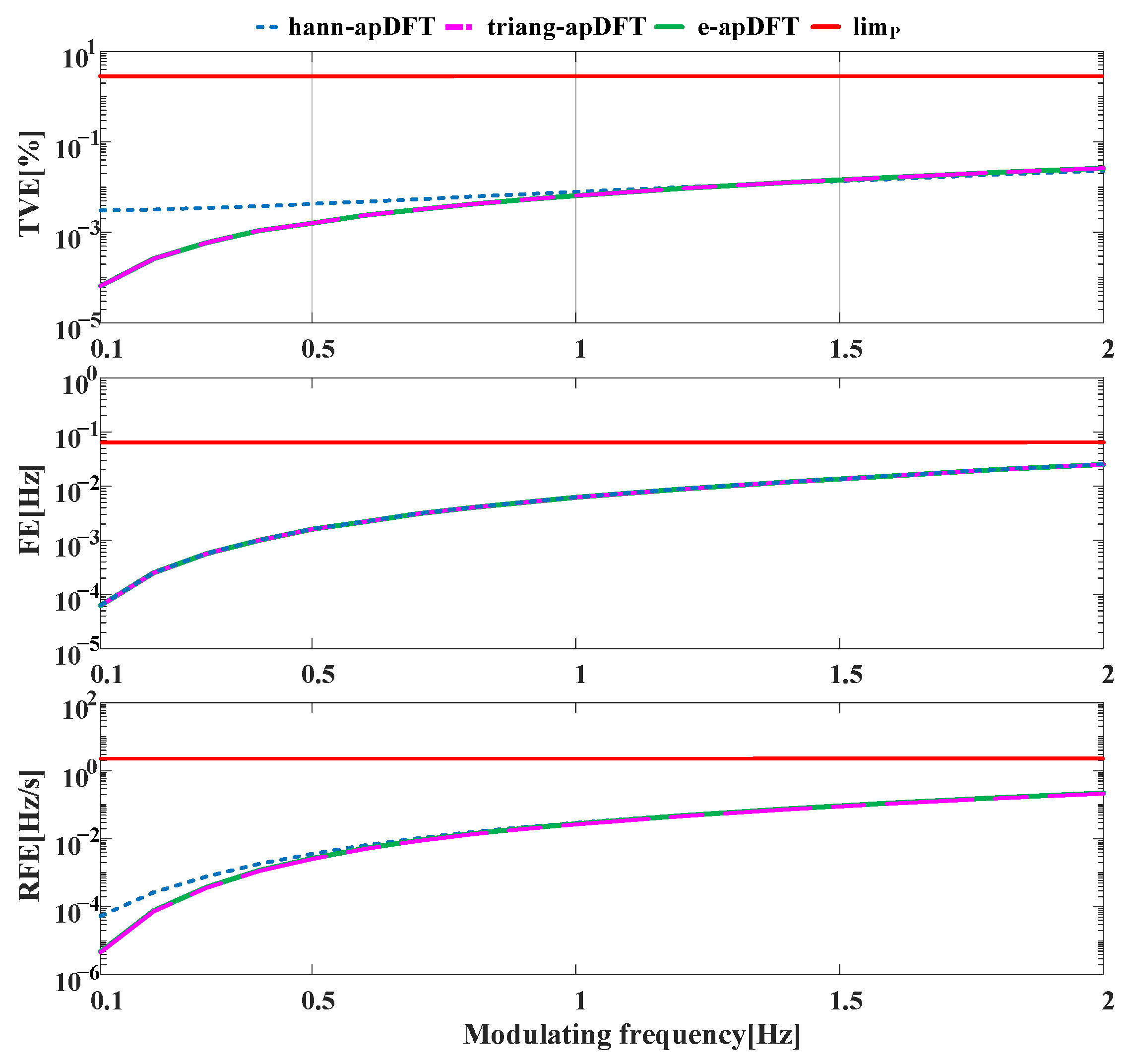
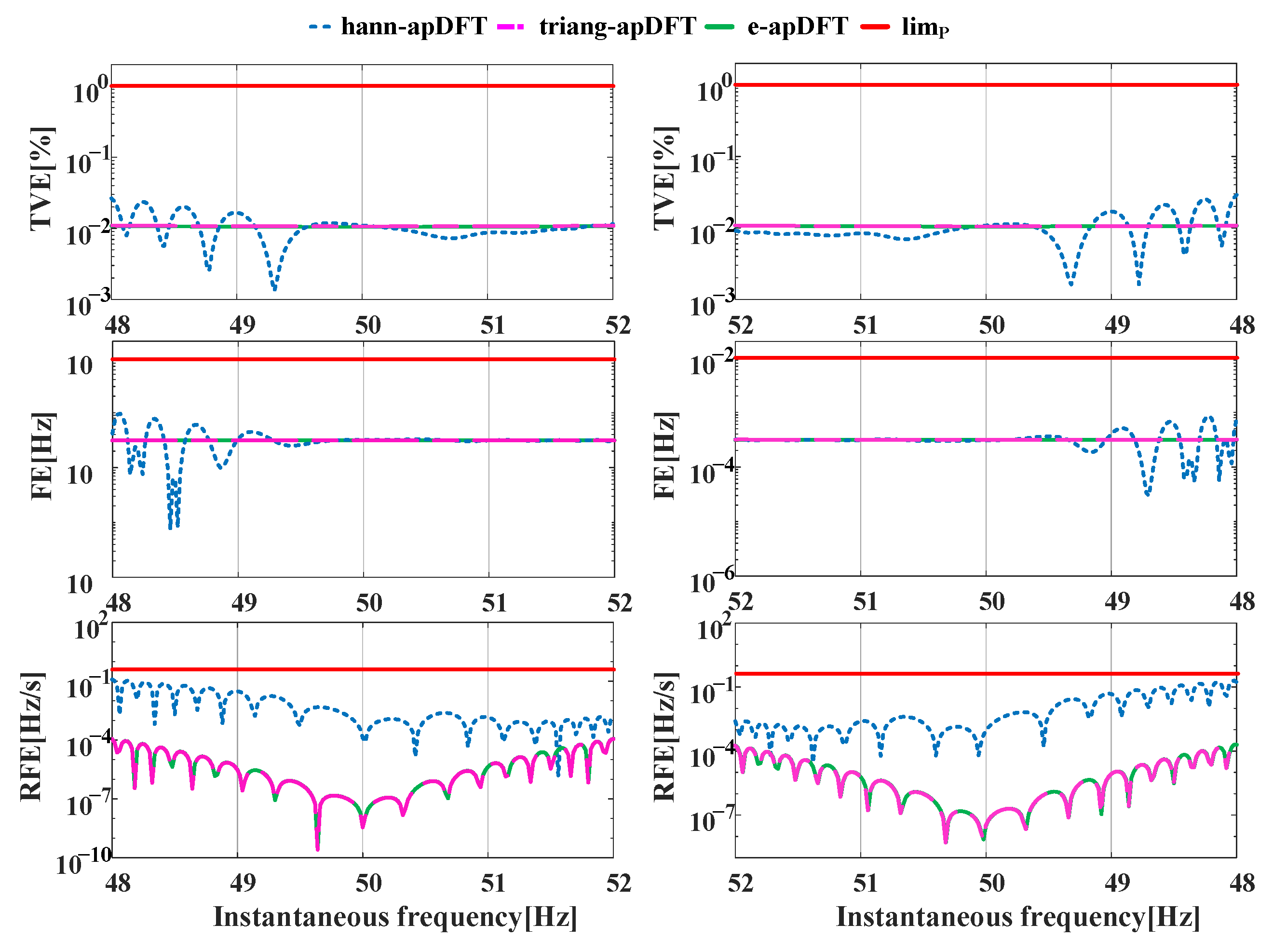
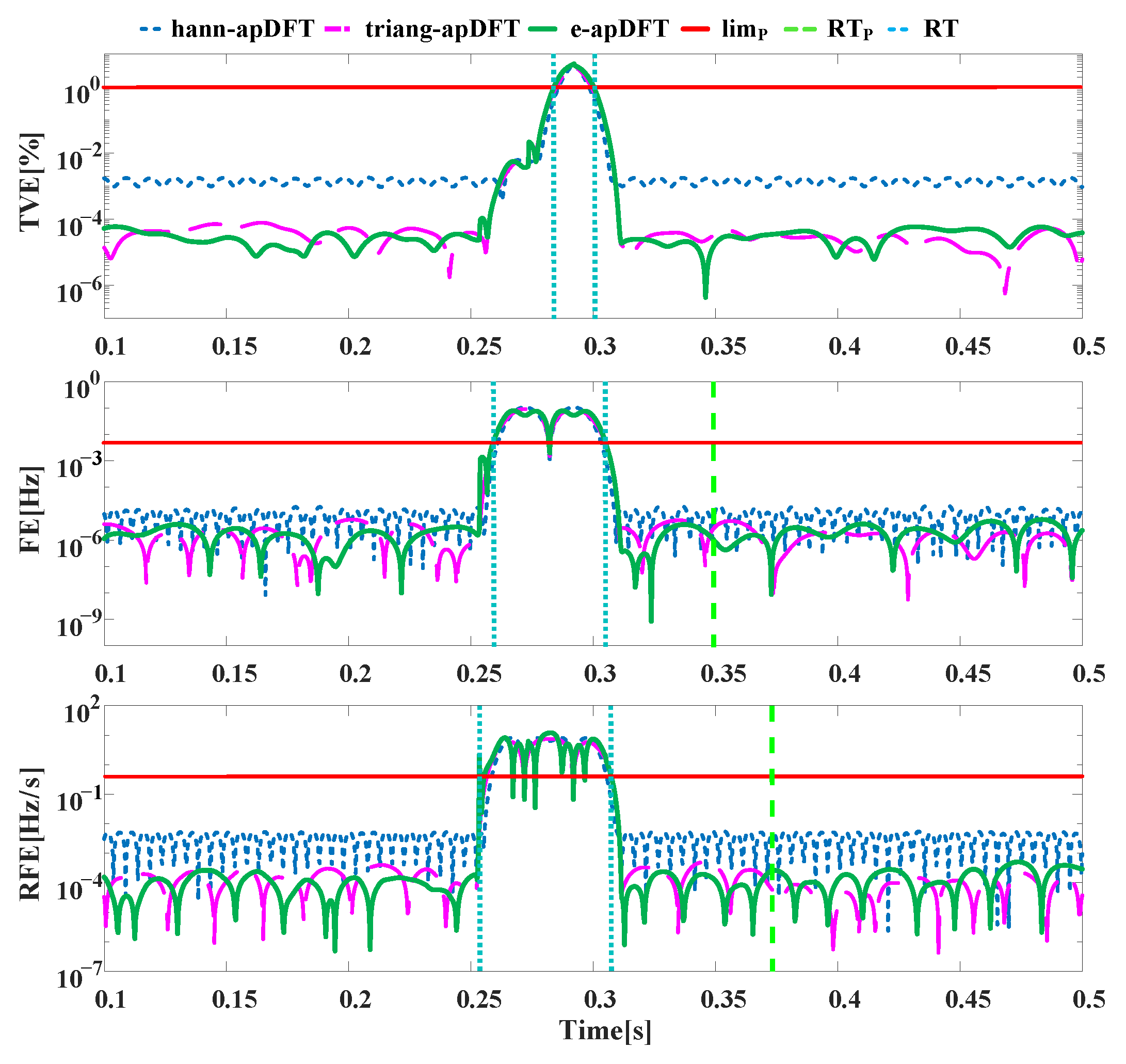
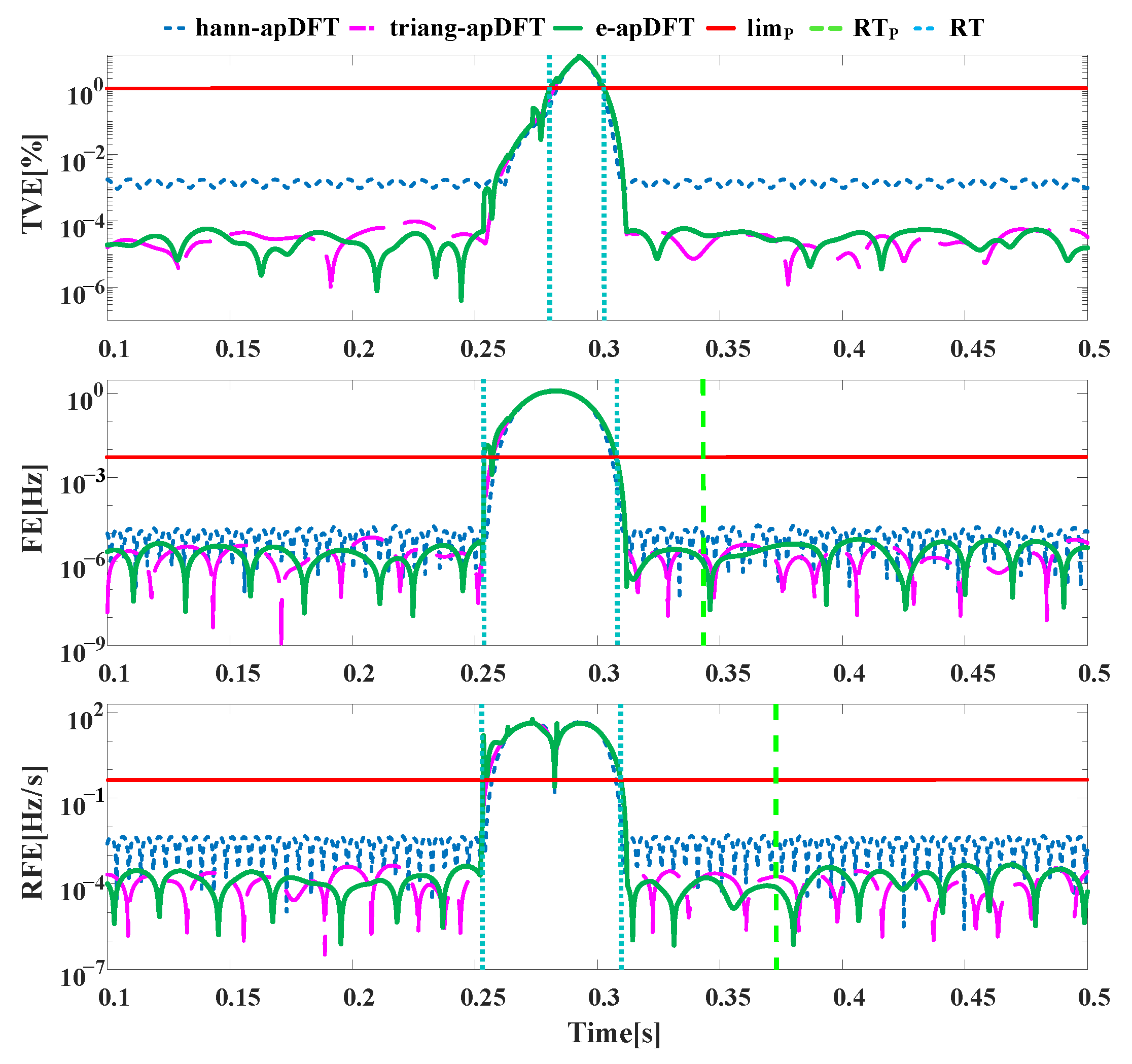
4. Simulation Analysis
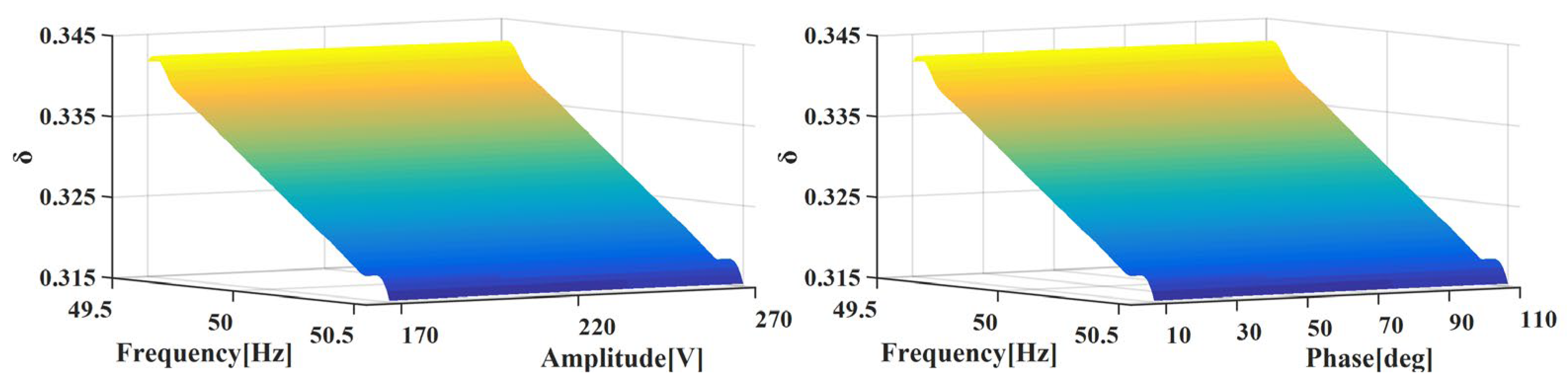
4.1. Static Tests
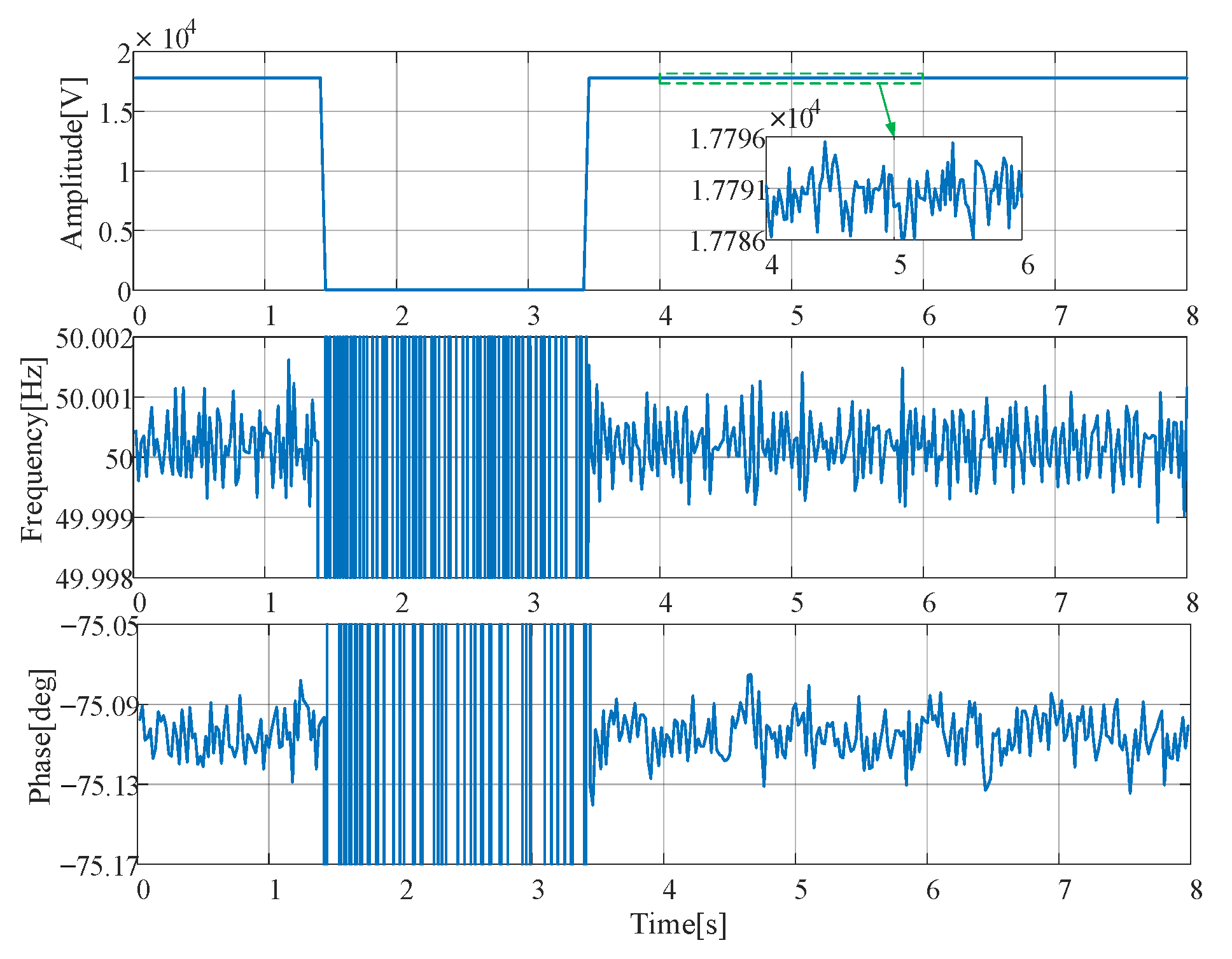
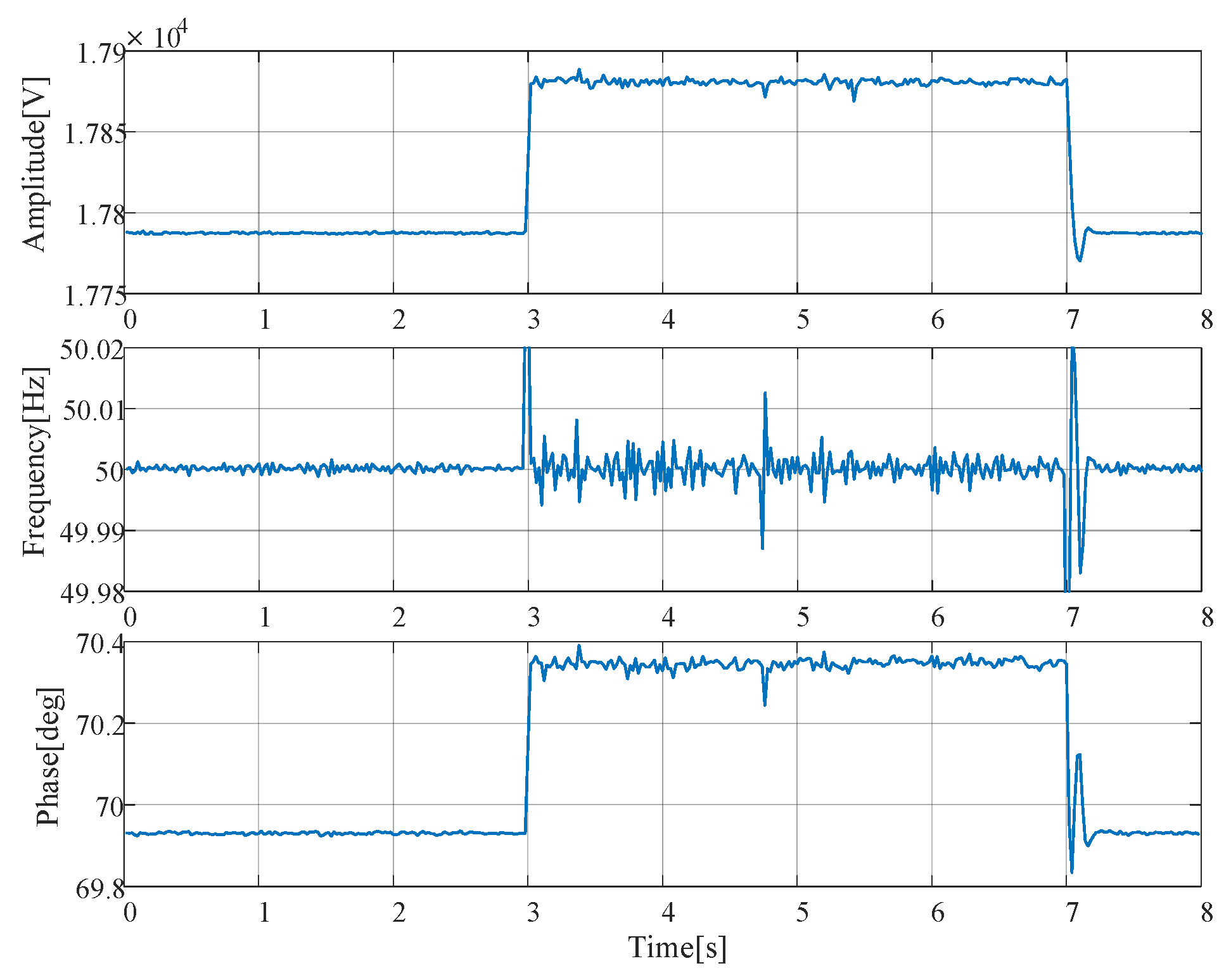
4.2. Dynamic Tests
5. Implementation in the DSP-Based Hardware Platform
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bhatt, N.B. Role of Synchrophasor Technology in the Development of A Smarter Transmission Grid. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010. [Google Scholar]
- Dusabimana, E.; Yoon, S. A Survey on the Micro-Phasor Measurement Unit in Distribution Networks. Electronics 2020, 9, 305. [Google Scholar] [CrossRef]
- Akrami, A.; Doostizadeh, M.; Aminifar, F. Optimal Reconfiguration of Distribution Network Using μPMU Measurements: A Data-Driven Stochastic Robust Optimization. IEEE Trans. Smart Grid 2020, 11, 420–428. [Google Scholar] [CrossRef]
- Fu, L.; Yu, L.; Xiong, S.; He, Z.; Mai, R.; Li, X. A Dynamic Synchrophasor Estimation Algorithm Considering Out-of-Band Interference. IEEE Trans. Power Deliv. 2022, 37, 1193–1202. [Google Scholar] [CrossRef]
- Huang, C.; Xie, X.; Jiang, H. Dynamic Phasor Estimation Through DSTKF Under Transient Conditions. IEEE Trans. Instrum. Meas. 2017, 66, 2929–2936. [Google Scholar] [CrossRef]
- Ferrero, R.; Pegoraro, P.A.; Toscani, S. Synchrophasor Estimation for Three-Phase Systems Based on Taylor Extended Kalman Filtering. IEEE Trans. Instrum. Meas. 2020, 69, 6723–6730. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.; Choi, S. Performance Criterion of Phasor Measurement Units for Distribution System State Estimation. IEEE Access 2019, 7, 106372–106384. [Google Scholar] [CrossRef]
- Rao, A.V.K.; Soni, K.M.; Sinha, S.K.; Nasiruddin, I. Accurate phasor and frequency estimation during power system oscillations using least squares. IET Sci. Meas. Technol. 2019, 13, 989–994. [Google Scholar]
- Oubrahim, Z.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H. Maximum-Likelihood Frequency and Phasor Estimations for Electric Power Grid Monitoring. IEEE Trans. Ind. Inform. 2018, 14, 167–177. [Google Scholar] [CrossRef]
- Choqueuse, V.; Belouchrani, A.; Auger, F.; Benbouzid, M. Frequency and Phasor Estimations in Three-Phase Systems: Maximum Likelihood Algorithms and Theoretical Performance. IEEE Trans. Smart Grid 2019, 10, 3248–3258. [Google Scholar] [CrossRef]
- Vejdan, S.; Sanaye-Pasand, M.; Malik, O.P. Accurate Dynamic Phasor Estimation Based on the Signal Model Under Off-Nominal Frequency and Oscillations. IEEE Trans. Smart Grid 2017, 8, 708–719. [Google Scholar] [CrossRef]
- Bi, T.; Liu, H.; Feng, Q.; Qian, C.; Liu, Y. Dynamic Phasor Model-Based Synchrophasor Estimation Algorithm for M-Class PMU. IEEE Trans. Power Deliv. 2015, 30, 1162–1171. [Google Scholar] [CrossRef]
- Narduzzi, C.; Bertocco, M.; Frigo, G.; Giorgi, G. Fast-TFM—Multifrequency Phasor Measurement for Distribution Networks. IEEE Trans. Instrum. Meas. 2018, 67, 1825–1835. [Google Scholar] [CrossRef]
- Chauhan, K.; Reddy, M.V.; Sodhi, R. A Novel Distribution-Level Phasor Estimation Algorithm Using Empirical Wavelet Transform. IEEE Trans. Ind. Electron. 2018, 65, 7984–7995. [Google Scholar] [CrossRef]
- Serbes, A. Fast and Efficient Sinusoidal Frequency Estimation by Using the DFT Coefficients. IEEE Trans. Commun. 2019, 67, 2333–2342. [Google Scholar] [CrossRef]
- Frigo, G.; Derviskadic, A.; Paolone, M. Reduced Leakage Synchrophasor Estimation: Hilbert Transform Plus Interpolated DFT. IEEE Trans. Instrum. Meas. 2019, 68, 3468–3483. [Google Scholar] [CrossRef]
- Sun, Y.; Zhuang, C.; Xiong, Z. A Switch-Based Interpolated DFT for the Small Number of Acquired Sine Wave Cycles. IEEE Trans. Instrum. Meas. 2016, 65, 846–855. [Google Scholar] [CrossRef]
- Macii, D.; Petri, D.; Zorat, A. Accuracy Analysis and Enhancement of DFT-Based Synchrophasor Estimators in Off-Nominal Conditions. IEEE Trans. Instrum. Meas. 2012, 61, 2653–2664. [Google Scholar] [CrossRef]
- Wen, H.; Li, C.; Tang, L. Novel Three-Point Interpolation DFT Method for Frequency Measurement of Sine-Wave. IEEE Trans. Ind. Inform. 2017, 13, 2333–2338. [Google Scholar] [CrossRef]
- Wen, H.; Li, C.; Yao, W. Power System Frequency Estimation of Sine-Wave Corrupted with Noise by Windowed Three-Point Interpolated DFT. IEEE Trans. Smart Grid 2018, 9, 5163–5172. [Google Scholar] [CrossRef]
- Romano, P.; Paolone, M. Enhanced Interpolated-DFT for Synchrophasor Estimation in FPGAs: Theory, Implementation, and Validation of a PMU Prototype. IEEE Trans. Instrum. Meas. 2014, 63, 2824–2836. [Google Scholar] [CrossRef]
- Derviškadić, A.; Romano, P.; Paolone, M. Iterative-Interpolated DFT for Synchrophasor Estimation: A Single Algorithm for P- and M-Class Compliant PMUs. IEEE Trans. Instrum. Meas. 2018, 67, 547–558. [Google Scholar] [CrossRef]
- Jin, T.; Zhang, W. A Novel Interpolated DFT Synchrophasor Estimation Algorithm with an Optimized Combined Cosine Self-convolution Window. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Su, T.; Yang, M.; Jin, T.; Flesch, R.C.C. Power Harmonic and Interharmonic Detection Method in Renewable Power Based on Nuttall Double-window All-phase FFT Algorithm. IET Renew. Power Gener. 2018, 12, 953–961. [Google Scholar] [CrossRef]
- Yang, M.; Chen, H. An Interharmonic Detection Method Based on Wavelet Packet and ApFFT. Prot. Control. Mod. Power Syst. 2017, 45, 112–117. [Google Scholar]
- Pan, Y.; Zhang, T.; Zhang, G.; Luo, Z. A Narrowband Anti-Jamming Acquisition Algorithm Based on All-Phase Processing for BOC Signals. IEEE Access 2019, 7, 41416–41425. [Google Scholar] [CrossRef]
- Shao, P.; Zhao, Q.; Guo, H.; Zhang, X. Realization of All Phase-mixed Radix FFT on the Phase Measurement Device. Power Syst. Prot. Control. 2016, 44, 65–69. [Google Scholar]
- Huang, X.; Bai, R.; Zhai, X. All-phase Time-shift Phase Difference Frequency Estimation Based on Frequency Shift Compensation. J. Tianjin Univ. 2017, 50, 649–655. [Google Scholar]
- IEC/IEEE 60255-118-1:2018; Measuring Relays and Protection Equipment—Part 118-1:”Synchrophasor for Power Systems—Measurements. IEC: Geneva, Switzerland, 2018; pp. 1–78.

| Variable | Parameter | Value |
|---|---|---|
| f0 | Nominal frequency | 50 Hz |
| L | Window length | 2N−1 (N = 64) |
| fs | Sampling rate | 3.2 kHz |
| fr | Resolution | 50 Hz |
| Fr | Reporting rate | 50 fps |
| NI | Iterations | 3 |
| Static/Dynamic Test | Parameter Setting | Max FE/Hz | Max RFE/(Hz/s) | Max TVE/% | |||
|---|---|---|---|---|---|---|---|
| Sta. 1 | Mea. 2 | Sta. | Mea. | Sta. | Mea. | ||
| Frequency offset | 48~52 Hz | 0.005 | 9.57 × 10−4 | 0.4 | 0.10 | 1 | 0.0194 |
| Harmonic distortion | Harmonic: 2~50th (1%) | 0.005 | 0.0012 | 0.4 | 0.11 | 1 | 0.1018 |
| Frequency ramp | ±1 Hz/s (48~52 Hz) | 0.01 | 0.0027 | 0.4 | 0.09 | 1 | 0.0832 |
| Amplitude modulation | Modulation frequency: 0~2 Hz | 0.06 | 8.66 × 10−4 | 2.3 | 0.11 | 3 | 0.0231 |
| Phase modulation | Modulation frequency: 0~2 Hz | 0.06 | 0.0251 | 2.3 | 0.99 | 3 | 0.0925 |
| Step Test | RTFE/s | RTRFE/s | RTTFE/s | |||
|---|---|---|---|---|---|---|
| Sta. | Mea. | Sta. | Mea. | Sta. | Mea. | |
| AS | 4.5/f0 | 2.6/f0 | 6/f0 | 3.1/f0 | 2/f0 | 0.8/f0 |
| PS | 4.5/f0 | 2.7/f0 | 6/f0 | 3.0/f0 | 2/f0 | 1.2/f0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhang, W.; Zhuang, Z.; Jin, T. A Novel Synchrophasor Estimation Based on Enhanced All-Phase DFT with Iterative Compensation and Its Implementation. Energies 2022, 15, 6964. https://doi.org/10.3390/en15196964
Li Z, Zhang W, Zhuang Z, Jin T. A Novel Synchrophasor Estimation Based on Enhanced All-Phase DFT with Iterative Compensation and Its Implementation. Energies. 2022; 15(19):6964. https://doi.org/10.3390/en15196964
Chicago/Turabian StyleLi, Zengqin, Weifeng Zhang, Zhiyuan Zhuang, and Tao Jin. 2022. "A Novel Synchrophasor Estimation Based on Enhanced All-Phase DFT with Iterative Compensation and Its Implementation" Energies 15, no. 19: 6964. https://doi.org/10.3390/en15196964
APA StyleLi, Z., Zhang, W., Zhuang, Z., & Jin, T. (2022). A Novel Synchrophasor Estimation Based on Enhanced All-Phase DFT with Iterative Compensation and Its Implementation. Energies, 15(19), 6964. https://doi.org/10.3390/en15196964





