Leakage Analysis and Hazardous Boundary Determination of Buried Gas Pipeline Considering Underground Adjacent Confined Space
Abstract
1. Introduction
2. Methods
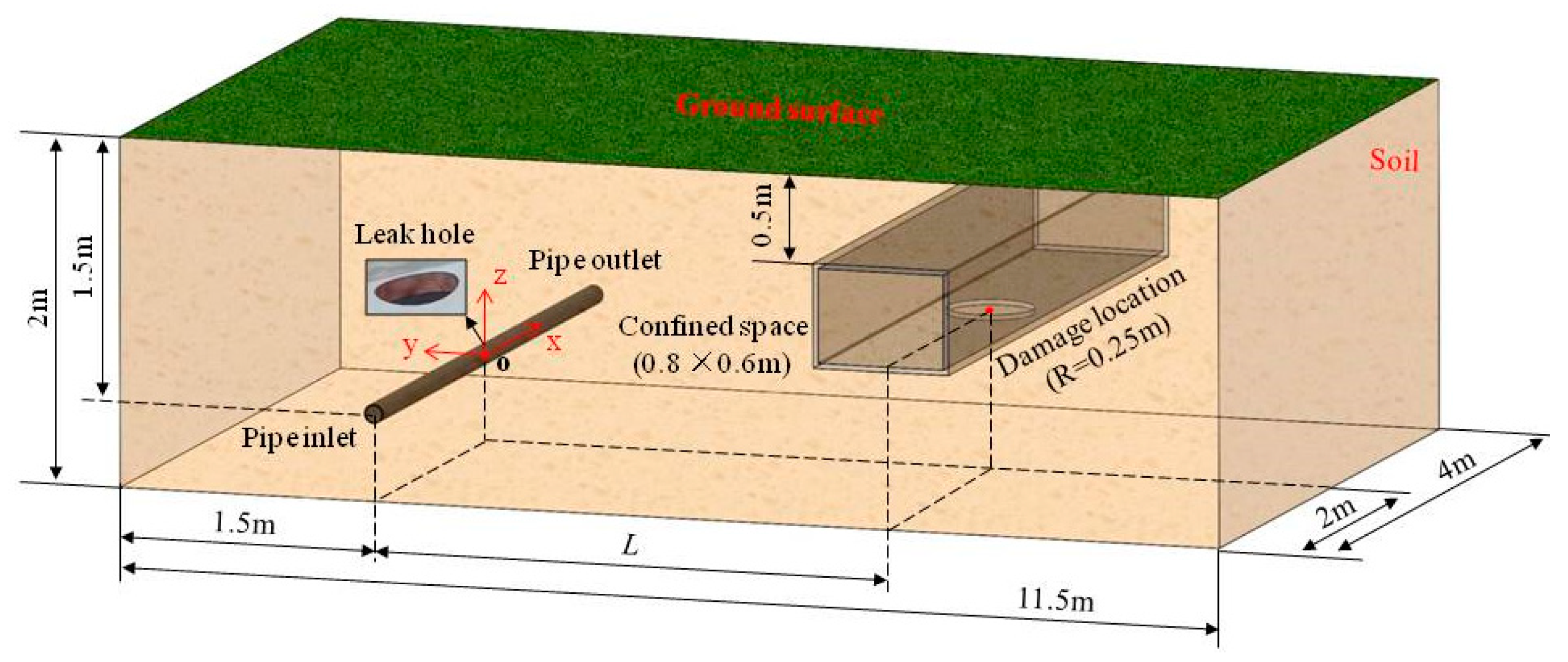
2.1. Physical Model
2.2. Mathematical Model
2.2.1. Basic Conservation Equation
2.2.2. Component Transport Equation
2.2.3. Gas-State Equation
2.2.4. Turbulence Model
2.3. Scenario Design
2.4. Grid Generation and Numerical Method
2.5. Boundary Conditions and Initial Conditions
3. Results and Discussion
3.1. Grid Independence
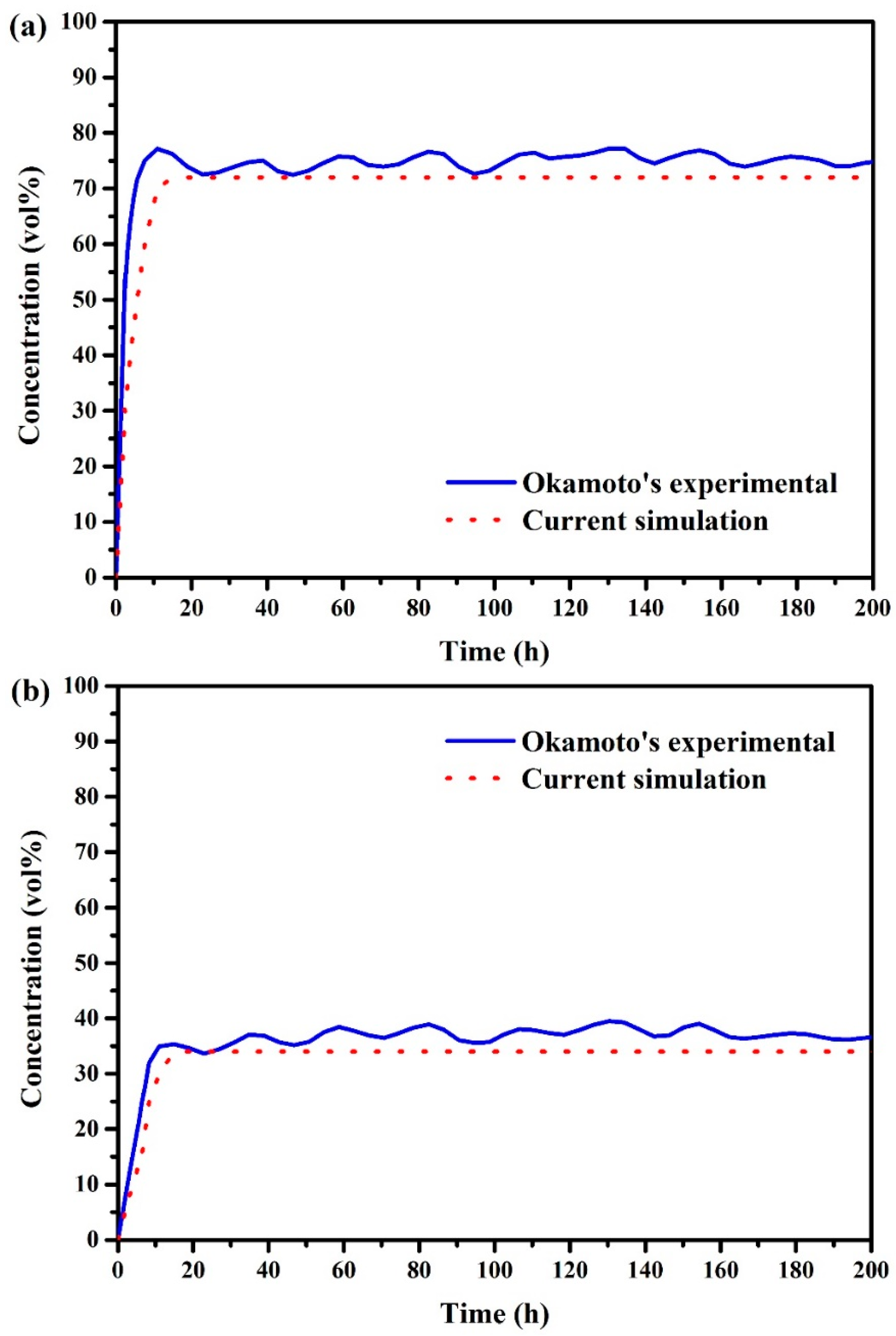
3.2. Model Validation
3.3. Analysis of Gas Leakage and Dispersiong Characteristics
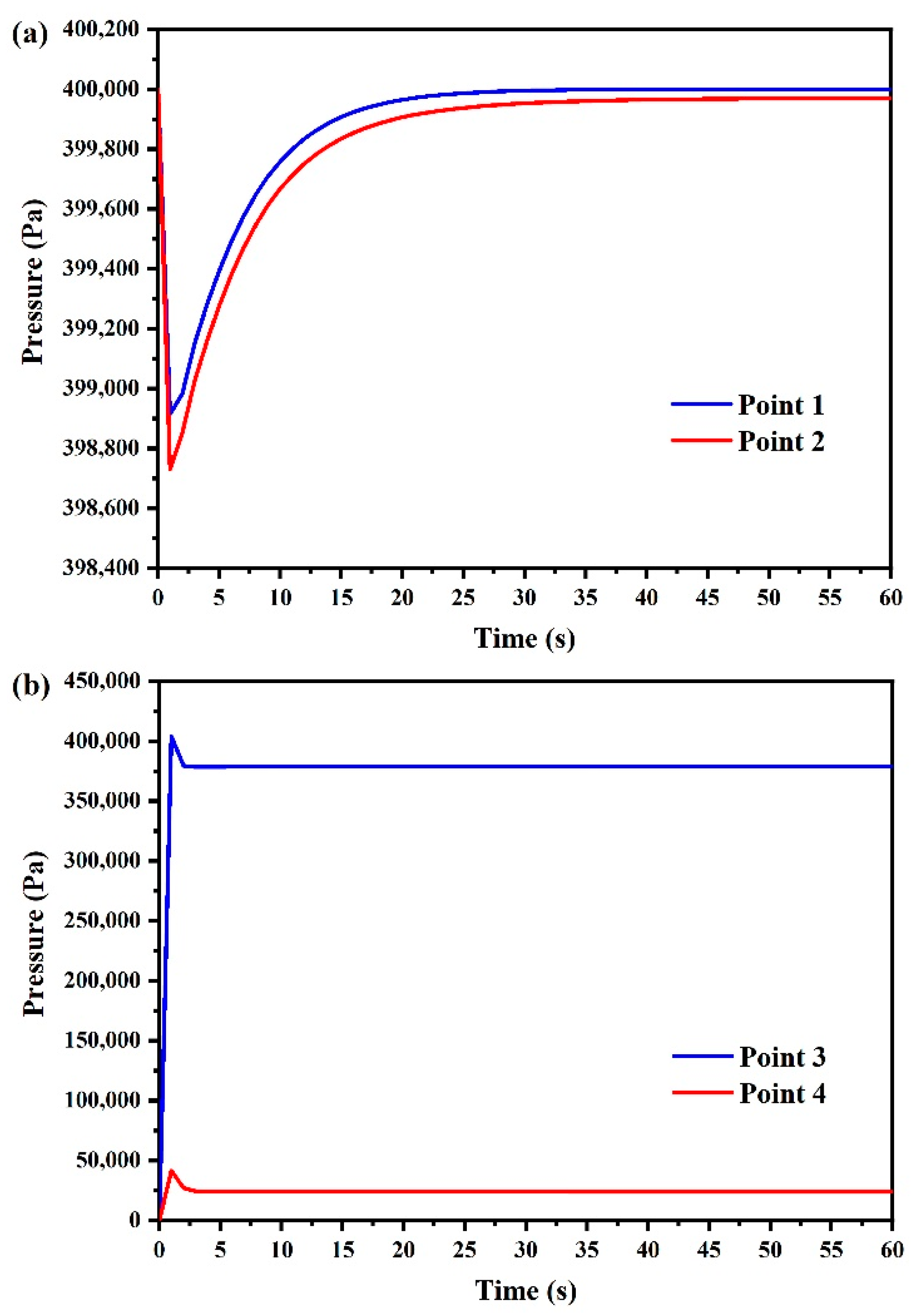
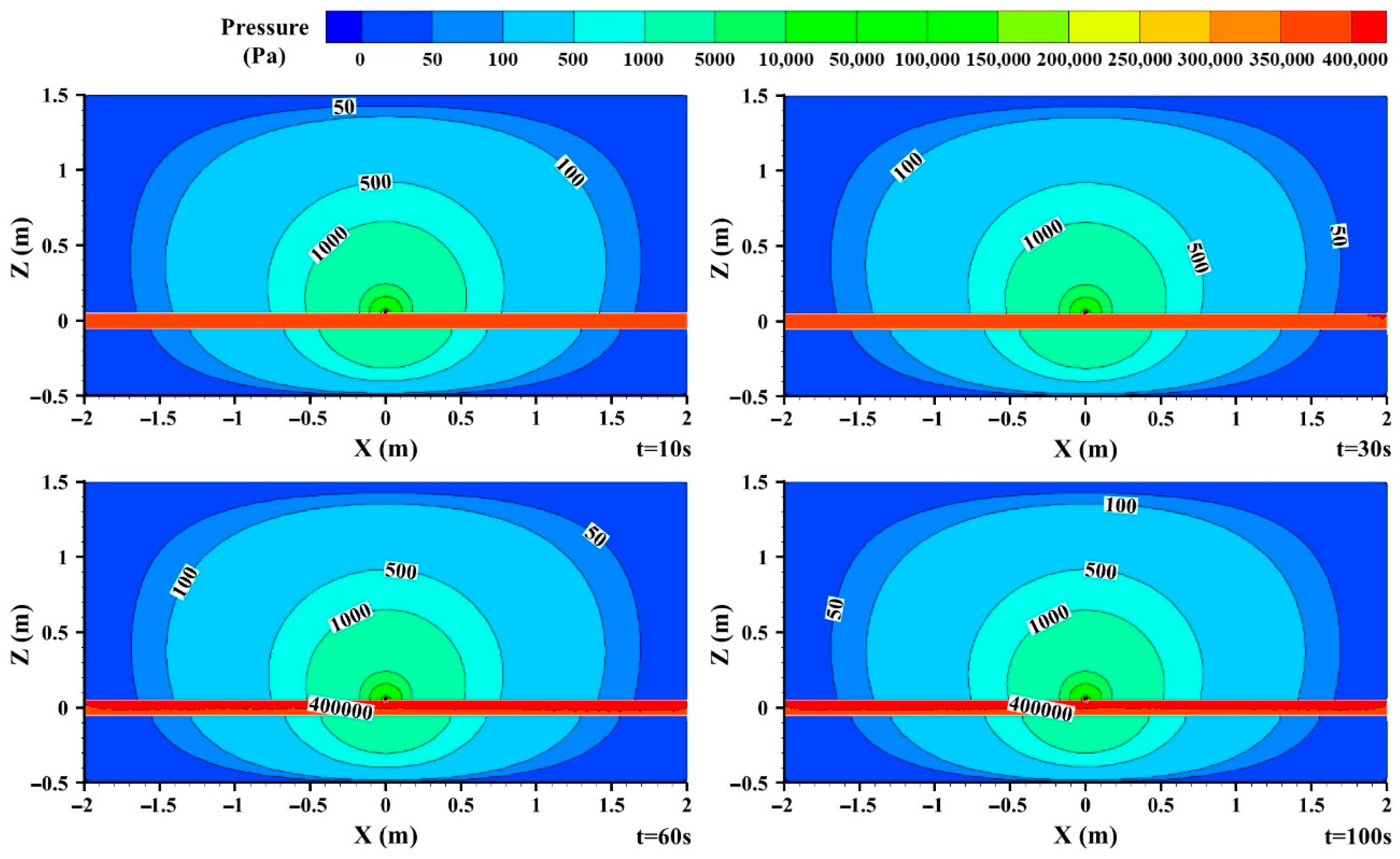
3.3.1. Pressure Distribution
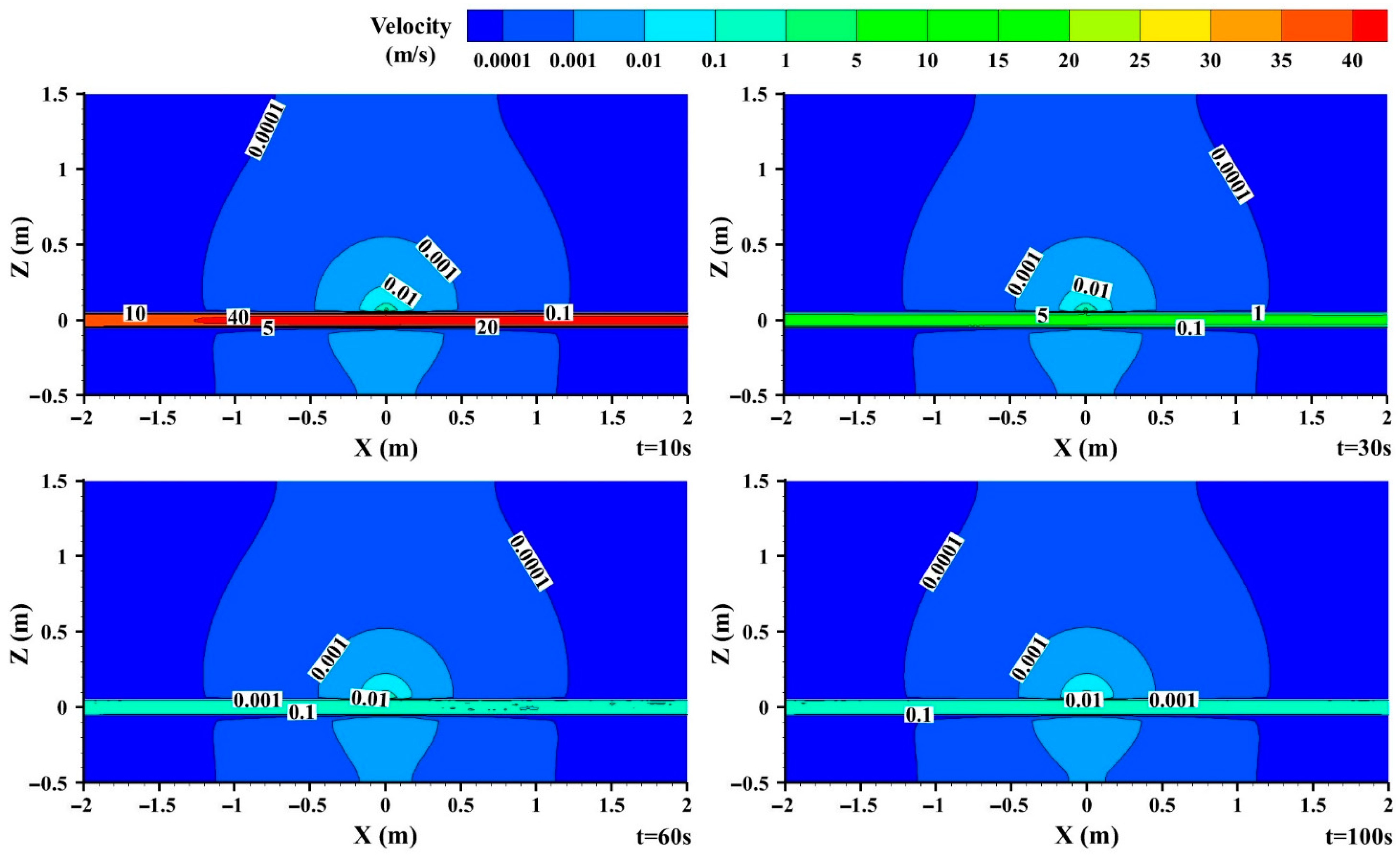
3.3.2. Velocity Distribution
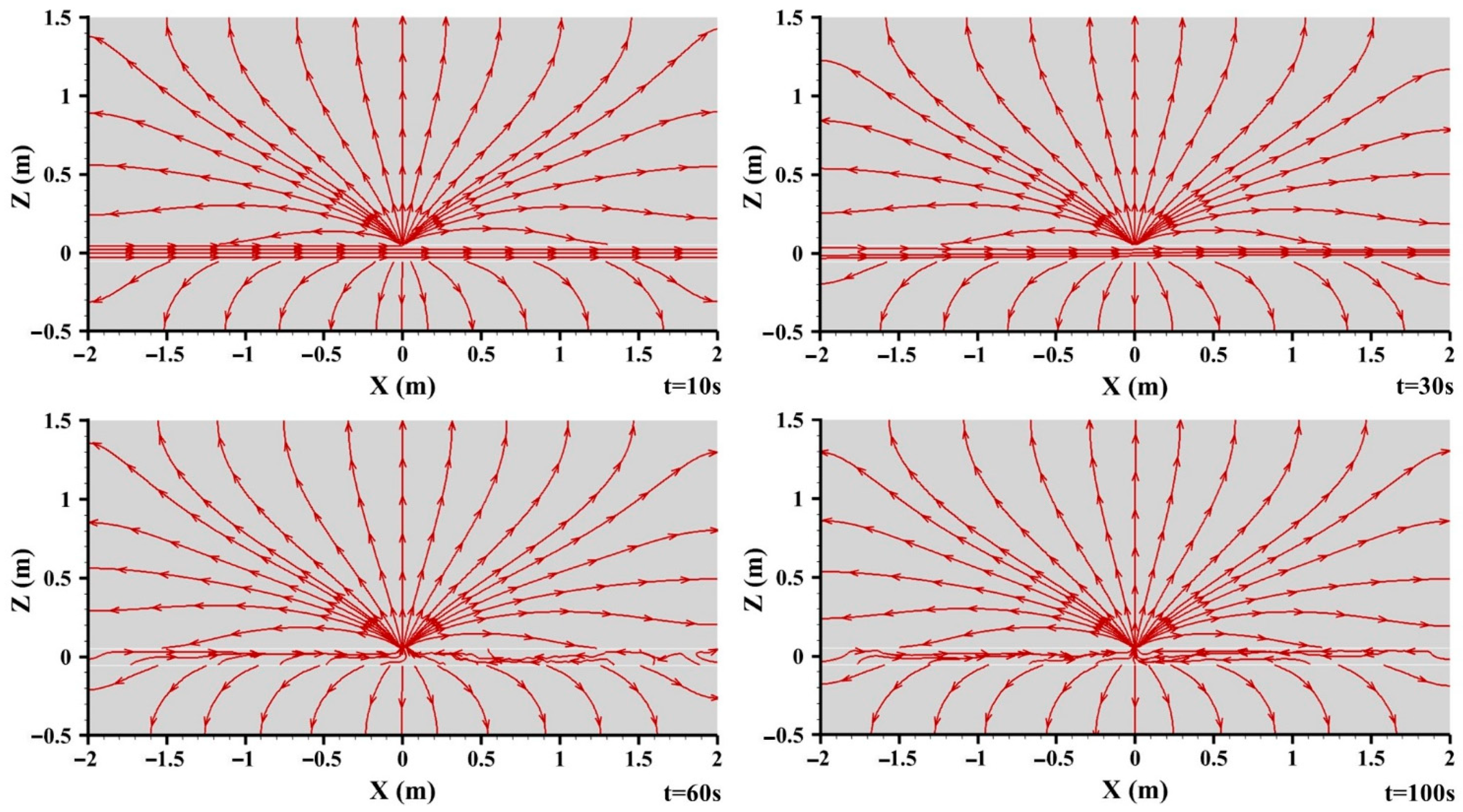
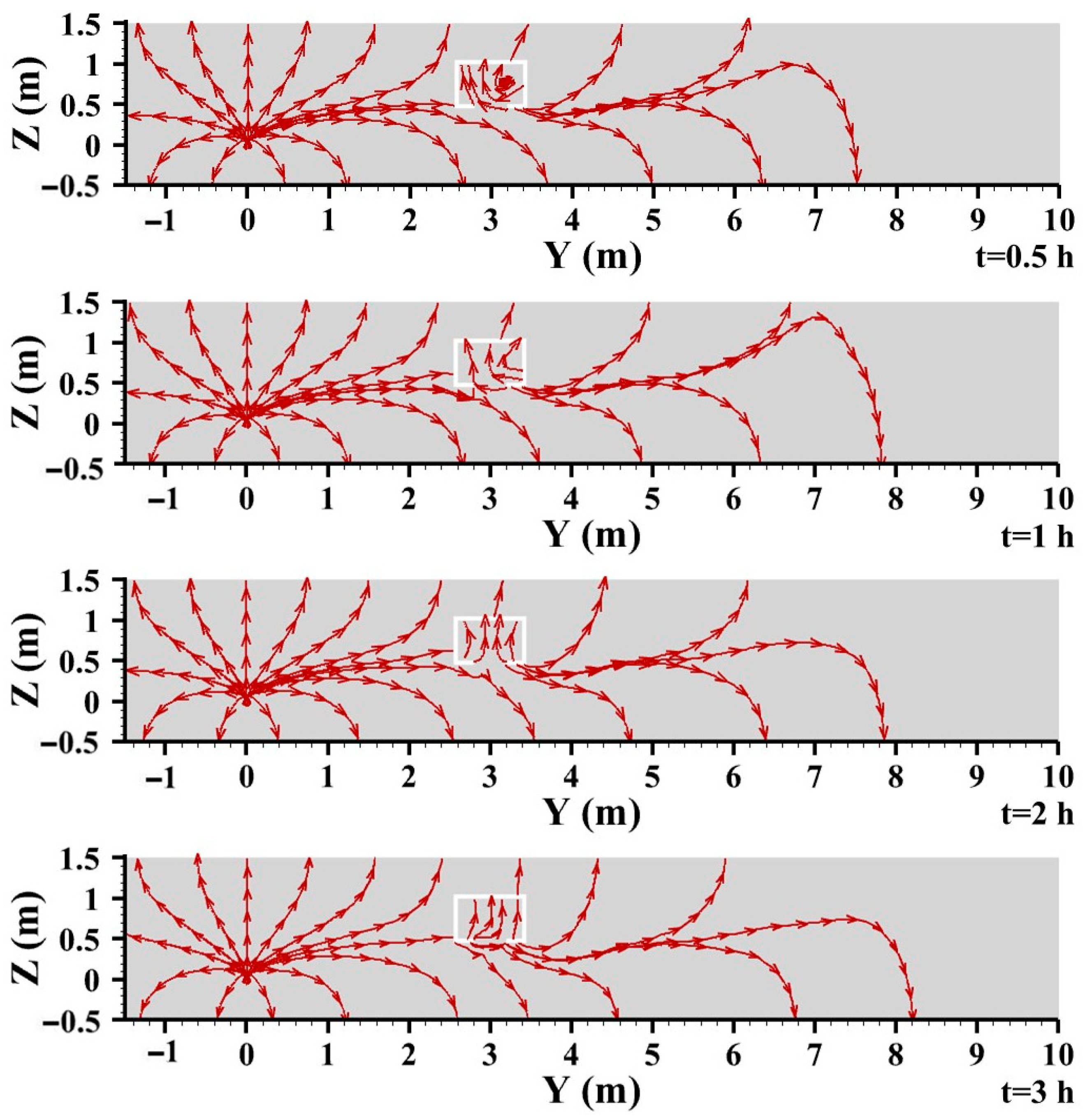
3.3.3. Streamline Distribution
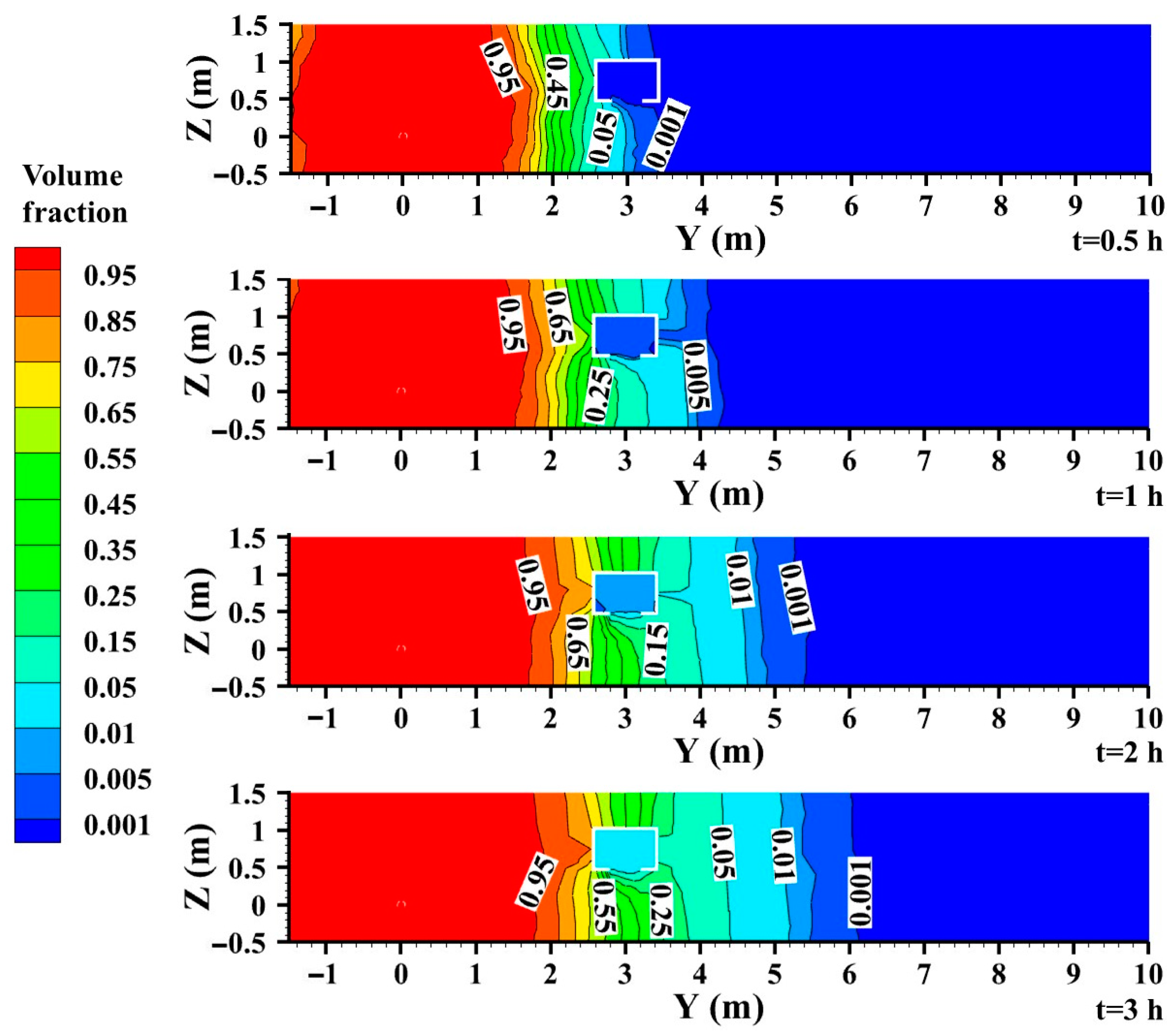
3.3.4. Gas Concentration Distribution
3.4. Determination of Underground Adjacent Confined Space Hazardous Boundary
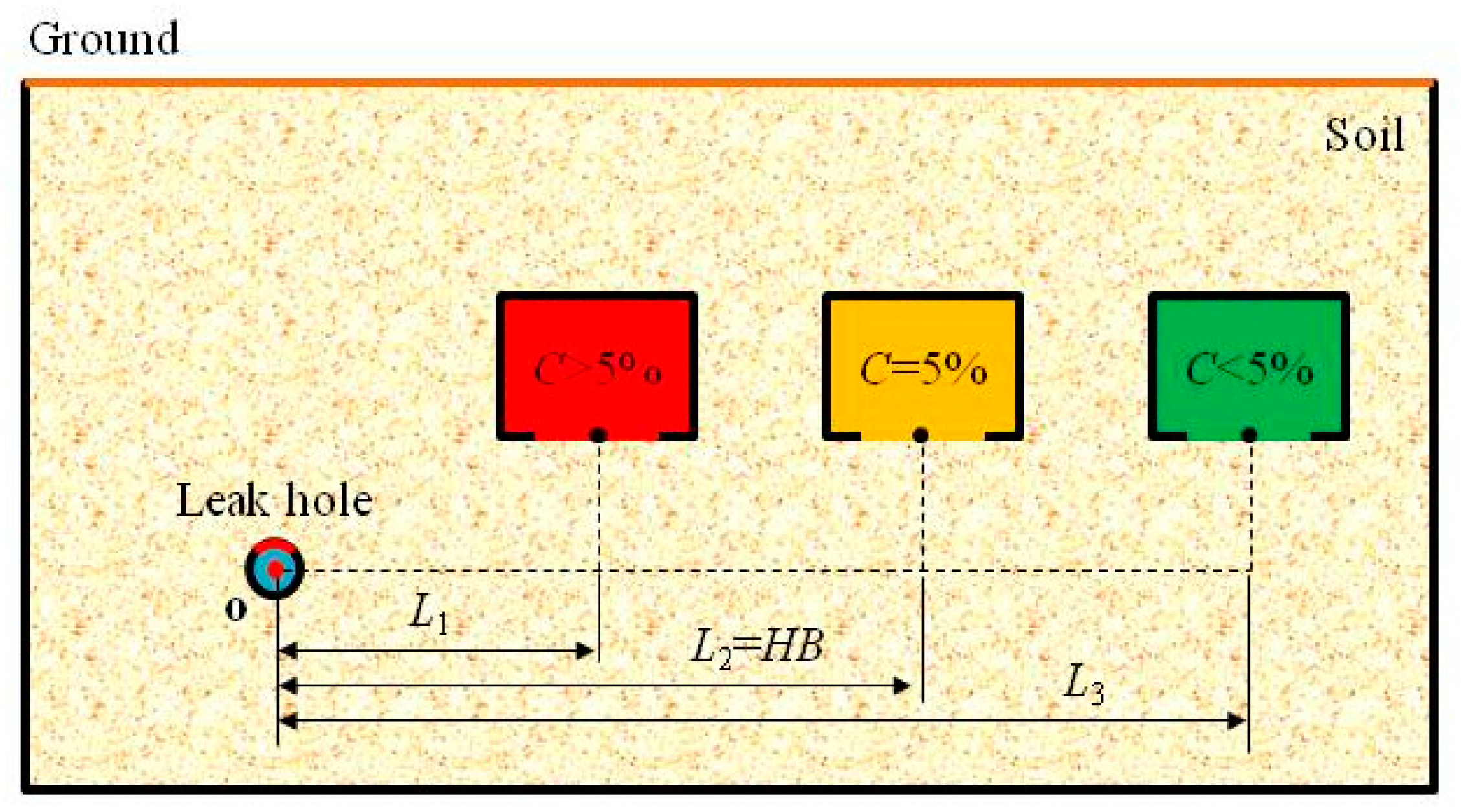
3.4.1. Definition for Hazardous Boundary of Underground Confined Space
3.4.2. Analysis on Influencing Factors of Gas Concentration in Confined Space
3.4.3. Gas Concentration Prediction Model and Hazardous Boundary Calculation Model
- (1)
- Gas concentration prediction model
- (2)
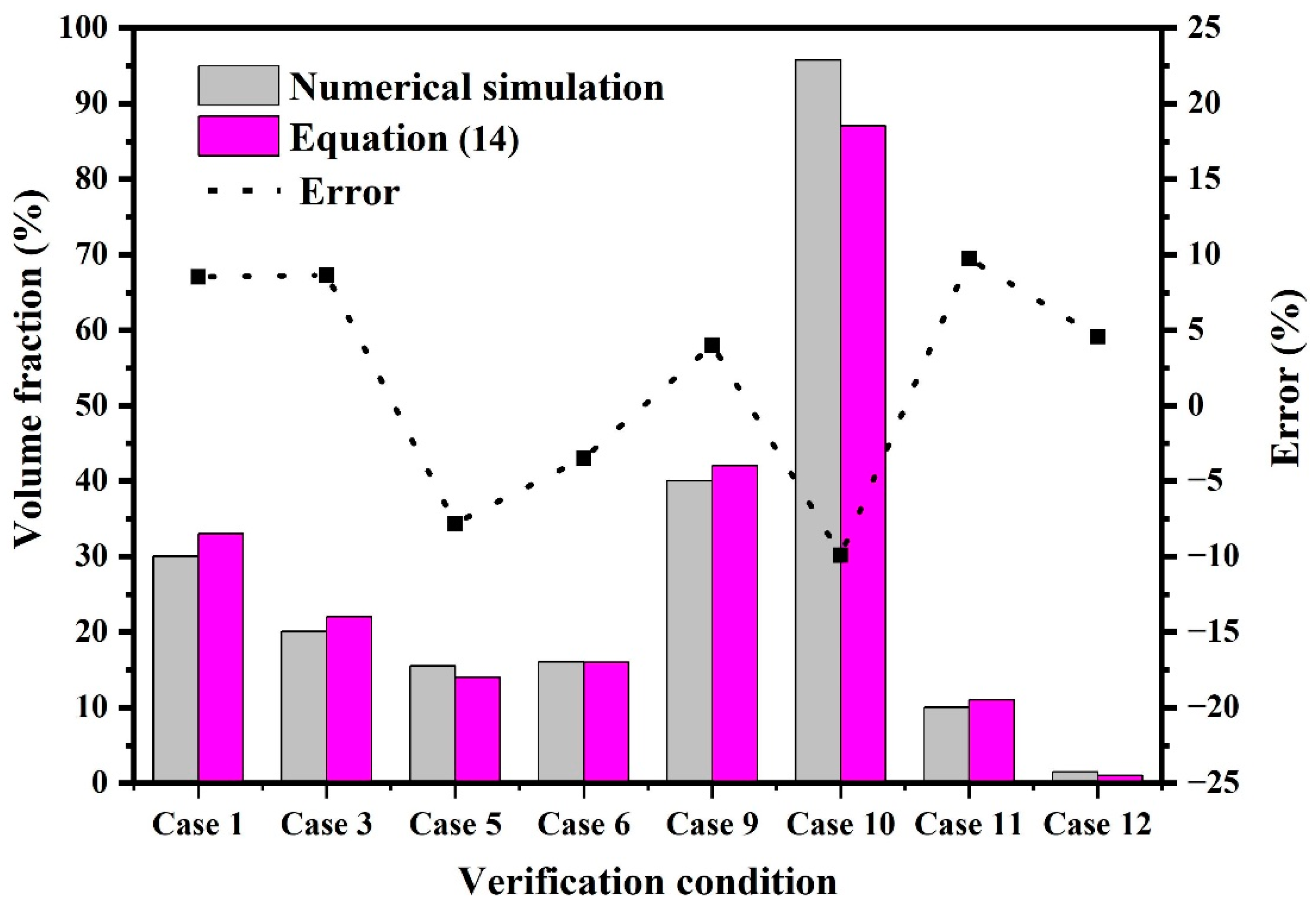
- Reliability verification
- (3)
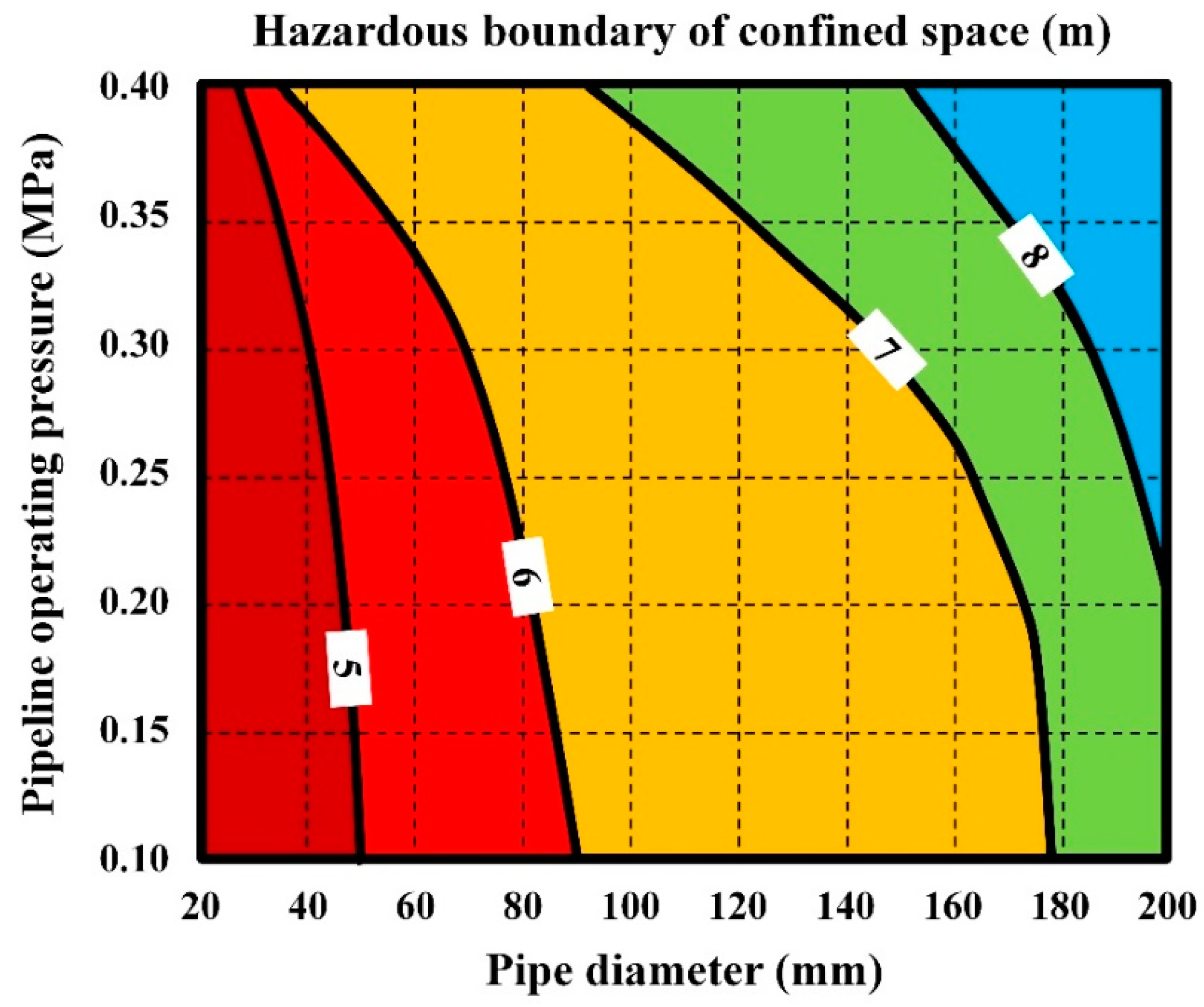
- Hazardous boundary calculation model
4. Conclusions
- (1)
- The buried gas pipeline leakage was affected by soil resistance, and there was no critical flow distribution at the leakage hole. At the initial stage of leakage, the internal and external pressure and velocity distribution of the pipeline near the leakage hole were unstable, reaching a stable state after 60 s, and then the reverse flow phenomenon occurred in the pipeline downstream of the leakage hole.
- (2)
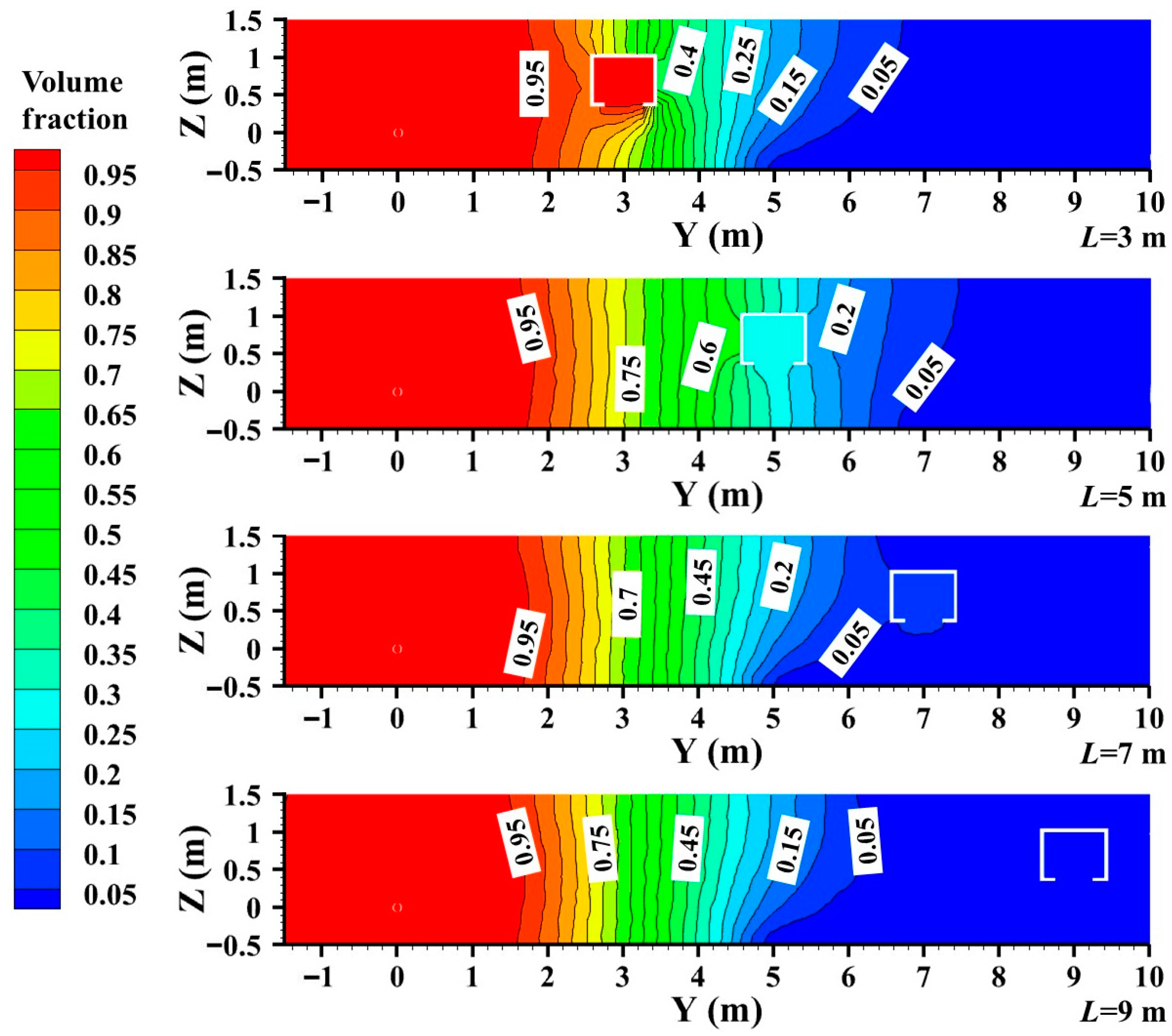
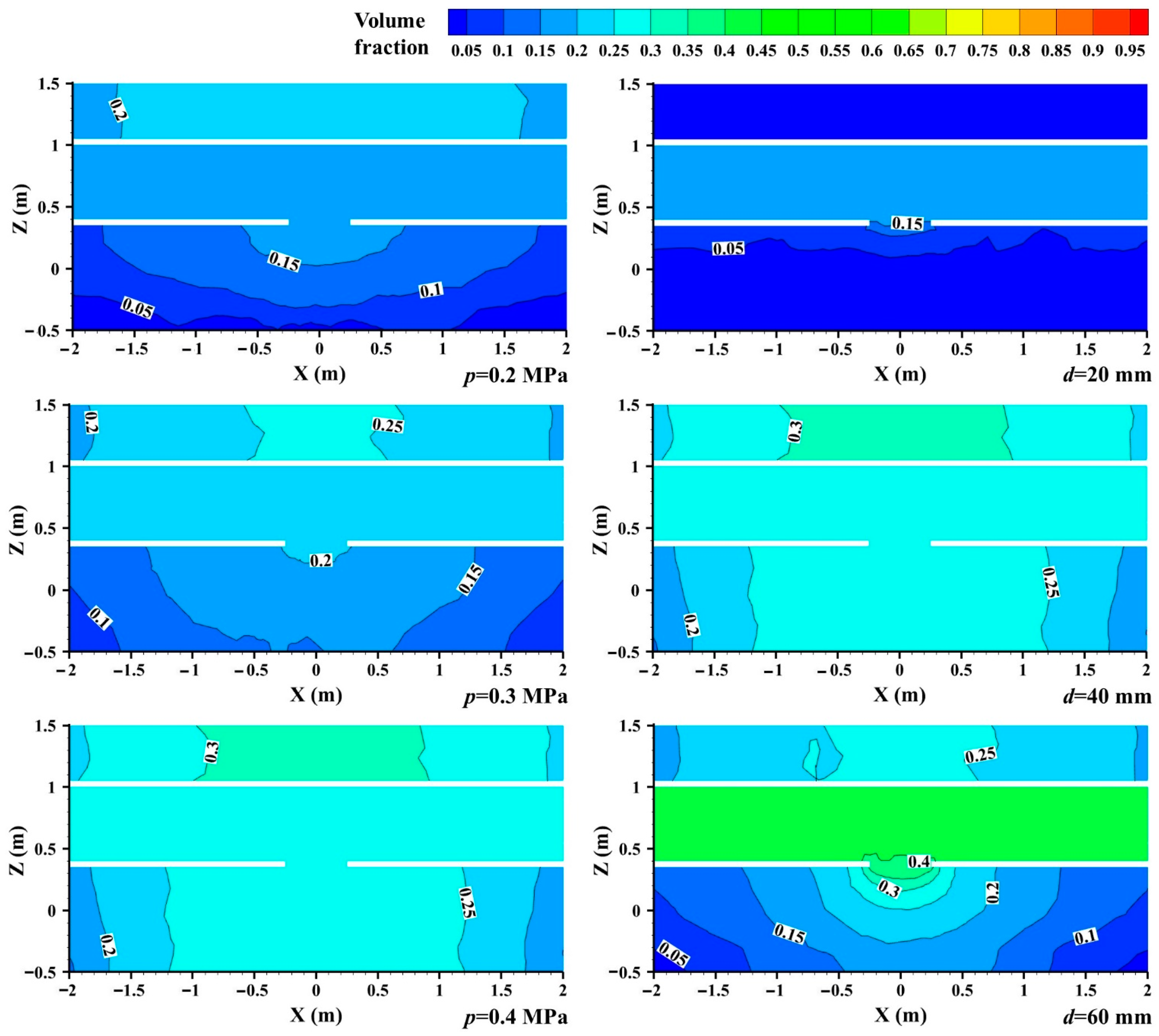
- Increasing the pipeline pressure and leakage size enhanced the gas concentration distribution in the confined space. When the pipeline pressure increased from 0.2 MPa to 0.4 MPa, the gas concentration distribution in the confined space enhanced from 15.51% to 29.98%. When the leak diameter enhanced from 20 mm to 60 mm, the gas concentration expanded from 16.05% to 40.02%. Increasing the minimum construction distance between the buried gas pipeline and the confined space reduced the gas concentration distribution in the confined space. When the minimum construction distance increased from 3 m to 9 m, the gas concentration distribution in the confined space decreased from 90.21% to 0.88%.
- (3)
- The prediction model for gas concentration in the underground adjacent closed space of the buried gas pipeline leakage was established, and the average error was 4.97%, which can realize the calculation of gas concentration distribution in the closed space under different leakage conditions.
- (4)
- Based on the principle of heavy risk, the calculation model of the hazardous boundary in a confined space was deduced and established by using the gas concentration prediction model, and the hazardous boundary drawing board was further drawn, which realized the rapid determination of the safety distance between the design and construction of a buried gas pipeline, and provided a more scientific basis for the design of the safety distance between a gas pipeline and a confined space in underground engineering construction.
- (5)
- This paper studied the continuous leakage and diffusion process of gas after the leakage of buried pipelines, and analyzed the distribution and danger of gas entering the confined space. However, the gas diffusion process after closing the valve in case of a leakage accident has not been paid attention to yet. The next step is to analyze the free dissipation process of gas after cutting off the valve at the upstream gas supply end, and effectively defining the hazard duration and range.
Author Contributions
Funding
Conflicts of Interest
References
- Boswell, R.; Collett, T.S. Current perspectives on gas hydrate resources. Energy Environ. Sci. 2011, 4, 1206–1215. [Google Scholar] [CrossRef]
- You, K.; Flemings, P.B.; Malinverno, A.; Collett, T.S.; Darnell, K. Mechanisms of methane hydrate formation in geological systems. Rev. Geophys. 2019, 57, 1146–1196. [Google Scholar] [CrossRef]
- Aguilera, R.F. The role of natural gas in a low carbon Asia Pacific. Appl. Energy 2014, 113, 1795–1800. [Google Scholar] [CrossRef]
- Biezma, M.V.; Agudo, D.; Barron, G. A fuzzy logic method: Predicting pipeline external corrosion rate. Int. J. Press. Vessel. Pip. 2018, 163, 55–62. [Google Scholar] [CrossRef]
- Parvini, M.; Gharagouzlou, E. Gas leakage consequence modeling for buried gas pipelines. J. Loss Prev. Process Ind. 2015, 37, 110–118. [Google Scholar] [CrossRef]
- Bu, F.X.; Liu, Y.; Chen, S.Q.; Wu, J.; Guan, B.; Zhang, N.; Lin, X.Q.; Liu, L.; Cheng, T.C.; Shi, Z.C. Real scenario analysis of buried natural gas pipeline leakage based on soil-atmosphere coupling. Int. J. Press. Vessel. Pip. 2022, 199, 104713. [Google Scholar] [CrossRef]
- Fan, Y.; van Perry, S.; Klemes, J.J.; Lee, C.T. A review on air emissions assessment: Transportation. J. Clean. Prod. 2018, 194, 673–684. [Google Scholar] [CrossRef]
- Badida, P.; Balasubramaniam, Y.; Jayaprakash, J. Risk evaluation of oil and natural gas pipelines due to natural hazards using fuzzy fault tree analysis. J. Nat. Gas Sci. Eng. 2019, 66, 284–292. [Google Scholar] [CrossRef]
- Hoeks, J. Effect of leaking natural gas on soil and vegetation in urban areas. Soil Sci. 1975, 120, 317–318. [Google Scholar] [CrossRef]
- Lovreglio, R.; Ronchi, E.; Maragkos, G.; Beji, T.; Merci, B. A dynamic approach for the impact of a toxic gas dispersion hazard considering human behaviour and dispersion modelling. J. Hazard. Mater. 2016, 318, 758–771. [Google Scholar] [CrossRef]
- Wakoh, H.; Hirano, T. Diffusion of leaked flammable-gas in soil. J. Loss Prev. Process Ind. 2011, 4, 260–264. [Google Scholar] [CrossRef]
- Houssin-Agbomson, D.; Blanchetiere, G.; McCollum, D. Consequences of a 12-mm diameter high pressure gas release on a buried pipeline. Experimental setup and results. J. Loss Prev. Process Ind. 2018, 54, 183–189. [Google Scholar] [CrossRef]
- Pokhrel, D.; Hettiaratchi, P.; Kumar, S. Methane diffusion coefficient in compost and soil-compost mixtures in gas phase biofilter. Chem. Eng. J. 2011, 169, 200–206. [Google Scholar] [CrossRef]
- Wilkening, H.; Baraldi, D. CFD modelling of accidental hydrogen release from pipelines. Int. J. Hydrogen Energy 2007, 32, 2206–2215. [Google Scholar] [CrossRef]
- Bezaatpour, J.; Fatehifar, E.; Rasoulzadeh, A. CFD investigation of natural gas leakage and propagation from buried pipeline for anisotropic and partially saturated multilayer soil. J. Clean. Prod. 2020, 277, 123940. [Google Scholar] [CrossRef]
- Bu, F.X.; Chen, S.Q.; Liu, Y.; Guan, B.; Wang, X.W.; Shi, Z.C.; Hao, G.W. CFD analysis and calculation models establishment of leakage of natural gas pipeline considering real buried environment. Energy Rep. 2022, 8, 3789–3808. [Google Scholar] [CrossRef]
- Bu, F.X.; Liu, Y.; Chen, S.Q.; Xu, Z.; Liu, Y.B.; Jiang, M.H.; Guan, B. Analysis and prediction of methane invasion distance considering real ground boundary. ACS Omega 2021, 6, 29111–29125. [Google Scholar] [CrossRef]
- Pontiggia, M.; Derudi, M.; Alba, M.; Scaioni, M.; Rota, R. Hazardous gas releases in urban areas: Assessment of consequences through CFD modelling. J. Hazard. Mater. 2010, 176, 589–596. [Google Scholar] [CrossRef]
- Sklavounos, S.; Rigas, F. Estimation of safety distances in the vicinity of fuel gas pipelines. J. Loss Prev. Process Ind. 2006, 19, 24–31. [Google Scholar] [CrossRef]
- Tan, Q.; Feng, G.L.; Yuan, H.Y.; Su, G.F.; Fu, M.; Zhu, Y.P. Applied research for the gas pipeline installation and the monitoring method for the safety of the adjacent under-ground spaces. J. Saf. Environ. 2019, 19, 902–908. [Google Scholar]
- Ebrahimi-Moghadam, A.; Farzaneh-Gord, M.; Deymi-Dashtebayaz, M. Correlations for estimating natural gas leakage from above-ground and buried urban distribution pipelines. J. Nat. Gas Sci. Eng. 2016, 34, 185–196. [Google Scholar] [CrossRef]
- Ebrahimi-Moghadam, A.; Farzaneh-Gord, M.; Arabkoohsar, A.; Moghadam, A.J. CFD analysis of natural gas emission from damaged pipelines: Correlation development for leakage estimation. J. Clean. Prod. 2018, 199, 257–271. [Google Scholar] [CrossRef]
- Water Supply and Drainage Design Manual Volume 5, Urban Drainage; China Construction Industry Press: Beijing, China, 1986.
- Montiel, H.; Vílchez, J.A.; Casal, J.; Arnaldos, J. Mathematical modelling of accidental gas releases. J. Hazard. Mater. 1998, 59, 211–233. [Google Scholar] [CrossRef]
- Luo, J.H.; Zheng, M.; Zhao, X.W.; Huo, C.Y.; Yang, L. Simplified expression for estimating release rate of hazardous gas from a hole on high-pressure pipelines. J. Loss Prev. Process Ind. 2006, 19, 362–366. [Google Scholar] [CrossRef]
- Deng, Y.J.; Hu, H.B.; Yu, B.; Sun, D.L.; Hou, L.; Liang, Y.T. A method for simulating the release of natural gas from the rupture of high-pressure pipelines in any terrain. J. Hazard. Mater. 2018, 342, 418–428. [Google Scholar] [CrossRef]
- Liu, A.H.; Huang, J.; Li, Z.W.; Chen, J.Y.; Huang, X.F.; Chen, K.; Xu, W.B. Numerical simulation and experiment on the law of urban natural gas leakage and diffusion for different building layouts. J. Nat. Gas Sci. Eng. 2018, 54, 1–10. [Google Scholar] [CrossRef]
- Pereira, T.W.C.; Marques, F.B.; Pereira, F.D.R.; Ribeiro, D.D.; Rocha, S.M.S. The influence of the fabric filter layout of in a flow mass filtrate. J. Clean. Prod. 2016, 111, 117–124. [Google Scholar] [CrossRef]
- Bu, F.X.; Liu, Y.; Liu, Y.B.; Xu, Z.; Chen, S.Q.; Jiang, M.H.; Guan, B. Leakage diffusion characteristics and harmful boundary analysis of buried natural gas pipeline under multiple working conditions. J. Nat. Gas Sci. Eng. 2021, 94, 104047. [Google Scholar] [CrossRef]
- Wang, X.M.; Tan, Y.F.; Zhang, T.T.; Xiao, R.; Yu, K.C.; Zhang, J.D. Numerical study on the diffusion process of pinhole leakage of natural gas from underground pipelines to the soil. J. Nat. Gas Sci. Eng. 2021, 87, 1–14. [Google Scholar] [CrossRef]
- GB 50028-2006; Code for Design of City Gas Engineering. Codeofchina Inc.: Beijing, China, 2022.
- Okamoto, H.; Gomi, Y. Empirical research on diffusion behavior of leaked gas in the ground. J. Loss Prev. Process Ind. 2011, 24, 531–540. [Google Scholar] [CrossRef]
- Torii, S. Numerical simulation of turbulent jet diffusion flames by means of two-equation heat transfer model. Energy Convers. Manag. 2001, 42, 1953–1962. [Google Scholar] [CrossRef]
- Jacobsen, Ø.; Magnussen, B.F. 3-D numerical simulation of heavy gas dispersion. J. Hazard. Mater. 1987, 16, 215–230. [Google Scholar] [CrossRef]
- Rieger, J.; Weiss, C.; Rummer, B. Modelling and control of pollutant formation in blast stoves. J. Clean. Prod. 2015, 88, 254–261. [Google Scholar] [CrossRef]
- Zhang, J.W.; Yin, X.X.; Xin, Y.A.; Zhang, J.; Zheng, X.P.; Jiang, C.M. Numerical Investigation on Three-dimensional Dispersion and Conversion Behaviors of Silicon Tetrachloride Release in the Atmosphere. J. Hazard. Mater. 2015, 288, 1–16. [Google Scholar] [CrossRef]
- Nahavandi, N.N.; Farzaneh-Gord, M. Numerical simulation of filling process of natural gas onboard vehicle cylinder. J. Braz. Soc. Mech. Sci. Eng. 2014, 36, 837–846. [Google Scholar] [CrossRef]
- Lu, J.S.; Xu, S.; Deng, J.J.; Wu, W.F.; Wu, H.X.; Yang, Z.B. Numerical prediction of temperature field for cargo containment system (CCS) of LNG carriers during pre-cooling operations. J. Nat. Gas Sci. Eng. 2016, 29, 382–391. [Google Scholar] [CrossRef]
- Liu, Y.; Bu, F.X.; Chen, S.Q.; Jiang, M.H. Investigating effect of polymer concentrations on separation performance of hydrocyclone by sensitivity analysis. Energy Sci. Eng. 2021, 9, 1202–1215. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, L.X.; Reifsnyder, S.; Gao, S.; Jiang, M.Z.; Huang, X.Q.; Jiang, M.H.; Liu, Y.; Rosso, D. Analysis of Hydrocyclone Geometry via Rapid Optimization based on Computational Fluid Dynamics. Chem. Eng. Technol. 2021, 44, 1693–1707. [Google Scholar] [CrossRef]
- Nordlund, M.; Stanic, M.; Kuczaj, A.K.; Frederix, E.M.A.; Geurts, B.J. Improved PISO algorithms for modeling density varying flow in conjugate fluid-porous domains. J. Comput. Phys. 2016, 306, 199–215. [Google Scholar] [CrossRef]
- Jarrahian, A.; Heidaryan, E. A new cubic equation of state for sweet and sour natural gases even when composition is unknown. Fuel 2014, 134, 333–342. [Google Scholar] [CrossRef]
- Sarkar, A.; Dey, P.; Rai, R.N.; Saha, S.C. A comparative study of multiple regression analysis and back propagation neural network approaches on plain carbon steel in submerged-arc welding. Sadhana 2016, 27, 82–89. [Google Scholar] [CrossRef]


| Case | p (MPa) | d (mm) | L (m) |
|---|---|---|---|
| 1 | 0.4 | 40 | 5 |
| 2 | 0.35 | 40 | 5 |
| 3 | 0.3 | 40 | 5 |
| 4 | 0.25 | 40 | 5 |
| 5 | 0.2 | 40 | 5 |
| 6 | 0.4 | 20 | 5 |
| 7 | 0.4 | 30 | 5 |
| 8 | 0.4 | 50 | 5 |
| 9 | 0.4 | 60 | 5 |
| 10 | 0.4 | 40 | 3 |
| 11 | 0.4 | 40 | 7 |
| 12 | 0.4 | 40 | 9 |
| Boundary Location | Boundary Type |
|---|---|
| Pipe inlet | Pressure inlet |
| Pipe outlet | Pressure outlet |
| Soil boundary | Pressure outlet |
| Local encryption boundary | Interface |
| Leakage hole of buried pipeline and confined space | Interior |
| Confined space sidewall | Wall |
| Grid Level | Grid Number | Leakage Rate | Error |
|---|---|---|---|
| 1 | 514,784 | 0.004738 kg/s | / |
| 2 | 1,133,662 | 0.004456 kg/s | 7.66% |
| 3 | 1,502,339 | 0.004352 kg/s | 2.39% |
| 4 | 1,887,451 | 0.004319 kg/s | 0.76% |
| Buried Medium | Porosity (%) | Permeability (m2) | Diffusion Coefficient (m2/s) |
|---|---|---|---|
| Asphalt | 5.0 | 0.4 | 0.21 |
| Crushed stone | 23.5 | 4.1 | 2.23 |
| Pit sand | 17.0 | 2.0 | 0.66 |
| Coefficient | Estimated Value | Confidence Interval |
|---|---|---|
| −247.4878 | [−367.6461, −127.3294] | |
| −9.3133 | [−15.0174, −3.6092] | |
| 3832.7156 | [1581, 6085] | |
| 80.0360 | [43.3944, 116.6775] | |
| R2 = 0.9109 F = 1.4350 × 103 P = 0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liu, Y.; Liang, H.; Xu, Z.; Bu, F.; Zhang, J.; Du, H.; Wang, Y.; Chen, S. Leakage Analysis and Hazardous Boundary Determination of Buried Gas Pipeline Considering Underground Adjacent Confined Space. Energies 2022, 15, 6859. https://doi.org/10.3390/en15186859
Wang Z, Liu Y, Liang H, Xu Z, Bu F, Zhang J, Du H, Wang Y, Chen S. Leakage Analysis and Hazardous Boundary Determination of Buried Gas Pipeline Considering Underground Adjacent Confined Space. Energies. 2022; 15(18):6859. https://doi.org/10.3390/en15186859
Chicago/Turabian StyleWang, Zhixue, Yongbin Liu, Haibin Liang, Zhe Xu, Fanxi Bu, Jina Zhang, Hua Du, Yan Wang, and Shuangqing Chen. 2022. "Leakage Analysis and Hazardous Boundary Determination of Buried Gas Pipeline Considering Underground Adjacent Confined Space" Energies 15, no. 18: 6859. https://doi.org/10.3390/en15186859
APA StyleWang, Z., Liu, Y., Liang, H., Xu, Z., Bu, F., Zhang, J., Du, H., Wang, Y., & Chen, S. (2022). Leakage Analysis and Hazardous Boundary Determination of Buried Gas Pipeline Considering Underground Adjacent Confined Space. Energies, 15(18), 6859. https://doi.org/10.3390/en15186859





