Power-Line Partial Discharge Recognition with Hilbert–Huang Transform Features
Abstract
:1. Introduction
- The possibility of HHT feature application in power-line PD recognition is explored. The HHT features were extracted from original signals and filtered.
- The filtered HHT feature was combined with peak features to train the light gradient boosting machine (LightGBM). The effectiveness of the HHT feature was then tested with the features used by the winner of a contest.
- An enhanced LightGBM methodology used for power-line PD recognition, based on HHT features, was constructed.
2. HHT and LightGBM Theories
2.1. HHT
2.2. LightGBM
3. PD Recognition Method with HHT Features
| Algorithm 1. PD recognition method with Hilbert–Huang Transform (HHT) features. |
| Input: dataset |
| Output: prediction for testing set |
| Initialize: LightGBM characteristics |
| Step 1: Flatten the signals of training set. |
| Step 2: Perform empirical mode decomposition for training and testing sets. |
| Step 3: Extract HHT features and peak features from training and testing sets. |
| Step 4: Filter the HHT features. |
| Step 5: Train the models and perform prediction. |
3.1. Step 1: Flattening the Original Signal
| Algorithm 2. Flatten the signal [20]. |
3.2. Step 2: EMD with Segmentation and Parallel Computing
3.3. Step 3: Obtaining the Hilbert Spectrum
3.4. Step 4: Filtering Features
3.5. Final Training
4. Experiments and Results
4.1. Contest and Dataset Description
4.2. Experiment and Test
4.2.1. Extracting the Features
4.2.2. Verifying the Effectiveness of the Features
4.2.3. Training with All 10 Features
4.2.4. Leave-One-Out Experiment
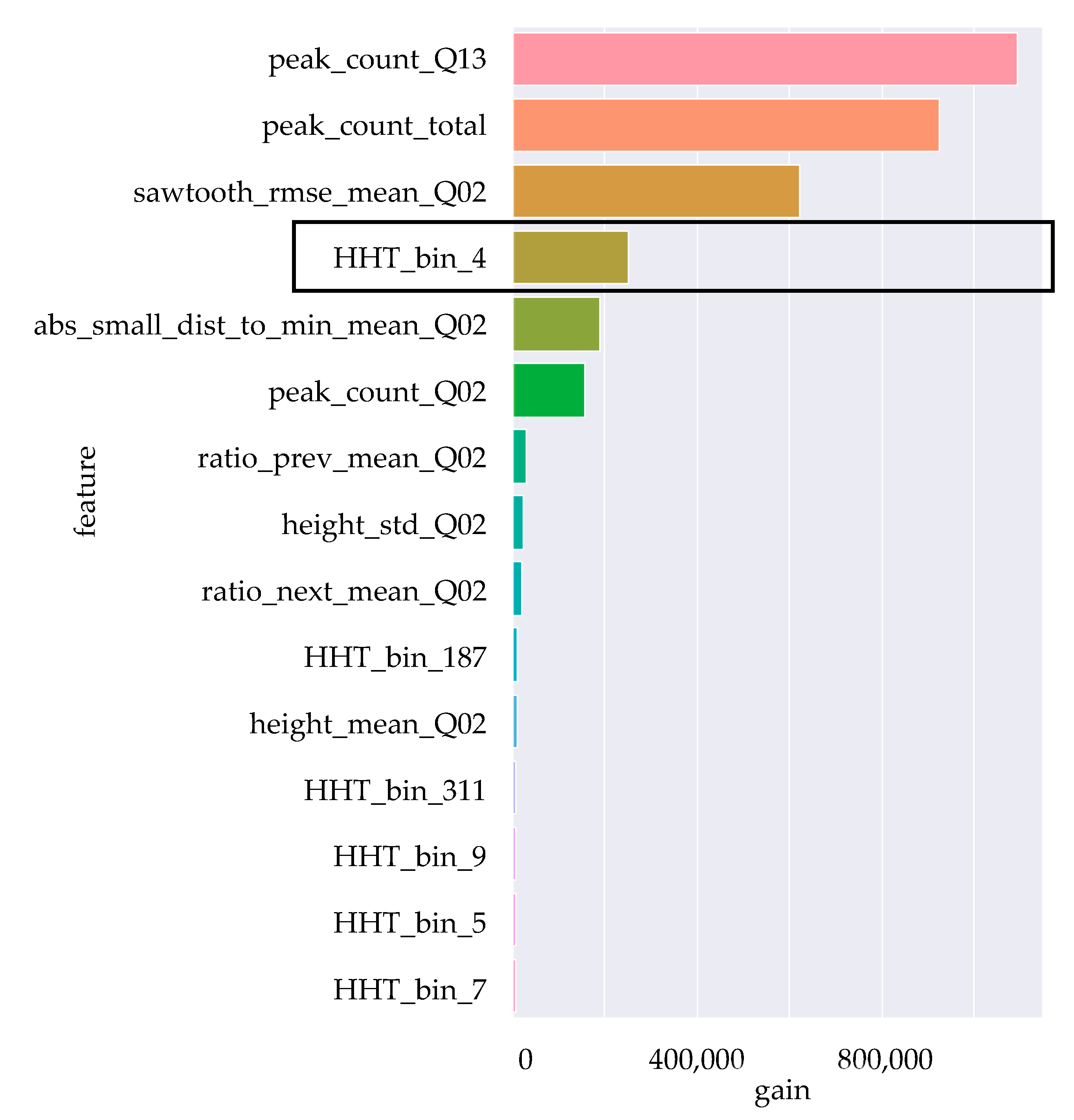
4.2.5. Decision-Tree Gain Analysis
4.3. Final Description of Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PD | Partial Discharge |
| WT | Wavelet Transform |
| GIS | Gas-Insulated Switchgear |
| LSTM | Long Short-Term Memory |
| HHT | Hilbert–Huang Transform |
| LightGBM | Light Gradient Boosting Machine |
| EMD | Empirical Mode Decomposition |
| IMF | Intrinsic Mode Functions |
| XGBoost | eXtreme Gradient Boosting |
| MCC | Matthews Correlation Coefficient |
References
- Karthikeyan, B.; Gopal, S.; Venkatesh, S. ART 2—An unsupervised neural network for PD pattern recognition and classification. Expert Syst. Appl. 2006, 31, 345–350. [Google Scholar] [CrossRef]
- Peng, X.; Yang, F.; Wang, G.; Wu, Y.; Li, L.; Li, Z.; Bhatti, A.A.; Zhou, C.; Hepburn, D.M.; Reid, A.J.; et al. A Convolutional Neural Network-Based Deep Learning Methodology for Recognition of Partial Discharge Patterns from High-Voltage Cables. IEEE Trans. Power Deliv. 2019, 34, 1460–1469. [Google Scholar] [CrossRef]
- Karimi, M.; Majidi, H.; MirSaeedi, M.; Arefi, M.; Oskuoee, M. A Novel Application of Deep Belief Networks in Learning Partial Discharge Patterns for Classifying Corona, Surface, and Internal Discharges. IEEE Trans. Ind. Electron. 2020, 67, 3277–3287. [Google Scholar] [CrossRef]
- Song, H.; Dai, J.; Sheng, G.; Jiang, X. GIS partial discharge pattern recognition via deep convolutional neural network under complex data source. IEEE Trans. Dielectr. Electr. Insul. 2018, 5, 678–685. [Google Scholar] [CrossRef]
- Li, J.; Jiang, T.; Wang, C.; Cheng, C. Optimization of UHF Hilbert Antenna for Partial Discharge Detection of Transformers. IEEE Trans. Antennas Propag. 2012, 60, 2536–2540. [Google Scholar] [CrossRef]
- Ma, G.-M.; Zhou, H.-Y.; Shi, C.; Li, Y.-B.; Zhang, Q.; Li, C.-R.; Zheng, Q. Distributed Partial Discharge Detection in a Power Transformer Based on Phase-Shifted FBG. IEEE Sens. J. 2018, 18, 2788–2795. [Google Scholar] [CrossRef]
- Li, J.; Han, X.; Liu, Z.; Yao, X. A Novel GIS Partial Discharge Detection Sensor with Integrated Optical and UHF Methods. IEEE Trans. Power Deliv. 2018, 33, 2047–2049. [Google Scholar] [CrossRef]
- Ahmad, D.; Wang, S. Bidirectional LSTM Based Partial Discharge Pattern Analysis for Fault Detection in Medium Voltage Overhead Lines with Covered Conductors. In Proceedings of the IEEE 18th International Conference on Industrial Informatics (INDIN), Warwick, UK, 20–23 July 2020; pp. 70–73. [Google Scholar] [CrossRef]
- Ding, B.; Zhu, H. A Novel Partial Discharge Detection Algorithm in Power Transmission Lines Based on Deep Learning. In Proceedings of the 3rd International Conference on Smart Power & Internet Energy Systems (SPIES), Shanghai, China, 25–28 September 2021; pp. 100–104. [Google Scholar] [CrossRef]
- Xu, N.; Gooi, H.B.; Wang, L.; Zheng, Y.; Yang, J. Partial Discharge Detection Based on Long Short-Term Memory Neural Network Classifier with Efficient Feature Extraction Methods. In Proceedings of the IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 2328–2333. [Google Scholar] [CrossRef]
- Salomon, D.; Motta, G.; Bryant, D. Data Compression: The Complete Reference, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Huang, N.E.; Zheng, S.; Long, S.R. A new view of nonlinear water waves: The Hilbert spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Gu, F.-C.; Chen, H.-C.; Chao, M.-H. Application of improved Hilbert-Huang transform to partial discharge signal analysis. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 668–677. [Google Scholar] [CrossRef]
- Chang, H.-C.; Gu, F.-C.; Kuo, C.-C. Applying Hilbert-Huang transform on partial discharge pattern recognition of a gas insulated switchgear. In Proceedings of the IEEE International Power Modulator and High Voltage Conference (IPMHVC), San Diego, CA, USA, 3–7 June 2012. [Google Scholar]
- Gu, F.-C.; Chang, H.-C.; Chen, F.-H. Application of the Hilbert–Huang transform with fractal feature enhancement on partial discharge recognition of power cable joints. IET Sci. Meas. Technol. 2012, 6, 440–448. [Google Scholar] [CrossRef]
- Gu, F.; Chang, H.; Cheng, C.; Meng, H.C. Application of improved Hilbert–Huang transform to partial discharge defect model recognition of power cables. Appl. Sci. 2017, 7, 1021. [Google Scholar] [CrossRef]
- VSB Power Line Fault Detection. Available online: https://www.kaggle.com/competitions/vsb-power-line-fault-detection (accessed on 23 June 2022).
- VSB_1st_Place_Solution. Available online: https://www.kaggle.com/mark4h/vsb-1st-place-solution#Preprocessing-Overview (accessed on 23 June 2022).
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 3149–3157. [Google Scholar]
- Flatiron. Available online: https://www.kaggle.com/miklgr500/flatiron (accessed on 23 June 2022).













| Variable | Description | Index Variable |
|---|---|---|
| Time | - | |
| An arbitrary time series | - | |
| - | ||
| - | ||
| Amplitude function of | ||
| Instantaneous frequency | ||
| Imaginary | - | |
| The number of intrinsic mode functions | ||
| RP | Real part | - |
| Flattened signal | - | |
| Medium variable | - | |
| Cycle count | ||
| Hilbert spectrum | - | |
| Hilbert marginal spectrum | - |
| Extreme Gradient Boosting | Light Gradient-Boosting Machine (LightGBM) | |
|---|---|---|
| Tree growth algorithm | Level-wise | Leaf-wise with maximum depth limitation |
| Split search algorithm | Pre-sorted algorithm | Histogram algorithm |
| Memory cost | 2*#feature*#data*4Bytes | #feature*#data*1 Bytes (8× smaller) |
| Calculation of split gain | O (#data* #features) | O (#bin *#features) |
| Seg/Parts | 104 | 103 | 400 | 200 | 160 | 100 | 80 | 50 | 20 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| One time/s | 0.0099 | 0.0100 | 0.0103 | 0.0110 | 0.0125 | 0.0125 | 0.0438 | 0.32 | 2.25 | 1876 |
| Label | Feature |
|---|---|
| 0 | Hilbert–Huang Transform (HHT) features from Steps 1–3 |
| 1 | The total number of peaks |
| 2 | The number of peaks in quarters 0 and 2 |
| 3 | The number of peaks in quarters 1 and 3 |
| 4 | The std height in quarters 0 and 2 |
| 5 | The mean “sawtooth” root mean square error (RMSE) value in quarters 0 and 2 |
| 6 | The mean height in quarters 0 and 2 |
| 7 | The mean value of the ratio with the previous data point feature in quarters 0 and 2 |
| 8 | The mean value of the ratio with the next data point feature in quarters 0 and 2 |
| 9 | The mean value of the absolute distance to the opposite polarity maximum |
| Predict 0 9 Features | Predict 0 10 Features | Predict 1 9 Features | Predict 1 10 Features | |
|---|---|---|---|---|
| Actual 0 | 19,497 | 19,496 | 186 | 187 |
| Actual 1 | 192 | 127 (−33.8%) | 462 | 527 (+14.1%) |
| Feature | Accuracy | Precision | Recall | F1_score | MCC | Sum | Rank |
|---|---|---|---|---|---|---|---|
| HHT | 4 | 3 | 4 | 3 | 3 | 17 | 3 |
| 1 | 3 | 6 | 1 | 1 | 1 | 12 | 1 |
| 2 | 7 | 8 | 5 | 6 | 6 | 32 | 6 |
| 3 | 1 | 1 | 9 | 4 | 4 | 19 | 4 |
| 4 | 9 | 9 | 6 | 8 | 8 | 40 | 8 |
| 5 | 5 | 5 | 3 | 5 | 5 | 23 | 5 |
| 6 | 2 | 4 | 2 | 2 | 2 | 12 | 1 |
| 7 | 10 | 10 | 7 | 9 | 9 | 45 | 10 |
| 8 | 8 | 7 | 8 | 10 | 10 | 43 | 9 |
| 9 | 6 | 2 | 10 | 7 | 7 | 32 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chiang, H.-d.; Dong, N. Power-Line Partial Discharge Recognition with Hilbert–Huang Transform Features. Energies 2022, 15, 6521. https://doi.org/10.3390/en15186521
Wang Y, Chiang H-d, Dong N. Power-Line Partial Discharge Recognition with Hilbert–Huang Transform Features. Energies. 2022; 15(18):6521. https://doi.org/10.3390/en15186521
Chicago/Turabian StyleWang, Yulu, Hsiao-dong Chiang, and Na Dong. 2022. "Power-Line Partial Discharge Recognition with Hilbert–Huang Transform Features" Energies 15, no. 18: 6521. https://doi.org/10.3390/en15186521
APA StyleWang, Y., Chiang, H.-d., & Dong, N. (2022). Power-Line Partial Discharge Recognition with Hilbert–Huang Transform Features. Energies, 15(18), 6521. https://doi.org/10.3390/en15186521





