Profitability and Revenue Uncertainty of Wind Farms in Western Europe in Present and Future Climate

Abstract

Investments into wind power generation may be hampered by the uncertainty of future revenues caused by the natural variability of the wind resource, the impact of climate change on wind potential and future electricity prices, and the regulatory risks. We quantify the uncertainty of the economic value of wind farms in France, Germany, and Denmark, and evaluate the cost of support mechanisms needed to ensure the profitability of wind farms under present and future climates. To this end, we built a localised model for wind power output and a country-level model for electricity demand and prices. Our study reveals that support mechanisms are needed for current market conditions and the current climate, as well as under future climate conditions according to several scenarios for climate change and energy transition. The cost of support mechanisms during a 15-year period is evaluated to EUR 3.8 to EUR 11.5 billion per year in France, from EUR 15.5 to EUR 26.5 billion per year in Germany, and from EUR 1.2 to EUR 3.3 billion per year in Denmark, depending on the scenario considered and the level of penetration of wind energy.

1. Introduction

To limit greenhouse gas emissions from power generation, as well as the dependence on energy imports, the use of renewable intermittent energy sources, such as wind and solar, has been encouraged in many European countries. Renewable energy generation, together with the electrification of carbon-intensive sectors, such as transport and heating, are the pillars of energy transition. In this context, wind energy plays a particularly important role because of high wind potential in Europe, rapidly decreasing costs of technology, regulated support mechanisms, and good acceptance by the public. In 2021, EUR 41 billion was spent on building new wind power plants in Europe, for a record total of 24.6 GW of new capacity, and this figure is expected to increase in the short term due to favourable economic conditions, policy initiatives, such as the European Green Deal, and the necessity to reduce dependence on the Russian gas exports in the current political context [1]. However, this still falls short of the declared energy transition objectives: in its REPowerEU roadmap the European Commission has fixed a new objective of 480 GW of installed wind power capacity in the EU by 2030 to reduce energy prices and enhance energy security. This requires the addition of 35 GW of wind capacity annually between 2022 and 2030.

The investment into wind energy production is hampered by the uncertainty of future revenues of wind power producers. This uncertainty arises from the natural variability of the resource, from climate change, which is likely to impact not only future wind energy production but also electricity prices and, last but not least, from the evolution of regulatory policies. A more precise understanding of the uncertainties at stake is, therefore, needed for a number of reasons. First, it will give the private sector investors a better view of risks and opportunities associated with wind energy industry. Second, it will enable the public authorities to quantify the level of support needed for long-term sustainability of the industry and to evaluate the long term costs of energy transition. Finally, it will allow the financial industry to develop suitable funding instruments.

The potential for future cost reduction in wind energy production is analysed in several recent articles. In [2], the authors summarise the results of a global expert survey of wind energy costs; they anticipate a 24–30% cost reduction by 2030 and a 35–41% reduction by 2050. Another recent article [3] also predicts a drop of 40% by 2050 in capital costs for onshore wind turbines. The articles [4,5] study the evolution of levelized cost of wind generated electricity, both anticipating cost reductions for this generation technology. The paper [6] identifies four main drivers for past cost changes: learning by deployment, learning by researching, supply chain dynamics, and market dynamics, including support policies. In [7], the authors study the impact of sector coupling on the cost of energy system development in Northern–Central Europe using the Balmorel energy system model [8], and in [9] the costs of increasing renewable energy penetration in the US are explored in the framework of the Regional Energy Deployment System (ReEDS) model [10]. When it comes to the value of wind power plants, several studies agree that it tends to decline as penetration rate increases [11,12,13]. A full model for the economic value of wind at increasing penetration taking into account hourly variation of wind and load is presented in [14]. An interesting model recently proposed in [15] analyses the effects of strategic behaviour of wind producers and heterogeneous resource availability.

Concerning support policies, real-options models with stochastic dynamics are developed in [16,17] to compare the costs of different policy schemes. Scenarios for future worldwide wind power deployment, associated costs, and policy options are reviewed in [18], while the papers [19,20] discuss the risks and risk management options of renewable energy projects, in particular revenue variability risks associated to resource intermittency and price volatility, that we also address in this paper. The article [21] evaluates the wind and solar subsidies in Spain and in Germany in terms of their cost for reducing carbon emissions and find that it is much cheaper for the regulator to reduce CO${}_2$ emissions by subsidizing the wind power production. At the same time, the paper [22] finds that wind subsidies in Germany may not be fully efficient since, in addition to helping wind producers, they also push land prices up, creating windfall revenues for land owners. Finally, a very recent preprint [23] considers optimal structuring of renewable energy subsidies taking into account the learning curves.

Regarding the impact of climate change on wind speed, the article [24] studies its consequences on the optimal power generation and transmission expansion plan in Chile. Some articles use reanalysis data to quantify wind potential and assess its uncertainty, see, e.g., [25]. The impact of climate change on wind potential and levelized cost of wind energy is analysed in [26,27] using CMIP5 scenarios. However, these papers, which use climate data to evaluate the wind potential, do not combine it with the price and electricity demand component. This is all the more important because the impact of climate change on electricity demand, due, in particular, to the global temperature change, is expected to be stronger than the impact on the wind potential [28]. The economics of wind energy is studied only in terms of costs but not in terms of actual revenues for the wind producers operating in the market, and, consequently, the cost of public support measures needed to make wind energy profitable is rarely evaluated.

We propose to fill this gap by quantifying the uncertainty of the net present value of standardized wind farms in European countries and by evaluating the level and the total cost of support mechanisms needed to guarantee the profitability of the wind fleet. To this end, we build a localized model for wind power output and a country-level model for electricity demand and prices taking into account hourly variation of wind, load and prices, using reanalysis data, climate projections, and integrated assessment model (IAM) scenarios. The main focus of our study is to quantify the uncertainty due to climate variability and climate change. Our model for the electricity demand is thus relatively simple compared to the literature, but allows to quantify the climate impacts very precisely. We develop a general methodology, focusing on the examples of France, Germany, and Denmark for specific evaluations. Our study shows that profitability of wind energy in these countries requires support mechanisms under current market prices and current climate. We then analyse several scenarios of climate change and energy transition, and show that, under future climate, support mechanisms will still be needed in these countries to ensure the economic sustainability of the wind energy.

The rest of the paper is structured as follows. In Section 2, we briefly describe the model that we use to generate long time series of synthetic electricity prices and wind energy output under present and future climate. In Section 3, we analyse the variability of wind farm revenues and value under present climate. Section 4 presents the analysis of wind farm value under future climate and various socio-economic scenarios. In this section we also evaluate the cost of public support schemes required to ensure the economic sustainability of wind energy in the future. Section 5 places our results in a wider context and discusses their policy implications, and Section 6 concludes the paper. A list of frequently used abbreviations is provided after this section.

2. Modelling Electricity Prices and Local Wind Production

Our methodology relies on constructing a long time series of synthetic local wind power production and national electricity prices, built assuming current market conditions. This is done by plugging a long time series of climate variables into a model for wind power production and for electricity prices, calibrated on recent market and energy system data. The time series of climate variables are obtained either from historical reanalysis data (for current climate analysis) or from regional climate model projections (for future climate analysis). The synthetic local wind power production and national electricity prices are then used to simulate the revenues of standardized wind farms depending on their location, under different scenarios. This approach allows to disentangle the different sources of variability and to quantify the variations in the revenues and expenditure of wind farms at current market design and network structure, under different support schemes.

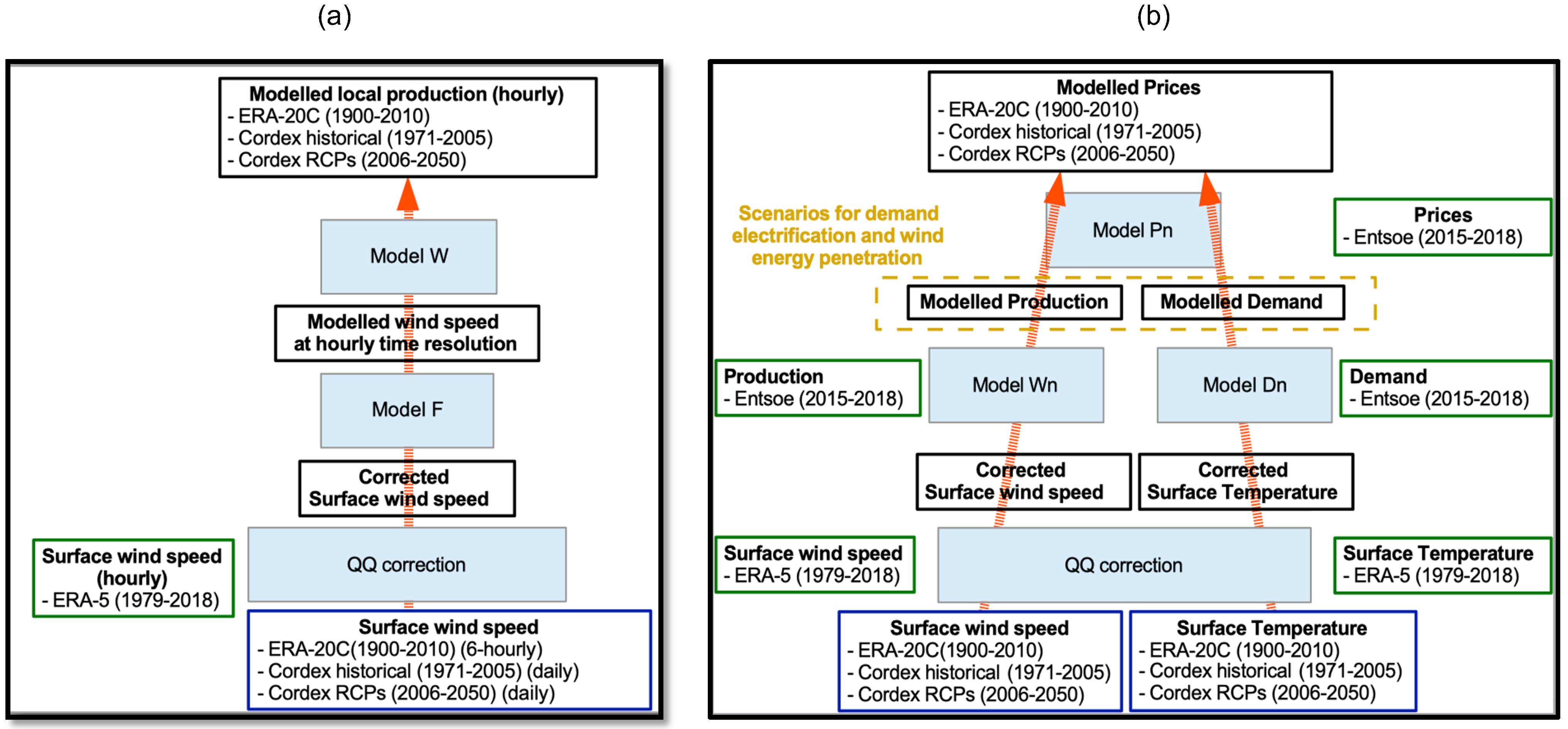
Here, we briefly describe the modelling approach to generate the time series. A summary of the variables and the data sources is provided in the Data section in the Appendix A and a detailed description of the modelling approach is presented in the Models section of the same appendix. Figure 1 presents the modelling process for wind energy infeed at each gridpoint of the considered domain (Figure 1a) and for day-ahead prices in each of the three considered countries (Figure 1b). Both models have three steps, going from the bottom to the top of Figure 1.

In the first step, which is common to the two models, we reduce the bias of the long time series of surface wind speed and temperature from the ERA20C reanalysis by comparing them to the ERA-5 reanalysis dataset, which is considered to be more reliable and less biased, and performing a quantile-quantile correction. Recall that reanalysis is a procedure wherein a single model for the atmosphere is run over an extended historical period, coupled with an assimilation system, which assimilates all available observations for this period. This results in a long homogeneous time series of the evolution of the atmosphere which represents our best guess of the state of the atmosphere given the available data. For the local production model, in the second modelling step, we downscale the wind speed time series to hourly frequency by generating the missing values from a stochastic wind model. In the third step, we combine the local wind speed with standardized production functions to obtain a time series of the synthetic local wind power production. For the price model, the second step consists in generating long time series of national production and demand, using models whose parameters are estimated from historical data from a recent period. The third step allows to obtain a time series of synthetic prices from the generated production and demand values.

As a result of these modelling processes, we obtain two datasets:

• The present climate dataset used to study the variability of wind farm revenues and value at current climate, i.e., at 20th century climate variability but with current market and energy system characteristics;
• The future climate dataset used to study the variability of the wind farm revenues and value under future climate and future realistic scenarios for demand and wind energy penetration, taking into account the climate model uncertainty.

We now proceed to describe the two datasets in detail. The present climate dataset contains synthetic local wind power production data at the spatial resolution of $1.{125}^{\circ }$ and synthetic day-ahead prices, electricity demand, and national wind energy production in France, Germany, and Denmark. All series have hourly time resolution and correspond to the climate data from 1900 to 2010.

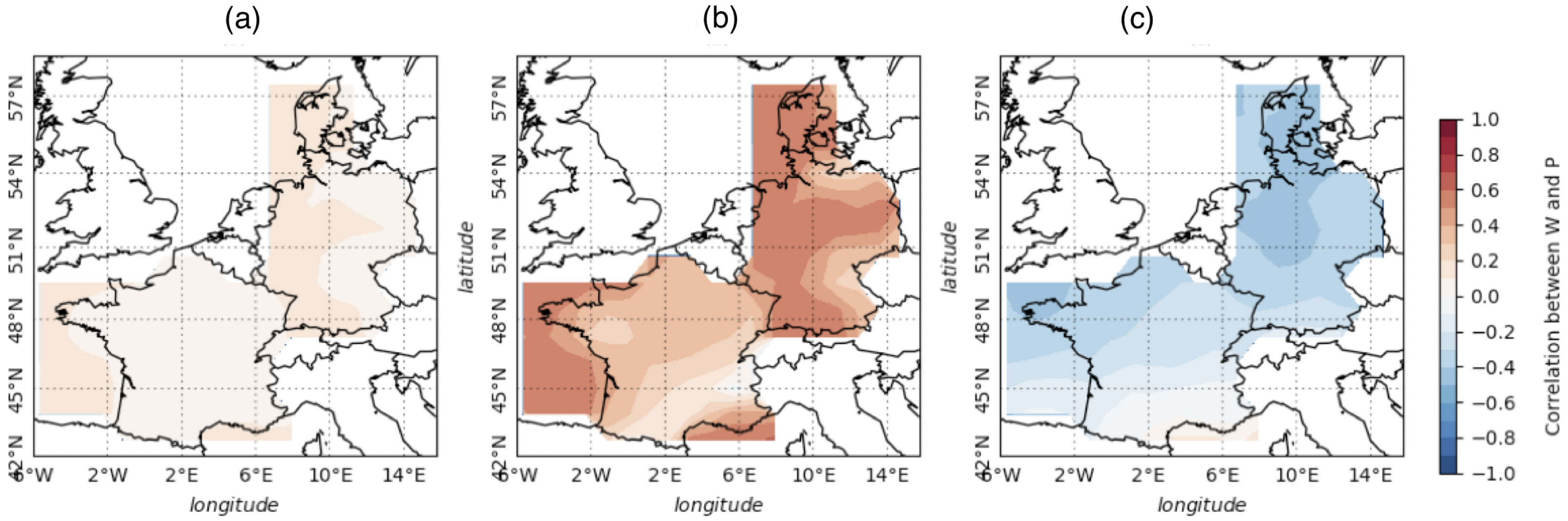
This dataset is illustrated in Figure 2, Figure 3 and Figure 4. Figure 2 displays the relative standard deviation (i.e., the ratio between the standard deviation and the mean, henceforth RSD) of onshore and offshore production capacity factor in panel (a), and of price in panel (b) for each considered country. It is clear that the variability of revenues is largely explained by that of the capacity factor, which is much more variable than the price in all countries under consideration. The standard deviation of the price is around 35% of the mean price, while the standard deviation of the capacity factor exceeds the mean capacity factor in most onshore regions, especially in locations where the mean capacity factor is low (e.g., mountainous regions). In France, the price RSD exceeds 45% because the seasonal cycle is more pronounced than in the other countries due to strong seasonal variations of the consumption.

At the hourly timescale (panel (c)), the correlation between prices and production is low but positive (<0.2). At the monthly timescale (panel (d)), wind energy production is significantly positively correlated with prices in all three countries under study. This is due to matching seasonal cycles of wind energy production and prices. Indeed, prices are high during cold seasons when demand increases. At the same time, wind production in Western Europe is also expected to be high during the cold season due to the enhanced activity of the storm track. In the long term (panel (e)), the correlation between wind energy production and prices becomes negative, especially in Denmark and the north of Germany. This may be related to the merit-order effect: a rise in wind production at the national level tends to push the wholesale electricity price down (see [29,30] for instance). It may also indicate a negative correlation between temperature (whose increase tends to push the demand and thus the prices down) and wind energy production. This correlation can also be related to the large scale weather regimes, such as the North Atlantic Oscillation (NAO) which, in the positive phase, enhances the storm track activity, increasing the wind production in Western Europe, and, at the same time, contributes to increasing the temperature and, therefore, decreasing energy demand and prices, by bringing warmer wet air in this region. In the negative phase, this phenomenon is reversed. The NAO displays long term cycles of the order of 3 to 7 years. Many studies have demonstrated a correlation of the NAO (and other weather regimes) with wind speed and production and electricity demand (see for instance [31,32]).

Figure 3 shows the correlation between synthetic prices and production at different timescales.

Figure 4 displays the long-term trends (10 years sliding mean) of the synthetic electricity prices, electricity consumption, and wind energy production in France, Germany, and Denmark (Figure 4a–c, respectively). As expected from our model, where the electricity prices are largely driven by consumption, these two time series tend to vary together. On the other hand, the negative correlations between electricity prices and wind energy production, discussed above, are not clearly visible on this graph due to averaging. We observe long-term trends in consumption and price trajectories, especially after the late 1960s when they both decrease, and very long-term trends in wind energy production, which increases in all three countries throughout the 20th century and appears to decrease afterwards. The authors of [33] identify such positive trends for wind speed in ERA20C, CERA20C reanalyses, as well as in the OFA observation dataset (assimilated in these reanalyses). They also identify negative trends in NOAA20CR reanalysis, and no trends in the free simulation ERA20CM which uses the same model as ERA20C. The study focuses on North Pacific and North Atlantic areas, but smaller and significant trends are found in continental Europe as well. They show that the positive trends in ERA20C may come from the assimilation of marine wind speed. The discussion of the reality of these trends is very instructive but does not conclude as to whether these trends are spurious or not. Arguments in favour of spurious trends are based on the changes in wind measurement techniques, the disagreement between mean sea level pressure (MSLP) over the Arctic in ERA20C and measurements (HadSLP2), and the low signal on wind speed in CMIP5/CORDEX simulations. Nevertheless, there are also some arguments in favour of real trends, such as the findings of trends in wave height in agreement with positive wind speed trends. We make the choice to keep the wind speed as it is in ERA20C. This choice can be justified by the purpose of a reanalysis which aims at representing the observations in the best possible way and by the fact that there is no proper correction methodology. In the following, we address this issue by giving in some cases an order of magnitude of the impact of this trend on our results.

The future climate dataset contains synthetic local wind production data at the spatial resolution of $0.{44}^{\circ }$ and synthetic day-ahead prices, demand, and national wind energy production in France, Germany, and Denmark. All series have hourly time resolution and correspond to projected climate from 2006 to 2050, under the RCP-4.5 and the RCP-8.5 scenarios, for 5 different regional climate models. Price, demand, and national wind energy production series are computed under 3 scenarios of future electricity demand (no electrification, medium electrification, and high electrification of demand) and 2 scenarios of wind energy penetration (low and high penetration of wind energy), which makes a total of 6 economic scenarios.

The three demand scenarios are based on the IMAGE 3.0 model scenarios [34]. The IMAGE 3.0 model output can be found at https://tntcat.iiasa.ac.at/LIMITSPUBLICDB/dsd?Action=htmlpage&page=welcome (last accesses on 8 August 2022). The choice of IMAGE 3.0 model for demand trend scenarios was somewhat arbitrary and guided mostly by the availability of data and documentation, global coverage, and a strong focus of this model on climate change. In our framework, IMAGE 3.0 scenarios are used only to determine the 2020–2050 demand trends and can be easily replaced with any other set of scenarios. For example, the International Energy Agency in its Net Zero by 2020 report [35] projects a 80% increase in global electricity demand in the stated policies scenario (STEPS), nearly a 100% increase in the announced pledges scenario (APS) and a 116% increase in the NZE2020 scenario. These values are much higher than the ones we use, however they are at a global level and are mainly driven by increased energy consumption in developing countries. In each scenario, the actual electricity demand projections are defined starting from the historical demand of each country, adding the temperature-dependent demand computed with the given climate projection and adding a common rate of growth defined for Europe as follows:

• In the first scenario, the electricity demand is only temperature dependent, there is no additional trend. As a result of temperature increase in the RCPs scenarios, the electricity demand tends to decrease in this scenario;
• The second scenario projects a medium electrification; the trends of electricity demand are based on the IMAGE 3.0 scenario LIMITS-Pledges, where the electricity demand increases almost linearly by 28% from 2020 to 2050;
• The third scenario projects a high electrification; the trends of electricity demand are based on the IMAGE 3.0 scenario LIMITS-baseline, where the electricity demand increases almost linearly by 42% from 2020 to 2050.

The two wind energy penetration scenarios are designed based on trends given in the report [36], which are different for each considered country. The first scenario projects a low increase in installed wind capacity and the second scenario projects a high increase in installed capacity. The six resulting scenarios are summarised in

Table 1. Wind energy penetration and electricity demand scenarios used to build price scenarios in each country.

		Wind Penetration in 2030
	Scenarios	Low Scenario (Onshore, Offshore in GW) In France: 31.0, 4.3 In Germany: 60.0, 14.0 In Denmark: 3.6, 3.4	High Scenario (Onshore, Offshore in GW) In France: 41.0, 11.1 In Germany: 71.0, 20.0 In Denmark: 6.5, 6.1
Demand increase from 2020 to 2050	0%	Scenario 1	Scenario 2
	28%	Scenario 3	Scenario 4
	42%	Scenario 5	Scenario 6

.

The electricity price projections are computed using these scenarios for electricity demand and wind energy production in each country and using the temperature and wind speed from the two RCPs as inputs. We thus have 60 different price projections for each country (2 RCPs, 5 models, 3 demand scenarios, and 2 penetration scenarios). In the following, for each of the 6 economic scenarios (3 demand times 2 penetration), we have 10 different physical simulations corresponding to different models and RCP. Note that the two RCPs are considered as two simulations, not as scenarios, because the results from the two RCPs are not significantly different. This is not unexpected as RCP scenarios begin to show diverging trajectories around 2050 in terms of global mean temperature for instance.

The change in future wind speed and future wind production has already been investigated in several studies. Tobin et al. [37] using the same CORDEX dataset (with 12 models) found a decrease in the wind speed by the end of the century of less than 2% and a decrease in the wind power generation potential in Western Europe of about 5 to 10%. We obtain similar results with our dataset.

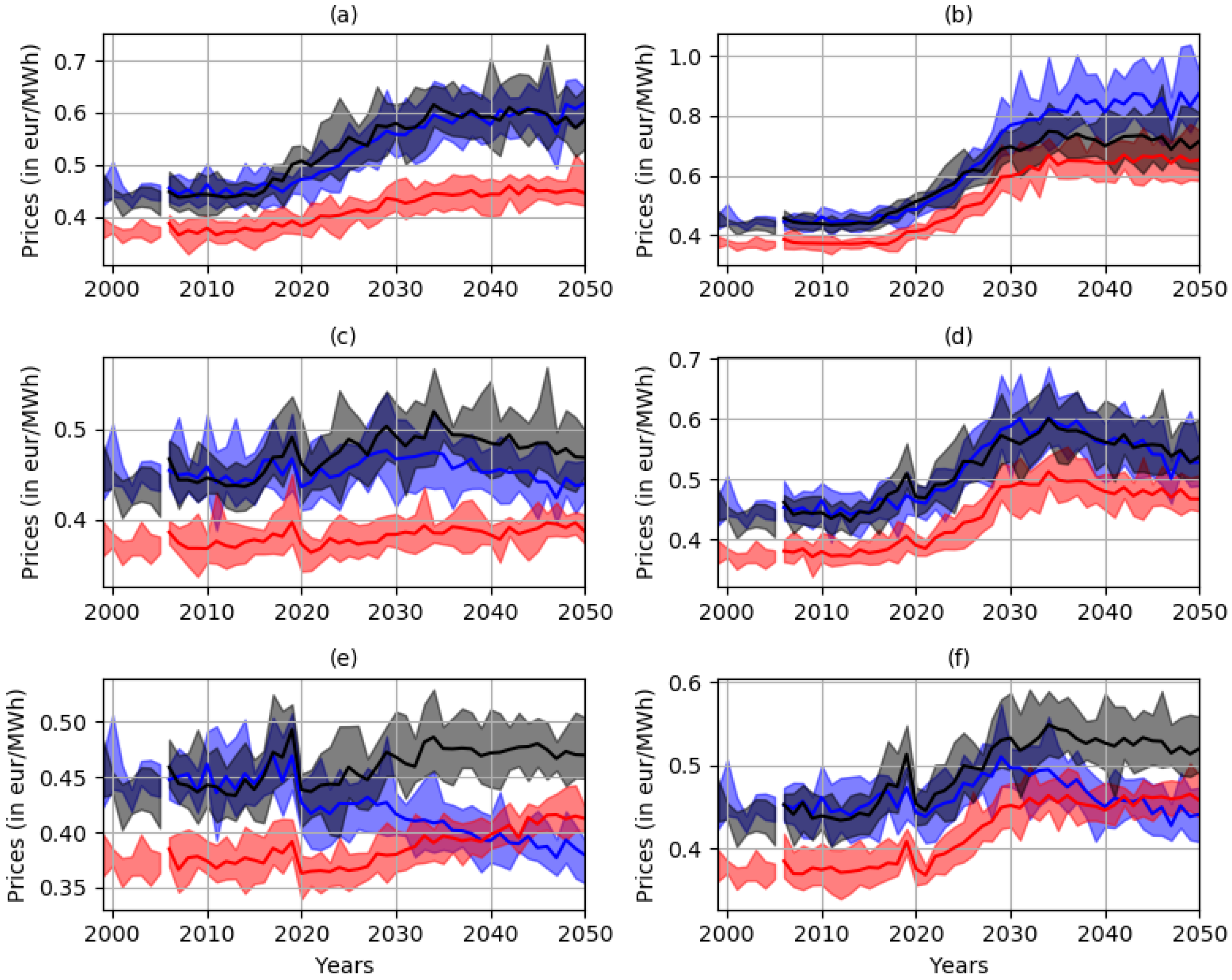
Figure 5 displays the projected yearly average prices in blue for France, in black for Germany, and in red for Denmark, in the 6 economic scenarios previously described. The shaded area corresponds to the minimum and maximum yearly average prices among the 10 simulations (5 models and 2 RCPs). Left panels correspond to low penetration scenarios and right panels to high penetration scenarios. Top panels correspond to no demand trend scenarios, middle panels to medium demand trend scenarios, and bottom panels to high demand trend scenarios.

Some discontinuities are visible in 2020 (Figure 5c–f). They correspond to the beginning of demand electrification and wind energy penetration scenarios. Price trajectories span a wide range of possible prices (from less than about 20 €/MWh in 2050 in Denmark (Figure 5b) to 70 €/MWh in 2050 in France (Figure 5e).

The 10 simulations (5 models and 2 RCPs—filled area) display uncertainties of about 2 €/MWh to 5 €/MWh. The trajectories of the scenarios are firstly driven by electricity consumption assumptions (comparing panels from top to bottom), secondly by wind energy penetration assumptions (comparing left and right panels) and thirdly by the RCP. In the scenario where the demand only depends on temperature, the prices drop slowly between 2010 and 2050 (Figure 5a,b). For a medium and high electrification of the system, the electricity demand increases after 2020, and proportionally so do the prices (Figure 5c–f).

Figure 6 shows the projected intra-annual RSD of prices for each scenario. The scenario of low demand and high penetration displays high values of RSD in all countries (Figure 6b). The increasing standard deviation relatively to the average price is due to decreasing average prices but also to increasing standard deviation due to the intermittency of wind energy production. Overall, there is an increase in the price RSD in every scenario due to wind energy penetration. The increase in RSD takes place between 2020 and 2030 when the installed wind capacity increases. In France, there is a decrease in the RSD after 2030 in the scenarios of medium and high electrification of demand and high penetration of wind energy (Figure 6d,f), and a decrease in RSD after 2020 in the scenario of high electrification of demand and low penetration (Figure 6e). We conclude that the penetration of renewable energy has less influence on prices variability in France than in Denmark and Germany.

3. Variability and Uncertainty of Wind Farm Value under Present Energy Economics and Recent Climate

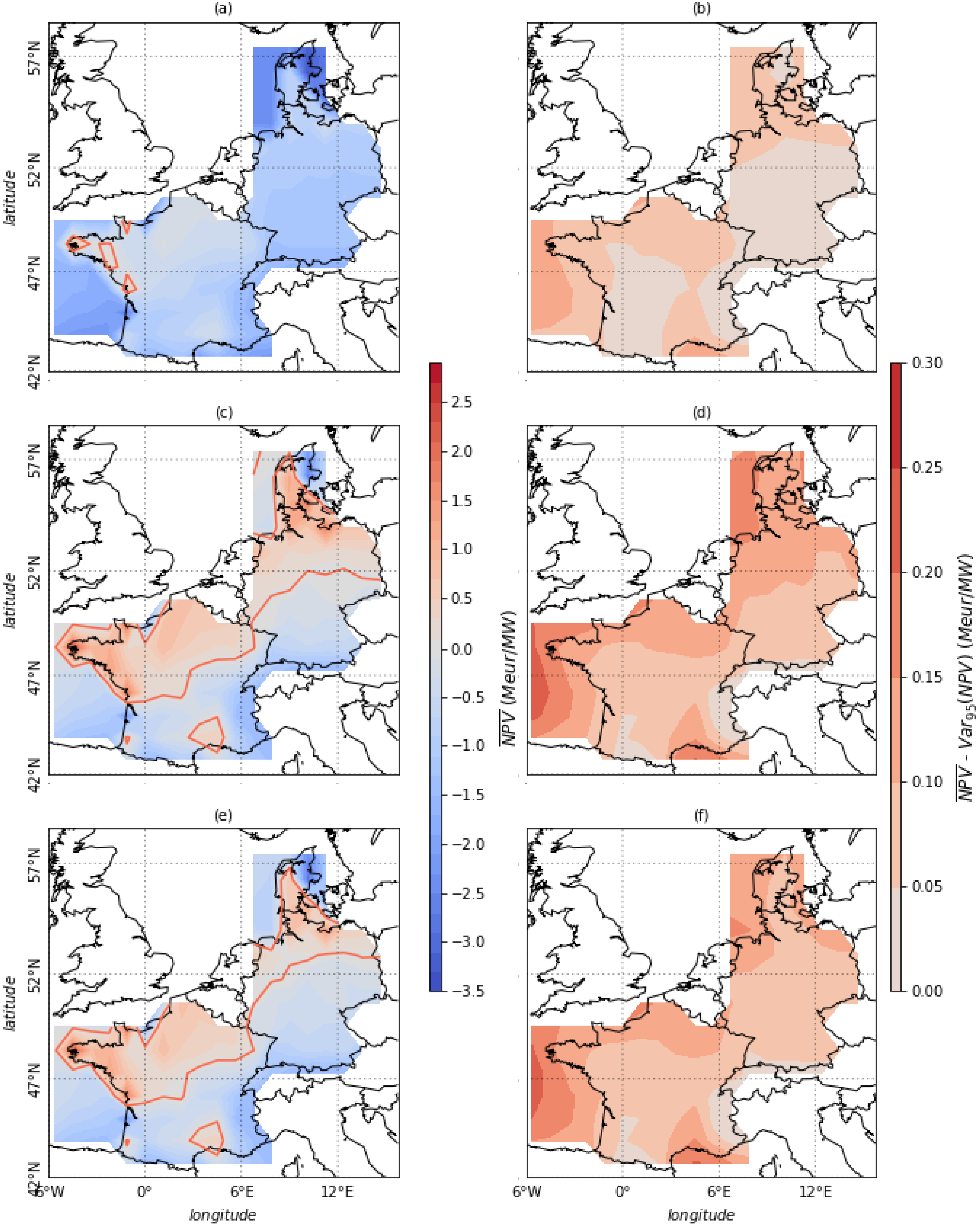
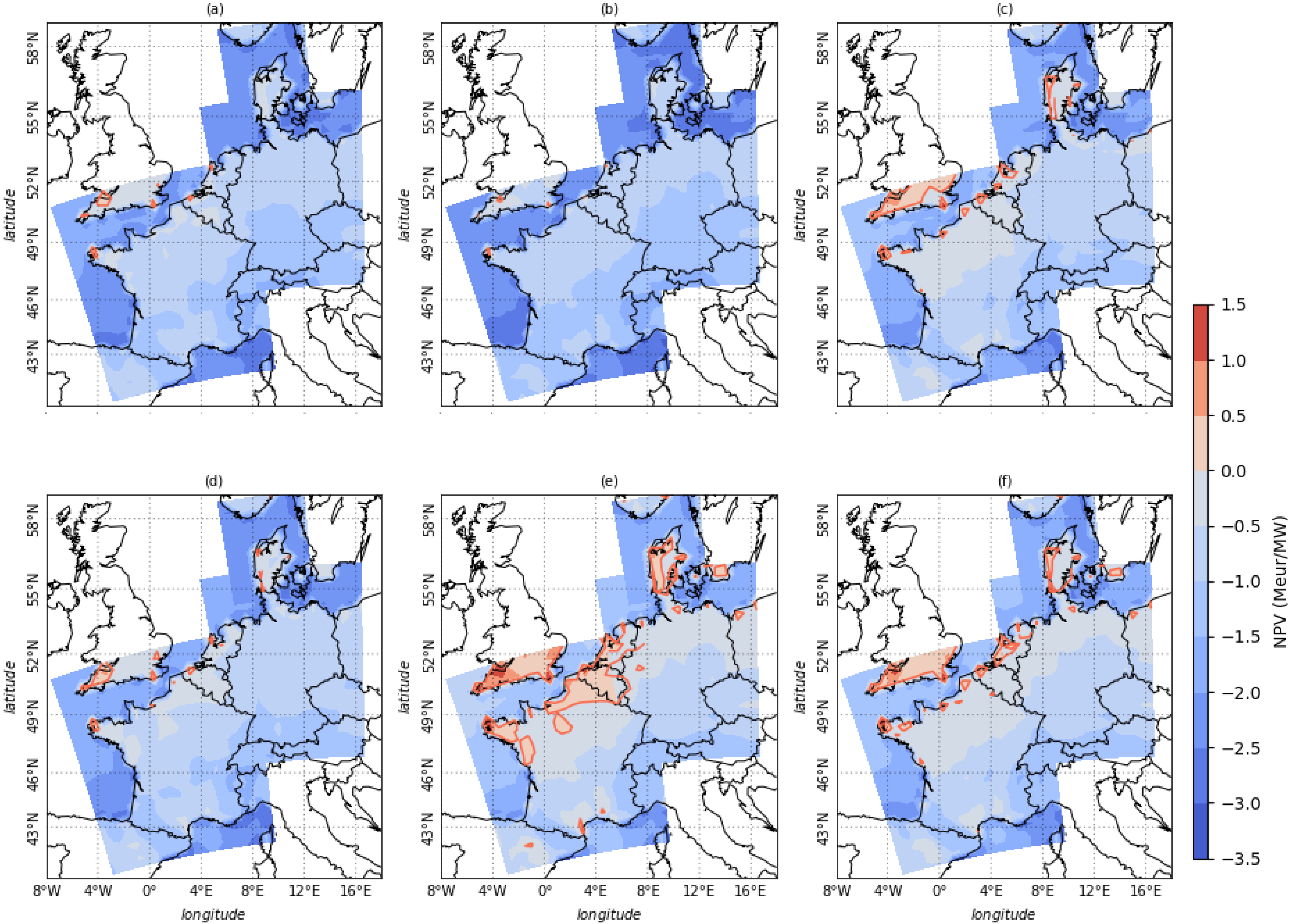
From our synthetic dataset of 111 years, we define 81 virtual wind farm projects at each gridpoint starting on the 1st of January of each year from year 1 to year 82 and lasting 30 years. Figure 7 displays the NPV averaged over 81 project at each gridpoint, as well as the corresponding $Va{R}_{95}$ (quantile at the 95% level).

For offshore wind farms operating without subsidies (Figure 7a,b), the NPV is negative due to the high initial investment and costs. Thus, offshore wind farms are not yet profitable if not supported by regulations mechanisms. Nevertheless, both investment costs and operational costs are rapidly decreasing [5,20,38]. For onshore wind farms, small areas in the west of France display small positive NPV of the order of the range between the mean and the 95th percentile of NPV. The difference between the mean and the $Va{R}_{95}$ is small, meaning that the NPV does not vary much on the long term. The standard deviation is less than 5% the mean of the NPV in most of the regions.

Note that removing the trends in the ERA20C wind speed to compute local production has a large impact on the inter-quartile range (IQR) for the 81 projects: using detrended production results in an IQR which is 30% to 100% lower than the IQR computed using production with trends. In other words, the very long-term trends in wind speed result in low profitability early in the century and higher profitability at the end of it. Detrending wind speed results in a less varying profitability along the 20th century. The decrease in IQR is larger for offshore wind farms and for onshore wind farms close to coast.

We model both the feed-in-tariff (henceforth FiT) and the feed-in-premium (henceforth FiP) subsidy. Under FiT, the producer receives a fixed guaranteed price of 82 €/MWh for 10 years after which the price decreases linearly for 5 years to 28 €/MWh. After 15 years the subsidy disappears and the remaining energy is sold in the day-ahead market. This corresponds to the support mechanism used in France until 2016. The function $f_t$, which defines the amount a producer receives for a MWh produced, is given by:

$$f_t^{FiT}=82€/\mathrm{MWh}{\mathbf{1}}_{0\le t<10}+\left(82-54\times \frac{t-10}{5}\right)€/\mathrm{MWh}{\mathbf{1}}_{10\le t<15}+P_t{\mathbf{1}}_{t>15}.$$

(1)

Several FiP procedures exist. We choose to use a simplified one under which the producer receives a guaranteed bonus of 33 €/MWh in addition to the market price. After 15 years, the subsidy disappears and the remaining energy is sold in the day-ahead market. The function $f_t$ is, in this case, given by:

$$f_t^{FiP}=(P_t+33€/\mathrm{MWh}){\mathbf{1}}_{0\le t<15}+P_t{\mathbf{1}}_{t>15}.$$

(2)

The formula for the bonus is inspired from the Danish FIP. In reality, the procedure is slightly different, as the bonus is guaranteed until the sum of the the price and the bonus is under $78€/\mathrm{MWh}$. In this last case, the producer receives a bonus to reach the target of $78€/\mathrm{MWh}$. Germany used a FiT mechanism similar to the French one until 2012 and now uses a FiP similar to the Danish one. We use the same mechanisms for onshore and offshore wind farms.

For wind farms supported by either FiT (Figure 7c,d) or FiP (Figure 7e,f) mechanisms, the wind farm value is higher, especially in the case of the FiT mechanism. Offshore wind farms are found to be profitable with FiT in the Western coast of France, Denmark, and Germany. The average NPV over the 81 projects for the FIT mechanism reaches 2.5M €/MW for a wind farm with a lifetime of 30 years (Figure 7c). For FiP mechanism, the average NPV reaches 2.3M €/MW (Figure 7e). The difference between the mean and the $Va{R}_{95}$ is still small and represents not more than 10% of the mean NPV, showing that the revenues are rather stable in this case. A sensitivity analysis of NPV with respect to the discount rate is reported in the Appendix (Methods section).

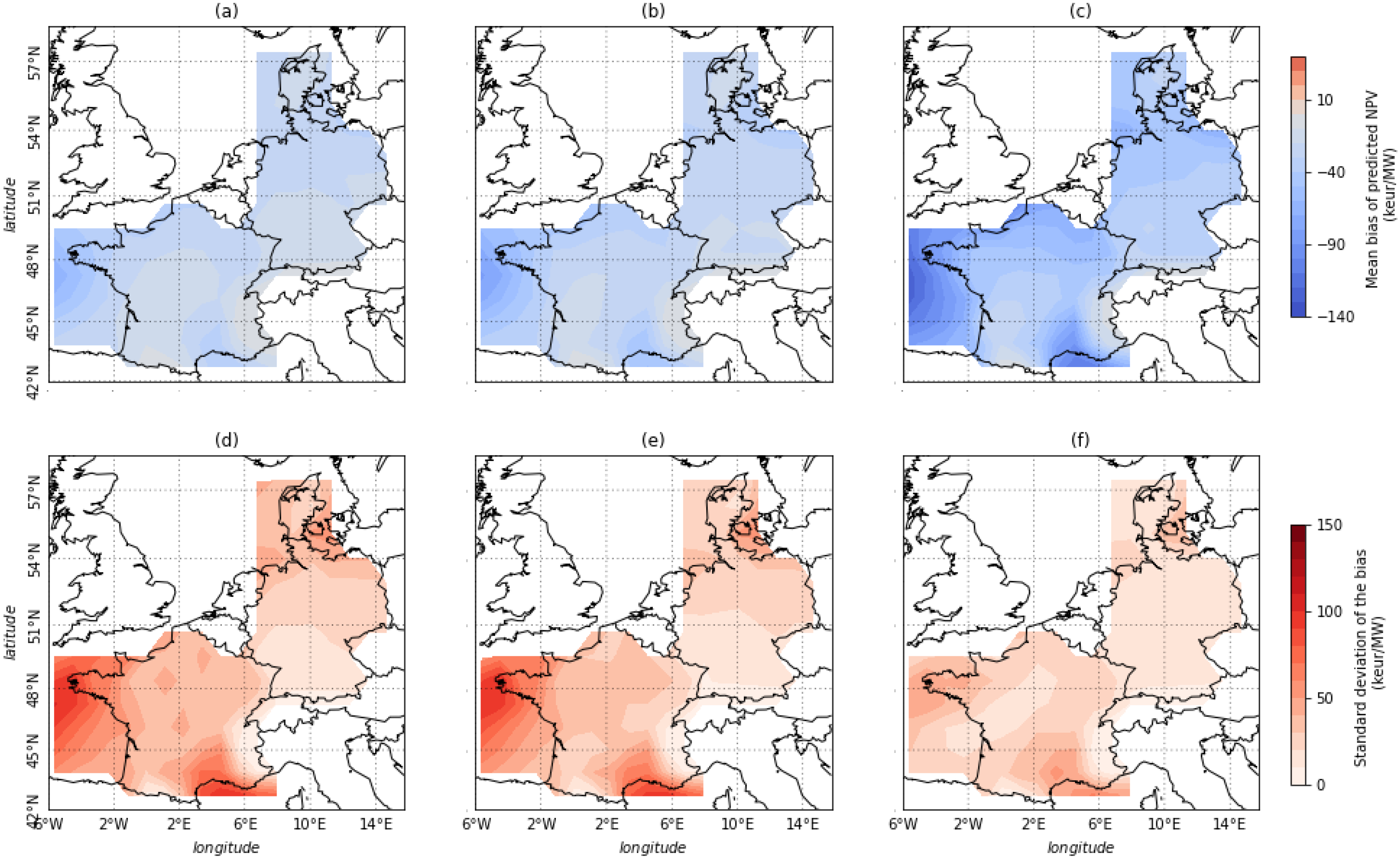
It is common for a wind farm project to base the projections for the future value of an asset on the historical wind speed recorded at the chosen location. To highlight the shortcomings of this approach, we define 51 wind farm projects at each gridpoint starting on the first of January of each year from year 31 to year 82 and lasting 30 years The choice of 51 projects is due to the fact that we have 111 years of data and would like to have 30 years of observations before the start of the project in order to test different projection strategies. We use three different strategies for estimating the wind farm value: the first one based on the wind speed recorded during 5 most recent years, the second one based on 10 most recent years, and the third one based on 30 most recent years before the project begins. Figure 8 displays the mean bias and standard deviation of the bias between projected NPV and actual NPV. We compare projections based on a historical period of 5 years (Figure 8a,d), 10 years (Figure 8b,e), and 30 years (Figure 8c,f).

Our results show that every method underestimates the average NPV. Using the past 30 years to project future revenues results in a larger mean error (underestimation) than using 5 or 10 past years (Figure 8a compared to Figure 8b,c). Nevertheless, the standard deviation is much lower using this method (Figure 8f than using the 5 or 10 past years of data (Figure 8d,e). Thus, using 5 or 10 past years results in higher risk to make large errors than when the projection is based on a longer period (e.g., 30 years). Using 30 years of data makes the projection more sensitive to very long term trends, resulting in a larger mean error, while using fewer historical years makes the projection more sensitive to shorter term interannual variability of revenues. Such projections can sometimes largely overestimate or underestimate the actual future production, revenues and wind farm value. For instance, if an investor projects future revenues based on the past 5 years when the NAO is in positive phase, he may highly overestimate future production concluding wrongly on the profitability of the project.

Note that this result is very sensitive to long term trends found in ERA-20C wind speed. Indeed, the fact that the mean error is larger for a projection based on 30 years than a projection based on 5 years is entirely due to these trends. When trends are removed from the data, using the past 30 years to project future revenues results in a lower mean bias than when using 5 or 10 past years, so that this method becomes the best in terms of both mean and standard deviation of the error.

4. Future Value of Wind Farms under Realistic Socio-Economic Scenarios and Climate Change

In this illustration we compute the NPV for virtual wind farms commissioned on 1st January 2021 with a lifetime of 30 years (decommissioning date is 31st December 2050). Figure 9 displays the NPV averaged over the 10 CORDEX simulations (5 models and 2 RCPs), for each of the 6 price scenarios, in the case of wind farms operating without support mechanism. In the scenario of high electrification and low penetration of wind energy (Figure 9d), several areas of the domain are found to be profitable for onshore wind farms. In the northwest of France and in the western coast of Denmark, the NPV attains 1 M €/MW without support mechanisms. In the remaining scenarios, positive NPV is very rare and in any case very low. As a consequence, in most cases, support mechanisms are needed to guarantee profitability of wind farms and thus ensure energy transition.

Level and Cost of Support Mechanisms under Future Climate

Figure 10 maps the FiP level needed to guarantee a positive or null NPV for wind farms installed in 2021 and operating for 30 years under each considered scenario. The FiP is a simple premium added to the market price for the first 15 years of plant’s operation: the FiP takes into account the evolution of the market price, contrary to the FiT which is less dependent on prices (the dependence only appears at the mechanisms’ expiration date, i.e., after 15 years).

Using the current spatial distribution of the wind farms in the three countries under study (Figure 11), we calculate for each country the premium level needed to guarantee a positive NPV for the 90% of the fleet. We assume that the new installed capacity will display the same spatial distribution as the current one. For offshore wind farms in France, where there is no currently installed capacity, we make the assumption that future wind farms will be mainly placed in the northern coast and in the south, close to the shore (see Figure 11).

In France, the premium level for onshore (offshore) wind farms varies from 33 €/MWh (45 €/MWh) in the best case scenario (Figure 10e) to 66 €/MWh (78 €/MWh) in the worst case scenario (Figure 10b). In Germany, the premium level for onshore (offshore) wind farms varies from 68 €/MWh (76 €/MWh) in the best case scenario (Figure 10e) to 93 €/MWh (102 €/MWh) in the worst case scenario (Figure 10b). Finally, in Denmark, the bonus level for onshore (offshore) wind farms varies from 1.5 €/MWh (83 €/MWh) in the best case scenario (Figure 10e) to 23 €/MWh (105 €/MWh) in the worst case scenario (Figure 10b).

With these data, we are able to calculate the cost of wind energy penetration (onshore and offshore) for each country and in each scenario. Remember that, for scenarios 2, 4, and 6, penetration is high, i.e., total (new) installed capacity in France in 2030 is 41 GW onshore and 11.1 GW offshore; in Germany 71 GW onshore and 20 GW offshore; and in Denmark 6.5 GW onshore and 6.1 GW offshore. In scenarios 1, 3, and 5, penetration is low, i.e., total (new) installed capacity in France is 31 GW onshore and 4.3 GW offshore; in Germany 60 GW onshore and 14 GW offshore; and in Denmark 3.6 GW onshore and 3.4 GW offshore. Note that we not only consider the cost of new installed wind farms, but also that of the replacement of current installed wind farms. Indeed, the vast majority of the currently installed wind farms will arrive at decomissioning date within the next 30 years so that they will need to be replaced to reach the penetration given by our scenarios. The costs are computed by simply adding up the future payments, without discounting, and, as a result, we may slightly overestimate the true costs. However, these are public support policy costs which should therefore be discounted with the sovereign borrowing rate, and the sovereign bond rates are presently quite low.

We find that supporting the penetration of wind energy (over the 15 years of support) will cost the regulator from EUR 57 to 172 billion in France, from EUR 232 to 397 billion in Germany, and from EUR 18 to 50 billion in Denmark, depending on the scenario considered and the level of penetration of wind energy. The results for each scenario are shown in Figure 12. Scenario 5 always results in lower cost for the regulator due to higher electricity prices and low penetration. Conversely, Scenario 2 results in higher costs for the regulator because of the price decreases coupled with high penetration.

5. Discussion and Policy Implications

The first objective of our paper was to evaluate the net present value of standardized wind farms and quantify the associated uncertainty. Our results show that the extreme variations of net present value along the 20th century are of the order of one year of revenues whatever the support mechanism used. We show that under recent climate and current market prices, profitability of wind farms is not guaranteed without support schemes. Using feed-in tariff (FiT) and feed-in premium (FiP) mechanisms with current level of support allows to guarantee profitability of wind farms in a large part of the domain. We also show that when projecting the future value of a wind farm based on historical production records, an investor can both overestimate or underestimate the profitability due to the natural variability of wind speed and to the presence of long-term trends.

Our second objective was to quantify the support level that will be needed in future to guarantee the profitability of the wind fleet, and to evaluate the cost of such support mechanisms. To address this objective, we simulated future price scenarios using electricity demand and renewable penetration projections from integrated assessment models. These scenarios were combined with wind speed and temperature projections from the regional climate model intercomparison project (CORDEX), corresponding to several Representative Concentration Pathways (RCP). This enabled us to model future local wind energy production and prices in a changing climate. Our approach allows to assess and quantify several relevant sources of uncertainty [39]: socio-economic uncertainties corresponding to the choices made by the society (e.g., the extent of climate change mitigation vs. adaptation), scientific uncertainties (corresponding to model simulations spread and associated with modelling errors), and natural/climate uncertainties (related to the natural variability of the earth system, including climate change).

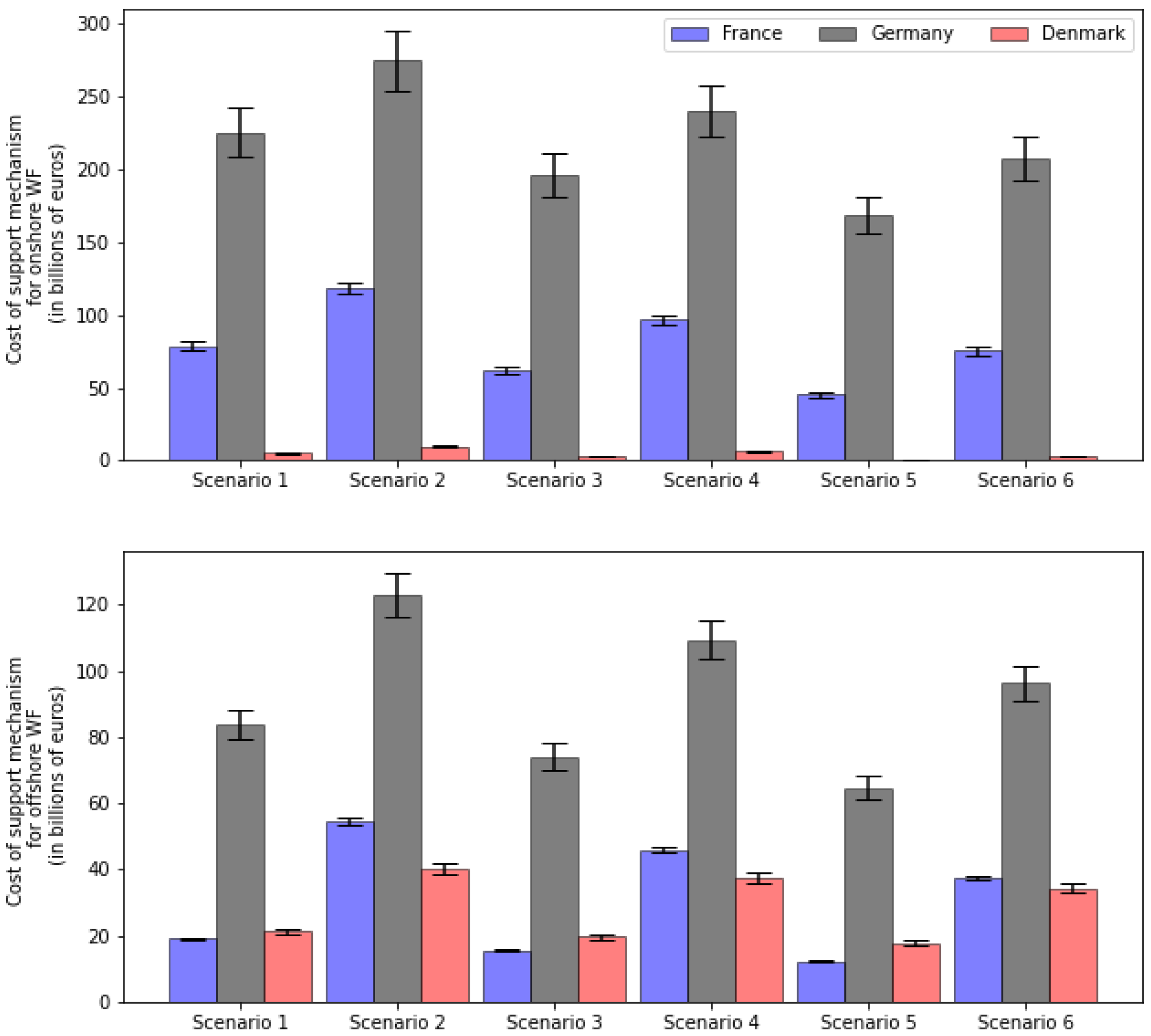
Under future climate scenarios, we show that profitability of wind farms is reached in several regions of the domain only in the specific scenario of high electrification and low penetration of wind energy. To guarantee profitability of 90% of the wind farms in the future, under the assumption that future wind fleet is installed following current spatial distribution, the required premium level in France for onshore (offshore) wind farms varies from 33 €/MWh (45 €/MWh) in the best case scenario to 66 €/MWh (78 €/MWh) in the worst case scenario. In Germany, the premium level for onshore (offshore) wind farms varies from 68 €/MWh (76 €/MWh) in the best case scenario to 93 €/MWh (102 €/MWh) in the worst case scenario. In Denmark, the premium level for onshore (onshore) wind farms varies from 1.5 €/MWh (83 €/MWh) in the best case scenario to 23 €/MWh (105 €/MWh) in the worst case scenario. According to these results, we find that supporting the penetration of wind energy in these countries during 15 years amounts to costs for the regulator ranging from EUR 3.8 to EUR 11.5 billion per year in France, from EUR 15.5 to EUR 26.5 billion per year in Germany, and from EUR 1.2 to EUR 3.3 billion per year in Denmark, depending on the scenario considered and the level of penetration of wind energy. In the preceding section, we computed aggregate costs for the period of 15 years, and here they are reported on a yearly basis to make comparisons easier.

These numbers should not be interpreted as global investment needs, but rather as costs of public support measures required to attract the necessary investments from the private sector. Let us compare them with the current support measures for wind energy in the three countries we analyse in this paper. In France, where the renewable energy penetration is the lowest among the three countries, the cost of public support measures for the wind energy industry amounted to EUR 1.2 billion in 2018, in Germany this number was EUR 9.7 billion, and in Denmark EUR 0.45 billion [40]. However, one needs to keep in mind that between 2012 and 2018, the renewable energy subsidies in the EU grew by about 4% per year, and given the current plans for massive deployment of renewables, further growth should be expected. The fact that our estimates for the future support needs are higher than the current subsidies can be explained, firstly, by the need to accelerate the energy transition to be able to meet the Paris Agreement goals, secondly, by the fact that at present when the number of wind farms is relatively low (especially in France), they are installed at the most profitable locations, which may no longer be available in future, and thirdly, by our modeling assumptions, some of which may introduce an upward bias. Let us briefly recall these assumptions here.

• Our analysis is based on the assumption (which is the actual situation in many countries) that the subsidy mechanism (feed-in tariff or feed-in premium) is the same for all wind farms within a country, and is not adjusted depending on the profitability of each specific farm. We have chosen, somewhat arbitrarily, to fix the parameters of the mechanism so that 90% of the farms are profitable. Our methodology can, of course, be used with any other number. This means that 10% of the farms do not receive a sufficient subsidy, and for 90% of the farms, the subsidy is higher than the minimum amount to ensure profitability. If the subsidy were determined individually for each site, as in renewable energy auctions, which are increasingly more common, each farm would receive just the required subsidy amount and the overall cost would be lower.
• Our analysis is completed assuming current market conditions, and, therefore, does not take into account the possible increase in carbon taxes/carbon costs, which are a key tool for energy transition and GHG emission reduction. By making electricity production with fossil fuels more expensive, carbon taxes make renewable producers more competitive. The revenues of renewable producers increase and this can be seen as an indirect subsidy, albeit at a cost to electricity consumers in the form of higher prices. For the same technology, this cost will generally be higher than the cost of direct subsidies, since higher electricity price is paid to all producers, whereas targeted subsidies are only paid to renewable producers. However, this can be partly compensated by distributing a part of the carbon tax to more vulnerable consumers, to also address the social issues of the energy transition. In our paper, the carbon prices are not taken into account directly, although the electricity demand scenarios from integrated assessment models we use may account for carbon pricing. We do not model carbon taxes directly since imposing carbon taxes is largely a political decision and their modeling requires assumptions on environmental policies of the concerned states, which may turn out to be incorrect. However, our results can be seen as an estimate of the cost of future renewable production, to be paid to renewable producers either in the form of subsidies or in the form of higher prices.
• Finally, our estimates do not take into account the potential reduction in costs of wind energy. Indeed, renewable energy production costs are declining. This decline is more significant for solar energy than for wind energy. For example, in a recent article [3], the capital expenditure for solar power plants is predicted to drop by 75%, while a drop of 40% is expected for onshore wind turbines. Since in our study new wind turbines are installed every year from 2020 to 2035, we can expect an average reduction of 10% in the CAPEX, which would lead to a reduction in the cost of public support measures of at least a similar magnitude.

Policy Implications

As the wind and solar energy industries mature, there is a tendency to phase out the subsidies for wind and solar energy production, and some new plants at particularly profitable locations are already being built without public support, see https://qz.com/1995355/the-era-of-subsidies-for-wind-and-solar-is-coming-to-a-close/ (last accessed on 8 August 2022). This is especially true for the solar energy, where, on the one hand, the capital costs are decreasing fast, and on the other hand, the cost of subsidies is higher in most countries [41], and their impact per euro spent in terms of GHG emission reductions is lower than for the wind energy [21]. However, our analysis shows that accelerating the deployment of wind energy at the rate required for a successful energy transition may require maintaining and even increasing the level of public support. This is consistent with the estimates of IRENA which projects a 26% increase in renewable energy subsidies between 2017 and 2050 [42]. Our second message is that while with the historical support measures, such as feed-in tariff and feed-in premium the required subsidies may be high, the variability of renewable energy output is such that using site-specific measures, such as renewable energy auctions may considerably reduce the need for public support.

6. Conclusions

In this study, we quantify the net present value of standardised wind power plants and the associated uncertainty in France, Germany, and Denmark under present and future climate, and we evaluate the cost of the support schemes needed to ensure the economic sustainability of the wind energy industry. The main contribution of our research is to combine, on the one hand, the information on the wind resource from reanalysis and climate scenarios, and on the other hand, information on energy prices from a model of electricity consumption based on climate data and economic scenarios. Building a realistic model for future wind farm revenues is a complex task and some important features had to be left to further research. First, the evolution of capital and operational costs of wind energy is not taken into account. The model for electricity prices does not include socio-economic factors other than electricity consumption and renewable energy production, such as, for example, fuel costs, or geopolitical uncertainty, which can temporarily lead to very high electricity prices as in 2021–2022. The economics of a wind farm is stylised, both in terms of revenues (we assume that it is given by the market price plus a premium but, for example, the role of aggregators is not taken into account) and in terms of wind production (we use the same turbine model everywhere with only a correction factor for offshore turbines). The price and consumption models are fitted over a relatively short 3-year period, and, for example, the bias in the reanalysis data is assumed to be constant in time.

Despite these limitations, our work provides an original integrated methodology to assess the uncertainties of wind farm net present value under current and future climate. The methodology is fairly general and it can be easily applied to other countries. The results of our analysis highlight the fundamental role that support schemes play and are likely to be playing in the future in guaranteeing the economic viability of wind power plants. Our study provides an estimate of the future costs of wind energy deployment, and a quantification of its uncertainty under different climate and socio-economic scenarios. We show that the final cost to achieve energy transition by supporting wind penetration is not negligible and that it can vary widely across countries.

In the future development of our methodology, the first step will be to include a more realistic model for electricity price formation, taking into account the merit order stack of electricity markets, the carbon price, and the stochastic evolution of fuel prices. The evolution of capital costs of wind power plants, with a realistic learning curve, will be an important building block. Finally, the social aspects of energy transition, from public acceptance of wind power plants to obstacles posed by rising energy prices will be taken into account.