Flexible Short-Term Electricity Certificates—An Analysis of Trading Strategies on the Continuous Intraday Market
Abstract
:1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contribution and Paper Organization
2. The Flexible Certificate
- Offering Period: daily 12:40 to 3 p.m.;
- Fulfillment: next day;
- Granularity: hourly;
- Price: day-ahead auction price + premium P;
- Volume: to be fixed in advance.
3. Data and Descriptive Statistic
3.1. Data
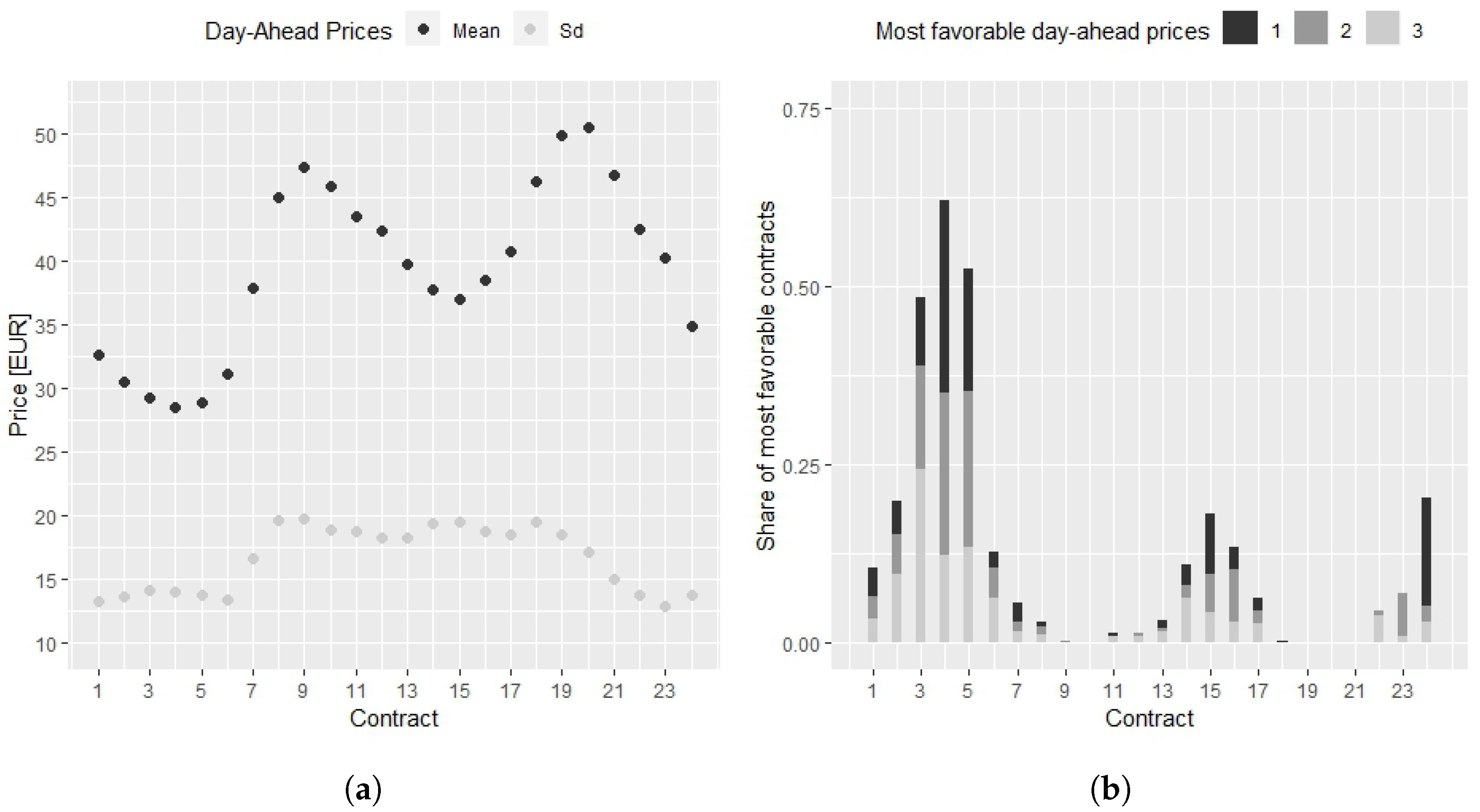
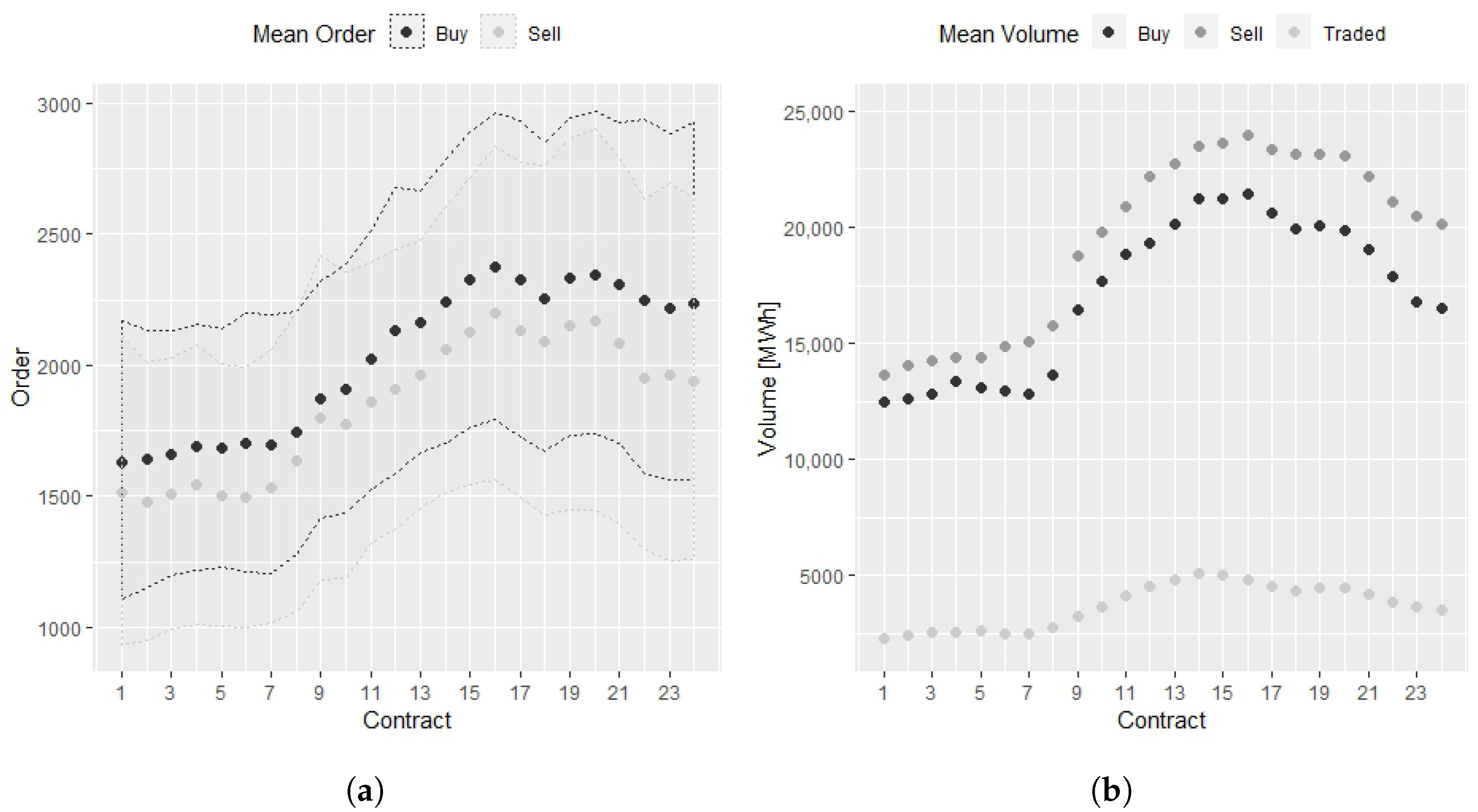
3.2. Descriptive Statistics and Implications
- The concentration could be on a few individual contracts on a daily basis;
- The market is liquid only in the hours before expiration;
- Due to forecast errors, early available prices might still be more attractive (despite high bid–ask spread);
- Bid–ask spreads are usually based on low-volume orders, so larger volumes should be bought/sold split;
- There are differences between 2017 and 2018 regarding liquidity.
4. Strategies
4.1. Definitions
- Up to 60 min before trading closes for a specific contract, the supplier buys (sells) any available volume (up to the required volume) at a price equal to or lower (higher) than the day-ahead auction price plus/minus an adjustment .
- If the necessary volume has not been reached 60 min before the close of trading, this criteria is softened for buying (selling) strategies by increasing (decreasing) linearly with remaining time.
- As a final option, the remaining required volume is bought (sold) five minutes before the close of trading at any price.
- Up to 60 min before the close of trading, besides the known criterion related to the day-ahead price, the supplier only trades if the bid–ask spread is smaller than a level S.
- Analogous to Strategy I, S is increased linearly if there is missing volume 60 min before close.
- As with Strategy I, the remaining required volume is bought (sold) five minutes before the close of trading at any price.
- Up to 240 min before the close of trading, the supplier only trades according to the day-ahead price criterion, analogous to Strategy I.
- Within the last 240 min before the close of trading, the strategy is identical to Strategy II.
4.2. Implementation
- We only consider orders where .
- If an order is executed, we remove any following orders with the same OrderID.
- The supplier of the certificate always buys (sells) at the best ask (bid) price for the quoted volume.
- We omit orders that would have been matched with another order that the supplier had previously executed.
- There are no transaction costs beyond the bid–ask spread.
5. Strategy Performance
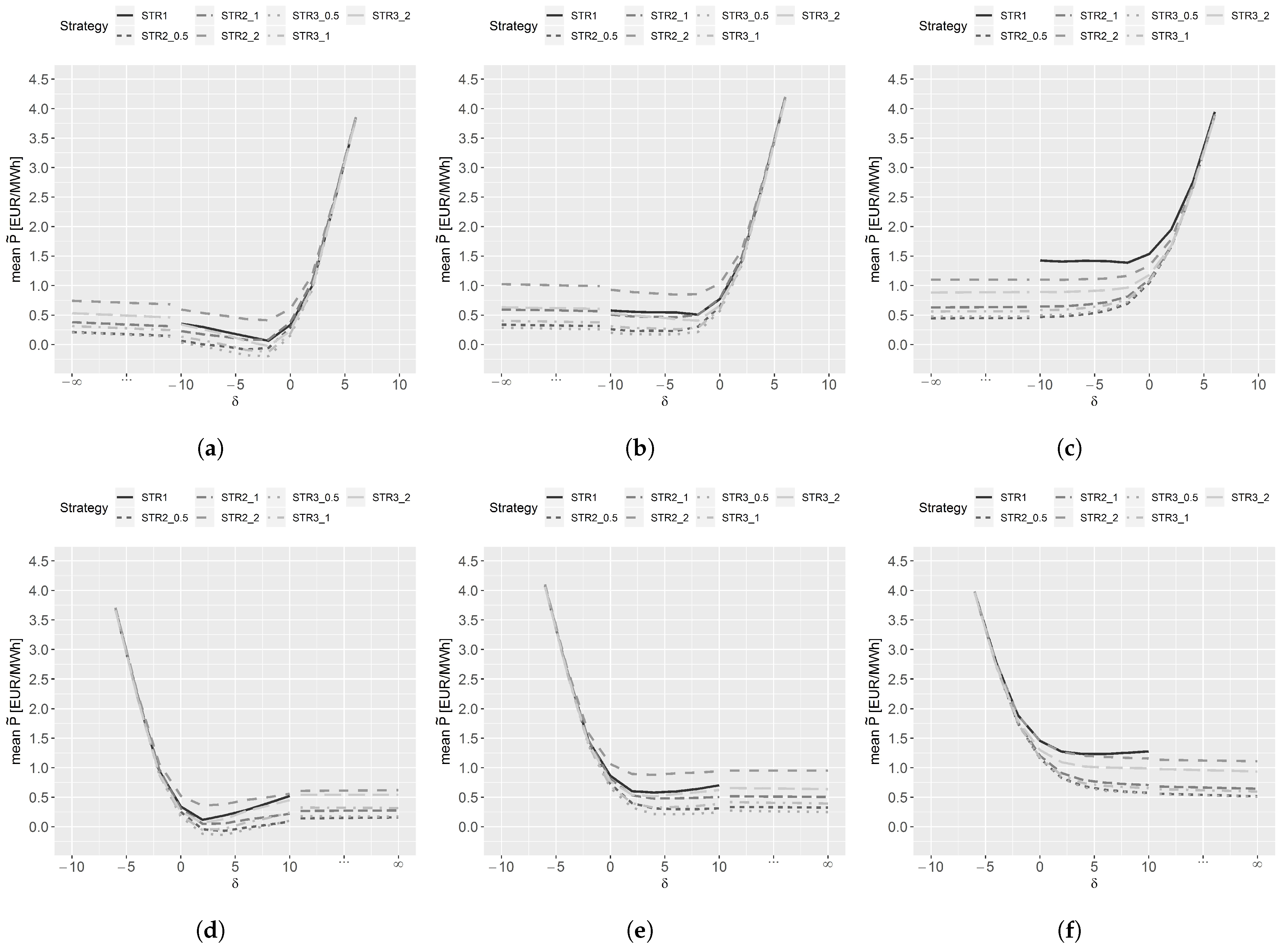
5.1. Average Premiums
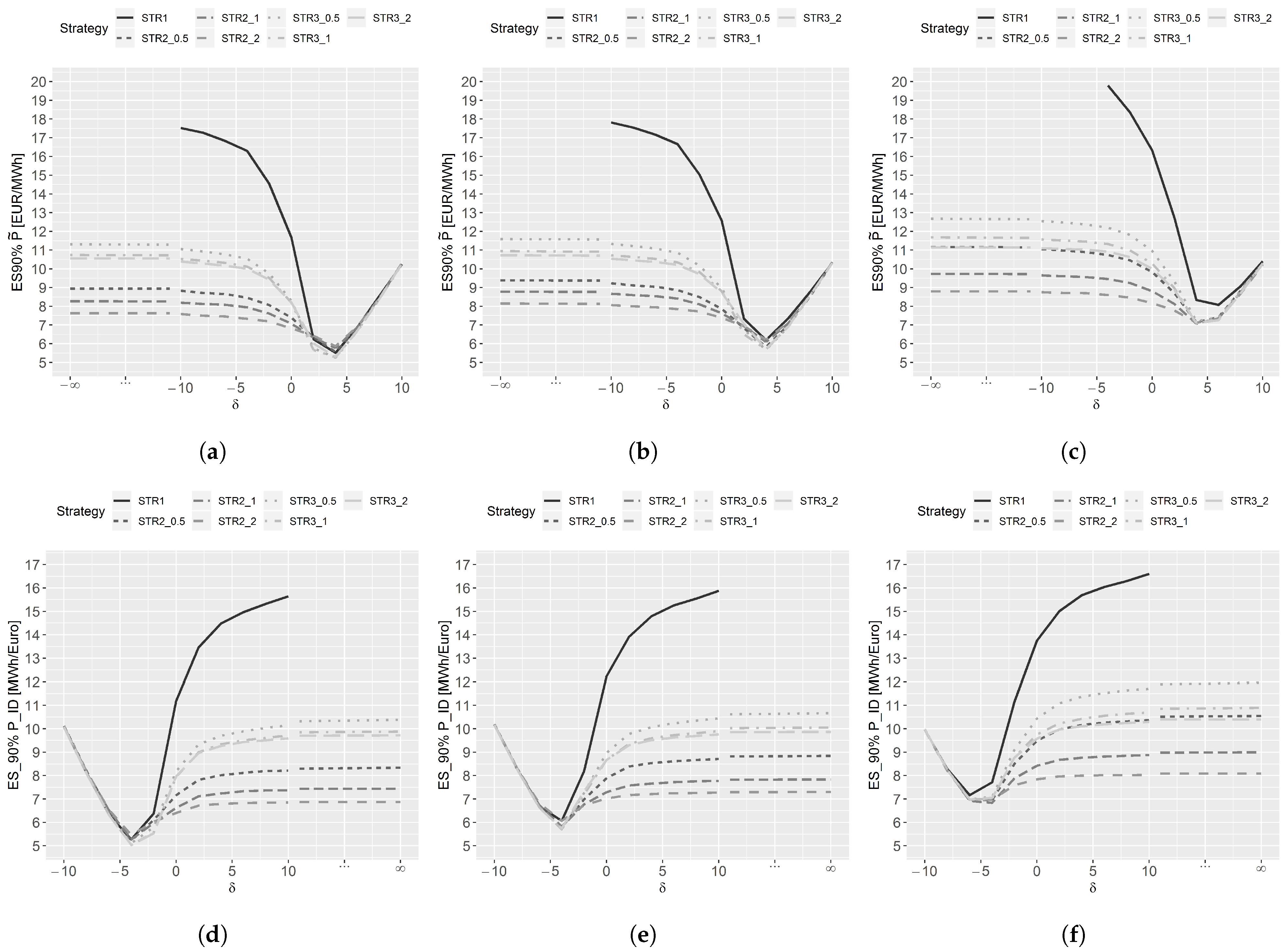
5.2. Risk
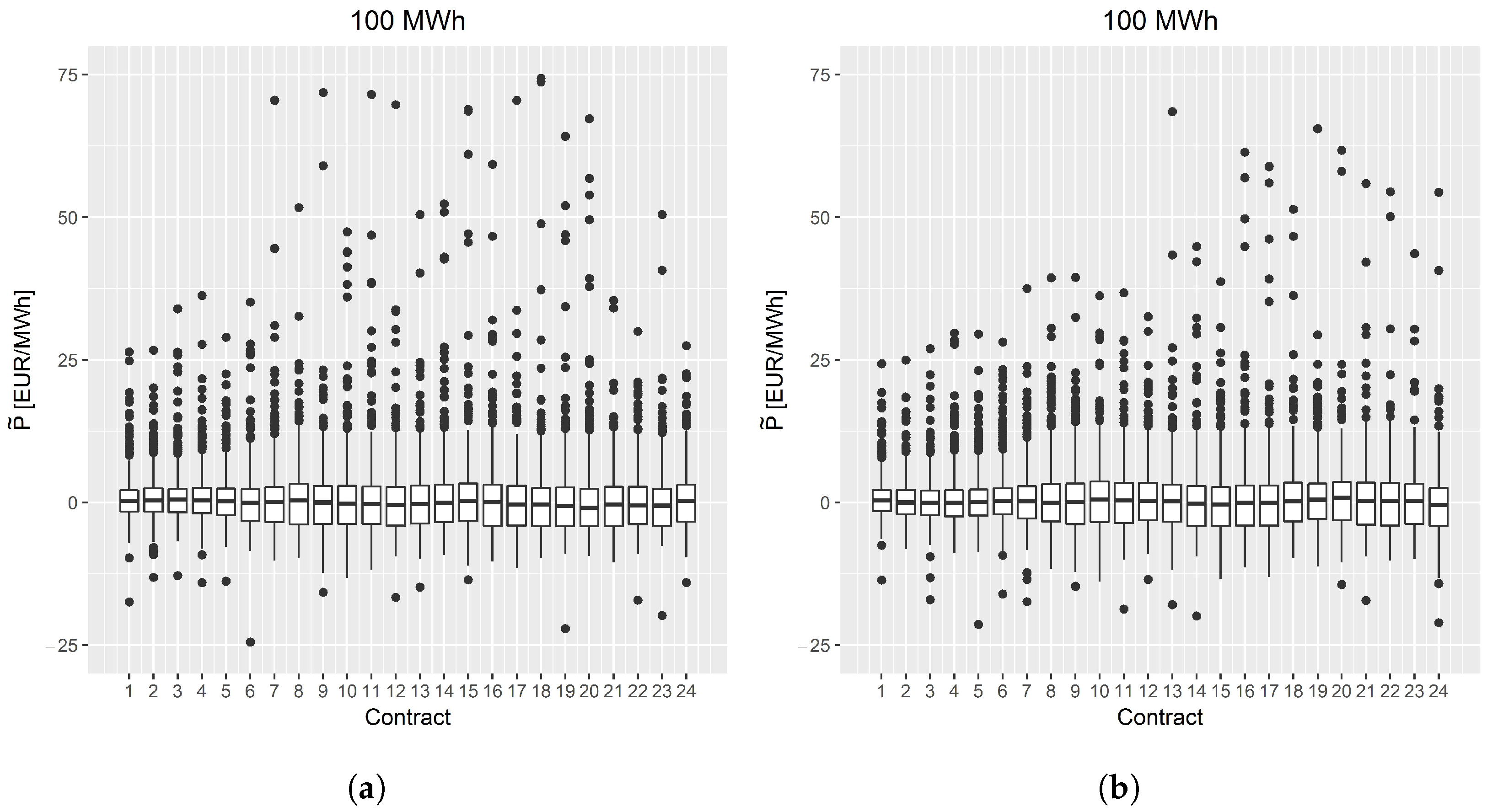
5.3. Analysis of Hourly Contracts
6. Time-Series Characteristics and External Drivers
7. Limit Prices
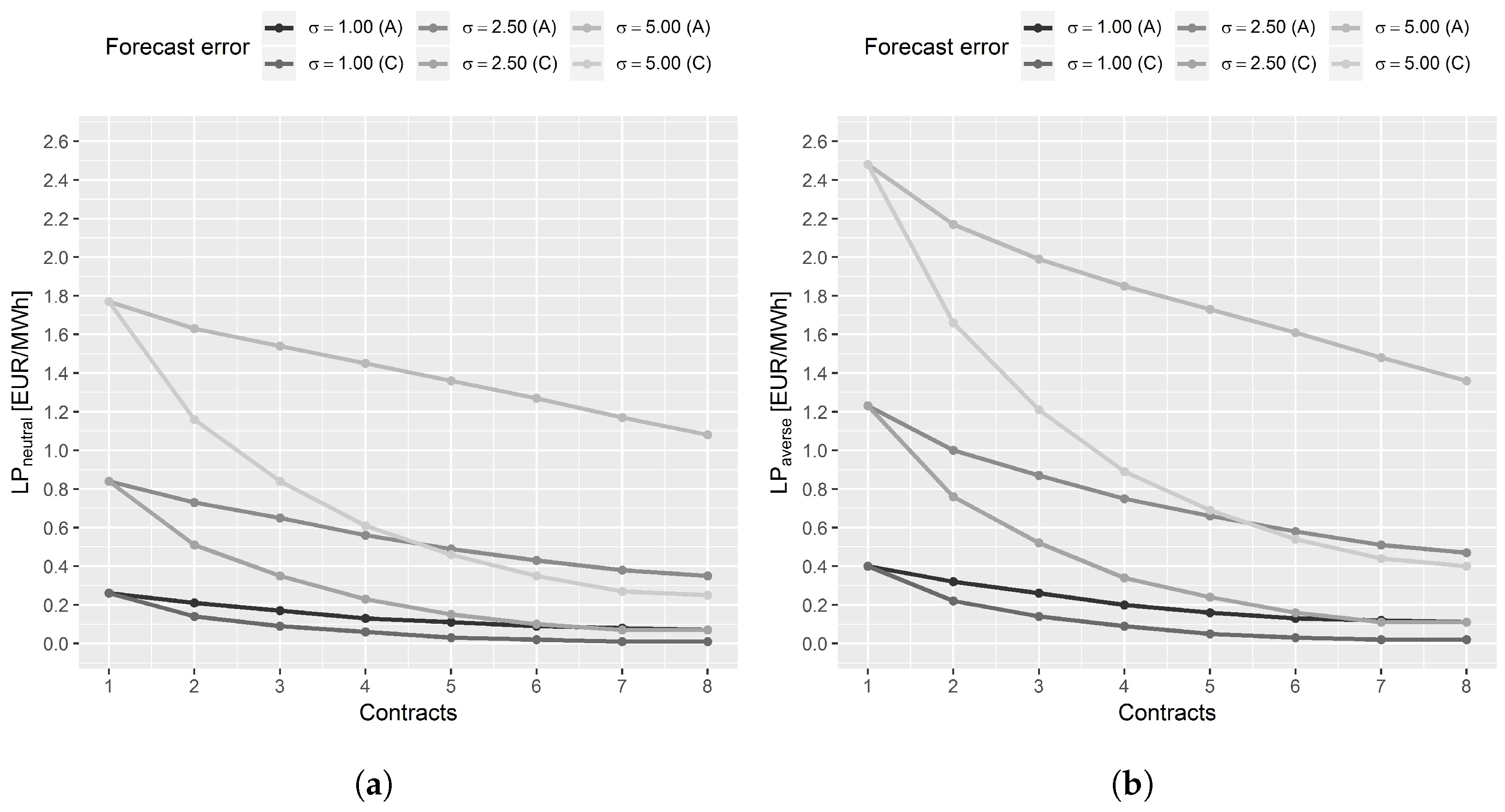
7.1. Methodology
7.2. Results
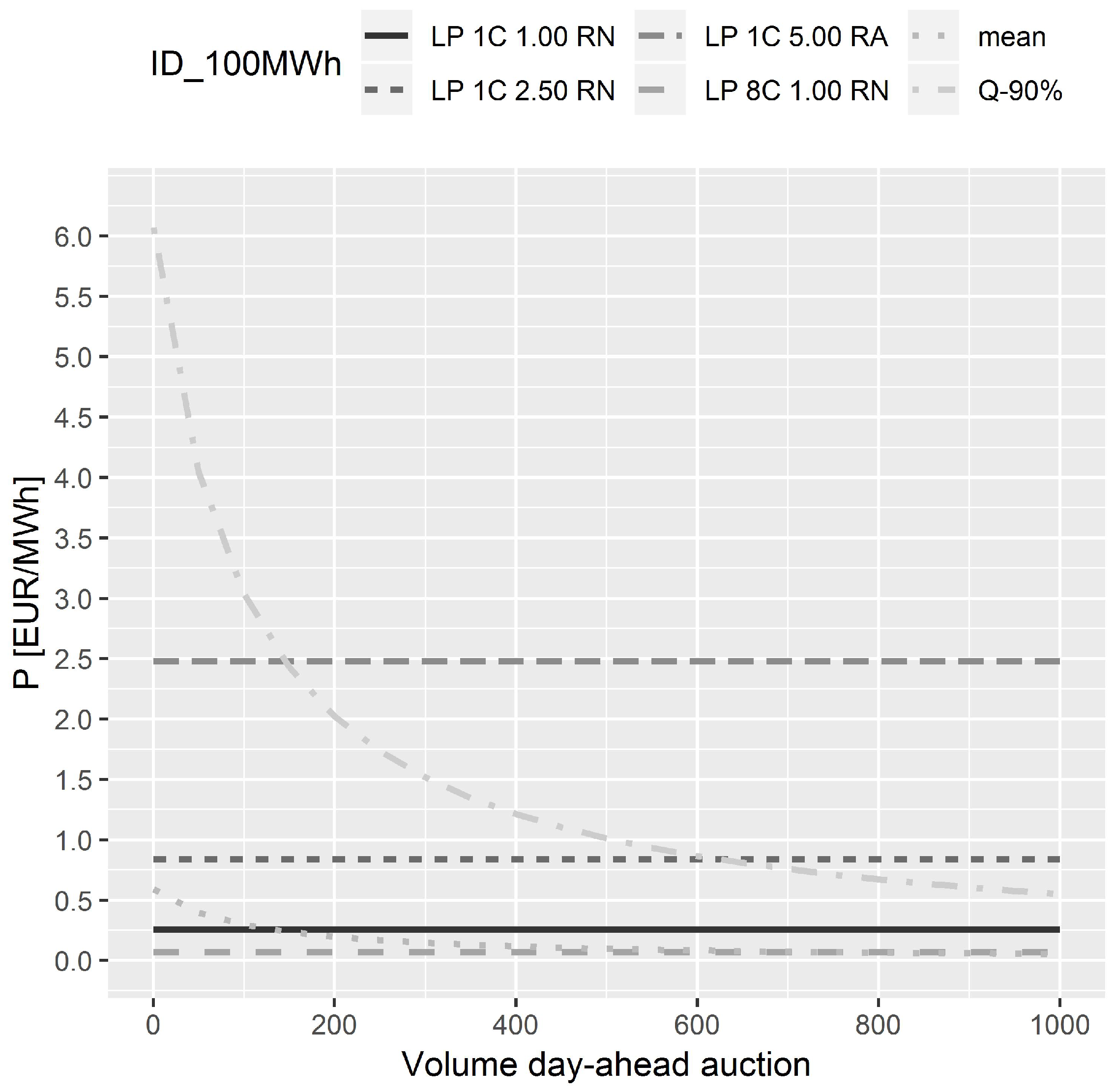
7.3. Relation to Strategy Premiums
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| P | Actual premium for the flexible certificate |
| Base premium for intraday trading | |
| Strategy premiums on the intraday market | |
| Traded volume on the intraday market | |
| Traded volume on the day-ahead market | |
| Add-on to day-ahead price | |
| Bid–ask spread | |
| S | Maximum bid–ask spread |
| Day-ahead price | |
| Forecast error | |
| Maximum price that a risk-neutral buyer would pay for the flexible certificate | |
| Maximum price that a risk/loss-averse buyer would pay for the flexible certificate | |
| MWh | Megawatt hour |
| GWh | Megawatt hour |
| TWh | Terawatt hour |
| C | Contract |
| ES | Expected shortfall |
| RA | Risk-neutral buyer |
| RN | Risk/loss-averse buyer |
| (A) | Arbitrary |
| (C) | Consecutive |
References
- Busse, J.; Rieck, J. Mid-term energy cost-oriented flow shop scheduling: Integration of electricity price forecasts, modeling, and solution procedures. Comput. Ind. Eng. 2022, 163, 107810. [Google Scholar] [CrossRef]
- Braschczok, D.; Dellnitz, A.; Hilbert, M.; Kleine, A.; Ostmeyer, J. Energy costs vs. carbon dioxide emissions in short-term production planning. J. Bus. Econ. 2020, 90, 1383–1407. [Google Scholar]
- Busse, J.; Windler, T.; Rieck, J. One month-ahead electricity price forecasting in the context of production planning. J. Clean. Prod. 2019, 238, 117910. [Google Scholar]
- Braunreuther, S.; Keller, F.; Reinhart, G.; Schultz, C. Enabling energy-flexibility of manufacturing systems through new approaches within production planning and control. Procedia CIRP 2016, 57, 752–757. [Google Scholar]
- Finnah, B.; Gönsch, J.; Ziel, F. Integrated day-ahead and intraday self-schedule bidding for energy storage systems using approximate dynamic programming. Eur. J. Oper. Res. 2022, 301, 726–746. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Anvari-Moghaddam, A.; Siano, P. Risk-averse probabilistic framework for scheduling of virtual power plants considering demand response and uncertainties. Int. J. Electr. Power Energy Syst. 2020, 121, 106126. [Google Scholar] [CrossRef]
- Wozabal, D.; Rameseder, G. Optimal bidding of a virtual power plant on the Spanish day-ahead and intraday market for electricity. Eur. J. Oper. Res. 2020, 280, 639–655. [Google Scholar] [CrossRef]
- Finnah, B. Optimal bidding functions for renewable energies in sequential electricity markets. OR Spectr. 2022, 44, 1–27. [Google Scholar] [CrossRef]
- Finnah, B.; Gönsch, J. Optimizing trading decisions of wind power plants with hybrid energy storage systems using backwards approximate dynamic programming. Int. J. Prod. Econ. 2021, 238, 108155. [Google Scholar] [CrossRef]
- Marijanovic, Z.; Theile, P.; Czock, B.H. Value of short-term heating system flexibility—A case study for residential heat pumps on the German intraday market. Energy 2022, 249, 123664. [Google Scholar] [CrossRef]
- Busse, J.; Rieck, J. Electricity price-oriented scheduling within production planning stage. In Operations Research Proceedings; Springer: Berlin/Heidelberg, Germany, 2018; pp. 161–166. [Google Scholar]
- Erdmann, G.; Praktiknjo, A.; Zweifel, P. Energy Economics: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Henriot, A. Market design with centralized wind power management: Handling low-predictability in intraday markets. Energy J. 2014, 35, 99–117. [Google Scholar] [CrossRef]
- Garnier, E.; Madlener, R. Balancing forecast errors in continuous-trade intraday markets. Energy Syst. 2015, 6, 362–388. [Google Scholar] [CrossRef]
- Skajaa, A.; Edlund, K.; Morales, J. Intraday trading of wind energy. IEEE Trans. Power Syst. 2015, 30, 3181–3189. [Google Scholar] [CrossRef]
- Gönsch, J.; Hassler, M. Sell or store? An ADP approach to marketing renewable energy. OR Spectr. 2016, 38, 633–660. [Google Scholar] [CrossRef]
- Hassler, M. Heuristic decision rules for short-term trading of renewable energy with co-located energy storage. Comput. Oper. Res. 2017, 83, 199–213. [Google Scholar] [CrossRef]
- Bertrand, G.; Papavasoliou, A. Adaptive Trading in Continuous Intraday Electricity Markets for a Storage Unit. IEEE Trans. Power Syst. 2020, 35, 2339–2350. [Google Scholar] [CrossRef]
- Boukas, I.; Ernst, D.; Tháte, T.; Bolland, A.; Huynen, A.; Buchwald, M.; Wynants, C.; Cornélusse, B. A deep reinforcement learning framework for continuous intraday market bidding. Mach. Lang. 2021, 110, 2335–2387. [Google Scholar] [CrossRef]
- Koch, C. Intraday imbalance optimization: Incentives and impact of strategic intraday bidding behavior. Energy Syst. 2022, 13, 409–435. [Google Scholar] [CrossRef]
- Serafin, T.; Marcjasz, G.; Weron, R. Trading on short-term path forecasts of intraday electricity prices. Energy Econ. 2022, 112, 106125. [Google Scholar] [CrossRef]
- Hagemann, S. Price determinants in the German intraday market for electricity: An empirical analysis. J. Energy Mark. 2015, 8, 21–45. [Google Scholar] [CrossRef]
- Gianfreda, A.; Parisio, L.; Pelagatti, M. The Impact of RES in the Italian Day–Ahead and Balancing Markets. Energy J. 2016, 37, 161–184. [Google Scholar] [CrossRef]
- Ziel, F. Modeling the impact of wind and solar power forecasting errors on intraday electricity prices. In Proceedings of the 14th International Conference on the European Energy Market, Dresden, Germany, 6–9 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Kulakov, S.; Ziel, F. The Impact of Renewable Energy Forecasts on Intraday Electricity Prices. Econ. Energy Environ. Policy 2021, 10. [Google Scholar] [CrossRef]
- Pape, C.; Hagemann, S.; Weber, C. Are fundamentals enough? Explaining price variations in the German day-ahead and intraday power market. Energy Econ. 2016, 54, 376–387. [Google Scholar] [CrossRef] [Green Version]
- Kiesel, R.; Paraschiv, F. Econometric analysis of 15-minute intraday electricity price. Energy Econ. 2017, 64, 77–90. [Google Scholar] [CrossRef]
- Karanfil, F.; Li, Y. The Role of Continuous Intraday Electricity Markets: The Integration of Large-Share Wind Power Generation in Denmark. Energy J. 2017, 38, 107–130. [Google Scholar] [CrossRef]
- Scharff, R.; Amelin, M. Trading behaviour on the continuous intraday market Elbas. Energy Policy 2016, 88, 544–557. [Google Scholar] [CrossRef]
- Narajewski, M.; Ziel, F. Econometric modelling and forecasting of intraday electricity prices. J. Commod. Mark. 2020, 19, 100107. [Google Scholar] [CrossRef]
- Kath, C. Modeling intraday markets under the new advances of the cross-border intraday project (XBID): Evidence from the German intraday market. Energies 2019, 12, 4339. [Google Scholar] [CrossRef]
- Baule, R.; Naumann, M. Volatility and Dispersion of Hourly Electricity Contracts on the German Continuous Intraday Market. Energies 2021, 14, 7531. [Google Scholar] [CrossRef]
- Steinert, R.; Ziel, F. Electricity price forecasting using sale and purchase curves: The X-Model. Energy Econ. 2016, 59, 435–454. [Google Scholar]
- Weron, R.; Ziel, F. Day-ahead electricity price forecasting with high-dimensional structures: Univariate vs. multivariate modeling frameworks. Energy Econ. 2018, 70, 396–420. [Google Scholar]
- Zhang, J.L.; Zhang, Y.J.; Li, D.Z.; Tan, Z.F.; Ji, J.F. Forecasting day-ahead electricity prices using a new integrated model. Int. J. Electr. Power Energy Syst. 2019, 105, 541–548. [Google Scholar] [CrossRef]
- Maciejowska, K.; Nitka, W.; Weron, T. Enhancing load, wind and solar generation for day-ahead forecasting of electricity prices. Energy Econ. 2021, 99, 105273. [Google Scholar] [CrossRef]
- Qussous, R.; Harder, N.; Weidlich, A. Understanding Power Market Dynamics by Reflecting Market Interrelations and Flexibility-Oriented Bidding Strategies. Energies 2022, 15, 494. [Google Scholar] [CrossRef]
- Kuppelwieser, T.; Wozabal, D. Liquidity costs on intraday power markets: Continuous trading versus auctions. Energy Policy 2021, 154, 112299. [Google Scholar] [CrossRef]
- Balardy, C. An Empirical Analysis of the Bid-ask Spread in the Continuous Intraday Trading of the German Power Market. Energy J. 2022, 43. [Google Scholar] [CrossRef]
- Martin, H.; Otterson, S. German intraday electricity market analysis and modeling based on the limit order book. In Proceedings of the 15th International Conference on the European Energy Market, Lodz, Poland, 27–29 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 639–644. [Google Scholar]
- Artzner, P.; Delbaen, F.; Eber, J.M.; Heath, D. Thinking coherently. Risk 1997, 10, 68–71. [Google Scholar]
- Koch, C.; Maskos, P. Passive Balancing Through Intraday Trading: Whether Interactions Between Short-term Trading and Balancing Stabilize Germany’s Electricity System. Int. J. Energy Econ. Policy 2020, 10, 101–112. [Google Scholar] [CrossRef]
- Newey, W.K.; West, K.D. Hypothesis testing with efficient method of moments estimation. Int. Econ. Rev. 1987, 28, 777–787. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–292. [Google Scholar] [CrossRef]
- Benartzi, S.; Thaler, R. Risk aversion or myopia? Choices in repeated gambles and retirement investmens. Manag. Sci. 1999, 45, 364–381. [Google Scholar] [CrossRef]
- Thaler, R.H. Toward a positive theory of consumer choice. J. Econ. Behav. Organ. 1980, 1, 39–60. [Google Scholar] [CrossRef]
- Thaler, R.H. Mental accounting and consumer choice. Mark. Sci. 1985, 4, 199–214. [Google Scholar] [CrossRef]
- Müller, T.; Möst, D. Demand response potential: Available when needed? Energy Policy 2018, 115, 181–198. [Google Scholar] [CrossRef]
- Pape, C. The impact of intraday markets on the market value of flexibility—Decomposing effects on profile and the imbalance costs. Energy Econ. 2018, 76, 186–201. [Google Scholar] [CrossRef] [Green Version]



| 2017 | 2018 | Total | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Q1 | Q2 | Q3 | Q4 | Q1 | Q2 | Q3 | Q4 | ||
| # Buy (Mio.) | 3.15 | 3.03 | 2.96 | 3.58 | 4.31 | 4.77 | 5.16 | 7.49 | 34.45 |
| Vol. Buy (TWh) | 40.61 | 34.00 | 34.67 | 42.06 | 43.82 | 45.11 | 40.14 | 50.70 | 331.11 |
| Buy (EUR) | 29.32 | 20.35 | 20.44 | 14.82 | 28.79 | 23.59 | 30.54 | 14.14 | 22.74 |
| # Sell (Mio) | 2.46 | 2.41 | 2.62 | 3.22 | 3.88 | 4.34 | 4.78 | 7.65 | 31.37 |
| Vol. Sell (TWh) | 31.66 | 27.43 | 30.13 | 36.64 | 37.87 | 40.37 | 36.30 | 50.04 | 290.43 |
| Sell (EUR) | 58.82 | 40.70 | 45.66 | 56.85 | 44.78 | 49.23 | 93.92 | 94.58 | 60.53 |
| Tr. Vol. (TWh) | 7.55 | 7.52 | 7.33 | 7.65 | 7.97 | 8.58 | 7.88 | 8.10 | 62.57 |
| # Contracts | 2073 | 2158 | 2176 | 2114 | 2066 | 2119 | 2159 | 2085 | 16,950 |
| Buying Strategy | Selling Strategy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: Strategy III with | |||||||||||
| min | −47.92 | −24.46 | −26.03 | −26.12 | −25.33 | −17.29 | −21.36 | −21.36 | −23.47 | −48.29 | |
| median | 0.28 | 0.25 | −0.01 | −0.28 | 2.59 | 2.69 | −0.24 | 0.14 | 0.38 | 0.44 | |
| mean | 0.48 | 0.50 | 0.59 | 1.07 | 2.66 | 2.72 | 1.16 | 0.67 | 0.57 | 0.51 | |
| max | 182.84 | 182.84 | 182.84 | 154.13 | 122.36 | 84.52 | 84.52 | 84.52 | 84.52 | 84.52 | |
| sd | 7.19 | 6.78 | 6.23 | 4.99 | 3.44 | 2.86 | 4.24 | 5.28 | 5.88 | 6.62 | |
| skewness | 4.15 | 5.59 | 7.21 | 8.92 | 14.20 | 8.98 | 4.87 | 2.78 | 1.81 | 0.10 | |
| kurtosis | 78.63 | 95.74 | 131.31 | 156.83 | 341.04 | 158.75 | 48.42 | 21.67 | 14.98 | 16.52 | |
| 12.68 | 12.55 | 12.20 | 10.96 | 7.21 | 7.09 | 10.44 | 11.37 | 11.70 | 11.96 | ||
| Panel B: Strategy III with | |||||||||||
| min | −45.33 | −26.03 | −26.03 | −26.12 | −25.33 | −17.29 | −21.36 | −21.36 | −23.47 | −48.23 | |
| median | 0.43 | 0.40 | 0.22 | −0.25 | 2.59 | 2.69 | −0.21 | 0.36 | 0.52 | 0.56 | |
| mean | 0.56 | 0.58 | 0.67 | 1.08 | 2.65 | 2.71 | 1.17 | 0.74 | 0.66 | 0.60 | |
| max | 160.04 | 160.04 | 160.04 | 160.04 | 118.79 | 74.49 | 74.49 | 74.49 | 74.49 | 74.49 | |
| sd | 6.65 | 6.30 | 5.82 | 4.69 | 3.24 | 2.75 | 3.97 | 4.89 | 5.41 | 6.09 | |
| skewness | 4.35 | 5.74 | 7.23 | 8.94 | 13.27 | 8.87 | 4.64 | 2.57 | 1.66 | −0.12 | |
| kurtosis | 85.41 | 102.18 | 135.61 | 171.07 | 310.02 | 161.58 | 48.27 | 21.63 | 15.51 | 18.39 | |
| 11.68 | 11.57 | 11.32 | 10.30 | 7.10 | 7.01 | 9.75 | 10.43 | 10.69 | 10.89 | ||
| Panel C: Strategy III with | |||||||||||
| min | −43.55 | −24.46 | −24.46 | −24.46 | −22.83 | −17.29 | −21.36 | −21.36 | −23.47 | −48.23 | |
| median | 0.77 | 0.75 | 0.62 | −0.21 | 2.59 | 2.69 | −0.16 | 0.79 | 0.90 | 0.92 | |
| mean | 0.88 | 0.89 | 0.92 | 1.18 | 2.65 | 2.72 | 1.30 | 1.02 | 0.99 | 0.94 | |
| max | 155.29 | 155.29 | 155.29 | 105.20 | 91.00 | 68.07 | 68.07 | 68.07 | 68.07 | 68.07 | |
| sd | 6.02 | 5.77 | 5.37 | 4.32 | 2.98 | 2.58 | 3.81 | 4.65 | 5.06 | 5.64 | |
| skewness | 3.42 | 4.50 | 5.51 | 6.60 | 10.58 | 7.15 | 3.71 | 1.98 | 1.18 | −0.53 | |
| kurtosis | 65.10 | 73.64 | 92.45 | 96.06 | 212.19 | 123.47 | 34.49 | 15.84 | 12.04 | 17.89 | |
| 11.15 | 11.10 | 10.92 | 10.00 | 7.10 | 7.05 | 9.58 | 10.11 | 10.29 | 10.40 | ||
| Buying Strategy | Selling Strategy | ||||||
|---|---|---|---|---|---|---|---|
| Mean | 90% | 95% | Mean | 90% | 95% | ||
| Panel A: Years | |||||||
| 2017 | 0.63 | 6.08 | 8.95 | 0.95 | 6.70 | 9.89 | 8521 |
| 2018 | 0.55 | 6.06 | 8.76 | 0.38 | 5.75 | 8.29 | 8429 |
| Panel B: Day-ahead auction prices | |||||||
| lowest | 1.88 | 8.18 | 11.95 | −0.35 | 4.69 | 8.71 | 707 |
| 2 lowest | 1.58 | 7.57 | 11.53 | −0.11 | 4.90 | 8.28 | 1417 |
| 3 lowest | 1.34 | 7.16 | 10.72 | −0.05 | 4.90 | 8.32 | 2118 |
| 4 lowest | 1.18 | 6.69 | 10.18 | 0.09 | 5.11 | 8.40 | 2821 |
| 5 lowest | 1.08 | 6.31 | 10.00 | 0.21 | 5.18 | 8.50 | 3513 |
| 6 lowest | 0.96 | 6.23 | 9.65 | 0.33 | 5.39 | 8.74 | 4220 |
| highest | −0.19 | 5.59 | 8.19 | 1.83 | 7.97 | 11.86 | 717 |
| 2 highest | −0.02 | 5.57 | 8.33 | 1.52 | 7.64 | 11.35 | 1426 |
| 3 highest | 0.03 | 5.56 | 8.34 | 1.45 | 7.43 | 10.82 | 2141 |
| 4 highest | 0.13 | 5.58 | 8.19 | 1.36 | 7.34 | 10.36 | 2851 |
| 5 highest | 0.15 | 5.59 | 8.11 | 1.24 | 7.27 | 9.96 | 3547 |
| 6 highest | 0.16 | 5.69 | 8.17 | 1.20 | 7.14 | 9.81 | 4267 |
| 8.77 | 27.39 | 36.25 | −2.33 | 5.47 | 18.69 | 254 | |
| min | −9.697 | −4.698 | −24.00 | −15.84 | 0.003 | 0.000 |
| 25% | −0.597 | −0.019 | −8.249 | −0.248 | 0.089 | 0.000 |
| median | 0.047 | 0.000 | −4.823 | 0.970 | 0.175 | 0.002 |
| mean | 0.138 | 0.004 | −5.381 | 1.081 | 0.214 | 0.072 |
| 75% | 0.841 | 0.008 | −2.217 | 2.351 | 0.306 | 0.113 |
| max | 10.78 | 4.662 | 19.42 | 10.26 | 0.848 | 0.584 |
| sd | 1.434 | 0.669 | 4.680 | 2.006 | 0.157 | 0.112 |
| Panel A: Buying Strategy | Panel B: Selling Strategy | |||||
|---|---|---|---|---|---|---|
| 0.1 MWh | 10 MWh | 100 MWh | 0.1 MWh | 10 MWh | 100 MWh | |
| −1.878 ** | −1.287 * | −1.178 | 0.348 | 1.148 * | 1.575 ** | |
| (0.642) | (0.632) | (0.644) | (0.541) | (0.49) | (0.497) | |
| −1.152 *** | −1.234 *** | −1.477 *** | 1.143 *** | 1.217 *** | 1.410 *** | |
| (0.088) | (0.085) | (0.079) | (0.074) | (0.069) | (0.069) | |
| −0.948 *** | -0.942 *** | −1.210 *** | 0.892 *** | 0.936 *** | 1.192 *** | |
| (0.116) | (0.115) | (0.13) | (0.119) | (0.116) | (0.112) | |
| 0.024 | 0.001 | 0.004 | −0.046 | −0.032 | −0.007 | |
| (0.036) | (0.035) | (0.038) | (0.038) | (0.035) | (0.035) | |
| 0.234 *** | 0.263 *** | 0.299 *** | −0.184 ** | −0.235 *** | −0.255*** | |
| (0.052) | (0.052) | (0.054) | (0.063) | (0.061) | (0.058) | |
| 2.424 * | 2.327 * | 3.356 ** | −2.223 * | −1.494 | −0.919 | |
| (1.13) | (1.13) | (1.214) | (1.006) | (0.984) | (1.08) | |
| 2.715 | 2.345 | 2.445 | −5.226 ** | −4.195 * | −2.05 | |
| (1.58) | (1.51) | (1.681) | (1.717) | (1.697) | (1.788) | |
| fixed effects | yes | yes | yes | yes | yes | yes |
| adj. | 0.092 | 0.111 | 0.154 | 0.120 | 0.144 | 0.184 |
| Observations | 16,631 | 16,631 | 16,631 | 16,631 | 16,631 | 16,631 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baule, R.; Naumann, M. Flexible Short-Term Electricity Certificates—An Analysis of Trading Strategies on the Continuous Intraday Market. Energies 2022, 15, 6344. https://doi.org/10.3390/en15176344
Baule R, Naumann M. Flexible Short-Term Electricity Certificates—An Analysis of Trading Strategies on the Continuous Intraday Market. Energies. 2022; 15(17):6344. https://doi.org/10.3390/en15176344
Chicago/Turabian StyleBaule, Rainer, and Michael Naumann. 2022. "Flexible Short-Term Electricity Certificates—An Analysis of Trading Strategies on the Continuous Intraday Market" Energies 15, no. 17: 6344. https://doi.org/10.3390/en15176344
APA StyleBaule, R., & Naumann, M. (2022). Flexible Short-Term Electricity Certificates—An Analysis of Trading Strategies on the Continuous Intraday Market. Energies, 15(17), 6344. https://doi.org/10.3390/en15176344





