Heat Transfer Enhancement through Thermodynamical Activity of H₂O/Clay Nanofluid Flow over an Infinite Upright Plate with Caputo Fractional-Order Derivative

Abstract

This paper presents a modelling of nanofluid flow using Caputo fractional derivatives through conservative equations of mass and momentum, and provides an exact solution on un-steady convective flow over a vertical plate with the mass diffusion effect, in association with an energy equation. H₂O is the base liquid with clay nanoparticles floating in it in a uniform way. Boussinessq’s approach is used in the momentum equation for pressure gradient. The non-dimensional fluid temperature, species concentration and fluid transport are derived together with Jacob Fourier sine and Laplace transform techniques in terms of exponential decay function, and the inverse is computed further in terms of the Mittag-Leffler function. The impact of various physical quantities is interpreted with the fractional order of the Caputo derivatives. The obtained temperature, transport and species concentration profiles show behaviors for 0 < $\mathsf{\alpha }$ < 1, where $\mathsf{\alpha }$ is the fractional parameter. The rate of heat and mass transfer coefficients for the significance of physical quantities of interest are also obtained and presented through graphs. The impact of the nanoparticle volume fraction on the flow field is observed. At larger values of the fractional parameter, the velocity, temperature, and concentration distributions grow more quickly. In addition to that, it is found the concentration profiles behave in the opposite way for the volume fraction of nanofluids.

1. Introduction

Nanofluid is a homogenous combination of convectional base fluids such as water, ethylene glycol, oils, polymer solutions, and other lubricants, and extremely small nanoparticles with diameters less than 100 nm. The significance of nanotechnology for enhancing the heat capacity of liquids by increasing heat and mass transport rates is gaining prominence. Nanofluids have been an issue for the academic community in recent years because of their wide variety of applications in heat exchangers, biomedicine, electrical device cooling, double windowpanes, food, transportation, and other sectors. Different kinds of nanoparticles may be added to the base fluids, such as graphene, silica, silver, gold, copper, alumina, carbon nanotubes, and so on, to boost the heat capacity of common fluids such as water, kerosene, and motor oils. Choi and Eastman [1] were first to introduce these nanofluids. A vast number of research papers dealing with enhancing the heat conductivity of base liquids by accumulating different kinds of nanoparticles have been published in the literature. Wong et al. [2] covered a wide range of nanofluid uses. To make nanofluids easier to understand, Mohain et al. [3] provided critical thinking and fresh innovations. A comprehensive elucidation of thermophysical properties and an accurate simulation of heat transfer in nanofluid flow were the main points of focus for the researchers. Eastman et al. [4,5] reported that when CuO nanoparticles with a volume fraction of 5% were introduced to the base fluid (water), the heat conduction of the considered base fluid increased, at most, 0.6, whereas when 1% copper nanoparticles were introduced into ethylene glycol or oil, thermal conductivity increased by 40%. This is due to metals having three times greater thermal conductivity of general fluids; this is one of the aspects of carrying out heat transmission by combining two elements that act as fluid matter. CNT nanofluid was studied by Mandal Gopinath [6] by examining the applied magnetic field under the impact of thermal radiation, variable thermal conductivity, and mass diffusivity, as well as binary chemical reaction with energy loss analysis across a linearly extending cylinder. Daniel [7] have studied the effects of variable thermal conductivity and the chemical reaction of the first order of MHD in the presence of non-linear thermal radiation with nanofluid over a flat plate in a porous zone. Chemically reactive magnetic nanofluid was heated by Dulal Pal’s [8] consideration of the aligned magnetic field on the pore surface under non-linear thermal radiation, variable thermal conductivity, and suction. References [9,10,11] provide a few studies on nanofluids.

In this paper, we investigate the heat transmission of a viscous (clay water-based) nanofluid across a surface of an upright vertical plate. Clay nanoparticles are natural nanoscale substances derived from clay. Due to their extensive use, they have received great attention in recent years. Owing to their high surface area and unique physical and chemical characteristics, there is a considerable interest in exploiting clay nanoparticles for a variety of applications. Clay nanoparticles have been used effectively to conserve artwork materials such as marble and porous stones, metal surfaces, bread-made items, and ancient woods and paper. Additionally, water-based clay nanofluid is called a drilling nanofluid; the drilling fluid used in the current research is mud that circulates in the cylindrical borehole and is a nanofluid designed to increase drilling operation efficiency and cost effectiveness. Drilling fluid removes the cuttings from the bottom of the hole while lubricating and cooling the drill bit to increase productivity and stability. The goal of the ongoing study is to increase the drilling fluid’s effectiveness. The following are some of the most important functions of the drilling fluid: (1) to block the pores in rock formations in wells, a thin, low-permeability filter cake is made; (2) by applying hydrostatic pressure, formation fluid entry into wells is prevented; (3) collecting the rock cuttings from the bottom of wells and bringing them to the surface for disposal; (4) bit and drill string cooling and lubrication; and (5) decreasing the friction between the drilling string and the hole. Using the Prabhakar fractional operato, Muhammad Imran Asjad et al. [12] deal with an unsteady flow of a Maxwell fluid including clay nanoparticles. The effect of radiation absorption on chemically reactive and heat-generating drilling liquids, such as water–clay, kerosene–clay or engine oil–clay nanofluids running down a vertical channel, was explored by Hamzat Afe Isede [13] in his paper.

Free convection flow past an infinite vertical plate has received much attention in the literature due to its industrial and engineering applications, namely, heat transfer from pipes and transmission lines, heat conduction from electrical devices, heat transfer from a heater, heat transfer in nuclear energy poles, extrusion and wiredrawing, heat debauchery from the spiral refrigerator element to surrounding air, and atmospheric and oceanic circulation. It is used in the cooling of nuclear reactors or in the study of environmental heat transfer processes. Thermal and entropy transport in ${\mathrm{Al}}_2{{O}}_3$-Ethylene glycol (EG) nanofluids are studied by Sayantan Mukherjee et al. [14] in a circular tube with a constant wall temperature. Using water as the base liquid, Huda Alfannakh et al. [15] performed a computational evaluation of the steady natural convective heat transfer problem and entropy production of both single-wall (SWCNT) and multi-wall (MWCNT) nanoparticles across two separated spheres. The combined effects of the Casson micropolar fluid model over a vertically variable stretching Riga sheet were examined by Nadeem Abbas et al. [16].

In the past decade, fractional derivatives have been used to represent a wide variety of practical events. Fractional calculus is rapidly expanding in various disciplines related to present contemporary issues due to its wide-ranging uses in a variety of real-world occurrences, such as in electromagnetism, modelling in biological, biomedical and epidemic problems, the dynamical behavior of fluid matters, wave traveling solutions, signal processing, economics, and the viscoelastic behavior of fluids. Many academics have recently come to the conclusion that fractional derivatives provide more reliable and accurate findings than ordinary derivatives. This is because an acceptable fractional parameter adaptation results in almost complete congruence between theoretical and experimental assessments. Some rheological properties of fluids can only be seen using fractional derivatives in the subject of fluid mechanics. As a result, scientists have realized that generating unique fractional derivatives with distinct benefits over regular derivatives is critical in confirming specifications for modelling computational and mathematical problems. Until now, all fractional derivatives have been presented using a unique kernel. Leibenitz and L. Hospital [17] studies on the fractional order approach in 1695 has received a lot of attention. Fractional operators in biological modelling are examined as a broad topic [18] in their physical model [19], in investigations of mathematical physics [20,21], and in applications of mathematics [22]. There are a great number of fractional derivatives, and they each offer some distinct benefits.

The Riemann-Liouville derivative and the integral associated with it are both considered to be fractional operators, as is the Caputo–Fabrizio derivative, as well as the integral that is connected with it. The use of fractional calculus has been extensively studied in the scientific literature [23]. For flow problems, academics such as Ali et al. [24,25] apply the fractional derivative technique. Caputo–Fabrizio fractional derivatives [26] are another form of fractional derivatives; they are sometimes referred to in the literature as derivatives with a non-singular kernel. In their study, Atangana and Koca [27] use fractional derivatives to demonstrate the existence and uniqueness of a solution. The Riemann–Liouville integral operator and Mittag–Leffler functions have been developed numerically by Diehelm and coworkers [28]. Using fractional derivatives, Aman, S. et al. [29] attempt to obtain accurate solutions for the flow field, fluid temperature, and species levels of a forced convective flow of graphene nanofluid prepared by graphene nanoparticles in an ambient stream of an upright surface. A viscous fluid with heat/sink was studied over an upright cylinder by considering a combination of 47 nm alumina nanoparticles in water as a heat source, as given by Shah, N.A. et al. [30]. In [31] Raza, A. et al., conduct research on the exact solutions of fractional nanofluids moving on an endless surface at a fixed temperature while accounting for heat flux and radiation impact. Ikram, M.D. et al. [32], estimated hybrid nanoparticles suspended in Brinkman-type fluid (BTF) using a fractional model. A Brinkman-type fluid flow with mass transfer in an unstable MHD flow was examined by Sheikh, N.A. et al. [33,34]. The majority of the research concentrated on fluid flow reports by examining various liquids connected to fractional-order derivatives in the process of heat transmission. Some pertinent works subject to fractionalized models are explored in depth in [35,36,37,38].

For fractions, the Caputo fractional operator frequently comes in handy. The aim of this research work is to use the Laplace and Fourier sine transform technique to provide analytical solutions to a fluid model. However, application to a fluid model with fractional operators with nanofluids is the major innovative element of the approach. To solve the fractional differential equation, we employ the Laplace transform of the Caputo derivative, which is extremely beneficial for this fractional operator. With the use of Laplace transforms, the solutions are expressed in terms of well-known functions such as Gaussian error function, exponential function, and Mittag–Leffler function. Additionally, even though there are many different forms to describe diffusion processes, the sub-diffusion process is investigated using the Caputo fractional operator by setting the range of fractional values 0 < $\mathsf{\alpha }$ < 1.

In the present work, the resulting flow of governing equations are translated into fractional PDEs and solved by utilizing a combination of Fourier sine transform and Laplace transform techniques. Computational results are obtained through MATLAB and MATHEMATICA to create graphs. Furthermore, the influences of some flow quantities on fluid velocity, temperature distribution and species concentration are demonstrated, and a fixed fractional order parameter is suggested through graphs and tables in the proposed research work.

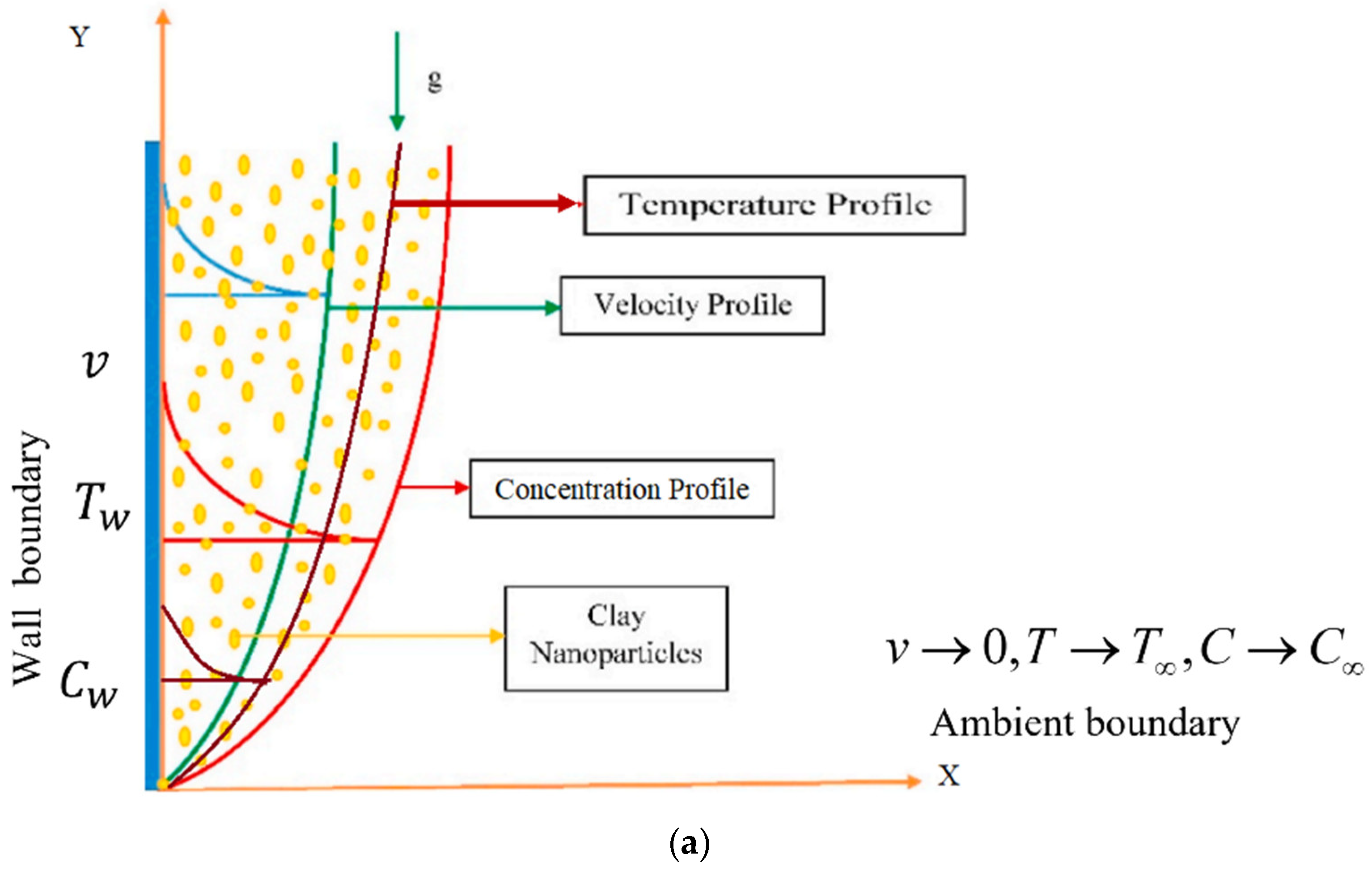
2. Mathematical Formulation

The rectilinear system of coordinates is cogitated. Let us consider the flow in the y direction and the x axis to be normal to the plate and the $xy-$plane filled with nanofluid to contain clay nanoparticles. In the initial state $t^{\prime }\le 0$, the plate surface and nanofluid in the region are in a static condition, and after elapsing at a certain time $t^{\prime }>0$, the plate moves with velocity U, and at the same time raises its temperature to $T_w$. The buoyant force is the essential mechanism in driving the fluid through gravity by pulling down. Since the plate has an infinite length, the boundary layer thickness is considerably small in comparison; hence, all the flow fields only function for one special coordinate and with respect to time. The geometry of the problem and the flow chart of the present work are shown in Figure 1a,b. The governing equations of momentum, energy, and concentration describing the fluid flow phenomena are formulated according to simplified pressure gradients and body force in the Navier–Stokes equation and presented in dimensionless form with the Caputo fractional derivative as follows [29,39]:

$${\mathsf{\rho }}_{nf}\frac{{\partial }^{\mathsf{\alpha }}v(x,t)}{\partial t^{\mathsf{\alpha }}}={\mu }_{nf}\frac{{\partial }^{2}v}{\partial x^2}+{(\mathsf{\rho }{g}_T)}_{nf}\gamma \left(T-T_{\infty }\right)+{(\mathsf{\rho }{g}_C)}_{nf}\phi \left(C-C_{\infty }\right)$$

(1)

$${({\mathsf{\rho }}_{cp})}_{nf}\frac{{\partial }^{\mathsf{\alpha }}T(x,t)}{\partial t^{\mathsf{\alpha }}}=K_{nf}\frac{{\partial }^{2}T}{\partial x^2}$$

(2)

$$\frac{{\partial }^{\mathsf{\alpha }}C(x,t)}{\partial t^{\mathsf{\alpha }}}=D_{nf}\frac{{\partial }^{2}C}{\partial x^2}$$

(3)

with appropriate initial and boundary conditions [29],

$$\hspace{0.17em}v(x,0)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}T(x,0)=T_{\infty },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}C(x,0)=C_{\infty }$$

$$v(0,t)=V,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}T(0,t)=T_w,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}C(0,t)=C_w$$

(4)

$$v(\infty ,t)\to 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}T(\infty ,t)\to T_{\infty },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}C(\infty ,t)\to C_{\infty }\hspace{0.17em}$$

The physical properties of the nanofluid provided by [40] are as follows:

$${\mathsf{\mu }}_{nf}={\left(1-\mathsf{\varphi }\right)}^{-2.5}{\mathsf{\mu }}_f$$

$${\mathsf{\rho }}_{nf}=\left(1-\mathsf{\varphi }\right){\mathsf{\rho }}_f+\mathsf{\varphi }{\mathsf{\rho }}_s$$

$${(\mathsf{\rho }Cp)}_{nf}={(\mathsf{\rho }Cp)}_s\mathsf{\varphi }+\left(1-\mathsf{\varphi }\right){(\mathsf{\rho }Cp)}_f$$

(5)

$${(\mathsf{\rho }\mathsf{\beta })}_{nf}=\left(1-\mathsf{\varphi }\right){(\mathsf{\rho }\mathsf{\beta })}_f+\mathsf{\varphi }{(\mathsf{\rho }\mathsf{\beta })}_s\hspace{0.17em}\hspace{0.17em}$$

$$knf=k_f\left[\frac{(k_s+2k_f)-2\mathsf{\varphi }(k_f-k_s)}{(k_s+2k_f)+\mathsf{\varphi }(k_f-k_s)}\right]$$

The subscript $f$ denotes base fluids and $s$ denotes nanoparticles, while the subscript $\mathsf{\varphi }$ stands for the nanoparticle volume concentration.

To obtain a prototype model, the following non-dimensional parameters are constructed with the help of Buckingham’s pi-theorem:

$$u^{*}=\frac{u}{v}\hspace{0.17em}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}{x}^{*}=\frac{U}{\gamma }x,\hspace{0.17em}\hspace{0.17em}{T}^{*}=\frac{U^2}{\gamma }t,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathsf{\theta }=\frac{T-T_{\infty }}{T_w-T_{\infty }}$$

$$C=\frac{C-C_{\infty }}{C_w-C_{\infty }}$$

(6)

$$pr=\frac{\mathsf{\mu }Cp}{k}$$

$$Gr=\frac{\mathsf{\beta }g\gamma \left(T_w-T_{\infty }\right)}{u_0{}^3}$$

$$Gm=\frac{\mathsf{\beta }g\mathsf{\phi }\left(C_w-C_{\infty }\right)}{u_0{}^3}$$

With the use of these dimensionless numbers, the governing Equations (1)–(3) and corresponding condition (4), after dropping the asterisk, can be yielded as

$$D_t^{\mathsf{\alpha }}v=a1\frac{{\partial }^{2}u}{\partial x^2}+a2GrV+a2GmC$$

(7)

$$D_t^{\mathsf{\alpha }}\mathsf{\theta }=a3\frac{1}{Pr}\frac{{\partial }^2\mathsf{\theta }}{\partial x^2}$$

(8)

$$\frac{sc}{a_4}{D}_t{}^{\mathsf{\alpha }}C=\frac{{\partial }^{2}C}{\partial x^2}$$

(9)

where

$$z_2=\left[1-\mathsf{\varphi }+\mathsf{\varphi }\frac{{(\mathsf{\rho }\mathsf{\beta })}_s}{{(\mathsf{\rho }\mathsf{\beta })}_f}\right]$$

$$z_3=\left[1-\mathsf{\varphi }+\mathsf{\varphi }\frac{{(\mathsf{\rho }Cp)}_s}{{(\mathsf{\rho }Cp)}_f}\right]$$

$$z_4=\left[1+\frac{k_s-2\mathsf{\varphi }\left(k_f-k_s\right)+2k_f}{k_s+\mathsf{\varphi }\left(k_f-k_s\right)+2k_f}\right]$$

(10)

$$a_1=\frac{{\mathsf{\mu }}_f}{{(1-\mathsf{\varphi })}^{2.5}{z}_1}$$

$$a_2=\frac{z_2}{z_1}$$

$$a_3=\frac{z_4}{z_3}$$

$$a_4=(1-\mathsf{\varphi })$$

The boundary conditions are taken into consideration

$$v\left(x,0\right)=0,\hspace{0.17em}\hspace{0.17em}\mathsf{\theta }\left(x,0\right)=0,\hspace{0.17em}\hspace{0.17em}c(x,0)=0$$

(11)

$$v\left(0,\mathsf{\tau }\right)=1,\hspace{0.17em}\hspace{0.17em}\mathsf{\theta }\left(0,\mathsf{\tau }\right)=1,\hspace{0.17em}\hspace{0.17em}c(0,\mathsf{\tau })=1$$

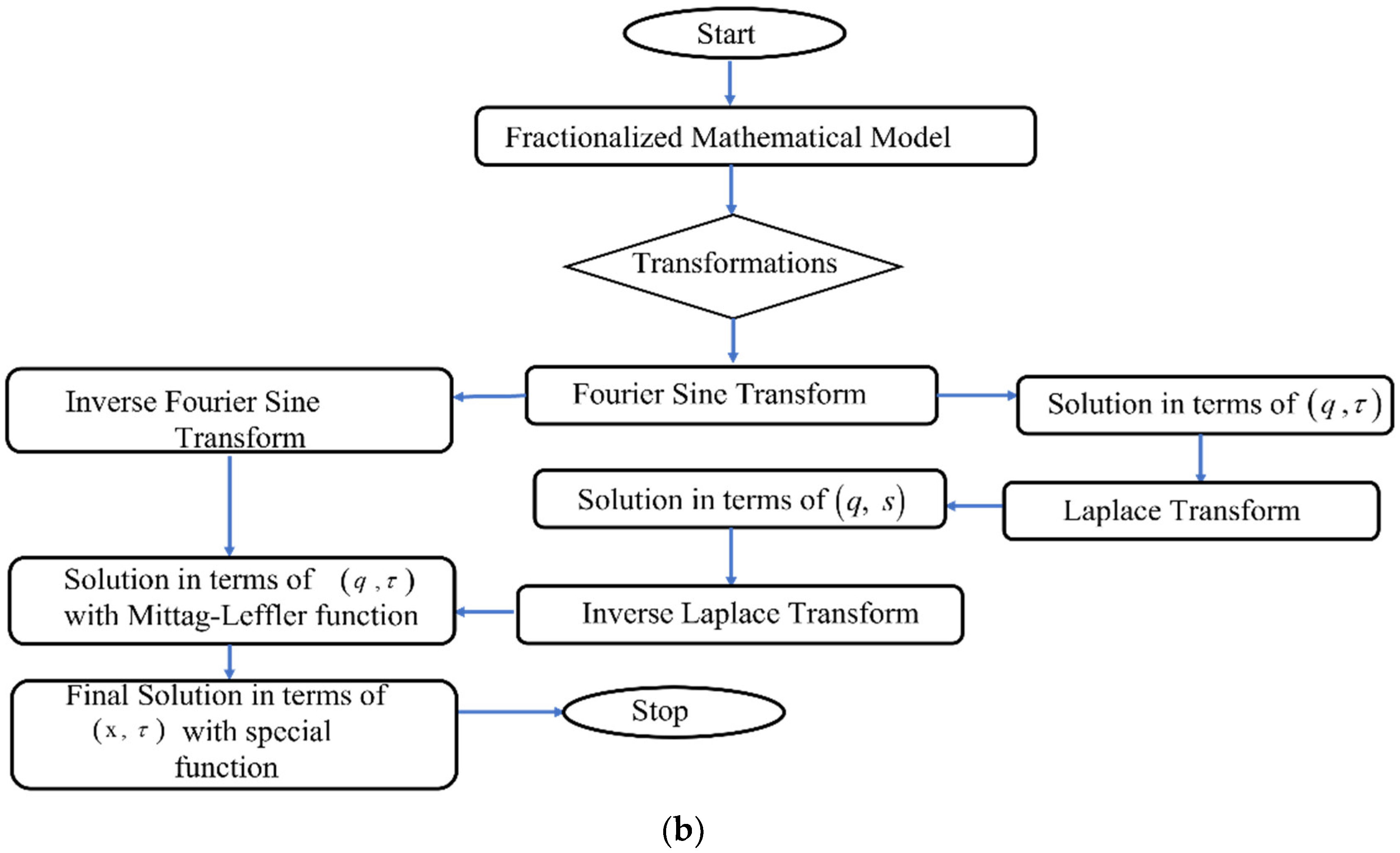
3. Solution of the Problem

For the fractional differential equations presented in Equations (7)–(9), various approaches exist for finding their solutions. In the present investigation, both integral transforms are employed, such as the Laplace transform of the Caputo fractional derivative and the Fourier sine transformation for classical derivatives, to find the precise results of the governing model.

3.1. Energy Equation

From Equation (8) the Fourier sine transformation is employed, yielding the following relationship:

$$F_s\left[D_{\mathsf{\tau }}^{\mathsf{\alpha }}\mathsf{\theta }\left(x,\mathsf{\tau }\right)\right]=\frac{1}{Pr}{a}_3{F}_s\left[\frac{{\partial }^2\mathsf{\theta }}{\partial x^2}\left(x,\mathsf{\tau }\right)\right]$$

(12)

$$D_{\mathsf{\tau }}^{\mathsf{\alpha }}\mathsf{\theta }\left(q,\mathsf{\tau }\right)=\frac{1}{Pr}{a}_3\left[q\mathsf{\theta }\left(0,\mathsf{\tau }\right)-q^2\mathsf{\theta }\left(q,\mathsf{\tau }\right)\right]$$

(13)

The next step is the integral transformation, which involves the integral transform to the Caputo derivative; with further simplification and rearrangement, we reach the following equations:

$$L\left(D_{\mathsf{\tau }}^{\mathsf{\alpha }}\mathsf{\theta }\left(q,\mathsf{\tau }\right)\right)=\frac{q}{Pr}{a}_{3}L\left[\mathsf{\theta }\left(0,\mathsf{\tau }\right)\right]-\frac{q^2}{Pr}{a}_{3}L\left[\mathsf{\theta }\left(0,\mathsf{\tau }\right)\right]$$

(14)

$$\mathsf{\theta }\left(q,s\right)=\frac{1}{q}\left\{\frac{1}{s}-\frac{S^{\mathsf{\alpha }-1}}{S^{\mathsf{\alpha }}+\frac{q^2{a}_3}{Pr}}\right\}$$

(15)

After determining the solution to the energy equation with fractional derivatives using the methods outlined in [41], apart from using the inverse integral transform, we obtain the following inverse Laplace transform form:

$$L^{-1}\left[\mathsf{\theta }\left(q,s\right)\right]=L^{-1}\left[\frac{1}{q}\left(\frac{1}{s}-\frac{s^{\mathsf{\alpha }-1}}{s^{\mathsf{\alpha }}+\frac{q^2{a}_3}{Pr}}\right)\right]$$

(16)

to find the value of $L^{-1}$$\left(\frac{s^{\mathsf{\alpha }-1}}{s^{\mathsf{\alpha }}+\frac{q^2{a}_3}{Pr}}\right)$, by using the Mittag-Leffler function [42].

$$E_{\mathsf{\alpha }}\left(-\frac{q^2}{Pr}{\mathsf{\tau }}^2\right)=L^{-1}\left[\frac{S^{\mathsf{\alpha }}-1}{S^{\mathsf{\alpha }}+\frac{q^2{a}_3}{Pr}}\right]$$

(17)

$$\mathsf{\theta }\left(q,\mathsf{\tau }\right)=\frac{1}{q}\left[1-E_{\mathsf{\alpha }}\left(-\frac{q^2{a}_3}{Pr}{\mathsf{\tau }}^2\right)\right]$$

(18)

As described in [43], employing the inverse Fourier transform in Equation (18) gives the temperature distribution as

$$\mathsf{\theta }\left(x,\mathsf{\tau }\right)=1-\frac{2}{\pi }\underset{0}{\overset{\infty }{\mathsf{\int }}}\frac{sin\hspace{0.17em}qx}{q}{E}_{\mathsf{\alpha }}\left(-\frac{q^2{a}_3}{Pr}{\mathsf{\tau }}^{\mathsf{\alpha }}\right)dq$$

(19)

3.2. Concentration Equation

From Equation (9), the Fourier sine transformation is applied to this equation, obtaining the following relationship:

$$F_s\left[\frac{sc}{a_4}{D}_t{}^{\mathsf{\alpha }}C\right]=F_s\left[\frac{{\partial }^{2}C}{\partial x^2}\right]$$

(20)

$$D_{\mathsf{\tau }}^{\mathsf{\alpha }}c\left(q,\mathsf{\tau }\right)=\frac{a_4}{sc}\left[qc\left(0,\mathsf{\tau }\right)-q^{2}c\left(q,\mathsf{\tau }\right)\right]$$

(21)

The next step is the integral transformation, which involves the integral transform to the Caputo derivative and the Fourier transform of the second-order classical derivative, reaching the following form:

$$L\left[D_{\mathsf{\tau }}^{\mathsf{\alpha }}c\left(q,\mathsf{\tau }\right)\right]=\frac{a_4}{sc}L\left[qc\left(0,\mathsf{\tau }\right)-q^{2}c\left(q,\mathsf{\tau }\right)\right]$$

(22)

$$c\left(q,s\right)=\frac{1}{q}\left\{\frac{1}{s^{\mathsf{\alpha }}}-\frac{s^{\mathsf{\alpha }-1}}{s^{\mathsf{\alpha }}+\frac{q^2{a}_4}{sc}}\right\}$$

(23)

After determining the solution to the concentration equation with fractional derivative using the methods outlined in [41], along with the inverse integral transform, we obtain the following inverse Laplace transform form:

$$L^{-1}\left[c\left(q,s\right)\right]=\frac{1}{q}{L}^{-1}\left\{\frac{1}{s^{\mathsf{\alpha }}}-\frac{s^{\mathsf{\alpha }-1}}{s^{\mathsf{\alpha }}+\frac{q^2{a}_4}{sc}}\right\}$$

(24)

to find the value of $L^{-1}$$\left(\frac{s^{\mathsf{\alpha }-1}}{s^{\mathsf{\alpha }}+\frac{q^2{a}_4}{sc}}\right)$ by using the Mittag-Leffler function [42].

$$E_{\mathsf{\alpha }}\left(-\frac{q^2{a}_4}{sc}{\mathsf{\tau }}^{\mathsf{\alpha }}\right)=L^{-1}\left[\frac{S^{\mathsf{\alpha }}-1}{S^{\mathsf{\alpha }}+\frac{q^2{a}_4}{sc}}\right]$$

(25)

$$c\left(q,\mathsf{\tau }\right)=\frac{1}{q}\left[1-E_{\mathsf{\alpha }}\left(-\frac{q^2{a}_4}{sc}{\mathsf{\tau }}^{\mathsf{\alpha }}\right)\right]$$

(26)

As described in [43], we perform the inverse Fourier transform on Equation (26)

$$c\left(x,\mathsf{\tau }\right)=1-\frac{2}{\pi }\underset{0}{\overset{\infty }{\int }}\frac{sinqx}{q}{E}_{\mathsf{\alpha }}\left(-\frac{q^2{a}_4}{sc}{\mathsf{\tau }}^{\mathsf{\alpha }}\right)dq$$

(27)

3.3. Velocity Equation

From Equation (7), the Fourier sine transformation is applied to this equation, yielding the following relationship:

$$F_s\left[D_t^{\mathsf{\alpha }}v\right]=F_s\left[a1\frac{{\partial }^{2}v}{\partial x^2}+a2Gr\mathsf{\theta }+a2GmC\right]$$

(28)

$$D_{\mathsf{\tau }}^{\mathsf{\alpha }}v\left(q,z\right)=a_{1}qv\left(0,\mathsf{\tau }\right)-a_1{q}^{2}v\left(q,\mathsf{\tau }\right)+Gr\mathsf{\theta }\left(q,\mathsf{\tau }\right)+GmC(q,\mathsf{\tau })$$

(29)

The second step is the integral transformation, which involves the integral transform to the Caputo derivative; we obtain the following equations:

$$L\left[D_{\mathsf{\tau }}^{\mathsf{\alpha }}v\left(q,z\right)\right]=a_{1}qL\left[v\left(0,\mathsf{\tau }\right)\right]-a_1{q}^{2}L\left[v\left(q,\mathsf{\tau }\right)\right]+GrL\left[\mathsf{\theta }\left(q,\mathsf{\tau }\right)\right]+GmL\left[C(q,\mathsf{\tau })\right]$$

(30)

$$v\left(q,s\right)=\frac{a_{1}q}{S\left(s^{\mathsf{\alpha }}+a_1{q}^2\right)}+\frac{Gr\hspace{0.17em}q\hspace{0.17em}{a}_2}{spr\left(s^{\mathsf{\alpha }}+\frac{q^2}{Pr}\right)\left(s^{\mathsf{\alpha }}+a_1{q}^2\right)}+\frac{Gm\hspace{0.17em}q\hspace{0.17em}{a}_2}{spr\left(s^{\mathsf{\alpha }}+\frac{q^2}{Pr}\right)\left(s^{\mathsf{\alpha }}+a_1{q}^2\right)}$$

(31)

where

$$a\left(q,s\right)=\frac{a_{1}q}{s\left(s^{\mathsf{\alpha }}+\frac{q^2{a}_4}{Pr}\right)}$$

$$b\left(q,s\right)=\frac{q\hspace{0.17em}Gr\hspace{0.17em}{a}_2}{Prs\left(s^{\mathsf{\alpha }}+\frac{q^2{a}_4}{Pr}\right)\left(s^{\mathsf{\alpha }}+a_1{q}^2\right)}$$

$$c\left(q,s\right)=\frac{q\hspace{0.17em}Gm\hspace{0.17em}{a}_2}{Prs\left(s^{\mathsf{\alpha }}+\frac{q^2{a}_4}{Pr}\right)\left(s^{\mathsf{\alpha }}+a_1{q}^2\right)}$$

After determining the solution to the velocity equation with fractional derivatives using the methods outlined in [41], in addition to the inverse integral transform, we obtain the following form:

$$L^{-1}\left[v\left(q,s\right)\right]=L^{-1}\left[\frac{a_{1}q}{S\left(s^{\mathsf{\alpha }}+a_1{q}^2\right)}+\frac{Gr\hspace{0.17em}q\hspace{0.17em}{a}_2}{spr\left(s^{\mathsf{\alpha }}+\frac{a_4{q}^2}{Pr}\right)\left(s^{\mathsf{\alpha }}+a_1{q}^2\right)}+\frac{Gm\hspace{0.17em}q\hspace{0.17em}{a}_2}{spr\left(s^{\mathsf{\alpha }}+\frac{a_4{q}^2}{Pr}\right)\left(s^{\mathsf{\alpha }}+a_1{q}^2\right)}\right]$$

(32)

$$a\left(q,\mathsf{\tau }\right)=\frac{1}{q}\left[1-E_{\mathsf{\alpha }}\left(-a_1{q}^2{\mathsf{\tau }}^{\mathsf{\alpha }}\right)\right]$$

$$b\left(q,\mathsf{\tau }\right)=\frac{Gr{\mathsf{\tau }}^{\mathsf{\alpha }}{a}_2}{Prq\left(a_1-\frac{1}{Pr}\right)}\left[E_{\mathsf{\alpha },\mathsf{\beta }}\left(\frac{-q^2{a}_3}{Pr}{\mathsf{\tau }}^{\mathsf{\alpha }}\right)-E_{\mathsf{\alpha },\mathsf{\beta }}\left(-a_1{q}^2{\mathsf{\tau }}^{\mathsf{\alpha }}\right)\right]$$

$$c(q,\mathsf{\tau })=\frac{Gm{\mathsf{\tau }}^{\mathsf{\alpha }}{a}_2}{prq(a_1-pr)}\left[E_{\mathsf{\alpha },\mathsf{\beta }}\left(-\frac{q^2{a}_3}{pr}{\mathsf{\tau }}^{\mathsf{\alpha }}\right)-E_{\mathsf{\alpha },\mathsf{\beta }}\left(-a_1{q}^2{\mathsf{\tau }}^{\mathsf{\alpha }}\right)\right]$$

$$v(q,\mathsf{\tau })=a(q,\mathsf{\tau })+b(q,\mathsf{\tau })+c(q,\mathsf{\tau })$$

(33)

As described in [42,43,44], after employing the inverse Fourier transform in Equation (33), it is obtained that

$$a(x,\mathsf{\tau })=1-\frac{2}{\pi }\underset{0}{\overset{\infty }{\int }}\frac{sinqx}{q}\hspace{0.17em}{E}_{\mathsf{\alpha }}(-a_1{q}^2\hspace{0.17em}{\mathsf{\tau }}^{\mathsf{\alpha }})\hspace{0.17em}dq$$

$$b\left(x,\mathsf{\tau }\right)=\frac{2a_{2}Gr}{k}\underset{0}{\overset{\infty }{\int }}sin\frac{qx\hspace{0.17em}{\mathsf{\tau }}^{\mathsf{\alpha }}}{q}\left[E_{\mathsf{\alpha },\mathsf{\beta }}\left(\frac{-a_3{q}^2}{Pr}{\mathsf{\tau }}^{\mathsf{\alpha }}-E_{\mathsf{\alpha },\mathsf{\beta }}\left(-a_1{q}^2{\mathsf{\tau }}^{\mathsf{\alpha }}\right)\right)\right]sin\hspace{0.17em}qx\hspace{0.17em}dq$$

$$c(x,\mathsf{\tau })=\frac{2a_{2}Gm}{\pi k}\underset{0}{\overset{\infty }{\int }}\frac{sinqx}{q}\hspace{0.17em}{\mathsf{\tau }}^{\mathsf{\alpha }}\hspace{0.17em}\left[E_{\mathsf{\alpha },\mathsf{\beta }}\left(\frac{-q^2{a}_3}{pr}{\mathsf{\tau }}^{\mathsf{\alpha }}\right)-E_{\mathsf{\alpha },\mathsf{\beta }}\left(-a_1{q}^2{\mathsf{\tau }}^{\mathsf{\alpha }}\right)\right]sinqx\hspace{0.17em}dq$$

where

$$K=\pi Pr\left(a_1-\frac{1}{Pr}\right)$$

$$v(x,\mathsf{\tau })=\hspace{0.33em}a(x,\mathsf{\tau })+b(x,\mathsf{\tau })+c(x,\mathsf{\tau })$$

(34)

3.4. Nusselt Number

The physical explanation of the Nusselt number is the increase in heat transfer due to convection over conduction alone. If $Nu$ = 1, the fluid is static, and all heat transmission is through conduction. Fluid motion improves heat transfer through convection when $Nu$ > 1. From the fluid temperature, heat flow rate can be computed from the non-dimensional form

$$Nu=-L^{-1}\left[{\left(\frac{\partial \overline{\mathsf{\theta }}(x,s)}{\partial x}\right)}_{x=0}\right]=L^{-1}\left[\frac{\sqrt{s^{\mathsf{\alpha }}\frac{pr}{a3}}}{s}\right]=\sqrt{\frac{pr}{a3}\hspace{0.17em}}\frac{t^{-\raisebox{1ex}{$\mathsf{\alpha }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\mathsf{\Gamma }\left(1-\raisebox{1ex}{$\mathsf{\alpha }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}$$

(35)

3.5. Sherwood Number

Sherwood number is the ratio of convective mass transfer to diffusive mass transport rate. From the concentration, mass flow rate can be computed from the non-dimensional form

$$Sh=-L^{-1}\left[{\left(\frac{\partial \overline{C}(x,s)}{\partial x}\right)}_{x=0}\right]=L^{-1}\left[\frac{\sqrt{s^{\mathsf{\alpha }}\hspace{0.17em}sc\hspace{0.17em}a4}}{s}\right]=\sqrt{sc\hspace{0.17em}a4\hspace{0.17em}}\frac{t^{-\raisebox{1ex}{$\mathsf{\alpha }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\mathsf{\Gamma }(1-\raisebox{1ex}{$\mathsf{\alpha }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}$$

(36)

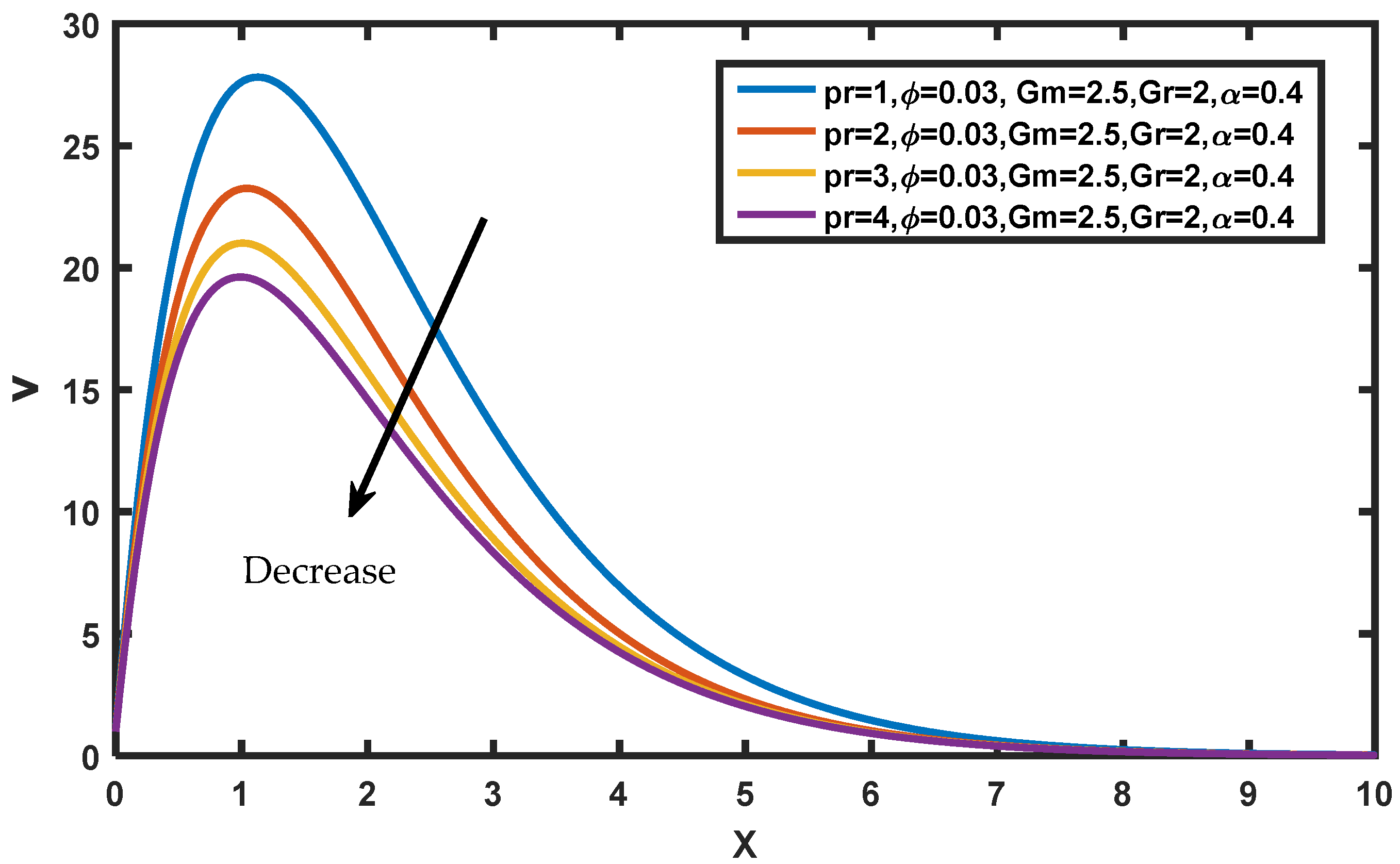
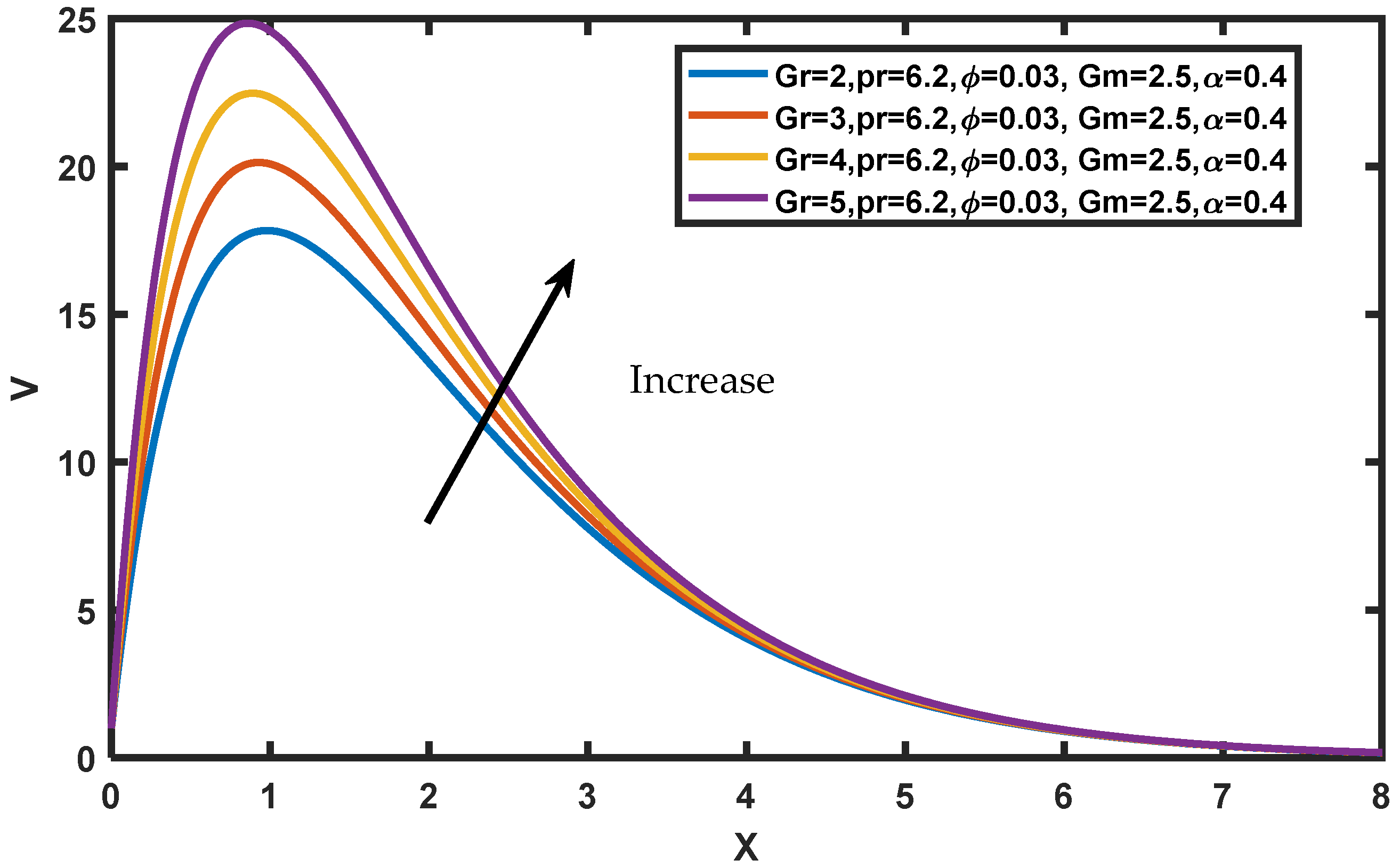
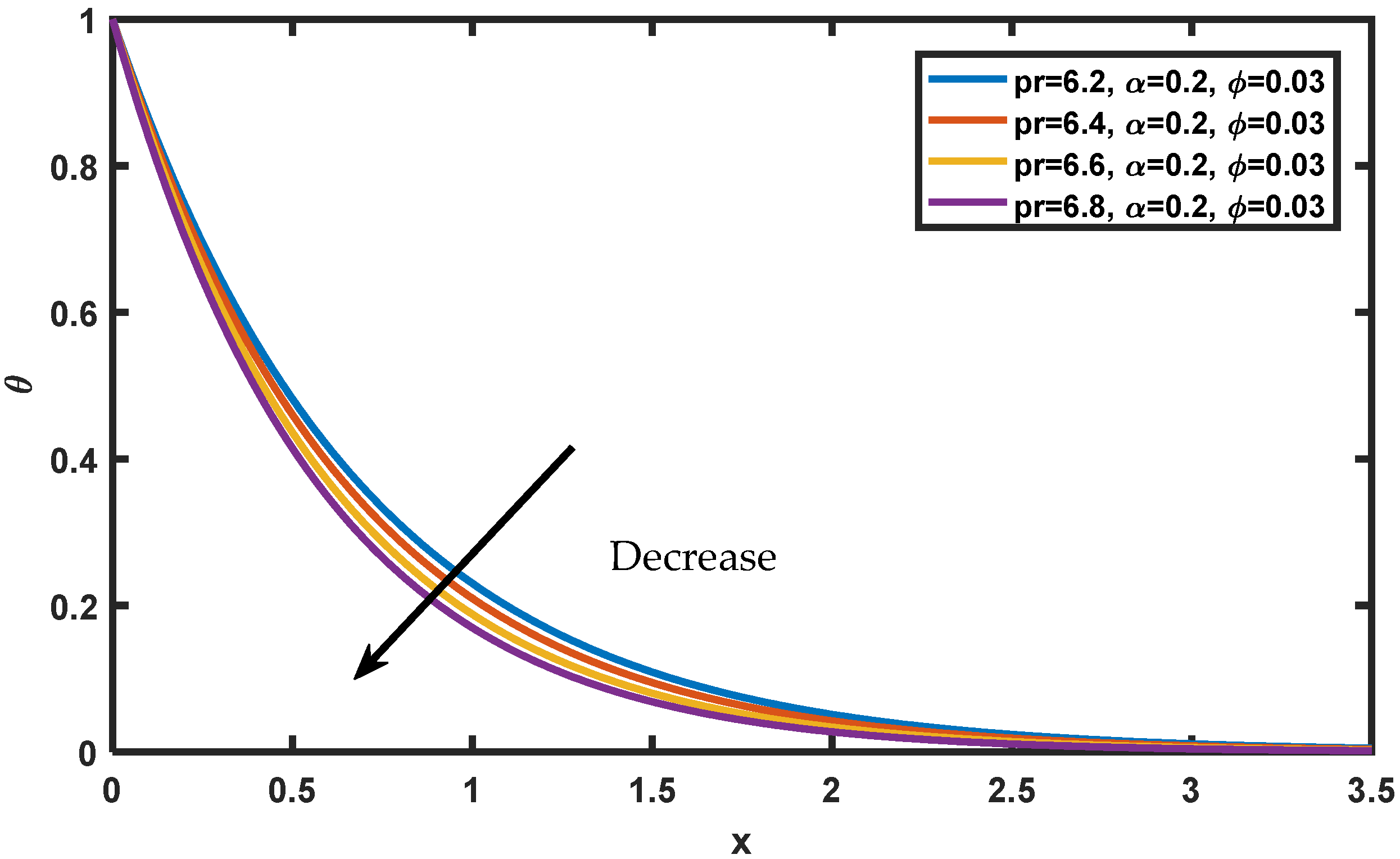
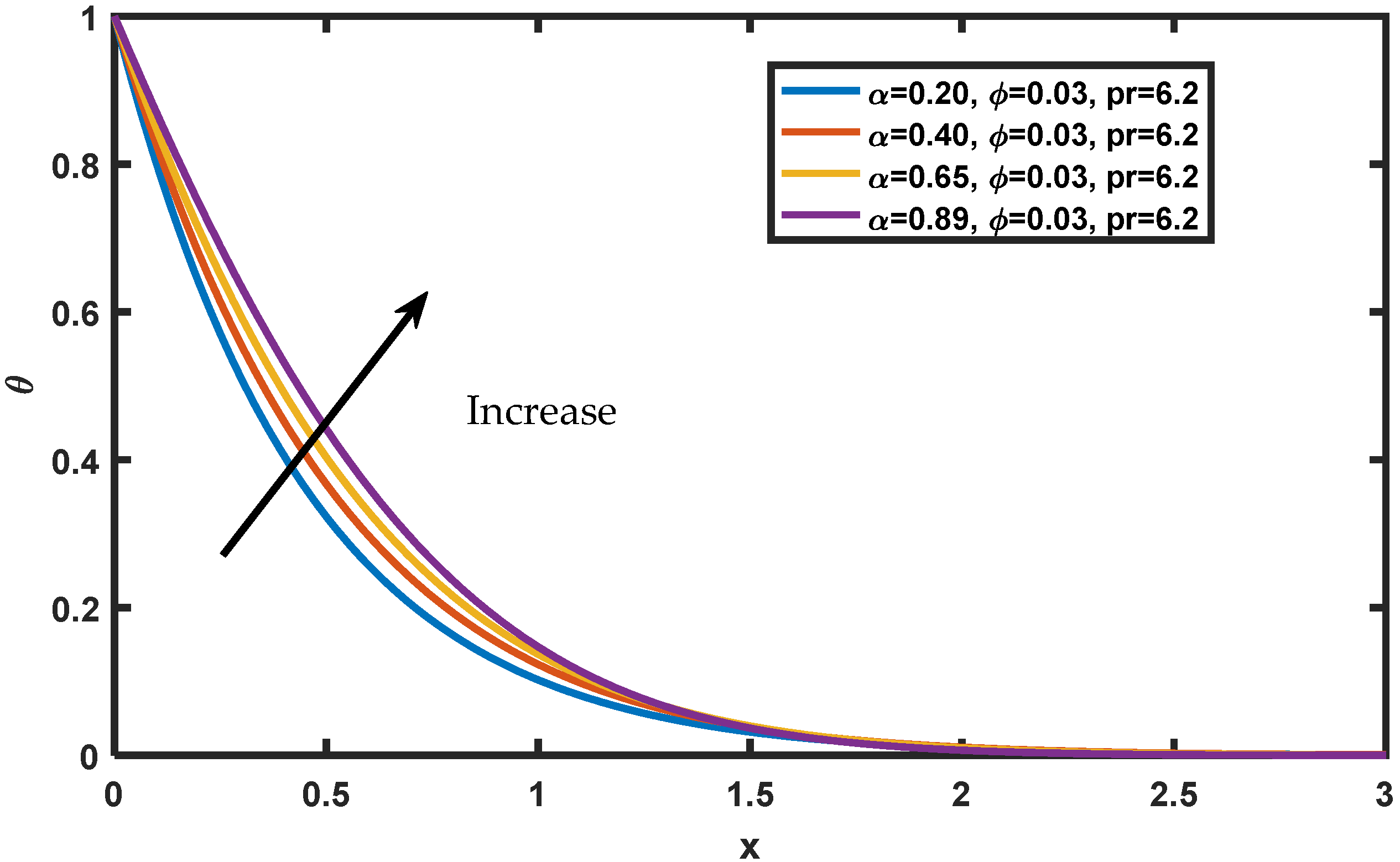
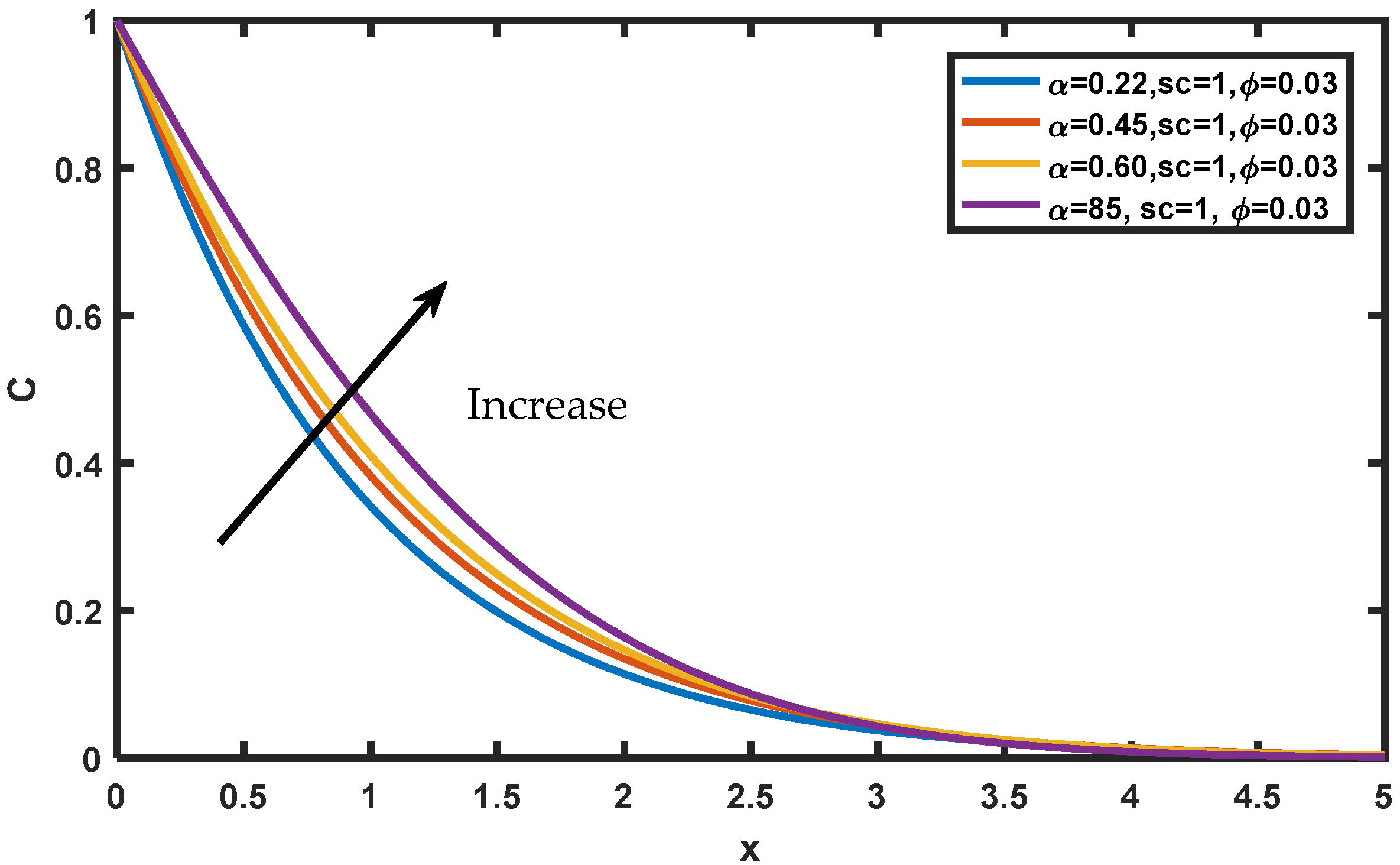
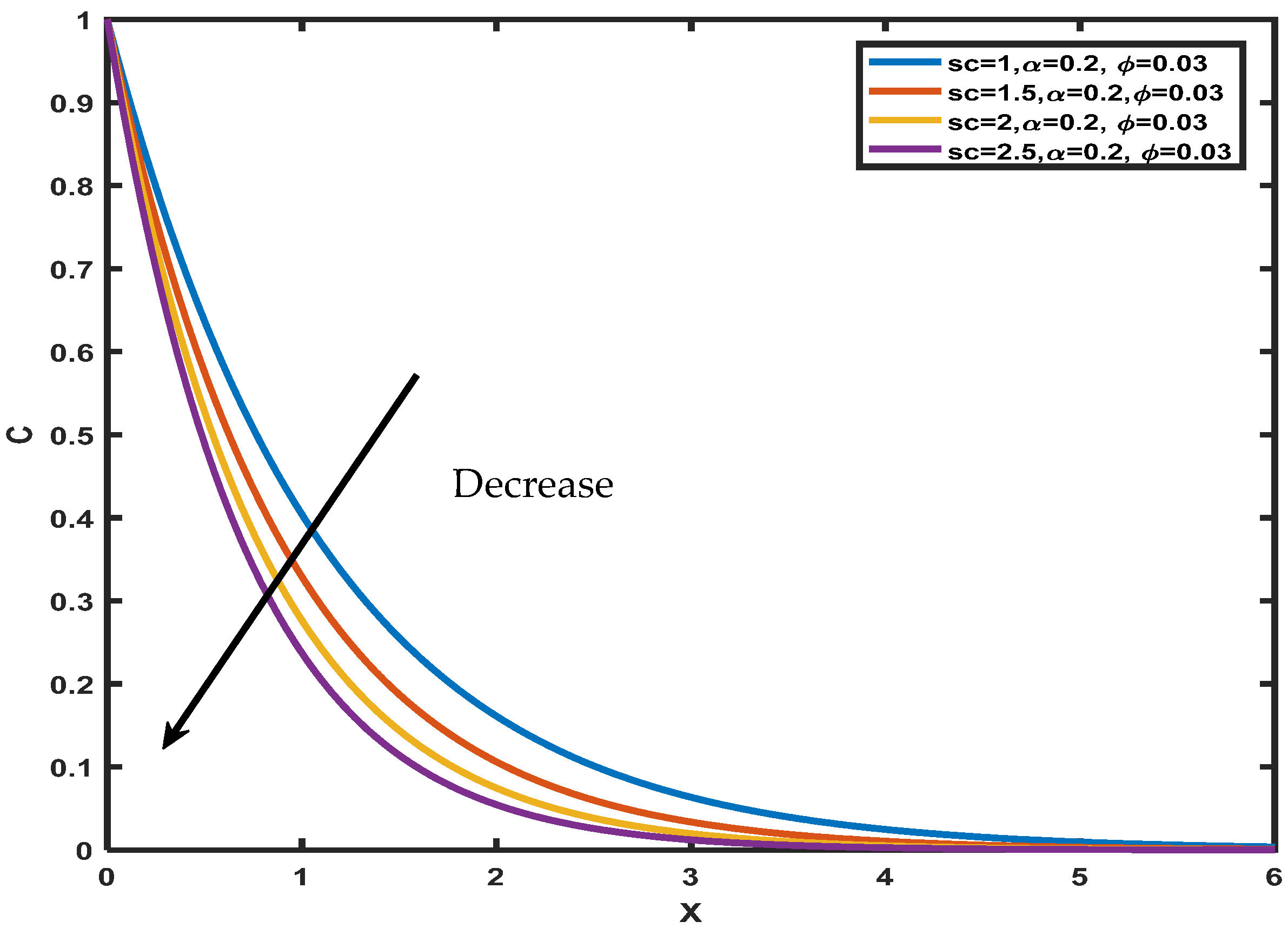
4. Results and Discussion

The fractional derivative is employed in this article to generalize the convective flow of the nanofluid. The Caputo fractional derivative is used to fractionalize the Brinkman-type fluid’s governing equation. The governing PDEs are more general fractional PDEs. The non-dimensional fluid temperature, species concentration, and fluid momentum equations are solved analytically using the Fourier sine and Laplace transform methods together. The results obtained from the solutions of the governing model are displayed in the form of graphs to investigate the impact of various physical terms, such as $\mathsf{\alpha }$, $\mathsf{\varphi }$, $Gr$,$Gm$,$Pr$, and $sc$. The nanofluid physical parameters are listed in

Table 1. Thermophoresis properties of water and clay [45].

Thermophysical Property	$\mathsf{\rho }\left(\mathbf{k}\mathbf{g}/{\mathbf{m}}^3\right)$	${\mathit{C}}_{\mathit{p}}(\mathbf{J}/\mathbf{k}\mathbf{g}\mathbf{K})$	$\mathit{k}\left(\mathbf{w}/\mathbf{m}\mathbf{K}\right)$	$\mathsf{\beta }\left(1/\mathbf{k}\right)$
$H_{2}O$	997.1	4179	0.613	21 × 10−5
Clay	6320	531.8	76.5	1.80 × 10−5

. Figure 2 displays the velocity profiles for different values of the prandtl number. The velocity profiles were found to be decreased as the Prandtl number increased. The prandtl number is defined as the ratio of momentum to thermal diffusivity. Prandtl number and momentum diffusivity are directly tied; therefore, with greater values of $Pr$, the fluid becomes thicker and more viscous with minimal capacity for heat conduction. As a result, the fluid moves more slowly.

As demonstrated in Figure 3 and Figure 4, the influence of Gr and Gm on the fluid flow behavior is discussed. Here, $Gr>0$ indicates that the plate is cooled down and $Gr<0$ denotes that the plate is heated up. The fluid temperature rises dramatically when the plate is cooled, while heating greatly slows it down. It is noticed that, from the flow pattern, fluid velocity increased in Gr and Gm when the surface of the plate is a coolant. This explains the physical fact that when Gr and Gm rise in buoyancy ratio, there is a better improvement and enhancement in the species buoyancy force. Figure 5 illustrates the impact of nanoparticle volume fraction $\mathsf{\varphi }$ on dimensionless velocity. Initially, the velocity of nanofluids is revealed to have an inverse relationship. Adding nanoparticles to a fluid increases its density, which reduces both the boundary layer thickness as well as nanofluid velocity; it is noted that with elapsed time velocity decelerates.

Figure 6 exhibits the flow curves for the variation in $\mathsf{\alpha }$ values; it can be seen that increasing the order of the fractional derivative causes an increase in the fluid momentum. It is true that increasing time leads to an increase in the flow field, which may explain this result. Figure 7 depicts the effect of $\mathsf{\varphi }$ (nano-sized particle volume fraction) on fluid temperature, and hence it is noticed that with increasing $\mathsf{\varphi }$ the nanoparticle increases the temperature profile. This is because the increase in the density of nanoparticles causes a rise in heat conductivity. Figure 8 depicts that increasing the value of the Prandtl number makes the fluid’s thermal conductivity go down, so the temperature of the nanofluid goes down due to low thermal diffusivity.

The temperature profiles for different values of $\mathsf{\alpha }$ are shown in Figure 9, while the other parameters are held constant. The Caputo fractional parameter’s rising function grows as the temperature increases. The uniqueness lies in explaining how temperature rises as the fractional operator’s order grows. Increases in order have a significant influence on time values because of the memory effect inherent in fractional operators, which leads to a large accumulation. When the order of the fractional operator is increased, it is seen that a rise in time consequently leads to an upturn in fluid temperature. A sub-diffusion in the range of (0, 1) is also noted. Caputo’s fractional derivative sub-diffusion is confirmed by the literature’s conclusions when the order is changed (0, 1). For different magnitudes $sc$,$\mathsf{\alpha }$ and $\mathsf{\varphi }$, the curve patterns on the species are represented in Figure 10, Figure 11 and Figure 12. It is noticed that the concentration drops with a rise in Schmidt number, but increases as $\mathsf{\alpha }$ increases. The concentration decreases for distinct values of volume fraction $\mathsf{\varphi }$, and it is observed that the concentration levels in the fluid become stationary as they move far away from the plate. Figure 13 and Figure 14 display the engineering interests via rate of change of heat and mass for various pertinent physical parameters. In Figure 13, it can be seen that Nusselt number increases significantly with an increase in Prandtl number and fractional value $\mathsf{\alpha }$ and then decreases with time. From Figure 14, a small amount of growth can be seen in the Sherwood number as $\mathsf{\alpha }$ rises, and with increasing Sherwood number increases.

In terms of comparative study, mathematical strategies have been employed to solve the current physical models, and similar published works have been observed; as an illustration, the Nusselt number is computed numerically and presented in

Table 2. Comparison of Nusselt number when $\mathsf{\varphi }=0\hspace{0.17em}$.

t	$\mathsf{\alpha }$	$\mathit{p}\mathit{r}$	Nodolane Sene [34]	Present Results
1	0.84	12	2.2539	2.25672
1		18	2.7605	2.7564
	0.94		3.1875	3.1645

in comparison to Ref. [34], and it is observed that the present results are in very good agreement with previous published work.

5. Conclusions

In the present investigation, a fractional calculus mathematical model with the Caputo fractional derivative is presented for constitutive conservation equations to study the free convection flow of nanofluid along an impulsive upright plate. An integral and sine Fourier transform technique was used in this study to solve the fractional order partial differential equations with the defined initial and boundary conditions. A water-based nanofluid suspended by clay nanoparticles is considered under the influence of gravitational force in a semi-infinite flow region. The analytical solutions are provided in terms of the Mittag-Leffler function. The consequences of different parameters are analyzed and explained. The main findings of this analysis are:

• For fractional model solutions, the considered hybrid transformation method is more reliable. Using this transformation, it is much simpler to solve the fractional model;
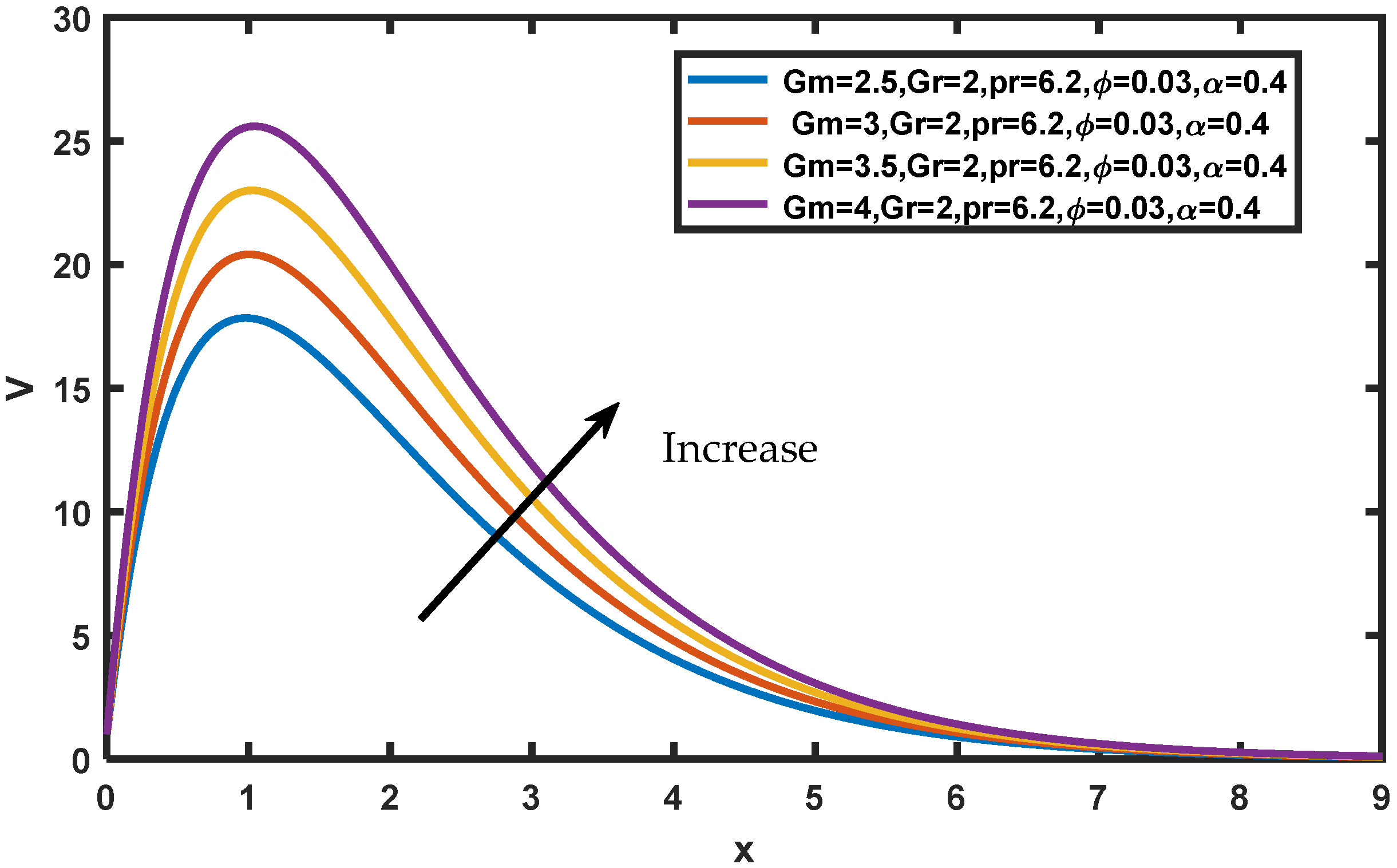
• Fluid velocity increases as the mass grashof $Gm$ number or thermal grashof $Gr$ number increases;
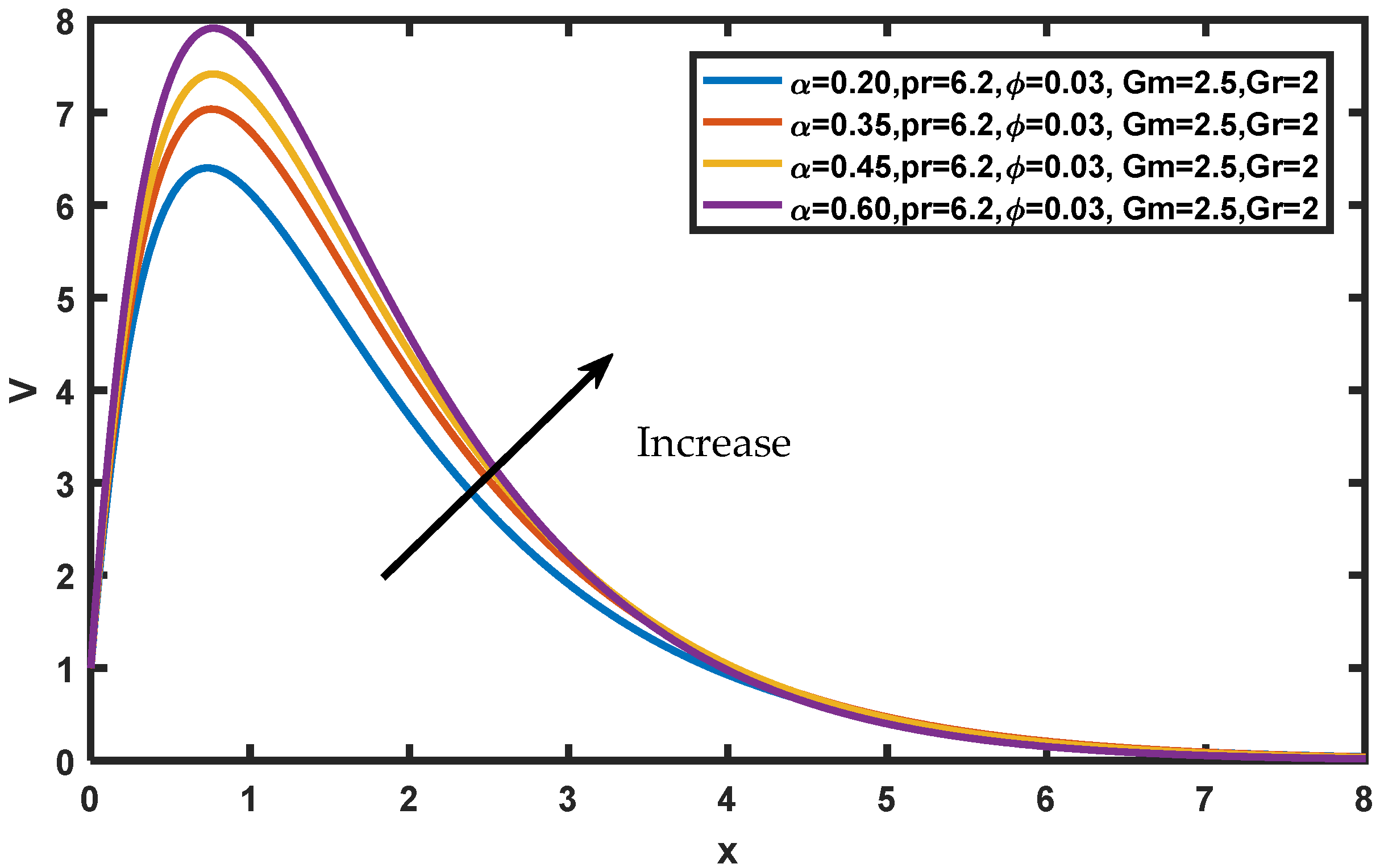
• The velocity, temperature and concentration profiles show an incremental behavior for increasing values of $\mathsf{\alpha }$;
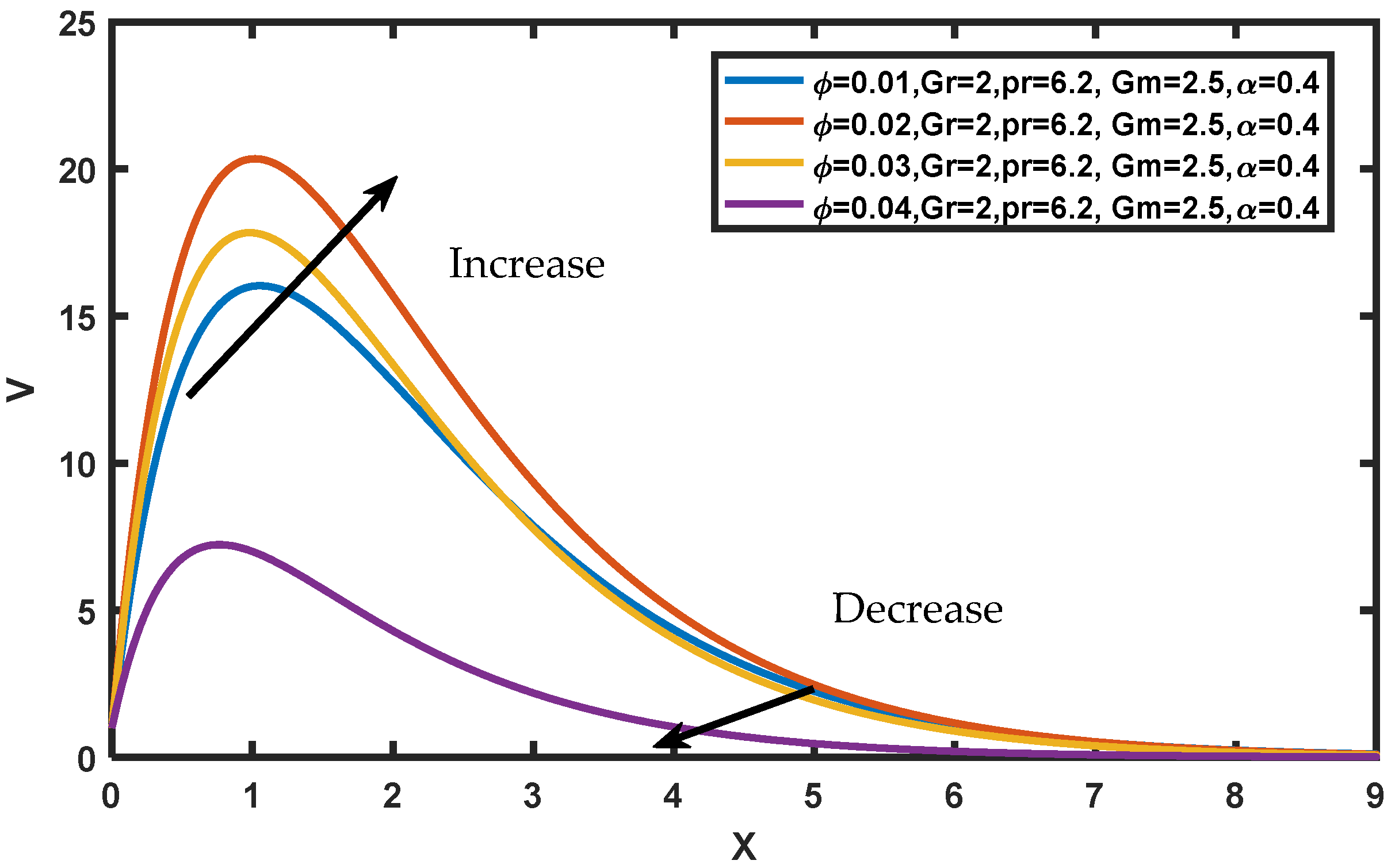
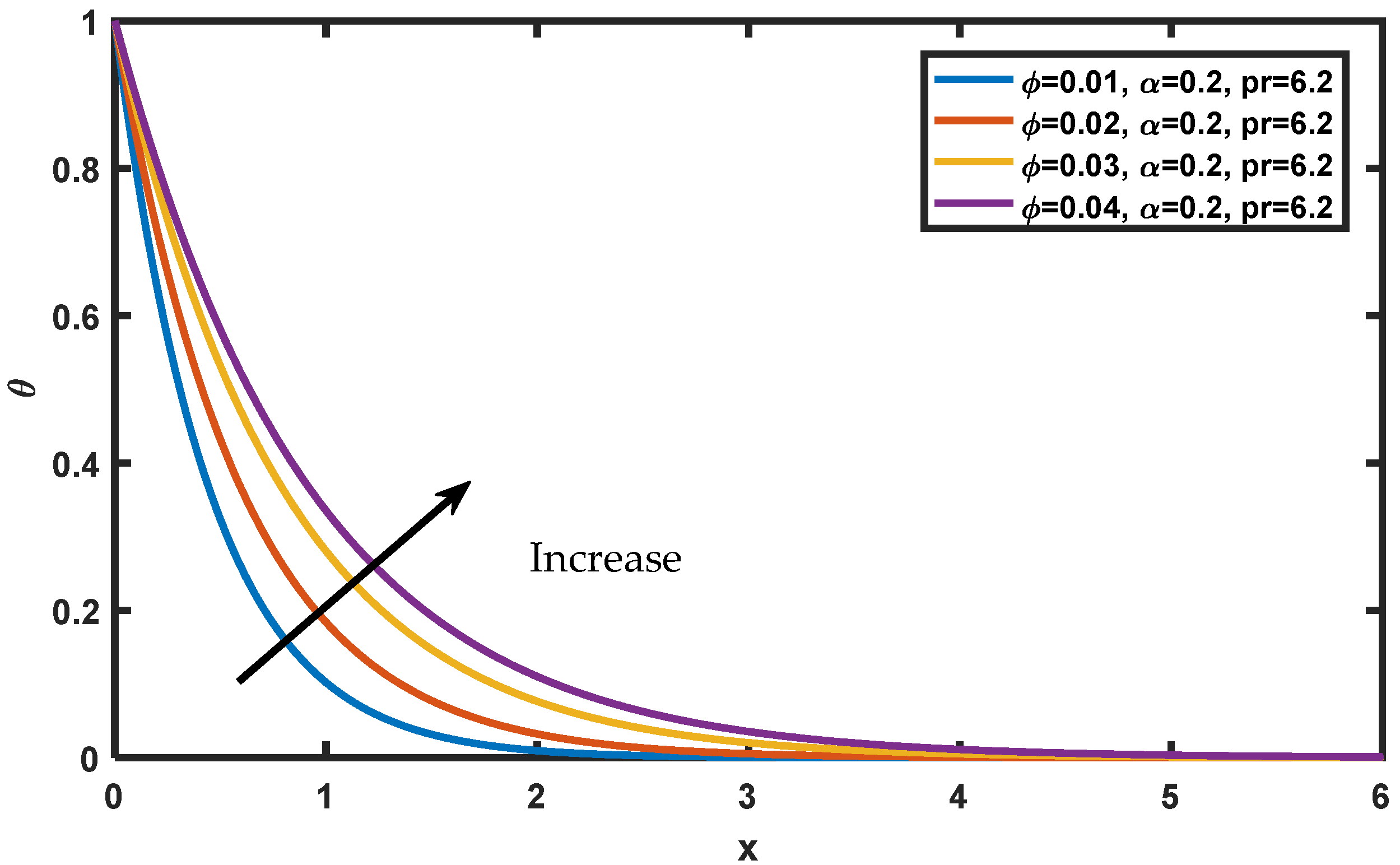
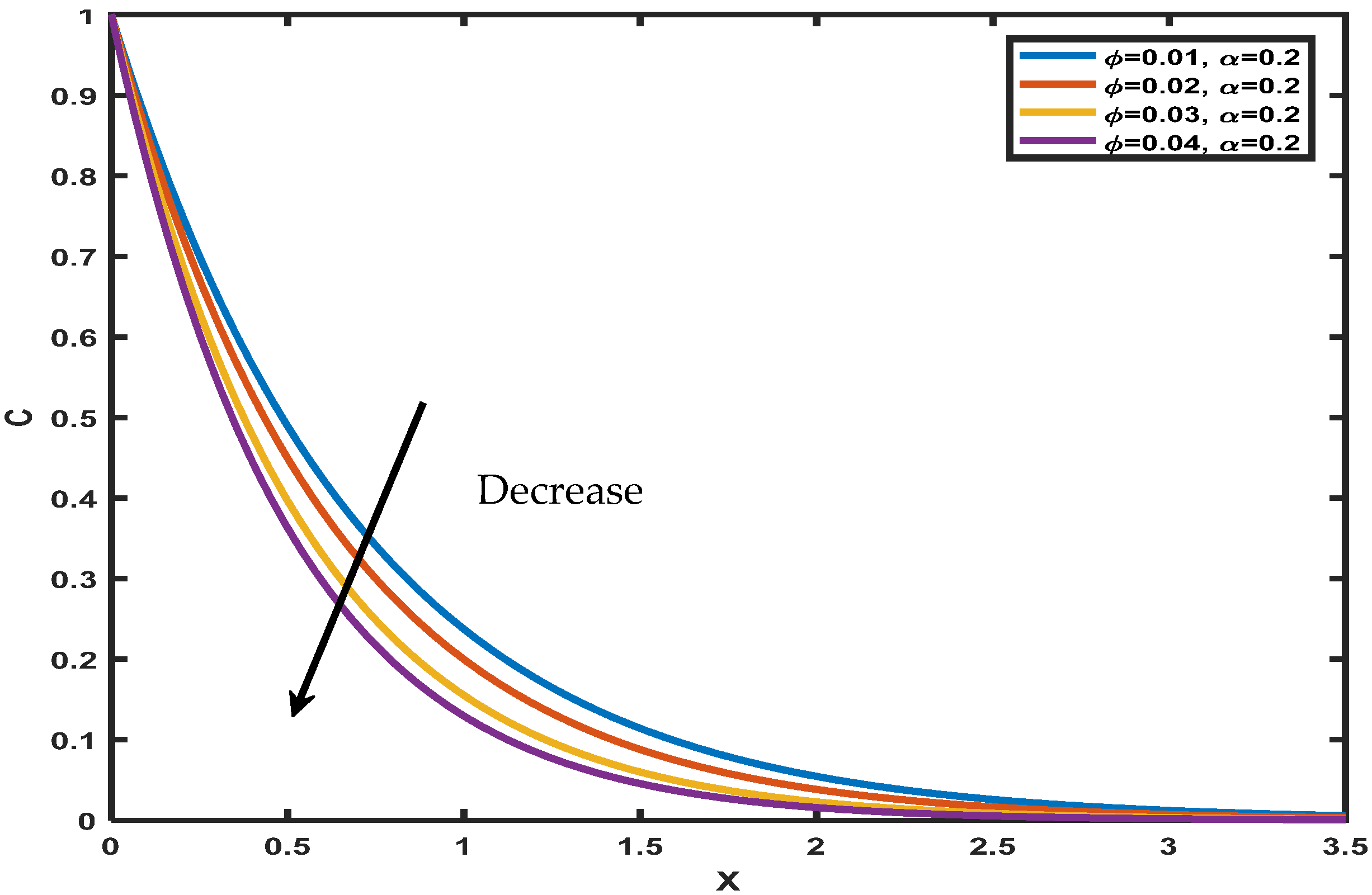
• The concentration boundary layer reduces with an increase in nanoparticle volume fraction while the energy boundary layer and momentum boundary layer increase with the volume fraction;
• Temperature decreases with increasing $Pr$ due to the diffusivity of the nanofluid;
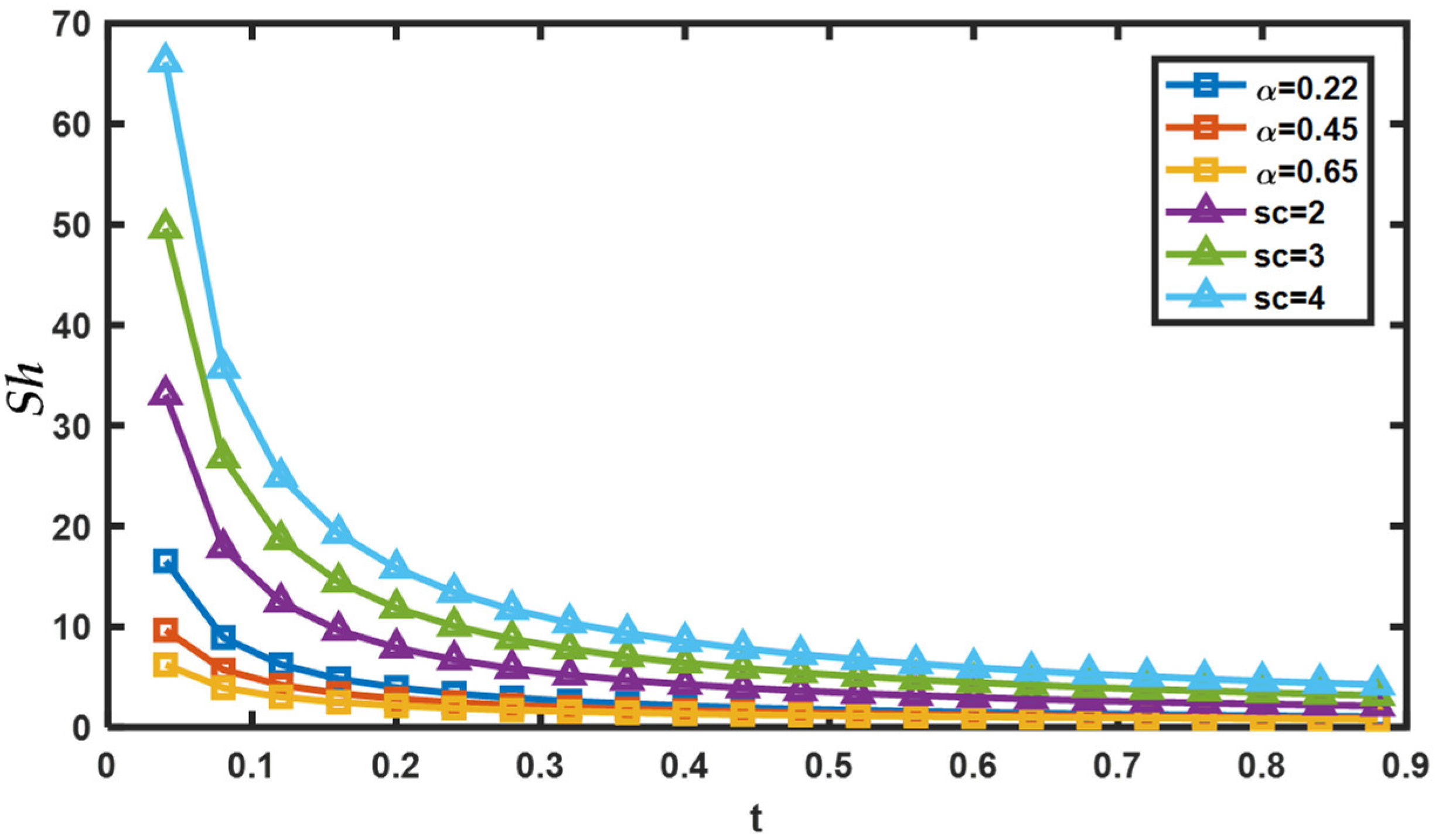
• Concentration decreases with an increase in Schmidt number $sc$;
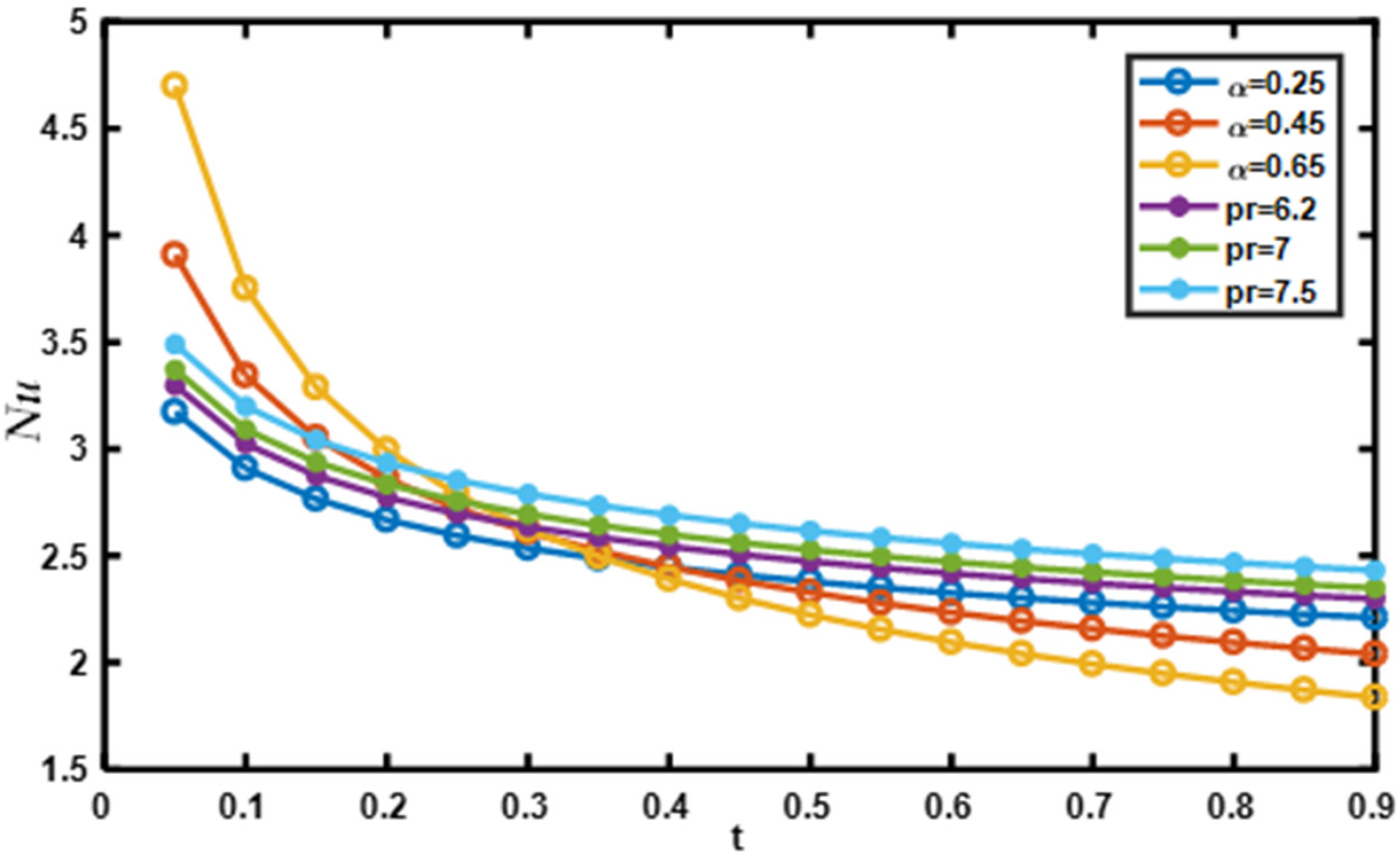
• As the fractional parameter increases, the Sherwood number or Nusselt number diminishes.