Porosity and Permeability Model of a Regionally Extending Unit (Upper Miocene Sandstones of the Western Part of Sava Depression, Croatia) Based on Vintage Well Data
Abstract
:1. Introduction
2. Geological Setting
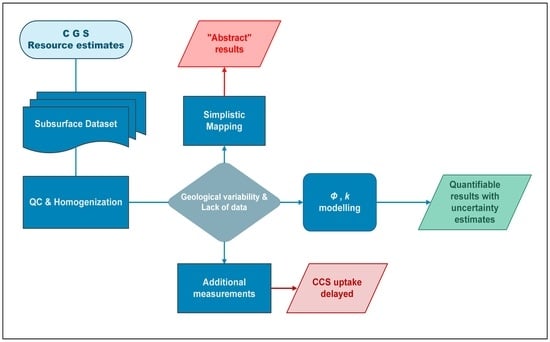
3. Porosity Estimates
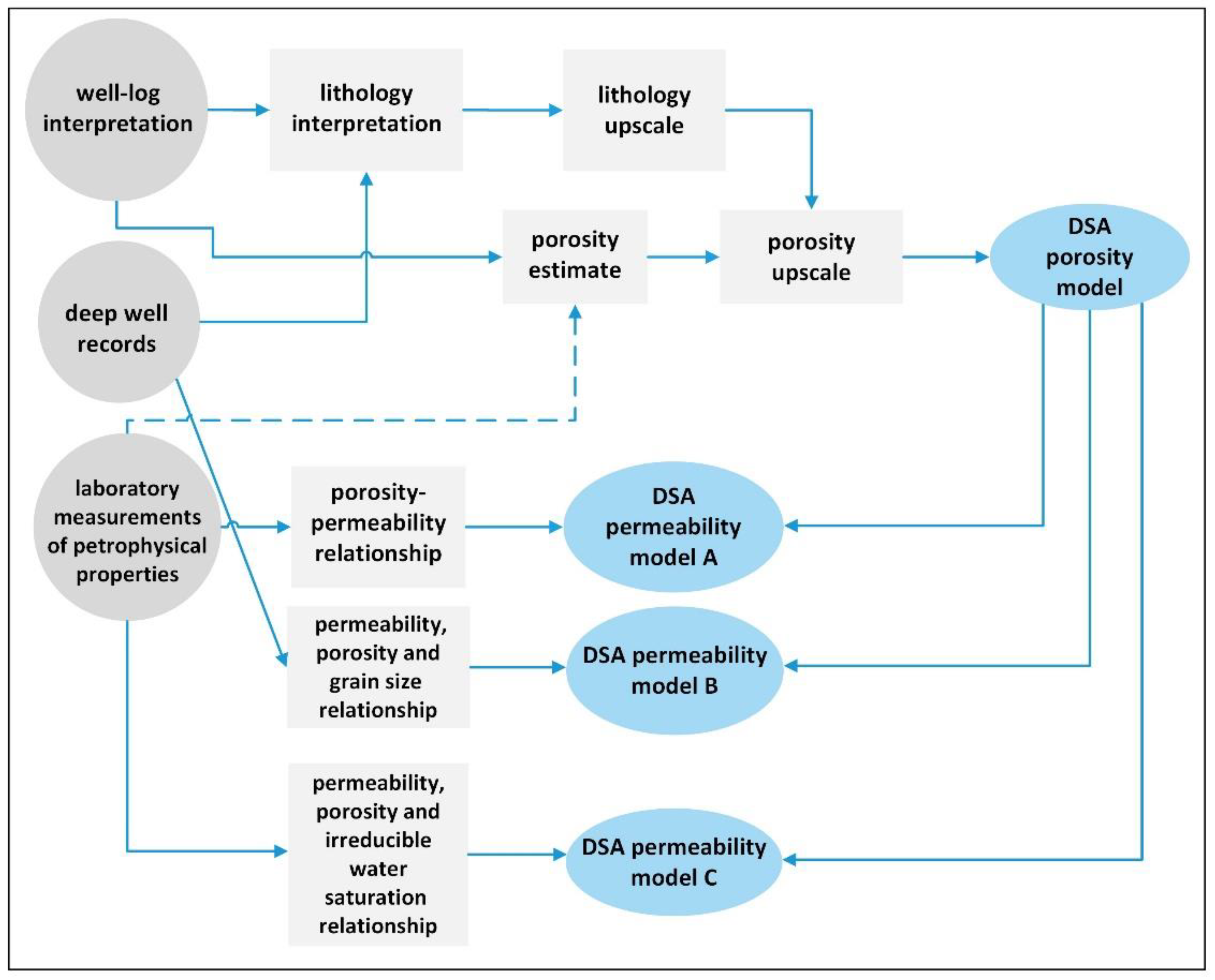
4. Materials and Methods
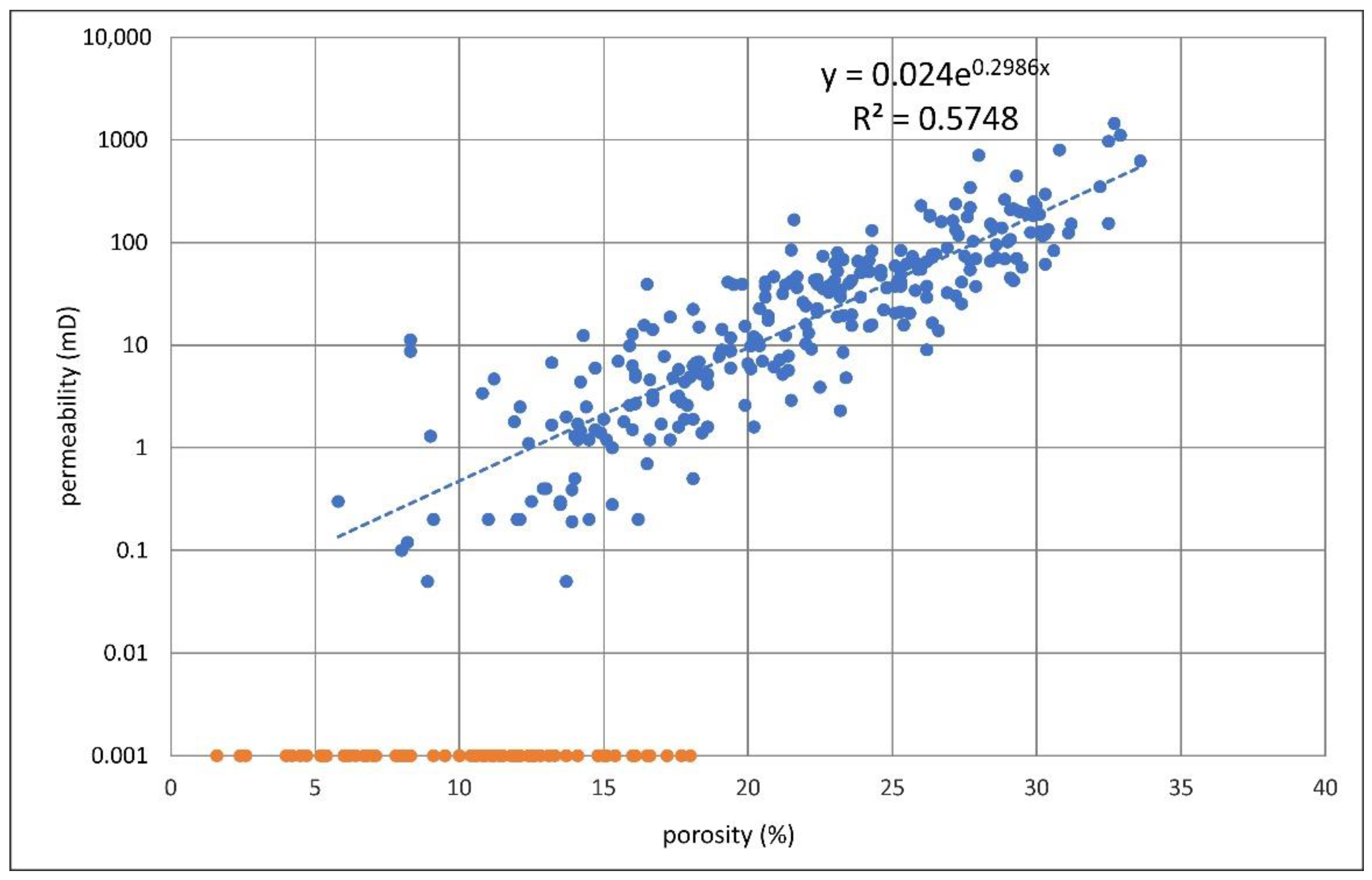
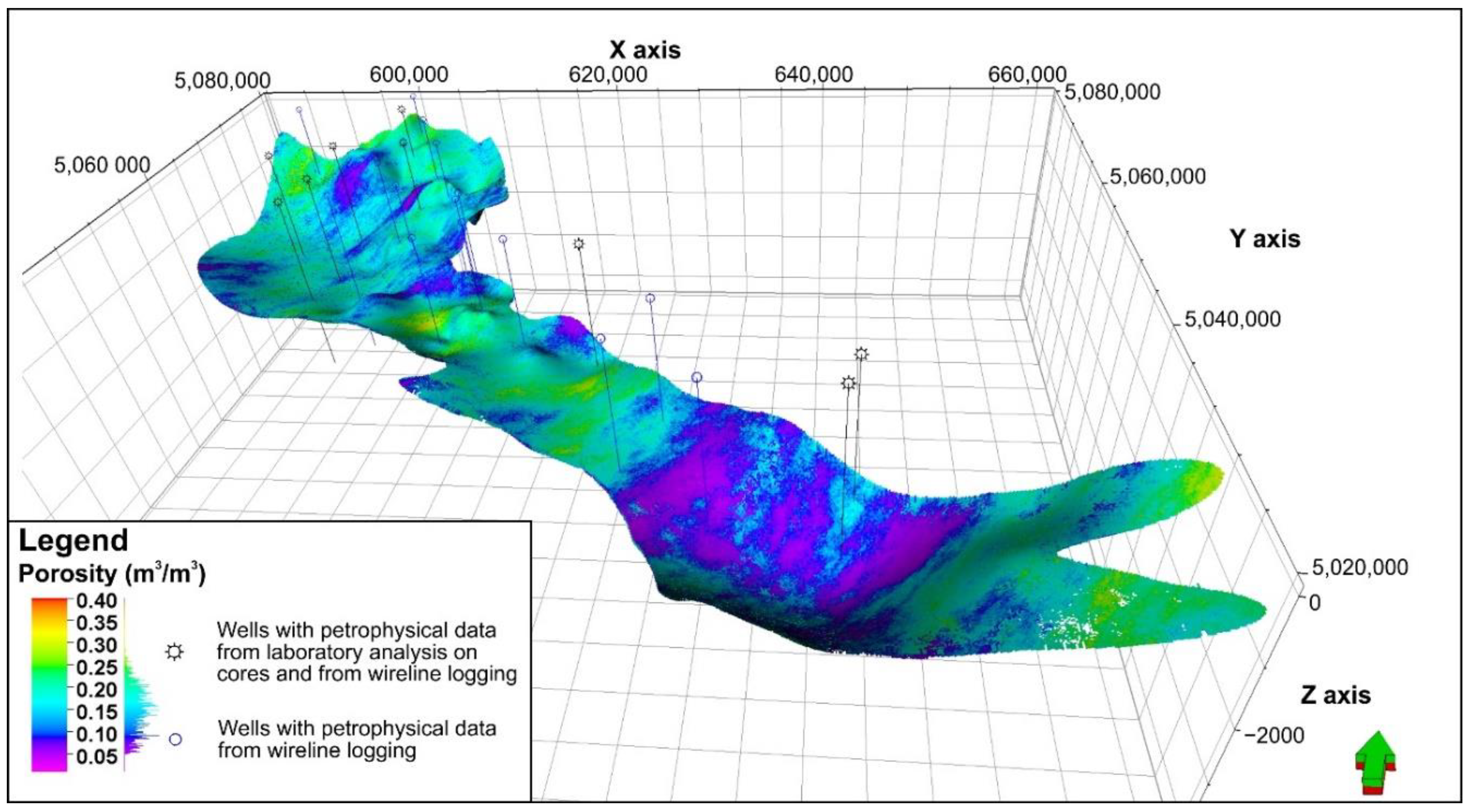
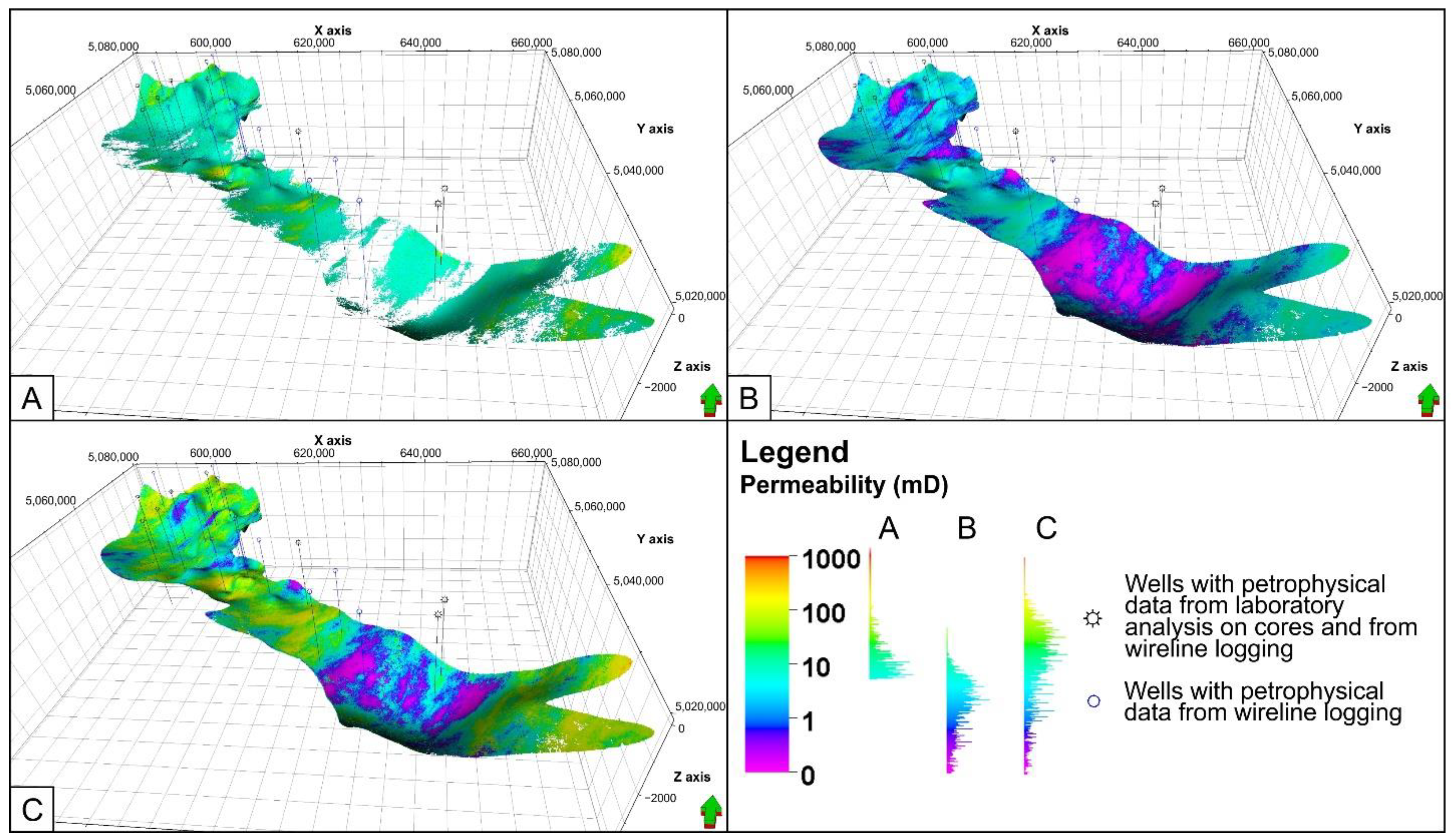
5. Results
6. Discussion
7. Conclusions
- The most obvious conclusion that can be drawn at this stage would be that further research is needed to reliably assess the DSA Poljana, including sedimentological analyses as well as micro-computed tomography, with the novel petrophysical analyses primarily focused on impermeable samples showing fair porosity.
- Additional analyses of cap rock petrophysical properties are needed, including CO2/brine relative permeability and capillary threshold pressure.
- The presented approach is suitable for DSAs characterized by variability of petrophysical properties and can be used in the rather early stage of investigation to direct further research towards more promising areas of clastic DSAs.
- Despite showing a significant drawback concerning the inability to adequately describe the permeability of the whole DSA Poljana, the permeability model A can be regarded as the most reliable, since it is based on a greater number of laboratory measurements and it indicates the zones where the diagenetic processes might have played a significant role, strongly influencing the permeability values.
- Using the Slichter equation to develop the meaningful permeability model B is practically impossible without a large dataset that would enable to assess the spatial distribution of the mean grain size.
- Attempts to make use of the Timur equation (model C) have run into a similar problem—the lack of reliable input data prohibits any estimate of the reliability of the results.
- Seismic data should be included to enable identification of structures suitable for underground storage of CO2 or energy and development of their structural models as a start point for site characterization and project development.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- UNDP. World Energy Assessment; Energy and the Challenge of Sustainability; UNDP: New York, NY, USA, 2000. [Google Scholar]
- Global Energy Assessment (GEA); Johansson, T.B.; Nakicenovic, N.; Patwardhan, A.; Gomez-Echeverri, L. (Eds.) Global Energy Assessment; Cambridge University Press: Cambridge, UK, 2012; ISBN 9780511793677. [Google Scholar]
- Howes, S.; Wyrwoll, P. Evaluation of Current Pledges, Actions, and Strategies. In Managing the Transition to a Low-Carbon Economy—Perspectives, Policies, and Practices from Asia; Nbumozhi, V., Kawai, M., Lohani, B.N., Eds.; Asian Development Bank Institute: Hong Kong, China, 2015; pp. 85–146. [Google Scholar]
- Bradshaw, J.; Bachu, S.; Bonijoly, D.; Burruss, R.; Holloway, S.; Christensen, N.P.; Mathiassen, O.M. CO2 storage capacity estimation: Issues and development of standards. Int. J. Greenh. Gas Control 2007, 1, 62–68. [Google Scholar] [CrossRef] [Green Version]
- Bachu, S.; Bonijoly, D.; Bradshaw, J.; Burruss, R.; Holloway, S.; Christensen, N.P.; Mathiassen, O.M. CO2 storage capacity estimation: Methodology and gaps. Int. J. Greenh. Gas Control 2007, 1, 62–68. [Google Scholar] [CrossRef] [Green Version]
- Doughty, C.; Pruess, K. Modeling Supercritical Carbon Dioxide Injection in Heterogeneous Porous Media. Vadose Zone J. 2004, 3, 837–847. [Google Scholar] [CrossRef]
- Goodman, A.; Hakala, A.; Bromhal, G.; Deel, D.; Rodosta, T.; Frailey, S.; Small, M.; Allen, D.; Romanov, V.; Fazio, J.; et al. U.S. DOE methodology for the development of geologic storage potential for carbon dioxide at the national and regional scale. Int. J. Greenh. Gas Control 2011, 5, 952–965. [Google Scholar] [CrossRef]
- Bachu, S. Review of CO2 storage efficiency in deep saline aquifers. Int. J. Greenh. Gas Control 2015, 40, 188–202. [Google Scholar] [CrossRef]
- Vangkilde-Pedersen, T.; Anthonsen, K.L.; Smith, N.; Kirk, K.; Neele, F.; van der Meer, B.; Le Gallo, Y.; Bossie-Codreanu, D.; Wojcicki, A.; Le Nindre, Y.-M.; et al. Assessing European capacity for geological storage of carbon dioxide–the EU GeoCapacity project. Energy Procedia 2009, 1, 2663–2670. [Google Scholar] [CrossRef] [Green Version]
- Höller, S.; Viebahn, P. Assessment of CO2 storage capacity in geological formations of Germany and Northern Europe. Energy Procedia 2011, 4, 4897–4904. [Google Scholar] [CrossRef] [Green Version]
- Bader, A.G.; Thibeau, S.; Vincké, O.; Delprat Jannaud, F.; Saysset, S.; Joffre, G.H.; Giger, F.M.; David, M.; Gimenez, M.; Dieulin, A.; et al. CO2 Storage Capacity Evaluation in Deep Saline Aquifers for an Industrial Pilot Selection. Methodology and Results of the France Nord Project. Energy Procedia 2014, 63, 2779–2788. [Google Scholar] [CrossRef] [Green Version]
- Koukouzas, N.; Tyrologou, P.; Karapanos, D.; Carneiro, J.; Pereira, P.; de Mesquita Lobo Veloso, F.; Koutsovitis, P.; Karkalis, C.; Manoukian, E.; Karametou, R. Carbon Capture, Utilisation and Storage as a Defense Tool against Climate Change: Current Developments in West Macedonia (Greece). Energies 2021, 14, 3321. [Google Scholar] [CrossRef]
- Burton, M.; Kumar, N.; Bryant, S.L. CO2 injectivity into brine aquifers: Why relative permeability matters as much as absolute permeability. Energy Procedia 2009, 1, 3091–3098. [Google Scholar] [CrossRef] [Green Version]
- Yusof, M.A.M.; Neuyam, Y.A.S.; Ibrahim, M.A.; Saaid, I.M.; Idris, A.K.; Mohamed, M.A. Experimental study of CO2 injectivity impairment in sandstone due to salt precipitation and fines migration. J. Pet. Explor. Prod. Technol. 2022, 12, 2191–2202. [Google Scholar] [CrossRef]
- Birkholzer, J.; Zhou, Q.; Tsang, C. Large-scale impact of CO2 storage in deep saline aquifers: A sensitivity study on pressure response in stratified systems. Int. J. Greenh. Gas Control 2009, 3, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.; Al-Shuhail, A.A.; Khulief, Y.A. Numerical modeling of the geomechanical behavior of Ghawar Arab-D carbonate petroleum reservoir undergoing CO2 injection. Environ. Earth Sci. 2016, 75, 1499. [Google Scholar] [CrossRef]
- Vilarrasa, V.; Silva, O.; Carrera, J.; Olivella, S. Liquid CO2 injection for geological storage in deep saline aquifers. Int. J. Greenh. Gas Control 2013, 14, 84–96. [Google Scholar] [CrossRef] [Green Version]
- Worden, R.H.; Burley, S.D. Sandstone Diagenesis: The Evolution of Sand to Stone. In Sandstone Diagenesis; Burley, S.D., Worden, R.H., Eds.; Blackwell Publishing Ltd.: Oxford, UK, 2003; pp. 1–44. [Google Scholar]
- Füchtbauer, H. Influence of Different Types of Diagenesis on Sandstone Porosity. In Proceedings of the 7th World Petroleum Congress, Mexico City, Mexico, 2–9 April 1967. [Google Scholar]
- Bjorlykke, K. Petroleum Geoscience; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-02331-6. [Google Scholar]
- Collen, J.D. Diagenetic Control of Porosity and Permeability in Pakawau and Kapuni Group Sandstones, Taranaki Basin, New Zealand. Energy Explor. Exploit. 1988, 6, 263–280. [Google Scholar] [CrossRef]
- Cnudde, V.; Boone, M.; Dewanckele, J.; Dierick, M.; Van Hoorebeke, L.; Jacobs, P. 3D characterization of sandstone by means of X-ray computed tomography. Geosphere 2011, 7, 54–61. [Google Scholar] [CrossRef]
- Neumann, R.F.; Barsi-Andreeta, M.; Lucas-Oliveira, E.; Barbalho, H.; Trevizan, W.A.; Bonagamba, T.J.; Steiner, M.B. High accuracy capillary network representation in digital rock reveals permeability scaling functions. Sci. Rep. 2021, 11, 11370. [Google Scholar] [CrossRef]
- Galkin, S.V.; Martyushev, D.A.; Osovetsky, B.M.; Kazymov, K.P.; Song, H. Evaluation of void space of complicated potentially oil-bearing carbonate formation using X-ray tomography and electron microscopy methods. Energy Rep. 2022, 8, 6245–6257. [Google Scholar] [CrossRef]
- Belozerov, I.; Gubaydullin, M. Concept of technology for determining the permeability and porosity properties of terrigenous reservoirs on a digital rock sample model. J. Min. Inst. 2020, 244, 402–407. [Google Scholar] [CrossRef]
- Tian, J.; Qi, C.; Sun, Y.; Yaseen, Z.M.; Pham, B.T. Permeability prediction of porous media using a combination of computational fluid dynamics and hybrid machine learning methods. Eng. Comput. 2021, 37, 3455–3471. [Google Scholar] [CrossRef]
- Medina, C.R.; Rupp, J.A.; Barnes, D.A. Effects of reduction in porosity and permeability with depth on storage capacity and injectivity in deep saline aquifers: A case study from the Mount Simon Sandstone aquifer. Int. J. Greenh. Gas Control 2011, 5, 146–156. [Google Scholar] [CrossRef]
- Grana, D.; Liu, M.; Ayani, M. Prediction of CO2 Saturation Spatial Distribution Using Geostatistical Inversion of Time-Lapse Geophysical Data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3846–3856. [Google Scholar] [CrossRef]
- Khanal, A.; Shahriar, M.F. Physics-Based Proxy Modeling of CO2 Sequestration in Deep Saline Aquifers. Energies 2022, 15, 4350. [Google Scholar] [CrossRef]
- Bandilla, K.W.; Celia, M.A.; Elliot, T.R.; Person, M.; Ellett, K.M.; Rupp, J.A.; Gable, C.; Zhang, Y. Modeling carbon sequestration in the Illinois Basin using a vertically-integrated approach. Comput. Vis. Sci. 2012, 15, 39–51. [Google Scholar] [CrossRef]
- Popov, S.V.; Shcherba, I.G.; Ilyina, L.B.; Nevesskaya, L.A.; Paramonova, N.P.; Khondkarian, S.O.; Magyar, I. Late Miocene to Pliocene palaeogeography of the Paratethys and its relation to the Mediterranean. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2006, 238, 91–106. [Google Scholar] [CrossRef]
- Palcu, D.V.; Patina, I.S.; Șandric, I.; Lazarev, S.; Vasiliev, I.; Stoica, M.; Krijgsman, W. Late Miocene megalake regressions in Eurasia. Sci. Rep. 2021, 11, 11471. [Google Scholar] [CrossRef]
- Pavelić, D. Tectonostratigraphic model for the North Croatian and North Bosnian sector of the Miocene Pannonian Basin System. Basin Res. 2001, 13, 359–376. [Google Scholar] [CrossRef]
- Saftić, B.; Velić, J.; Sztanó, O.; Juhász, G.; Ivković, Ž. Tertiary subsurface facies, source rocks and hydrocarbon reservoirs in the SW part of the Pannonian Basin (Northern Croatia and south-western Hungary). Geol. Croat. 2003, 56, 101–122. [Google Scholar] [CrossRef]
- Balázs, A.; Magyar, I.; Matenco, L.; Sztanó, O.; Tőkés, L.; Horváth, F. Morphology of a large paleo-lake: Analysis of compaction in the Miocene-Quaternary Pannonian Basin. Glob. Planet. Chang. 2018, 171, 134–147. [Google Scholar] [CrossRef]
- Pavelić, D.; Kovačić, M. Sedimentology and stratigraphy of the Neogene rift-type North Croatian Basin (Pannonian Basin System, Croatia): A review. Mar. Pet. Geol. 2018, 91, 455–469. [Google Scholar] [CrossRef]
- Lučić, D.; Saftić, B.; Krizmanić, K.; Prelogović, E.; Britvić, V.; Mesić, I.; Tadej, J. The Neogene evolution and hydrocarbon potential of the Pannonian Basin in Croatia. Mar. Pet. Geol. 2001, 18, 133–147. [Google Scholar] [CrossRef]
- Šimon, J. On some results of regional lithostratigraphic correlation in the south-western part of Pannonian basin (In Croatian: O nekim rezultatima regionalne korelacije litostratigrafskih jedinica u jugozapadnom području Panonskog bazena). Nafta 1973, 24, 623–630. [Google Scholar]
- Kolenković, I.; Saftić, B.; Perešin, D. Regional capacity estimates for CO2 geological storage in deep saline aquifers—Upper Miocene sandstones in the SW part of the Pannonian basin. Int. J. Greenh. Gas Control 2013, 16, 180–186. [Google Scholar] [CrossRef]
- US DOE. Carbon Sequestration Atlas of United States and Canada, 3rd ed.; US DOE: Washington, DC, USA, 2010.
- Spencer, L.K.; Bradshaw, J.; Bradshaw, B.E.; Lahtinen, A.-L.; Chirinos, A. Regional storage capacity estimates: Prospectivity not statistics. Energy Procedia 2011, 4, 4857–4864. [Google Scholar] [CrossRef] [Green Version]
- Ramm, M.; Bjørlykke, K. Porosity/depth trends in reservoir sandstones: Assessing the quantitative effects of varying pore-pressure, temperature history and mineralogy, Norwegian Shelf data. Clay Miner. 1994, 29, 475–490. [Google Scholar] [CrossRef]
- Tadej, J.; Marić Đureković, Ž.; Slavković, R. Porosity, Cementation, Diagenesis and Their Influence on the Productive Capability of Sandstone Reservoirs in the Sava Depression (Croatia). Geol. Croat. 1996, 49, 311–316. [Google Scholar]
- Matošević, M.; Kovačić, M.; Pavelić, D. Provenance and diagenesis of the Upper Miocene sandstones from the Pannonian Basin System. In Proceedings of the Book of Abstracts of 35th IAS Meeting of Sedimentology, Prague, Czech Republic, 21–25 June 2021. [Google Scholar]
- Dutton, S.P. Calcite cement in Permian deep-water sandstones, Delaware Basin, west Texas: Origin, distribution, and effect on reservoir properties. Am. Assoc. Pet. Geol. Bull. 2008, 92, 765–787. [Google Scholar] [CrossRef]
- Pittman, E.D.; Lumsden, D.N. No TitleRelationship between chlorite coating on quartz grain and porosity, Spiro Sand, Oklahoma. J. Sediment. Petrol. 1968, 38, 668–670. [Google Scholar] [CrossRef]
- Ahmad, N.; Khan, S.; Al-Shuhail, A. Seismic Data Interpretation and Petrophysical Analysis of Kabirwala Area Tola (01) Well, Central Indus Basin, Pakistan. Appl. Sci. 2021, 11, 2911. [Google Scholar] [CrossRef]
- Slichter, S.C. Theoretical investigation of the motion of ground water. In US Geological Survey, 19th Annual Report, Part II; Government Printing Office: Washington, DC, USA, 1899; pp. 295–384. [Google Scholar]
- Tiab, D.; Donaldson, E.C. Petrophysics: Theory and Practice of Measuring Reservoir Rock and Fluid Transport Properties; Gulf Professional Publishing: Houston, TX, USA, 2015. [Google Scholar]
- Tixier, M.P. Evaluation of Permeability from Resistivity Gradient on Electric Logs. Tulsa Geol. Soc. Dig. 1949, 17, 68–73. [Google Scholar]
- Wyllie, M.R.J.; Rose, W.D. Some Theoretical Considerations Related to Quantitative Evaluation of Physical Characteristics of Reservoir Rocks from Electrical Log Data. Trans. AIME 1950, 189, 105–118. [Google Scholar] [CrossRef]
- Morris, R.L.; Biggs, W.P. Using log-derived values of water saturation and porosity. In Proceedings of the SPWLA Annual Logging Symposium, Denver, CO, USA, 12–14 June 1967. [Google Scholar]
- Timur, A. Pulsed Nuclear Magnetic Resonance Studies of Porosity, Movable Fluid, and Permeability of Sandstones. J. Pet. Technol. 1969, 21, 775–786. [Google Scholar] [CrossRef]
- Coates, G.R.; Denoo, S. The producibility answer product. Tech. Rev. 1981, 29, 54–63. [Google Scholar]
- Peng, L.; Zhang, C.; Ma, H.; Pan, H. Estimating irreducible water saturation and permeability of sandstones from nuclear magnetic resonance measurements by fractal analysis. Mar. Pet. Geol. 2019, 110, 565–574. [Google Scholar] [CrossRef]
- Lis-Śledziona, A.; Stadtmüller, M. Determining irreducible water saturation based on well log data and laboratory measurements. Nafta-Gaz 2019, 75, 239–246. [Google Scholar] [CrossRef]
- Shi, J.-Q.; Xue, Z.; Durucan, S. History matching of CO2 core flooding CT scan saturation profiles with porosity dependent capillary pressure. Energy Procedia 2009, 1, 3205–3211. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Zhang, C.; Chen, D.; Yang, F.; Li, H.; Li, M. Microscopic Seepage Mechanism of Gas and Water in Ultra-Deep Fractured Sandstone Gas Reservoirs of Low Porosity: A Case Study of Keshen Gas Field in Kuqa Depression of Tarim Basin, China. Front. Earth Sci. 2022, 10, 893701. [Google Scholar] [CrossRef]
- Buckles, R.S. Correlating and Averaging Connate Water Saturation Data. J. Can. Pet. Technol. 1965, 4, 42–52. [Google Scholar] [CrossRef]
- Vulin, D.; Čogelja, Z.; Biljanović, T. Determination of representative capillary pressure curve by adjusting the laboratory and well logging data (in Croatian, original title: Određivanje reprezentativne krivulje kapilarnog tlaka usklađivanjem laboratorijskih i karotažnih podataka). Naft. I Plin 2016, 36, 33–40. (In Croatian) [Google Scholar]
- Baker, R.O.; Yarranton, H.W.; Jensen, J.L. Special Core Analysis—Rock–Fluid Interactions. In Practical Reservoir Engineering and Characterization; Elsevier: Amsterdam, The Netherlands, 2015; pp. 239–295. [Google Scholar]
- Asquith, G.B.; Gibosn, C.R. Basic Well Log Analysis for Geologists; American Association of Petroleum Geologists: Tulsa, OK, USA, 1982; ISBN 978-1-6298-1171-0. [Google Scholar]
- Coates, G.R.; Dumanoir, J.L. A new approach to improved log derived permeability. Log Anal. 1974, 15, 17–29. [Google Scholar]
- Torskaya, T.; Shabro, V.; Torres-Verdín, C.; Salazar-Tio, R.; Revil, A. Grain Shape Effects on Permeability, Formation Factor, and Capillary Pressure from Pore-Scale Modeling. Transp. Porous Media 2014, 102, 71–90. [Google Scholar] [CrossRef]
- El Sharawy, M.S.; Gaafar, G.R. Impacts of petrophysical properties of sandstone reservoirs on their irreducible water saturation: Implication and prediction. J. Afr. Earth Sci. 2019, 156, 118–132. [Google Scholar] [CrossRef]
- Ge, Z.; Nemec, W.; Vellinga, A.J.; Gawthorpe, R.L. How is a turbidite actually deposited? Sci. Adv. 2022, 8, eabl9124. [Google Scholar] [CrossRef] [PubMed]
- Jelić, K. Porosity and permeability relation to burial depth for lithostratigraphic units of Sava and Drava Depressions (Odnos gustoće i poroznosti s dubinom litostratigrafskih formacija Savske i Dravske potoline). Nafta 1984, 35, 952–965. (In Croatian) [Google Scholar]
- Paxton, S.T.; Szabo, J.O.; Ajdukiewicz, J.M.; Klimentidis, R.E. Construction of an intergranular volume compaction curve for evaluating and predicting compaction and porosity loss in rigid-grain sandstone reservoirs. Am. Assoc. Pet. Geol. Bull. 2002, 86, 2047–2067. [Google Scholar] [CrossRef]
- Cheng, C.-L.; Gragg, M.J.; Perfect, E.; White, M.D.; Lemiszki, P.J.; McKay, L.D. Sensitivity of injection costs to input petrophysical parameters in numerical geologic carbon sequestration models. Int. J. Greenh. Gas Control 2013, 18, 277–284. [Google Scholar] [CrossRef]
- Yang, J.; Busen, H.; Scherb, H.; Hürkamp, K.; Guo, Q.; Tschiersch, J. Modeling of radon exhalation from soil influenced by environmental parameters. Sci. Total Environ. 2019, 656, 1304–1311. [Google Scholar] [CrossRef] [PubMed]
- Trask, P. Origin and Environment of Source Sediments of Petroleum; Gulf Publishing Co.: Huston, TX, USA, 1932. [Google Scholar]
- Folk, R.L. The Distinction between Grain Size and Mineral Composition in Sedimentary-Rock Nomenclature. J. Geol. 1954, 62, 344–359. [Google Scholar] [CrossRef]
- Folk, R.L.; Ward, W.C. Brazos River bar: A study in the significance of grain size parameters. J. Sediment. Petrol. 1957, 27, 3–26. [Google Scholar] [CrossRef]
- Friedman, G.M. On Sorting, Sorting Coefficients, and the Lognormality of the Grain-Size Distribution of Sandstones. J. Geol. 1962, 70, 737–753. [Google Scholar] [CrossRef]
- Coskun, S.B.; Wardlaw, N.C.; Haverslew, B. Effects of composition, texture and diagenesis on porosity, permeability and oil recovery in a sandstone reservoir. J. Pet. Sci. Eng. 1993, 8, 279–292. [Google Scholar] [CrossRef]


| Sample | Depth (m) | kmeasured (mD) | Φ | Swirr Estimated | k after Wyllie and Rose (mD) | k after Tixier (mD) | k after Timur (mD) | k after Coates and Denoo (mD) | k after Morris and Biggs (mD) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1528.9 | 10.32 | 0.2013 | 0.1618 | 281.4103 | 158.8494 | 283.4618 | 440.6699 | 15.86207 |
| 2 | 1528.44 | 14.49 | 0.2024 | 0.2642 | 108.1637 | 61.557 | 108.8929 | 130.1655 | 6.146836 |
| 3 | 1526.97 | 15.21 | 0.2105 | 0.2178 | 189.8973 | 114.6243 | 190.4287 | 253.2376 | 11.44593 |
| 4 | 1526.55 | 45.53 | 0.2162 | 0.1799 | 313.8978 | 197.2204 | 313.9364 | 454.0399 | 19.69364 |
| 5 | 1528.55 | 23.3 | 0.2189 | 0.1417 | 535.0153 | 342.464 | 534.4174 | 842.4062 | 34.19708 |
| 6 | 1526.86 | 33.95 | 0.2206 | 0.1099 | 920.9359 | 596.3726 | 919.1952 | 1553.475 | 59.55138 |
| 7 | 1527.64 | 34.79 | 0.2225 | 0.1282 | 703.4108 | 461.4069 | 701.4794 | 1133.386 | 46.07424 |
| 8 | 1528.65 | 38.07 | 0.2229 | 0.102 | 1120.198 | 736.7838 | 1116.922 | 1913.342 | 73.57229 |
| 9 | 1528.34 | 71.5 | 0.254 | 0.166 | 761.2644 | 609.0685 | 749.1885 | 1050.632 | 60.81914 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolenković Močilac, I.; Cvetković, M.; Saftić, B.; Rukavina, D. Porosity and Permeability Model of a Regionally Extending Unit (Upper Miocene Sandstones of the Western Part of Sava Depression, Croatia) Based on Vintage Well Data. Energies 2022, 15, 6066. https://doi.org/10.3390/en15166066
Kolenković Močilac I, Cvetković M, Saftić B, Rukavina D. Porosity and Permeability Model of a Regionally Extending Unit (Upper Miocene Sandstones of the Western Part of Sava Depression, Croatia) Based on Vintage Well Data. Energies. 2022; 15(16):6066. https://doi.org/10.3390/en15166066
Chicago/Turabian StyleKolenković Močilac, Iva, Marko Cvetković, Bruno Saftić, and David Rukavina. 2022. "Porosity and Permeability Model of a Regionally Extending Unit (Upper Miocene Sandstones of the Western Part of Sava Depression, Croatia) Based on Vintage Well Data" Energies 15, no. 16: 6066. https://doi.org/10.3390/en15166066
APA StyleKolenković Močilac, I., Cvetković, M., Saftić, B., & Rukavina, D. (2022). Porosity and Permeability Model of a Regionally Extending Unit (Upper Miocene Sandstones of the Western Part of Sava Depression, Croatia) Based on Vintage Well Data. Energies, 15(16), 6066. https://doi.org/10.3390/en15166066