Blind Source Separation of Transformer Acoustic Signal Based on Sparse Component Analysis
Abstract
:1. Introduction
2. Principle of Blind Source Separation for Transformer Acoustic Signal
2.1. Characteristic Analysis of Interference Signals
2.2. Sparse Component Analysis
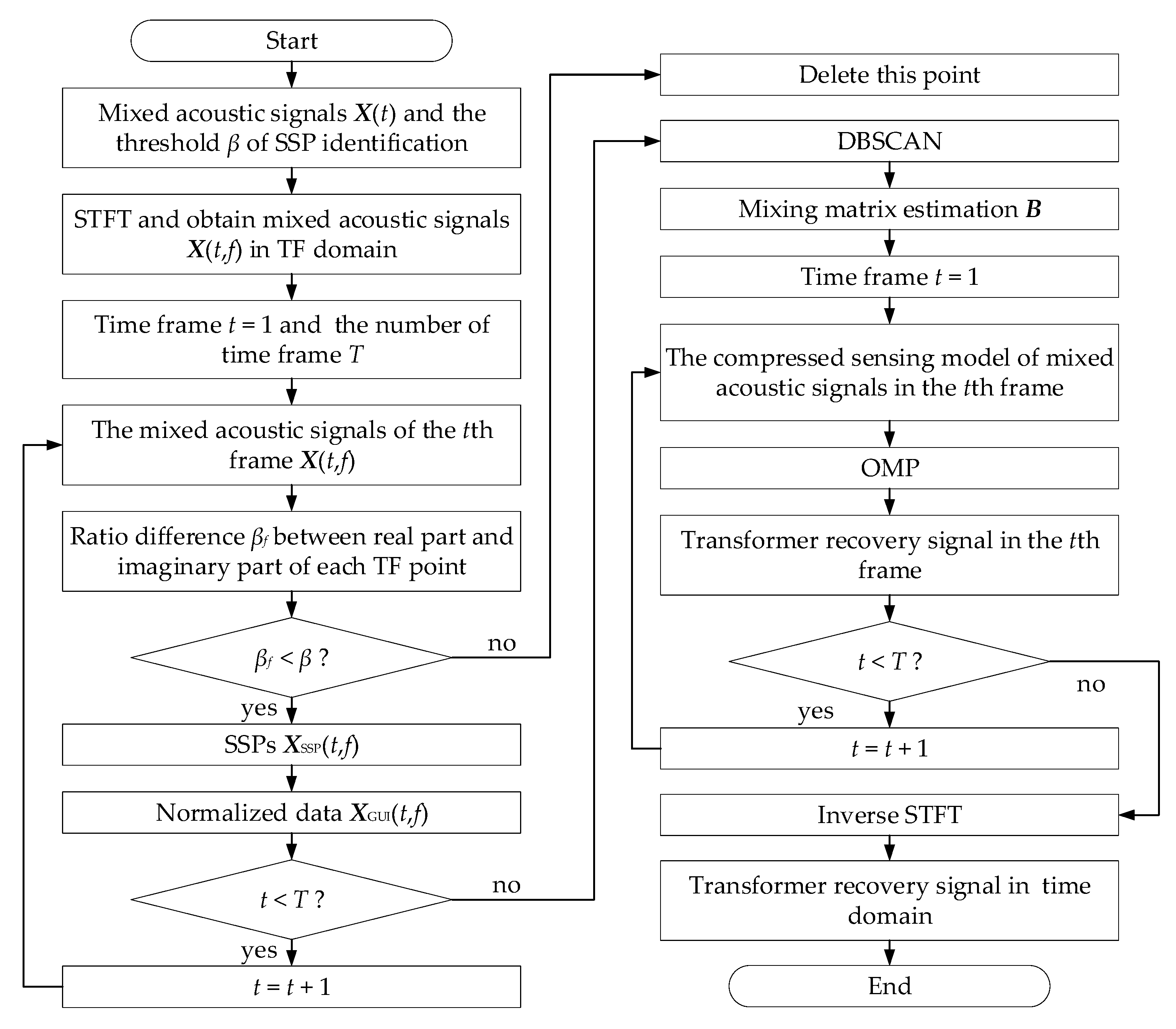
3. Blind Source Separation Method of Transformer Acoustic Signal
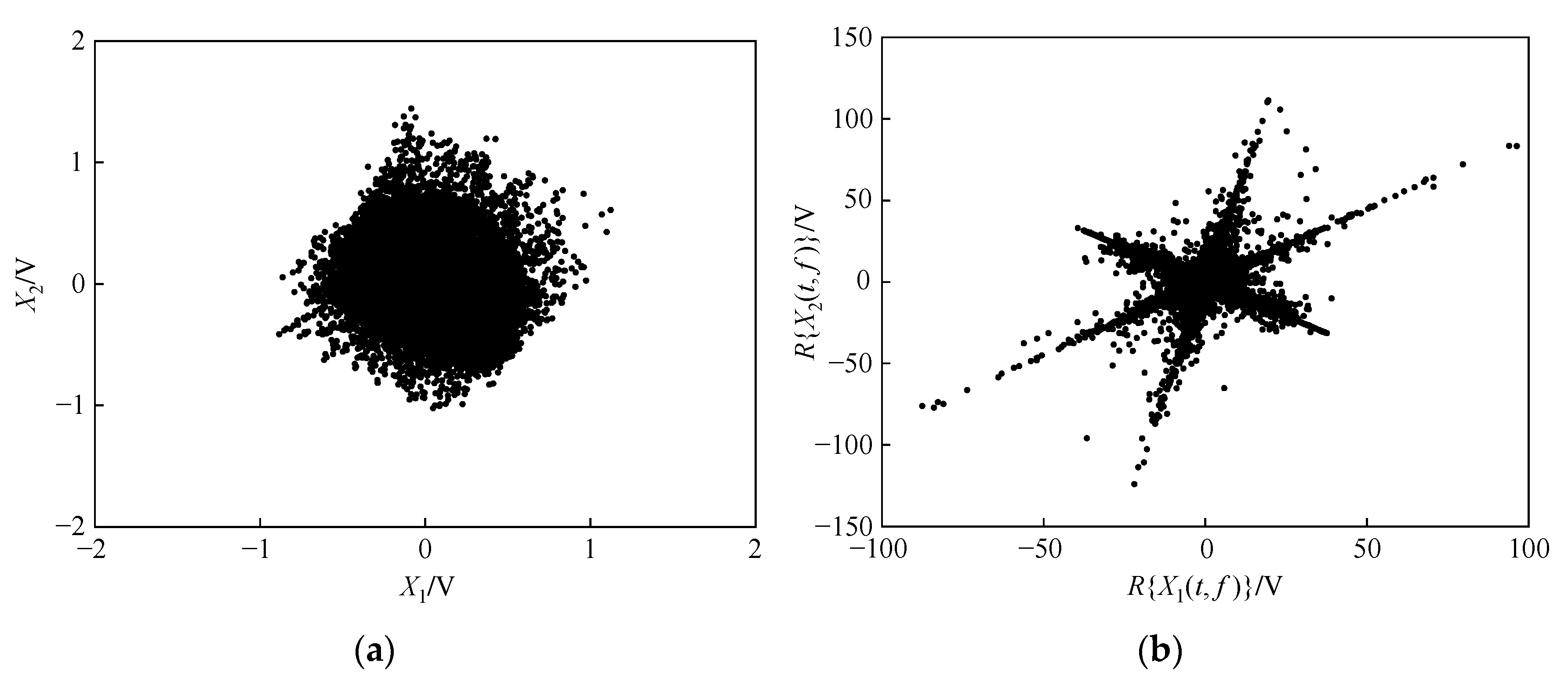
3.1. Sparse Enhancement of Mixed Acoustic Signals
3.2. Mixing Matrix Estimation Based on Density Space Clustering
- (1)
- Eps-neighborhood: for P ∈ C, the set of sample points contained in the hypersphere region with P as the center and Eps as the radius is called the Eps-neighborhood of P, i.e., . Where dist(P, Q) is the distance between sample point P and Q in C.
- (2)
- Core point: for P ∈ C, if the number of sample points contained in NE(P) is more than or equal to mps, i.e., , P is called the core point of C.
- (3)
- Directly density reachable: for Q ∈ C, if and Q ∈ NE(P), Q is directly density reachable from P.
- (4)
- Density reachable: for P1, P2, ..., PC ∈ C, if Pc+1 is directly density reachable from Pc, where 1 ≤ c ≤ C−1, PC is density reachable from P1.
- (5)
- Boundary point: for Q ∈ C, if NE(Q) < mps, NE(P) ≥ mps and Q ∈ NE(P), Q is the boundary point of C.
- (6)
- Noise point: for Q ∈ C, if Q does not belong to Eps-neighborhood of any core point, Q is the noise point of C.
3.3. Source Signals Recovery Based on Compressed Sensing
3.3.1. Compressed Sensing
3.3.2. Source Signals Recovery
4. Simulation Analysis
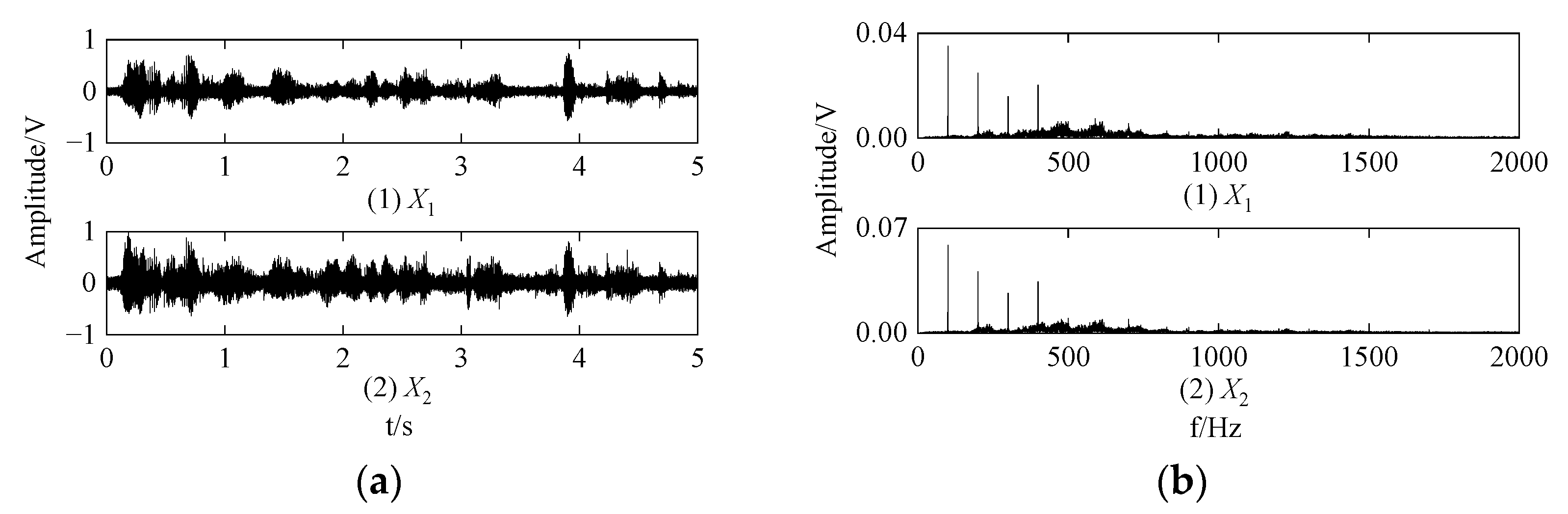
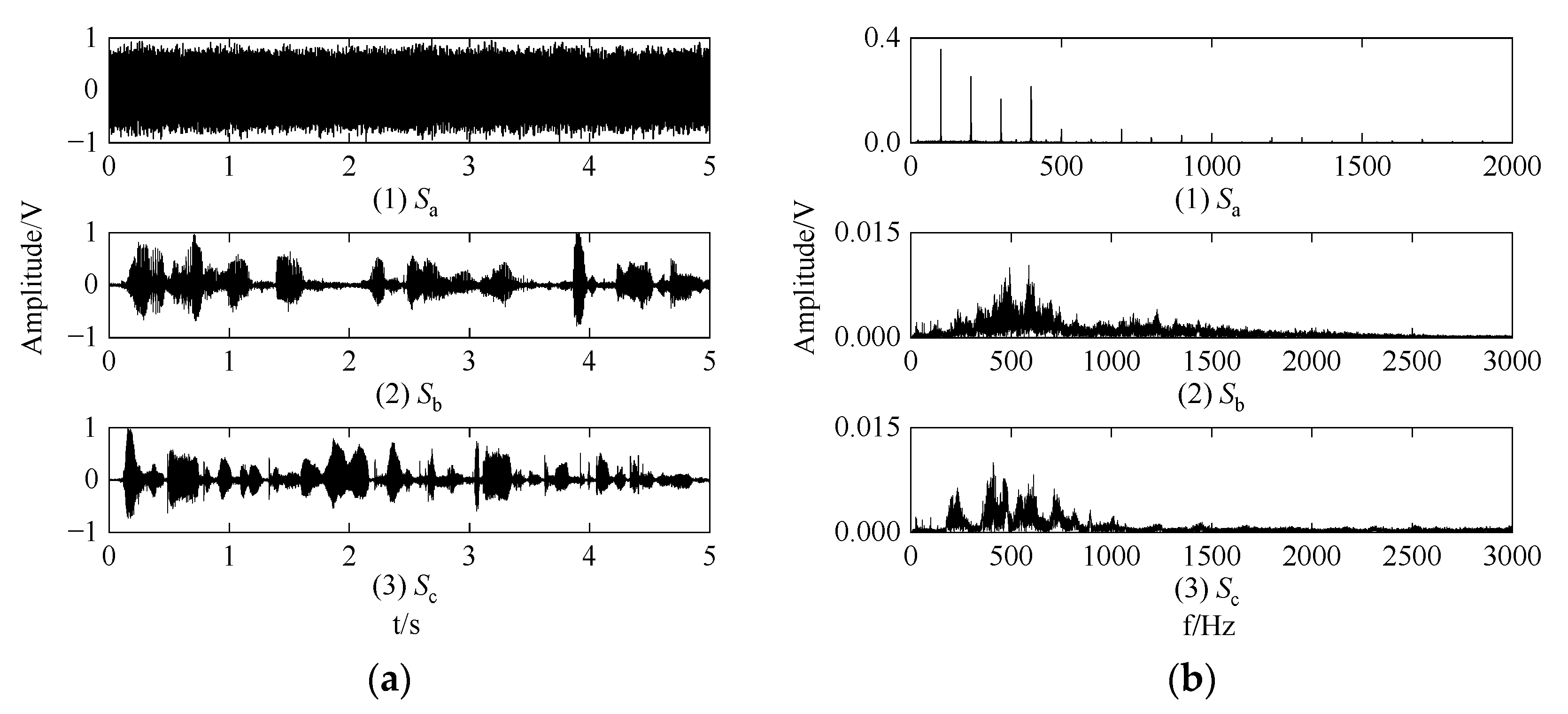
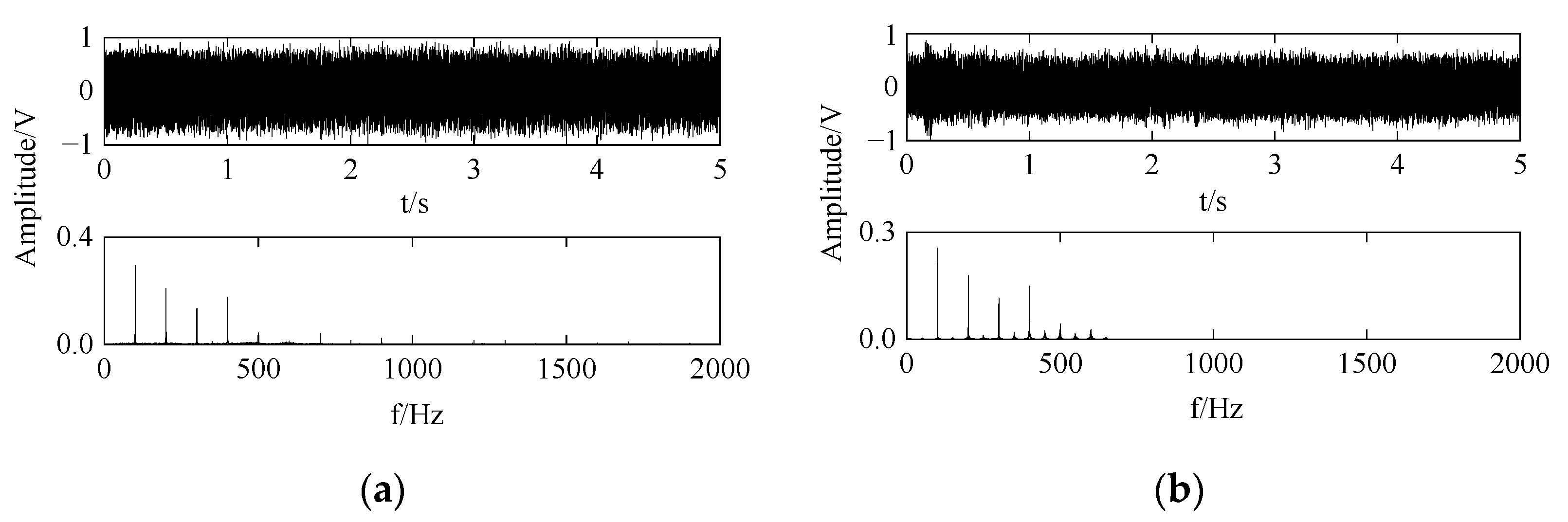
4.1. Simulation Signals
4.2. Simulation Experiment and Analysis
4.3. Comparison with Other Methods
5. Experimental Analysis
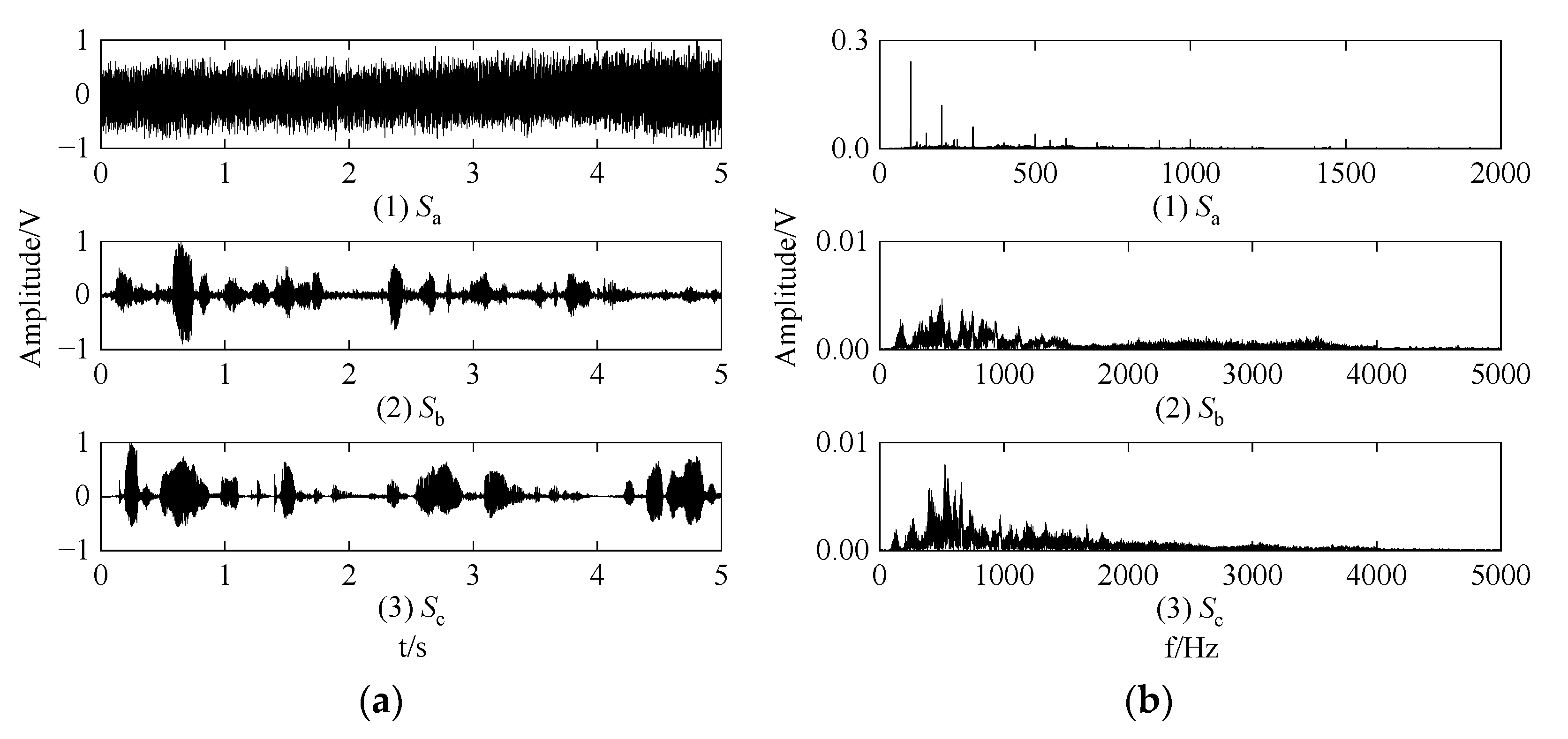
5.1. Experimental Setup
5.2. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zou, L.; Guo, Y.K.; Liu, H.; Zhang, L.; Zhao, T. A Method of Abnormal States Detection Based on Adaptive Extraction of Transformer Vibro-Acoustic Signals. Energies 2017, 10, 2076. [Google Scholar] [CrossRef]
- Adnan, S.; Matej, K.; Igor, K. Vibro-Acoustic Methods in the Condition Assessment of Power Transformers: A Survey. IEEE Access 2019, 7, 83915–83931. [Google Scholar]
- Liu, Y.P.; Wang, B.W.; Yue, H.T.; Gao, F.; Han, S.; Luo, S.H.; Zhang, C.C. Identification of Transformer Bias Voiceprint Based on 50Hz Frequency Multiplication Cepstrum Coefficients and Gated Recurrent Unit. Proc. CSEE 2020, 40, 4681–4694. [Google Scholar]
- Pan, L.L.; Zhao, S.T.; Li, B.S. Electrical equipment fault diagnosis based on acoustic wave signal analysis. Electr. Power Autom. Equip. 2009, 29, 87–90. [Google Scholar]
- Shams, M.A.; Anis, H.I.; El-Shahat, M. Denoising of heavily contaminated partial discharge signals in high-voltage cables using maximal overlap discrete wavelet transform. Energies 2021, 14, 6540. [Google Scholar] [CrossRef]
- Wu, X.W.; Zhou, N.G.; Pei, C.M.; Hu, S.; Huang, T.; Ying, L.M. Separation methodology of audible noises of UHV AC substations. High Volt. Eng. 2016, 42, 2625–2632. [Google Scholar]
- Liu, Z.Y.; Liu, Z.Y.; Fan, H.M. Study on signal de-noising of high voltage cable partial discharge based on EMD-ICA. Power Syst. Prot. Control 2018, 46, 83–87. [Google Scholar]
- Chan, J.C.; Hui, M.; Saha, T.K.; Ekanayakel, C. Self-adaptive partial discharge signal denoising based on ensemble empirical mode decomposition and automatic morphological thresholding. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 294–303. [Google Scholar] [CrossRef]
- Hao, L.; Lewin, P.L.; Hunter, J.A.; Swaffielf, D.J.; Contin, A.; Walton, C.; MIchel, M. Discrimination of multiple PD sources using wavelet decomposition and principal component analysis. IEEE Trans. Dielectrics Electr. Insul. 2011, 18, 1702–1711. [Google Scholar] [CrossRef]
- Alvarez, F.; Garnacho, F.; Ortego, J.; Sanchez-Uran, M.A. A clustering technique for partial discharge and noise sources identifification in power cables by means of waveform parameters. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 469–481. [Google Scholar] [CrossRef]
- Wang, Y.B.; Chang, D.C.; Qin, S.R.; Fan, Y.H.; Mu, H.B.; Zhang, G.J. Separating multi-source partial discharge signals using linear prediction analysis and isolation forest algorithm. IEEE Trans. Instrum. Meas. 2020, 69, 2734–2742. [Google Scholar] [CrossRef]
- Han, S.; Gao, F.; Wang, B.W.; Liu, Y.P.; Wang, K.; Wu, D.; Zhang, C.C. Audible sound identification of on load tap changer based on mel spectrum filtering and CNN. Power Syst. Technol. 2021, 45, 3609–3617. [Google Scholar]
- Stergiadis, C.; Kostaridou, V.D.; Klados, M.A. Which BSS method separates better the EEG Signals? A comparison of five different algorithms. Biomed. Signal Process. Control 2022, 72, 103292. [Google Scholar] [CrossRef]
- Dorothea, K.; Ramon, F.A.; Eugen, H.; Reinhold, O. Independent component analysis and time-frequency masking for speech recognition in multitalker conditions. EURASIP J. Audio Speech Music Process. 2010, 1, 1–13. [Google Scholar] [CrossRef]
- Reju, V.G.; Koh, S.N.; Soon, I.Y. An algorithm for mixing matrix estimation in instantaneous blind source separation. Signal Process. 2009, 89, 1762–1773. [Google Scholar] [CrossRef]
- Guo, J.; Ji, S.C.; Shen, Q.; Zhu, L.Y.; Ou, X.B.; Du, L.M. Blind source separation technology for the detection of transformer fault based on vibration method. Trans. China Electrotech. Soc. 2017, 27, 68–78. [Google Scholar]
- Lin, S.F.; Li, Y.; Tang, B.; Fu, Y.; Li, D.D. System harmonic impedance estimation based on improved fastica and partial least squares. Power Syst. Technol. 2018, 42, 308–314. [Google Scholar]
- Zhou, D.X.; Wang, F.H.; Dang, X.J.; Zhang, X.; Liu, S.G. Blind Separation of UHV Power Transformer Acoustic Signal Preprocessing Based on Sparse Representation Theory. Power Syst. Technol. 2020, 44, 3139–3148. [Google Scholar]
- Bofill, P.; Zibulevsky, M. Underdetermined blind source separation using sparse representations. Signal Process. 2001, 81, 2353–2362. [Google Scholar] [CrossRef]
- Bofill, P. Underdetermined blind separation of delayed sound sources in the frequency domain. Neurocomputing 2003, 55, 627–641. [Google Scholar] [CrossRef]
- Li, M.Z.; Li, S.M.; Lu, J.T. Underdetermined blind source separation based on density peak clustering for gear fault identification. J. Aerosp. Power 2022, 37, 1010–1019. [Google Scholar]
- Li, X.; Zhang, P.; Zhu, G. DBSCAN clustering algorithms for non-uniform density data and its application in urban rail passenger aggregation distribution. Energies 2019, 12, 3722. [Google Scholar] [CrossRef]
- Nooshin, H.; Hamid, S. A fast DBSCAN algorithm for big data based on efficient density calculation. Expert Syst. Appl. 2022, 203, 117501. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Ruiz, M.; Montalvo, I. Electrical faults signals restoring based on compressed sensing techniques. Energies 2020, 13, 2121. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Zhang, S.Z.; Qi, R. Compressed sensing Construction for Underdetermined Source Separation. Circuits Syst. Signal Process. 2017, 36, 4741–4755. [Google Scholar] [CrossRef]
- Zhao, H.F.; Zhang, Y.; Li, S.Z. Undetermined blind source separation and feature extraction of penetration overload signals. Chin. J. Sci. Instrum. 2019, 40, 208–218. [Google Scholar]



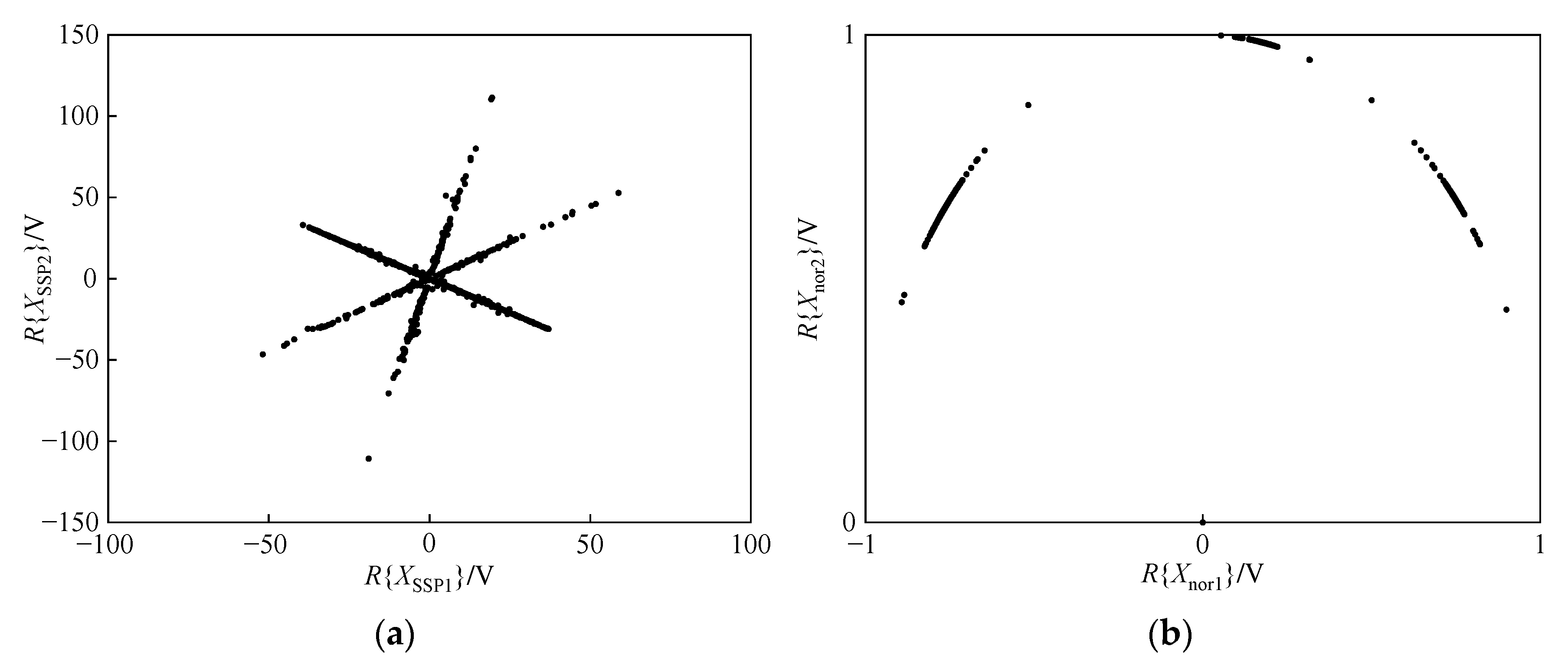



| Interference Source | Interference Factor | Duration/s | Frequency Band/Hz |
|---|---|---|---|
| Transformer structure | Cooling fan sound | continued | 0–1000 |
| OLTC action sound | 0.2 | 0–20,000 | |
| power equipment | Reactor sound | continued | 0–2000 |
| Capacitor sound | continued | 0–2000 | |
| Corona discharge sound | continued | 5000–20,000 | |
| operation environment | Speech sound | 0.4 | 150–5000 |
| Musical sound | 0.5 | 0–20,000 | |
| vehicle sound | 0.5 | 2000–8000 | |
| Bird sound | 0.2 | 3000–8000 |
| Evaluation Index | Proposed Method | Method 1 | Method 2 |
|---|---|---|---|
| NCC(S1, Sa) | 0.9941 | 0.9648 | 0.8413 |
| SNR(S1, Sa)/dB | 20.1829 | 13.8940 | 4.9459 |
| Evaluation Index | (X1, Sa) | (X2, Sa) | (S1, Sa) |
|---|---|---|---|
| NCC | 0.4927 | 0.6472 | 0.9254 |
| SNR/dB | 0.7885 | 1.6663 | 8.8580 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Wang, Y.; Min, Y.; Lei, W. Blind Source Separation of Transformer Acoustic Signal Based on Sparse Component Analysis. Energies 2022, 15, 6017. https://doi.org/10.3390/en15166017
Wang G, Wang Y, Min Y, Lei W. Blind Source Separation of Transformer Acoustic Signal Based on Sparse Component Analysis. Energies. 2022; 15(16):6017. https://doi.org/10.3390/en15166017
Chicago/Turabian StyleWang, Guo, Yibin Wang, Yongzhi Min, and Wu Lei. 2022. "Blind Source Separation of Transformer Acoustic Signal Based on Sparse Component Analysis" Energies 15, no. 16: 6017. https://doi.org/10.3390/en15166017
APA StyleWang, G., Wang, Y., Min, Y., & Lei, W. (2022). Blind Source Separation of Transformer Acoustic Signal Based on Sparse Component Analysis. Energies, 15(16), 6017. https://doi.org/10.3390/en15166017






