Lead–Acid Battery SOC Prediction Using Improved AdaBoost Algorithm
Abstract
:1. Introduction
1.1. Background
1.2. Related Works
1.3. Limitations of Current Methods
1.4. Research Method of This Paper
2. Related Deep Learning Theories
2.1. Extreme Learning Machine (ELM)
2.2. Online Sequence Extreme Learning Machine (OSELM)
2.3. AdaBoost Algorithm
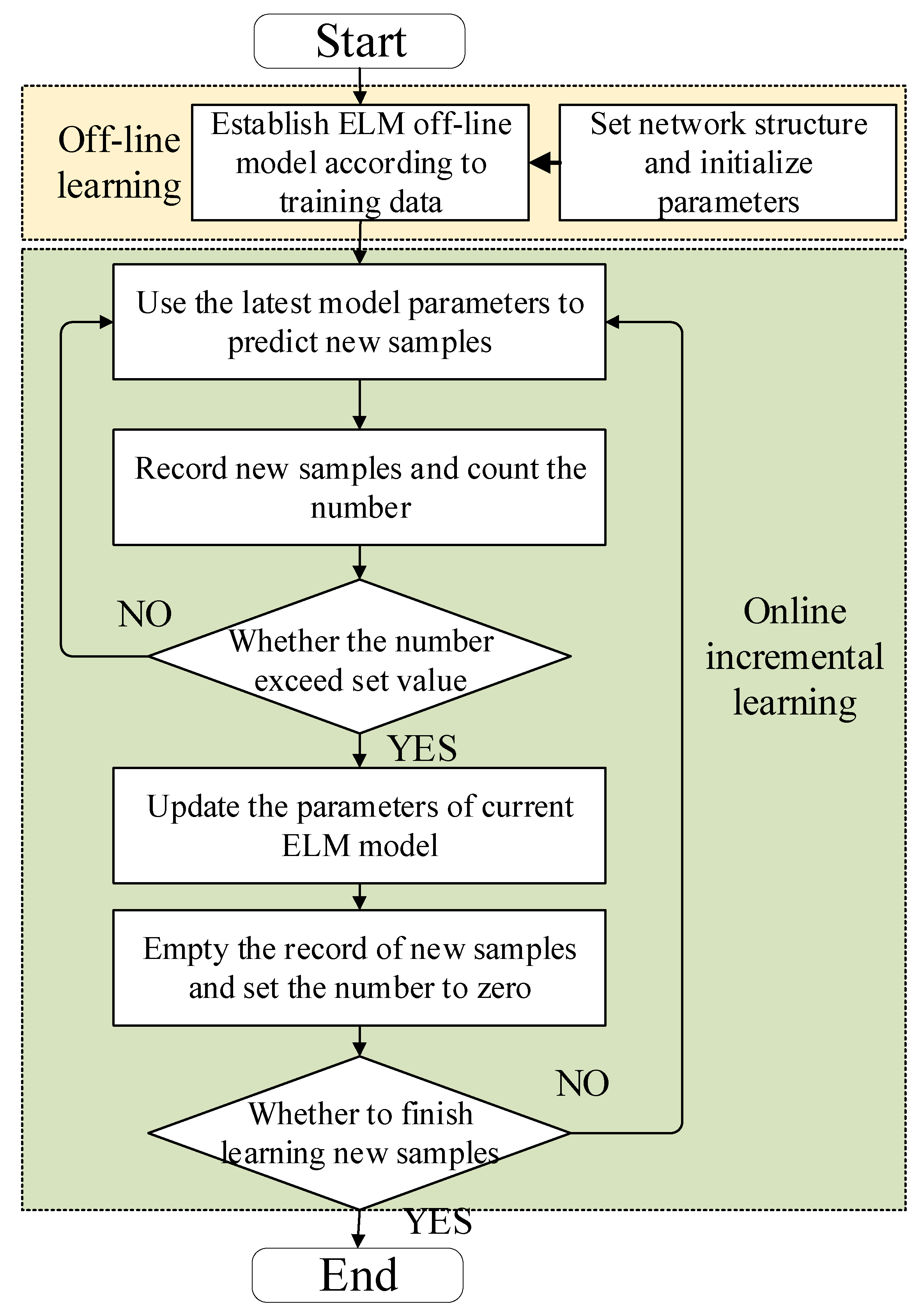
3. Battery SOC Prediction Process Based on the AdaBoost.I-OSELM Model
3.1. Computation Process of the AdaBoost.I-OSELM Model
3.2. Prediction Process of Battery SOC Based on the AdaBoost.I-OSELM Model
3.2.1. Data Content
3.2.2. Prediction Process of Battery SOC Based on the AdaBoost.I-OSELM Model
3.3. Experimental Evaluation Indicators
4. Case Analysis
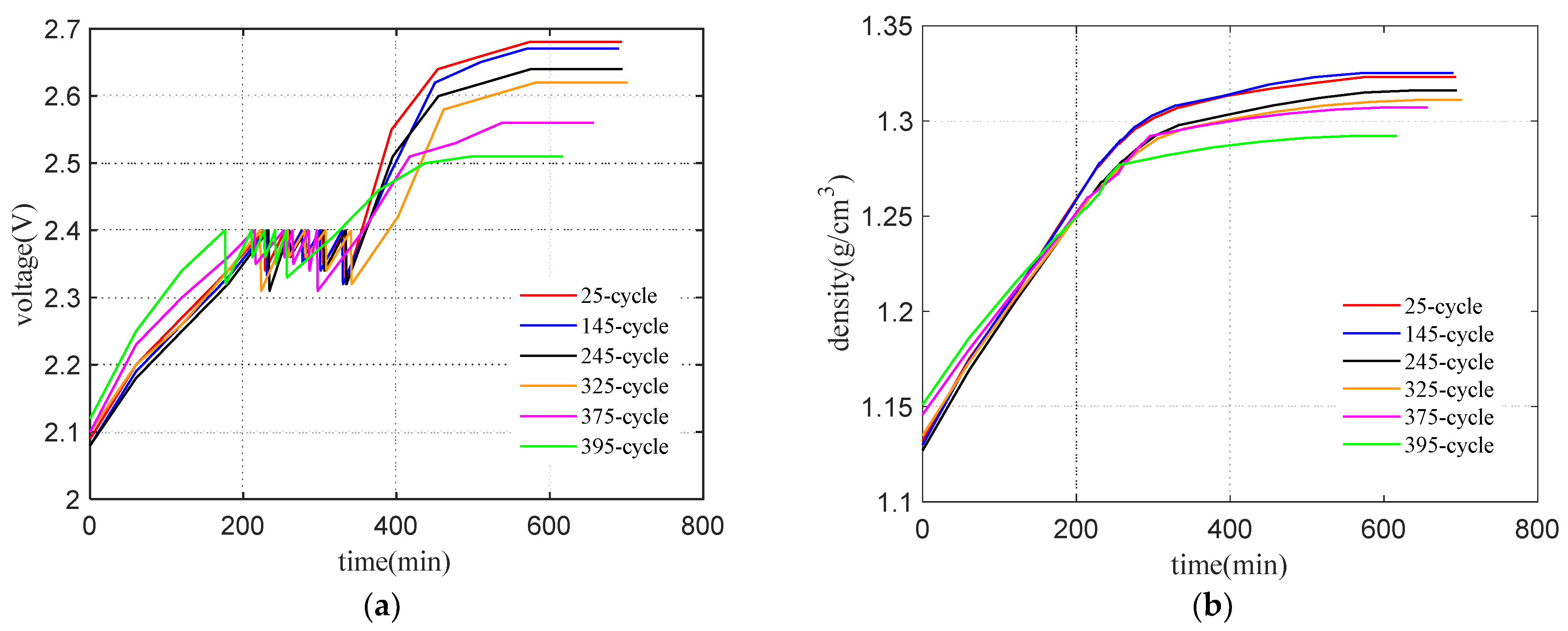
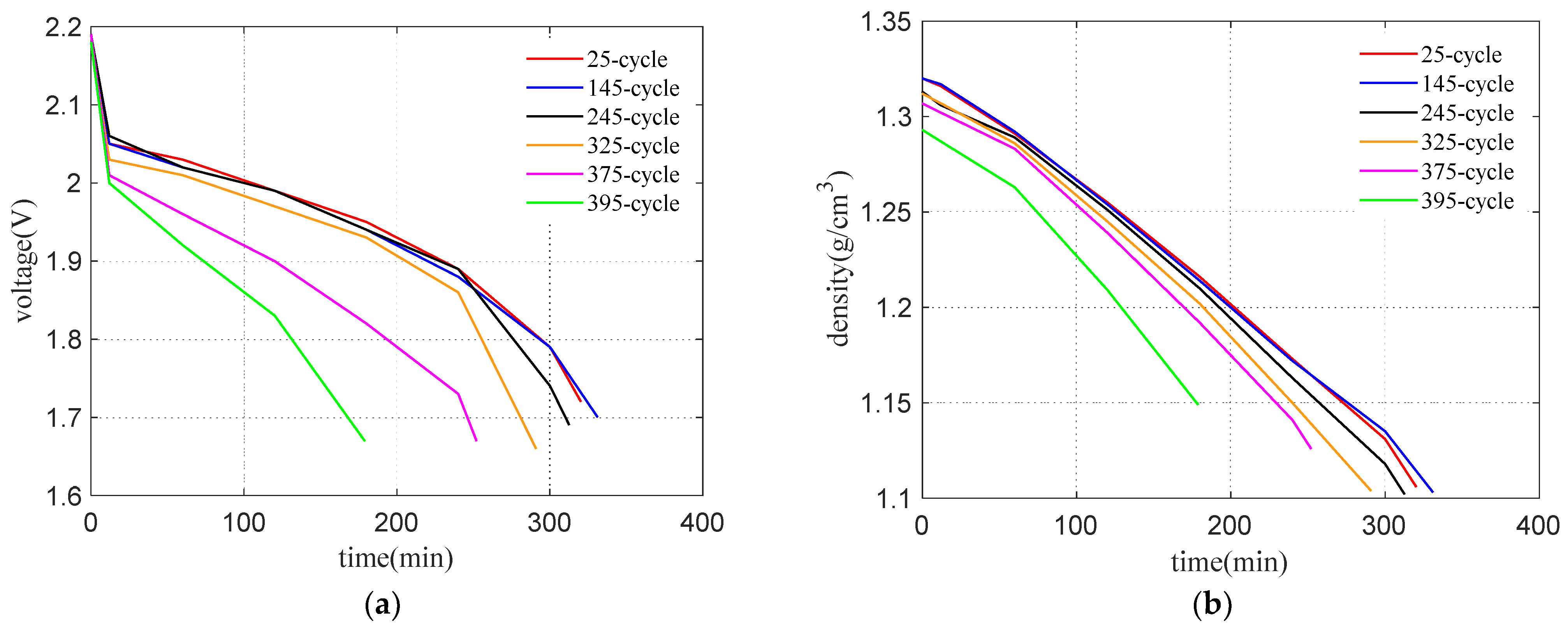
4.1. Experiment Scheme
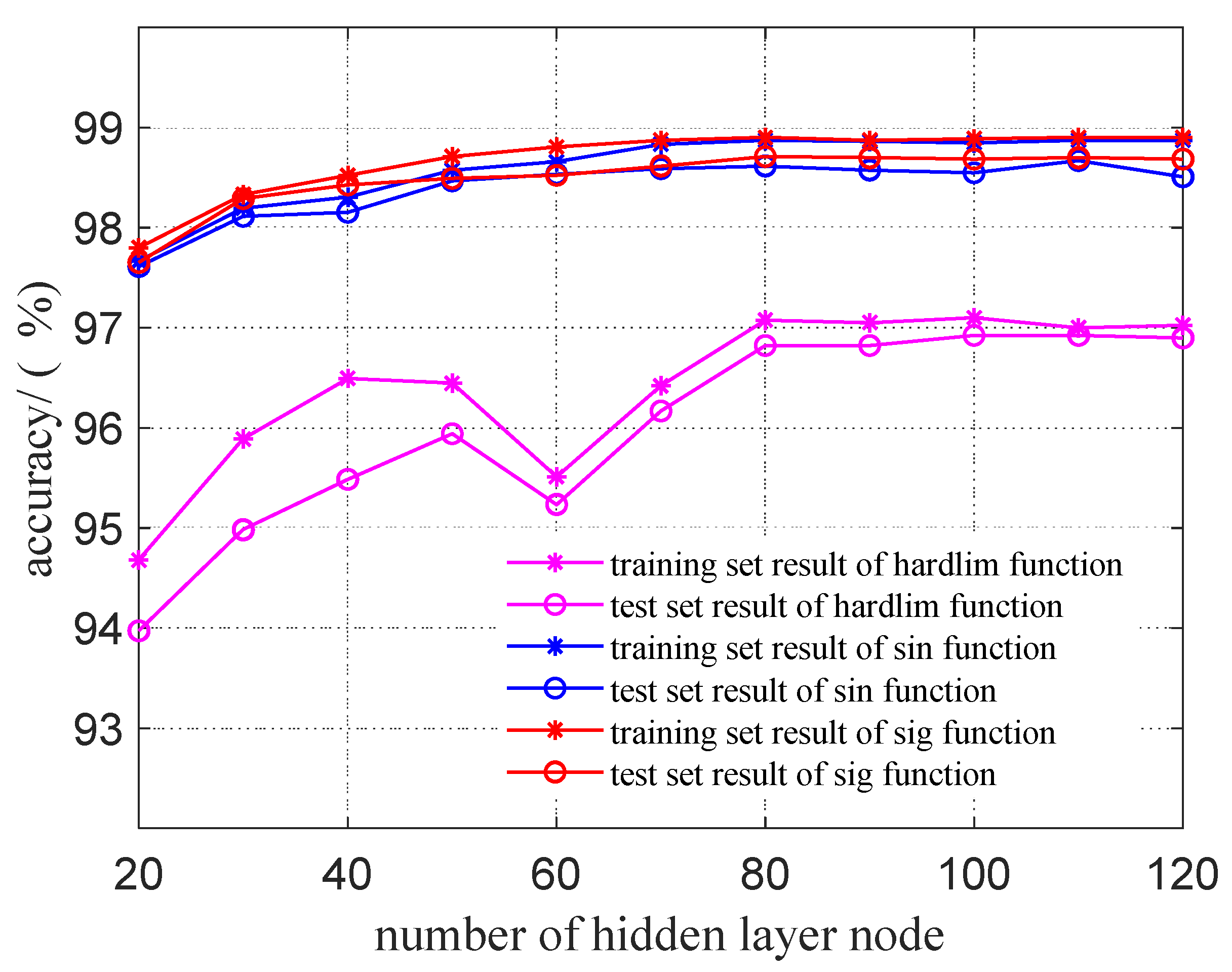
4.2. Selection of Model Parameters
4.3. Verification of Effectiveness and Adaptability
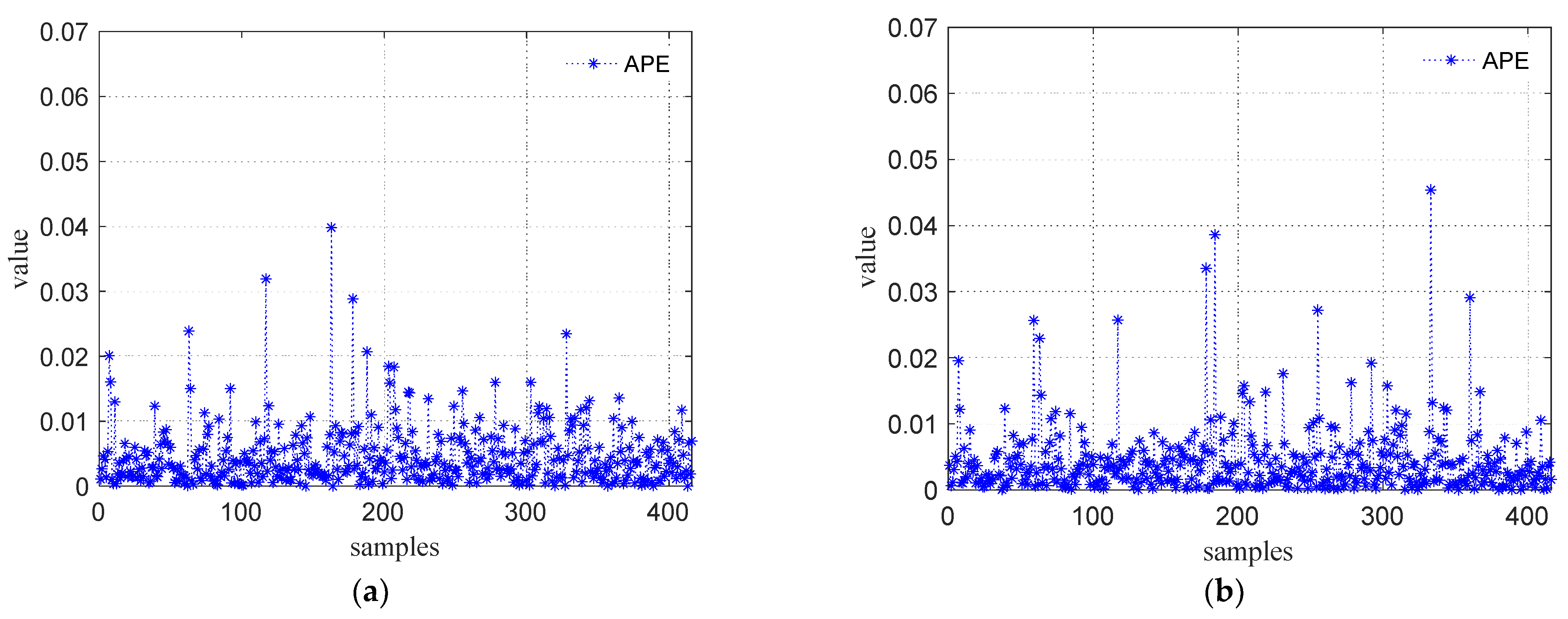
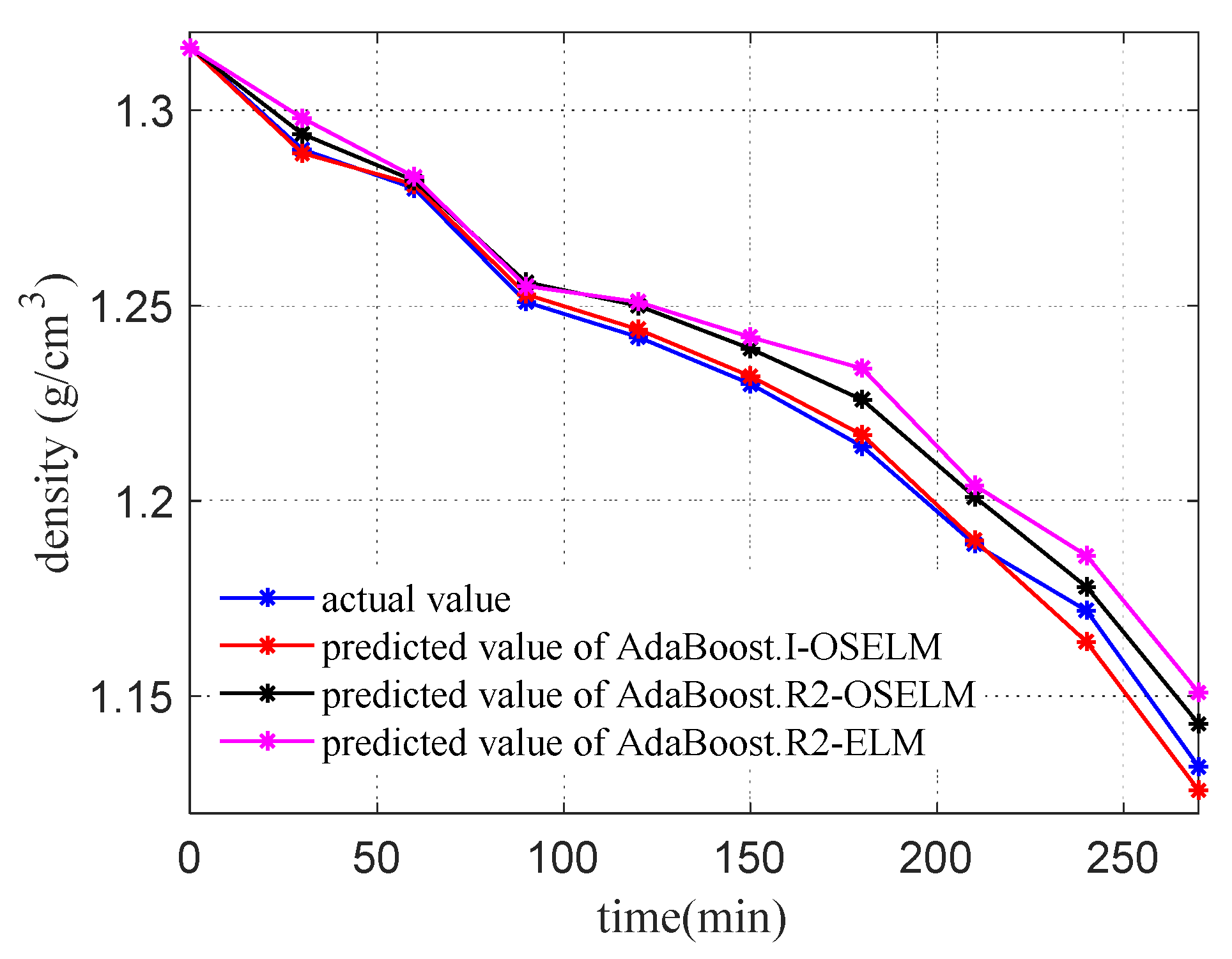
4.3.1. Verification of Effectiveness
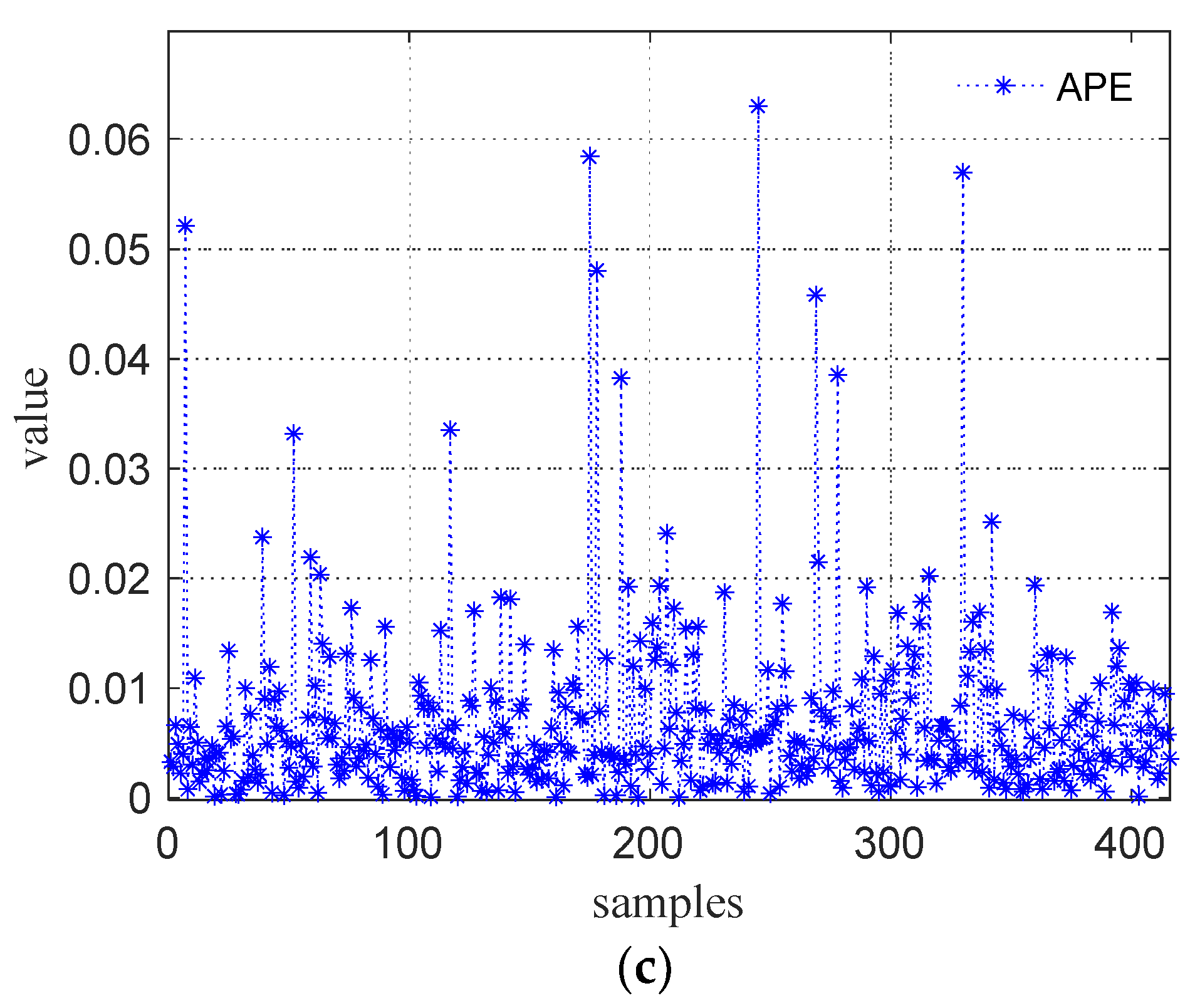
4.3.2. Verification of Adaptability
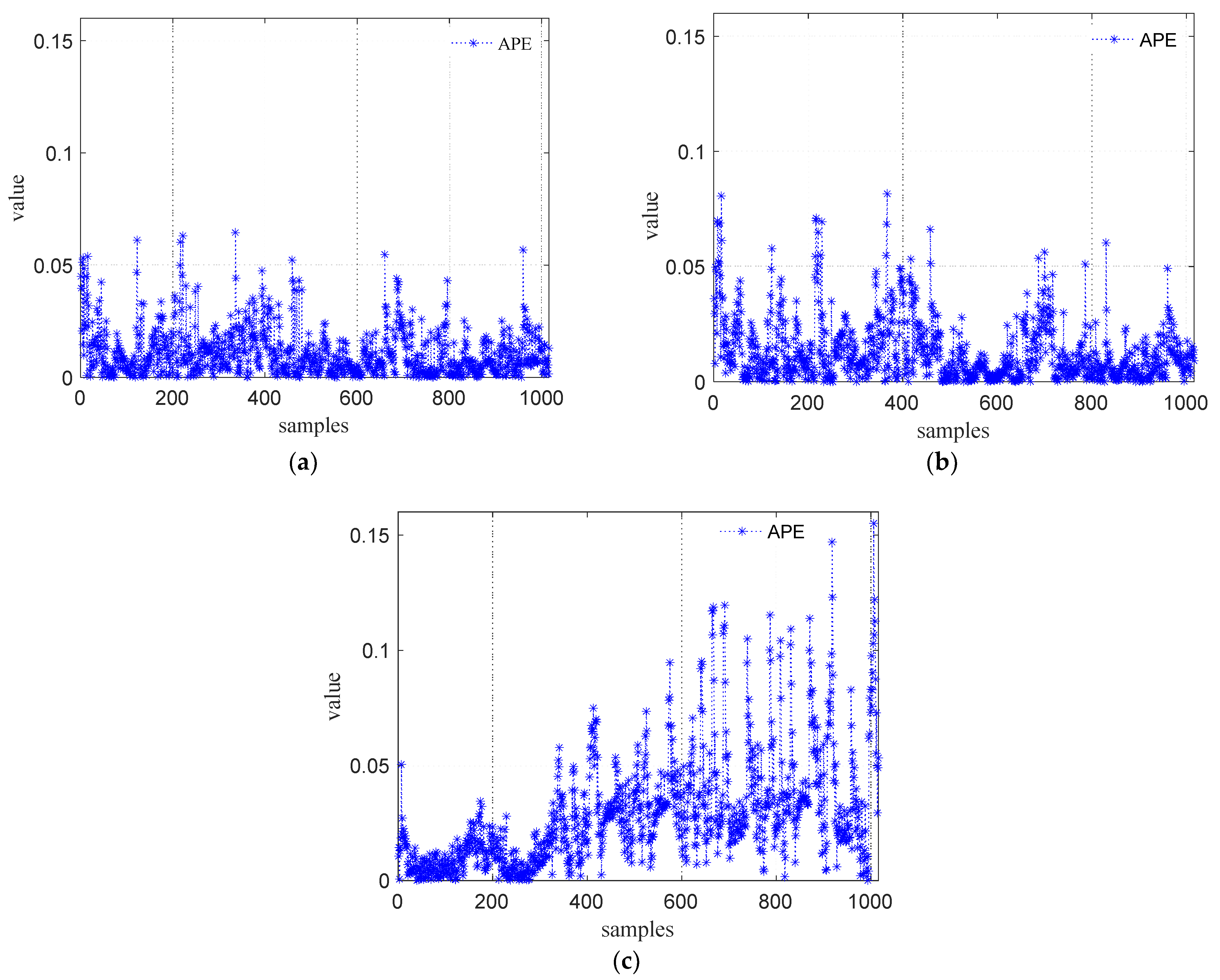
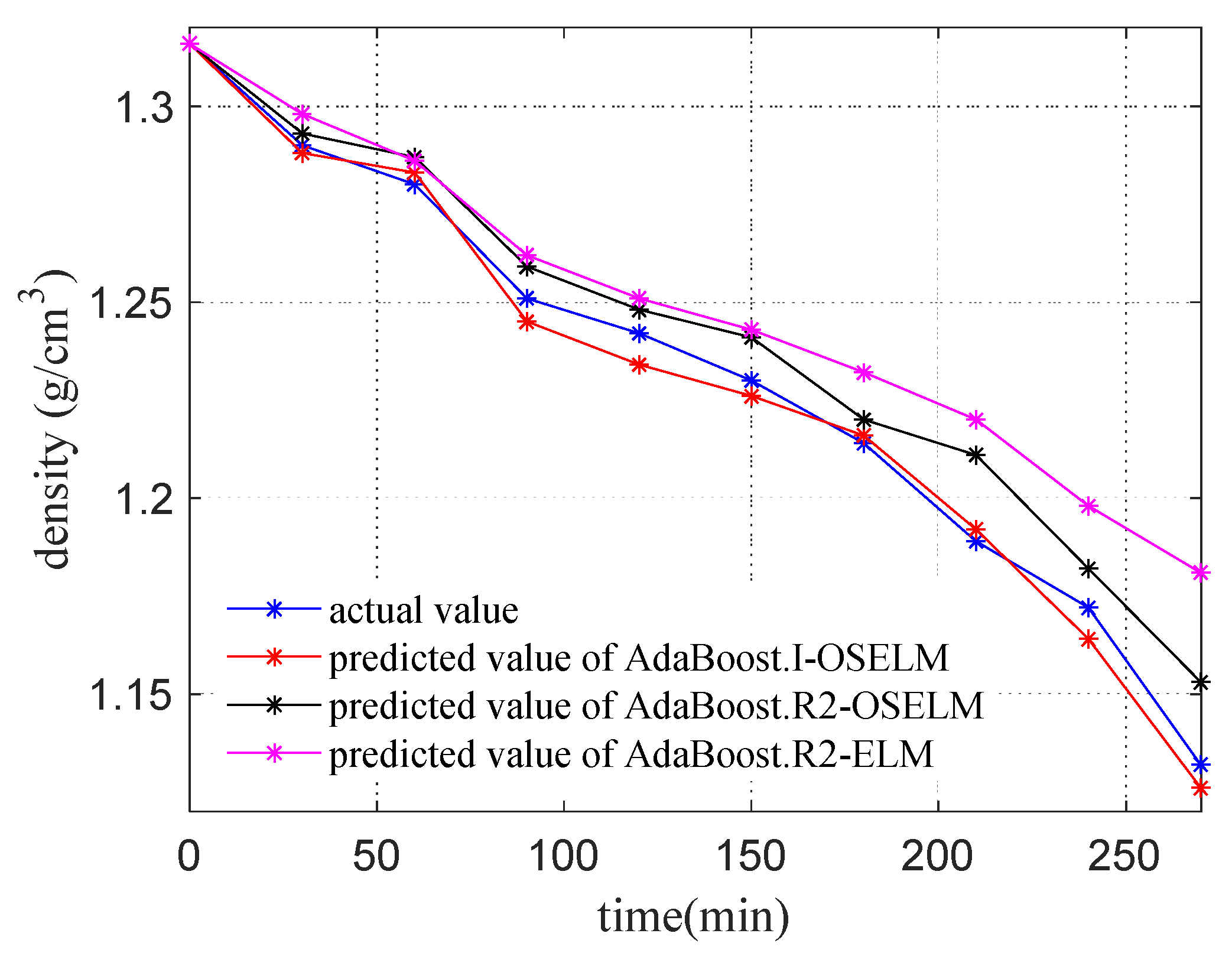
4.4. Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Campillo-Robles, J.M.; Goonetilleke, D.; Soler, D.; Sharma, N.; Rodriguez, D.M.; Bucherl, T.; Makowska, M.; Turkilmaz, P.; Karahan, V. Monitoring lead-acid battery function using operando neutron radiography. J. Power Sources 2019, 438, 226976. [Google Scholar] [CrossRef]
- Luo, X.; Barreras, J.V.; Chambon, C.L.; Wu, B.; Batzelis, E. Hybridizing lead-acid batteries with supercapacitors: A methodology. Energies 2021, 14, 507. [Google Scholar] [CrossRef]
- Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthanb, N. A review on the state-of-the-arttechnologies of electric vehicle, its impacts and prospects. Renew. Sustain. Energy Rev. 2015, 49, 365–385. [Google Scholar] [CrossRef]
- Liu, J.W.; Wu, G.; Shi, C. Ampere hour integrated state of charge estimation method based on available capacity estimation and power increment curve. Instrum. Technol. 2021, 3, 33–37. [Google Scholar]
- Lashway, C.R.; Mohammed, O.A. Adaptive battery management and parameter estimation through physics-based modeling and experimental verification. IEEE Trans. Transp. Electrif. 2016, 2, 454–464. [Google Scholar] [CrossRef]
- Luo, Y.; Qi, P.; Huang, H.; Wang, J.; Wang, Y.; Li, P. Study on battery SOC estimation by ampere-hour integral method with capacity correction. Automot. Eng. 2020, 42, 681–687. [Google Scholar]
- Ping, S.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The co-estimation of state of charge, state of health, and state of function for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2018, 67, 92–103. [Google Scholar]
- Yang, F.; Song, X.; Xu, F.; Tsui, K.L. State-of-charge estimation of lithium-ion batteries via long short-term memory network. IEEE Access 2019, 7, 53792–53799. [Google Scholar] [CrossRef]
- Guoliang, W.; Zhiyu, Z.; Daren, Y. Unsteady open circuit voltage method for state of charge estimation of electric vehicle batteries. Electr. Mach. Control. 2013, 17, 110–116. [Google Scholar]
- Yang, X.J.; Zhou, E.Z. Study of improved battery SOC estimation method. Chin. J. Power Sources 2016, 40, 1840–1844. [Google Scholar]
- Krivik, P.; Vaculik, S.; Baca, P.; Kazelle, J. Determination of state of charge of lead-acid battery by EIS. J. Energy Srorage 2019, 21, 581–585. [Google Scholar] [CrossRef]
- Ma, W.W.; Zheng, J.Y.; You, J.; Zhang, X.F. Kalman filter for estimating state-of-charge of VRLA batteries. Chin. Labat Man 2010, 47, 19–23. [Google Scholar]
- Pan, H.; Lü, Z.; Lin, W.; Li, J.; Chen, L. State of charge estimation of lithium-ion batteries using a grey extended Kalman filter and a novel open-circuit voltage model. Energy 2017, 138, 764–775. [Google Scholar] [CrossRef]
- Cui, W.H.; Wang, J.S.; Chen, Y.Y. Equivalent Circuit Model of Lead-acid Battery in Energy Storage Power Station and Its State-of-Charge Estimation Based on Extended Kalman Filtering Method. Eng. Lett. 2018, 26, 504–517. [Google Scholar]
- Shao, S.; Bi, J.; Yang, F.; Guan, W. On-line estimation of state-of-charge of Li-ion batteries in electric vehicle using the resampling particle filter. Transp. Res. Part D Transp. Environ. 2014, 32, 207–217. [Google Scholar] [CrossRef]
- Pola, D.A.; Navarrete, H.F.; Orchard, M.E.; Rabié, R.S.; Cerda, M.A.; Olivares, B.E.; Pérez, A. Particle-filtering-based discharge time prognosis for lithium-ion batteries with a statistical characterization of use profiles. IEEE Trans. Reliab. 2015, 64, 710–720. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, H.; Dong, G.; Wei, J.; Wu, J.I. Particle filter-based state-of-charge estimation and remaining-dischargeable-time prediction method for lithium-ion batteries. J. Power Sources 2019, 414, 158–166. [Google Scholar] [CrossRef]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Li, C.; Xiao, F.; Fan, Y. An approach to state of charge estimation of lithium-ion batteries based on recurrent neural networks with gated recurrent unit. Energies 2019, 12, 1592. [Google Scholar] [CrossRef]
- Xia, K.G.; Qian, X.Z.; Yu, Y.H.; Zhang, J.Y. Accurate estimation of charge state of lithium battery based on BP neural network. Electron. Des. Eng. 2019, 27, 61–65. [Google Scholar]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Saad, M.H.; Ayob, A.; Uddin, M.N. Extreme learning machine model for state-of-charge estimation of lithium-ion battery using gravitational search algorithm. IEEE Trans. Ind. Appl. 2019, 55, 4225–4234. [Google Scholar] [CrossRef]
- Li, R.; Xu, S.; Li, S.; Zhou, Y.; Zhou, K.; Liu, X.; Yao, J. State of charge prediction algorithm of lithium-ion battery based on PSO-SVR cross validation. IEEE Access 2020, 8, 10234–10242. [Google Scholar] [CrossRef]
- Wu, Z.Q.; Shang, M.Y.; Shen, D.D.; QI, S.Q. Prediction of SOC of lead-acid battery in pure electric vehicle based on BSA-RELM. J. Renew. Sustain. Energy 2018, 10, 054103. [Google Scholar] [CrossRef]
- Li, X.J.; Zhao, J.H.; Yang, J.B.; Zhang, J.T. Research on the charge model of lead-acid batteries onboard modern submarines. Ship Sci. Technol. 2011, 33, 58–61. [Google Scholar]
- Zhang, Y.; Yu, Y.; Zhang, B.; Zhao, J.; Xu, W.; Zhou, Q. Overview of the current situation and development of lead-acid battery. Chin. Labat Man 2021, 58, 27–31. [Google Scholar]
- Han, Y.B. Life cycle comparative study of lithium batteries and lead-acid batteries. Chin. Labat Man 2014, 51, 186–189. [Google Scholar]
- Wu, H.B.; Gu, X.; Zhao, B.; Zhu, C.Z. Comparison study on model and state of charge estimation of typical battery. J. Electron. Meas. Instrum. 2014, 28, 717–723. [Google Scholar]
- Liu, B.; Bi, X.X.; Dang, J.P.; Liu, Q.; Wang, J. Degradation trend prediction of battery in substation based on support vectorregression. J. Power Supply 2020, 18, 207–214. [Google Scholar]
- Galar, M.; Fernandez, A.; Barrenechea, E.; Bustince, H.; Herrera, F. A review on ensembles for the class imbalance problem: Bagging, boosting, and hybrid-based approaches. IEEE Trans. Syst. Man Cybern. Part C 2012, 42, 463–484. [Google Scholar] [CrossRef]
- Wang, Y.W.; Feng, L.Z. Improved AdaBoost algorithm using group degree and membership degree based noise detection and dynamic feature selction. J. ZheJiang Univ. 2021, 55, 367–376. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Liang, N.Y.; Huang, G.B.; Saratchandran, P.; Sundararajan, N. A fast and accurate online sequential learning algorithm for feedforward networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Lan, Y.; Huang, G.B.; Xu, Z.B. Universal approximation of extreme learning machine with adaptive growth of hidden nodes. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 365–371. [Google Scholar] [CrossRef] [PubMed]
- Nie, Q.; Jin, L.; Fei, S.; Ma, J. Neural network for multi-class classification by boosting composite stumps. Neurocomputing 2015, 149, 949–956. [Google Scholar] [CrossRef]
- Li, L.; Wang, C.; Li, W.; Chen, J. Hyperspectral image classification by AdaBoost weighted composite kernel extreme learning machines. Neurocomputing 2018, 275, 1725–1733. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of online learning and all application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Schapire, R.E.; Singer, Y. Improved boosting algorithms using confidence-rated predictions. Mach. Learn. 1999, 37, 297–336. [Google Scholar] [CrossRef]
- Reddy, T.B. Linden’s Handbook of Batteries, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hype parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Chen, W.; Chen, J.X.; Jiang, Y.Q.; Song, D.L.; Zhang, W.D. Fault identification of rolling bearing based on RS-LSTM. China Sci. Pap. 2018, 13, 1134–1140. [Google Scholar]
- Ma, L.Y.; Yu, S.L.; Zhao, S.Y.; Sun, J.M. Superheated steam temperature prediction models based on XGBoost optimized with random search algorithm. J. North China Electr. Power Univ. 2021, 48, 99–105. [Google Scholar]
- How, D.; Hannan, M.A.; Lipu, M.; Ker, P.J. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: A review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]

| p | 1 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
|---|---|---|---|---|---|---|---|---|---|
| Accuracy (%) | 98.91 | 98.89 | 98.91 | 98.90 | 98.52 | 98.43 | 98.39 | 98.40 | 90.38 |
| Time (s) | 0.241 | 0.165 | 0.141 | 0.126 | 0.119 | 0.112 | 0.109 | 0.107 | 0.106 |
| Model | AdaBoost.R2-ELM | AdaBoost.R2-OSELM | AdaBoost.I-OSELM |
|---|---|---|---|
| MAPE | 0.0098 | 0.0075 | 0.0062 |
| MAE | 0.0129 | 0.0098 | 0.0084 |
| MSE | 4.54 × 10−4 | 3.50 × 10−4 | 3.22 × 10−4 |
| AEmax | 0.1026 | 0.0712 | 0.0663 |
| APEmax | 0.0630 | 0.0445 | 0.0406 |
| Model | AdaBoost R2-ELM | AdaBoost R2-OSELM | AdaBoost.I-OSELM |
|---|---|---|---|
| MAPE | 0.0415 | 0.0145 | 0.0102 |
| MAE | 0.0492 | 0.0176 | 0.0205 |
| MSE | 0.0057 | 0.0011 | 0.0009 |
| AEmax | 0.1762 | 0.0863 | 0.0693 |
| APEmax | 0.1550 | 0.0816 | 0.0645 |
| Algorithm | ELM | SVM | LSTM | RF | BP | AdaBoost.I-OSELM |
|---|---|---|---|---|---|---|
| MAPE | 0.0102 | 0.0096 | 0.0121 | 0.0074 | 0.0104 | 0.0062 |
| MAE | 0.0132 | 0.0123 | 0.0156 | 0.0093 | 0.0134 | 0.0084 |
| MSE | 4.78 × 10−4 | 3.66 × 10−4 | 5.25 × 10−4 | 3.41 × 10−4 | 4.29 × 10−4 | 3.22 × 10−4 |
| AEmax | 0.1036 | 0.0874 | 0.1203 | 0.0669 | 0.0839 | 0.0663 |
| APEmax | 0.0853 | 0.0671 | 0.1022 | 0.0436 | 0.0635 | 0.0406 |
| Time/s | 0.002 | 0.071 | 0.199 | 0.102 | 0.016 | 0.021 |
| Algorithm | ELM | SVM | LSTM | RF | BP | AdaBoost.I-OSELM |
|---|---|---|---|---|---|---|
| MAPE | 0.0461 | 0.0433 | 0.0521 | 0.0388 | 0.0446 | 0.0102 |
| MAE | 0.0522 | 0.0501 | 0.0598 | 0.0426 | 0.0515 | 0.0205 |
| MSE | 0.0068 | 0.0062 | 0.0079 | 0.0048 | 0.0063 | 0.0009 |
| AEmax | 0.2301 | 0.2131 | 0.3125 | 0.1132 | 0.1923 | 0.0693 |
| APEmax | 0.2105 | 0.1922 | 0.2863 | 0.0901 | 0.1625 | 0.0645 |
| Time/s | 0.003 | 0.233 | 0.92 | 0.524 | 0.066 | 0.082 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Zhang, Q.; Sun, J.; Cai, W.; Zhou, Z.; Yang, Z.; Wang, Z. Lead–Acid Battery SOC Prediction Using Improved AdaBoost Algorithm. Energies 2022, 15, 5842. https://doi.org/10.3390/en15165842
Sun S, Zhang Q, Sun J, Cai W, Zhou Z, Yang Z, Wang Z. Lead–Acid Battery SOC Prediction Using Improved AdaBoost Algorithm. Energies. 2022; 15(16):5842. https://doi.org/10.3390/en15165842
Chicago/Turabian StyleSun, Shuo, Qianli Zhang, Junzhong Sun, Wei Cai, Zhiyong Zhou, Zhanlu Yang, and Zongliang Wang. 2022. "Lead–Acid Battery SOC Prediction Using Improved AdaBoost Algorithm" Energies 15, no. 16: 5842. https://doi.org/10.3390/en15165842
APA StyleSun, S., Zhang, Q., Sun, J., Cai, W., Zhou, Z., Yang, Z., & Wang, Z. (2022). Lead–Acid Battery SOC Prediction Using Improved AdaBoost Algorithm. Energies, 15(16), 5842. https://doi.org/10.3390/en15165842








