Optimal Planning of Electric Vehicle Charging Stations Considering User Satisfaction and Charging Convenience
Abstract
:1. Introduction
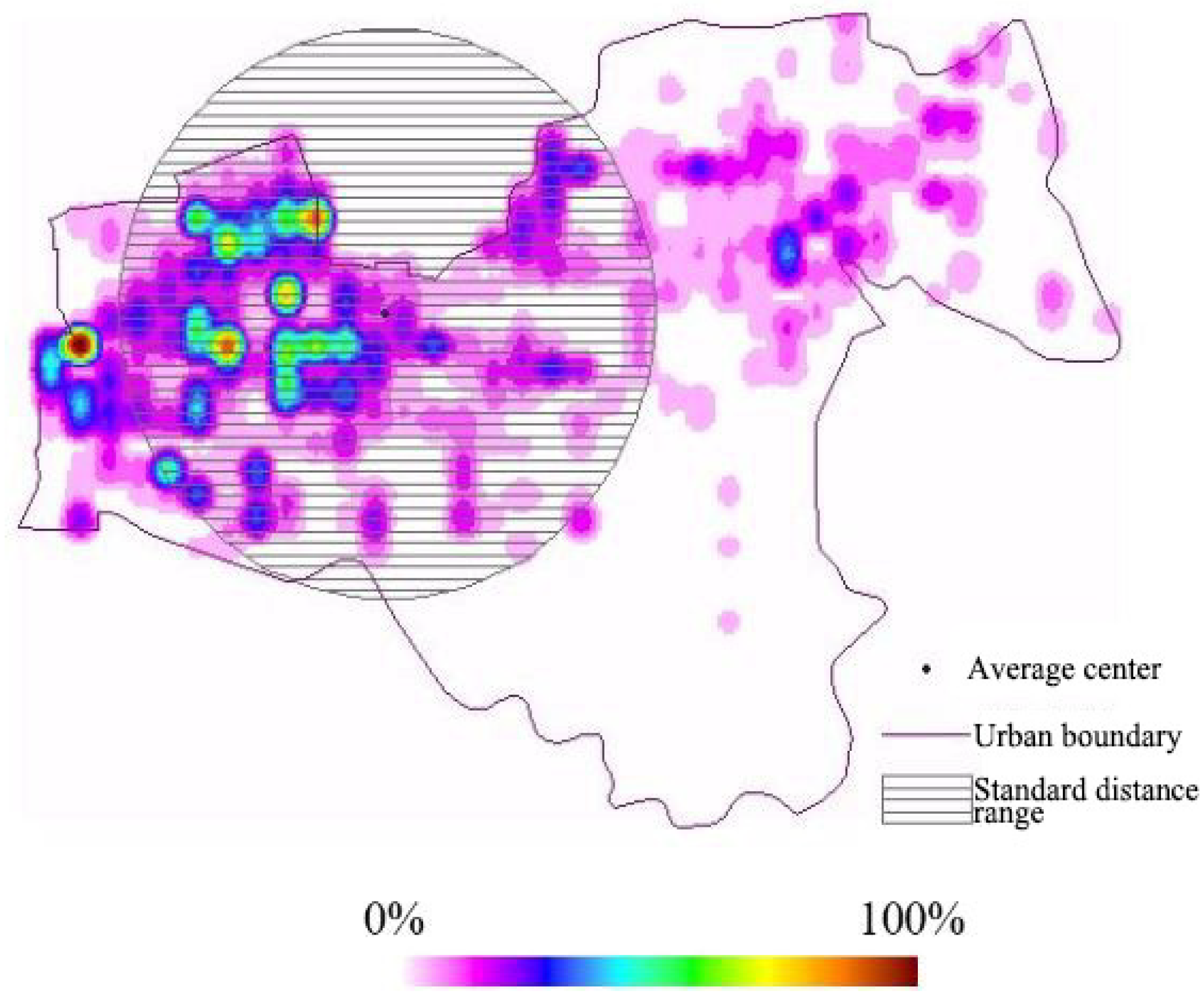
2. Aernel Density Analysis
3. Electric Vehicle User Satisfaction Model
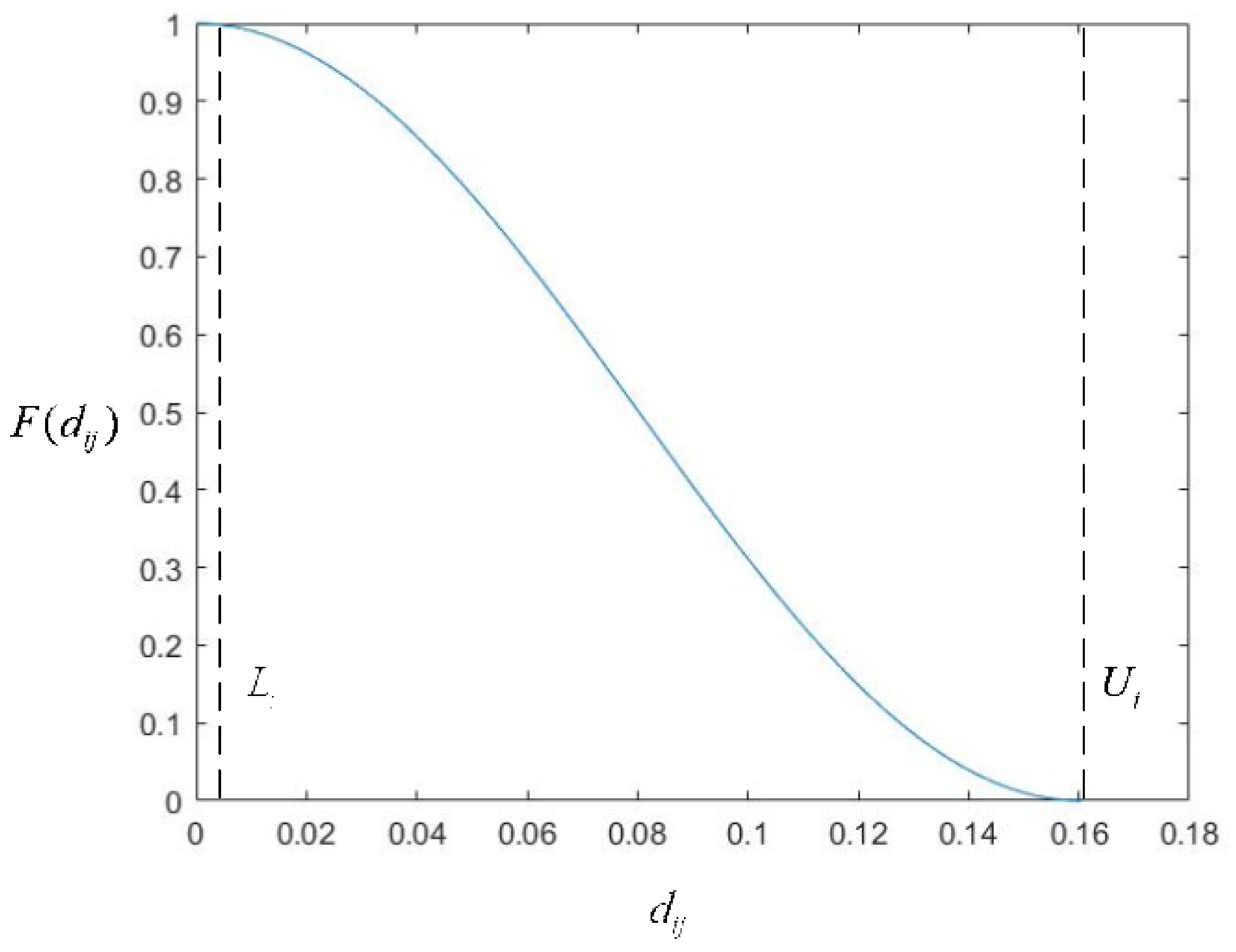
4. User Charging Convenience
5. Electric Vehicle Charging Station Site-Selection Model
5.1. Suppose
- (1)
- Each demand point only goes to the nearest charging station for charging;
- (2)
- Each demand point represents a small area of fixed area;
- (3)
- All electric vehicles have the same battery capacity and model;
- (4)
- While going to the charging station to charge, the driving speed of the electric vehicle remains constant;
- (5)
- In the study area, the demand for the demand point is the same every day, and the demand density is equal to the population density value expressed as a percentage.
5.2. Goals and Constraints
- -
- Objective function one: Maximize user satisfaction
- -
- Objective function two: Maximize the charging convenience
- (1)
- Each demand point can only correspond to one to-be-taken point.
- (2)
- Meeting priority conditions and charging needs of electric vehicles. Formula (13) indicates that the user satisfaction is satisfied under the condition that the charging convenience of the electric vehicle charging station is satisfied. Meanwhile, the charging demand of electric vehicles is met at the to-be-taken point .
- (3)
- Meeting demand points are allocated to corresponding charging stations. Formula (14) indicates that the built electric vehicle charging station meets the changing needs of all demand points.
- (4)
- Meeting the capacity requirements of the site-selection scheme. Formula (15) represents the number of charging stations in all site-selection schemes.
- (5)
- indicates that the user is satisfied with the electric vehicle charging station at the to-be-taken point . indicates that the user is not satisfied with the electric vehicle charging station at the to-be-taken point . indicates that the charging convenience of the electric vehicle charging station is high in the to-be-taken point . indicates that the charging convenience of the electric vehicle charging station is low at the to-be-taken point . Analyzing conditions are:
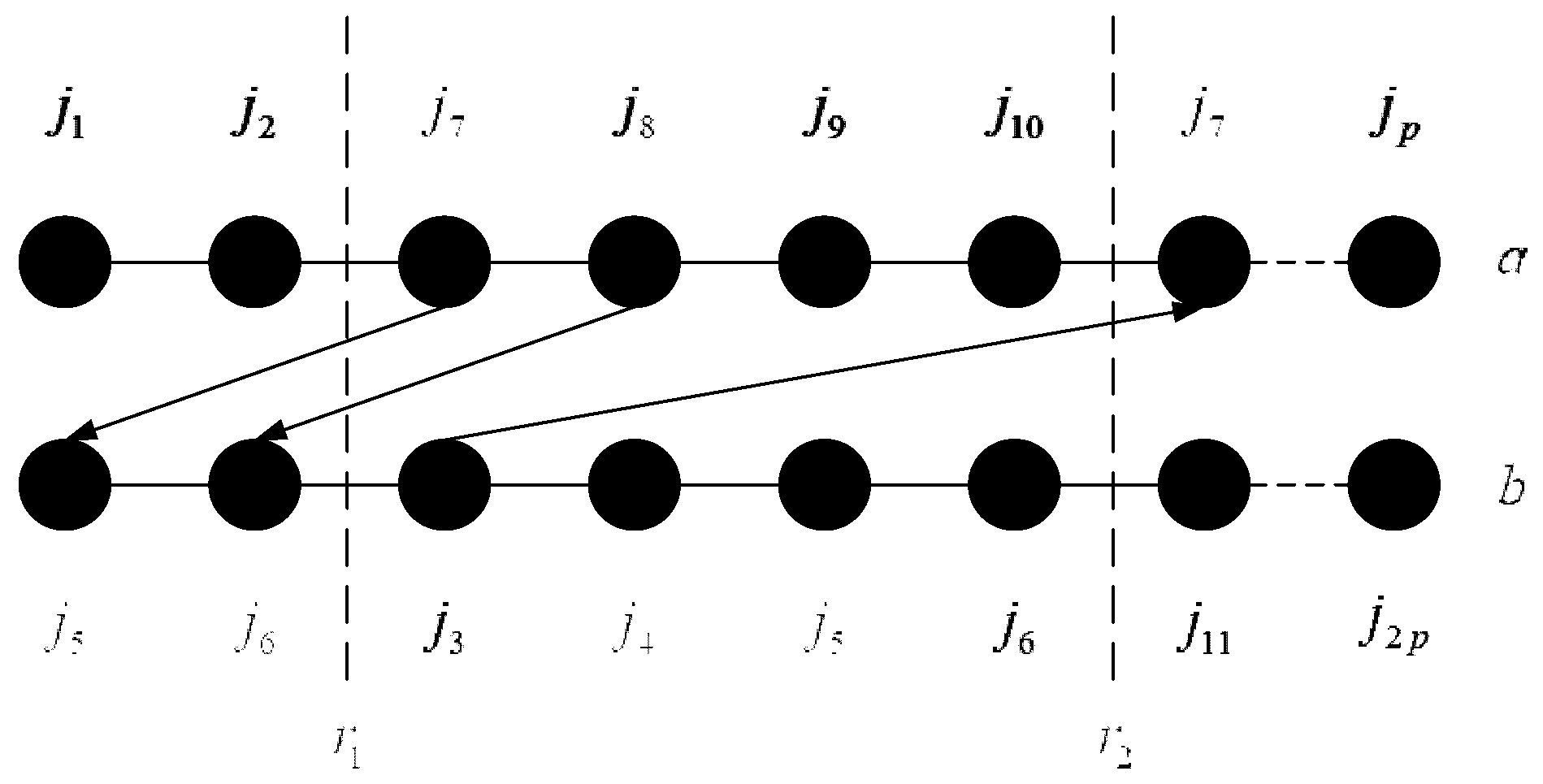
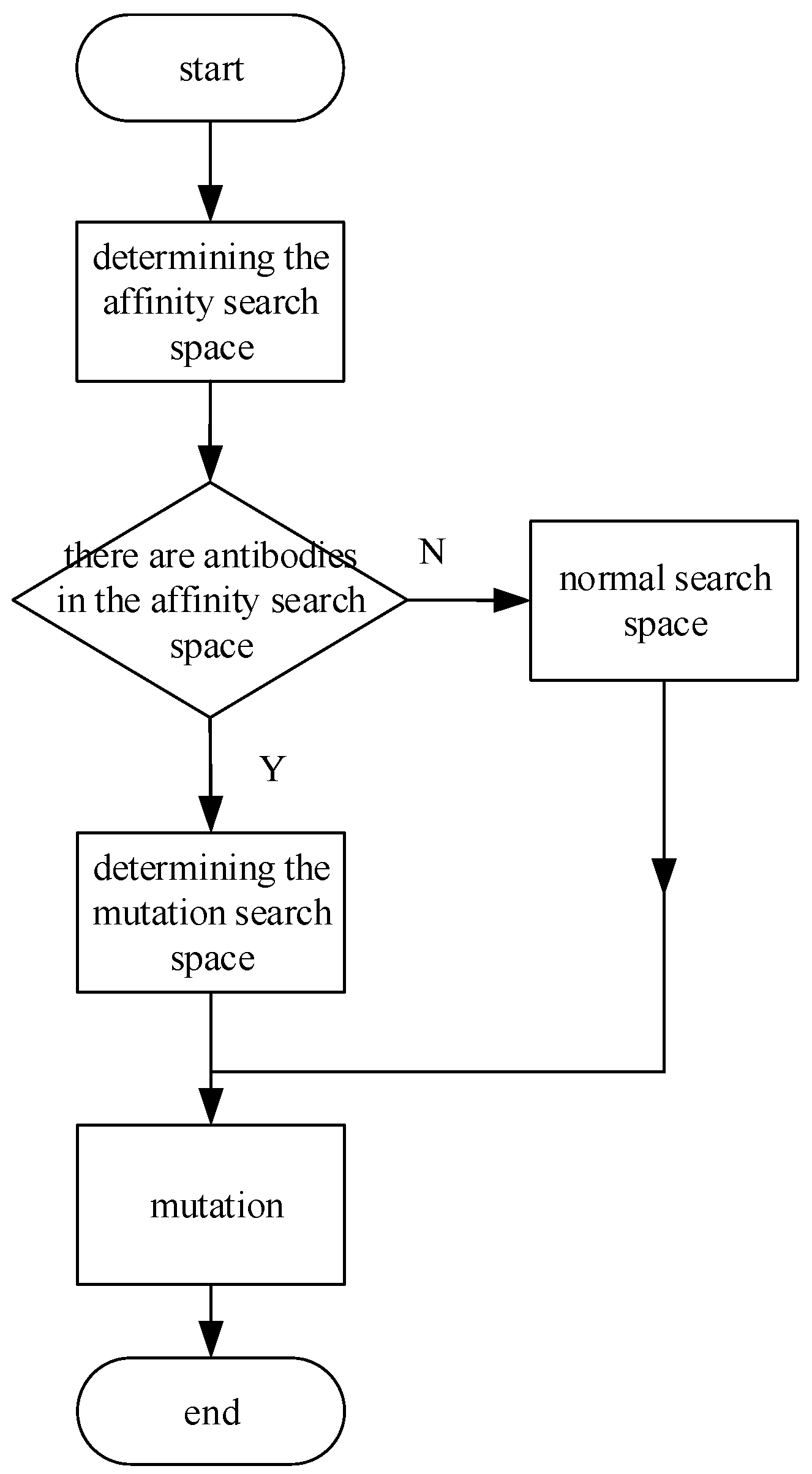
6. Optimized Immune Algorithm
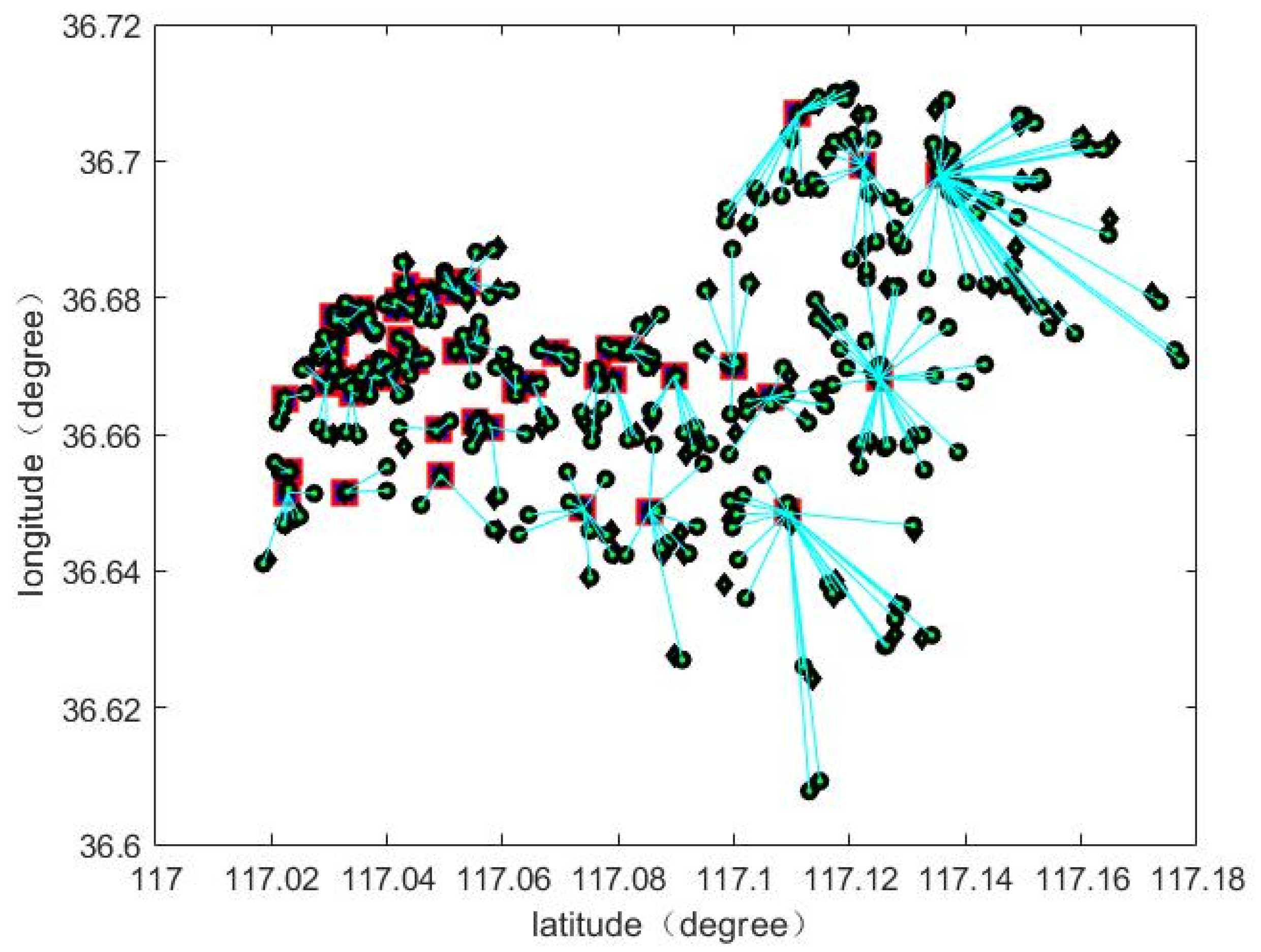
7. Region and Points Are Selected
8. Simulation
8.1. Analysis of the Example
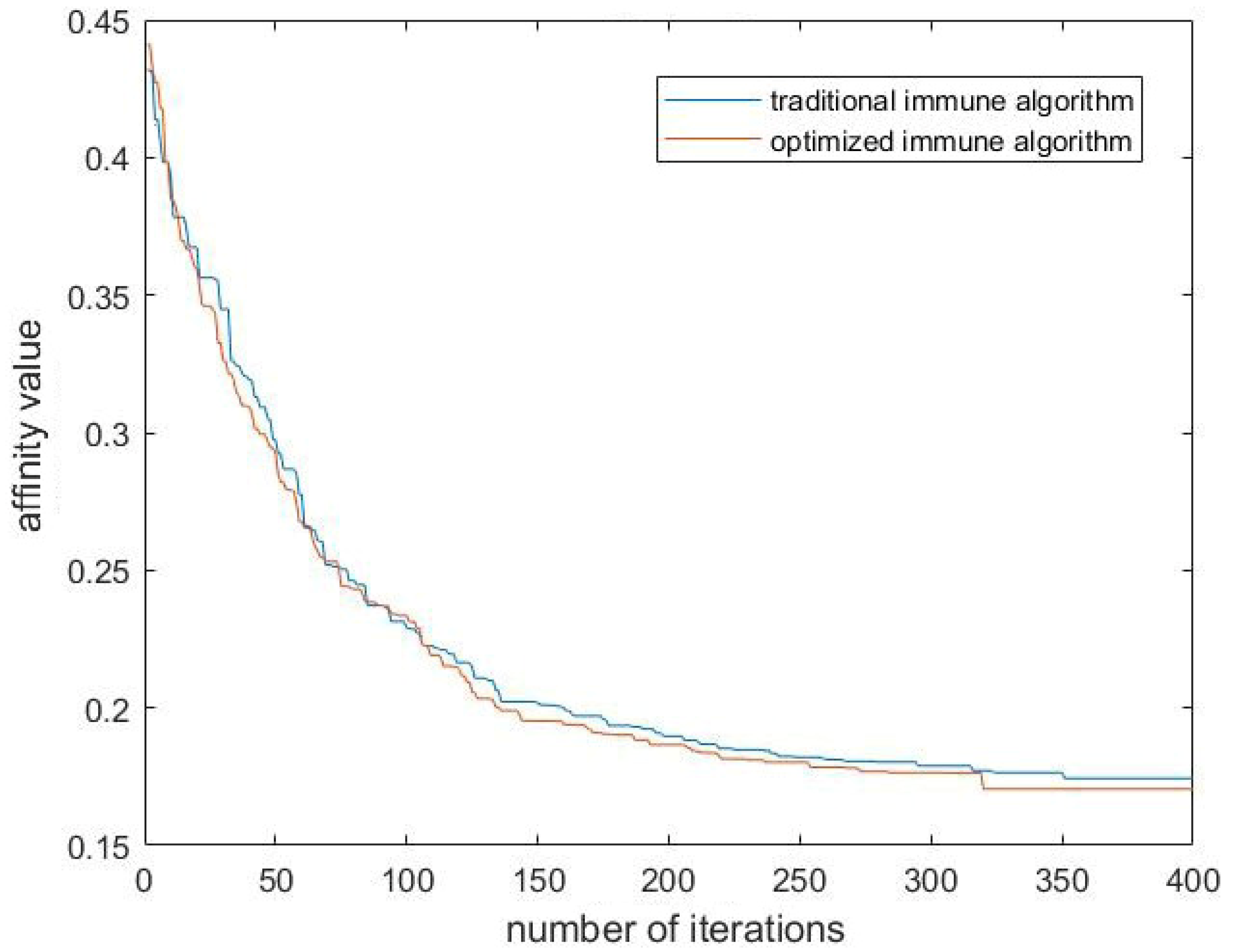
8.2. Algorithm Comparison
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, G.; Liu, H.; Han, N. Optimization method for charging station location and capacity considering the spatiotemporal distribution of electric vehicles. Chin. J. Electr. Eng. 2021, 41, 1–14. [Google Scholar]
- Yu, J. Research and application of electric vehicle fast charging station site selection and capacity. Master Thesis, Northeast Agricultural University, Harbin, China, 2019. [Google Scholar]
- Hosseini, S.; Sarder, M.D. Development of a Bayesian network model for optimal site selection of electric vehicle charging station. Int. J. Electr. Power Energy Syst. 2019, 105, 110–112. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, H. Optimal site selection of electric vehicle charging station by using fuzzy TOPSIS based on sustainability perspective. Appl. Energy 2015, 158, 390–402. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, H.; Hu, R.; Qiu, Y. Location of Electric Vehicle Charging Stations: A Perspective Using the Grey Decision-making Model. Energy 2019, 173, 548–553. [Google Scholar] [CrossRef]
- Wu, Y.; Xie, C.; Xu, C.; Li, F. A Decision Framework for Electric Vehicle Charging Station Site Selection for Residential Communities under an Intuitionistic Fuzzy Environment: A Case of Beijing. Energies 2017, 10, 1270. [Google Scholar] [CrossRef]
- You, P.; Hsieh, Y. A hybrid heuristic approach to the problem of the location of vehicle charging stations. Comput. Ind. Eng. 2014, 70, 195–204. [Google Scholar] [CrossRef]
- Zhou, G.; Zhu, Z.; Luo, S. Location optimization of electric vehicle charging stations: Based on cost model and genetic algorithm. Energy 2022, 247, 0360–5442. [Google Scholar] [CrossRef]
- Jia, Y.; Xing, F. Site selection of electric vehicle charging station based on Satisfactory Optimization. J. Donghua Univ. 2017, 43, 1671–1680. [Google Scholar]
- Rezvani, Z.; Jansson, J. Advances in consumer electric vehicle adoption research: A review and research agenda. Transp. Res. Part D Transp. Environ. 2015, 34, 122–136. [Google Scholar] [CrossRef] [Green Version]
- Di, S. Research on Hierarchical Location Planning and Capacity Determination Method of Urban Electric Vehicle Charging Facilities. Master Thesis, Southeast University, Nanjing, China, 2017. [Google Scholar]
- Church, R.L.; ReVelle, C.S. Theoretical and computational links between the p-median location set-covering and the maximal covering location problem. Geogr. Anal. 1976, 8, 406–415. [Google Scholar] [CrossRef]
- Yang, F.; Hua, G.; Deng, M.; Li, J. Some advances in the study of location problem Operations. Res. Manag. 2002, 14, 1–7. [Google Scholar]
- Hakimi, S.L. Optimum locations of switching centers in a communication network and medians of graph. Oper. Res. 1964, 12, 450–459. [Google Scholar] [CrossRef]
- Lin, Z.; Ogden, J.; Fan, Y.; Chen, C.W. The Fuel-Travel-Back Approach to Hydrogen Station Siting. Int. J. Hydroge. Energy 2008, 33, 3096–3101. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wang, C.R. Locating Passenger Vehicle Refueling Stations. Transp. Res. Part E 2010, 46, 791–801. [Google Scholar] [CrossRef]
- Wang, Y.W.; Wang, C.R. Locating multiple types of recharging stations for battery powered electric vehicle transport. Transp. Res. Part E Logist. Transp. Rev. 2013, 58, 76–87. [Google Scholar] [CrossRef]
- Zhao, S.; Li, Z. Optimal planning of urban electric vehicle charging station based on differential evolution particle swarm optimization algorithm Draw. J. North China Electr. Power Univ. (Nat. Sci. Ed.) 2015, 42, 1–7. [Google Scholar]
- Hui, W.; Guibin, W.; Junhua, Z. Electric vehicle charging station planning considering traffic network flow. Powersystem Autom. 2013, 37, 63–69. [Google Scholar]
- Song, Z.; Wang, X.; Lun, L. Location planning of electric vehicle charging station based on revenue maximization. East China J. Jiaotong Univ. 2014, 31, 50–55. [Google Scholar]
- Zhang, D.; Jiang, J.; Zhang, W. Economic operation of electric vehicle replacement station based on genetic algorithm. Power Grid Technol. 2013, 8, 2101–2107. [Google Scholar]
- Riemann, R.; Wang, D.Z.W.; Busch, F. Optimal location of wireless charging facilities for electric vehicles: Flow-capturing location model with stochastic user equilibrium. Transp. Res. Part C Emerg. Technol. 2015, 58, 1–12. [Google Scholar] [CrossRef]
- Ge, S.; Feng, L.; Liu, H. Electric vehicle charging station planning considering user convenience. Electr. Energy Electr. New Technol. 2014, 33, 70–75. [Google Scholar]
- Ren, Y.; Shi, L.; Zhang, Q.; Han, W.; Huang, S. Study on the optimal distribution and scale of electric vehicle charging stations. Power Syst. Autom. 2011, 35, 53–57. [Google Scholar]
- Sun, X.; Liu, K.; Zuo, Z. Layout model of electric vehicle charging station considering time and space constraints. Land Prog. Sci. 2012, 6, 686–692. [Google Scholar]
- Jerne, N.K. Towards a network theory of the immune system. Annu. Immunol. 1974, 125, 373–389. [Google Scholar]
- Liu, Z.; Li, Z.; Chen, W.; Zhao, Y.; Yue, H.; Wu, Z. Path Optimization of Medical Waste Transport Routes in the Emergent Public Health Event of COVID-19: A Hybrid Optimization Algorithm Based on the Immuneâ “Ant Colony Algorithm. Int. J. Environ. Res. Public Health 2020, 17, 5831. [Google Scholar] [CrossRef]
- Li, R.; Ma, L.; Liu, Y. Site selection simulation of capacity-limited factory based on improved immune algorithm. Comput. Simul. 2021, 38, 401–405. [Google Scholar]
- Yıldız, A.R. A novel hybrid immune algorithm for global optimization in design and manufacturing. Robot. Comput.-Integr. Manuf. 2009, 25, 261–270. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, J. Improved immune algorithm to solve TSP problem. Comput. Eng. Des. 2005, 4, 978–980+984. [Google Scholar]
- Meng, W.C.; Qiu, J.J.; Bian, X.M. Artificial immune algorithm integrated with chaotic optimization for economic dispatch of power system. Power Syst. Technol. 2006, 23, 41–44. [Google Scholar]
- Wang, B.; Hu, J.; Zhang, K.; Li, X.; Zhang, Y.; Sun, S. Research and Application of Improved Immune Algorithm Based on Solution Space Oriented Optimization. Firepower Command. Control. 2020, 45, 64–67. [Google Scholar]
- Ping, H.; Song, C.; Jiang, J.Q. Application of self-adaptive mutation immune algorithm in logistics distribution. J. Inn. Mong. Univ. Natl. Nat. 2017, 32, 406–411. [Google Scholar]
- Xu, Y.; Zhang, J. Regional Integrated Energy Site Layout Optimization Based on Improved Artificial Immune Algorithm. Energies 2020, 13, 4381. [Google Scholar] [CrossRef]
- Cao, X.; Hu, P.; Liu, D. Research progress on site selection of electric vehicle charging stations. Adv. Geogr. Sci. 2019, 38, 139–152. [Google Scholar]
- Dong, J.; Liu, C.; Lin, Z. Charging infrastructure planning for promoting battery electric vehicles: An activity—Based approach using multiday travel data. Transp. Res. Part C Emerg. Technol. 2014, 38, 44–55. [Google Scholar] [CrossRef] [Green Version]
- Sathaye, N.; Kelley, S. An approach for the optimal planning of electric vehicle infrastructure for highway corridors. Transp. Res. Part E Logist. Transp. Review. 2013, 59, 15–33. [Google Scholar] [CrossRef]
- Li, N.; Xu, G. Grid analysis of land use data based on natural discontinuous point classification method. Bull. Surv. Mapp. 2020, 60, 106–110+156. [Google Scholar]
- Ma, Y.; Yang, C.; Zhang, M. The problem of maximum coverage location selection based on time satisfaction. Chin. Manag. Sci. 2006, 14, 45–51. [Google Scholar]
- Zhou, Y.; Zhang, H.; Ma, L. Improved immune algorithm for solving hierarchical and progressive location problem of emergency medical facilities. J. Oper. Res. 2021, 25, 15–34. [Google Scholar]
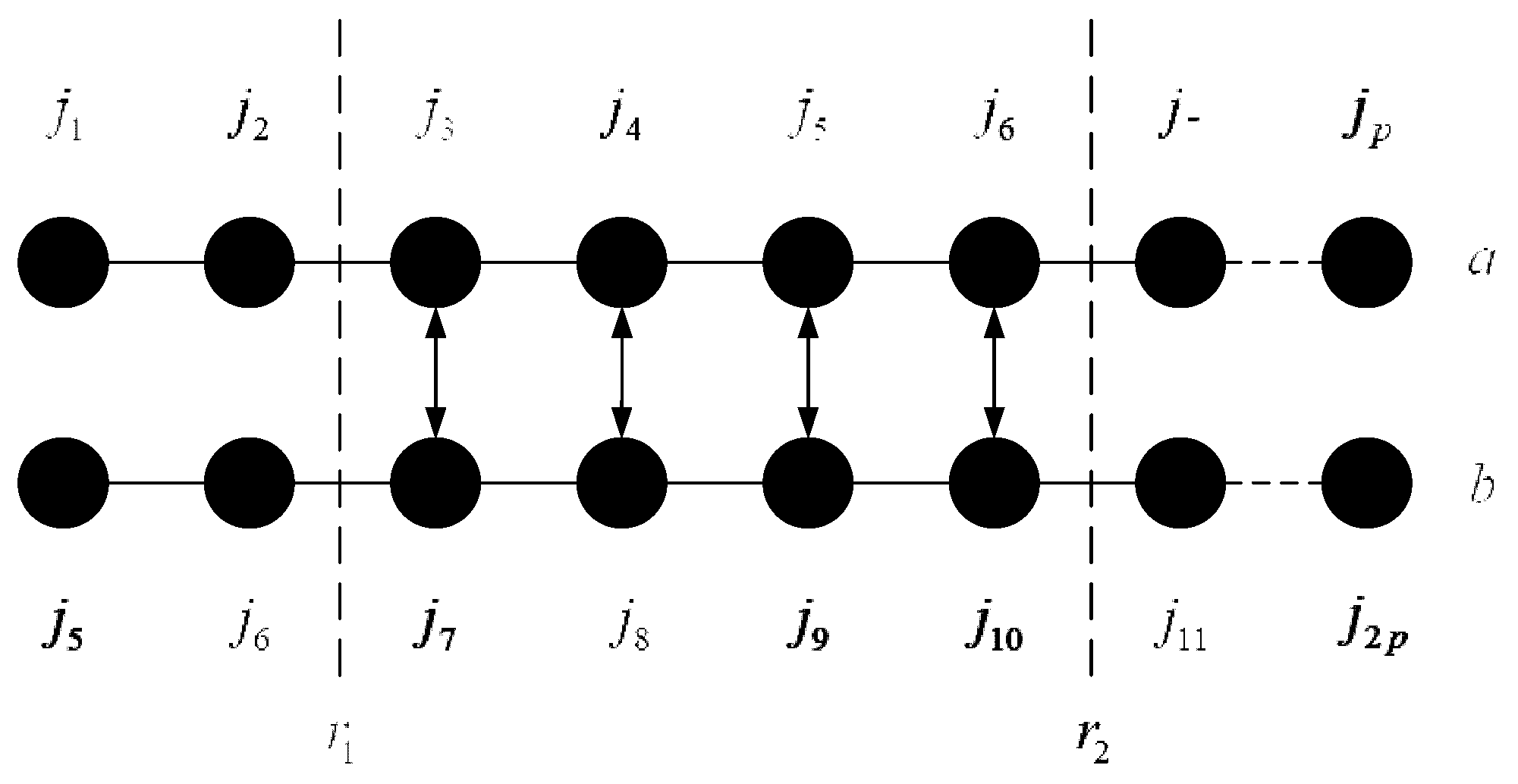
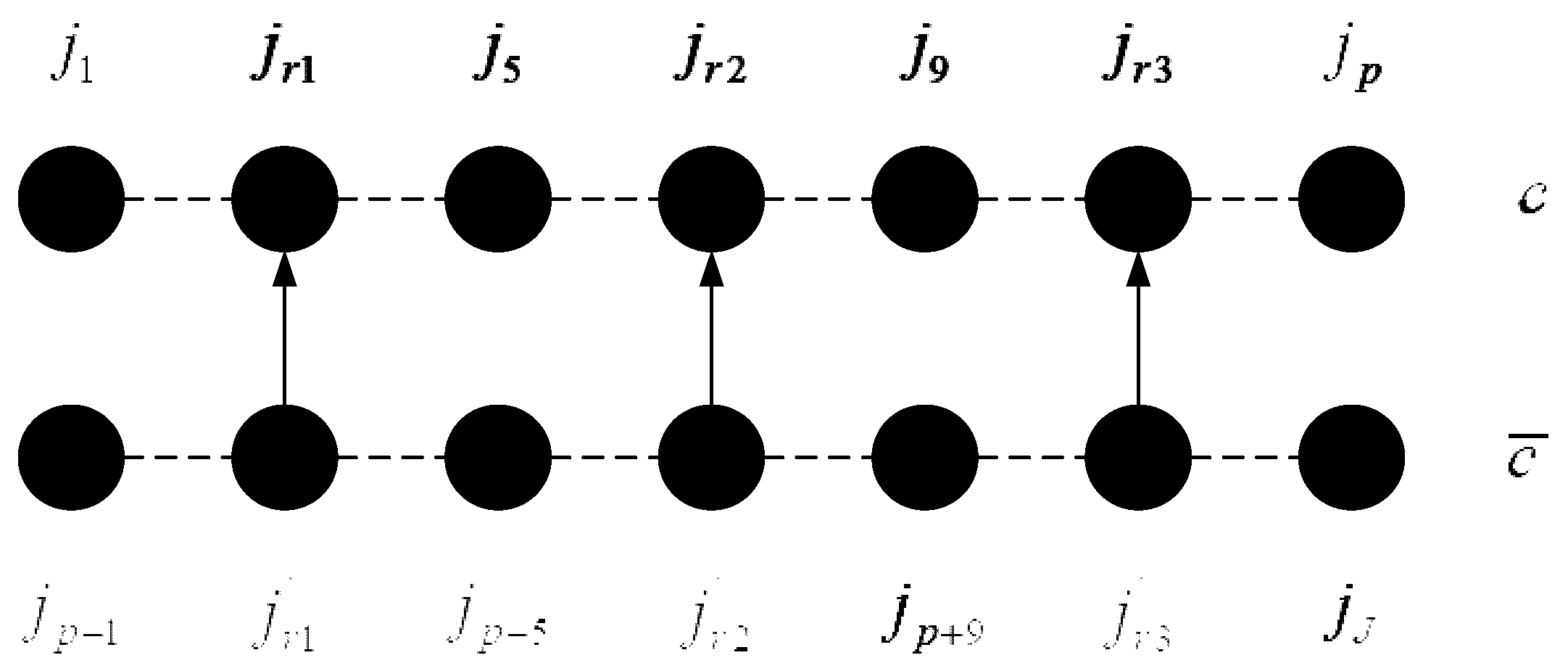



| Degree | Score |
|---|---|
| Big impact | 5 |
| Greater impact | 4 |
| General impact | 3 |
| Lesser impact | 2 |
| No impact | 1 |
| Number of Sites Built | Average Satisfaction |
|---|---|
| 51 | 60.63% |
| 52 | 65.82% |
| 53 | 74.7% |
| 54 | 79.94% |
| 55 | 83.18% |
| 56 | 85.04% |
| Average Service Capacity | Average User Density | Average Charging Convenience | |
|---|---|---|---|
| Traditional site selection | 116 | 70% | 4195 |
| Site-selection plan in this paper | 128 | 73% | 4657 |
| Optimal Solution | Average Solution | Standard Deviation | |
|---|---|---|---|
| Traditional immune algorithm | 0.17493 | 0.21110 | 0.04843 |
| Optimized immune algorithm | 0.16975 | 0.18391 | 0.01712 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Pei, W.; Zhang, Q. Optimal Planning of Electric Vehicle Charging Stations Considering User Satisfaction and Charging Convenience. Energies 2022, 15, 5027. https://doi.org/10.3390/en15145027
Xu D, Pei W, Zhang Q. Optimal Planning of Electric Vehicle Charging Stations Considering User Satisfaction and Charging Convenience. Energies. 2022; 15(14):5027. https://doi.org/10.3390/en15145027
Chicago/Turabian StyleXu, Di, Wenhui Pei, and Qi Zhang. 2022. "Optimal Planning of Electric Vehicle Charging Stations Considering User Satisfaction and Charging Convenience" Energies 15, no. 14: 5027. https://doi.org/10.3390/en15145027
APA StyleXu, D., Pei, W., & Zhang, Q. (2022). Optimal Planning of Electric Vehicle Charging Stations Considering User Satisfaction and Charging Convenience. Energies, 15(14), 5027. https://doi.org/10.3390/en15145027








