Planning of Multi-Vector Energy Systems with High Penetration of Renewable Energy Source: A Comprehensive Review
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Related Reviews on Planning of Energy Hub
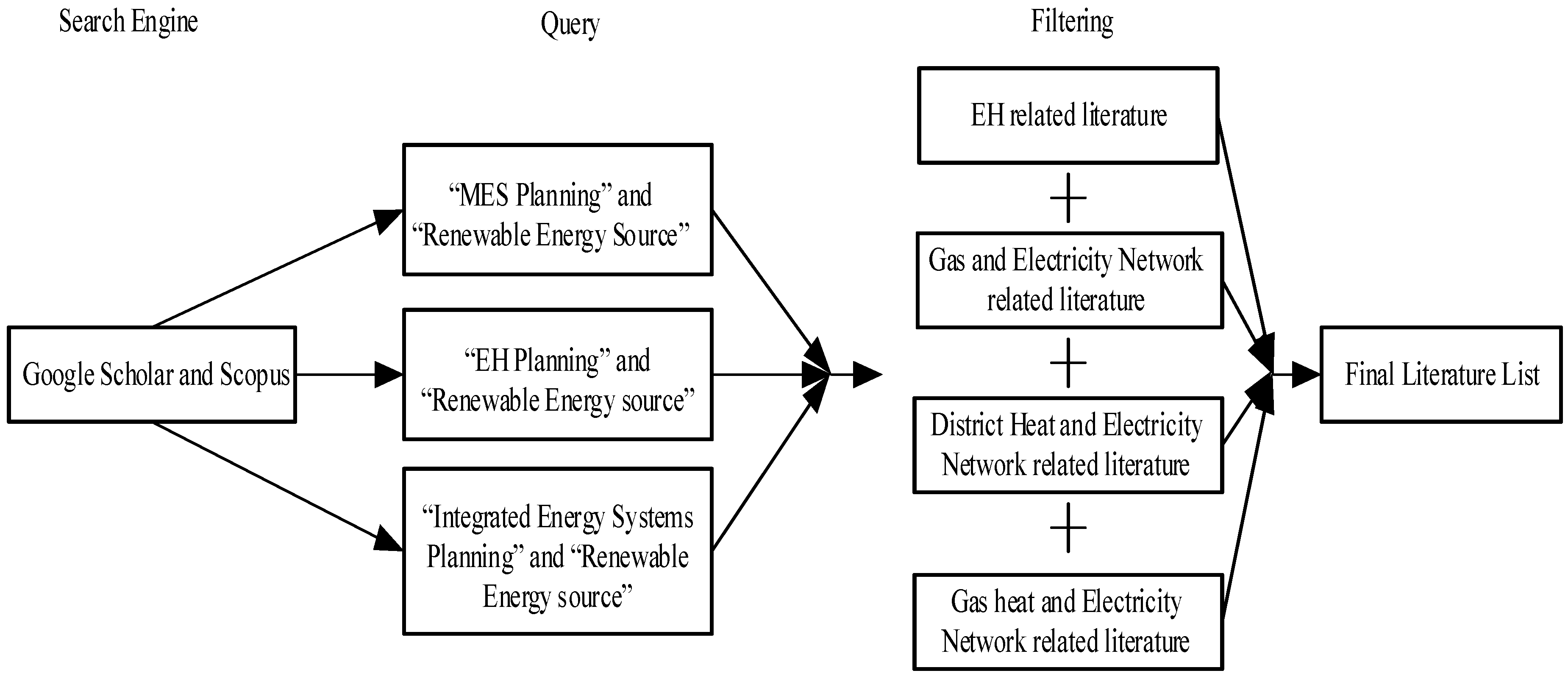
1.3. Literature Search Strategy
- “Multi-vector energy systems planning” AND “Renewable energy source”.
- “Energy hub planning” AND “Renewable energy source”.
- “Integrated Energy systems planning” AND “Renewable energy source”.
1.4. Structure of the Review
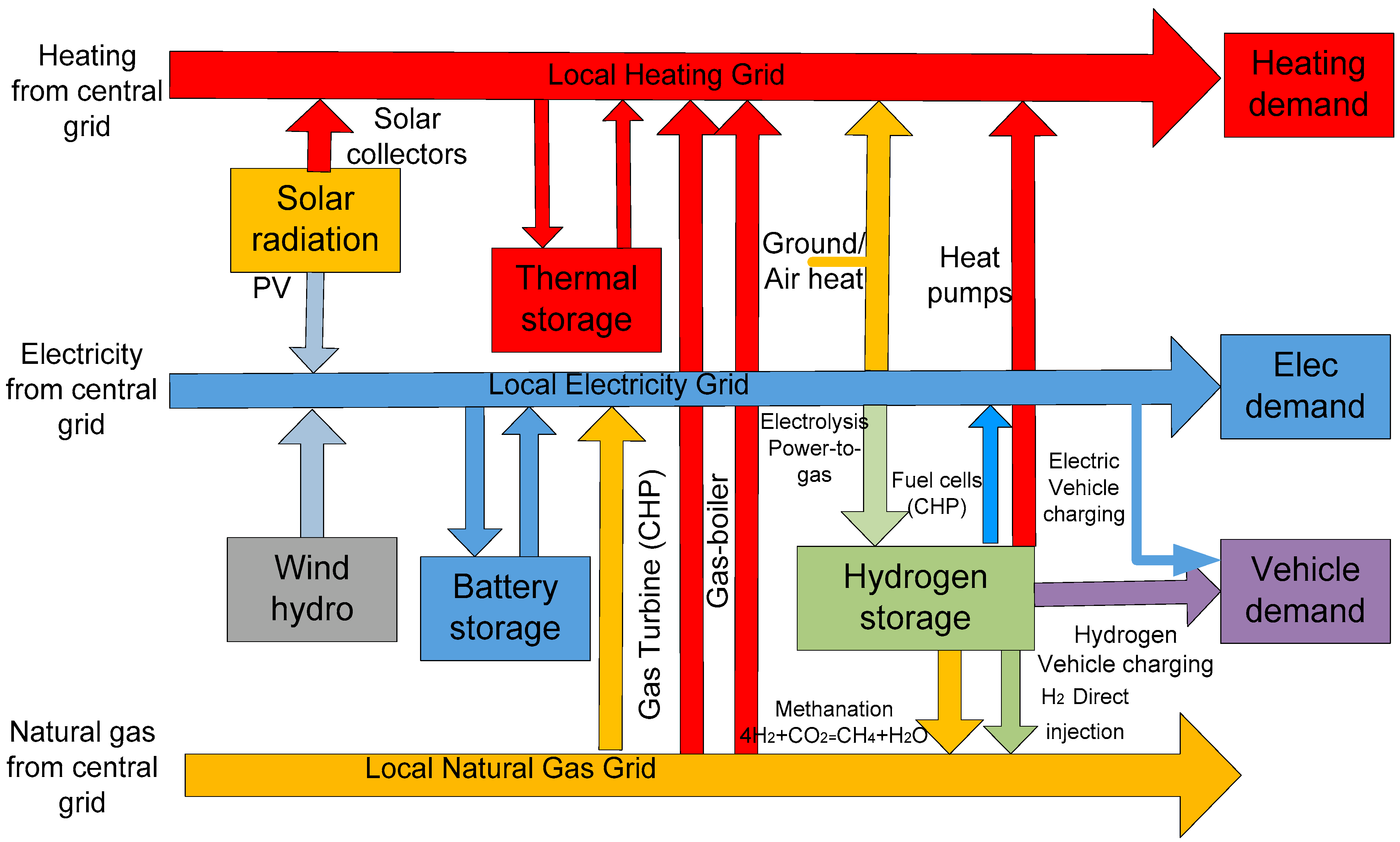
2. Multi-Vector Energy System
2.1. Definition of Multi-Vector Energy Systems
2.1.1. Various Categories of Energy Vectors Interactions and Interdependencies
- Natural gas and electricity networks.
- District heat and electricity networks.
- Natural gas, district heat, and electricity networks.
2.1.2. Natural Gas and Electricity Networks Interdependencies
2.1.3. District Heat and Electricity Networks Interdependencies
2.1.4. Natural Gas, District Heat, and Electricity Networks Interdependencies
2.2. Benefits
2.3. Challenges
3. Multi-Vector Energy Systems Models
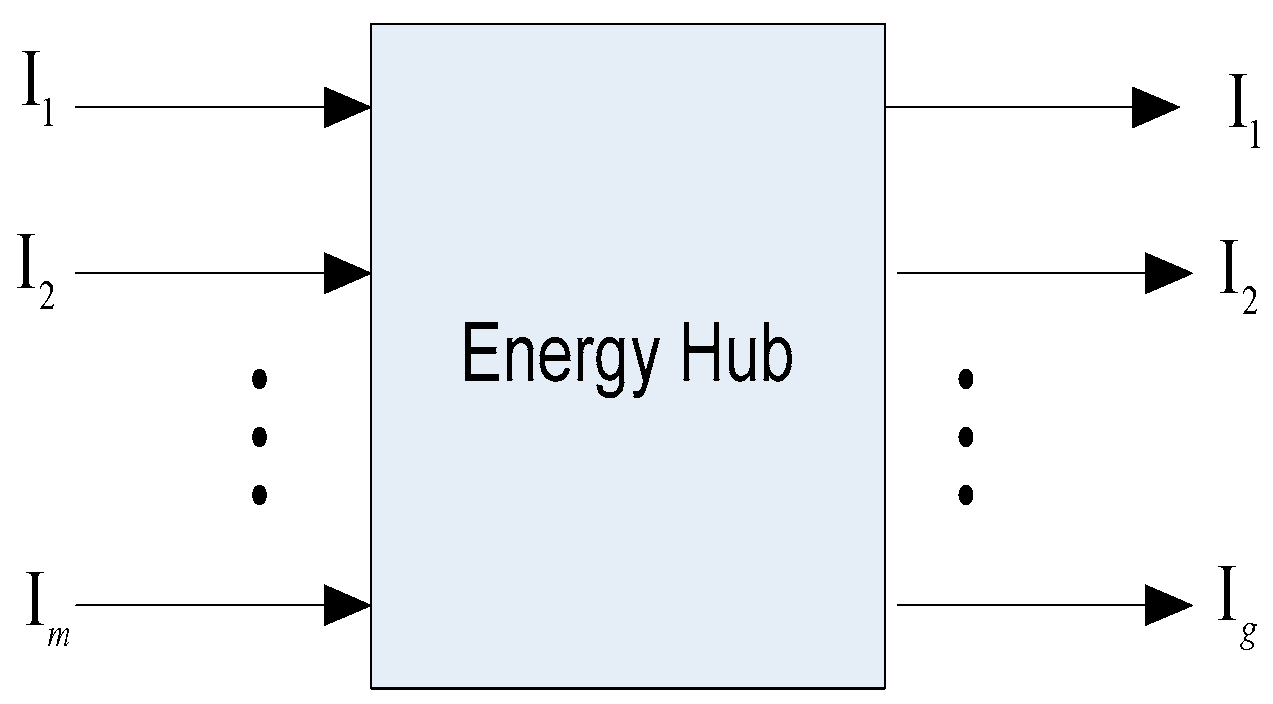
3.1. What Is an Energy Hub (EH)?
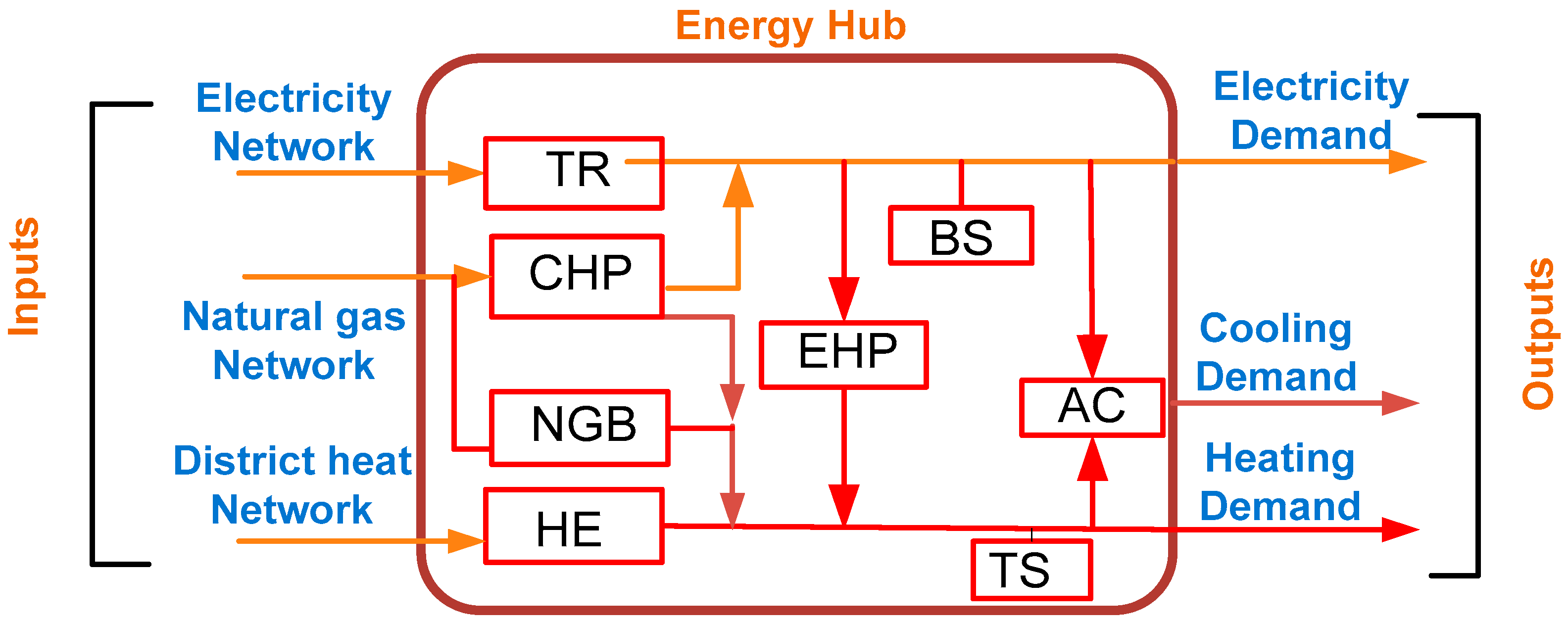
3.1.1. Energy Hub Model
3.1.2. The Energy Hub Basic Concept
- Inputs: Energy vectors at the input (fossil fuels, solar and wind energy, electricity, hydrogen, water, gas).
- Converters: Used in the conversion of different energy resources (boilers, chillers, CHP unit, heat pump, fuel cell, electrolyser (P2G)).
- Energy storage systems (ESSs): Used to store or preserve surplus energy (heat storage, hot water tank, hydrogen tank, battery, ice storage, and flywheel).
- Output: The hub energy demands for end users (electricity, heat, cooling, gas, water, hydrogen) [75].
4. Planning and Management
4.1. Deterministic Models
4.2. Probabilistic Models
4.3. Planning Objective Functions (OFs) of Energy Hubs
- Minimization of investment and operating cost.
- Minimization of lifecycle cost (LCC).
- Maximization of the share of RESs penetration.
- Minimization of energy cost and emissions.
- Minimization of primary energy consumption.
- Maximization of system reliability and profits.
- Maximization of social welfare.
4.3.1. Energy Hubs Planning Constraints
4.3.2. Decision Variables
- Binary variable: e.g., identifying if the energy converter or storage device is chosen.
- Continuous variable: e.g., the energy flow of scenario at time [64].
4.3.3. Basic Framework for EH Optimization
- Structural optimization (i.e., finding the optimal topology and structure of an EH based on a specific demand and corresponding OFs).
- Operational optimization (optimal power dispatch in an EH or optimal power flow in the network of interconnected EHs for a given structure of the system).
4.3.4. Simulation Results
4.4. Uncertainty Modelling Methods
4.5. Mathematical Techniques and Solution Algorithm for Planning Energy Hubs
5. Demand Response (DR)
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hosseini, S.E.; Andwari, A.M.; Wahid, M.A.; Bagheri, G. A review on green energy potentials in Iran. Renew. Sustain. Energy Rev. 2013, 27, 533–545. [Google Scholar] [CrossRef]
- Dincer, I.; Acar, C. Potential energy solutions for better sustainability. In Exergetic, Energetic and Environmental Dimensions; Elsevier: Amsterdam, The Netherlands, 2018; pp. 3–37. [Google Scholar]
- Field, C.B.; Barros, V.R.; Mastrandrea, M.D.; Mach, K.J.; Abdrabo, M.-K.; Adger, N.; Anokhin, Y.A.; Anisimov, O.A.; Arent, D.J.; Barnett, J. Summary for policymakers. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; pp. 1–32. [Google Scholar]
- Larsen, H.H.; Petersen, L.S. DTU International Energy Report 2015: Energy Systems Integration for the Transition to Non-Fossil Energy Systems. Technical University of Denmark, Version of Record. 2015. Available online: orbit.dtu.dk (accessed on 1 April 2022).
- Reynolds, J.; Ahmad, M.W.; Rezgui, Y. Holistic modelling techniques for the operational optimisation of multi-vector energy systems. Energy Build. 2018, 169, 397–416. [Google Scholar] [CrossRef]
- Wang, C.; Dong, S.; Xu, S.; Yang, M.; He, S.; Dong, X.; Liang, J. Impact of power-to-gas cost characteristics on power-gas-heating integrated system scheduling. IEEE Access 2019, 7, 17654–17662. [Google Scholar] [CrossRef]
- Kholardi, F.; Assili, M.; Lasemi, M.A.; Hajizadeh, A. Optimal management of energy hub with considering hydrogen network. In Proceedings of the 2018 International Conference on Smart Energy Systems and Technologies (SEST), Seville, Spain, 10–12 September 2018; pp. 1–6. [Google Scholar]
- Rosa, R.N. The role of synthetic fuels for a carbon neutral economy. C.—J. Carbon Res. 2017, 3, 11. [Google Scholar] [CrossRef] [Green Version]
- Park, C.; Sedundo, R.; Knazkins, V.; Korbakorba, P. Feasibility Analysis of the Power-to-Gas Concept in the Future Swiss Power System; CIRED Workshop, Zurich University of Applied Sciences: Zurich, Switzerland, 2016; pp. 1768–1772. [Google Scholar] [CrossRef]
- Yang, J.; Sun, W.; Harrison, G.; Robertson, J. A Novel Planning Method for Multi-Scale Integrated Energy System. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Zhang, X.; Karady, G.G.; Ariaratnam, S.T. Optimal allocation of CHP-based distributed generation on urban energy distribution networks. IEEE Trans. Sustain. Energy 2013, 5, 246–253. [Google Scholar] [CrossRef]
- Pazouki, S.; Haghifam, M.-R. Optimal planning and scheduling of energy hub in presence of wind, storage and demand response under uncertainty. Int. J. Electr. Power Energy Syst. 2016, 80, 219–239. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, C.; Wang, Y.; Li, W. Optimal expansion co-planning of reconfigurable electricity and natural gas distribution systems incorporating energy hubs. Energies 2017, 10, 124. [Google Scholar] [CrossRef] [Green Version]
- Unsihuay-Vila, C.; Marangon-Lima, J.W.; De Souza, A.Z.; Perez-Arriaga, I.J.; Balestrassi, P.P. A model to long-term, multiarea, multistage, and integrated expansion planning of electricity and natural gas systems. IEEE Trans. Power Syst. 2010, 25, 1154–1168. [Google Scholar] [CrossRef]
- Saldarriaga, C.A.; Hincapié, R.A.; Salazar, H. A holistic approach for planning natural gas and electricity distribution networks. IEEE Trans. Power Syst. 2013, 28, 4052–4063. [Google Scholar] [CrossRef]
- Qiu, J.; Dong, Z.Y.; Zhao, J.H.; Xu, Y.; Zheng, Y.; Li, C.; Wong, K.P. Multi-stage flexible expansion co-planning under uncertainties in a combined electricity and gas market. IEEE Trans. Power Syst. 2014, 30, 2119–2129. [Google Scholar] [CrossRef]
- Salimi, M.; Ghasemi, H.; Adelpour, M.; Vaez-ZAdeh, S. Optimal planning of energy hubs in interconnected energy systems: A case study for natural gas and electricity. IET Gener. Transm. Distrib. 2015, 9, 695–707. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, C.B.; Bent, R.; Backhaus, S.; Blumsack, S.; Hijazi, H.; Van Hentenryck, P. Convex optimization for joint expansion planning of natural gas and power systems. In Proceedings of the 2016 49th Hawaii International Conference on System Sciences (HICSS), Koloa, HI, USA, 5–8 January 2016; pp. 2536–2545. [Google Scholar]
- Ni, L.; Liu, W.; Wen, F.; Xue, Y.; Dong, Z.; Zheng, Y.; Zhang, R. Optimal operation of electricity, natural gas and heat systems considering integrated demand responses and diversified storage devices. J. Mod. Power Syst. Clean Energy 2018, 6, 423–437. [Google Scholar] [CrossRef] [Green Version]
- Maroufmashat, A.; Elkamel, A.; Fowler, M.; Sattari, S.; Roshandel, R.; Hajimiragha, A.; Walker, S.; Entchev, E. Modeling and optimization of a network of energy hubs to improve economic and emission considerations. Energy 2015, 93, 2546–2558. [Google Scholar] [CrossRef]
- Bracco, S.; Dentici, G.; Siri, S. Economic and environmental optimization model for the design and the operation of a combined heat and power distributed generation system in an urban area. Energy 2013, 55, 1014–1024. [Google Scholar] [CrossRef]
- Fan, H.; Yuan, Q.; Xia, S.; Lu, J.; Li, Z. Optimally Coordinated Expansion Planning of Coupled Electricity, Heat and Natural Gas Infrastructure for Multi-Energy System. IEEE Access 2020, 8, 91139–91149. [Google Scholar] [CrossRef]
- Galus, M.D.; Andersson, G. Integration of plug-in hybrid electric vehicles into energy networks. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–8. [Google Scholar]
- Cheng, Y.; Zhang, N.; Kang, C. Bi-Level Expansion Planning of Multiple Energy Systems under Carbon Emission Constraints. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Ojeda-Esteybar, D.M.; Rubio-Barros, R.G.; Vargas, A. Integrated operational planning of hydrothermal power and natural gas systems with large scale storages. J. Mod. Power Syst. Clean Energy 2017, 5, 299–313. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Che, L.; Shahidehpour, M.; Alabdulwahab, A.S.; Abusorrah, A. Reliability-based optimal planning of electricity and natural gas interconnections for multiple energy hubs. IEEE Trans. Smart Grid 2015, 8, 1658–1667. [Google Scholar] [CrossRef]
- Zhang, X.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Optimal expansion planning of energy hub with multiple energy infrastructures. IEEE Trans. Smart Grid 2015, 6, 2302–2311. [Google Scholar] [CrossRef]
- Ceseña, E.A.M.; Mancarella, P. Distribution network support from multi-energy demand side response in smart districts. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Melbourne, VIC, Australia, 28 November–1 December 2016; pp. 753–758. [Google Scholar]
- Xunjie, W.; Bowen, L.; Hainan, Z.; Chengfu, W.; Donglei, S.; Zhe, L. Optimal Planning Method of IES with Multi-energy Storage and Wind Power. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 2869–2872. [Google Scholar]
- Yang, F.; Yuan, X.; Bai, H.; Yin, S.; Liu, H. Collaborative planning of integrated natural gas and power supply system considering P2G technique. In Proceedings of the 2018 China International Conference on Electricity Distribution (CICED), Tianjin, China, 17–19 September 2018; pp. 2216–2220. [Google Scholar]
- Wang, X.; Bie, Z.; Liu, F. Optimal expansion planning of multi-energy generations and natural gas storages in integrated energy system. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Zhang, H.; Cao, Q.; Gao, H.; Wang, P.; Zhang, W.; Yousefi, N. Optimum design of a multi-form energy hub by applying particle swarm optimization. J. Clean. Prod. 2020, 260, 121079. [Google Scholar] [CrossRef]
- Fan, H.; Lu, J.; Li, Z.; Shahidehpour, M.; Zhang, S. Optimal Planning of Integrated Electricity-Gas System with Demand Side Management. IEEE Access 2019, 7, 176790–176798. [Google Scholar] [CrossRef]
- Eid, C.; Codani, P.; Perez, Y.; Reneses, J.; Hakvoort, R. Managing electric flexibility from Distributed Energy Resources: A review of incentives for market design. Renew. Sustain. Energy Rev. 2016, 64, 237–247. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef] [Green Version]
- Antonopoulos, I.; Robu, V.; Couraud, B.; Kirli, D.; Norbu, S.; Kiprakis, A.; Flynn, D.; Elizondo-Gonzalez, S.; Wattam, S. Artificial intelligence and machine learning approaches to energy demand-side response: A systematic review. Renew. Sustain. Energy Rev. 2020, 130, 109899. [Google Scholar] [CrossRef]
- Hussain, B.; Thirkill, A. Multi-Energy Vector Integration Innovation Opportunities; Catapult Energy Systems: Birmingham, UK, 2018; Available online: https://es.catapult.org.uk/ (accessed on 5 May 2022).
- Mancarella, P. MES (multi-energy systems): An overview of concepts and evaluation models. Energy 2014, 65, 1–17. [Google Scholar] [CrossRef]
- Lowe, R.; Chiu, L.; Pye, S.; Gallo Cassarino, T.; Barrett, M.; Scamman, D.; Smith, A.; Solano-Rodriguez, B. Lost Generation: System Resilience and Flexibility. In Proceedings of the Proceedings of the 2020 MIT “A+ B” Applied Energy Symposium, Cambridge, MA, USA, 1 August 2020. [Google Scholar]
- O’Malley, M.; Kroposki, B.; Hannegan, B.; Madsen, H.; Andersson, M.; D’haeseleer, W.; McGranaghan, M.F.; Dent, C.; Strbac, G.; Baskaran, S. Energy Systems Integration. Defining and Describing the Value Proposition; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2016. [Google Scholar]
- Carradore, L.; Turri, R. Modeling and simulation of multi-vector energy systems. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–7. [Google Scholar]
- Clegg, S.; Mancarella, P. Storing renewables in the gas network: Modelling of power-to-gas seasonal storage flexibility in low-carbon power systems. IET Gener. Transm. Distrib. 2016, 10, 566–575. [Google Scholar] [CrossRef]
- Qadrdan, M.; Wu, J.; Jenkins, N.; Ekanayake, J. Operating strategies for a GB integrated gas and electricity network considering the uncertainty in wind power forecasts. IEEE Trans. Sustain. Energy 2013, 5, 128–138. [Google Scholar] [CrossRef]
- Abeysekera, M.; Jenkins, N.; Wu, J. Integrated Energy Systems: An Overview of Benefits, Analysis, Research Gaps and Opportunities. Hubnet, UK. 2016. Available online: www.hubnet.org.uk (accessed on 10 May 2022).
- Salgado, F.; Pedrero, P. Short-term operation planning on cogeneration systems: A survey. Electr. Power Syst. Res. 2008, 78, 835–848. [Google Scholar] [CrossRef]
- Houwing, M.; Negenborn, R.R.; De Schutter, B. Demand response with micro-CHP systems. Proc. IEEE 2010, 99, 200–213. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Mancarella, P. Modelling, assessment and Sankey diagrams of integrated electricity-heat-gas networks in multi-vector district energy systems. Appl. Energy 2016, 167, 336–352. [Google Scholar] [CrossRef]
- Vandewalle, J.; Keyaerts, N.; D’haeseleer, W. The role of thermal storage and natural gas in a smart energy system. In Proceedings of the 2012 9th International Conference on the European Energy Market, Florence, Italy, 10–12 May 2012; pp. 1–9. [Google Scholar]
- Krause, T.; Andersson, G.; Fröhlich, K.; Vaccaro, A. Multiple-energy carriers: Modeling of production, delivery, and consumption. Proc. IEEE 2010, 99, 15–27. [Google Scholar] [CrossRef]
- Geidl, M. Integrated Modeling and Optimization of Multi-Carrier Energy Systems; ETH: Zurich, Switzerland, 2007. [Google Scholar]
- Robertson, E.; Galloway, S. Multienergy vector modelling of a Scottish Energy System: Transitions and technology implications. Proc. Inst. Mech. Eng. Part A J. Power Energy 2017, 231, 580–589. [Google Scholar] [CrossRef] [Green Version]
- Kriechbaum, L.; Scheiber, G.; Kienberger, T. Grid-based multi-energy systems—Modelling, assessment, open source modelling frameworks and challenges. Energy Sustain. Soc. 2018, 8, 35. [Google Scholar] [CrossRef] [Green Version]
- Pudjianto, D.; Ramsay, C.; Strbac, G. Microgrids and virtual power plants: Concepts to support the integration of distributed energy resources. Proc. Inst. Mech. Eng. Part A J. Power Energy 2008, 222, 731–741. [Google Scholar] [CrossRef]
- Kampouropoulos, K. Multi-Objective Optimization of an Energy Hub Using Artificial Intelligence; Centre Technologies: Barcelona, Spain, 2018; Available online: http://www.tdx.cat/ (accessed on 2 May 2022).
- Shabanpour-Haghighi, A.; Seifi, A.R. An integrated steady-state operation assessment of electrical, natural gas, and district heating networks. IEEE Trans. Power Syst. 2015, 31, 3636–3647. [Google Scholar] [CrossRef]
- Cesena, E.A.M.; Loukarakis, E.; Good, N.; Mancarella, P. Integrated electricity–heat–gas systems: Techno–economic modeling, optimization, and application to multienergy districts. Proc. IEEE 2020, 108, 1392–1410. [Google Scholar] [CrossRef]
- Martinez-Mares, A.; Fuerte-Esquivel, C.R. A unified gas and power flow analysis in natural gas and electricity coupled networks. IEEE Trans. Power Syst. 2012, 27, 2156–2166. [Google Scholar] [CrossRef]
- Liu, C.; Shahidehpour, M.; Fu, Y.; Li, Z. Security-constrained unit commitment with natural gas transmission constraints. IEEE Trans. Power Syst. 2009, 24, 1523–1536. [Google Scholar]
- Mancarella, P.; Andersson, G.; Peças-Lopes, J.; Bell, K.R. Modelling of integrated multi-energy systems: Drivers, requirements, and opportunities. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–22. [Google Scholar]
- Van Beuzekom, I.; Gibescu, M.; Slootweg, J. A review of multi-energy system planning and optimization tools for sustainable urban development. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–7. [Google Scholar]
- Liu, X.; Wu, J.; Jenkins, N.; Bagdanavicius, A. Combined analysis of electricity and heat networks. Appl. Energy 2016, 162, 1238–1250. [Google Scholar] [CrossRef] [Green Version]
- Good, N.; Karangelos, E.; Navarro-Espinosa, A.; Mancarella, P. Optimization under uncertainty of thermal storage-based flexible demand response with quantification of residential users’ discomfort. IEEE Trans. Smart Grid 2015, 6, 2333–2342. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. A modeling and optimization approach for multiple energy carrier power flow. In Proceedings of the 2005 IEEE Russia Power Tech, St. Petersburg, Russia, 27–30 June 2005; pp. 1–7. [Google Scholar]
- Soroudi, A. Power System Optimization Modeling in GAMS.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 78. [Google Scholar]
- Wang, Y.; Zhang, N.; Zhuo, Z.; Kang, C.; Kirschen, D. Mixed-integer linear programming-based optimal configuration planning for energy hub: Starting from scratch. Appl. Energy 2018, 210, 1141–1150. [Google Scholar] [CrossRef]
- Maroufmashat, A.; Taqvi, S.T.; Miragha, A.; Fowler, M.; Elkamel, A. Modeling and optimization of energy hubs: A comprehensive review. Inventions 2019, 4, 50. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-Ivatloo, B. An introduction to smart energy systems and definition of smart energy hubs. In Operation, Planning, and Analysis of Energy Storage Systems in Smart Energy Hubs; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–21. [Google Scholar]
- Liu, T.; Zhang, D.; Dai, H.; Wu, T. Intelligent modeling and optimization for smart energy hub. IEEE Trans. Ind. Electron. 2019, 66, 9898–9908. [Google Scholar] [CrossRef]
- Geidl, M.; Koeppel, G.; Favre-Perrod, P.; Klockl, B.; Andersson, G.; Frohlich, K. Energy hubs for the future. IEEE Power Energy Mag. 2006, 5, 24–30. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Optimal power flow of multiple energy carriers. IEEE Trans. Power Syst. 2007, 22, 145–155. [Google Scholar] [CrossRef]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-Ivatloo, B.; Yousefi, H. Energy hub: From a model to a concept–A review. Renew. Sustain. Energy Rev. 2017, 80, 1512–1527. [Google Scholar] [CrossRef]
- Walker, S.; Labeodan, T.; Maassen, W.; Zeiler, W. A review study of the current research on energy hub for energy positive neighborhoods. Energy Procedia 2017, 122, 727–732. [Google Scholar] [CrossRef]
- Walker, S.B.; Mukherjee, U.; Fowler, M.; Elkamel, A. Benchmarking and selection of Power-to-Gas utilizing electrolytic hydrogen as an energy storage alternative. Int. J. Hydrog. Energy 2016, 41, 7717–7731. [Google Scholar] [CrossRef]
- Schulze, M.; Friedrich, L.; Gautschi, M. Modeling and optimization of renewables: Applying the energy hub approach. In Proceedings of the 2008 IEEE International Conference on Sustainable Energy Technologies, Singapore, 24–27 November 2008; pp. 83–88. [Google Scholar]
- Suslov, K.; Piskunova, V.; Gerasimov, D.; Ukolova, E.; Akhmetshin, A.; Lombardi, P.; Komarnicki, P. Development of the methodological basis of the simulation modelling of the multi-energy systems. E3S Web Conf. 2019, 124, 01049. [Google Scholar] [CrossRef] [Green Version]
- Payasi, R.P.; Singh, A.K.; Singh, D. Review of distributed generation planning: Objectives, constraints, and algorithms. Int. J. Eng. Sci. Technol. 2011, 133–153. [Google Scholar] [CrossRef]
- Aien, M.; Hajebrahimi, A.; Fotuhi-Firuzabad, M. A comprehensive review on uncertainty modeling techniques in power system studies. Renew. Sustain. Energy Rev. 2016, 57, 1077–1089. [Google Scholar] [CrossRef]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-ivatloo, B.; Yousefi, H.; Jalilinasrabady, S. Optimal scheduling of energy hubs in the presence of uncertainty-A review. J. Energy Manag. Technol. 2017, 1, 1–17. [Google Scholar]
- Zubo, R.H.; Mokryani, G.; Rajamani, H.-S.; Aghaei, J.; Niknam, T.; Pillai, P. Operation and planning of distribution networks with integration of renewable distributed generators considering uncertainties: A review. Renew. Sustain. Energy Rev. 2017, 72, 1177–1198. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Liu, Y.; Han, S.; Wang, Y.; Feng, S. Reviews on uncertainty analysis of wind power forecasting. Renew. Sustain. Energy Rev. 2015, 52, 1322–1330. [Google Scholar] [CrossRef]
- Alharbi, W.; Raahemifar, K. Probabilistic coordination of microgrid energy resources operation considering uncertainties. Electr. Power Syst. Res. 2015, 128, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Pazouki, S.; Haghifam, M.-R.; Moser, A. Uncertainty modeling in optimal operation of energy hub in presence of wind, storage and demand response. Int. J. Electr. Power Energy Syst. 2014, 61, 335–345. [Google Scholar] [CrossRef]
- Nosratabadi, S.M.; Hooshmand, R.-A.; Gholipour, E. A comprehensive review on microgrid and virtual power plant concepts employed for distributed energy resources scheduling in power systems. Renew. Sustain. Energy Rev. 2017, 67, 341–363. [Google Scholar] [CrossRef]
- Zarif, M.; Khaleghi, S.; Javidi, M.H. Assessment of electricity price uncertainty impact on the operation of multi-carrier energy systems. IET Gener. Transm. Distrib. 2015, 9, 2586–2592. [Google Scholar] [CrossRef]
- Kienzle, F.; Ahčin, P.; Andersson, G. Valuing investments in multi-energy conversion, storage, and demand-side management systems under uncertainty. IEEE Trans. Sustain. Energy 2011, 2, 194–202. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J.; Tian, C. Capacity optimization of hybrid energy storage in microgrid based on statistic method. Power Syst. Technol. 2018, 42, 187–194. [Google Scholar]
- Suganthi, L.; Iniyan, S.; Samuel, A.A. Applications of fuzzy logic in renewable energy systems—A review. Renew. Sustain. Energy Rev. 2015, 48, 585–607. [Google Scholar] [CrossRef]
- Datta, M.; Senjyu, T.; Yona, A.; Funabashi, T. A fuzzy based method for leveling output power fluctuations of photovoltaic-diesel hybrid power system. Renew. Energy 2011, 36, 1693–1703. [Google Scholar] [CrossRef]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton and Oxford, Oxfordshire, UK, 2009. [Google Scholar]
- Akbari, K.; Nasiri, M.M.; Jolai, F.; Ghaderi, S.F. Optimal investment and unit sizing of distributed energy systems under uncertainty: A robust optimization approach. Energy Build. 2014, 85, 275–286. [Google Scholar] [CrossRef]
- Stott, B.; Hobson, E. Power system security control calculations using linear programming, Part I. IEEE Trans. Power Appar. Syst. 1978, PAS-97, 1713–1720. [Google Scholar] [CrossRef]
- Koeppel, G.; Andersson, G. The influence of combined power, gas, and thermal networks on the reliability of supply. In Proceedings of The Sixth World Energy System Conference, Torino, Italy, 10–12 July 2006; pp. 10–12. [Google Scholar]
- Maroufmashat, A.; Fowler, M.; Elkamel, A.; Sattari, S. Optimal operation of an energy hub network in the context of hydrogen economy. In Proceedings of the 6th International Conference on Hydrogen Production, Oshawa, ON, Canada, 3–6 May 2015; pp. 3–6. [Google Scholar]
- Evins, R.; Orehounig, K.; Dorer, V.; Carmeliet, J. New formulations of the ‘energy hub’model to address operational constraints. Energy 2014, 73, 387–398. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Optimal power dispatch and conversion in systems with multiple energy carriers. In Proceedings of the 15th Power Systems Computation Conference (PSCC), Liege, Belgium, 22 August 2005. [Google Scholar]
- Pantaleo, A.; Shah, N.; Keirstead, J. Bioenergy and other renewables in urban energy systems. In Urban Energy Systems, 1st ed.; Routledge: London, UK, 2013; pp. 96–117. [Google Scholar]
- Chehreghani Bozchalui, M. Optimal Operation of Energy Hubs in the Context of Smart Grids; University of Waterloo Library: Waterloo, ON, Canada, 2011; Available online: http://hdl.handle.net/10012/6085 (accessed on 4 April 2022).
- Chrysikou, V.; Alamaniotis, M.; Tsoukalas, L.H. A review of incentive based demand response methods in smart electricity grids. Int. J. Monit. Surveill. Technol. Res. 2015, 3, 62–73. [Google Scholar] [CrossRef] [Green Version]
- Sheen, J.-N.; Chen, C.-S.; Yang, J.-K. Time-of-use pricing for load management programs in Taiwan Power Company. IEEE Trans. Power Syst. 1994, 9, 388–396. [Google Scholar] [CrossRef]
- Neumann, S.; Sioshansi, F.; Vojdani, A.; Yee, G. How to get more response from demand response. Electr. J. 2006, 19, 24–31. [Google Scholar] [CrossRef]
- Bao, Z.; Qiu, W.; Wu, L.; Zhai, F.; Xu, W.; Li, B.; Li, Z. Optimal multi-timescale demand side scheduling considering dynamic scenarios of electricity demand. IEEE Trans. Smart Grid 2018, 10, 2428–2439. [Google Scholar] [CrossRef]


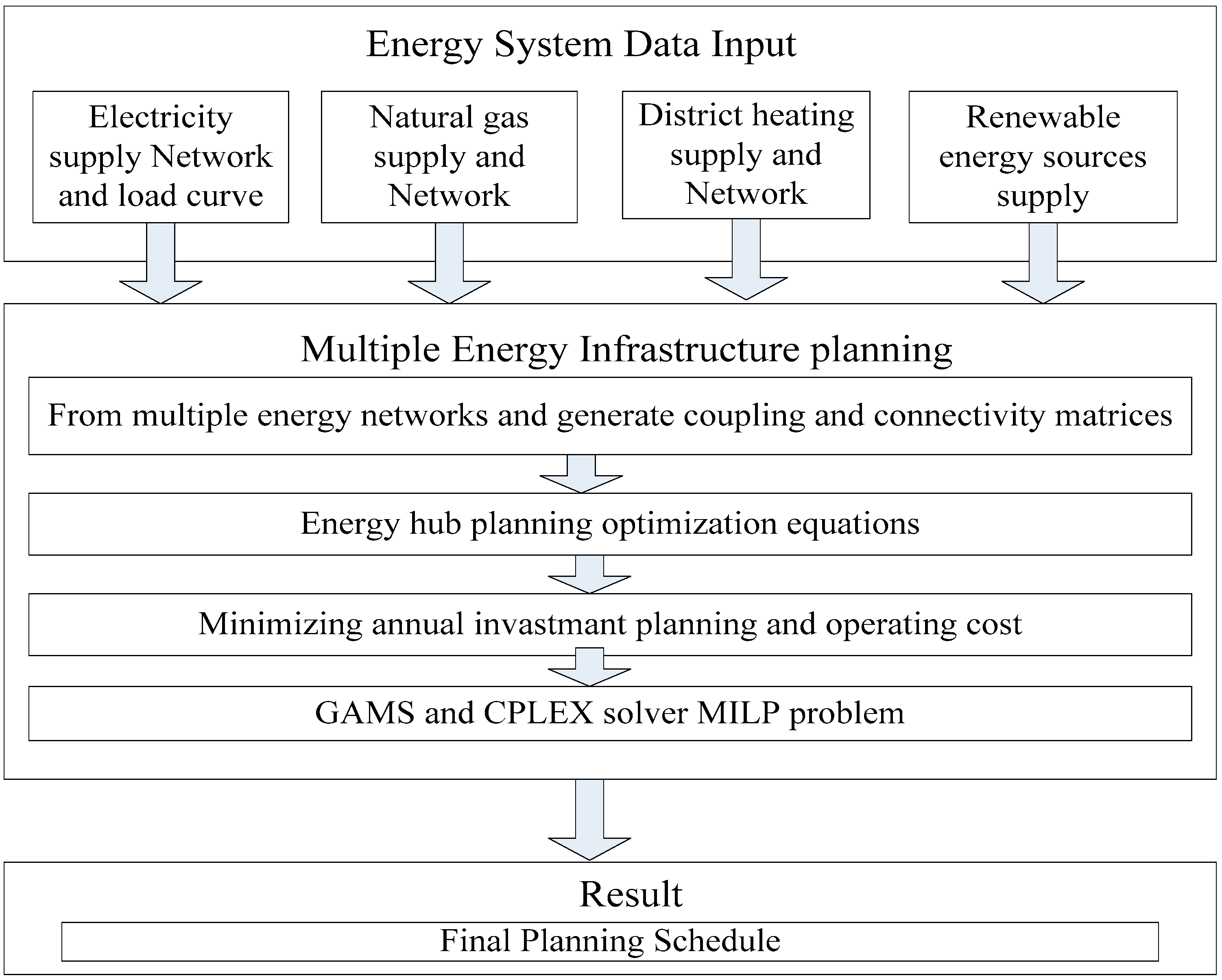

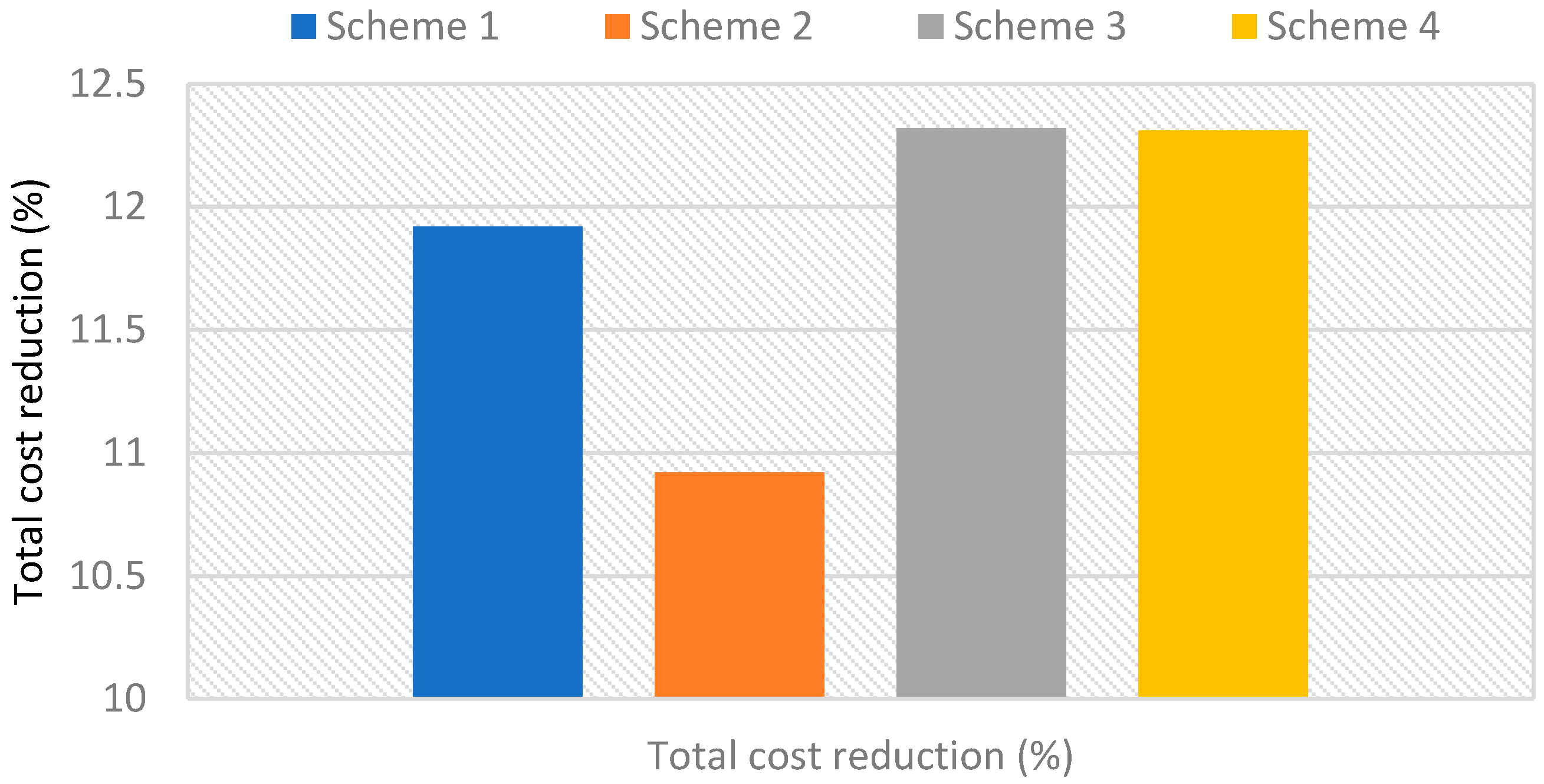
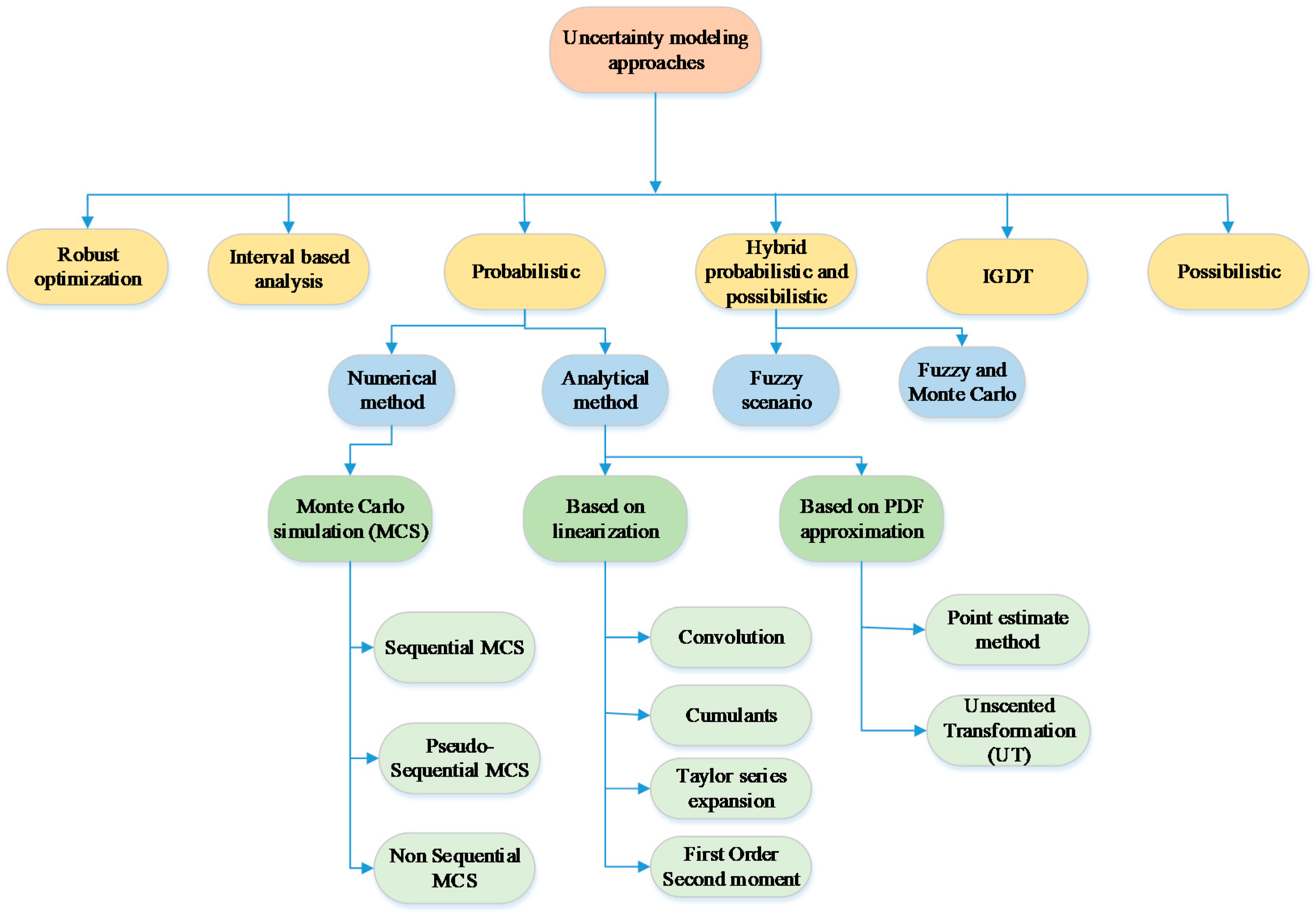
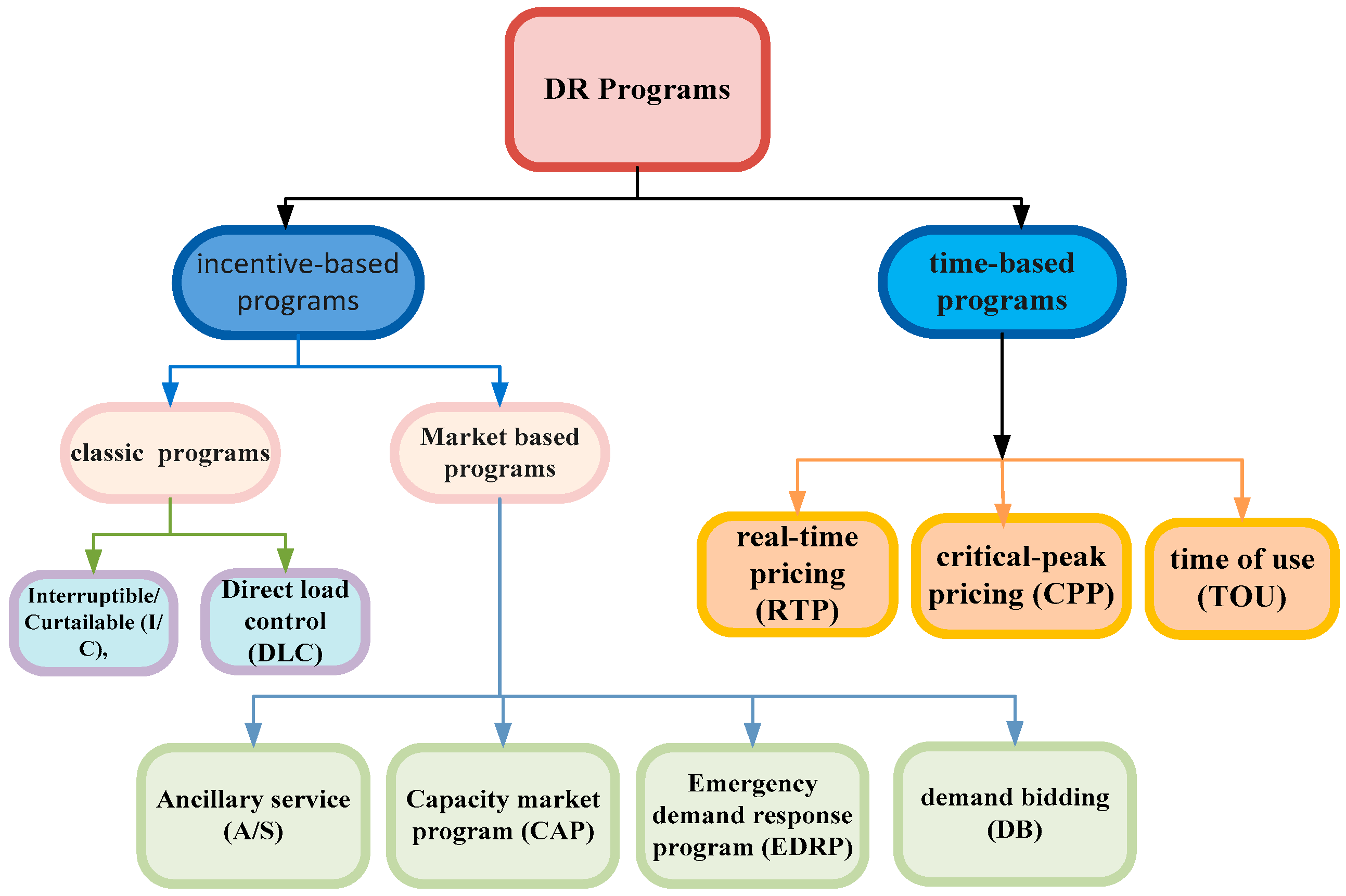
| Refs. | Energy Vector | Conversion Technologies | Objective Function | HorizonTime | Problem | Solution Method | Mathematical Modelling Uncertainty | Emission | DR | Contribution | Energy Demand |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [10] 2019 | EN, NGN | Minimize net present value of total costs | 6 years | MILP | GAMS Optimization Solver | Y | Y | A new planning framework is proposed that will allow for two-level integration with multiple subsystems, including the lower-level of several local communities and the upper-level of a combined gas and electricity distribution network. | E, H | ||
| [12] 2016 | EN, WP, NGN, Water | T, CHP, GB, Wind Turbine | Minimize investment, operation. Reliability cost and emission | One year | MILP | GAMS Optimization Solver | Monte Carlo simulation (MCS) | Y | Y | Mathematical formulation was used for optimal planning of a developed EH considering operation constraints. | E, H, NG, Water |
| [13] 2017 | EN, NGN | T, CHP, GB, AC | Minimize net present value, investment, operation, | Five years | MIQP | Fast iteration solver | Numerical method | Y | A new method is presented to model and formulate the optimal design of reconfiguration electricity and natural gas distribution systems. | E, C, H | |
| [14] 2010 | EN, NGN HYP LNG | T, | Minimize annual investment, operation costs | One year | MILP | GAMS Optimization Solver | Y | A new idea to analyse long-term multi-area expansion plan of gas systems was considered. It was seen that there is more benefit when electricity and gas are combined within the same system. | E, NG | ||
| [15] 2013 | EN, NGN, | T, | Minimize energy and investment cost | One year | MINLP | GAMS Optimization Solver | Y | Y | A new direction of study towards the distribution expansion model that looks at the electricity distribution and natural gas networks as a system with a high penetration of DER. | E, NG | |
| [17] 2015 | EN, NGN, DHN | T, CHP, GB, AC, CC, HE | Minimize net present value | 15 years | Nonlinear problem | MATLAB optimization toolbox | Monte Carlo scenario (MCS) | Y | Y | This study optimally designs and sizes interconnected energy hubs. The constraints on gas and electricity are analysed. | E, H, C |
| [18] 2016 | EN, NGN | T | Minimize investment cost. Reliability | MILP | GAMS Optimization Solver | Y | The paper considered the designing of integrated gas and electricity network to solve the continuous demand. | E, H | |||
| [20] 2020 | EN, NGN, DHN | CHP, GB | Minimize of MES total cost | 10 years | MILP | Bender’s decomposition method | Y | A long-term coordinated planning model is proposed to determine the optimal expansion plans of generation units, GB, and CHP. | E, H | ||
| [22] 2018 | EN, NGN | T, CHP, EB, GF | Minimize energy investment cost | One day | MILP | GAMS Optimization Solver | Y | This paper proposes a bi-level expansion planning model for MES to investigate the optimal planning scheme under the district emission constraints. | E, H | ||
| [24] 2015 | EN, NGN | T, CHP, GF | Minimize energy costs, investment costs | Ten years | MILP | GAMS Optimization solvers | Y | The proposed planning model could be applied by system planners to evaluate and analyse efficiency of energy. | E, H | ||
| [26] 2019 | EN, NGN, WP, DHN | CHP, GF, | Minimize net present value for planning cost | One year | MILP | GAMS Optimization Solver | Scenario Based Approached | Y | The optimal planning model of multi-type energy storage with wind power is established with the goal of minimum cost. | E, H | |
| [27] 2018 | EN, NGN, DHN | CHP, EB | Minimize energy cost, operation costs | One day | MILP | GAMS Optimization Solver | Y | An optimal expansion planning model was proposed to determine the candidate CHPs, EBs, and natural gas storages which satisfy the needs of various energy loads. | E, H | ||
| [29] 2020 | EN, NGN, WC | CHP, EH, T, GF | Minimize overall power expenses | 2 & 5 years | Limitation Optimization problem | Particle swarm optimization | Y | Y | An optimal expansion planning is proposed to mathematically model an optimization problem considering the optimal combination of services. | E, H | |
| [30, 31] 2018 | EN, NGN | GT, T | Minimize total energy cost | MILP | Particle swarm optimization (PSO) algorithm | Y | A collaborative planning model of the natural gas network and power system was built to configure the equipment capacity. | E, NG | |||
| [32, 33] 2019 | EN, NGN, SP | CHP, HP, GB, PV | Minimize energy cost | One day | MILP | MATLAB Optimization toolbox | Scenario Based Approached | Y | This paper proposes a planning framework for integrating energy systems at different scales using a decentralized approach. | E, H |
| Technical | Economic | Environmental |
|---|---|---|
|
|
|
| Challenges | Description |
|---|---|
| Technical |
|
| Economic |
|
| Social |
|
| Regulatory |
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onen, P.S.; Mokryani, G.; Zubo, R.H.A. Planning of Multi-Vector Energy Systems with High Penetration of Renewable Energy Source: A Comprehensive Review. Energies 2022, 15, 5717. https://doi.org/10.3390/en15155717
Onen PS, Mokryani G, Zubo RHA. Planning of Multi-Vector Energy Systems with High Penetration of Renewable Energy Source: A Comprehensive Review. Energies. 2022; 15(15):5717. https://doi.org/10.3390/en15155717
Chicago/Turabian StyleOnen, Patrick Sunday, Geev Mokryani, and Rana H. A. Zubo. 2022. "Planning of Multi-Vector Energy Systems with High Penetration of Renewable Energy Source: A Comprehensive Review" Energies 15, no. 15: 5717. https://doi.org/10.3390/en15155717
APA StyleOnen, P. S., Mokryani, G., & Zubo, R. H. A. (2022). Planning of Multi-Vector Energy Systems with High Penetration of Renewable Energy Source: A Comprehensive Review. Energies, 15(15), 5717. https://doi.org/10.3390/en15155717







