Novel Magnetic Suspension Platform with Three Types of Magnetic Bearings for Mass Transfer
Abstract
:1. Introduction
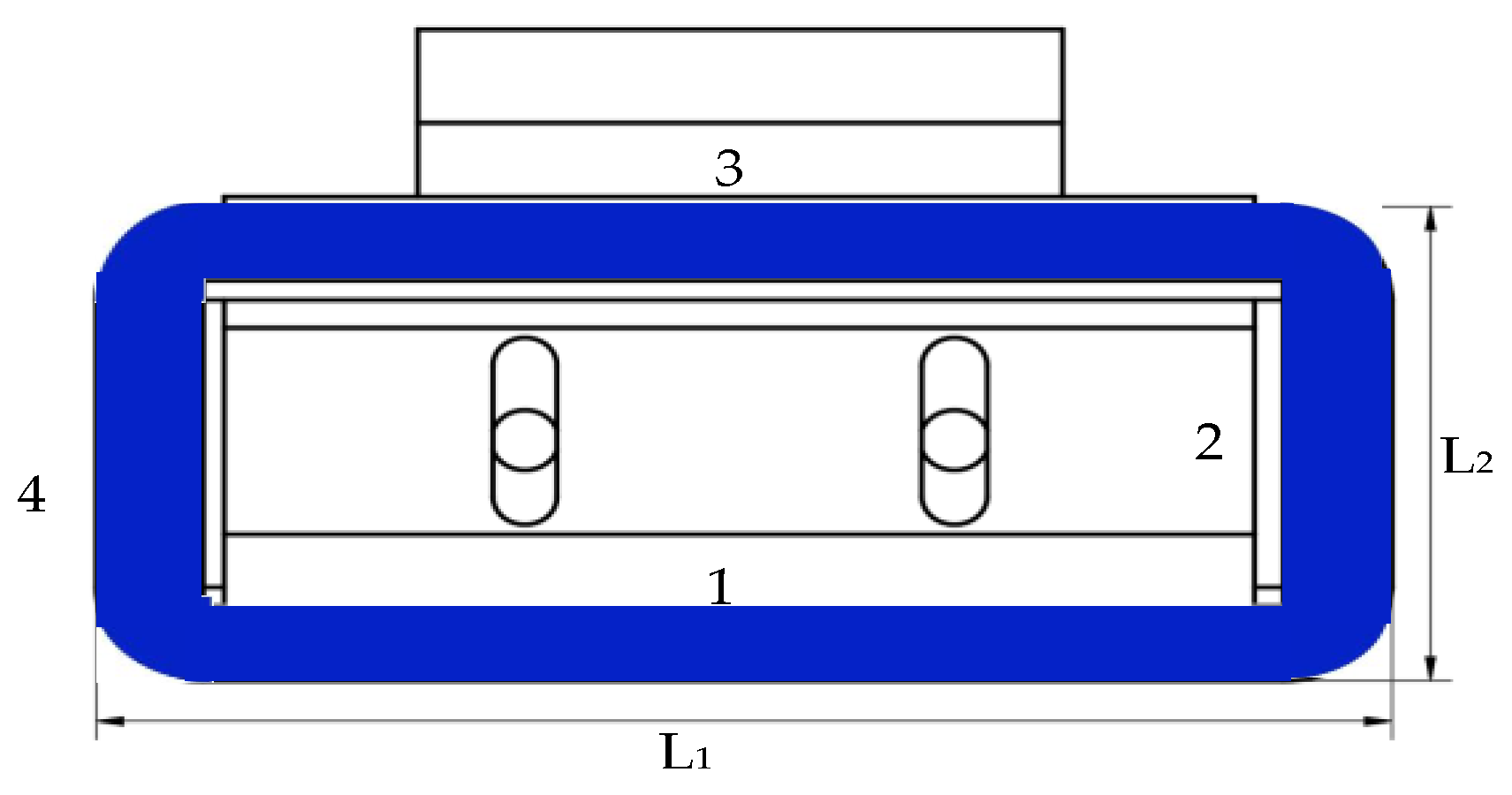
2. Structure and Working Principle
3. Improved Halbach Magnetic Array
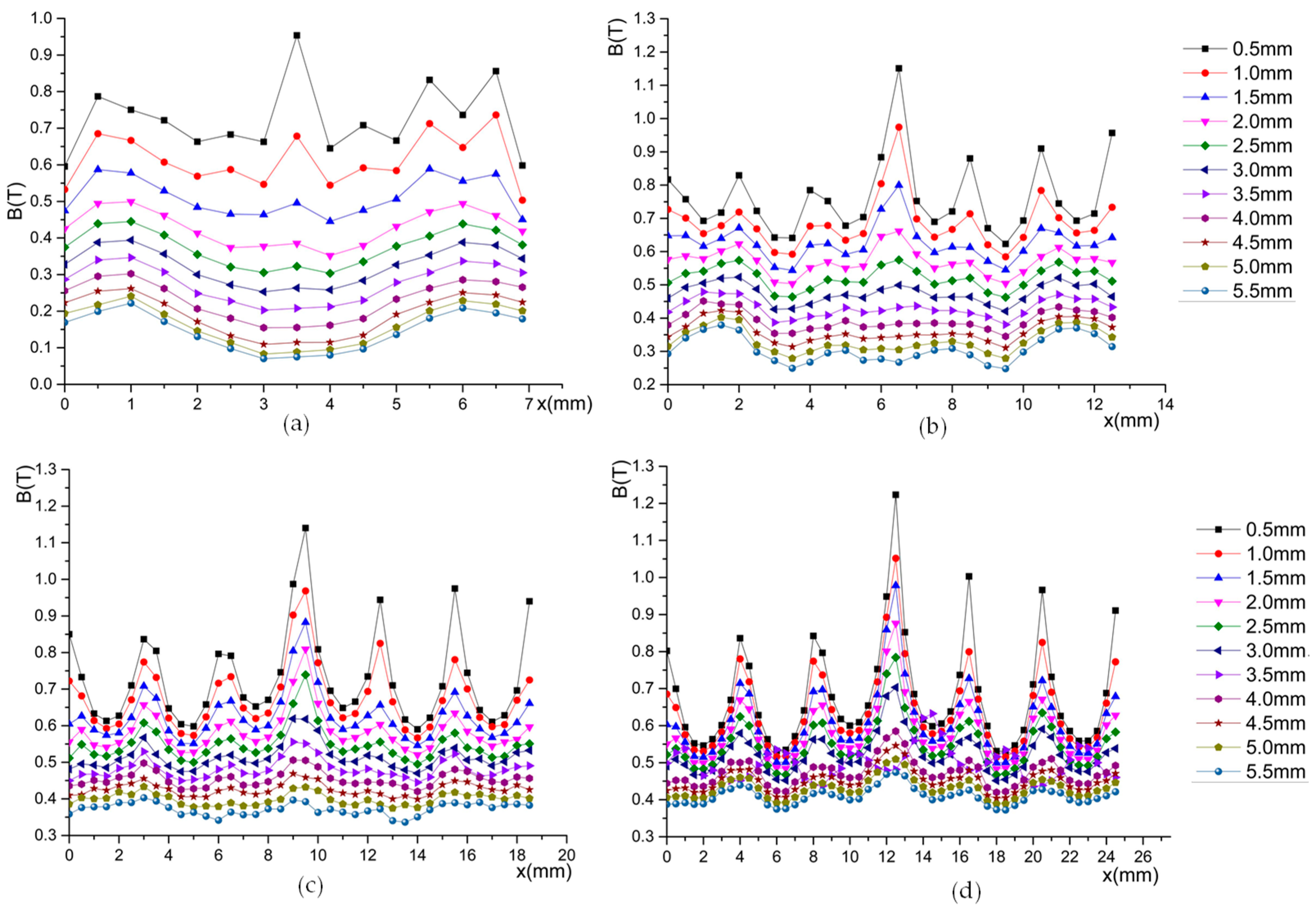
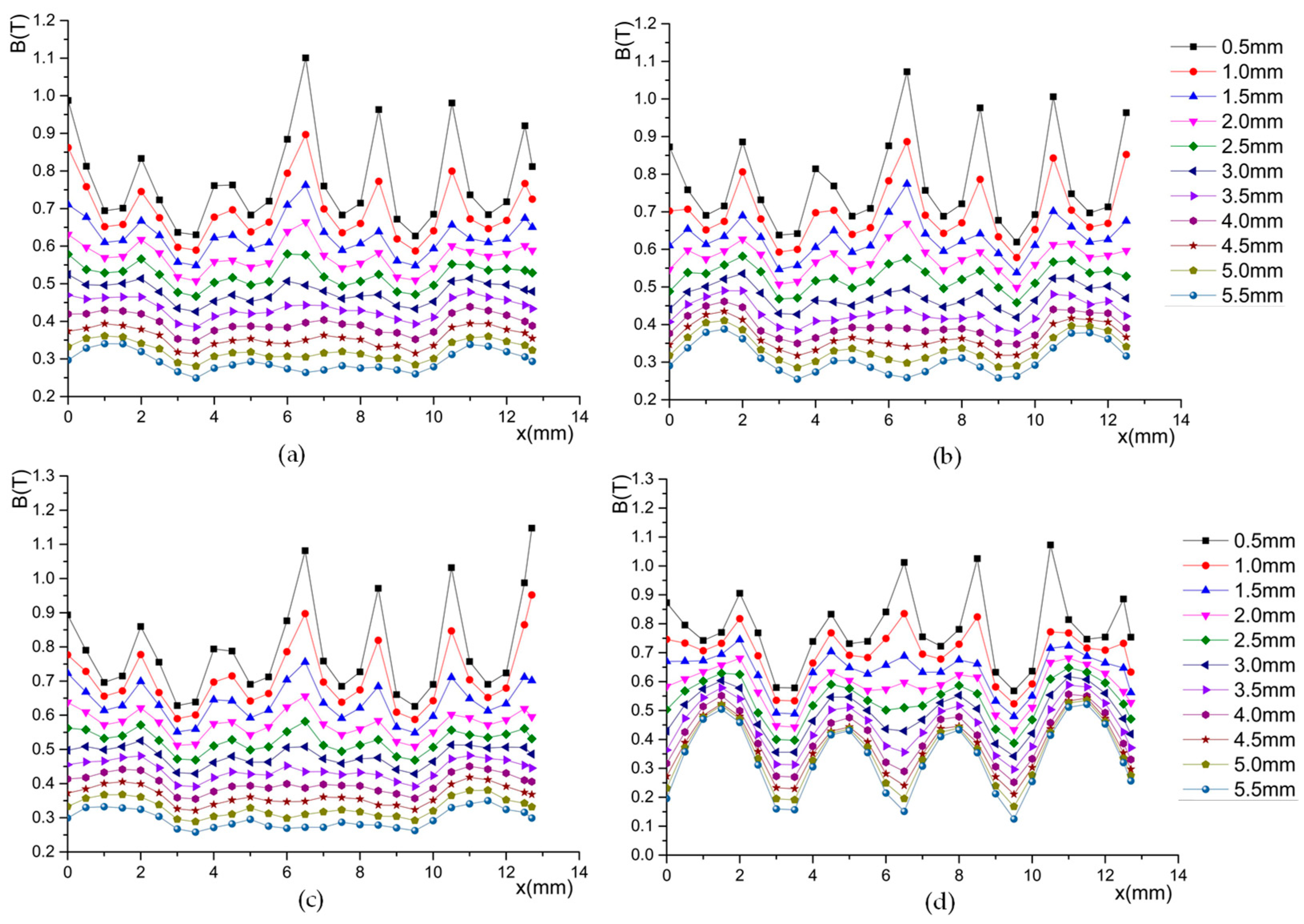
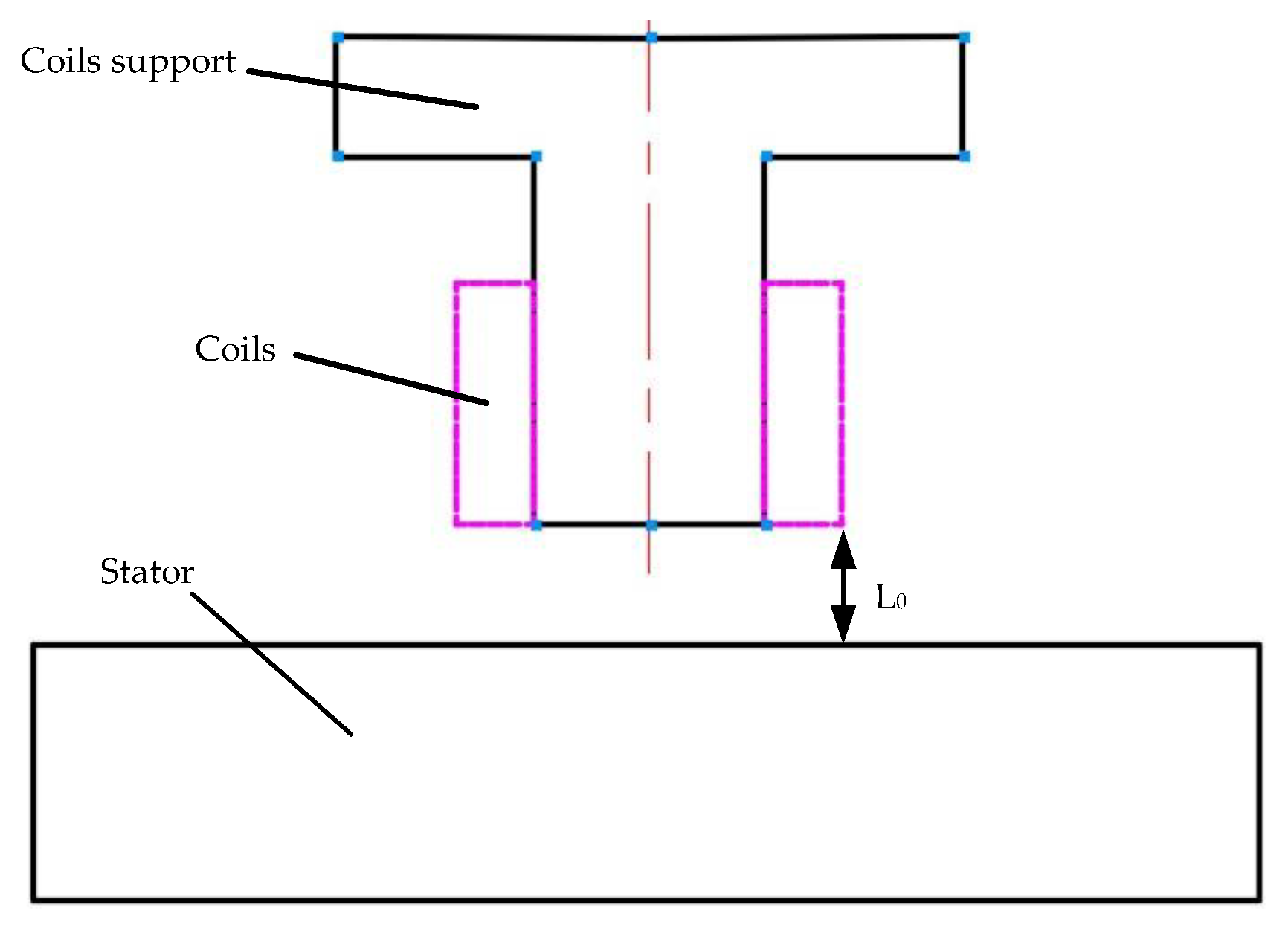
3.1. Model of the Magnetic Flux Density
3.2. Size Optimization of the Permanent Magnet
4. Stiffness of Magnetic Bearing
4.1. Stiffness of Lorentz-Force-Type Magnetic Bearings
4.2. Stiffness of Passive Magnetic Bearing
4.3. Stiffness of Electromagnetic Suspension Bearings
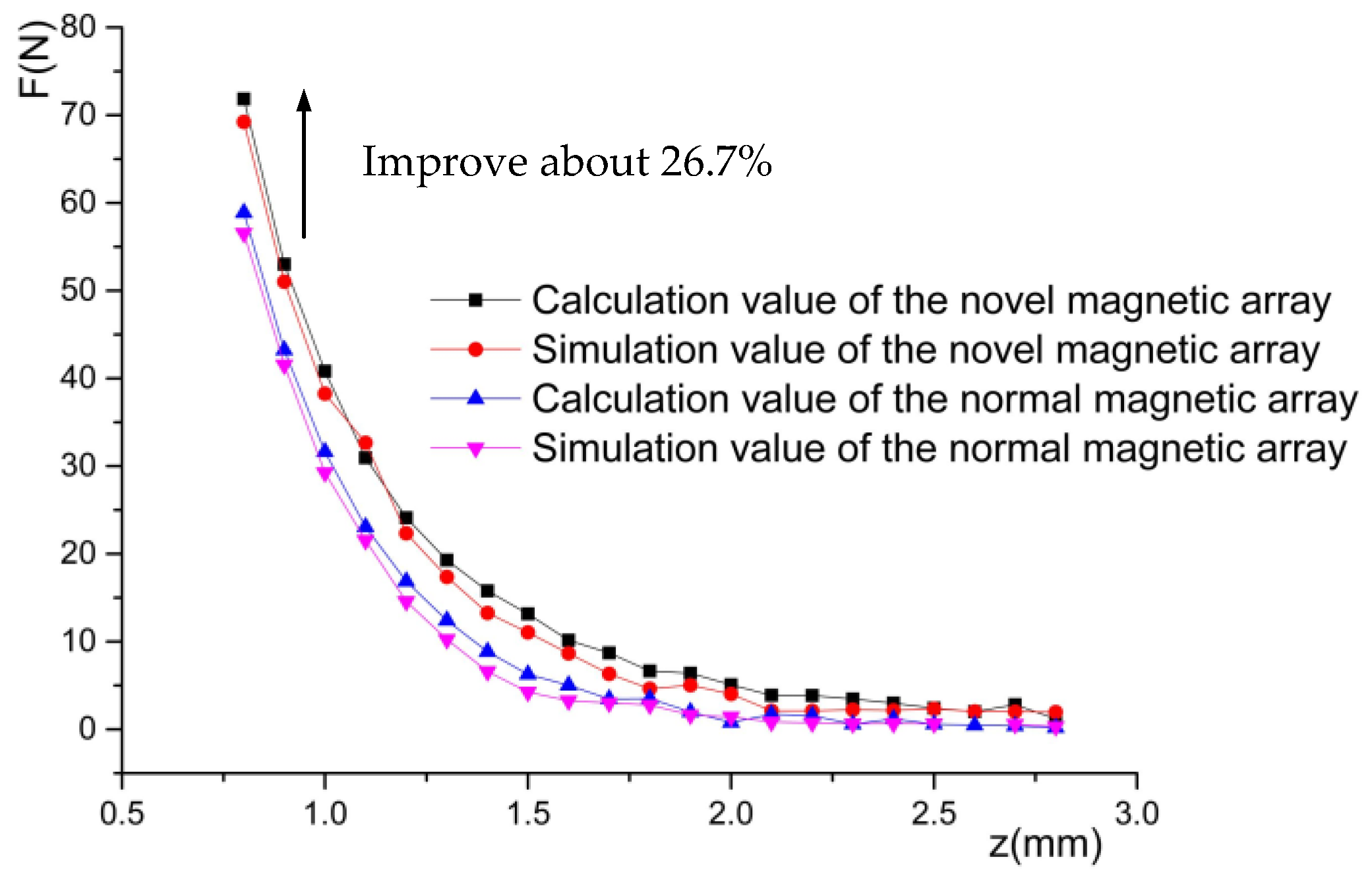
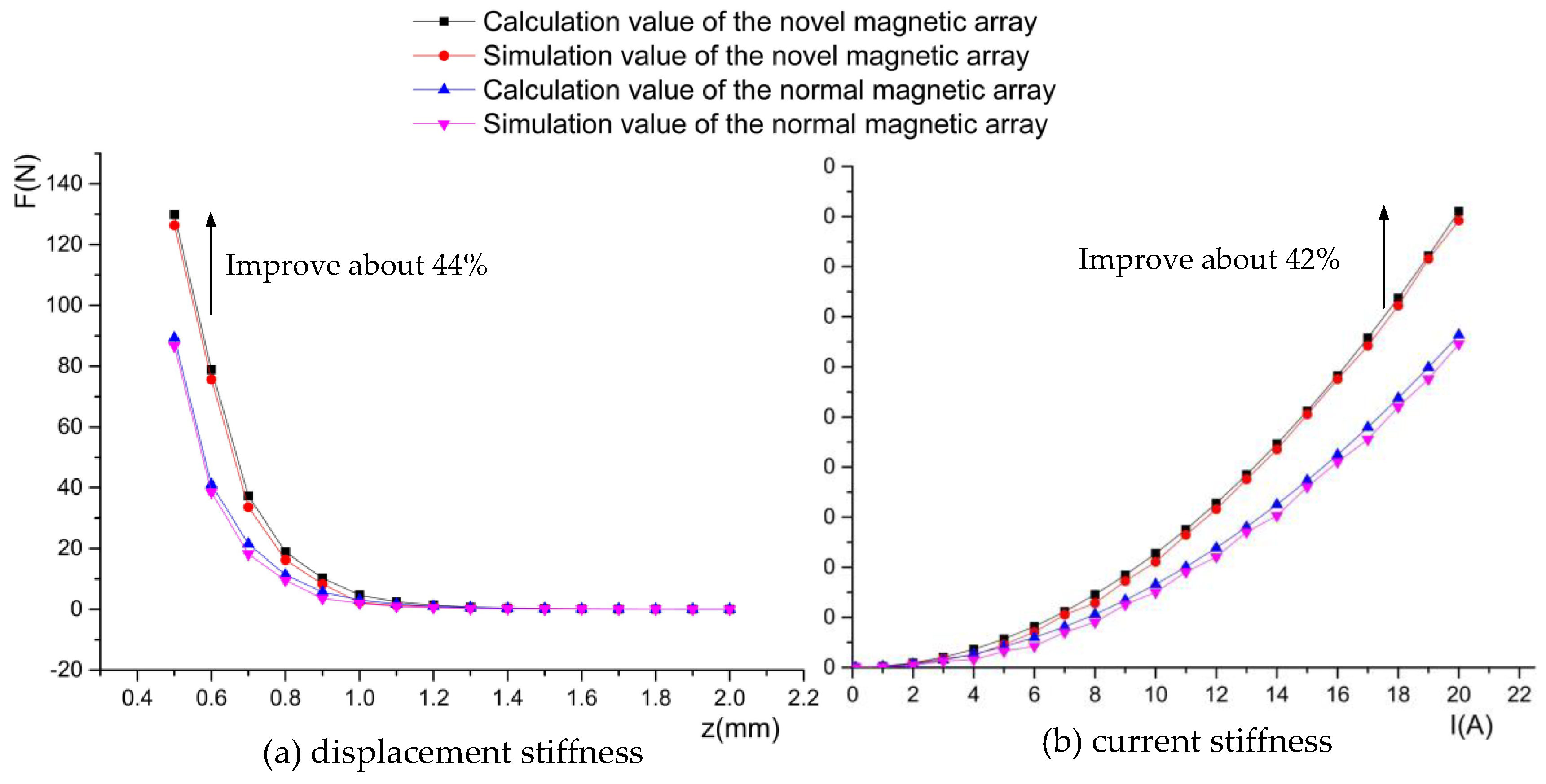
5. Analysis of the Stiffness
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, W.; Dejima, S.; Yanai, H.; Katakura, K.; Kiyono, S.; Tomita, Y. A surface motor-driven planar motion stage integrated with an XYθZ surface encoder for precision positioning. Precis. Eng. 2004, 28, 329–337. [Google Scholar] [CrossRef]
- Kim, J.H. Robust Discrete-Time Variable Structure Control Method. Trans. Asme J. Dyn. Syst. Meas. Control 1992, 122, 766–775. [Google Scholar] [CrossRef]
- Kunioka, T.; Takeda, Y.; Matsuda, T.; Shimazu, N.; Nakayama, Y. XY stage driven by ultrasonic linear motors for the electron-beam x-ray mask writer EB-X3. J. Vac. Sci. Technol. B 1999, 17, 2917–2920. [Google Scholar] [CrossRef]
- Stevenson, J.; Jordan, J.R. Dynamic position measurement technique for flash-on-the-fly wafer exposure. Precis. Eng. 1989, 11, 127–133. [Google Scholar] [CrossRef]
- Kim, W.J.; Trumper, D.L. High-precision magnetic levitation stage for photolithography. Precis. Eng. 1998, 22, 66–77. [Google Scholar] [CrossRef]
- Whorton, M. g-LIMIT-A Vibration Isolation System for the Microgravity Science Glovebox. In Proceedings of the 37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 11–14 January 1999. [Google Scholar]
- Kim, W.J.; Maheshwari, H. In High-precision control of a maglev linear actuator with nanopositioning capability. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002. [Google Scholar]
- Sang, H.L.; Baek, Y.S. Magnetically Suspended Contact-Free Linear Actuator for Precision Stage. Ksme Int. J. 2003, 17, 708–717. [Google Scholar]
- Kim, W.J.; Bhat, N.; Hu, T. Integrated multidimensional positioner for precision manufacturing. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2008, 431–442. [Google Scholar] [CrossRef] [Green Version]
- Verma, S.; Shakir, H.; Kim, W.J. Novel Electromagnetic Actuation Scheme for Multiaxis Nanopositioning. IEEE Trans. Magn. 2006, 42, 2052–2062. [Google Scholar] [CrossRef] [Green Version]
- Estevez, P.; Mulder, A.; Schmidt, R. 6-DoF miniature maglev positioning stage for application in haptic micro-manipulation. Mechatronics 2012, 22, 1015–1022. [Google Scholar] [CrossRef]
- Zhang, Z.; Menq, C.H. Six-axis magnetic levitation and motion control. IEEE Trans. Robot. 2007, 23, 196–205. [Google Scholar] [CrossRef]
- Dejima, S.; Gao, W.; Shimizu, H.; Kiyono, S.; Tomita, Y. Precision positioning of a five degree-of-freedom planar motion stage. Mechatronics 2005, 15, 969–987. [Google Scholar] [CrossRef]
- Chen, M.Y. Design and Experiment of a Macro–Micro Planar Maglev Positioning System. IEEE Trans. Ind. Electron. 2012, 59, 4128–4139. [Google Scholar] [CrossRef]
- Xu, F.; Xu, X.; Chen, M. Prototype of 6-DOF Magnetically Levitated Stage Based on Single Axis Lorentz force Actuator. J. Electr. Eng. Technol. 2016, 11, 1216–1228. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Zhao, Y.; Li, H.; Mu, X.; Zhang, W.; Yue, H.; Liu, R. Design and Analysis of a 2-DOF Electromagnetic Actuator with an Improved Halbach Array for the Magnetic Suspension Platform. Sensors 2022, 22, 790. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.J.; Lee, K.N.; Park, N.C.; Park, Y.P.; Lee, D.J. Development of 3-axis nano stage for precision positioning in lithography system. In Proceedings of the Mechatronics & Automation, IEEE International Conference, Niagara Falls, ON, Canada, 29 July–1 August 2005. [Google Scholar]
- Zhang, H.; Kou, B.; Zhou, Y. Analysis and design of a novel magnetic levitation gravity compensator with low passive force variation in a large vertical displacement. IEEE Trans. Ind. Electron. 2019, 67, 4797–4805. [Google Scholar] [CrossRef]
- Takahashi, M.; Ogawa, H.; Kato, T. Compact maglev stage system for nanometer-scale positioning. Precis. Eng. 2020, 66, 519–530. [Google Scholar] [CrossRef]
- Prosen, N.; Milanovič, M.; Domajnko, J. Magnetic Flux Density Measurement Platform for an Inductive Wireless Power Transmitter Coil Design. Sensors 2022, 22, 479. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Liu, Z.; Wang, L.; Li, Y. Design of Hybrid Magnetic Stage for a Magnetic–Pneumatic Levitation System. IEEE Trans. Magn. 2022, 58, 8001108. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Q.; Liu, B.; Gong, Z. Optimal Design of Magneto-Force-Thermal Parameters for Electromagnetic Actuators with Halbach Array. Actuators 2021, 10, 231. [Google Scholar] [CrossRef]
- Choi, Y.; Gweon, D. A High-Precision Dual-Servo Stage Using Halbach Linear Active Magnetic Bearings. IEEE/ASME Trans. Mechatron. 2011, 16, 925–931. [Google Scholar] [CrossRef]
- Britcher, C.P.; Ghofrani, M. A magnetic suspension system with a large angular range. Rev. Sci. Instrum. 1993, 64, 1910–1917. [Google Scholar] [CrossRef] [Green Version]
- Molenaar, L.; Zaaijer, E. A Novel Long Stroke Planar Magnetic Bearingactuator. In Proceedings of the 4th International Conference on Motion and Vibration Control, Zurich, Switzerland, 25–28 August 1998; pp. 1071–1076. [Google Scholar]
- Jabben, L.; Overschie, P.M.; Molenaar, A. Lorentz Motor with Stationary Magnets and Coils Applied in a 6DOF Contactless Motion Stage. In Proceedings of the ASPE Spring Topical Meeting on Control of Precision Systems, Philadelphia, PA, USA, 18–20 April 2014. [Google Scholar]
- Rovers, J.; Jansen, J.W.; Compter, J.C.; Lomonova, E.A. Analysis Method of the Dynamic Force and Torque Distribution in the Magnet Array of a Commutated Magnetically Levitated Planar Actuator. IEEE Trans. Ind. Electron. 2012, 59, 2157–2166. [Google Scholar] [CrossRef]
- Cao, S.; Niu, P.; Liu, Q.; Li, J.; Gao, Q.; Peng, C. In Design and Analysis of the Magnetic Circuit and Vibration of LMLP for Mass Transfer. In Proceedings of the 2021 IEEE 15th International Conference on Electronic Measurement & Instruments (ICEMI), Nanjing, China, 2–4 November 2021; pp. 104–108. [Google Scholar]
- Schaeffel, C.; Katzschmann, M.; Mohr, H.U.; Gloess, R.; Walenda, C. 6D planar magnetic levitation system-PIMag 6D. Mech. Eng. J. 2015, 3, 15-00111. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, M. Design Concept and Structural Configuration of Magnetic Levitation Stage with Z-Assist System. Int. J. Autom. Technol. 2021, 15, 706–714. [Google Scholar] [CrossRef]
- Berkelman, P.; Lu, Y.-S. Long range six degree-of-freedom magnetic levitation using low cost sensing and control. J. Robot. Mechatron. 2020, 32, 683–691. [Google Scholar] [CrossRef]
- Zhang, X.; Trakarnchaiyo, C.; Zhang, H.; Khamesee, M.B. MagTable: A tabletop system for 6-DOF large range and completely contactless operation using magnetic levitation. Mechatronics 2021, 77, 102600. [Google Scholar] [CrossRef]
- Arief, I.; Mukhopadhyay, P. Magnetorheology in CoNi nanoplatelet-based MRFs: Effect of platelet orientation and oscillatory shear. J. Magn. Magn. Mater. 2019, 479, 326–331. [Google Scholar] [CrossRef]
- Arief, I.; Mukhopadhyay, P. Two-step yielding in novel CoNi nanoplatelet-based magnetic fluids under oscillatory rheology. Mater. Lett. 2016, 167, 192–196. [Google Scholar] [CrossRef]

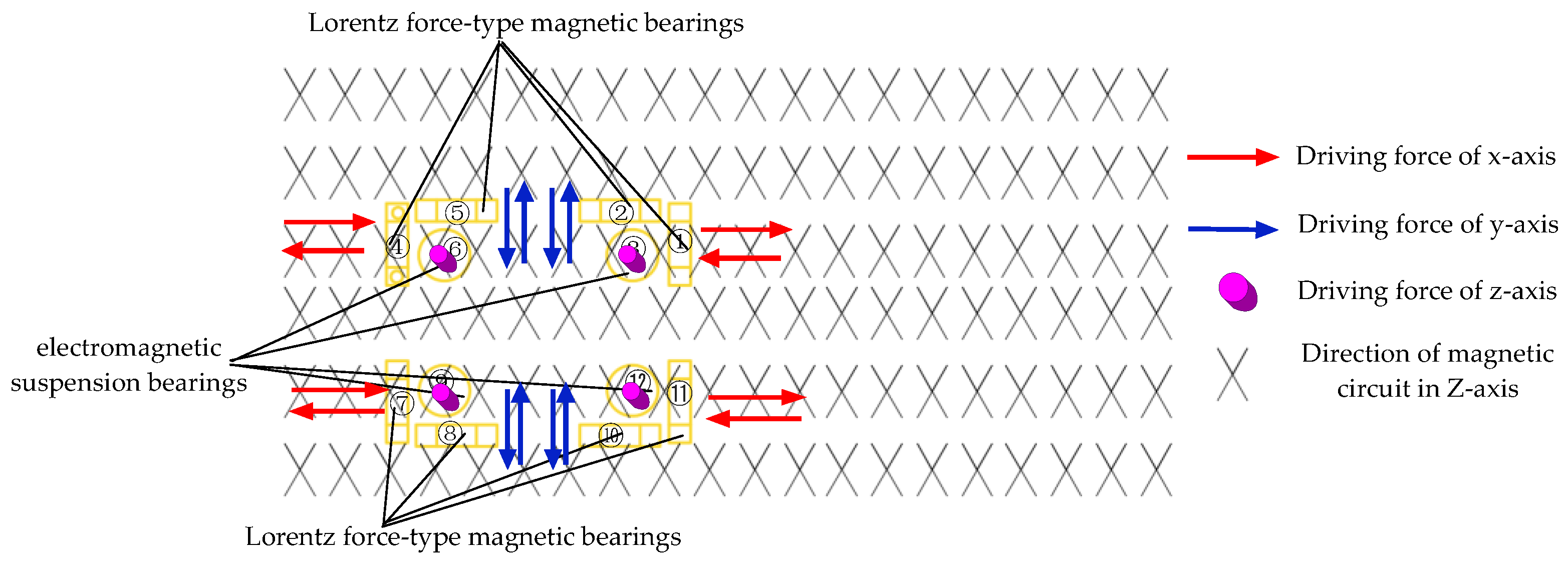
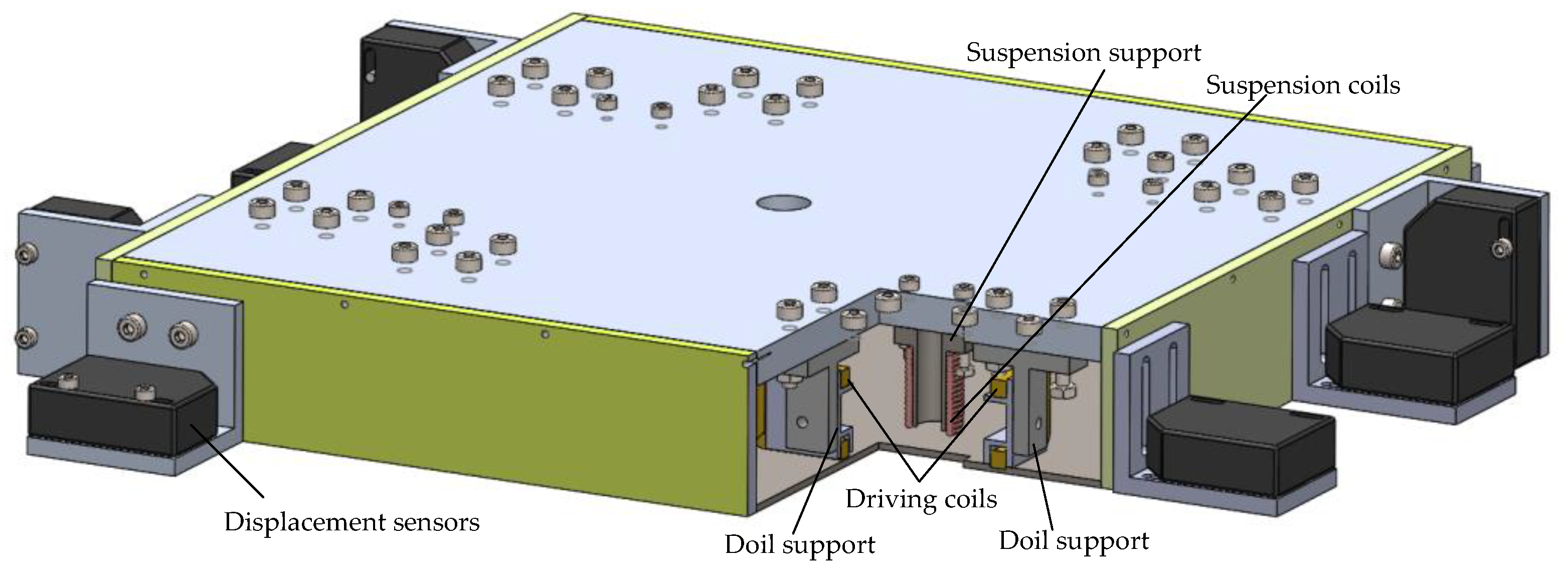
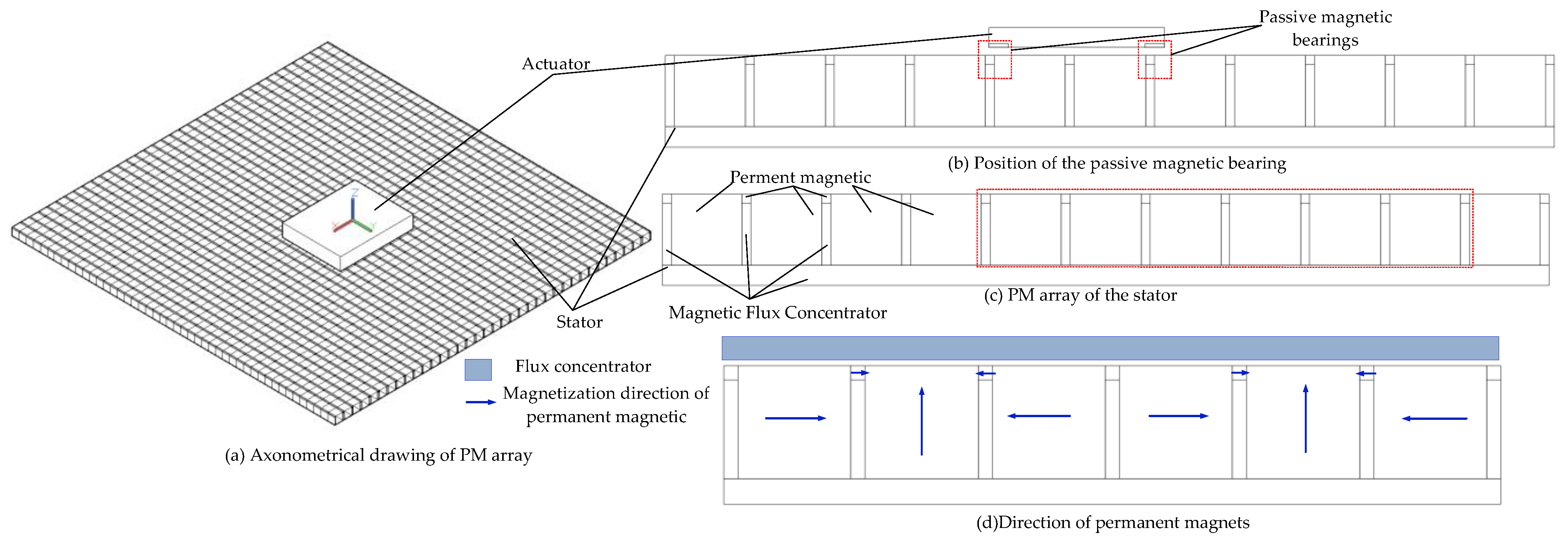

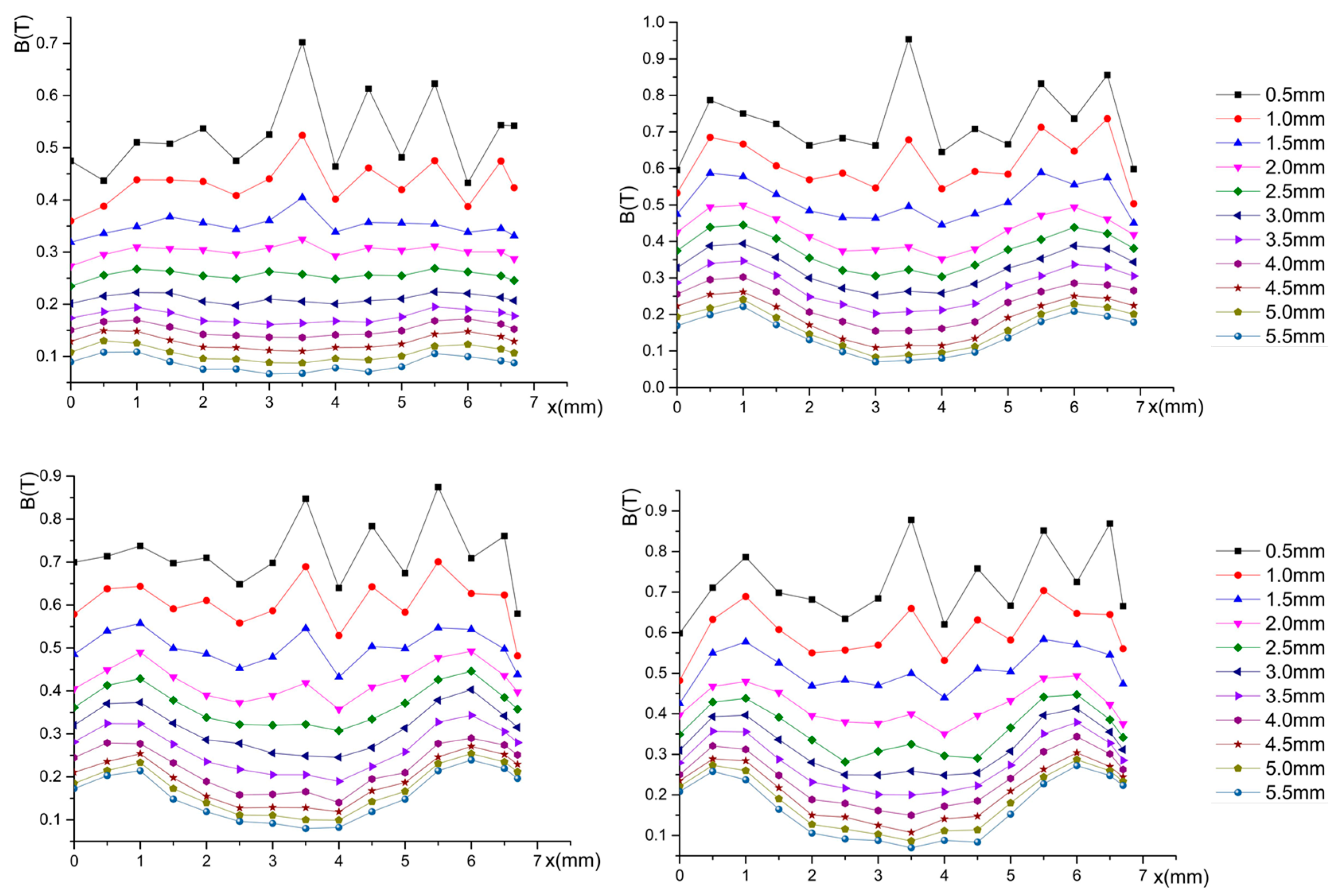


| Movement of the Platform | Driving Force/Torque |
|---|---|
| Translation in X-axis direction of O-XYZ | Lorentz-force-type magnetic bearings 1 and 7 or 4 and 11 |
| Translation in Y-axis direction of O-XYZ | Lorentz-force-type magnetic bearings 5 and 10 or 2 and 8 |
| Translation in Z-axis direction of O-XYZ | electromagnetic suspension bearings 3, 6, 9, 12 |
| Rotate around X-axis of O-XYZ | electromagnetic suspension bearings 3, 6 and 9, 12 |
| Rotate around Y-axis of O-XYZ | electromagnetic suspension bearings 3, 12 and 6, 9 |
| Rotate around Z-axis of O-XYZ | Lorentz force-type magnetic bearings 1 and 7 or 4 and 11 or 5 and 10 or 2 and 8 |
| Size | Value (Unite: mm) |
|---|---|
| L1 | 8 |
| L2 | 4 |
| L3 | ≤L1/4 |
| L4 | ≤L2/4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, S.; Niu, P.; Wang, W.; Zhao, T.; Liu, Q.; Bai, J.; Sheng, S. Novel Magnetic Suspension Platform with Three Types of Magnetic Bearings for Mass Transfer. Energies 2022, 15, 5691. https://doi.org/10.3390/en15155691
Cao S, Niu P, Wang W, Zhao T, Liu Q, Bai J, Sheng S. Novel Magnetic Suspension Platform with Three Types of Magnetic Bearings for Mass Transfer. Energies. 2022; 15(15):5691. https://doi.org/10.3390/en15155691
Chicago/Turabian StyleCao, Shinan, Pingjuan Niu, Wei Wang, Tiantian Zhao, Qiang Liu, Jie Bai, and Sha Sheng. 2022. "Novel Magnetic Suspension Platform with Three Types of Magnetic Bearings for Mass Transfer" Energies 15, no. 15: 5691. https://doi.org/10.3390/en15155691
APA StyleCao, S., Niu, P., Wang, W., Zhao, T., Liu, Q., Bai, J., & Sheng, S. (2022). Novel Magnetic Suspension Platform with Three Types of Magnetic Bearings for Mass Transfer. Energies, 15(15), 5691. https://doi.org/10.3390/en15155691






