Numerical Investigation of Multi-Floater Truss-Type Wave Energy Convertor Platform
Abstract
:1. Introduction
2. Mathematical Formulation
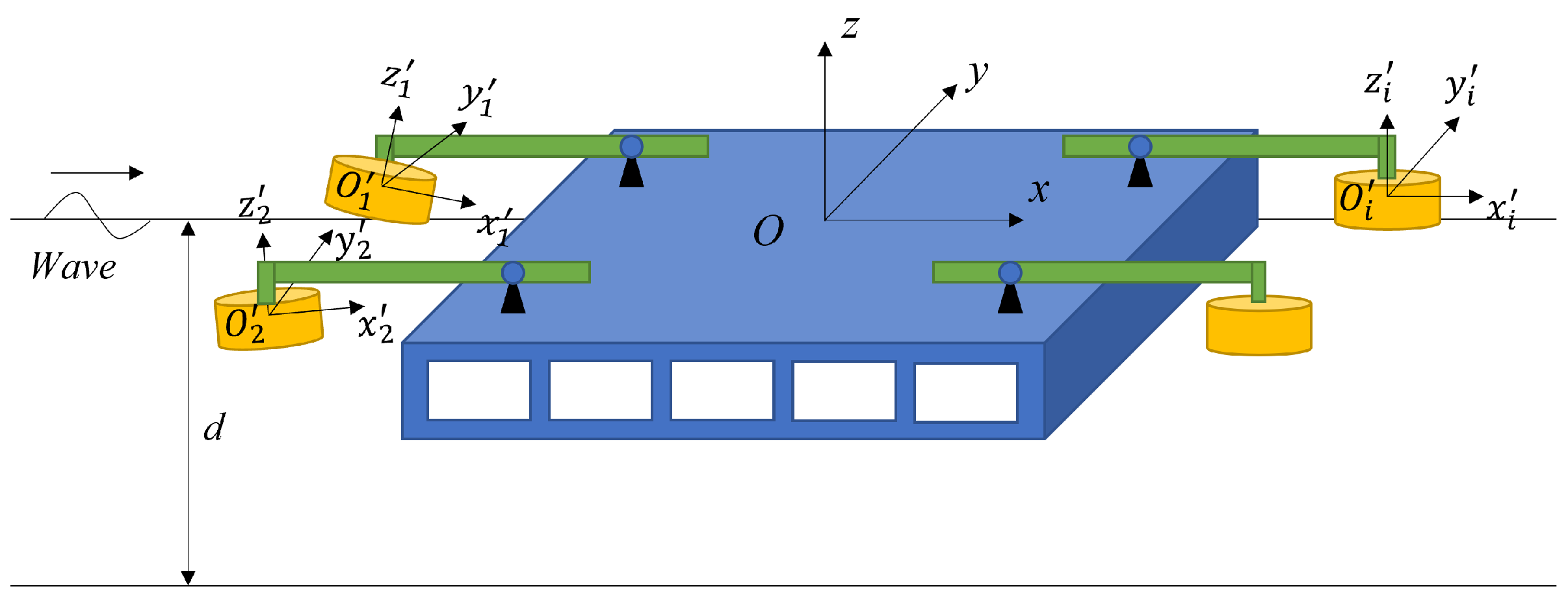
2.1. Calculation of Platform and Floaters
2.2. Calculation of the Truss Structure
2.3. Motion Response
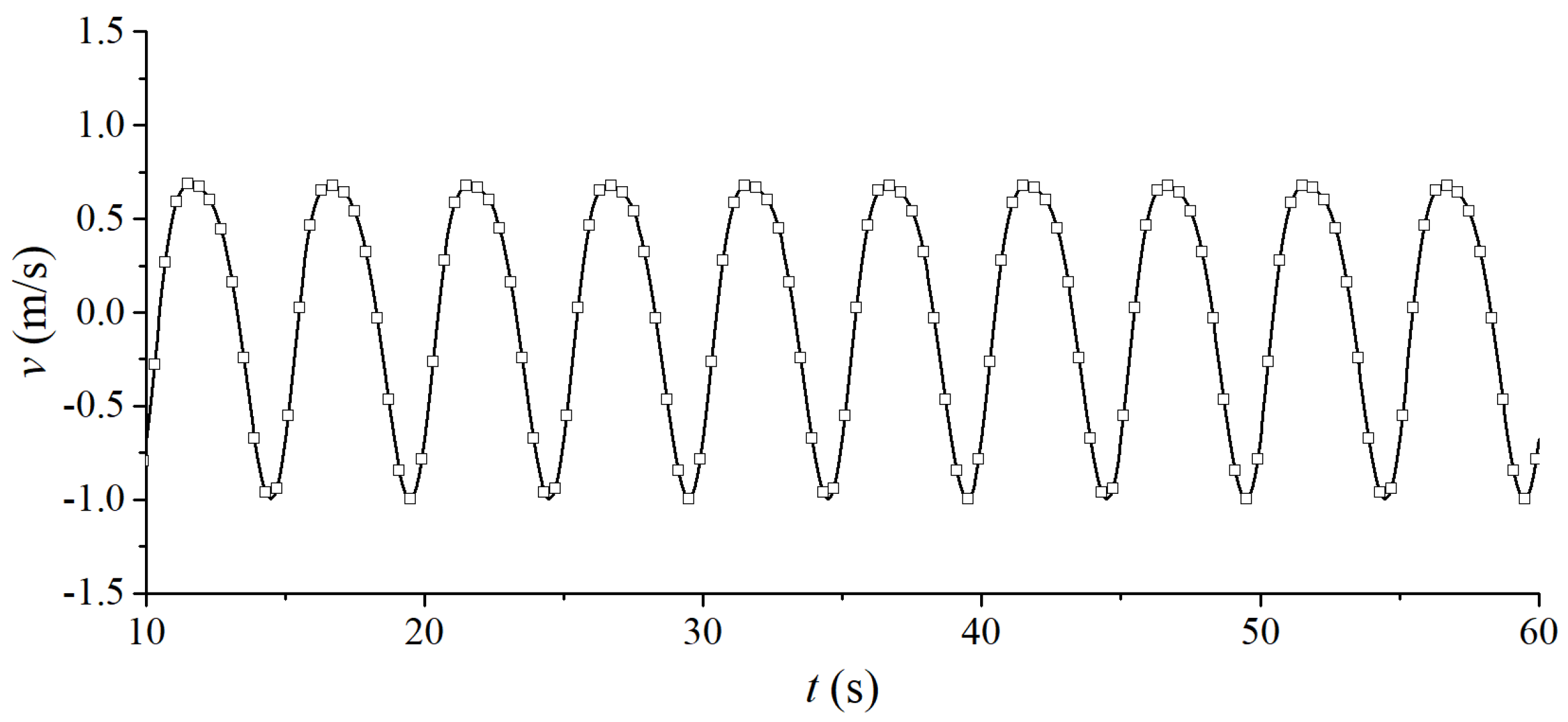
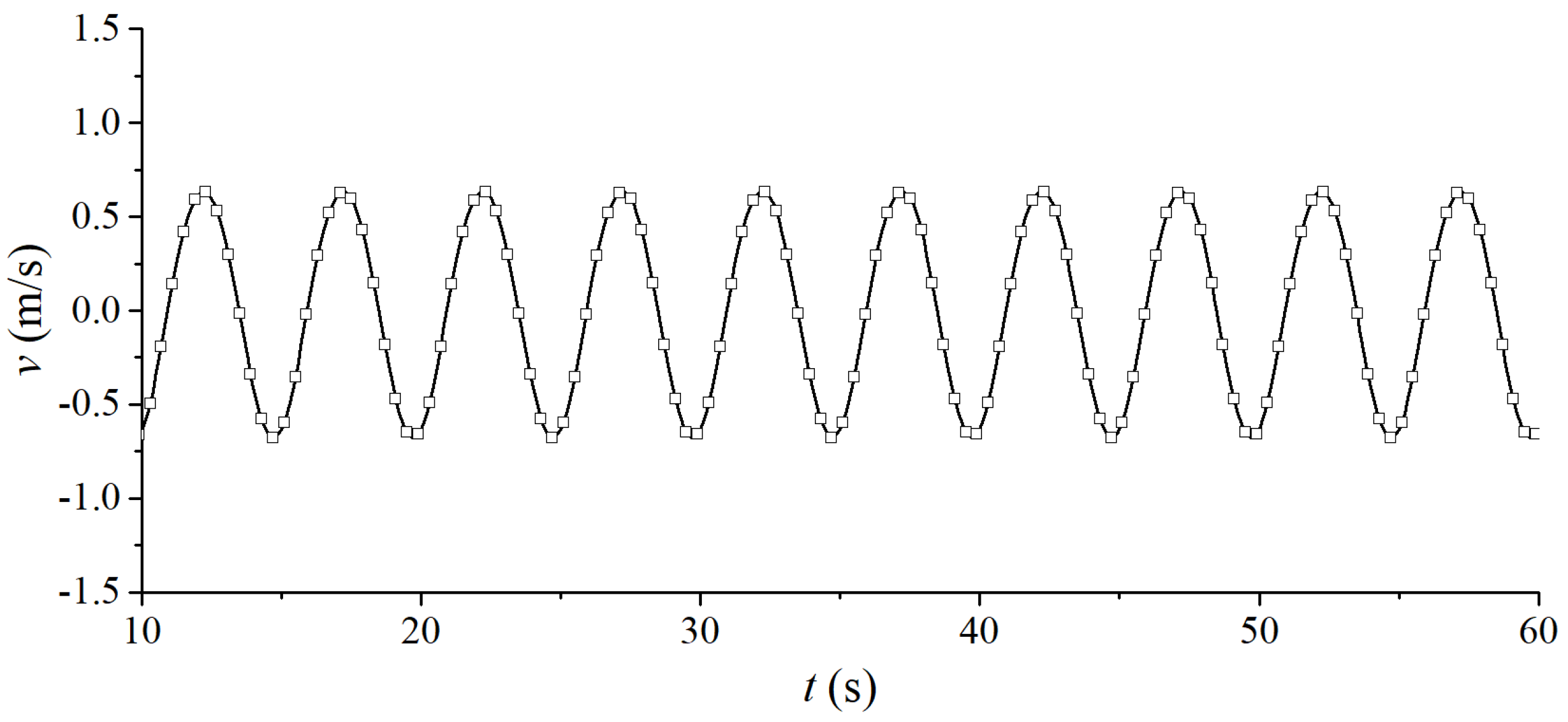
3. Model Validation
4. Results and Discussions
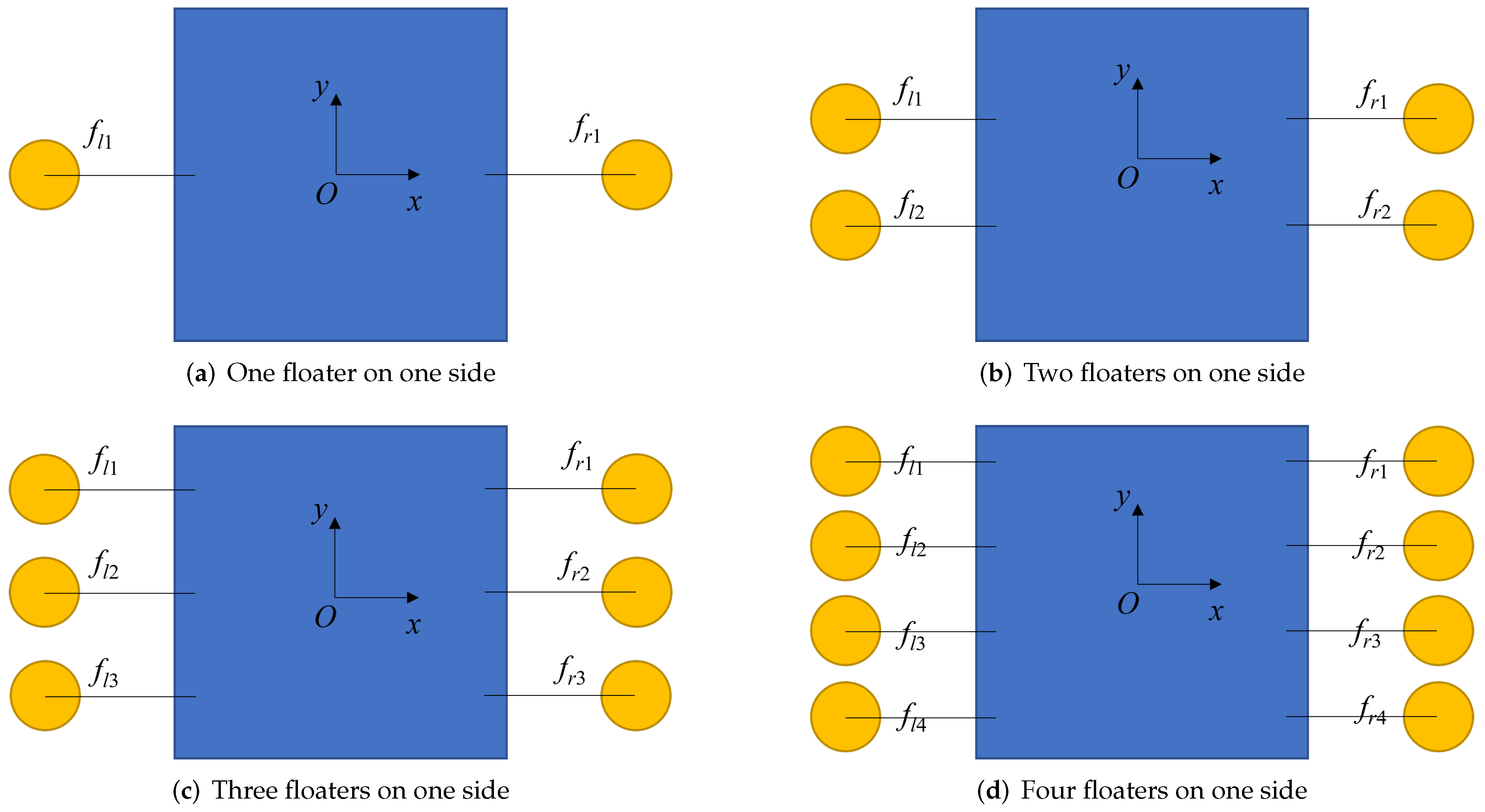
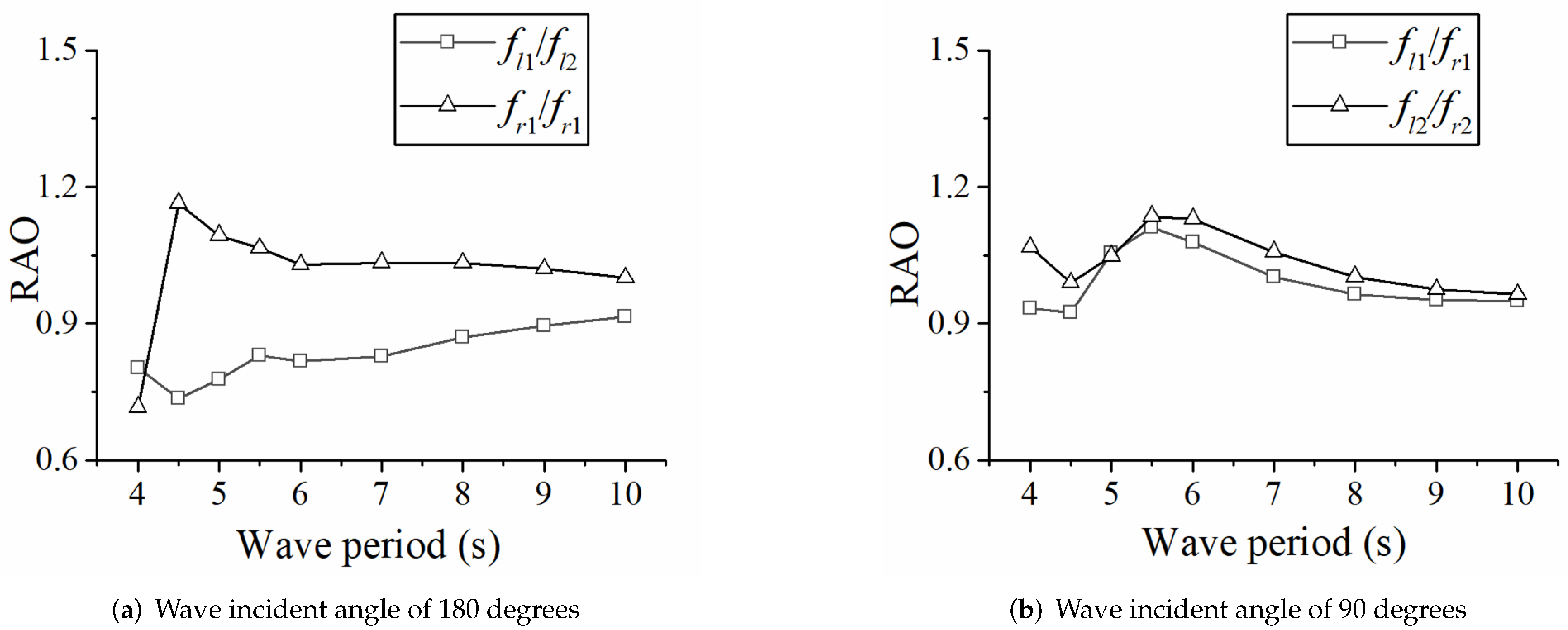
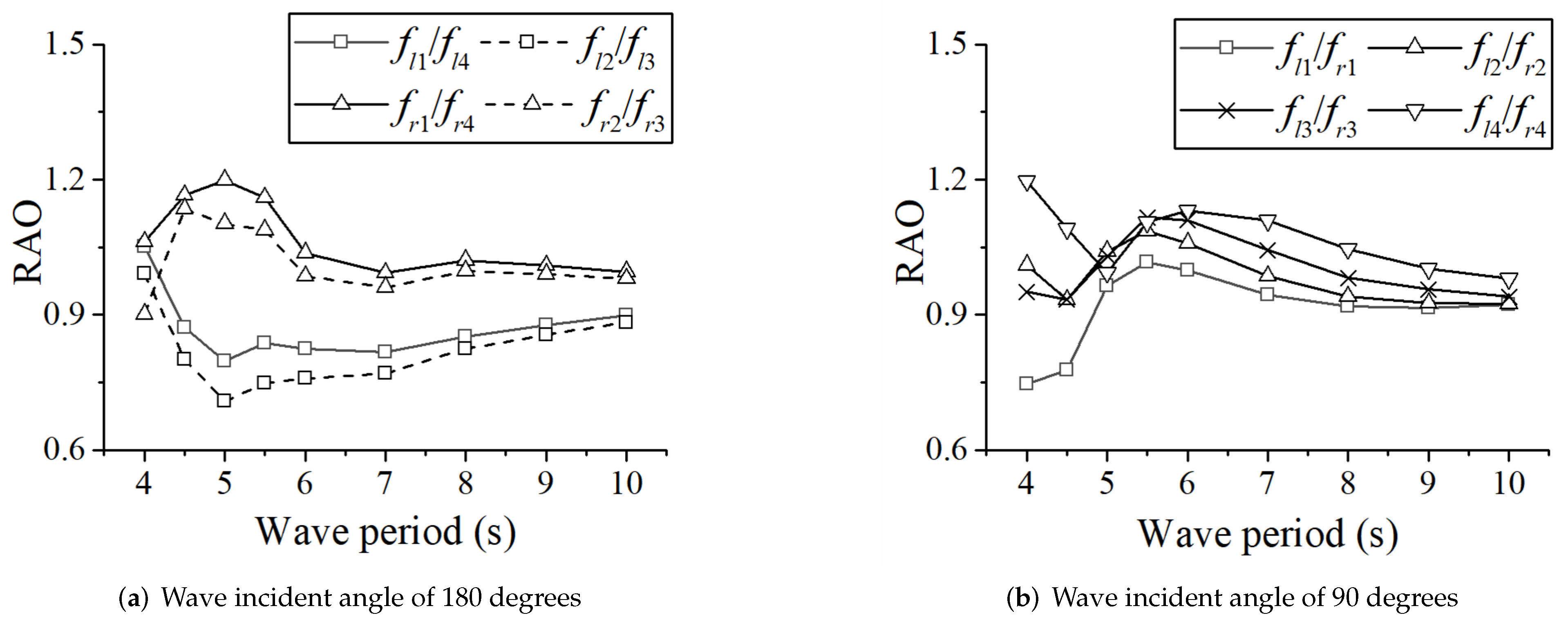
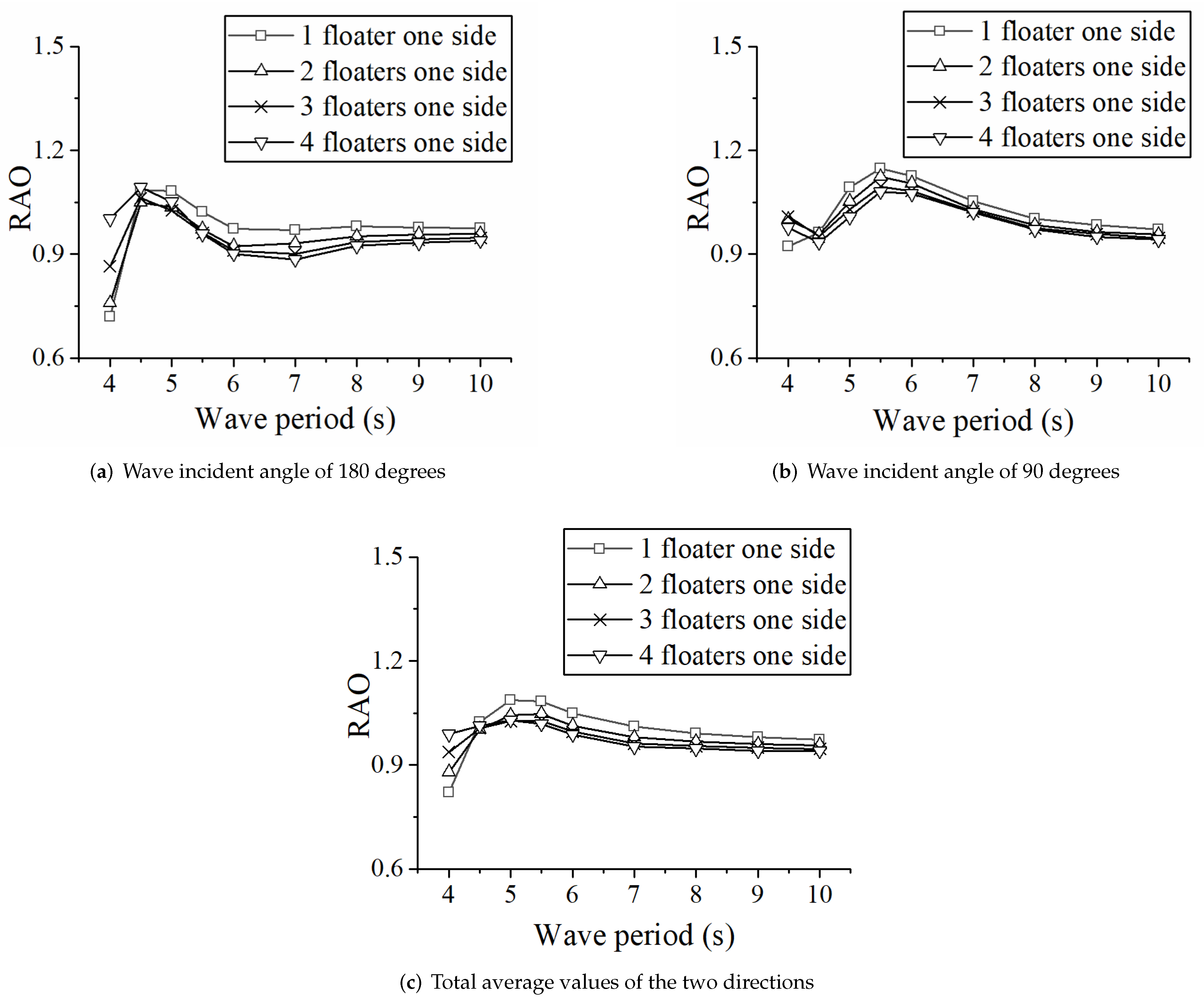
4.1. The Influence of Floater Number on the Motion Response
4.2. The Selection of Floater Arrangement
5. Calculation of Energy Utilization Efficiency of WEC Platform
5.1. Theory of Capture Efficiency
5.2. Capture Efficiency of WEC Platform
6. Conclusions
- Since the platform is composed of a truss structure, the floaters’ motion responses under wave action in all directions are very close, and each floater has good wave-following performance. The motion response of the up-wave floater is slightly greater than that of the back-wave floater, and the motion response of the side floaters is slightly greater than that of the middle floater.
- With an increase in the number of floaters arranged at one side, the average RAO of the floats is smaller, but the overall difference is small. Multiple floaters as a whole show very good wave-following performance. Therefore, if conditions permit, arranging as many floats as possible can effectively improve the power generation efficiency of the platform.
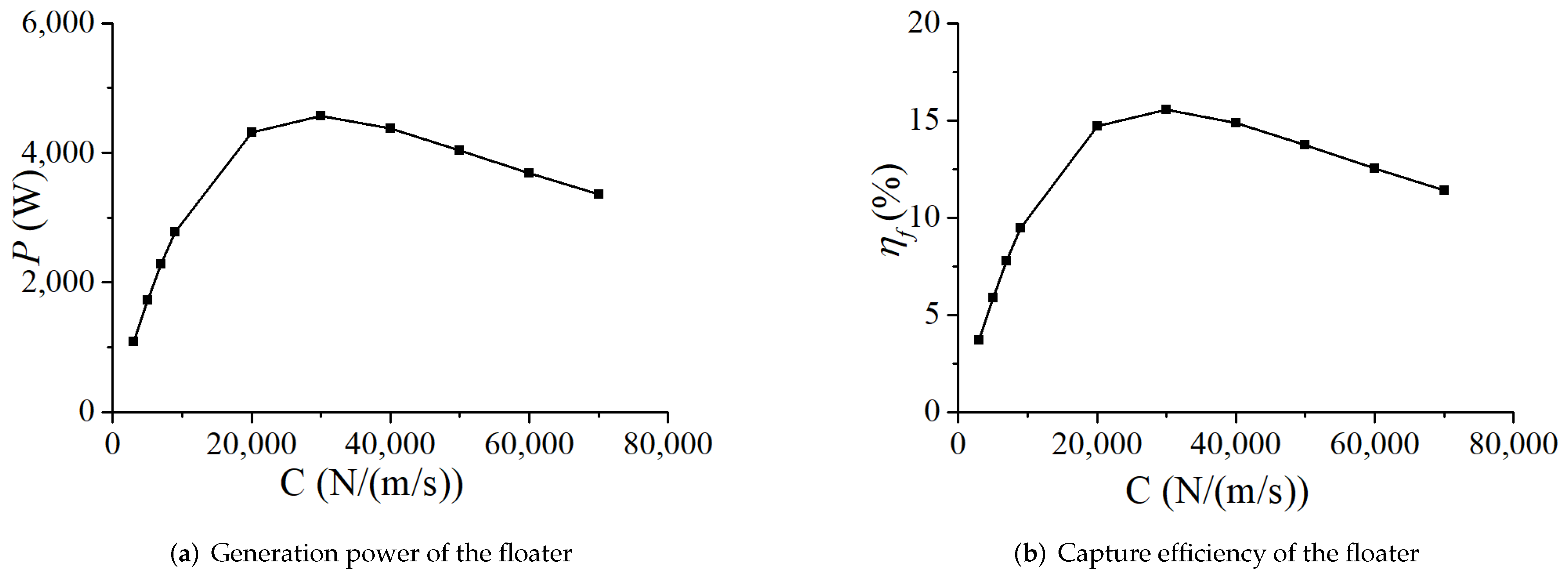
- The power and efficiency of a single float first increase and then decrease with the increase of linear damping under the regular wave action. When the damping is 30,000 N/(m/s), the power generation efficiency is the highest, and the capture efficiency of the whole platform is 9.7%
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhang, D.H.; Li, W.; Lin, Y.G. Wave energy in China: Current status and perspectives. Renew. Energy 2009, 34, 2089–2092. [Google Scholar] [CrossRef]
- Nielsen, K.; Smed, P.F. Point absorber-optimization and survival testing. In Proceedings of the Third European Wave Energy Conference, Patras, Greece, 30 September–2 October 1998; Volume 18. [Google Scholar]
- Prado, M. Archimedes wave swing (AWS). In Ocean Wave Energy; Springer: Berlin, Germany, 2008; pp. 297–304. [Google Scholar]
- Cleason, L.; Forsberg, J.; Ryler, A.; Sjöström, B.O. Contribution to the theory and experience of energy production and transmission from the buoy-concept. In Proceedings of the 2nd International Symposium on Wave Energy Utilization, Trondheim, Norway, 22–24 June 1982; pp. 345–370. [Google Scholar]
- Chang-Lei, M.A.; Xia, D.W.; Wang, M. Review on the Progress of Marine Renewable Energy Technologies in the World. J. Ocean Technol. 2017, 36, 70–75. (In Chinese) [Google Scholar]
- Korde, U.A. On controlled oscillating bodies with submerged reaction mass. In Proceedings of the OMAE 2003 22nd International Conference on Offshore Mechanics and Arctic Engineering, Cancun, Mexico, 8–13 June 2003. [Google Scholar]
- Caska, A.J.; Finnigan, T.D. Hydrodynamic characteristics of a cylindrical bottom-pivoted wave energy absorber. Ocean Eng. 2008, 35, 6–16. [Google Scholar] [CrossRef]
- Zhao, X.L.; Ning, D.Z.; Zhang, C.W.; Kang, H.G. Hydrodynamic Investigation of an Oscillating Buoy Wave Energy Converter Integrated into a Pile-Restrained Floating Breakwater. Energies 2017, 10, 712. [Google Scholar] [CrossRef] [Green Version]
- Cao, C. Investigation on Hydrodynamic Performance of Wave Energy Float Pendulum System. Master’s Thesis, Suzhou University, Suzhou, China, 2019. (In Chinese). [Google Scholar]
- Zhou, Z. Mooring Hydrodynamics Analysis of Oscillating Float Wave Power Generator. Master’s Thesis, Ningbo University, Ningbo, China, 2019. (In Chinese). [Google Scholar]
- Zhou, B.H. The Research of Pitching Float Type Wave Energy Conversion Device. Master’s Thesis, Harbin Engineering University, Harbin, China, 2018. [Google Scholar]
- Zhang, H.M.; Zhou, B.Z.; Vogel, C.; Willden, R.; Zang, J.; Geng, J. Hydrodynamic performance of a dual-floater hybrid system combining a floating breakwater and an oscillating-buoy type wave energy converter. Appl. Energy 2020, 259, 114212. [Google Scholar] [CrossRef]
- Finnegan, W.; Rosa-Santos, P.; Taveira-Pinto, F.; Geooins, J. Development of a numerical model of the CECO wave converter using computational fluid dynamics. Ocean Eng. 2021, 219, 108416. [Google Scholar] [CrossRef]
- Luan, Z.X.; He, G.H.; Zhang, Z.G.; Jing, P.L.; Jin, R.J.; Geng, B.L.; Liu, C.G. Study on the optimal wave energy absorption power of a float in waves. J. Mar. Sci. Eng. 2019, 7, 269. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.L. Study on the Wave Energy Conversion Characteristics of an Array of Floating Point Absorbers. Ph.D. Thesis, Tsinghua University, Beijing, China, 2016. (In Chinese). [Google Scholar]
- Yang, S.H.; He, G.Y.; He, H.Z. Response and Efficiency Analysis of Oscillating Float Array Based on Hydrodynamic Simulation. In Proceedings of the State Oceanic Administration of the State Oceanic Technology Center Proceedings of the 4th China Marine renewable Energy Development Annual Conference and Forum, Suzhou, China, 21–23 October 2015; pp. 58–64. (In Chinese). [Google Scholar]
- Chrasekaran, S.; Sricharan, V.V.S. Numerical study of bean-float wave energy converter with float number parametrization using WEC-Sim in regular waves with the Levelized Cost of Electricity assessment for Indian sea states. Ocean Eng. 2021, 237, 109591. [Google Scholar] [CrossRef]
- Marchesi, E.; Negri, M.; Malavasi, S. Development and analysis of a numerical model for a two-oscillating-body wave energy converter in shallow water. Ocean Eng. 2020, 214, 107765. [Google Scholar] [CrossRef]
- He, G.H.; Luan, Z.X.; Jin, R.J.; Zhang, W.; Wang, W.; Zhang, Z.G.; Jing, P.L.; Liu, P.F. Numerical and experimental study on absorber-type wave energy converters concentrically arranged on an octagonal platform. Renew. Energy 2022, 188, 504–523. [Google Scholar] [CrossRef]
- Negri, M.; Malavasi, S. Wave Energy Harnessing in Shallow Water through Oscillating Bodies. Energies 2018, 11, 2730. [Google Scholar] [CrossRef] [Green Version]
- Ramadanad, A.; Mohamedbc, M.H.; Gabbard, H.A. Experimental analysis of an enhanced design of float with inverted cup for wave energy conversion. Ocean Eng. 2022, 249, 110910. [Google Scholar] [CrossRef]
- Moreno, E.C.; Stansby, P.K. The 6-float wave energy converter M4: Ocean basin tests giving capture width, response and energy yield for several sites. Renew. Sustain. Energy Rev. 2019, 104, 307–318. [Google Scholar] [CrossRef] [Green Version]
- Stansby, P.K.; Moreno, E.C. Hydrodynamics of the multi-float wave energy converter M4 with slack moorings: Time domain linear diffraction-radiation modeling with mean force and experimental comparison. Appl. Ocean Res. 2020, 97, 102070. [Google Scholar] [CrossRef]
- Santo, H.; Taylor, P.H.; Stansby, P.K. The performance of the three-float M4 wave energy converter off Albany, on the south coast of western Australia, compared to Orkney (EMEC) in the U.K. Renew. Energy 2020, 146, 444–459. [Google Scholar] [CrossRef]
- Jin, R.J.; Gou, Y. Motion response analysis of large-scale structures with small-scale cylinders under wave action. Ocean. Eng. 2018, 115, 65–74. [Google Scholar] [CrossRef]
- Choi, Y.; Hong, S. An Analysis of Hydrodynamic Interaction of Floating Multi-Body Using Higher-Order Boundary Element Method. In Proceedings of the International Offshore and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002; Volume 12, pp. 303–308. [Google Scholar]
- Chrasekaran, S.; Sricharan, V.V.S. Numerical analysis of a new multi-body floating wave energy converter with a linear power take-off system. Renew. Energy 2020, 159, 250271. [Google Scholar]
- Kim, K.H.; Park, S.; Kim, J.R.; Cho, I.H.; Hong, K. Numerical and experimental analyses on motion responses on heaving point Absorbers connected to large semi-submersibles. Processes 2021, 9, 1363. [Google Scholar] [CrossRef]







| Symbol | Meaning | Value |
|---|---|---|
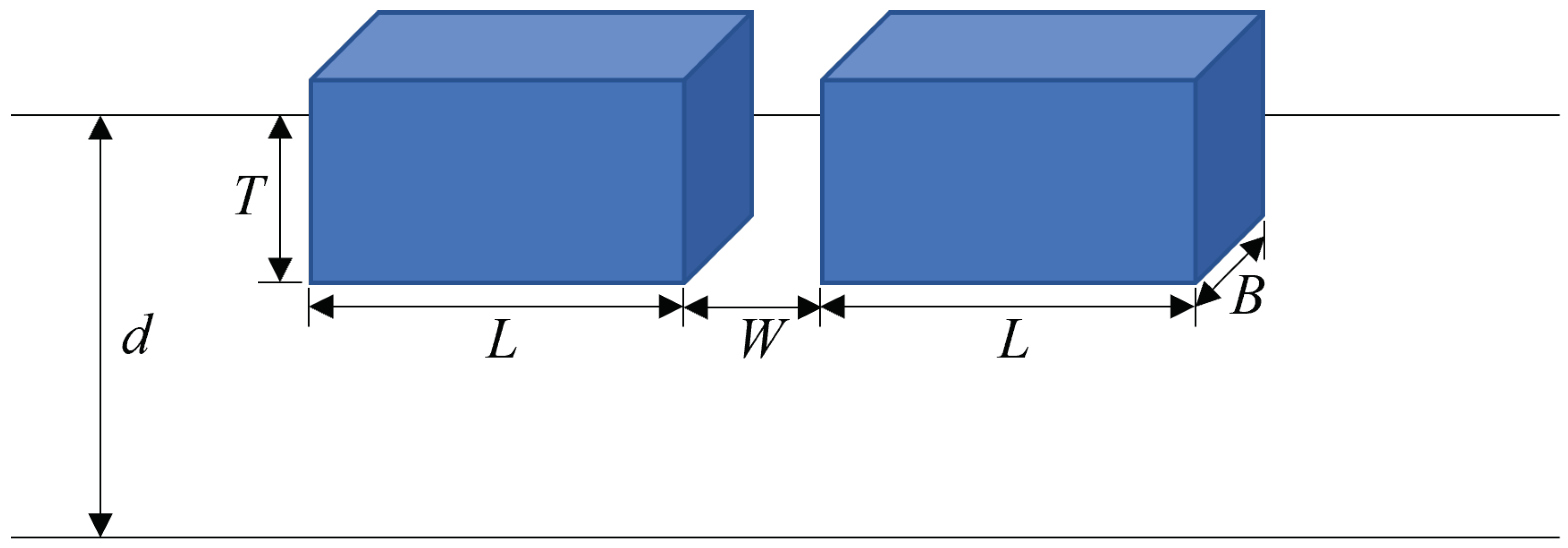
| L | Length (m) | 30 |
| B | Width (m) | 22 |
| T | Draft (m) | 1.5 |
| d | Water depth (m) | 15 |
| W | Distance of twin-boxes (m) | 8 |
| Rotation radius around x-axis (m) | 9.0 | |
| Rotation radius around y-axis (m) | 6.6 | |
| Rotation radius around z-axis (m) | 10.8 |
| Meaning | Value |
|---|---|
| Size of platform | 20 m |
| Mass of platform | kg |
| Mass center of platform | (0.0, 0.0, 0.0) |
| Rotation center of platform | (0.0, 0.0, 0.0) |
| Platform moment of inertia | kg·m |
| Platform moment of inertia | kg·m |
| Platform moment of inertia | kg·m |
| Distance between floater and platform edge | 5 m |
| Distance between adjacent floater edge | 1 m |
| Truss diameter | m |
| Truss number in one side | 6 |
| Meaning | Value |
|---|---|
| Diameter of floater | 3 m |
| Mass of floater | 3000 kg |
| Draft of floater | 1 m |
| Mass of floating arm | 300 kg |
| Length of floating arm | 7 m |
| Displacement | 7.07 m |
| Floater moment of inertia | 2687 kg·m |
| Floater moment of inertia | 2687 kg·m |
| Floater moment of inertia | 3375 kg·m |
| Damping Box 1 | Damping Box 2 | Damping Box 3 | Damping Box 4 | Damping Box 5 |
|---|---|---|---|---|
| (8.35, 8.35) | (8.35, −8.35) | (−8.35, −8.35) | (−8.35, 8.35) | (0.0, 0.0) |
| Floater number | ||||
| 5.38 | 4.07 | 4.07 | 5.38 | |
| Floater number | ||||
| 15.55 | 13.80 | 13.80 | 15.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, R.; Wang, J.; Chen, H.; Geng, B.; Liu, Z. Numerical Investigation of Multi-Floater Truss-Type Wave Energy Convertor Platform. Energies 2022, 15, 5675. https://doi.org/10.3390/en15155675
Jin R, Wang J, Chen H, Geng B, Liu Z. Numerical Investigation of Multi-Floater Truss-Type Wave Energy Convertor Platform. Energies. 2022; 15(15):5675. https://doi.org/10.3390/en15155675
Chicago/Turabian StyleJin, Ruijia, Jiawei Wang, Hanbao Chen, Baolei Geng, and Zhen Liu. 2022. "Numerical Investigation of Multi-Floater Truss-Type Wave Energy Convertor Platform" Energies 15, no. 15: 5675. https://doi.org/10.3390/en15155675
APA StyleJin, R., Wang, J., Chen, H., Geng, B., & Liu, Z. (2022). Numerical Investigation of Multi-Floater Truss-Type Wave Energy Convertor Platform. Energies, 15(15), 5675. https://doi.org/10.3390/en15155675






